Experimental and Numerical Study of Cyclic Stress–Strain Response and Fatigue Crack Initiation Life of Mid-Carbon Steel under Constant and Multi-Step Amplitude Loading
Abstract
:1. Introduction
2. Experiment
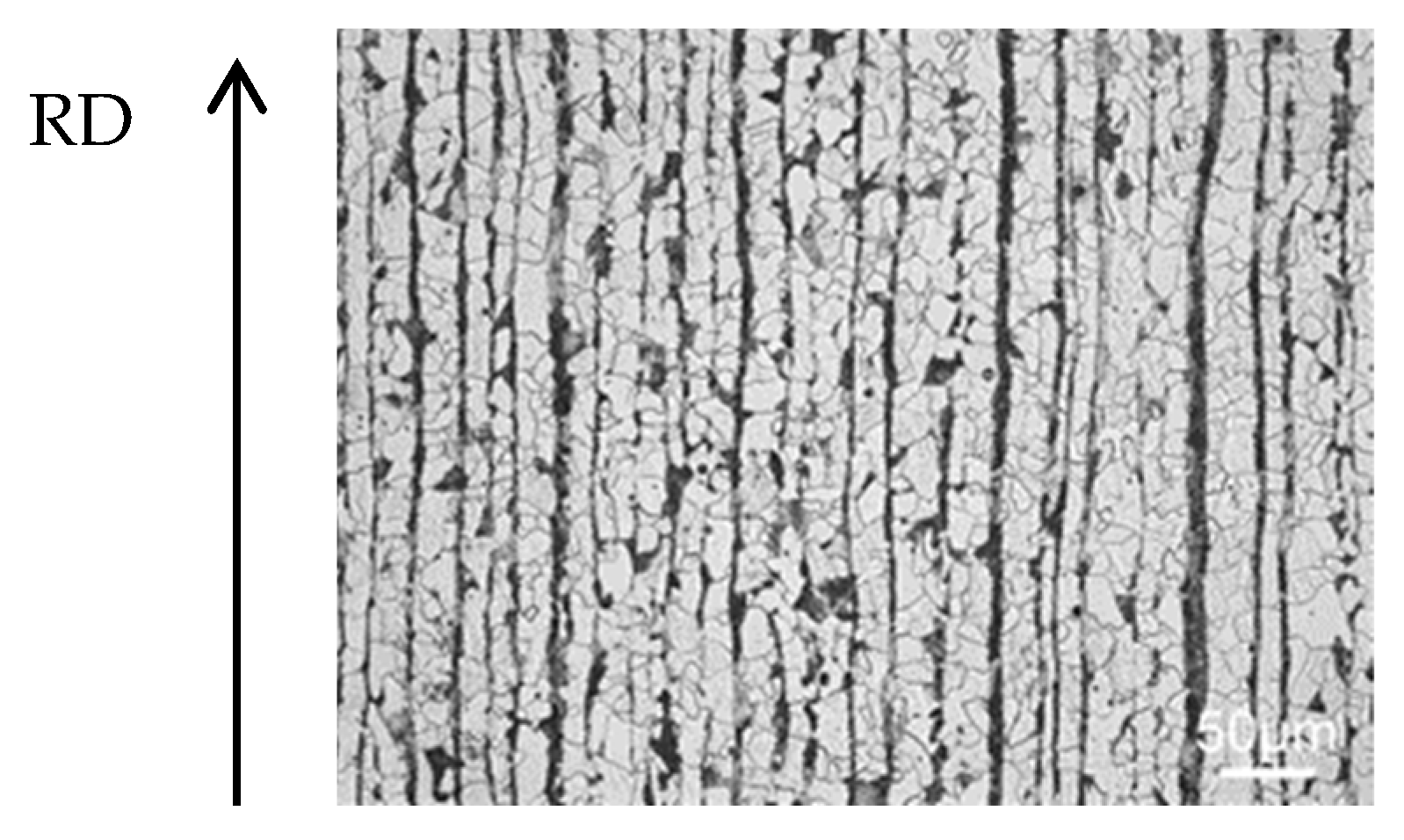
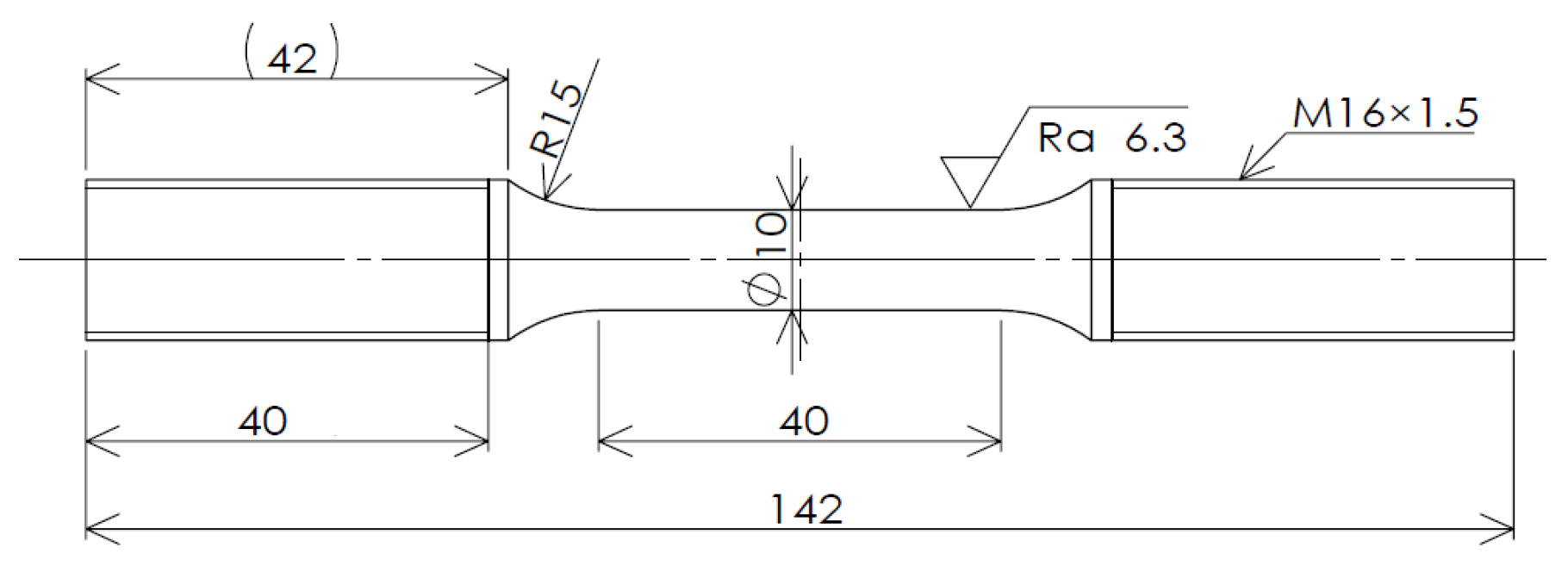
2.1. Uniaxial Tensile Tests
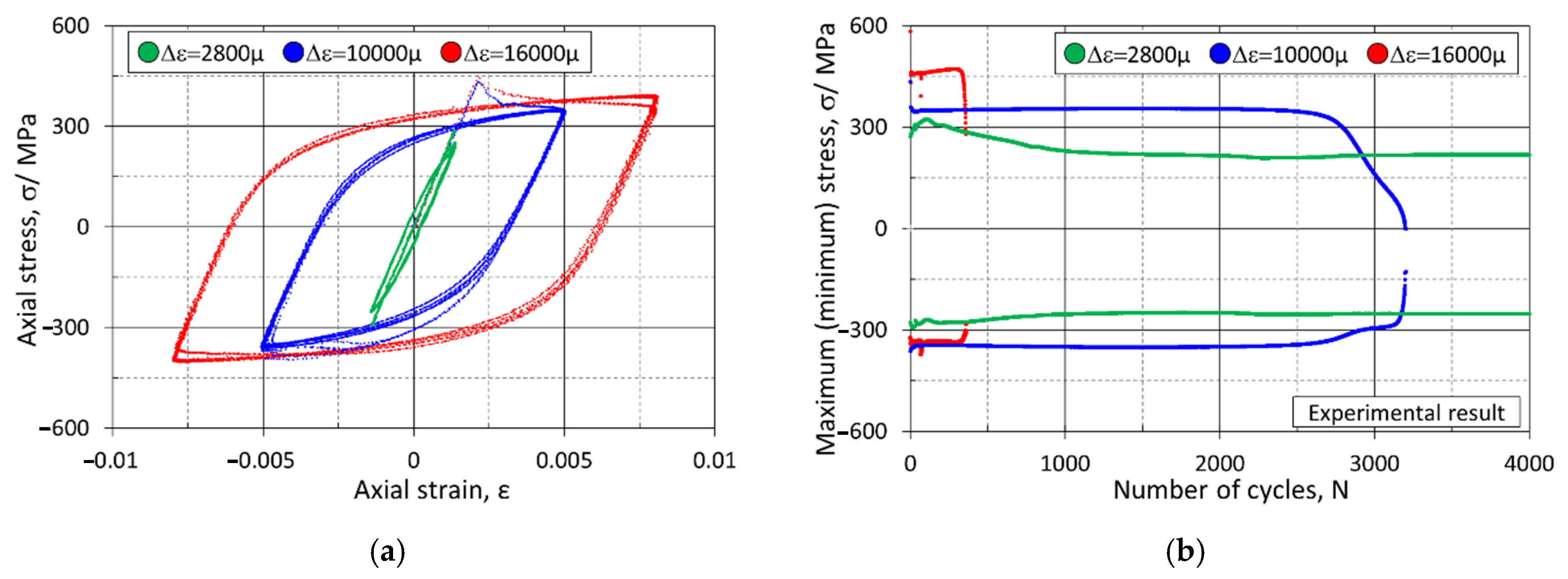
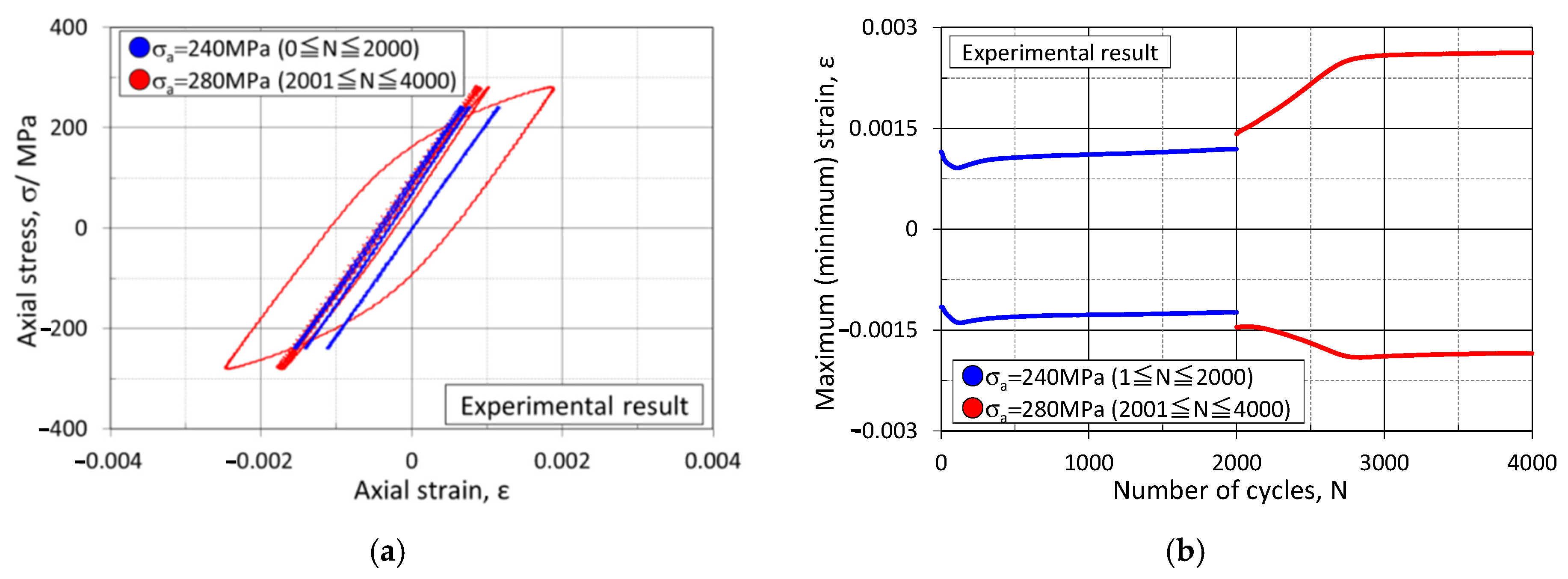
2.2. Fatigue Tests
3. Numerical Simulation of the Cyclic Stress–Strain Response
3.1. The FSS Model
3.2. Calibration of the FSS Model
4. Prediction of Crack Initiation Life
5. Conclusions
- Uniaxial tensile tests were carried out to obtain the mechanical properties of SM490A.
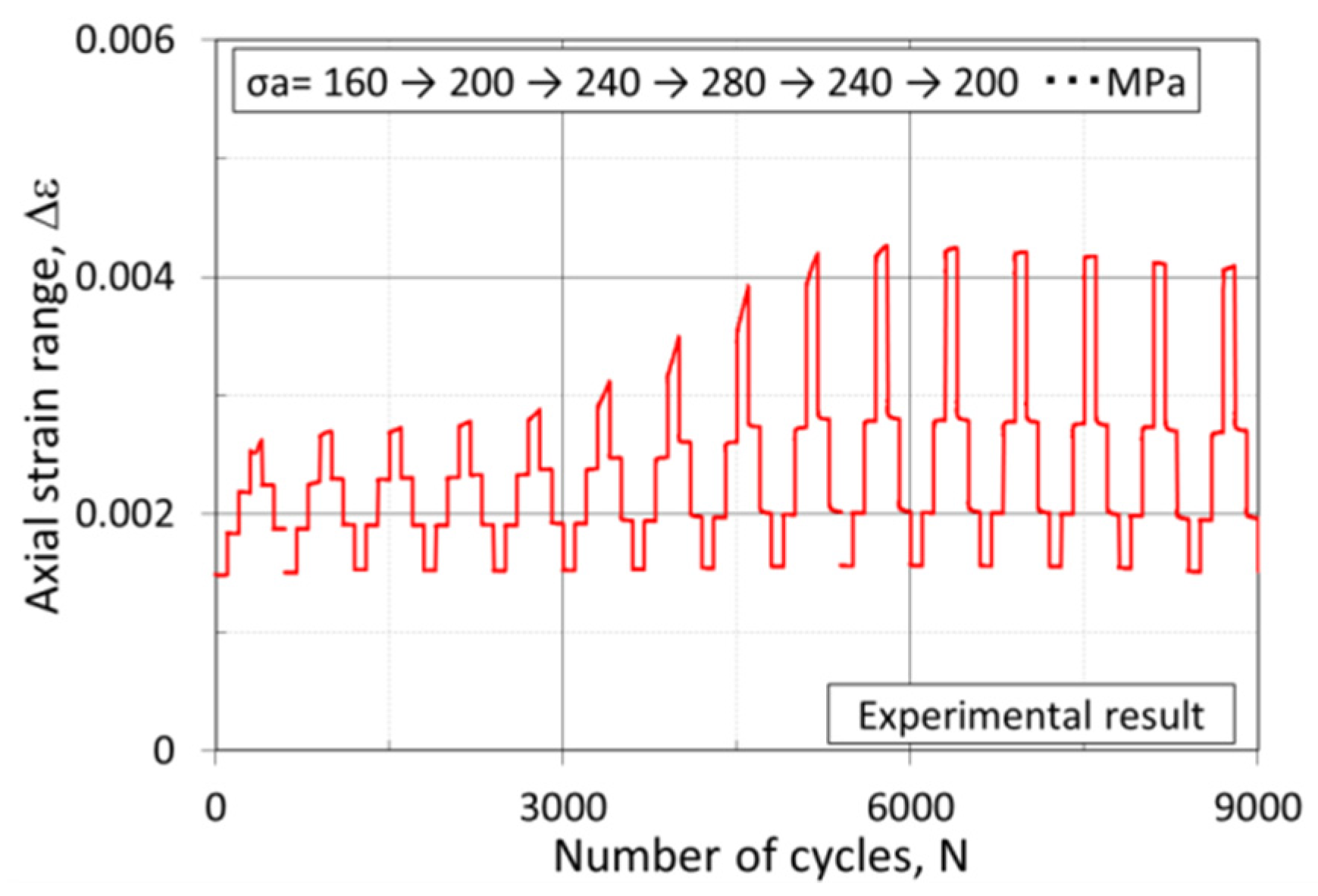
- Fatigue tests with various loading conditions were carried out to investigate the cyclic response of SM490A. Cyclic softening/hardening and cyclic shakedown were observed under different loading conditions.
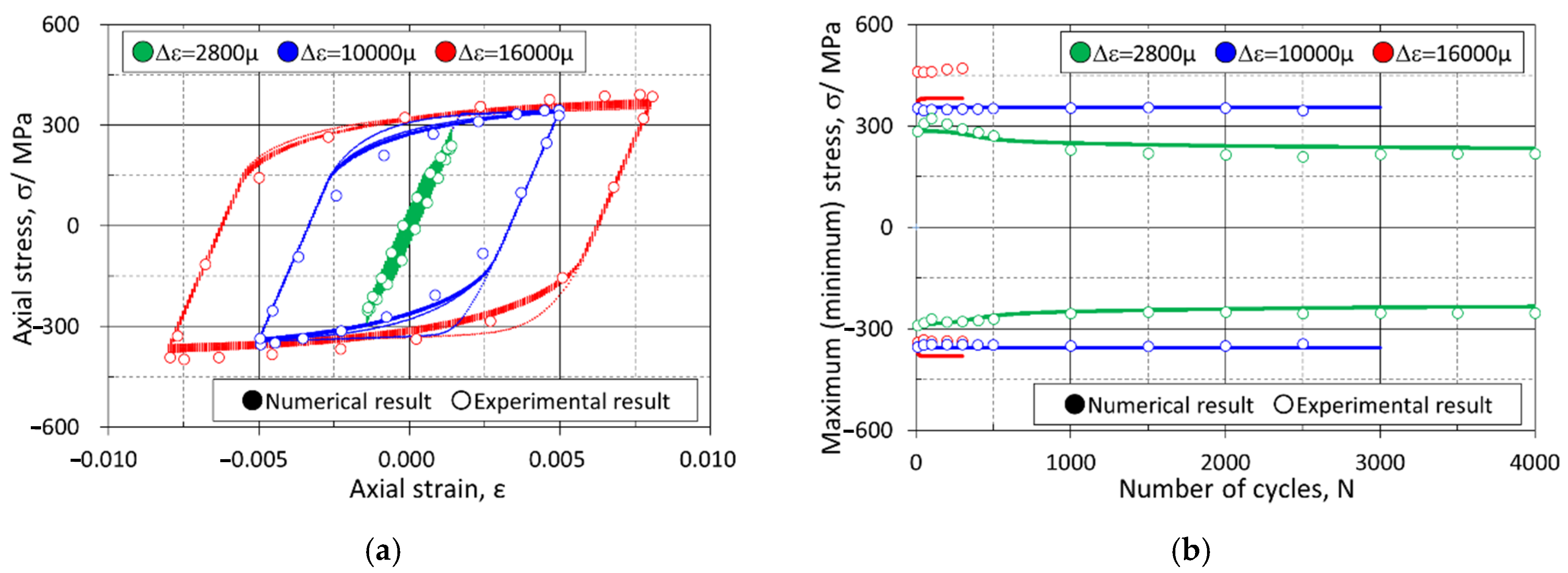
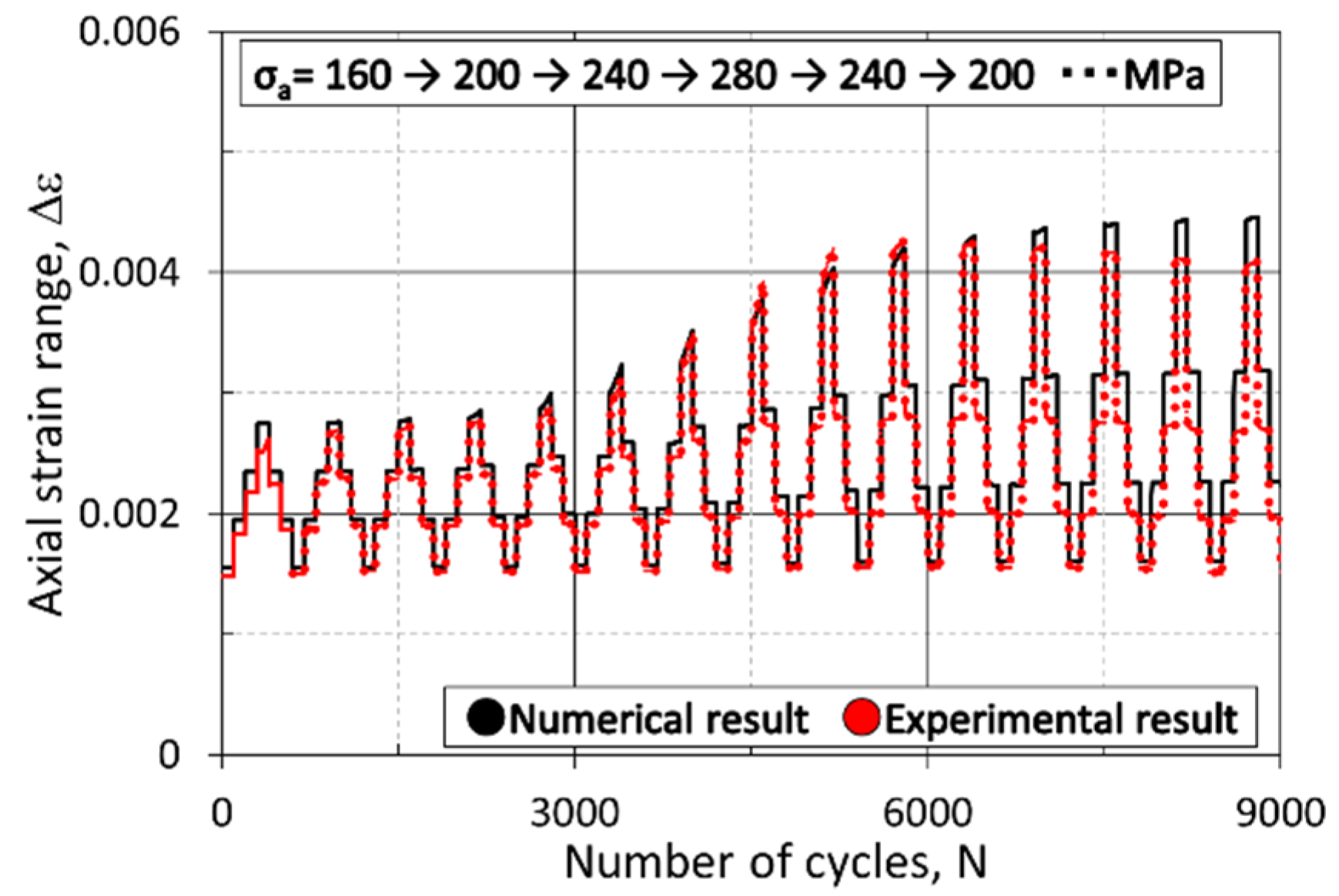
- The calibration of the material constants using the FSS model was performed under constant and two-step amplitude loading and repeated increasing and decreasing conditions. The numerical results in terms of stress and strain responses showed good agreement with the experimental results.
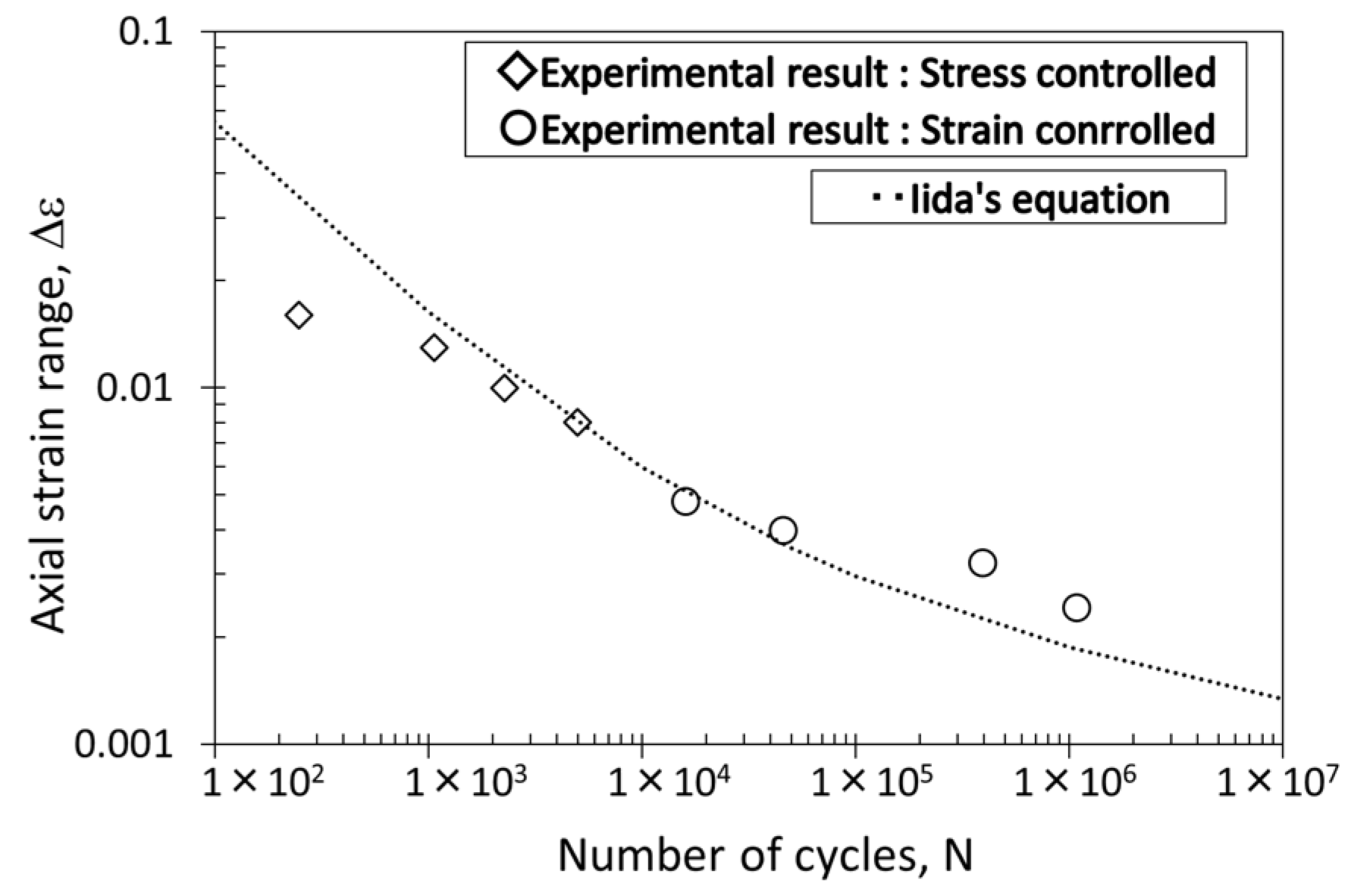
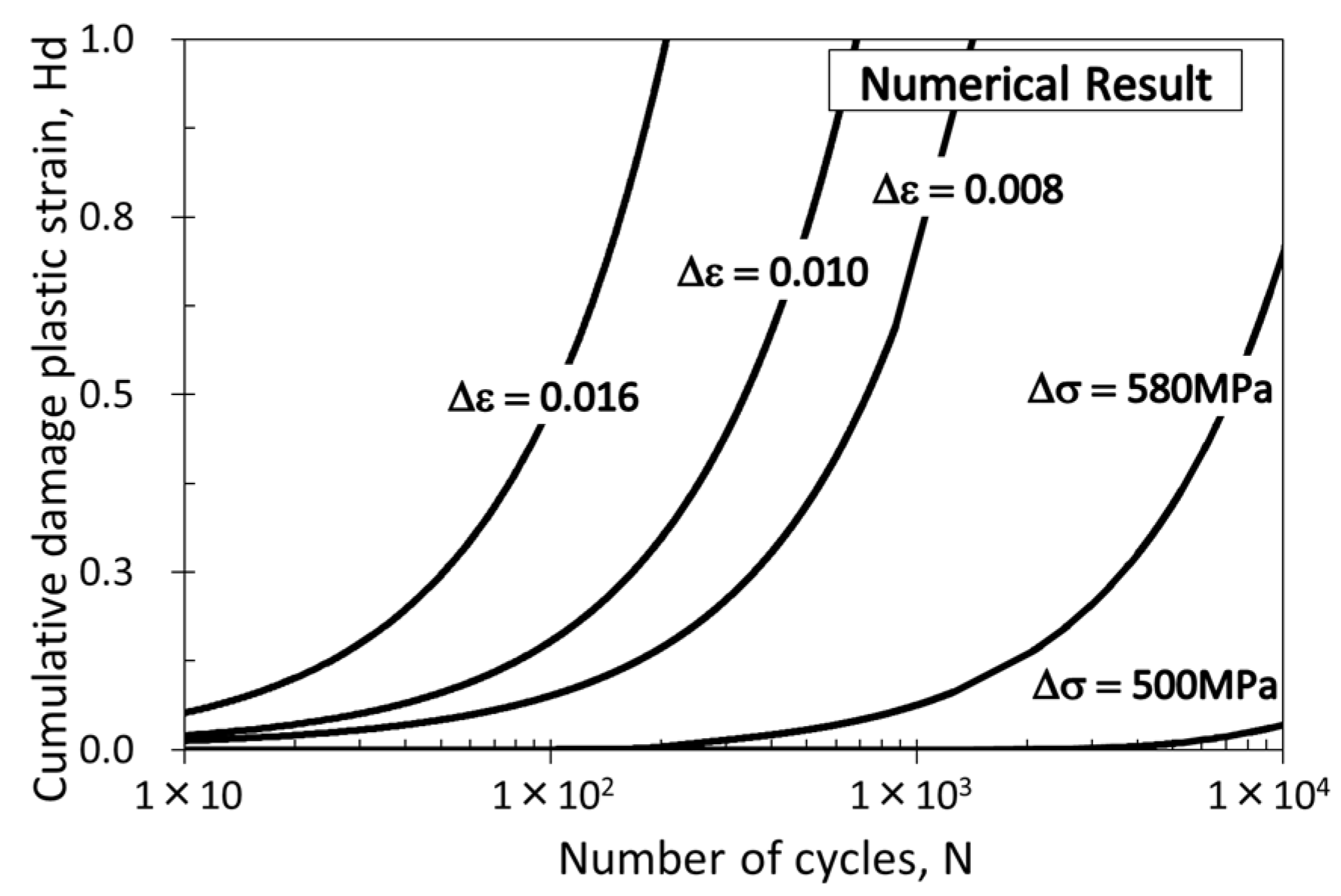
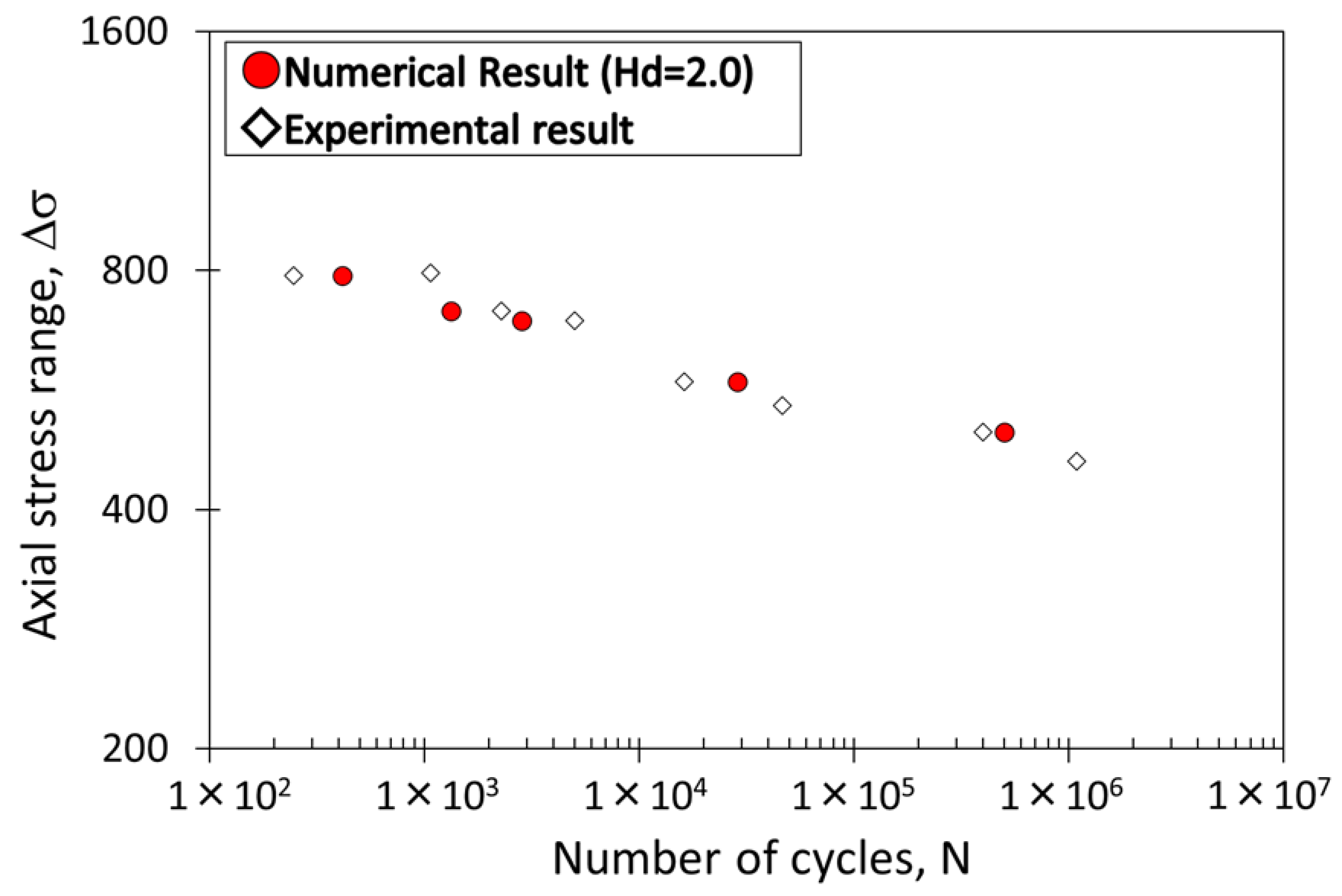
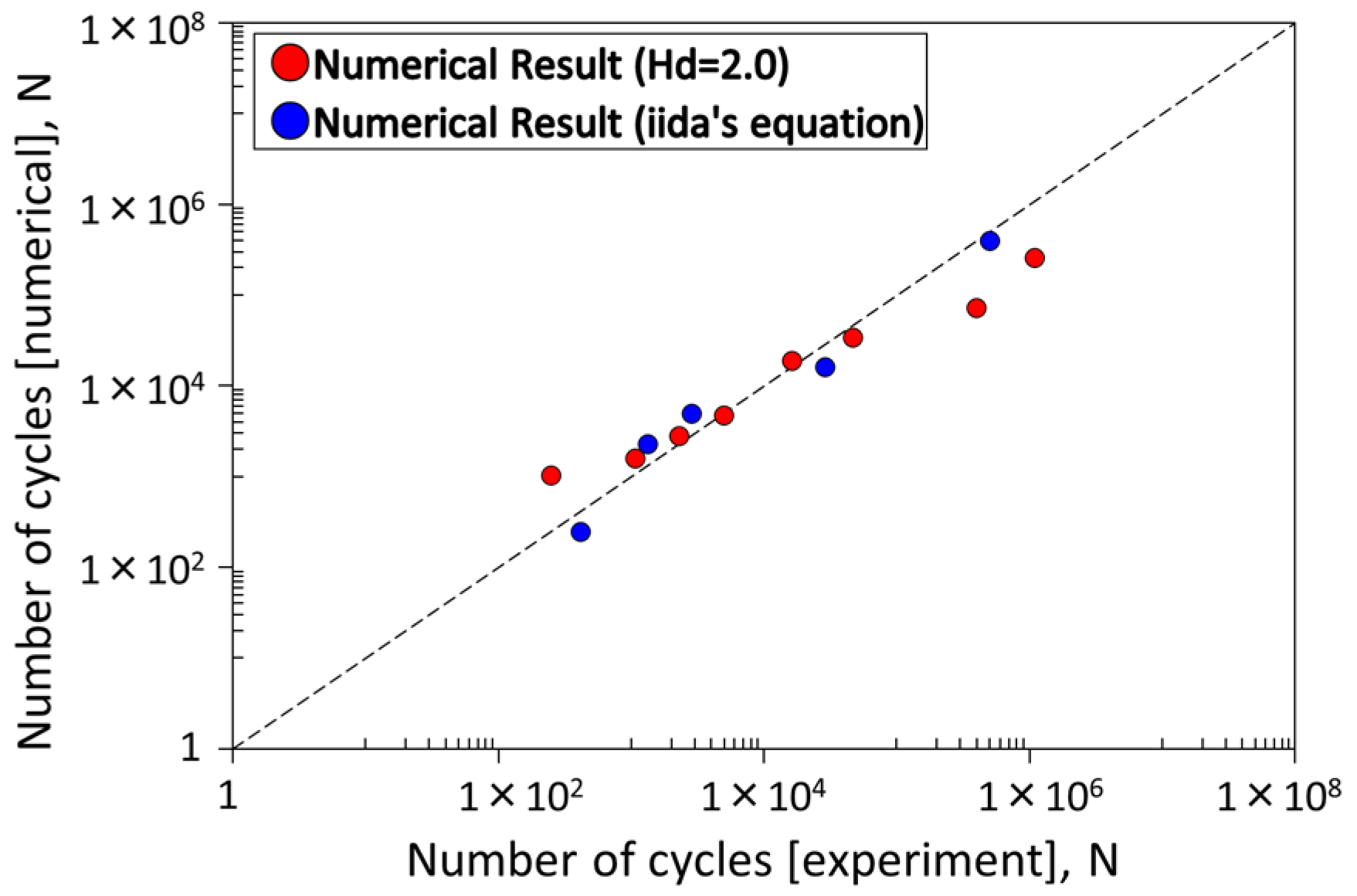
- Fatigue crack initiation life prediction using Iida’s equation, based on the total strain range, agreed quite well with the experiment under constant amplitude loading. The criterion based on the cumulative plastic damage strain calculated by the FSS model predicted a realistic fatigue crack initiation life as well as Iida’s equation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stephens, A.; Fatemi, R.R.; Stephens, H.F. Metal Fatigue in Engineering [Hardcover]; John Wiley & Sons: Hoboken, NJ, USA, 2000; ISBN 0471510599. [Google Scholar]
- Plumtree, A. Cyclic Stress–Strain Response and Substructure. Int. J. Fatigue 2001, 23, 799–805. [Google Scholar] [CrossRef]
- Jones, A. Cyclic Stress-Strain Curves Generated from Random Cyclic Strain Amplitude Tests. Int. J. Fatigue 1999, 21, 521–530. [Google Scholar] [CrossRef]
- Paul, S.K.; Sivaprasad, S.; Dhar, S.; Tarafder, S. Cyclic Plastic Deformation and Cyclic Hardening/Softening Behavior in 304LN Stainless Steel. Theor. Appl. Fract. Mech. 2010, 54, 63–70. [Google Scholar] [CrossRef]
- Gorash, Y.; MacKenzie, D. On Cyclic Yield Strength in Definition of Limits for Characterisation of Fatigue and Creep Behaviour. Open Eng. 2017, 7, 126–140. [Google Scholar] [CrossRef]
- Hilditch, T.B.; Timokhina, I.B.; Robertson, L.T.; Pereloma, E.V.; Hodgson, P.D. Cyclic Deformation of Advanced High-Strength Steels: Mechanical Behavior and Microstructural Analysis. Metall. Mater. Trans. A 2009, 40, 342–353. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Jiang, Y. An Experimental Study of Inhomogeneous Cyclic Plastic Deformation of 1045 Steel under Multiaxial Cyclic Loading. Int. J. Plast. 2005, 21, 2174–2190. [Google Scholar] [CrossRef]
- Belattar, A.; Taleb, L.; Hauet, A.; Taheri, S. Dependence of the Cyclic Stress–Strain Curve on Loading History and Its Interaction with Fatigue of 304L Stainless Steel. Mater. Sci. Eng. A 2012, 536, 170–180. [Google Scholar] [CrossRef]
- Drucker, D.C. Conventional and Unconventional Plastic Response and Representation. Appl. Mech. Rev. 1988, 41, 151–167. [Google Scholar] [CrossRef]
- Hashiguchi, K. Subloading Surface Model in Unconventional Plasticity. Int. J. Solids Struct. 1989, 25, 917–945. [Google Scholar] [CrossRef]
- Iwan, W.D. On a Class of Models for the Yielding Behavior of Continuous and Composite Systems. J. Appl. Mech. 1967, 34, 612–617. [Google Scholar] [CrossRef]
- Mróz, Z. On the Description of Anisotropic Workhardening. J. Mech. Phys. Solids 1967, 15, 163–175. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Popov, E.P. A Model of Nonlinearly Hardening Materials for Complex Loading. Acta Mech. 1975, 21, 173–192. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.-D. Kinematic Hardening Rules with Critical State of Dynamic Recovery, Part I: Formulation and Basic Features for Ratchetting Behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Lesne, P.M. A Non-Linear continuous fatigue damage model. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 1–17. [Google Scholar] [CrossRef]
- Oller, S.; Salomón, O.; Oñate, E. A Continuum Mechanics Model for Mechanical Fatigue Analysis. Comput. Mater. Sci. 2005, 32, 175–195. [Google Scholar] [CrossRef]
- Barbu, L.G.; Oller, S.; Martinez, X.; Barbat, A. High Cycle Fatigue Simulation: A New Stepwise Load-Advancing Strategy. Eng. Struct. 2015, 97, 118–129. [Google Scholar] [CrossRef] [Green Version]
- Van Do, V.N. The Numerical High Cycle Fatigue Damage Model of Fillet Weld Joint under Weld-Induced Residual Stresses. IOP Conf. Ser. Earth Environ. Sci. 2018, 143, 012037. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Yue, P.; Yu, Z.-Y.; Wang, Q. A Combined High and Low Cycle Fatigue Model for Life Prediction of Turbine Blades. Materials 2017, 10, 698. [Google Scholar] [CrossRef] [Green Version]
- Fatemi, A.; Yang, L. Cumulative Fatigue Damage and Life Prediction Theories: A Survey of the State of the Art for Homogeneous Materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Socie, D.F. Fatigue-Life Prediction Using Local Stress-Strain Concepts. Exp. Mech. 1977, 17, 50–56. [Google Scholar] [CrossRef]
- Conle, F.A.; Chu, C.-C. Fatigue Analysis and the Local Stress–Strain Approach in Complex Vehicular Structures. Int. J. Fatigue 1997, 19, 317–323. [Google Scholar] [CrossRef]
- Maier, H.; Christ, H.-J. Modeling of Cyclic Stress–Strain Behavior and Damage Mechanisms under Thermomechanical Fatigue Conditions. Int. J. Fatigue 1997, 19, 267–274. [Google Scholar] [CrossRef]
- Li, B.; Reis, L.; Defreitas, M. Simulation of Cyclic Stress/Strain Evolutions for Multiaxial Fatigue Life Prediction. Int. J. Fatigue 2006, 28, 451–458. [Google Scholar] [CrossRef]
- Manson, S.S. Fatigue: A Complex Subject–Some Simple Approximation. Exp. Mech. 1965, 5, 193–226. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Fan, J.; Xu, L.; Nie, X. Cyclic Hardening and Softening Behavior of the Low Yield Point Steel: Implementation and Validation. Eng. Struct. 2020, 210, 110220. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Murakami, K.; Gotoh, K.; Toyosada, M. Cyclic Stress-Strain Relation under High Cycle Fatigue Process. J. Japan Soc. Nav. Archit. Ocean Eng. 2008, 7, 243–250. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Fincato, R. Cyclic Plasticity Model for Fatigue with Softening Behaviour below Macroscopic Yielding. Mater. Des. 2019, 165, 107573. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Toyosada, M.; Hashiguchi, K. Extended Subloading Surface Model Incorporating Elastic Boundary Concept. J. Appl. Mech. 2006, 9, 455–462. [Google Scholar] [CrossRef] [Green Version]
- JIS G 3106:2008; Rolled Steels for Welded Structure. Japanese Industrial Standards Committee: Tokyo, Japan, 2008.
- A Theory of the Yielding and Plastic Flow of Anisotropic Metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [CrossRef] [Green Version]
- van den Boogaard, T.; Havinga, J.; Belin, A.; Barlat, F. Parameter Reduction for the Yld2004-18p Yield Criterion. Int. J. Mater. Form. 2016, 9, 175–178. [Google Scholar] [CrossRef]
- Cazacu, O.; Barlat, F. Generalization of Drucker’s Yield Criterion to Orthotropy. Math. Mech. Solids 2001, 6, 613–630. [Google Scholar] [CrossRef]
- JIS 2241:2011; Metallic Materials-Tensile Testing-Method of Test at Room Temperature. Japanese Industrial Standards Committee: Tokyo, Japan, 2009.
- Hashiguchi, K. Elastoplasticity Theory; Lecture Notes in Applied and Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 69, ISBN 978-3-642-35848-7. [Google Scholar]
- Hashiguchi, K.; Tsutsumi, S. Elastoplastic Constitutive Equation with Tangential Stress Rate Effect. Int. J. Plast. 2001, 17, 117–145. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S. Numerical Study of a Welded Plate Instability Using the Subloading Surface Model. Mar. Struct. 2017, 55, 104–120. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S. An Overstress Elasto-Viscoplasticity Model for High/Low Cyclic Strain Rates Loading Conditions: Part I–Formulation and Computational Aspects. Int. J. Solids Struct. 2020, 207, 279–294. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S. An Overstress Elasto-Viscoplasticity Model for High/Low Cyclic Strain Rates Loading Conditions: Part II–Numerical Analyses. Int. J. Solids Struct. 2021, 208–209, 247–261. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S.; Sakai, T.; Terada, K. 3D Crystal Plasticity Analyses on the Role of Hard/Soft Inclusions in the Local Slip Formation. Int. J. Fatigue 2020, 134, 105518. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S. Numerical Modeling of the Evolution of Ductile Damage under Proportional and Non-Proportional Loading. Int. J. Solids Struct. 2019, 160, 247–264. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S. A Return Mapping Algorithm for Elastoplastic and Ductile Damage Constitutive Equations Using the Subloading Surface Method. Int. J. Numer. Methods Eng. 2018, 113, 1729–1754. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Kitamura, T.; Fincato, R. Ductile Behaviour of Carbon Steel for Welded Structures: Experiments and Numerical Simulations. J. Constr. Steel Res. 2020, 172, 106185. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Morita, K.; Fincato, R.; Momii, H. Fatigue Life Assessment of a Non-Load Carrying Fillet Joint Considering the Effects of a Cyclic Plasticity and Weld Bead Shape. Frat. ed Integrità Strutt. 2016, 10, 240–250. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Fincato, R.; Momii, H. Effect of Tangential Plasticity on Structural Response under Non-Proportional Cyclic Loading. Acta Mech. 2019, 230, 2425–2446. [Google Scholar] [CrossRef]
- Fincato, R.; Tsutsumi, S. A Numerical Study of the Return Mapping Application for the Subloading Surface Model. Eng. Comput. 2018, 35, 1314–1343. [Google Scholar] [CrossRef]
- The Society of Materials Science. The Handbook of Fatigue Design; The Society of Materials Science: Yokendo, Japan, 2015. [Google Scholar]
- Iida, K. Micro-Crack Initiation Life and Micro-Fractographic Analysis in Strain Cycling Fatigue of a 60 kg/mm2 High Strength Steel. J. Soc. Nav. Archit. Japan 1970, 128, a331–a342. [Google Scholar] [CrossRef]
- Iida, K. Crack Initiation Life and Microfractographic Analysis in Strain Cycling Fatigue. Trans. Jpn. Weld. Soc. 1971, 2, 86–95. [Google Scholar]
- Nieslony, A.; Dsoki, C.; Kaufmann, H.; Krug, P. New Method for Evaluation of the Manson–Coffin–Basquin and Ramberg–Osgood Equations with Respect to Compatibility. Int. J. Fatigue 2008, 30, 1967–1977. [Google Scholar] [CrossRef]
- Muralidharan, U.; Manson, S.S. A Modified Universal Slopes Equation for Estimation of Fatigue Characteristics of Metals. J. Eng. Mater. Technol. 1988, 110, 55–58. [Google Scholar] [CrossRef]



| Chemical Composition /% | ||||
|---|---|---|---|---|
| C | Si | Mn | P | S |
| 0.16 | 0.36 | 1.42 | 0.015 | 0.004 |
| Upper yield stress/MPa | 402 |
| Lower yield stress/MPa | 336 |
| Young’s modulus/GPa | 208 |
| Name | Control | Stress Ratio (R = σmin/σmax) | Cyclic Amplitude |
|---|---|---|---|
| Constant amplitude loading test | Strain | −1 | εa = 0.0014/0.005/0.008 |
| Load | −1 | σa = 210/230/250/270/290 MPa | |
| Two-step amplitude loading test | Load | −1 | σa1 = 240 (2000 cycles) →σa2 = 280 MPa (2000 cycles) |
| Repeated increasing and decreasing amplitude loading test | Load | −1 | σa = 160→200→240→280→240→200→160→200 MPa (Every 100 cycles, changing the amplitude) |
| Poisson’s Ratio | Isotropic Hardening Parameter | Kinematic Hardening Parameter | High-Cycle Fatigue Parameter for the Computation of Damage | |||||
|---|---|---|---|---|---|---|---|---|
| μ | h1 | h2 | a1 | a2 | a3 | d1 | d2 | d3 |
| 0.3 | 0.1 | 4.0 | 1.0 | 740 | 1.0 | 0.0004 | 0.0096 | 2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morita, K.; Mouri, M.; Fincato, R.; Tsutsumi, S. Experimental and Numerical Study of Cyclic Stress–Strain Response and Fatigue Crack Initiation Life of Mid-Carbon Steel under Constant and Multi-Step Amplitude Loading. J. Mar. Sci. Eng. 2022, 10, 1535. https://doi.org/10.3390/jmse10101535
Morita K, Mouri M, Fincato R, Tsutsumi S. Experimental and Numerical Study of Cyclic Stress–Strain Response and Fatigue Crack Initiation Life of Mid-Carbon Steel under Constant and Multi-Step Amplitude Loading. Journal of Marine Science and Engineering. 2022; 10(10):1535. https://doi.org/10.3390/jmse10101535
Chicago/Turabian StyleMorita, Kasumi, Masashi Mouri, Riccardo Fincato, and Seiichiro Tsutsumi. 2022. "Experimental and Numerical Study of Cyclic Stress–Strain Response and Fatigue Crack Initiation Life of Mid-Carbon Steel under Constant and Multi-Step Amplitude Loading" Journal of Marine Science and Engineering 10, no. 10: 1535. https://doi.org/10.3390/jmse10101535
APA StyleMorita, K., Mouri, M., Fincato, R., & Tsutsumi, S. (2022). Experimental and Numerical Study of Cyclic Stress–Strain Response and Fatigue Crack Initiation Life of Mid-Carbon Steel under Constant and Multi-Step Amplitude Loading. Journal of Marine Science and Engineering, 10(10), 1535. https://doi.org/10.3390/jmse10101535







