A Method for Vessel’s Trajectory Prediction Based on Encoder Decoder Architecture
Abstract
:1. Introduction
2. Related Work
3. Our Approach and Other Models
3.1. Problem Formulation
3.2. Encoder–Decoder Architecture
3.3. Transformer
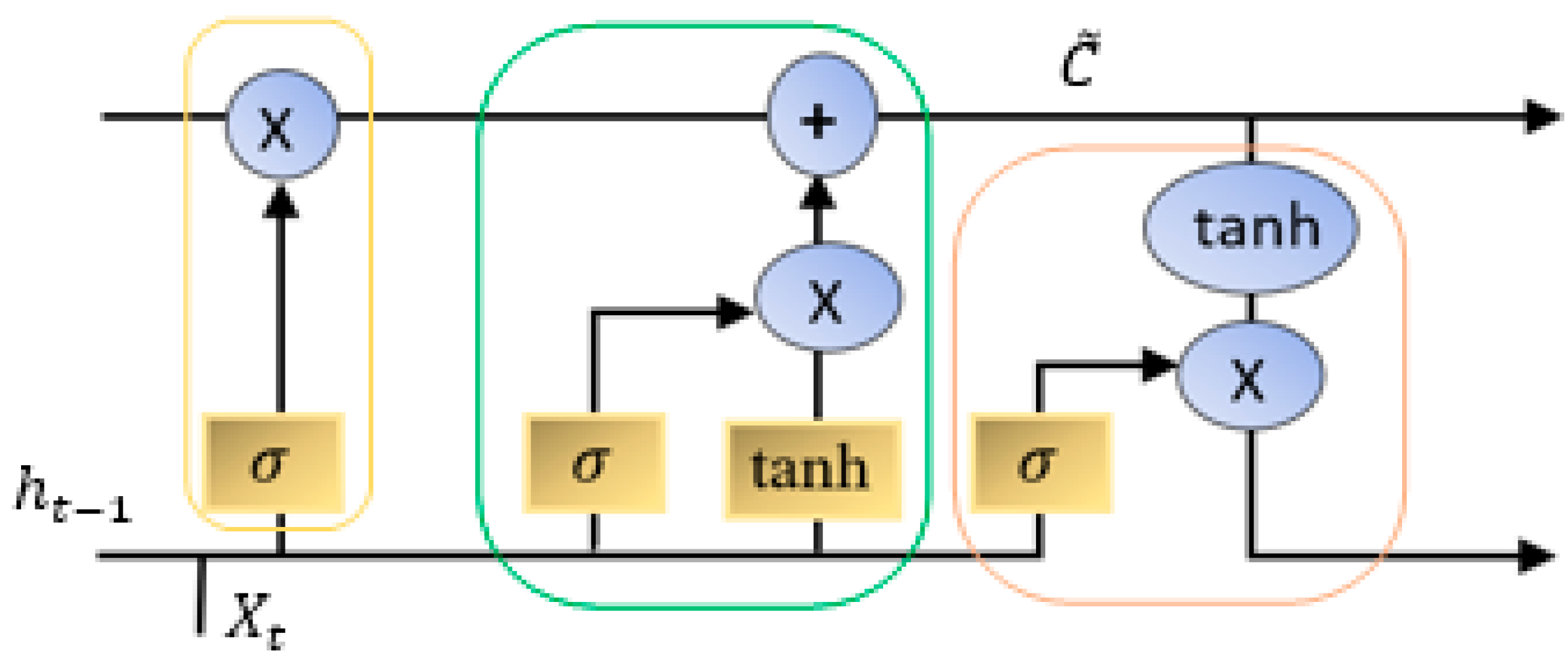
3.4. LSTNet (Long- and Short-Term Time-Series Network)
4. AIS Data Preparation
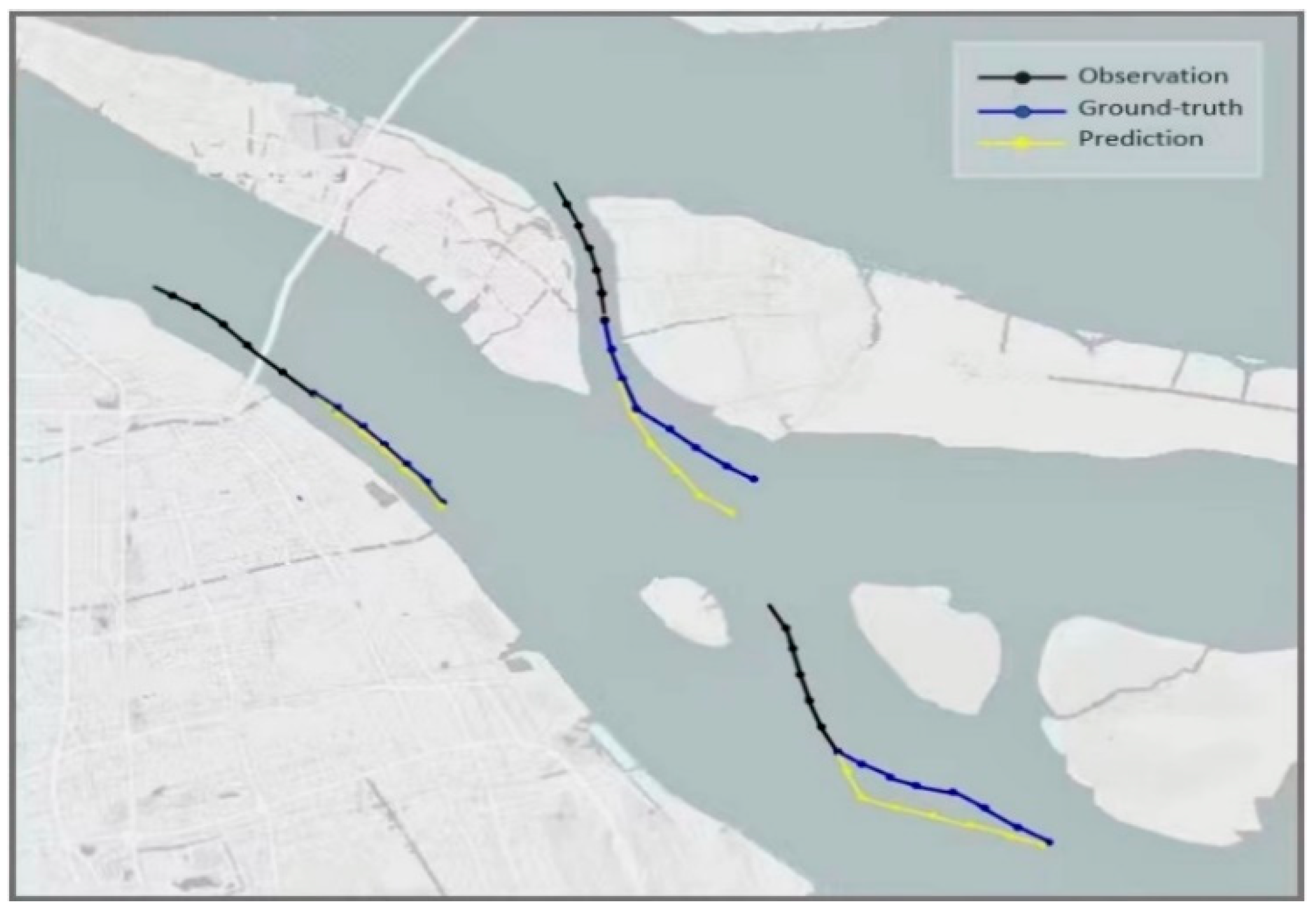
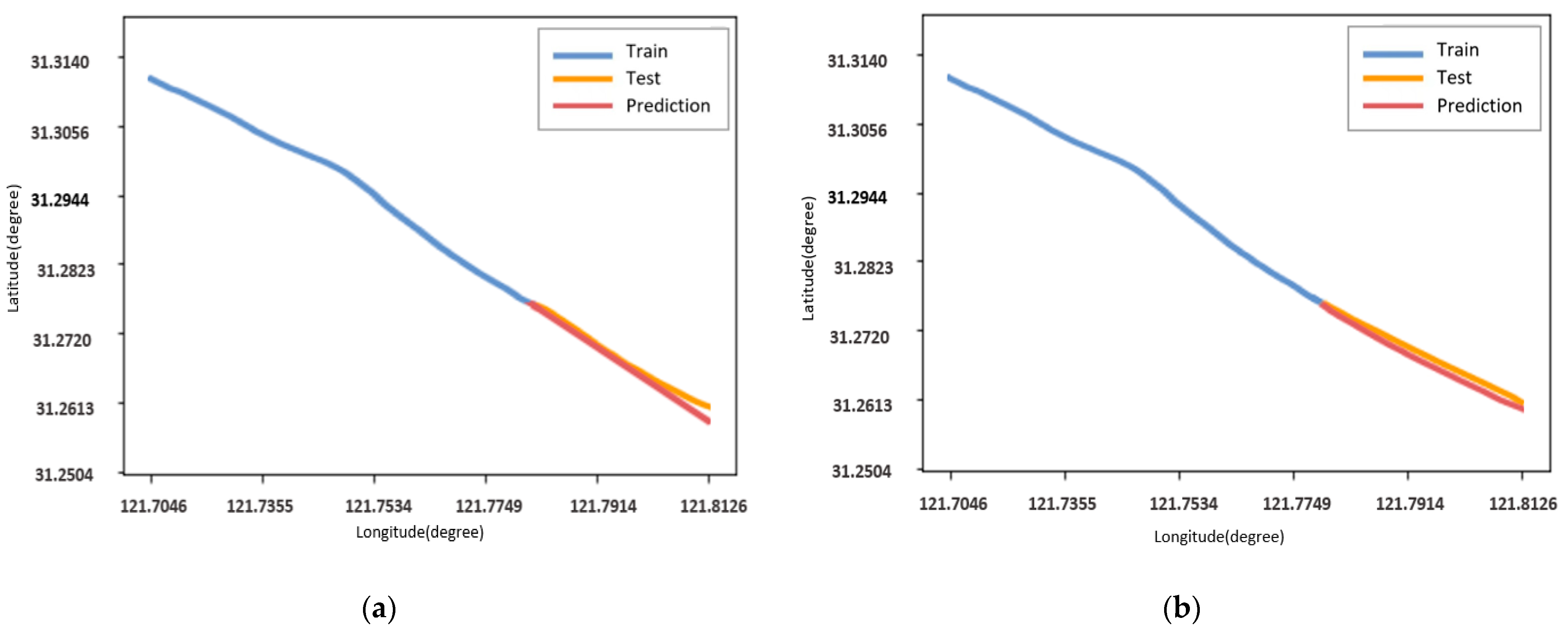
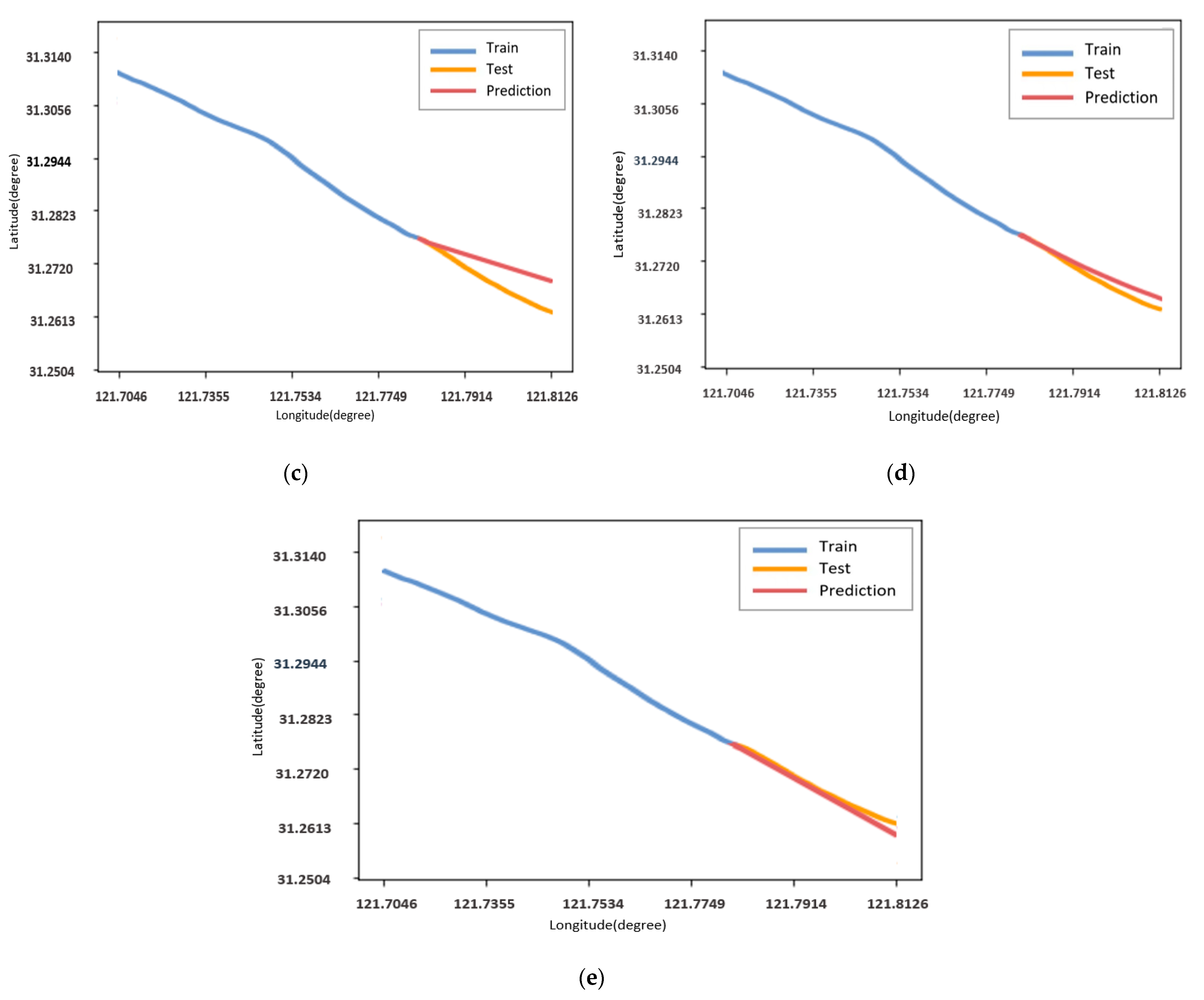
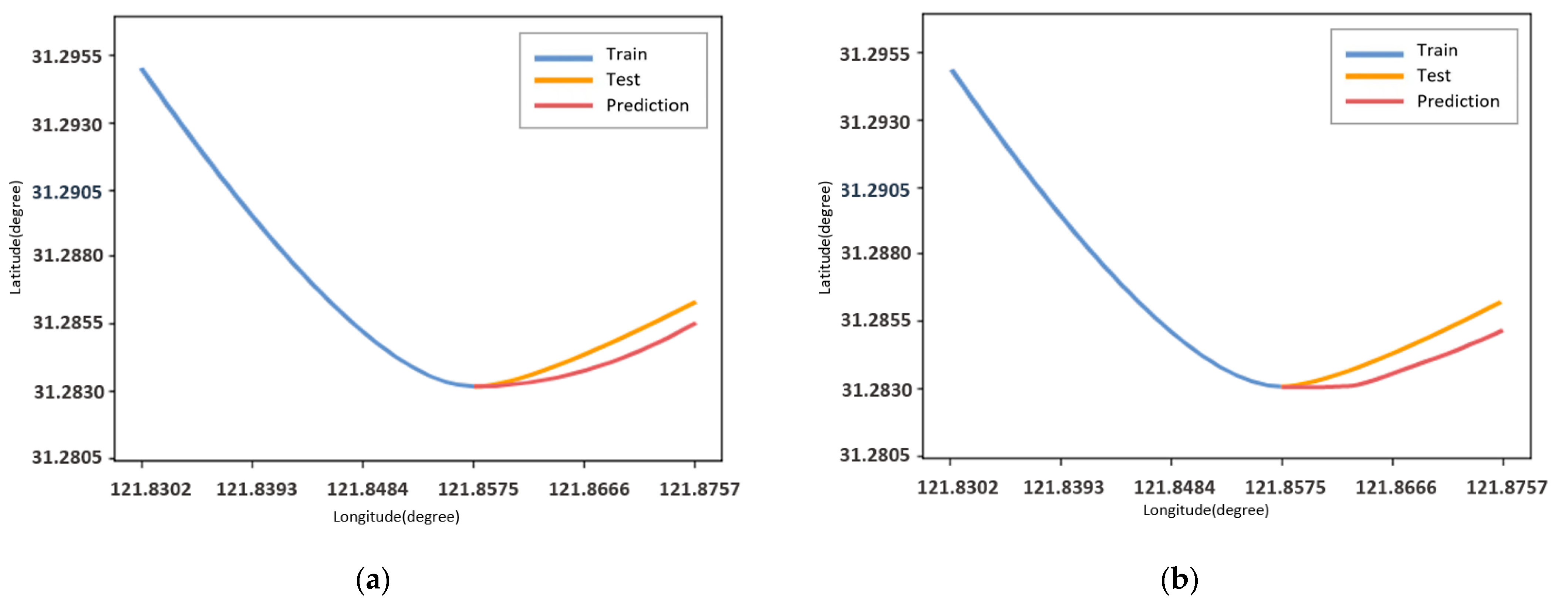
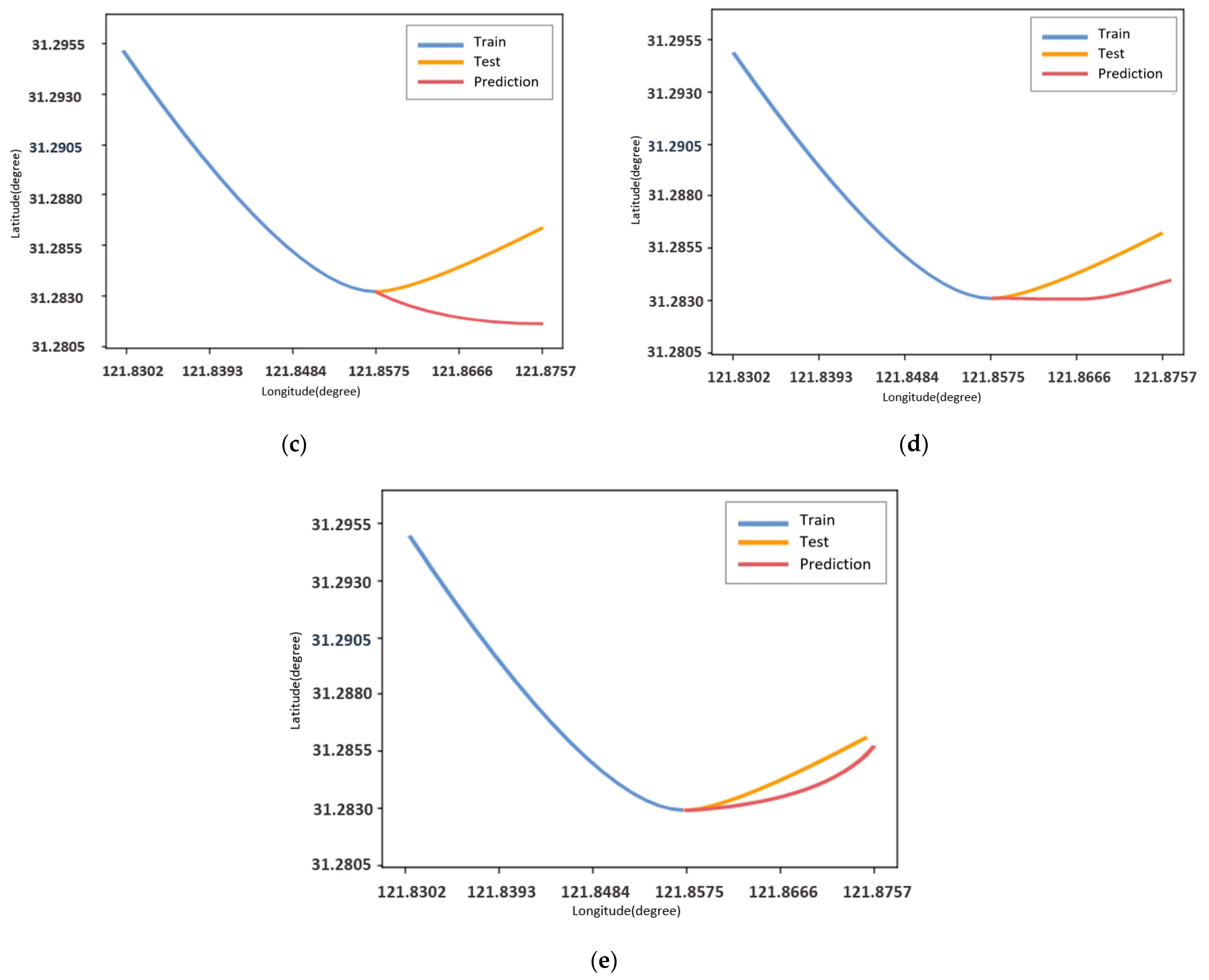
5. Experimental Setup and Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Available online: https://www.agcs.allianz.com/news-and-insights/reports/shipping-safety.html#download (accessed on 15 October 2022).
- Özkan, U.; Erol, S.; Başar, E. The analysis of life safety and economic loss in marine accidents occurring in the Turkish Straits. Marit. Policy Manag. 2016, 43, 356–370. [Google Scholar]
- Chen, X.; Wang, S.; Shi, C.; Wu, H.; Zhao, J.; Fu, J. Robust ship tracking via multi-view learning and sparse representation. J. Navig. 2019, 72, 176–192. [Google Scholar] [CrossRef]
- Chen, X.; Xu, X.; Yang, Y.; Wu, H.; Tang, J.; Zhao, J. Augmented ship tracking under occlusion conditions from maritime surveillance videos. IEEE Access 2020, 8, 42884–42897. [Google Scholar] [CrossRef]
- Fang, Z.; Jian-Yu, L.; Jin-Jun, T.; Xiao, W.; Fei, G. Identifying activities and trips with GPS data. IET Intell. Transp. Syst. 2018, 12, 884–890. [Google Scholar] [CrossRef]
- Available online: https://artes.esa.int/satellite-%E2%80%93-automatic-identification-system-satais-overview (accessed on 30 July 2022).
- Mozaffari, S.; Al-Jarrah, O.Y.; Dianati, M.; Jennings, P.; Mouzakitis, A. Deep learning-based vehicle behavior prediction for autonomous driving applications: A review. IEEE Trans. Intell. Transp. Syst. 2020, 23, 33–47. [Google Scholar] [CrossRef]
- Available online: https://www.imo.org/en/About/Conventions/Pages/COLREG.aspx (accessed on 13 July 2022).
- Bye, R.J.; Almklov, P.G. Normalization of maritime accident data using AIS. Mar. Policy 2019, 109, 103675. [Google Scholar] [CrossRef]
- Iphar, C.; Ray, C.; Napoli, A. Data integrity assessment for maritime anomaly detection. Expert Syst. Appl. 2020, 147, 113219. [Google Scholar] [CrossRef]
- Millefiori, L.M.; Braca, P.; Bryan, K.; Willett, P. Modeling vessel kinematics using a stochastic mean-reverting process for long-term prediction. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2313–2330. [Google Scholar] [CrossRef]
- Pallotta, G.; Vespe, M.; Bryan, K. Vessel Pattern Knowledge Discovery from AIS Data: A Framework for Anomaly Detection and Route Prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef] [Green Version]
- Perera, L.P.; Oliveira, P.; Soares, C.G. Maritime Traffic Monitoring Based on Vessel Detection, Tracking, State Estimation, and Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1188–1200. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Uney, M.; Millefiori, L.M.; Braca, P. Data driven vessel trajectory forecasting using stochastic generative models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8459–8463. [Google Scholar]
- Coscia, P.; Braca, P.; Millefiori, L.M.; Palmieri, F.A.N.; Willett, P. Multiple Ornstein–Uhlenbeck processes for maritime traffic graph representation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2158–2170. [Google Scholar] [CrossRef]
- Forti, N.; Millefiori, L.M.; Braca, P. Unsupervised extraction of maritime patterns of life from Automatic Identification System data. In Proceedings of the IEEE/MTS OCEANS, Marseille, France, 17–20 June 2019. [Google Scholar]
- Forti, N.; Millefiori, L.M.; Braca, P.; Willett, P. Anomaly detection and tracking based on mean–reverting processes with unknown parameters. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8449–8453. [Google Scholar]
- Mazzarella, F.; Arguedas, V.F.; Vespe, M. Knowledge-based vessel position prediction using historical AIS data. In Proceedings of the Sensor Data Fusion: Trends, Solutions, Applications, Bonn, Germany, 6–8 October 2015. [Google Scholar]
- Hexeberg, S.; Flaten, A.L.; Eriksen, B.H.; Brekke, E.F. AIS-based vessel trajectory prediction. In Proceedings of the International Conference on Information Fusion, Xi’an, China, 10–13 July 2017. [Google Scholar]
- Nguyen, D.; Vadaine, R.; Hajduch, G.; Garello, R.; Fablet, R. A multi-task deep learning architecture for maritime surveillance using AIS data streams. In Proceedings of the IEEE International Conference on Data Science and Advanced Analytics, Turin, Italy, 1–3 October 2018; pp. 331–340. [Google Scholar]
- Zhou, T.; Li, Z.; Zhang, C.; Ma, H. Classify multi-label images via improved CNN model with adversarial network. Multimed. Tools Appl. 2020, 79, 6871–6890. [Google Scholar] [CrossRef]
- Khalil, R.A.; Jones, E.; Babar, M.I.; Jan, T.; Zafar, M.H.; Alhussain, T. Speech Emotion Recognition Using Deep Learning Techniques: A Review. IEEE Access 2019, 7, 117327–117345. [Google Scholar] [CrossRef]
- Available online: https://builtin.com/data-science/recurrent-neural-networks-and-lstm (accessed on 15 October 2022).
- Fujita, T.; Luo, Z.; Quan, C.; Mori, K. Simplification of RNN and Its Performance Evaluation in Machine Translation. Transactions of the Institute of Systems. Control Inf. Eng. 2020, 33, 267–274. [Google Scholar]
- Singh, S.P.; Kumar, A.; Darbari, H.; Singh, L.; Rastogi, A.; Jain, S. Machine translation using deep learning: An overview. In Proceedings of the 2017 International Conference on Computer, Communications and Electronics (Comptelix), Jaipur, India, 1–2 July 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018. [Google Scholar]
- Karahalios, H. The contribution of risk management in ship management: The case of ship collision. Saf. Sci. 2014, 63, 104–114. [Google Scholar] [CrossRef]
- Available online: https://www8.cao.go.jp/koutu/kihon/keikaku8/english/part2.html (accessed on 10 October 2022).






| Name | Value |
|---|---|
| Batches | 32 |
| Optimizer | Adam |
| Epochs | 160 |
| Loss Function | MSE |
| Activation | ReLU |
| Model | Learning Rate | Input Layer | Hidden Layer | Batch Size | Activation |
|---|---|---|---|---|---|
| GRU | 0.001 | 16 | 100 | 32 | ReLU |
| LSTNet | 0.001 | 16 | 100 | 20 | ReLU |
| Transformer | 0.001 | 16 | 100 | 20 | ReLU |
| LSTM | 0.001 | 16 | 100 | 32 | ReLU |
| CNN | 0.001 | 16 | 100 | 32 | ReLU |
| Models | RMSE | MAE | |
|---|---|---|---|
| Straight-line navigation | LSTNet | 0.0210 | 0.0135 |
| Transformer | 0.0238 | 0.0185 | |
| LSTM | 0.0263 | 0.0216 | |
| CNN | 0.0270 | 0.0219 | |
| GRU | 0.0536 | 0.0480 | |
| Waypoint navigation | LSTNet | 0.0389 | 0.0310 |
| Transformer | 0.0426 | 0.0384 | |
| LSTM | 0.0519 | 0.0475 | |
| CNN | 0.0536 | 0.0441 | |
| GRU | 0.0734 | 0.0677 |
| Models (∆ l − 10) | RMSE (∆ h + 4) | MAE (∆ h + 4) | |
|---|---|---|---|
| Straight-line navigation | LSTNet | 0.0218 | 0.0133 |
| Transformer | 0.0244 | 0.0190 | |
| LSTM | 0.0280 | 0.0231 | |
| CNN | 0.0283 | 0.0232 | |
| GRU | 0.0563 | 0.0503 | |
| Waypoint navigation | LSTNet | 0.0458 | 0.0399 |
| Transformer | 0.0489 | 0.0438 | |
| LSTM | 0.0614 | 0.0549 | |
| CNN | 0.0635 | 0.0586 | |
| GRU | 0.0841 | 0.0778 |
| LSTM | CNN | |
|---|---|---|
| East China Sea | 0.0238 | 0.0.265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billah, M.M.; Zhang, J.; Zhang, T. A Method for Vessel’s Trajectory Prediction Based on Encoder Decoder Architecture. J. Mar. Sci. Eng. 2022, 10, 1529. https://doi.org/10.3390/jmse10101529
Billah MM, Zhang J, Zhang T. A Method for Vessel’s Trajectory Prediction Based on Encoder Decoder Architecture. Journal of Marine Science and Engineering. 2022; 10(10):1529. https://doi.org/10.3390/jmse10101529
Chicago/Turabian StyleBillah, Mohammad Masum, Jing Zhang, and Tianchi Zhang. 2022. "A Method for Vessel’s Trajectory Prediction Based on Encoder Decoder Architecture" Journal of Marine Science and Engineering 10, no. 10: 1529. https://doi.org/10.3390/jmse10101529
APA StyleBillah, M. M., Zhang, J., & Zhang, T. (2022). A Method for Vessel’s Trajectory Prediction Based on Encoder Decoder Architecture. Journal of Marine Science and Engineering, 10(10), 1529. https://doi.org/10.3390/jmse10101529






