Detecting Maritime Obstacles Using Camera Images
Abstract
1. Introduction and Background
2. Methods
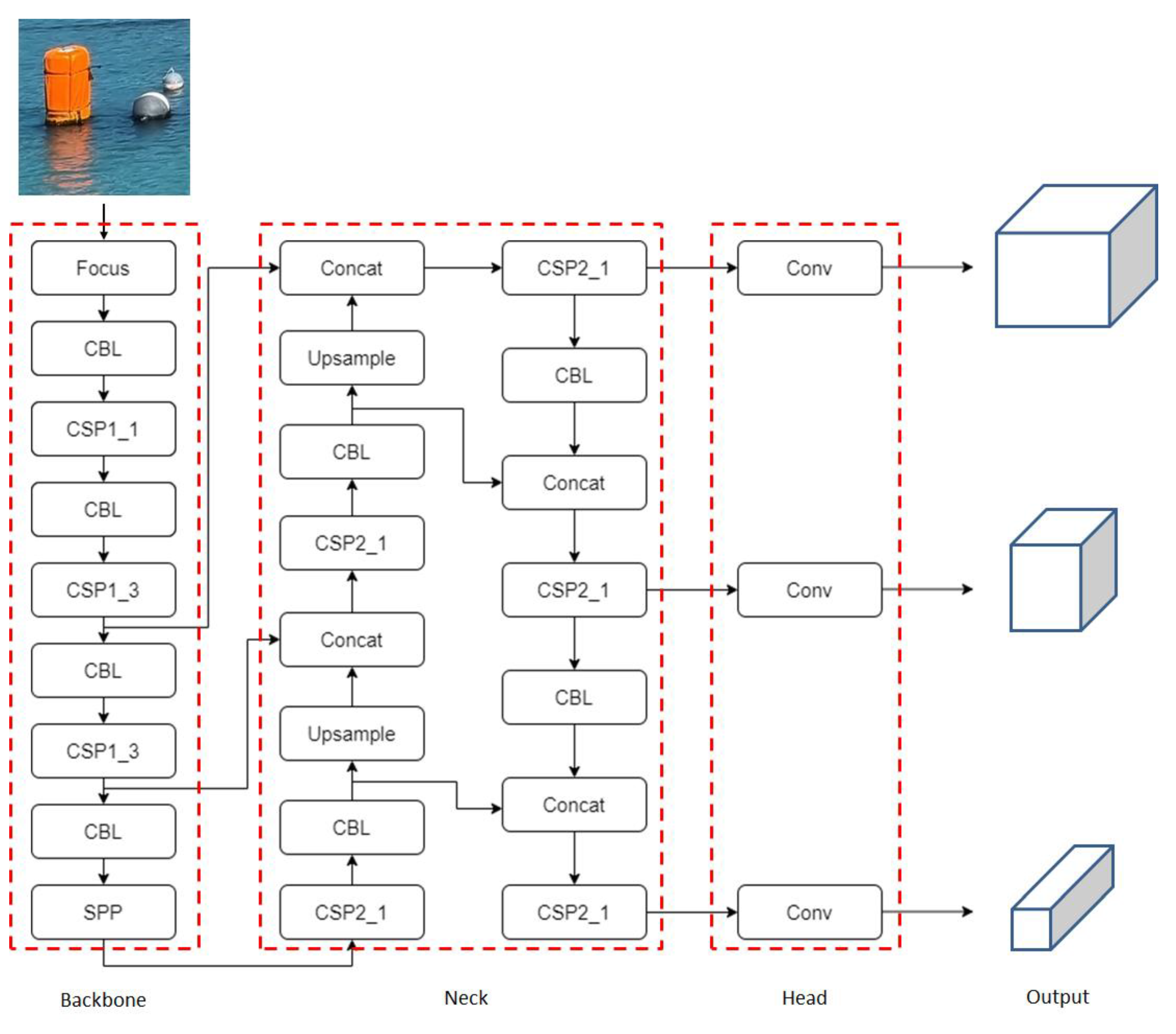
2.1. YOLOv5
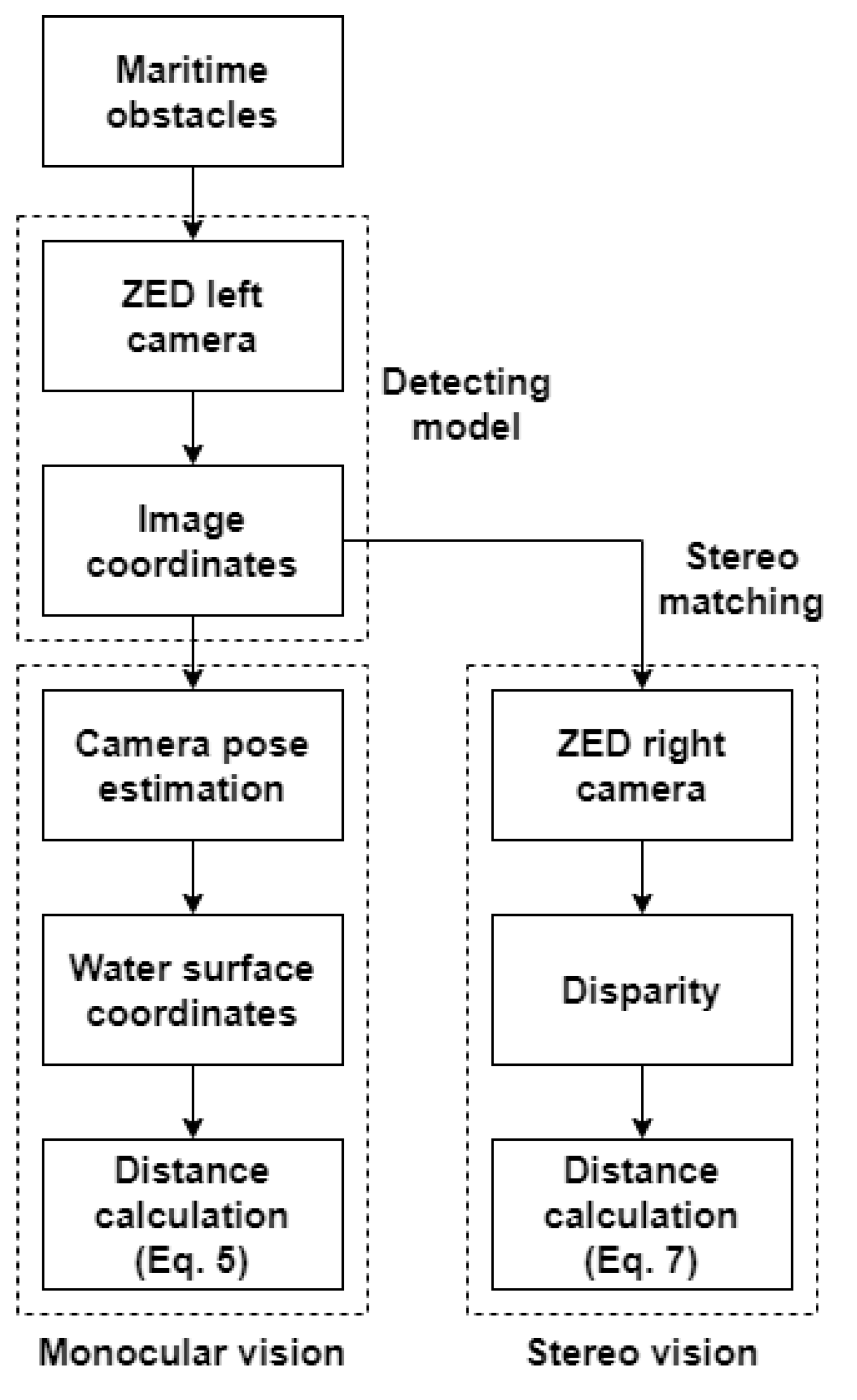
2.2. Monocular Vision
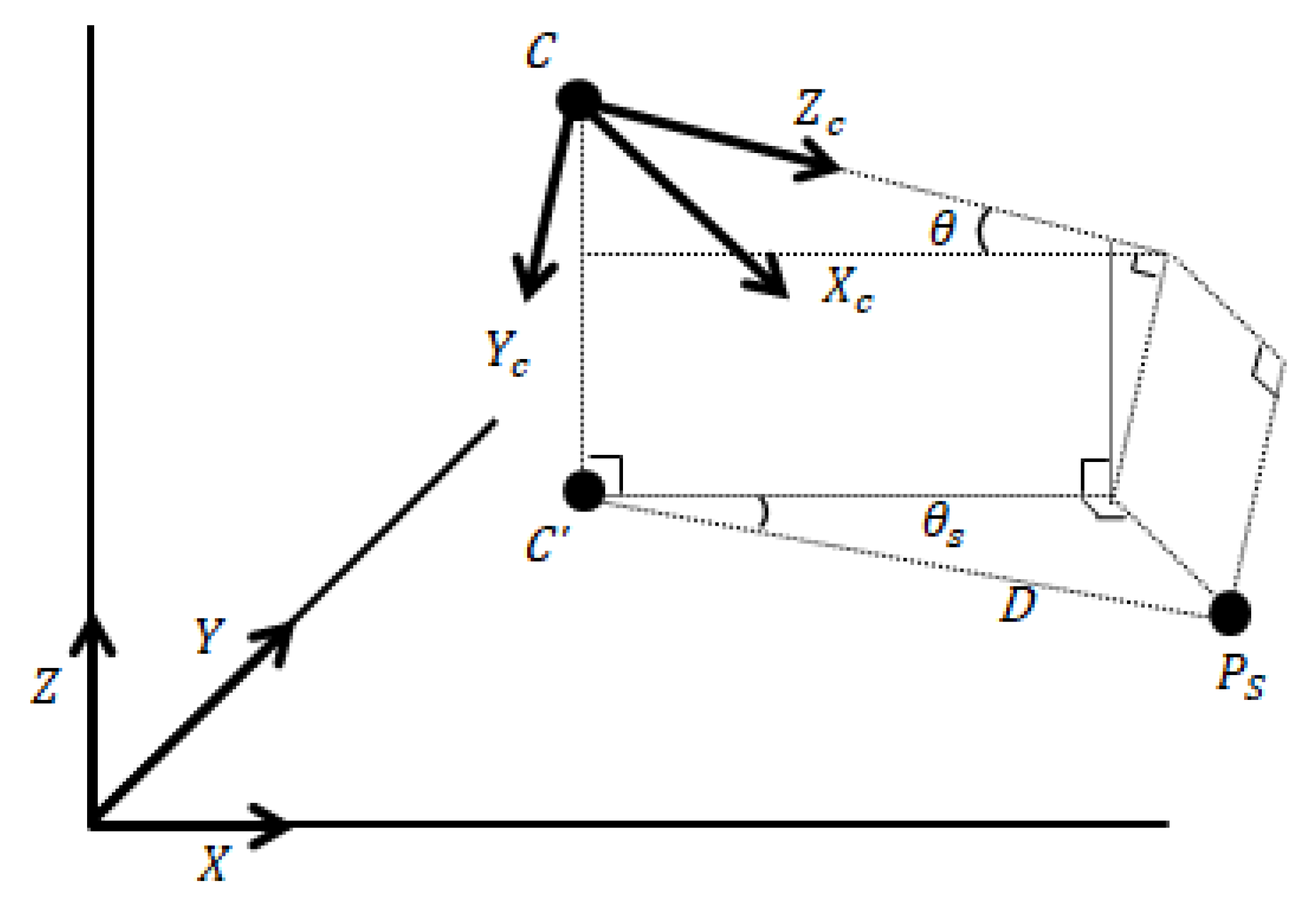
2.2.1. Projection Transformation
2.2.2. Distance Calculation
2.3. Stereo Vision
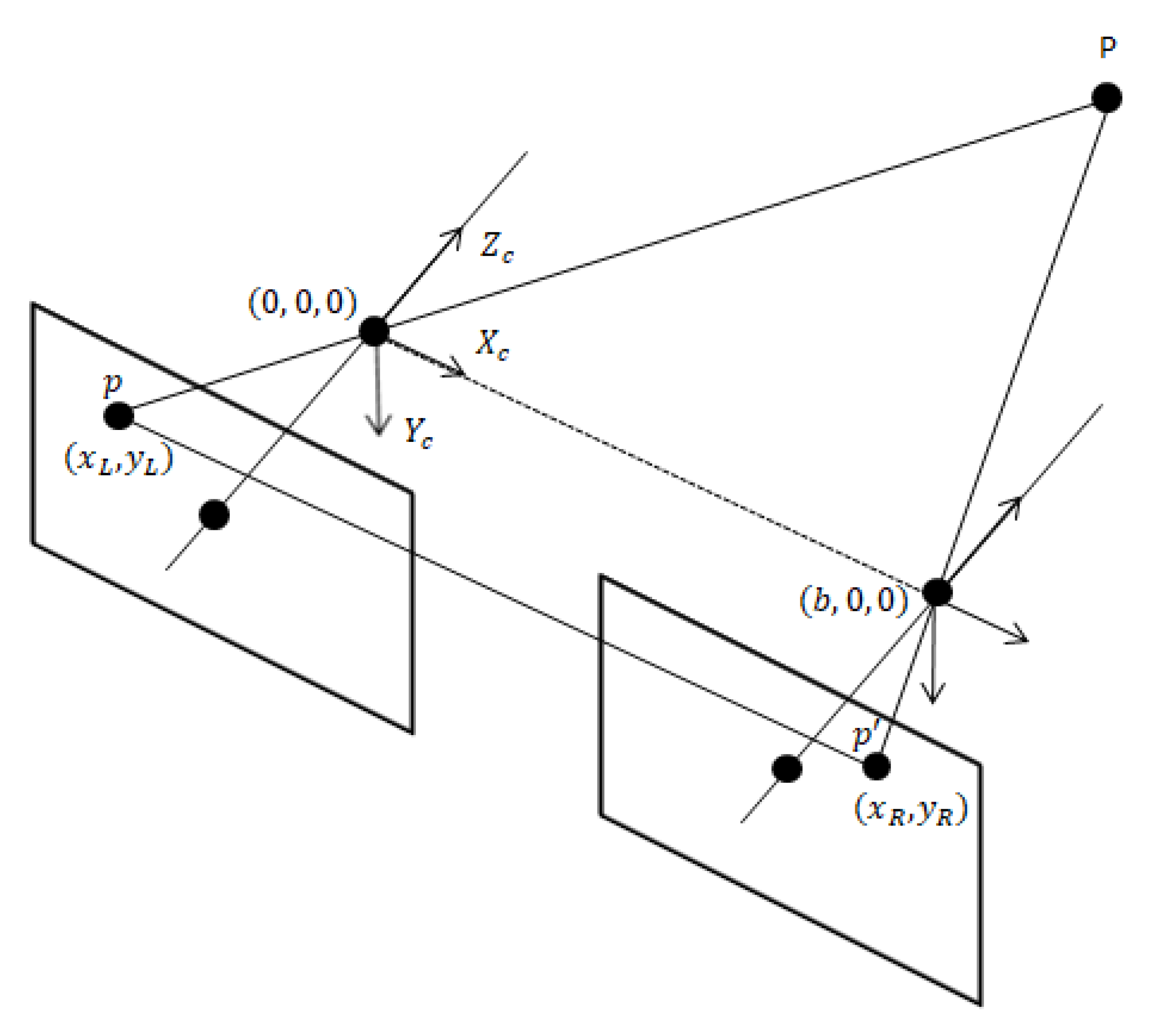
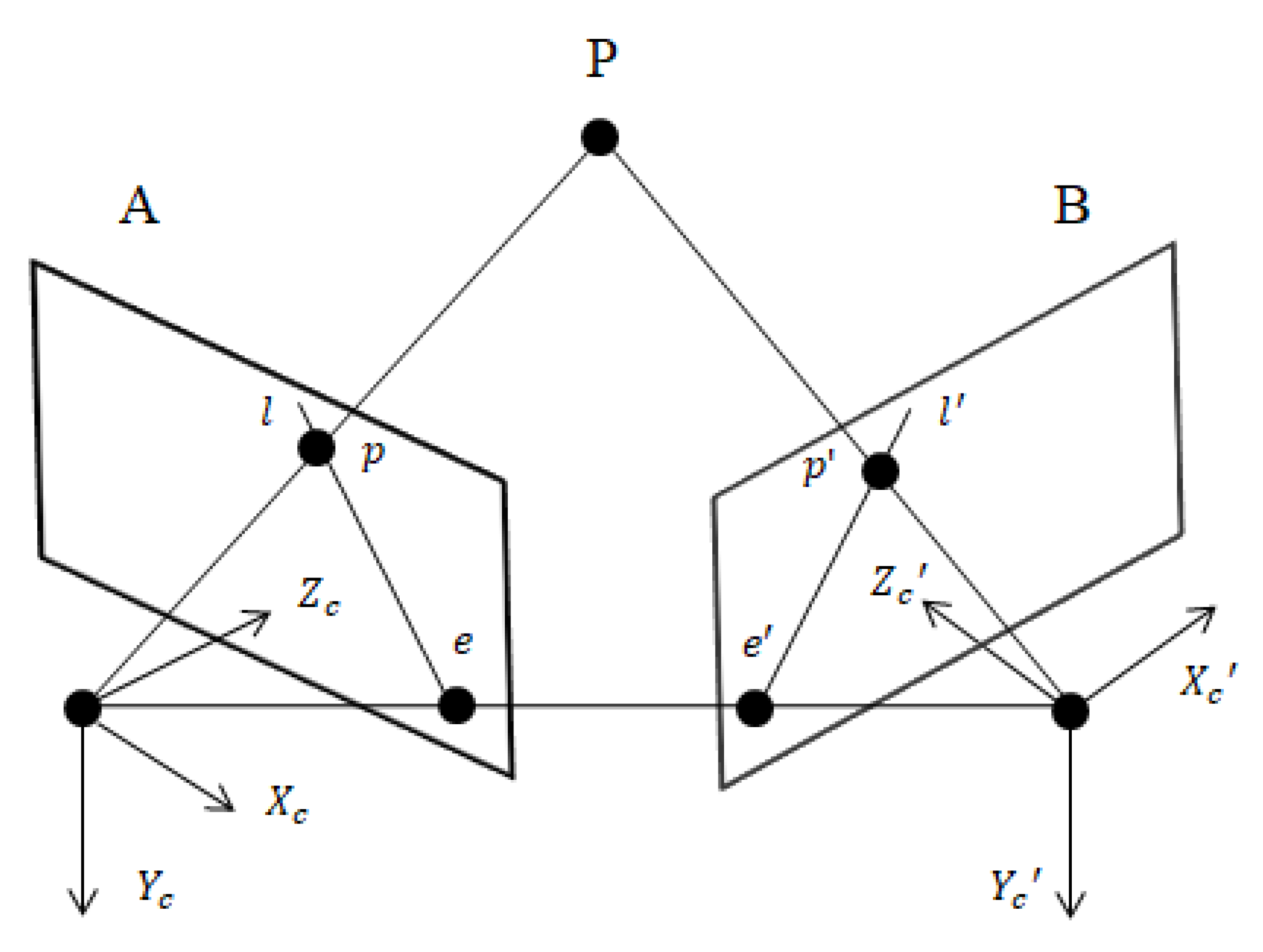
2.3.1. Distance Calculation
2.3.2. Epipolar Geometry
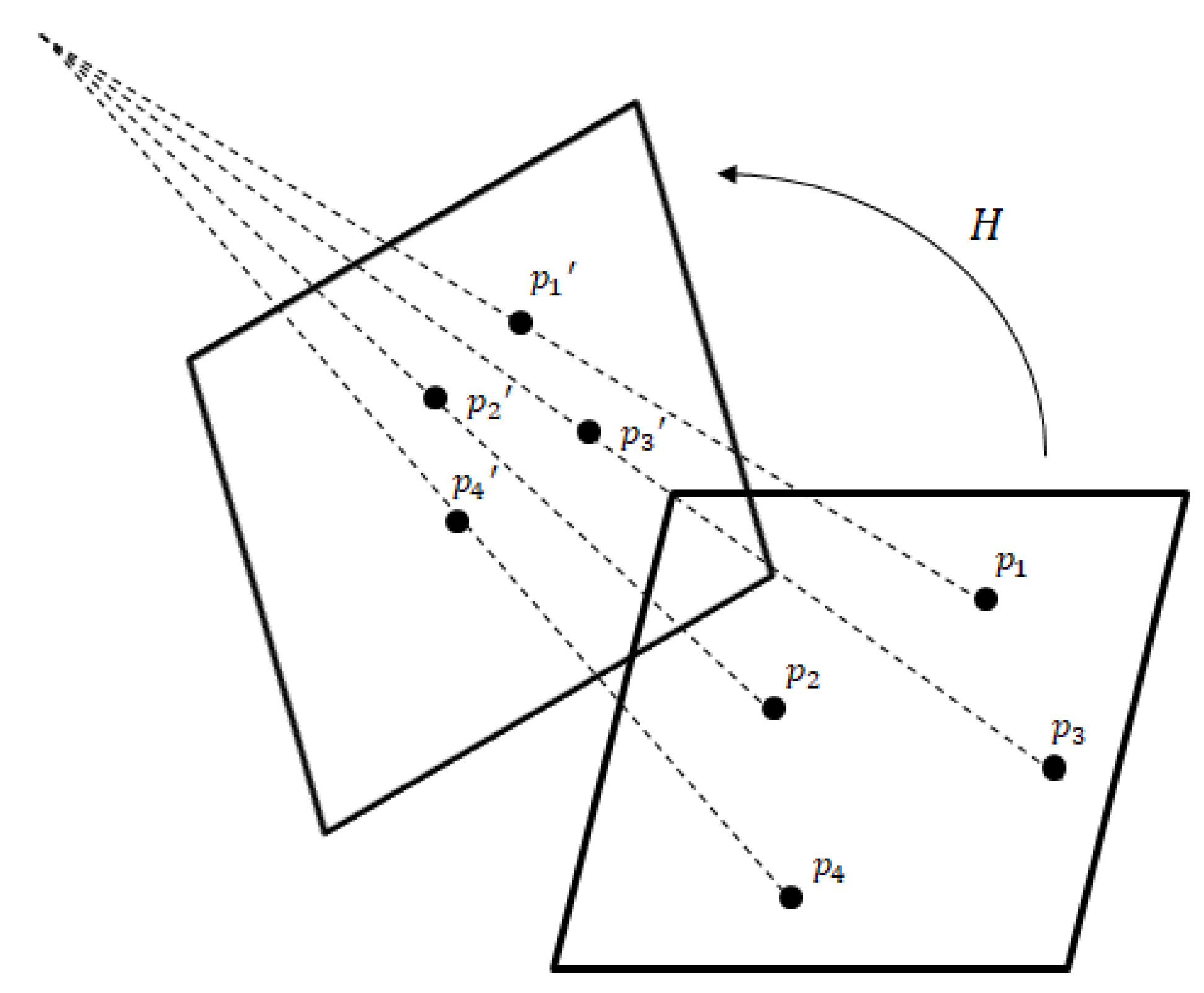
2.3.3. Area-Based Matching
- SSD
- 2.
- NCC
2.3.4. Feature-Based Matching
3. Experiment Results
3.1. Detecting Model
3.1.1. Introduction of Dataset
3.1.2. Mosaic Augmentation
3.1.3. Training Results
3.2. Distance Calculation
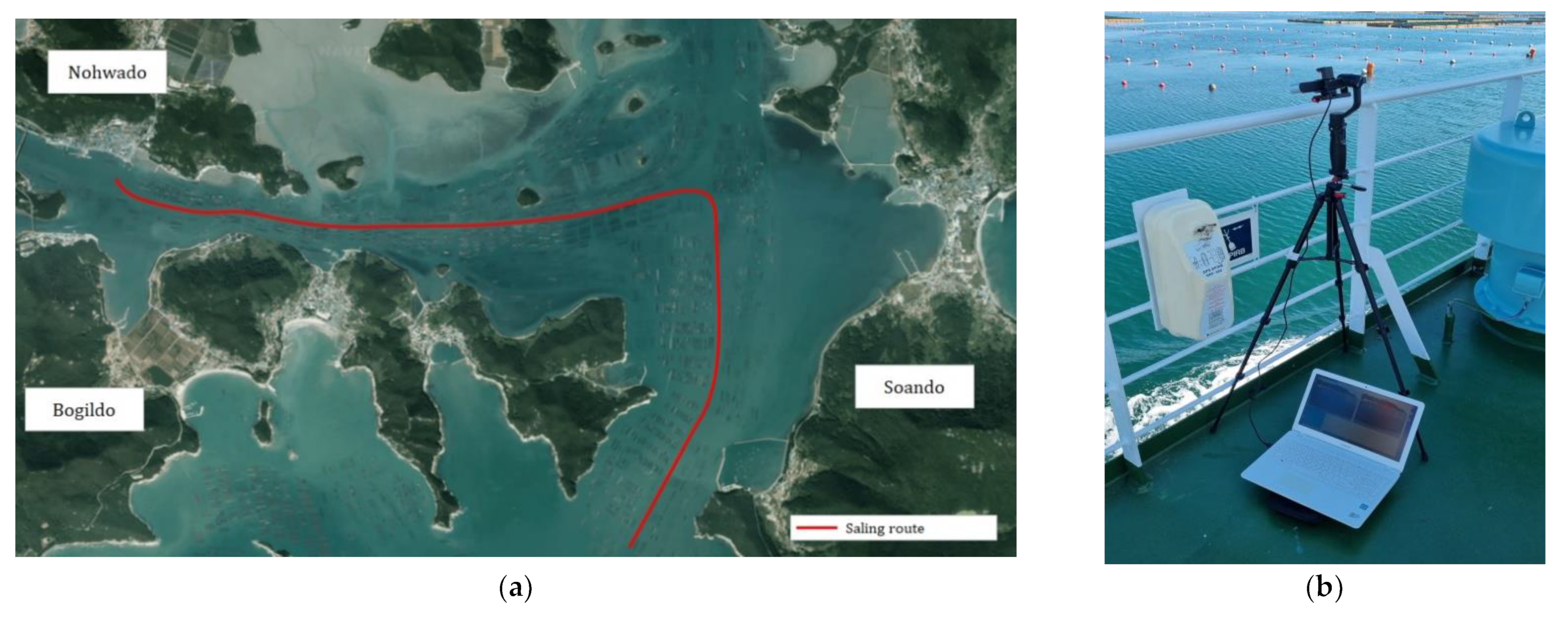
3.2.1. Experimental Environment and Equipment
3.2.2. Camera Calibration
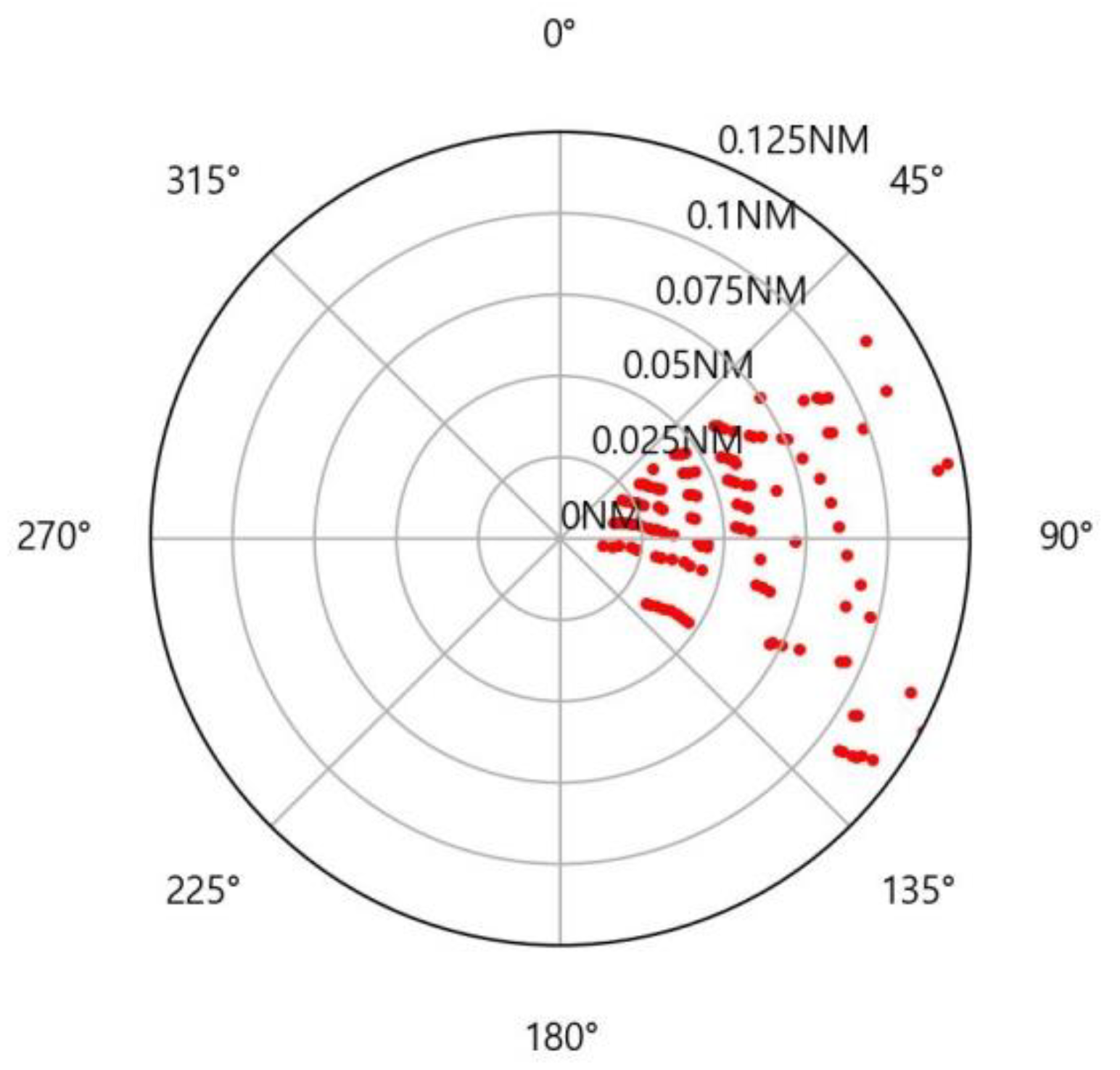
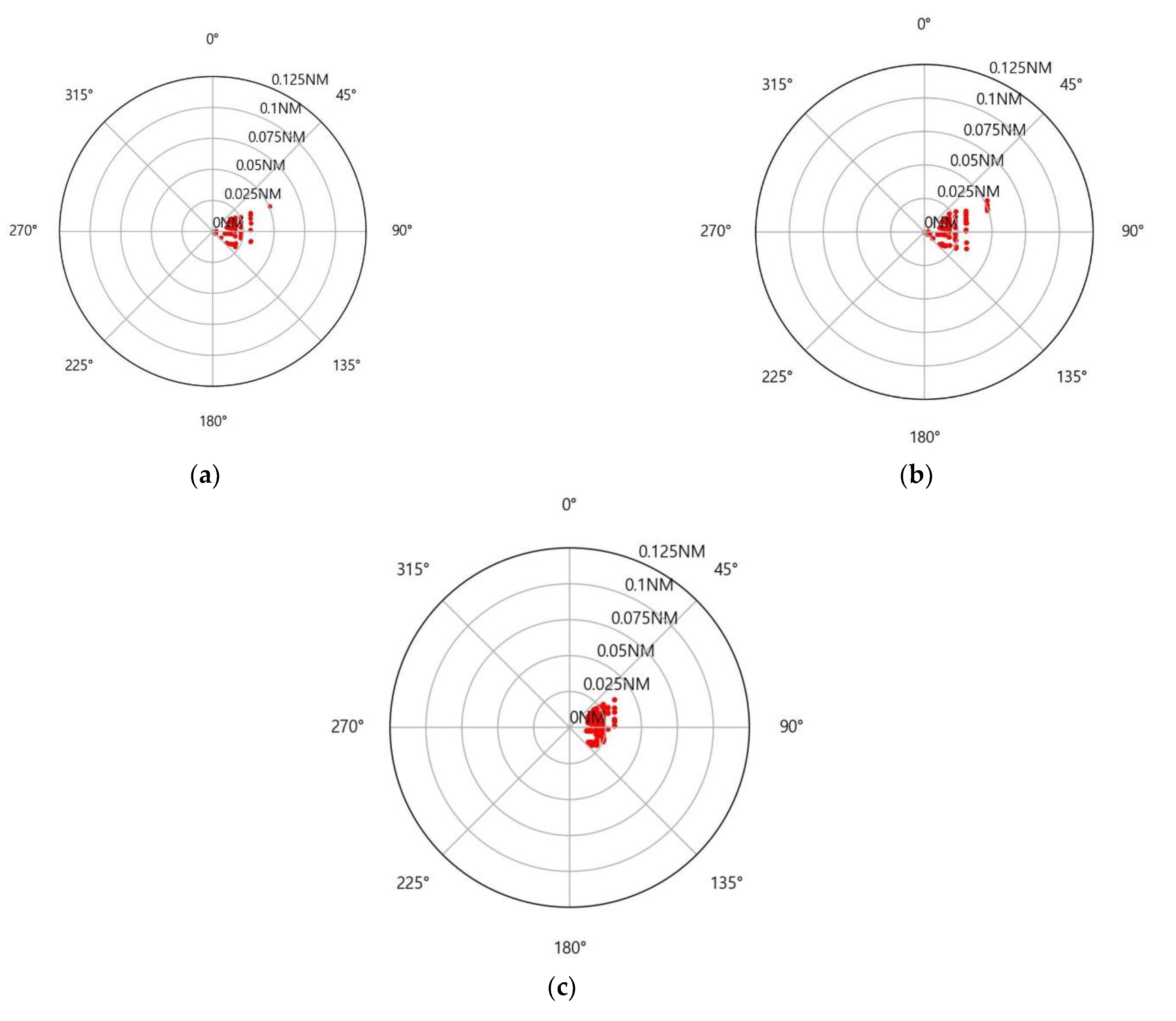
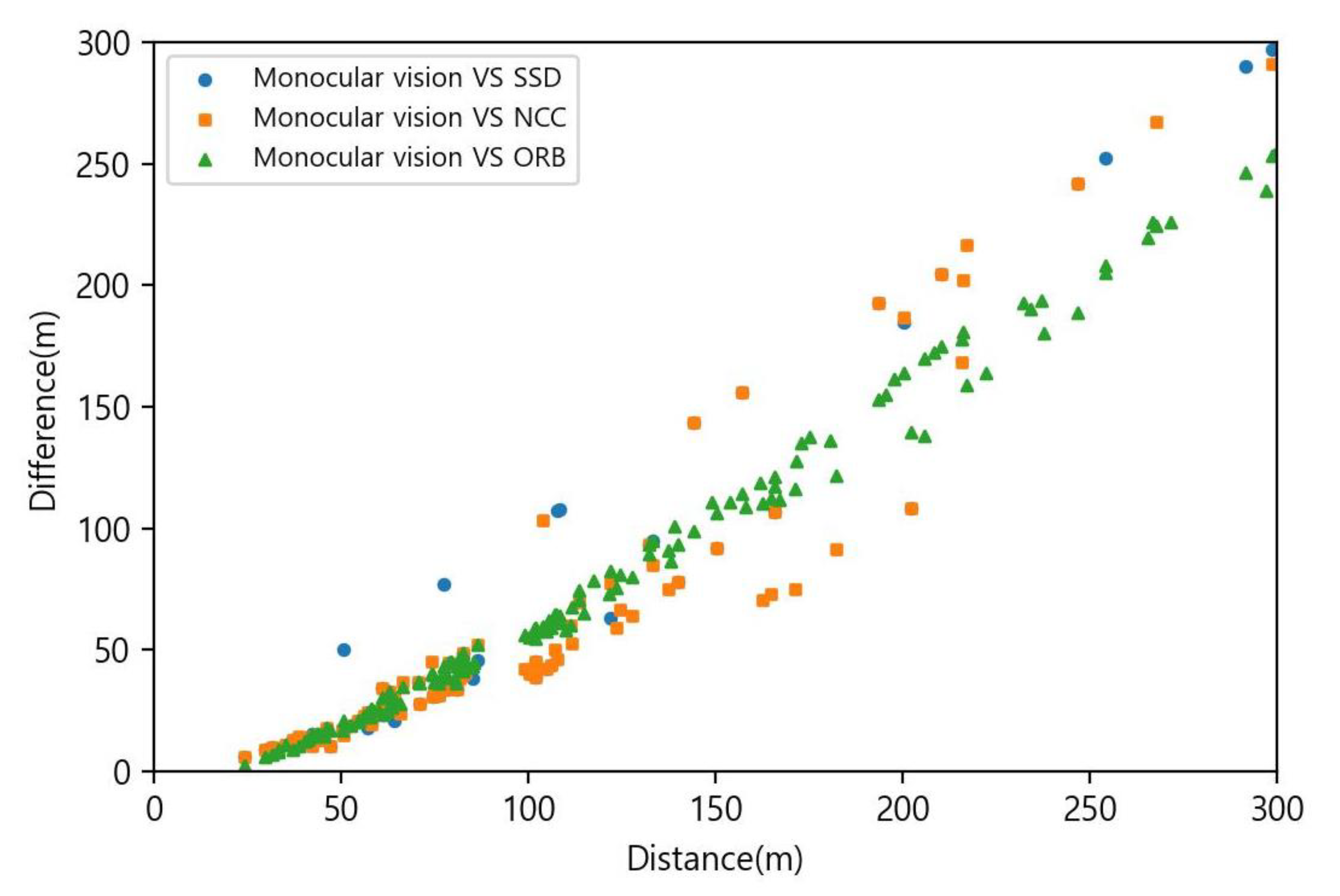
3.2.3. Experiment A
3.2.4. Experiment B
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, C.M.; Lee, S.C.; Kim, S.I.; Yoon, M.G. A Study on Environmental Improvements of Aquaculture Farms; Korea Maritime Institute: Busan, Korea, 2018; pp. 22–24. [Google Scholar]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 11, 3212–3232. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 17, 1137–1149. [Google Scholar] [CrossRef]
- Cai, Z.; Vasconcelos, N. Cascade r-cnn: Delving into high quality object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar]
- Lee, Y.H.; Kim, Y.S. Comparison of CNN and YOLO for object detection. J. Semicond. Display Technol. 2020, 19, 85–92. [Google Scholar]
- Li, Q.; Ding, X.; Wang, X.; Chen, L.; Son, J.; Song, J.Y. Detection and identification of moving objects at busy traffic road based on YOLO v4. J. Inst. Internet Broadcast. Commun. 2021, 21, 141–148. [Google Scholar]
- Kim, J.; Cho, J. YOLO-based real time object detection scheme combining RGB image with LiDAR point cloud. J. KIIT 2019, 17, 93–105. [Google Scholar] [CrossRef]
- Zhang, Z.; Hang, Y.; Zhou, Y.; Dai, M. A novel absolute localization estimation of a target with monocular vision. Optik-Int. J. Light Electron Opt. 2012, 124, 1218–1223. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, Q.Z. Monocular vision based 6D object localization for service robots intelligent grasping. Comput. Math. Appl. 2012, 64, 1235–1241. [Google Scholar] [CrossRef]
- Qi, S.H.; Sun, Z.P.; Zhang, J.T.; Sun, Y. Distance estimation of monocular based on vehicle pose information. J. Phys. Conf. Ser. 2019, 1168, 1–8. [Google Scholar] [CrossRef]
- Dhall, A. Real-time 3D posed estimation with a monocular camera using deep learning and object priors on an autonomous racecar. arXiv 2018, arXiv:1809.10548. [Google Scholar]
- Fusiello, A.; Roberto, V.; Trucco, E. Efficient stereo with multiple windowing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, 17–19 June 1997; pp. 858–868. [Google Scholar]
- Gong, M.; Yang, M. Fast unambiguous stereo matching using reliability-based dynamic programming. IEEE Trans. Pattern Anal. March. Intell. 2005, 27, 998–1003. [Google Scholar] [CrossRef]
- Klaus, A.; Sormann, M.; Karner, K. Segment-based stereo matching using belief propagation and a self-adapting dissimilarity measure. In Proceedings of the International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; pp. 15–18. [Google Scholar]
- Kim, J.C.; Lee, K.M.; Choi, B.T.; Lee, S.U. A dense stereo matching using two-pass dynamic programming with generalized ground control points. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 1075–1082. [Google Scholar]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. March. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Hamzah, R.A.; Ibrahim, H. Literature survey on stereo vision disparity map algorithms. J. Sens. 2016, 2016, 1–23. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image feature from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded Up Robust Features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE Features. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 214–227. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Yang, Y.; Lu, C. A stereo matching method for 3D image measurement of long-distance sea surface. J. Mar. Sci. Eng. 2021, 9, 1281. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, P.; Qian, L.; Qin, S.; Liu, X.; Ma, Y.; Cheng, G. Recognition and depth estimation of ships based on binocular stereo vision. J. Mar. Sci. Eng. 2022, 10, 1153. [Google Scholar] [CrossRef]
- GitHub. YOLO V5-Master. Available online: https://github.com/ultralytics/yolov5.git/ (accessed on 11 September 2022).
- Bloomenthal, J.; Rokne, J. Homogeneous coordinates. Vis. Comput. 1994, 11, 15–26. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, Z. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003; pp. 151–176. [Google Scholar]
- Taryudi; Wang, M.S. Eye to hand calibration using ANFIS for stereo vision-based object manipulation system. Microsyst. Technol. 2018, 24, 305–317. [Google Scholar] [CrossRef]
- Bennamoun, M.; Mamic, G.J. Object Recognition Fundamentals and Case Studies, 1st ed.; Springer: London, UK; Berlin/Heidelberg, Germany, 2002; pp. 34–38. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Calondar, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Oberkampf, D.; Dementhon, D.F.; Davis, L.S. Iterative pose estimation using coplanar feature points. Comput. Vis. Image Underst. 1996, 63, 495–511. [Google Scholar] [CrossRef]
- Marchang, E.; Uchiyama, H.; Spindler, F. Pose estimation for augmented reality: A hands-on survey. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2633–2651. [Google Scholar] [CrossRef]
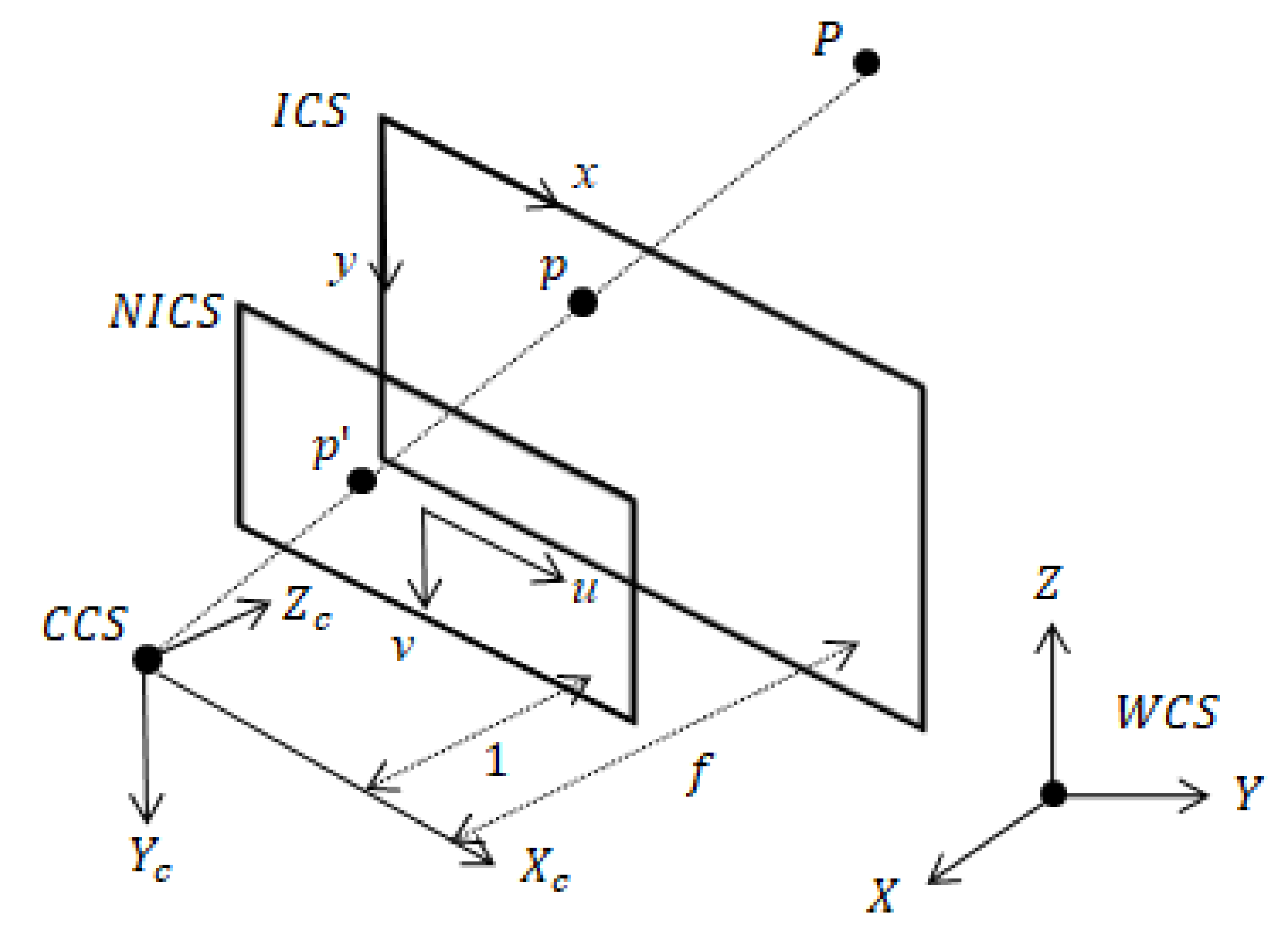
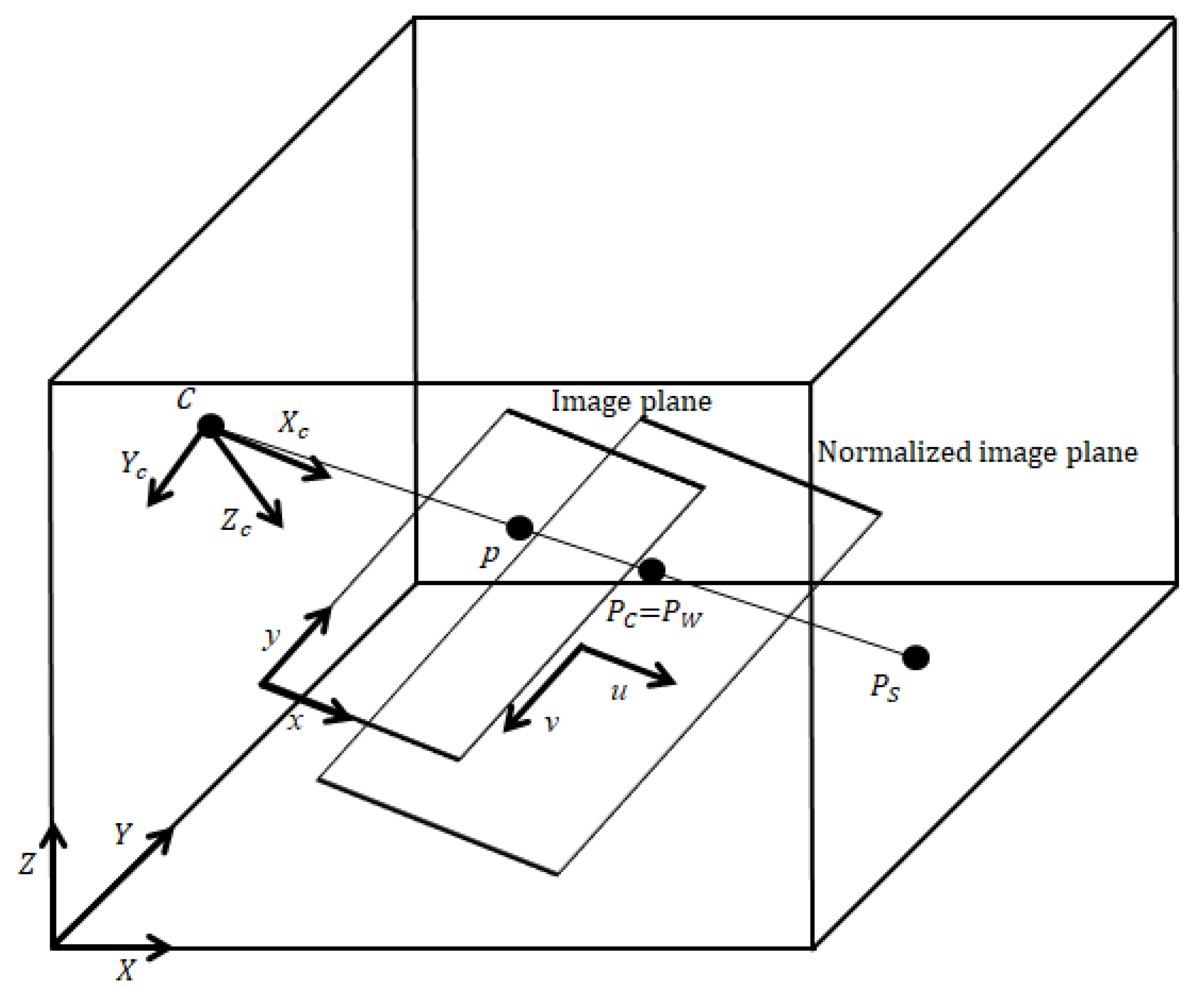













| Term | Definition |
|---|---|
| World Coordinate System (WCS) | 3D coordinate system used to provide an object’s location—can be arbitrarily set. |
| Camera Coordinate System (CCS) | 3D coordinate system with respect to the camera focus. The center of the camera lens is the origin, the front direction is the z-axis, the downward direction is the y-axis, and the right direction is the x-axis. |
| Image Coordinate System (ICS) | 2D coordinate system for an image obtained with a camera. The top-left corner of the image is the origin, the right direction is the x-axis, and the downward direction is the y-axis. |
| Normalized Image Coordinate System (NICS) | 2D coordinate system for a virtual image plane. The distance from the camera focus is 1 and the effects of a camera’s intrinsic parameters are removed. The center of the plane is the origin. |
| Class | Instances | Percentage |
|---|---|---|
| buoy 1 | 22,422 | 89.1% |
| buoy 2 | 2744 | 10.9% |
| Class | Precision | Recall | AP | mAP | FPS |
|---|---|---|---|---|---|
| Buoy 1 | 0.938 | 0.902 | 94.0% | 94.3% | 39.1 |
| Buoy 2 | 0.934 | 0.904 | 94.6% |
| Parameter | Information |
|---|---|
| Sensor type | 1/3” 4MP CMOS |
| Output resolution | 2 × (2208 × 1242) @ 15 fps 2 × (1920 × 1080) @ 30 fps 2 × (1280 × 720) @ 60 fps 2 × (672 × 376) @ 100 fps |
| Field of view | Max. 90° (H) × 60° (V) × 100° (D) |
| Focal length | 2.8 mm |
| Baseline | 120 mm |
| Parameter | Left Camera | Right Camera |
|---|---|---|
| Internal parameter matrix | ||
| Extrinsic parameter matrix | ||
| Distortion coefficient matrix | ||
| Parameter | Value |
|---|---|
| Rotation matrix | |
| Translation vector |
| Buoy | Laser (mm) | Error Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SSD | Error Rate | NCC | Error Rate | ORB | Error Rate | ||||
| A | 2254 | 2245 | −0.40% | 2157 | −4.50% | 2185 | −3.16% | 2157 | −4.50% |
| B | 2037 | 2001 | −1.80% | 1997 | −2.00% | 1971 | −3.35% | 2010 | −1.34% |
| C | 2378 | 2448 | 2.86% | 2335 | −1.84% | 2356 | −0.93% | 2436 | 2.38% |
| Radar (mm) | Error Rate | |||||||
|---|---|---|---|---|---|---|---|---|
| SSD | Error Rate | NCC | Error Rate | ORB | Error Rate | |||
| 25,093 | 24,129 | −4.00% | 18,214 | −37.77% | 18,214 | −37.77% | 21,857 | −14.81% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, B.-S.; Jung, C.-H. Detecting Maritime Obstacles Using Camera Images. J. Mar. Sci. Eng. 2022, 10, 1528. https://doi.org/10.3390/jmse10101528
Kang B-S, Jung C-H. Detecting Maritime Obstacles Using Camera Images. Journal of Marine Science and Engineering. 2022; 10(10):1528. https://doi.org/10.3390/jmse10101528
Chicago/Turabian StyleKang, Byung-Sun, and Chang-Hyun Jung. 2022. "Detecting Maritime Obstacles Using Camera Images" Journal of Marine Science and Engineering 10, no. 10: 1528. https://doi.org/10.3390/jmse10101528
APA StyleKang, B.-S., & Jung, C.-H. (2022). Detecting Maritime Obstacles Using Camera Images. Journal of Marine Science and Engineering, 10(10), 1528. https://doi.org/10.3390/jmse10101528






