An Interface Parametric Evaluation on Wellbore Integrity during Natural Gas Hydrate Production
Abstract
:1. Introduction

2. Soil–Structure Interface Properties
- (1)
- testing technology
- (2)
- Mechanical Response and Deformation Mechanism
- (3)
- constitutive model
3. Interaction between Natural Gas Hydrate Production Well and Soil under Multi-Process Coupling
4. Wellbore Integrity Assessment
5. Wellbore Integrity Evaluation System by the Interface Parameters for Hydrate Production
- (1)
- Research and development of test equipment and testing technology for deep-water hydrate extraction wells
- (i)
- Temperature–pressure precise dual-control interface shear test system: the modification of the direct shearing instrument for soil containing hydrate can carry out the monotonic and cyclic shear tests of the interface. On this basis, the interface temperature and pore pressure real-time control and measurement modules are further developed to realize the interface shear test under the condition of precise dual control of temperature and pressure. Develop a structure acquisition and measurement module for hydrates in the interface, and develop a real-time high-precision measurement system for the interface strain field combined with digital image correlation technology (DIC).
- (ii)
- Wellbore response physics test platform in the process of hydrate production: Based on the existing large-scale 3D physical model test equipment for hydrate production, develop a real-time measurement module for the temperature and deformation of the wellbore and its interface with soil, and integrate the research and development of depressurization water inflow units, sand production collect monitoring units and permeability measurement units to form a test module for hydrate mining and sand production.
- (2)
- Revealing the coupling mechanism of interface weakening properties and fabric evolution under the condition of hydrate decomposition.
- (i)
- The influence of temperature and pore pressure changes on interface mechanical properties: changing normal boundary conditions, shear stress levels, and soil physical and mechanical parameters, etc. The interface direct shear test was carried out under the condition of no phase transformation, and the structural changes such as the stress–displacement response and porosity of the interface are observed. Based on the idea of combining macro and micro, the correlation mechanism between the weakening characteristics of the interface and the fabric evolution is analyzed, and the influence of temperature and pore pressure changes on the mechanical properties of the interface is revealed.
- (ii)
- Coupling mechanism of interface weakening properties and fabric evolution under phase transition conditions: change normal boundary conditions, shear stress levels, and soil physical and mechanical parameters, simulate hydrate phase transition, conduct interface direct shear tests, and interface the stress-displacement response, porosity change, and phase transition of the interface are observed, and the response of the missing solid skeleton and the output (gas, liquid) fluid involved in the decomposition process of the phase transition is measured. Based on the idea of combining macro and microscopic features, the correlation mechanism between interface weakening properties and fabric evolution, especially phase transition is analyzed, and the coupling mechanism between interface weakening properties and fabric evolution under phase transition conditions is revealed.
- (iii)
- The influence of sand production on the interface weakening characteristics: simulate different sand production forms (pore liquefaction type, earthworm-like cave type, etc.). By changing the normal boundary conditions, shear stress levels and other factors, the direct shear test of the interface between the hydrate-containing soil and the structure was carried out, and the stress–displacement response and porosity of the interface after the sand mining were observed. Based on the idea of combining macro and micro, the correlation mechanism between interface weakening characteristics and fabric evolution is analyzed, and the influence law of sand production on interface weakening characteristics is revealed.
- (iv)
- Coupling mathematical model of interface weakening characteristics and fabric evolution: comprehensively analyze the coupling characteristics of interface weakening characteristics and fabric evolution under the conditions of variable temperature and pressure, phase transition, and sand production, and obtain the interface weakening under multi-factor coupling mechanism, study the mathematical description of the mechanism, and establish a coupled-variable mathematical model of interface weakening characteristics and fabric evolution.
- (3)
- Explore the failure mode of production wells considering interface weakening.
- (i)
- Interaction analysis of deep-sea soil and hydrate production wells: establishing multiphase flow control equations in the wellbore and calculating the evolution law of the temperature field and pressure field in the well during the production process; through multi-process coupled numerical simulation, the deep-sea soil phase transition, heat transfer, seepage, and deformation processes under the disturbance of the temperature field and pressure field in the well are studied, and the stress evolution around the well is obtained.
- (ii)
- Exploration of the failure mode of wellbore integrity: based on the results of the above interaction analysis, combined with the response test simulation of the hydrate mining wellbore, the weakening process of the interface between the deep-sea soil and the mining well is studied; the failure modes of wellbore integrity, such as reservoir subsidence and collapse, sand production blockage, etc., are revealed under different mining techniques and working conditions.
- (4)
- A wellbore integrity analysis method for hydrate production considering the interface weakening effect is proposed.
- (i)
- Hydration prediction method of sand production in hydrate mining: summarize and analyze the sand production mechanism, sand production form, and plugging law under different hydrate production techniques and working conditions, as well as the main controlling factors of sand production in deep-sea hydrate production; sand production prediction model based on onshore oil and gas production, establish a deep-water hydrate mining sand production model with interface weakening effect under multi-process coupling conditions, predict whether sand production, sand production amount and sand production form during the mining process and verify the effectiveness of the method by comparing with the model test.
- (ii)
- Reservoir settlement prediction model and collapse evaluation method for hydrate extraction: summarize the main controlling factors and influence laws of reservoir settlement during hydrate extraction, and establish a deep-water hydrate extraction reservoir settlement prediction model. The interaction characteristics between the production well and the soil are analyzed, the mathematical description method of the relationship between the interface weakening and the failure mode is studied, and the evaluation criteria for reservoir collapse considering the interface weakening characteristics are proposed. Compared with the numerical simulation and model test results, the validity of the settlement prediction model and the collapse evaluation method is verified.
6. Conclusions
- (1)
- Revealing the phase transition characteristics and weakening coupling laws of the interface between deep-sea soil and hydrate extraction wells and establishing a mathematical model of interface weakening characteristics considering the phase transition conditions;
- (2)
- Revealing the multi-process interaction between deep-sea soil and hydrate mining wells, and exploring the failure mode of hydrate mining wells under mining disturbances;
- (3)
- Establishing and proposing a wellbore integrity analysis method considering the interface weakening effect and form natural gas hydrate sand production prediction method and reservoir subsidence prediction model and collapse evaluation method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, N.; Bai, R.; Zhou, S.; Luo, Y.; Zhao, J.; Zhang, Y.; Xue, J. China’s Deepwater Gas Hydrate Development Strategies under the Goal of Carbon Peak. Nat. Gas Ind. 2022, 42, 156–165. [Google Scholar]
- Li, N.; Wang, J.; Liu, R.; Tang, X. Multi-scenario Conception on the Development of Natural Gas Industry under the Goal of Carbon Neutrality. Nat. Gas Ind. 2021, 41, 183–192. [Google Scholar]
- Lee, S.Y.; Holder, G.D. Methane Hydrates Potential as a Future Energy Source. Fuel Process. Technol. 2001, 71, 181–186. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S. Current Perspectives on Gas Hydrate Resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Luo, M.; Wang, H.; Yang, S.; Chen, D. Research Advancement of Natural Gas Hydrate in South China Sea. Bull. Miner. Petrol. Geochem. 2013, 32, 56–79. [Google Scholar]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qiu, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C.; et al. Main Progress of the Second Gas Hydrate Trial Production in the South China Sea. Geol. China 2020, 47, 557–568. [Google Scholar]
- Sahu, C.; Kumar, R.; Sangwai, J.S. A comprehensive review on well completion operations and artificial lift techniques for methane gas production from natural gas hydrate reservoirs. Energy Fuels 2021, 35, 11740–11760. [Google Scholar] [CrossRef]
- Wei, H.; Yan, R.; Wei, C.; Wu, E.; Chen, P.; Tian, H. Summary of Researches for Phase-equilibrium of Natural Gas Hydrates in Bearing Sediments. Rock Soil Mech. 2011, 32, 9. [Google Scholar]
- Fitzgerald, G.C.; Castaldi, M.J.; Schicks, J.M. Methane Hydrate Formation and Thermal Based Dissociation Behavior in Silica Glass Bead Porous Media. Ind. Eng. Chem. Res. 2014, 53, 6840–6854. [Google Scholar] [CrossRef]
- Khlebnikov, V.N.; Antonov, S.V.; Mishin, A.S.; Bakulin, D.A.; Khamidullina, I.V.; Liang, M.; Vinokurov, V.A.; Gushchin, P.A. A New Method for the Replacement of CH4 with CO2 in Natural Gas Hydrate Production. Nat. Gas Ind. B 2016, 3, 445–451. [Google Scholar] [CrossRef]
- Konno, Y.; Jin, Y.; Shinjou, K.; Nagao, J. Experimental Evaluation of the Gas Recovery Factor of Methane Hydrate in Sandy Sediment. RSC Adv. 2014, 4, 51666–51675. [Google Scholar] [CrossRef]
- Ota, M.; Morohashi, K.; Abe, Y.; Watanabe, M.; Smith, R.L., Jr.; Inomata, H. Replacement of CH4 in the Hydrate by Use of Liquid CO2. Energy Convers. Manag. 2005, 46, 1680–1691. [Google Scholar] [CrossRef]
- Pooladi-Darvish, M.; Hong, H. Effect of Conductive and Convective Heat Flow on Gas Production from Natural Hydrates by Depressurization; Springer: New York, NY, USA, 2004. [Google Scholar]
- Uchida, S.; Klar, A.; Yamamoto, K. Sand Production Model in Gas Hydrate-bearing Sediments. Int. J. Rock Mech. Min. Sci. 2016, 86, 303–316. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Y.; Cheng, J.; Han, Q.; Hu, Z.; Wang, L. Geomechanics involved in gas hydrate recovery. Chin. J. Chem. Eng. 2019, 27, 2099–2106. [Google Scholar] [CrossRef]
- Zhang, J. New Advances in Basic Theories of Sand Dynamics. Chin. J. Geotech. Eng. 2012, 34, 50. [Google Scholar]
- Li, G. The Six Disadvantages of the Rock Altar. Miner. Explor. 2006, 3, 20–22. [Google Scholar]
- Feng, D.; Zhang, J. Influence of Initial Static Shear Stress on Cycle Mechanical Behavior of Interface between Structure and Gravelly Soil. Rock Soil Mech. 2012, 33, 7. [Google Scholar]
- Feng, D.; Zhang, J. Monotonic and Cyclic Behaviors of Coarse-grained Soil-structure Interface Using Large-scale Simple Shear Device. Chin. J. Geotech. Eng. 2012, 34, 8. [Google Scholar]
- Potyondy, J.G. Skin Friction between Various Soils and Construction Materials. Géotechnique 1961, 11, 339–353. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H. Frictional Resistance at Yield between Dry Sand and Mild Steel-ScienceDirect. Soils Found. 1986, 26, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Desai, C.; Drumm, E.; Zaman, M. Cyclic Testing and Modeling of Interfaces. J. Geotech. Eng. 1985, 111, 793–815. [Google Scholar] [CrossRef]
- Fakharian, K.; Evgin, E. Cyclic Simple-shear Behavior of Sand-steel Interfaces under Constant Normal Stiffness Condition. J. Geotech. Geoenviron. Eng. 1997, 123, 1096–1105. [Google Scholar] [CrossRef]
- Gao, J.; Yu, H.; Zhao, W. Characteristics Study of Interface Between Soil and Concrete by Using Large Size Since Shear Apparatus and Numerical Analysis. China Civ. Eng. J. 2000, 33, 5. [Google Scholar]
- Wang, J.; Zhou, Y.; Tang, X.; Huang, S. Development and Application of Large Size Direct Shear Test Apparatus with Visual and Digital Collection Functions for Reinforced soil. Rock Soil Mech. 2017, 38, 1533–1540. [Google Scholar]
- Zhang, G.; Zhang, J. Development and Application of Cyclic Shear Apparatus for Soil-structure Interface. Chin. J. Geotech. Eng. 2003, 25, 149–153. [Google Scholar]
- Xu, H.; Dai, S. Research Progress of Pile-soil Interface Shear Test Apparatus Under Temperature Effect and Manufacture of New Apparatus. Bull. Sci. Technol. 2019, 35, 139–142. [Google Scholar]
- AbdelSalam, S.S.; Suleiman, M.T.; Sritharan, S. Enhanced Load-Transfer Analysis for Friction Piles Using a Modified Borehole Shear Test. Geotech. Test. J. 2012, 35, 879–889. [Google Scholar] [CrossRef]
- Vogelsang, J.; Huber, G.; Triantafyllidis, T. A Large-Scale Soil-Structure Interface Testing Device. Geotech. Test. J. 2013, 36, 20120213. [Google Scholar] [CrossRef]
- Eid, H.T. Undrained Interface Shear Strength of Fine-Grained Soils for Near-Shore Marine Pipelines. Geotech. Test. J. 2019, 43, 20180188. [Google Scholar] [CrossRef]
- Liang, Y.; Xia, R.; Liu, Z.; Ma, C.; Zhang, H.; Sun, Z. Experimental Investigation into Cyclic Shear Behaviors in the Interface Between Steel and Crushed Mudstone Particles. Transp. Res. Rec. J. Transp. Res. Board 2021, 2676, 499–509. [Google Scholar] [CrossRef]
- Xu, C.; Liao, X.; Ye, G.; Li, Z. Researches on Frictional Properties of HDPE Geomembrane Using Tilt Table Device. Chin. J. Geotech. Eng. 2006, 28, 989–993. [Google Scholar]
- Cho, K.; Cho, J.R.; Chin, W.J.; Kim, B.S. Bond-slip Model for Coarse Sand Coated Interface between FRP and Concrete from Optimization Technique. Comput. Struct. 2006, 84, 439–449. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H. Influential Factors of Friction between Steel and Dry Sands. Soils Found. 1986, 26, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Tsubakihara, Y.; Kishida, H.; Nishiyama, T. Friction between Cohesive Soils and Steel. J. Jpn. Soc. Soil Mech. Found. Eng. 1993, 33, 145–156. [Google Scholar] [CrossRef]
- Yoshimi, Y.; Kishida, T. A Ring Torsion Apparatus for Evaluating Friction Between Soil and Metal Surfaces. Geotechnol. Test. J. 1981, 4, 8. [Google Scholar] [CrossRef]
- Yin, Z.; Xu, G. Numerical Simulation of the Deformation in the Interface between Soil and Structural Material. Chin. J. Geotechnol. Eng. 1994, 16, 14–22. [Google Scholar]
- Clough, G.W.; Duncan, J.M. Finite Element Analyses of Retaining Wall Behavior. ASCE Soil Mech. Found. Div. J. 1971, 97, 1657–1673. [Google Scholar] [CrossRef]
- Bathe, K.-J.; Chaudhary, A. A Solution Method for Planar and Axisymmetric Contact Problems. Int. J. Numer. Methods Eng. 1985, 21, 65–88. [Google Scholar] [CrossRef] [Green Version]
- Desai, C. Some Aspects of Constitutive Models for Geologic Media. In Proceedings of the Third International Conference on Numerical Methods in Geomechanics, Aachen, Germany, 2–6 April 1979. [Google Scholar]
- Zeghal, M. In Soil Structure Interaction Analysis: Modelling the Interface, Engineering in Medicine & Biology. In Proceedings of the Conference & the Fall Meeting of the Biomedical Engineering Society Embs/Bmes, Second Joint, Houston, TX, USA, 23–26 October 2002. [Google Scholar]
- Tsubakihara, Y.; Kishida, H. Frictional Behaviour between Normally Consolidated Clay and Steel by Two Direct Shear Type Apparatuses. J. Jpn. Soc. Soil Mech. Found. Eng. 1993, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Zhang, J. Monotonic and Cyclic Constitutive Law of Interface Between Structure and Coarse Grained Soil. Chin. J. Geotech. Eng. 2005, 27, 515–520. [Google Scholar]
- Hou, W. Research on Monotonic and Cyclic Behavior and Constitutive Model of Three-Dimensional Soil-Structure Interface; Tsinghua University: Beijing, China, 2008. [Google Scholar]
- Peterson, M.; Kulhawy, F.; Nucci, L.; Wasil, B. Stress-Deformation Behavior of Soil-Concrete Interfaces; Contract Report B-49; Niagara Mohawk Power Corporation: Syracuse, NY, USA, 1976. [Google Scholar]
- Boulon, M. Basic Features of Soil Structure Interface Behaviour. Comput. Geotech. 1989, 7, 115–131. [Google Scholar] [CrossRef]
- Hryciw, R.D.; Irsyam, M. Behavior of Sand Particles around Rigid Ribbed Inclusions during Shear. Soils Found. 2008, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Fakharian, K.; Evgin, E. An Automated Apparatus for Three-Dimensional Monotonic and Cyclic Testing of Interfaces. Geotechnol. Test. J. 1996, 19, 22–31. [Google Scholar]
- Gomez, J.E.; Filz, G.M.; Ebeling, R.M. Development of an Improved Numerical Model for Concrete-to-Soil Interfaces in Soil-Structure Interaction Analyses; Technical Report ITL-99-1; Defense Technical Information Center: Fairfax, VA, USA, 1999. [Google Scholar]
- Zhang, G.; Zhang, J. Reversible and irreversible dilatancy of soil-structure interface. Rock Soil Mech. 2005, 5, 699–704. [Google Scholar]
- Wang, T.-L.; Wang, H.-H.; Hu, T.-F.; Song, H.-F. Experimental Study on the Mechanical Properties of Soil-structure Interface under Frozen Conditions Using an Improved Roughness Algorithm. Cold Reg. Sci. Technol. 2019, 158, 62–68. [Google Scholar] [CrossRef]
- Saberi, M.; Annan, C.-D.; Konrad, J.-M. On the Mechanics and Modeling of Interfaces between Granular Soils and Structural Materials. Arch. Civ. Mech. Eng. 2018, 18, 1562–1579. [Google Scholar] [CrossRef]
- Kong, L.; Xiong, C.; Guo, A.; Yang, A. Effects of Shear Rate on Strength Properties and Pile-soil Interface of Marine Soft Clay. Chin. J. Geotech. Eng. 2017, 39 (Suppl. S2), 13–16. [Google Scholar]
- Yan, P.; Lin, P.; Jia, Z.; Lang, R. Large-scale Direct Shear Tests on Shear Strength of Interface Between Marine Soil and Steel Piles. Chin. J. Geotech. Eng. 2018, 40, 495–501. [Google Scholar]
- Guo, J.; Kou, H.; Xu, H.; Lei, S. Experimental Study on Shear Behaviors of Interface Between Pile and Marine Clay. J. Yangtze River Sci. Res. Inst. 2019, 36, 104–108, 117. [Google Scholar]
- Li, Y.; Guo, Z.; Wang, L.; Li, Y.; Liu, Z. Shear Resistance of MICP Cementing Material at the Interface between Calcareous Sand and Steel. Mater. Lett. 2020, 274, 128009. [Google Scholar] [CrossRef]
- Andersen, K.H.; Pool, J.H.; Brown, S.F.; Rosebrand, W.F. Cyclic and Static Laboratory Tests on Drammen clay. J. Geotech. Eng. Div. 1980, 106, 499–529. [Google Scholar] [CrossRef]
- Bea, R.G. Pile capacity for axial cyclic loading. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1992, 29, 34–50. [Google Scholar]
- Stutz, H.H.; Wuttke, F. Hypoplasticmodeling of Soil-structure Interfaces in Offshore Applications. J. Zhejiang Univ. Sci. A 2018, 19, 624–637. [Google Scholar] [CrossRef]
- Cui, L.; Jeng, D.S. Seabed liquefaction around breakwater heads at a river mouth: An integrated 3D model. Ocean. Eng. 2021, 242, 110036. [Google Scholar] [CrossRef]
- Lu, T.; Bao, F. A Coupled Constitutive Model for Interface Thin layer Element. J. Hydraul. Eng. 2000, 2, 5. [Google Scholar]
- Gens, A.; Carol, I.; Alonso, E.E. A constitutive model for rock joints formulation and numerical implementation. Comput. Geotech. 1990, 9, 3–20. [Google Scholar] [CrossRef]
- Gens, A.; Carol, I.; Alonso, E.E. An interface element formulation for the analysis of soil-reinforcement interaction. Comput. Geotech. 1989, 7, 133–151. [Google Scholar] [CrossRef]
- Luan, M.; Wu, Y. A Nonlinear Elasto-perfectly Plastic Model of Interface Element for Soil-structure Interaction and Its Applications. Rock Soil Mech. 2004, 25, 7. [Google Scholar]
- Vatsala, A. Discussion: Dilatancy for cohesionless soils. Géotechnique 2001, 51, 729–730. [Google Scholar] [CrossRef]
- Sheng, D.; Sloan, S.W.; Gens, A.; Smith, D.W. Finite element formulation and algorithms for unsaturated soils. Part I: Theory. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 745–765. [Google Scholar] [CrossRef]
- Airey, D.W.; Ghorbani, J. Analysis of unsaturated soil columns with application to bulk cargo liquefaction in ships. Comput. Geotech. 2021, 140, 104402. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Manzari, M.T.; Papadimitriou, A.G. SANICLAY: Simple anisotropic clay plasticity model. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1231–1257. [Google Scholar] [CrossRef]
- Ghorbani, J.; Nazem, M.; Kodikara, J.; Wriggers, P. Finite element solution for static and dynamic interactions of cylindrical rigid objects and unsaturated granular soils. Comput. Methods Appl. Mech. Eng. 2021, 384, 113974. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y. Constitutive Model of Calcareous Sand Structure Interface. Chin. Q. Mech. 2006, 27, 5. [Google Scholar]
- Luo, J.; Yao, Y. Dilatancy Behavior of Soil-structure Interfaces and Its Simulation. Ind. Constr. 2006, 36, 4. [Google Scholar]
- Desai, C.S.; Ma, Y. Modeling of Joints and Interfaces Using the Disturbed State Concept. Int. J. Numer. Anal. Methods Geomech. 1992, 16, 623–653. [Google Scholar] [CrossRef]
- Desai, C.S.; Pradhan, S.K.; Cohen, D. Cyclic Testing and Constitutive Modeling of Saturated Sand–concrete Interfaces Using the Disturbed State Concept. Int. J. Geomech. 2005, 5, 286–294. [Google Scholar] [CrossRef]
- Hu, L.; Pu, J. Application the Damage Model to Soil Interface in Finite Element. China Civ. Eng. J. 2002, 35, 5. [Google Scholar]
- Pradhan, S.K.; Desai, C.S. DSC Model for Soil and Interface including Liquefaction and Prediction of Centrifuge Test. J. Geotech. Geoenviron. Eng. 2006, 132, 214–222. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, J. Unified Modeling of Soil-structure Interface and Its Test Confirmation. Chin. J. Geotech. Eng. 2005, 27, 1175–1179. [Google Scholar]
- Zhang, G.; Zhang, J.M. Unified Modeling of Monotonic and Cyclic Behavior of Interface Between Structure and Gravelly Soil. Soils Found. 2011, 48, 231–245. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G. A Study on the Static and Dynamic Characteristics and Elastic-Plastic Damage Theory of the Interface between Coarse-Grained Soil and Structure; Tsinghua University: Beijing, China, 2002. [Google Scholar]
- Zhang, G.; Zhang, J.-M. Constitutive Rules of Cyclic Behavior of Interface Between Structure and Gravelly Soil. Mech. Mater. 2009, 41, 48–59. [Google Scholar] [CrossRef]
- Sun, J.; Shi, G. Bounding Surface Model for Soil-structure Interface Under Cyclic Loading. Rock Soil Mech. 2007, 28, 311–314. [Google Scholar]
- Kong, X.; Liu, J.; Zou, D.; Song, Y.; Chen, K.; Qu, Y.; Gong, J. State-of-the-art: Computational Model for Soil-interface-structure System. Chin. J. Geotech. Eng. 2021, 43, 397–405. [Google Scholar]
- Uddin, M.; Wright, F.; Coombe, D.A. Numerical Study of Gas Evolution and Transport Behaviours in Natural Gas-Hydrate Reservoirs. J. Can. Pet. Technol. 2010, 50, 70–88. [Google Scholar] [CrossRef]
- Hao, E.; Wei, H.; Yan, R.; Wei, C. Constitutive Model for Gas Hydrate-bearing Sediments Considering Gamage. Chin. J. Rock Mech. Eng. 2012, 31, 6. [Google Scholar]
- Liu, X.; Flemings, P.B. Dynamic Multiphase Flow Model of Hydrate Formation in Marine Sediments. J. Geophys. Res. Solid Earth 2007, 112, B3. [Google Scholar] [CrossRef] [Green Version]
- Minagawa, H.; Nishikawa, Y.; Ikeda, I.; Miyazaki, K.; Takahara, N.; Sakamoto, Y.; Komai, T.; Narita, H. Characterization of Sand Sediment by Pore Size Distribution and Permeability Using Proton Nuclear Magnetic Resonance Measurement. J. Geophys. Res. Solid Earth 2008, 113, B07210. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Dai, S.; Terzariol, M.; Jang, J.; Waite, W.F.; Winters, W.J.; Nagao, J.; Yoneda, J.; Konno, Y.; Fujii, T. Hydro-bio-geomechanical Properties of Hydrate-bearing Sediments from Nankai Trough. Mar. Pet. Geol. 2015, 66, 434–450. [Google Scholar] [CrossRef] [Green Version]
- Konno, Y.; Yoneda, J.; Egawa, K.; Ito, T.; Jin, Y.; Kida, M.; Suzuki, K.; Fujii, T.; Nagao, J. Permeability of Sediment Cores from Methane Hydrate Deposit in the Eastern Nankai Trough. Mar. Pet. Geol. 2015, 66, 487–495. [Google Scholar] [CrossRef]
- Delli, M.L.; Grozic, J. Experimental Determination of Permeability of Porous Media in the Presence of Gas Hydrates. J. Pet. Sci. Eng. 2014, 120, 1–9. [Google Scholar] [CrossRef]
- Goel, N.; Shah, S.; Wiggins, M. Analytical Modeling of Gas Recovery from in Situ Hydrates Dissociation. J. Pet. Sci. Eng. 2001, 29, 115–127. [Google Scholar] [CrossRef]
- Moridis, G.J.; Sloan, E.D. Gas Production Potential of Disperse Low-saturation Hydrate Accumulations in Oceanic Sediments. Energy Convers. Manag. 2007, 48, 1834–1849. [Google Scholar] [CrossRef] [Green Version]
- Kurihara, M.; Ouchi, H.; Inoue, T.; Yonezawa, T.; Masuda, Y.; Dallimore, S.R.; Collett, T.S. Analysis of the JAPEX/JNOC/GSC et al. Mallik 5L-38 Gas Hydrate Thermal-Production Test through Numerical Simulation; Scientific Results from the Mallik 2002 Gas Hydrate Production Well Program; Geological Survey of Canada: Vancouver, BC, Canada, 2005; p. 139. [Google Scholar]
- Liu, Z.; Yu, X. Thermo-Hydro-Mechanical-Chemical Simulation of Methane Hydrate Dissociation in Porous Media. Geotech. Geol. Eng. 2013, 31, 1681–1691. [Google Scholar] [CrossRef]
- Kimoto, S.; Oka, F.; Fushita, T.; Fujiwaki, M. A Chemo-thermo-mechanically Coupled Numerical Simulation of the Subsurface Ground Deformations Due to Methane Hydrate Dissociation. Comput. Geotech. 2007, 34, 216–228. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G. Coupled Hydrological, Thermal and Geomechanical Analysis of Wellbore Stability in Hydrate-Bearing Sediments. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008. [Google Scholar]
- Soga, K.; Ng, M.; Klar, A. Coupled deformation–flow Analysis for Methane Hydrate Extraction. Géotechnique 2010, 60, 765–776. [Google Scholar]
- Kakumoto, M.; Tenma, N.; Sakamoto, Y.; Miyazakai, K.; Mori, J. Development of the Geo-Mechanical Simulation Code COTHMA. Paper presented at the Ninth ISOPE Ocean Mining Symposium, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Gao, Y.; Sun, B.; Zhao, X.; Wang, Z.; Yin, Z.; Wang, J. Multiphase Flow in Wellbores and Variation Laws of the Bottom Hole Pressure in Gas Hydrate Drilling. Acta Pet. Sin. 2012, 33, 6. [Google Scholar]
- Qiu, K.; Yamamoto, K.; Birchwood, R.; Chen, Y. Well-integrity Evaluation for Methane-hydrate Production in the Deepwater Nankai Trough. SPE Drill. Complet. 2015, 30, 52–67. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, Z.; Zhao, Y.; Guo, Y.; Zhang, J.; Sun, B. Flow Assurance during Gas Hydrate Production: Hydrate Regeneration Behavior and Blockage Risk Analysis in Wellbore. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirate, 13–16 November 2017. [Google Scholar]
- Moridis, G.J.; Collett, T.S.; Pooladi-Darvish, M.; Hancock, S.H.; Santamarina, J.C.; Boswell, R.; Kneafsey, T.J.; Rutqvist, J.; Reagan, M.T.; Sloan, E.D. Challenges, Uncertainties and Issues Facing Gas Production from Hydrate Deposits in Geologic Systems. Soc. Pet. Eng. 2010, 14, 76–112. [Google Scholar]
- Li, L.; Cheng, Y.; Mei, W.; Li, Q.; Gao, L. Finite Element Simulation of Temperature Impact on Wellbore Stability of Gas-hydrate-bearing Sediments. Nat. Gas Ind. 2012, 32, 74–78. [Google Scholar]
- Cao, Y.; Deng, J. Wellbore Stability Research of Heterogeneous Formation. J. Appl. Sci. 2014, 14, 33–39. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Jin, Y.; Lu, Y.; Chen, M.; Hou, B.; Chen, W.; Wen, X.; Yu, X. A Wellbore Stability Model for a Deviated Well in a Transversely Isotropic Formation Considering Poroelastic Effects. Rock Mech. Rock Eng. 2016, 49, 3671–3686. [Google Scholar] [CrossRef]
- Tan, C.P.; Freij-Ayoub, R.; Clennell, M.B.; Tohidi, B.; Yang, J. Managing Wellbore Instability Risk in Gas Hydrate-Bearing Sediments. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 5–7 April 2007. [Google Scholar]
- Wenke, C.; Jingen, D.; Baohua, Y.; Wei, L.; Qiang, T. Offshore wellbore Stability Analysis Based on Fully Coupled Poro-thermo-elastic Theory. J. Geophys. Eng. 2017, 14, 380–396. [Google Scholar]
- Freij-Ayoub, R.; Tan, C.; Clennell, B.; Tohidi, B.; Yang, J. A Wellbore Stability Model for Hydrate Bearing Sediments. J. Pet. Sci. Eng. 2007, 57, 209–220. [Google Scholar] [CrossRef]
- Yin, Y.; Cai, Y.; Chen, C.; Liu, J. Theoretical Solution of Casing Loading in Non-uniform Ground Stress Field. Acta Pet. Sin. 2006, 27, 6. [Google Scholar]
- Wan, X. Research on Cement Hull Mechanics of Oil and Gas Well Cementing; Southwest Petroleum University: Chengdu, China, 2006. [Google Scholar]
- Li, J.; Lin, C.; Yang, S.; Zhi, Y.; Chen, S. Theoretical solution of thermal stress for casing-cement-formation coupling system. J. China Univ. Pet. 2009, 33, 63–69. [Google Scholar]
- Chu, W.; Shen, J.; Yang, Y.; Li, Y.; Gao, D. Calculation of Micro-annulus Size in Casing-cement Sheath-formation System under Continuous Internal Casing Pressure Change. Pet. Explor. Dev. 2015, 42, 379–385. [Google Scholar] [CrossRef]
- Salehabadi, M.; Jin, M.; Yang, J.; Haghighi, H.; Ahmed, R.; Tohidi, B. Finite Element Modeling of Casing in Gas-Hydrate-Bearing Sediments. SPE Drill. Complet. 2009, 24, 545–552. [Google Scholar] [CrossRef]
- Kim, J.; Moridis, G.J.J.; Yang, D.; Rutqvist, J. Numerical Studies on Two-Way Coupled Fluid Flow and Geomechanics in Hydrate Deposits. SPE J. 2012, 17, 485–501. [Google Scholar] [CrossRef] [Green Version]
- Fereidounpour, A.; Vatani, A. An Investigation of Interaction of Drilling Fluids with Gas Hydrates in Drilling Hydrate Bearing Sediments. J. Nat. Gas Sci. Eng. 2014, 20, 422–427. [Google Scholar] [CrossRef]
- Golmohammadi, S.M.; Nakhaee, A. A Cylindrical Model for Hydrate Dissociation near Wellbore during Drilling Operations. J. Nat. Gas Sci. Eng. 2015, 27, 1641–1648. [Google Scholar] [CrossRef]
- Sasaki, T.; Soga, K.; Elshafie, M.Z.E.B. Simulation of Wellbore Construction in Offshore Unconsolidated Methane Hydrate-bearing formation. J. Nat. Gas Sci. Eng. 2018, 60, 312–326. [Google Scholar] [CrossRef] [Green Version]
- Shengyu, J.; Guoming, C.; Xiangkun, M.; Dongdong, Y.; Yuan, Z.; Kang, L.; Yuanjiang, C. Integrity Control Analysis of Natural Gas Hydrate Production Wellbore Using System Method and Game Theory. J. Loss Prev. Process Ind. 2021, 75, 104696. [Google Scholar]
- Chen, Z.; You, C.; Lv, T.; Li, X.; Zhang, Y.; Xu, L. Numerical simulation of the depressurization production of natural gas hydrate reservoirs by vertical well patterns in the northern South China Sea. Natural Gas Ind. 2020, 8, 177–185. [Google Scholar]
- Chang, Y.; Huang, S.; Wang, K.; Sun, B.; Li, H.; Sun, H.; Chen, G. Study on 3D Nonlinear Coupling Wellbore-soil Model of Natural Gas Hydrate Production Test. J. Cent. South Univ. Sci. Technol. 2022, 53, 942–951. [Google Scholar]
- Sun, J.; Ning, F.; Lei, H.; Gai, X.; Sánchez, M.; Lu, J.; Li, Y.; Liu, L.; Liu, C.; Wu, N.; et al. Wellbore Stability Analysis during Drilling through Marine Gas Hydrate-bearing Sediments in Shenhu area: A case study. J. Pet. Sci. Eng. 2018, 170, 345–367. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S. Advances in Study of Mechanical Properties of Gas Hydrate-bearing sediments. Open Ocean. Eng. J. 2013, 6, 26–40. [Google Scholar]
- Lu, J.; Li, D.; Liang, D.; Shi, L.; Zhou, X.; He, Y. An innovative experimental apparatus for the analysis of sand production during natural gas hydrate exploitation. Rev. Sci. Instrum. 2021, 92, 105110. [Google Scholar] [CrossRef]
- Hiroyuki, O.; Jiro, N.; Kiyofumi, S.; Hideo, N. Experimental Analysis of Sand Production from Methane Hydrate Bearing Sediments Applying Depressurization Method. Shigen Sozai 2011, 126, 497–502. [Google Scholar]
- Jung, J.W.; Jang, J.; Santamarina, J.C.; Tsouris, C.; Phelps, T.J.; Rawn, C.J. Gas Production from Hydrate-Bearing Sediments: The Role of Fine Particles. Energy Fuels 2012, 26, 480–487. [Google Scholar] [CrossRef]
- Murphy, A.; Soga, K.; Yamamoto, K. A Laboratory Investigation of Sand Production Simulating the 2013 Daini-Atsumi Knoll Gas Hydrate Production Trial Using a High Pressure Plane Strain Testing Apparatus. In Proceedings of the 9th International Conferences on Gas Hydrate, Denver, CO, USA, 25 June 2017. [Google Scholar]
- Uchida, S.; Klar, A.; Charas, Z.; Yamamoto, K. Thermo-hydro-mechanical Sand Production Model in Hydrate-bearing Sediments. In Proceedings of the EAGE International Workshop on Geomechanics and Energy—The Ground as Energy Source and Storage, Lausanne, Switzerland, 26–28 November 2013. [Google Scholar]
- Uchida, S.; Klar, A.; Yamamoto, K. Sand Production Modeling of the 2013 Nankai Offshore Gas Production Test. In Proceedings of the 1st International Conference on Energy Geotechnics, Kiel, Germany, 29 August–1 September 2016. [Google Scholar]
- Xu, E.; Soga, K.; Zhou, M.; Uchida, S.; Yamamoto, K. Numerical Analysis of Wellbore Behaviour during Methane Gas Recovery from Hydrate Bearing Sediments. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar]
- Zhou, M.; Xu, E.; Soga, K.; Uchida, S.; Yamamoto, K. Numerical Study on Eastern Nankai Trough gas Hydrate Production Test. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar]
- Ning, F.; Sun, J.; Liu, Z.; Liang, J. Prediction of Sand Production in Gas Recovery from the Shenhu Hydrate Reservoir by Depressurization. In Proceedings of the 9th International Conference on Gas Hydrate, Denver, CO, USA, 25–30 June 2017. [Google Scholar]
- Yu, T.; Liu, Y.; Song, Y. Experimental Study on Sand Production Characteristics in Natural Gas Hydrate Deposits. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Yan, C.; Ren, X.; Cheng, Y.; Song, B.; Li, Y.; Tian, W. Geomechanical Issues in the Exploitation of Natural Gas Hydrate. Gondwana Res. 2020, 81, 403–422. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, T.; Yuan, Y.; Xia, Y.; Xin, X. Numerical Investigation of the Natural Gas Hydrate Production Tests in the Nankai Trough by incorporating sand migration. Appl. Energy 2020, 275, 115384. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, L.; Lv, X.; Xue, K.; Zhao, J.; Liu, Y.; Yang, S. Fine Sand Migration in Hydrate-bearing Sediments and Median Grain Size Ratio Optimization of Gravel Pack. J. Nat. Gas Sci. Eng. 2021, 88, 103809. [Google Scholar] [CrossRef]
- Hao, Y.; Liang, J.; Kong, C.; Fan, M.; Xu, H.; Yang, F.; Yang, S. Study on the Influence of Sand Production on Seepage Capacity in Natural Gas Hydrate Reservoirs. Geofluids 2021, 2021, 6647647. [Google Scholar] [CrossRef]
- Ding, J.; Cheng, Y.; Yan, C.; Lu, C.; Li, Y.; Xue, M. Numerical Simulation on Sand Production in the Exploitation Process of Gas Hydrates Based on Skeleton Failure of Reservoirs. J. Nat. Gas Sci. Eng. 2021, 94, 104052. [Google Scholar] [CrossRef]
- Jin, Y.; Li, Y.; Wu, N.; Yang, D. Characterization of Sand Production for Clayey-Silt Sediments Conditioned to Openhole Gravel-Packing: Experimental Observations. SPE J. 2021, 26, 3591–3608. [Google Scholar] [CrossRef]
- Song, J.; Fu, J.; Xiong, Y.; Pang, W.; He, Y.; Liu, L.; Huang, T.; Liu, C.; Li, Y.; Li, J. State-of-the-art Brief Review on Sanding Problem of Offshore Natural Gas Hydrates Sediments. Energy Sci. Eng. 2021, 10, 253–273. [Google Scholar] [CrossRef]
- Xiangyu, F.; Dianheng, Y.; Fulong, N.; Linjie, W.; Zhichao, L.; Yanjiang, Y.; Wenwei, X.; Hongfeng, L.; Yanlong, L.; Meng, X. Experimental Study on Sand Production and Reservoir Response of Clayey Silt Hydrate during Depressurization. Petroleum 2021, in press. [CrossRef]
- Zhang, Y.; Wang, W.; Zhang, P.; Li, G.; Tian, S.; Lu, J.; Zhang, B. A Solution to Sand Production from Natural Gas Hydrate Deposits with Radial Wells: Combined Gravel Packing and Sand Screen. J. Mar. Sci. Eng. 2022, 10, 71. [Google Scholar] [CrossRef]
- Chuanliang, Y.; Yang, L.; Yuanfang, C.; Jia, W.; Wanqing, T.; Shuxia, L.; Zhiyuan, W. Multifield Coupling Mechanism in Formations around a Wellbore during the Exploitation of Methane Hydrate with CO2 Replacement. Energy 2022, 245, 123283. [Google Scholar]
- Ya-Ting, X.; Yi, W.; Xiao-Sen, L.; Xiao-Yan, L.; Gang, L.; Fu-Cheng, D. Experimental Research on the Influence of Particle Size on Sand Production during Gas Hydrate Dissociation via Depressurization. Energy Fuels 2022, 36, 10541–10551. [Google Scholar]
- Zhang, P.; Zhou, Y.; Liu, B.; Deng, W. Multiphase Flow Model Coupled with Fine Particle Migration for Applications in Offshore Gas Hydrate Extraction. J. Nat. Gas Sci. Eng. 2022, 102, 104586. [Google Scholar] [CrossRef]
- Haiyan, Z.; Xuanhe, T.; Fengshou, Z.; David, M.J. Mechanical Behavior of Methane–Hydrate–Bearing Sand with Nonlinear Constitutive Model. Arab. J. Sci. Eng. 2022, 47, 12141–12167. [Google Scholar]
- Jiping, D.; Yuanfang, C.; Chuanliang, Y. Research on Sand Control Effect and Micro-plugging Mechanism of Sand Control Medium in the Development of Natural Gas Hydrate Reservoir. J. Pet. Sci. Eng. 2022, 215, 110703. [Google Scholar]
- Xiao-Yan, L.; Heng-Qi, H.; Yi, W.; Xiao-Sen, L. Experimental Study of Gas-liquid-sand Production Behaviors during Gas Hydrates Dissociation with Sand Control Screen. Energy 2022, 254, 124414. [Google Scholar]
- Bin, G.; Ruiqi, Z.; Tianwei, S.; Yujing, J.; Naser, G.; Yanlong, L.; Shanilka, G.F.; Madusanka, N.J. Coupling Model of Submarine Deformation Response Prediction during Methane Hydrate Exploitation. Energy Fuels 2022, 36, 6785–6809. [Google Scholar]
- Fang, X.; Ning, F.; Wang, L.; Liu, Z.; Lu, H.; Yu, Y.; Li, Y.; Sun, J.; Shi, H.; Zhao, Y.; et al. Dynamic Coupling Responses and Sand Production Behavior of Gas Hydrate-bearing Sediments during Depressurization: An Experimental Study. J. Pet. Sci. Eng. 2021, 201, 108506. [Google Scholar] [CrossRef]
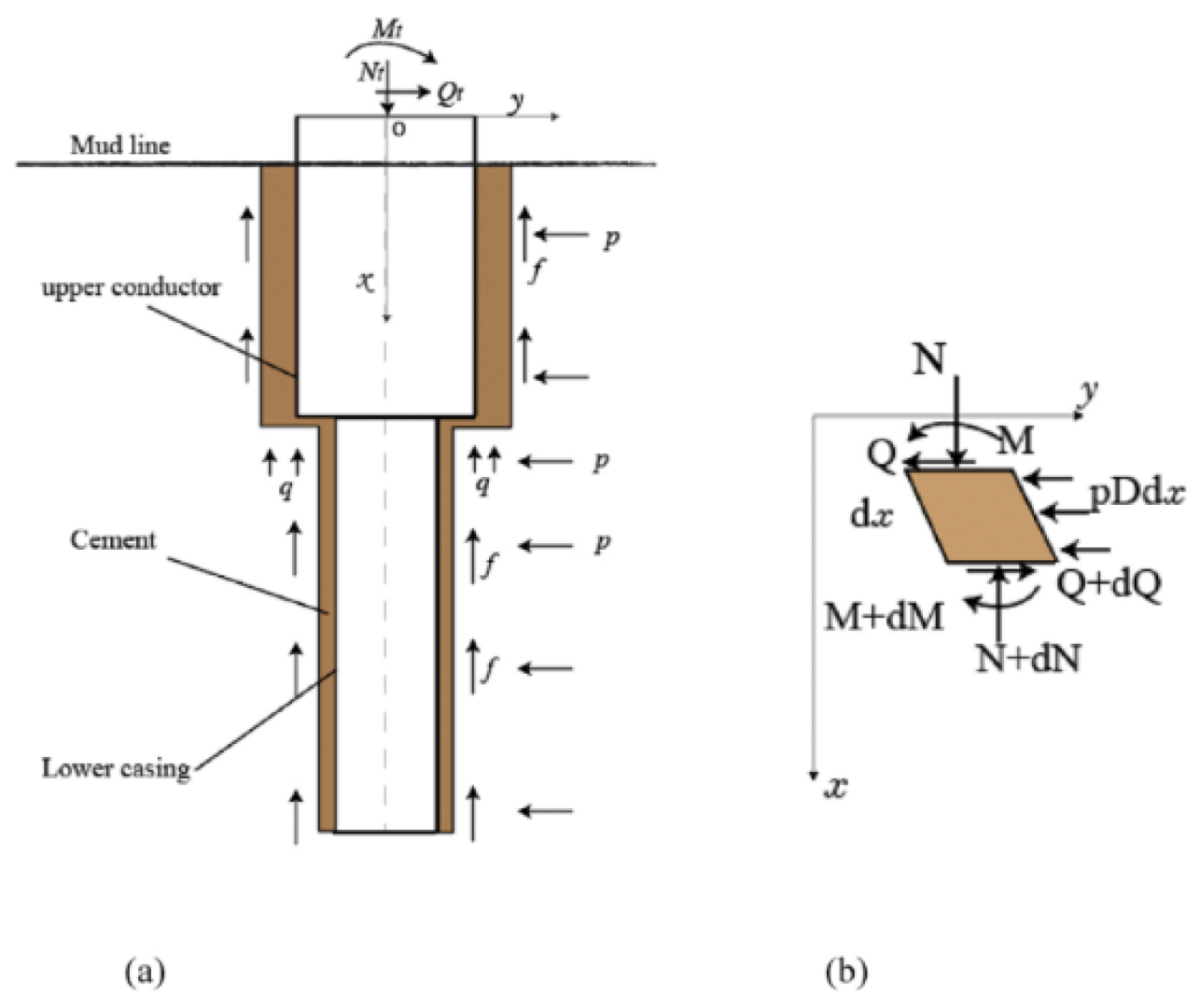
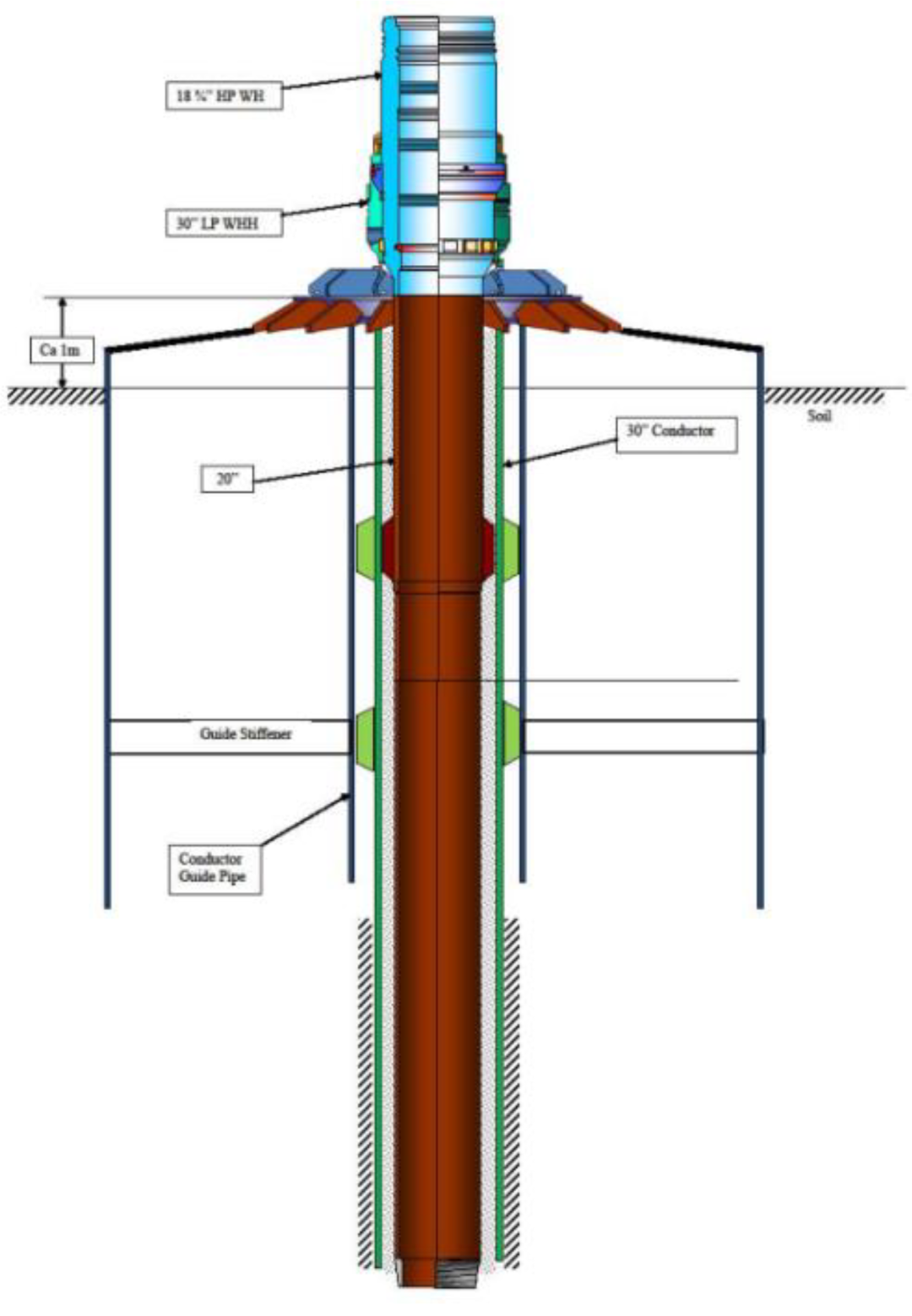
- Wang, Y.; Gao, D.; Fang, J. Finite Element Analysis of Deepwater Conductor Bearing Capacity to Analyze the Subsea Wellhead Stability with Consideration of Contact Interface Models between Pile and Soil. J. Pet. Sci. Eng. 2014, 126, 48–54. [Google Scholar] [CrossRef]
- Li, J.; Chang, Y.; Xiu, Z.; Liu, H.; Xue, A.; Chen, G.; Xu, L.; Sheng, L. A Local Stress-strain Approach for Fatigue Damage Prediction of Subsea Wellhead System Based on Semi-decoupled Model. Appl. Ocean. Res. 2020, 102, 102306. [Google Scholar] [CrossRef]
- Yan, W.; Chen, Z.-J.; Deng, J.-G.; Zhu, H.-Y.; Deng, F.-C.; Liu, Z.-L. Numerical Method for Subsea Wellhead Stability Analysis in Deepwater Drilling. Ocean. Eng. 2015, 98, 50–56. [Google Scholar] [CrossRef]
- Adamiec-Wójcik, I.; Wojciech, S. Application of The Finite Segment Method to Stabilisation of the Force in A Riser Connection with A Wellhead. Nonlinear Dyn. 2018, 93, 1853–1874. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Gao, D.; Yang, J.; Hu, Z.; Abimbola, F. Subsea Wellhead Stability Study of Composite Casing for Deepwater Drilling. Ocean. Eng. 2020, 214, 107780. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, Z.; Jin, Y.; Liu, Y.; Sun, Y.; Zhang, B.; Sheng, Y. Risk Assessment Method of Subsea Wellhead Instability in Consideration of Uncertain Factors in Deepwater Drilling. Arab. J. Sci. Eng. 2017, 43, 2659–2672. [Google Scholar] [CrossRef]
- Su, K.; Guang, Z.; Su, Y. Mechanical Stability Analysis of Subsea Wellhead for Deepwater Drilling. Oil Drill. Prod. Technol. 2008, 30, 1–4, 15. [Google Scholar]
- Guan, D.; Yan, W. Stability Analysis of Underwater Wellhead in Deepwater Drilling. China Pet. Mach. 2012, 40, 85–89. [Google Scholar]
- Zhang, J.; Pang, D.; Xu, J.; Hu, J.; Cao, Y.; Chen, Q. Wellhead stability analysis of surface casing running for deepwater drilling. Oil Drill. Prod. Technol. 2018, 40 (Suppl. S1), 101–103. [Google Scholar]
- Zhou, Y.; Zhou, B.; Li, L.; Wang, K.; Wang, J.; Yang, X. Influence of the Top Tension of Riser on the Stability of Subsea Wellhead System. Oil Drill. Prod. Technol. 2018, 40 (Suppl. S1), 98–100. [Google Scholar]
- Yang, J.; Li, W.; Hu, Z.; Yin, Q.; Li, S. Research Progresses on Subsea Wellhead Stability of Deep Water Drilling. China Offshore Oil Gas 2020, 32 (Suppl. S1), 98–100. [Google Scholar]
- Wu, Y.; Xing, X.; Pang, Z.; Huang, Z. Research and Application of Key Technologies of Integrated Drilling and Completion for Offshore Exploration and Development. China Offshore Oil Gas 2022, 34, 128–133. [Google Scholar]
- Li, Q.; Cheng, Y.; Zhang, H.; Yan, C.; Liu, Y. Simulating the Effect of Hydrate Dissociation on Wellhead Stability during Oil and Gas Development in Deepwater. J. Ocean. Univ. China 2018, 17, 35–45. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J. Effect of Depressurized Hydrate on Soil Layer Around Wellhead. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Li, P.; Yang, J.; Lu, B.; Ke, K.; Wang, L.; Chen, K. Research on Stratum Settlement and Wellhead Stability in Deep Water during Hydrate Production TestingChinese Full Text. Pet. Drill. Tech. 2020, 48, 61–68. [Google Scholar]
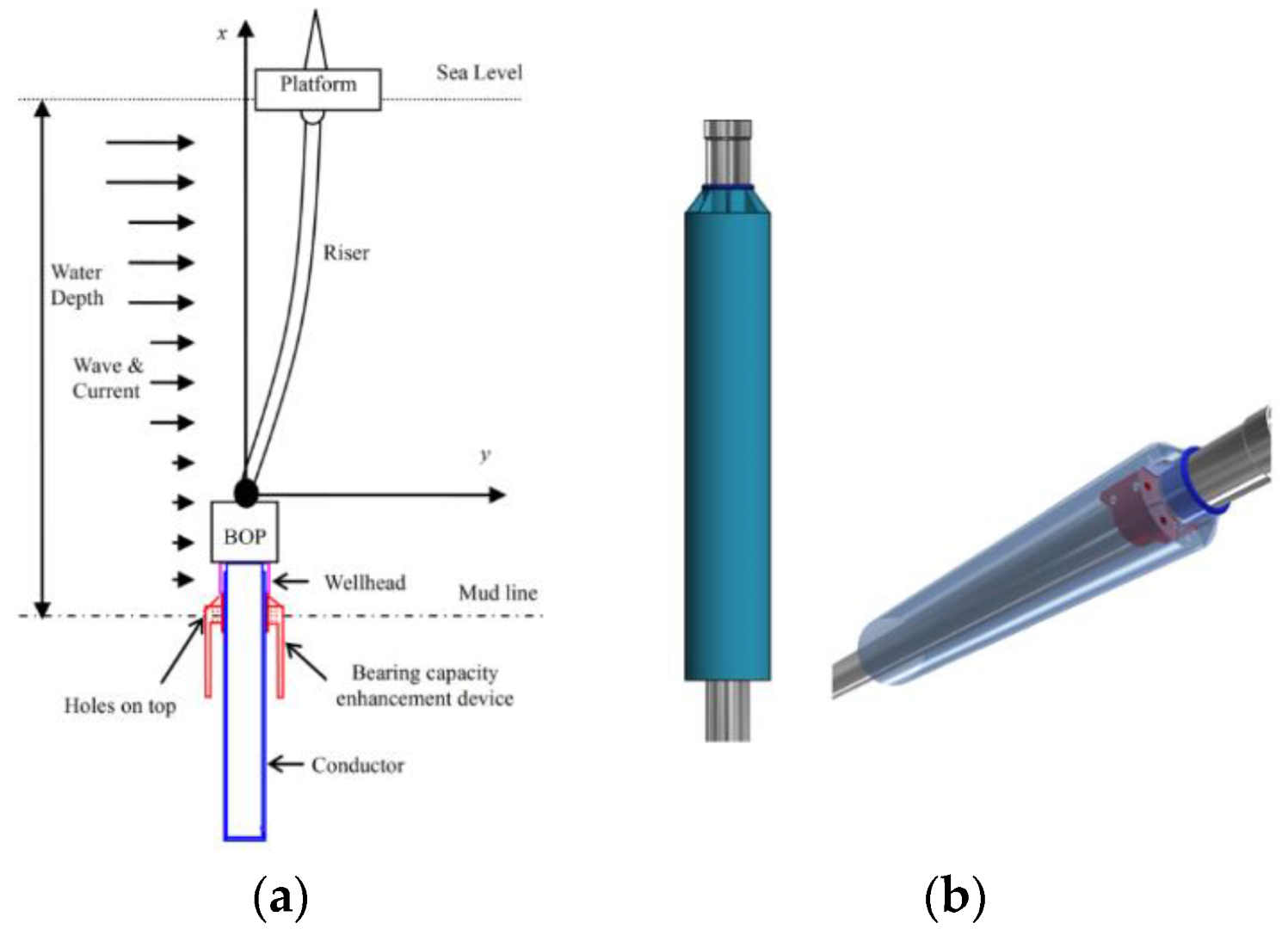
- Su, K. A Device for Preventing the Instability of Underwater Wellhead in Deep Water. Drilling. Patent CN202451101U, 26 September 2012. [Google Scholar]
- Su, K.; Yang, J.; Butt, S. An Innovative Device to Enhance Conductor Bearing Capacity in Deepwater Drilling Operations. J. Offshore Mech. Arct. Eng. 2018, 140, 011302. [Google Scholar] [CrossRef]
- Kan, C.; Yang, J.; Yu, X.; Dong, T.; Wu, X.; Liu, M.; Li, C.; Zhang, C.; Fu, J. Load Bearing Characteristics Study on Novel Deepwater Composite Drilling Conductor by Simulation and Experimental Methods. J. Pet. Sci. Eng. 2018, 171, 289–301. [Google Scholar] [CrossRef]
- Su, K.; Guang, Z.; Wei, L.; Liu, Y. Analysis on Subsea Wellhead Stability of Surface BOP Drilling System in Deepwater Operations. China Offshore Oil Gas 2009, 21, 180–185. [Google Scholar]
- Dib, M.W.; Lou, J.; Zhu, L.; Bassey, M. SBOP Drilling Enables Efficient Drilling in Extreme Water Depths. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2009. [Google Scholar]
- Cheng, G.; Duan, M.; Ye, M.; Li, M.; Sun, C.; Wang, F. Bearing Capacity of Suction Piles Used in Deep Water Subsea System. Oil Field Equip. 2013, 42, 46–50. [Google Scholar]
- Sivertsen, T.; Strand, H. New Well Foundation Concept, as Used at a Norwegian Sea well. In Proceedings of the SPE Arctic and Extreme Environments Conference and Exhibition, Moscow, Russia, 18–20 October 2011. [Google Scholar]
- Qin, Y.; Liu, K.; Chen, G.; Zhang, A.; Zhu, J.; Xia, K. Negative Pressure Analysis for the Penetration Installation of Conductor Suction Anchor in Marine Hydrate Reservoirs. Oil Drill. Prod. Technol. 2021, 43, 737–743. [Google Scholar]
- Gong, Z.; Zhang, L.; Cheng, H.; Liu, Y.; Ren, S. The Influence of Subsea Natural Gas Hydrate Dissociation on the Safety of Offshore Drilling. Pet. Drill. Tech. 2015, 43, 19–24. [Google Scholar]
- Li, W.; Gao, D.; Yang, J. Challenges and Prospect of the Drilling and Completion Technologies Used for the Natural Gas Hydrate Reservoirs in Sea Areas. Oil Drill. Prod. Technol. 2019, 41, 681–689. [Google Scholar]
- Zhou, S.; Chen, W.; Li, Q.; Chen, J.; Shi, H. Research on the Solid Fluidization Well Testing and Production for Shallow Non-diagenetic Natural Gas Hydrate in Deep Water Area. China Offshore Oil Gas 2017, 29, 1–8. [Google Scholar]
- Zhou, S.; Chen, W.; Li, Q.; Zhou, J.; Shi, H. Thinking and Suggestions on Research Direction of Natural Gas Hydrate Development. China Offshore Oil Gas 2019, 31, 1–8. [Google Scholar]
- Wang, B.; Huo, P.; Luo, T.; Fan, Z.; Liu, F.; Xiao, B.; Yang, M.; Zhao, J.; Song, Y. Analysis of the Physical Properties of Hydrate Sediments Recovered from the Pearl River Mouth Basin in the South China Sea: Preliminary Investigation for Gas Hydrate Exploitation. Energies 2017, 10, 531. [Google Scholar] [CrossRef]



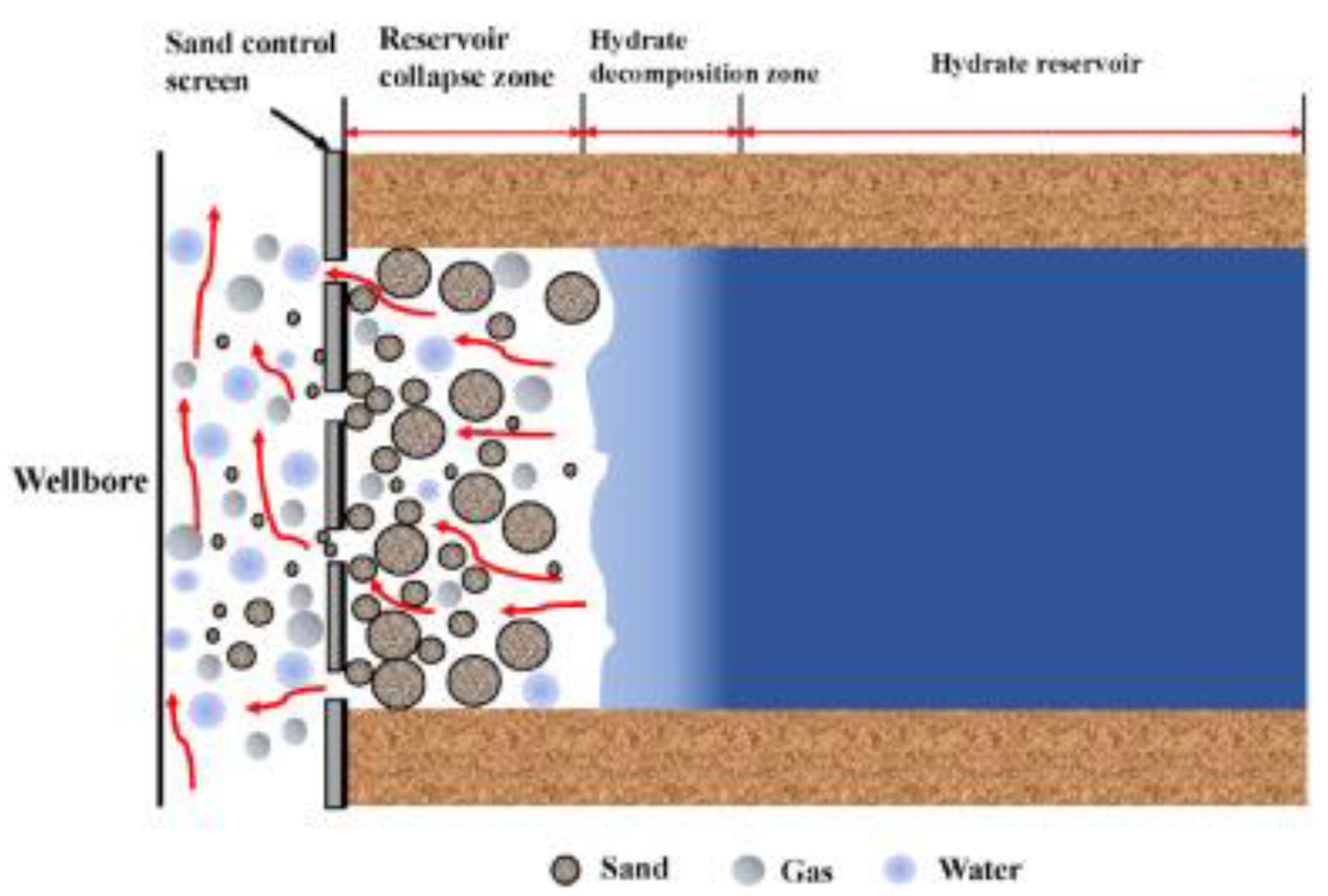
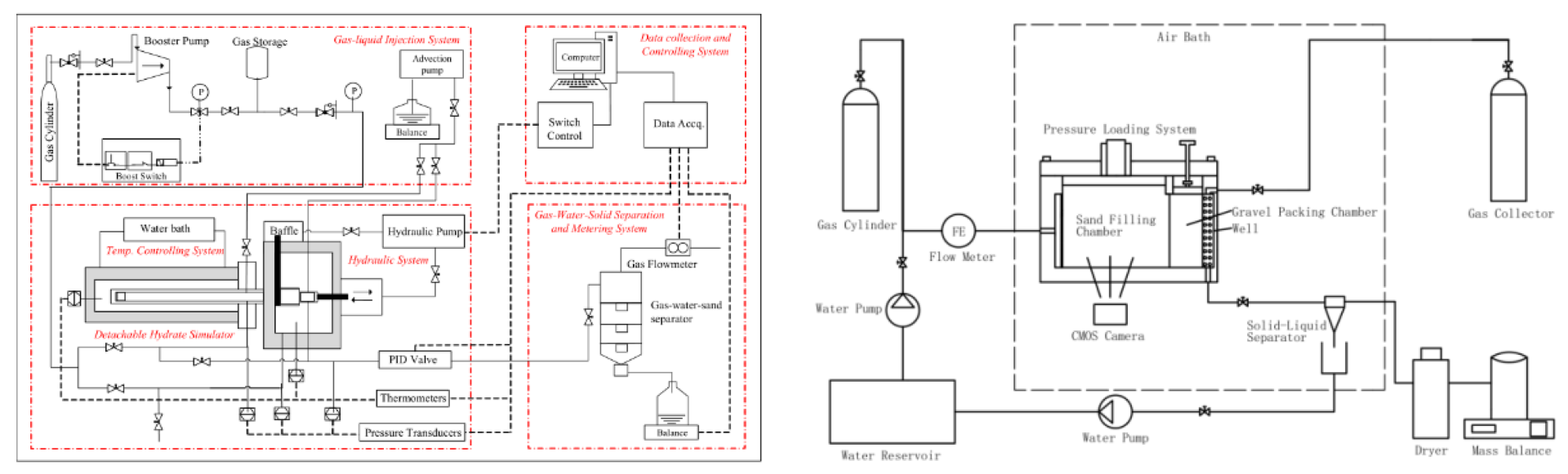



| Project | Reservoir Properties | Mining Method | Whether Sand Controlled and Effects |
|---|---|---|---|
| Messo Yaha, former Soviet Union (1967) | Depth 700~800 m; thickness 84 m; sandstone | Reduce pressure, inject chemicals | Perforation completion; poorly unconsolidated sand production of gas hydrate reservoir |
| Mackenzie, Canada (2002, 2007–2008) | Depth 800~1100 m; thickness 110 m; sandstone | 2002, heat injection 2007, reduce pressure + heat injection 2008, reduce pressure | Mechanical sand control; sand production perforation completion; not sand controlled; ESP damage caused by sand production mechanical sand control; add sand prevention meshwork to pump inlet; sand production |
| Alaska North Slope (2008, 2012) | Thickness 40~130 m; saturation 75%; sandstone | Reduce pressure, Carbon dioxide replacement | Perforated sand screen for sand control; sand production |
| Japan’s sea of love (2013) | Water depth 1000 m; burial depth 300 m; sandstone | Reduce pressure | Open-hole gravel sand screen for sand control; sand production caused the failure of the ESP work and was forced to terminate |
| Japan’s South China Sea Trough (2017) | Thickness 50 m | Reduce pressure | Geoform sand control system, the pre-expand of Geoform sand control system and geoform sand control system which expands after going down well (active) |
| Shenhu, South China South (2017) | Water depth 1266 m; burial depth 203~277 m; silty mud reservoir | Formation fluid extraction | the sand control of undiagenetic ultrafine reservoir; effective sand control |
| Liwan, South China Sea (2017) | Water depth 1310 m; buried depth 117~196 m; non-diagenetic reservoir | Solid-state fluidized mining | without sand control, the sand was separated from gas, water and hydrate inside the lifting pipeline |
| Shenhu, South China South (2020) | Water depth 1255 m; burial depth 203~277 m; silty shale reservoir | Formation fluid extraction | An innovative combination of bypass pipe technology and pre-packed screen technology, a new type of bypass pre-packed screen was developed; sand control is effective |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, M.; Yang, R.; Zhang, J.; Liu, Y.; Gao, S.; Duan, M. An Interface Parametric Evaluation on Wellbore Integrity during Natural Gas Hydrate Production. J. Mar. Sci. Eng. 2022, 10, 1524. https://doi.org/10.3390/jmse10101524
Zheng M, Yang R, Zhang J, Liu Y, Gao S, Duan M. An Interface Parametric Evaluation on Wellbore Integrity during Natural Gas Hydrate Production. Journal of Marine Science and Engineering. 2022; 10(10):1524. https://doi.org/10.3390/jmse10101524
Chicago/Turabian StyleZheng, Miaozi, Renjie Yang, Jianmin Zhang, Yongkai Liu, Songlin Gao, and Menglan Duan. 2022. "An Interface Parametric Evaluation on Wellbore Integrity during Natural Gas Hydrate Production" Journal of Marine Science and Engineering 10, no. 10: 1524. https://doi.org/10.3390/jmse10101524





