Hydrodynamic Analysis of a Modular Integrated Floating Structure System Based on Dolphin-Fender Mooring
Abstract
:1. Introduction
2. Numerical Model of the MIFS
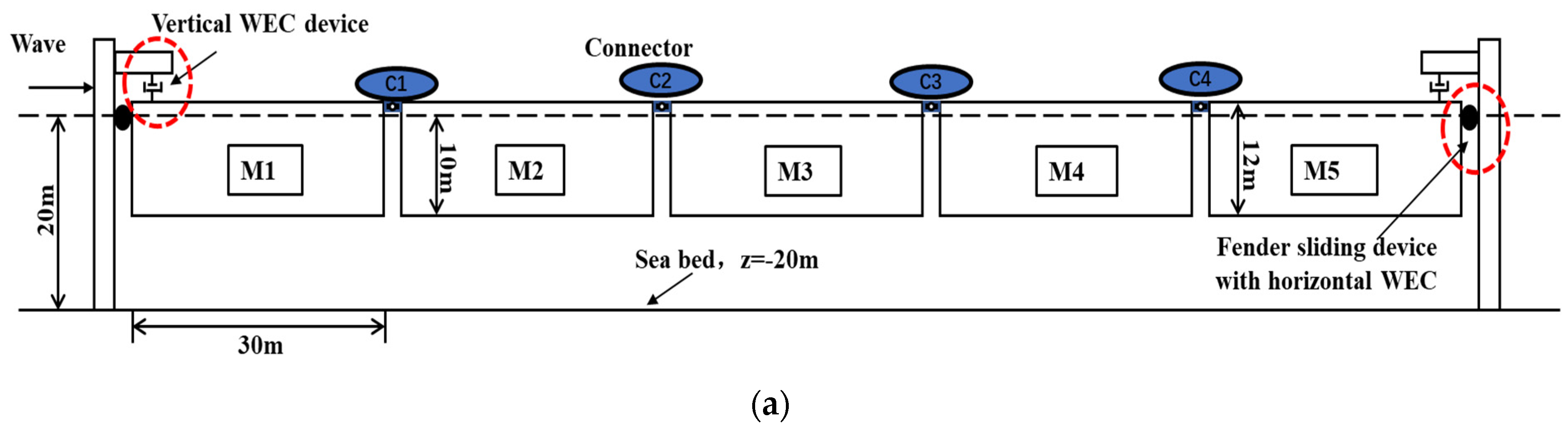
2.1. Description of the MIFS System
- (1)
- Pontoon-type floating module
- (2)
- Tidal self-adaptive dolphin-fender mooring (DFM)
- (3)
- Module connector
- (a)
- The hinge connector (denoted as “Hinge”): is only free for the relative pitch motion between the two connected modules;
- (b)
- The hinge connector coupled with an additional WEC (denoted as “HWK”): the PTO system of the WEC has been simplified as a linear pitch damper, which can effectively mitigate the relative pitch motion of the two adjacent modules, as well as generate power;
- (c)
- The fixed connector (denoted as “Fixed”): There is no relative motion in all degrees of freedom between the two connected modules;
- (4)
- Wave energy converter (WEC).
2.2. Multi-Body Dynamic Coupling Model
2.3. Hydrodynamic Model
3. Numerical Results of the 5-Module MIFS
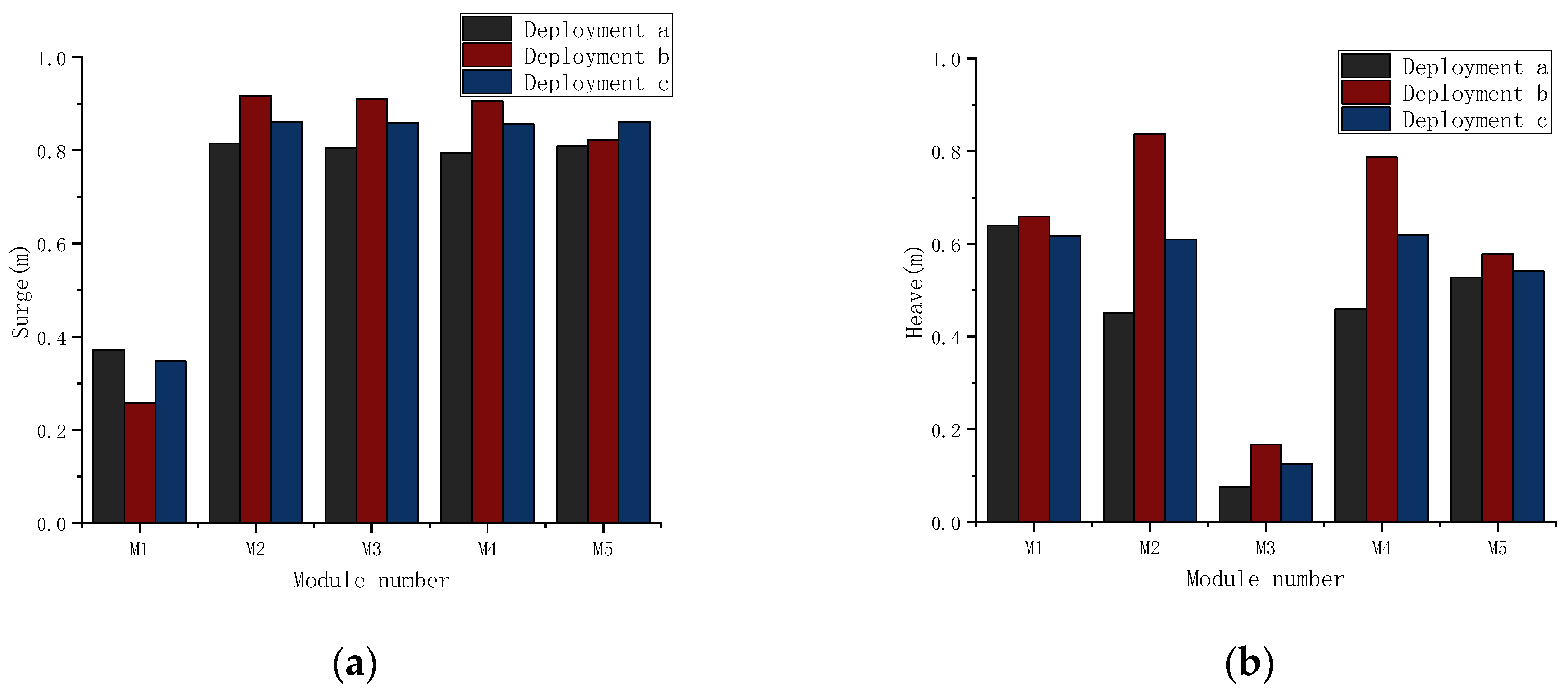
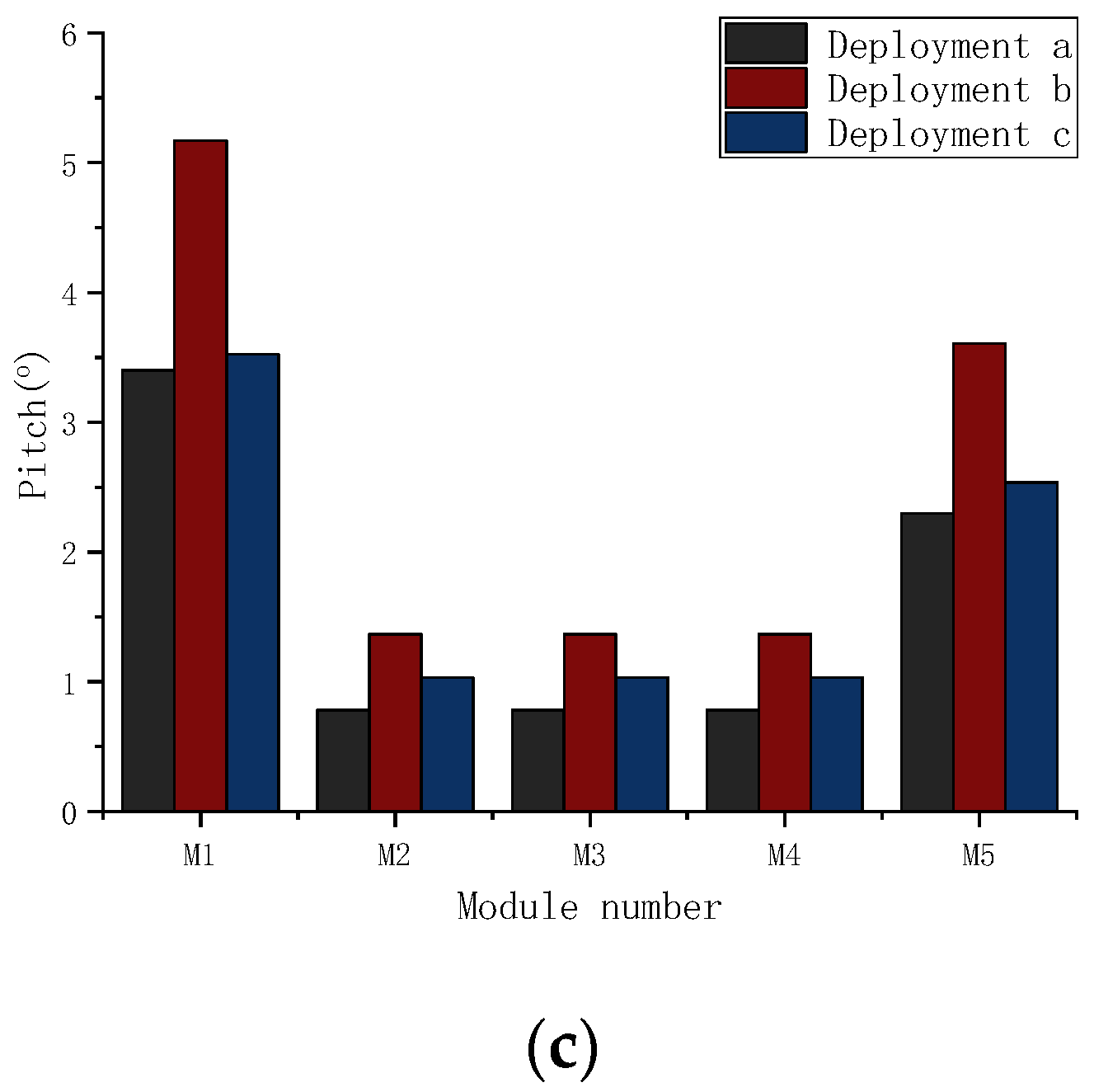
3.1. Deployment Effects of the DFM and Connectors
- The Kp is 1.0 × 109 Nms/rad, and each module is provided with vertical restraint devices;
- The C1 and the C4 are changed into the Hinge type, and each module is provided with vertical restraint devices;
- The Kp is 1.0 × 109 Nms/rad, and the inner three modules (M2~M4) are without vertical constraint devices.
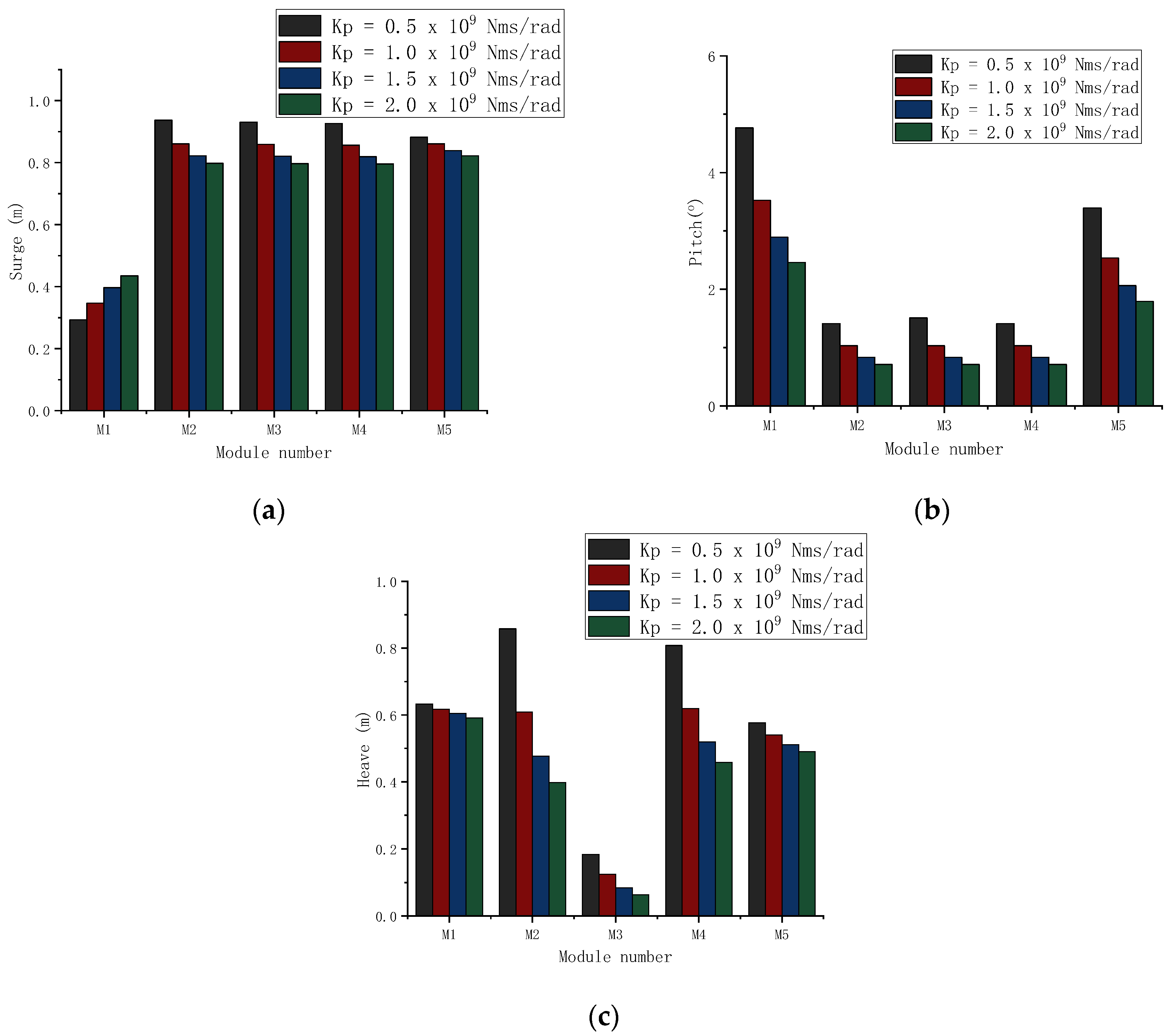
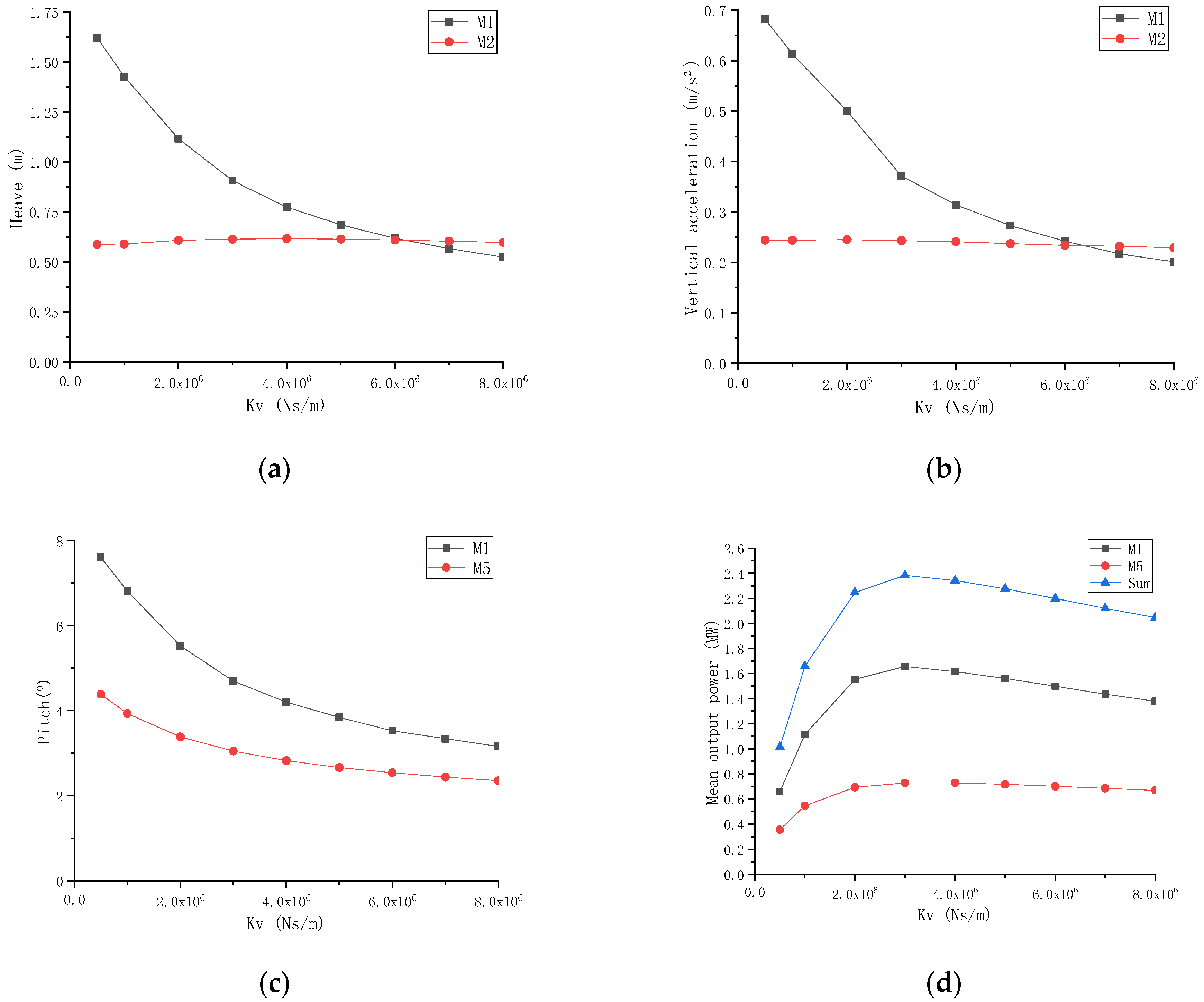
3.2. Effect of the HWK Key Parameter
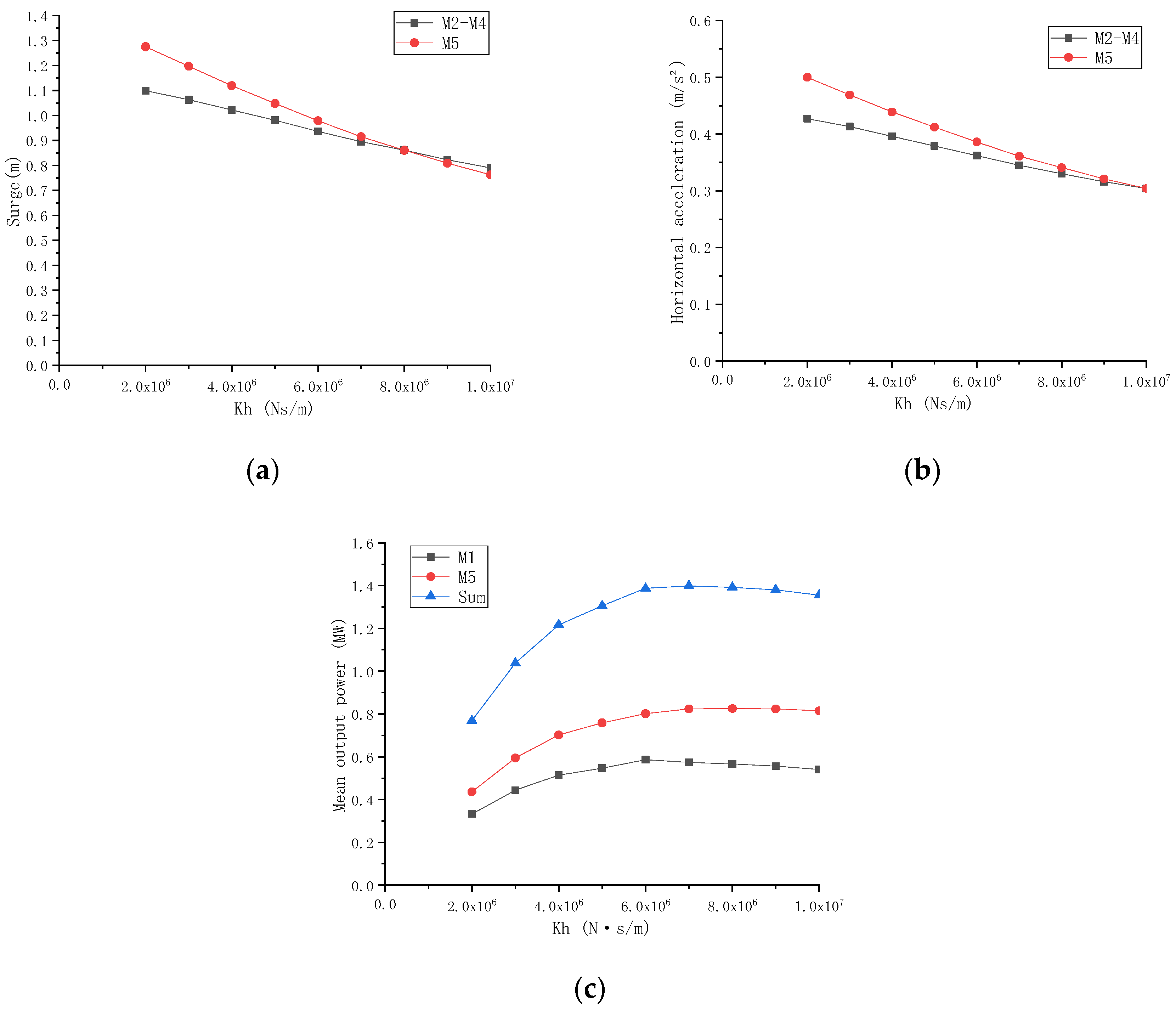
3.3. Effects of Key Parameters of the DFM’s WECs
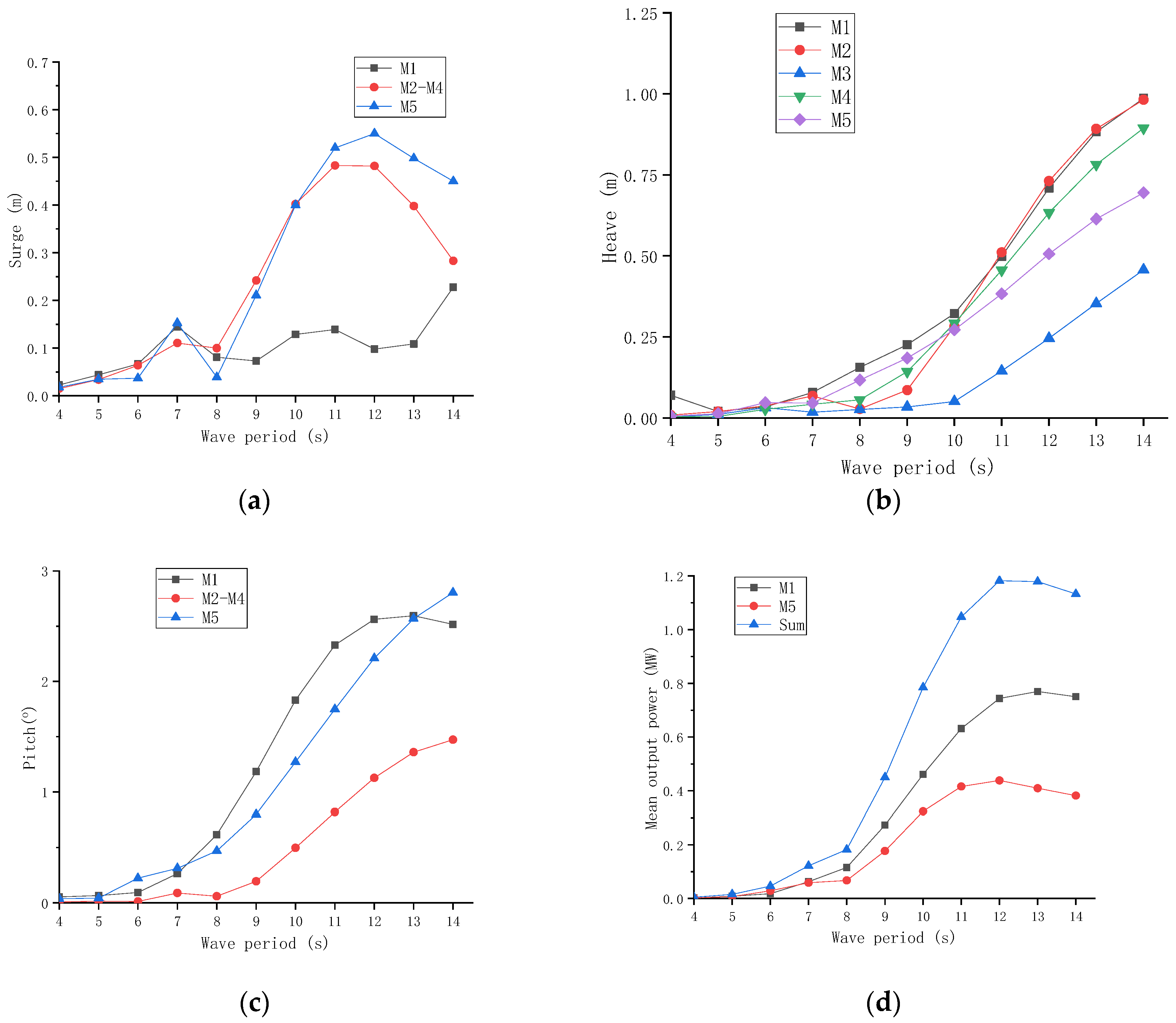
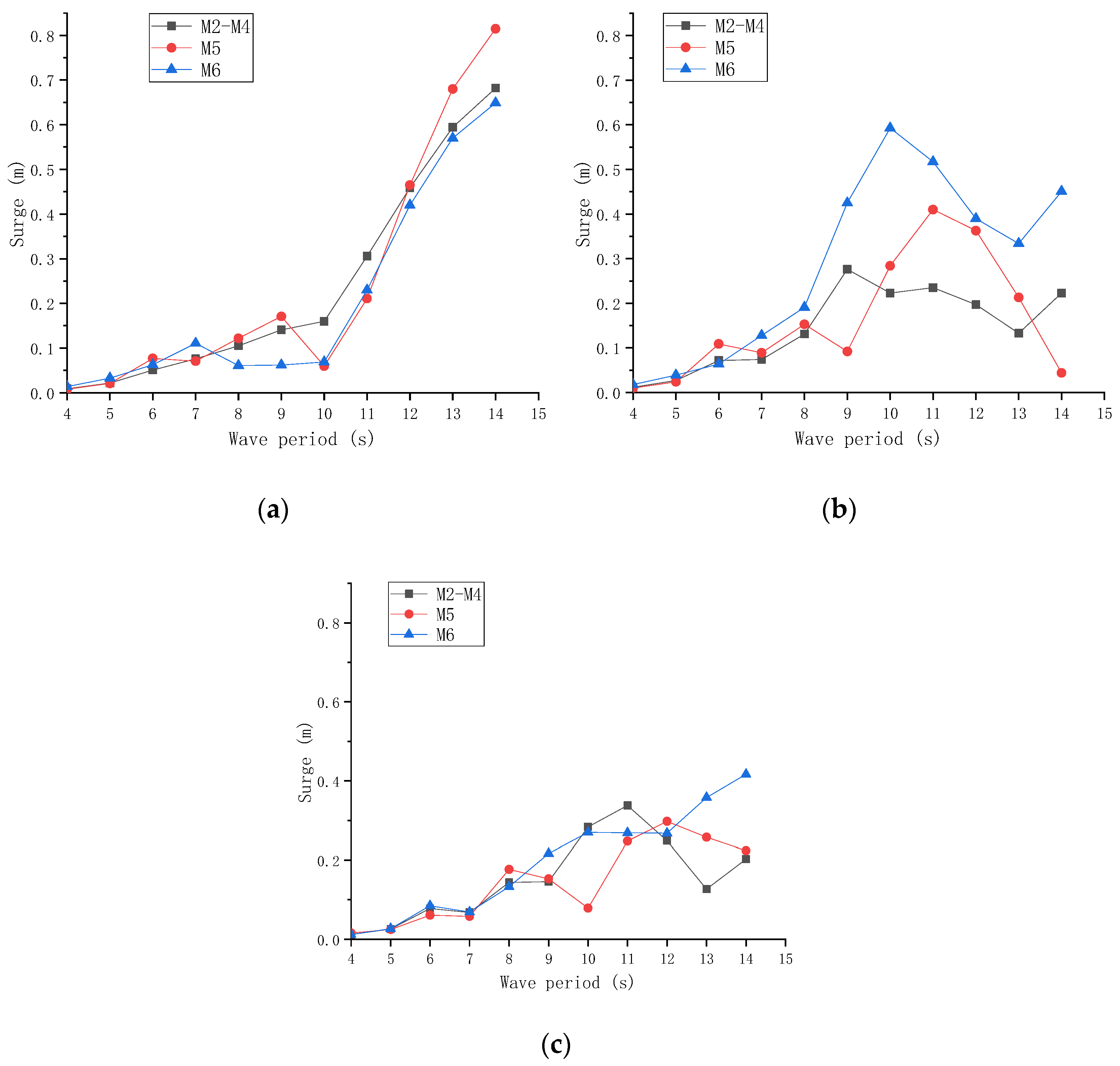
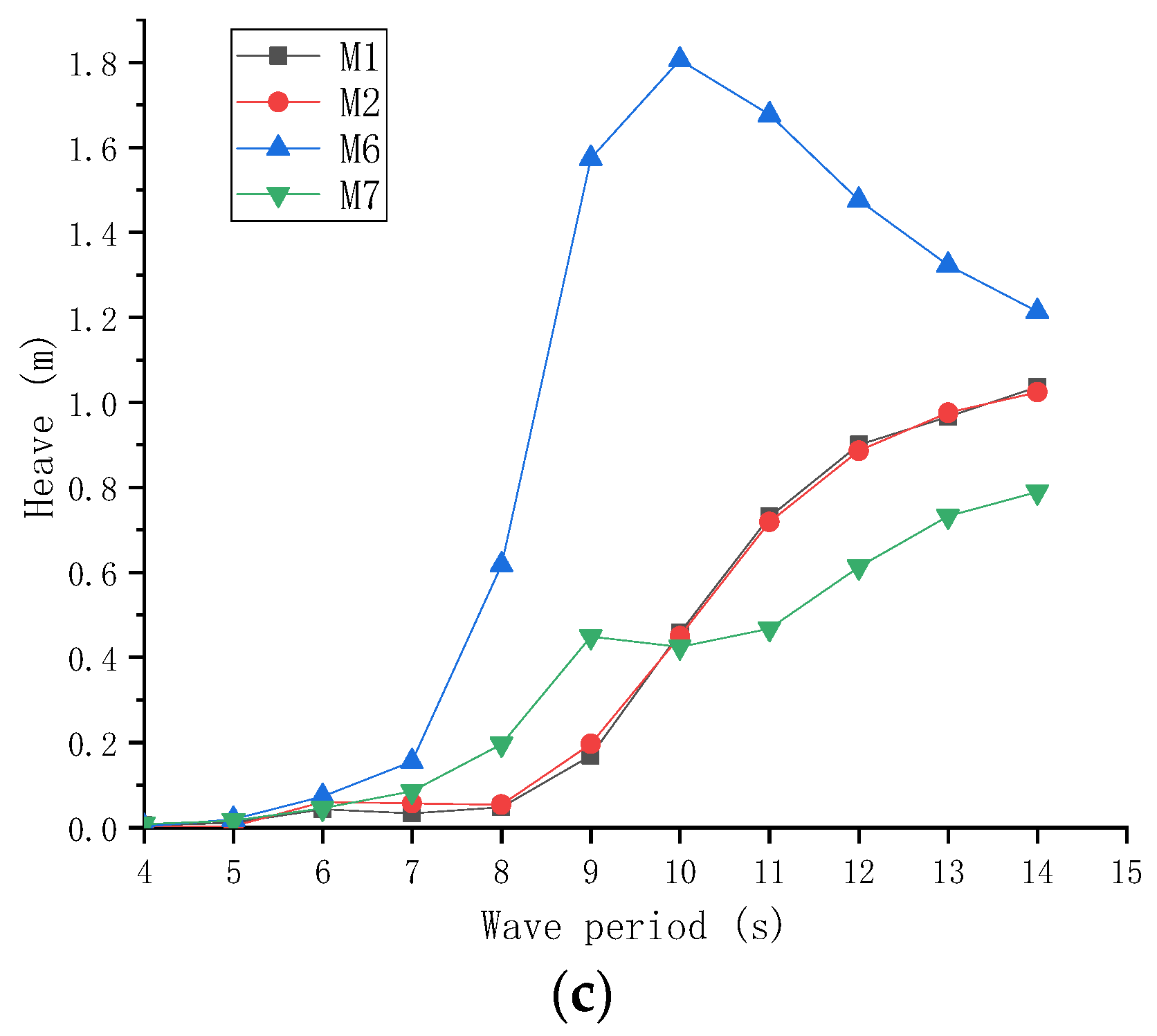
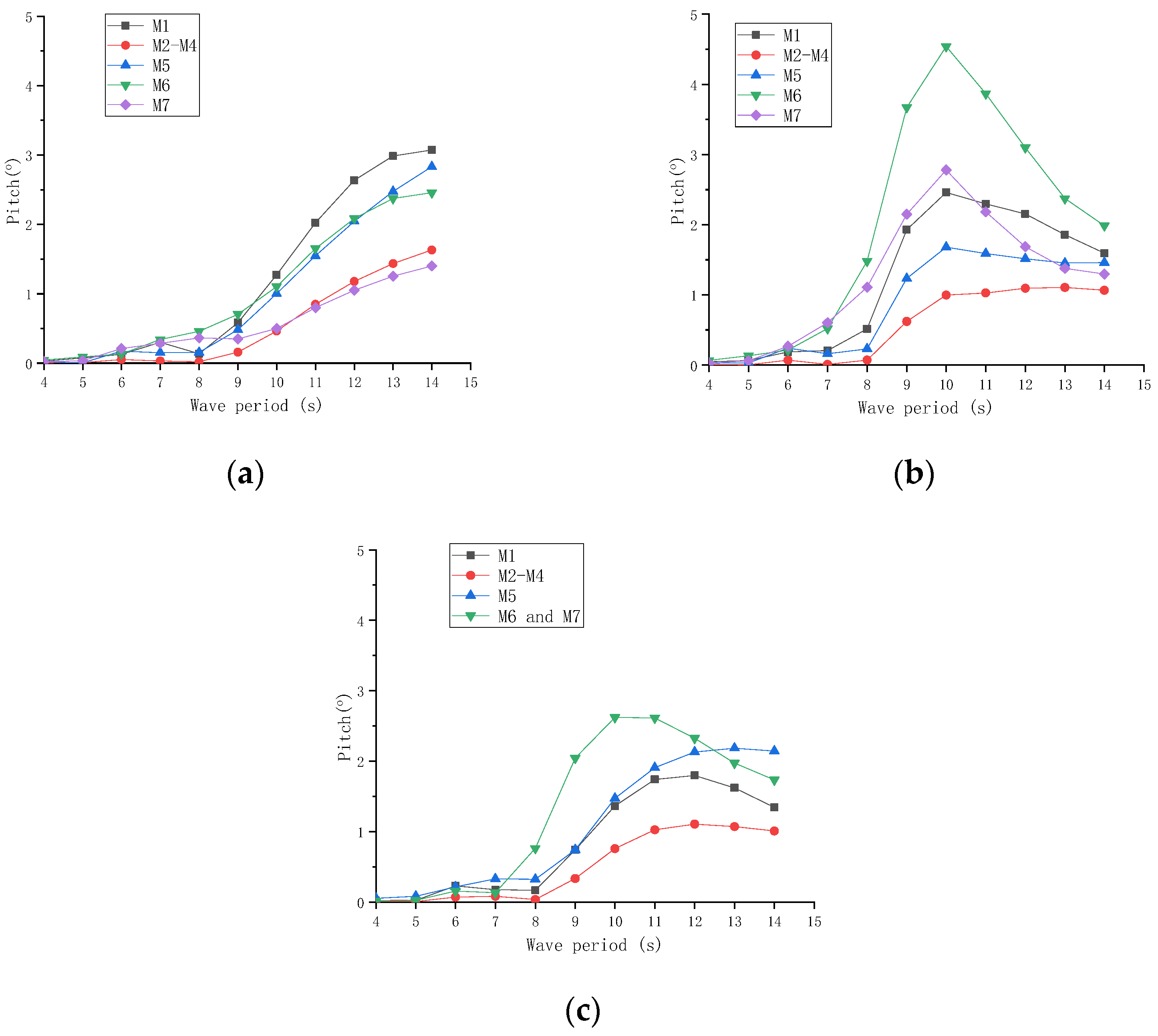
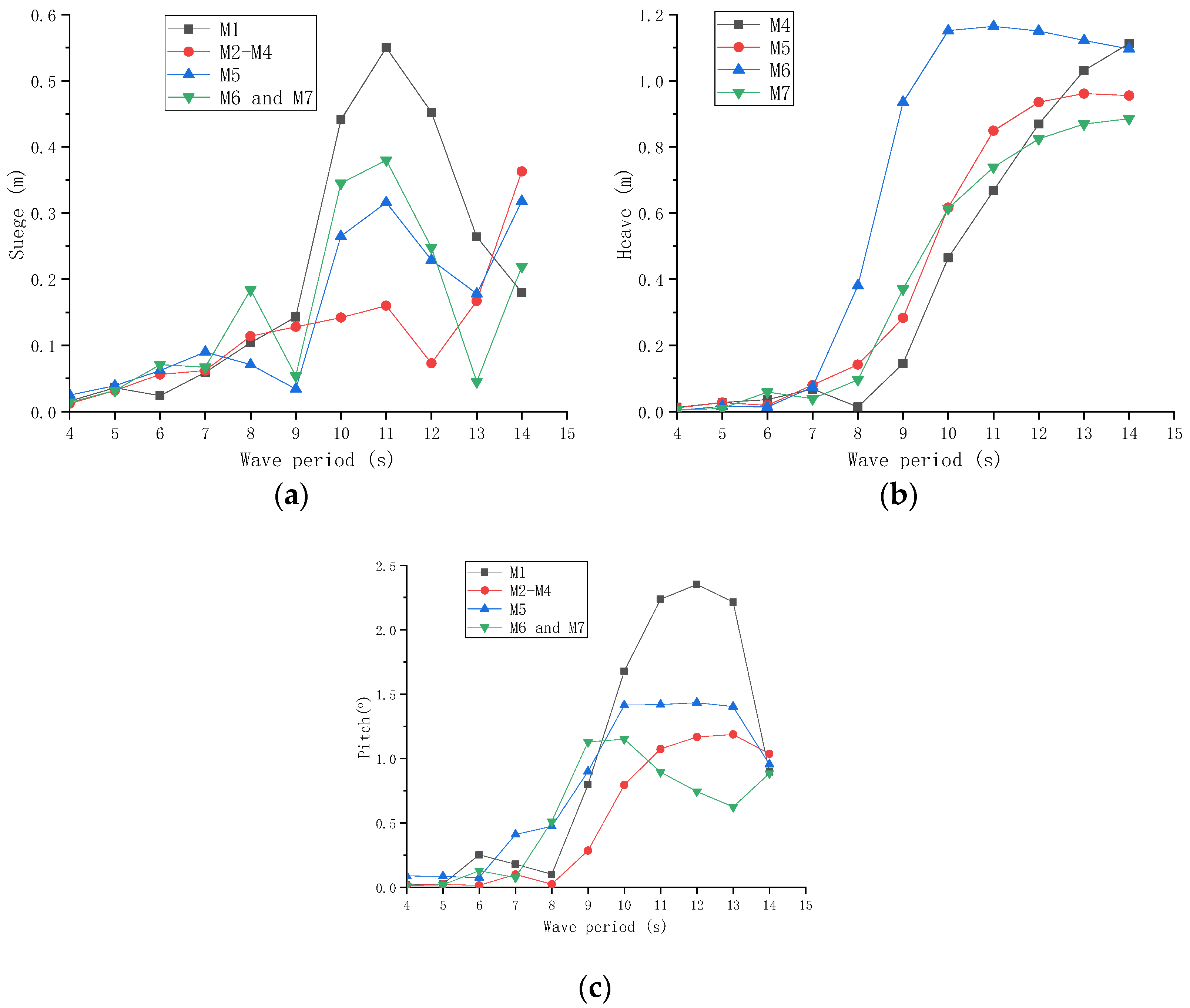
3.4. Typical Operational Sea Conditions
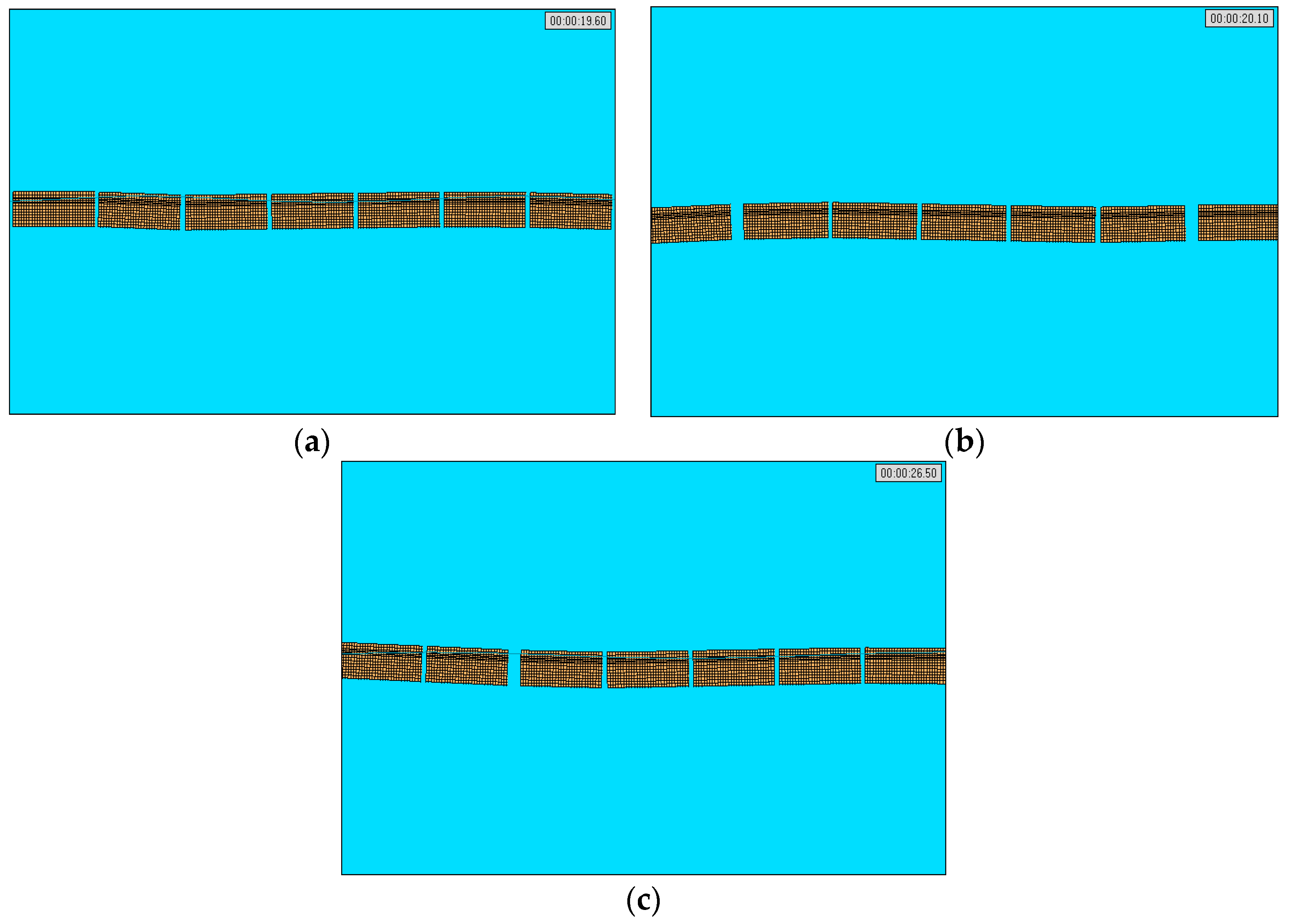
3.5. Extreme Sea Condition
4. Modular Expansion Scheme Research
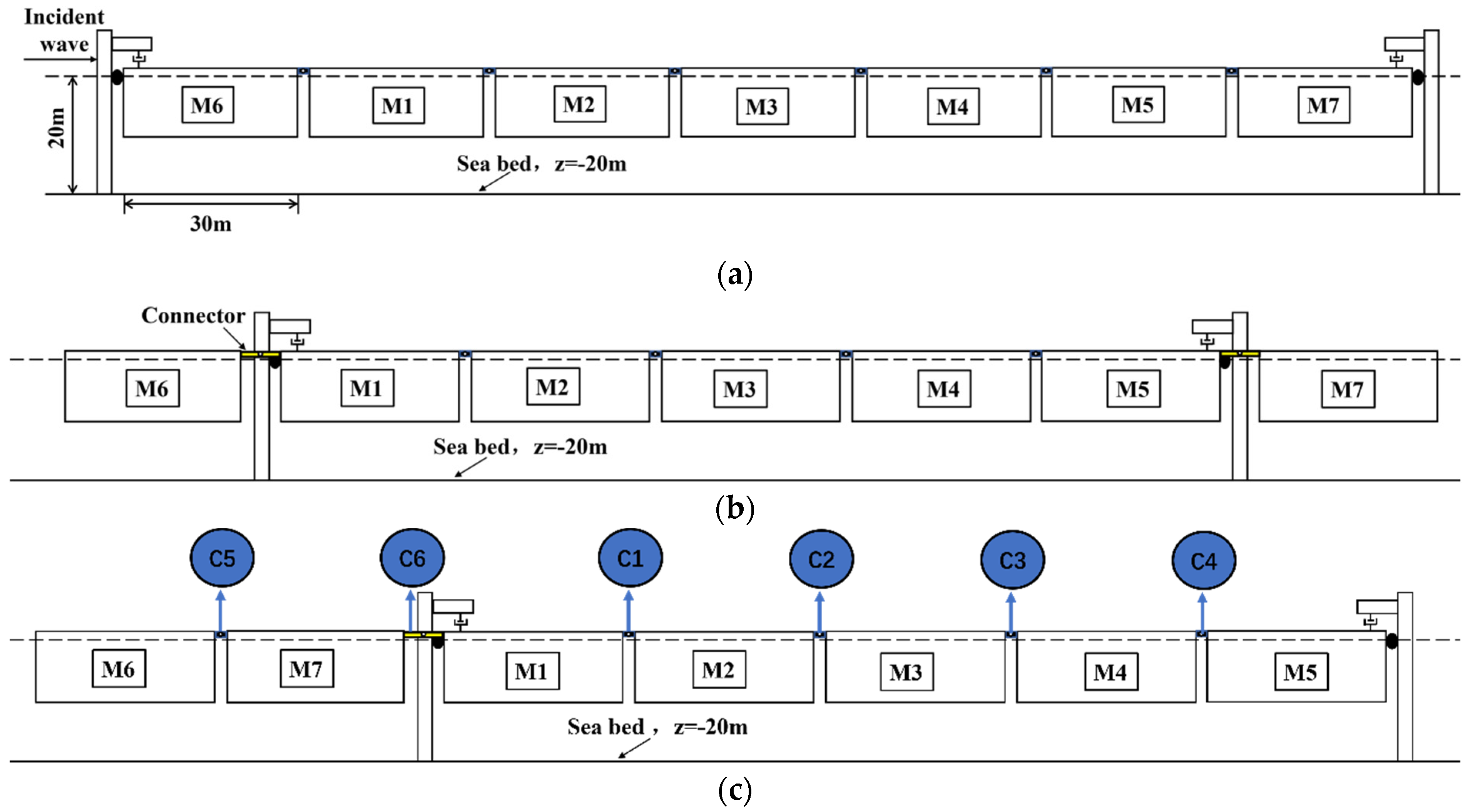
4.1. Modular Expansion Scheme
4.2. Reverse Incident Wave Sea Conditions for the Scheme C
4.3. Extreme Responses of the Scheme C
5. Conclusions
- (1)
- When the wave period is large than 10 s, the global dynamic responses of the MIFS system increase obviously. However, considering the wave period for such shallow water (20 m) is usually smaller than 10 s, the hydrodynamic performance of the proposed MIFS system can be acceptable. Under extreme irregular sea conditions, the safety of the MIFS system has been checked. It should be noticed the fixed connector for the inner modules tends to suffer considerable large loads, which might be challenging for the safety of the MIFS system. Therefore, the HWK connector is recommended to replace the inner fixed connector for reducing the huge connector loads, with sacrificing the modules’ pitch responses to a certain degree. The results indicate that this strategy can effectively make the MIFS system safer;
- (2)
- An effective modular expansion scheme has been proposed, which can improve the performance of inner modules. It indicates that the natural characteristic periods of the MIFS system tend to become larger with the modular expansion, which is more suitable for the shallow water environment. As a result, main dynamic responses of expanded MIFS systems are much better than those of the original MIFS system, especially for extreme irregular wave sea conditions. Therefore, the proposed MIFS system is of promising expansibility.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| DFM | Dolphin-Fender Mooring |
| DOF | Degree of Freedom |
| JONSWAP | Joint North Sea Wave Project |
| Fixed | Fixed Connector |
| Fx | Horizontal Force of Connector |
| Kp | Pitch Damping Coefficient |
| Fz | Vertical Shear Force of Connector |
| Kv | Vertical WEC Damping Coefficient |
| Kh | Horizontal WEC Damping Coefficient |
| MIFS | Modular Integrated Floating Structure |
| My | Pitch Bending Moment of Connector |
| PTO | Power Take-Off |
| WEC | Wave Energy Converter |
| VLFS | Very Large Floating Structure |
References
- Wang, G.; Drimer, N.; Goldfeld, Y. Modular floating structures (MFS) for offshore dwelling a hydrodynamic analysis in the frequency domain. Ocean Eng. 2020, 216, 107996. [Google Scholar] [CrossRef]
- Wang, C.; Tay, Z. Very large floating structures: Applications, research and development. Procedia Eng. 2011, 14, 62–72. [Google Scholar] [CrossRef] [Green Version]
- Lamas-Pardo, M.; Iglesias, G.; Carral, L. A review of very large floating structures (VLFS) for coastal and offshore uses. Ocean Eng. 2015, 109, 677–690. [Google Scholar] [CrossRef]
- Wang, C.M.; Watanabe, E.; Utsunomiya, T. Very Large Floating Structures; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Kim, J.-H.; Hong, S.-Y.; Cho, S.-k.; Park, S.-H. In Experimental Study on a Dolphin-Fender Moored Pontoon-Type Structure. In Proceedings of the The Fourteenth International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004; OnePetro: Richardson, TX, USA, 2004. [Google Scholar]
- Cho, K.-N. A Study on the Design of Dolphin System for VLFS. J. Comput. Struct. Eng. Inst. Korea 2006, 19, 105–111. [Google Scholar]
- Nguyen, H.; Dai, J.; Wang, C.; Ang, K.; Luong, V. Reducing hydroelastic responses of pontoon-type VLFS using vertical elastic mooring lines. Mar. Struct. 2018, 59, 251–270. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Soares, C.G. Hydroelastic Response to Oblique Wave Incidence on a Floating Plate with a Submerged Perforated Base. J. Mar. Sci. Eng. 2022, 10, 1205. [Google Scholar] [CrossRef]
- Xia, D.; Kim, J.; Ertekin, R.C. Review on conceptual designs and key technologies of very large floating structures. J. Ship Mech. 2000, 24, 135–148. [Google Scholar]
- Wang, D.; Ertekin, R.C.; Riggs, H.R. Three-dimensional hydroelastic response of a very large floating structure. Int. J. Offshore Polar 1991, 1, 307–316. [Google Scholar]
- Wang, Y.-T.; Wang, X.-F.; Xu, S.-W.; Wang, L.; Shang, Y.-Z. Numerical and experimental investigation of hydrodynamic interactions of two VLFS modules deployed in Tandem. China Ocean Eng. 2020, 34, 46–55. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Ding, J.; Xie, Z.; Wu, Y.; Xu, S.; Qiu, G.; Wang, Y.; Wang, Q. Numerical and experimental investigation on hydroelastic responses of an 8-module VLFS near a typical island. Ocean Eng. 2020, 214, 107841. [Google Scholar] [CrossRef]
- Lu, Y.; Teng, B.; Wang, Y.; Zhou, Y.; Cheng, X.; Qi, E. Structural Design of Hinge Connector for Very Large Floating Structures; Practical Design of Ships and Other Floating Structures; Springer: Berlin/Heidelberg, Germany, 2019; pp. 197–208. [Google Scholar]
- Ren, N.X.; Wu, H.B.; Ma, Z.; Ou, J.P. Hydrodynamic analysis of a novel modular floating structure system with central tension-leg platforms. Ships Offshore Struc. 2020, 15, 1011–1022. [Google Scholar] [CrossRef]
- Ren, N.X.; Wu, H.B.; Liu, K.; Zhou, D.C.; Ou, J.P. Hydrodynamic Analysis of a Modular Floating Structure with Tension-Leg Platforms and Wave Energy Converters. J. Mar. Sci. Eng. 2021, 9, 424. [Google Scholar] [CrossRef]
- Ren, N.X.; Zhang, C.; Magee, A.R.; Hellan, Ø.; Dai, J.; Ang, K.K. Hydrodynamic analysis of a modular multi-purpose floating structure system with different outermost connector types. Ocean Eng. 2019, 176, 158–168. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xu, S.; Wang, L.; Ding, A.; Deng, Y. Experimental and Numerical Investigation of Influences of Connector Stiffness and Damping on Dynamics of a Multimodule VLFS. Int. J. Offshore Polar 2020, 30, 427–436. [Google Scholar] [CrossRef]
- Drummen, I.; Olbert, G. Conceptual design of a modular floating multi-purpose island. Front. Mar. Sci. 2021, 8, 615222. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Lentsiou, E.N.; Aksel, M.; Yagci, O. Experimental investigation of the hydroelastic and the structural response of a moored pontoon-type modular floating breakwater with flexible connectors. Coast. Eng. 2017, 121, 240–254. [Google Scholar] [CrossRef]
- Tay, Z.Y. Energy extraction from an articulated plate anti-motion device of a very large floating structure under irregular waves. Renew. Energy 2019, 130, 206–222. [Google Scholar] [CrossRef]
- Praveen, K.; Karmakar, D.; Guedes Soares, C. Hydroelastic analysis of periodic arrays of multiple articulated floating elastic plate. Ships Offshore Struc. 2020, 15, 280–295. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, C.; Luong, V. Two-mode WEC-type attachment for wave energy extraction and reduction of hydroelastic response of pontoon-type VLFS. Ocean Eng. 2020, 197, 106875. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.; Ji, C.; Cocard, M.; Yuan, Z.; Incecik, A. Performance characteristics and parametric analysis of a novel multi-purpose platform combining a moonpool-type floating breakwater and an array of wave energy converters. Appl. Energy 2021, 292, 116888. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.S.; Ji, C.Y.; Collu, M.; Li, M.X.; Yuan, Z.M.; Incecik, A. Wave Energy extraction and hydroelastic response reduction of modular floating breakwaters as array wave energy converters integrated into a very large floating structure. Appl. Energy 2022, 306, 117953. [Google Scholar] [CrossRef]
- Li, Y.W.; Ren, N.X.; Li, X.; Ou, J.P. Hydrodynamic Analysis of a novel modular floating structure system integrated with floating artificial reefs and wave energy converters. J. Mar. Sci. Eng. 2022, 10, 1091. [Google Scholar] [CrossRef]
- ANSYS Inc. Aqwa User’s Manual; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Gourlay, T.; von Graefe, A.; Shigunov, V.; Lataire, E. Comparison of AQWA, GL RANKINE, MOSES, OCTOPUS, PDSTRIP and WAMIT with Model Test Results for Cargo Ship Wave-Induced Motions in Shallow Water. In Proceedings of the 34th International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, May 31–June 5 2015; American Society of Mechanical Engineers: New York NY, USA, 2015; p. V011T12A006. [Google Scholar]
- Nordforsk. Assessment of Ship Performance in a Seaway: The Nordic Cooperative Project: “Seakeeping Performance of Ships”; Nordforsk: Oslo, Norway, 1987. [Google Scholar]



| Parameters | Value | Units |
|---|---|---|
| Single module size | 30 × 30 × 12 | m |
| Draft; Operating water depth | 10; 20 | m |
| Height of center of gravity | −5.47 | m |
| Mass = Displacement | 9225 | t |
| Ixx = Iyy,Izz | 1.08 × 109;1.46 × 109 | kg·m2 |
| HWK Damping (Nms/rad) | Mean Output Power (MW) | Maximum C1 Load | ||
|---|---|---|---|---|
| Fx (N) | Fz (N) | My (Nm) | ||
| 0.5 × 109 | 1.707 | 1.590 × 107 | 0.484 × 107 | 3.221 × 107 |
| 1.0 × 109 | 1.818 | 1.560 × 107 | 0.534 × 107 | 4.882 × 107 |
| 1.5 × 109 | 1.744 | 1.545 × 107 | 0.565 × 107 | 5.884 × 107 |
| 2.0 × 109 | 1.637 | 1.533 × 107 | 0.587 × 107 | 6.583 × 107 |
| HWK | Fixed | Module with Vertical Restrain Device | Kp (Nms/rad) | Kh (Ns/m) | Kv (Ns/m) |
|---|---|---|---|---|---|
| C1; C4 | C2; C3 | Only M1 and M5 | 1.0 × 109 | 7.0 × 106 | 6.0 × 106 |
| Module | Surge (m) | Heave (m) | Pitch (m) | Horizontal Acceleration (m/s2) | Vertical Acceleration (m/s2) | Horizontal Force of Monopile (N) | My of Connector (Nm) | |
|---|---|---|---|---|---|---|---|---|
| M1 | Max | 0.348 | 0.716 | 3.814 | 0.238 | 0.296 | 1.071 × 107 | |
| Stdev | 0.274 | 0.284 | 2.168 | 0.131 | 0.170 | C1: 4.623 × 107 | ||
| M2 | Max | 0.840 | 0.599 | 1.042 | 0.379 | 0.257 | ||
| Stdev | 0.601 | 0.211 | 0.408 | 0.214 | 0.067 | C2: 14.092 × 107 | ||
| M3 | Max | 0.840 | 0.168 | 1.042 | 0.379 | 0.007 | ||
| Stdev | 0.601 | 0.007 | 0.408 | 0.214 | 0.023 | C3: 14.291 × 107 | ||
| M4 | Max | 0.840 | 0.617 | 1.042 | 0.379 | 0.234 | ||
| Stdev | 0.601 | 0.245 | 0.408 | 0.214 | 0.113 | C4: 3.634 × 107 | ||
| M5 | Max | 0.869 | 0.551 | 2.684 | 0.385 | 0.259 | 1.146 × 107 | |
| Stdev | 0.476 | 0.214 | 0.525 | 0.219 | 0.085 | |||
| Module | Surge (m) | Heave (m) | Pitch (m) | Horizontal Acceleration (m/s2) | Vertical Acceleration (m/s2) | Horizontal Force of Monopile (N) | My of Connector (N·m) | |
|---|---|---|---|---|---|---|---|---|
| M1 | Max | 0.540 | 1.035 | 3.842 | 0.250 | 0.427 | 1.055 × 107 | |
| Stdev | 0.310 | 0.466 | 2.116 | 0.158 | 0.269 | C1: 4.009 × 107 | ||
| M2 | Max | 0.515 | 0.907 | 3.019 | 0.256 | 0.358 | ||
| Stdev | 0.411 | 0.408 | 1.268 | 0.155 | 0.192 | C2: 5.168 × 107 | ||
| M3 | Max | 1.049 | 0.897 | 3.089 | 0.502 | 0.374 | ||
| Stdev | 0.816 | 0.298 | 1.915 | 0.381 | 0.329 | C3: 4.554 × 107 | ||
| M4 | Max | 0.991 | 0.823 | 2.415 | 0.425 | 0.332 | ||
| Stdev | 0.640 | 0.407 | 0.618 | 0.273 | 0.196 | C4: 3.208 × 107 | ||
| M5 | Max | 0.736 | 0.775 | 2.295 | 0.335 | 0.363 | 1.114 × 107 | |
| Stdev | 0.426 | 0.308 | 0.978 | 0.186 | 0.125 | |||
| Module | Surge (m) | Heave (m) | Pitch (m) | Horizontal Acceleration (m/s2) | Vertical Acceleration (m/s2) | Horizontal Force of Monopile (N) | My of Connector (Nm) | |
|---|---|---|---|---|---|---|---|---|
| M1 | Max | 0.498 | 0.610 | 2.102 | 0.285 | 0.269 | 0.956 × 107 | C1: 3.182 × 107 |
| Stdev | 0.063 | 0.053 | 0.258 | 0.041 | 0.016 | |||
| M2 | Max | 0.487 | 0.689 | 0.949 | 0.239 | 0.310 | C2: 10.482 × 107 | |
| Stdev | 0.006 | 0.033 | 0.015 | 0.016 | 0.031 | |||
| M6 | Max | 0.447 | 3.300 | 4.530 | 0.259 | 1.440 | C5: 7.830 × 107 | |
| Stdev | 0.100 | 0.706 | 0.970 | 0.064 | 0.285 | |||
| M7 | Max | 0.447 | 0.873 | 4.530 | 0.259 | 0.401 | C6: 5.836 × 107 | |
| Stdev | 0.100 | 0.164 | 0.970 | 0.064 | 0.030 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, N.; Yu, Y.; Li, X.; Ou, J. Hydrodynamic Analysis of a Modular Integrated Floating Structure System Based on Dolphin-Fender Mooring. J. Mar. Sci. Eng. 2022, 10, 1470. https://doi.org/10.3390/jmse10101470
Ren N, Yu Y, Li X, Ou J. Hydrodynamic Analysis of a Modular Integrated Floating Structure System Based on Dolphin-Fender Mooring. Journal of Marine Science and Engineering. 2022; 10(10):1470. https://doi.org/10.3390/jmse10101470
Chicago/Turabian StyleRen, Nianxin, Yuekai Yu, Xiang Li, and Jinping Ou. 2022. "Hydrodynamic Analysis of a Modular Integrated Floating Structure System Based on Dolphin-Fender Mooring" Journal of Marine Science and Engineering 10, no. 10: 1470. https://doi.org/10.3390/jmse10101470
APA StyleRen, N., Yu, Y., Li, X., & Ou, J. (2022). Hydrodynamic Analysis of a Modular Integrated Floating Structure System Based on Dolphin-Fender Mooring. Journal of Marine Science and Engineering, 10(10), 1470. https://doi.org/10.3390/jmse10101470







