COLREGs-Compliant Multi-Ship Collision Avoidance Based on Multi-Agent Reinforcement Learning Technique
Abstract
1. Introduction
2. Literature Review and Motivation
3. Ship Collision Avoidance Problem
3.1. Problem Definition
- Single-agent collision avoidance: The own-ship (OS) is considered as an agent, the target-ship (TS) is seen as a dynamic obstacle;
- Multi-agent collision avoidance: Each ship is an agent, and there are partnerships between them.
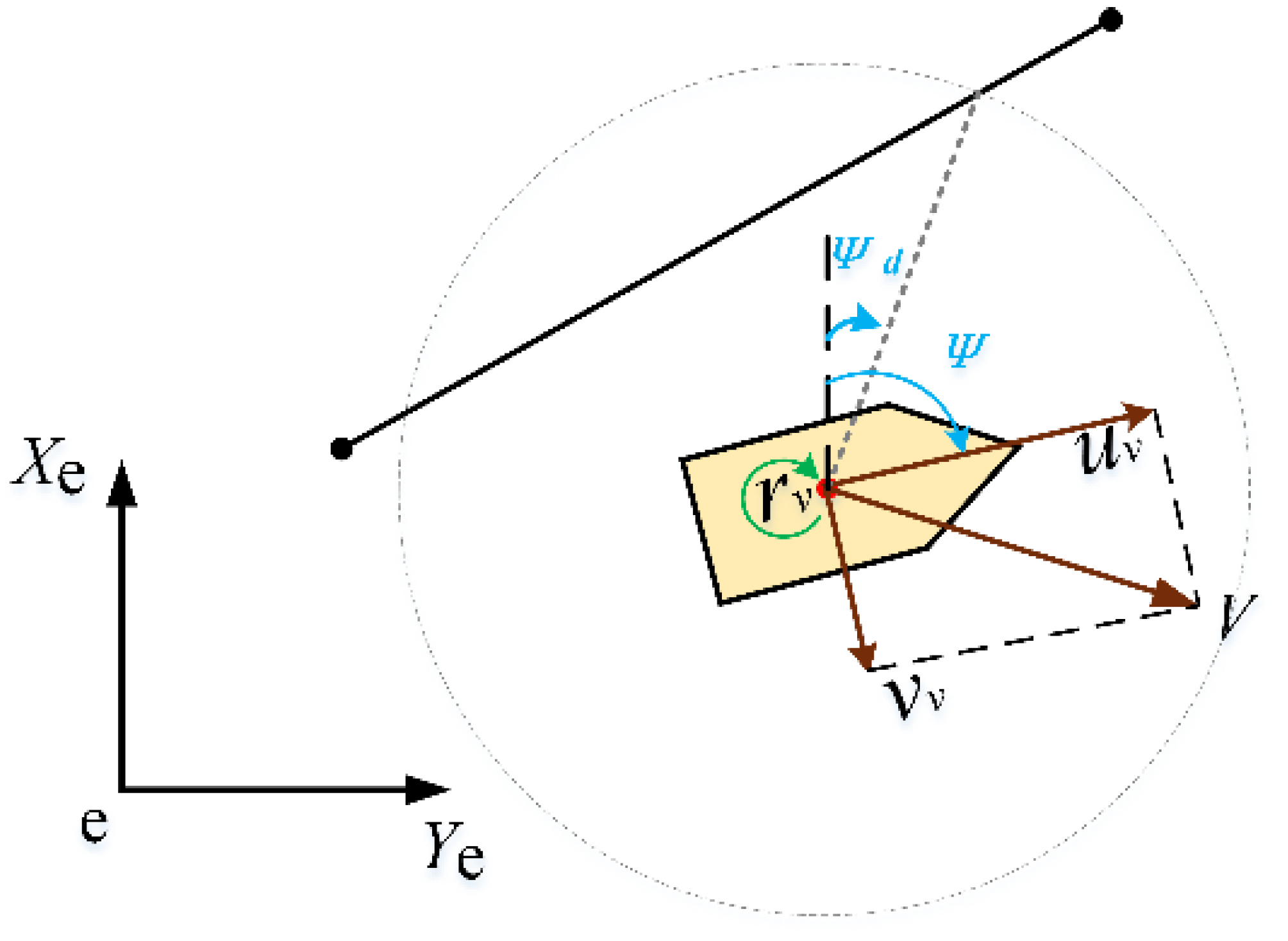
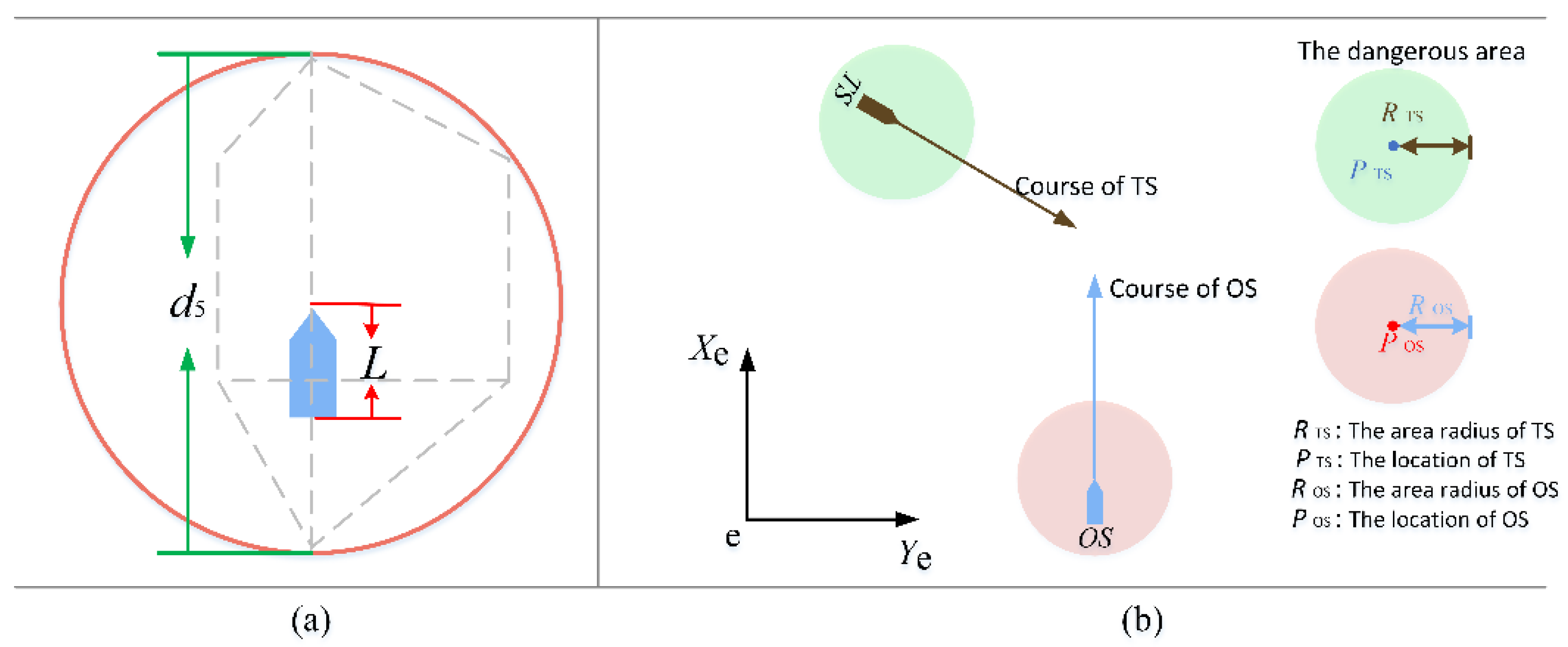
3.2. The Ship Motion Model and Collision Detection
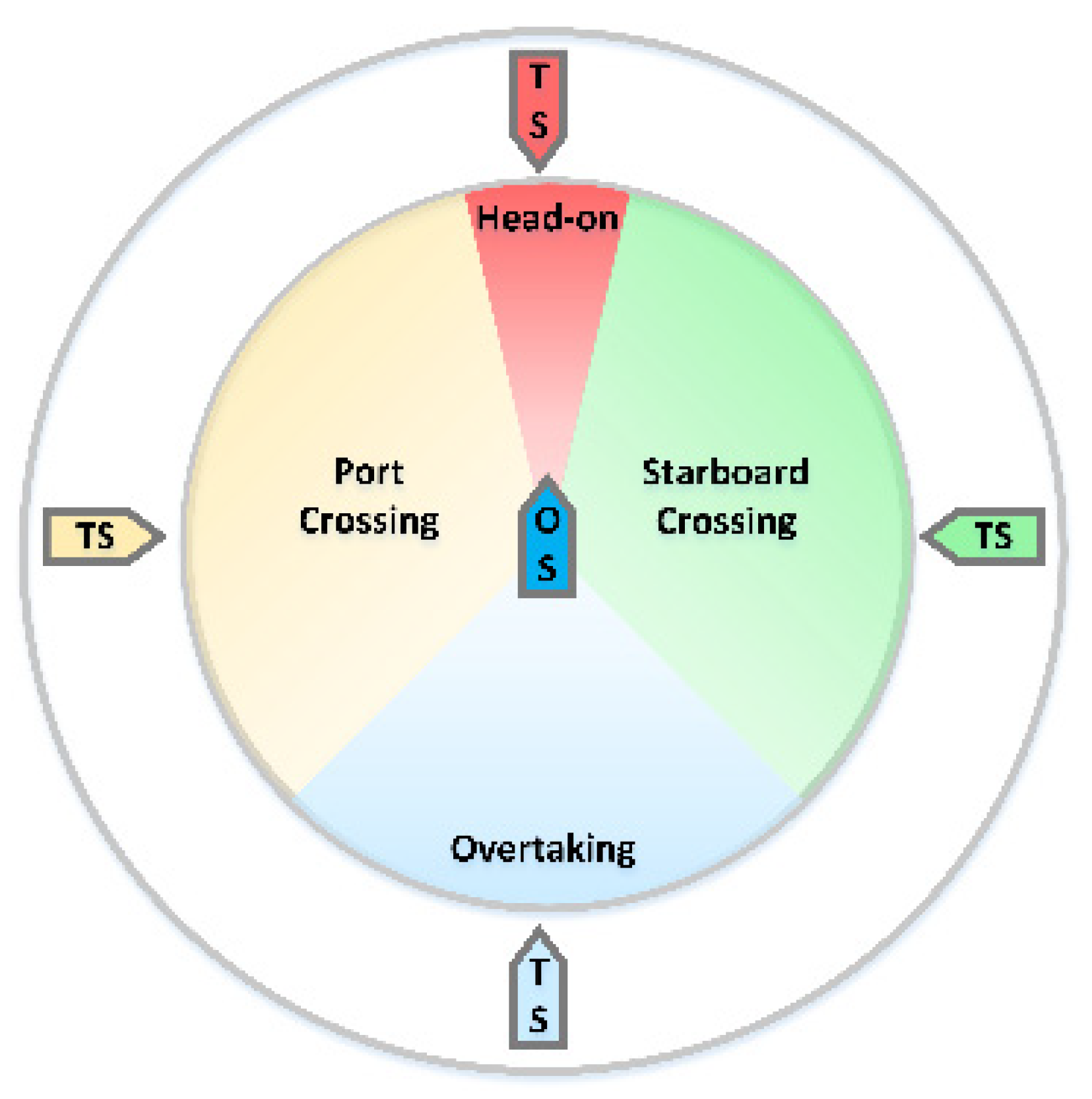
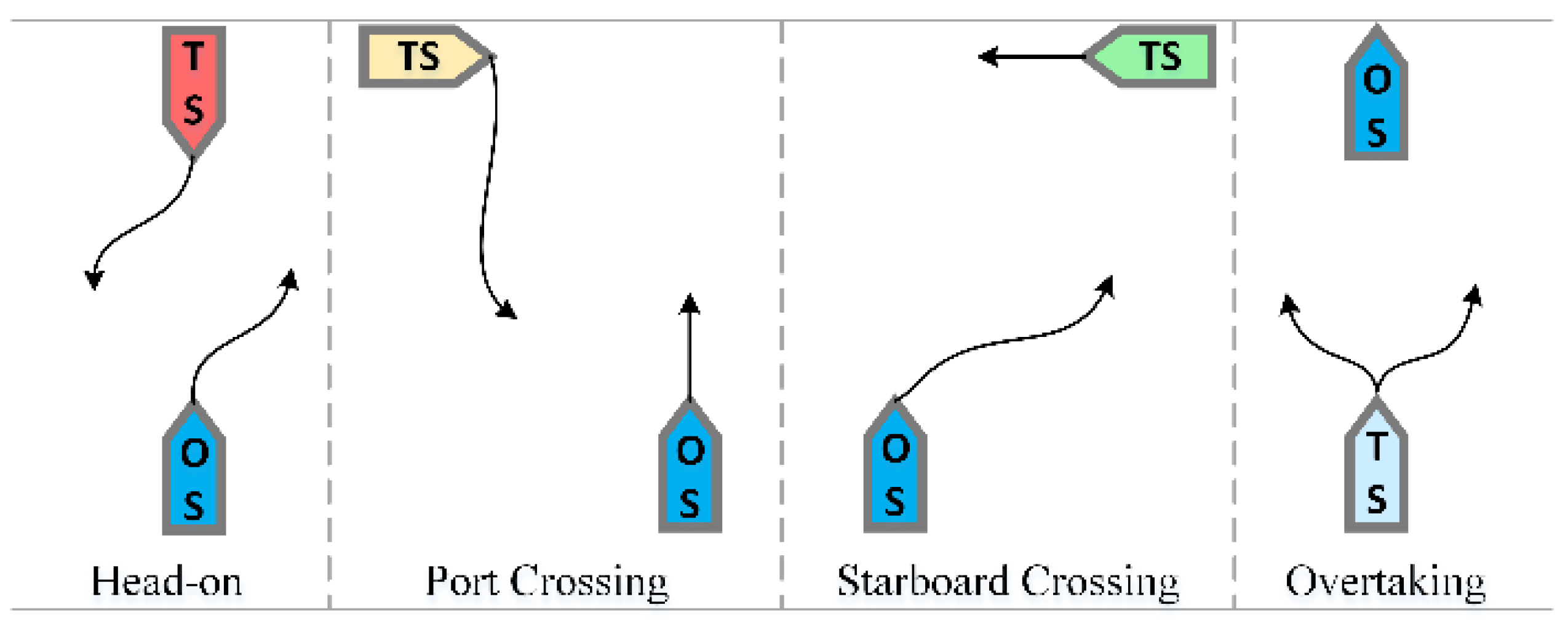
3.3. COLREGs
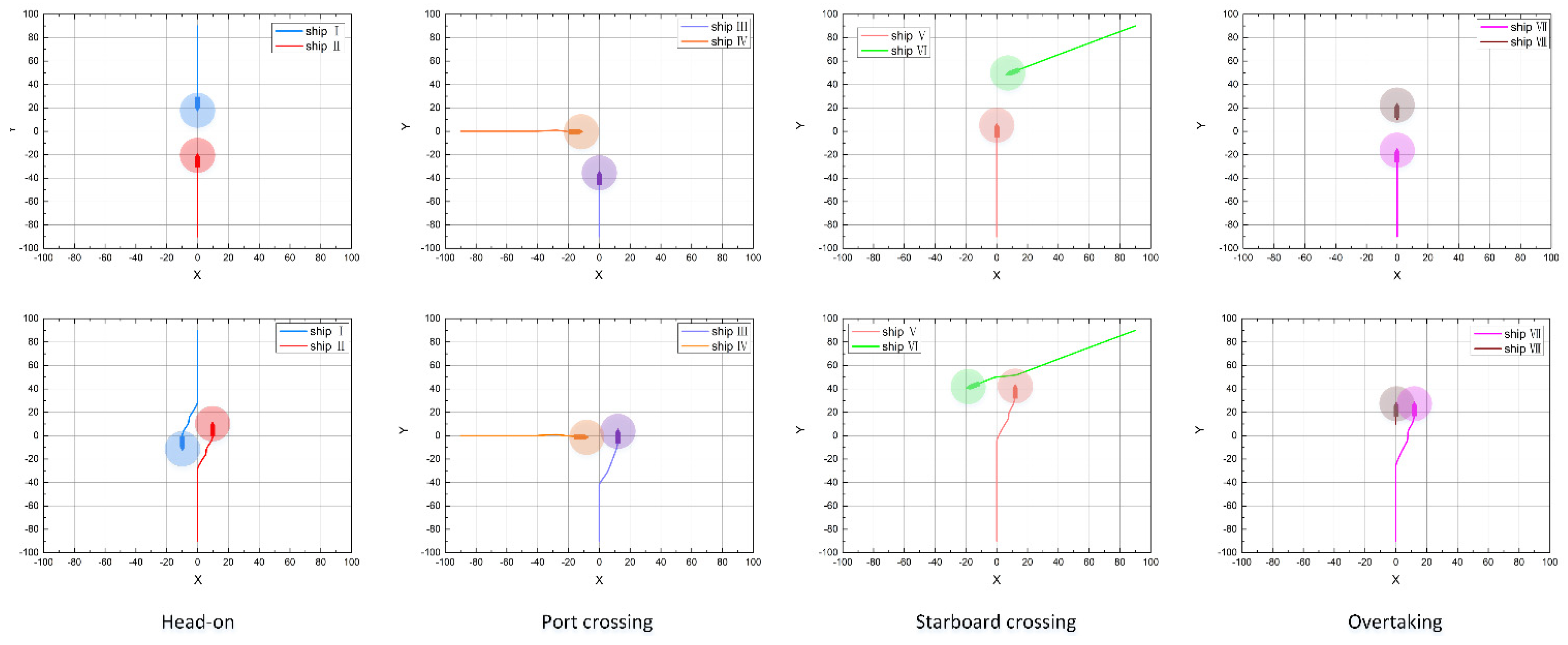
- Head-on: When two vessels (OS and TS) are meeting on opposite or approximately opposite routes within an azimuth angle of (0°, 5°) or (355°, 360°), this situation should be judged as a head-on situation. The two vessels (OS and TS) should alter their course to starboard, so that each vessel should pass on the port side of the other to avoid collision;
- Port crossing: When a vessel (OS) is crossing on its port side within an azimuth angle of 247.5–355°, this situation should be judged as a port crossing situation. The vessels (OS) are not the give-way vessels so they shall keep their original course and speed;
- Starboard crossing: When a vessel (OS) is crossing on its starboard side within an azimuth angle of 5–112.5°, this situation should be judged as the starboard crossing situation. The vessels (OS) shall alter their course to the starboard side to avoid collision;
- Overtaking: When a vessel (OS) is chasing another vessel (target-ship, TS) within an azimuth angle of 112.5–247.5° directly behind it, this situation should be judged as overtaking. The vessels (OS) shall alter their course to starboard or port side to avoid collision.
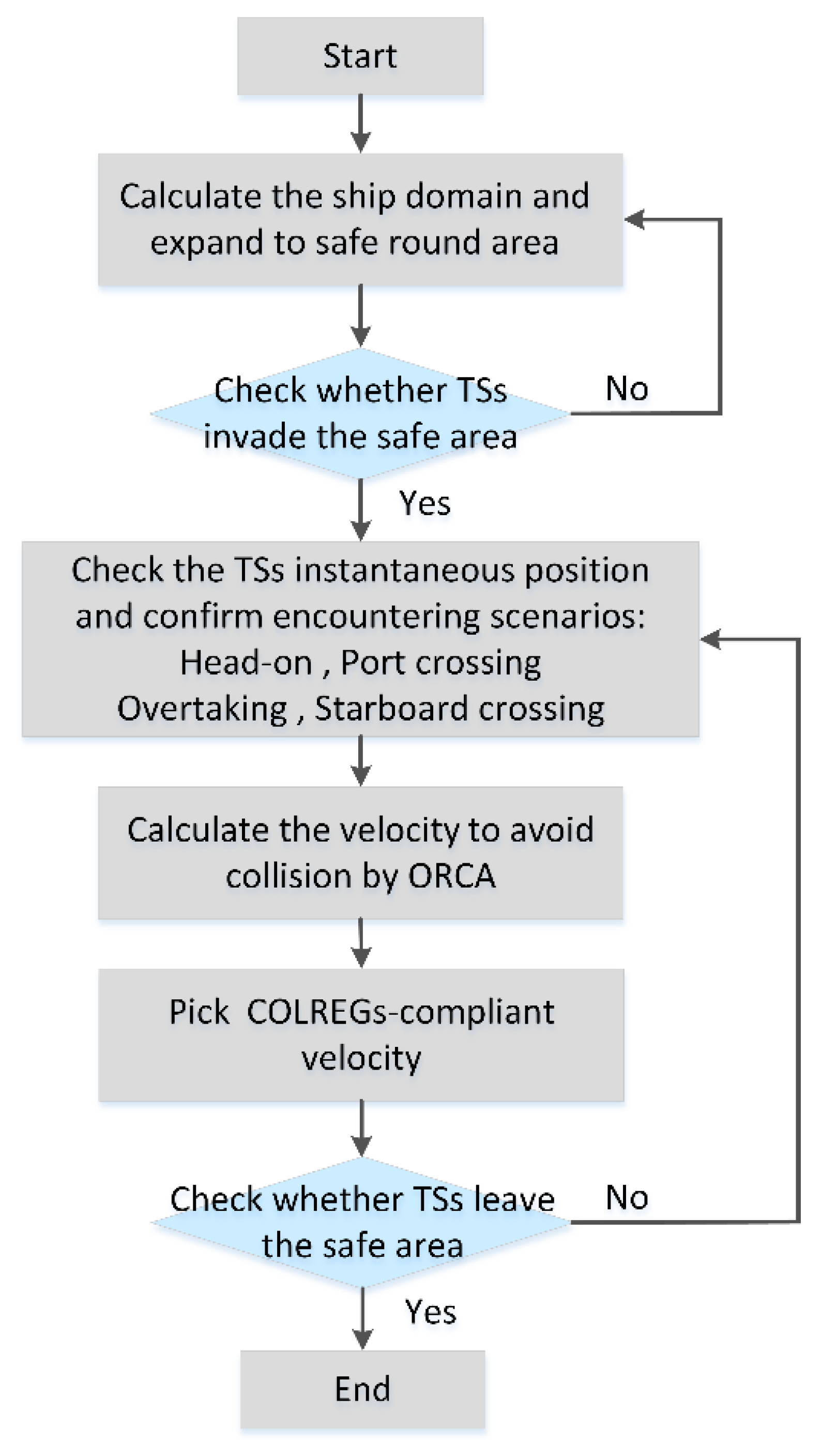
3.4. COLREGs-Based Multi-Ship Collision Avoidance
4. Algorithm Background
4.1. Algorithm Model and CTDE
4.1.1. CTDE
- Observational limitations: When the agent interacts with the environment, the agent cannot obtain the global state of the environment, and can only see the local observation information within its own observation range ;
- Instability: When multiple agents learn together, the changing strategies and the mutative actions caused mean that the value function of agent cannot stably update.
4.1.2. DEC-POMDP Model
4.2. IQL and VDN
4.3. QMIX Algoritnm
4.3.1. IGM Condition and Constraint
4.3.2. Overall Framework
- Agent network (Figure 8a): It is represented by the DRQN network. In the partially observable setting, agents using RNN can use all their action-observation history information to get the current state. Its input at each step is the current individual observation of the agent and the action at each time step;
- Hypernetwork: Hypernetwork [30] is used to calculate network weights and biases in the mixing network. Its inputs are global state inputs. The outputs are the weights and the bias, where the weights need to be greater than 0 , so the activation function is the absolute activation function. Biases use the common Relu activation function, because it does not have a requirement for the value range;
- Mixing network (Figure 8c): Its weights and biases are generated by the Hypernetwork, and its role is to mix the of each agent into a monotonic of the whole system, and to also make the training more stable by increasing the system information.
4.3.3. Algorithm Implementation
4.4. CA-QMIX Algoritnm
4.4.1. Action Space
4.4.2. State Space
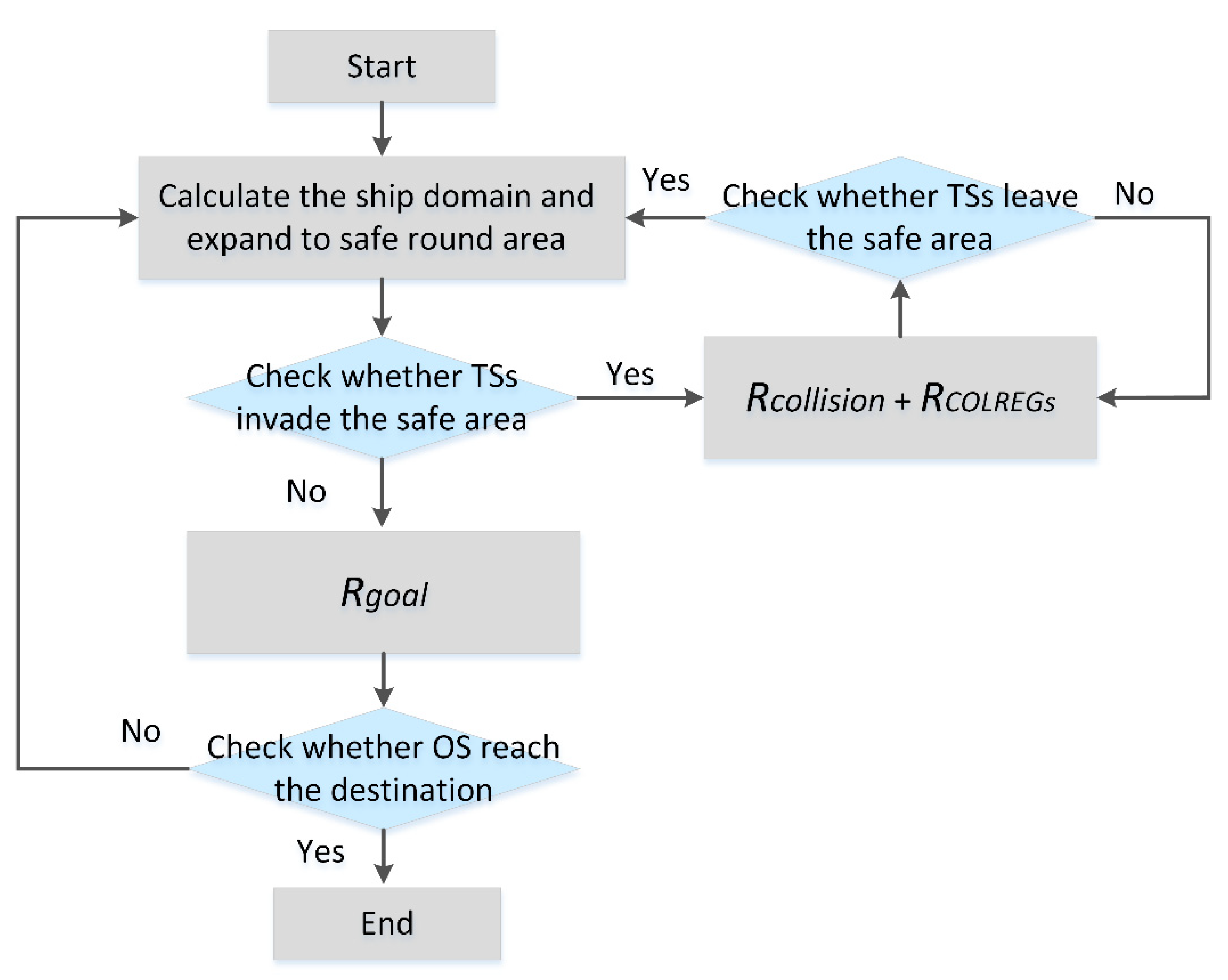
4.4.3. Reward Function
5. Method for Path Planning and Collision Avoidance Based on CA-QMIX
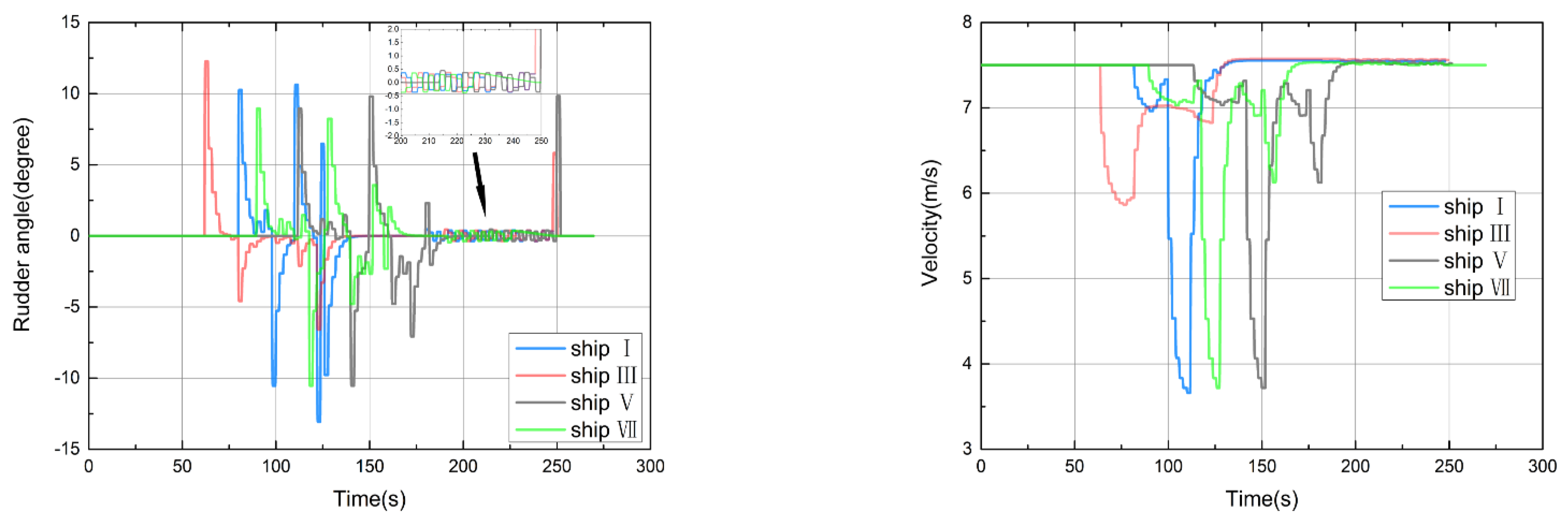
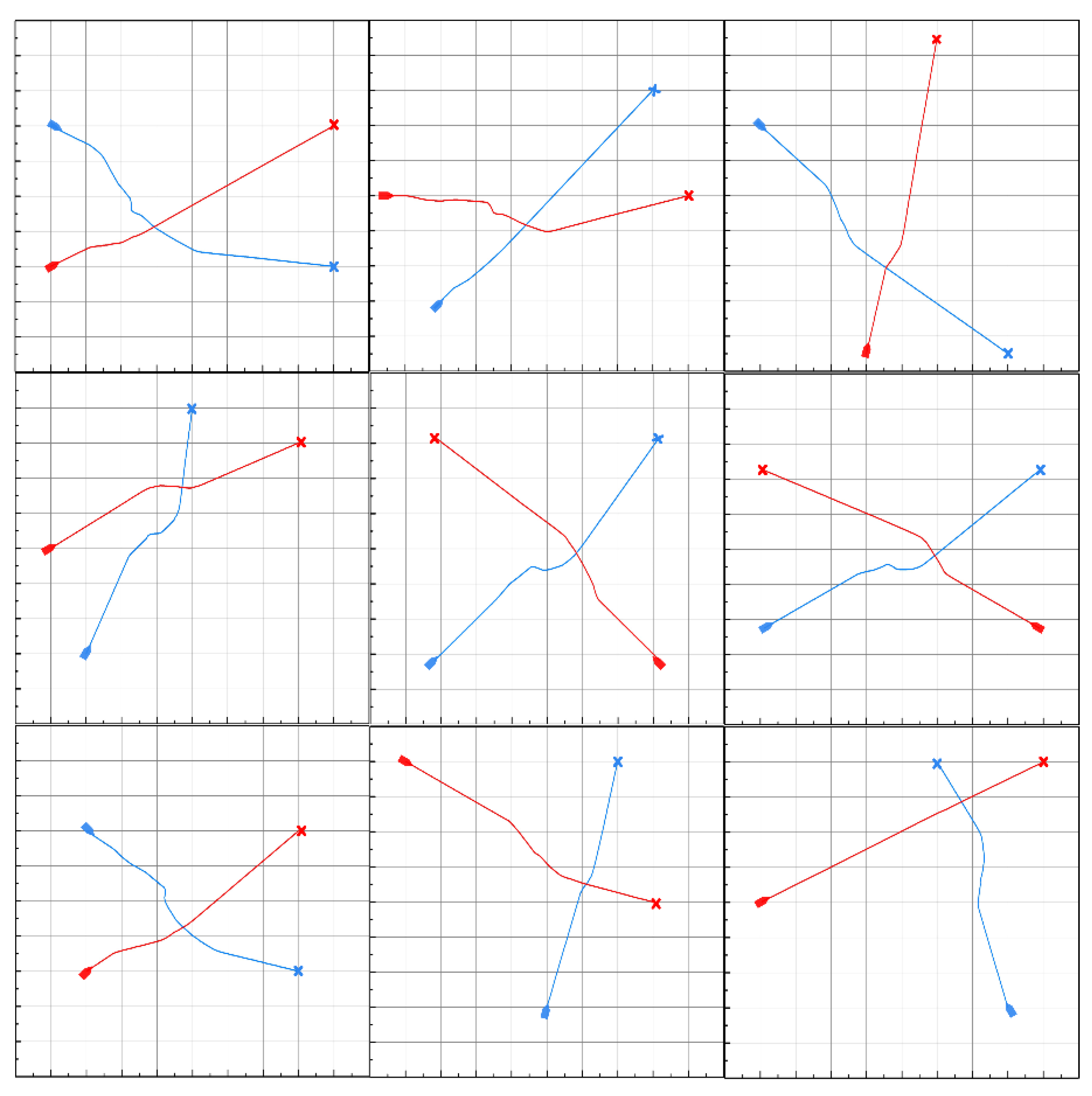
5.1. Two Ships Collision Avoidance in Four Scenarios
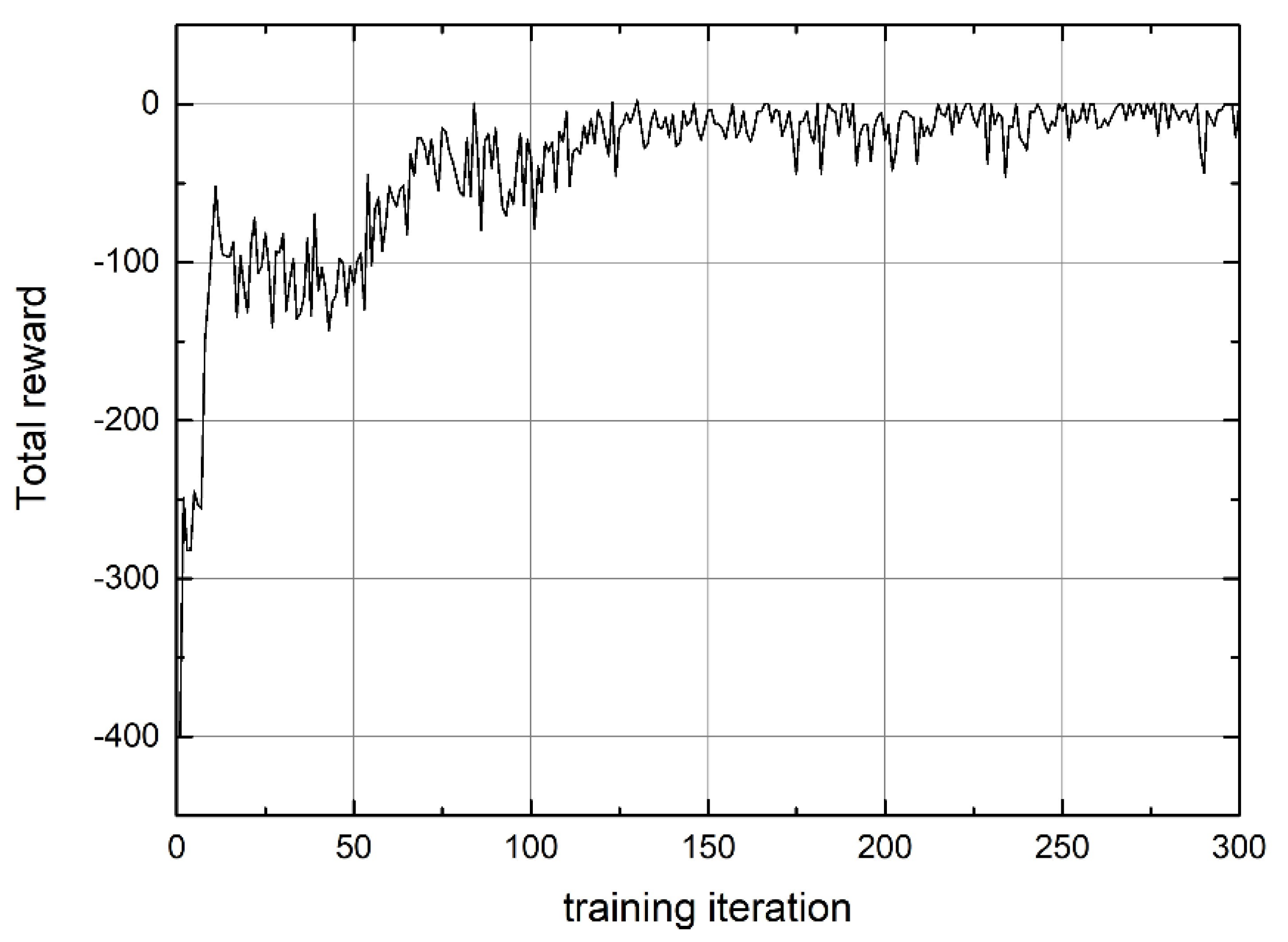
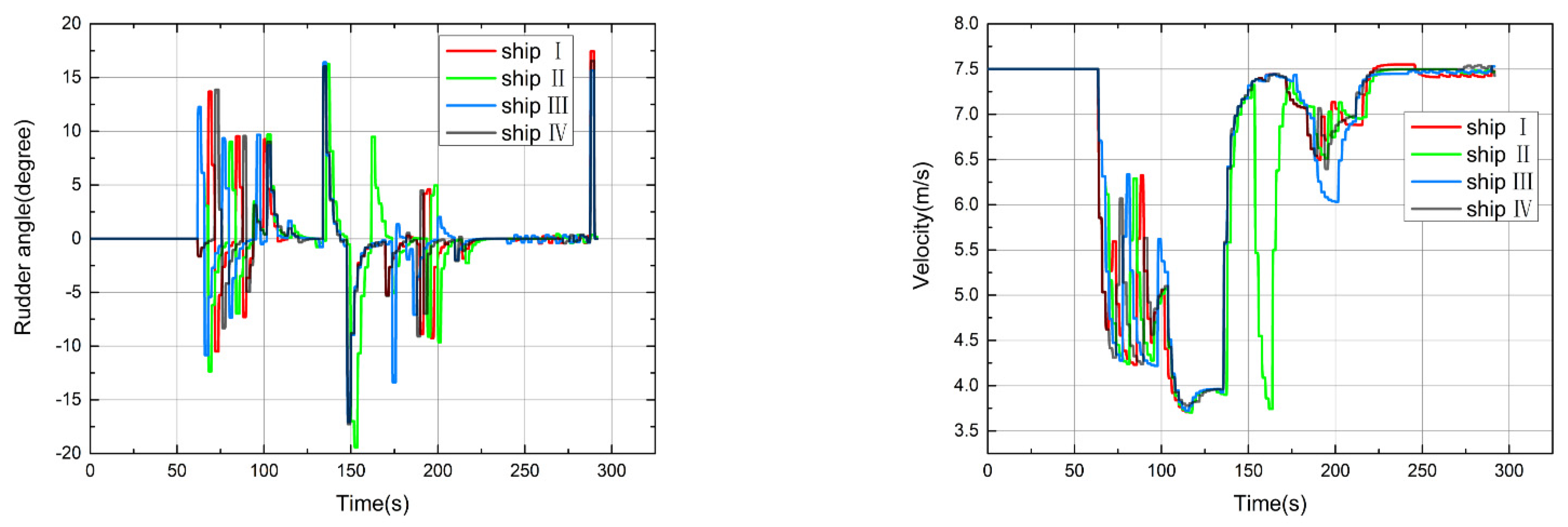
5.2. Simulation for Multi-Ship Collision Avoidance
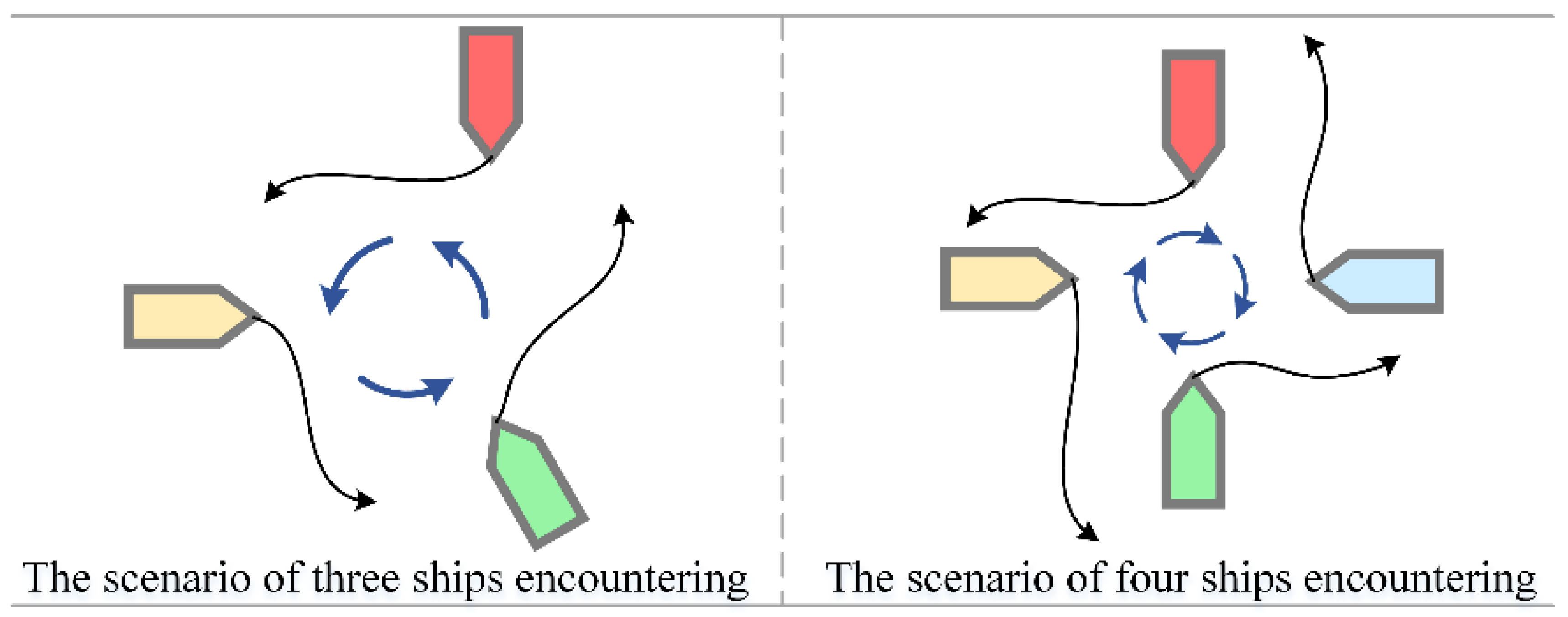
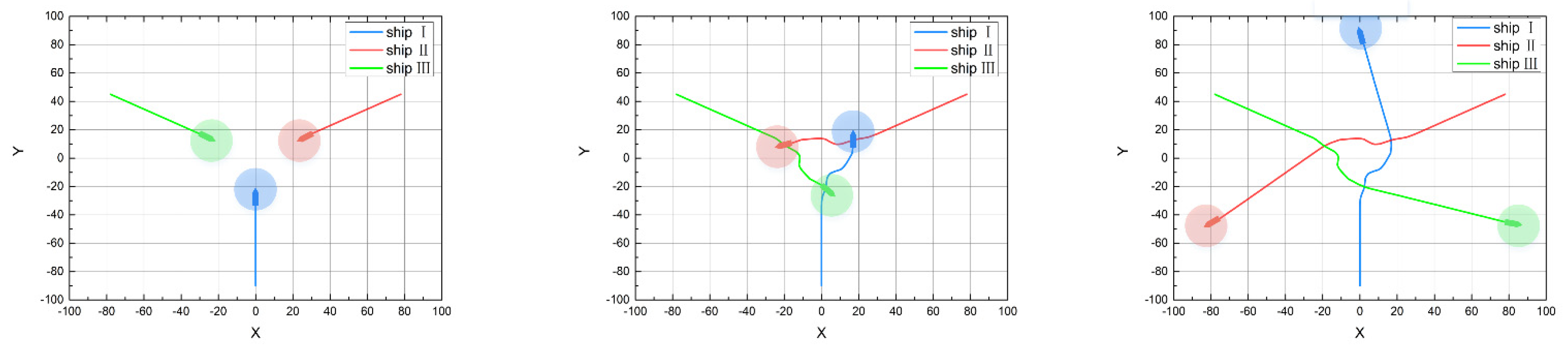
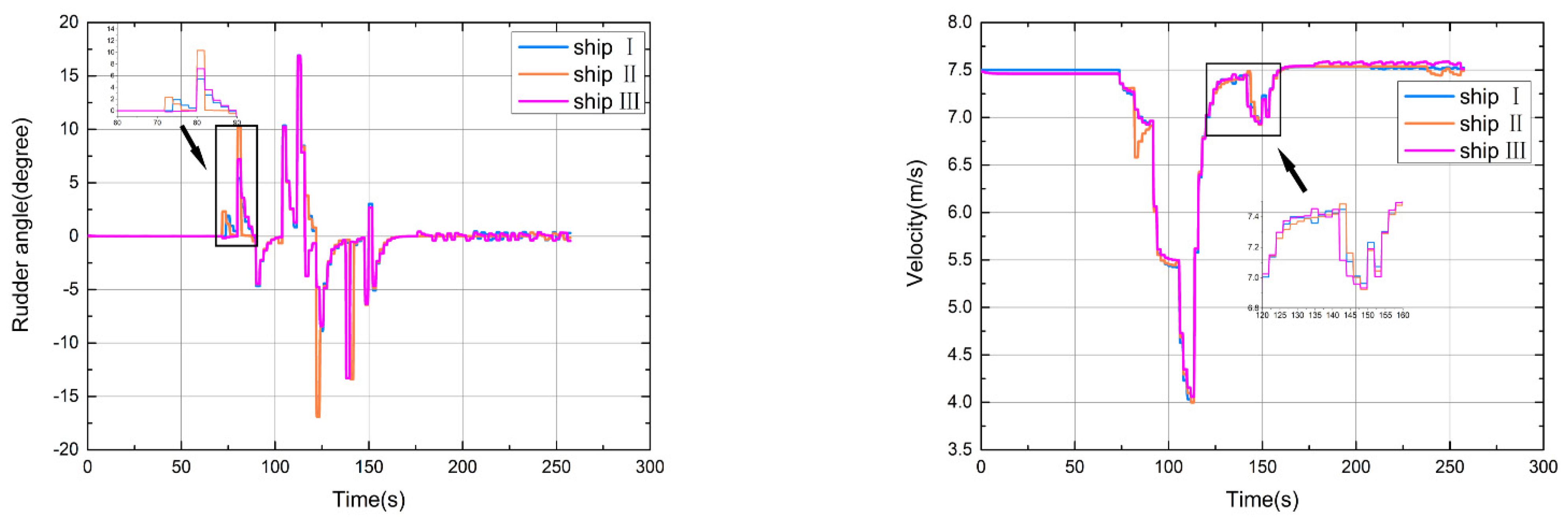
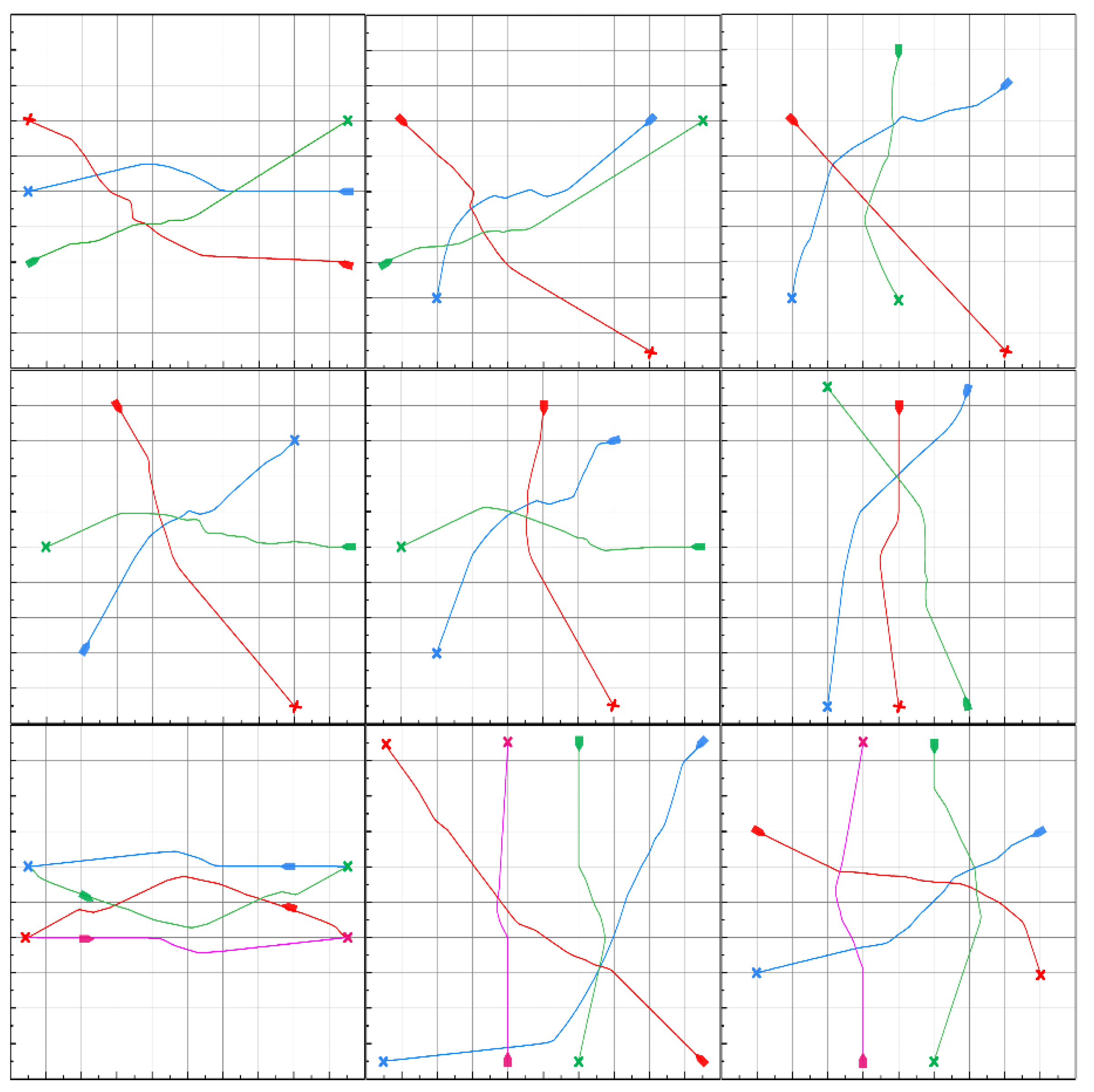
5.2.1. Three Ships Collision Avoidance Scenarios
5.2.2. Four Ships Collision Avoidance Scenarios
5.3. Complementary Simulation for Multi-Ship Collision Avoidance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, W.; Peng, H.; Zhang, X.; Sun, H. Ship Steering Adaptive CGS Control Based on EKF Identification Method. J. Mar. Sci. Eng. 2022, 10, 294. [Google Scholar] [CrossRef]
- Statheros, T.; Howells, G.; Maier, K.M.D. Autonomous ship collision avoidance navigation concepts, technologies and techniques. J. Navig. 2008, 61, 129–142. [Google Scholar] [CrossRef]
- Zhao, D.; Shao, K. Deep reinforcement learning overview: The development of computer go. Control. Theory Appl. 2016, 6, 17. [Google Scholar] [CrossRef]
- Liu, Q.; Zhai, J. A brief overview of deep reinforcement learning. Chin. J. Comput. 2018, 1, 27. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vision 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech Recognition with Deep Recurrent Neural Networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; Volume 38, pp. 6645–6649. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Miele, A.; Wang, T. Maximin approach to the ship collision avoidance problem via multiple-subarc sequential gradient-restoration algorithm. J. Optim. Theory Appl. 2005, 124, 29–53. [Google Scholar] [CrossRef]
- Phanthong, T.; Maki, T.; Ura, T.; Sakamaki, T.; Aiyarak, P. Application, Application of A* algorithm for real-time path re-planning of an unmanned surface vehicle avoiding underwater obstacles. J. Mar. Sci. Appl. 2014, 13, 105–116. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, Z.; Zhang, X. In Trajectory Optimization for ship Collision Avoidance System Using Genetic Algorithm. In Proceedings of the OCEANS 2006-Asia Pacific, Singapore, 16–19 May 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, X.; Watanabe, Y.; Deng, Y. Autonomous collision avoidance of unmanned surface vehicles based on improved a star and minimum course alteration algorithms. Appl. Ocean. Res. 2021, 113, 102755. [Google Scholar] [CrossRef]
- Wilson, P.A.; Harris, C.J.; Hong, X. A line of sight counteraction navigation algorithm for ship encounter collision avoidance. J. Navig. 2003, 56, 111–121. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Ellis-Tiew, M.-Z.; Chen, W.-C.; Wang, C.-Z. Fuzzy risk evaluation and collision avoidance control of unmanned surface vessels. Appl. Sci. 2021, 11, 6338. [Google Scholar] [CrossRef]
- Johansen, T.A.; Perez, T.; Cristofaro, A. Ship collision avoidance and COLREGS compliance using simulation-based control behavior selection with predictive hazard assessment. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3407–3422. [Google Scholar] [CrossRef]
- Hu, L.; Naeem, W.; Rajabally, E.; Watson, G.; Mills, T.; Bhuiyan, Z.; Raeburn, C.; Salter, I.; Pekcan, C. A multiobjective optimization approach for COLREGs-compliant path planning of autonomous surface vehicles verified on networked bridge simulators. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1167–1179. [Google Scholar] [CrossRef]
- Shen, H.; Hashimoto, H.; Matsuda, A.; Taniguchi, Y.; Terada, D.; Guo, C. Automatic collision avoidance of multiple ships based on deep Q-learning. Appl. Ocean. Res. 2019, 86, 268–288. [Google Scholar] [CrossRef]
- Sawada, R.; Sato, K.; Majima, T. Automatic ship collision avoidance using deep reinforcement learning with LSTM in continuous action spaces. J. Mar. Sci. Technol. 2021, 26, 509–524. [Google Scholar] [CrossRef]
- Li, L.; Wu, D.; Huang, Y.; Yuan, Z.-M. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean. Res. 2021, 113, 102759. [Google Scholar] [CrossRef]
- Zhao, L.; Roh, M.-I. COLREGs-compliant multiship collision avoidance based on deep reinforcement learning. Ocean. Eng. 2019, 191, 106436. [Google Scholar] [CrossRef]
- Xu, X.; Lu, Y.; Liu, X.; Zhang, W. Intelligent collision avoidance algorithms for USVs via deep reinforcement learning under COLREGs. Ocean. Eng. 2020, 217, 107704. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley and Sons: Chichester, UK, 1999; ISBN 0 471 94113 1. [Google Scholar]
- Perez, T.; Ross, A.; Fossen, T. A 4-dof Simulink Model of a Coastal Patrol Vessel for Manoeuvring in Waves. In Proceedings of the 7th IFAC Conference on Manoeuvring and Control of Marine Craft, International Federation for Automatic Control, Lisbon, Portugal, 20–22 September 2006; pp. 1–6. [Google Scholar]
- Alonso-Mora, J.; Breitenmoser, A.; Rufli, M.; Beardsley, P.; Siegwart, R. Optimal Reciprocal Collision Avoidance for Multiple Non-Holonomic Robots; Springer: Berlin/Heidelberg, Germany, 2013; pp. 203–216. [Google Scholar] [CrossRef]
- Śmierzchalski, R. Ships’ Domains as Collision Risk at Sea in the Evolutionary Method of Trajectory Planning. In Information Processing and Security Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 411–422. [Google Scholar] [CrossRef]
- Oliehoek, F.A.; Span, M.T.; Vlassis, N. Optimal and approximate q-value functions for decentralized POMDPs. J. Artif. Intell. Res. 2008, 32, 289–353. [Google Scholar] [CrossRef]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Busoniu, L.; Babuška, R.; De Schutter, B. Multi-Agent Reinforcement Learning: An Overview. In Innovations in Multi-Agent Systems and Applications-1; Springer: Berlin/Heidelberg, Germany, 2008; Volume 38, pp. 156–172. [Google Scholar] [CrossRef]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-decomposition networks for cooperative multi-agent learning. arXiv 2017, arXiv:1706.05296. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. Qmix: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4295–4304. [Google Scholar]
- Ha, D.; Dai, A.; Le, Q. Hypernetworks. arXiv 2016, arXiv:1609.09106. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]




| Type | Reference | Technique | Advantages | Disadvantages |
|---|---|---|---|---|
| Ship collision avoidance | [8] | ulti-subarc sequential gradient-restoration algorithm | Solving two cases of the collision avoidance problem | Ship‘s actions do not conform to COLREGs |
| [9] | A star algorithm | Avoiding against the stationary and dynamic obstacles with the optimal trajectory | ||
| [10] | Genetic algorithm | Avoiding collision and seek the trajectory | ||
| COLREGs-compliant ship collision avoidance | [11] | A line of sight counteraction navigation algorithm | Two-ship collision avoidance complied with COLREGs | When the ship encounters more complex scenarios, such as four ships will collide at the same time, these methods cannot achieve collision avoidance navigation |
| [12] | Minimum course alteration algorithm | Avoid moving ships or obstacles constrained by COLREGs | ||
| [13] | Nonlinear optimal control method | Collision risk and collision avoidance acting timing are developed | ||
| [14] | Model predictive control | COLREGs and collision hazards associated with each of the alternative control behaviors are evaluated on a finite prediction horizon | ||
| [15] | Multi-objective optimization algorithm | Cooperating a hierarchical sorting rule | ||
| COLREGs-compliant multi-ship collision avoidance based on DRL | [16] | DRL incorporated the ship maneuverability, human experience and COLREGs | The experimental validation of three self-propelled ships | Discrete action element |
| [17] | DRL in continuous action space | The risk of collision is reduced | Poor convergence | |
| [18] | Utilizing the artificial potential field (APF) algorithm to improve DRL | Improving the action space and reward function of DRL | - | |
| [19] | The policy-gradient based DRL algorithm | Multi-ship collision avoidance | Heading angle retention | |
| [20] | DDPG | The method can give reasonable collision avoidance actions and realize effective collision avoidance | - |
| Parameters | Value |
|---|---|
| Length (m) | 52.5 |
| Beam (m) | 8.6 |
| Draft (m) | 2.29 |
| Rudder area (m2) | 1.5 |
| Max rudder angle (deg) | 40 |
| Max rudder angle rate (deg/s) | 20 |
| Nominal speed (kt) | 15 |
| K index | −0.085 |
| T index | 4.2 |
| Parameter | Value | |
|---|---|---|
| Discounted rate | 0.99 | |
| Lambda | 0.95 | |
| Time steps | T max | 10,000 |
| The epoch of target network | E | 100 |
| The learning rate for RMSprop | r RMS | 5 × 10–4 |
| Clipping hyperparameter | 1 | |
| Scenario | Ship Number | Origin (m) | Destination (m) |
|---|---|---|---|
| Head-on | I | (0, 900) | (0, −900) |
| II | (0, −900) | (0, 900) | |
| Port crossing | III | (0, −900) | (0, 900) |
| IV | (−900, 0) | (900, 0) | |
| Starboard crossing | V | (0, −900) | (0, 900) |
| VI | (900, 900) | (−900, 0) | |
| Overtaking | VII | (0, −900) | (0, 900) |
| VIII | (0, 100) | (0, 300) |
| Scenario | Ship Number | Origin (m) | Destination (m) |
|---|---|---|---|
| Three ships | Ship I | (0, 900) | (0, −900) |
| Ship II | (779.4, 450) | (−779.4, −450) | |
| Ship III | (−779.4, 450) | (779.4, −450) | |
| Four ships | Ship I | (0, −900) | (0, 900) |
| Ship II | (−900, 0) | (900, 0) | |
| Ship III | (0, 900) | (0, −900) | |
| Ship IV | (900, 0) | (−900, 0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, G.; Kuo, W. COLREGs-Compliant Multi-Ship Collision Avoidance Based on Multi-Agent Reinforcement Learning Technique. J. Mar. Sci. Eng. 2022, 10, 1431. https://doi.org/10.3390/jmse10101431
Wei G, Kuo W. COLREGs-Compliant Multi-Ship Collision Avoidance Based on Multi-Agent Reinforcement Learning Technique. Journal of Marine Science and Engineering. 2022; 10(10):1431. https://doi.org/10.3390/jmse10101431
Chicago/Turabian StyleWei, Guan, and Wang Kuo. 2022. "COLREGs-Compliant Multi-Ship Collision Avoidance Based on Multi-Agent Reinforcement Learning Technique" Journal of Marine Science and Engineering 10, no. 10: 1431. https://doi.org/10.3390/jmse10101431
APA StyleWei, G., & Kuo, W. (2022). COLREGs-Compliant Multi-Ship Collision Avoidance Based on Multi-Agent Reinforcement Learning Technique. Journal of Marine Science and Engineering, 10(10), 1431. https://doi.org/10.3390/jmse10101431







