Mechanism of Mechanical Analysis on Torsional Buckling of U-Shaped Bellows in FLNG Cryogenic Hoses
Abstract
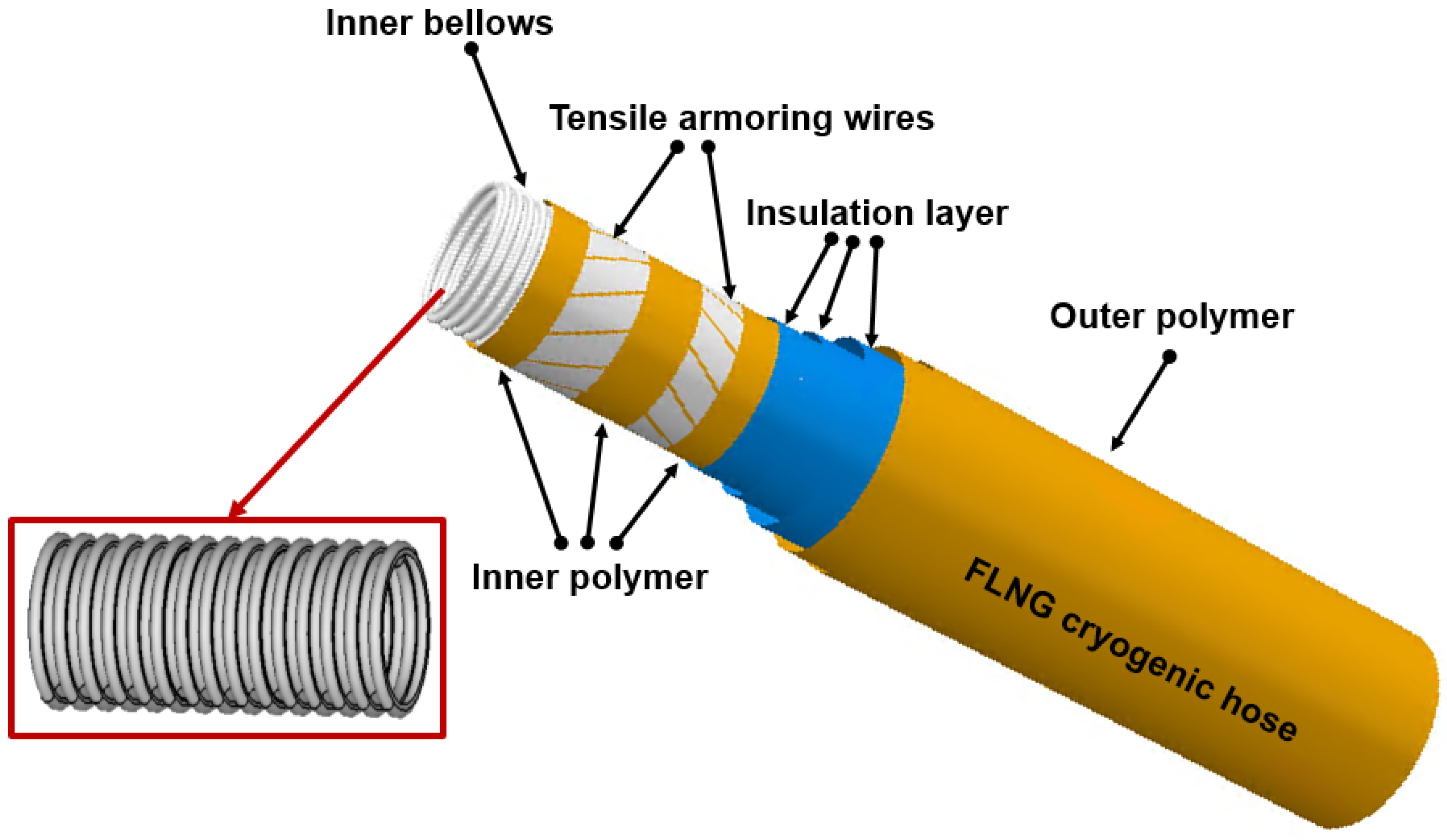
:1. Introduction
2. Linear Buckling Analysis of Bellows under Torque
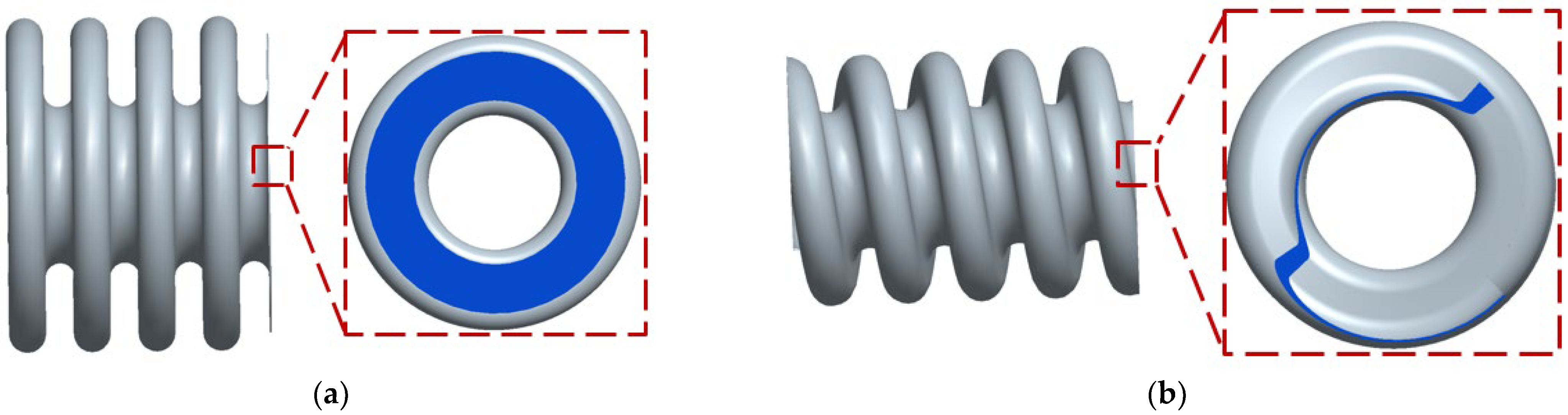
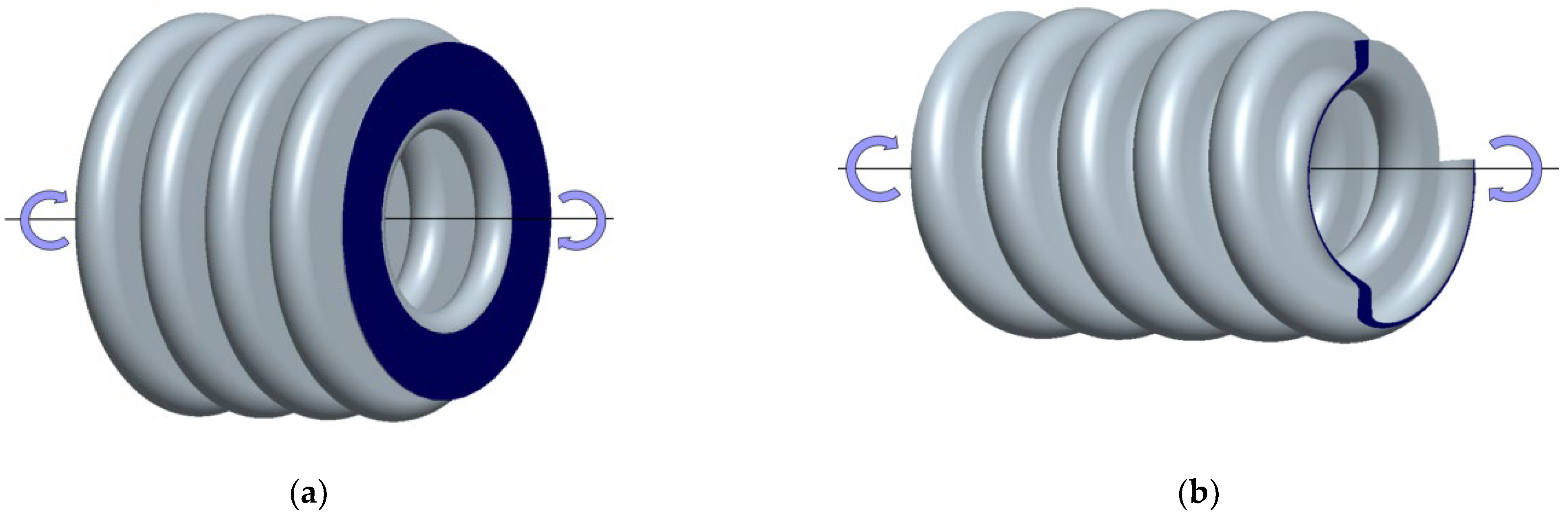
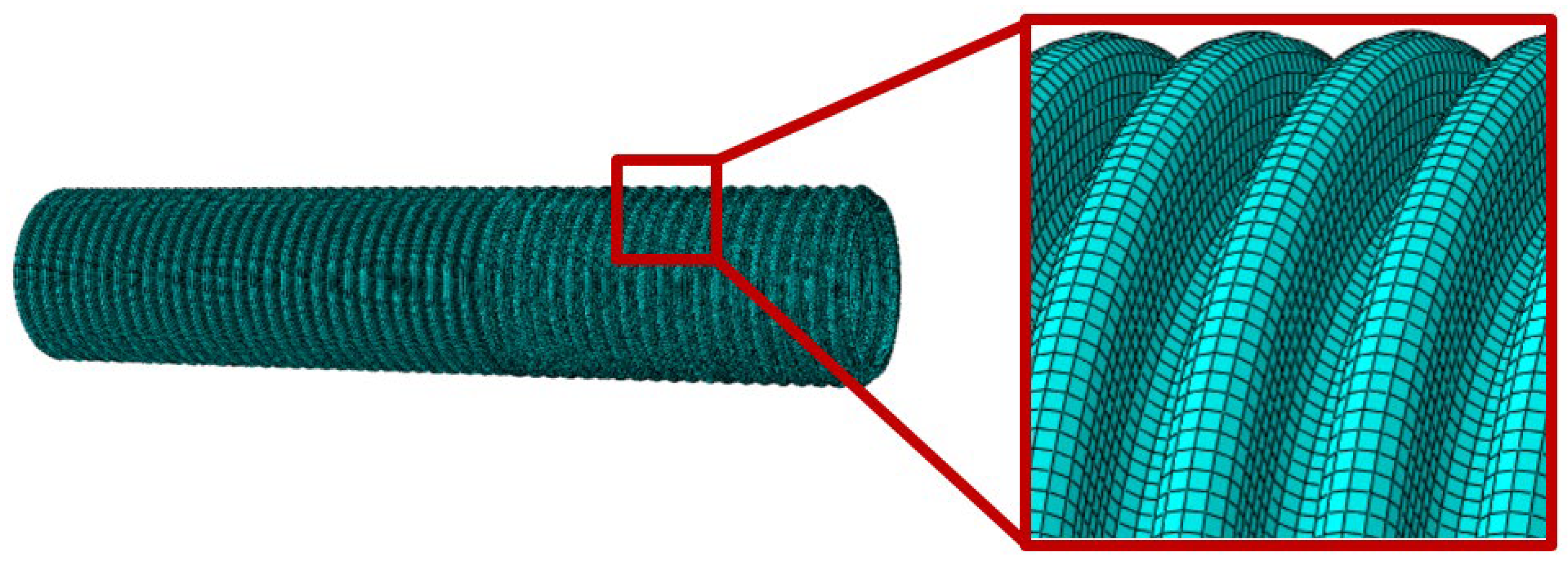
2.1. Bellow Models
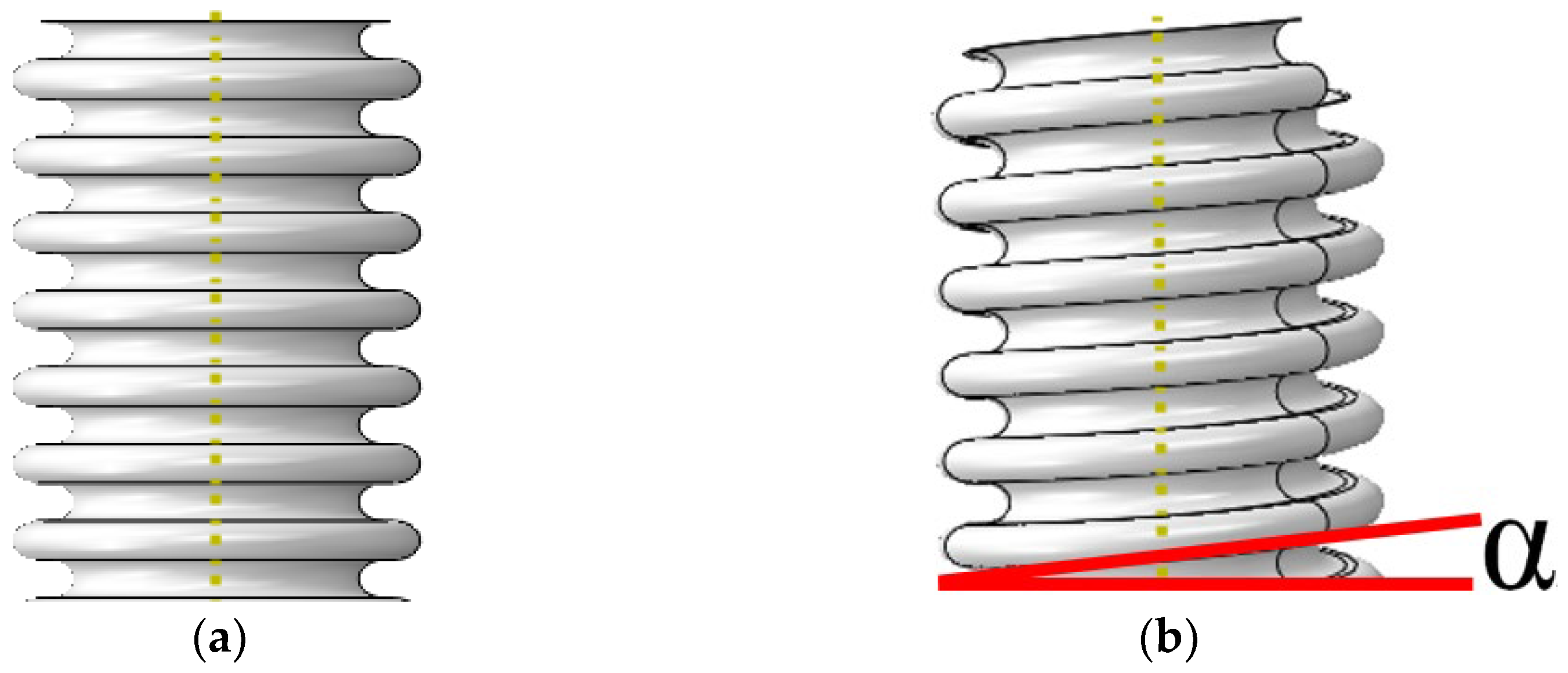
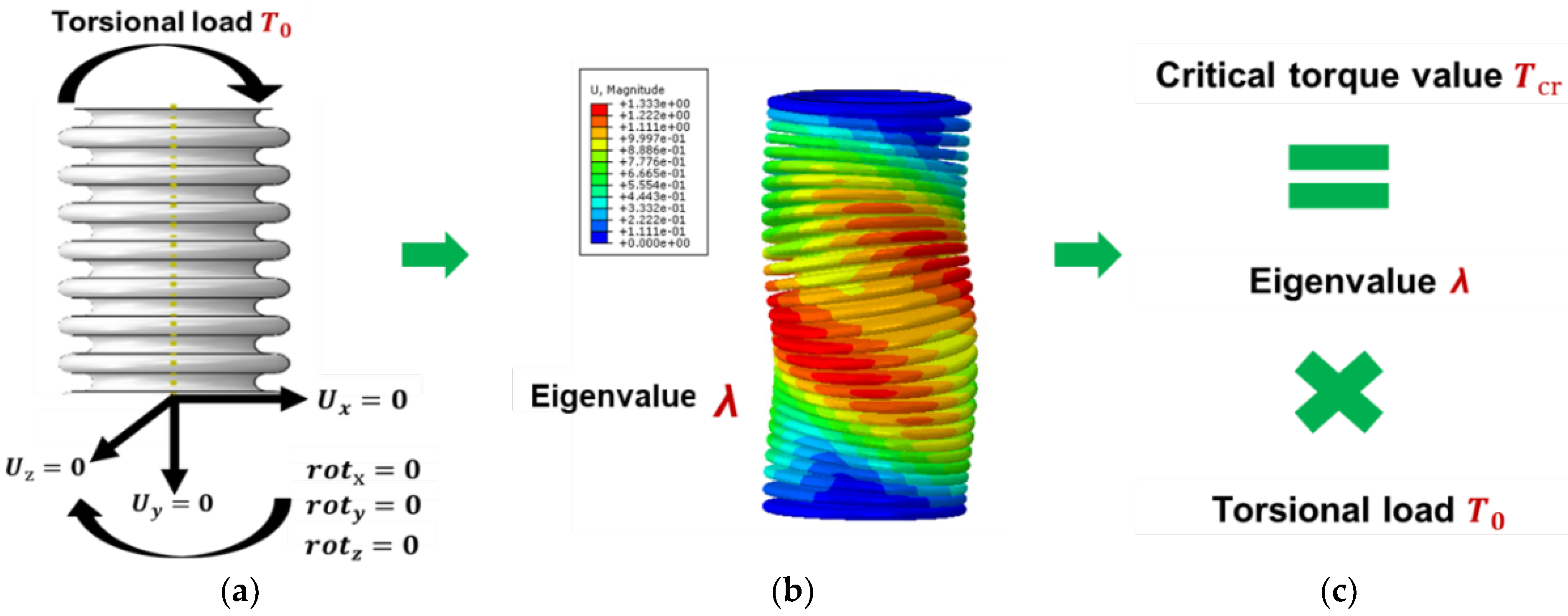
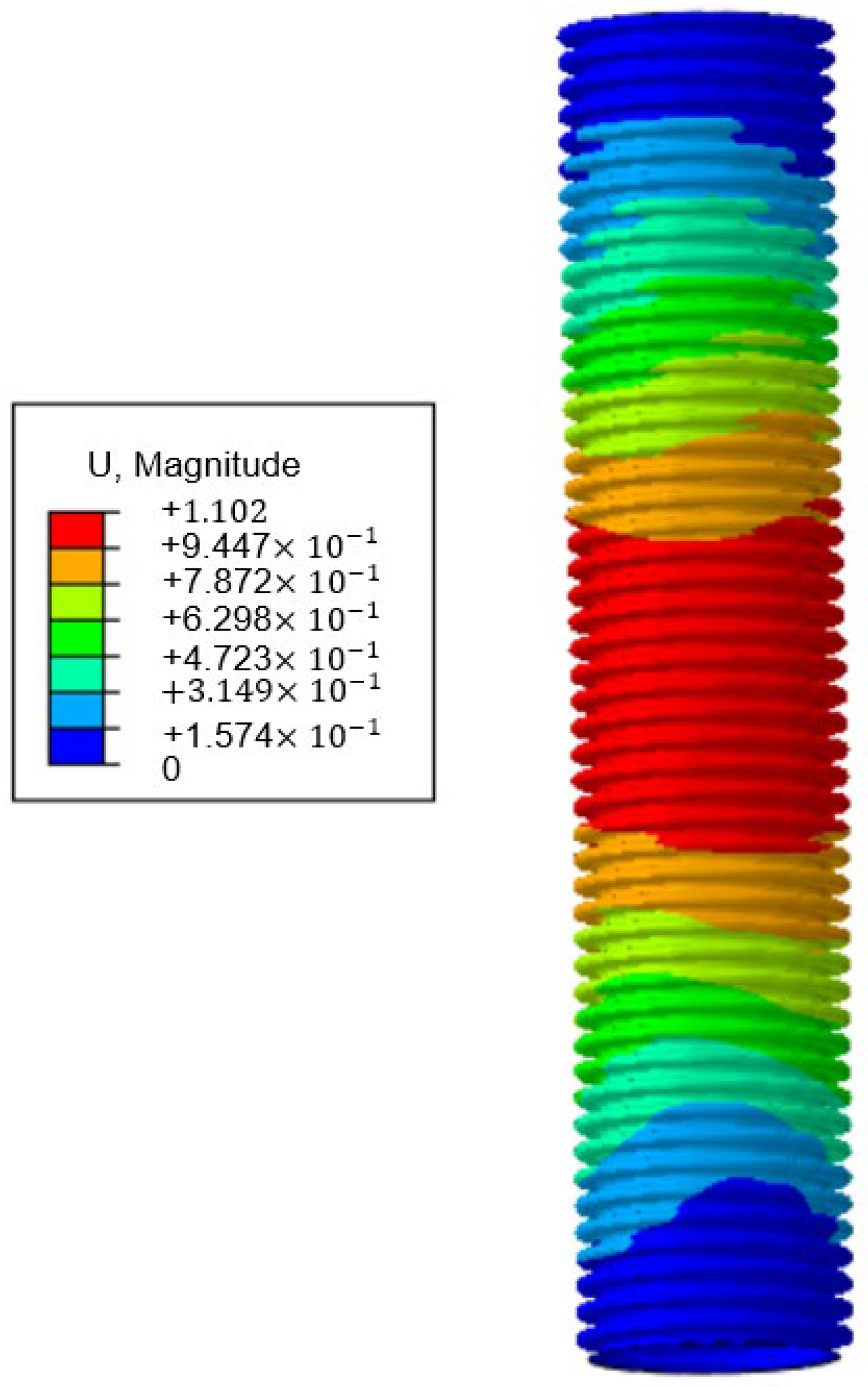
2.2. Linear Torsional Buckling Mode
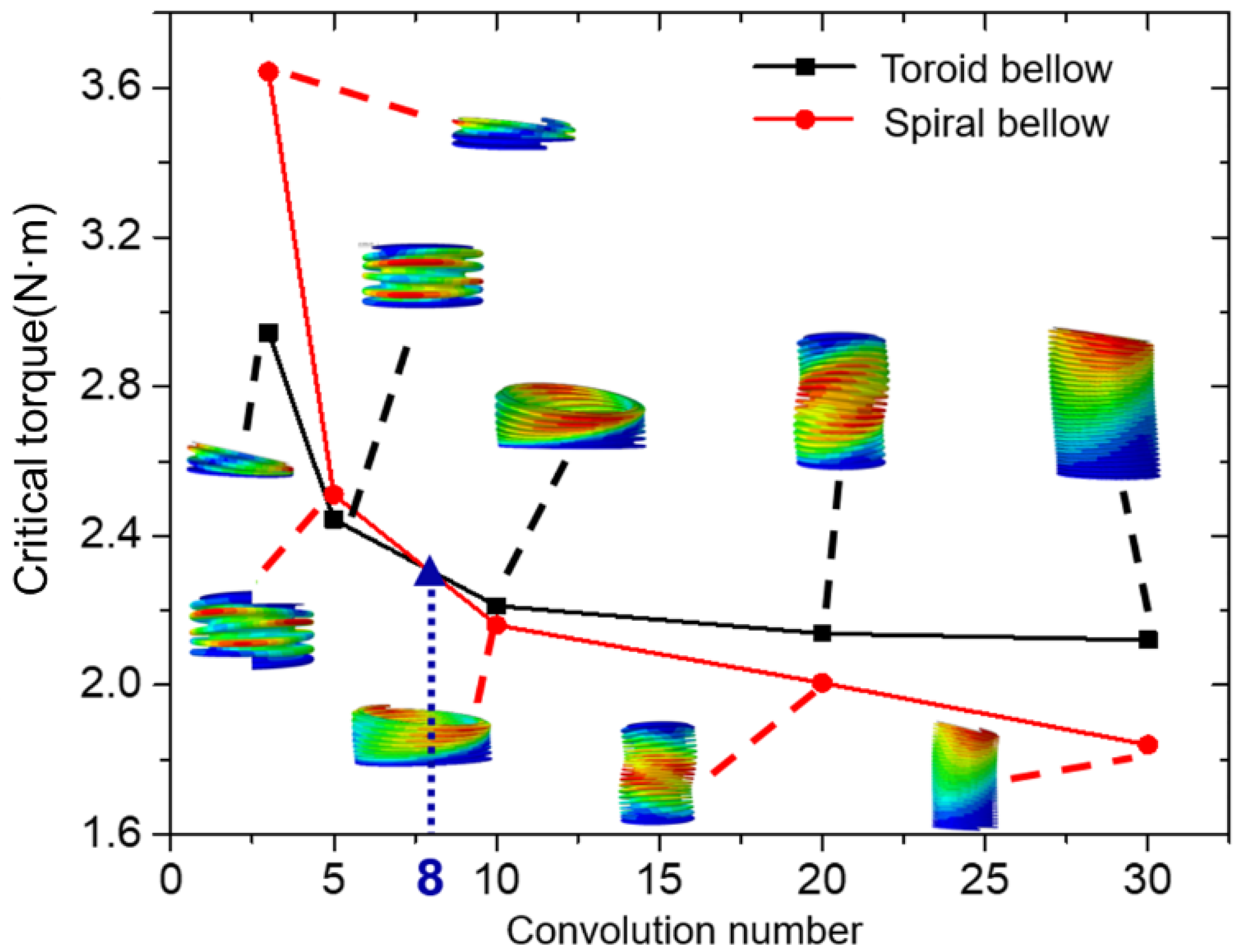
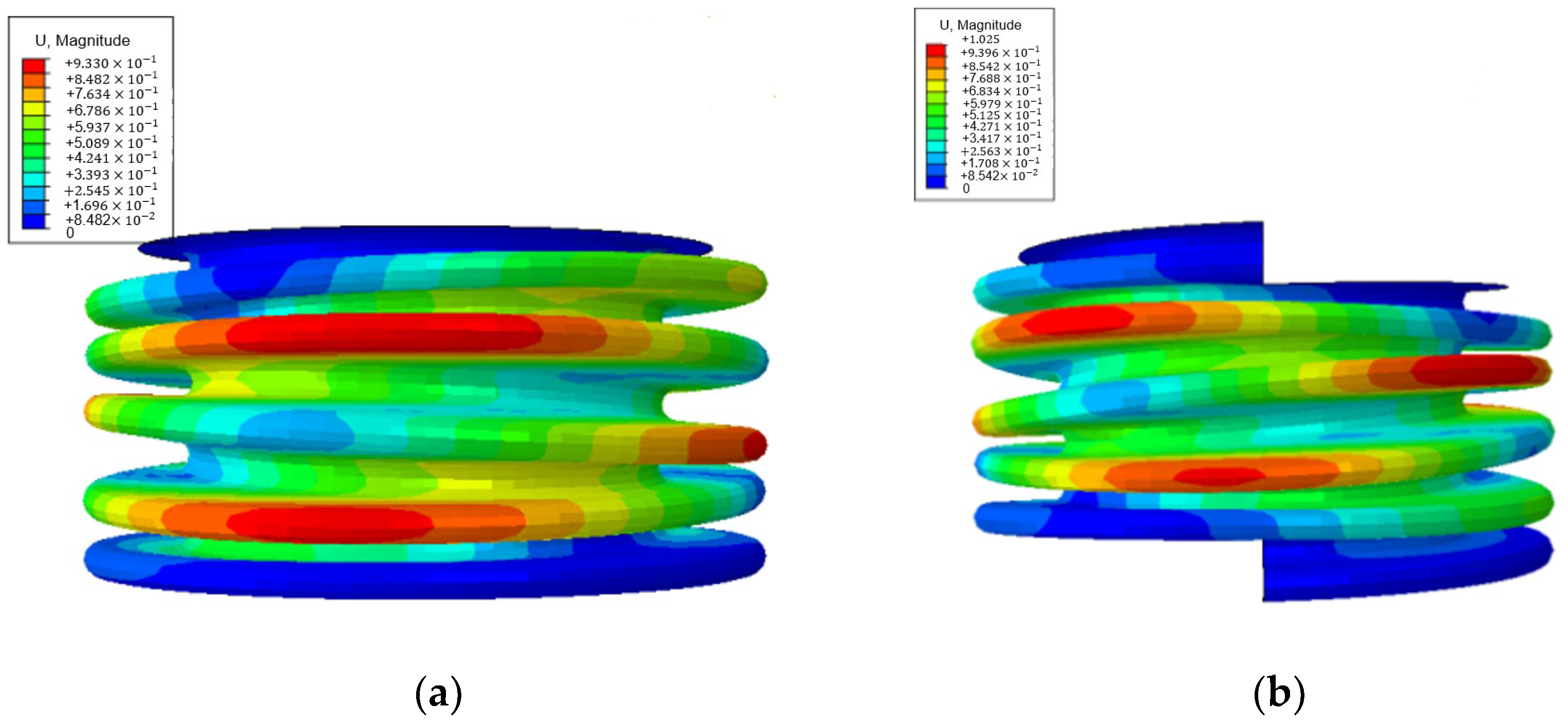
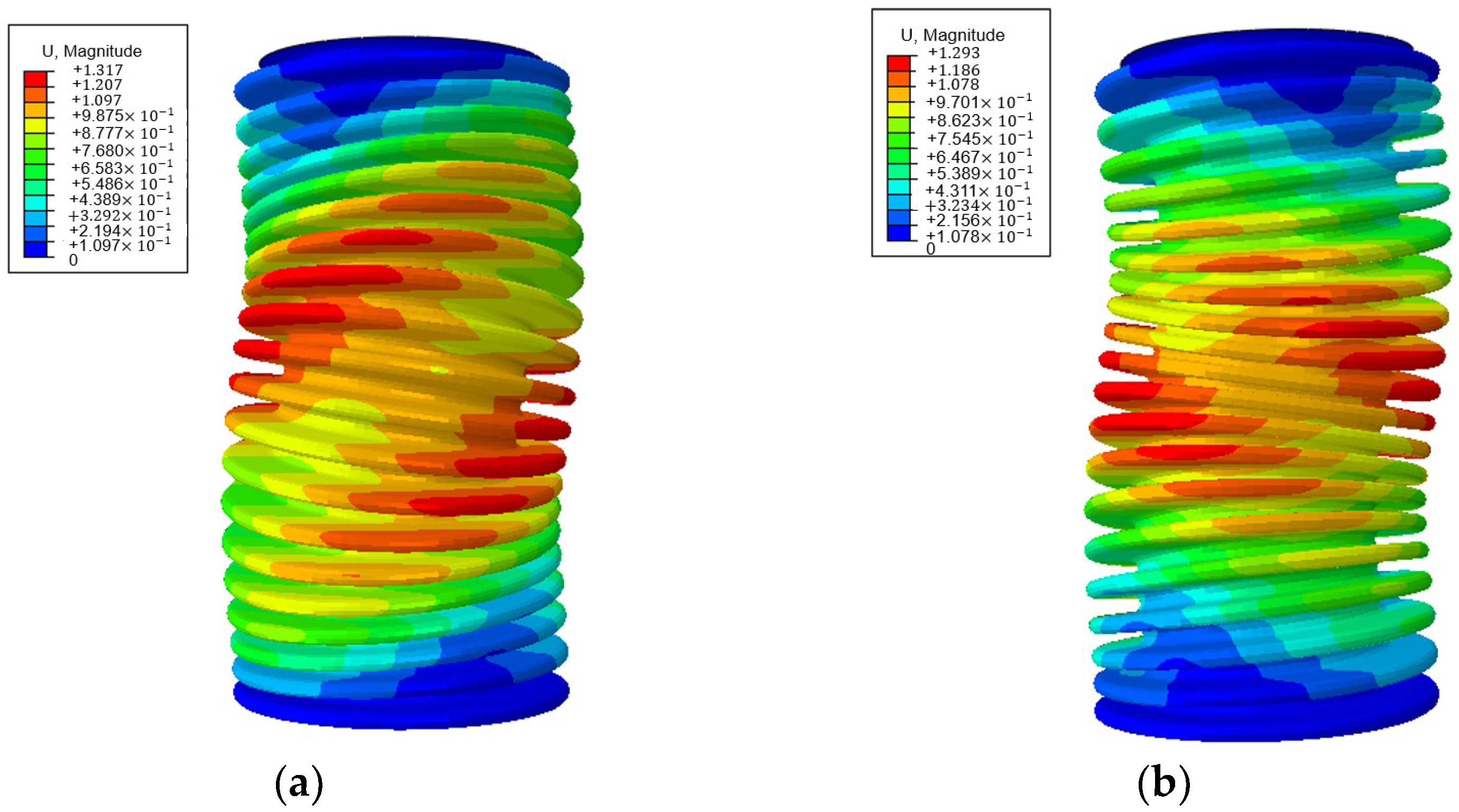
2.3. Torsional Buckling Performance Influenced by Convolution Number
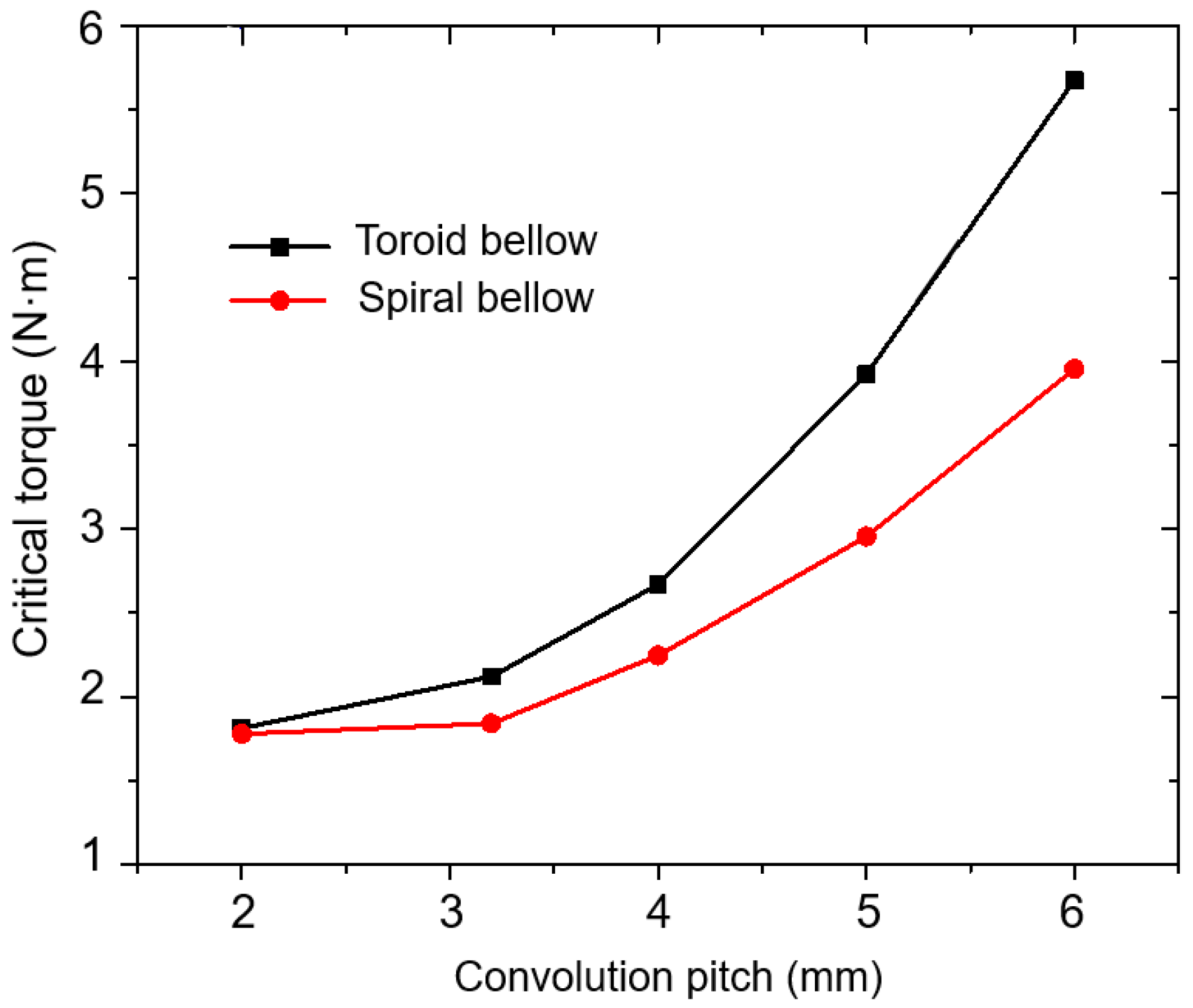
2.4. Torsional Buckling Performance Influenced by Convolution Pitch
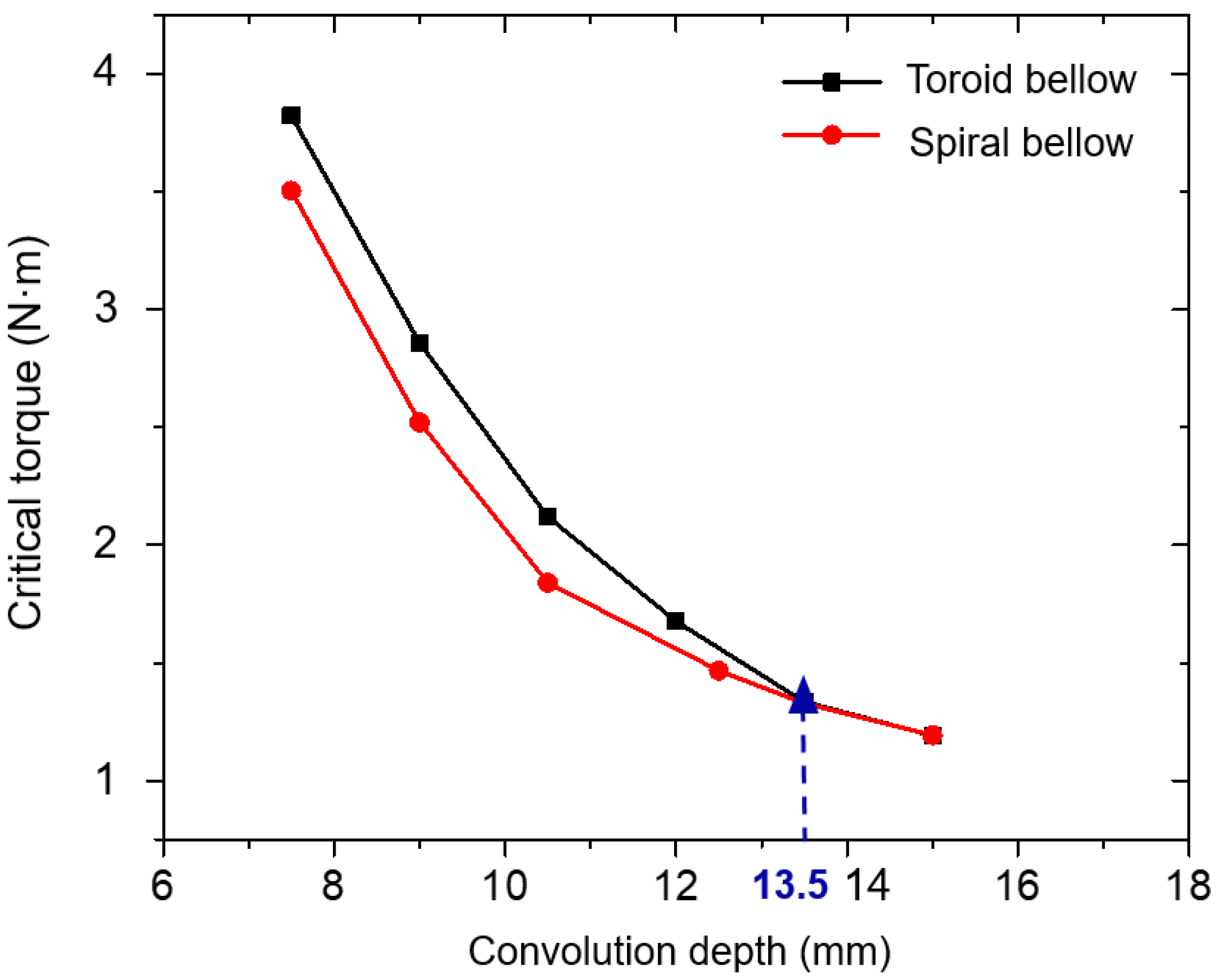
2.5. Torsional Buckling Performance Influenced by Convolution Depth
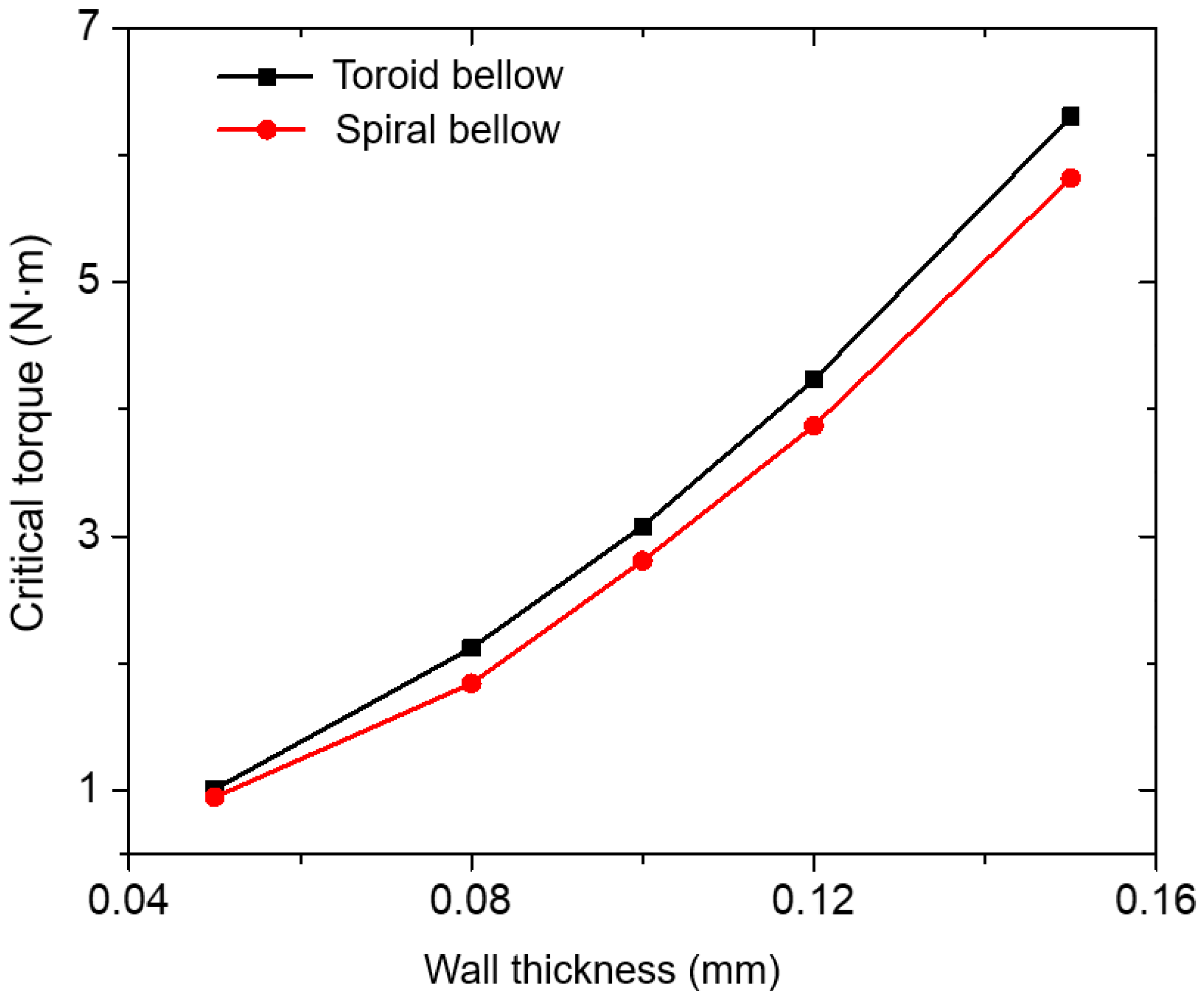
2.6. Torsional Buckling Performance Influenced by Wall Thickness
3. Post-Buckling of Torsional Buckling Analysis of Bellows
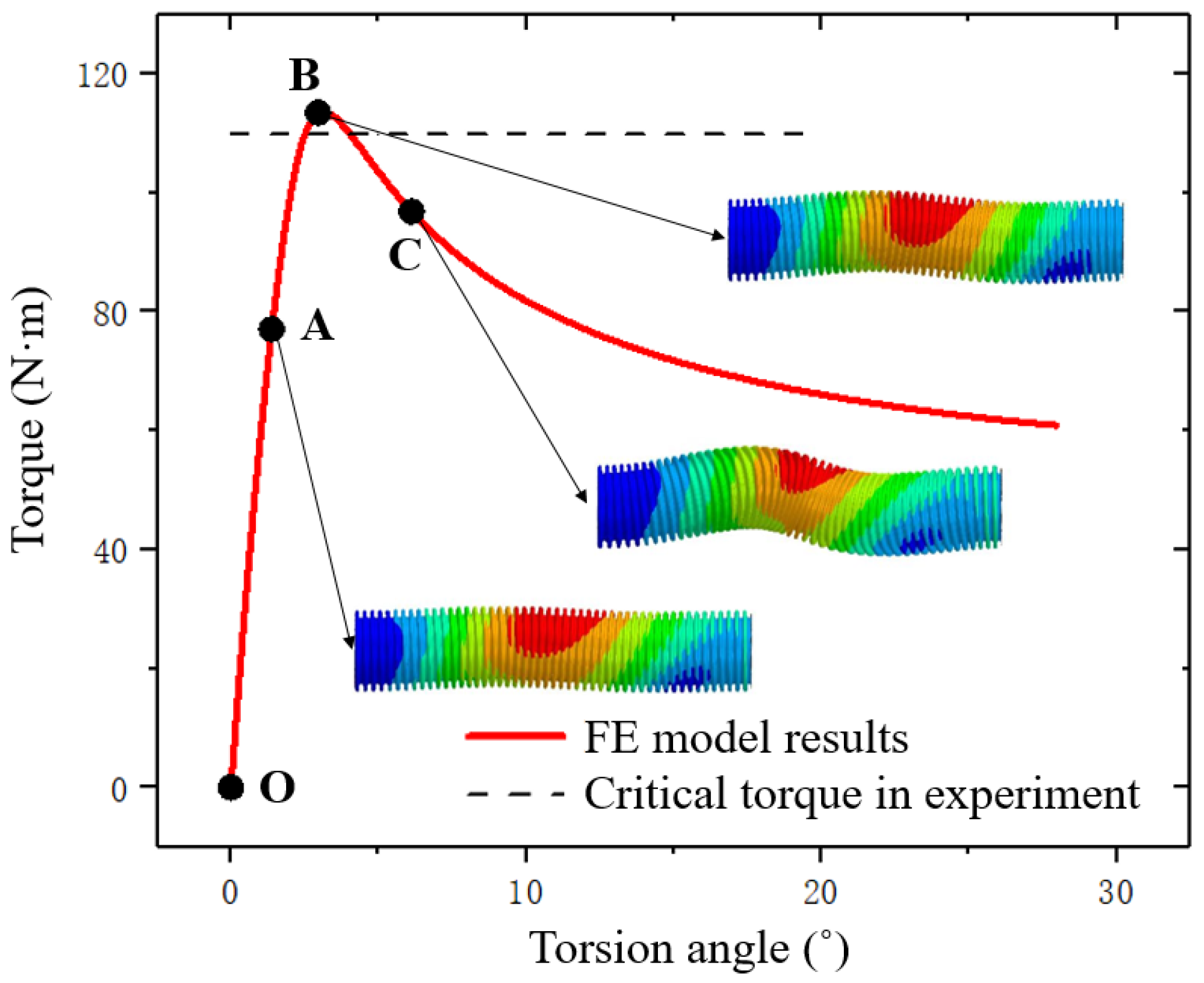
3.1. Torsional Buckling Experiment
3.2. Post-Buckling Analysis of Bellows
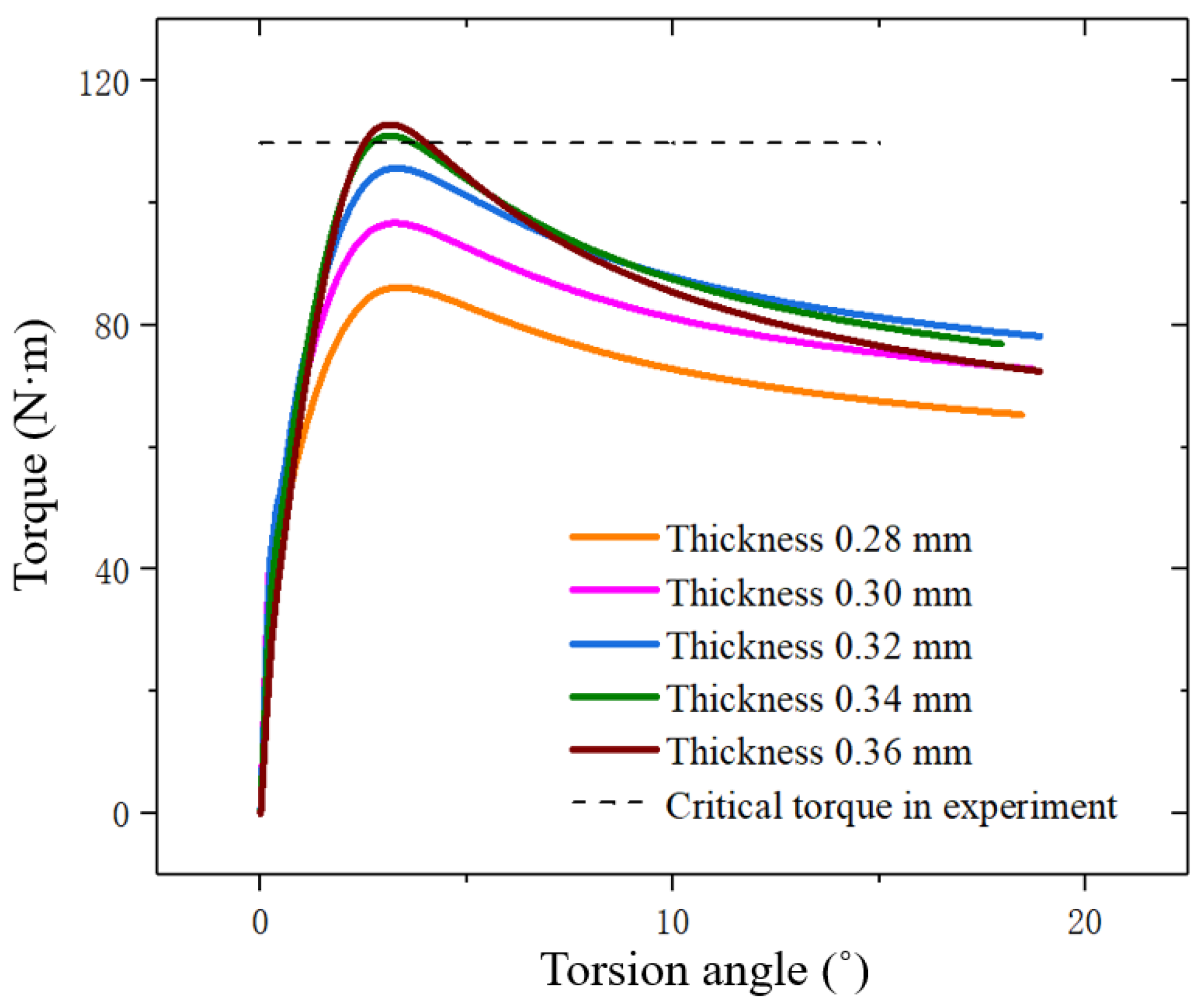
3.3. The Influence of Geometric Structural Defects on the Post-Buckling Analysis of Bellows under Torsional Loads
4. Conclusions
- (1)
- The mechanism of mechanical analysis on torsional buckling of U-shaped bellows in FLNG cryogenic hoses was carried out. The reason for becoming a spiral mode during torsional deformation of the bellows with a large slenderness ratio was that warping internal forces and tangential displacements were generated. The type of torsional buckling of U-shaped bellows at this time belonged to column instability.
- (2)
- There were two kinds of torsional buckling modes of bellows, including column instability and plane instability. When the slenderness ratio of the bellows was small (slenderness ratio was less than 1), the plane instability mode could occur, and the critical torque of the spiral bellows was larger than that of the toroid bellows. When the slenderness ratio of the bellows was large (slenderness ratio was larger than 1), the column instability mode could occur, and the critical torque of the spiral bellows was smaller than that of the toroid bellows.
- (3)
- In the sensitivity analysis of structural parameters of bellows in torsional buckling, the critical torque of the bellows decreased with the increase of convolution number or convolution depth and increased with the increase of convolution pitch or wall thickness.
- (4)
- As the extension of torsional buckling analysis, post-buckling behavior was analyzed by means of experiment and finite element simulation. Critical torque value in FE model was compared with experimental results, showed that the error of critical torque was only about 3.3% and the deformation of the bellows presented the same changing trends and instability modes.
- (5)
- It was analyzed that the most likely reason of the error of 3.3% was the decrease of the thickness of bellows. After considering and correcting the defects of numerical model, the errors of the results obtained in this work were controlled to only about 0.9%. Therefore, the effect of the decrease of the bellows thickness on post-buckling instability performance had to be considered in practical engineering designs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Snedden, N. Analysis and design guidance for the lateral stiffness of bellows expansion joints. Thin-Walled Struct. 1985, 3, 145–162. [Google Scholar] [CrossRef]
- Felice, R.; Nisticò, A.; Fausto, T. Marine Application of Fiber Reinforced Composites: A Review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Krovvidi, K.; Padmakumar, G.; Bhaduri, K. Design and analysis of bellows for high temperature application as per RCC-MR. Trans. Indian Inst. Met. 2016, 69, 531–535. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, J.; Lu, Q.; Chen, J.; Wu, S.; Wang, L.; Yue, Q. Multi-Objective Shape Optimization Design for LNG Cryogenic Helical Corrugated Steel Pipe. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar] [CrossRef]
- EJMA. Standards of the Expansion Joint Manufactures Association; Expansion Joint Manufactures Association: White Plains, NY, USA, 1998. [Google Scholar]
- Watanabe, O.; Ohtsubo, H. Stress Analysis and Torsional Buckling Analysis of U-Shaped Bellows. Des. Anal. 1989, 1, 619–626. [Google Scholar] [CrossRef]
- Broman, G.; Hermann, M.; Jönsson, A. Modelling Flexible Bellows by Standard Beam Finite Elements; University of Karlskrona/Ronneby: Karlskrona, Sweden, 1999. [Google Scholar]
- Radhakrishna, M.; Rao, C.K. Axial vibrations of U-shaped bellows with elastically restrained end conditions. Thin-Walled Struct. 2004, 42, 415–426. [Google Scholar] [CrossRef]
- Kondapalli, S.; Gudla, P. Investigation of stresses in U-shaped metal bellow using EJMA standards. Adv. Des. Manuf. Technol. 2017, 10, 25–35. [Google Scholar]
- Rieger, W. Torsion of expansion joints-first information and test results for stability properties and behaviour under stress. In Proceedings of the International Conference on Structural Mechanics in Reactor Technology, Chicago, IL, USA, 22–26 August 1983. [Google Scholar]
- Lu, C.; Zhou, Y.; Ye, Q. The Torsional Buckling of Bellows. J. Shanghai Jiaotong Univ. 2007, 41, 1017–1020. [Google Scholar]
- Dennis, K. Buckling considerations for U-shaped bellows utilized in flexible metal hoses. In Proceedings of the ASME Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005. [Google Scholar]
- Yang, Z.; Ying, X.; Yan, J. Study of equivalent mechanical properties of corrugated structure based on asymptotic homogenization method. J. Dalian Univ. Technol. 2021, 61, 498–505. [Google Scholar] [CrossRef]
- Wang, B.; Du, K.; Hao, P.; Zhou, C.; Tian, K.; Xu, S.; Ma, Y.; Zhang, X. Numerically and experimentally predicted knockdown factors for stiffened shells under axial compression. Thin-Walled Struct. 2016, 109, 13–24. [Google Scholar] [CrossRef]
- Hao, P.; Wang, B.; Li, G.; Tian, K.; Du, K.; Wang, X.; Tang, X. Surrogate-based optimization of stiffened shells including load-carrying capacity and imperfection sensitivity. Thin-Walled Struct. 2013, 72, 164–174. [Google Scholar] [CrossRef]
- Jiao, P.; Chen, Z.; Ma, H.; Ge, P.; Gu, Y.; Miao, H. Buckling behaviors of thin-walled cylindrical shells under localized axial compression loads, Part 1: Experimental study. Thin-Walled Struct. 2021, 166, 108118. [Google Scholar] [CrossRef]
- Jiao, P.; Chen, Z.; Ma, H.; Ge, P.; Gu, Y.; Miao, H. Buckling behaviors of thin-walled cylindrical shells under localized axial compression loads, Part 2: Numerical study. Thin-Walled Struct. 2021, 169, 108330. [Google Scholar] [CrossRef]
- Mohammad, R.; Amir, R.; Ali, A. Critical buckling moment of functionally graded tapered mono-symmetric I-beam. Steel Compos. Struct. 2021, 39, 599–614. [Google Scholar] [CrossRef]
- Mohammad, R.; Amir, R.; Ali, A. Lateral-Torsional Buckling of a Bidirectional Exponentially Graded Thin-Walled C-Shaped Beam. Mech. Compos. Mater. 2022, 58, 53–68. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Liu, Y.; Li, L.; Sun, C. “Size effect” related hydroforming characteristics of thin-walled 316-L bellow considering pressure change. Int. J. Adv. Manuf. Technol. 2018, 98, 505–522. [Google Scholar] [CrossRef]
- Teng, J.; Song, C. Numerical models for nonlinear analysis of elastic shells with eigenmode-affine imperfections. Int. J. Solids Struct. 2001, 38, 3263–3280. [Google Scholar] [CrossRef]
- Angelina, C.; Priyadarsini, R. Influence of crack on the instability of GFRP composite cylindrical shells under combined loading. Appl. Mech. Mater. 2018, 877, 453–459. [Google Scholar] [CrossRef]
- Riks, E. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- Silvestre, N. Buckling behavior of elliptical cylindrical shells and tubes under compression. Int. J. Solids Struct. 2008, 45, 4427–4447. [Google Scholar] [CrossRef] [Green Version]
- Powell, G.; Simons, J. Improved iteration strategy for nonlinear structures. Int. J. Numer. Methods Eng. 1981, 17, 1455–1467. [Google Scholar] [CrossRef]
- Pang, T.; Sun, G.Y.; Ruan, D.; Huang, X.D.; Lu, G.X. Experimental Study on Crushing Resistance of Square CFRP Frusta under Axial Loading. Key Eng. Mater. 2019, 794, 194–201. [Google Scholar] [CrossRef]
- Hilburger, M.W.; Nemeth, M.P.; Starnes, J.H. Shell Buckling Design Criteria Based on Manufacturing Imperfection Signatures. AIAA J. 2006, 44, 654–663. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhou, T.; Wang, W. Buckling of a composite cylindrical shell considering mode imperfections. Acta Mater. Compos. Sin. 2017, 34, 588–596. [Google Scholar]
- Haynie, W.; Hilburger, M. Comparison of methods to predict lower bound buckling loads of cylinders under axial compression. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010. [Google Scholar]
- EN 1993-1-6; Eurocode 3: Design of Steel Structures. European Committee for Standardizations: Brussels, Belgium, 1999.
- Wagner, H.; Hühne, C.; Elishakoff, I. Probabilistic and deterministic lower-bound design benchmarks for cylindrical shells under axial compression. Thin-Walled Struct. 2020, 146, 106451. [Google Scholar] [CrossRef]
- Wagner, H.; Hühne, C. Robust knockdown factors for the design of cylindrical shells under axial compression: Potentials, practical application and reliability analysis. Int. J. Mech. Sci. 2018, 135, 410–430. [Google Scholar] [CrossRef]
- Wagner, H.; Hühne, C.; Rohwer, K.; Niemann, S.; Wiedemann, M. Stimulating the realistic worst case buckling scenario of axially compressed unstiffened cylindrical composite shells. Compos. Struct. 2017, 160, 1095–1104. [Google Scholar] [CrossRef]
- Degenhardt, R.; Castro, S.G.; Arbelo, M.A.; Zimmerman, R.; Khakimova, R.; Kling, A. Future structural stability design for composite space and airframe structures. Thin-Walled Struct. 2014, 81, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Castro, S.G.; Zimmermann, R.; Arbelo, M.A.; Degenhardt, R. Exploring the constancy of the global buckling load after a critical geometric imperfection level in thin-walled cylindrical shells for less conservative knock-down factors. Thin-Walled Struct. 2013, 72, 76–87. [Google Scholar] [CrossRef]
- Castro, S.G.; Zimmermann, R.; Arbelo, M.A.; Khakimova, R.; Hilburger, M.W.; Degenhardt, R. Geometric imperfections and lower-bound methods used to calculate knock-down factors for axially compressed composite cylindrical shells. Thin-Walled Struct. 2014, 74, 118–132. [Google Scholar] [CrossRef]
- Castro, S.G.; Mittelstedt, C.; Monteiro, F.A.; Degenhardt, R.; Ziegmann, G. Evaluation of non-linear buckling loads of geometrically imperfect composite cylinders and cones with the Ritz method. Compos. Struct. 2015, 122, 284–299. [Google Scholar] [CrossRef]
- Degenhardt, R.; Kling, A.; Bethge, A.; Orf, J.; Kärger, L.; Zimmermann, R.; Rohwer, K.; Calvi, A. Investigations on imperfection sensitivity and deduction of improved knock-down factors for unstiffened CFRP cylindrical shells. Compos. Struct. 2010, 92, 1939–1946. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, B.; Sun, G.; Yang, S. A Two-Phase Differential Evolution for Uniform Designs in Constrained Experimental Domains. IEEE Trans. Evol. Comput. 2017, 21, 665–680. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z. Influence of wall-thickness variation on non-linear behavior of U-shaped bellows calculations by iteration method of integral equation and gradient method. Int. J. Numer. Meth. Biomed. 2015, 15, 203–218. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H. Static and dynamic bending collapse of thin-walled square beams with tube filler. Int. J. Impact Eng. 2018, 112, 165–179. [Google Scholar] [CrossRef]
- Haj-Ali, R.; Choi, J.; Wei, B.-S.; Popil, R.; Schaepe, M. Refined nonlinear finite element models for corrugated fiberboards. Compos. Struct. 2009, 87, 321–333. [Google Scholar] [CrossRef]
- Davalos, J.F.; Qiao, P.; Xu, X.F.; Robinson, J.; Barth, K.E. Modeling and characterization of fiber-reinforced plastic honeycomb sandwich panels for highway bridge applications. Compos. Struct. 2001, 52, 441–452. [Google Scholar] [CrossRef]
- Aboura, Z.; Talbi, N.; Allaoui, S.; Benzeggagh, M. Elastic behavior of corrugated cardboard: Experiments and modeling. Compos. Struct. 2004, 63, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Yokozeki, T.; Takeda, S.-I.; Ogasawara, T.; Ishikawa, T. Mechanical properties of corrugated composites for candidate materials of flexible wing structures. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1578–1586. [Google Scholar] [CrossRef]
- Talbi, N.; Batti, A.; Ayad, R.; Guo, Y. An analytical homogenization model for finite element modelling of corrugated cardboard. Compos. Struct. 2009, 88, 280–289. [Google Scholar] [CrossRef]
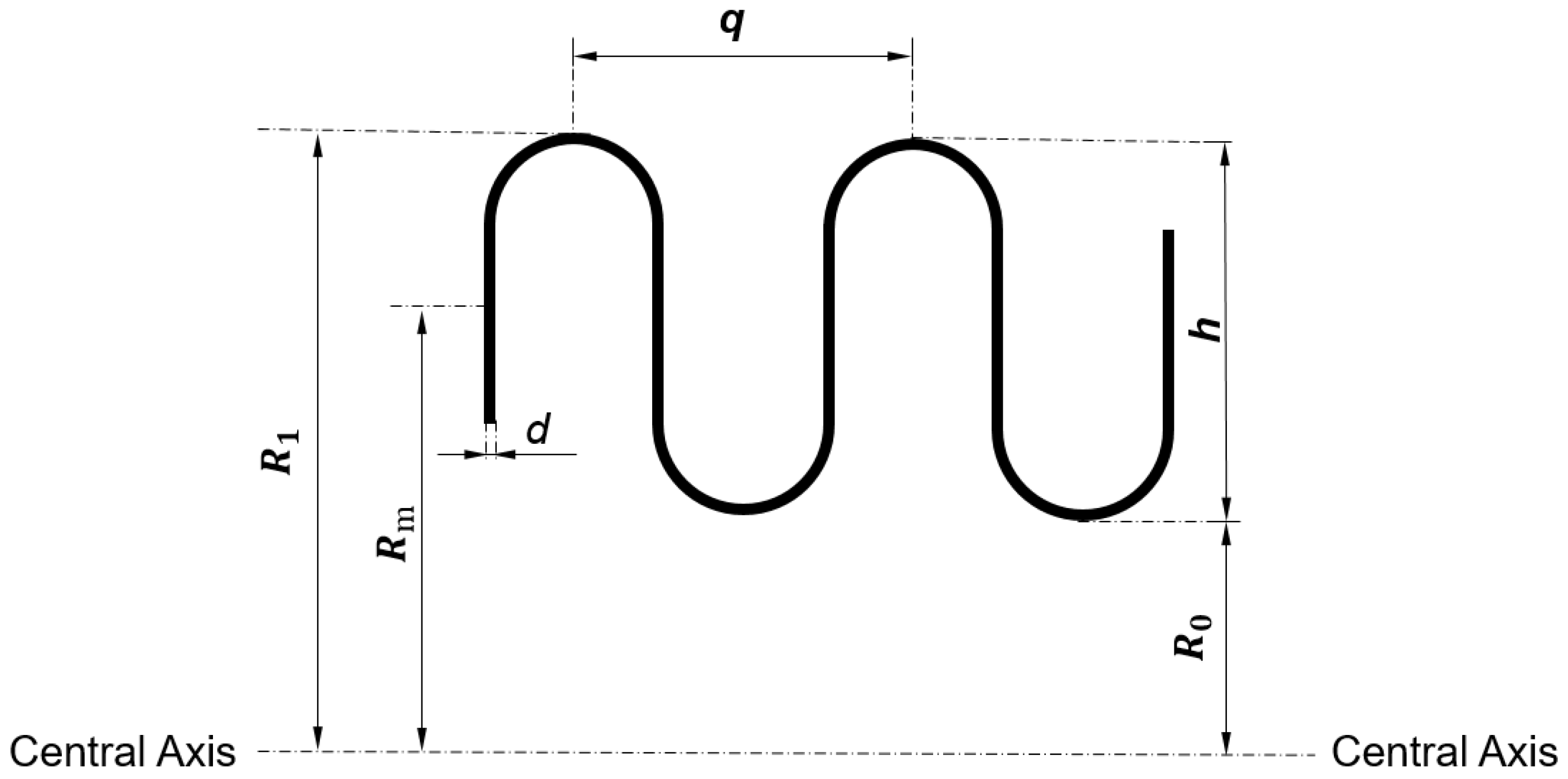





| Structural Parameters (mm) | Material Parameters | |||||
|---|---|---|---|---|---|---|
| R1 | R0 | d | h | q | Elasticity Modulus (GPa) | Poisson’s Ratio |
| 17.00 | 11.75 | 0.10 | 5.25 | 2.20 | 103.00 | 0.30 |
| Convolution Number | Toroid Bellows | Spiral Bellows | ||
|---|---|---|---|---|
| Critical Torque (N·m) | Instability Model | Critical Torque (N·m) | Instability Model | |
| 3 | 2.94 | Plane instability | 3.64 | Plane instability |
| 5 | 2.44 | Plane instability | 2.51 | Plane instability |
| 10 | 2.21 | Column instability | 2.16 | Column instability |
| 20 | 2.14 | Column instability | 2.01 | Column instability |
| 30 | 2.12 | Column instability | 1.84 | Column instability |
| Convolution Pitch (mm) | Critical Torque (N·m) | |
|---|---|---|
| Toroid Bellows | Spiral Bellows | |
| 2.0 | 1.81 | 1.78 |
| 3.2 | 2.12 | 1.84 |
| 4.0 | 2.67 | 2.25 |
| 5.0 | 3.92 | 2.96 |
| 6.0 | 5.68 | 3.95 |
| Structural Parameters (mm) | Material Parameters | ||||||
|---|---|---|---|---|---|---|---|
| R1 | R0 | d | h | q | Elasticity Modulus (GPa) | Poisson’s Ratio | Yield Stress (MPa) |
| 31.38 | 25.38 | 0.38 | 6.00 | 6.00 | 193.00 | 0.30 | 298 |
| Analysis Method | Critical Torque Value (N·m) | Error (%) |
|---|---|---|
| Experimental results | 109.85 | - |
| FE model results | 113.50 | 3.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Ying, X.; Cao, H.; Xiong, F.; Zhang, K.; Yang, Z. Mechanism of Mechanical Analysis on Torsional Buckling of U-Shaped Bellows in FLNG Cryogenic Hoses. J. Mar. Sci. Eng. 2022, 10, 1405. https://doi.org/10.3390/jmse10101405
Yan J, Ying X, Cao H, Xiong F, Zhang K, Yang Z. Mechanism of Mechanical Analysis on Torsional Buckling of U-Shaped Bellows in FLNG Cryogenic Hoses. Journal of Marine Science and Engineering. 2022; 10(10):1405. https://doi.org/10.3390/jmse10101405
Chicago/Turabian StyleYan, Jun, Xipeng Ying, Huixin Cao, Feiyu Xiong, Kailun Zhang, and Zhixun Yang. 2022. "Mechanism of Mechanical Analysis on Torsional Buckling of U-Shaped Bellows in FLNG Cryogenic Hoses" Journal of Marine Science and Engineering 10, no. 10: 1405. https://doi.org/10.3390/jmse10101405





