A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines
Abstract
:1. Introduction
2. Component-Level Studies
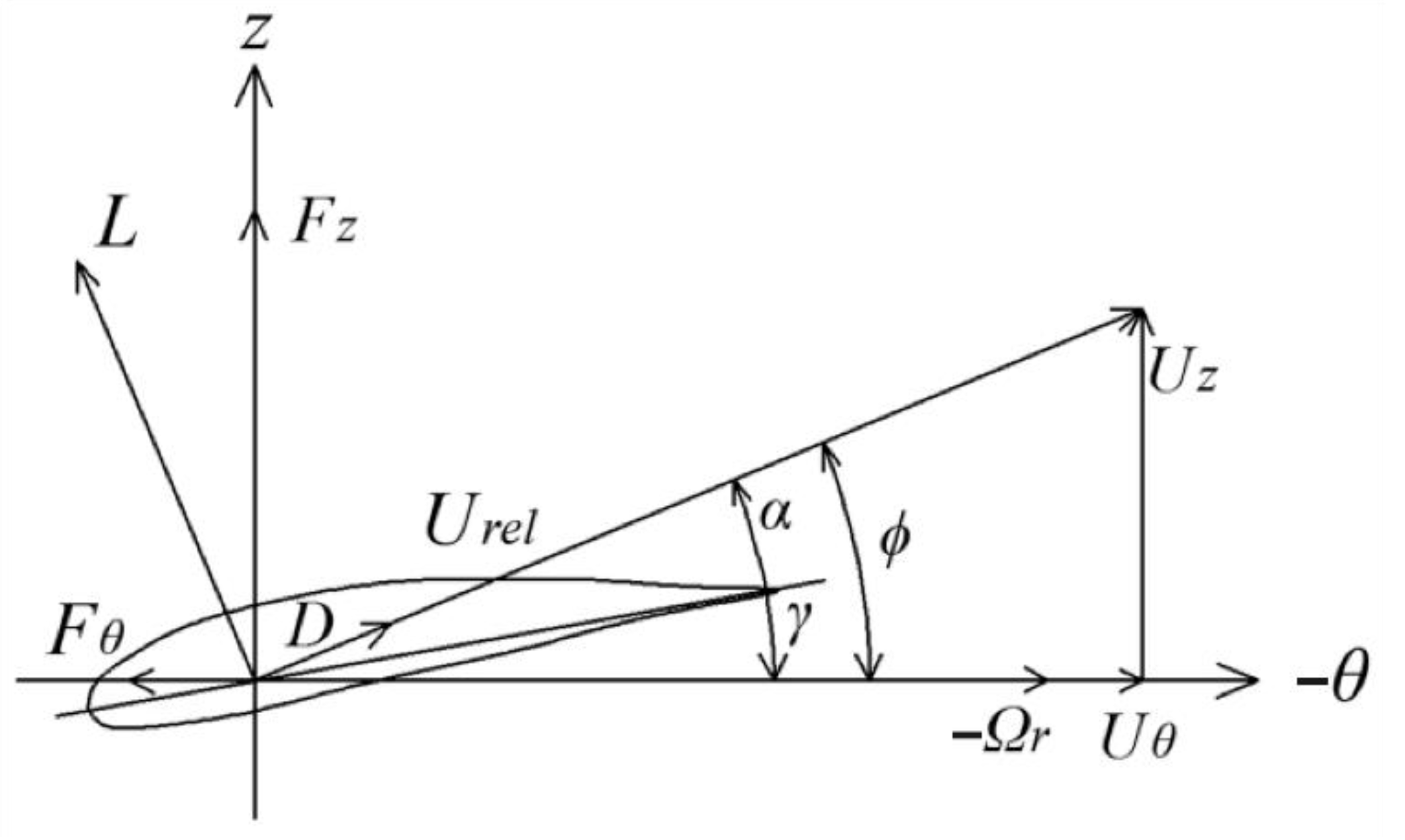
2.1. Aerodynamics
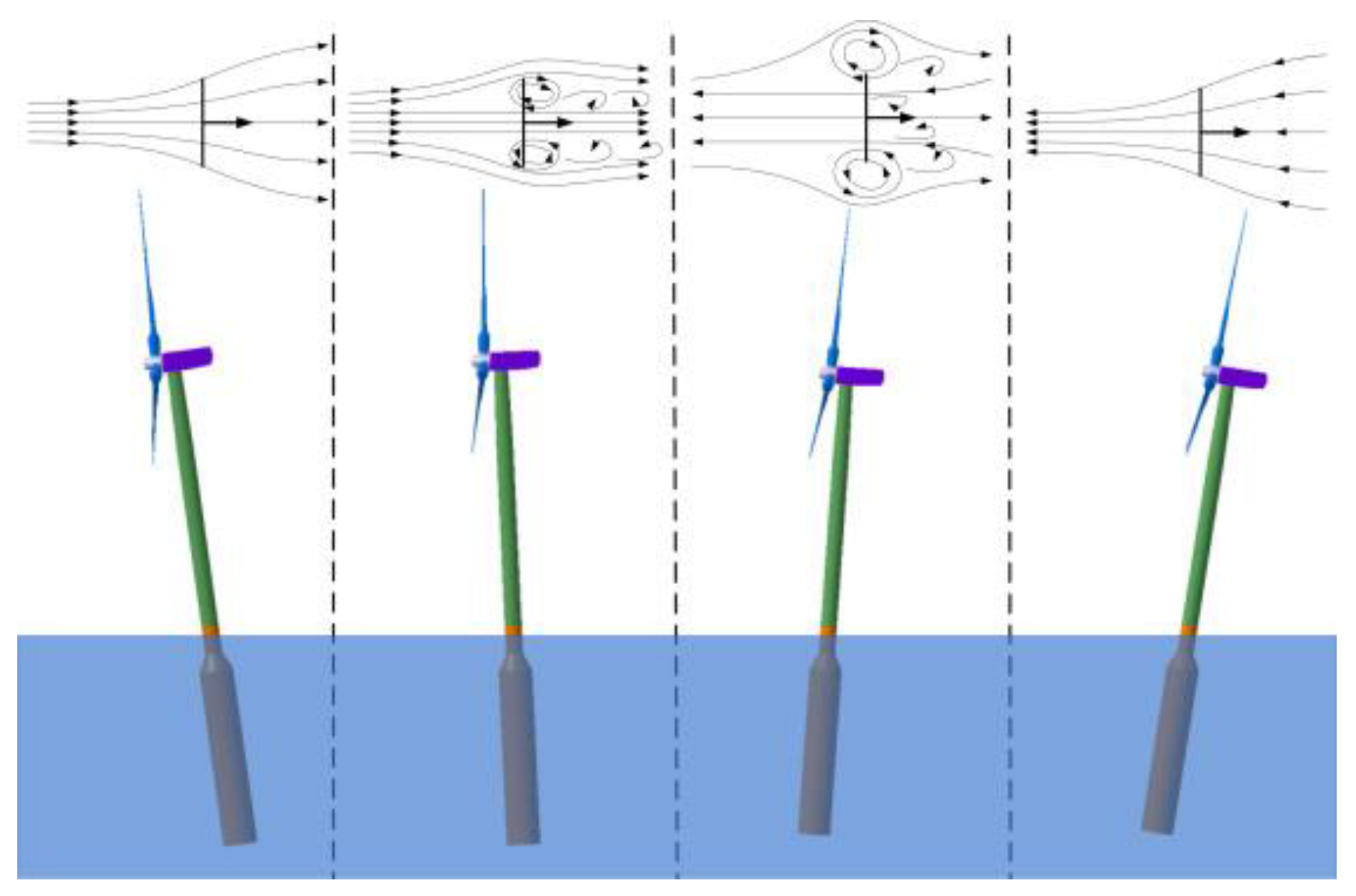
2.1.1. Actuator Disk Model
2.1.2. Actuator Line Model
2.1.3. Actuator Surface Model
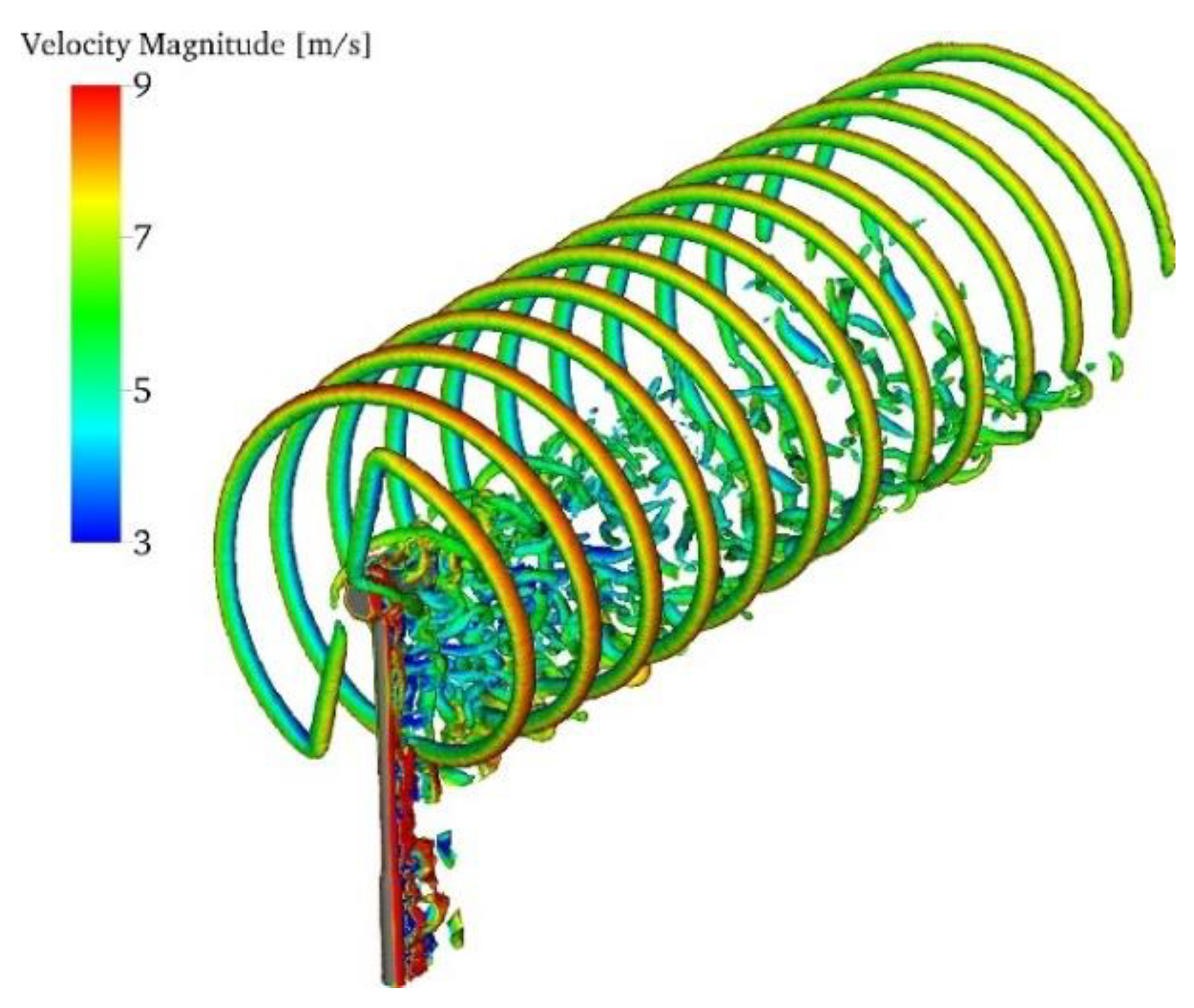
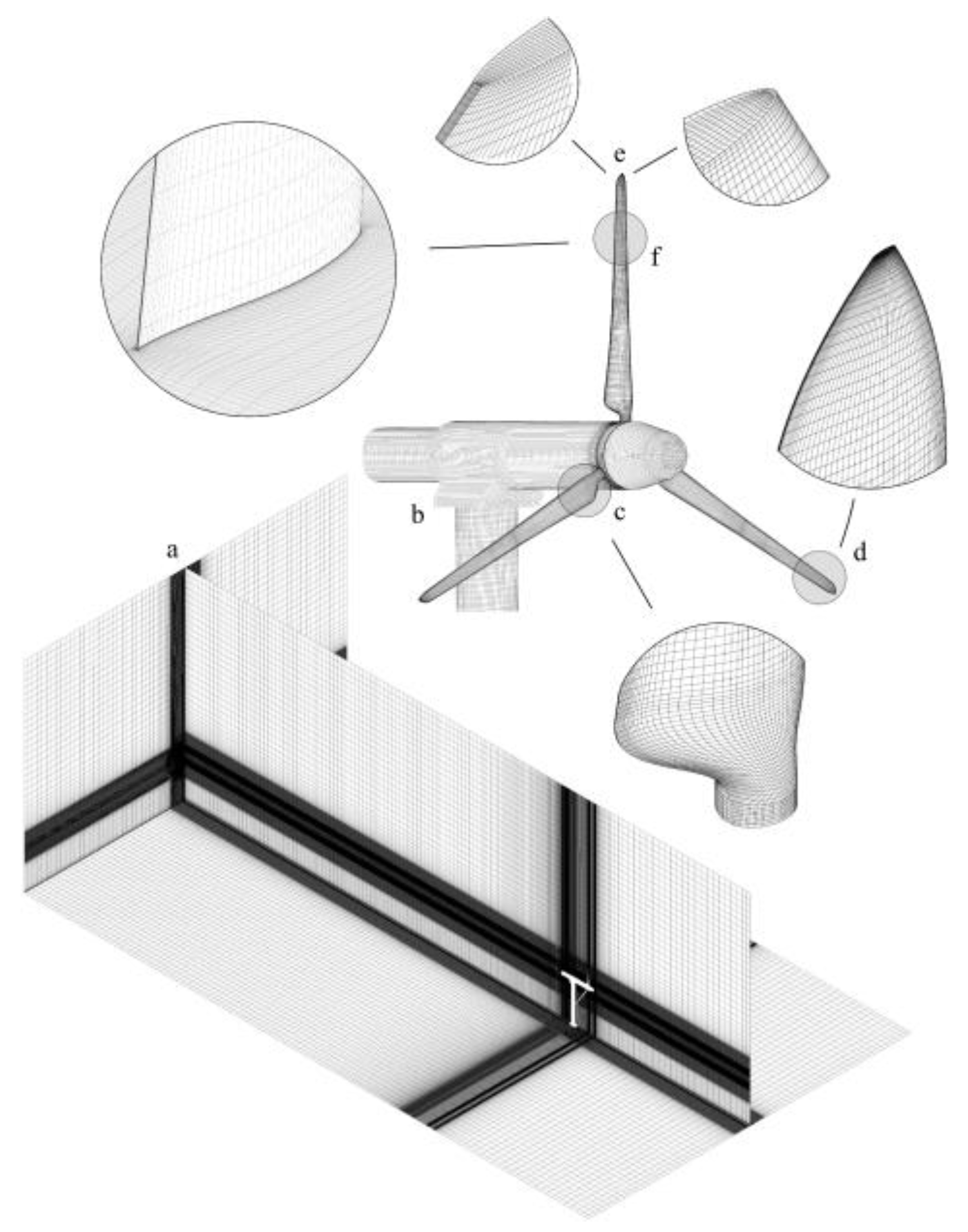
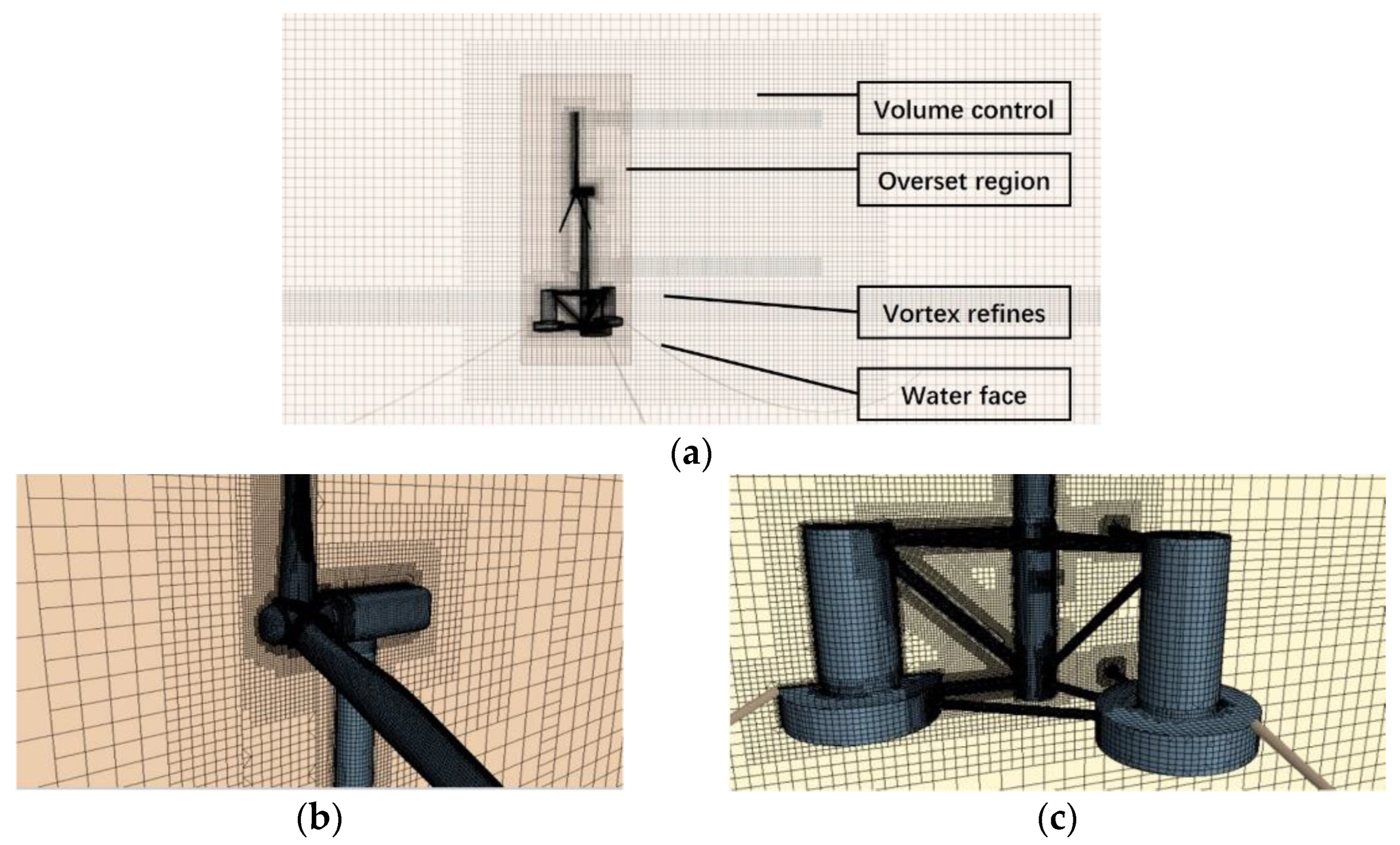
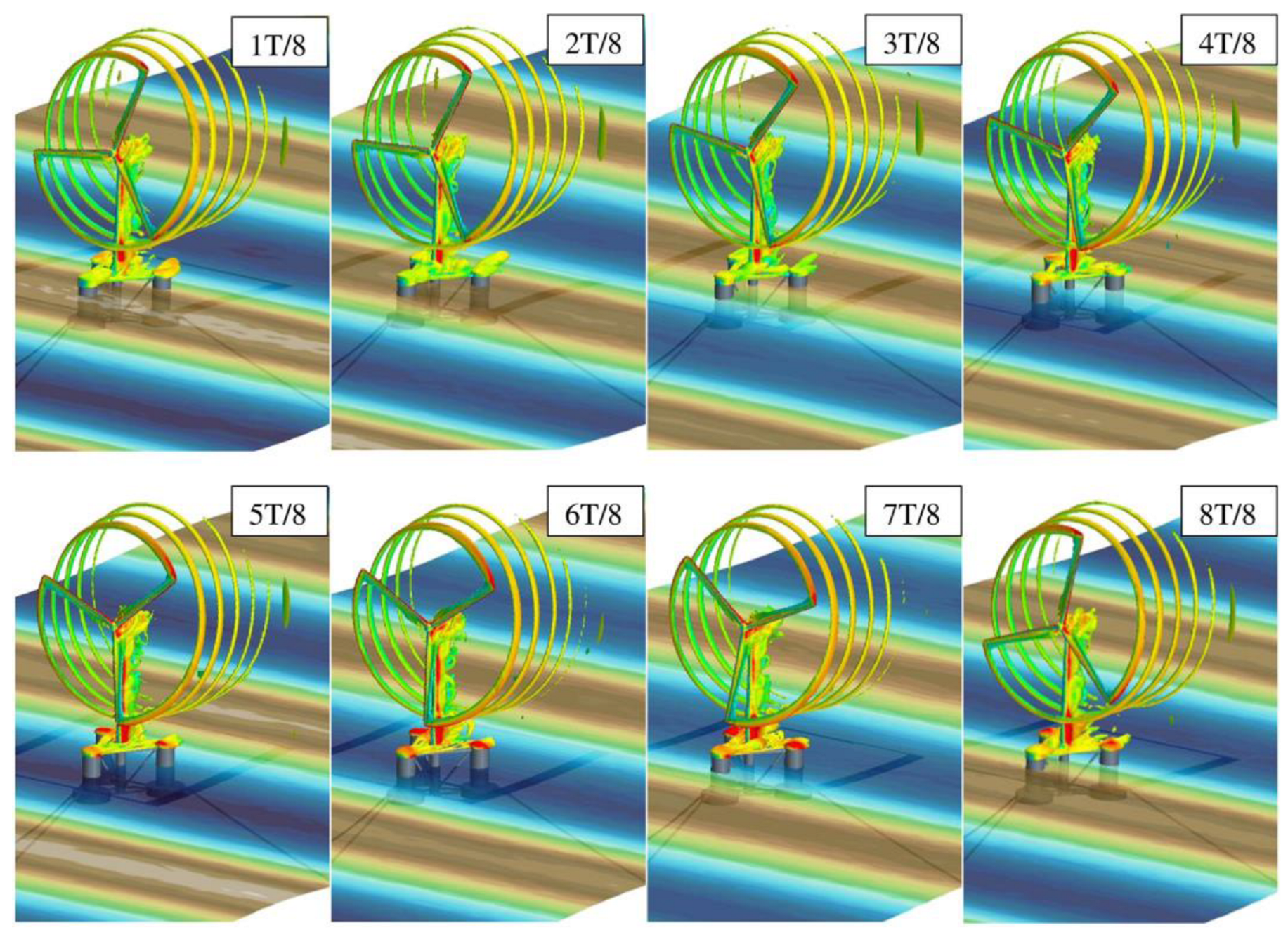
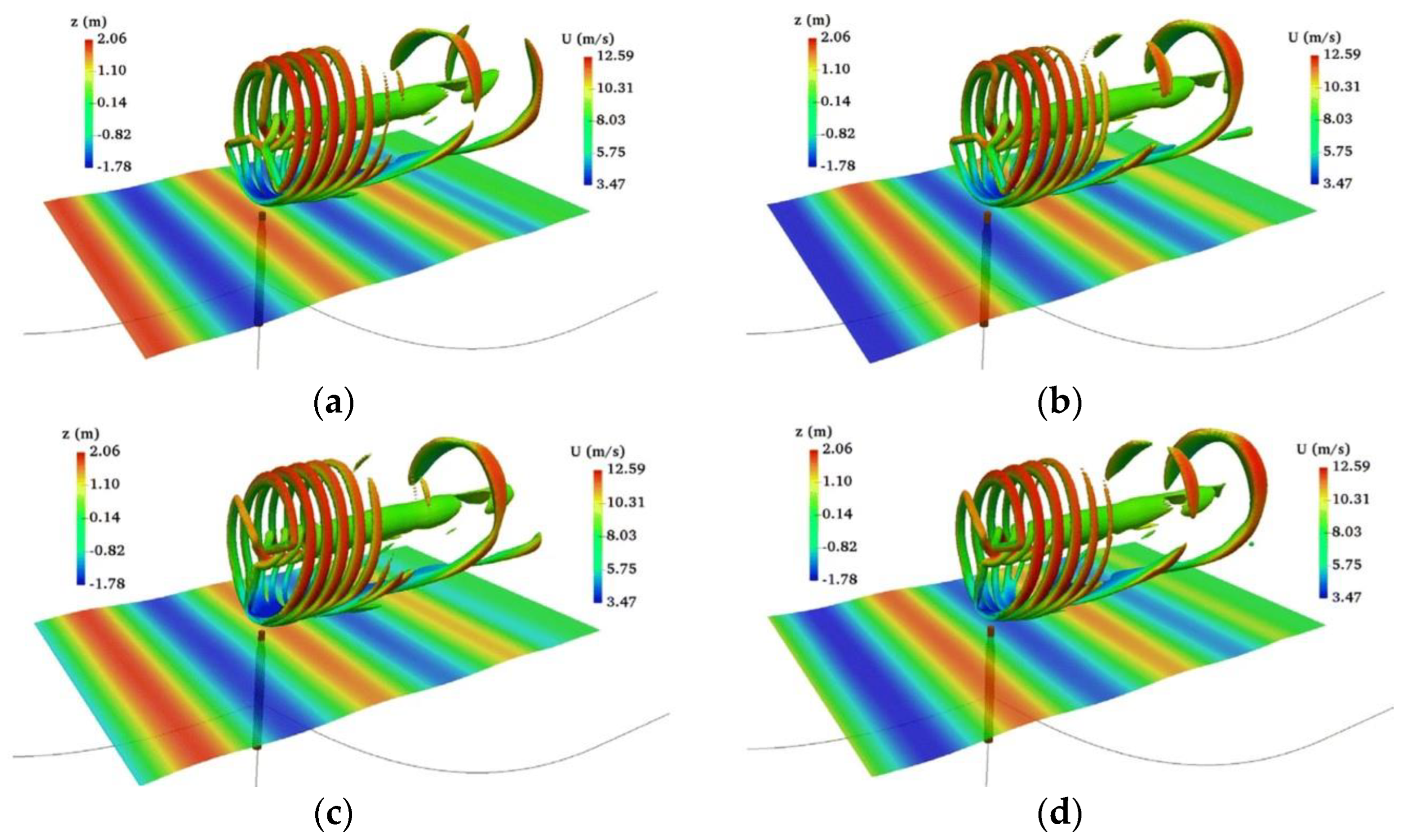
2.1.4. Direct Modeling
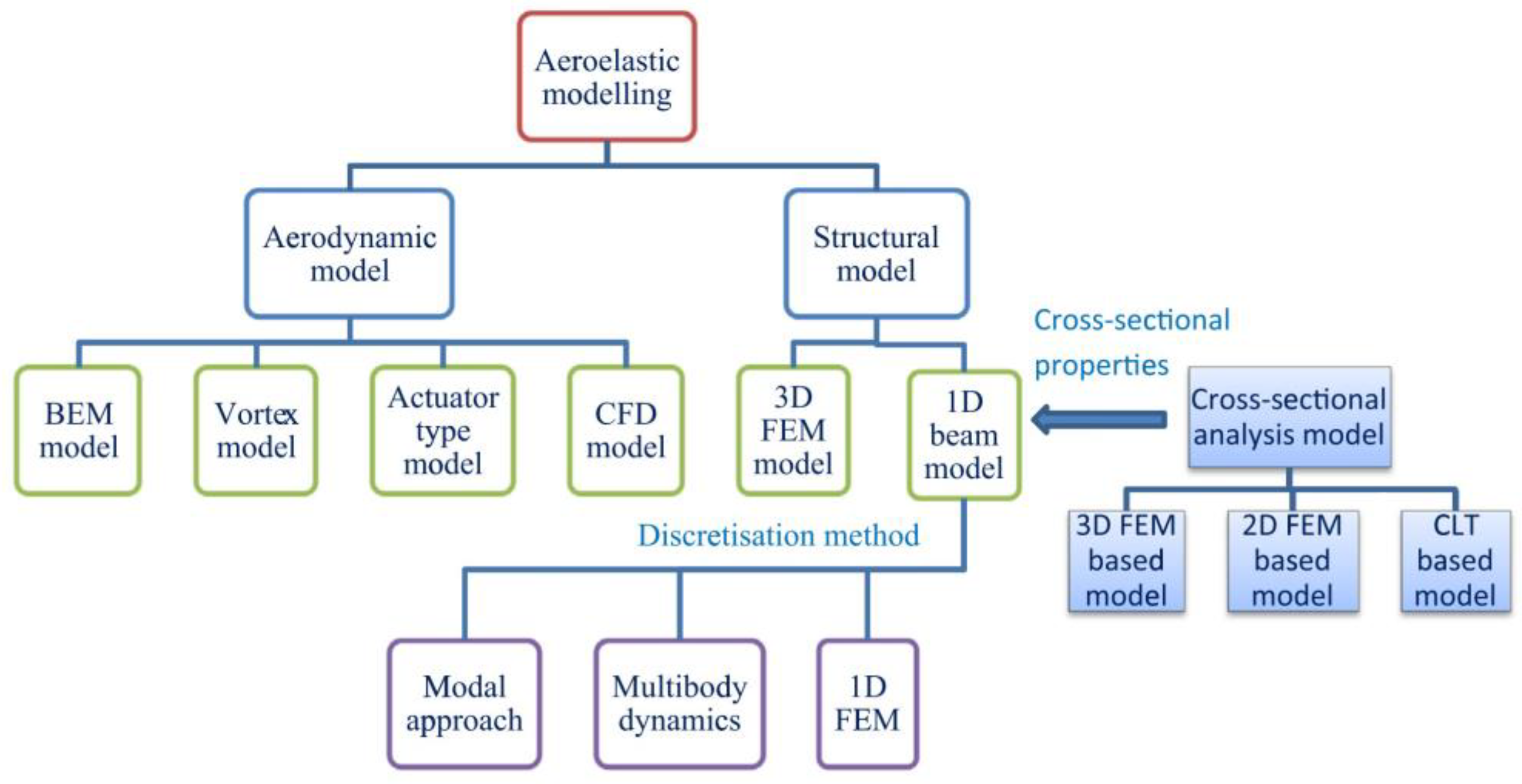
2.2. Aeroelasticity
2.2.1. One-Dimensional Equilibrium Beam Model
2.2.2. Three-Dimensional Finite Element Method
2.3. Hydrodynamics
2.3.1. Spar Buoy Platform
2.3.2. Semi-Submersible Platform
2.3.3. Tension Leg Platform
2.3.4. Barge Platform
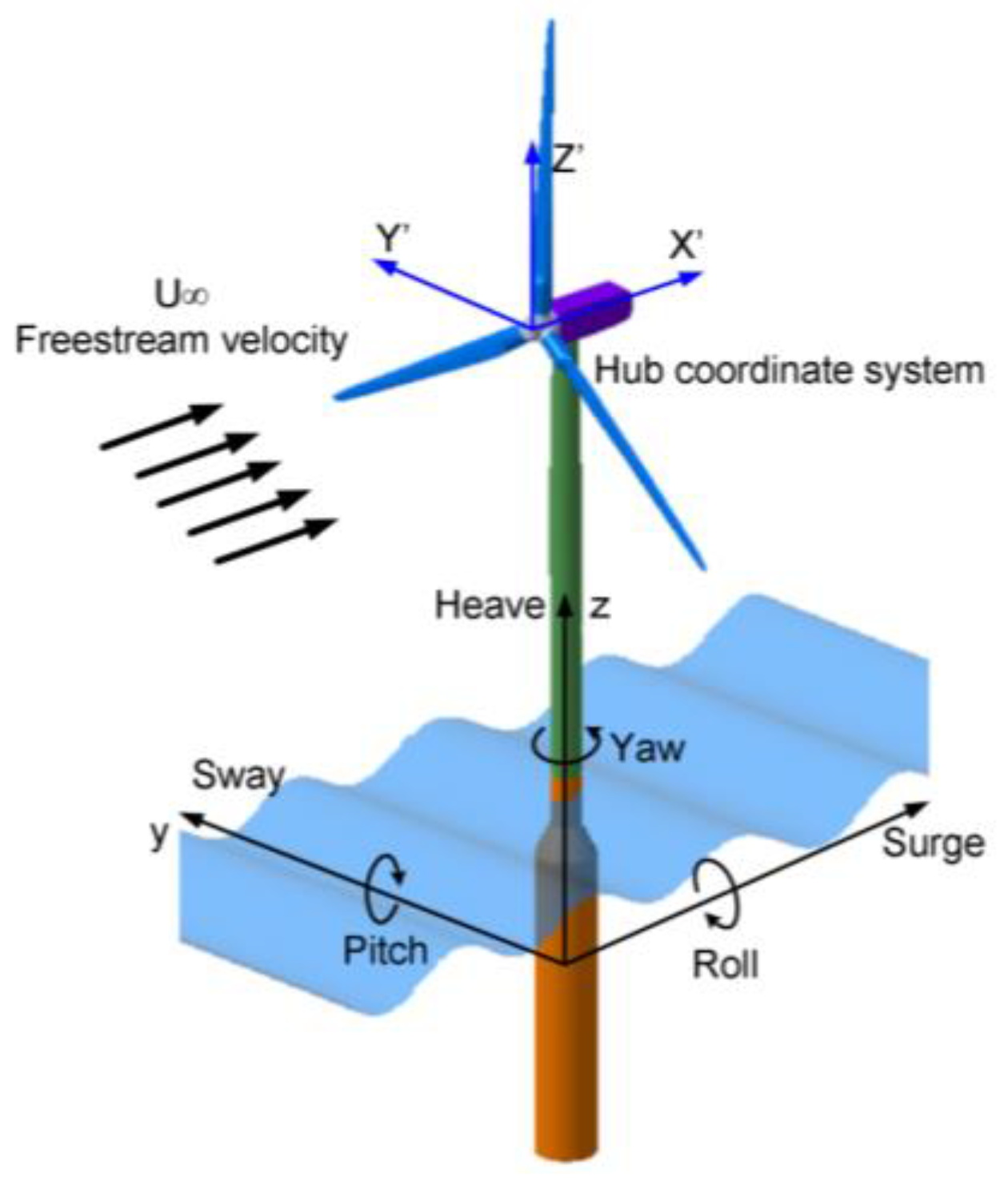
3. System-Level Studies
3.1. Simplified Aerodynamics
3.2. Prescribed Platform Motions
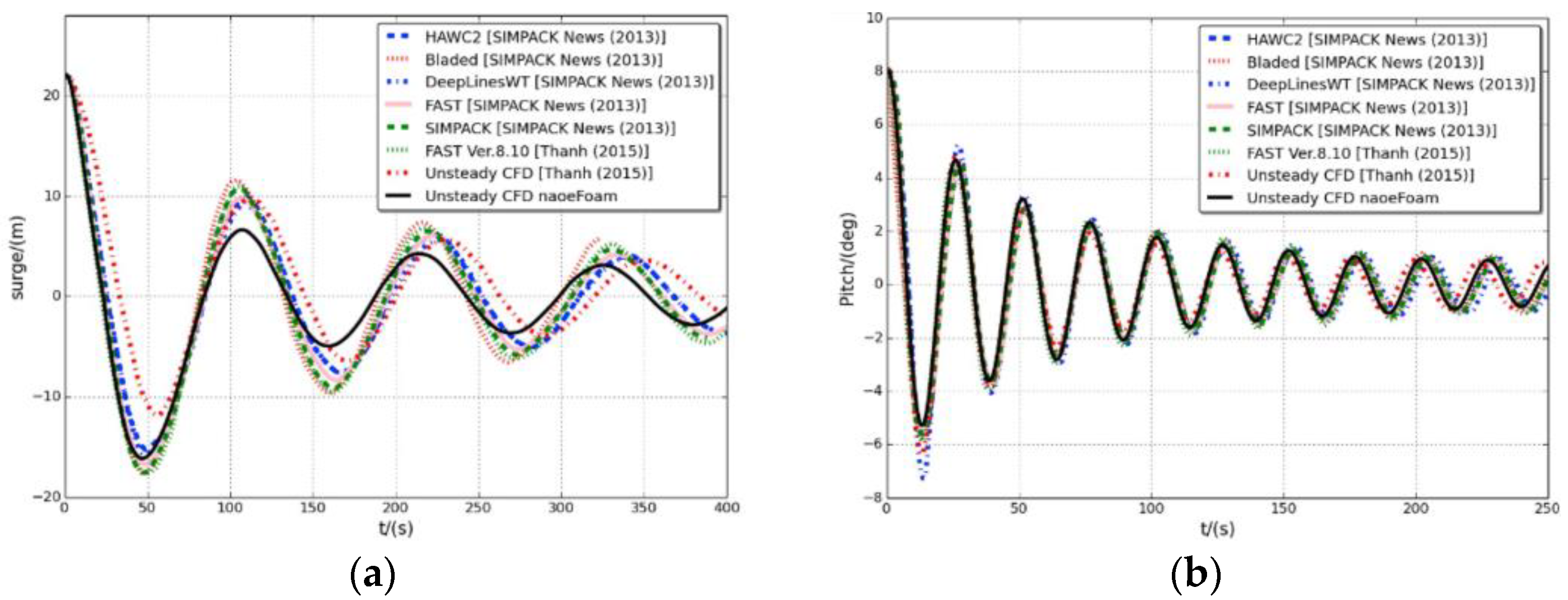
3.3. Fully Coupled Aero-Hydrodynamic Performance
3.4. Fully Coupled Aero-Hydro-Elastic Performance
4. Future Recommendations
4.1. Fully Coupled Aero-Hydro-Elastic Performance
4.2. Complex Atmospheric Inflow
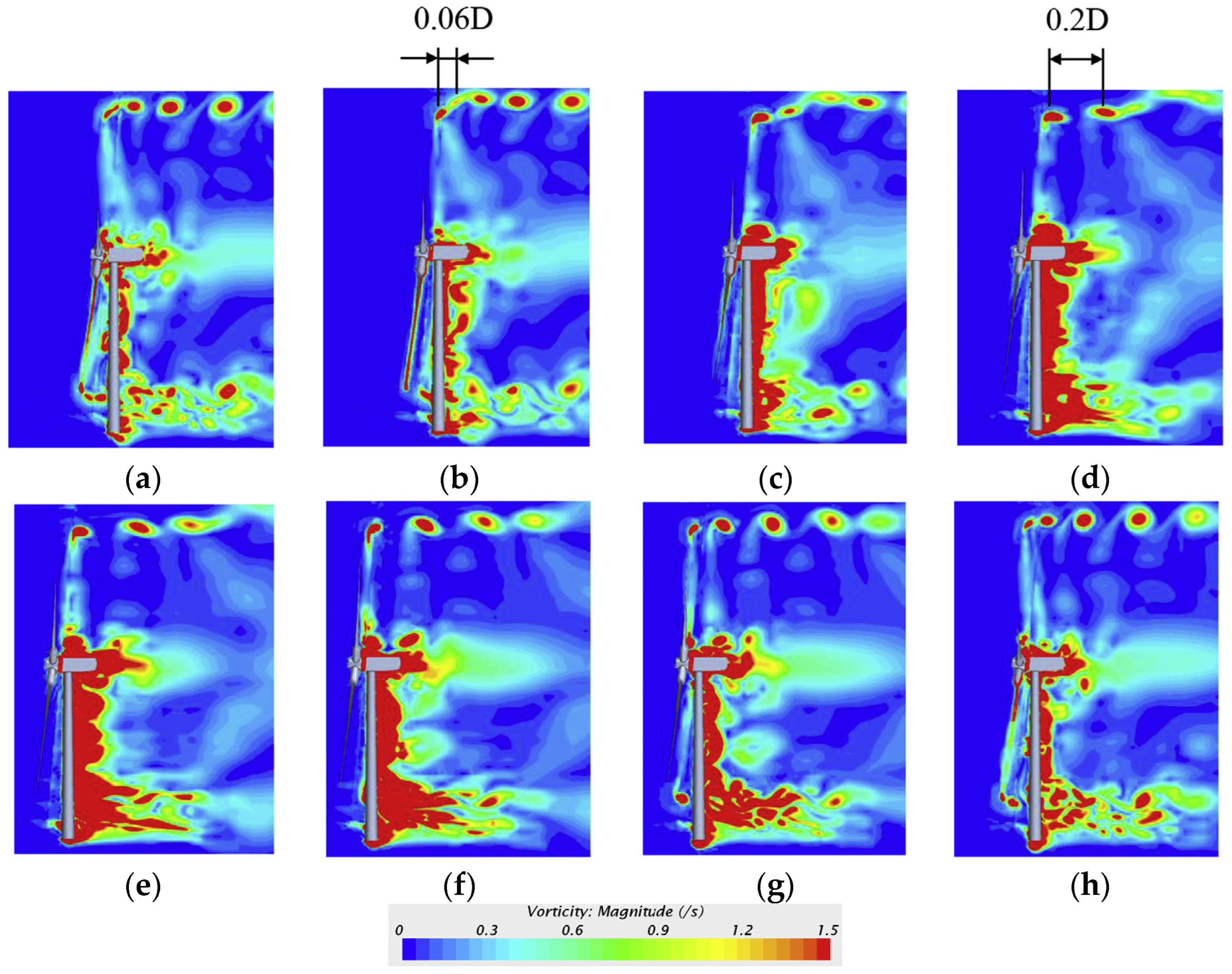
4.3. Wake Interactions between Multi-FOWT
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| GWEC | Global Wind Energy Council |
| FOWTs | floating offshore wind turbines |
| LCOE | levelized cost of energy |
| HPC | high-performance computers |
| BEM | blade element momentum |
| PF | potential flow |
| CFD | computational fluid dynamics |
| AD | actuator disk |
| AL | actuator line |
| AS | actuator surface |
| 3D | three-dimensional |
| LES | Large Eddy Simulation |
| ACE | actuator curve embedding |
| RANS | Reynolds-Averaged Navier-Stokes |
| uRANS | unsteady Reynolds-Averaged Navier-Stokes |
| DES | Detached Eddy Simulation |
| IDDES | Improved and Delayed Detached Eddy Simulation |
| DDES | Delayed Detached Eddy Simulation |
| FVM | free vortex wake |
| FEM | finite element method |
| EBM | equilibrium beam model |
| MBD | multi-body dynamics |
| GEBT | geometrically exact beam theory |
| CSD | computational structure dynamics |
| EAL | elastic actuator line |
| FSI | fluid-structure interaction |
| ME | Morison equation |
| 6-DOF | six degrees-of-freedom |
| FDM | finite difference model |
| FSM | finite segment model |
| FEM | finite element model |
| LMM | lumped mass model |
| MBS | multi-body system |
| VIM | vortex-induced motions |
| AMI | arbitrary mesh interface |
| IEC | International Electrotechnical Commission |
References
- Esteban, M.D.; Diez, J.J.; López, J.S.; Negro, V. Why offshore wind energy? Renew. Energy 2011, 36, 444–450. [Google Scholar] [CrossRef]
- Global Wind Report 2022. Available online: https://gwec.net/global-wind-report-2022/ (accessed on 10 July 2022).
- Future of Wind. Available online: https://www.irena.org/publications/2019/Oct/Future-of-wind (accessed on 10 July 2022).
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A review of recent advancements in offshore wind turbine technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Bashetty, S.; Ozcelik, S. Review on Dynamics of Offshore Floating Wind Turbine Platforms. Energies 2021, 14, 6026. [Google Scholar] [CrossRef]
- Musial, W. Overview of Floating Offshore Wind; National Renewable Energy Laboratory: Golden, CO, USA, 2020. [Google Scholar]
- Jiang, Z. Installation of offshore wind turbines: A technical review. Renew. Sust. Energ. Rev. 2021, 139, 110576. [Google Scholar] [CrossRef]
- Martinez, A.; Iglesias, G. Mapping of the levelised cost of energy for floating offshore wind in the European Atlantic. Renew. Sust. Energ. Rev. 2022, 154, 111889. [Google Scholar] [CrossRef]
- Wiser, R.; Rand, J.; Seel, J.; Beiter, P.; Baker, E.; Lantz, E.; Gilman, P. Expert elicitation survey predicts 37% to 49% declines in wind energy costs by 2050. Nat. Energy 2021, 6, 555–565. [Google Scholar] [CrossRef]
- Matha, D.; Schlipf, M.; Pereira, R.; Jonkman, J. Challenges in simulation of aerodynamics, hydrodynamics, and mooring-line dynamics of floating offshore wind turbines. In Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Tran, T.T.; Kim, D.H. The platform pitching motion of floating offshore wind turbine: A preliminary unsteady aerodynamic analysis. J. Wind Eng. Ind. Aerodyn. 2015, 142, 65–81. [Google Scholar] [CrossRef]
- Röckmann, C.; Lagerveld, S.; Stavenuiter, J. Operation and Maintenance Costs of Offshore Wind Farms and Potential Multi-Use Platforms in the Dutch North Sea. In Aquaculture Perspective of Multi-Use Sites in the Open Ocean; Springer: Cham, Switzerland, 2017; pp. 97–113. [Google Scholar]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2022, 25, 831–857. [Google Scholar] [CrossRef]
- Chen, P.; Chen, J.; Hu, Z. Review of Experimental-Numerical Methodologies and Challenges for Floating Offshore Wind Turbines. J. Mar. Sci. Eng. Appl. 2020, 19, 339–361. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Y.; Yan, J.; Zhou, Y.; Yan, S.; Shi, W.; Li, X. Integrated Dynamics Response Analysis for IEA 10-MW Spar Floating Offshore Wind Turbine. J. Mar. Sci. Eng. 2022, 10, 542. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Cai, X.; Xie, J.; Wang, Y.; Zhang, N. Research on the Dynamic Performance of a Novel Floating Offshore Wind Turbine Considering the Fully-Coupled-Effect of the System. J. Mar. Sci. Eng. 2022, 10, 341. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Z.; Liu, G.; Wan, D. Coupled aero-hydro-servo-elastic methods for floating wind turbines. Renew. Energy 2019, 130, 139–153. [Google Scholar] [CrossRef]
- Madsen, H.A.; Bak, C.; Døssing, M.; Mikkelsen, R.; Øye, S. Validation and modification of the blade element momentum theory based on comparisons with actuator disc simulations. Wind Energy 2010, 13, 373–389. [Google Scholar] [CrossRef]
- Sebastian, T.; Lackner, M. Characterization of the unsteady aerodynamics of offshore floating wind turbines. Wind Energy 2013, 16, 339–352. [Google Scholar] [CrossRef]
- Oguz, E.; Clelland, D.; Day, A.H.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and numerical analysis of a TLP floating offshore wind turbine. Ocean Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef]
- Sanderse, B.; Van der Pijl, S.P.; Koren, B. Review of computational fluid dynamics for wind turbine wake aerodynamics. Wind Energy 2011, 14, 799–819. [Google Scholar] [CrossRef]
- Prospathopoulos, J.M.; Politis, E.S.; Rados, K.G.; Chaviaropoulos, P.K. Enhanced CFD modelling of wind turbine wakes. In Proceedings of the Wind Turbine Wakes, Madrid, Spain, 20–22 October 2009. [Google Scholar]
- Wu, Y.T.; Porté-Agel, F. Large-eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound. Layer Meteor. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2009. [Google Scholar]
- Yang, X.; Zhang, X.; Li, Z.; He, G.W. A smoothing technique for discrete delta functions with application to immersed boundary method in moving boundary simulations. J. Comput. Phys. 2009, 228, 7821–7836. [Google Scholar] [CrossRef]
- Revaz, T.; Porté-Agel, F. Large-Eddy Simulation of Wind Turbine Flows: A New Evaluation of Actuator Disk Models. Energies 2021, 14, 3745. [Google Scholar] [CrossRef]
- Micallef, D.; Ferreira, C.; Herráez, I.; Höning, L.; Yu, W.; Capdevila, H. Assessment of actuator disc models in predicting radial flow and wake expansion. J. Wind Eng. Ind. Aerodyn. 2020, 207, 104396. [Google Scholar] [CrossRef]
- Li, N.; Liu, Y.; Li, L.; Chang, S.; Han, S.; Zhao, H.; Meng, H. Numerical simulation of wind turbine wake based on extended k-epsilon turbulence model coupling with actuator disc considering nacelle and tower. IET Renew. Power Gener. 2020, 14, 3834–3842. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Nilsson, K.; Ivanell, S.; Asmuth, H.; Mikkelsen, R.F. Analytical body forces in numerical actuator disc model of wind turbines. Renew. Energy 2020, 147, 2259–2271. [Google Scholar] [CrossRef]
- Naderi, S.; Parvanehmasiha, S.; Torabi, F. Modeling of horizontal axis wind turbine wakes in Horns Rev offshore wind farm using an improved actuator disc model coupled with computational fluid dynamic. Energy Conv. Manag. 2018, 171, 953–968. [Google Scholar] [CrossRef]
- Behrouzifar, A.; Darbandi, M. An improved actuator disc model for the numerical prediction of the far-wake region of a horizontal axis wind turbine and its performance. Energy Conv. Manag. 2019, 185, 482–495. [Google Scholar] [CrossRef]
- Amini, S.; Golzarian, M.R.; Mahmoodi, E.; Jeromin, A.; Abbaspour-Fard, M.H. Numerical simulation of the Mexico wind turbine using the actuator disk model along with the 3D correction of aerodynamic coefficients in OpenFOAM. Renew. Energy 2021, 163, 2029–2036. [Google Scholar] [CrossRef]
- Sorensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Yu, Z.; Zheng, X.; Ma, Q. Study on actuator line modeling of two NREL 5-MW wind turbine wakes. Appl. Sci. 2018, 8, 434. [Google Scholar] [CrossRef]
- Martinez-Tossas, L.A.; Churchfield, M.J.; Yilmaz, A.E.; Sarlak, H.; Johnson, P.L.; Sørensen, J.N.; Meyers, J.; Meneveau, C. Comparison of four large-eddy simulation research codes and effects of model coefficient and inflow turbulence in actuator-line-based wind turbine modeling. J. Renew. Sustain. Energy 2018, 10, 033301. [Google Scholar] [CrossRef]
- Ravensbergen, M.; Mohamed, A.B.; Korobenko, A. The actuator line method for wind turbine modelling applied in a variational multiscale framework. Comput. Fluids 2020, 201, 104465. [Google Scholar] [CrossRef]
- Onel, H.C.; Tuncer, I.H. Investigation of wind turbine wakes and wake recovery in a tandem configuration using actuator line model with LES. Comput. Fluids 2021, 220, 104872. [Google Scholar] [CrossRef]
- Draper, M.; Guggeri, A.; Mendina, M.; Usera, G.; Campagnolo, F. A large eddy simulation-actuator line model framework to simulate a scaled wind energy facility and its application. J. Wind Eng. Ind. Aerodyn. 2018, 182, 146–159. [Google Scholar] [CrossRef]
- Jha, P.K.; Schmitz, S. Actuator curve embedding–an advanced actuator line model. J. Fluid Mech. 2018, 834, R2. [Google Scholar] [CrossRef]
- Xie, S. An actuator-line model with Lagrangian-averaged velocity sampling and piecewise projection for wind turbine simulations. Wind Energy 2021, 24, 1095–1106. [Google Scholar] [CrossRef]
- Xue, F.; Duan, H.; Xu, C.; Han, X.; Shangguan, Y.; Li, T.; Fen, Z. Research on the Power Capture and Wake Characteristics of a Wind Turbine Based on a Modified Actuator Line Model. Energies 2022, 15, 282. [Google Scholar] [CrossRef]
- Shen, W.Z.; Sørensen, J.N.; Zhang, J. Actuator surface model for wind turbine flow computations. In Proceedings of the European Wind Energy Conference, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Shen, W.Z.; Zhang, J.H.; Sørensen, J.N. The actuator surface model: A new Navier–Stokes based model for rotor computations. J. Sol. Energy Eng. 2009, 131, 011002. [Google Scholar] [CrossRef]
- Sibuet Watters, C.; Breton, S.P.; Masson, C. Application of the actuator surface concept to wind turbine rotor aerodynamics. Wind Energy 2010, 13, 433–447. [Google Scholar] [CrossRef]
- Yang, X.; Sotiropoulos, F. A new class of actuator surface models for wind turbines. Wind Energy 2018, 21, 285–302. [Google Scholar] [CrossRef]
- Yang, X.; Sotiropoulos, F. Wake characteristics of a utility-scale wind turbine under coherent inflow structures and different operating conditions. Phys. Rev. Fluids 2019, 4, 024604. [Google Scholar] [CrossRef]
- Foti, D.; Yang, X.; Campagnolo, F.; Maniaci, D.; Sotiropoulos, F. Wake meandering of a model wind turbine operating in two different regimes. Phys. Rev. Fluids 2018, 3, 054607. [Google Scholar] [CrossRef]
- Foti, D.; Yang, X.; Shen, L.; Sotiropoulos, F. Effect of wind turbine nacelle on turbine wake dynamics in large wind farms. J. Fluid Mech. 2019, 869, 1–26. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X. Evaluation of actuator disk model relative to actuator surface model for predicting utility-scale wind turbine wakes. Energies 2020, 13, 3574. [Google Scholar] [CrossRef]
- Sutrisno; Deendarlianto; Rohmat, T.A.; Indarto; Setyawan, B.W.; Iswahyudi, S.; Dhanu, A.; Djatmiko. The structured and unstructured CFD characteristic studies of 3-D backward wind turbine blades. AIP Conf. Proc. 2018, 2001, 040003. [Google Scholar] [CrossRef]
- Regodeseves, P.G.; Morros, C.S. Unsteady numerical investigation of the full geometry of a horizontal axis wind turbine: Flow through the rotor and wake. Energy 2020, 202, 117674. [Google Scholar] [CrossRef]
- Wang, Q.; Liao, K.; Ma, Q. The influence of tilt angle on the aerodynamic performance of a wind turbine. Appl. Sci. 2020, 10, 5380. [Google Scholar] [CrossRef]
- Zahle, F.; Sørensen, N.N.; Johansen, J. Wind turbine rotor-tower interaction using an incompressible overset grid method. Wind Energy 2009, 12, 594–619. [Google Scholar] [CrossRef]
- Li, Y.; Paik, K.J.; Xing, T.; Carrica, P.M. Dynamic overset CFD simulations of wind turbine aerodynamics. Renew. Energy 2012, 37, 285–298. [Google Scholar] [CrossRef]
- Purohit, S.; Kabir, I.F.S.A.; Ng, E. On the accuracy of uRANS and LES-based CFD modeling approaches for rotor and wake aerodynamics of the (New) MEXICO wind turbine rotor phase-iii. Energies 2021, 14, 5198. [Google Scholar] [CrossRef]
- Sedano, C.A.; Berger, F.; Rahimi, H.; Lopez Mejia, O.D.; Kühn, M.; Stoevesandt, B. CFD validation of a model wind turbine by means of improved and delayed detached eddy simulation in OpenFOAM. Energies 2019, 12, 1306. [Google Scholar] [CrossRef]
- Pinto, M.L.; Franzini, G.R.; Simos, A.N. A CFD analysis of NREL’s 5MW wind turbine in full and model scales. J. Ocean Eng. Mar. Energy 2020, 6, 211–220. [Google Scholar] [CrossRef]
- Bangga, G. Comparison of blade element method and CFD simulations of a 10 MW wind turbine. Fluids 2018, 3, 73. [Google Scholar] [CrossRef] [Green Version]
- Carreno Ruiz, M.; Manavella, A.; D’Ambrosio, D. Numerical and experimental validation and comparison of reduced order models for small scale rotor hovering performance prediction. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0154. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Kolios, A. State of the art in the aeroelasticity of wind turbine blades: Aeroelastic modelling. Renew. Sust. Energ. Rev. 2016, 64, 195–210. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Euler-Bernoulli Beam Theory. Structural Analysis; Springer: Dordrecht, The Netherlands, 2009; pp. 173–221. [Google Scholar]
- Oñate, E. Structural Analysis with the Finite Element Method. In Linear Statics: Volume 2: Beams, Plates and Shells; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Hodges, D.H. Geometrically exact, intrinsic theory for dynamics of curved and twisted anisotropic beams. AIAA J. 2003, 41, 1131–1137. [Google Scholar] [CrossRef]
- Shabana, A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Hansen, M.O.L.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aeosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Gözcü, O.; Verelst, D.R. The effects of blade structural model fidelity on wind turbine load analysis and computation time. Wind Energy Sci. 2020, 5, 503–517. [Google Scholar] [CrossRef]
- Sayed, M.; Klein, L.; Lutz, T.; Krämer, E. The impact of the aerodynamic model fidelity on the aeroelastic response of a multi-megawatt wind turbine. Renew. Energy 2019, 140, 304–318. [Google Scholar] [CrossRef]
- Li, Y.; Castro, A.M.; Martin, J.E.; Sinokrot, T.; Prescott, W.; Carrica, P.M. Coupled computational fluid dynamics/multibody dynamics method for wind turbine aero-servo-elastic simulation including drivetrain dynamics. Renew. Energy 2017, 101, 1037–1051. [Google Scholar] [CrossRef]
- Guma, G.; Bangga, G.; Lutz, T.; Krämer, E. Aeroelastic analysis of wind turbines under turbulent inflow conditions. Wind Energy Sci. 2021, 6, 93–110. [Google Scholar] [CrossRef]
- Grinderslev, C.; González Horcas, S.; Sørensen, N.N. Fluid–structure interaction simulations of a wind turbine rotor in complex flows, validated through field experiments. Wind Energy 2021, 24, 1426–1442. [Google Scholar] [CrossRef]
- Sayed, M.; Lutz, T.; Krämer, E.; Shayegan, S.; Ghantasala, A.; Wüchner, R.; Bletzinger, K.U. High fidelity CFD-CSD aeroelastic analysis of slender bladed horizontal-axis wind turbine. J. Phys. Conf. Ser. 2016, 753, 042009. [Google Scholar] [CrossRef] [Green Version]
- Sayed, M.; Lutz, T.; Krämer, E.; Shayegan, S.; Wüchner, R. Aeroelastic analysis of 10 MW wind turbine using CFD–CSD explicit FSI-coupling approach. J. Fluids Struct. 2019, 87, 354–377. [Google Scholar] [CrossRef]
- Dose, B.; Rahimi, H.; Herráez, I.; Stoevesandt, B.; Peinke, J. Fluid-structure coupled computations of the NREL 5 MW wind turbine by means of CFD. Renew. Energy 2018, 129, 591–605. [Google Scholar] [CrossRef]
- Della Posta, G.; Leonardi, S.; Bernardini, M. A two-way coupling method for the study of aeroelastic effects in large wind turbines. Renew. Energy 2022, 190, 971–992. [Google Scholar] [CrossRef]
- Yu, Z.; Hu, Z.; Zheng, X.; Ma, Q.; Hao, H. Aeroelastic performance analysis of wind turbine in the wake with a new Elastic Actuator Line model. Water 2020, 12, 1233. [Google Scholar] [CrossRef]
- Ma, Z.; Zeng, P.; Lei, L. Analysis of the coupled aeroelastic wake behavior of wind turbine. J. Fluids Struct. 2019, 84, 466–484. [Google Scholar] [CrossRef]
- Meng, H.; Lien, F.S.; Glinka, G.; Li, L.; Zhang, J. Study on wake-induced fatigue on wind turbine blade based on elastic actuator line model and two-dimensional finite element model. Wind Eng. 2019, 43, 64–82. [Google Scholar] [CrossRef]
- Meng, H.; Li, L.; Zhang, J. A preliminary numerical study of the wake effects on the fatigue load for wind farm based on elastic actuator line model. Renew. Energy 2020, 162, 788–801. [Google Scholar] [CrossRef]
- Sayed, M.; Bucher, P.; Guma, G.; Lutz, T.; Wüchner, R. Aeroelastic Simulations Based on High-Fidelity CFD and CSD Models. In Handbook of Wind Energy Aerodynamics; Springer: Cham, Switzerland, 2022; pp. 1–76. [Google Scholar] [CrossRef]
- Peeters, M.; Santo, G.; Degroote, J.; Van Paepegem, W. Comparison of shell and solid finite element models for the static certification tests of a 43 m wind turbine blade. Energies 2018, 11, 1346. [Google Scholar] [CrossRef]
- Tojo, B.M.; Marta, A.C. Aero-Structural blade design of a high-power wind turbine. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar]
- Zhangaskanov, D.; Batay, S.; Kamalov, B.; Zhao, Y.; Su, X.; Ng, E.Y.K. High-Fidelity 2-Way FSI Simulation of a Wind Turbine Using Fully Structured Multiblock Meshes in OpenFoam for Accurate Aero-Elastic Analysis. Fluids 2022, 7, 169. [Google Scholar] [CrossRef]
- Guma, G.; Bucher, P.; Letzgus, P.; Lutz, T.; Wüchner, R. High-fidelity aeroelastic analyses of wind turbines in complex terrain: Fluid–structure interaction and aerodynamic modeling. Wind Energy Sci. 2022, 7, 1421–1439. [Google Scholar] [CrossRef]
- Shkara, Y.; Cardaun, M.; Schelenz, R.; Jacobs, G. Aeroelastic response of a multi-megawatt upwind horizontal axis wind turbine (HAWT) based on fluid–structure interaction simulation. Wind Energy Sci. 2020, 5, 141–154. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Effect of rotor–tower interaction, tilt angle, and yaw misalignment on the aeroelasticity of a large horizontal axis wind turbine with composite blades. Wind Energy 2020, 23, 1578–1595. [Google Scholar] [CrossRef]
- Micallef, D.; Rezaeiha, A. Floating offshore wind turbine aerodynamics: Trends and future challenges. Renew. Sust. Energ. Rev. 2021, 152, 111696. [Google Scholar] [CrossRef]
- Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcón, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B.; et al. OC6 Phase I: Investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine. J. Phys. Conf. Ser. 2020, 1618, 032033. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The aerodynamic interference effects of a floating offshore wind turbine experiencing platform pitching and yawing motions. J. Mech. Sci. Technol. 2015, 29, 549–561. [Google Scholar] [CrossRef]
- Huang, Y.; Zhuang, Y.; Wan, D. Hydrodynamic Study and Performance Analysis of the OC4-DeepCWind Platform by CFD Method. Int. J. Comput. Methods 2021, 18, 2050020. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Li, J.; Bian, J.; Ma, Y.; Jiang, Y. Impact of typhoons on floating offshore wind turbines: A case study of typhoon Mangkhut. J. Mar. Sci. Eng. 2021, 9, 543. [Google Scholar] [CrossRef]
- Davidson, J.; Ringwood, J.V. Mathematical modelling of mooring systems for wave energy converters—A review. Energies 2017, 10, 666. [Google Scholar] [CrossRef] [Green Version]
- Quallen, S.; Xing, T.; Carrica, P.; Li, Y.; Xu, J. CFD simulation of a floating offshore wind turbine system using a quasi-static crowfoot mooring-line model. In Proceedings of the Twenty-Third International Offshore and Polar Engineering Conference, Anchorage, AL, USA, 30 June–5 July 2013. [Google Scholar]
- Faraggiana, E.; Giorgi, G.; Sirigu, M.; Ghigo, A.; Bracco, G.; Mattiazzo, G. A review of numerical modelling and optimisation of the floating support structure for offshore wind turbines. J. Ocean Eng. Mar. Energy 2022, 8, 433–456. [Google Scholar] [CrossRef]
- Leonard, J.W.; Nath, J.H. Comparison of finite element and lumped parameter methods for oceanic cables. Eng. Struct. 1981, 3, 153–167. [Google Scholar] [CrossRef]
- Beyer, F.; Arnold, M.; Cheng, P.W. Analysis of floating offshore wind turbine hydrodynamics using coupled CFD and multibody methods. In Proceedings of the Twenty-Third International Offshore and Polar Engineering Conference, Anchorage, AL, USA, 30 June–5 July 2013. [Google Scholar]
- Quallen, S.; Xing, T. CFD simulation of a floating offshore wind turbine system using a variable-speed generator-torque controller. Renew. Energy 2016, 97, 230–242. [Google Scholar] [CrossRef]
- Liu, B.; Yu, J. Dynamic Response of SPAR-Type Floating Offshore Wind Turbine under Wave Group Scenarios. Energies 2022, 15, 4870. [Google Scholar] [CrossRef]
- Nematbakhsh, A.; Olinger, D.J.; Tryggvason, G. Nonlinear simulation of a spar buoy floating wind turbine under extreme ocean conditions. J. Renew. Sustain. Energy 2014, 6, 033121. [Google Scholar] [CrossRef]
- Zhao, W.; Shen, Z.; Wan, D. Numerical investigation of the vortex induced motion of SPAR in uniform current. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
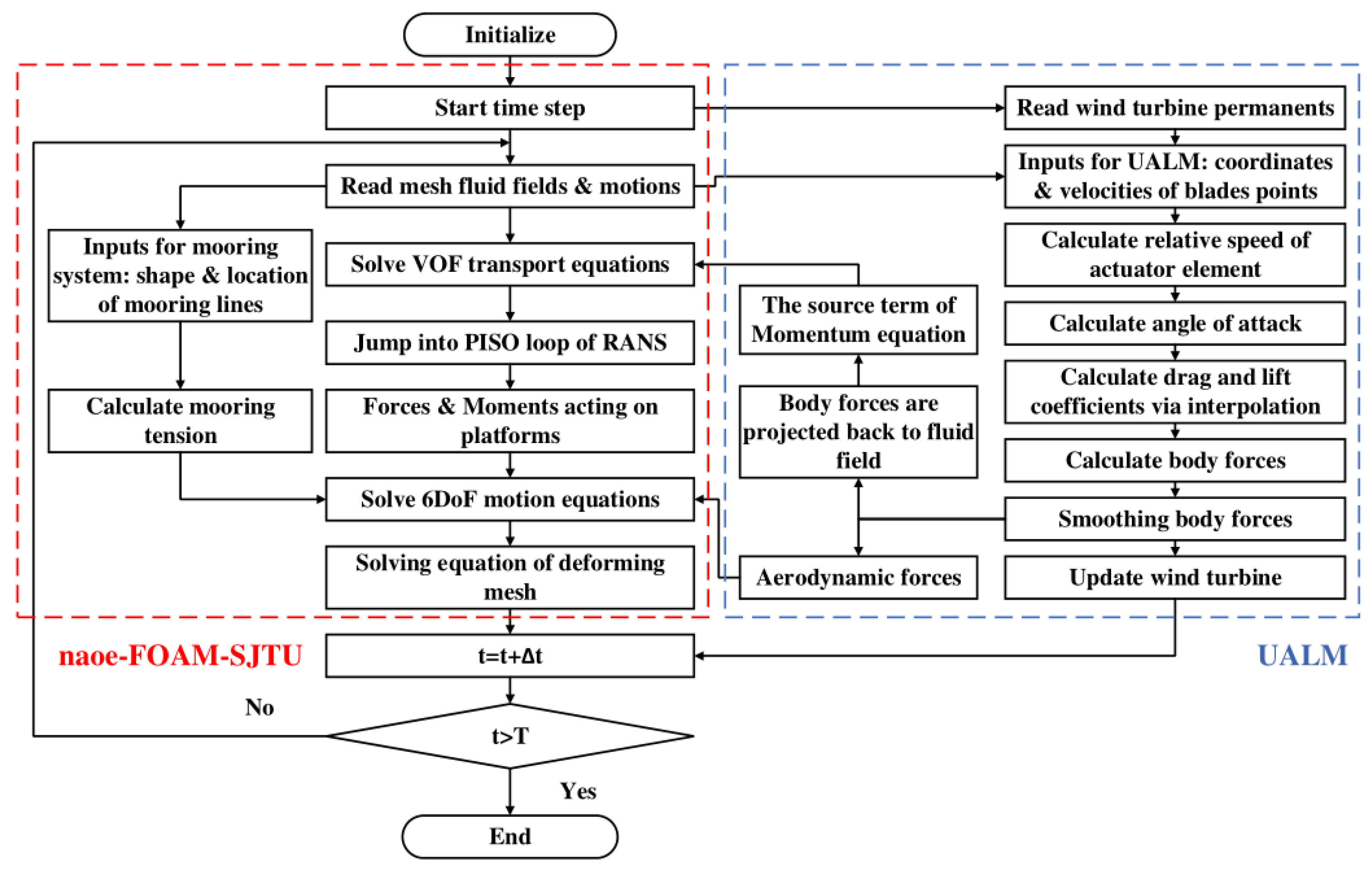
- Wang, J.; Zhao, W.; Wan, D. Development of naoe-FOAM-SJTU solver based on OpenFOAM for marine hydrodynamics. J. Hydrodyn. 2019, 31, 1–20. [Google Scholar] [CrossRef]
- Wang, B.; Xu, Z.; Li, C.; Wang, D.; Ding, Q. Hydrodynamic characteristics of forced oscillation of heave plate with fractal characteristics based on floating wind turbine platform. Ocean Eng. 2020, 212, 107621. [Google Scholar] [CrossRef]
- Subbulakshmi, A.; Sundaravadivelu, R. Heave damping of spar platform for offshore wind turbine with heave plate. Ocean Eng. 2016, 121, 24–36. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, Y.; Wan, D. Numerical Study of Coupled Aero-Hydrodynamics Performances of a Floating Offshore Wind Turbine with Heave Plate. In Proceedings of the Thirty-First International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021. [Google Scholar]
- Dunbar, A.J.; Craven, B.A.; Paterson, E.G. Development and validation of a tightly coupled CFD/6-DOF solver for simulating floating offshore wind turbine platforms. Ocean Eng. 2015, 110, 98–105. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Benitz, M.A.; Schmidt, D.P.; Lackner, M.A.; Stewart, G.M.; Jonkman, J.; Robertson, A. Validation of hydrodynamic load models using CFD for the OC4-DeepCwind semisubmersible. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NF, Canada, 31 May–5 June 2015. [Google Scholar] [CrossRef]
- Rivera-Arreba, I.; Bruinsma, N.; Bachynski, E.E.; Viré, A.; Paulsen, B.T.; Jacobsen, N.G. Modeling of a semisubmersible floating offshore wind platform in severe waves. J. Offshore Mech. Arct. Eng. 2019, 141, 061905. [Google Scholar] [CrossRef]
- Liu, C.; Hu, C. CFD simulation of a floating wind turbine platform in rough sea conditions. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.H. Uncertainty assessment of CFD investigation of the nonlinear difference-frequency wave loads on a semisubmersible FOWT platform. Sustainability 2020, 13, 64. [Google Scholar] [CrossRef]
- Li, H.; Bachynski, E.E. Experimental and numerical investigation of nonlinear diffraction wave loads on a semi-submersible wind turbine. Renew. Energy 2021, 171, 709–727. [Google Scholar] [CrossRef]
- Bandringa, H.; Helder, J.A. On the validity and sensitivity of CFD simulations for a deterministic breaking wave impact on a semi submersible. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Tan, J.H.C.; Magee, A.; Kim, J.W.; Teng, Y.J.; Ahmad Zukni, N. CFD simulation for vortex induced motions of a multi-column floating platform. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
- Kim, S.J.; Spernjak, D.; Mejia-Alvarez, R.; Vinayan, V.; Sterenborg, J.; Antony, A.; Holmes, S.; Halkyard, J. Numerical simulation of vortex-induced motion of a deep-draft paired-column semi-submersible offshore platform. Ocean Eng. 2018, 149, 291–304. [Google Scholar] [CrossRef]
- Zhao, W.; Zou, L.; Wan, D.; Hu, Z. Numerical investigation of vortex-induced motions of a paired-column semi-submersible in currents. Ocean Eng. 2018, 164, 272–283. [Google Scholar] [CrossRef]
- Zhao, W.; Wei, Z.; Wan, D. Numerical investigation on the effects of current headings on vortex induced motions of a semi-submersible. J. Hydrodyn. 2022, 34, 382–394. [Google Scholar] [CrossRef]
- Nematbakhsh, A.; Bachynski, E.E.; Gao, Z.; Moan, T. Comparison of wave load effects on a TLP wind turbine by using computational fluid dynamics and potential flow theory approaches. Appl. Ocean Res. 2015, 53, 142–154. [Google Scholar] [CrossRef]
- Dai, S.S.; Chaplin, J.R.; Younis, B.A.; Tang, D.; Zhai, T.L. Computations and measurements of the global drag force on a Tension-Leg Platform. Ocean Eng. 2021, 239, 109710. [Google Scholar] [CrossRef]
- Nam, B.W.; Hong, S.Y.; Kim, H.J. An experimental study on characteristics of relative wave elevations around a tension leg platform in irregular waves. Appl. Ocean Res. 2022, 122, 103133. [Google Scholar] [CrossRef]
- Beyer, F.; Choisnet, T.; Kretschmer, M.; Cheng, P.W. Coupled MBS-CFD simulation of the IDEOL floating offshore wind turbine foundation compared to wave tank model test data. In Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference, Big Island, HI, USA, 21–26 June 2015. [Google Scholar]
- Tan, L.; Ikoma, T.; Aida, Y.; Masuda, K. Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools. J. Mar. Sci. Eng. 2021, 9, 709. [Google Scholar] [CrossRef]
- Kristiansen, T.; Sauder, T.; Firoozkoohi, R. Validation of a hybrid code combining potential and viscous flow with application to 3D moonpool. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
- Nematbakhsh, A.; Olinger, D.J.; Tryggvason, G. A nonlinear computational model for floating wind turbines. In Proceedings of the ASME 2012 Fluids Engineering Summer Meeting, Rio Grande, PR, USA, 8–12 July 2012. [Google Scholar] [CrossRef]
- Zhao, W.; Wan, D. Numerical study of interactions between phase II of OC4 wind turbine and its semi-submersible floating support system. J. Ocean Wind Energy 2015, 2, 45–53. [Google Scholar]
- Tran, T.T.; Kim, D.H. A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion. Renew. Energy 2016, 90, 204–228. [Google Scholar] [CrossRef]
- Chen, G.; Liang, X.F.; Li, X.B. Modelling of wake dynamics and instabilities of a floating horizontal-axis wind turbine under surge motion. Energy 2022, 239, 122110. [Google Scholar] [CrossRef]
- Kopperstad, K.M.; Kumar, R.; Shoele, K. Aerodynamic characterization of barge and spar type floating offshore wind turbines at different sea states. Wind Energy 2020, 23, 2087–2112. [Google Scholar] [CrossRef]
- Kyle, R.; Lee, Y.C.; Früh, W.G. Propeller and vortex ring state for floating offshore wind turbines during surge. Renew. Energy 2020, 155, 645–657. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Micallef, D. Wake interactions of two tandem floating offshore wind turbines: CFD analysis using actuator disc model. Renew. Energy 2021, 179, 859–876. [Google Scholar] [CrossRef]
- Tran, T.; Kim, D.; Song, J. Computational fluid dynamic analysis of a floating offshore wind turbine experiencing platform pitching motion. Energies 2014, 7, 5011–5026. [Google Scholar] [CrossRef]
- Lei, H.; Zhou, D.; Lu, J.; Chen, C.; Han, Z.; Bao, Y. The impact of pitch motion of a platform on the aerodynamic performance of a floating vertical axis wind turbine. Energy 2017, 119, 369–383. [Google Scholar] [CrossRef]
- Fang, Y.; Duan, L.; Han, Z.; Zhao, Y.; Yang, H. Numerical analysis of aerodynamic performance of a floating offshore wind turbine under pitch motion. Energy 2020, 192, 116621. [Google Scholar] [CrossRef]
- Cai, X.; Gu, R.; Pan, P.; Zhu, J. Unsteady aerodynamics simulation of a full-scale horizontal axis wind turbine using CFD methodology. Energy Conv. Manag. 2016, 112, 146–156. [Google Scholar] [CrossRef]
- Leble, V.; Barakos, G. 10-MW wind turbine performance under pitching and yawing motion. J. Sol. Energy Eng. 2017, 139, 041003. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Wan, D. Investigation of the effects of platform motion on the aerodynamics of a floating offshore wind turbine. J. Hydrodyn. 2016, 28, 95–101. [Google Scholar] [CrossRef]
- Li, P.; Cheng, P.; Wan, D.; Xiao, Q. Numerical simulations of wake flows of floating offshore wind turbines by unsteady actuator line model. In Proceedings of the 9th International Workshop on Ship and Marine Hydrodynamics, Glasgow, UK, 26–28 August 2015. [Google Scholar]
- Lin, L.; Wang, K.; Vassalos, D. Detecting wake performance of floating offshore wind turbine. Ocean Eng. 2018, 156, 263–276. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Guo, Y.; Kang, S. Numerical analysis of unsteady aerodynamic performance of floating offshore wind turbine under platform surge and pitch motions. Renew. Energy 2021, 163, 1849–1870. [Google Scholar] [CrossRef]
- Ren, N.; Li, Y.; Ou, J. Coupled wind-wave time domain analysis of floating offshore wind turbine based on Computational Fluid Dynamics method. J. Renew. Sustain. Energy 2014, 6, 023106. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Zhang, Y.; Kim, B. A fully coupled computational fluid dynamics method for analysis of semi-submersible floating offshore wind turbines under wind-wave excitation conditions based on OC5 data. Appl. Sci. 2018, 8, 2314. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.T.; Kim, D.H. A CFD study of coupled aerodynamic-hydrodynamic loads on a semisubmersible floating offshore wind turbine. Wind Energy 2018, 21, 70–85. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Li, S.; Pan, G. Numerical modelling of dynamic responses of a floating offshore wind turbine subject to focused waves. Energies 2019, 12, 3482. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Peyrard, C.; Pan, G. Assessing focused wave applicability on a coupled aero-hydro-mooring FOWT system using CFD approach. Ocean Eng. 2021, 240, 109987. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, D. Investigation of interference effects between wind turbine and spar-type floating platform under combined wind-wave excitation. Sustainability 2019, 12, 246. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, P.; Wan, D. Numerical analysis of a floating offshore wind turbine by coupled aero-hydrodynamic simulation. J. Mar. Sci. Eng. Appl. 2019, 18, 82–92. [Google Scholar] [CrossRef]
- Rodriguez, S.N.; Jaworski, J.W. Strongly-coupled aeroelastic free-vortex wake framework for floating offshore wind turbine rotors. Part 1: Numerical framework. Renew. Energy 2019, 141, 1127–1145. [Google Scholar] [CrossRef]
- Rodriguez, S.N.; Jaworski, J.W. Strongly-coupled aeroelastic free-vortex wake framework for floating offshore wind turbine rotors. Part 2: Application. Renew. Energy 2020, 149, 1018–1031. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C. Aeroelastic analysis of a floating offshore wind turbine in platform-induced surge motion using a fully coupled CFD-MBD method. Wind Energy 2019, 22, 1–20. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q. Development of a fully coupled aero-hydro-mooring-elastic tool for floating offshore wind turbines. J. Hydrodyn. 2019, 31, 21–33. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, D.; Hu, C. Numerical Analysis of Aero-Hydrodynamic Responses of Floating Offshore Wind Turbine Considering Blade Deformation. In Proceedings of the Thirty-First International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021. [Google Scholar]
- Huang, Y.; Xiao, Q.; Wan, D. Wake interaction between two floating offshore wind turbines with blade deformation. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering, Hamburg, Germany, 5–10 June 2022. [Google Scholar]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Wan, D.; Pan, G.; Li, S. Exploring inflow wind condition on floating offshore wind turbine aerodynamic characterisation and platform motion prediction using blade resolved CFD simulation. Renew. Energy 2022, 182, 1060–1079. [Google Scholar] [CrossRef]
- Mann, J. The spatial structure of neutral atmospheric surface-layer turbulence. J. Fluid Mech. 1994, 273, 141–168. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.J.; Izumi, Y.; Coté, O.R. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Yuan, Z.; Gao, Y. Wind field effect on the power generation and aerodynamic performance of offshore floating wind turbines. Energy 2018, 157, 379–390. [Google Scholar] [CrossRef]
- Doubrawa, P.; Churchfield, M.J.; Godvik, M.; Sirnivas, S. Load response of a floating wind turbine to turbulent atmospheric flow. Appl. Energy 2019, 242, 1588–1599. [Google Scholar] [CrossRef]
- Nybø, A.; Nielsen, F.G.; Reuder, J.; Churchfield, M.J.; Godvik, M. Evaluation of different wind fields for the investigation of the dynamic response of offshore wind turbines. Wind Energy 2020, 23, 1810–1830. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Xu, W.; Gao, Z.; Fang, L.; Li, R.; Ding, B.; Zhao, B.; Leng, J.; He, F. Systematic analysis of performance and cost of two floating offshore wind turbines with significant interactions. Appl. Energy 2022, 321, 119341. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Xue, Y.; Zhao, W.; Wan, D. A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2022, 10, 1357. https://doi.org/10.3390/jmse10101357
Xu S, Xue Y, Zhao W, Wan D. A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines. Journal of Marine Science and Engineering. 2022; 10(10):1357. https://doi.org/10.3390/jmse10101357
Chicago/Turabian StyleXu, Shun, Yingjie Xue, Weiwen Zhao, and Decheng Wan. 2022. "A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines" Journal of Marine Science and Engineering 10, no. 10: 1357. https://doi.org/10.3390/jmse10101357
APA StyleXu, S., Xue, Y., Zhao, W., & Wan, D. (2022). A Review of High-Fidelity Computational Fluid Dynamics for Floating Offshore Wind Turbines. Journal of Marine Science and Engineering, 10(10), 1357. https://doi.org/10.3390/jmse10101357






