The Numerical Simulation and Experimental Study of Heat Flow in Seabed Sediments Based on COMSOL
Abstract
:1. Introduction
2. Design of Sediment Thermal Conductivity Test System
2.1. In Situ Heat Transfer Analysis of Sediments
2.1.1. Calculating Heat Conduction in Cylindrical Coordinate System
2.1.2. One-Dimensional Heat Conduction Flow Calculation for a Large Flat Plate
2.2. Sediment Thermal Conductivity Test Experiment
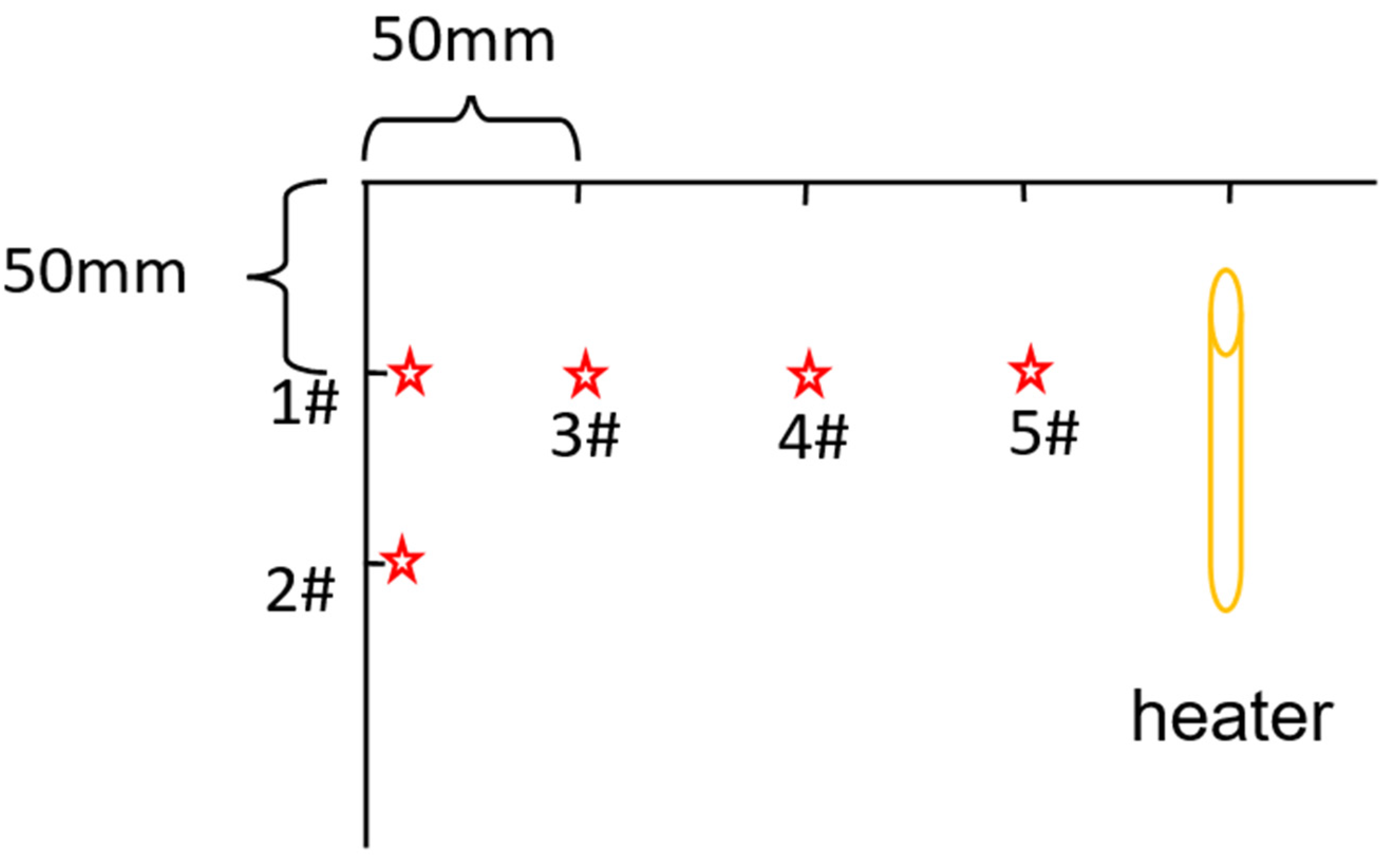
2.2.1. Test Method Construction
2.2.2. Analysis of Results
3. Simulation
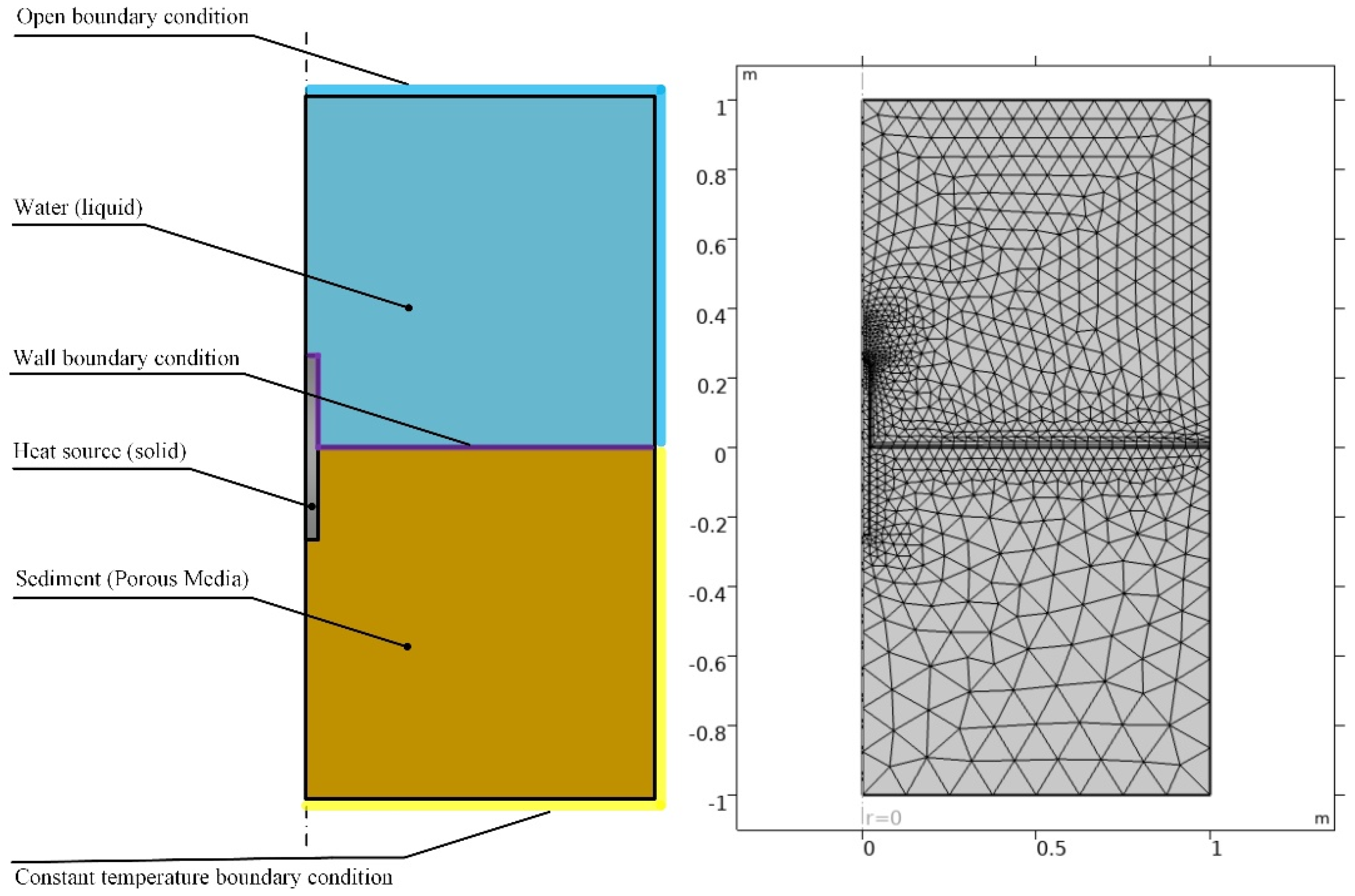
3.1. Finite Element Model
- (1)
- The thermal deformation of the soil during the heating process is ignored;
- (2)
- Contact thermal resistance between heating the heat source and soil is ignored;
- (3)
- Changes in basic property parameters during soil heating are ignored and the soil is considered to be homogeneous and isotropic, so the physical parameters of the porous medium (density, heat capacity, thermal conductivity, etc.) are assumed to be constant;
- (4)
- The porous medium is assumed to be homogeneous, isotropic, and fully saturated;
- (5)
- The thermally-induced pore flow in porous media is described by Darcy’s law [30].
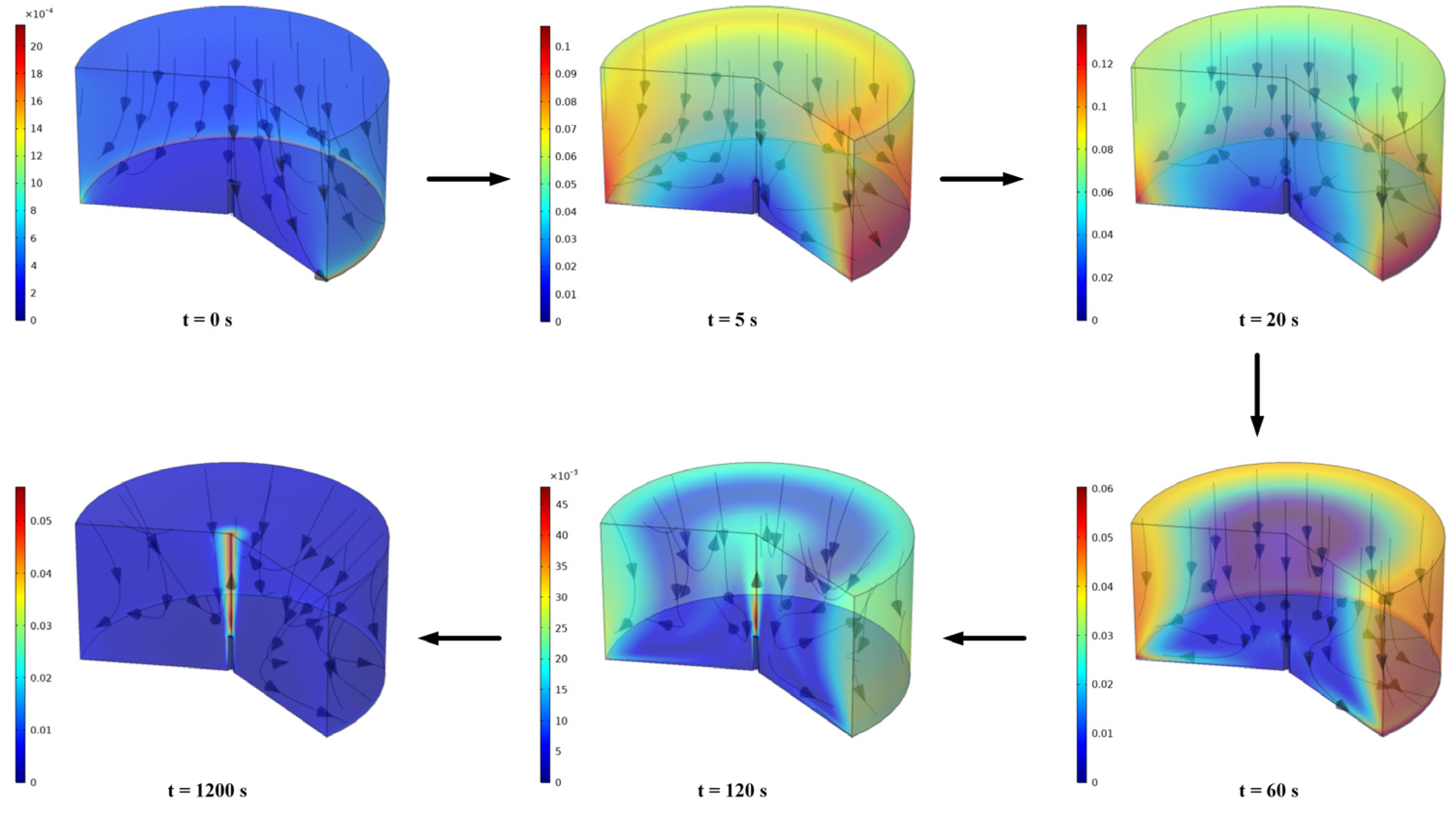
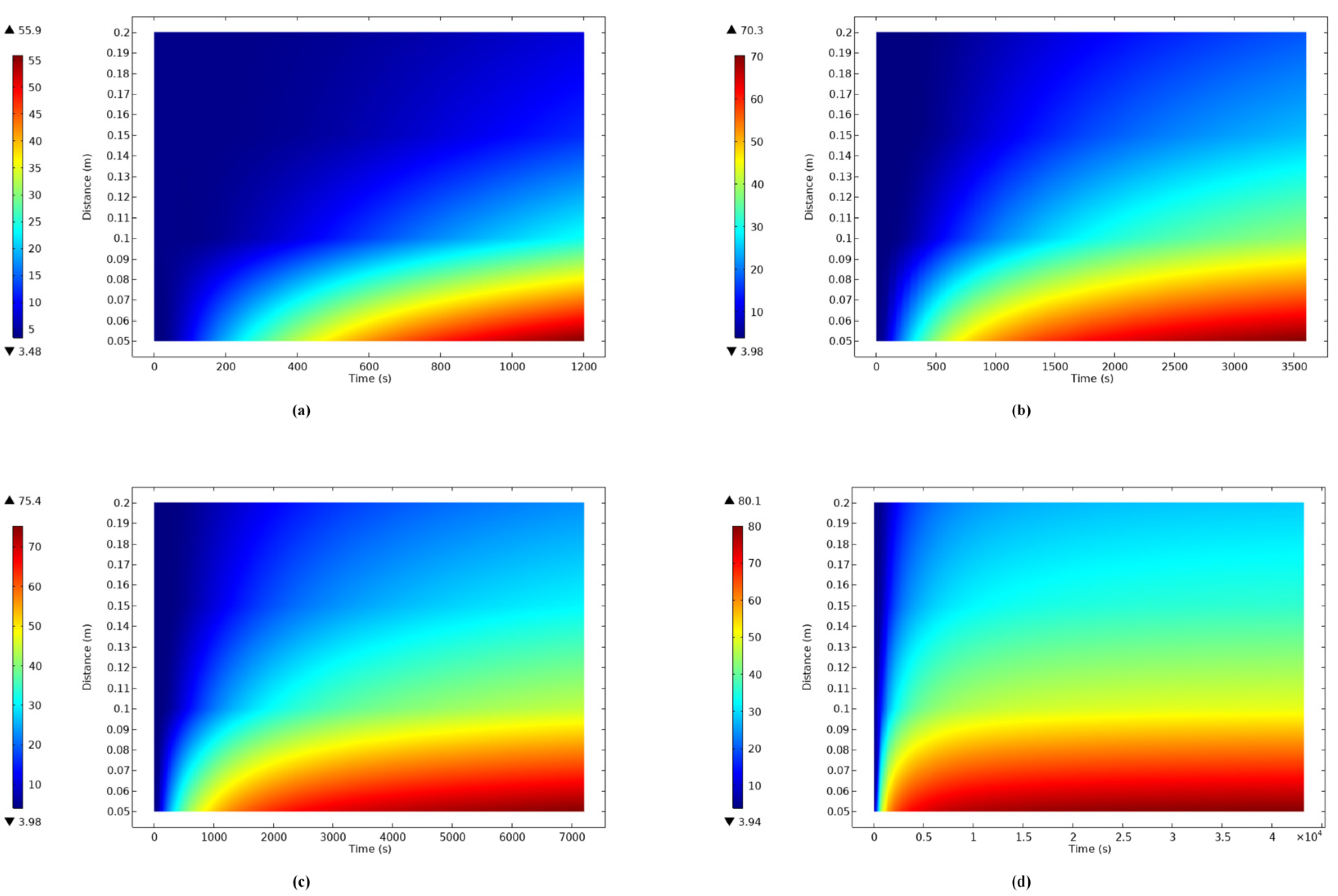
3.2. Simulation Analysis and Discussion
4. Experimental Verification
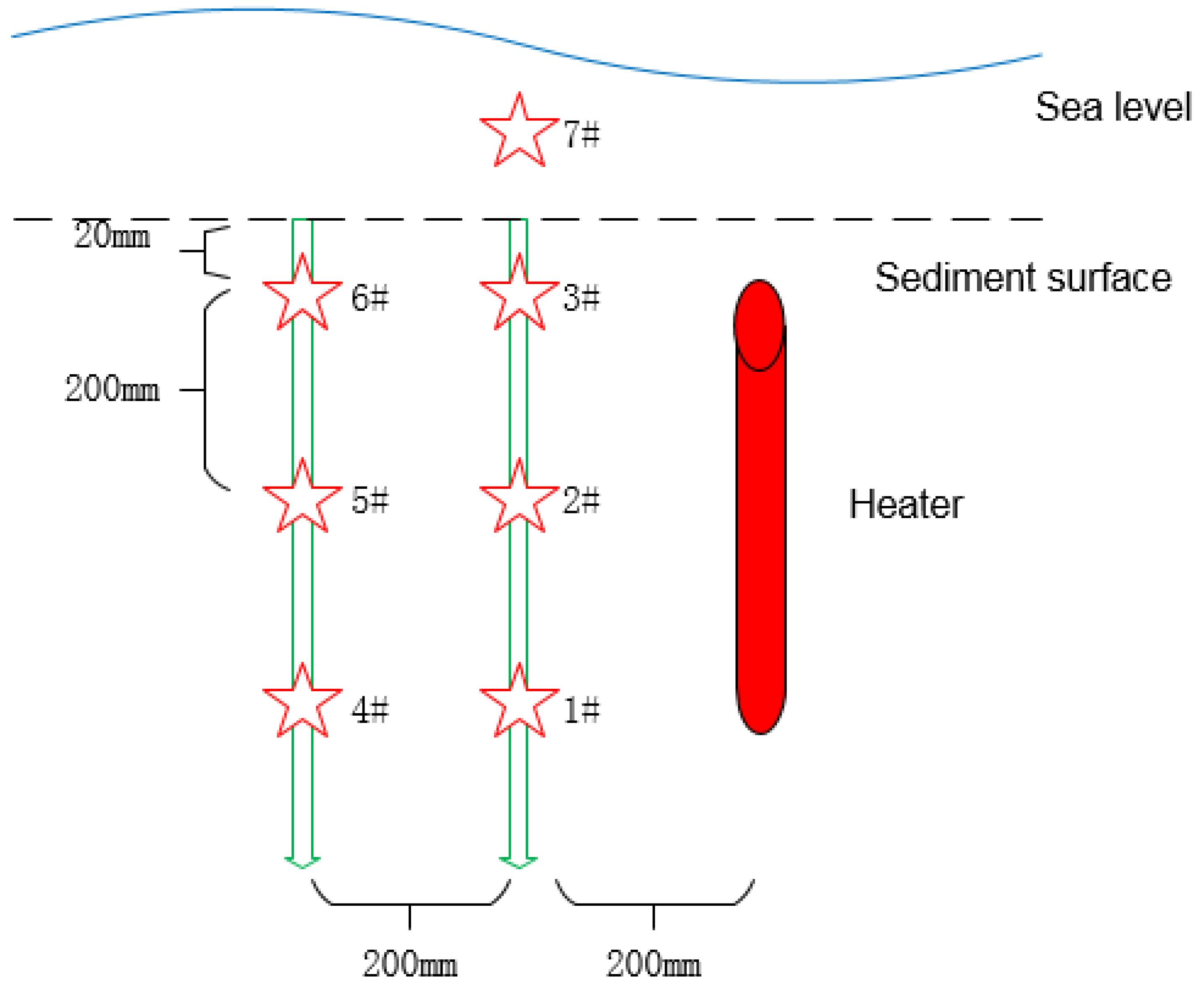
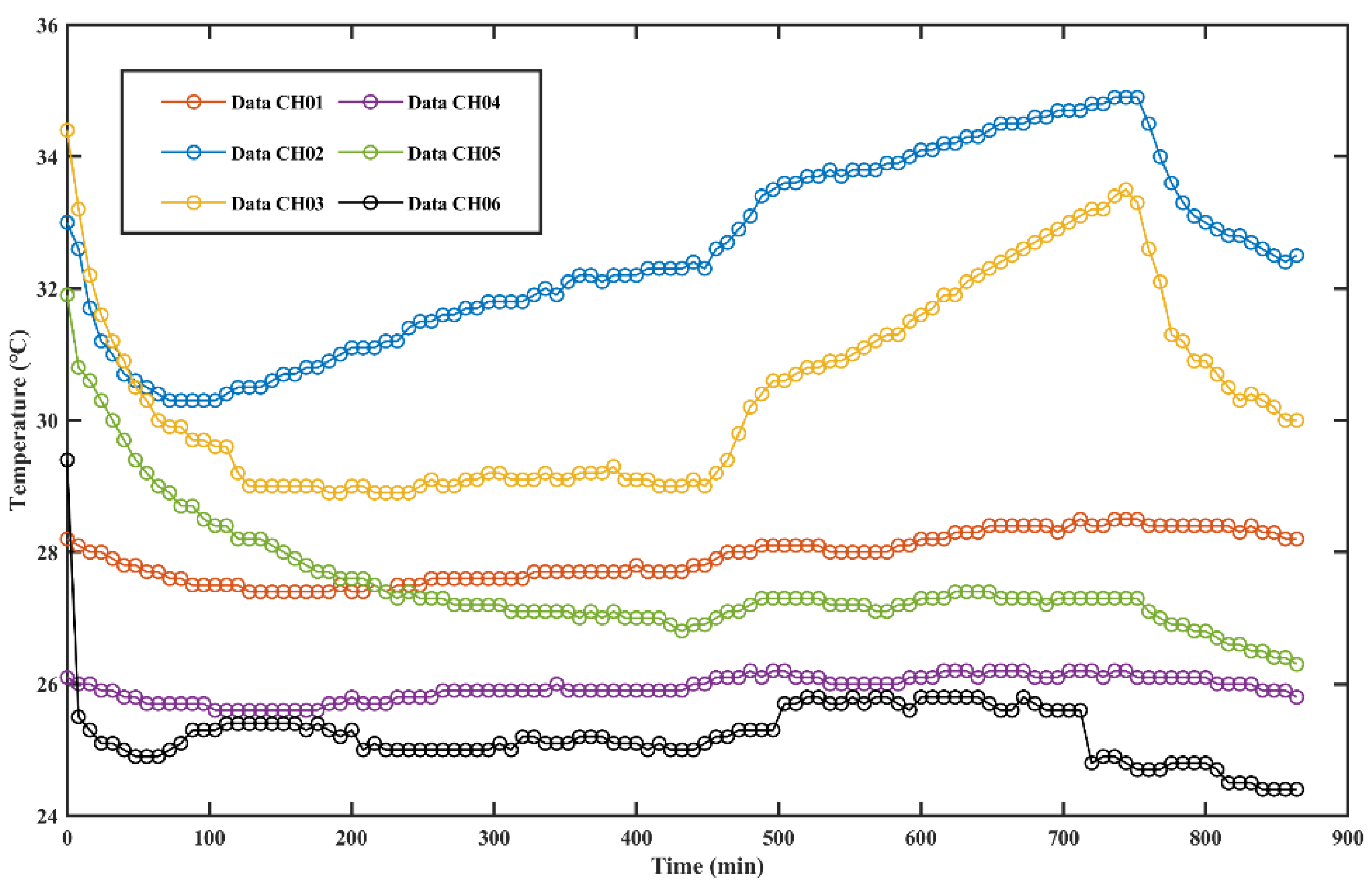
4.1. Incubator Experiment
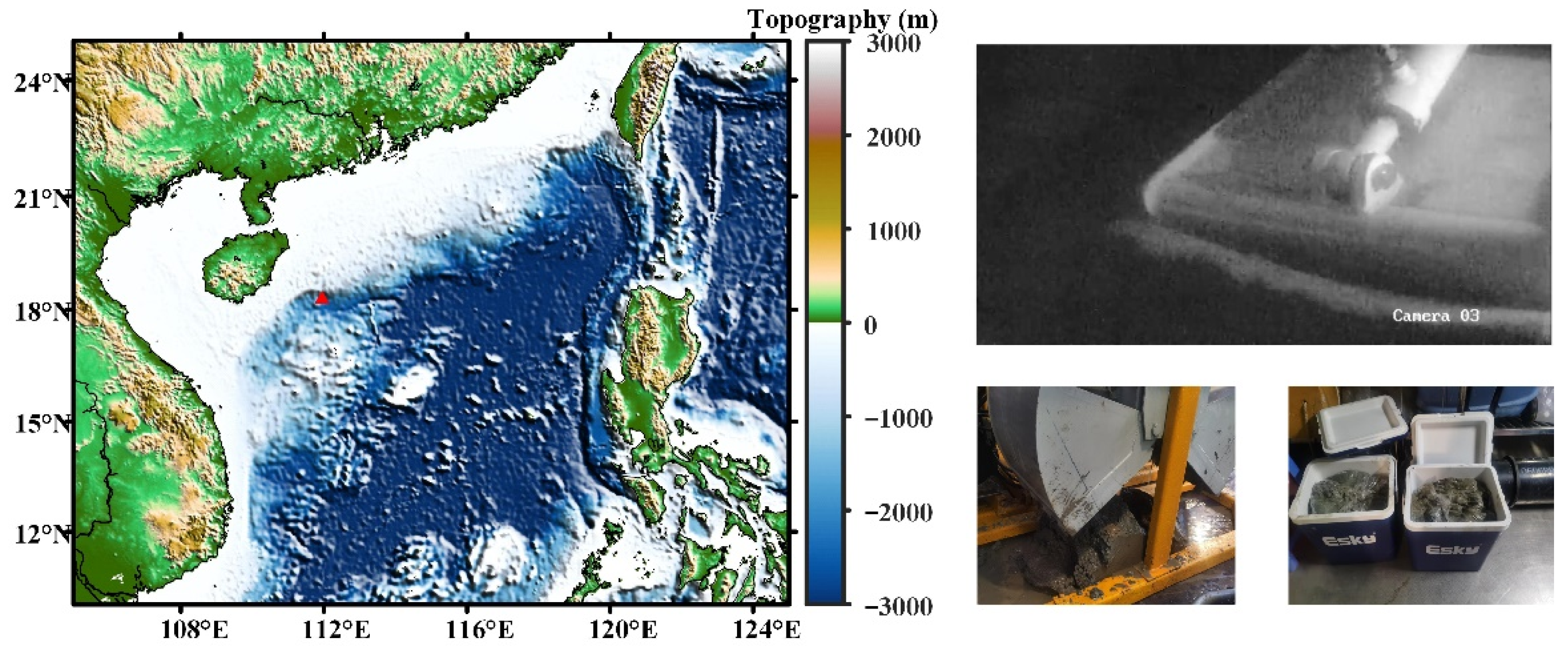
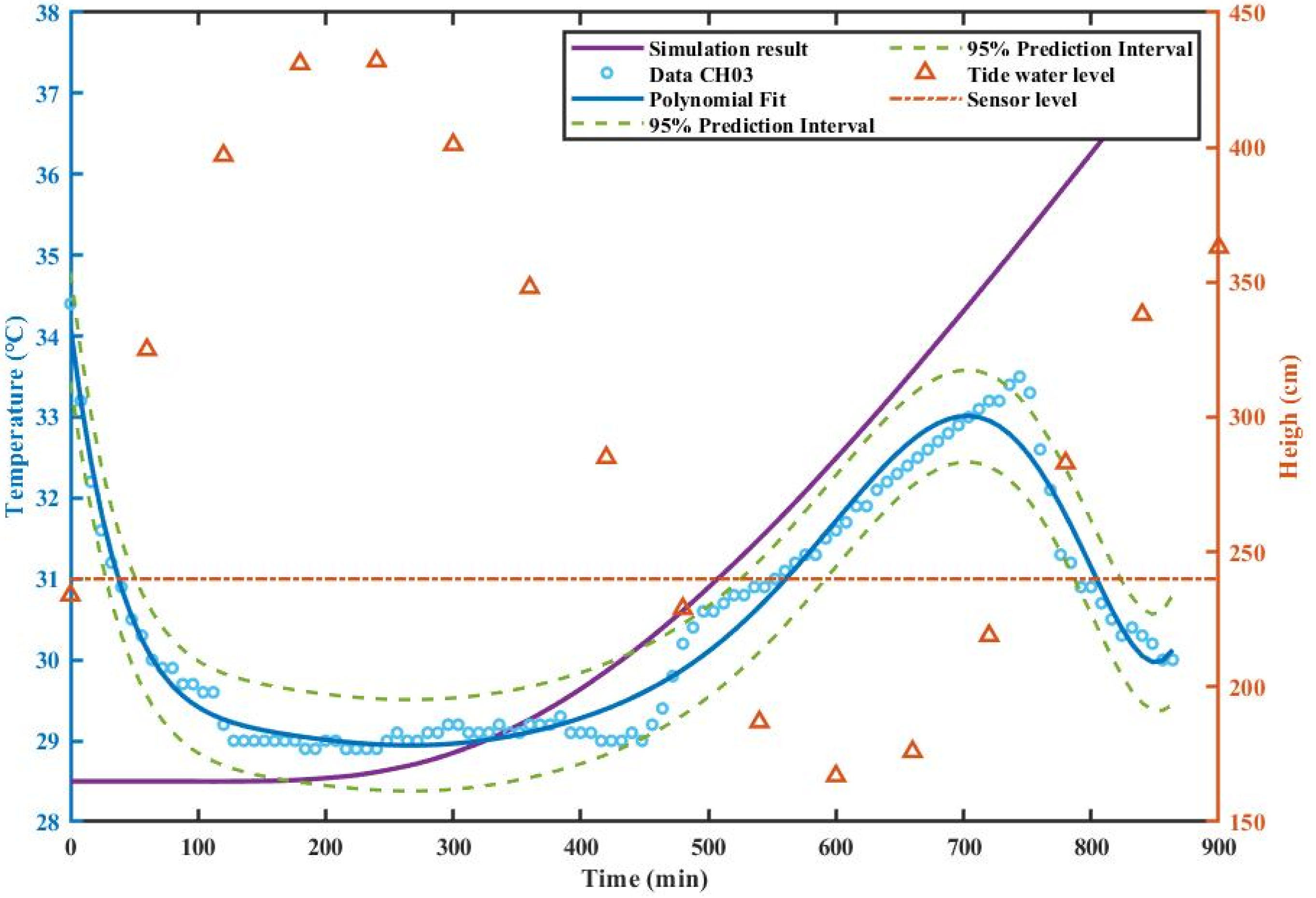
4.2. Experiment on the Shallows by the Sea
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Aguilar-Ojeda, J.A.; Campos-Gaytán, J.R.; Villela, A.; Herrera-Oliva, C.S.; Ramírez-Hernández, J.; Kretzschmar, T.G. Understanding hydrothermal behavior of the maneadero geothermal system, Ensenada, Baja California, Mexico. Geothermics 2020, 89, 101985. [Google Scholar] [CrossRef]
- Stein, C.A. Geophysical Heat Flow; Univ Illinois: Chicago, IL, USA, 2019; pp. 1–8. [Google Scholar]
- Miao, W. Development of Data Acquisition and Process Software for Multi-Channel Thermal Conductivity Meter. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2011. [Google Scholar]
- Kvenvolden, K.A. Potential effects of gas hydrate on human welfare. Proc. Natl. Acad. Sci. USA 1999, 96, 3420–3426. [Google Scholar] [CrossRef] [PubMed]
- Hornbach, M.J.; Harris, R.N.; Phrampus, B.J. Heat flow on the U.S. beaufort margin, arctic ocean: Implications for ocean warming, methane hydrate stability, and regional tectonics. Geochem. Geophys. Geosyst. 2020, 21, e2020GC008933. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Insights into the climate-driven evolution of gas hydrate-bearing permafrost sediments: Implications for prediction of environmental impacts and security of energy in cold regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. Research on Several Key Technologies of Sediment Thermal Conductivity Meter. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2008. [Google Scholar]
- Gerard, R.; Langseth, M.G.; Ewing, M. Thermal gradient measurements in the water and bottom sediment of the western Atlantic. J. Geophys. Res. Earth Surf. 1962, 67, 785–803. [Google Scholar] [CrossRef]
- Von Herzen, R.; Maxwell, A.E. The measurement of thermal conductivity of deep-sea sediments by a needle-probe method. J. Geophys. Res. Earth Surf. 1959, 64, 1557–1563. [Google Scholar] [CrossRef]
- Sclater, J.G.; Corry, C.E.; Vacquier, V. In situ measurement of the thermal conductivity of ocean-floor sediments. J. Geophys. Res. Earth Surf. 1969, 74, 1070–1081. [Google Scholar] [CrossRef]
- Lister, C.R.B. Measurement of in situ sediment conductivity by means of a bullard-type probe. Geophys. J. Int. 1970, 19, 521–532. [Google Scholar] [CrossRef]
- Lee, T.-C.; Von Herzen, R.P. In situ determination of thermal properties of sediments using a friction-heated probe source. J. Geophys. Res. Earth Surf. 1994, 99, 12121–12132. [Google Scholar] [CrossRef]
- Lee, T.-C.; Duchkov, A.D.; Morozov, S.G. Determination of thermal conductivity and formation temperature from cooling history of friction-heated probes. Geophys. J. Int. 2003, 152, 433–442. [Google Scholar] [CrossRef] [Green Version]
- Duchkov, A.D.; Manakov, A.Y.; Kazantsev, S.A.; Permyakov, M.E.; Ogienko, A.G. Thermal conductivity measurement of the synthetic samples of bottom sediments containing methane hydrates. Izv. Phys. Solid Earth 2009, 45, 661–669. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, J.F.; Wang, B.; Liu, W.G.; Yang, M.J.; Song, Y.C. Effective thermal conductivity of methane hydrate-bearing sediments: Experiments and correlations. Fuel 2016, 179, 87–96. [Google Scholar] [CrossRef]
- Chuvilin, E.; Bukhanov, B. Thermal conductivity of frozen sediments containing self-preserved pore gas hydrates at atmospheric pressure: An experimental study. Geosciences 2019, 9, 65. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.H.; Tohidi, B. Heat transfer in unfrozen and frozen porous media: Experimental measurement and pore-scale modeling. Water Resour. Res. 2020, 56, e2020WR027885. [Google Scholar] [CrossRef]
- Kim, D.; Oh, S. Measurement and comparison of thermal conductivity of porous materials using box, dual-needle, and single-needle probe methods—A case study. Int. Commun. Heat Mass Transf. 2020, 118, 104815. [Google Scholar] [CrossRef]
- Wang, B. Engineering Heat and Mass Transfer; Science Press: Beijing, China, 2015. [Google Scholar]
- Klauda, J.B.; Sandler, S.I. Global distribution of methane hydrate in ocean sediment. Energy Fuels 2005, 19, 459–470. [Google Scholar] [CrossRef]
- Wang, S.; Lu, X.; Zhang, X. Advances in the laboratory apparatus and research on mechanical properties of gas hydrate sediment. J. Exp. Mech. 2009, 24, 413–420. [Google Scholar]
- Chuvilin, E.; Bukhanov, B. Effect of hydrate formation conditions on thermal conductivity of gas-saturated sediments. Energy Fuels 2017, 31, 5246–5254. [Google Scholar] [CrossRef]
- Muraoka, M.; Ohtake, M.; Susuki, N.; Yamamoto, Y.; Suzuki, K.; Tsuji, T. Thermal properties of methane hydrate-bearing sediments and surrounding mud recovered from nankai trough wells. J. Geophys. Res. Solid Earth 2014, 119, 8021–8033. [Google Scholar] [CrossRef]
- Kim, Y.; Yun, T. Thermal conductivity of methane hydrate-bearing Ulleung basin marine sediments: Laboratory testing and numerical evaluation. Mar. Pet. Geol. 2013, 47, 77–84. [Google Scholar] [CrossRef]
- Cortes, D.; Martin, A.; Yun, T.; Francisca, F.; Santamarina, J.; Ruppel, C. Thermal conductivity of hydrate-bearing sediments. J. Geophys. Res. Earth Surf. 2009, 114, B11103. [Google Scholar] [CrossRef] [Green Version]
- Munholland, J.L.; Mumford, K.G.; Kueper, B.H. Factors affecting gas migration and contaminant redistribution in heterogeneous porous media subject to electrical resistance heating. J. Contam. Hydrol. 2016, 184, 14–24. [Google Scholar] [CrossRef] [PubMed]
- Yiqing, W. Study on High Temperature Treatment of Silty Clay Based on In-Situ Electrical Thermal Conductivity; Dalian Maritime University: Dalian, China, 2020. [Google Scholar]
- Rupeng, W. Experimental Study and Prediction Model of Thermal Conductivity of Hydrate-Bearing Sediment; Dalian University of Technology: Dalian, China, 2019. [Google Scholar]
- GB/T 10297-1988; Test Method for Thermal Conductivity of Nonmetal Solid Materials—Hot-Wire Method. Standards Press of China: Beijing, China, 2015.
- Fu, G.; Yang, Y. A hybrid-mixed finite element method for single-phase darcy flow in fractured porous media. Adv. Water Resour. 2022, 161, 104129. [Google Scholar] [CrossRef]
- Zhang, X.; Kong, G.-Q.; Li, H.; Wang, L.; Yang, Q. Thermal conductivity of marine sediments influenced by porosity and temperature in the South China Sea. Ocean Eng. 2022, 260, 111992. [Google Scholar] [CrossRef]
- Gallo-Villanueva, R.; Perez-Gonzalez, V.; Cardenas-Benitez, B.; Jind, B.; Martinez-Chapa, S.O.; Lapizco-Encinas, B. Joule heating effects in optimized insulator-based dielectrophoretic devices: An interplay between post geometry and temperature rise. Electrophoresis 2019, 40, 1408–1416. [Google Scholar] [CrossRef] [PubMed]
- Hassanzadeh, H.; Harding, T. Analysis of conductive heat transfer during in-situ electrical heating of oil sands. Fuel 2016, 178, 290–299. [Google Scholar] [CrossRef]

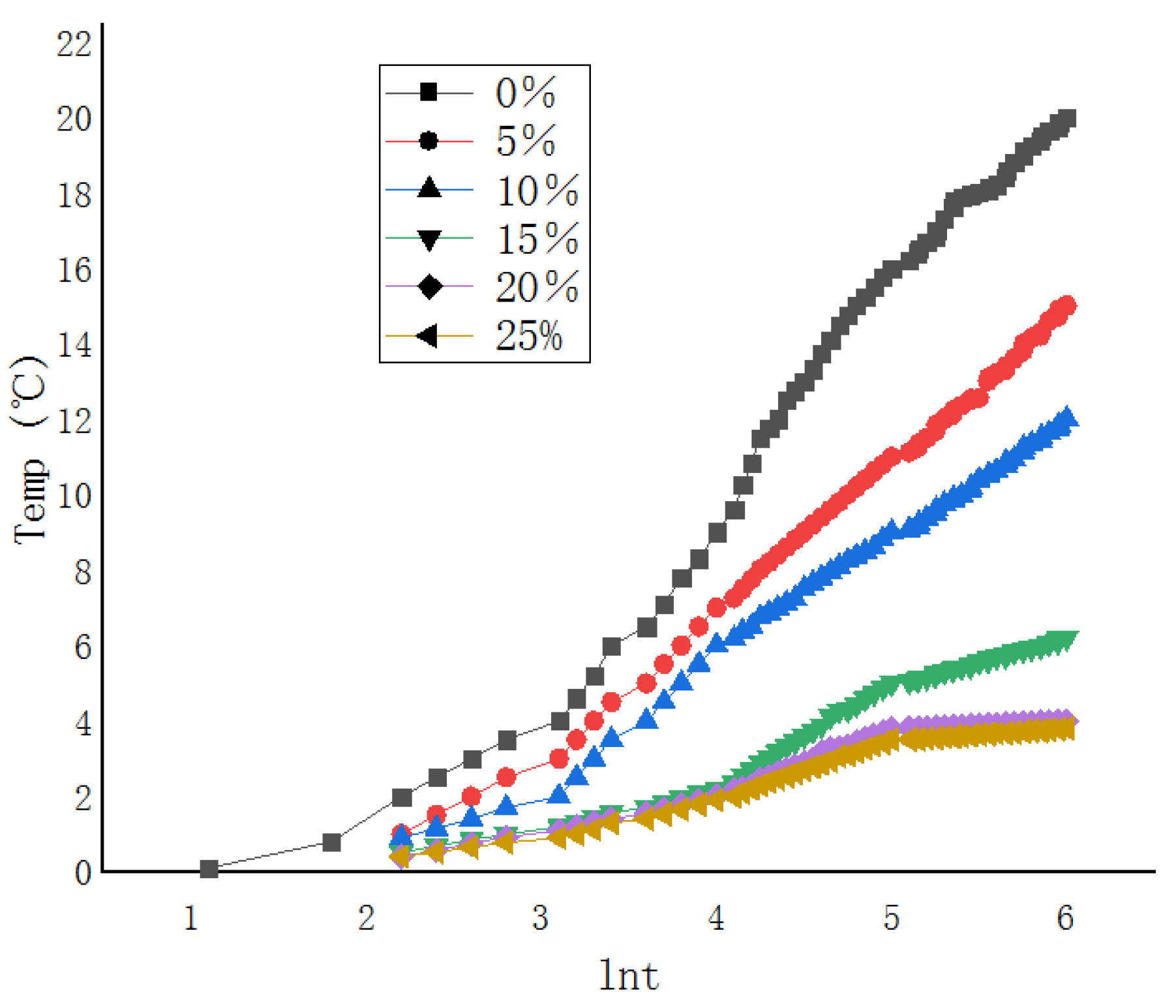






| Moisture Content | U (V) | I (A) | L (m) | λ (W/(m·K)) | |
|---|---|---|---|---|---|
| 0% | 4 | 1 | 0.22 | 5.0012 | 0.289 |
| 5% | 4 | 1 | 0.22 | 3.8501 | 0.3759 |
| 10% | 4 | 1 | 0.22 | 3.1253 | 0.4631 |
| 15% | 4 | 1 | 0.22 | 1.7584 | 0.8232 |
| 20% | 4 | 0.9 | 0.22 | 0.8841 | 1.4736 |
| 25% | 4 | 0.9 | 0.22 | 1.0342 | 1.2597 |
| Distance (m) | 0.05 | 0.1 | 0.15 | 0.2 |
|---|---|---|---|---|
| p1 | −1.603 × 10−13 | 2.608 × 10−13 | 8.317 × 10−14 | 1.993 × 10−14 |
| p2 | 9.218 × 10−11 | −1.366 × 10−10 | −4.59 × 10−11 | −1.143 × 10−11 |
| p3 | −2.244 × 10−8 | 2.963 × 10−8 | 1.065 × 10−8 | 2.794 × 10−9 |
| p4 | 3.013 × 10−9 | −3.434 × 10−6 | −1.346 × 10−6 | −3.803 × 10−7 |
| p5 | −0.000244 | 0.0002279 | 0.0001003 | 3.14 × 10−5 |
| p6 | 0.01227 | −0.00849 | −0.004403 | −0.001581 |
| p7 | −0.3827 | 0.15 | 0.102 | 0.04351 |
| p8 | 7.31 | 0.04844 | −0.5358 | −0.2418 |
| p9 | −5.342 | 3.016 | 4.605 | 4.298 |
| Coefficients of Determination (%) | 99.95 | 99.97 | 99.99 | 99.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Zhang, C.; Ai, J.; Ge, Y.; Peng, X.; Gao, Q.; Wang, W.; Zhou, Z.; Chen, J. The Numerical Simulation and Experimental Study of Heat Flow in Seabed Sediments Based on COMSOL. J. Mar. Sci. Eng. 2022, 10, 1356. https://doi.org/10.3390/jmse10101356
Zhou P, Zhang C, Ai J, Ge Y, Peng X, Gao Q, Wang W, Zhou Z, Chen J. The Numerical Simulation and Experimental Study of Heat Flow in Seabed Sediments Based on COMSOL. Journal of Marine Science and Engineering. 2022; 10(10):1356. https://doi.org/10.3390/jmse10101356
Chicago/Turabian StyleZhou, Peng, Chunyue Zhang, Jingkun Ai, Yongqiang Ge, Xiaoqing Peng, Qiaoling Gao, Wei Wang, Zhonghui Zhou, and Jiawang Chen. 2022. "The Numerical Simulation and Experimental Study of Heat Flow in Seabed Sediments Based on COMSOL" Journal of Marine Science and Engineering 10, no. 10: 1356. https://doi.org/10.3390/jmse10101356
APA StyleZhou, P., Zhang, C., Ai, J., Ge, Y., Peng, X., Gao, Q., Wang, W., Zhou, Z., & Chen, J. (2022). The Numerical Simulation and Experimental Study of Heat Flow in Seabed Sediments Based on COMSOL. Journal of Marine Science and Engineering, 10(10), 1356. https://doi.org/10.3390/jmse10101356







