Numerical Investigation of Internal Solitary Wave Forces on a Moving Submarine
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
2.2. ISW Generation
3. Model Verification
3.1. Computational Domain and Grids
3.2. Grid Convergence Study
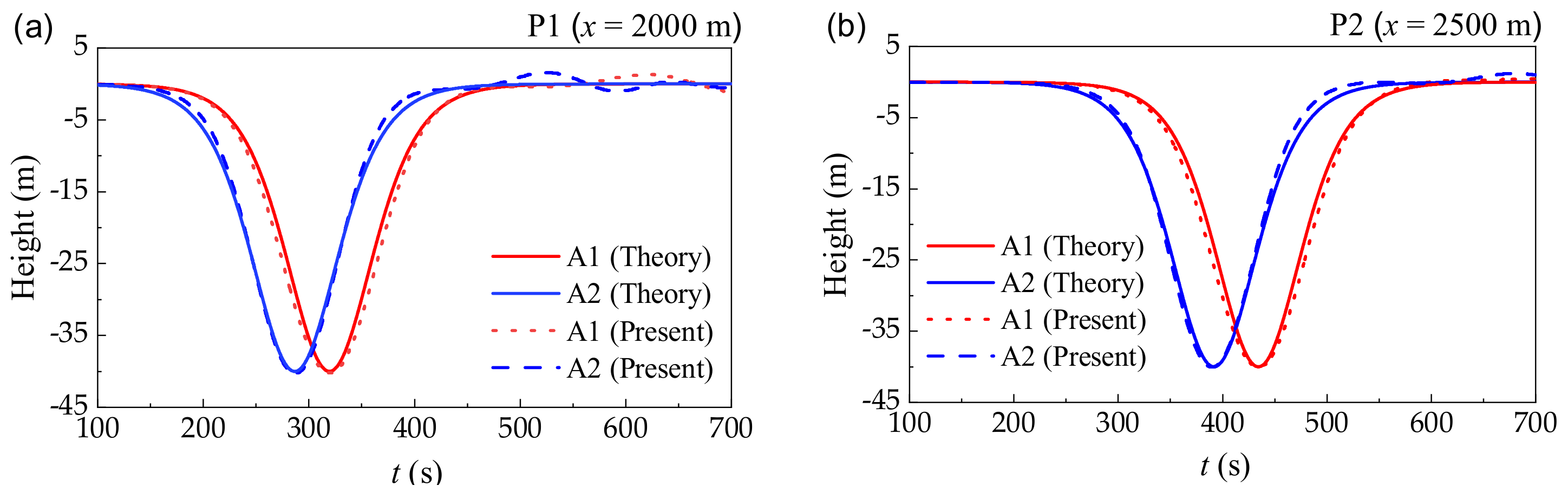
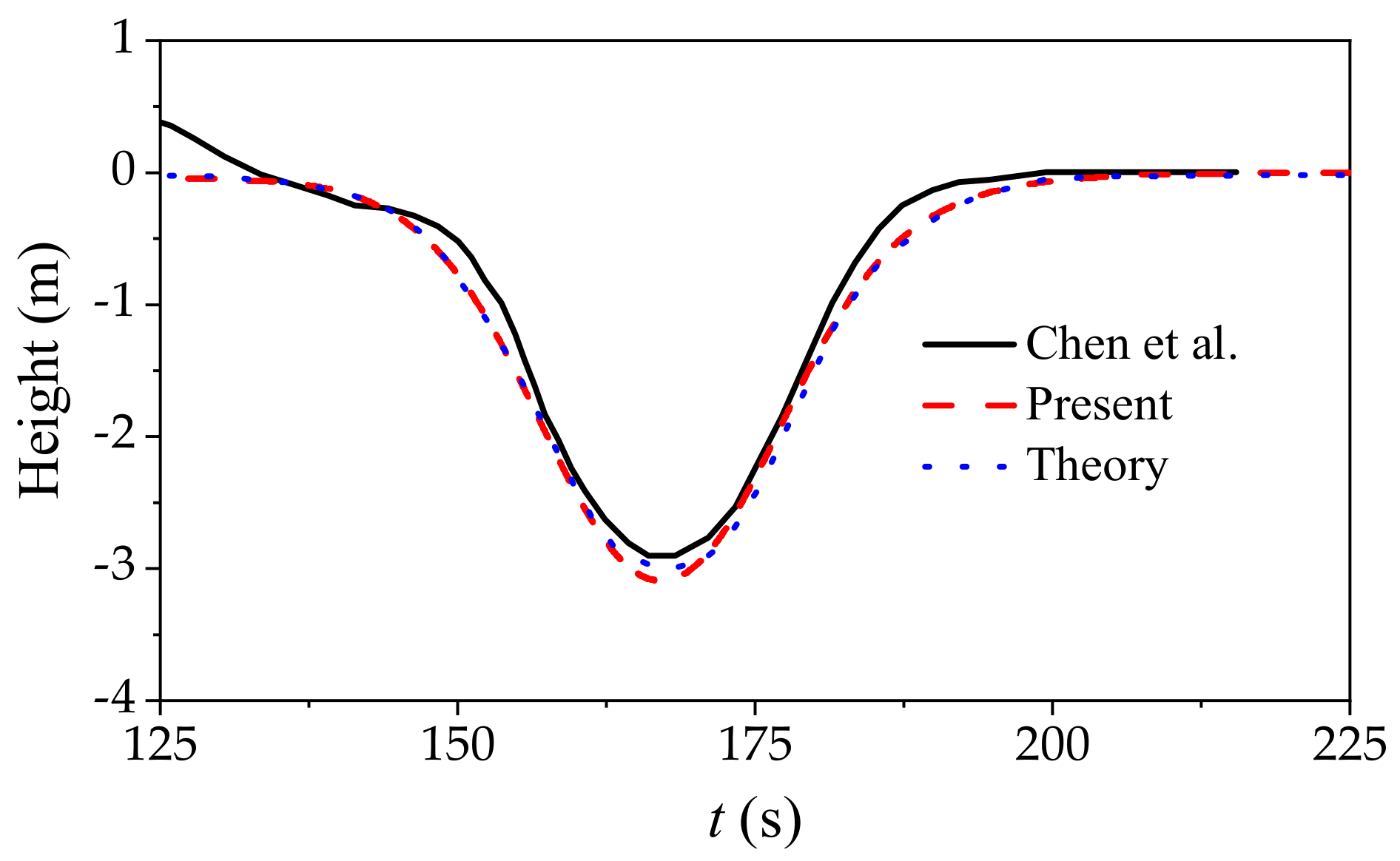
3.3. Comparison between Numerical and Experimental Results
4. Results and Discussion
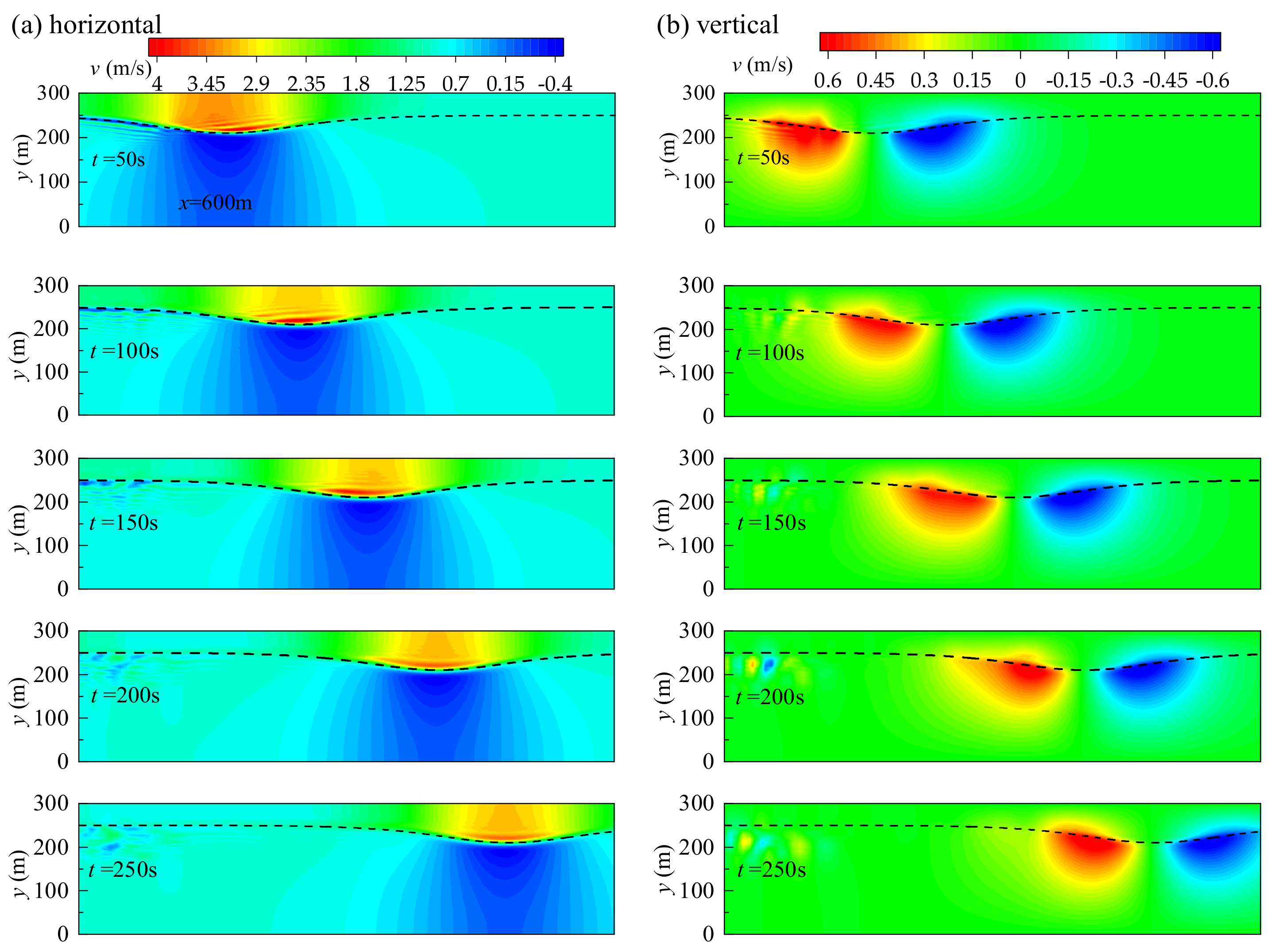
4.1. ISW Propagation under the Action of Current
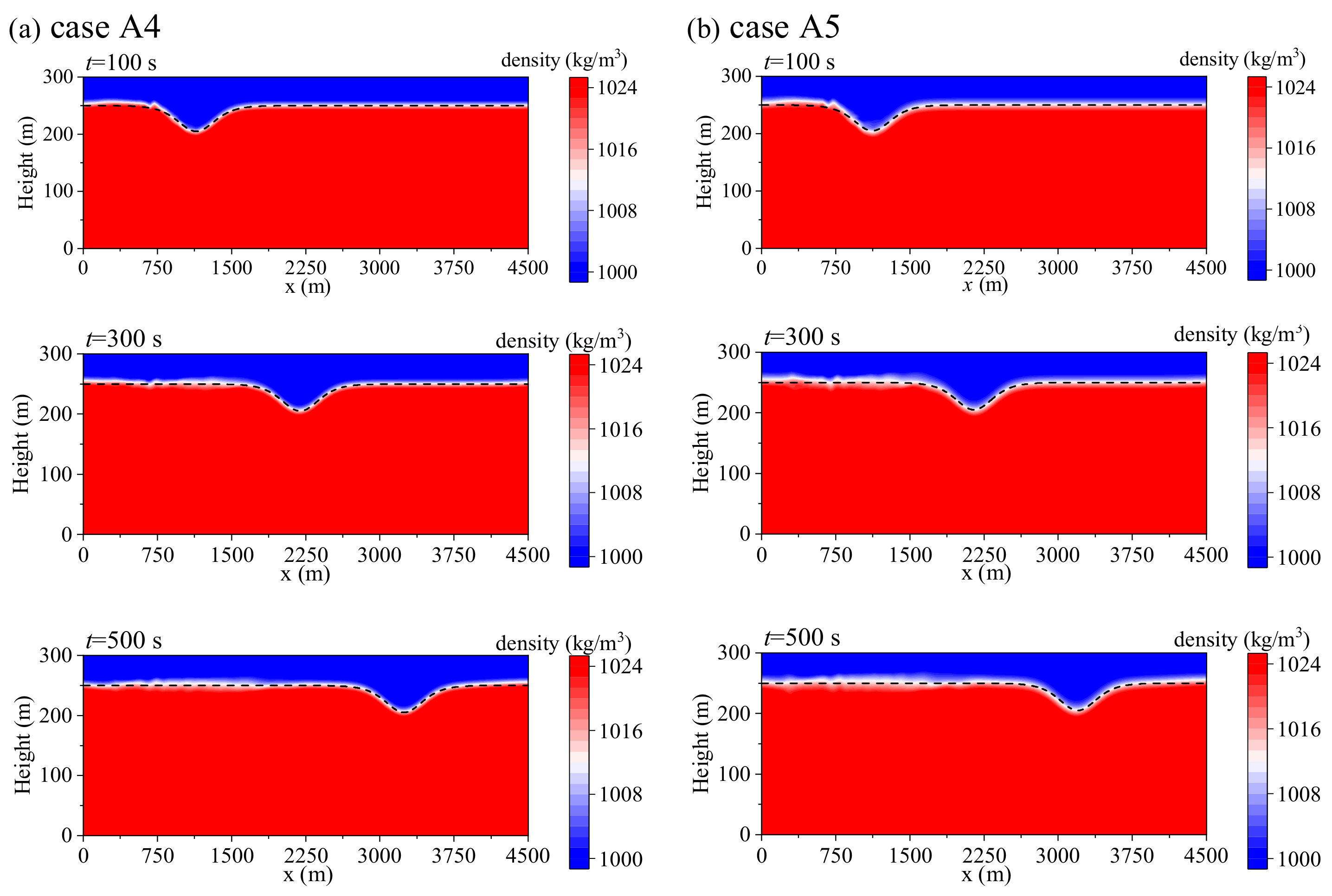
4.2. Interaction between Submarine and ISWs with Different Pycnocline Thickness
4.3. Interaction between ISWs and the Submarine with Different Velocities
5. Conclusions
- A series of ISWs coupled with the current against various flow speeds and pycnocline thicknesses were made using the proposed numerical method. Based on the waveform analysis of the ISWs and the comparison with theoretical results, the propagation of the ISWs was validated to be accurate and stable.
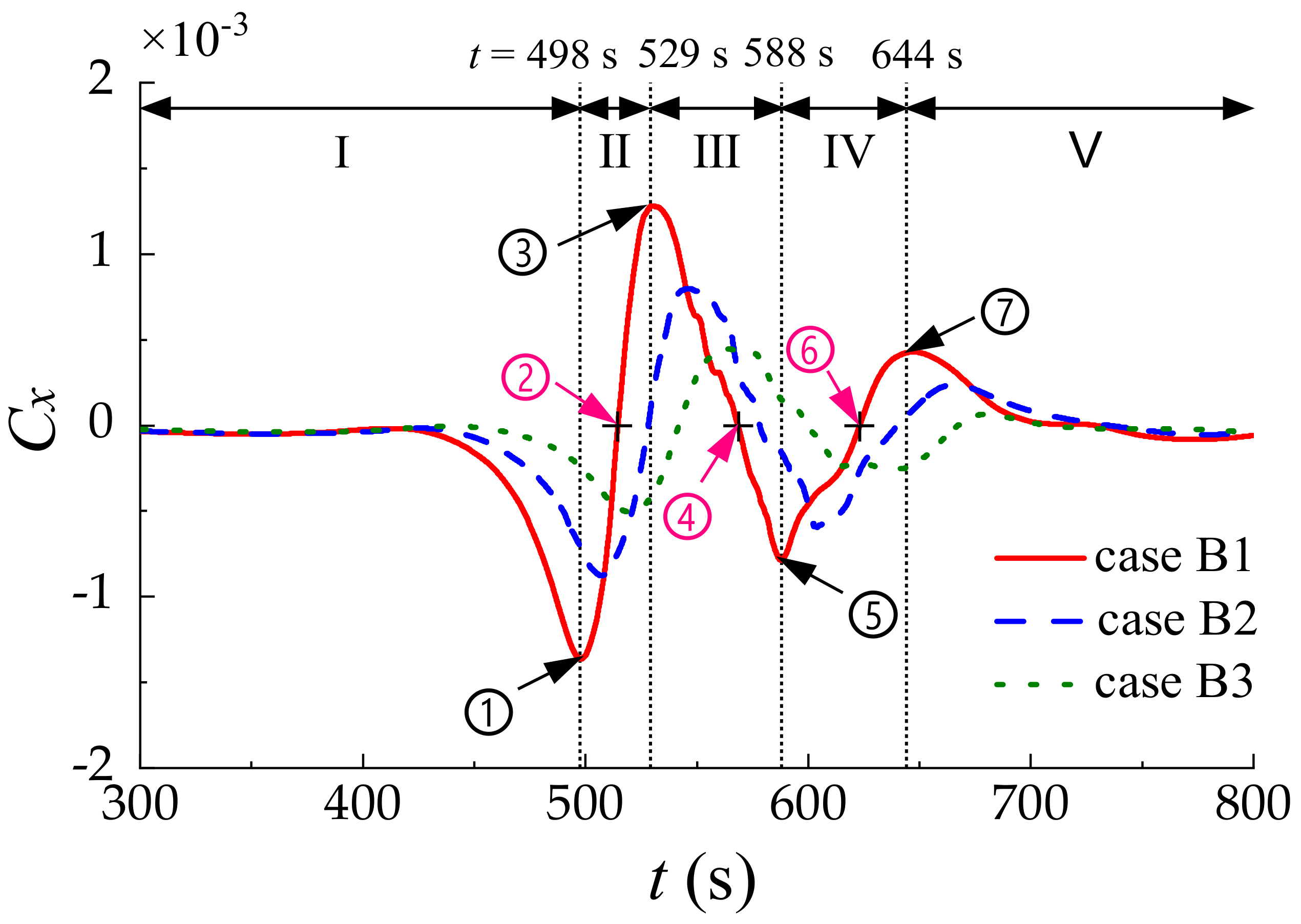
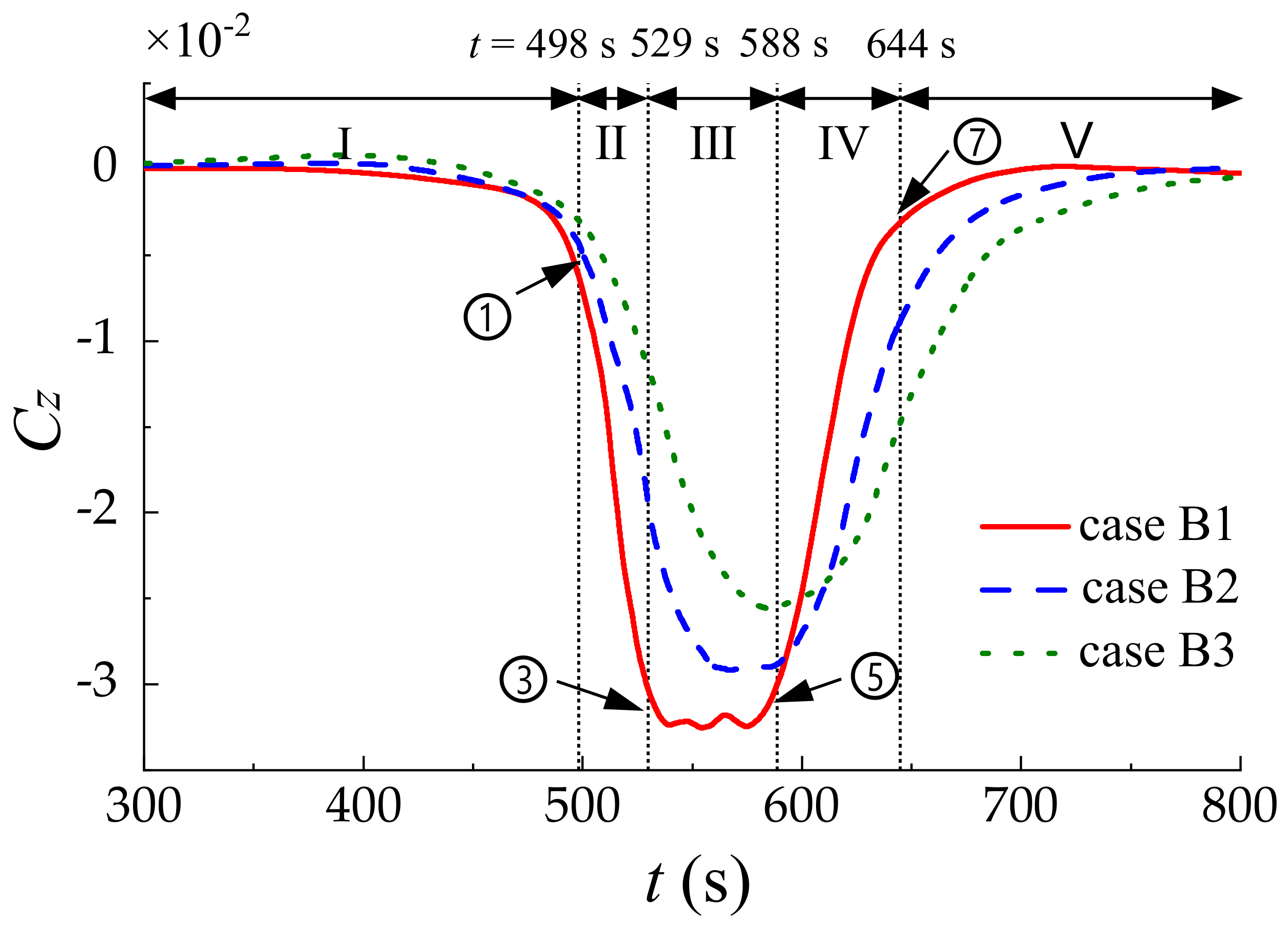
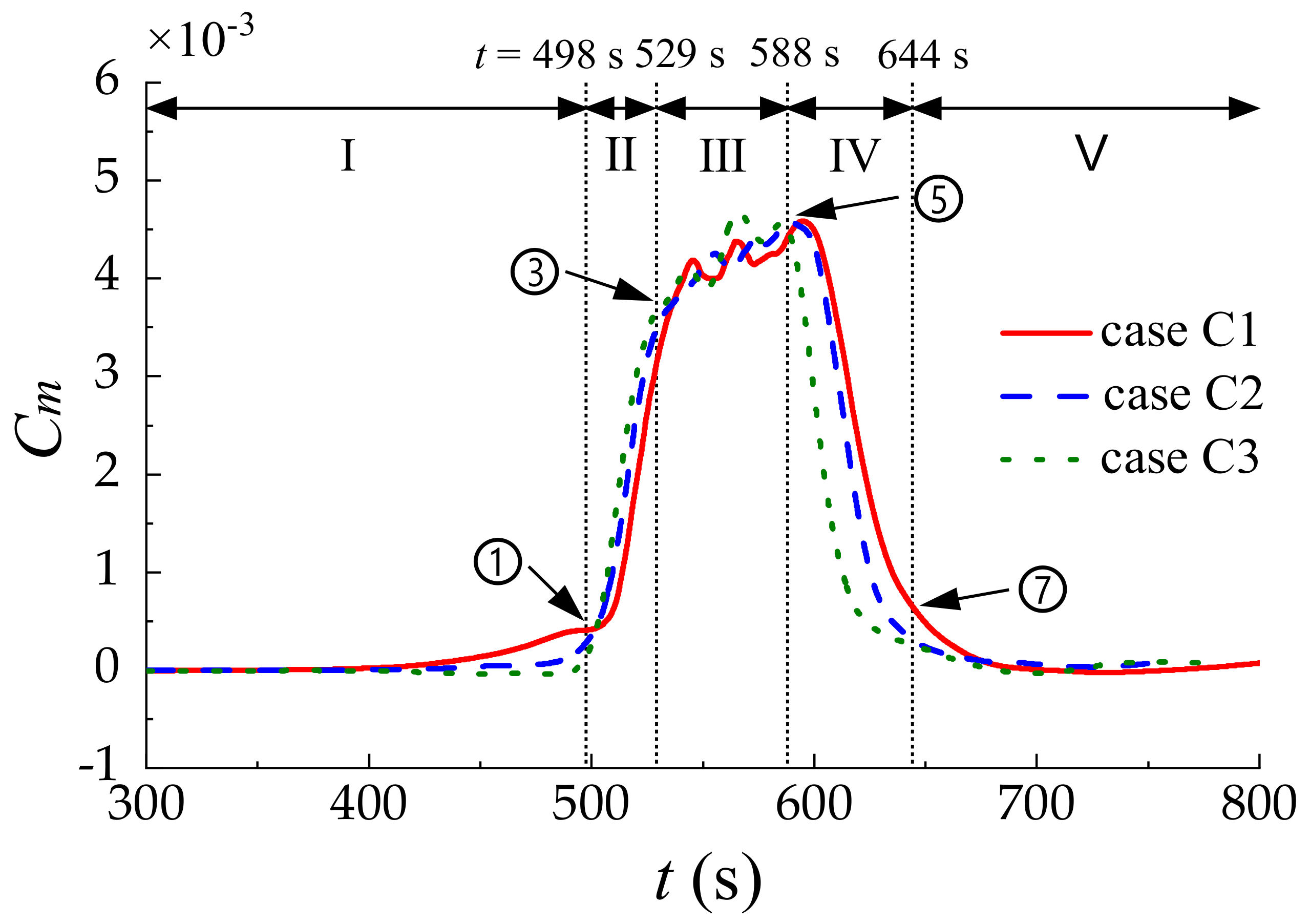
- The ISWs-induced horizontal force Cx, the vertical force Cz and the torque Cm on the submarine against various pycnocline thicknesses were investigated. It was found that the hydrodynamic forces are closely related to the dynamic pressure around the submarine. The direction of the vertical force Cz is downward in the five stages, which can cause the sinking of the submarine. Besides, the maximum values of |Cx|, |Cz|, |Cm| decrease with the increment of the pycnocline thickness.
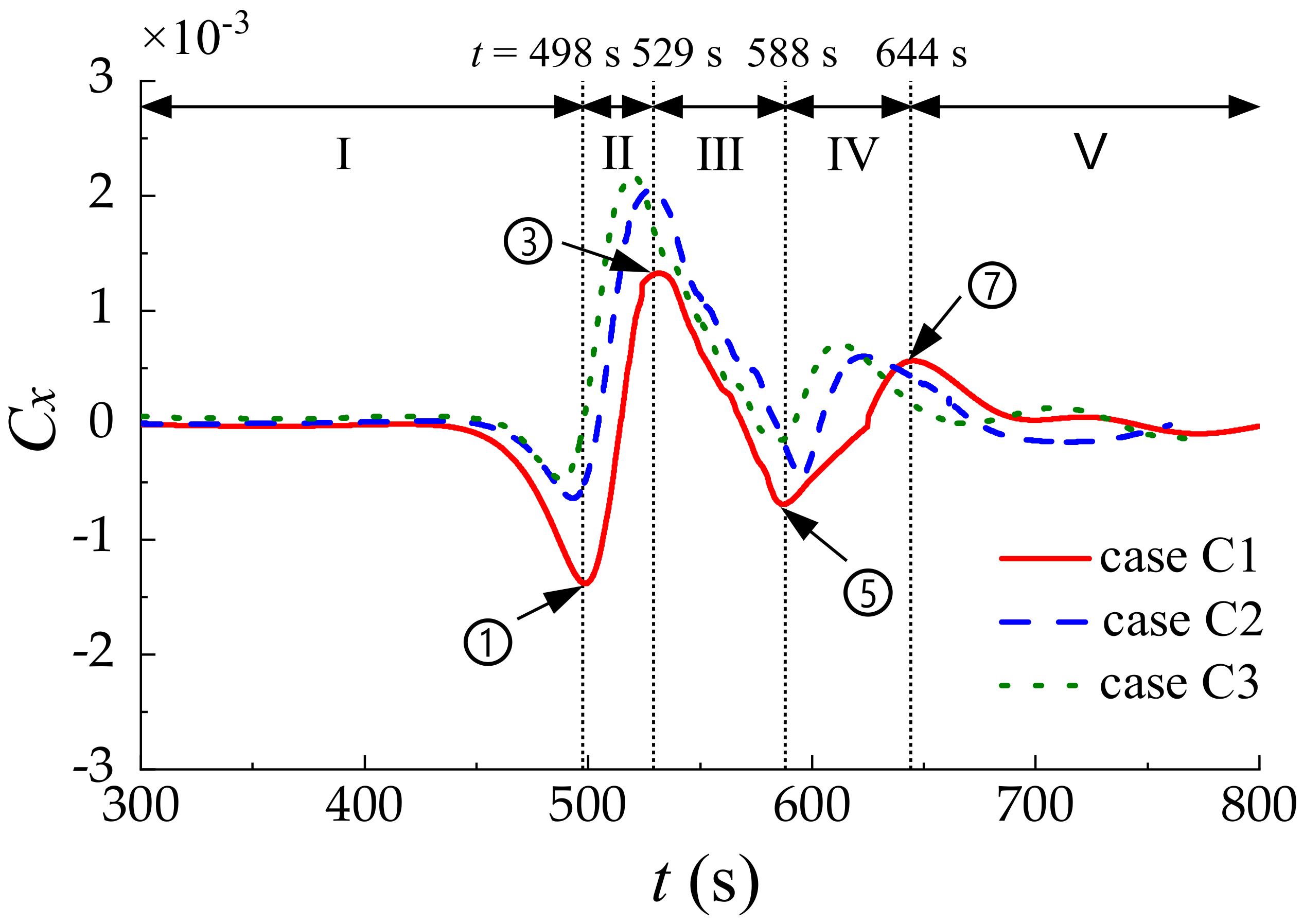
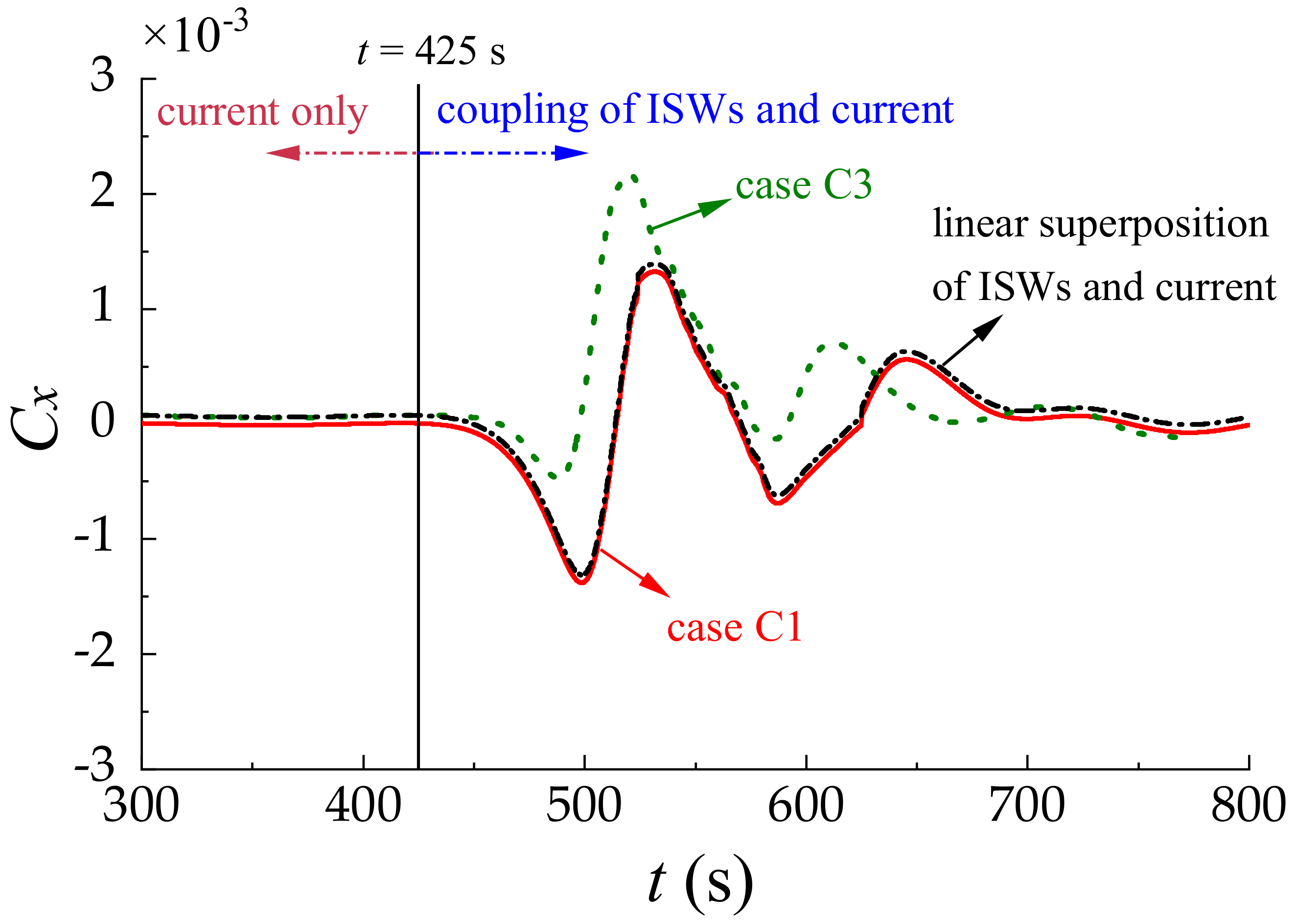
- The horizontal force Cx, the vertical force Cz and the torque Cm on the submarine induced by the coupling of the ISWs and the current were studied. Different flow speeds were considered to demonstrate their effects on the hydrodynamic forces. It was found that peak values of Cx increase with the increment of the flow speed. Moreover, the flow speed performs significant effects on Cx but ignorable effects on Cz and Cm.
- The interaction between the submarine and the ISWs coupled with the current is complicated. When the submarine is far from the ISWs, the hydrodynamic forces on the submarine can be thought to be caused only by the current. However, when the submarine encounters the ISWs, the hydrodynamic forces on the submarine cannot be simply regarded as the superposition of the ISWs-induced forces and the steady flow resistance, which means the coupling of ISWs and the current is nonlinear.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, J.; Zhao, W.; Chen, H.; Meng, Z.; Shi, X.; Tian, J. Asymmetry of internal waves and its effects on the ecological environment observed in the northern South China Sea. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2015, 98, 94–101. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J. Wave loading on floating platforms by internal solitary waves. In Proceedings of the Fifth International Conference on Fluid Mechanics, Shanghai, China, 15–19 August 2007; pp. 304–307. [Google Scholar]
- Song, Z.J.; Teng, B.; Gou, Y.; Lu, L.; Shi, Z.M.; Xiao, Y.; Qu, Y. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses. Appl. Ocean. Res. 2011, 33, 120–129. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.F.; Wang, Z.; You, Y.X. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean. Eng. 2018, 150, 298–308. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.F. Numerical and experimental study of internal solitary wave loads on tension leg platforms. J. Hydrodyn. 2021, 33, 93–103. [Google Scholar] [CrossRef]
- Chen, M.; Chen, K.; You, Y.X. Experimental investigation of internal solitary wave forces on a semi-submersible. Ocean. Eng. 2017, 141, 205–214. [Google Scholar] [CrossRef]
- Ding, W.; Ai, C.F.; Jin, S.; Lin, J.B. 3D numerical investigation of forces and flow field around the semi-submersible platform in an internal solitary wave. Water 2020, 12, 208. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Huang, X.; Zhao, W.; Zheng, S.H.; Yang, Y.C.; Tian, J.W. Internal Solitary Wave Activities near the Indonesian Submarine Wreck Site Inferred from Satellite Images. J. Mar. Sci. Eng. 2022, 10, 197. [Google Scholar] [CrossRef]
- Gong, Y.K.; Xie, J.S.; Xu, J.X.; Chen, Z.W.; He, Y.H.; Cai, S.Q. Oceanic internal solitary waves at the Indonesian submarine wreckage site. Acta Oceanol. Sin. 2022, 41, 109–113. [Google Scholar] [CrossRef]
- Fu, D.M.; You, Y.X.; Li, W. Numerical simulation of internal solitary waves with a submerged body in a two-layer fluid. Ocean. Eng. 2009, 37, 38–44. [Google Scholar]
- Chen, J.; You, Y.X.; Liu, X.D.; Wu, C.S. Numerical simulation of interaction of internal solitary waves with a moving submarine. Chin. J. Hydrodyn. 2010, 25, 344–350. [Google Scholar]
- Huang, M.M.; Zhang, N.N.; Zhu, A.J. Numerical simulation of the interaction motion features for a submarine with internal solitary wave. In Proceedings of the 30th International Ocean and Polar Engineering Conference, OnePetro, Shanghai, China, 11–16 October 2020; pp. 1805–1812. [Google Scholar]
- Li, J.Y.; Zhang, Q.H.; Chen, T.Q. Numerical Investigation of Internal Solitary Wave Forces on Submarines in Continuously Stratified Fluids. J. Mar. Sci. Eng. 2021, 9, 1374. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhang, Q.H.; Chen, T. ISWFoam: A numerical model for internal solitary wave simulation in continuously stratified fluids. Geosci. Model Dev. Discuss. 2021, 15, 105–127. [Google Scholar] [CrossRef]
- Ur, K.; Rehman, Q.M.; AI-Mdallal, E.-S.; Sherif, M.; Junaedi, H.; Lv, Y.-P. Numerical study of low Reynolds hybrid discretized convergent-divergent (CD) channel rooted with obstructions in left/right vicinity of CD throat. Results Phys. 2021, 24, 104141. [Google Scholar]
- Ur, K.; Rehman, Q.M.; AI-Mdallal, E.-S.; Sherif, M.; Junaedi, H.; Lv, Y.-P. On magnetized Newtonian liquid suspension in single backward facing-step(SBFS) with centrally translated obstructions. J. Mol. Liq. 2021, 337, 116265. [Google Scholar]
- Liu, S.; He, G.H.; Wang, Z.K.; Luan, Z.X.; Zhang, Z.G.; Wang, W.; Gao, Y. Resistance and flow field of a submarine in a density stratified fluid. Ocean. Eng. 2020, 217, 107934. [Google Scholar] [CrossRef]
- Hsieh, C.M.; Hwang, R.R.; Hsu, J.R.C.; Cheng, M.H. Numerical modeling of flow evolution for an internal solitary wave propagating over a submerged ridge. Wave Motion 2015, 55, 48–72. [Google Scholar] [CrossRef]
- Wilcox, D.C. Comparison of two-equation turbulence models for boundary layers with pressure gradient. AIAA J. 1993, 31, 1414–1421. [Google Scholar] [CrossRef]
- Bardina, J.E.; Huang, P.G.; Coakley, T.J. Turbulence modeling validation. In Proceedings of the 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997; pp. 1–16. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows; Imperial College London: London, UK, 1996. [Google Scholar]
- Cui, J.N.; Dong, S.; Wang, Z.F. Study on applicability of internal solitary wave theories by theoretical and numerical method. Appl. Ocean. Res. 2021, 111, 102629. [Google Scholar] [CrossRef]
- Aghsaee, P.; Boegman, L.; Lamb, K.G. Breaking of shoaling internal solitary waves. J. Fluid Mech. 2010, 659, 289–317. [Google Scholar] [CrossRef] [Green Version]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA Suboff Models: (DTRC Model Nos. 5470 and 5471); David Taylor Research Center: Bethesda, MD, USA, 1989. [Google Scholar]
- Day, S.; Penesis, I.; Babarit, A.; Fontaine, A.; He, Y.; Kraskowski, M.; Murai, M.; Salvatore, F.; Shin, H.K. Ittc recommended guidelines: Wave energy converter model test experiments (7.5-02-07-03.7). In Proceedings of the 27th International Towing Tank Conference, Copenhagen, Denmark, 31 August–5 September 2014. [Google Scholar]
- Liu, H.L.; Huang, T.T. Summary of DARPA SUBOFF Experimental Program Data; Defense Technical Information Center (DTIC): Fort Belvoir, VA, USA, 1998. [Google Scholar]
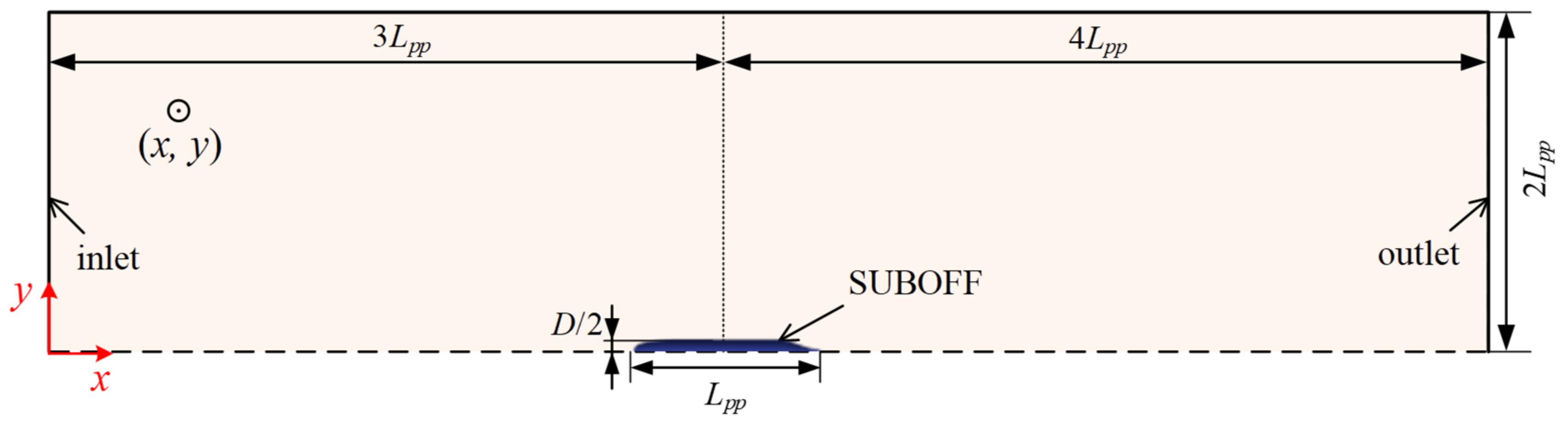

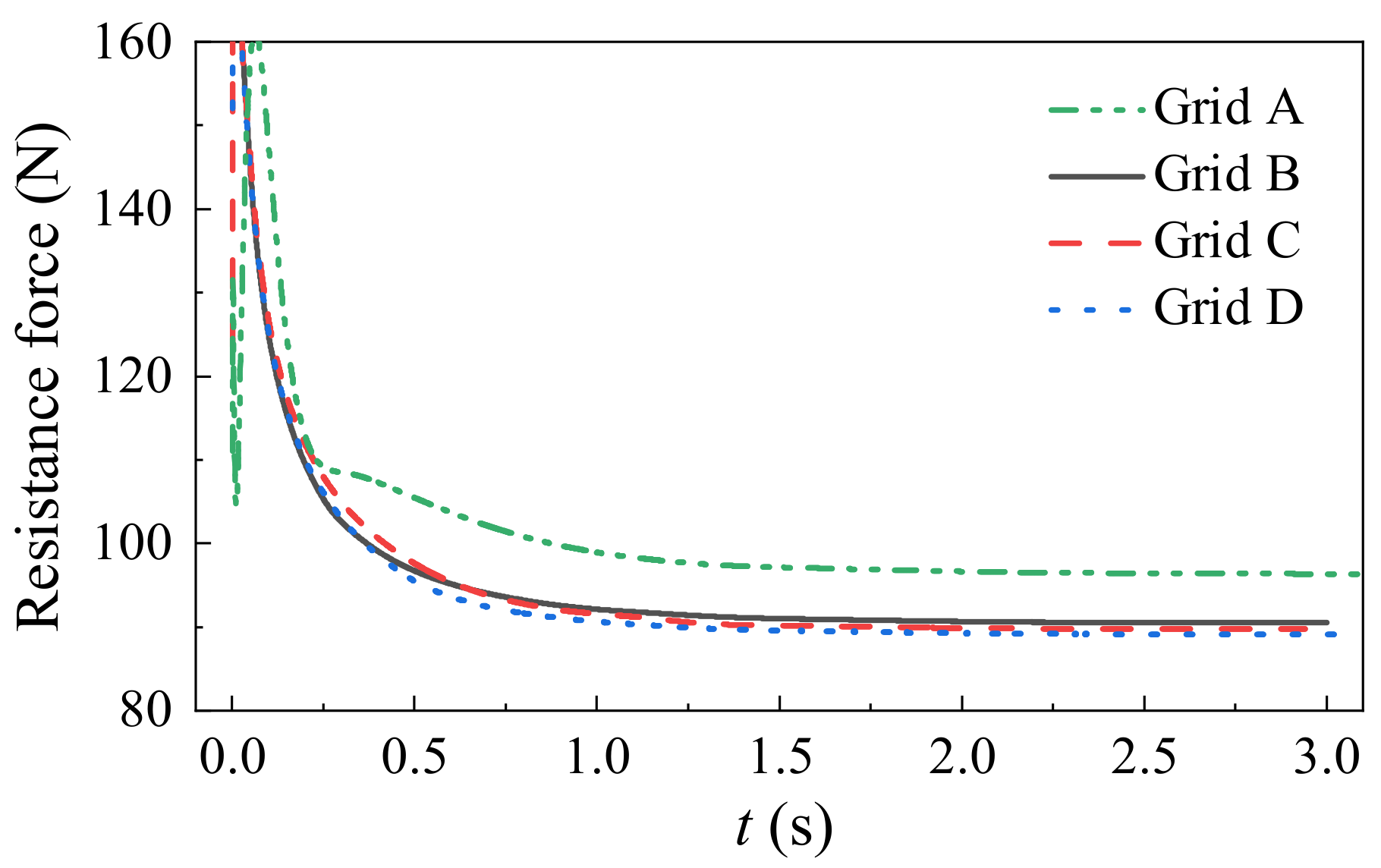
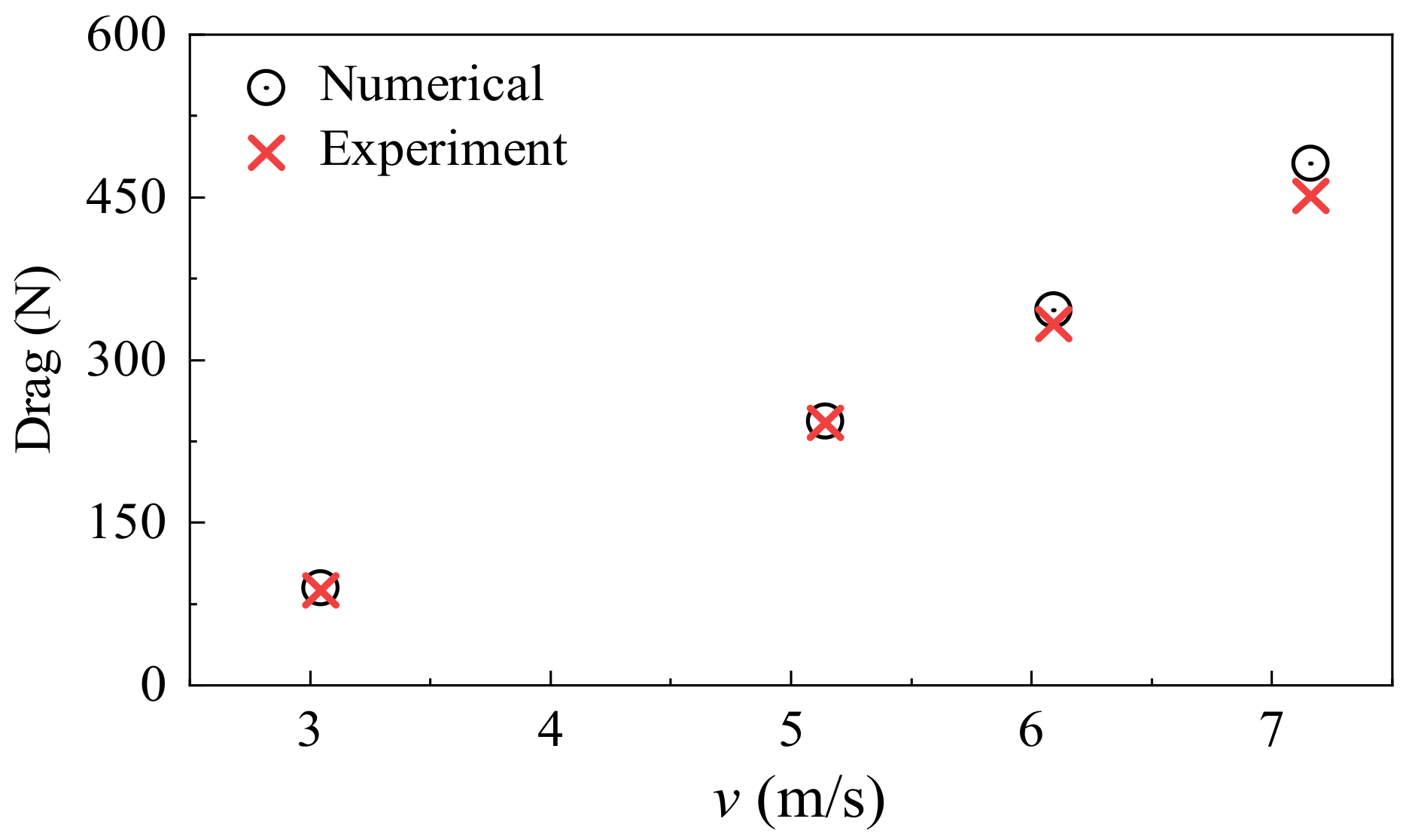
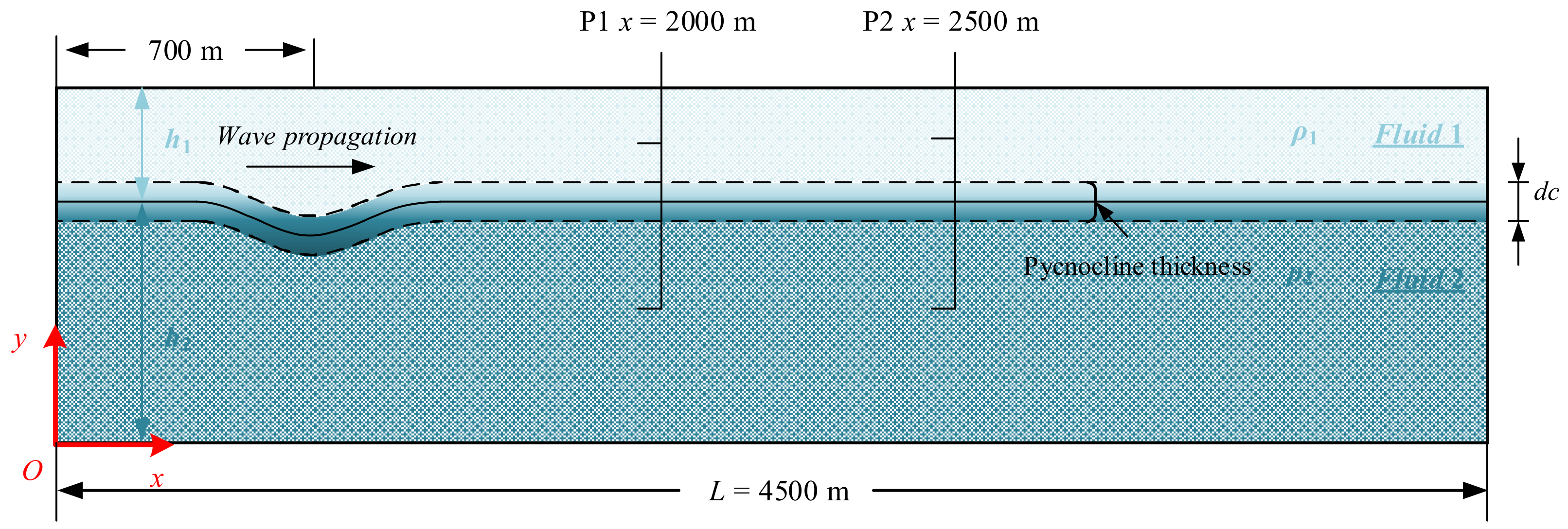
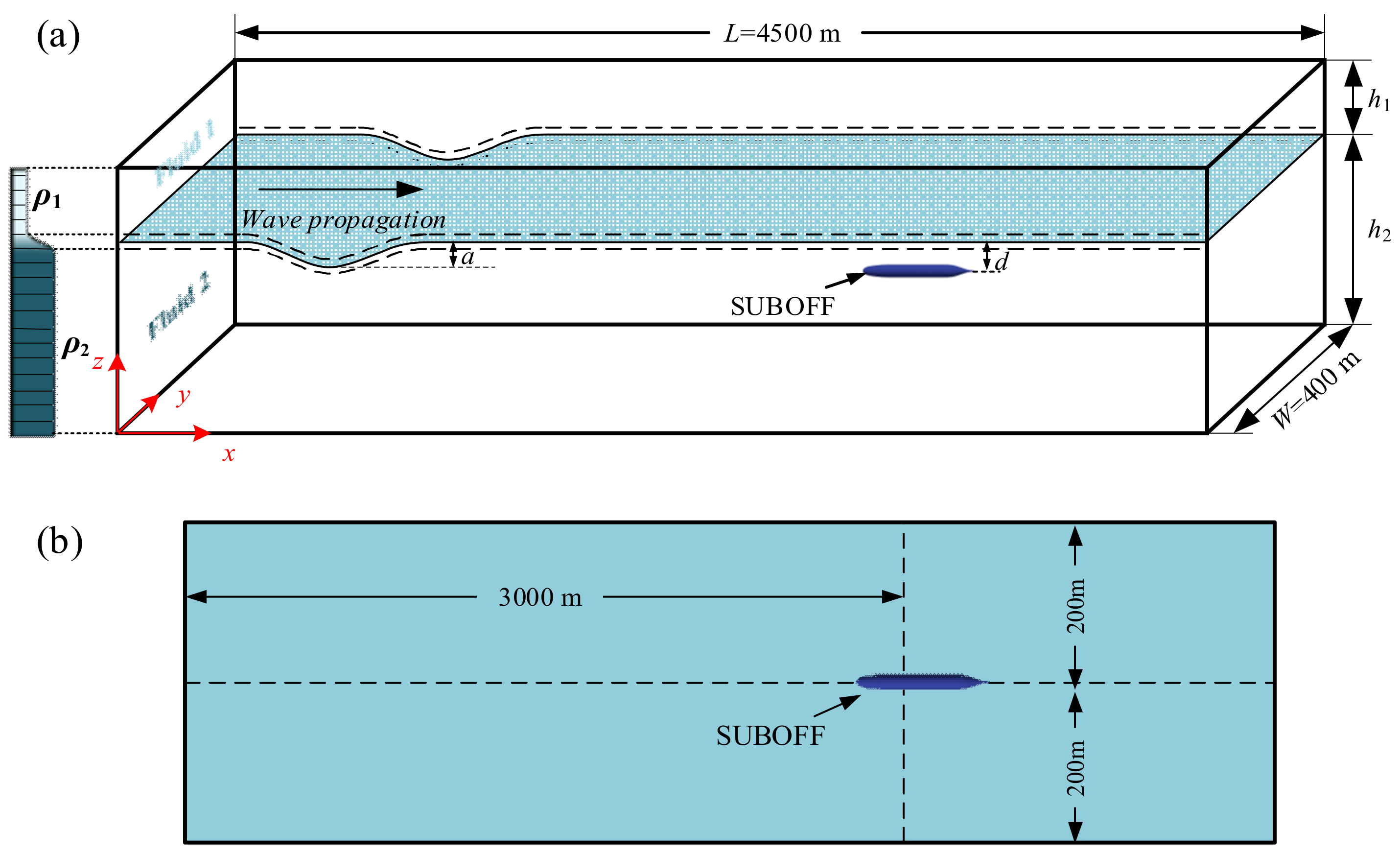



| Label | Grid Size (mm) | Grid Number (×104) | Resistance (N) | Experiment (N) | Relative Error (%) |
|---|---|---|---|---|---|
| Grid A | 90 | 57.8 | 96.42 | 87.4 | 10.32 |
| Grid B | 70 | 109.8 | 90.52 | 87.4 | 3.57 |
| Grid C | 65 | 169.1 | 89.76 | 87.4 | 2.7 |
| Grid D | 60 | 271.5 | 89.11 | 87.4 | 1.95 |
| Velocity (m/s) | Numerical Results (N) | Experimental Results (N) | Relative Error (%) |
|---|---|---|---|
| 3.046 | 89.76 | 87.4 | 2.7 |
| 5.144 | 243.59 | 242.2 | 0.6 |
| 6.091 | 345.975 | 332.9 | 3.9 |
| 7.161 | 481.226 | 451.5 | 6.5 |
| Label | Velocity (m/s) | Pycnocline Thickness (m) |
|---|---|---|
| A1 | 0 | 5 |
| A2 | 0.5 | 5 |
| A3 | 1 | 5 |
| A4 | 1 | 10 |
| A5 | 1 | 15 |
| Label | Velocity (m/s) | Pycnocline Thickness (m) |
|---|---|---|
| B1 | 0 | 5 |
| B2 | 0 | 10 |
| B3 | 0 | 15 |
| Label | Velocity (m/s) | Pycnocline Thickness (m) |
|---|---|---|
| C1 | 0 | 5.0 |
| C2 | 0.5 | 5.0 |
| C3 | 1 | 5.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, G.; Xie, H.; Zhang, Z.; Liu, S. Numerical Investigation of Internal Solitary Wave Forces on a Moving Submarine. J. Mar. Sci. Eng. 2022, 10, 1020. https://doi.org/10.3390/jmse10081020
He G, Xie H, Zhang Z, Liu S. Numerical Investigation of Internal Solitary Wave Forces on a Moving Submarine. Journal of Marine Science and Engineering. 2022; 10(8):1020. https://doi.org/10.3390/jmse10081020
Chicago/Turabian StyleHe, Guanghua, Hongfei Xie, Zhigang Zhang, and Shuang Liu. 2022. "Numerical Investigation of Internal Solitary Wave Forces on a Moving Submarine" Journal of Marine Science and Engineering 10, no. 8: 1020. https://doi.org/10.3390/jmse10081020
APA StyleHe, G., Xie, H., Zhang, Z., & Liu, S. (2022). Numerical Investigation of Internal Solitary Wave Forces on a Moving Submarine. Journal of Marine Science and Engineering, 10(8), 1020. https://doi.org/10.3390/jmse10081020







