Dynamic Lifetime Prediction of Fishing Nets Based on the Model of Wave Return Period and Residual Strength
Abstract
:1. Introduction
2. Adopted Approaches
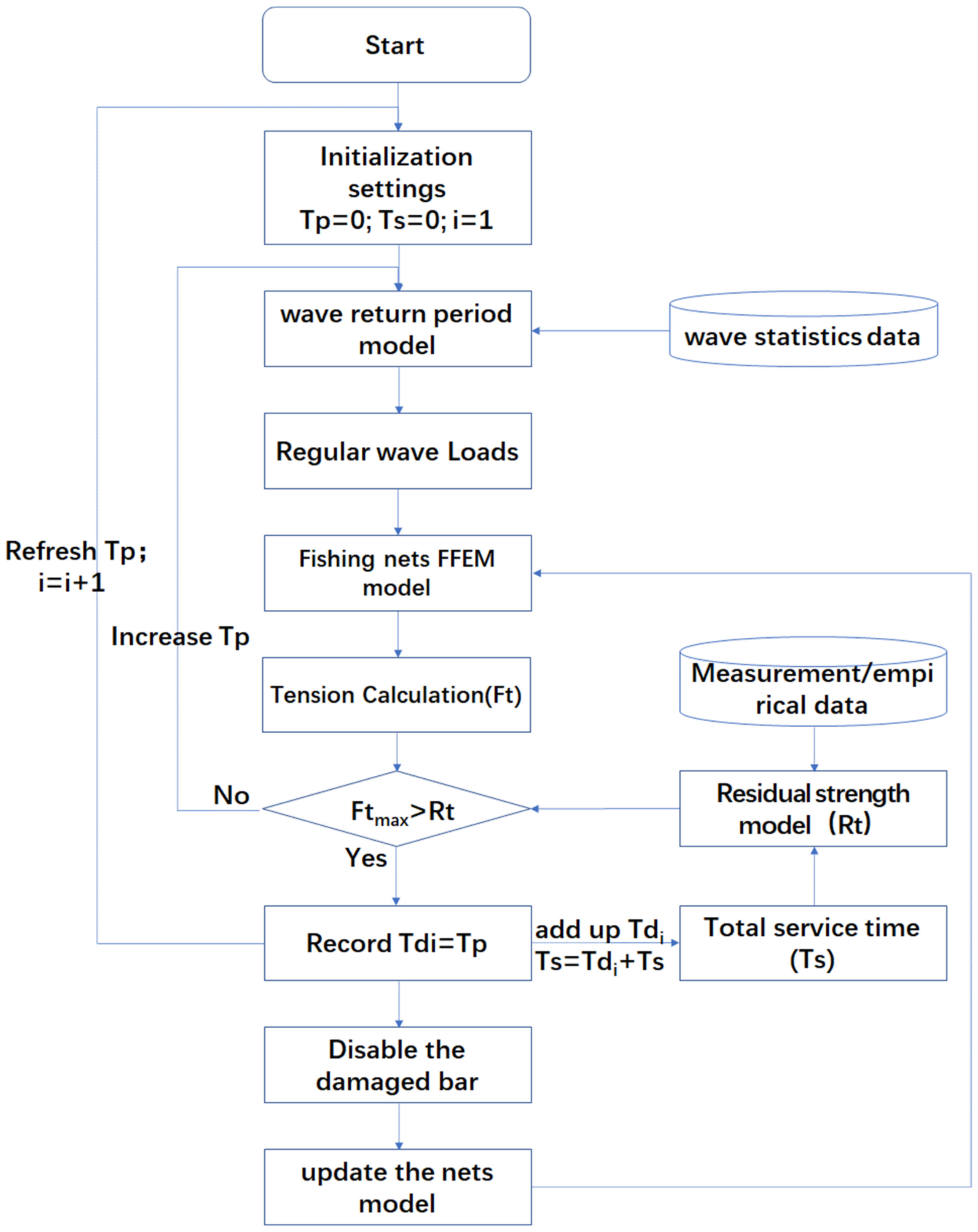
2.1. Basic Workflow of The Dynamic Lifetime Calculation
- Step 1: The wave return period model is obtained from the wave statistics data by integrating the wave probability density function (described in detail in Section 2.2). Then, the relationship between the wave load level and the wave return period (Tp) is established.
- Step 2: By applying the Flexible Finite Element Method (described in detail in Section 2.3), the tension (FT) distribution of the fishing net is analyzed under the wave loads; the tension is determined by the increasing wave return period (Tp) and the corresponding wave load level.
- Step 3: The residual strength model of the netting twine is estimated by fitting the actual measured tensile strength data with an exponential function (described in detail in Section 2.4), through which the tensile strength (Rt) can be calculated under the different expected total service times (Ts).
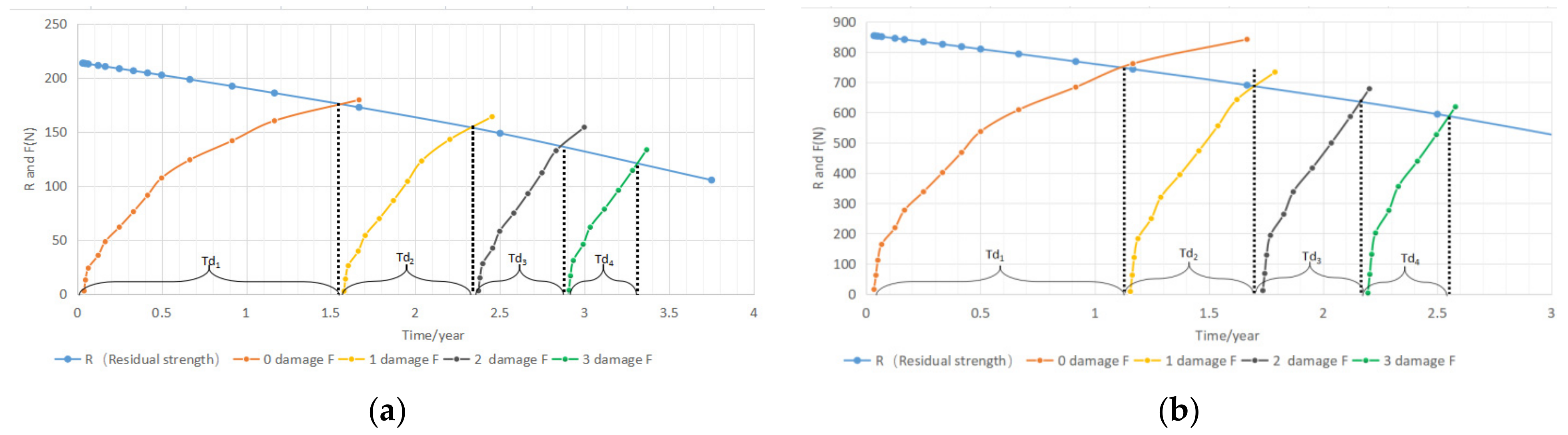
- Step 4: To determine whether the fishing net is damaged, the maximum tension is compared with the residual strength. The netting twine is judged as damaged if the maximum tension value exceeds the residual strength. The corresponding wave return period is set as the first dynamic lifetime Td1, and then the dynamic lifetime Td1 is added to the total service time (Ts).
- Step 5: To rebuild the fishing net model, the damaged twines are set as disabled and removed from the calculation model.
- Step 6: The dynamic lifetime Tdi is calculated by repeating steps 2–5.
2.2. Wave Return Period Model
2.3. Flexible Finite Element Method (FFEM)
2.3.1. Numerical Model Assumptions
- A fishing net is composed of several identical netting bars. Each netting bar is regarded as a cylinder.
- Every netting twine is built as a spatial beam-type line with two end super-nodes.
- Since the number of finite elements of the beam-type line has no influence on the convergence, each line is composed of only one finite element.
- The netting bars are entirely flexible and soft, having only tensile stiffness, which can be realized by setting minimal values to replace the compression, shear modulus, and bending stiffness in the calculation.
- Each bar is connected by nodes that can rotate freely without resistance. Each node has three translational degrees of freedom.
- The mutual interference of the flow field between bars is not considered.
2.3.2. Force Analysis
- (1)
- For an ideal smooth cylinder, the added mass coefficient in the normal direction is 1, or 0 in the axial direction, that is, = 0, = ρ∀.
- (2)
- is the characteristic area in the axial direction, and is the component in the normal direction, and are the diameter and length of the netting bars, respectively.
- (3)
- The flow force coefficient CD refers to the formula given by Blevins [19] in the Applied Fluid Dynamics Handbook, = .
2.3.3. Dynamic Equilibrium Equations
2.3.4. Equation Solving Method
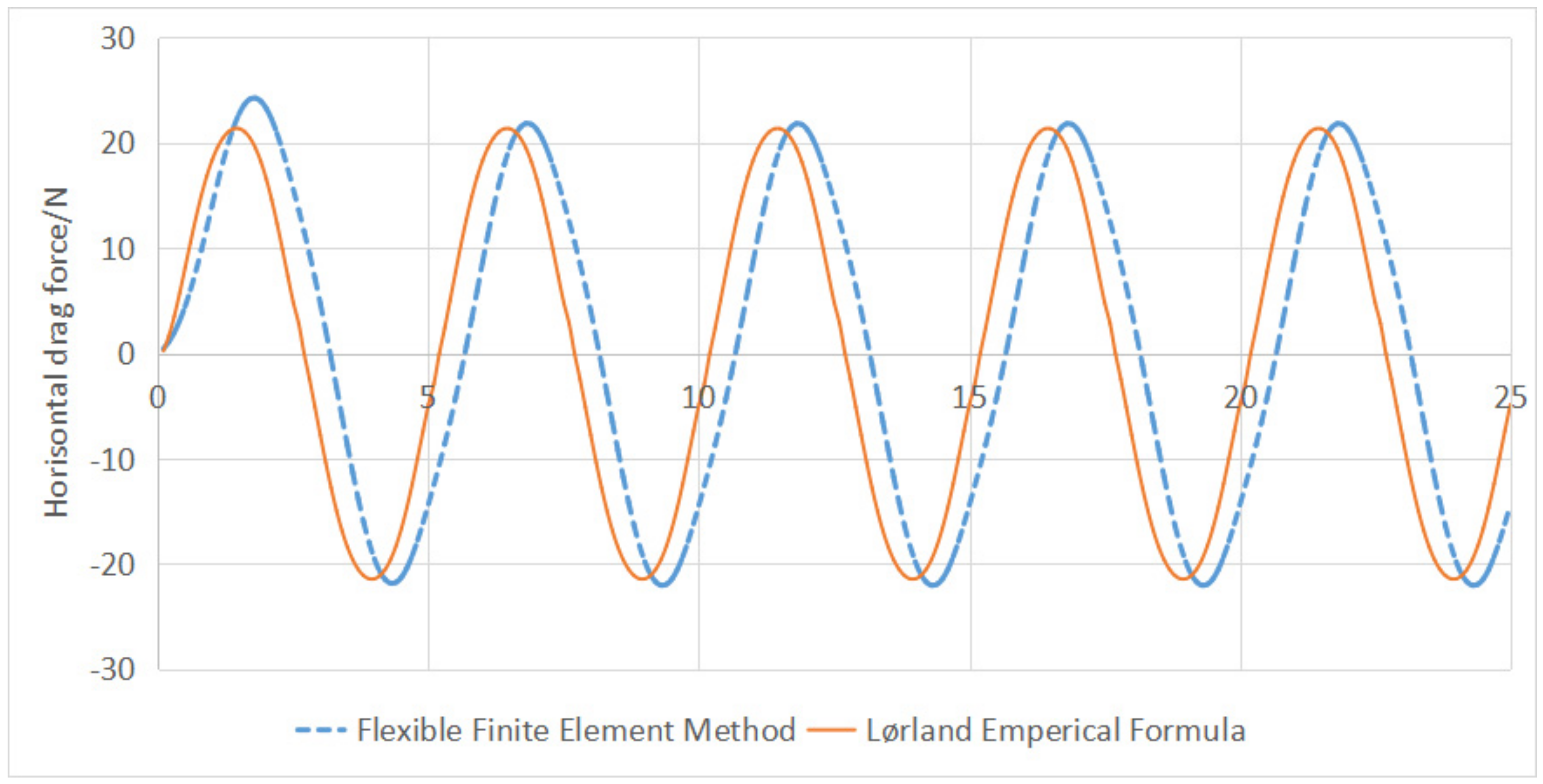
2.3.5. Checking the Force Calculation Result by Løland’s Empirical Formula
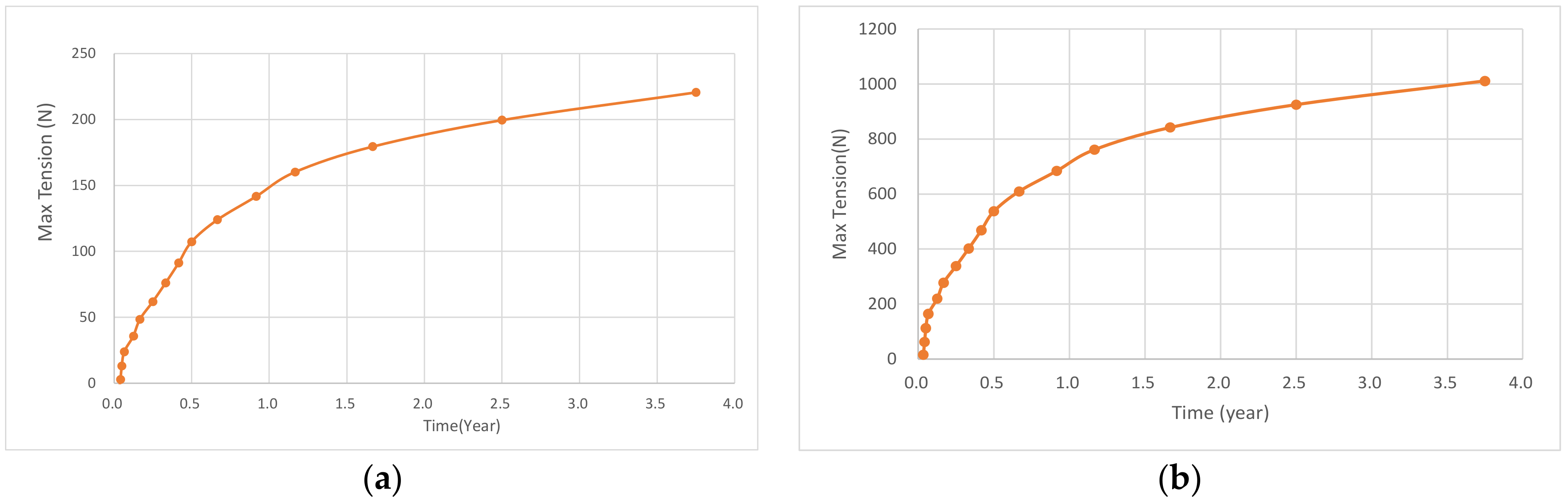
2.4. Residual Strength Model and Breaking Criterion
3. Results and Discussion
3.1. Calculation Model
3.2. Checking the Force Calculation Result
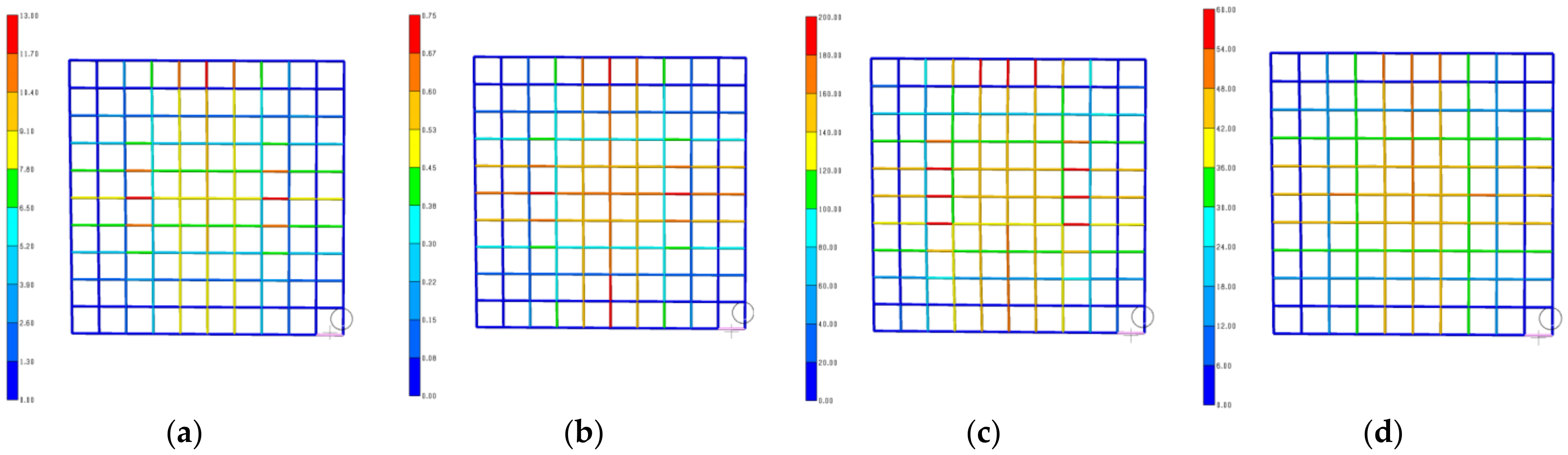
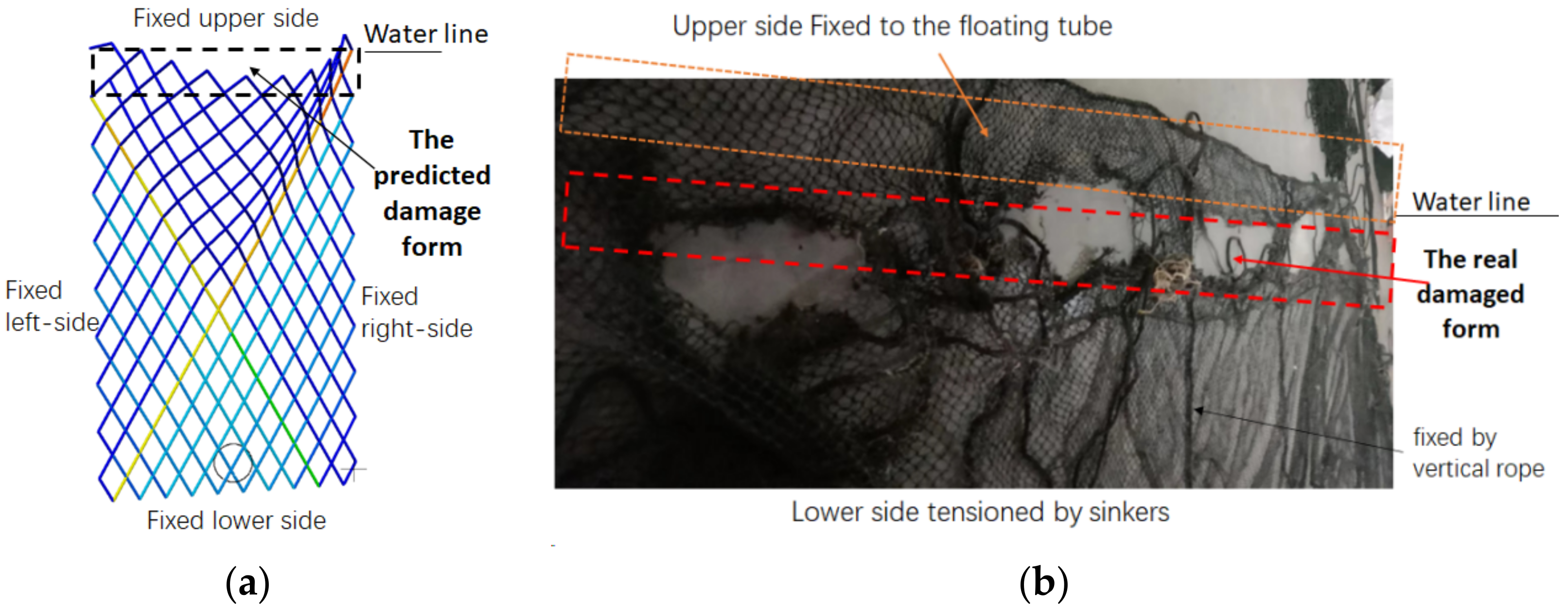
3.3. Determination of Hotspot Areas
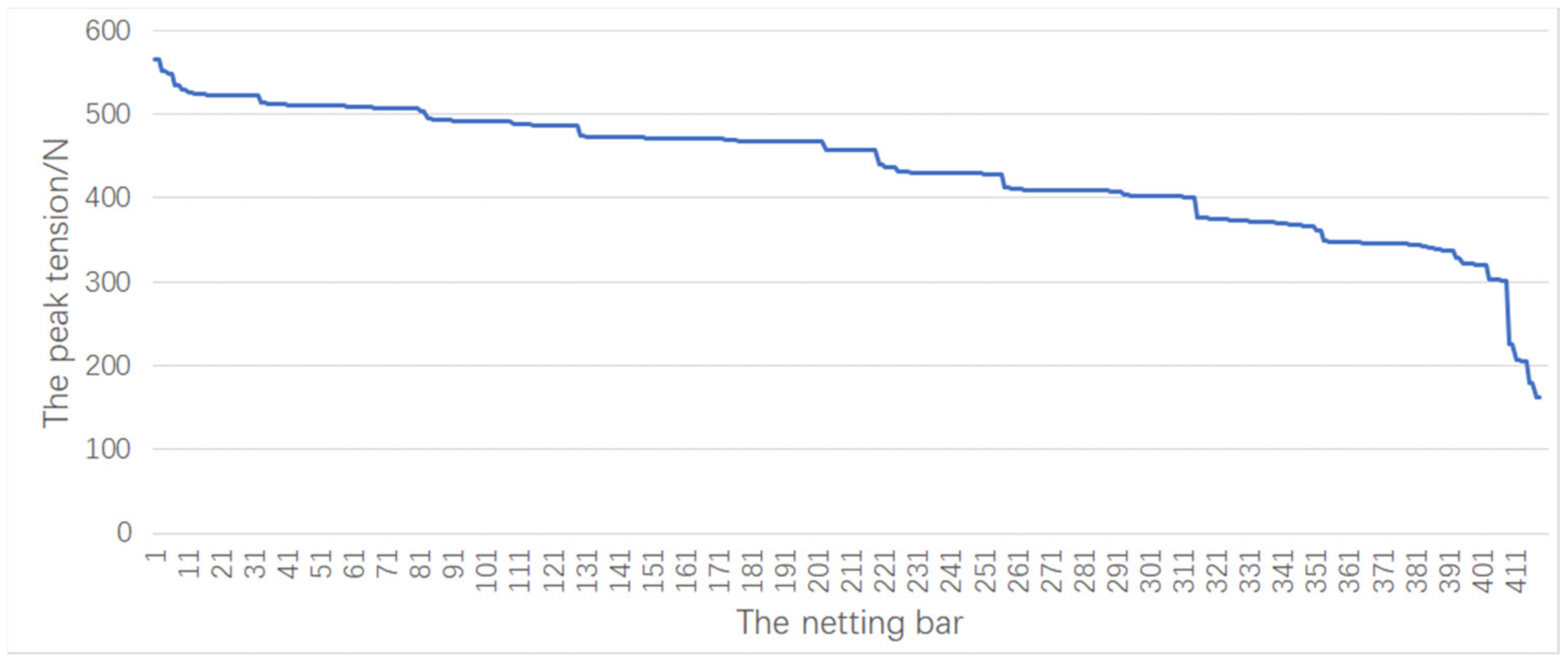
- The peak tension value of the bars follows a ladder distribution. Compared with the diamond mesh netting, the tension distribution of the square mesh netting is steeper.
- In the square mesh netting, the peak tension of nearly half the bars is less than the median value of the maximum tension of the netting. However, most of the bars in the diamond mesh netting have a peak tension exceeding the median value of the maximum tension of the netting.
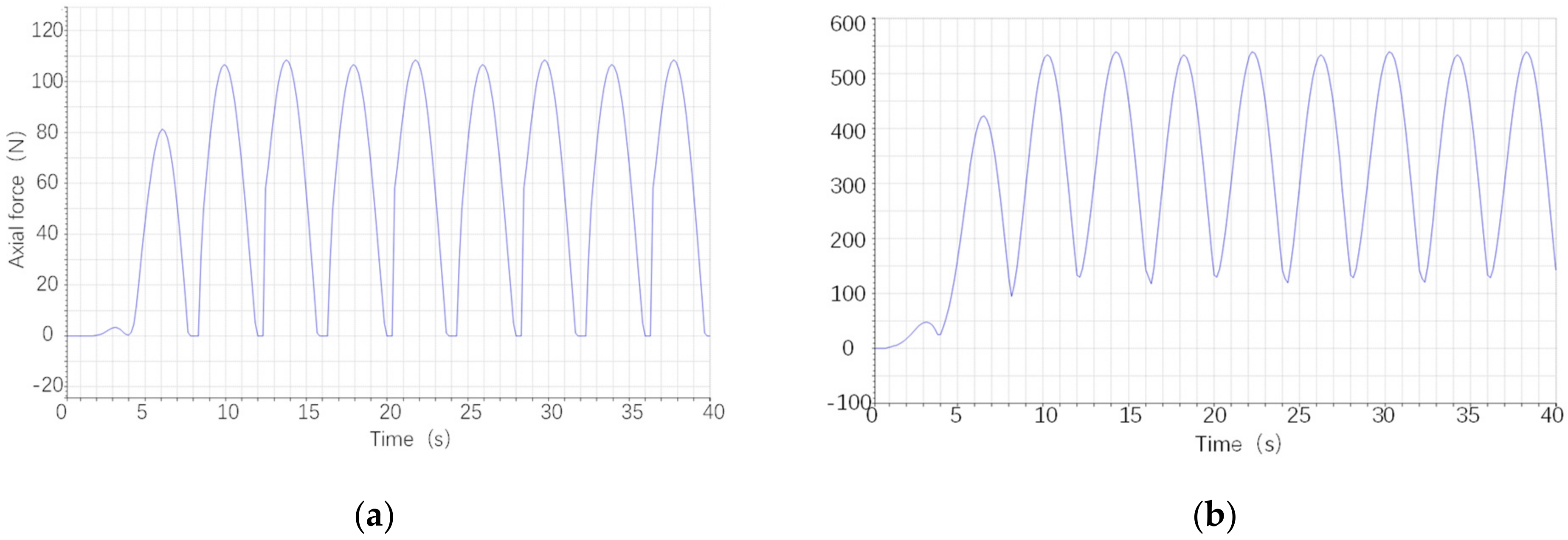
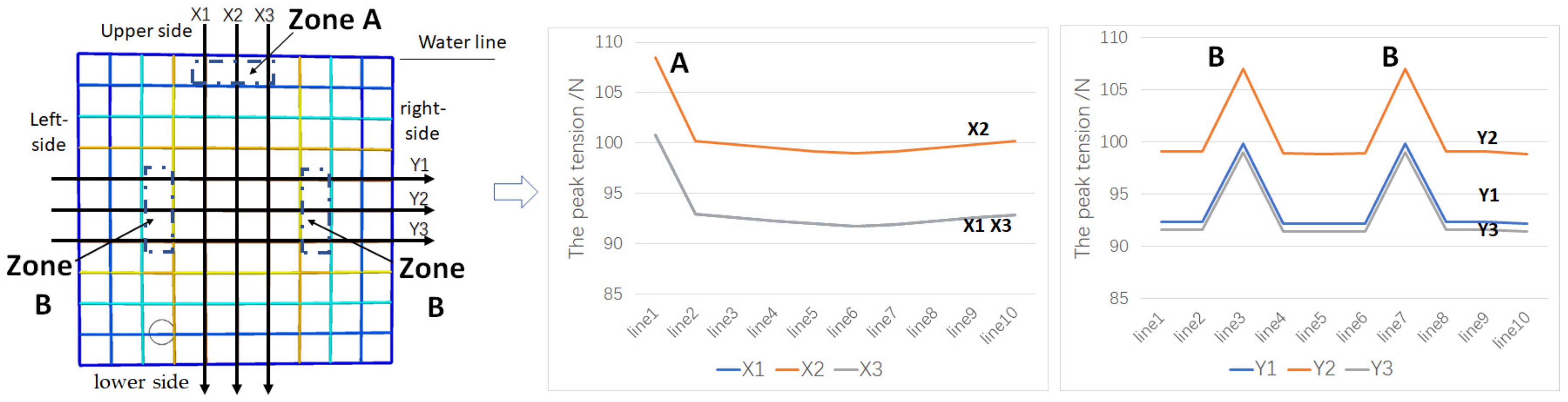
3.4. Influence of Wave Parameters on the Tension
3.5. Prediction of Damage Development in the Netting
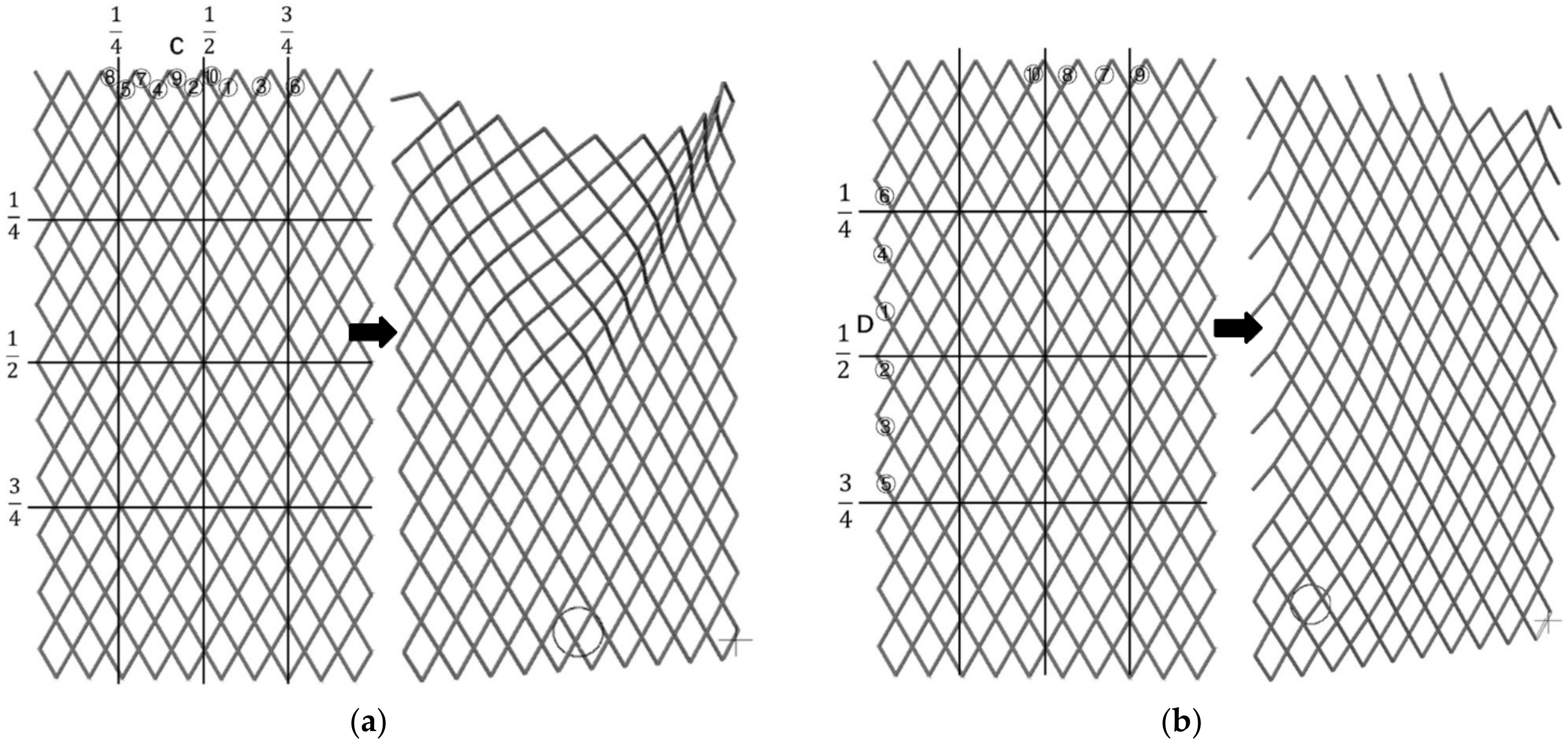
- Whether the square mesh netting is damaged from zone A or B, the netting bars in zone B or A will rupture in the subsequent damage process, and the netting will eventually show the same damaged form.
- The maximum tension changing trends along the two paths of damage development are similar at the beginning stage of the damage process and the same in the subsequent process. The maximum tension will generally increase at the beginning stage of the damage process and decrease rapidly when the destructive area expands to a large enough extent.
- The diamond mesh netting will result in different damaged forms when damaged from either zone C or zone D. When the damage begins from zone C, the area of the continuous damaged hole is more significant than that from zone D.
- The maximum tension of the diamond mesh netting increases at first and then drops at the beginning stage of the breakage process. When the net is damaged to a certain extent, the maximum tension will increase rapidly in a volatile pattern. The growth rate of the maximum tension from zone C is greater than that of zone D.
3.6. Dynamic Lifetime Prediction of the Netting
4. Conclusions and Future Works
Future works
- The residual strength and wave return period data in this paper’s calculation come from assumptions. The size of the calculated mesh model is relatively small compared with the actual mesh. Therefore, a prediction calculation based on a measured residual strength, actual wave return period data, and real-sized netting models would be more valuable in the future.
- Different wave parameters have a great effect on the tension of the netting. It is necessary to conduct more studies on the site selection of cages, as well as installation, operation, and maintenance to reduce the maximum tension and increase the lifetime of fishing nets.
- The nettings with different mesh types may have different performances in the material utilization rate, technical economy, or applicability for deep-sea aquaculture cages. Therefore, it is also worthwhile to further study these issues from the perspective of netting tension distribution or lifetime.
- Further study is necessary to find the general rule of the relative dynamic lifetime within different types of settings, different wave return periods, and residual strength models.
- In the future, considering that the structure has significant dimensions and displacement, it is necessary to conduct research with a nonlinear model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Basic parameters of fishing nets: | |
| d | diameter of netting bar |
| initial length of netting bar | |
| length of element i after deformation | |
| mass density of the fishnet net | |
| elastic modules of the netting bar | |
| cross-sectional area of the netting bar | |
| ∀ | volume of displacement |
| coefficient of knot shrinkage in T-direction | |
| coefficient of knot shrinkage in N-direction | |
| solidity of the netting | |
| Parameters about residual strength model: | |
| Ts | total service time |
| Rt | residual strength after time t |
| R0 | initial tensile strength |
| RL | residual strength after time L |
| a, b | parameters reflecting the material ability and work condition comprehensively |
| Parameters of wave and force analysis: | |
| wave amplitude | |
| wave period | |
| θ | incident angle of waves |
| ρ | mass density of seawater |
| initial phase angle | |
| the angle between the flow direction and the normal direction of the netting | |
| wave round frequency | |
| k | wave number |
| h | water depth |
| velocity potential of waves | |
| Tp | wave return period |
| probability of wave return period | |
| a characteristic parameter of wave in general | |
| f | probability density function of waves |
| X, Y, Z | coordinate of microelement position in the overall coordinate system |
| V | velocity of water |
| fluid velocity component | |
| added mass | |
| added mass coefficient | |
| drag coefficients | |
| characteristic area | |
| drag coefficients in the normal direction | |
| drag coefficients in the tangential direction | |
| FT | tension of the netting bar |
| Gravity | |
| buoyancyforce | |
| hydrodynamics load force | |
| tension force | |
| tension force from element i | |
| Parameters of FFEM calculation: | |
| Piola–Kirchhoff stress tensor | |
| E | Green strain tensor |
| surface forces | |
| body forces | |
| translational displacement vector | |
| displacement vector | |
| virtual quantities | |
| viscous damping density function | |
| surface of the initial configuration | |
| volume of the initial configuration | |
| tangential mass, damping, and stiffness matrices | |
| internal structural reaction force vector | |
| external force | |
| Others: | |
| Td1 | first damage lifetime of the netting |
| Tdi | dynamic lifetime of the netting |
| / | relative dynamic lifetime |
| i | imaginary unit or element label |
| g | gravitational acceleration |
References
- Sun, M.C. Fishing Gear Materials and Technology; China Agricultural Press: Beijing, China, 2009; p. 5. [Google Scholar]
- Sun, B.; Yu, W.W. Progress in research on high-performance netting materials for fishing. Fish. Mod. 2020, 47, 1–7. [Google Scholar]
- Zhou, Y.Q.; Xu, L.X. Mechanics of Fishing Gear (Revision); Science Press: Beijing, China, 2018; pp. 2–8. [Google Scholar]
- Zhanjiang Jingwei Net Factory: Zhanjiang, China, 2022. Available online: https://jwnetting.en.alibaba.com/ (accessed on 1 August 2022).
- Yang, P.; Kang, G.X. Comparison of fatigue lifetime assessment methods for semi-submerged platform structures. Ship Sci. Technol. 2012, 34, 112–118. [Google Scholar]
- CCS. Guidelines for Fatigue Strength of Ship Structure. In Guidance Notes GD18-2021; CCS: Beijing, China, 2021. [Google Scholar]
- ABS. Fatigue Assessment of Offshore Structures; ABS: Singapore, 2003. [Google Scholar]
- DNV. Fatigue Design of Offshore Steel Structures; DNV: Bærum, Norway, 2005. [Google Scholar]
- Mansour, A.E.; Ertekin, R.C. Fatigue Loading (Committee VI.1). In Proceedings of the 15th International Ship and Offshore Structures Congress (ISSC), San Diego, CA, USA, 26 June 2003. [Google Scholar]
- Li, Y.; Zhao, Y.; Gui, F.; Teng, B. Numerical simulation of the hydrodynamic behaviour of submerged plane nets in current. Ocean. Eng. 2006, 33, 2352–2368. [Google Scholar] [CrossRef]
- Miao, Y.J.; Ding, J.; Tian, C. Experimental study on hydrodynamic characteristics of net clothing in regular wave environments. In Proceedings of the 31st National Hydrodynamic Symposium, Xiamen, China, 30 October 2020; p. 7. [Google Scholar]
- Huang, C.-C.; Tang, H.-J.; Liu, J.-Y. Dynamical analysis of net cage structures for marine aquaculture: Numerical simulation and model testing. Aquac. Eng. 2006, 35, 258–270. [Google Scholar] [CrossRef]
- Tsukrov, I.; Eroshkin, O.; Fredriksson, D.; Swift, M.; Celikkol, B. Finite element modeling of net panels using a consistent net element. Ocean Eng. 2003, 30, 251–270. [Google Scholar] [CrossRef]
- Shi, J.G.; Wang, L.M. Study on fishing UHMWPE fiber rope. JSOU 2003, 4, 371–375. [Google Scholar]
- Liu, Y.; Yu, W.; Shi, J. Study on UV aging and fatigue properties of polyethylene fishing net material. Mar. Fish. 2018, 40, 734–739. [Google Scholar]
- Moe-Føre, H.; Endresen, P.C.; Jensen, Ø. Temporary-creep and postcreep properties of aquaculture netting materials with UHMWPE fibers. J. Offshore Mech. Arct. Eng. 2016, 3, 138. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhao, H.; Li, X.; Shi, W. Hydrodynamic Responses of a Barge-Type Floating Offshore Wind Turbine Integrated with an Aquaculture Cage. J. Mar. Sci. Eng. 2022, 10, 854. [Google Scholar] [CrossRef]
- DNV. RIFLEX-Theory-Manual_4.10.3; DNV: Bærum, Norway, 2017. [Google Scholar]
- Blevins, R.D. Applied Fluid Dynamics Handbook; Van Nostrand Reinhold Company: New York, NY, USA, 1984; p. 334. [Google Scholar]
- Løland, G. Current Forces on and Flow through Fish Farms. Ph.D. Thesis, The Norwegian Institute of Technology, Trondheim, Norway, 1991; p. 87. [Google Scholar]
- Friedman, A. Fishing Gear Theory and Design; Ocean Press: Beijing, China, 1988; p. 12. [Google Scholar]
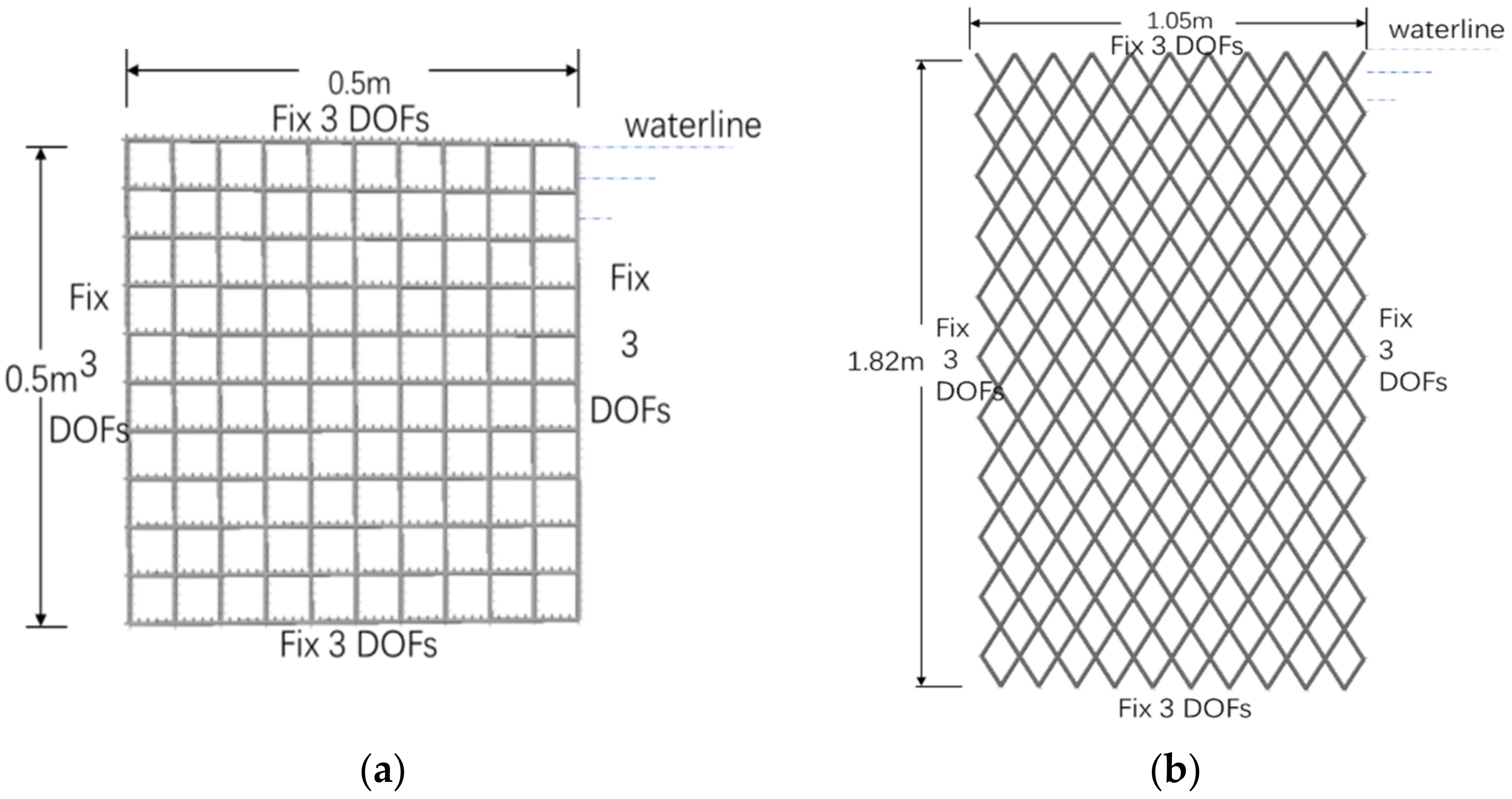


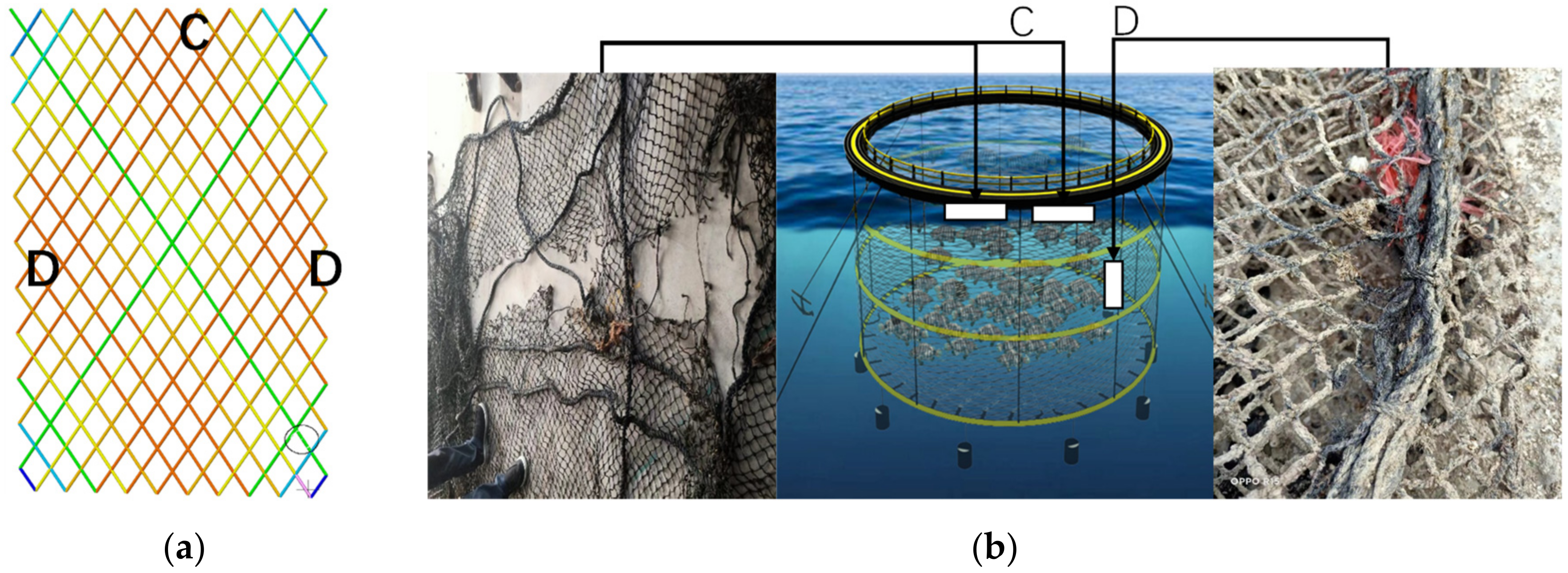


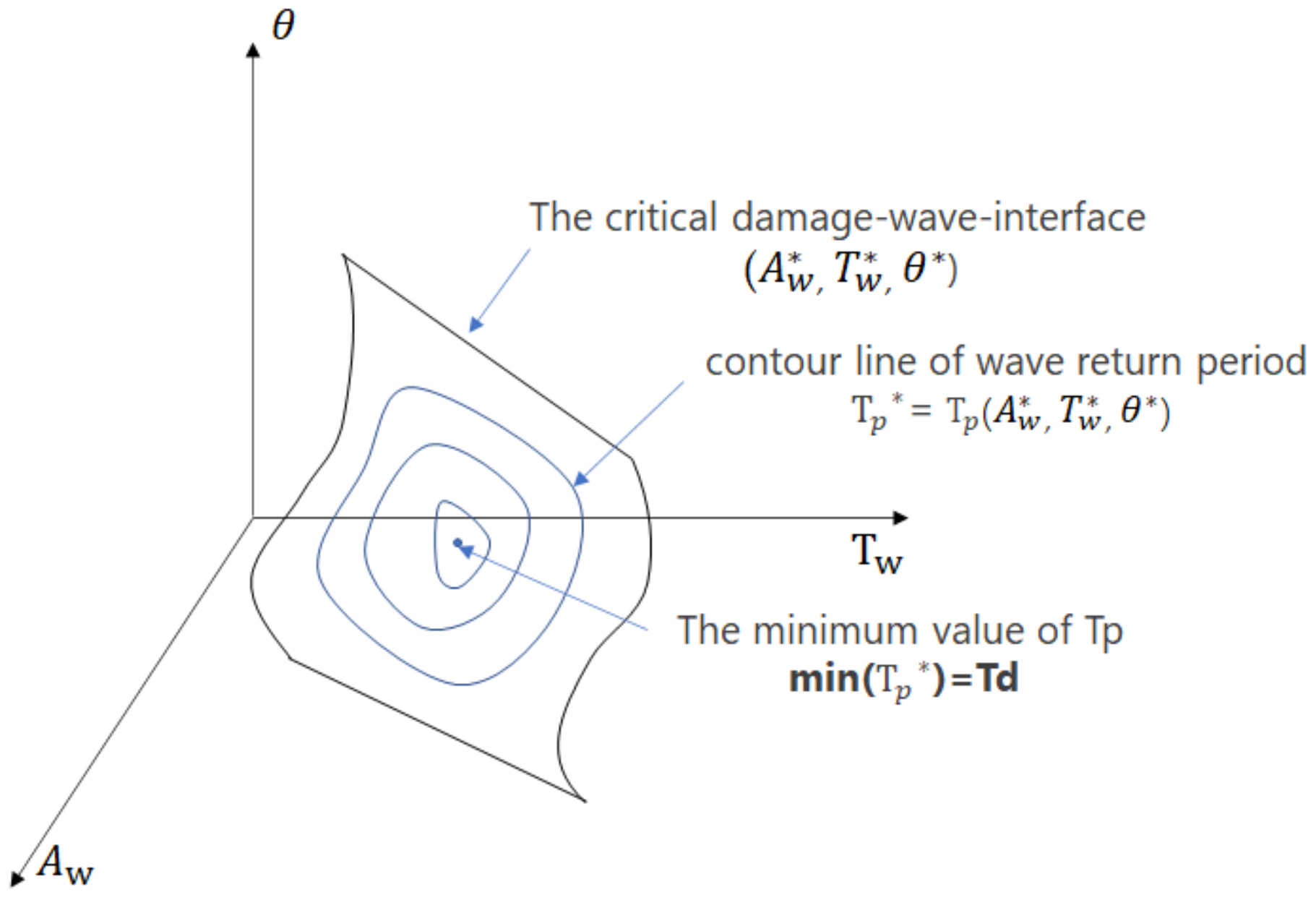
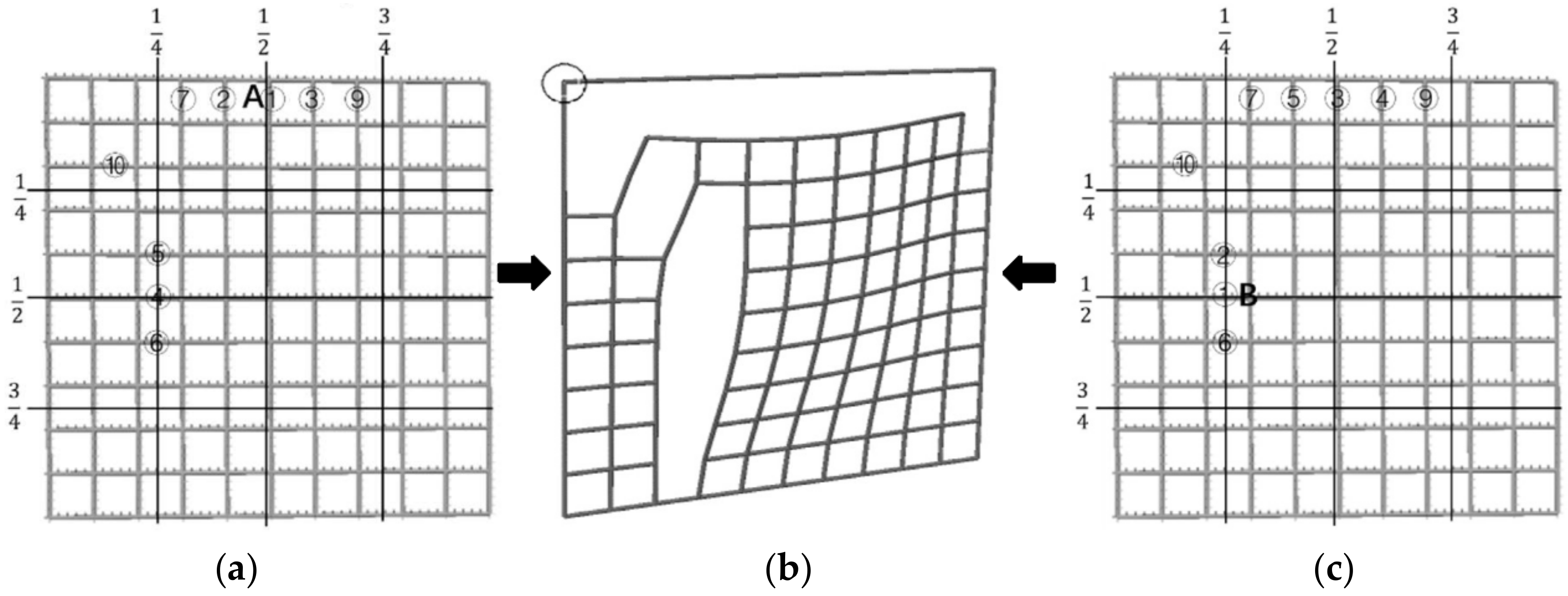
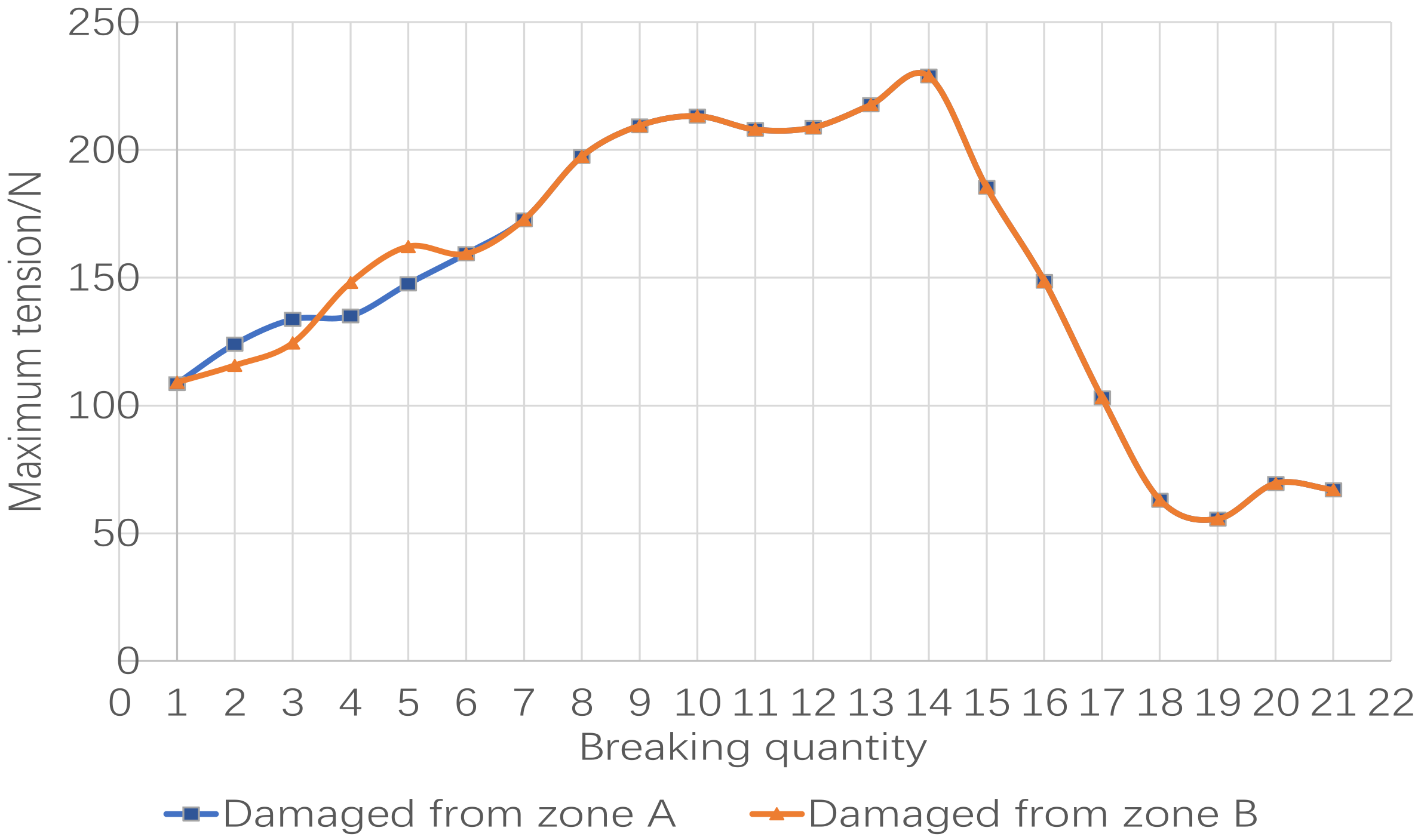



| Mesh Type | Twine Diameter | Bar Size | Material Density | Axial Stiffness | Coefficient of Knot Shrinkage | Netting Size | Number of Elements |
|---|---|---|---|---|---|---|---|
| m | m | kg/m3 | N/m | m | |||
| Square | 3.8 × 10−3 | 0.05 | 917.5 | 1.69 × 106 | 0.5 × 0.5 | 220 | |
| Diamond | 7.6 × 10−3 | 0.1 | 917.5 | 3.37 × 106 | 1.05 × 1.82 | 452 |
| Mesh Type | t/year | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| Square | R(t)/N | 214 | 190 | 163 | 133 | 95 | 21 |
| Diamond | 856 | 760 | 653 | 531 | 379 | 86 |
| Wave Amplitude/m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Return Period/years | 0.042 | 0.067 | 0.17 | 0.33 | 0.5 | 0.92 | 1.67 | 3.75 |
| Netting | Dynamic Lifetime (Year) | |||
|---|---|---|---|---|
| Td1 | Td2 | Td3 | Td3 | |
| Square mesh | 1.56 | 0.79 | 0.53 | 0.45 |
| Diamond mesh | 1.1 | 0.58 | 0.46 | 0.39 |
| Netting | Relative Dynamic Lifetime | |||
|---|---|---|---|---|
| Td1/Td1 | Td2/Td1 | Td3/Td1 | Td3/Td1 | |
| Square mesh | 1 | 0.51 | 0.34 | 0.29 |
| Diamond mesh | 1 | 0.53 | 0.42 | 0.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yuan, H.; Zhao, Y.; Yan, J. Dynamic Lifetime Prediction of Fishing Nets Based on the Model of Wave Return Period and Residual Strength. J. Mar. Sci. Eng. 2022, 10, 1353. https://doi.org/10.3390/jmse10101353
Wang H, Yuan H, Zhao Y, Yan J. Dynamic Lifetime Prediction of Fishing Nets Based on the Model of Wave Return Period and Residual Strength. Journal of Marine Science and Engineering. 2022; 10(10):1353. https://doi.org/10.3390/jmse10101353
Chicago/Turabian StyleWang, Hong, Hua Yuan, Yao Zhao, and Jun Yan. 2022. "Dynamic Lifetime Prediction of Fishing Nets Based on the Model of Wave Return Period and Residual Strength" Journal of Marine Science and Engineering 10, no. 10: 1353. https://doi.org/10.3390/jmse10101353
APA StyleWang, H., Yuan, H., Zhao, Y., & Yan, J. (2022). Dynamic Lifetime Prediction of Fishing Nets Based on the Model of Wave Return Period and Residual Strength. Journal of Marine Science and Engineering, 10(10), 1353. https://doi.org/10.3390/jmse10101353





