A Numerical Study on the Effects of Perforated and Imperforate Baffles on the Sloshing Pressure of a Rectangular Tank
Abstract
:1. Introduction
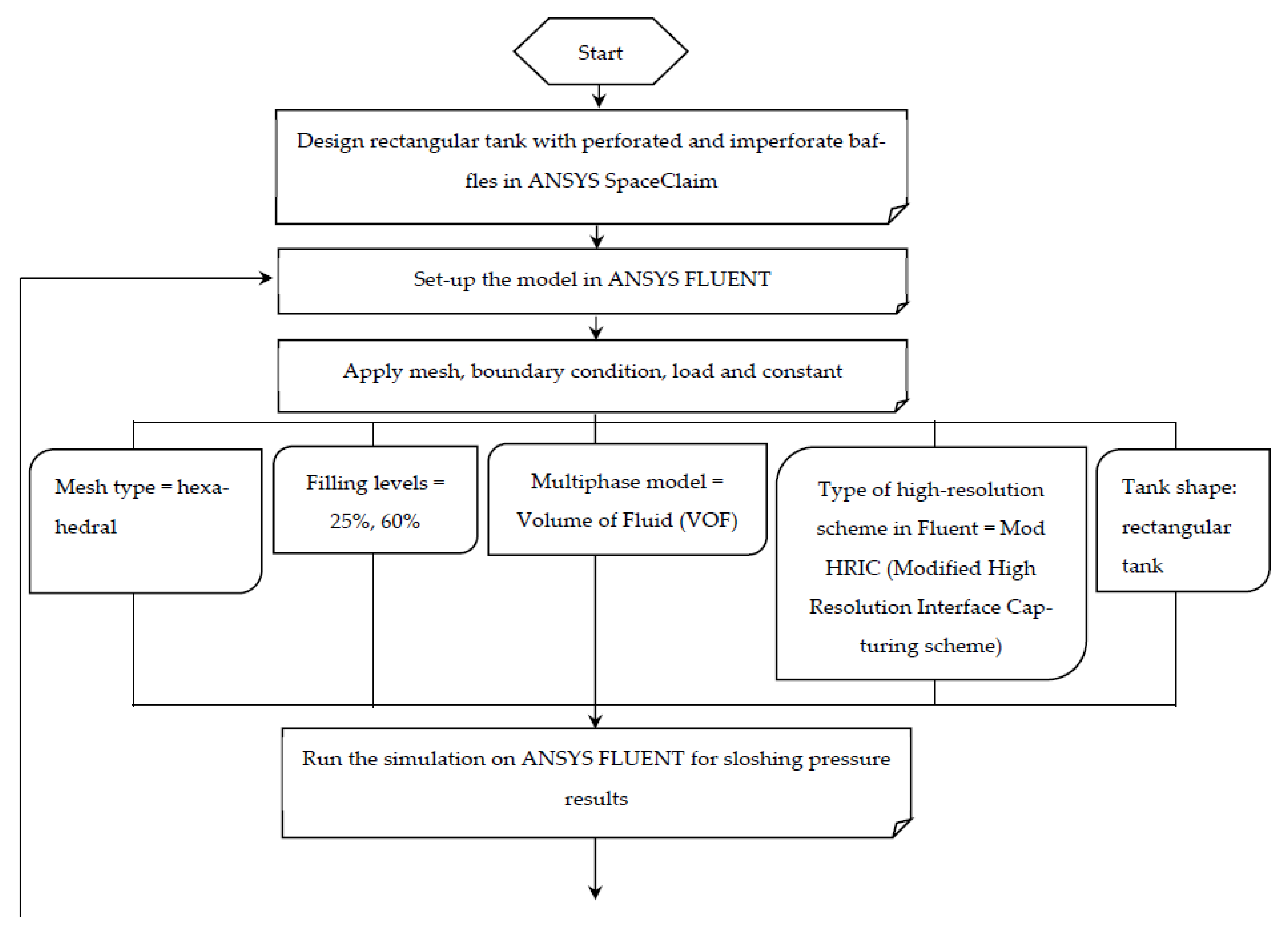
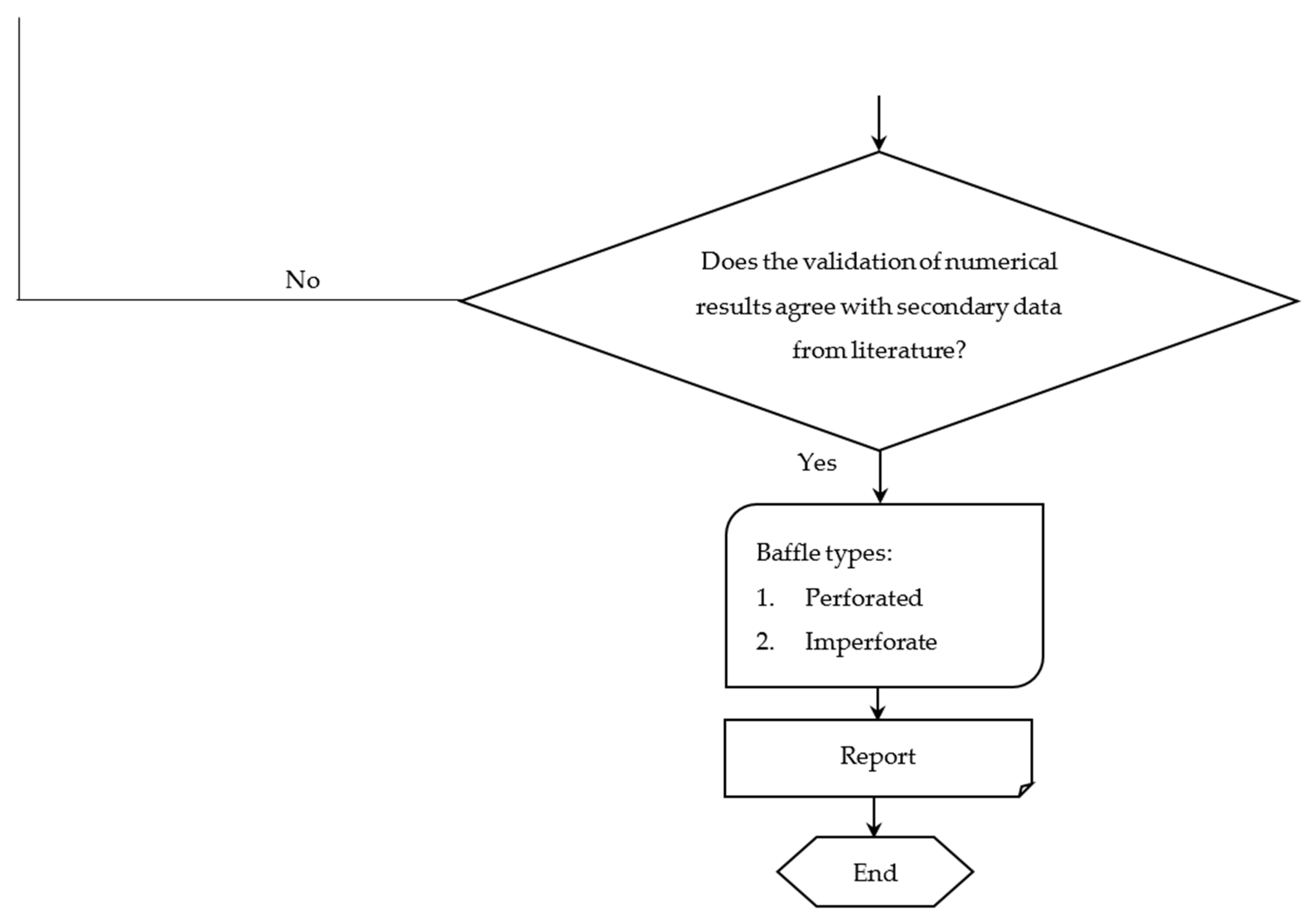
2. Methodology
2.1. Numerical Flow of ANSYS Software
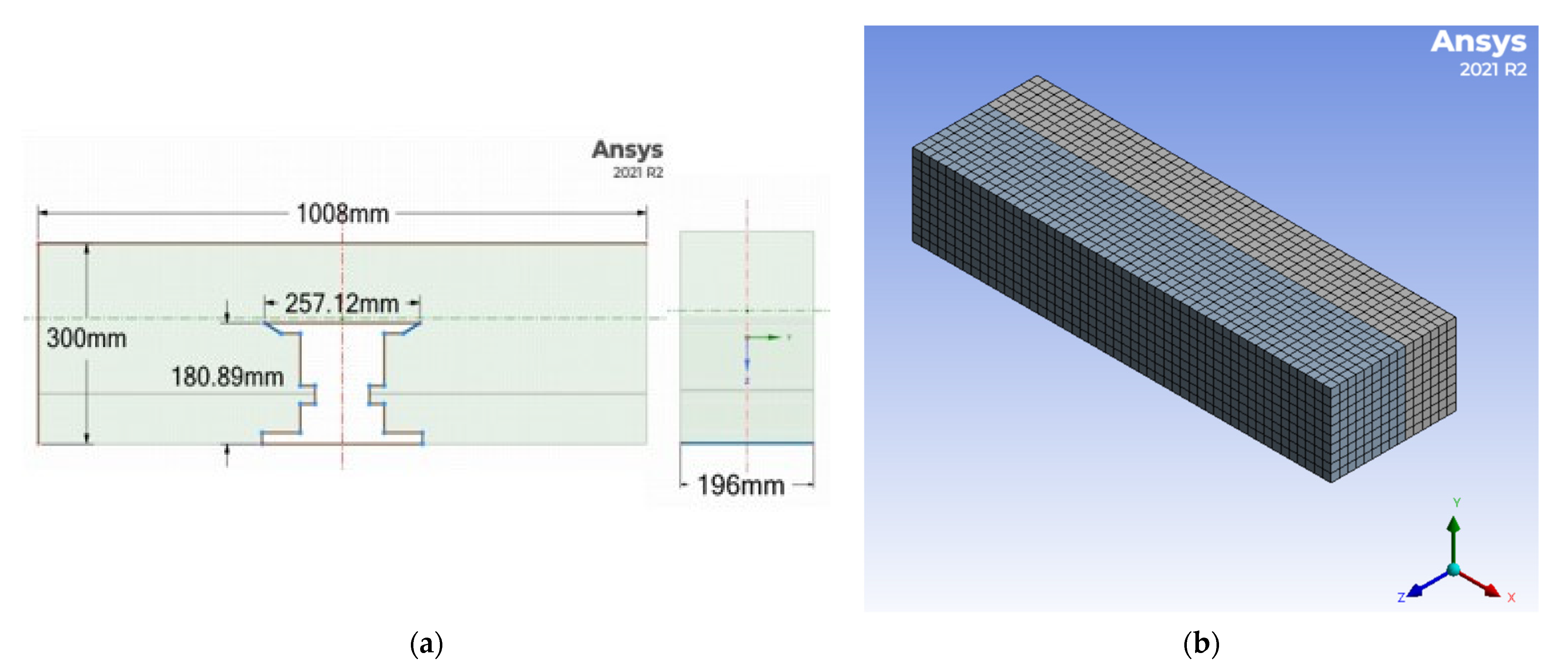
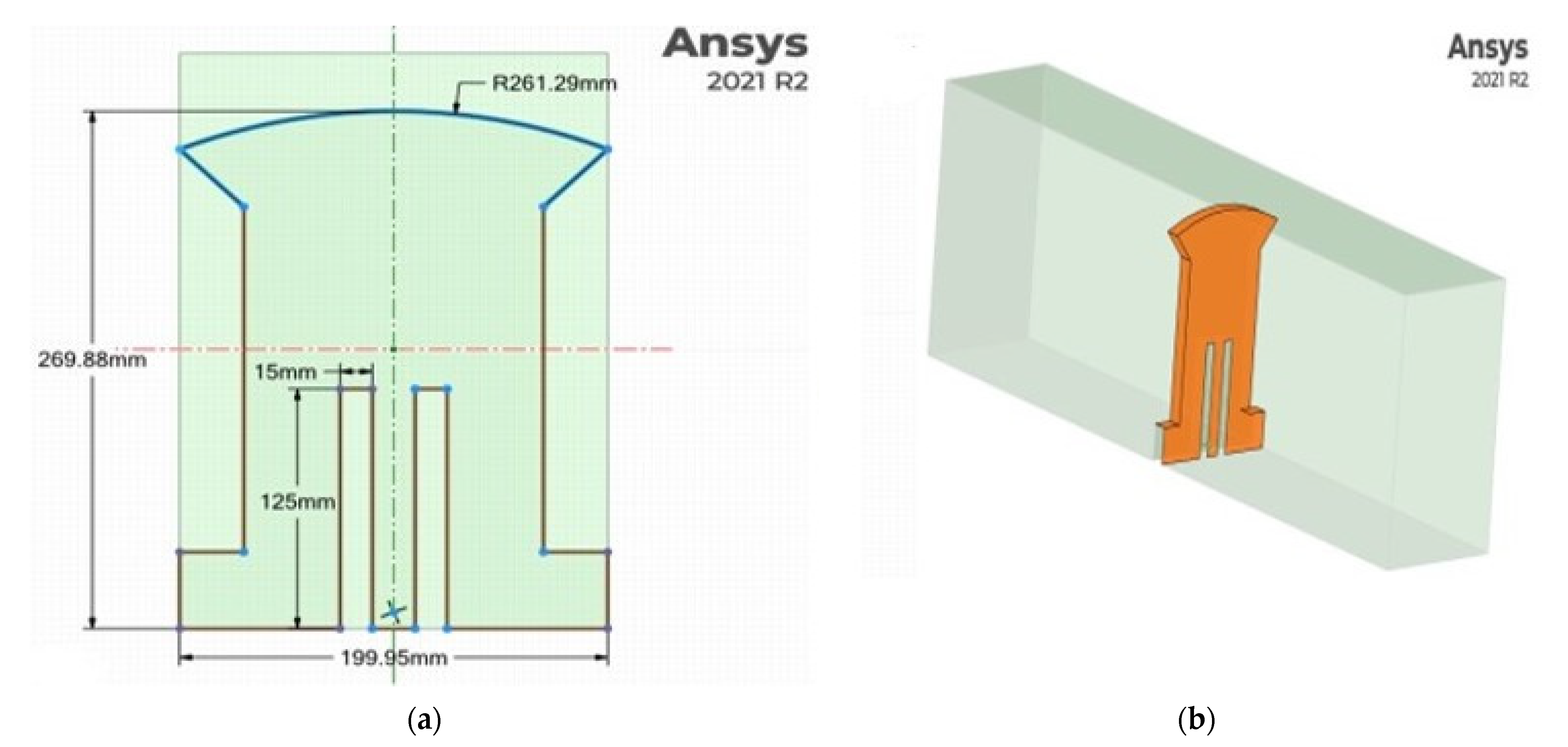
2.2. Geometrical Particulars of Rectangular Tank and Baffles
2.3. Theoretical Background
Volume of Fluid (VOF) Method in ANSYS Fluent
- α = 0; the cell is empty
- α = 1; the cell is full
- 0 < α < 1; the cell is partially filled and contains the interface
3. Results and Discussion
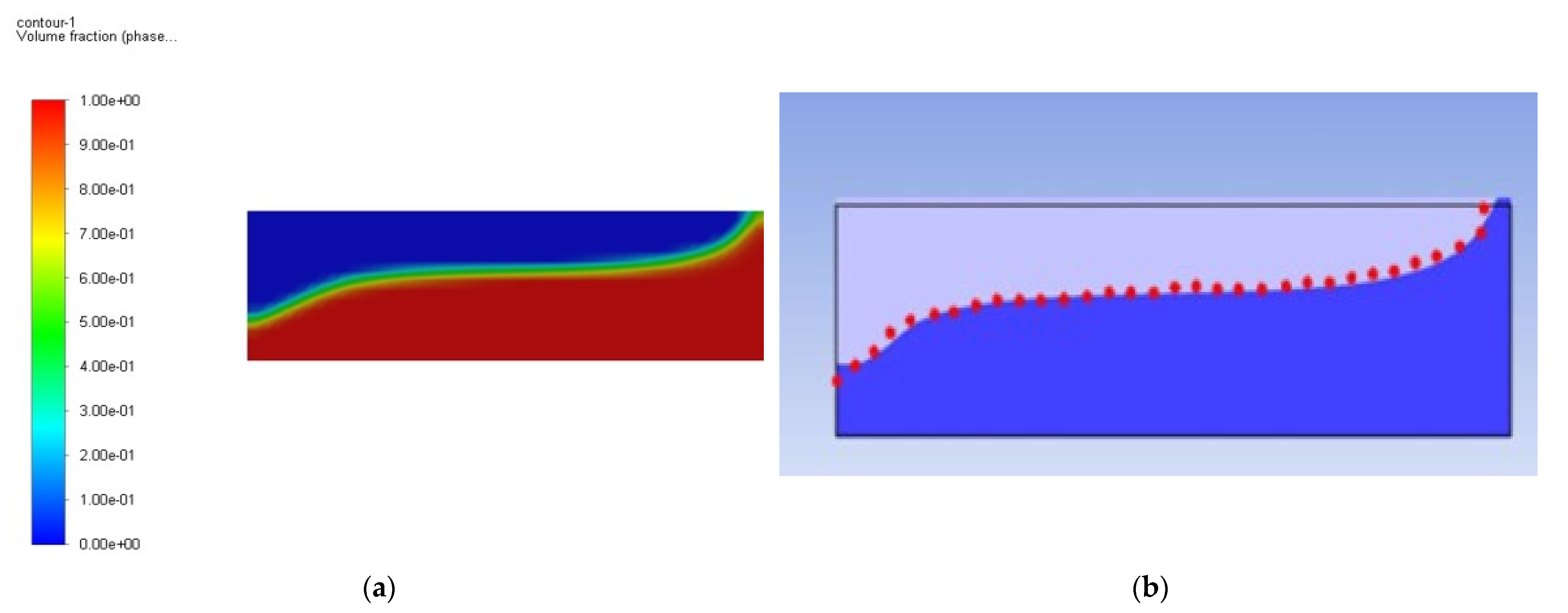
3.1. Validation of Sloshing Pressure Results in Unbaffled Rectangular Tank under 60% Filling
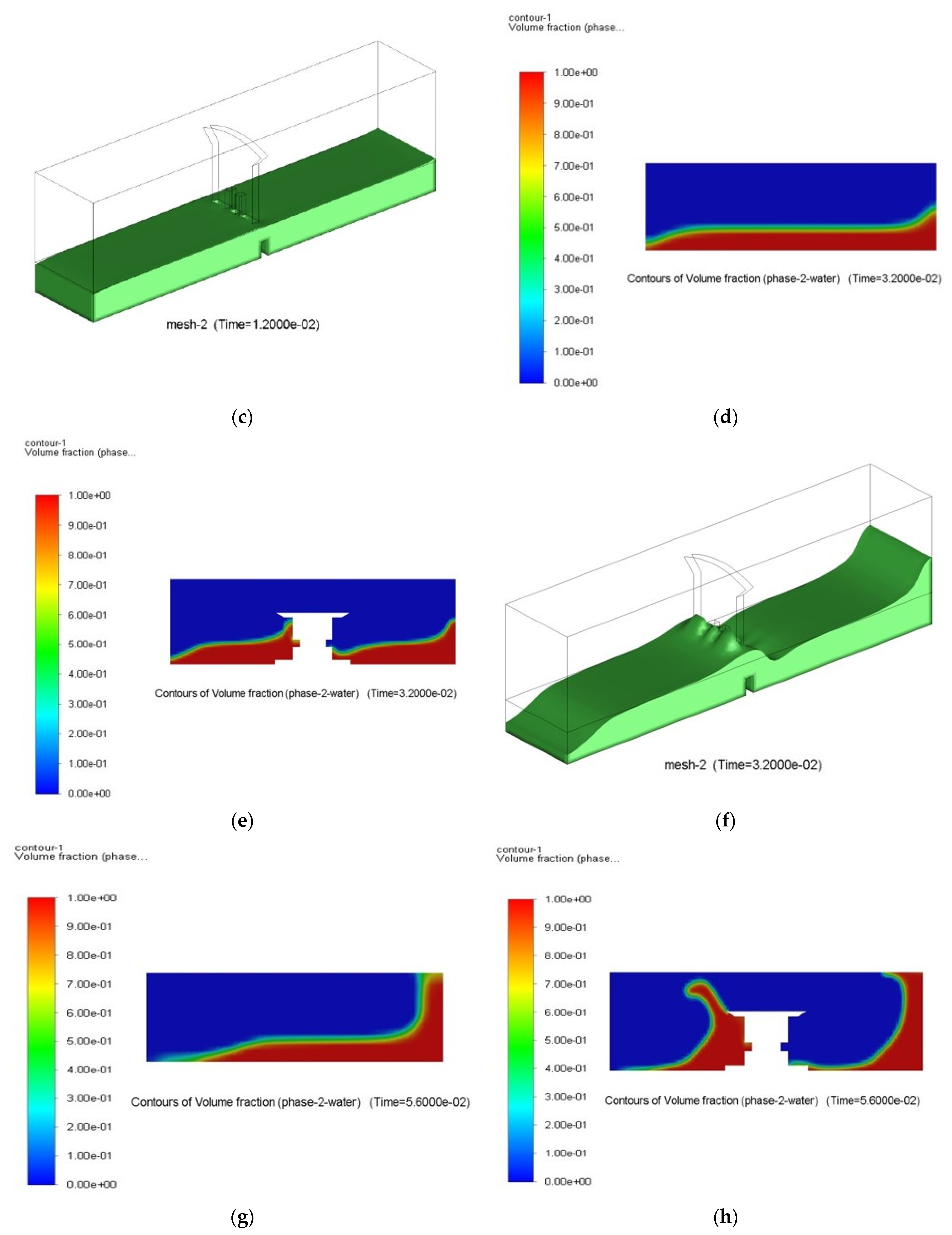
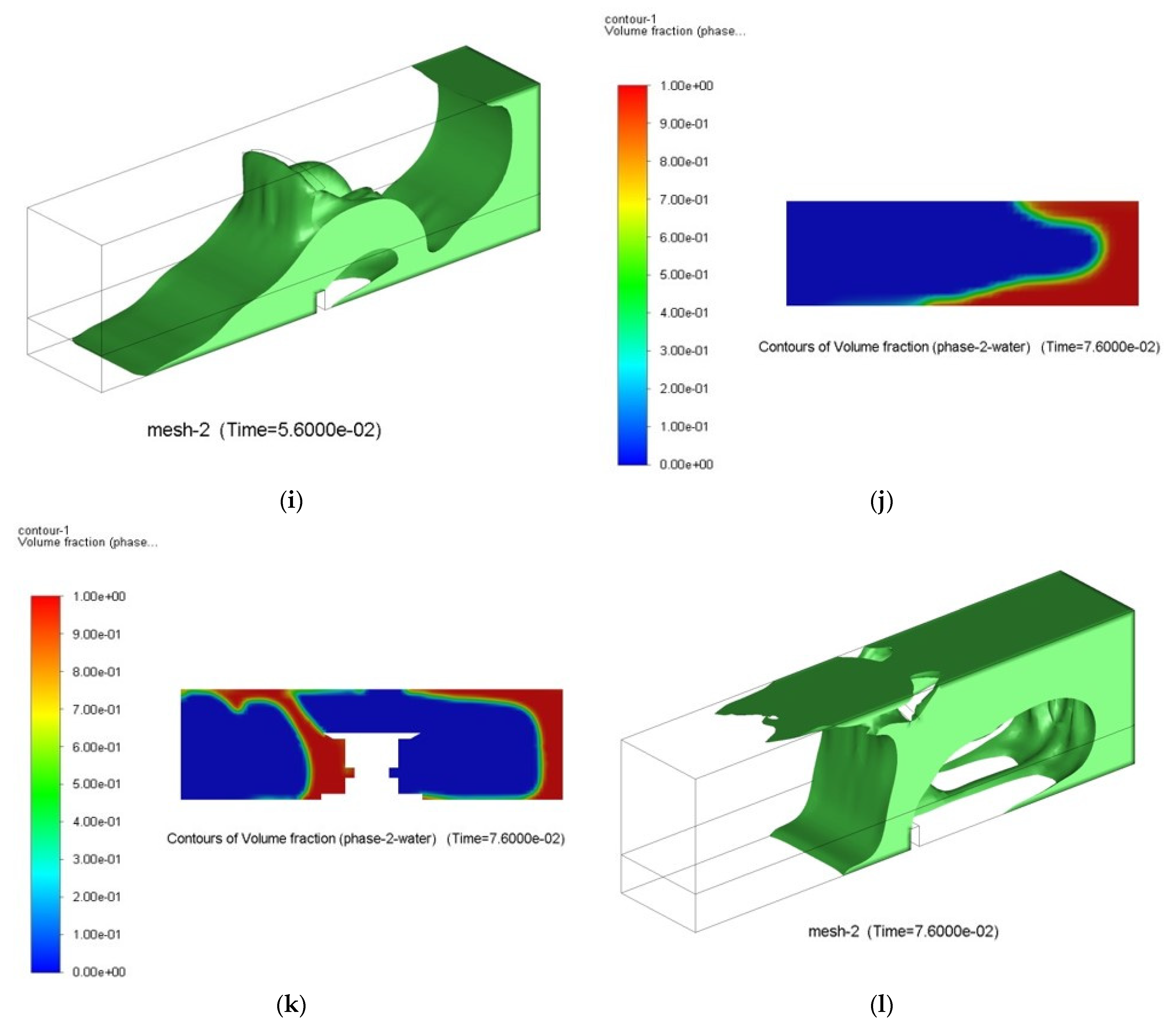
3.2. Comparison of Sloshing Pressure between Unbaffled and Baffled Tanks under 25% Filling
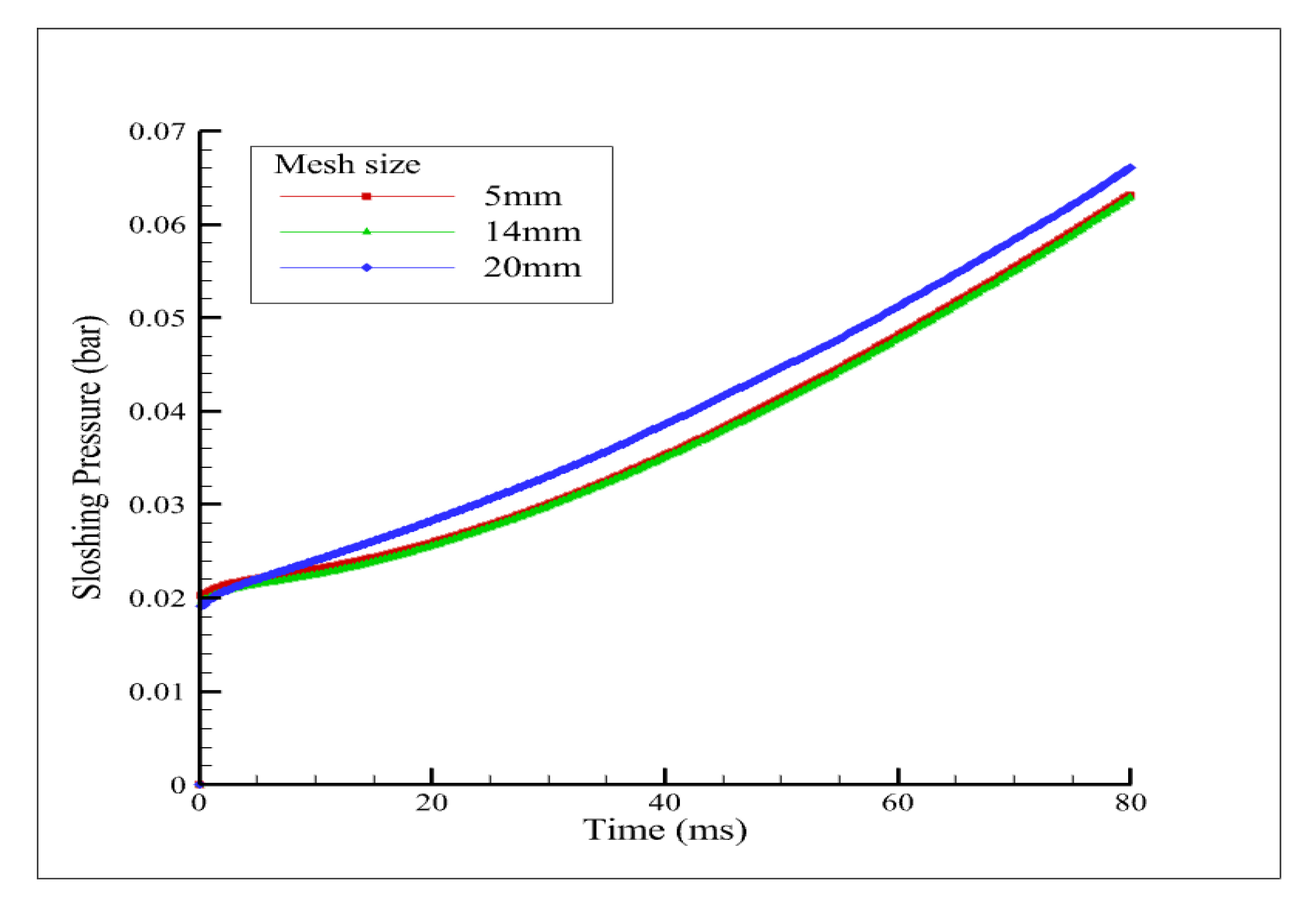
3.3. Mesh Sensitivity Analysis
4. Conclusions
- The analysis of sloshing pressure for a rectangular tank with perforated and imperforate baffles under 25% and 60% filling rates was discussed and presented. The validation of the correlation of the sloshing pressure results under 60% filling level for the unbaffled tank case is found to be in good agreement with the numerical data published by Agrawal and Rahumathulla [30] and the experimental data by Vesenjak et al. [33].
- On the other hand, the 25% filling level was extensively investigated considering three conditions: unbaffled tank, baffled tank with perforated baffle, and baffled tank with imperforate baffle for addressing the sloshing pressure problem. It is remarkably observed that the lowest sloshing pressure was in the case of perforated baffle with value of 0.886 bar, followed by the imperforate baffle with value of 0.891 bar, and finally the unbaffled tank with a pressure value of 0.982 bar.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choudhary, N.; Bora, S.N. Linear sloshing frequencies in the annular region of a circular cylindrical container in the presence of a rigid baffle. Sādhanā 2017, 42, 805–815. [Google Scholar] [CrossRef]
- Jena, D.; Biswal, K.C. A numerical study of violent sloshing problems with modified MPS method. J. Hydrodyn. 2017, 29, 659–667. [Google Scholar] [CrossRef]
- Wang, X.; Arai, M. A numerical study on coupled sloshing and ship motions of a liquefied natural gas carrier in regular and irregular waves. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2015, 229, 3–13. [Google Scholar] [CrossRef]
- Zheng, M.Z.; Gou, Y.; Teng, B.; Jo, H. A practical prescreening method for sloshing severity evaluation. Pet. Sci. 2020, 17, 1119–1134. [Google Scholar] [CrossRef]
- Ma, C.; Oka, M.; Ando, T. A Study on Sloshing Behavior for Moss-type LNG Tank Based on SPH Numerical Simulation and Large-scale Model Experiment. Int. J. Offshore Polar Eng. 2018, 28, 350–360. [Google Scholar] [CrossRef]
- Kawahashi, T.; Arai, M.; Wang, X.; Cheng, L.Y.; Nishimoto, K.; Nakashima, A. A study on the coupling effect between sloshing and motion of FLNG with partially filled tanks. J. Mar. Sci. Technol. 2019, 24, 917–929. [Google Scholar] [CrossRef]
- Luo, M.; Koh, C.G.; Bai, W. A three-dimensional particle method for violent sloshing under regular and irregular excitations. Ocean Eng. 2016, 120, 52–63. [Google Scholar] [CrossRef]
- Singal, V.; Bajaj, J.; Awalgaonkar, N.; Tibdewal, S. CFD analysis of a kerosene fuel tank to reduce liquid sloshing. Procedia Eng. 2014, 69, 1365–1371. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.; Lee, J. Comparison of sloshing-induced pressure in different scale tanks. J. Ships Off. Str. 2016, 5302, 1744–5302. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Khan, I.; Wang, S.; Xu, Q. Comprehensive Study on Sloshing Impacts for an Offshore 3D Vessel via the Integration of Computational Fluid Dynamics Simulation, Experimental Unit, and Artificial Neural Network Prediction. Ind. Eng. Chem. Res. 2020, 59, 22187–22204. [Google Scholar] [CrossRef]
- Su, Y.; Liu, Z.Y. Coupling effects of barge motion and sloshing. Ocean Eng. 2017, 140, 352–360. [Google Scholar] [CrossRef]
- Yu, Y.; Ma, N.; Fan, S.; Gu, X. Experimental and numerical studies on sloshing in a membrane-type LNG tank with two floating plates. Ocean Eng. 2017, 129, 217–227. [Google Scholar] [CrossRef]
- Kim, S.; Chung, S.; Shin, W.; Cho, D.; Park, J. Experimental study on sloshing reduction effects of baffles linked to a spring system. Ocean Eng. 2018, 170, 136–147. [Google Scholar] [CrossRef]
- Xue, M.; Chen, Y.; Zheng, J.; Qian, L.; Yuan, X. Fluid dynamics analysis of sloshing pressure distribution in storage vessels of different shapes. Ocean Eng. 2019, 192, 106–582. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Han, F. LNG Tank Sloshing Simulation of Multidegree Motions Based on Modified 3D MPS Method. Math. Probl. Eng. 2020, 4018925. [Google Scholar] [CrossRef]
- Kargbo, O.; Xue, M.; Zheng, J.; Yuan, X. Multiphase sloshing dynamics of a two-layered fluid and interfacial wave interaction with a porous T-shaped baffle in a tank. Ocean Eng. 2021, 229, 108664. [Google Scholar] [CrossRef]
- Saripilli, J.R. Numerical Studies of Coupling Effect of Sloshing on 3D Ship Motions. Int. J. Offshore Polar Eng. 2017, 27, 27–35. [Google Scholar] [CrossRef]
- Bai, W.; Liu, X.; Koh, C.G. Numerical study of violent LNG sloshing induced by realistic ship motions using level set method. Ocean Eng. 2015, 97, 100–113. [Google Scholar] [CrossRef]
- Ma, C.; Xiong, C.; Ma, G. Numerical study on suppressing violent transient sloshing with single and double vertical baffles. Ocean Eng. 2021, 223, 108557. [Google Scholar] [CrossRef]
- Kim, H.; Parthasarathy, N.; Choi, Y.; Lee, Y. Reduction of sloshing effects in a rectangular tank through an air-trapping mechanism—A numerical study. J. Mech. Sci. Technol. 2018, 32, 1049–1056. [Google Scholar] [CrossRef]
- Ye, W.; Liu, J.; Lin, G.; Zhou, Y.; Yu, L. High performance analysis of lateral sloshing response in vertical cylinders with dual circular or arc-shaped porous structures. Appl. Ocean Res. 2018, 81, 47–71. [Google Scholar] [CrossRef]
- Wang, W.; Peng, Y.; Wei, Z.; Guo, Z.; Jiang, Y. Engineering Analysis with Boundary Elements High performance analysis of liquid sloshing in horizontal circular tanks with internal body by using IGA-SBFEM. Eng. Anal. Bound. Elem. 2019, 101, 1–16. [Google Scholar] [CrossRef]
- Zhu, A.; Xue, M.A.; Yuan, X.; Zhang, F.; Zhang, W. Effect of Double-Side Curved Baffle on Reducing Sloshing in Tanks under Surge and Pitch Excitations. Shock Vib. 2021, 6647604. [Google Scholar] [CrossRef]
- Ma, L.; Wei, C.; Zhao, Y. Research on the Suppression Effect Law of Different Baffle Positions on Liquid Sloshing in Spherical Tank. In Proceedings of the 2018 9th International Conference on Mechanical and Aerospace Engineering (ICMAE), Budapest, Hungary, 10–13 July 2018; pp. 457–461. [Google Scholar] [CrossRef]
- Zheng, X.; You, Y.; Ma, Q.; Khayyer, A.; Shao, S. Applied sciences A Comparative Study on Violent Sloshing with Complex Baffles Using the ISPH Method. Appl. Sci. 2018, 8, 904. [Google Scholar] [CrossRef]
- Chen, X.; Tang, Z.; Wan, D. The effects of T type baffle on liquid sloshing by MPS method. In Proceedings of the 3rd International Conference on Violent Flows (VF-2016), Osaka, Japan, 9–11 March 2016; pp. 9–11. [Google Scholar]
- Wang, W.; Tang, G.; Song, X.; Zhou, Y. Transient Sloshing in Partially Filled Laterally Excited Horizontal Elliptical Vessels with T-Shaped Baffles. J. Press. Vessel Technol. Trans. ASME 2017, 139, 1–13. [Google Scholar] [CrossRef]
- Shivanian, E.; Aslefallah, M. Stability and convergence of spectral radial point interpolation method locally applied on two-dimensional pseudoparabolic equation. Numer. Methods Partial Differ. Equ. 2017, 33, 724–741. [Google Scholar] [CrossRef]
- Aslefallah, M.; Abbasbandy, S.; Shivanian, E. Meshless singular boundary method for two-dimensional pseudo-parabolic equation: Analysis of stability and convergence. J. Appl. Math. Comput. 2020, 63, 585–606. [Google Scholar] [CrossRef]
- Agrawal, M.; Rahumathulla, L. Numerical simulation of liquid sloshing in floating LNG. In Proceedings of the Annual Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014; Volume 3, pp. 1848–1858. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two equation k-w turbulence models for aerodynamic flows. In Proceedings of the AIAA 24th Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Waclawczyk, T.; Koronowicz, T. Comparison of cicsam and hric high-resolution schemes for interface capturing. J. Theor. Appl. Mech. 2008, 46, 325–345. [Google Scholar]
- Vesenjak, M.; Müllerschön, H.; Hummel, A.; Ren, Z. Simulation of Fuel Sloshing—Comparative Study. 2004. Available online: https://www.semanticscholar.org/paper/Simulation-of-Fuel-Sloshing-Comparative-Study-Verfahren-Vesenjak/23c434469e479820e214973a905c15d3b1e53db6 (accessed on 1 April 2022).




| Designation | Dimensions |
|---|---|
| Rectangular tank | |
| Length (mm) | 1008 |
| Breadth (mm) | 196 |
| Height (mm) | 300 |
| Imperforate baffle parameters | |
| Length (mm) | 257.12 |
| Height (mm) | 180.89 |
| Perforated baffle parameters | |
| Length (mm) | 199.95 |
| Height (mm) | 269.88 |
| Hole Length (mm) | 15 |
| Hole Height (mm) | 125 |
| Baffle arc radius (mm) | 261.29 |
| Mesh parameters | |
| Mesh type | Hexahedral |
| Maximum mesh size | 20 mm |
| Number of elements | 7500 |
| Number of nodes | 8976 |
| Max Sloshing Pressure (Bar) | ||
|---|---|---|
| Present Study | Numerical Study [30] | Experimental Study [33] |
| 3.099 | 3.189 | 3.327 |
| Mesh Type | Mesh Size | Sloshing Pressure (Bar) under 25% Filling Rate for Unbaffled Tank |
|---|---|---|
| Automatic | 5 mm | 0.0632 |
| Tetrahedral | 14 mm | 0.0629 |
| Hexahedral | 20 mm | 0.0661 |
| Type of Viscous Model | Sloshing Pressure (Bar) under 25% Filling Rate for Unbaffled Tank |
|---|---|
| Laminar | 0.9032 |
| SST k-omega | 0.9309 |
| k-epsilon | 1.9317 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Yacouby, A.M.; Ahmed, M.M. A Numerical Study on the Effects of Perforated and Imperforate Baffles on the Sloshing Pressure of a Rectangular Tank. J. Mar. Sci. Eng. 2022, 10, 1335. https://doi.org/10.3390/jmse10101335
Al-Yacouby AM, Ahmed MM. A Numerical Study on the Effects of Perforated and Imperforate Baffles on the Sloshing Pressure of a Rectangular Tank. Journal of Marine Science and Engineering. 2022; 10(10):1335. https://doi.org/10.3390/jmse10101335
Chicago/Turabian StyleAl-Yacouby, Ahmad Mahamad, and Mostafa Mohamed Ahmed. 2022. "A Numerical Study on the Effects of Perforated and Imperforate Baffles on the Sloshing Pressure of a Rectangular Tank" Journal of Marine Science and Engineering 10, no. 10: 1335. https://doi.org/10.3390/jmse10101335
APA StyleAl-Yacouby, A. M., & Ahmed, M. M. (2022). A Numerical Study on the Effects of Perforated and Imperforate Baffles on the Sloshing Pressure of a Rectangular Tank. Journal of Marine Science and Engineering, 10(10), 1335. https://doi.org/10.3390/jmse10101335






