Quantitative Evaluation of Submerged Cavitation Jet Performance Based on Image Processing Method
Abstract
:1. Introduction
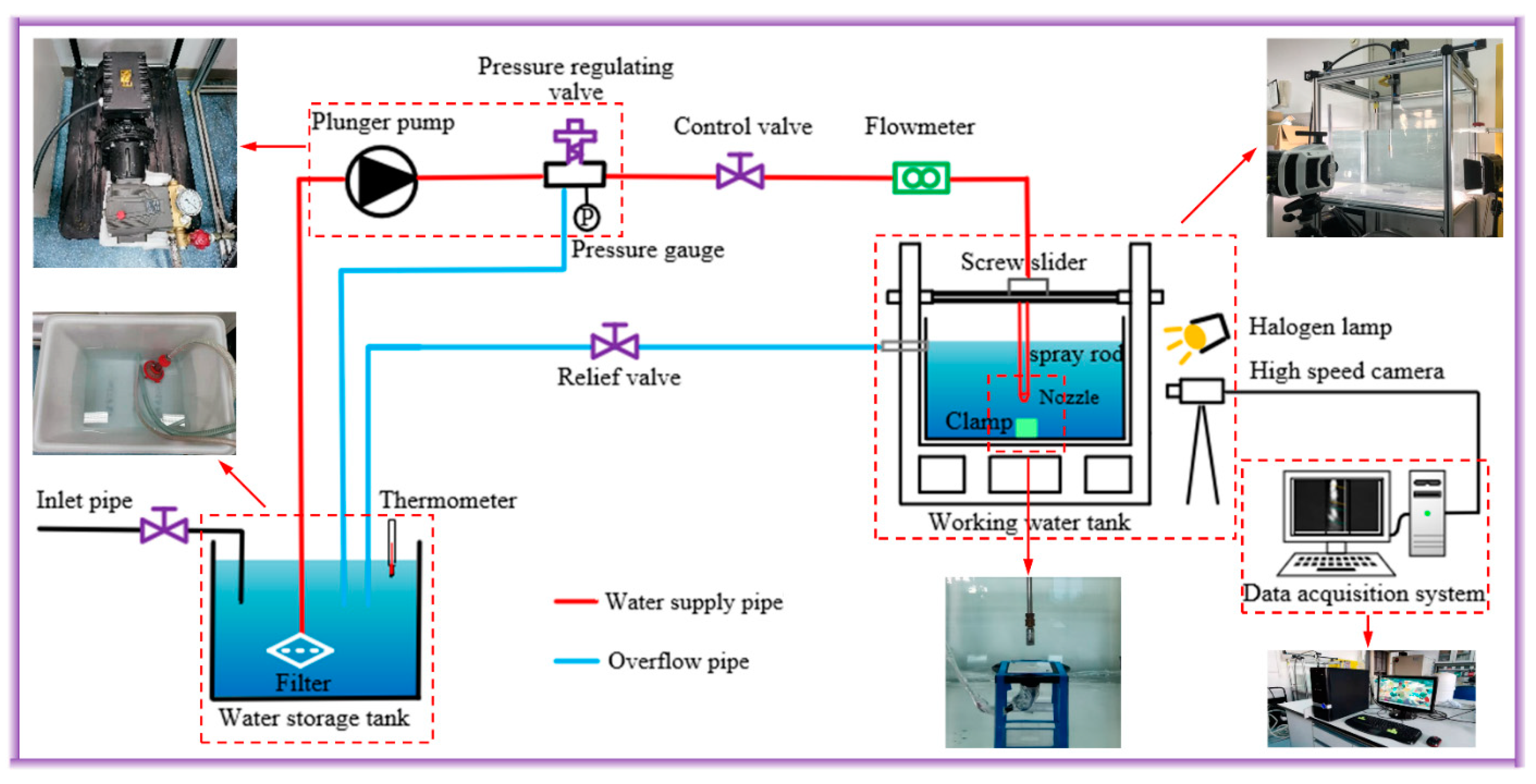
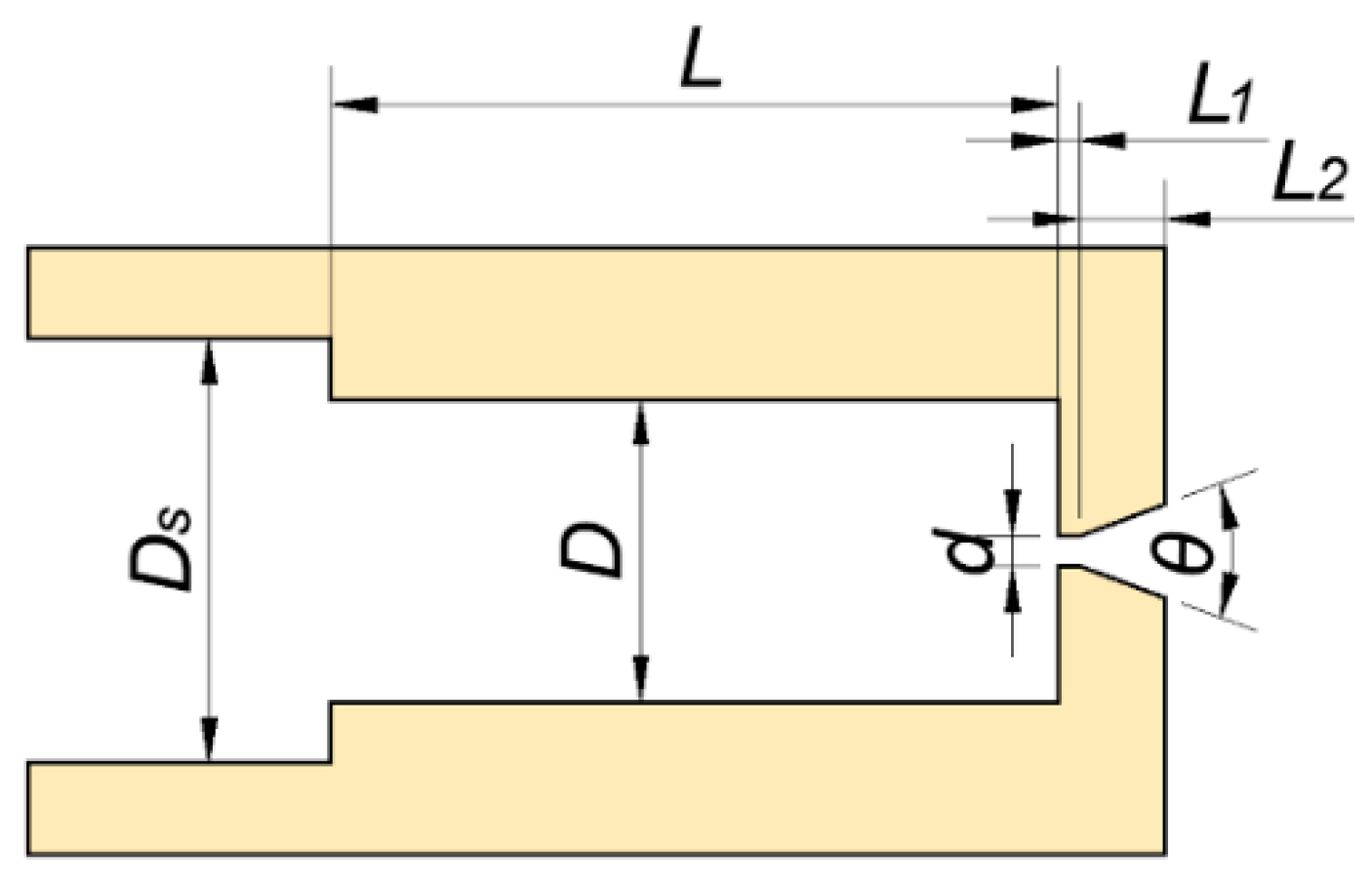
2. Experimental Setup and Methodology
2.1. Experimental Setup
2.2. Image Processing Method
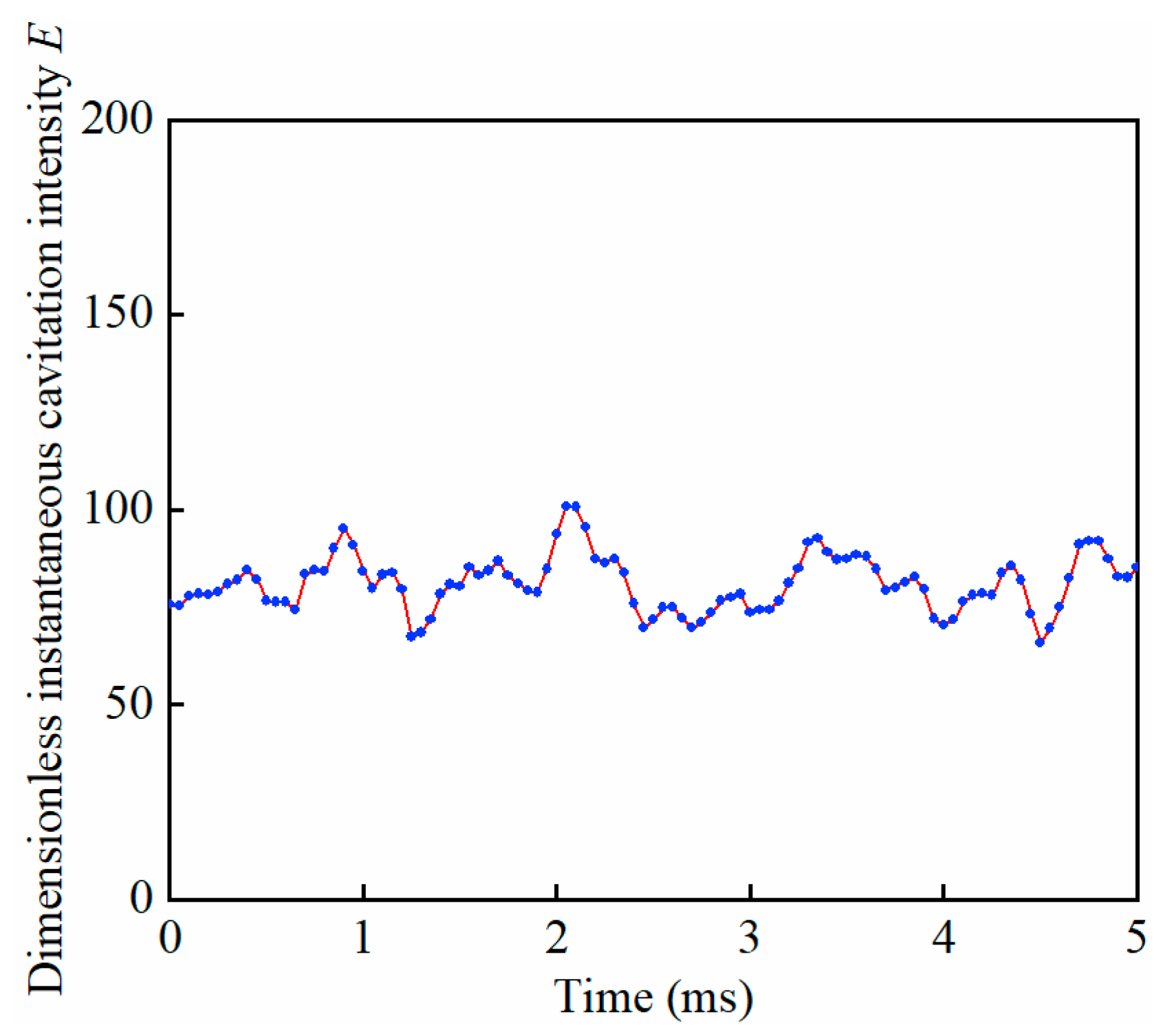
2.3. Erosion Intensity Evaluation
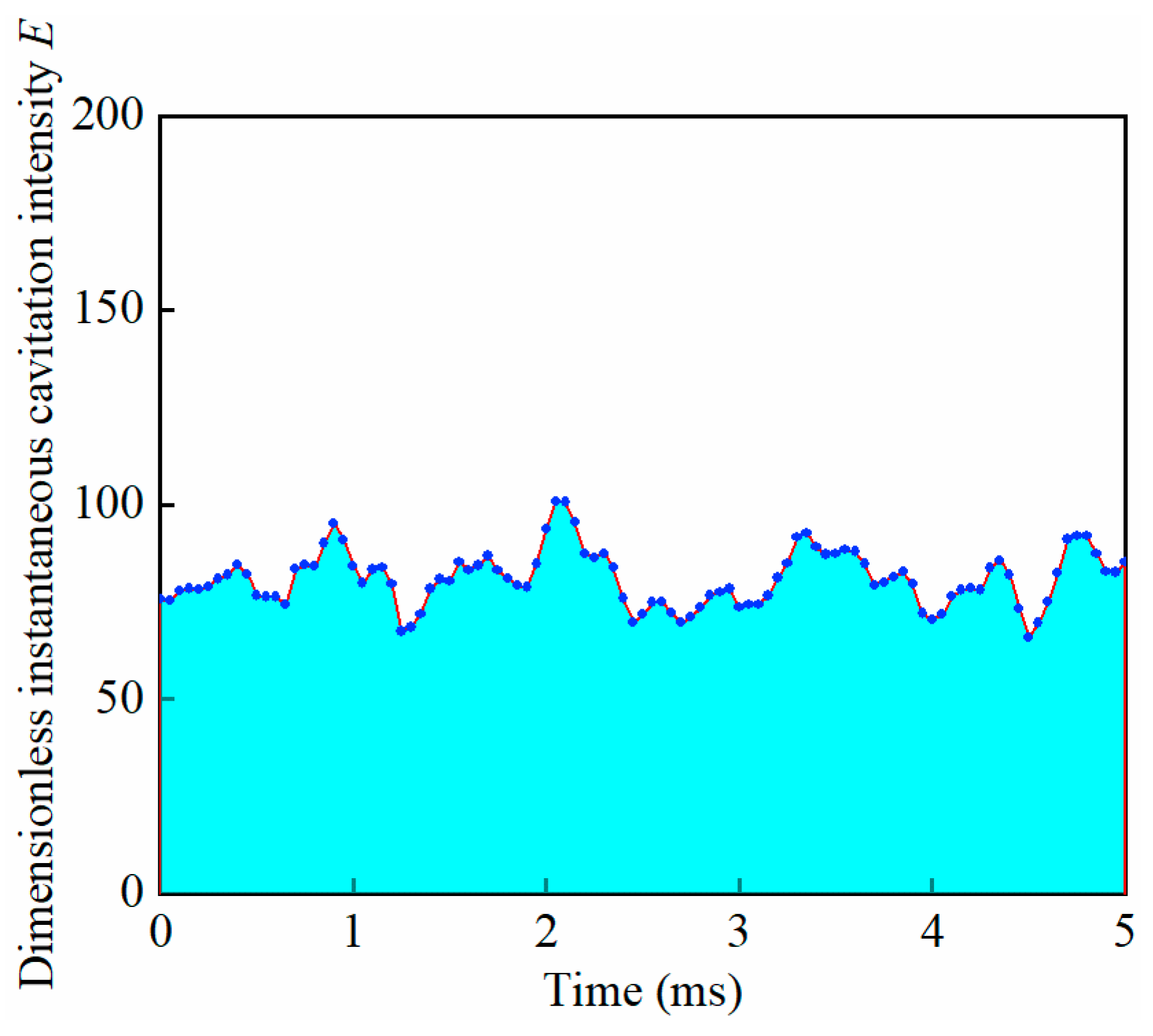
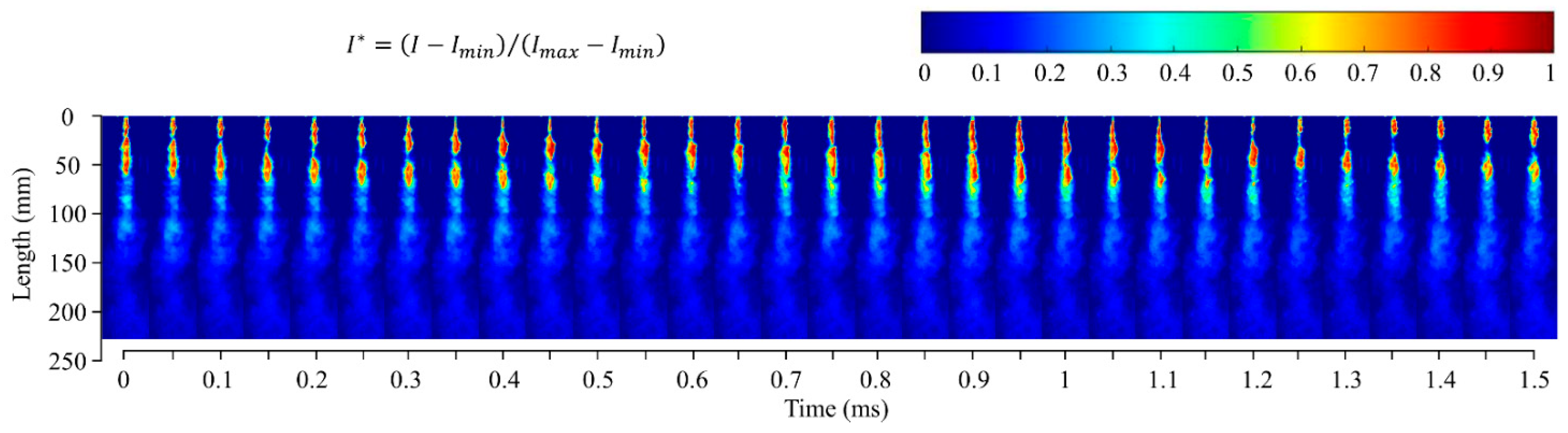
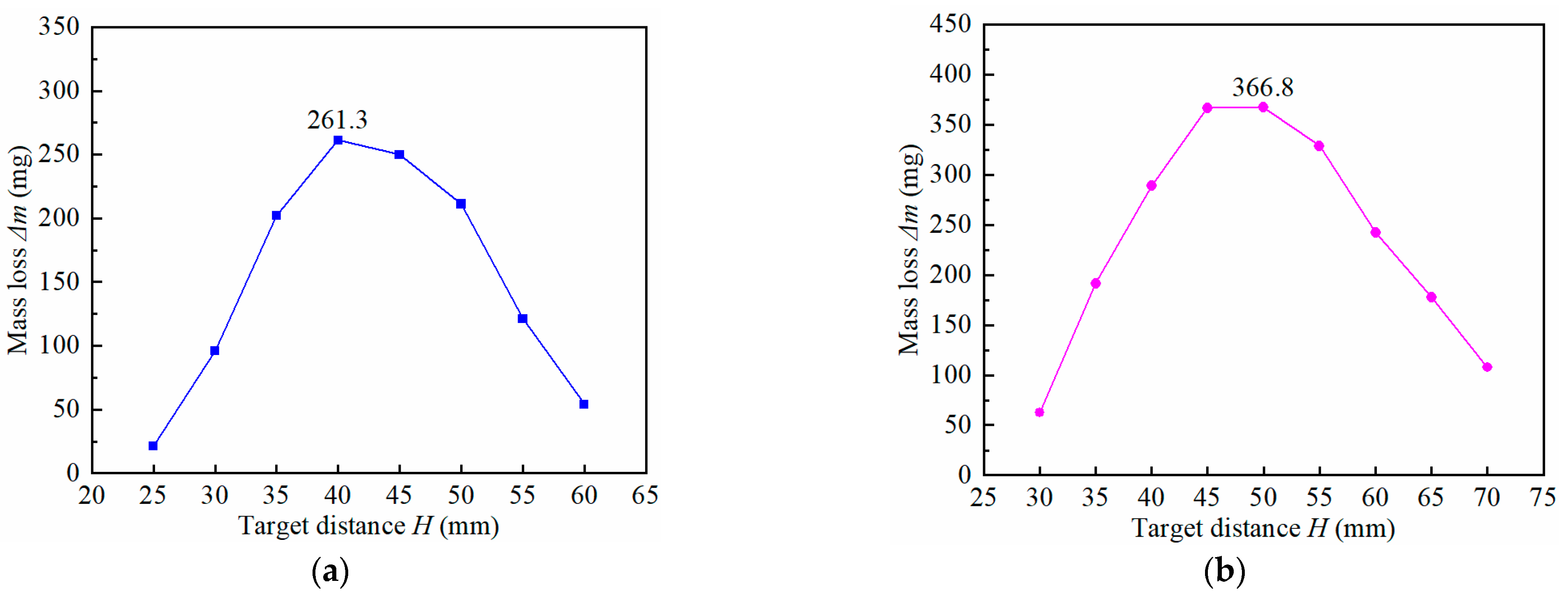
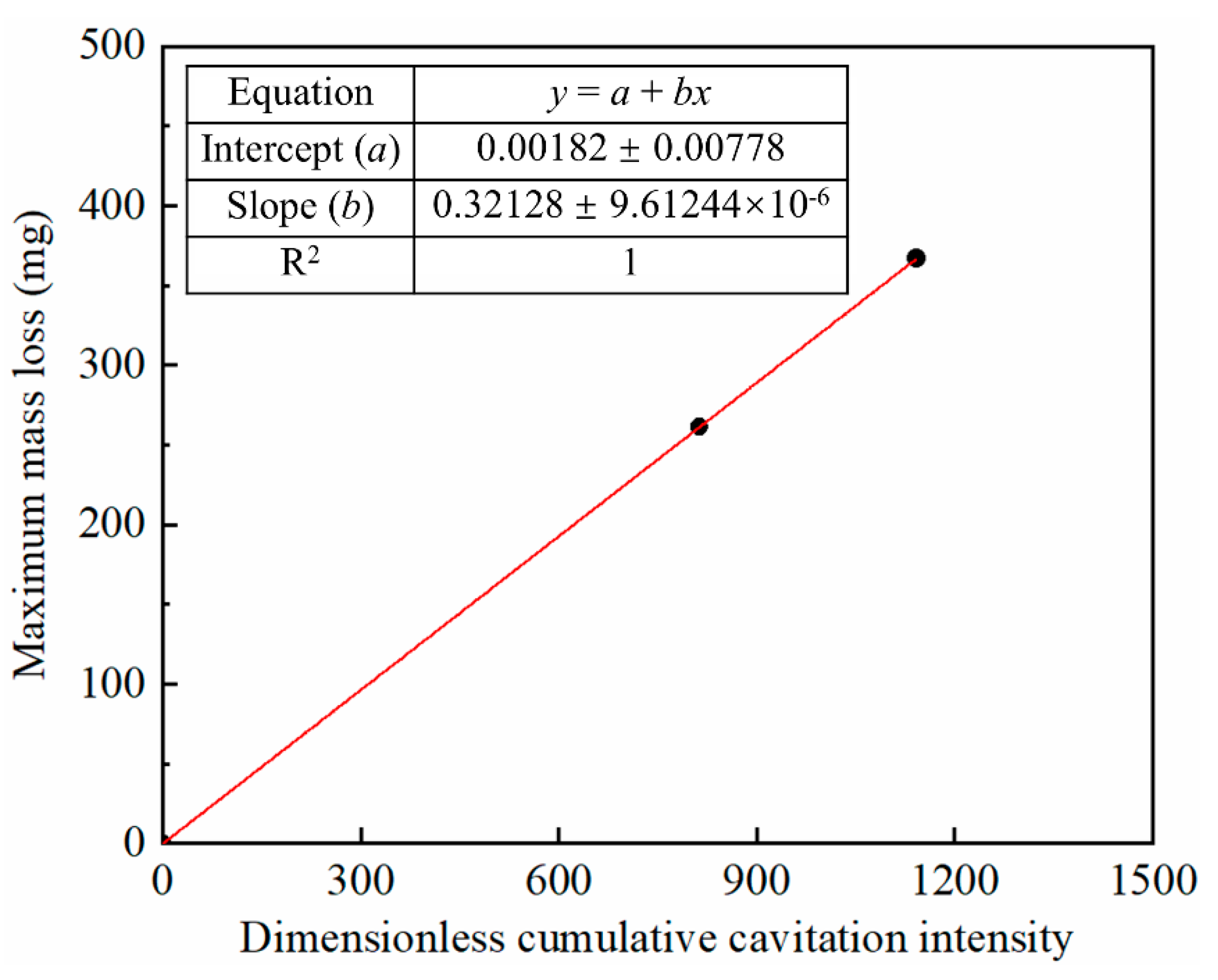
3. Results and Discussion
4. Conclusions
- (1)
- The image processing method based on the dimensionless grayscale intensity can quantitatively and accurately evaluate the performance of the submerged cavitation jet.
- (2)
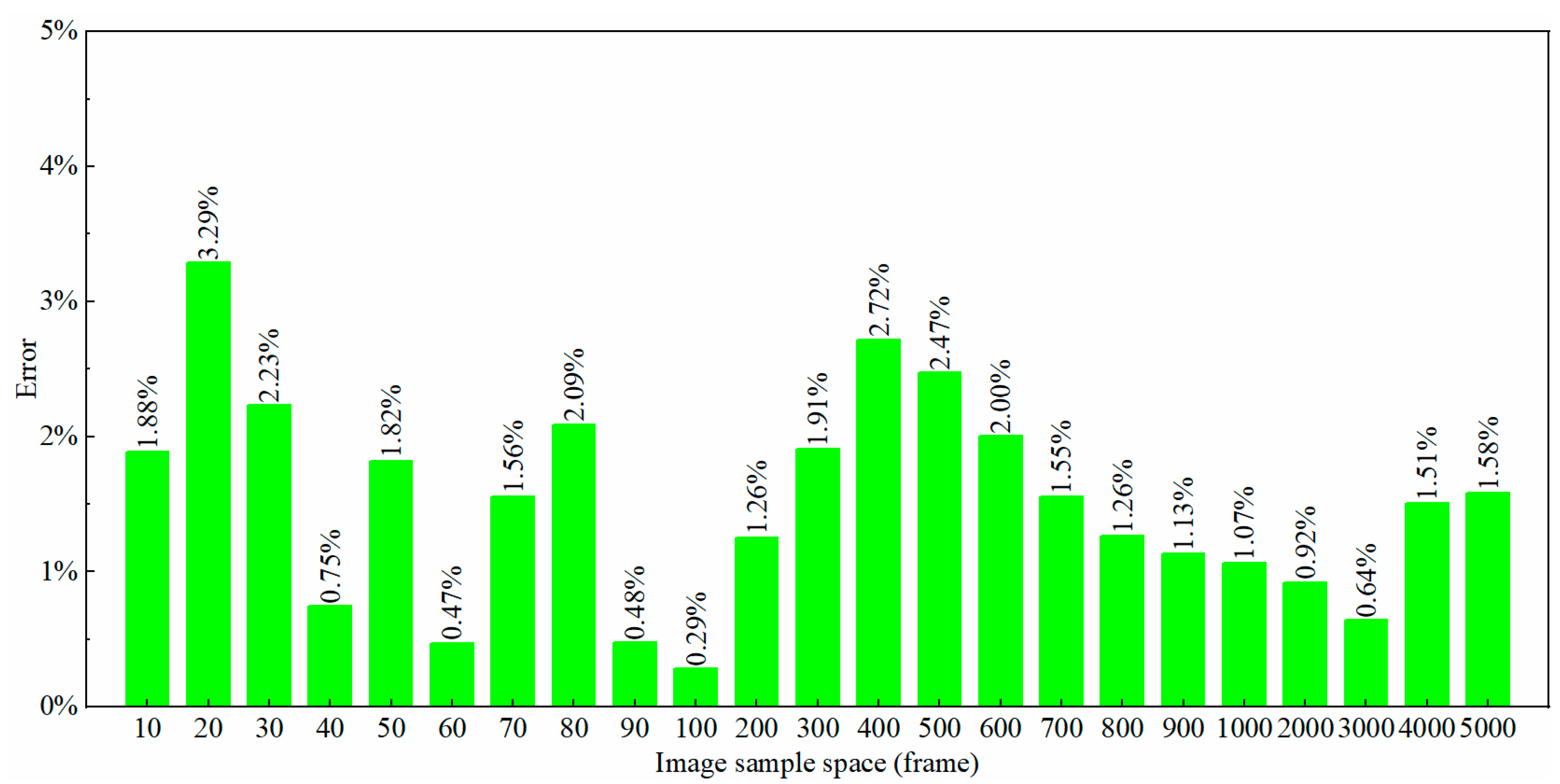
- When the sample space is 200 images and the working pressure was 20 MPa, the calculation error of the image processing method for the maximum mass loss of the sample was 1.26%.
- (3)
- For the sample space of 10–5000 images, the calculation errors of the image processing method for the maximum mass loss of samples were all within 3.29%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Song, C.; Cui, W. Review of Underwater Ship Hull Cleaning Technologies. J. Mar. Sci. Appl. 2020, 19, 415–429. [Google Scholar] [CrossRef]
- Perrin, L.; Colombet, D.; Ayela, F. Comparative study of luminescence and chemiluminescence in hydrodynamic cavitating flows and quantitative determination of hydroxyl radicals production. Ultrason. Sonochem. 2020, 70, 105277. [Google Scholar] [CrossRef] [PubMed]
- Podbevšek, D.; Colombet, D.; Ayela, F.; Ledoux, G. Localization and quantification of radical production in cavitating flows with luminol chemiluminescent reactions. Ultrason. Sonochem. 2020, 71, 105370. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Wang, X.; Xu, W.; Zhao, Y.; Zhao, G.; Zhu, H. Study on Different Parameters of the Self-Excited Oscillation Nozzle for Cavitation Effect under Multiphase Mixed Transport Conditions. J. Mar. Sci. Eng. 2021, 9, 1159. [Google Scholar] [CrossRef]
- El Hassan, M.; Bukharin, N.; Al-Kouz, W.; Zhang, J.-W.; Li, W.-F. A Review on the Erosion Mechanism in Cavitating Jets and Their Industrial Applications. Appl. Sci. 2021, 11, 3166. [Google Scholar] [CrossRef]
- Bukharin, N.; El Hassan, M.; Omelyanyuk, M.; Nobes, D. Applications of cavitating jets to radioactive scale cleaning in pipes. Energy Rep. 2020, 6, 1237–1243. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.-S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, K.; Wu, X.; Tian, S.; Shi, H.; Wang, W.; Zhang, P. An innovative experimental apparatus for the analysis of natural gas hydrate erosion process using cavitating jet. Rev. Sci. Instrum. 2020, 91, 095107. [Google Scholar] [CrossRef]
- Hutli, E.; Nedeljkovic, M.S.; Bonyár, A.; Légrády, D. Experimental study on the influence of geometrical parameters on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2017, 80, 281–292. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.; Li, G.; Wei, M. Enhancement of cavitation intensity and erosion ability of submerged cavitation jet by adding micro-particles. Ocean Eng. 2020, 209, 107516. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Ding, X.; Liu, W. Experimental study on the effects of feeding pipe diameter on the cavitation erosion performance of self-resonating cavitating waterjet. Exp. Therm. Fluid Sci. 2017, 82, 314–325. [Google Scholar] [CrossRef]
- Cai, T.; Pan, Y.; Ma, F. Effects of nozzle lip geometry on the cavitation erosion characteristics of self-excited cavitating waterjet. Exp. Therm. Fluid Sci. 2020, 117, 110137. [Google Scholar] [CrossRef]
- Hutli, E.; Petrović, P.B.; Nedeljkovic, M.; Legrady, D. Automatic Edge Detection Applied to Cavitating Flow Analysis: Cavitation Cloud Dynamics and Properties Measured through Detected Image Regions. Flow Turbul. Combust. 2021, 108, 865–893. [Google Scholar] [CrossRef]
- Soyama, H. Cavitating Jet: A Review. Appl. Sci. 2020, 10, 7280. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, H.; Xu, J.; Tang, C. Experimental investigation on noise of cavitation nozzle and its chaotic behaviour. Chin. J. Mech. Eng. 2013, 26, 758–762. [Google Scholar] [CrossRef]
- Liao, H.-L.; Zhao, S.-L.; Cao, Y.-F.; Zhang, L.; Yi, C.; Niu, J.-L.; Zhu, L.-H. Erosion characteristics and mechanism of the self-resonating cavitating jet impacting aluminum specimens under the confining pressure conditions. J. Hydrodyn. 2020, 32, 375–384. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Hu, Y.; Ding, X.; Xiang, M.; Li, D. An Experimental Study on the Jet Pressure Performance of Organ–Helmholtz (O-H), Self-Excited Oscillating Nozzles. Energies 2020, 13, 367. [Google Scholar] [CrossRef]
- Liu, C.; Liu, G.; Yan, Z. Study on Cleaning Effect of Different Water Flows on the Pulsed Cavitating Jet Nozzle. Shock Vib. 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Shafaghi, A.H.; Talabazar, F.R.; Zuvin, M.; Gevari, M.T.; Villanueva, L.G.; Ghorbani, M.; Koşar, A. On cavitation inception and cavitating flow patterns in a multi-orifice microfluidic device with a functional surface. Phys. Fluids 2021, 33, 032005. [Google Scholar] [CrossRef]
- Talabazar, F.R.; Jafarpour, M.; Zuvin, M.; Chen, H.; Gevari, M.T.; Villanueva, L.G.; Grishenkov, D.; Koşar, A.; Ghorbani, M. Design and fabrication of a vigorous “cavitation-on-a-chip” device with a multiple microchannel configuration. Microsystems Nanoeng. 2021, 7, 1–13. [Google Scholar] [CrossRef]
- Hutli, E.A.F.; Nedeljkovic, M. Frequency in Shedding/Discharging Cavitation Clouds Determined by Visualization of a Submerged Cavitating Jet. J. Fluids Eng. 2008, 130, 021304. [Google Scholar] [CrossRef]
- Wright, M.M.; Epps, B.; Dropkin, A.; Truscott, T.T. Cavitation of a submerged jet. Exp. Fluids 2013, 54, 1541. [Google Scholar] [CrossRef]
- Sato, K.; Taguchi, Y.; Hayashi, S. High Speed Observation of Periodic Cavity Behavior in a Convergent-Divergent Nozzle for Cavitating Water Jet. J. Flow Control. Meas. Vis. 2013, 01, 102–107. [Google Scholar] [CrossRef]
- Hutli, E.; Nedeljkovic, M.; Bonyár, A. Dynamic behaviour of cavitation clouds: Visualization and statistical analysis. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 281. [Google Scholar] [CrossRef]
- Wu, Q.; Wei, W.; Deng, B.; Jiang, P.; Li, D.; Zhang, M.; Fang, Z. Dynamic characteristics of the cavitation clouds of submerged Helmholtz self-sustained oscillation jets from high-speed photography. J. Mech. Sci. Technol. 2019, 33, 621–630. [Google Scholar] [CrossRef]
- Hayashi, S.; Sato, K. Unsteady Behavior of Cavitating Waterjet in an Axisymmetric Convergent-Divergent Nozzle: High Speed Observation and Image Analysis Based on Frame Difference Method. J. Flow Control. Meas. Vis. 2014, 02, 94–104. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Shi, W.; Wang, C.; Zhang, W. Experimental Study on Submerged High-Pressure Jet and Parameter Optimization for Cavitation Peening. Mechanika 2020, 26, 346–353. [Google Scholar] [CrossRef]
- Sekyi-Ansah, J.; Wang, Y.; Tan, Z.; Zhu, J.; Li, F. The Dynamic Evolution of Cavitation Vacuolar Cloud with High-Speed Camera. Arab. J. Sci. Eng. 2020, 45, 4907–4919. [Google Scholar] [CrossRef]
- Dong, J.; Li, S.; Meng, R.; Zhong, X.; Pan, X. Research on Cavitation Characteristics of Two-Throat Nozzle Submerged Jet. Appl. Sci. 2022, 12, 536. [Google Scholar] [CrossRef]
- Fujisawa, N.; Fujita, Y.; Yanagisawa, K.; Fujisawa, K.; Yamagata, T. Simultaneous observation of cavitation collapse and shock wave formation in cavitating jet. Exp. Therm. Fluid Sci. 2018, 94, 159–167. [Google Scholar] [CrossRef]
- Watanabe, R.; Yanagisawa, K.; Yamagata, T.; Fujisawa, N. Simultaneous shadowgraph imaging and acceleration pulse measurement of cavitating jet. Wear 2016, 358–359, 72–79. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.; Li, G. Joint experiments of cavitation jet: High-speed visualization and erosion test. Ocean Eng. 2018, 149, 1–13. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.-C.; Li, G.-S. Determination of the shedding frequency of cavitation cloud in a submerged cavitation jet based on high-speed photography images. J. Hydrodyn. 2021, 33, 127–139. [Google Scholar] [CrossRef]
- Zhong, X.; Dong, J.; Liu, M.; Meng, R.; Li, S.; Pan, X. Experimental study on ship fouling cleaning by ultrasonic-enhanced submerged cavitation jet: A preliminary study. Ocean Eng. 2022, 258. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Shi, W.; Zhou, L.; Zhang, W. Experimental Study on the Unsteady Characteristics and the Impact Performance of a High-Pressure Submerged Cavitation Jet. Shock Vib. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
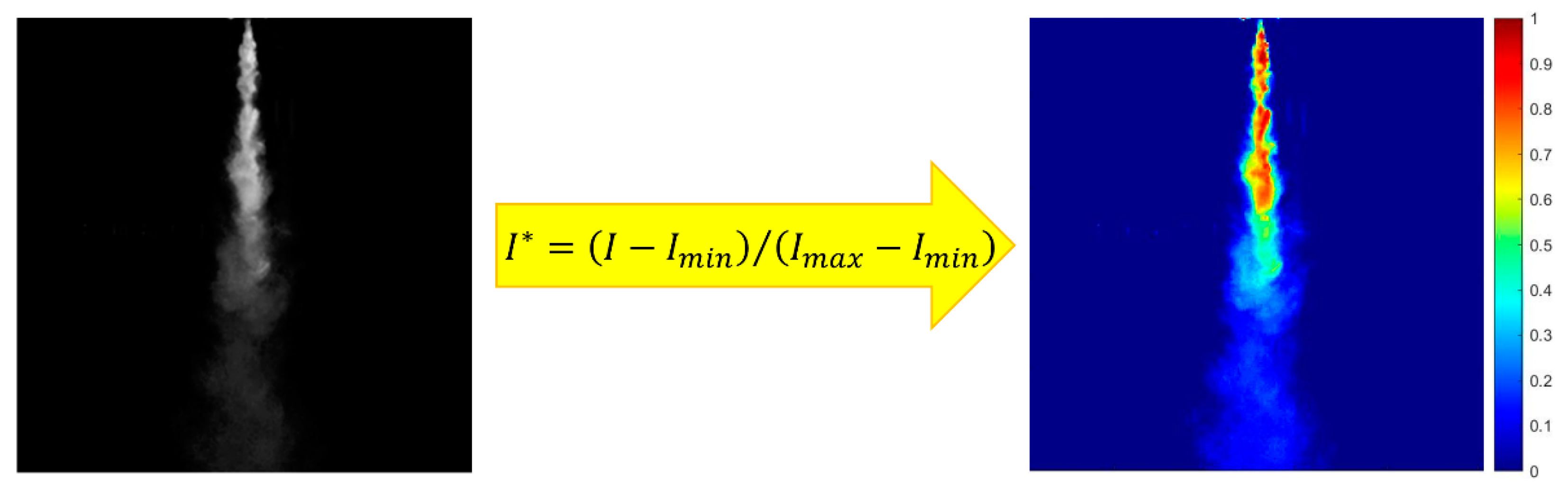


| Parameter Description | Symbol | Value | Units |
|---|---|---|---|
| Diameter of nozzle inlet | Ds | 14 | mm |
| Diameter of resonant cavity | D | 10 | mm |
| Diameter of minimum throat diameter | d | 1 | mm |
| Length of resonant cavity | L | 24 | mm |
| Length of minimum throat | L1 | 0.7 | mm |
| Length of nozzle exit lip | L2 | 2.8 | mm |
| Nozzle exit expansion angle | θ | 40 | ° |
| Al | Fe | Si | Cu | Zn | V | Mn | Mg | Ti |
|---|---|---|---|---|---|---|---|---|
| 99.6 | ≤0.35 | ≤0.25 | ≤0.05 | ≤0.05 | ≤0.05 | ≤0.03 | ≤0.03 | ≤0.03 |
| Density /kg∙m3 | Tensile Strength /MPa | Elasticity Modulus /GPa | Offset Yield Strength /MPa | Vickers Hardness HV0.2 | Surface Roughness /μm |
|---|---|---|---|---|---|
| 2710 | 80 | 71 | 35 | 31 | 1 |
| Working Pressure /MPa | Image Processing Result /mg | Experimental Result /mg | Error |
|---|---|---|---|
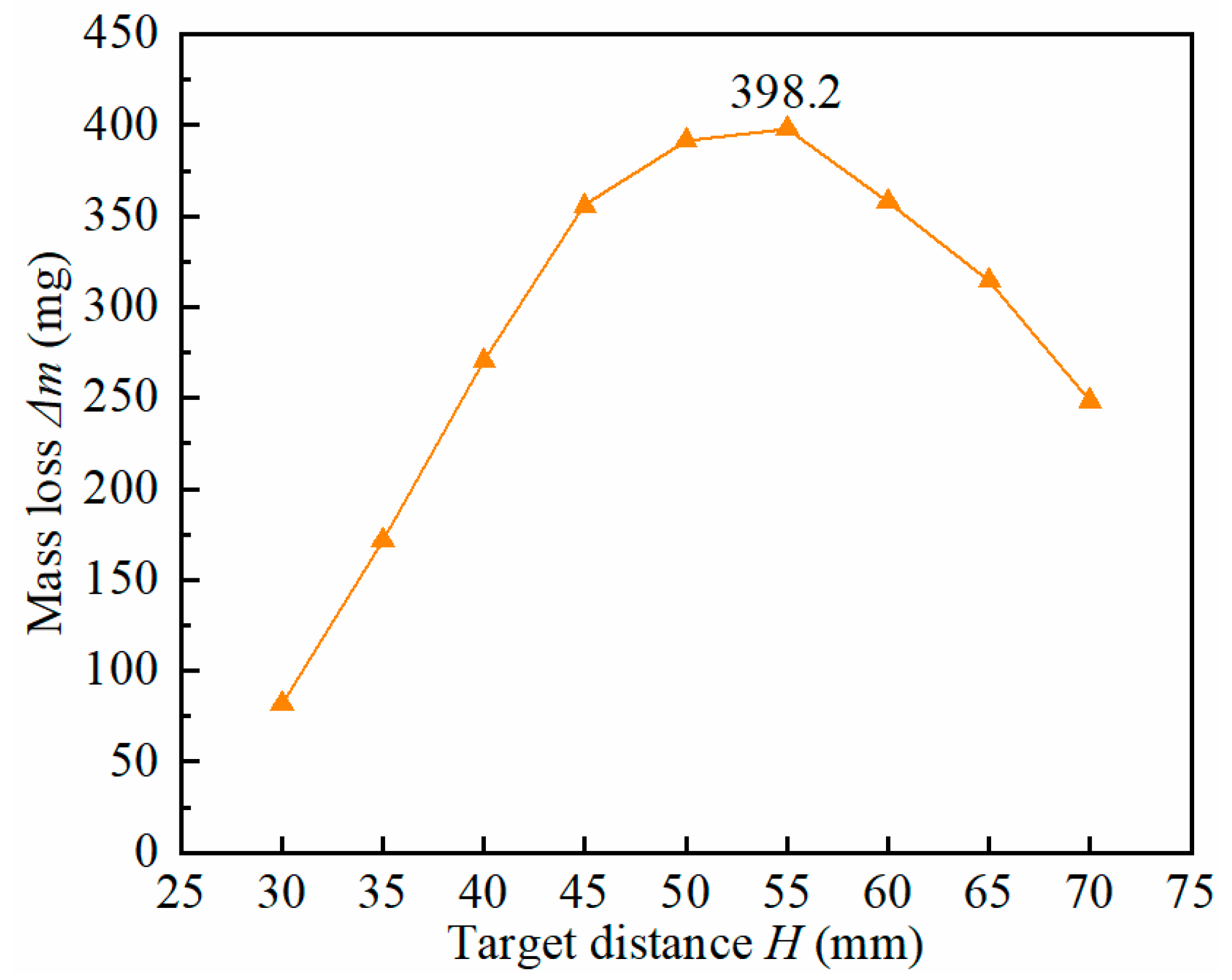
| 20 | 403.2 | 398.2 | 1.26% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, X.; Dong, J.; Meng, R.; Liu, M.; Pan, X. Quantitative Evaluation of Submerged Cavitation Jet Performance Based on Image Processing Method. J. Mar. Sci. Eng. 2022, 10, 1336. https://doi.org/10.3390/jmse10101336
Zhong X, Dong J, Meng R, Liu M, Pan X. Quantitative Evaluation of Submerged Cavitation Jet Performance Based on Image Processing Method. Journal of Marine Science and Engineering. 2022; 10(10):1336. https://doi.org/10.3390/jmse10101336
Chicago/Turabian StyleZhong, Xiao, Jingming Dong, Rongxuan Meng, Mushan Liu, and Xinxiang Pan. 2022. "Quantitative Evaluation of Submerged Cavitation Jet Performance Based on Image Processing Method" Journal of Marine Science and Engineering 10, no. 10: 1336. https://doi.org/10.3390/jmse10101336
APA StyleZhong, X., Dong, J., Meng, R., Liu, M., & Pan, X. (2022). Quantitative Evaluation of Submerged Cavitation Jet Performance Based on Image Processing Method. Journal of Marine Science and Engineering, 10(10), 1336. https://doi.org/10.3390/jmse10101336






