Experimental and Numerical Studies on Fluid-Structure Interaction for Underwater Drop of a Stone-Breaking Crusher
Abstract
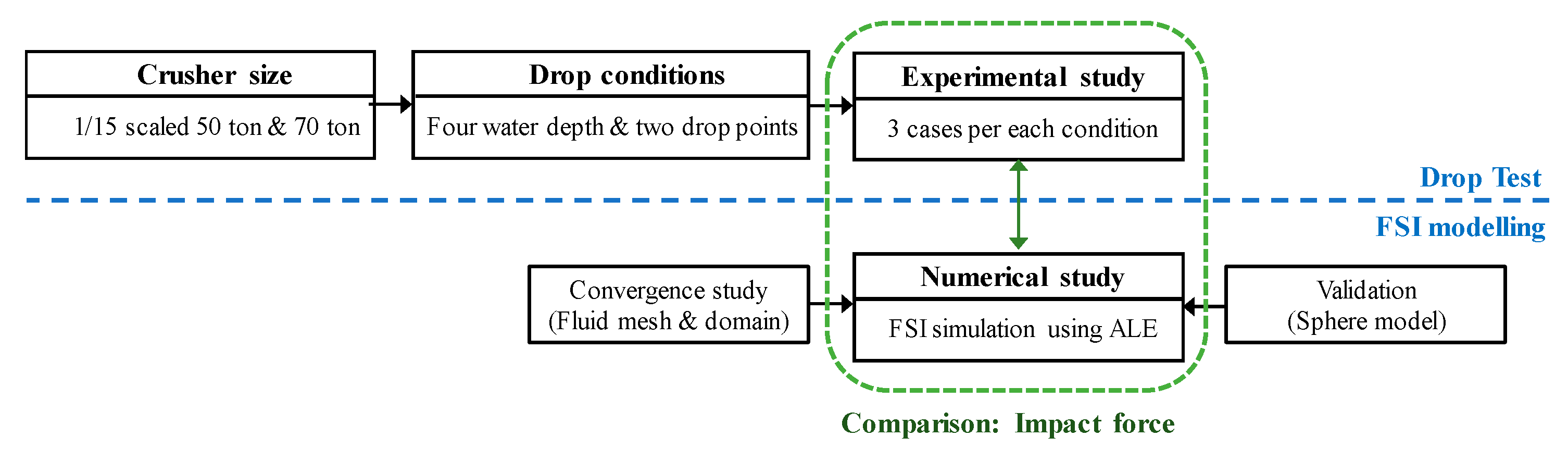
:1. Introduction
2. Validation for FSI Modelling
2.1. Equation of State
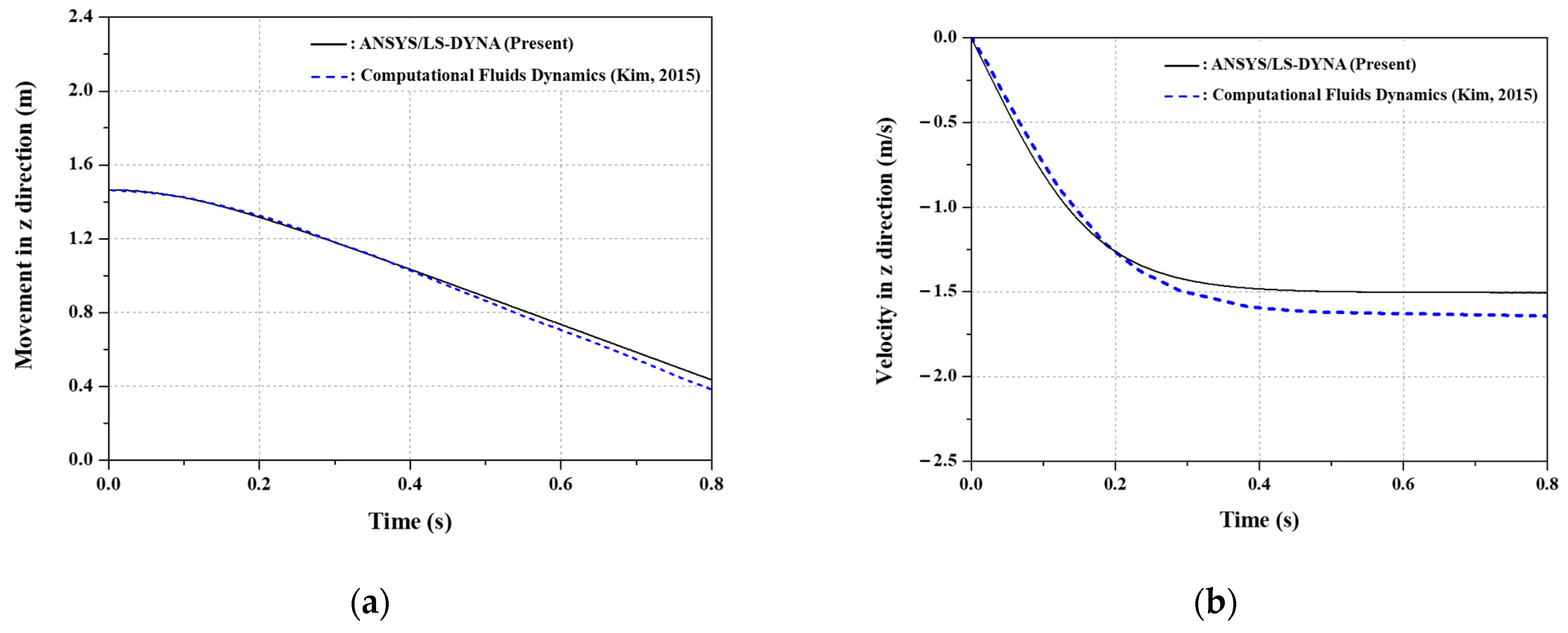
2.2. Comparison with CFD Model
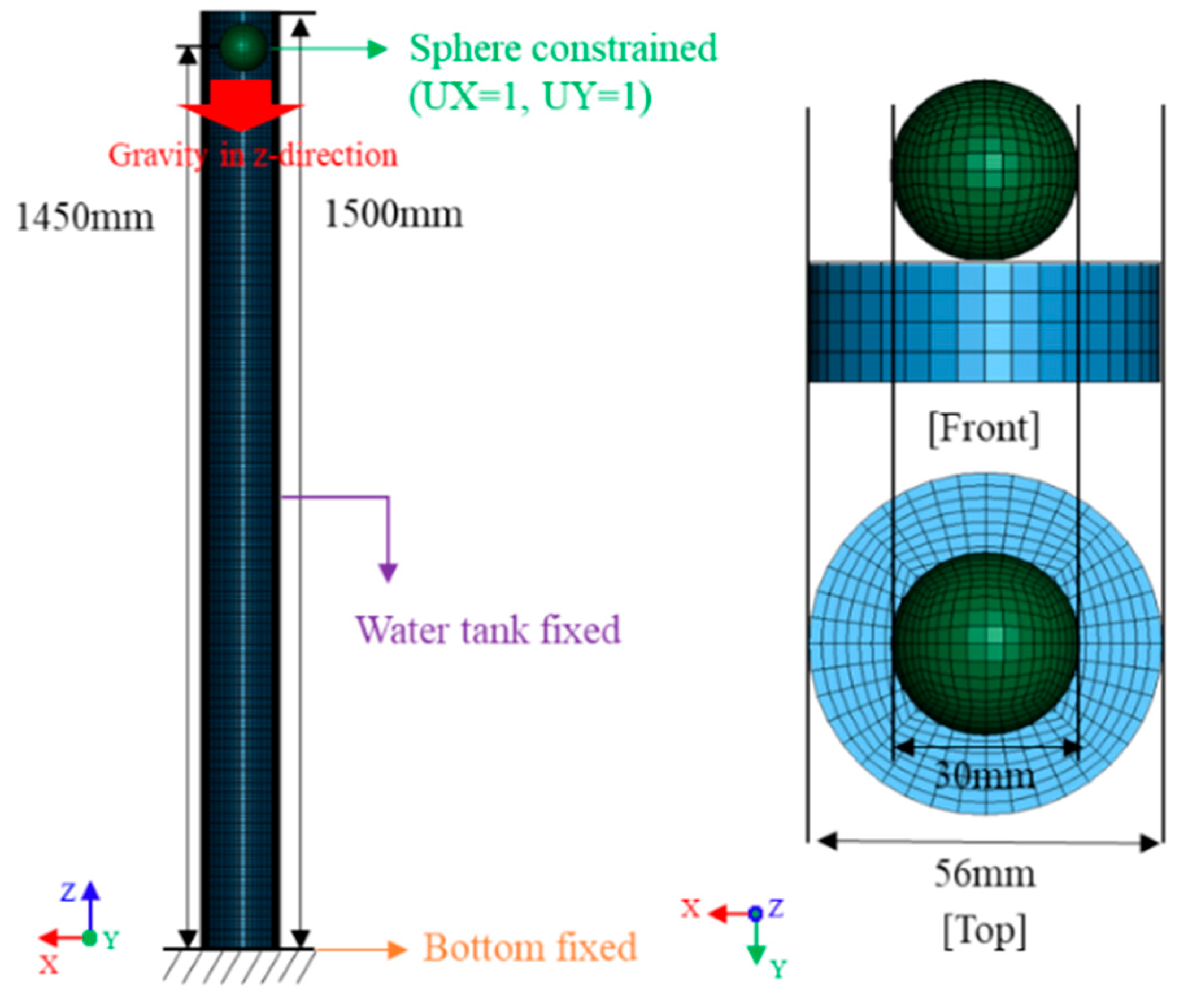
2.3. Comparison with Experimental Model
3. Experiment for the Underwater Drop of a Crusher
3.1. Stone-Breaking Crusher
3.2. Experimental Conditions
3.3. Test Results
4. FSI Analysis for the Underwater Drop of a Crusher
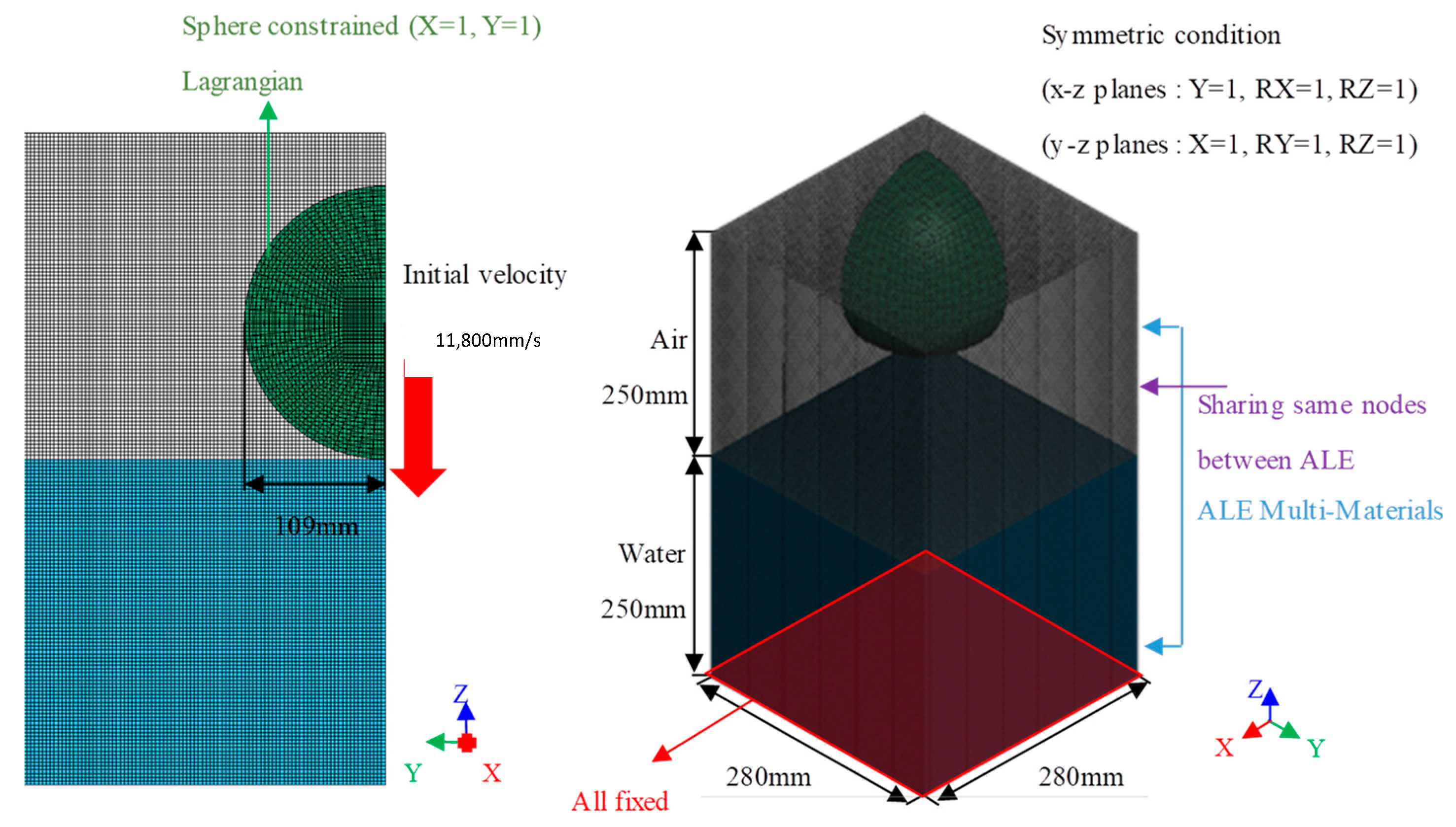
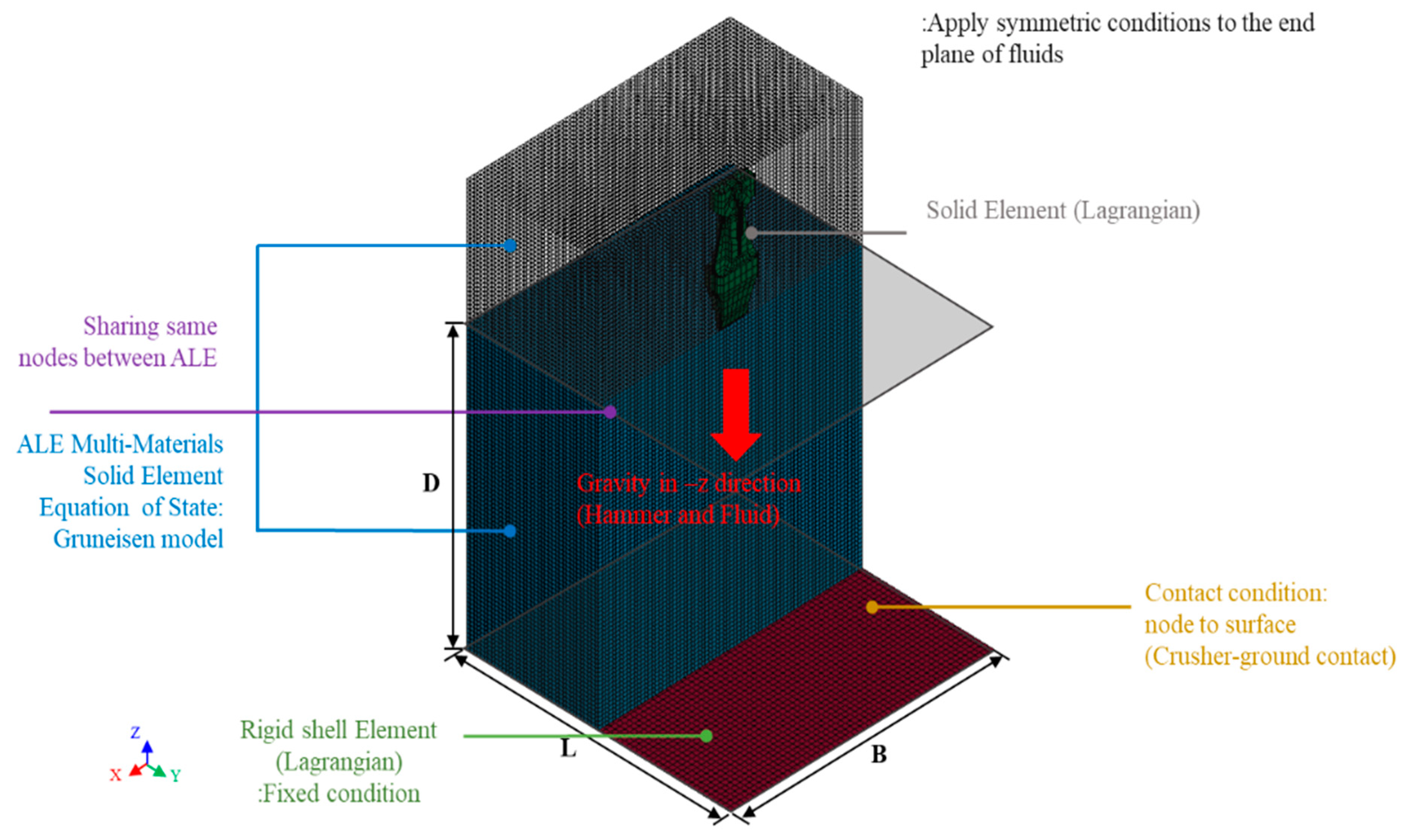
4.1. Model Description and Analysis Settings
4.2. Fluid Mesh Determination
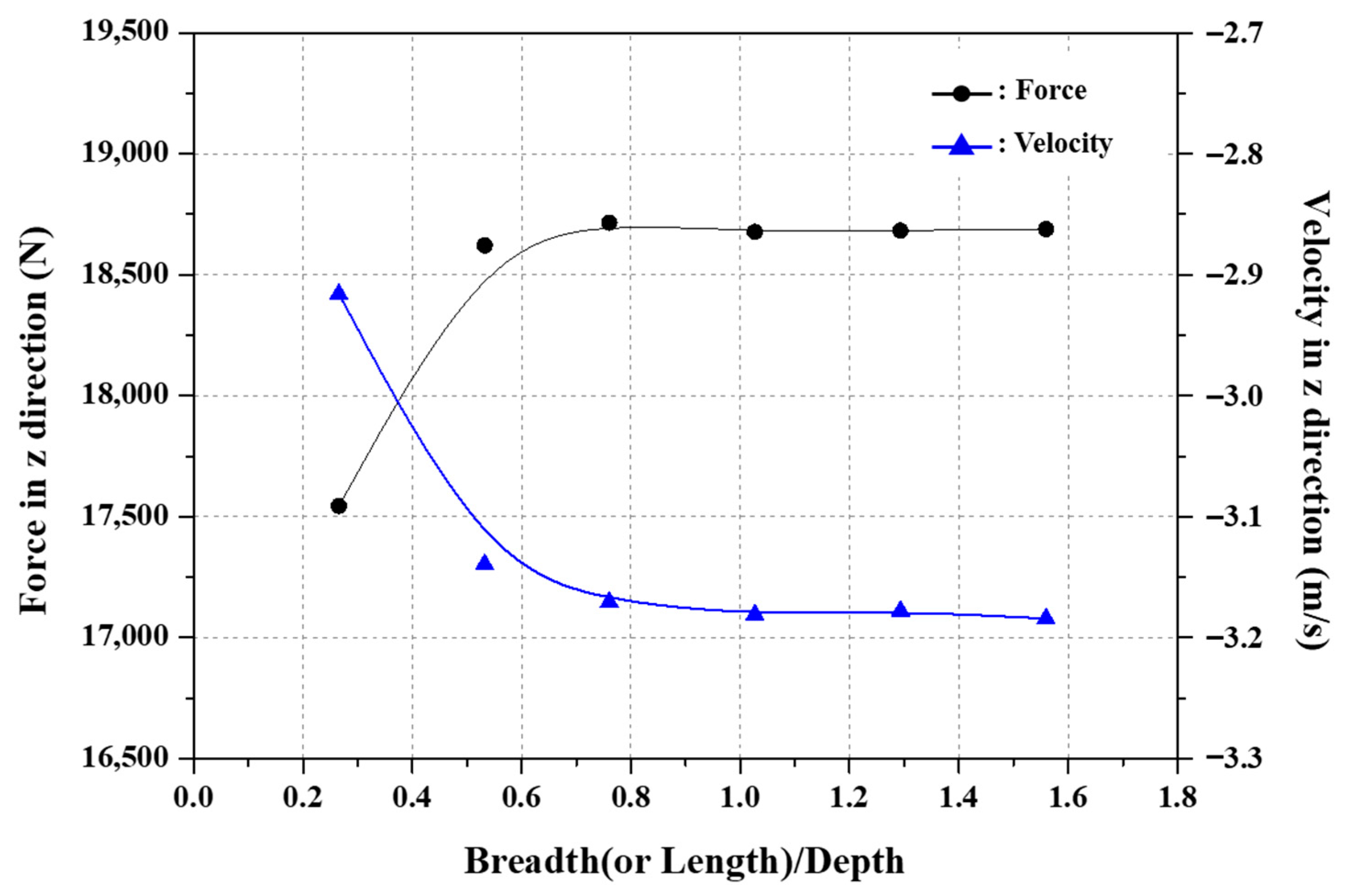
4.3. Fluid Domain Determination
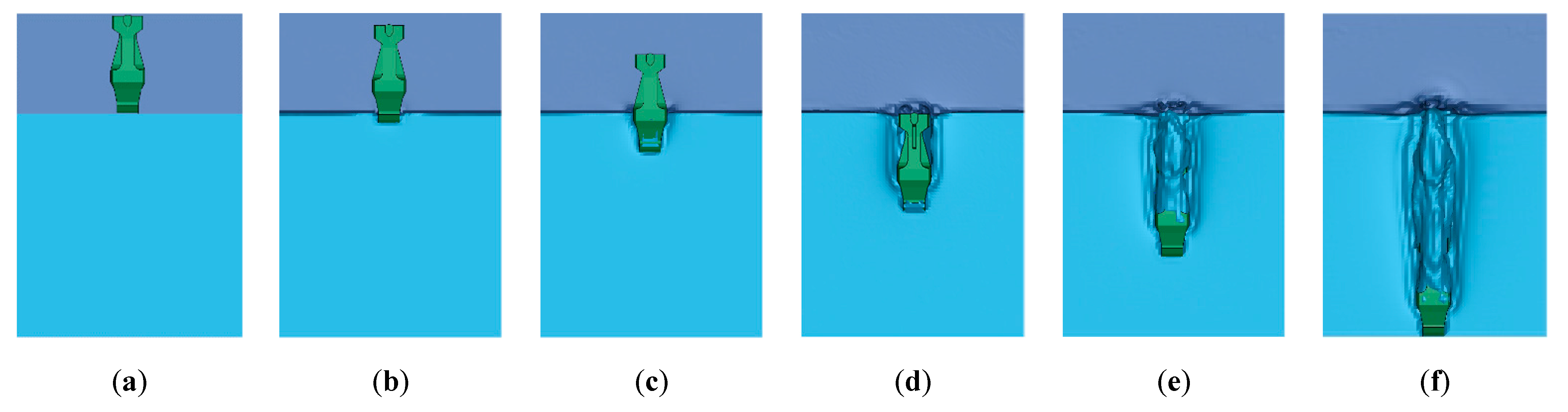
4.4. Results of Numerical Analysis
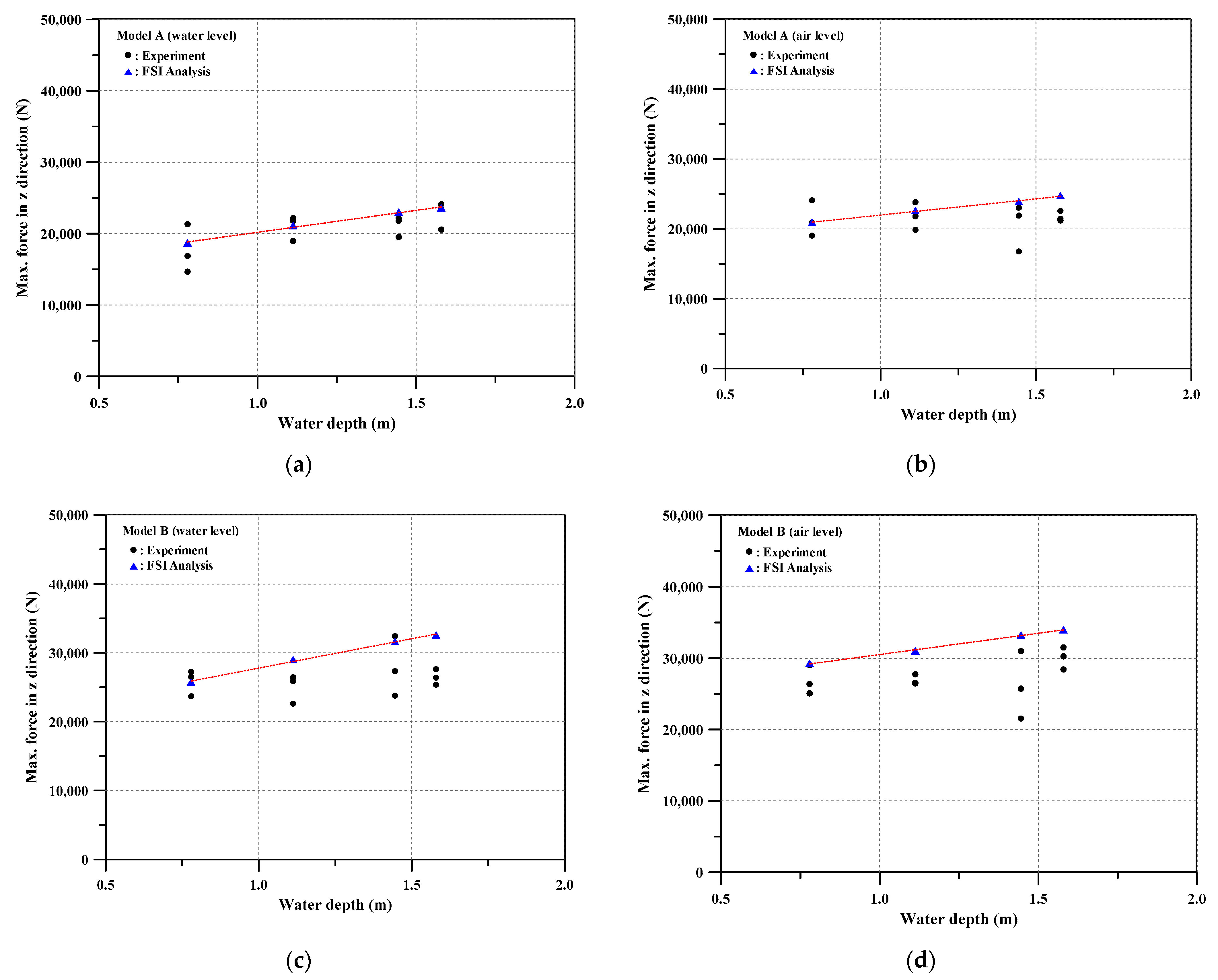
4.5. Comparison between Experimental and Numerical Results
5. Conclusions
- Experimental tests for two different scaled-down models and multiple water depths with two different dropping levels were conducted to confirm that the impact loads linearly increase with increase in mass. In addition, this will be a good reference for validating numerical methods on dropping object into the water.
- Numerical techniques using FSI analysis for a free-falling crusher were established by applying the ALE element and Grüneisen EoS to the fluid models. To increase accuracy, two validation methods comprising CFD and experiment models for a rigid sphere were performed. Furthermore, modeling size and extent were determined by multiple computations.
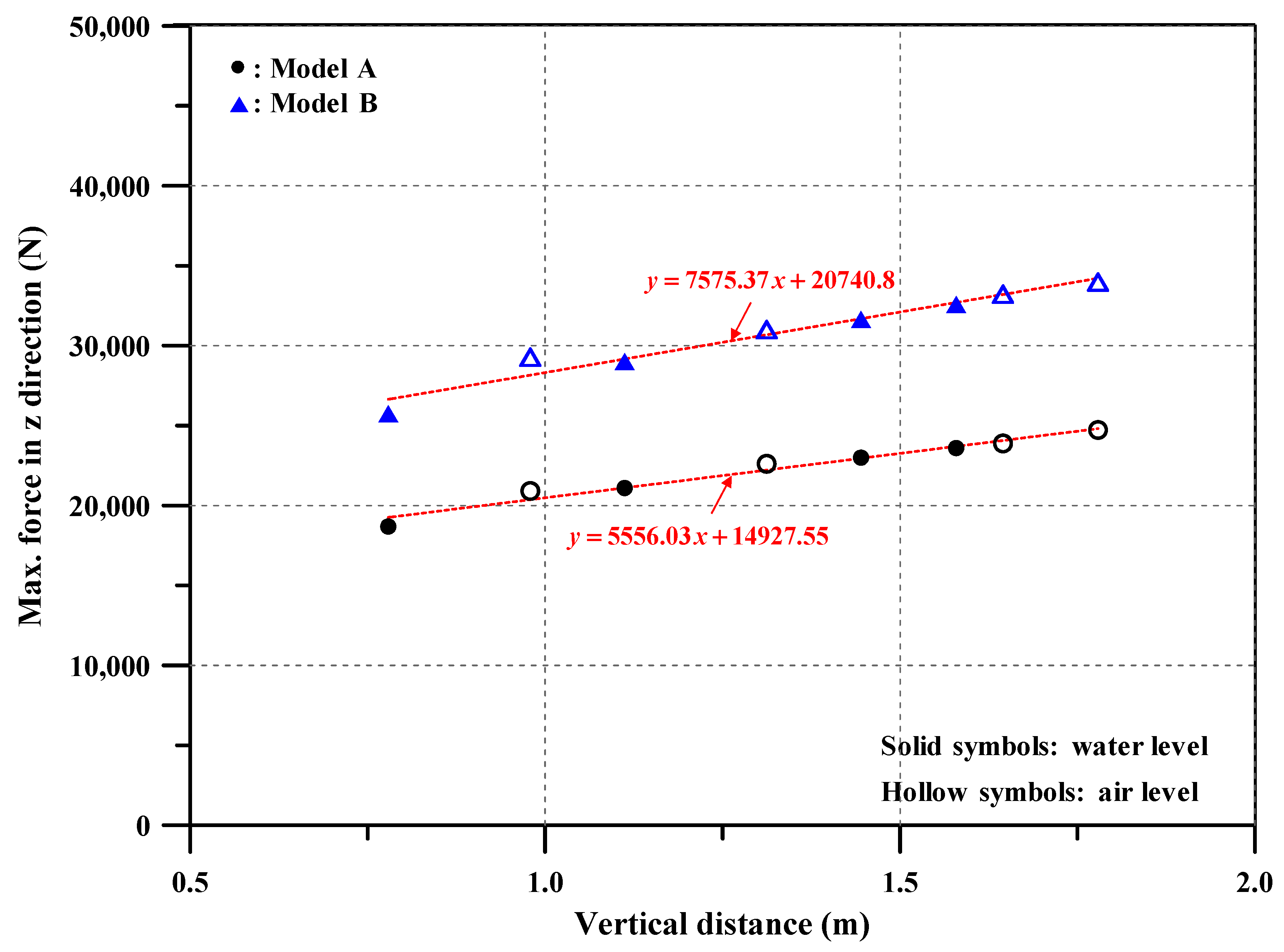
- Model size and water depth are the most influential factors to increase impact force on the ground. The impact force increases as water depth increases. Moreover, the air-level drop shows typically greater impact force than that of a water-level drop. Higher impact force was measured for model B than A; however, there is no specific ratio between them. Therefore, there is no linear relationship based on model weight or, in other words, there is no dynamic similarity of impact force between the model and prototype.
- Similar trends were observed between numerical and experimental data. Certain cases demonstrate good agreement while others have >20% error because there is large variance in experimental data. In particular, there is a higher CoV for increase in water depths. Moreover, certain cases do not show constant results because of angular rotation between the crusher and ground when the crusher hits the ground.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALE | Arbitrary Lagrangian-Eulerian |
| COV | Coefficient of Variation |
| CFD | Computational Fluid Dynamics |
| DoF | Degree of Freedom |
| FE | Finite Element |
| MSL | Mean Sea Level |
| RIMS | Research Institute of Medium and Small Shipbuilding |
| ALLW | Approximate Lowest Low Water |
| CEL | Coupled Eulerian-Lagrangian |
| DL | Datum Level |
| EoS | Equation of State |
| FSI | Fluid-Structure Interaction |
| RANS | Reynolds-averaged Navier-Stokes |
| SPH | Smoothed Particle Hydrodynamics |
References
- Bray, R.N.; Richard, N.; Bates, A.D.; Land, J.M. Dredging: A Handbook for Engineers; Arnold: London, UK, 1997. [Google Scholar]
- Keevin, T.M.; Hempen, G.L. The Environmental Effects of Underwater Explosions with Methods to Mitigate Impacts; U.S. Army Corps of Engineers: St. Louis, MO, USA, 1997.
- Tripathy, G.R.; Shirke, R.R. Underwater drilling and blasting for hard rock dredging in indian ports—A case study. Aquat. Procedia 2015, 4, 248–255. [Google Scholar] [CrossRef]
- Nikolov, S.A. performance model for impact crushers. Miner. Eng. 2002, 15, 715–721. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D.; Cummins, S.; Delaney, G.W. Analysis of cone crusher performance with changes in material properties and operating conditions using DEM. Miner. Eng. 2017, 100, 49–70. [Google Scholar] [CrossRef]
- Kim, S.J.; Kõrgersaara, M.; Ahmadi, N.; Taimuri, G.; Kujala, P.; Hirdaris, S. The influence of fluid structure interaction modelling on the dynamic response of ships subject to collision and grounding. Mar. Struct. 2021, 75, 102875. [Google Scholar] [CrossRef]
- Lee, S.; Zhao, T.; Nam, J. Structural safety assessment of ship collision and grounding using FSI analysis technique. In Proceedings of the 6th International Conference on Collision and Grounding of Ships and Offshore Structures, ICCGS, Trondheim, Norway, 17–19 June 2013; Jørgan Amdahl. CRC Press/Balkema: Boca Raton, FL, USA, 2013; pp. 197–204. [Google Scholar]
- Song, M.; Ma, J.; Huang, Y. Fluid-structure interaction analysis of ship-ship collisions. Mar. Struct. 2017, 55, 121–136. [Google Scholar] [CrossRef]
- Kim, J.Y. A Study on Unsteady Drag Coefficient of Free Falling Structure in the Water. Ph.D. Thesis, Chungnam National University, Daejeon, Korea, 2015. [Google Scholar]
- Jang, G.H.; Kim, J.H.; Song, C.Y. Comparison of Underwater Drop Characteristics for Hazard Apparatuses on Subsea Cable Using Fluid-Structure Interaction Analysis. J. Ocean. Eng. Technol. 2018, 32, 324–332. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.Y.; Yoon, K.H.; Oh, S.H.; Ko, S.H. CFD Analysis to Estimate Drop Time and Impact Velocity of a Control Rod Assembly in the Sodium Cooled Faster Reactor. KSFM J. Fluid Mach. 2015, 18, 5–11. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.; Shen, C.; Zhen, C.; Tang, H.; Wang, T. Parametric Study on the Free-Fall Water Entry of a Sphere by Using the RANS Method. J. Mar. Sci. Eng. 2019, 5, 122. [Google Scholar] [CrossRef] [Green Version]
- Troesch, A.W.; Kang, C. Hydrodynamic impact loads on three-dimensional bodies. In Proceedings of the Symposium on Naval Hydrodynamics, Berkeley, CA, USA, 13–16 July 1986. [Google Scholar]
- Toso, N.R.S. Contribution to the Modelling and Simulation of Aircraft Structures Impacting on Water. Ph.D. Thesis, University Stuttgart, Stuttgart, Germany, 2009. [Google Scholar]
- Abelev, A.V.; Valent, P.J.; Holland, K.T. Behavior of a large cylinder in free-fall through water. IEEE J. Ocean. Eng. 2007, 32, 10–20. [Google Scholar] [CrossRef]
- Fallah-Kharmiani, S.; Khozeymeh-Nezhad, H.; Niazmand, H. Numerical study of free-fall cylinder water entry using an efficient three-phase lattice Boltzmann method with automatic interface capturing capability. Ocean. Eng. 2021, 235, 109328. [Google Scholar] [CrossRef]
- ANSYS/LS-DYNA. In ANSYS/LS-DYNA 2020 R1; ANSYS Inc: Canonsburg, PA, USA, 2020.
- Olovsson, L.; Souli, M.; Do, I. LS-DYNA-ALE capabilities (Arbitrary-Lagrangian-Eulerian) Fluid-Structure Interaction Modeling. Available online: https://ftp.lstc.com/anonymous/outgoing/jday/aletutorial-278p.pdf (accessed on 8 November 2021).
- LS-DYNA. In LS-DYNA Keywords User’s Manual, 12th ed.; Livermore Software Technology Corporation: Livermore, CA, USA, 2020.
- Khazraiyan, N.; Gerami, N.D.; Damircheli, M. Numerical Simulation of Fluid-Structure Interaction and its Application in Impact of Low-Velocity Projectiles with Water Surface. ADMT J. 2015, 8, 81–90. [Google Scholar]
- Bisagni, C.; Pigazzini, M.S. Modelling strategies for numerical simulation of aircraft ditching. Int. J. Crashworthiness 2018, 23, 377–394. [Google Scholar] [CrossRef] [Green Version]
- Benson, D.J. An efficient, accurate, simple ALE method for nonlinear finite element programs. Comput. Methods Appl. Mech. Eng. 1989, 72, 305–350. [Google Scholar] [CrossRef]
- Truong, D.D.; Jang, B.S.; Ju, H.B.; Han, S.W. Prediction of slamming pressure considering fluid-structure interaction. Part II: Derivation of empirical formulations. Mar. Struct. 2021, 75, 102700. [Google Scholar] [CrossRef]
- Souli, M.; Ouahsine, A.; Lewin, L. ALE formulation for Fluid-Structure interaction problems. Comput. Methods Appl. Mech. Eng. 2000, 190, 659–675. [Google Scholar] [CrossRef]
- Jang, I.H. Sloshing Response Analysis of LNG Carrier Tank Using Fluid-Structure Interaction Analysis Technique of LS-DYNA3D. Master’s Thesis, Korea Maritime and Ocean University, Busan, Korea, 2007. [Google Scholar]
- Hypermesh. HyperWorks14.0 User’s Guide; Altair: Troy, MI, USA, 2020. [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; Mcgraw-Hill College: New York, NY, USA, 2009. [Google Scholar]






| References | Object | Method | Result | Remark | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | CFD | FSI | Dis. | Vel. | Acc. | Pres. | Force | |||
| [9] | Sphere | o | o | o | ||||||
| [10] | Sphere Anchor, Rocket pile | o | o | o | o | CEL method | ||||
| [11] | Control rod assembly | o | o | o | ||||||
| [12] | Sphere | o | o | o | RANS model | |||||
| [13] | Sphere | o | ||||||||
| [14] | Aircraft Structure | o | o | o | o | o | o | SPH model | ||
| [15] | ||||||||||
| [16] | ||||||||||
| Present study | Crusher | o | o | o | ALE method | |||||
| Material | C (m/s) | ||||||
|---|---|---|---|---|---|---|---|
| Air | 343.7 | 0 | 0 | 0 | 1.4 | 0 | 0 |
| Water | 1647 | 1.921 | −0.096 | 0 | 0.35 | 0 | 0 |
| Model | Mass (kg) | Volume (m3) | Remark |
|---|---|---|---|
| A | 14.81 | 0.001628 | 1/15 scale down of 50 ton |
| B | 20.74 | 0.002876 | 1/15 scale down of 70 ton |
| Model | Dimension (mm) | |||||
|---|---|---|---|---|---|---|
| a | b | c | d | e | f | |
| A | 1330 | 2100 | 2100 | 2670 | 3405 | R75.00 |
| B | 1609 | 2541 | 2541 | 3230 | 4120 | R90.75 |
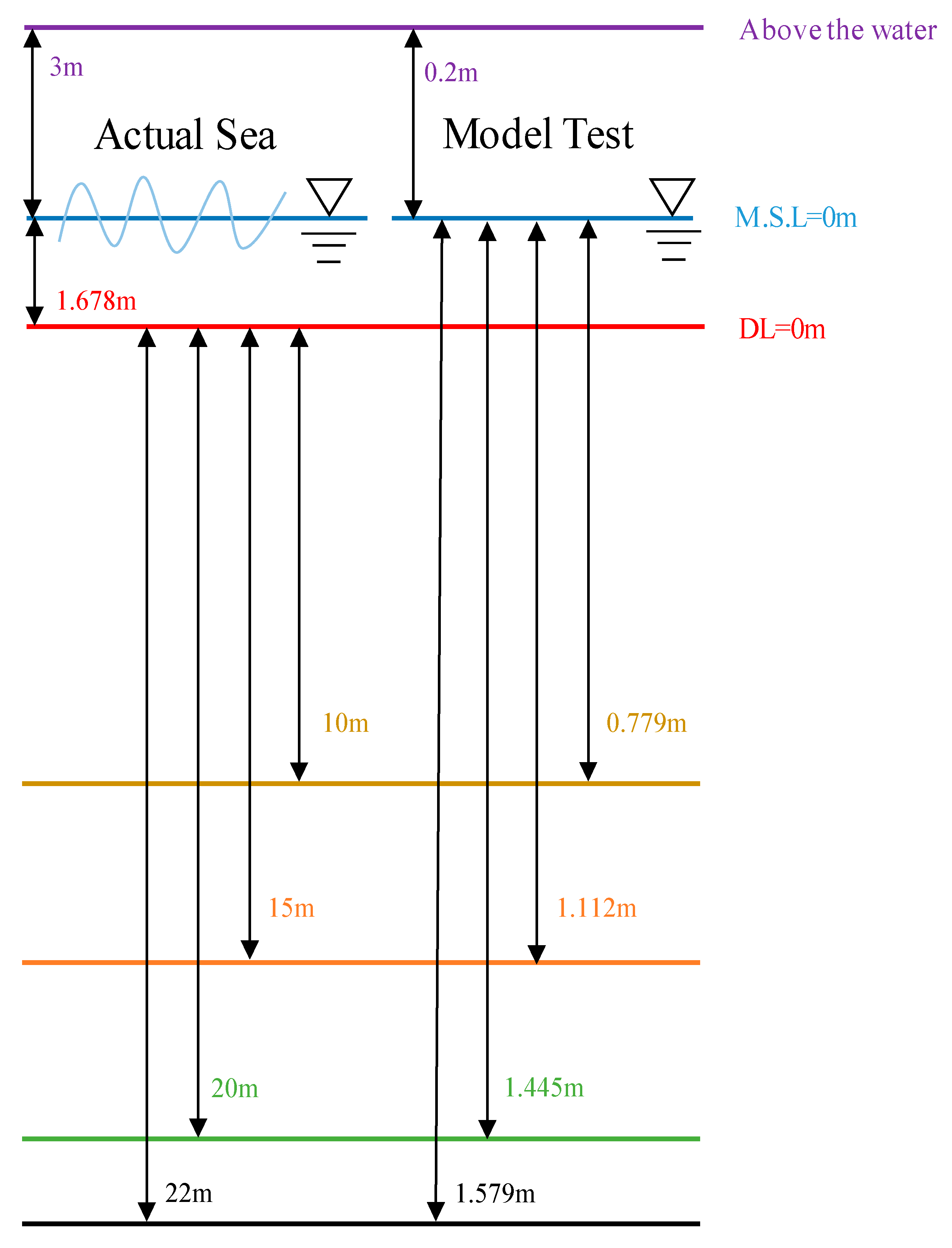
| Drop Level | Case | Actual Sea | Model Test | ||
|---|---|---|---|---|---|
| Drop Point | Water Depth | Drop Point | Water Depth | ||
| Water | 1 | M.S.L (DL(+)1.678 m) | DL(−) 10 m | 0.0 m | 0.779 m |
| 2 | DL(−) 15 m | 1.112 m | |||
| 3 | DL(−) 20 m | 1.445 m | |||
| 4 | DL(−) 22 m | 1.579 m | |||
| Air | 5 | On the surface 3 m (DL(+)4.678 m) | DL(−) 10 m | 0.2 m | 0.779 m |
| 6 | DL(−) 15 m | 1.112 m | |||
| 7 | DL(−) 20 m | 1.445 m | |||
| 8 | DL(−) 22 m | 1.579 m | |||
| Model | Scenario No. | Water Level | Air Level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| A (N) | S1 | 21,315 | 18,956 | 21,792 | 20,558 | 20,898 | 19,849 | 23,023 | 22,552 |
| S2 | 14,655 | 22,146 | 19,515 | 24,104 | 24,069 | 23,804 | 21,890 | 21,174 | |
| S3 | 16,859 | 21,788 | 22,106 | 23,430 | 19,020 | 21,786 | 16,749 | 21,429 | |
| Min. | 14,655 | 18,956 | 19,515 | 20,558 | 19,020 | 19,849 | 16,749 | 21,174 | |
| Max. | 21,315 | 22,146 | 22,106 | 24,104 | 24,069 | 23,804 | 23,023 | 22,552 | |
| Ave. | 17,613 | 20,964 | 21,138 | 22,697 | 21,329 | 21,813 | 20,554 | 21,718 | |
| CoV (%) | 15.7 | 6.8 | 5.5 | 6.8 | 9.8 | 7.4 | 13.3 | 2.8 | |
| B (N) | S1 | 27,244 | 22,605 | 23,780 | 27,617 | 29,017 | 26,558 | 21,548 | 28,435 |
| S2 | 26,498 | 25,900 | 32,430 | 25,378 | 26,380 | 26,467 | 30,980 | 31,506 | |
| S3 | 23,690 | 26,468 | 27,362 | 26,384 | 25,079 | 27,753 | 25,744 | 30,256 | |
| Min. | 23,690 | 22,605 | 23,780 | 22,927 | 25,079 | 26,467 | 21,548 | 28,435 | |
| Max. | 27,244 | 26,468 | 32,430 | 27,617 | 29,017 | 27,753 | 30,980 | 31,506 | |
| Ave. | 25,811 | 24,991 | 27,858 | 26,460 | 26,825 | 26,926 | 26,091 | 30,066 | |
| CoV (%) | 5.9 | 6.8 | 12.7 | 3.5 | 6.1 | 2.2 | 14.8 | 4.2 | |
| C/F | 0.5 | 0.6 | 0.75 | 1.0 | 1.2 | 1.5 |
|---|---|---|---|---|---|---|
 |  |  |  |  | 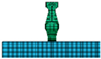 | |
| Fluid mesh size (m) | 0.030 | 0.025 | 0.020 | 0.015 | 0.0125 | 0.100 |
| No. of element | 36,894 | 65,280 | 128,000 | 246,612 | 522,240 | 1,024,000 |
| Computational time | 1 h 30 min | 2 h 30 min | 6 h | 13 h 30 min | 40 h | 91 h 30 min |
| B(or L)/D | 0.27 | 0.53 | 0.76 | 1.03 | 1.29 | 1.56 |
 |  |  |  |  |  | |
| B, L m) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
| No. of element | 18,502 | 68,782 | 138,642 | 246,612 | 391,502 | 569,908 |
| Computational time | 2 h | 4 h 30 min | 7 h | 13 h 30 min | 18 h 30 min | 27 h |
| Model | Water Level | Air Level | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A (N) | Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Experiment | 17,613 | 20,964 | 21,138 | 22,697 | 21,329 | 21,813 | 20,554 | 21,718 | |
| ANSYS/ LS-DYNA | 18,683 | 21,093 | 22,990 | 23,590 | 20,911 | 22,605 | 23,885 | 24,724 | |
| Error (%) | 6.08 | 0.62 | 8.76 | 3.93 | 1.96 | 3.63 | 16.21 | 13.84 | |
| B (N) | Experiment | 25,811 | 24,991 | 27,858 | 26,460 | 26,825 | 26,926 | 26,091 | 30,066 |
| ANSYS/ LS-DYNA | 25,735 | 28,999 | 31,634 | 32,576 | 29,286 | 31,010 | 33,227 | 33,986 | |
| Error (%) | 0.29 | 16.04 | 13.55 | 23.11 | 9.17 | 15.17 | 27.35 | 13.04 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohn, J.M.; Kim, J.W.; Kim, S.H. Experimental and Numerical Studies on Fluid-Structure Interaction for Underwater Drop of a Stone-Breaking Crusher. J. Mar. Sci. Eng. 2022, 10, 30. https://doi.org/10.3390/jmse10010030
Sohn JM, Kim JW, Kim SH. Experimental and Numerical Studies on Fluid-Structure Interaction for Underwater Drop of a Stone-Breaking Crusher. Journal of Marine Science and Engineering. 2022; 10(1):30. https://doi.org/10.3390/jmse10010030
Chicago/Turabian StyleSohn, Jung Min, Ji Woo Kim, and Sang Ho Kim. 2022. "Experimental and Numerical Studies on Fluid-Structure Interaction for Underwater Drop of a Stone-Breaking Crusher" Journal of Marine Science and Engineering 10, no. 1: 30. https://doi.org/10.3390/jmse10010030
APA StyleSohn, J. M., Kim, J. W., & Kim, S. H. (2022). Experimental and Numerical Studies on Fluid-Structure Interaction for Underwater Drop of a Stone-Breaking Crusher. Journal of Marine Science and Engineering, 10(1), 30. https://doi.org/10.3390/jmse10010030




