Improved BiLSTM-TDOA-Based Localization Method for Laying Hen Cough Sounds
Abstract
1. Introduction
- (1)
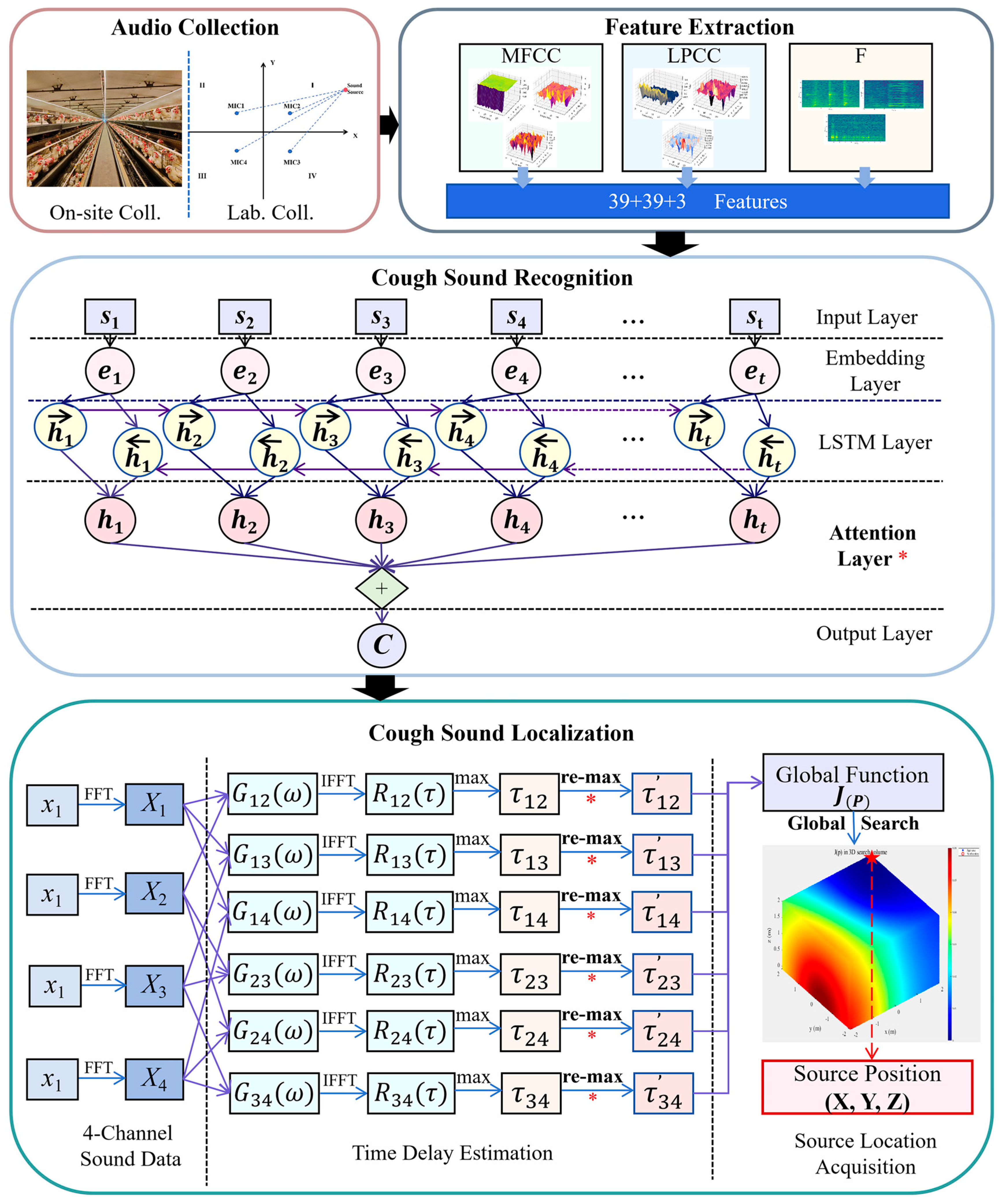
- Acoustic feature fusion-based recognition: For laying hen cough sounds, a fusion of extracted acoustic features—including formants, MFCCs, LPCCs, and their first—and second-order derivatives was employed. An attention mechanism was integrated into the BiLSTM-Attention model to enhance the network’s focus and capture key acoustic features of coughs, thereby achieving high-accuracy recognition.
- (2)
- Improved TDOA-based 3D localization in a laying-hen house: In the TDOA-based sound source localization framework, a novel combination of PHAT-weighted peak refitting and global grid search strategies was proposed to significantly improve time delay estimation and spatial search performance. Considering the acoustic environment of 3D cage structures in poultry houses, a 3D localization algorithm was optimized; unlike conventional 2D plane-based methods, it incorporates the vertical dimension to account for height-related propagation differences and enhance overall spatial accuracy.
2. Materials and Methods
2.1. Materials
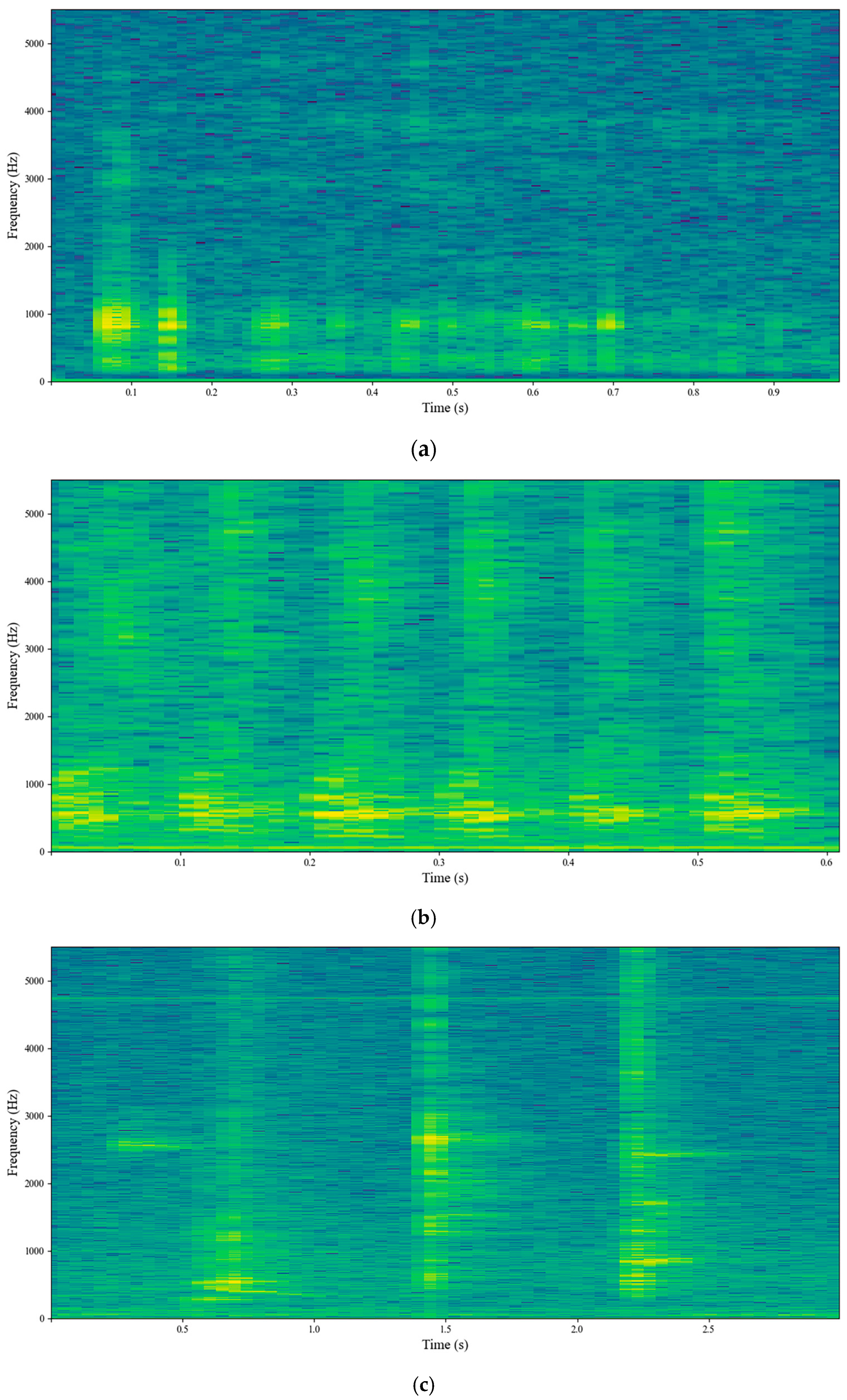
2.1.1. Sound Recognition Dataset of Laying Hens
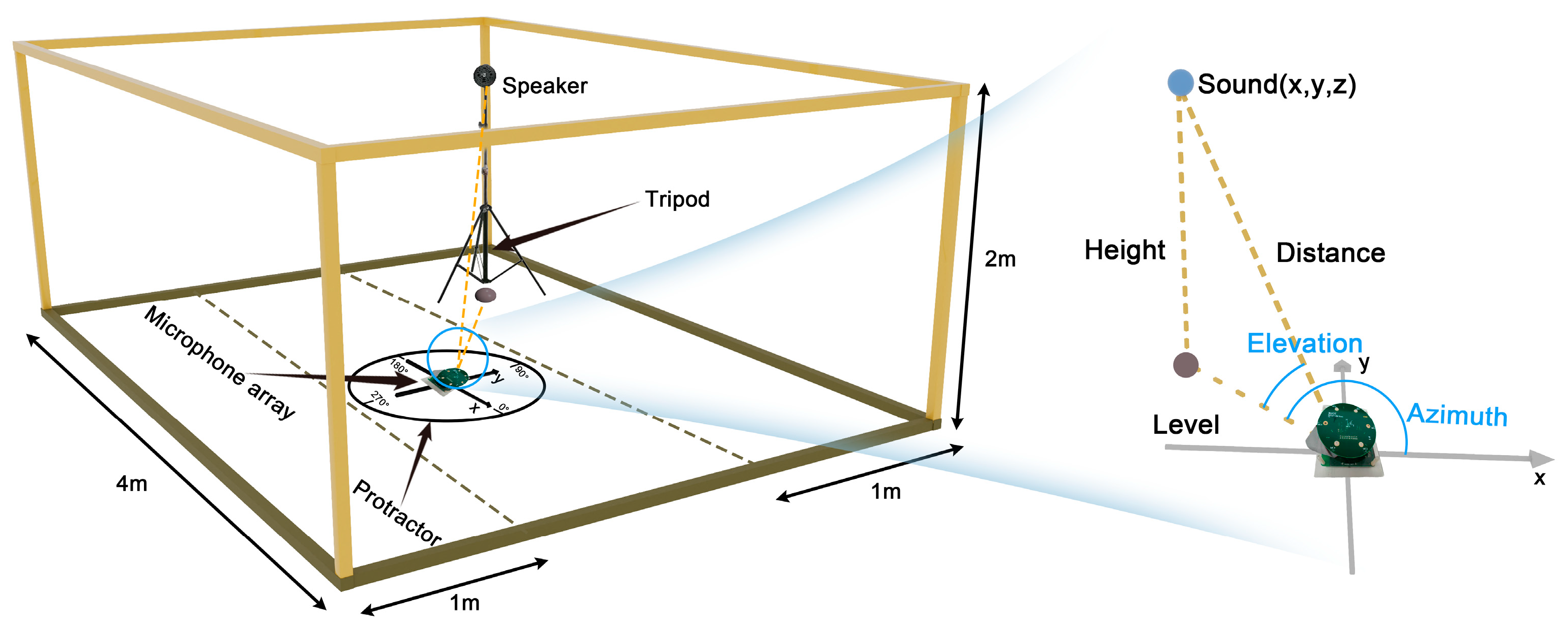
2.1.2. Setup of Localization Experimental Platform and Dataset Construction
2.2. Methods
2.2.1. Acoustic Feature Extraction of Laying Hens
- (1)
- MFCC extraction
- (2)
- LPCC extraction
- (3)
- Formant extraction
2.2.2. BiLSTM-Attention Cough Sound Classification of Laying Hens
- (1)
- BiLSTM model structure
- (2)
- Attention mechanism
- (3)
- Classification layer
- (4)
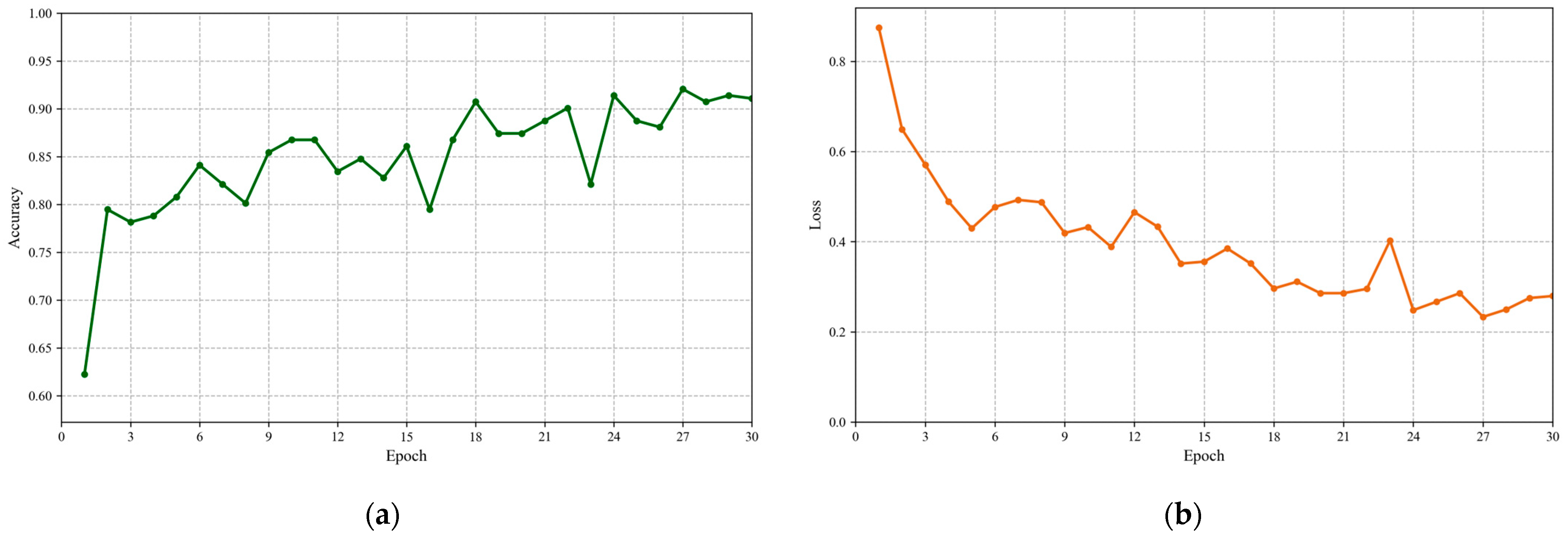
- Model training
2.2.3. Sound Source Localization of Laying Hen Coughs
- (1)
- Time delay estimation method
- (2)
- Sound Source Position Estimation
2.2.4. Evaluation Methods
3. Results and Discussion
3.1. Recognition Results of Laying Hen Sounds
3.2. Improved TDOA Localization of Laying Hen Coughs
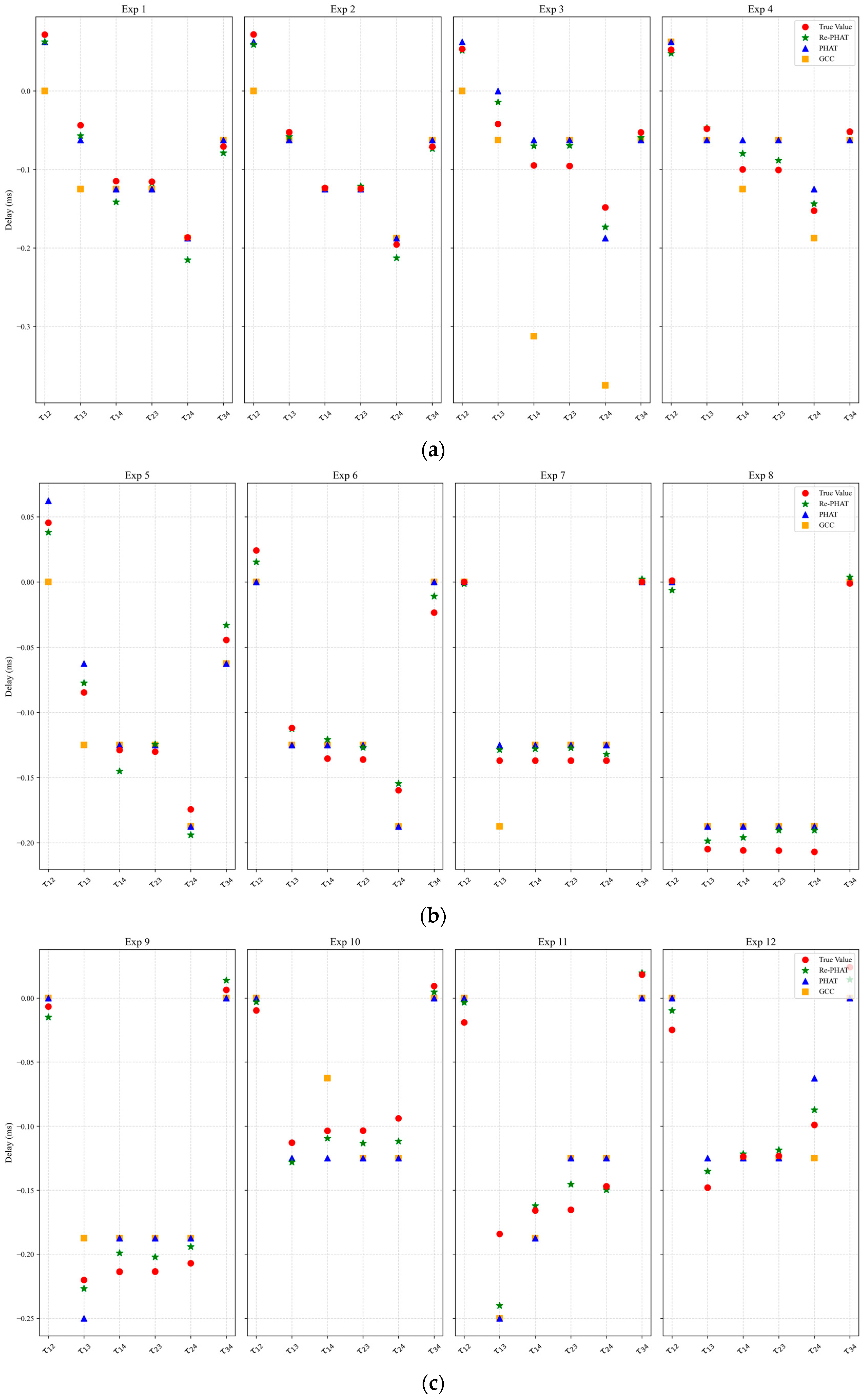
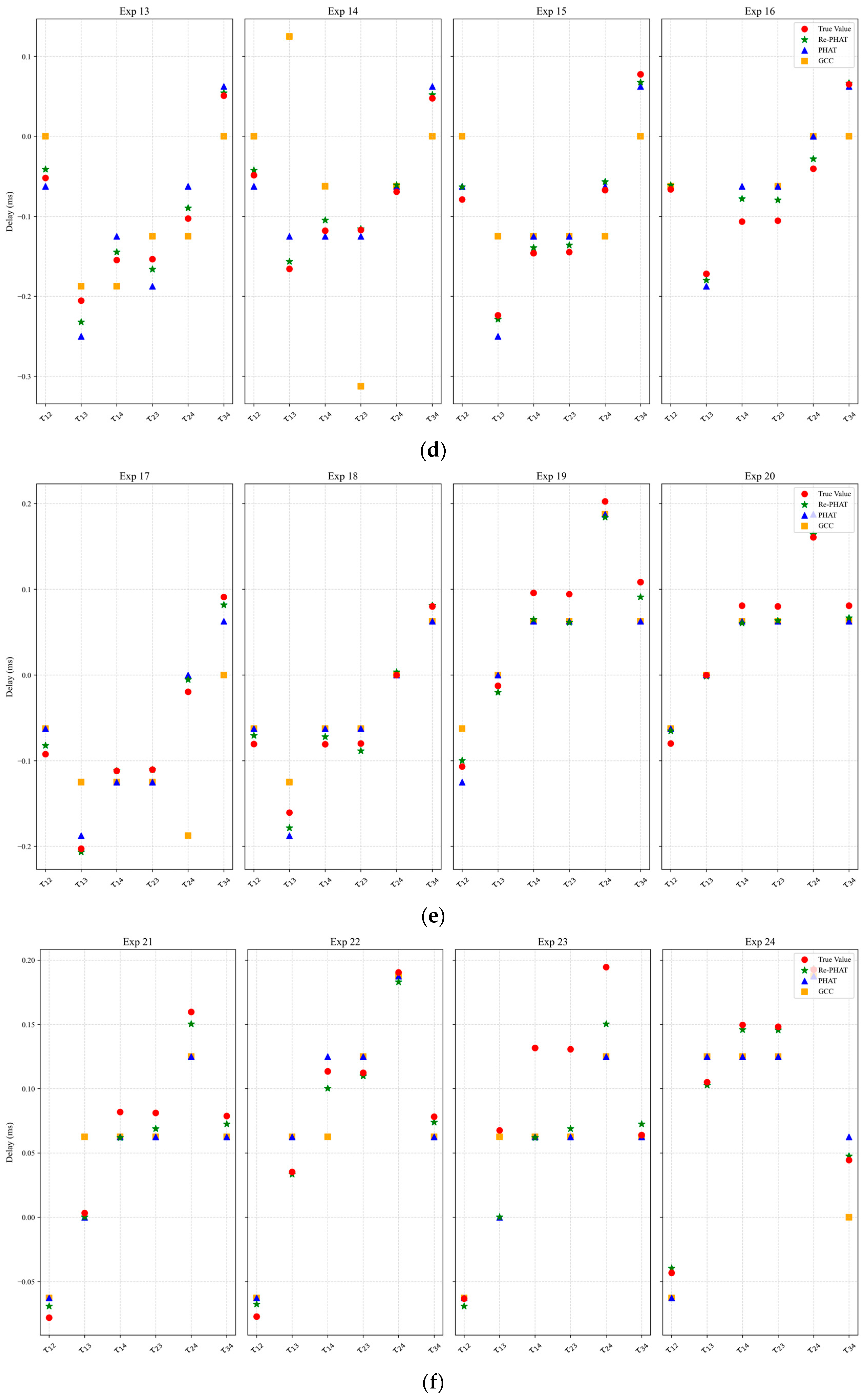
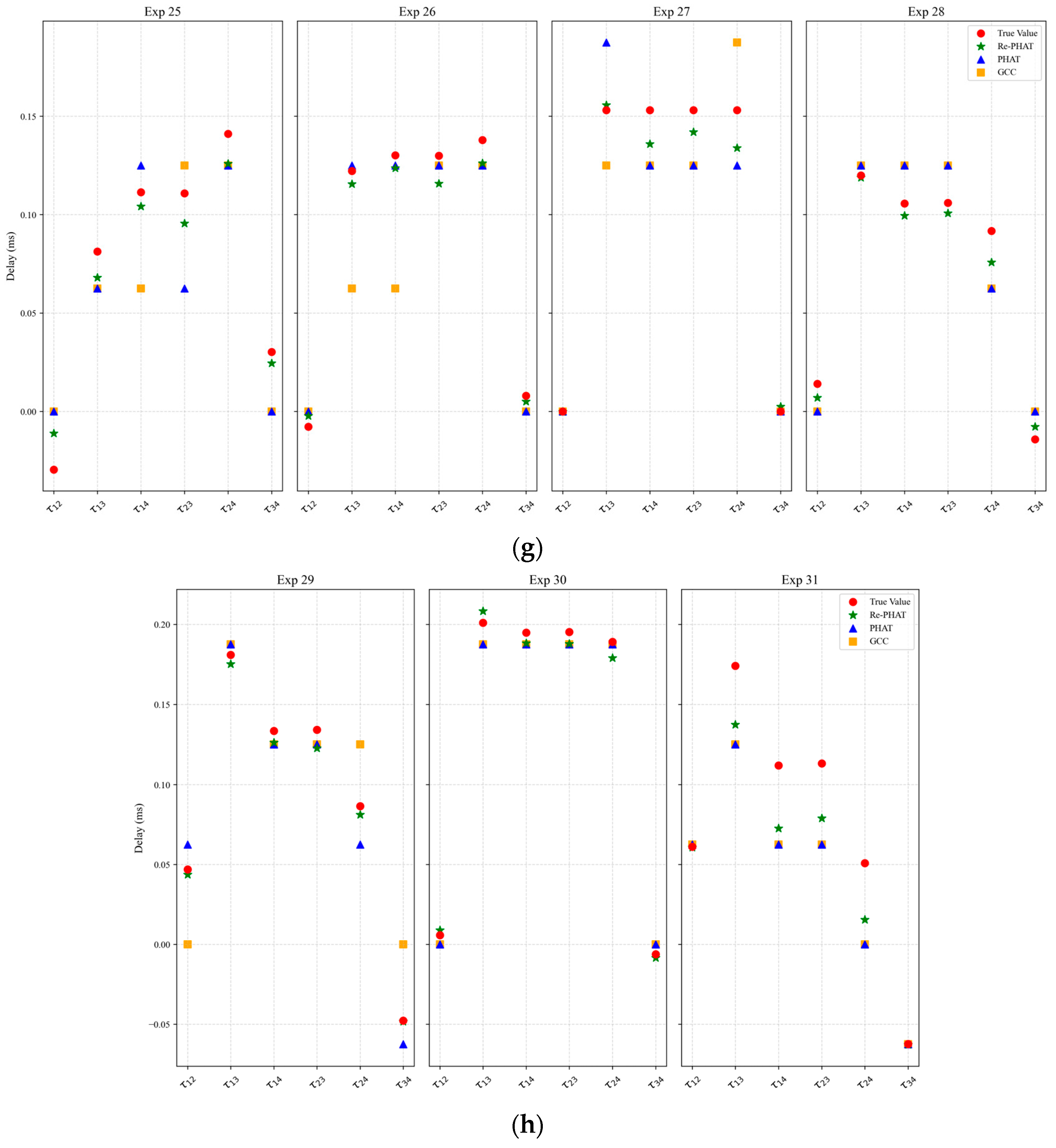
3.2.1. Analysis of Cough Sound Time Delay Estimation Based on TDOA
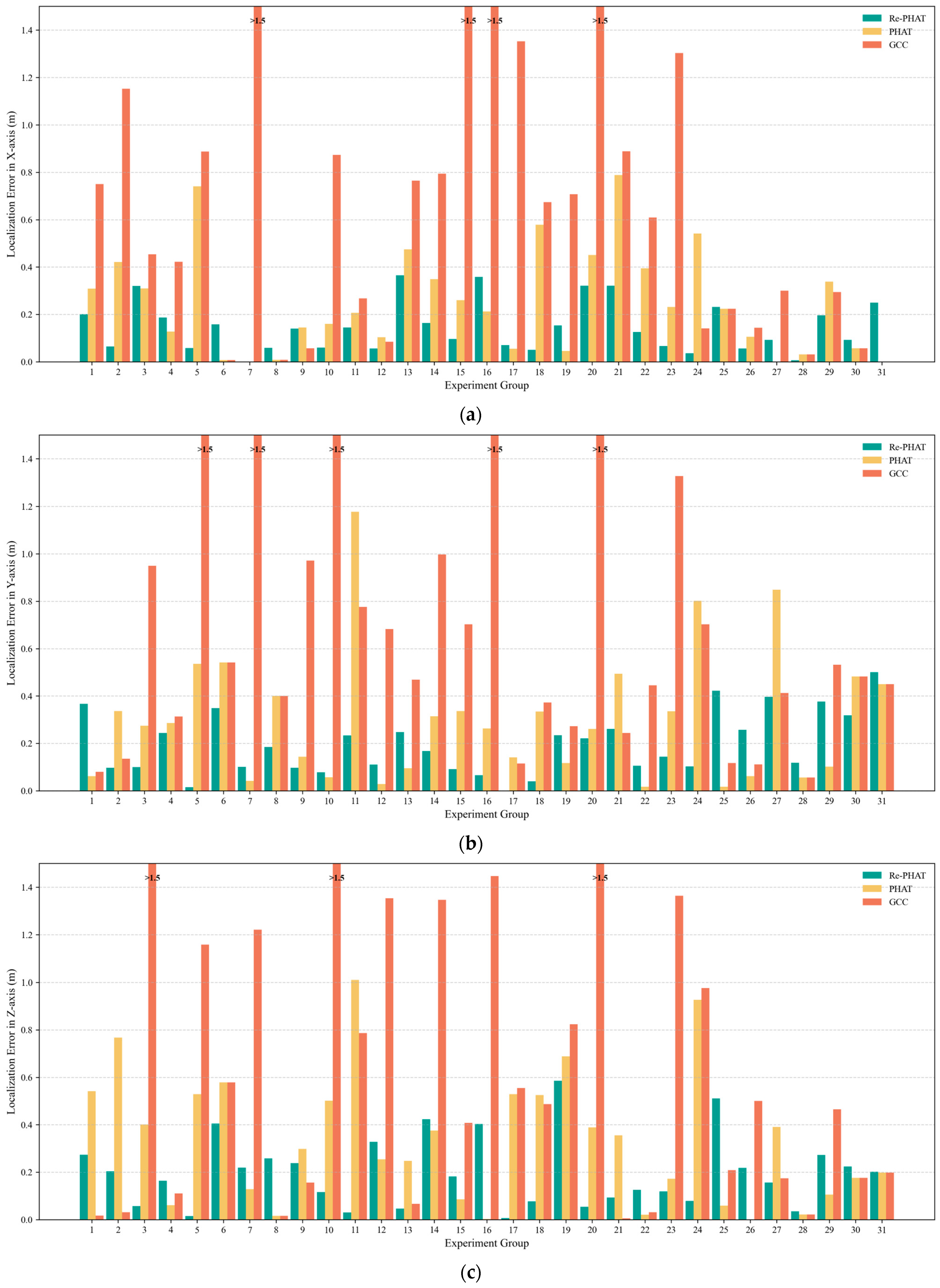
3.2.2. Analysis of Cough Sound Position Search Based on TDOA
4. Limitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Z.; Willems, S.; Liu, D.; Norton, T. How AI Improves Sustainable Chicken Farming: A Literature Review of Welfare, Economic, and Environmental Dimensions. Agriculture 2025, 15, 2028. [Google Scholar] [CrossRef]
- Natsir, M.H.; Mahmudy, W.F.; Tono, M.; Nuningtyas, Y.F. Advancements in artificial intelligence and machine learning for poultry farming: Applications, challenges, and future prospects. Smart Agric. Technol. 2025, 12, 101307. [Google Scholar] [CrossRef]
- Ahmed, N.Q.; Dawood, R.A.; Al-Mastafa, A.; Jassim, S.T.; Ali, A.; Ahmed, A.M.; Hammady, F.J. Investigating the correlation between stocking density and respiratory diseases in poultry. J. Anim. Health Prod. 2025, 13, 65–72. [Google Scholar] [CrossRef]
- He, P.; Chen, Z.; Yu, H.; Hayat, K.; He, Y.; Pan, J.; Lin, H. Research progress in the early warning of chicken diseases by monitoring clinical symptoms. Appl. Sci. 2022, 12, 5601. [Google Scholar] [CrossRef]
- Italiya, J.; Ahmed, A.A.; Abdel-Wareth, A.A.; Lohakare, J. An AI-based system for monitoring laying hen behavior using computer vision for small-scale poultry farms. Agriculture 2025, 15, 1963. [Google Scholar] [CrossRef]
- Neethirajan, S. Rethinking poultry welfare—Integrating behavioral science and digital innovations for enhanced animal well-being. Poultry 2025, 4, 20. [Google Scholar] [CrossRef]
- Zhou, H.; Zhu, Q.; Norton, T. Cough sound recognition in poultry using portable microphones for precision medication guidance. Comput. Electron. Agric. 2025, 237, 110541. [Google Scholar] [CrossRef]
- Manikandan, V.; Neethirajan, S. AI-driven bioacoustics in poultry farming: A critical systematic review on vocalization analysis for stress and disease detection. Preprint 2025. [Google Scholar]
- Liu, M.; Chen, H.; Zhou, Z.; Du, X.; Zhao, Y.; Ji, H.; Teng, G. Development of an intelligent service platform for a poultry house facility environment based on the Internet of Things. Agriculture 2024, 14, 1277. [Google Scholar] [CrossRef]
- Yu, L.; Du, T.; Yu, Q.; Liu, T.; Meng, R.; Li, Q. Recognition method of laying hens’ vocalizations based on multi-feature fusion. Trans. Chin. Soc. Agric. Eng. 2022, 53, 259–265, (In Chinese with English abstract). [Google Scholar]
- Rizwan, M.; Carroll, B.T.; Anderson, D.V.; Daley, W.; Harbert, S.; Britton, D.F.; Jackwood, M.W. Identifying rale sounds in chickens using audio signals for early disease detection in poultry. In Proceedings of the 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, USA, 7–9 December 2016; pp. 55–59. [Google Scholar]
- Banakar, A.; Sadeghi, M.; Shushtari, A. An intelligent device for diagnosing avian diseases: Newcastle, infectious bronchitis, avian influenza. Comput. Electron. Agric. 2016, 127, 744–753. [Google Scholar] [CrossRef] [PubMed]
- Cuan, K.; Zhang, T.; Li, Z.; Huang, J.; Ding, Y.; Fang, C. Automatic Newcastle disease detection using sound technology and deep learning method. Comput. Electron. Agric. 2022, 194, 106740. [Google Scholar] [CrossRef]
- Silva, M.; Ferrari, S.; Costa, A.; Aerts, J.; Guarino, M.; Berckmans, D. Cough localization for the detection of respiratory diseases in pig houses. Comput. Electron. Agric. 2008, 64, 286–292. [Google Scholar] [CrossRef]
- Du, X.; Lao, F.; Teng, G. A sound source localisation analytical method for monitoring the abnormal night vocalisations of poultry. Sensors 2018, 18, 2906. [Google Scholar] [CrossRef]
- Yu, L.; Zhuang, Y.; Qiu, F.; Ding, X.; He, J.; Zhao, Y.; Yang, G.; Wu, Y.; Zhao, C.; Li, Q. Research progress of audio information technology in agricultural field. Trans. Chin. Soc. Agric. Eng. 2025, 56, 1–26, (In Chinese with English abstract). [Google Scholar]
- Bottigliero, S.; Milanesio, D.; Saccani, M.; Maggiora, R. A low-cost indoor real-time locating system based on TDOA estimation of UWB pulse sequences. IEEE Trans. Instrum. Meas. 2021, 70, 5502211. [Google Scholar] [CrossRef]
- Motie, S.; Zayyani, H.; Salman, M.; Bekrani, M. Self UAV localization using multiple base stations based on TDoA measurements. IEEE Wirel. Commun. Lett. 2024, 13, 2432–2436. [Google Scholar] [CrossRef]
- Kita, S.; Kajikawa, Y. Fundamental study on sound source localization inside a structure using a deep neural network and computer-aided engineering. J. Sound Vib. 2021, 513, 116400. [Google Scholar] [CrossRef]
- Fan, W.; Peng, H.; Yang, D. The application and challenges of advanced detection technologies in poultry farming. Poult. Sci. 2025, 104, 105870. [Google Scholar] [CrossRef]
- García-Barrios, G.; Gutiérrez-Arriola, J.M.; Sáenz-Lechón, N.; Osma-Ruiz, V.J.; Fraile, R. Analytical model for the relation between signal bandwidth and spatial resolution in steered-response power phase transform (SRP-PHAT) maps. IEEE Access 2021, 9, 121549–121560. [Google Scholar] [CrossRef]
- Ramamurthy, A.; Unnikrishnan, H.; Donohue, K.D. Experimental performance analysis of sound source detection with SRP PHAT-β. In Proceedings of the IEEE Southeastcon 2009, Atlanta, GA, USA, 5–8 March 2009; IEEE: New York, NY, USA, 2009; pp. 422–427. [Google Scholar]
- Wang, L.; Hon, T.; Reiss, J.D.; Cavallaro, A. Self-localization of ad-hoc arrays using time difference of arrivals. IEEE Trans. Signal Process. 2015, 64, 1018–1033. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F. Positioning using time-difference of arrival measurements. In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 6–10 April 2003; p. 553. [Google Scholar]
- Krishnaveni, V.; Kesavamurthy, T. Beamforming for direction-of-arrival (DOA) estimation—A survey. Int. J. Comput. Appl. 2013, 61, 4–11. [Google Scholar] [CrossRef]
- Heydari, Z.; Mahabadi, A. Scalable real-time sound source localization method based on TDOA. Multimed. Tools Appl. 2023, 82, 23333–23372. [Google Scholar] [CrossRef]
- Ma, H.; Xin, P.; Ma, J.; Yang, X.; Zhang, R.; Liang, C.; Liu, Y.; Qi, F.; Wang, C. End-to-end detection of cough and snore based on ResNet18-TF for breeder laying hens: A field study. Artif. Intell. Agric. 2026, 16, 412–422. [Google Scholar] [CrossRef]
- Ali, S.; Tanweer, S.; Khalid, S.S.; Rao, N. Mel frequency cepstral coefficient: A review. In Proceedings of the 2nd International Conference on ICT for Digital, Smart, and Sustainable Development, ICIDSSD 2020, New Delhi, India, 27–28 February 2020. [Google Scholar]
- Kamarudin, N.; Al-Haddad, S.; Khmag, A.; Hassan, A.B.; Hashim, S.J. Analysis on Mel frequency cepstral coefficients and linear predictive cepstral coefficients as feature extraction on automatic accents identification. Int. J. Appl. Eng. Res. 2016, 11, 7301–7307. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: New York, NY, USA, 2019; pp. 3285–3292. [Google Scholar]
- Oppenheim, A.V. Speech spectrograms using the fast Fourier transform. IEEE Spectr. 2009, 7, 57–62. [Google Scholar] [CrossRef]
- Hartcher, K.M.; Jones, B. The welfare of layer hens in cage and cage-free housing systems. World’s Poult. Sci. J. 2017, 73, 767–782. [Google Scholar] [CrossRef]
- Özhan, O. Short-Time Fourier Transform. In Basic Transforms for Electrical Engineering; Springer International Publishing: Cham, Switzerland, 2022; pp. 441–464. [Google Scholar]
- Wang, X.; Xu, X.; Sun, K.; Jiang, Z.; Li, M.; Wen, J. A color image encryption and hiding algorithm based on hyperchaotic system and discrete cosine transform. Nonlinear Dyn. 2023, 111, 14513–14536. [Google Scholar] [CrossRef]
- Ashtekar, S.; Kumar, P.; Kumar, R. Study of generalized cross correlation techniques for direction finding of wideband signals. In Proceedings of the 5th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 8–10 April 2021; pp. 707–714. [Google Scholar]
| Parameter | Parameter Value |
|---|---|
| Input size | 81 |
| Hidden size | 512 |
| LSTM layers | 2 |
| Dropout rate | 0.5 |
| Optimizer | AdamW |
| Learning rate | 1 × 10−4 |
| Batch size | 16 |
| Model | Class | Precision | Recall | F1-Score |
|---|---|---|---|---|
| SVM [11] | cough | 89.71% | 84.72% | 0.8714 |
| normal | 80.00% | 73.17% | 0.7643 | |
| environment | 77.38% | 89.04% | 0.8280 | |
| macro | 82.36% | 82.31% | 0.8213 | |
| MLP | cough | 86.96% | 86.96% | 0.8696 |
| normal | 60.27% | 84.62% | 0.7040 | |
| environment | 84.85% | 51.85% | 0.6437 | |
| macro | 77.36% | 74.47% | 0.7391 | |
| BP [10] | cough | 90.48% | 82.61% | 0.8636 |
| normal | 72.73% | 76.92% | 0.7477 | |
| environment | 80.00% | 81.48% | 0.8073 | |
| macro | 81.07% | 80.34% | 0.8062 | |
| LSTM | cough | 84.21% | 87.67% | 0.8591 |
| normal | 91.80% | 69.14% | 0.7887 | |
| environment | 73.33% | 90.41% | 0.8098 | |
| macro | 83.12% | 82.41% | 0.8192 | |
| BiLSTM [13] | cough | 91.94% | 85.07% | 0.8837 |
| normal | 78.95% | 77.92% | 0.7843 | |
| environment | 84.27% | 90.36% | 0.8721 | |
| macro | 85.05% | 84.45% | 0.8467 | |
| BiLSTM-attention | cough | 98.08% | 94.44% | 0.9623 |
| normal | 90.74% | 83.05% | 0.8673 | |
| environment | 78.26% | 92.31% | 0.8471 | |
| macro | 89.03% | 89.93% | 0.8922 |
| Class | Precision | Recall | F1-Score |
|---|---|---|---|
| cough | 97.50% | 90.70% | 0.9398 |
| normal | 84.62% | 86.27% | 0.8544 |
| environment | 86.67% | 89.66% | 0.8814 |
| macro | 89.59% | 88.88% | 0.8918 |
| Time Delay Difference | True Value (ms) | Re-PHAT (ms) | PHAT (ms) | GCC (ms) |
|---|---|---|---|---|
| τ12 | −0.0779007 | −0.0690572 | −0.0625 | −0.0625 |
| τ13 | 0.0031888 | 0.0000808 | 0 | 0.0625 |
| τ14 | 0.0818758 | 0.0619728 | 0.0625 | 0.0625 |
| τ23 | 0.0810895 | 0.0687775 | 0.0625 | 0.0625 |
| τ24 | 0.1597765 | 0.1502702 | 0.1250 | 0.1250 |
| τ34 | 0.0786870 | 0.0725368 | 0.0625 | 0.0625 |
| Group | True Position (m) | Re-PHAT (m) | PHAT (m) | GCC (m) |
|---|---|---|---|---|
| 1 | (1.752, 1.633, 1.936) | (1.953, 2, 1.662) | (1.443, 1.571, 1.395) | (1.002, 1.553, 1.953) |
| 2 | (1.901, 1.901, 1.961) | (1.966, 1.998, 1.757) | (1.48, 1.564, 1.194) | (0.749, 1.766, 1.993) |
| 3 | (0.99, 1.025, 1.851) | (1.31, 0.925, 1.908) | (1.3, 0.75, 1.45) | (1.444, 1.974, 0.082) |
| 4 | (0.978, 1.086, 1.839) | (0.791, 0.842, 1.675) | (0.85, 0.8, 1.9) | (1.4, 1.4, 1.95) |
| 5 | (0.609, 1.014, 1.221) | (0.667, 1.029, 1.236) | (1.35, 1.55, 1.75) | (−0.278, −0.562, 0.063) |
| 6 | (0.308, 1.009, 1.221) | (0.15, 0.66, 0.816) | (0.3, 1.55, 1.8) | (0.3, 1.55, 1.8) |
| 7 | (0, 0.992, 1.221) | (0, 1.093, 1.44) | (0, 0.95, 1.35) | (2.168, −1.006, 0) |
| 8 | (0.009, 1, 0.334) | (−0.05, 1.185, 0.592) | (0, 0.6, 0.35) | (0, 0.6, 0.35) |
| 9 | (−0.105, 1.994, 0.352) | (−0.245, 1.897, 0.59) | (−0.25, 1.85, 0.65) | (−0.048, 1.023, 0.508) |
| 10 | (−0.16, 1.007, 1.851) | (−0.1, 1.085, 1.735) | (0, 0.95, 1.35) | (0.713, −1.122, 0) |
| 11 | (−0.268, 1.376, 1.136) | (−0.413, 1.61, 1.105) | (−0.061, 0.199, 0.127) | (0, 0.6, 0.35) |
| 12 | (−0.354, 1.029, 1.445) | (−0.298, 1.14, 1.773) | (−0.25, 1, 1.7) | (−0.439, 1.711, 0.092) |
| 13 | (−0.998, 1.728, 1.397) | (−1.363, 1.976, 1.35) | (−1.473, 1.823, 1.149) | (−0.234, 1.259, 1.33) |
| 14 | (−0.744, 1.047, 1.447) | (−0.908, 1.215, 1.87) | (−1.093, 1.362, 1.823) | (0.05, 0.05, 0.1) |
| 15 | (−1.76, 1.887, 1.136) | (−1.664, 1.795, 1.318) | (−1.5, 1.55, 1.05) | (−0.091, 1.185, 1.544) |
| 16 | (−1.087, 1.013, 1.447) | (−1.445, 1.079, 1.85) | (−1.3, 0.75, 1.45) | (1.119, −1.996, 0) |
| 17 | (−1.655, 1.159, 1.021) | (−1.726, 1.16, 1.014) | (−1.6, 1.3, 1.55) | (−0.303, 1.274, 1.576) |
| 18 | (−1.879, 1.085, 1.975) | (−1.93, 1.125, 1.898) | (−1.3, 0.75, 1.45) | (−1.205, 0.712, 1.488) |
| 19 | (−2.007, −1.023, 0.627) | (−1.853, −0.788, 1.212) | (−1.961, −0.906, 1.315) | (−1.3, −0.75, 1.45) |
| 20 | (−1.751, −1.011, 1.839) | (−1.43, −0.79, 1.785) | (−1.3, −0.75, 1.45) | (1.332, 1.726, 0) |
| 21 | (−1.738, −1.044, 1.906) | (−1.417, −0.783, 1.812) | (−0.95, −0.55, 1.55) | (−0.85, −0.8, 1.9) |
| 22 | (−1.786, −1.499, 1.699) | (−1.66, −1.393, 1.825) | (−1, −1.516, 1.72) | (−1.177, −1.054, 1.731) |
| 23 | (−1.582, −1.886, 1.923) | (−1.515, −1.742, 1.804) | (−1.35, −1.55, 1.75) | (−0.279, −0.559, 0.559) |
| 24 | (−0.559, −1.098, 1.024) | (−0.523, −0.995, 0.945) | (−1.1, −1.9, 1.95) | (−0.7, −1.8, 2) |
| 25 | (−0.474, −1.017, 1.641) | (−0.242, −0.595, 1.13) | (−0.25, −1, 1.7) | (−0.25, −0.9, 1.85) |
| 26 | (−0.106, −1.012, 1.35) | (−0.05, −0.755, 1.132) | (0, −0.95, 1.35) | (−0.25, −0.9, 1.85) |
| 27 | (0, −1.963, 1.975) | (0.093, −1.566, 1.819) | (0, −1.115, 1.584) | (−0.3, −1.55, 1.8) |
| 28 | (0.218, −0.944, 1.678) | (0.211, −0.826, 1.643) | (0.25, −1, 1.7) | (0.25, −1, 1.7) |
| 29 | (1.012, −1.652, 1.856) | (0.816, −1.275, 1.583) | (1.35, −1.55, 1.75) | (0.717,−1.12, 1.391) |
| 30 | (0.057, −1.082, 0.526) | (0.15, −1.4, 0.75) | (0, −0.6, 0.35) | (0, −0.6, 0.35) |
| 31 | (0.95, −1, 1.352) | (0.7, −0.5, 1.15) | (0.95, −0.55, 1.55) | (0.95, −0.55, 1.55) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Qiu, F.; Li, Q.; Zhuang, Y.; Ding, X.; Wu, Y.; Wang, Y.; Zhao, Y.; Zhang, H.; Ren, Z.; Lai, C.; et al. Improved BiLSTM-TDOA-Based Localization Method for Laying Hen Cough Sounds. Agriculture 2026, 16, 28. https://doi.org/10.3390/agriculture16010028
Qiu F, Li Q, Zhuang Y, Ding X, Wu Y, Wang Y, Zhao Y, Zhang H, Ren Z, Lai C, et al. Improved BiLSTM-TDOA-Based Localization Method for Laying Hen Cough Sounds. Agriculture. 2026; 16(1):28. https://doi.org/10.3390/agriculture16010028
Chicago/Turabian StyleQiu, Feng, Qifeng Li, Yanrong Zhuang, Xiaoli Ding, Yue Wu, Yuxin Wang, Yujie Zhao, Haiqing Zhang, Zhiyu Ren, Chengrong Lai, and et al. 2026. "Improved BiLSTM-TDOA-Based Localization Method for Laying Hen Cough Sounds" Agriculture 16, no. 1: 28. https://doi.org/10.3390/agriculture16010028
APA StyleQiu, F., Li, Q., Zhuang, Y., Ding, X., Wu, Y., Wang, Y., Zhao, Y., Zhang, H., Ren, Z., Lai, C., & Yu, L. (2026). Improved BiLSTM-TDOA-Based Localization Method for Laying Hen Cough Sounds. Agriculture, 16(1), 28. https://doi.org/10.3390/agriculture16010028






