Mitigating Catastrophic Forgetting in Pest Detection Through Adaptive Response Distillation
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets and Evaluation Metric
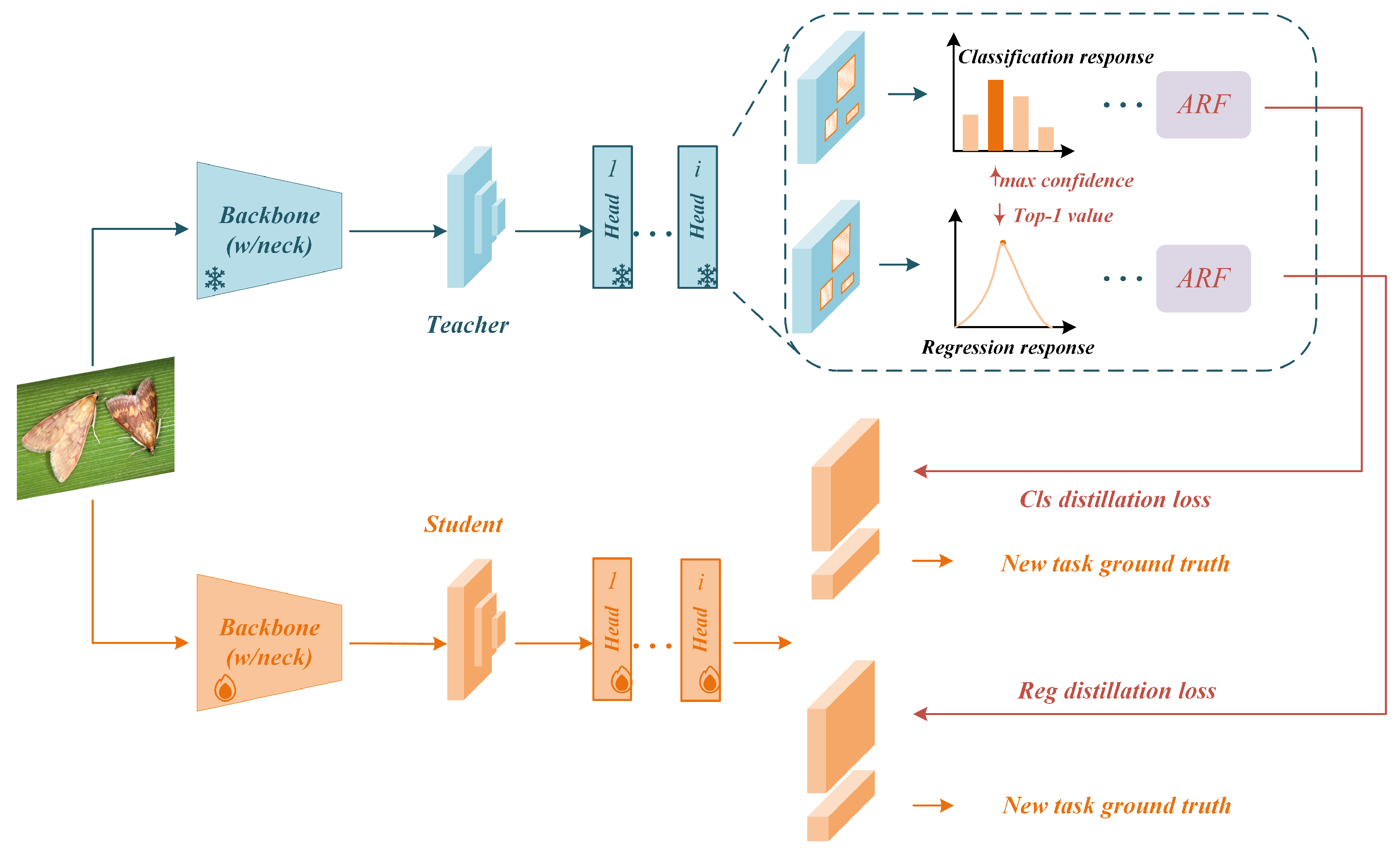
2.2. Overall Framework
2.3. Classification and Regression Head
2.4. Application of ARD in the Classification Head
2.5. Application of ARD in the Regression Head
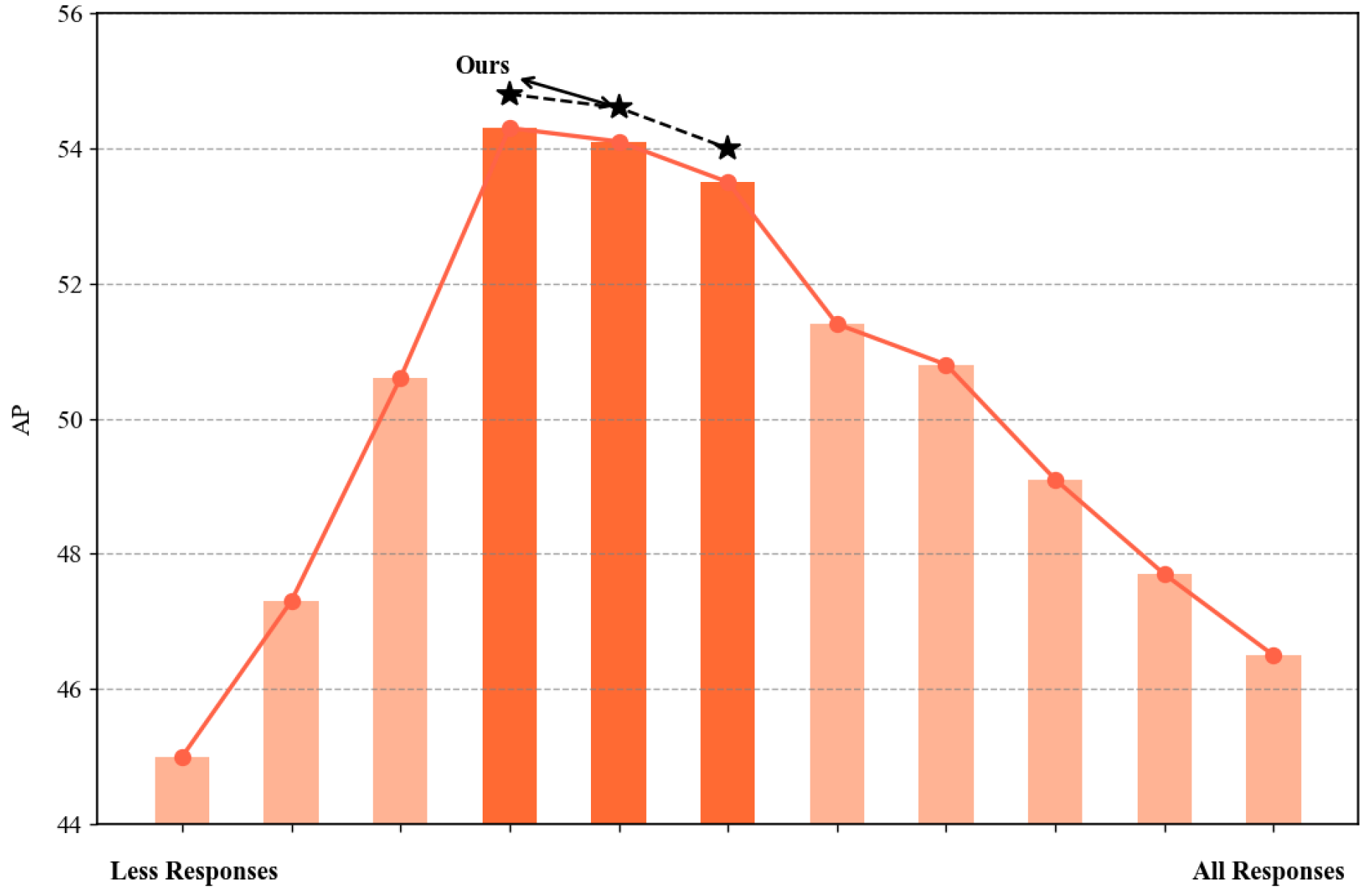
2.6. Adaptive Response Filtering
2.6.1. Ensure Fairness Among Different Types of Responses
2.6.2. Statistical Analysis-Based ARF
2.6.3. ARF in Classification Head
2.6.4. ARF in Regression Head
3. Results
3.1. Implementation Details
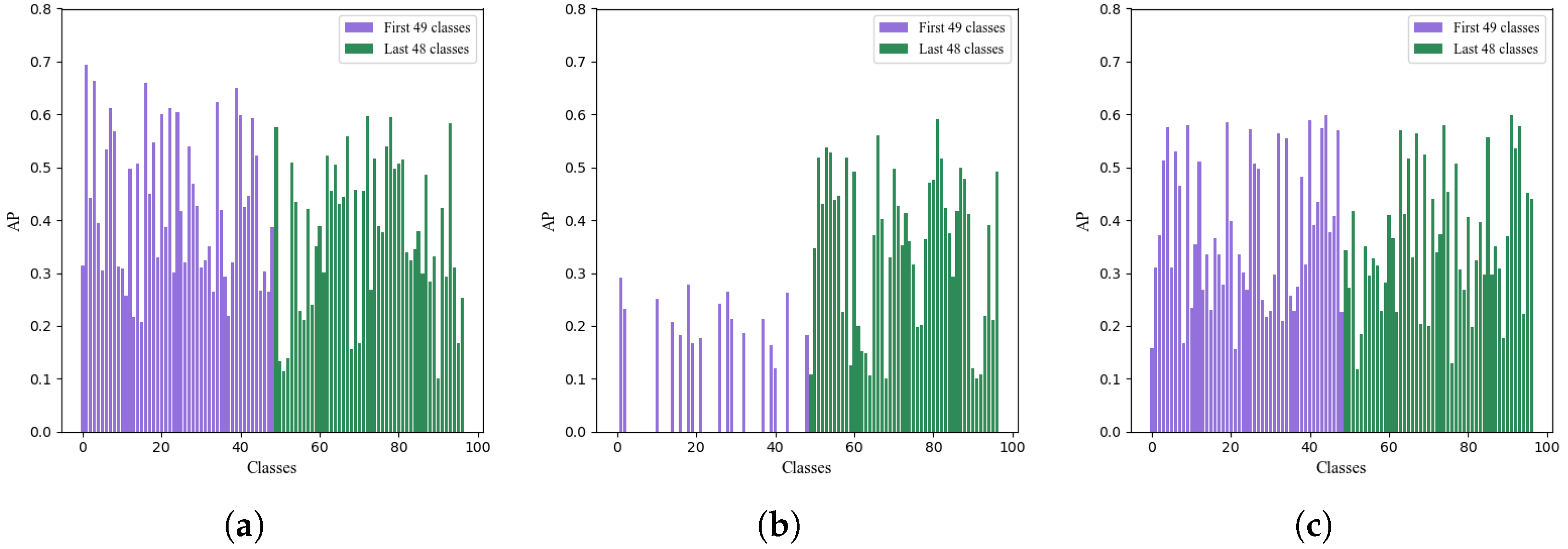
3.2. Single-Step Incremental Learning
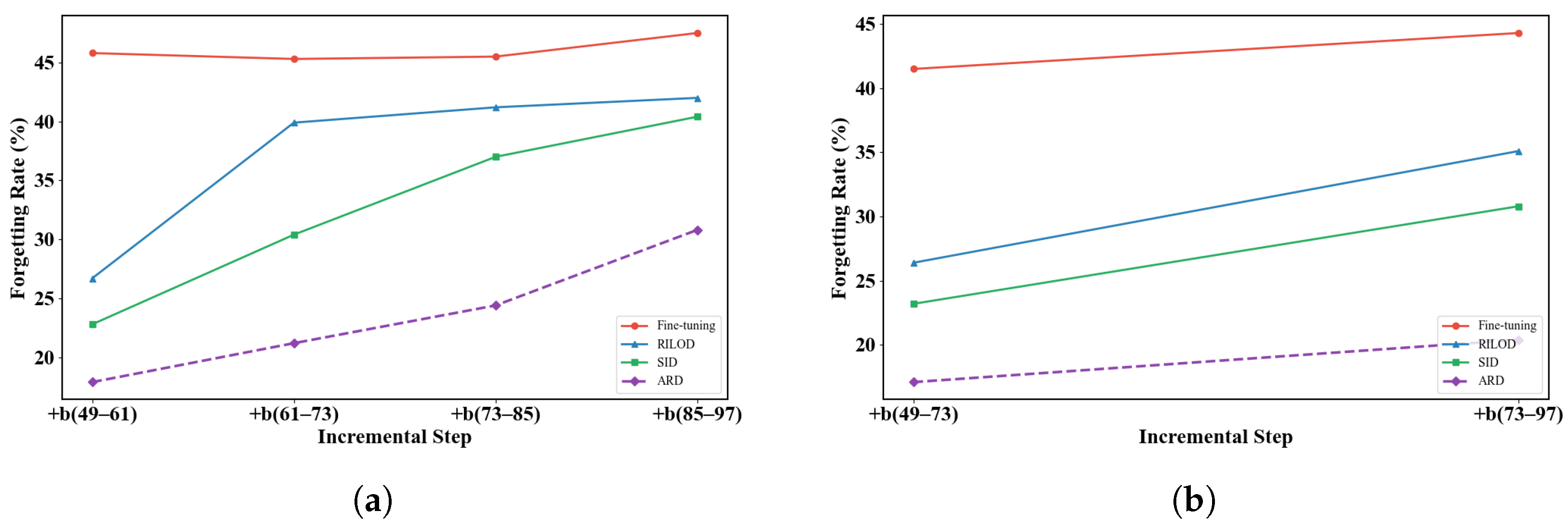
3.3. Multi-Step Incremental Learning
3.4. Ablation Study
3.5. Computational Cost Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Leong, D.P.; Teo, K.K.; Rangarajan, S.; Lopez-Jaramillo, P.; Avezum, A., Jr.; Orlandini, A. World Population Prospects 2019. World 2018, 73, 362. [Google Scholar]
- Ennouri, K.; Kallel, A. Remote sensing: An advanced technique for crop condition assessment. Math. Probl. Eng. 2019, 2019, 9404565. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of remote sensing in precision agriculture: A review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A review on UAV-based applications for precision agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Ahmad, N.; Hussain, A.; Ullah, I.; Zaidi, B.H. IOT based wireless sensor network for precision agriculture. In Proceedings of the 2019 7th International Electrical Engineering Congress (IEECON), Phetchaburi, Thailand, 7–9 March 2019; pp. 1–4. [Google Scholar]
- Condran, S.; Bewong, M.; Islam, M.Z.; Maphosa, L.; Zheng, L. Machine learning in precision agriculture: A survey on trends, applications and evaluations over two decades. IEEE Access 2022, 10, 73786–73803. [Google Scholar] [CrossRef]
- Kasinathan, T.; Singaraju, D.; Uyyala, S.R. Insect classification and detection in field crops using modern machine learning techniques. Inf. Process. Agric. 2021, 8, 446–457. [Google Scholar] [CrossRef]
- Ang, K.L.M.; Seng, J.K.P. Big data and machine learning with hyperspectral information in agriculture. IEEE Access 2021, 9, 36699–36718. [Google Scholar] [CrossRef]
- Butera, L.; Ferrante, A.; Jermini, M.; Prevostini, M.; Alippi, C. Precise agriculture: Effective deep learning strategies to detect pest insects. IEEE/CAA J. Autom. Sin. 2021, 9, 246–258. [Google Scholar] [CrossRef]
- Saranya, T.; Deisy, C.; Sridevi, S.; Anbananthen, K.S.M. A comparative study of deep learning and Internet of Things for precision agriculture. Eng. Appl. Artif. Intell. 2023, 122, 106034. [Google Scholar] [CrossRef]
- Lima, M.C.F.; de Almeida Leandro, M.E.D.; Valero, C.; Coronel, L.C.P.; Bazzo, C.O.G. Automatic detection and monitoring of insect pests—A review. Agriculture 2020, 10, 161. [Google Scholar] [CrossRef]
- Kundur, N.C.; Mallikarjuna, P. Insect pest image detection and classification using deep learning. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 411–421. [Google Scholar] [CrossRef]
- Du, L.; Sun, Y.; Chen, S.; Feng, J.; Zhao, Y.; Yan, Z.; Zhang, X.; Bian, Y. A novel object detection model based on faster R-CNN for spodoptera frugiperda according to feeding trace of corn leaves. Agriculture 2022, 12, 248. [Google Scholar] [CrossRef]
- Lippi, M.; Bonucci, N.; Carpio, R.F.; Contarini, M.; Speranza, S.; Gasparri, A. A yolo-based pest detection system for precision agriculture. In Proceedings of the 2021 29th Mediterranean Conference on Control and Automation (MED), Virtually, 22–25 June 2021; pp. 342–347. [Google Scholar]
- Wang, R.; Liu, L.; Xie, C.; Yang, P.; Li, R.; Zhou, M. Agripest: A large-scale domain-specific benchmark dataset for practical agricultural pest detection in the wild. Sensors 2021, 21, 1601. [Google Scholar] [CrossRef]
- Mittal, M.; Gupta, V.; Aamash, M.; Upadhyay, T. Machine learning for pest detection and infestation prediction: A comprehensive review. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2024, 14, e1551. [Google Scholar] [CrossRef]
- Huang, M.L.; Chuang, T.C.; Liao, Y.C. Application of transfer learning and image augmentation technology for tomato pest identification. Sustain. Comput. Inform. Syst. 2022, 33, 100646. [Google Scholar] [CrossRef]
- Pang, H.; Zhang, Y.; Cai, W.; Li, B.; Song, R. A real-time object detection model for orchard pests based on improved YOLOv4 algorithm. Sci. Rep. 2022, 12, 13557. [Google Scholar] [CrossRef]
- Arun, R.A.; Umamaheswari, S. Effective and efficient multi-crop pest detection based on deep learning object detection models. J. Intell. Fuzzy Syst. 2022, 43, 5185–5203. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, S.; Li, E.; Yang, G.; Liang, Z.; Tan, M. MD-YOLO: Multi-scale Dense YOLO for small target pest detection. Comput. Electron. Agric. 2023, 213, 108233. [Google Scholar] [CrossRef]
- Khairunniza-Bejo, S.; Ibrahim, M.F.; Hanafi, M.; Jahari, M.; Ahmad Saad, F.S.; Mhd Bookeri, M.A. Automatic Paddy Planthopper Detection and Counting Using Faster R-CNN. Agriculture 2024, 14, 1567. [Google Scholar] [CrossRef]
- Yang, S.; Xing, Z.; Wang, H.; Dong, X.; Gao, X.; Liu, Z.; Zhang, X.; Li, S.; Zhao, Y. Maize-YOLO: A new high-precision and real-time method for maize pest detection. Insects 2023, 14, 278. [Google Scholar] [CrossRef] [PubMed]
- Albanese, A.; Nardello, M.; Brunelli, D. Automated pest detection with DNN on the edge for precision agriculture. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 458–467. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized focal loss v2: Learning reliable localization quality estimation for dense object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11632–11641. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. Fcos: Fully convolutional one-stage object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9627–9636. [Google Scholar]
- Lesort, T.; Lomonaco, V.; Stoian, A.; Maltoni, D.; Filliat, D.; Díaz-Rodríguez, N. Continual learning for robotics: Definition, framework, learning strategies, opportunities and challenges. Inf. Fusion 2020, 58, 52–68. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Mirza, M.; Xiao, D.; Courville, A.; Bengio, Y. An empirical investigation of catastrophic forgetting in gradient-based neural networks. arXiv 2013, arXiv:1312.6211. [Google Scholar]
- McCloskey, M.; Cohen, N.J. Catastrophic interference in connectionist networks: The sequential learning problem. Psychol. Learn. Motiv. 1989, 24, 109–165. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Chen, P.; Liu, S.; Zhao, H.; Jia, J. Distilling knowledge via knowledge review. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 5008–5017. [Google Scholar]
- Chen, G.; Choi, W.; Yu, X.; Han, T.; Chandraker, M. Learning efficient object detection models with knowledge distillation. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Sun, R.; Tang, F.; Zhang, X.; Xiong, H.; Tian, Q. Distilling object detectors with task adaptive regularization. arXiv 2020, arXiv:2006.13108. [Google Scholar]
- Dai, X.; Jiang, Z.; Wu, Z.; Bao, Y.; Wang, Z.; Liu, S.; Zhou, E. General instance distillation for object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7842–7851. [Google Scholar]
- Jia, Z.; Sun, S.; Liu, G.; Liu, B. Mssd: Multi-scale self-distillation for object detection. Vis. Intell. 2024, 2, 8. [Google Scholar] [CrossRef]
- Li, Q.; Jin, S.; Yan, J. Mimicking very efficient network for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6356–6364. [Google Scholar]
- Wang, T.; Yuan, L.; Zhang, X.; Feng, J. Distilling object detectors with fine-grained feature imitation. In Proceedings of the EEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4933–4942. [Google Scholar]
- Guo, J.; Han, K.; Wang, Y.; Wu, H.; Chen, X.; Xu, C.; Xu, C. Distilling object detectors via decoupled features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2154–2164. [Google Scholar]
- Li, G.; Li, X.; Wang, Y.; Zhang, S.; Wu, Y.; Liang, D. Knowledge distillation for object detection via rank mimicking and prediction-guided feature imitation. AAAI Conf. Artif. Intell. 2022, 36, 1306–1313. [Google Scholar] [CrossRef]
- Zhixing, D.; Zhang, R.; Chang, M.; Liu, S.; Chen, T.; Chen, Y. Distilling object detectors with feature richness. Adv. Neural Inf. Process. Syst. 2021, 34, 5213–5224. [Google Scholar]
- Cao, W.; Zhang, Y.; Gao, J.; Cheng, A.; Cheng, K.; Cheng, J. Pkd: General distillation framework for object detectors via pearson correlation coefficient. Adv. Neural Inf. Process. Syst. 2022, 35, 15394–15406. [Google Scholar]
- Yang, Z.; Li, Z.; Jiang, X.; Gong, Y.; Yuan, Z.; Zhao, D.; Yuan, C. Focal and global knowledge distillation for detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4643–4652. [Google Scholar]
- Yao, L.; Pi, R.; Xu, H.; Zhang, W.; Li, Z.; Zhang, T. G-detkd: Towards general distillation framework for object detectors via contrastive and semantic-guided feature imitation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3591–3600. [Google Scholar]
- Zhang, L.; Ma, K. Improve object detection with feature-based knowledge distillation: Towards accurate and efficient detectors. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- Zhengetal, Z. Localization distillation for object detection. IEEE Trans. Pattern Anal. Mach. Intell 2023, 45, 10070–10083. [Google Scholar]
- Wu, X.; Zhan, C.; Lai, Y.K.; Cheng, M.M.; Yang, J. Ip102: A large-scale benchmark dataset for insect pest recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8787–8796. [Google Scholar]
- Li, Z.; Hoiem, D. Learning without forgetting. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2935–2947. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Tasci, S.; Ghosh, S.; Zhu, J.; Zhang, J.; Heck, L. RILOD: Near real-time incremental learning for object detection at the edge. In Proceedings of the 4th ACM/IEEE Symposium on Edge Computing, Washington, DC, USA, 7–9 November 2019; pp. 113–126. [Google Scholar]
- Peng, C.; Zhao, K.; Maksoud, S.; Li, M.; Lovell, B.C. Sid: Incremental learning for anchor-free object detection via selective and inter-related distillation. Comput. Vis. Image Underst. 2021, 210, 103229. [Google Scholar] [CrossRef]
- Chaudhry, A.; Dokania, P.K.; Ajanthan, T.; Torr, P.H. Riemannian walk for incremental learning: Understanding forgetting and intransigence. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 532–547. [Google Scholar]
- Lopez-Paz, D.; Ranzato, M. Gradient episodic memory for continual learning. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Müller, R.; Kornblith, S.; Hinton, G.E. When does label smoothing help? In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32.
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized focal loss: Learning qualified and distributed bounding boxes for dense object detection. Adv. Neural Inf. Process. Syst. 2020, 33, 21002–21012. [Google Scholar]
- Chen, K.; Wang, J.; Pang, J.; Cao, Y.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Xu, J.; et al. MMDetection: Open mmlab detection toolbox and benchmark. arXiv 2019, arXiv:1906.07155. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]

| Dimensions | LwF | RILOD | SID | ARD (Ours) |
|---|---|---|---|---|
| Incremental Sample Handling | No replay of old samples | Replays old samples (replay buffer) | No replay of old samples | No replay of old samples |
| Old-Class Knowledge Retention | Classification logits | Sample replay + fine-tuning | Classification logits; Feature maps | Classification logits; Localization logits |
| Distillation Loss | KL | No distillation; relies on replay | KL; L2 | L2; KL |
| Node/Region Selection | All classification responses | N/A | Main region (positives) + VLR (based on DIoU) | ARF: threshold |
| Training Overhead | Low | High (replay cost grows with dataset size) | Medium (feature-hint + VLR computation) | Low (output-layer statistics + L2/KL distillation) |
| Scenarios (Classes) | Method | ||||
|---|---|---|---|---|---|
| 49 + 48 | Fine-tuning | 19.4 | 28.3 | 16.1 | 23.1 |
| LwF | 15.5 | 28.6 | 13.9 | 27.0 | |
| RILOD | 26.3 | 43.5 | 28.8 | 16.2 | |
| SID | 32.8 | 47.9 | 31.4 | 9.7 | |
| ARD | 35.8 | 54.3 | 33.6 | 6.7 | |
| 61 + 36 | Fine-tuning | 14.2 | 22.5 | 14.2 | 28.3 |
| LwF | 10.1 | 15.8 | 9.6 | 32.4 | |
| RILOD | 25.5 | 42.3 | 28.6 | 17.0 | |
| SID | 29.2 | 46.0 | 30.3 | 13.3 | |
| ARD | 34.3 | 52.7 | 32.8 | 8.2 | |
| 73 + 24 | Fine-tuning | 9.8 | 16.9 | 9.5 | 32.7 |
| LwF | 7.3 | 12.4 | 8.4 | 35.2 | |
| RILOD | 24.6 | 40.4 | 27.8 | 17.9 | |
| SID | 30.4 | 43.2 | 28.9 | 12.1 | |
| ARD | 34.0 | 51.2 | 32.5 | 8.5 | |
| 85 + 12 | Fine-tuning | 7.6 | 9.2 | 7.4 | 34.9 |
| LwF | 8.9 | 13.3 | 8.7 | 33.6 | |
| RILOD | 23.7 | 38.4 | 24.8 | 18.8 | |
| SID | 29.4 | 41.1 | 29.1 | 13.1 | |
| ARD | 32.6 | 50.5 | 31.7 | 9.9 | |
| All classes | Joint Training | 42.5 | 58.4 | 38.6 |
| Method | a (1–49) | +b (49–61) | +b (61–73) | +b (73–85) | +b (85–97) | a (1–97) |
|---|---|---|---|---|---|---|
| Fine-tuning | 7.8/9.7 | 8.3/10.3 | 8.1/10.5 | 6.1/8.4 | 42.5/58.4 | |
| RILOD | 53.6/68.7 | 26.9/41.3 | 13.7/18.6 | 12.4/17.7 | 11.6/14.2 | |
| SID | 30.8/48.1 | 23.2/34.3 | 16.6/25.6 | 13.2/23.8 | ||
| ARD | 35.7/54.2 | 32.4/47.6 | 29.2/40.8 | 22.8/32.5 |
| Method | a (1–49) | +b (49–73) | +b (73–97) | a (1–97) |
|---|---|---|---|---|
| Fine-tuning | 12.1/17.3 | 9.3/11.6 | 42.5/58.4 | |
| RILOD | 53.6/68.7 | 27.2/44.9 | 18.5/26.0 | |
| SID | 30.4/47.8 | 22.8/31.2 | ||
| ARD | 36.5/55.8 | 33.2/46.9 |
| Threshold | ||||
|---|---|---|---|---|
| 35.7 | 54.1 | 33.6 | 6.7 | |
| 35.5 | 54.6 | 33.9 | 6.7 | |
| 35.3 | 54.3 | 33.4 | 6.7 | |
| 35.8 | 54.3 | 33.6 | 6.7 |
| Method | ||||
|---|---|---|---|---|
| KD:cls + reg | 30.7 | 47.3 | 29.2 | 11.5 |
| KD:cls | 24.8 | 35.7 | 24.9 | 18.9 |
| KD:reg | 15.7 | 22.1 | 16.2 | 26.0 |
| ARD:cls | 30.4 | 49.2 | 31.3 | 12.6 |
| ARD:cls + reg | 35.8 | 54.3 | 33.6 | 6.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yin, Z.; Li, D.; Zhao, Y. Mitigating Catastrophic Forgetting in Pest Detection Through Adaptive Response Distillation. Agriculture 2025, 15, 1006. https://doi.org/10.3390/agriculture15091006
Zhang H, Yin Z, Li D, Zhao Y. Mitigating Catastrophic Forgetting in Pest Detection Through Adaptive Response Distillation. Agriculture. 2025; 15(9):1006. https://doi.org/10.3390/agriculture15091006
Chicago/Turabian StyleZhang, Hongjun, Zhendong Yin, Dasen Li, and Yanlong Zhao. 2025. "Mitigating Catastrophic Forgetting in Pest Detection Through Adaptive Response Distillation" Agriculture 15, no. 9: 1006. https://doi.org/10.3390/agriculture15091006
APA StyleZhang, H., Yin, Z., Li, D., & Zhao, Y. (2025). Mitigating Catastrophic Forgetting in Pest Detection Through Adaptive Response Distillation. Agriculture, 15(9), 1006. https://doi.org/10.3390/agriculture15091006






