The Effect of Climate Change on Important Climate Variables in Taiwan and Its Potential Impact on Crop Production
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Analysis of Correlation and Relative Impact of Climate Variables
2.3. Trend Analysis
2.4. Statistical Software
3. Results
3.1. Relationship Between ET0 and the Related Climate Variables
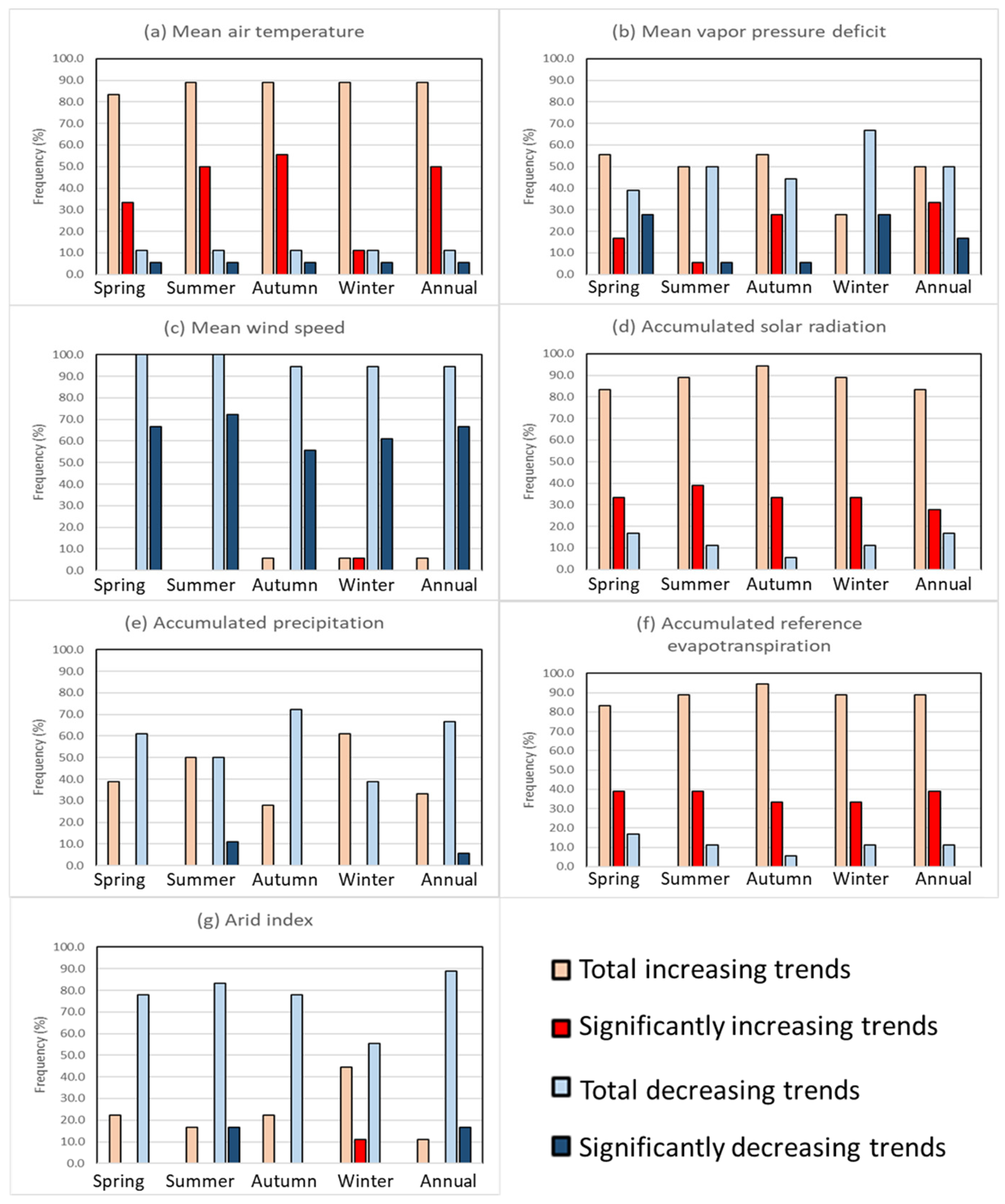
3.2. Trends of Important Climate Variables in Taiwan
3.3. Findings from Multi-Station Trend Analysis
3.4. Trends of the Arid Index for the Geographic Regions in Taiwan
4. Discussion
4.1. Comparison of the Effects of Climate Change in Taiwan and Other Regions
4.2. Changes in Important Climate Variables and Their Possible Impacts on Crop Production
4.3. Comparison of Different Multi-Station Analysis Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stern, N. A time for action on climate change and a time for change in economics. Econ. J. 2022, 132, 1259–1289. [Google Scholar] [CrossRef]
- Malhi, G.S.; Kaur, M.; Kaushik, P. Impact of climate change on agriculture and its mitigation strategies: A review. Sustainability 2021, 13, 1318. [Google Scholar] [CrossRef]
- Ming, A.; Rowell, I.; Lewin, S.; Rouse, R.; Aubry, T.; Boland, E. Key Messages from the IPCC AR6 Climate Science Report; IPCC: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]
- Abdul-Aziz, O.I.; Burn, D.H. Trends and variability in the hydrological regime of the Mackenzie River Basin. J. Hydrol. 2006, 319, 282–294. [Google Scholar] [CrossRef]
- Li, M.H.; Tien, W.; Tung, C.P. Assessing the impact of climate change on the land hydrology in Taiwan. Paddy Water Environ. 2009, 7, 283–292. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Chen, X. Reference evapotranspiration changes in China: Natural processes or human influences? Theor. Appl. Climatol. 2011, 103, 479–488. [Google Scholar] [CrossRef]
- Croitoru, A.-E.; Piticar, A.; Dragotă, C.S.; Burada, D.C. Recent changes in reference evapotranspiration in Romania. Glob. Planet. Change 2013, 111, 127–136. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration–A review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Maček, U.; Bezak, N.; Šraj, M. Reference evapotranspiration changes in Slovenia, Europe. Agric. For. Meteorol. 2018, 260, 183–192. [Google Scholar] [CrossRef]
- Łabędzki, L.; Bąk, B.; Smarzyńska, K. Spatio-temporal variability and trends of Penman-Monteith reference evapotranspiration (FAO-56) in 1971–2010 under climatic conditions of Poland. Pol. J. Environ. Stud. 2014, 23, 2083–2091. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend analysis in reference evapotranspiration using Mann-Kendall and Spearman’s Rho tests in arid regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in China during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Katerji, N.; Rana, G. Crop reference evapotranspiration: A discussion of the concept, analysis of the process, and validation. Water Resour. Manag. 2011, 25, 1581–1600. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Revuelto, J.; López-Moreno, J.I.; González-Hidalgo, J.C.; Moran-Tejeda, E.; Espejo, F. Reference evapotranspiration variability and trends in Spain, 1961–2011. Glob. Planet. Change 2014, 121, 26–40. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Hong, H. Assessing the effect of climate change on reference evapotranspiration in China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1871–1881. [Google Scholar] [CrossRef]
- De la Casa, A.C.; Ovando, G.G. Variation of reference evapotranspiration in the central region of Argentina between 1941 and 2010. J. Hydrol. Reg. Stud. 2016, 5, 66–79. [Google Scholar] [CrossRef][Green Version]
- Fan, J.; Wu, L.; Zhang, F.; Xiang, Y.; Zheng, J. Climate change effects on reference crop evapotranspiration across different climatic zones of China during 1956–2015. J. Hydrol. 2016, 542, 923–937. [Google Scholar] [CrossRef]
- Fan, Z.X.; Thomas, A. Spatiotemporal variability of reference evapotranspiration and its contributing climatic factors in Yunnan Province, SW China, 1961–2004. Clim. Change 2013, 116, 309–325. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. The cause of decreased pan evaporation over the past 50 years. Science 2002, 298, 1410–1411. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend analysis of reference evapotranspiration in the western half of Iran. Agric. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Thas, O.; Van Vooren, L.; Ottoy, J.P. Nonparametric test performance for trends in water quality with sampling design applications. J. Am. Water Resour. Assoc. 1998, 34, 347–357. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.; Duong, T.C. Testing for multivariate trends in hydrologic frequency analysis. J. Hydrol. 2013, 486, 519–530. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Clement, L.; Thas, O. Nonparametric trend detection in river monitoring network data: A spatio-temporal approach. Environmetrics 2009, 20, 283–297. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Water Resources Agency. Annual Water Consumption Report for 2020. Available online: https://wuss.wra.gov.tw/annualreports/20220006109%E5%B9%B4%E6%B0%B4%E7%B5%B1%E8%A8%88%E5%B9%B4%E5%A0%B1_compressed%20(1).pdf (accessed on 28 February 2024).
- Sharma, V.; Irmak, S. Mapping spatially interpolated precipitation, reference evapotranspiration, actual crop evapotranspiration, and net irrigation requirements in Nebraska: Part I. Precipitation and reference evapotranspiration. Trans. ASABE 2012, 55, 907–921. [Google Scholar] [CrossRef]
- Hsu, H.-H.; Chen, C.-T. Observed and projected climate change in Taiwan. Meteorol. Atmos. Phys. 2002, 79, 87–104. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Wu, C.-K. Effects of climate change on evapotranspiration from paddy fields in southern Taiwan. Clim. Change 2002, 54, 165–179. [Google Scholar] [CrossRef]
- Decorte, T.; Mortier, S.; Lembrechts, J.J.; Meysman, F.J.R.; Latré, S.; Mannens, E.; Verdonck, T. Missing value imputation of wireless sensor data for environmental monitoring. Sensors 2024, 24, 2416. [Google Scholar] [CrossRef]
- Narapusetty, B.; DelSole, T.; Tippett, M.K. Optimal estimation of the climatological mean. J. Clim. 2009, 22, 4845–4859. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Yang, J.; Wang, Y. Potential evapotranspiration and its attribution over the past 50 years in the arid region of Northwest China. Hydrol. Process 2014, 28, 1025–1031. [Google Scholar] [CrossRef]
- Oudin, L.; Moulin, L.; Bendjoudi, H.; Ribstein, P. Estimating potential evapotranspiration without continuous daily data: Possible errors and impact on water balance simulations. Hydrol. Sci. J. 2010, 55, 209–222. [Google Scholar] [CrossRef]
- Tao, X.H.C.; Xu, C. Characteristics of drought variations in Hanjiang Basin in 1961–2014 based on SPI/SPEI. J. Water Resour. Res. 2015, 4, 404–415. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, F.; Xu, J.; Chen, Y.; Sang, Y.F.; Liu, C. Dependence of trends in and sensitivity of drought over China (1961–2013) on potential evaporation model. Geophys. Res. Lett. 2016, 43, 206–213. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Rustum, R.; Kariyama, I.D. Neural computing modeling of the reference crop evapotranspiration. Environ. Model. Softw. 2012, 29, 61–73. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2011, 29, 11–25. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fang, S.-L.; Tu, Y.-K.; Kang, L.; Chen, H.-W.; Chang, T.-J.; Yao, M.-H.; Kuo, B.-J. CART model to classify the drought status of diverse tomato genotypes by VPD, air temperature, and leaf–air temperature difference. Sci. Rep. 2023, 13, 602. [Google Scholar] [CrossRef]
- Fang, S.-L.; Cheng, Y.-J.; Tu, Y.-K.; Yao, M.-H.; Kuo, B.-J. Exploring efficient methods for using multiple spectral reflectance indices to establish a prediction model for early drought stress detection in greenhouse tomato. Horticulturae 2023, 9, 1317. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 14, 2225–2236. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendalls tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the power of the Mann-Kendall test for detecting monotonic trends in hydrometeorological time series. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
- Lettenmaier, D.P. Multivariate nonparametric tests for trend in water quality. J. Am. Water Resour. Assoc. 1988, 24, 505–512. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. WIREs Data. Mining. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L. To tune or not to tune the number of trees in random forest. J. Mach. Learn. Res. 2018, 18, 1–18. [Google Scholar]
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Sharma, G.; Singh, A.; Jain, S. A hybrid deep neural network approach to estimate reference evapotranspiration using limited climate data. Neural Comput. Applic. 2022, 34, 4013–4032. [Google Scholar] [CrossRef]
- Fang, S.-L.; Lin, Y.-S.; Chang, S.-C.; Chang, Y.-L.; Tsai, B.-Y.; Kuo, B.-J. Using artificial intelligence algorithms to estimate and short-term forecast the daily reference evapotranspiration with limited meteorological variables. Agriculture 2024, 14, 510. [Google Scholar] [CrossRef]
- Sharma, V.; Irmak, S. Mapping spatially interpolated precipitation, reference evapotranspiration, actual crop evapotranspiration, and net irrigation requirements in Nebraska: Part II. Actual crop evapotranspiration and net irrigation requirements. Trans. ASABE 2012, 55, 923–936. [Google Scholar]
- Zhang, Q.; Zhang, J. Drought hazard assessment in typical corn cultivated areas of China at present and potential climate change. Nat. Hazards 2016, 81, 1323–1331. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Meza, I.; Eyshi Rezaei, E.; Siebert, S.; Ghazaryan, G.; Nouri, H.; Dubovyk, O.; Gerdener, H.; Herbert, C.; Kusche, J.; Popat, E.; et al. Drought risk for agricultural systems in South Africa: Drivers, spatial patterns, and implications for drought risk management. Sci. Total Environ. 2021, 799, 149505. [Google Scholar] [CrossRef]
- Shahpari, G.; Ashena, M.; Martinez-Cruz, A.L.; León, D.G. Implications for the Iranian economy from climate change effects on agriculture—A static computable general equilibrium approach. Theor. Appl. Climatol. 2023, 153, 1221–1235. [Google Scholar] [CrossRef]
- Kumar, S.; Chatterjee, U.; David Raj, A.; Sooryamol, K.R. Global Warming and Climate Crisis/Extreme Events. In Climate Crisis: Adaptive Approaches and Sustainability; Chatterjee, U., Shaw, R., Kumar, S., Raj, A.D., Das, S., Eds.; Sustainable Development Goals Series; Springer: Cham, Switzerland, 2024; pp. 3–18. [Google Scholar] [CrossRef]
- Bordoni, S.; Kang, S.M.; Shaw, T.A.; Simpson, I.R.; Zanna, L. The futures of climate modeling. npj Clim. Atmos. Sci. 2025, 8, 99. [Google Scholar] [CrossRef]
- Peng, S.; Huang, J.; Sheehy, J.E.; Laza, R.C.; Visperas, R.M.; Zhong, X.; Centeno, G.S.; Khush, G.S.; Cassman, K.G. Rice yields decline with higher night temperature from global warming. Proc. Natl. Acad. Sci. USA 2004, 101, 9971–9975. [Google Scholar] [CrossRef]
- Zhu, C.; Kobayashi, K.; Loladze, I.; Zhu, J.; Jiang, Q.; Xu, X.; Liu, G.; Seneweera, S.; Ebi, K.L.; Drewnowski, A.; et al. Carbon dioxide (CO2) levels this century will alter the protein, micronutrients, and vitamin content of rice grains with potential health consequences for the poorest rice-dependent countries. Sci. Adv. 2018, 4, eaaq1012. [Google Scholar] [CrossRef]
- Rezvi, H.U.A.; Tahjib-Ul-Arif, M.; Azim, M.A.; Tumpa, T.A.; Tipu, M.M.H.; Najnine, F.; Dawood, M.F.A.; Skalicky, M.; Brestič, M. Rice and food security: Climate change implications and the future prospects for nutritional security. Food Energy Secur. 2022, 12, 430. [Google Scholar] [CrossRef]
- Parker, L.E.; Abatzoglou, J.T. Warming winters reduce CHILL accumulation for peach production in the southeastern United States. Climate 2019, 7, 94. [Google Scholar] [CrossRef]
- Simelton, E.; Carew-Reid, J.; Coulier, M.; Damen, B.; Howell, J.; Pottinger-Glass, C.; Tran, H.V.; Van Der Meiren, M. NBS framework for agricultural landscapes. Front. Environ. Sci. 2021, 9, 678367. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A. Assessment of climate change impacts on chilling and forcing for the main fresh fruit regions in Portugal. Front. Plant Sci. 2021, 12, 689121. [Google Scholar] [CrossRef] [PubMed]
- Yao, F.; Livneh, B.; Rajagopalan, B.; Wang, J.; Crétaux, J.F.; Wada, Y.; Berge-Nguyen, M. Satellites reveal widespread decline in global lake water storage. Science 2023, 380, 743–749. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J. Anthropogenic warming has caused hot droughts more frequently in China. J. Hydrol. 2017, 544, 306–318. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J. Characterizing present and future drought changes over eastern China. Int. J. Climatol. 2017, 37, 138–156. [Google Scholar] [CrossRef]
- Dai, A. Hydroclimatic trends during 1950–2018 over global land. Clim. Dyn. 2021, 56, 4027–4049. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, Q.; Zhao, X.; Wu, P.; Pan, W.; Gao, X.; Sun, M. Temporal and spatial evolution of the standardized precipitation evapotranspiration index (SPEI) in the Loess Plateau under climate change from 2001 to 2050. Sci. Total Environ. 2017, 595, 191–200. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, A. Uncertainties in historical Changes and future projections of drought. Part II: Model-simulated historical and future drought Changes. Clim. Change 2017, 144, 535–548. [Google Scholar] [CrossRef]
- Sloat, L.L.; Davis, S.J.; Gerber, J.S.; Moore, F.C.; Ray, D.K.; West, P.C.; Mueller, N.D. Climate adaptation by crop migration. Nat. Commun. 2020, 11, 1243. [Google Scholar] [CrossRef]
- Su, Y.-C.; Wu, C.-Y.; Kuo, B.-J. Characterizing spatiotemporal patterns of disasters and climates to evaluate hazards to crop production in Taiwan. Agriculture 2024, 14, 1384. [Google Scholar] [CrossRef]
- Su, Y.-C.; Kuo, B.-J. Risk assessment of rice damage due to heavy rain in Taiwan. Agriculture 2023, 13, 630. [Google Scholar] [CrossRef]
- Fang, S.-L.; Chang, T.-J.; Tu, Y.-K.; Chen, H.-W.; Yao, M.-H.; Kuo, B.-J. Plant-response-based control strategy for irrigation and environmental controls for greenhouse tomato seedling cultivation. Agriculture 2022, 12, 633. [Google Scholar] [CrossRef]
- Surendran, U.; Raja, P.; Jayakumar, M.; Rama Subramoniam, S. Use of efficient water saving techniques for production of rice in India under climate change scenario: A critical review. J. Clean Prod. 2021, 309, 127272. [Google Scholar] [CrossRef]
- Du, T.; Kang, S.; Zhang, J.; Davies, W.J. Deficit irrigation and sustainable water-resource strategies in agriculture for China’s food security. J. Exp. Bot. 2015, 66, 2253–2269. [Google Scholar] [CrossRef]
- Yang, B.; Fu, P.; Lu, J.; Ma, F.; Sun, X.; Fang, Y. Regulated deficit irrigation: An effective way to solve the shortage of agricultural water for horticulture. Stress Biol. 2022, 2, 28. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Charlesworth, S.M.; Perales-Momparler, S.; Andrés-Doménech, I. Prediction of evapotranspiration in a Mediterranean region using basic meteorological variables. J. Hydrol. Eng. 2017, 22, 04016064. [Google Scholar] [CrossRef]
- Miller, H.J. Tobler’s first law and spatial analysis. Ann. Am. Assoc. Geogr. 2004, 94, 284–289. [Google Scholar] [CrossRef]
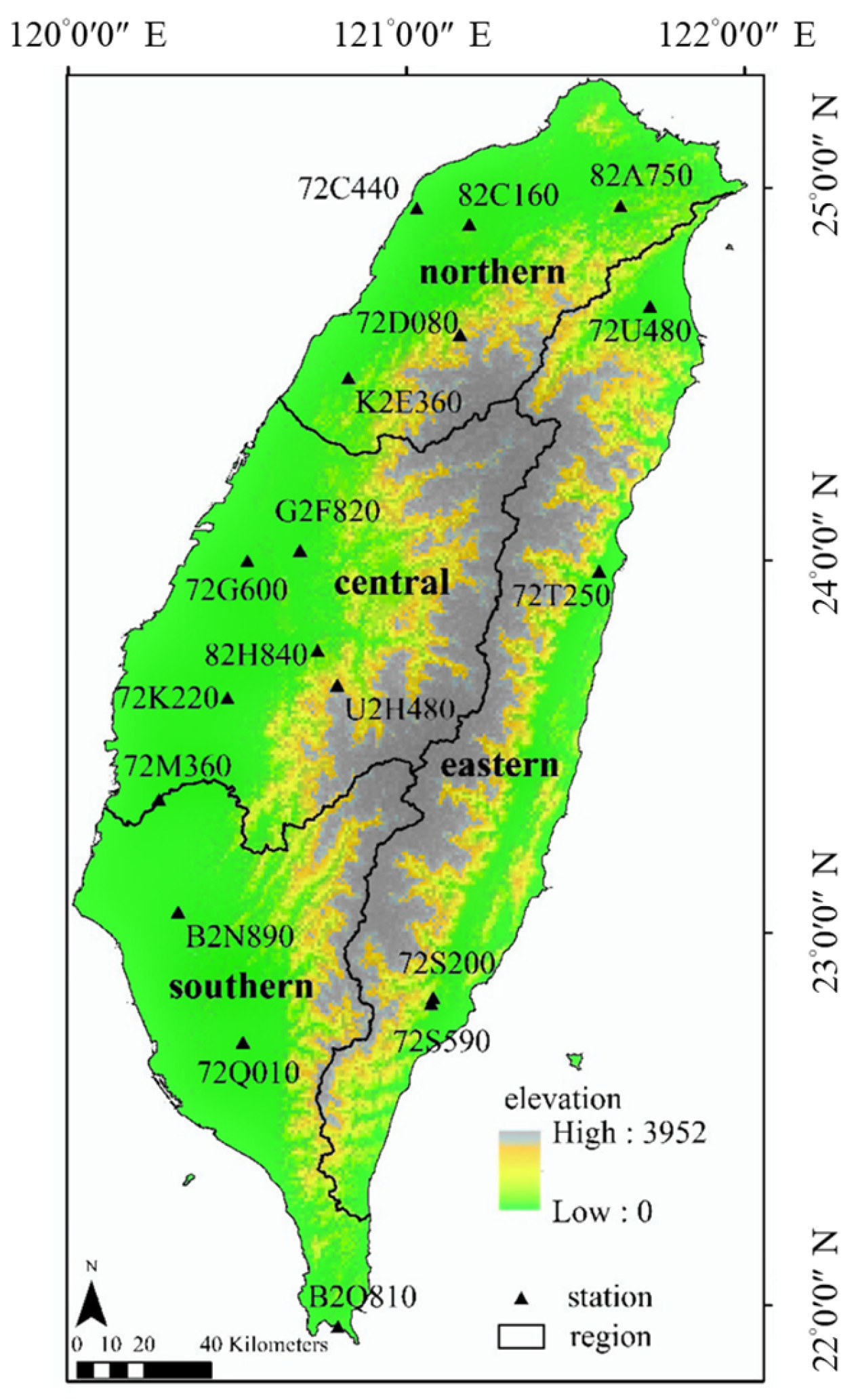
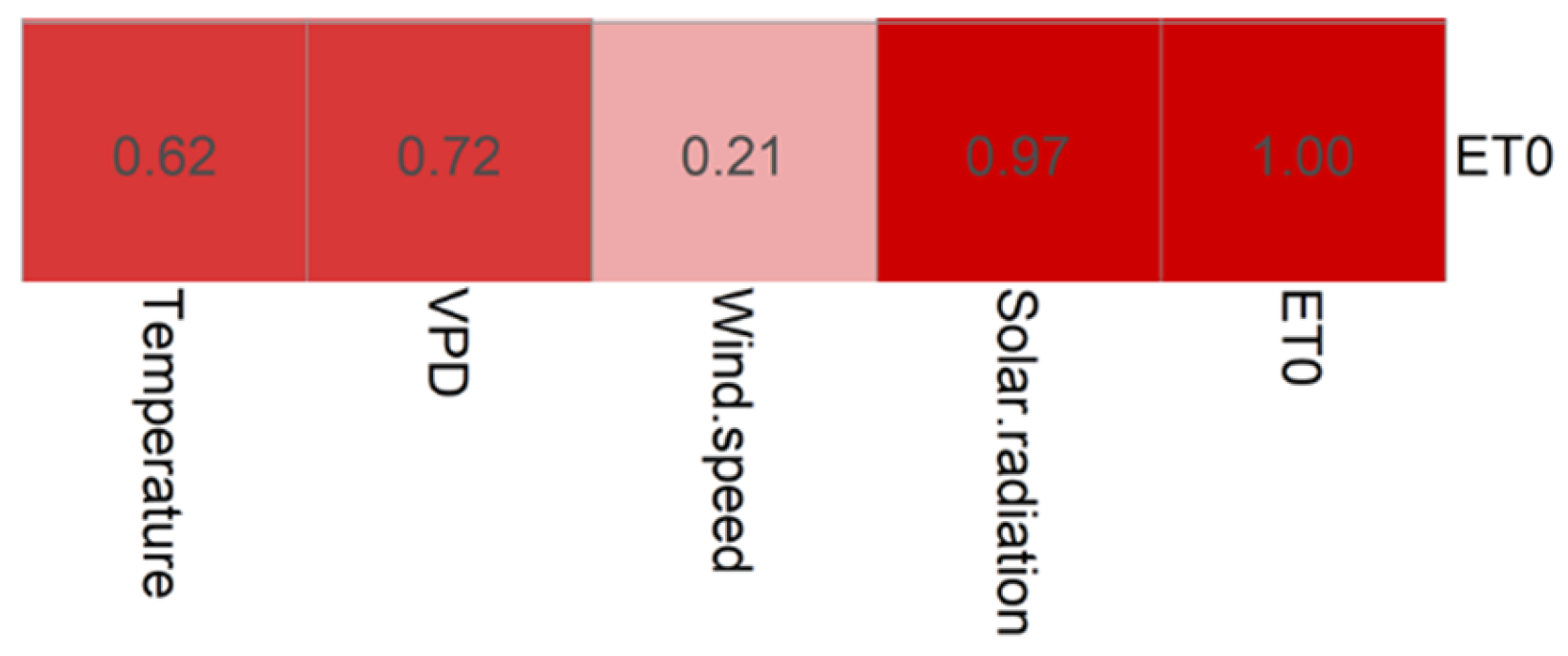
| Region | Station | Latitude (N) | Longitude (E) | Altitude (m.a.s.l.) | T (°C) | VPD (kPa) | u2 (m/s) | Rs (MJ/m2/yr) | PP (mm/yr) | ET0 (mm/yr) | Arid Index |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Northern | 72C440 | 24.95 | 121.03 | 70 | 22.27 | 0.55 | 3.94 | 4736.69 | 1451.56 | 1530.90 | 0.96 |
| 72D080 | 24.61 | 121.16 | 1048 | 17.32 | 0.25 | 0.50 | 3589.81 | 2711.03 | 999.20 | 2.91 | |
| 82A750 | 24.96 | 121.63 | 401 | 20.06 | 0.37 | 1.45 | 3810.00 | 3547.91 | 1136.49 | 3.50 | |
| 82C160 | 24.91 | 121.19 | 195 | 21.56 | 0.50 | 2.89 | 4295.31 | 2098.84 | 1354.76 | 1.58 | |
| K2E360 | 24.50 | 120.83 | 100 | 22.23 | 0.51 | 2.36 | 4812.51 | 1748.37 | 1476.00 | 1.20 | |
| Central | 72G600 | 24.00 | 120.53 | 19 | 23.39 | 0.58 | 1.99 | 4236.69 | 1380.61 | 1359.50 | 1.05 |
| 72K220 | 23.63 | 120.48 | 60 | 23.38 | 0.56 | 1.87 | 4510.79 | 1787.60 | 1416.42 | 1.29 | |
| 72M360 | 23.36 | 120.28 | 6 | 23.59 | 0.52 | 3.02 | 5491.08 | 1501.06 | 1648.99 | 0.93 | |
| 82H840 | 23.76 | 120.74 | 390 | 21.52 | 0.34 | 0.91 | 4633.75 | 2279.39 | 1330.67 | 1.73 | |
| G2F820 | 24.03 | 120.69 | 90 | 23.52 | 0.55 | 2.21 | 4575.15 | 1667.58 | 1440.28 | 1.19 | |
| U2H480 | 23.67 | 120.80 | 1150 | 17.05 | 0.21 | 1.06 | 3373.81 | 2473.58 | 909.84 | 2.76 | |
| Southern | BSQ810 | 21.95 | 120.80 | 20 | 25.34 | 0.73 | 4.12 | 5989.74 | 2022.48 | 1997.92 | 1.04 |
| B2N890 | 23.06 | 120.34 | 31 | 23.71 | 0.53 | 1.82 | 4452.66 | 2035.04 | 1386.30 | 1.53 | |
| 72Q010 | 22.71 | 120.53 | 45 | 24.98 | 0.69 | 1.45 | 4509.98 | 2360.49 | 1468.69 | 1.70 | |
| Eastern | 72S200 | 22.83 | 121.08 | 240 | 22.50 | 0.53 | 1.51 | 3184.27 | 1980.31 | 1053.10 | 1.96 |
| 72S590 | 22.81 | 121.07 | 290 | 22.43 | 0.39 | 1.30 | 2862.04 | 1897.40 | 905.51 | 2.35 | |
| 72T250 | 23.98 | 121.56 | 36 | 22.92 | 0.54 | 1.13 | 3857.17 | 2050.43 | 1218.36 | 1.75 | |
| 72U480 | 24.69 | 121.72 | 27 | 22.45 | 0.48 | 1.82 | 4250.42 | 2946.22 | 1325.94 | 2.24 |
| Region | Station | Statistic | T (°C /yr) | VPD (kPa/yr) | u2 (m/s/yr) | Rs (MJ/m2/yr) | PP (mm/yr) | ET0 (mm/yr) | Arid Index |
|---|---|---|---|---|---|---|---|---|---|
| Northern | All | z | 1.76 | 0.86 | −4.71 | 3.42 | −0.06 | 3.53 | −0.72 |
| 72C440 | Slope | 0.0274 | 0.0017 | −0.0379 | 64.4018 | −2.8776 | 14.8468 | −0.0121 | |
| z | 1.85 | 1.66 | −3.08 | 5.13 | −0.26 | 4.48 | −2.80 | ||
| 72D080 | Slope | 0.0287 | 0.0006 | −0.0069 | −7.3054 | −10.8861 | −1.6226 | −0.0040 | |
| z | 1.27 | 2.02 | −1.02 | −0.15 | −0.57 | −0.24 | −0.14 | ||
| 82A750 | Slope | −0.0269 | −0.0060 | −0.0170 | −51.2209 | 11.1150 | −18.5568 | 0.0477 | |
| z | −1.31 | −1.62 | −0.97 | −0.68 | 0.69 | −1.15 | 1.24 | ||
| 82C160 | Slope | 0.0285 | −0.0005 | −0.0636 | 66.2084 | −3.6080 | 14.7723 | −0.0222 | |
| z | 1.75 | −0.21 | −3.88 | 4.68 | −0.34 | 3.09 | −1.56 | ||
| K2E360 | Slope | 0.0300 | 0.0049 | −0.0153 | 38.2372 | 2.4963 | 13.5855 | −0.0111 | |
| z | 1.98 | 2.10 | −1.88 | 3.48 | 0.10 | 6.13 | −1.13 | ||
| Central | All | z | 3.40 | 1.43 | −4.40 | 2.83 | 0.11 | 3.50 | −1.40 |
| 72G600 | Slope | 0.0337 | 0.0026 | 0.0029 | 54.7603 | −0.2111 | 16.7439 | −0.0162 | |
| z | 2.54 | 2.20 | 1.03 | 1.02 | 0.00 | 1.15 | −1.80 | ||
| 72K220 | Slope | 0.0451 | 0.0000 | −0.0283 | 2.8293 | −1.2749 | 5.4492 | −0.0104 | |
| z | 4.33 | 0.14 | −2.93 | 0.07 | −0.10 | 0.70 | −1.05 | ||
| 72M360 | Slope | 0.0336 | 0.0081 | −0.0335 | 28.2188 | 0.8462 | 12.9502 | −0.0066 | |
| z | 3.52 | 2.59 | −3.42 | 1.47 | 0.06 | 2.36 | −0.93 | ||
| 82H840 | Slope | 0.0092 | −0.0010 | −0.0041 | 29.9815 | 6.2557 | 8.2366 | −0.0095 | |
| z | 0.36 | −0.49 | −2.08 | 1.90 | 0.41 | 2.22 | −0.89 | ||
| G2F820 | Slope | 0.0359 | 0.0053 | −0.0103 | 82.7472 | −1.1488 | 26.2093 | −0.0216 | |
| z | 3.42 | 2.38 | −1.19 | 2.38 | −0.14 | 3.53 | −2.00 | ||
| U2H480 | Slope | 0.0233 | −0.0025 | −0.0231 | 22.7595 | 6.0904 | 4.9367 | −0.0073 | |
| z | 3.32 | −3.89 | −3.43 | 1.89 | 0.39 | 2.39 | −0.41 | ||
| Southern | All | z | 2.32 | 1.53 | −5.74 | 1.75 | 0.03 | 2.00 | −1.02 |
| B2Q810 | Slope | 0.0080 | 0.0007 | −0.0487 | 3.2620 | −1.1748 | 0.1380 | −0.0350 | |
| z | 1.34 | 0.54 | −3.24 | 0.36 | −0.22 | 0.03 | 0.06 | ||
| B2N890 | Slope | 0.0224 | 0.0039 | −0.0316 | 63.2969 | 9.4717 | 19.6473 | −0.0102 | |
| z | 2.77 | 2.00 | −4.35 | 0.97 | 0.69 | 1.44 | −0.81 | ||
| 72Q010 | Slope | 0.0178 | −0.0019 | −0.0446 | 44.1143 | −8.2721 | 14.592 | 0.0005 | |
| z | 2.29 | −0.42 | −4.34 | 1.22 | −0.38 | 1.15 | −1.88 | ||
| Eastern | All | z | 1.22 | −3.40 | −5.02 | 2.92 | −1.94 | 2.02 | −2.33 |
| 72S200 | Slope | 0.0337 | −0.0038 | −0.0156 | −3.6189 | −18.5293 | 0.4108 | −0.0185 | |
| z | 3.30 | −2.11 | −2.82 | −0.13 | −1.64 | 0.10 | −1.48 | ||
| 72S590 | Slope | −0.0394 | −0.0129 | −0.0110 | 59.6778 | −34.4626 | 11.3245 | −0.0639 | |
| z | −2.56 | −2.21 | −3.68 | 1.43 | −3.06 | 0.99 | −1.72 | ||
| 72T250 | Slope | 0.0194 | −0.0045 | −0.0015 | 34.5151 | −19.3100 | 10.3225 | −0.0404 | |
| z | 1.15 | −1.65 | −0.12 | 1.87 | −1.52 | 1.73 | −2.98 | ||
| 72U480 | Slope | 0.0215 | −0.0043 | −0.0400 | 17.3881 | −1.0984 | 2.1031 | −0.0032 | |
| z | 1.54 | −2.40 | −3.38 | 3.68 | −0.02 | 1.29 | −0.18 |
| Region | Station | Statistic | T (°C /yr) | VPD (kPa/yr) | u2 (m/s/yr) | Rs (MJ/m2/yr) | PP (mm/yr) | ET0 (mm/yr) | Arid Index |
|---|---|---|---|---|---|---|---|---|---|
| Northern | All | z | 0.69 | −0.03 | −4.27 | 3.08 | 0.33 | 2.77 | 0.18 |
| 72C440 | Slope | 0.0138 | 0.0013 | −0.0415 | 15.9971 | −0.8813 | 3.8408 | −0.0138 | |
| z | 0.90 | 0.75 | −3.52 | 4.07 | −0.09 | 4.45 | −0.85 | ||
| 72D080 | Slope | 0.0095 | 0.0000 | −0.0050 | 0.5928 | 1.6524 | 0.4268 | 0.0330 | |
| z | 0.61 | −0.08 | −0.82 | 0.04 | 0.30 | 0.11 | 0.97 | ||
| 82A750 | Slope | −0.0272 | −0.0050 | −0.0249 | −13.2194 | 6.6875 | −4.6200 | 0.0598 | |
| z | −0.86 | −0.96 | −2.00 | −0.70 | 0.89 | −1.14 | 1.96 | ||
| 82C160 | Slope | 0.0223 | −0.0025 | −0.0568 | 17.7454 | −0.5704 | 4.2049 | −0.0248 | |
| z | 0.91 | −0.75 | −3.58 | 4.05 | −0.14 | 3.22 | −1.80 | ||
| K2E360 | Slope | 0.0188 | 0.0038 | −0.0154 | 12.5493 | 2.007 | 3.6716 | −0.0084 | |
| z | 1.49 | 1.25 | −1.52 | 3.34 | 0.55 | 3.18 | −0.26 | ||
| Central | All | z | 2.26 | 1.44 | −4.14 | 2.55 | −0.42 | 3.36 | −1.14 |
| 72G600 | Slope | 0.0312 | 0.0023 | 0.0050 | 15.8833 | −0.7666 | 4.4678 | −0.0153 | |
| z | 2.57 | 1.61 | 0.99 | 0.99 | −0.26 | 1.57 | −1.48 | ||
| 72K220 | Slope | 0.0276 | 0.0006 | −0.0223 | −0.9159 | −3.7076 | 0.8555 | −0.0102 | |
| z | 3.03 | 0.20 | −3.62 | −0.31 | −0.81 | 0.76 | −1.01 | ||
| 72M360 | Slope | 0.0271 | 0.0080 | −0.0315 | 10.5334 | 1.7123 | 3.2939 | −0.0018 | |
| z | 2.57 | 2.39 | −3.22 | 1.55 | 0.49 | 1.75 | −0.18 | ||
| 82H840 | Slope | 0.0117 | 0.0011 | −0.0039 | 6.0227 | −5.4466 | 2.1120 | −0.0214 | |
| z | 0.59 | 0.34 | −1.15 | 1.70 | −1.21 | 2.23 | −1.40 | ||
| G2F820 | Slope | 0.0304 | 0.0070 | −0.0121 | 18.0075 | −1.4439 | 5.3146 | −0.0172 | |
| z | 3.17 | 2.59 | −1.18 | 4.40 | −0.26 | 4.64 | −1.36 | ||
| U2H480 | Slope | 0.0181 | −0.0018 | −0.0218 | 4.3164 | −0.6457 | 1.0435 | −0.0133 | |
| z | 1.42 | −2.48 | −3.37 | 2.19 | −0.16 | 2.11 | −0.77 | ||
| Southern | All | z | 1.30 | 1.35 | −5.41 | 1.26 | −0.25 | 2.20 | −0.75 |
| B2Q810 | Slope | 0.0000 | 0.0000 | −0.0503 | 2.1671 | 0.9743 | 0.5306 | −0.0171 | |
| z | 0.00 | 0.00 | −2.80 | 1.27 | 0.26 | 0.65 | 0.49 | ||
| B2N890 | Slope | 0.0184 | 0.0054 | −0.0300 | 16.3192 | −0.1426 | 4.9767 | −0.0060 | |
| z | 1.67 | 2.22 | −5.44 | 0.95 | 0.00 | 1.92 | −0.65 | ||
| 72Q010 | Slope | 0.0243 | 0.0030 | −0.0460 | 8.5095 | −2.0792 | 4.2178 | 0.0029 | |
| z | 2.08 | 0.83 | −4.57 | 0.28 | −0.89 | 0.90 | −1.68 | ||
| Eastern | All | z | 0.04 | −3.34 | −4.91 | 1.46 | −0.04 | 0.79 | −0.45 |
| 72S200 | Slope | 0.0253 | −0.0050 | −0.0147 | −0.1023 | −0.4531 | −0.2667 | −0.0044 | |
| z | 2.29 | −2.22 | −3.58 | −0.01 | –0.38 | −0.04 | −0.42 | ||
| 72S590 | Slope | −0.0455 | −0.0118 | −0.0128 | 9.5870 | −2.1091 | 1.2536 | −0.0155 | |
| z | −2.61 | −2.57 | −3.15 | 0.84 | −0.69 | 0.44 | −0.85 | ||
| 72T250 | Slope | 0.0113 | −0.0057 | −0.0084 | 12.9683 | 0.1131 | 3.1416 | −0.0119 | |
| z | 1.05 | −2.42 | −0.66 | 2.59 | 0.08 | 2.07 | −1.42 | ||
| 72U480 | Slope | 0.0078 | −0.0067 | −0.0339 | 0.4366 | 3.0147 | −0.4624 | 0.0147 | |
| z | 0.63 | −3.01 | −3.26 | 0.18 | 0.47 | −0.49 | 0.69 |
| Region | Station | Statistic | T (°C /yr) | VPD (kPa/yr) | u2 (m/s/yr) | Rs (MJ/m2/yr) | PP (mm/yr) | ET0 (mm/yr) | Arid Index |
|---|---|---|---|---|---|---|---|---|---|
| Northern | All | z | 2.33 | 1.82 | −4.65 | 3.05 | −0.34 | 3.23 | −0.33 |
| 72C440 | Slope | 0.0273 | 0.0038 | −0.0313 | 22.5775 | 0.0663 | 6.1090 | −0.0056 | |
| z | 2.65 | 1.88 | −3.08 | 7.11 | 0.00 | 4.88 | −0.61 | ||
| 72D080 | Slope | 0.0198 | 0.0019 | −0.0063 | −8.8424 | −5.1326 | −2.7048 | 0.0131 | |
| z | 1.51 | 0.89 | −1.02 | −0.68 | −0.40 | −0.82 | 0.30 | ||
| 82A750 | Slope | −0.0034 | −0.0058 | −0.0289 | −13.2536 | −4.8894 | −4.8098 | 0.0193 | |
| z | −0.16 | −1.02 | −1.54 | −0.68 | −0.59 | −0.94 | 0.61 | ||
| 82C160 | Slope | 0.0367 | 0.0023 | −0.0571 | 21.7534 | −1.6133 | 6.2891 | −0.0160 | |
| z | 1.84 | 0.20 | −5.89 | 3.23 | −0.34 | 3.58 | −1.17 | ||
| K2E360 | Slope | 0.0345 | 0.0123 | −0.0300 | 8.4488 | 0.7233 | 4.0278 | −0.0103 | |
| z | 3.16 | 2.67 | −4.35 | 3.32 | 0.02 | 4.33 | −0.38 | ||
| Central | All | z | 3.15 | 0.01 | −4.67 | 2.96 | 0.49 | 3.18 | −0.72 |
| 72G600 | Slope | 0.0276 | 0.0039 | −0.0080 | 17.4792 | 4.7500 | 5.1360 | −0.0140 | |
| z | 2.55 | 1.37 | −1.94 | 1.08 | 0.36 | 1.00 | −0.69 | ||
| 72K220 | Slope | 0.0361 | −0.0015 | −0.0416 | 6.6182 | 4.685 | 2.4933 | −0.0020 | |
| z | 3.46 | −0.37 | −3.38 | 0.90 | 0.30 | 0.99 | −0.02 | ||
| 72M360 | Slope | 0.0237 | 0.0100 | −0.0310 | 3.3041 | 5.5972 | 2.1189 | 0.0007 | |
| z | 3.75 | 1.74 | −2.99 | 1.10 | 0.43 | 1.64 | 0.06 | ||
| 82H840 | Slope | 0.0004 | −0.0034 | −0.0084 | 19.4879 | 8.1727 | 5.8423 | −0.0579 | |
| z | 0.00 | −1.15 | −2.29 | 7.31 | 0.73 | 4.26 | −1.48 | ||
| G2F820 | Slope | 0.0310 | 0.0038 | −0.0169 | 26.4735 | 5.7336 | 7.8225 | −0.0292 | |
| z | 3.03 | 1.51 | −1.81 | 2.35 | 0.53 | 3.28 | −1.32 | ||
| U2H480 | Slope | 0.0220 | −0.0038 | −0.0228 | 3.9075 | 2.2013 | 0.9119 | −0.0031 | |
| z | 2.59 | −3.10 | −3.12 | 1.40 | 0.15 | 1.13 | −0.02 | ||
| Southern | All | z | 1.53 | 0.73 | −5.93 | 1.79 | −0.15 | 2.26 | −0.87 |
| B2Q810 | Slope | 0.0120 | 0.0011 | −0.0356 | 0.9970 | −3.6320 | 0.8960 | −0.0597 | |
| z | 1.09 | 0.61 | −4.74 | 0.18 | −0.49 | 0.58 | −0.34 | ||
| B2N890 | Slope | 0.0132 | 0.0028 | −0.0366 | 16.4809 | 5.3810 | 5.5894 | −0.0223 | |
| z | 1.35 | 1.31 | −4.09 | 1.43 | 0.45 | 1.75 | −0.89 | ||
| 72Q010 | Slope | 0.0207 | −0.0031 | −0.0547 | 18.6575 | −9.0125 | 5.8650 | −0.0113 | |
| z | 1.56 | −0.36 | −5.52 | 1.12 | −0.34 | 1.27 | −1.01 | ||
| Eastern | All | z | 1.55 | −2.55 | −5.03 | 2.95 | −2.89 | 2.69 | −3.02 |
| 72S200 | Slope | 0.0439 | −0.0024 | −0.0139 | 5.0445 | −12.4762 | 1.5901 | −0.0416 | |
| z | 3.04 | −0.90 | −3.20 | 0.68 | −1.88 | 0.66 | −2.00 | ||
| 72S590 | Slope | −0.0265 | −0.0123 | −0.0163 | 27.8268 | −17.7186 | 6.2989 | −0.0914 | |
| z | −3.35 | −1.92 | −3.94 | 1.34 | −5.17 | 1.41 | −1.95 | ||
| 72T250 | Slope | 0.0286 | −0.0041 | −0.0026 | 17.7681 | −15.8333 | 5.3625 | −0.0533 | |
| z | 2.02 | −1.09 | −0.53 | 2.51 | −2.00 | 2.67 | −3.14 | ||
| 72U480 | Slope | 0.0327 | −0.0045 | −0.0419 | 8.7681 | −7.5373 | 2.1215 | −0.0180 | |
| z | 1.38 | −1.46 | −5.53 | 2.94 | −1.50 | 3.76 | −2.19 |
| Region | Station | Statistic | T (°C /yr) | VPD (kPa/yr) | u2 (m/s/yr) | Rs (MJ/m2/yr) | PP (mm/yr) | ET0 (mm/yr) | Arid Index |
|---|---|---|---|---|---|---|---|---|---|
| Northern | All | z | 1.85 | 0.99 | −3.66 | 2.52 | 0.22 | 2.76 | −0.03 |
| 72C440 | Slope | 0.0348 | 0.0046 | −0.0515 | 14.3124 | 0.8896 | 3.7999 | −0.0033 | |
| z | 4.00 | 2.45 | −3.26 | 3.14 | 0.34 | 3.50 | −0.44 | ||
| 72D080 | Slope | 0.0421 | 0.0011 | −0.0054 | 1.2075 | −3.1292 | 0.5960 | 0.0019 | |
| z | 2.39 | 1.01 | −1.06 | 0.20 | −0.32 | 0.32 | 0.15 | ||
| 82A750 | Slope | −0.0168 | −0.0062 | −0.0141 | −8.4723 | 14.2560 | −2.7750 | 0.0760 | |
| z | −1.01 | −1.42 | −0.99 | −0.38 | 1.17 | −0.87 | 1.09 | ||
| 82C160 | Slope | 0.0268 | −0.0021 | −0.0732 | 14.4537 | 2.9914 | 3.1722 | 0.0012 | |
| z | 1.84 | −0.71 | −4.64 | 2.51 | 0.61 | 2.79 | 0.06 | ||
| K2E360 | Slope | 0.0263 | 0.0046 | −0.0063 | 10.0347 | −2.8631 | 3.2296 | −0.0111 | |
| z | 2.02 | 1.10 | −0.73 | 2.85 | −0.88 | 7.92 | −1.15 | ||
| Central | All | z | 2.92 | 2.27 | −3.60 | 2.51 | −0.49 | 3.30 | −0.72 |
| 72G600 | Slope | 0.0385 | 0.0038 | 0.0079 | 15.5101 | −0.8418 | 5.3769 | −0.0052 | |
| z | 3.08 | 2.96 | 1.51 | 1.12 | −0.49 | 1.69 | −0.65 | ||
| 72K220 | Slope | 0.0563 | 0.0005 | −0.0222 | 3.9542 | −3.2175 | 2.3691 | −0.0100 | |
| z | 3.62 | 0.40 | −2.68 | 1.02 | −0.78 | 1.46 | −0.82 | ||
| 72M360 | Slope | 0.0382 | 0.0125 | −0.0350 | 7.1597 | −2.6696 | 3.9382 | −0.0066 | |
| z | 2.57 | 3.52 | −3.30 | 1.95 | −1.32 | 5.50 | −1.28 | ||
| 82H840 | Slope | 0.0206 | 0.0000 | −0.0055 | 1.8700 | −1.8821 | 0.5400 | −0.0056 | |
| z | 1.80 | 0.00 | −1.64 | 0.38 | −0.40 | 0.46 | −0.55 | ||
| G2F820 | Slope | 0.0384 | 0.0079 | −0.0106 | 21.3231 | −0.0025 | 6.7380 | −0.0055 | |
| z | 2.73 | 2.71 | −0.65 | 2.52 | 0.00 | 3.06 | −0.53 | ||
| U2H480 | Slope | 0.0267 | −0.0023 | −0.0235 | 3.3565 | 2.0857 | 0.6812 | 0.0077 | |
| z | 1.52 | −2.83 | −3.52 | 1.91 | 0.71 | 1.19 | 0.58 | ||
| Southern | All | z | 2.35 | 1.47 | −5.42 | 2.42 | −0.84 | 2.35 | −1.51 |
| B2Q810 | Slope | 0.0080 | 0.0019 | −0.0500 | 15.8513 | −7.0033 | 5.0068 | −0.0241 | |
| z | 1.80 | 1.13 | −3.24 | 0.00 | −0.97 | −0.03 | −0.97 | ||
| B2N890 | Slope | 0.0274 | 0.0050 | −0.0316 | 16.6725 | −3.0893 | 5.0218 | −0.0159 | |
| z | 2.98 | 2.36 | −5.57 | 1.29 | −0.73 | 1.53 | −1.36 | ||
| 72Q010 | Slope | 0.0259 | −0.0029 | −0.0435 | 15.8513 | −1.2771 | 5.0068 | −0.0152 | |
| z | 2.35 | −1.33 | −4.31 | 1.78 | −0.20 | 1.55 | −1.00 | ||
| Eastern | All | z | 0.82 | −2.90 | −4.14 | 2.57 | −0.47 | 1.81 | −0.78 |
| 72S200 | Slope | 0.0373 | −0.0033 | −0.0159 | 2.1030 | −0.1292 | 0.5913 | −0.0263 | |
| z | 2.55 | −1.70 | −3.74 | 0.43 | 0.00 | 0.44 | −0.41 | ||
| 72S590 | Slope | −0.0420 | −0.0150 | −0.0055 | 14.5092 | −9.7230 | 2.1243 | −0.0634 | |
| z | −3.85 | −1.93 | −1.37 | 1.52 | −1.17 | 0.61 | −1.32 | ||
| 72T250 | Slope | 0.0224 | −0.0050 | −0.0022 | 10.4072 | 0.9208 | 2.8632 | −0.0247 | |
| z | 1.68 | −1.51 | −0.15 | 2.37 | 0.14 | 2.40 | −0.45 | ||
| 72U480 | Slope | 0.0180 | −0.0032 | −0.0442 | 4.3741 | −8.2595 | 0.3188 | −0.0211 | |
| z | 1.03 | −1.25 | −3.38 | 1.66 | −0.55 | 0.30 | −0.38 |
| Region | Station | Statistic | T (°C /yr) | VPD (kPa/yr) | u2 (m/s/yr) | Rs (MJ/m2/yr) | PP (mm/yr) | ET0 (mm/yr) | Arid Index |
|---|---|---|---|---|---|---|---|---|---|
| Northern | All | z | 0.46 | −1.31 | −3.74 | 2.16 | 0.32 | 0.52 | 0.42 |
| 72C440 | Slope | 0.0117 | −0.0028 | 0.0373 | 10.1099 | 1.4158 | 0.1685 | 0.0026 | |
| z | 0.67 | −1.57 | −2.75 | 3.18 | 0.46 | 0.12 | 0.17 | ||
| 72D080 | Slope | 0.0211 | 0.0000 | −0.0050 | 1.6807 | −2.9744 | 0.4835 | −0.0132 | |
| z | 1.38 | 0.18 | −0.74 | 0.47 | −0.66 | 0.43 | −0.41 | ||
| 82A750 | Slope | −0.0526 | −0.0025 | −0.0174 | −9.0904 | 6.0176 | −3.4102 | 0.1324 | |
| z | 1.31 | −1.10 | −1.02 | −0.98 | 1.13 | −1.61 | 2.27 | ||
| 82C160 | Slope | 0.0207 | −0.0018 | −0.0720 | 10.6727 | 0.2100 | 1.4448 | −0.0006 | |
| z | 1.25 | −1.40 | −3.26 | 3.18 | 0.02 | 1.64 | 0.00 | ||
| K2E360 | Slope | 0.0074 | −0.0009 | −0.0048 | 8.3438 | 0.6833 | 1.5369 | 0.0007 | |
| z | 0.38 | −0.72 | −0.81 | 2.63 | 0.34 | 2.26 | 0.02 | ||
| Central | All | z | 1.37 | 0.38 | −3.60 | 2.69 | −0.16 | 3.14 | −0.66 |
| 72G600 | Slope | 0.0219 | −0.0002 | 0.0118 | 13.7243 | −0.5242 | 2.8750 | −0.0051 | |
| z | 1.05 | −0.26 | 2.08 | 1.69 | −0.36 | 2.20 | −1.17 | ||
| 72K220 | Slope | 0.0393 | 0.0011 | −0.0211 | 3.7026 | 0.6141 | 1.6703 | 0.0008 | |
| z | 2.17 | 0.81 | −3.22 | 0.54 | 0.54 | 1.54 | −0.14 | ||
| 72M360 | Slope | 0.0187 | 0.0036 | −0.0374 | 8.9057 | 0.4833 | 2.4898 | 0.0011 | |
| z | 0.97 | 1.56 | −3.84 | 1.64 | 0.67 | 2.81 | 0.50 | ||
| 82H840 | Slope | 0.0088 | −0.0008 | −0.0044 | −3.2119 | −0.6905 | −0.9288 | −0.0024 | |
| z | 0.30 | −0.68 | −1.09 | −0.76 | −1.03 | −0.87 | −0.59 | ||
| G2F820 | Slope | 0.0308 | 0.0033 | −0.0133 | 13.4413 | −0.4618 | 3.9408 | −0.0063 | |
| z | 1.68 | 1.44 | −0.68 | 4.50 | −0.38 | 6.25 | −1.28 | ||
| U2H480 | Slope | 0.0212 | −0.0013 | −0.0234 | 7.0263 | −0.5671 | 1.6263 | −0.0105 | |
| z | 1.05 | −1.99 | −3.72 | 2.87 | −0.26 | 4.60 | −0.81 | ||
| Southern | All | z | 0.54 | 0.67 | −4.95 | 2.36 | 0.44 | 2.20 | −0.44 |
| B2Q810 | Slope | 0.0035 | 0.0010 | −0.0443 | 0.0951 | 1.5446 | 0.0244 | −0.0034 | |
| z | 0.36 | 0.49 | −4.11 | 0.00 | 1.03 | 0.02 | 1.05 | ||
| B2N890 | Slope | 0.0180 | 0.0020 | −0.0264 | 16.3217 | −0.1795 | 3.8575 | −0.0023 | |
| z | 0.79 | 1.71 | −4.07 | 1.49 | −0.08 | 2.24 | −1.39 | ||
| 72Q010 | Slope | 0.0075 | −0.0024 | −0.0329 | 10.7046 | 0.1898 | 2.4606 | 0.0036 | |
| z | 0.43 | −1.13 | −3.50 | 2.19 | 0.14 | 1.39 | −1.24 | ||
| Eastern | All | z | 0.11 | −3.52 | −4.77 | 2.26 | 1.09 | 1.28 | 0.16 |
| 72S200 | Slope | 0.0280 | −0.0015 | −0.0195 | 0.9660 | 1.2325 | 0.8138 | 0.0041 | |
| z | 2.14 | −5.18 | −11.71 | 0.30 | 1.93 | 0.38 | 0.71 | ||
| 72S590 | Slope | −0.0548 | −0.0133 | −0.0092 | 9.4480 | 1.8243 | 0.4558 | 0.0027 | |
| z | −3.95 | −2.07 | 2.41 | 0.81 | 1.54 | 0.16 | 0.22 | ||
| 72T250 | Slope | 0.0139 | −0.0040 | −0.0026 | 9.3053 | −2.0009 | 1.8083 | −0.0229 | |
| z | 0.87 | −2.32 | −0.38 | 1.80 | −1.30 | 1.88 | −1.68 | ||
| 72U480 | Slope | 0.0100 | −0.0033 | −0.0417 | 3.6258 | 9.4475 | 0.0444 | 0.0539 | |
| z | 0.71 | −2.26 | −3.64 | 1.96 | 1.48 | 0.06 | 2.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, S.-L.; Tsai, B.-Y.; Wu, C.-Y.; Chang, S.-C.; Chang, Y.-L.; Kuo, B.-J. The Effect of Climate Change on Important Climate Variables in Taiwan and Its Potential Impact on Crop Production. Agriculture 2025, 15, 766. https://doi.org/10.3390/agriculture15070766
Fang S-L, Tsai B-Y, Wu C-Y, Chang S-C, Chang Y-L, Kuo B-J. The Effect of Climate Change on Important Climate Variables in Taiwan and Its Potential Impact on Crop Production. Agriculture. 2025; 15(7):766. https://doi.org/10.3390/agriculture15070766
Chicago/Turabian StyleFang, Shih-Lun, Bing-Yun Tsai, Chun-Yi Wu, Sheng-Chih Chang, Yi-Lung Chang, and Bo-Jein Kuo. 2025. "The Effect of Climate Change on Important Climate Variables in Taiwan and Its Potential Impact on Crop Production" Agriculture 15, no. 7: 766. https://doi.org/10.3390/agriculture15070766
APA StyleFang, S.-L., Tsai, B.-Y., Wu, C.-Y., Chang, S.-C., Chang, Y.-L., & Kuo, B.-J. (2025). The Effect of Climate Change on Important Climate Variables in Taiwan and Its Potential Impact on Crop Production. Agriculture, 15(7), 766. https://doi.org/10.3390/agriculture15070766







