Apple Watercore Grade Classification Method Based on ConvNeXt and Visible/Near-Infrared Spectroscopy
Abstract
1. Introduction
2. Experiments and Methods
2.1. Experiment
2.1.1. Experimental Samples
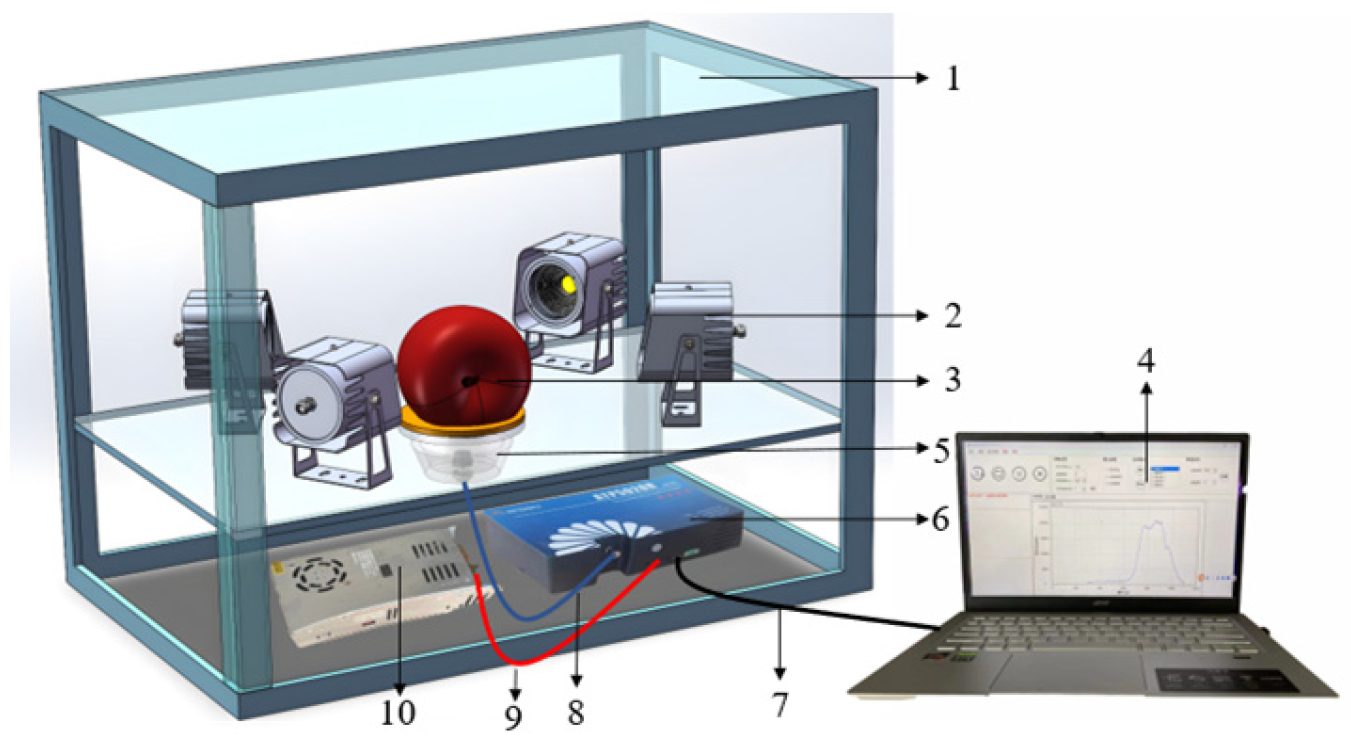
2.1.2. Experimental Instruments
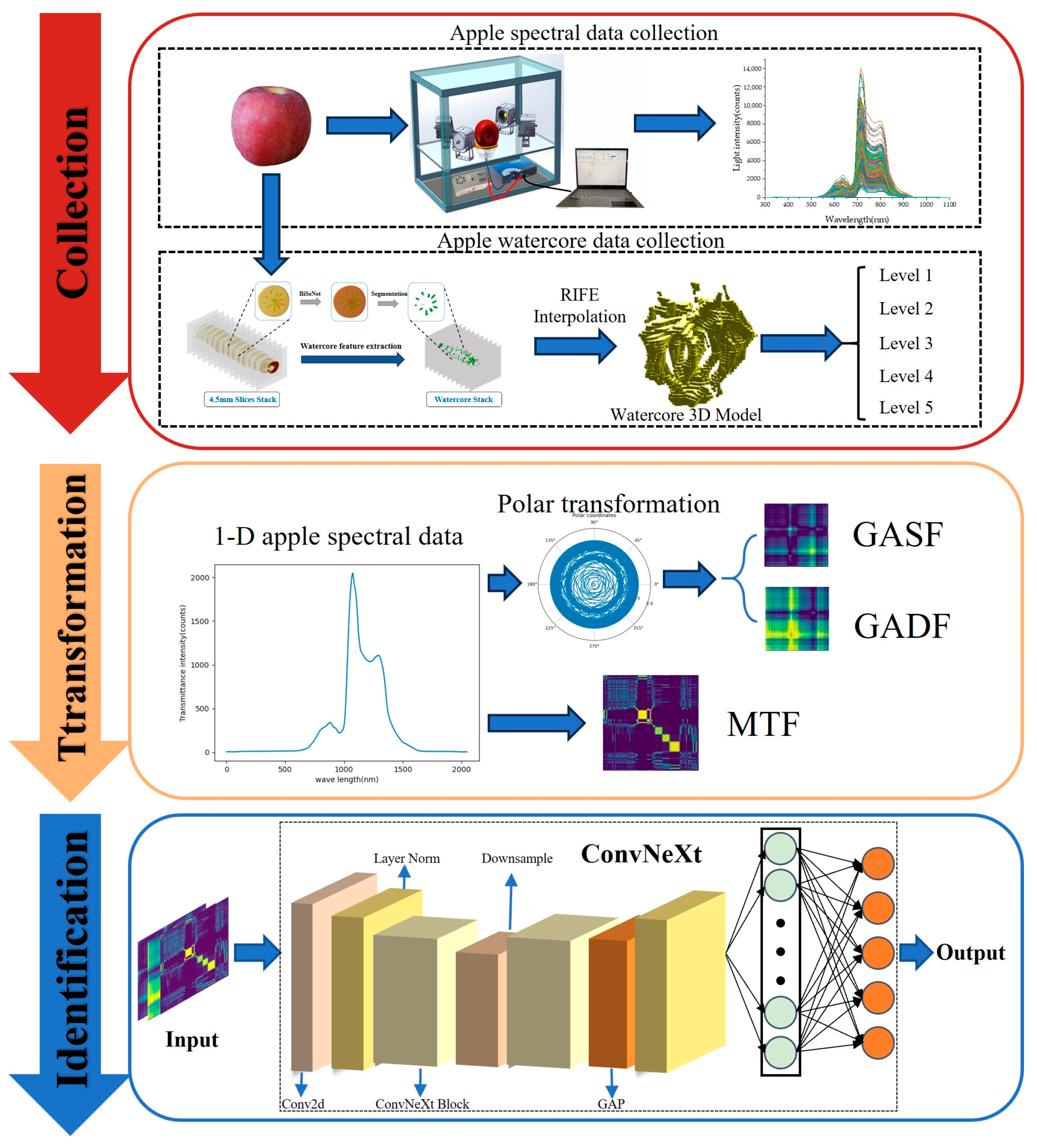
2.1.3. Data Collection
2.2. Methods
2.2.1. The Method of One-Dimensional Spectral Data Transformation to Two-Dimensional Images
2.2.2. The Method for Quantifying Apple Watercore Severity
2.2.3. Apple Watercore Grading Method Based on Deep Convolutional Neural Networks and Visible/Near-Infrared Spectroscopy
3. Results
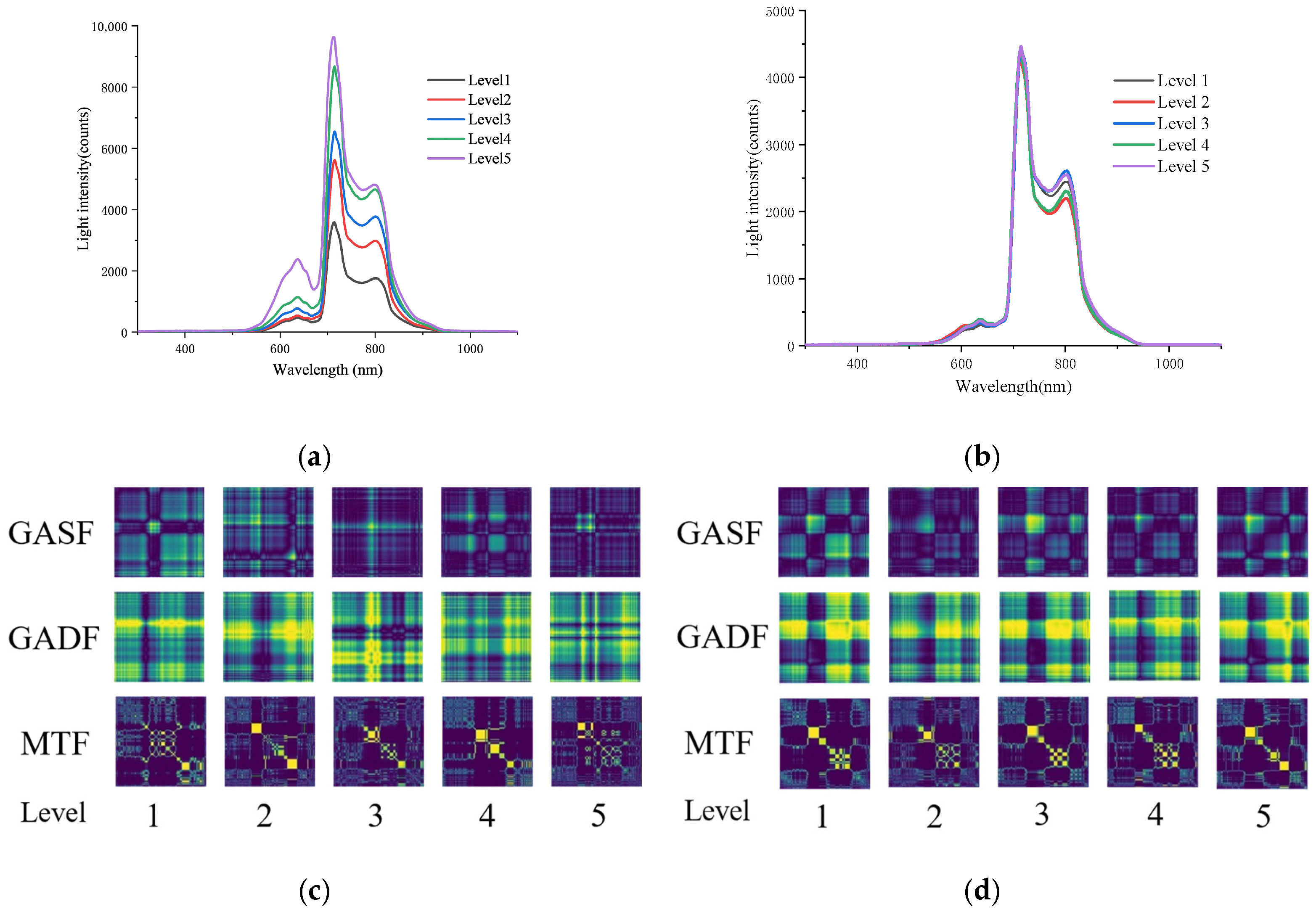
3.1. Results of Data Collection
3.2. Transformation of One-Dimensional Spectral Data into Two-Dimensional Images
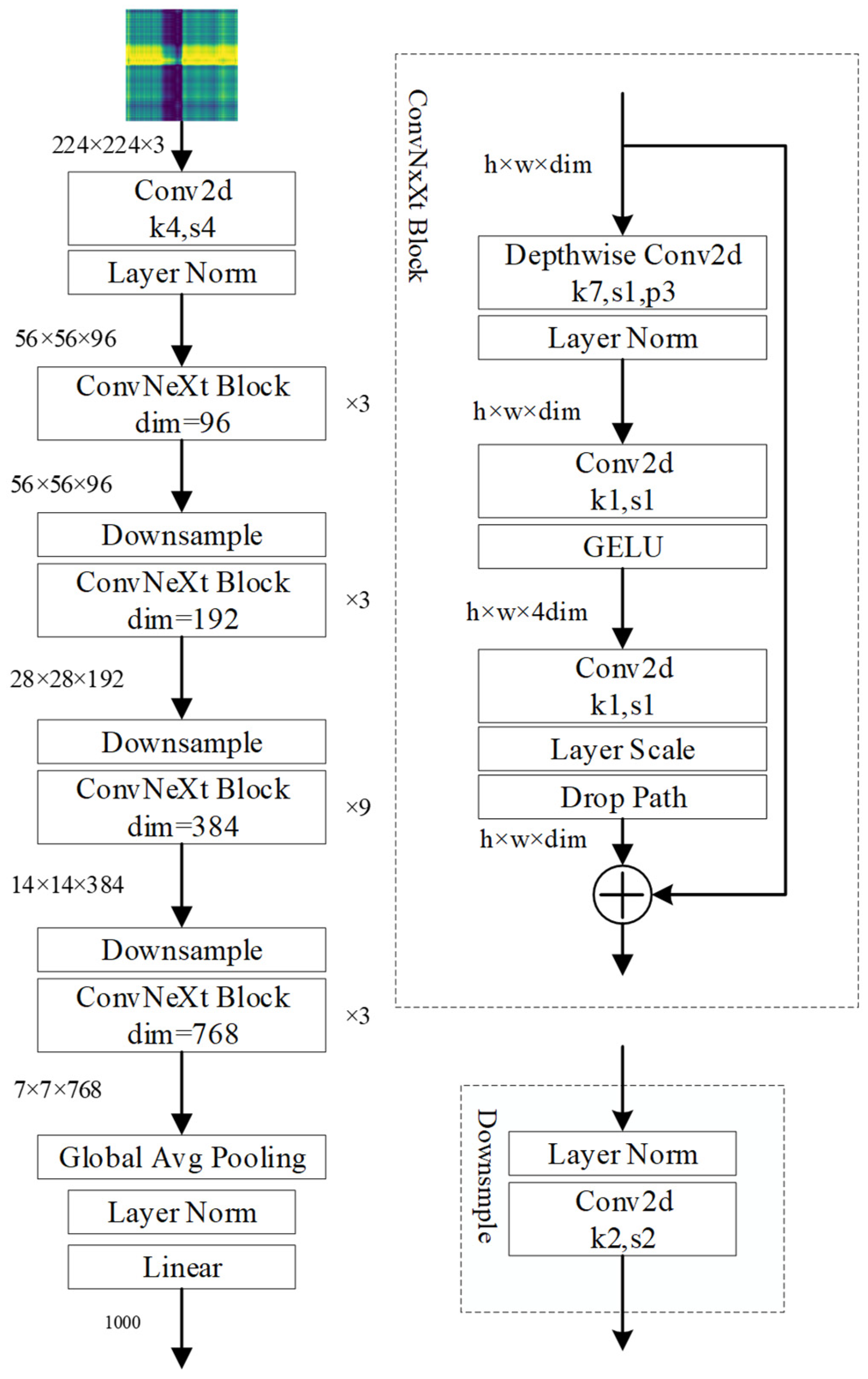
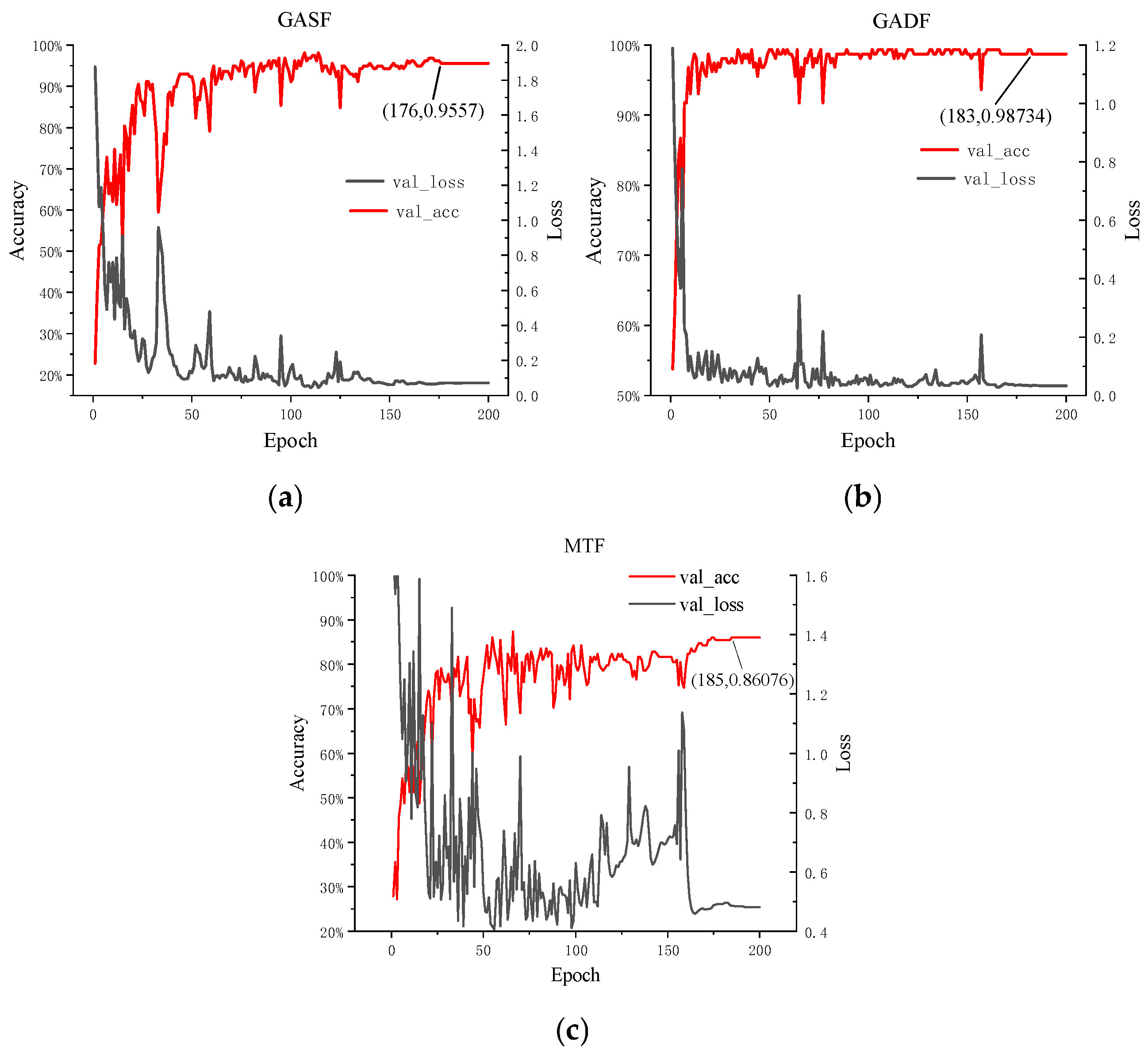
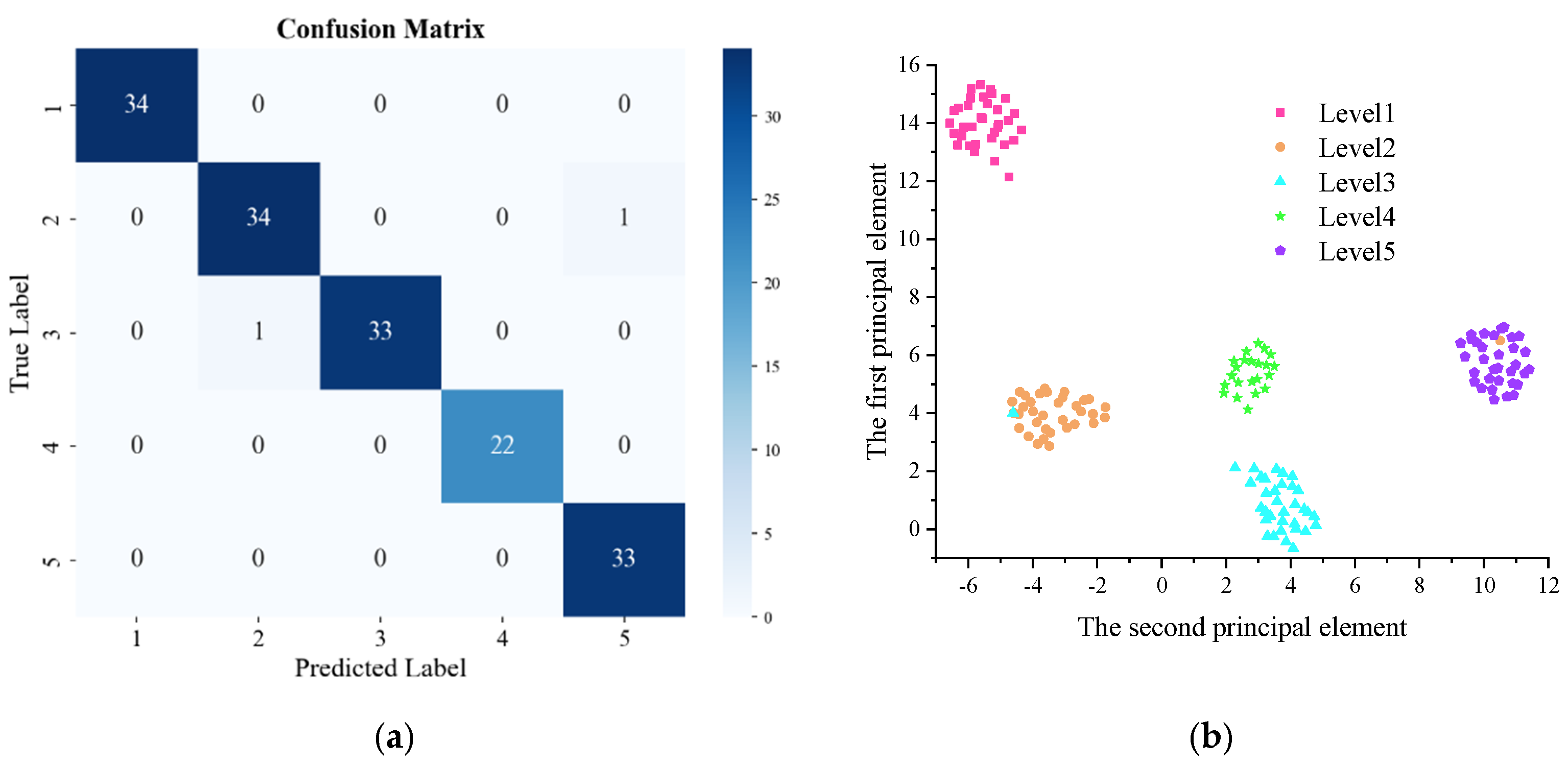
3.3. Training Results of ConvNeXt
4. Discussion
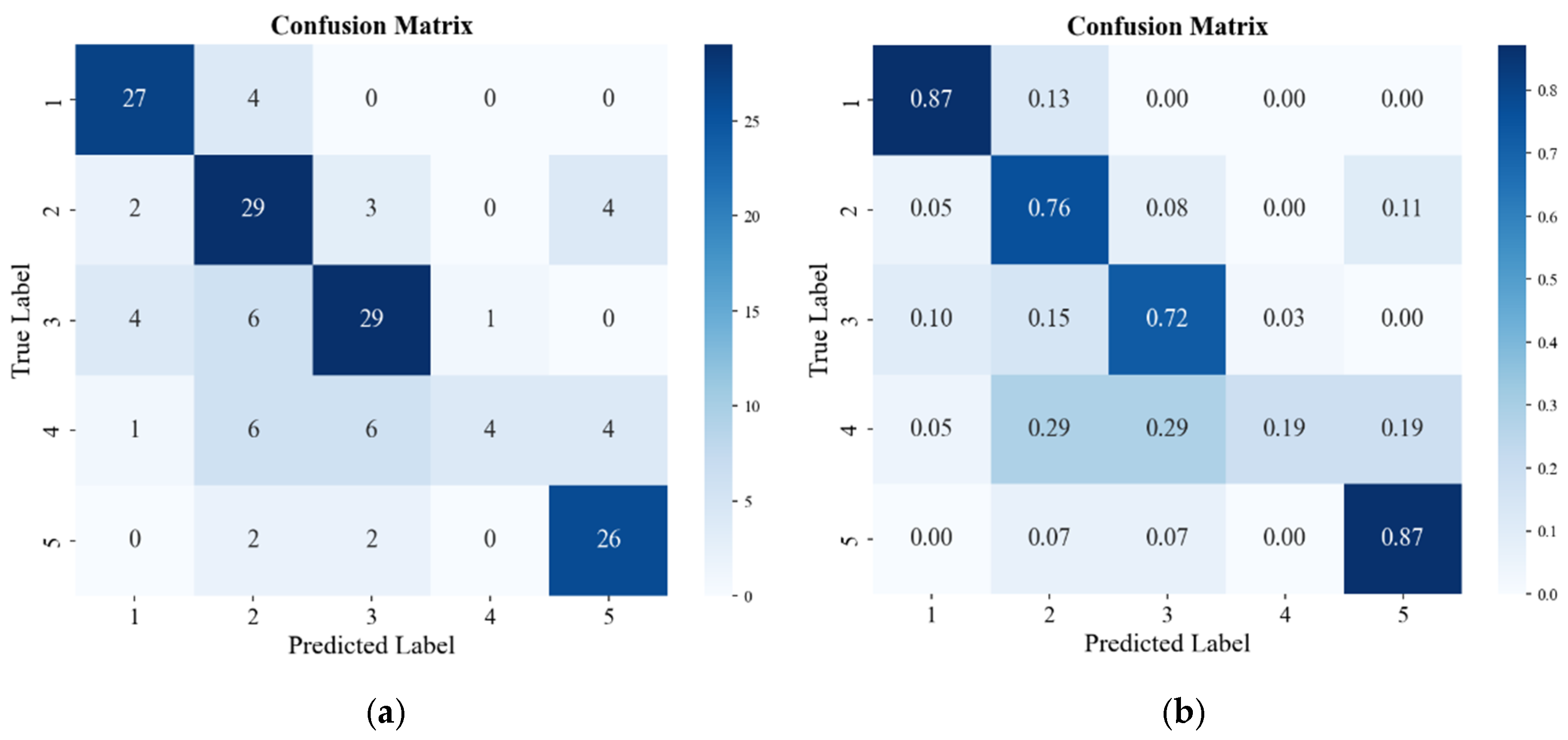
4.1. Recognition Results of Traditional Methods
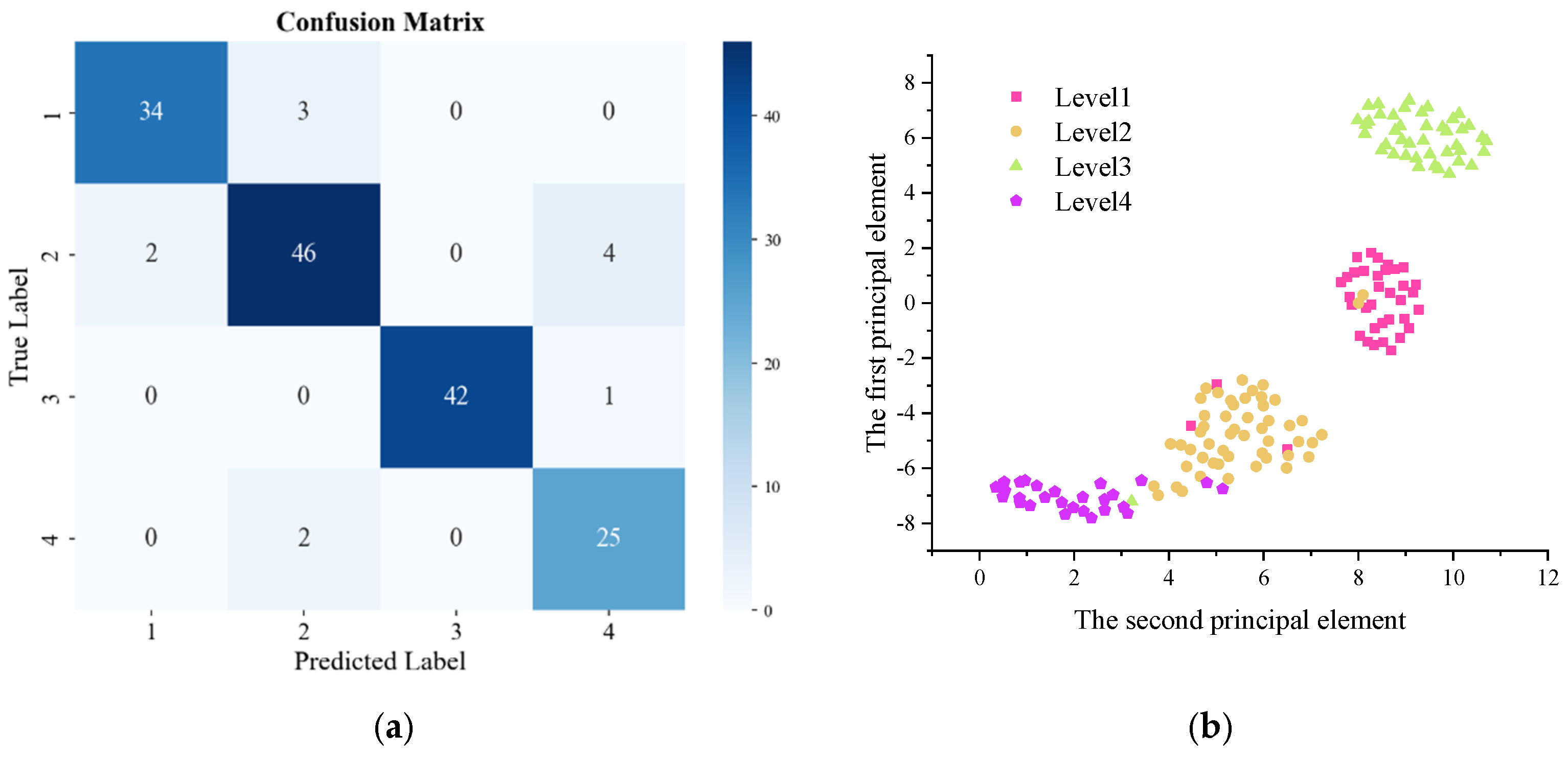
4.2. Classification Results of Existing Apple Watercore Quantification Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, Y.; Wang, Z.; Jia, C. Research progress on pathogenesis of watercore in apple. China Fruits 2022, 1, 8–14. [Google Scholar] [CrossRef]
- Feng, J.; Han, X.; Song, S.; Wang, H.; Xie, P.; Yang, H.; Li, S.; Wu, Y. Fruit quality characters and causes of watercore apple in high altitude areas of Guizhou. J. South. Agric. 2021, 52, 1273–1281. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, Y.; Li, M.; Fu, Q.; Liu, S.; Zhu, Z.; Zhang, X. Analysis and Microscopic Observation of Paraffin Sections of Pineapple Pulp in Watercore. Chin. J. Trop. Crops 2023, 44, 2514–2519. [Google Scholar] [CrossRef]
- Xu, S.; Lu, H.; Wang, X.; Qiu, G.; Wang, C.; Liang, X. Nondestructive detection method for pineapple water core based on visible/near infrared spectroscopy. Trans. Chin. Soc. Agric. Eng. 2021, 37, 287–294. [Google Scholar] [CrossRef]
- Gao, J.; Ma, H.; Liu, D.; Fang, X.; Liu, X. The Difference Analysis of Non Targeted Metabonomics on Different Metabolites in Watercore Pyrus pyrifolia. Mol. Plant Breed. 2021, 19, 8297–8304. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Dong, T.; Wang, F. Advances in rsearch on nondestructive detection method for apple watercore disease and its control. J. Fruit Sci. 2008, 5, 721–726. Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/20083263939 (accessed on 24 March 2025).
- Zhou, W.; Li, W.; Wang, A.; Wu, Z.; Hu, A. Quality Changes of Sugar Core Red Fuji Apple under Two Storage Conditions. Xinjiang Agric. Sci. 2020, 57, 1431–1442. [Google Scholar] [CrossRef]
- Cavalieri, R.P.; Hyde, G.M.; MacQuarrie, P.R. Hydraulic sorting of watercore apples. In Proceedings of the International Postharvest Science Conference Postharvest 96 464, Taupo, New Zealand, 4–9 August 1996; pp. 103–108. [Google Scholar] [CrossRef]
- Herremans, E.; Melado-Herreros, A.; Defraeye, T.; Verlinden, B.; Hertog, M.; Verboven, P.; Val, J.; Fernández-Valle, M.; Bongaers, E.; Estrade, P.; et al. Comparison of X-ray CT and MRI of watercore disorder of different apple cultivars. Postharvest Biol. Technol. 2014, 87, 42–50. [Google Scholar] [CrossRef]
- Wang, R.; Wang, D.; Ren, X.; Ma, H. Nondestructive detection of apple watercore disease based on electric features. Trans. Chin. Soc. Agric. Eng. 2018, 34, 129–136. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Q. Non-destructive testing of red globe grape sugar content and moisture content based on visible/near infrared spectroscopy transmission technology. Chin. Opt. 2021, 14, 566–577. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, H.; Sun, X.; Rao, Y. Non-destructive measurement of tomato maturity by near-infrared diffuse transmission spectroscopy. Laser Technol. 2019, 43, 25–29. [Google Scholar] [CrossRef]
- Zhang, P.; Li, J.; Feng, X.; Wang, B.; Chen, S.; Zhou, Z. Prediction of Maturity of Mopan persimmon Using Near Infrared Diffuse Reflectance Spectroscopy. Food Res. Dev. 2013, 34, 91–94. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, R.; Yu, D.; Lv, Y.; Han, Y. Identification of fig maturity based on near-infrared spectroscopy and partial least square-discriminant analysis. Food Mach. 2020, 36, 107–111. [Google Scholar] [CrossRef]
- Wang, X.; Hua, Z.; He, W. Research progress in infrared spectroscopy for detection of pesticide residue in jujube. J. Food Saf. Qual. 2020, 11, 4394–4400. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Q.; Dong, D. Application of Near Infrared Spectroscopy Combined with Comparative Principal Component Analysis for Pesticide Residue Detection in Fruit. Spectrosc. Spectr. Anal. 2020, 40, 917–921. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, X.; Zhang, N.; Shi, L. Detection of Chlorpyrifos Residue in Aksu Red Fuji Apples Using Near-Infrared Spectroscopy. Jiangsu Agric. Sci. 2018, 46, 162–166. [Google Scholar] [CrossRef]
- Han, D.; Liu, X.; Zhao, L.; Wang, Z.; Tu, R.; Qiao, W. Research of Nondestructive Detection of Apple Watercore by Optical Means. Trans. Chin. Soc. Agric. Mach. 2004, 35, 143–146. [Google Scholar] [CrossRef]
- Wang, J.; Sun, X.; Pan, L.; Sun, Q.; Han, H. Discrimination of Brownheart and Watercore of Apples Based on Energy Spectrum of Visible /Near Infrared Transmittance. Spectrosc. Spectr. Anal. 2008, 28, 2098–2102. [Google Scholar] [CrossRef]
- Guo, J.; Ma, Y.; Guo, Z.; Huang, H.; Shi, Y.; Zhou, J. Watercore Identification of Xinjiang Fuji Apple Based on Manifold Learning Algorithm and Near Infrared Transmission Spectroscopy. Spectrosc. Spectr. Anal. 2020, 40, 2415–2420. [Google Scholar] [CrossRef]
- Chang, H.; Wu, Q.; Yan, J.; Luo, X.; Xu, H. On-line evaluation of watercore in apples by visible/near infrared spectroscopy. In Proceedings of the 2019 ASABE Annual International Meeting, American Society of Agricultural and Biological Engineers, Boston, MA, USA, 7–10 July 2019; p. 1. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, H.; Wang, J.; Xu, H.; Mei, N.; Zhang, S. Non-Destructive Detection Method of Apple Watercore: Optimization Using Optical Property Parameter Inversion and MobileNetV3. Agriculture 2024, 14, 1450. [Google Scholar] [CrossRef]
- Guo, Z.; Zou, Y.; Sun, C.; Jayan, H.; Jiang, S.; EI-Seedi, H.R.; Zou, X. Nondestructive determination of edible quality and watercore degree of apples by portable Vis/NIR transmittance system combined with CARS-CNN. J. Food Meas. Charact. 2024, 18, 4058–4073. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, J.; Liu, T.; Chen, L.; Ban, Z.; Duan, L.; Wang, L.; Tang, Y.; Li, X.; Li, J. Fruit canopy position and harvest period affect watercore development and quality of the ′Fuji′ apple cultivar fruit. Sci. Hortic. 2023, 311, 111793. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z.; Tian, X.; Yang, X.; Cai, Z.; Li, J. Online analysis of watercore apples by considering different speeds and orientations based on Vis/NIR full-transmittance spectroscopy. Infrared Phys. Technol. 2022, 122, 104090. [Google Scholar] [CrossRef]
- Wang, C.; Zhai, M.; Li, H.; Mo, X.; Zha, Z.; Wu, J. Detection of sub-healthy apples with watercore based on visible/near-infrared transmission spectroscopy. Food Mach. 2024, 40, 117–125+182. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Tong, P.; Tang, L.; Xu, Q.; Wang, J. Effects of Different Storage Conditions on Quality and Saccharine of Aksu Apple. Xinjiang Agric. Sci. 2021, 58, 493–501. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. Available online: https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf (accessed on 25 March 2025).
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. Available online: https://proceedings.mlr.press/v97/tan19a/tan19a.pdf (accessed on 25 March 2025).
- Cai, J.; Huang, C.; Ma, L.; Zhai, L.; Guo, Z. Hand-Held Visible/Near Infrared Nondestructive Detection System for Soluble Solid Content in Mandarin by 1D-CNN Model. Spectrosc. Spectr. Anal. 2023, 43, 2792–2798. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, X.; Wang, Z.; Lei, C.; Song, W. Rice variety detection based on near-infrared spectroscopy and deep learning data augmentation. Trans. Chin. Soc. Agric. Eng. 2023, 39, 250–257. [Google Scholar] [CrossRef]
- Chen, C.; Wang, T.; Hu, K.; Bao, B.; Yan, H.; Yang, C. Identification Method of Pollen Typhae Processed Products Based on Convolutional Neural Network and Voting Mechanism. Spectrosc. Spectr. Anal. 2022, 42, 3361–3367. [Google Scholar] [CrossRef]
- Guo, P.; Zhang, W.; Cui, B.; Guo, Z.; Zhao, C.; Yin, Z.; Liu, B. Multi-condition fault diagnosis method of rolling bearing based on enhanced deep convolutional neural network. J. Vib. Eng. 2025, 38, 96–108. [Google Scholar] [CrossRef]
- Huang, H.; Li, Y.; Zhang, Z. A NIR Prediction Model for Forest Soil Carbon Content Based on ResNet. For. Eng. 2023, 39, 164–171. [Google Scholar] [CrossRef]
- Xu, X.; Fu, C.; Gao, Y.; Kang, Y.; Zhang, W. Research on the Identification Method of Maize Seed Origin Using NIR Spectroscopy and GAF-VGGNet. Agriculture 2024, 14, 466. [Google Scholar] [CrossRef]
- Feng, G.; Li, Z.; Zhang, J.; Wang, M. Multi-Scale Spatial Attention-Based Multi-Channel 2D Convolutional Network for Soil Property Prediction. Sensors 2024, 24, 4728. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Zhao, C.; Zhang, W.; Guo, P.; Ma, Y.; Wu, H.; Hu, D.; Lu, Q. Nondestructive detection of apple watercore disease content based on 3D watercore model. Ind. Crops Prod. 2025, 34, 129–136. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Menlo Park, CA, USA, 25–30 January 2015; p. 1. Available online: https://cdn.aaai.org/ocs/ws/ws0115/10179-46015-1-PB.pdf (accessed on 25 March 2025).
- Huang, Z.; Zhang, T.; Heng, W.; Shi, B.; Zhou, S. Real-time intermediate flow estimation for video frame interpolation. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022; pp. 624–642. Available online: https://arxiv.org/pdf/2011.06294 (accessed on 25 March 2025).
- Yin, Z.; Zhang, W.; Zhao, C. Method of extracting characteristics of watercore in cross section of watercore apple based on BiSeNet. Huazhong Agric. Univ. 2023, 42, 209–215. [Google Scholar] [CrossRef]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. Available online: https://openaccess.thecvf.com/content/CVPR2022/papers/Liu_A_ConvNet_for_the_2020s_CVPR_2022_paper.pdf (accessed on 25 March 2025).
- Chang, H. Research and Development of On-Line Non-Destructive Detecting Method and Grading Equipment of Apple Watercore and Soluble Solids Content. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar] [CrossRef]
- Zhao, C.; Yin, Z.; Zhang, W.; Guo, P.; Ma, Y. Identification of apple watercore based on ConvNeXt and Vis/NIR spectra. Infrared Phys. Technol. 2024, 142, 105575. [Google Scholar] [CrossRef]
- Zhao, C.; Yin, Z.; Zhang, W.; Guo, P.; Ma, Y. Classification of Watercore Apples Based on Visible/Near Infrared Transmission Spectroscopy Combined with Honey Badger Algorithm- Support Vector Machine. Food Sci. Technol. 2023, 48, 253–259. [Google Scholar] [CrossRef]




| Categories | Total | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Quantity | 800 | 174 | 177 | 170 | 112 | 167 |
| Proportion | 100% | 21.75% | 22.13% | 21.25% | 14% | 20.88% |
| Categories | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Total |
|---|---|---|---|---|---|---|
| Training set | 140 | 142 | 136 | 90 | 134 | 642 |
| Test set | 34 | 35 | 34 | 22 | 33 | 158 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Yin, Z.; Tan, Y.; Zhang, W.; Guo, P.; Ma, Y.; Wu, H.; Hu, D.; Lu, Q. Apple Watercore Grade Classification Method Based on ConvNeXt and Visible/Near-Infrared Spectroscopy. Agriculture 2025, 15, 756. https://doi.org/10.3390/agriculture15070756
Zhao C, Yin Z, Tan Y, Zhang W, Guo P, Ma Y, Wu H, Hu D, Lu Q. Apple Watercore Grade Classification Method Based on ConvNeXt and Visible/Near-Infrared Spectroscopy. Agriculture. 2025; 15(7):756. https://doi.org/10.3390/agriculture15070756
Chicago/Turabian StyleZhao, Chunlin, Zhipeng Yin, Yushuo Tan, Wenbin Zhang, Panpan Guo, Yaxing Ma, Haijian Wu, Ding Hu, and Quan Lu. 2025. "Apple Watercore Grade Classification Method Based on ConvNeXt and Visible/Near-Infrared Spectroscopy" Agriculture 15, no. 7: 756. https://doi.org/10.3390/agriculture15070756
APA StyleZhao, C., Yin, Z., Tan, Y., Zhang, W., Guo, P., Ma, Y., Wu, H., Hu, D., & Lu, Q. (2025). Apple Watercore Grade Classification Method Based on ConvNeXt and Visible/Near-Infrared Spectroscopy. Agriculture, 15(7), 756. https://doi.org/10.3390/agriculture15070756





