Path Tracking Control of a Large Rear-Wheel–Steered Combine Harvester Using Feedforward PID and Look-Ahead Ackermann Algorithms
Abstract
1. Introduction
2. Materials and Methods
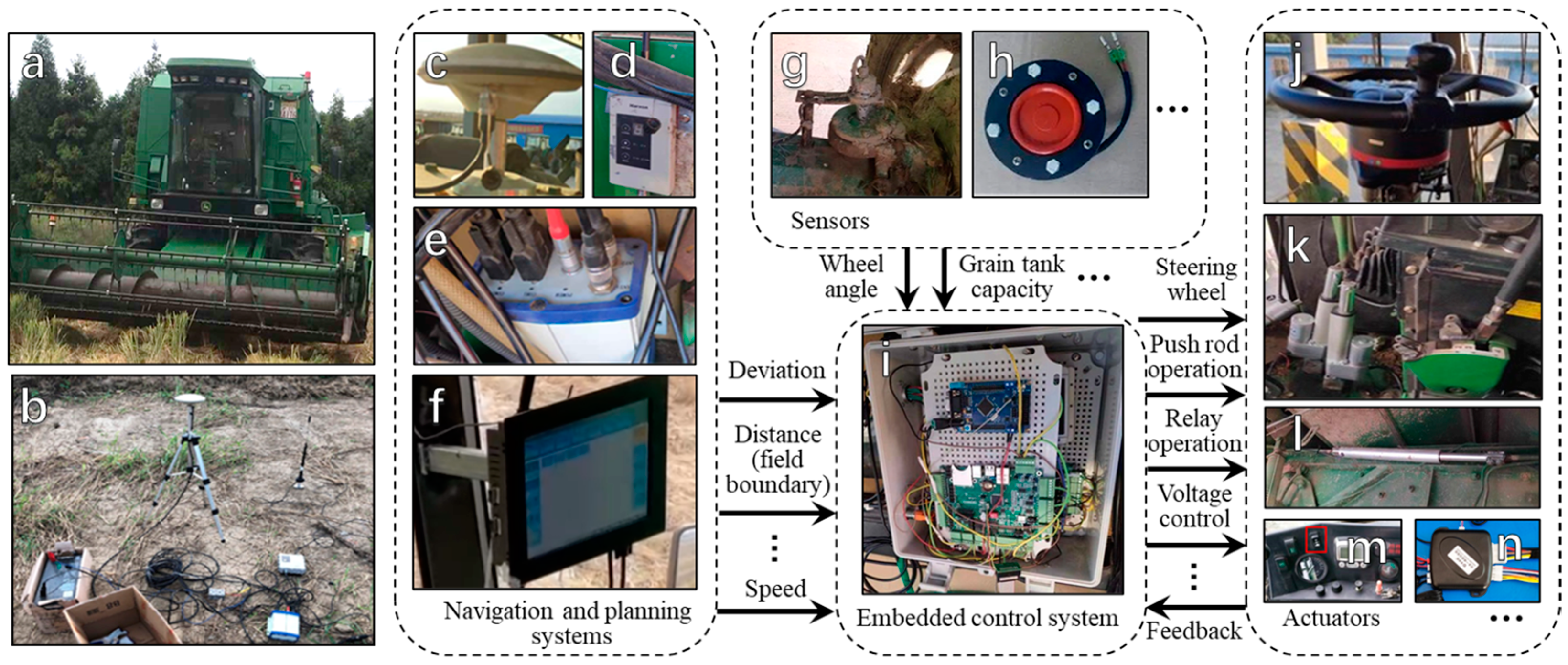
2.1. Overall Design of the Autonomous Driving System
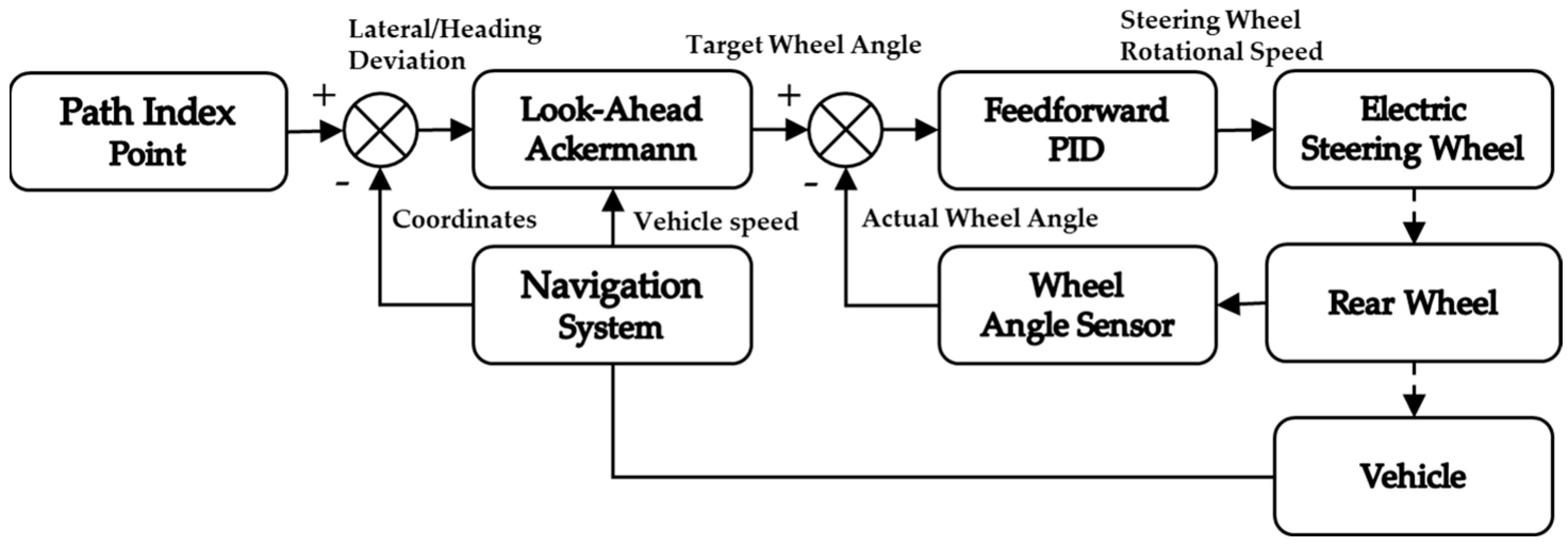
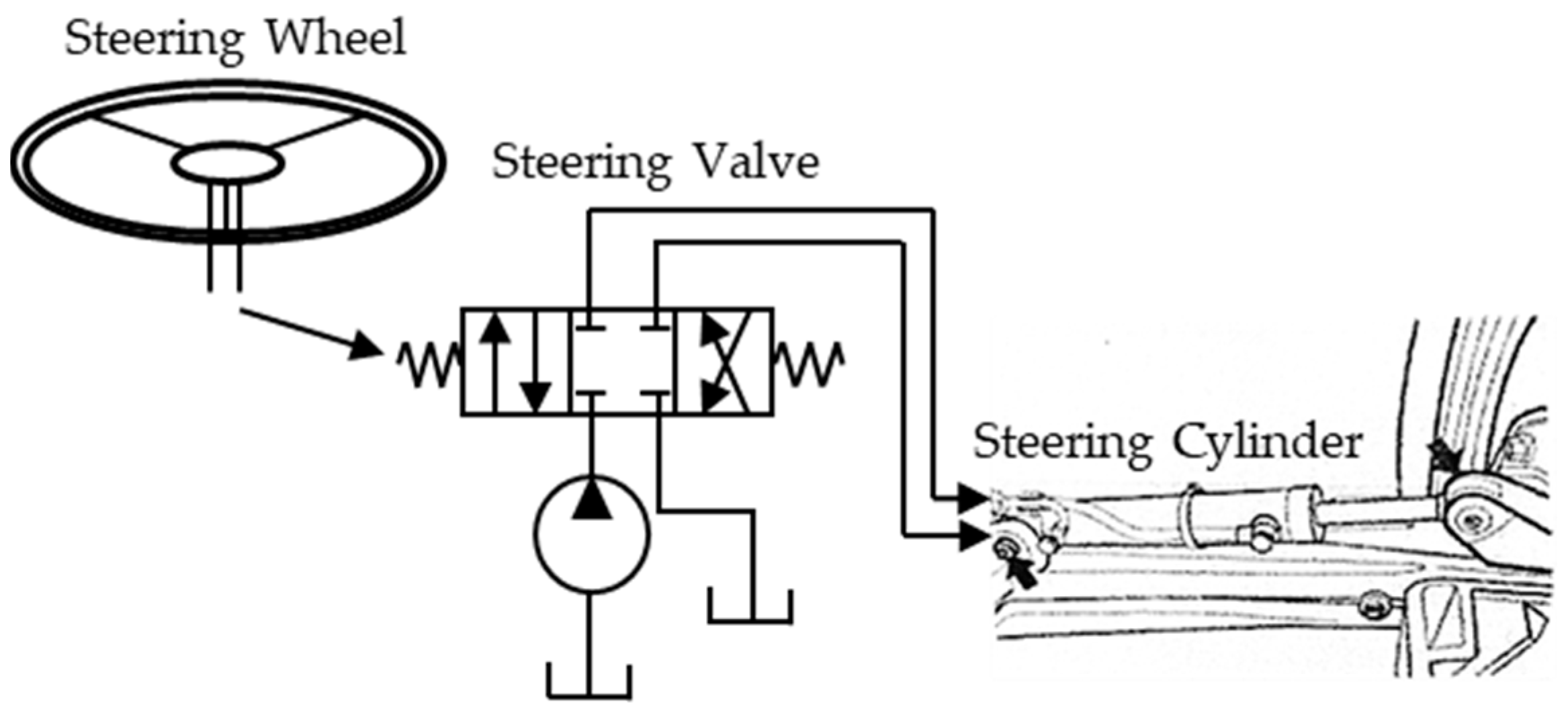
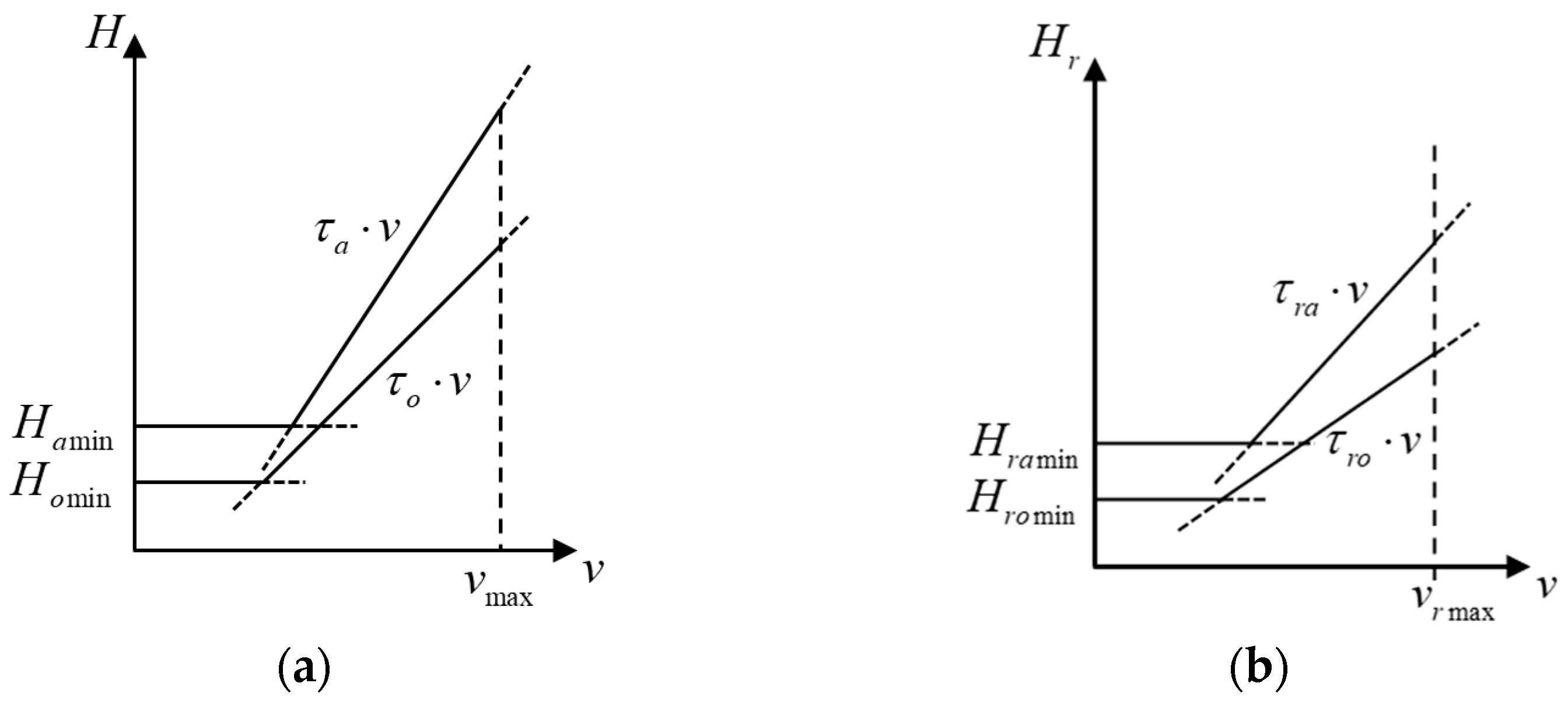
2.2. Feedforward PID Control of the Steering Wheel-Hydraulic Steering System
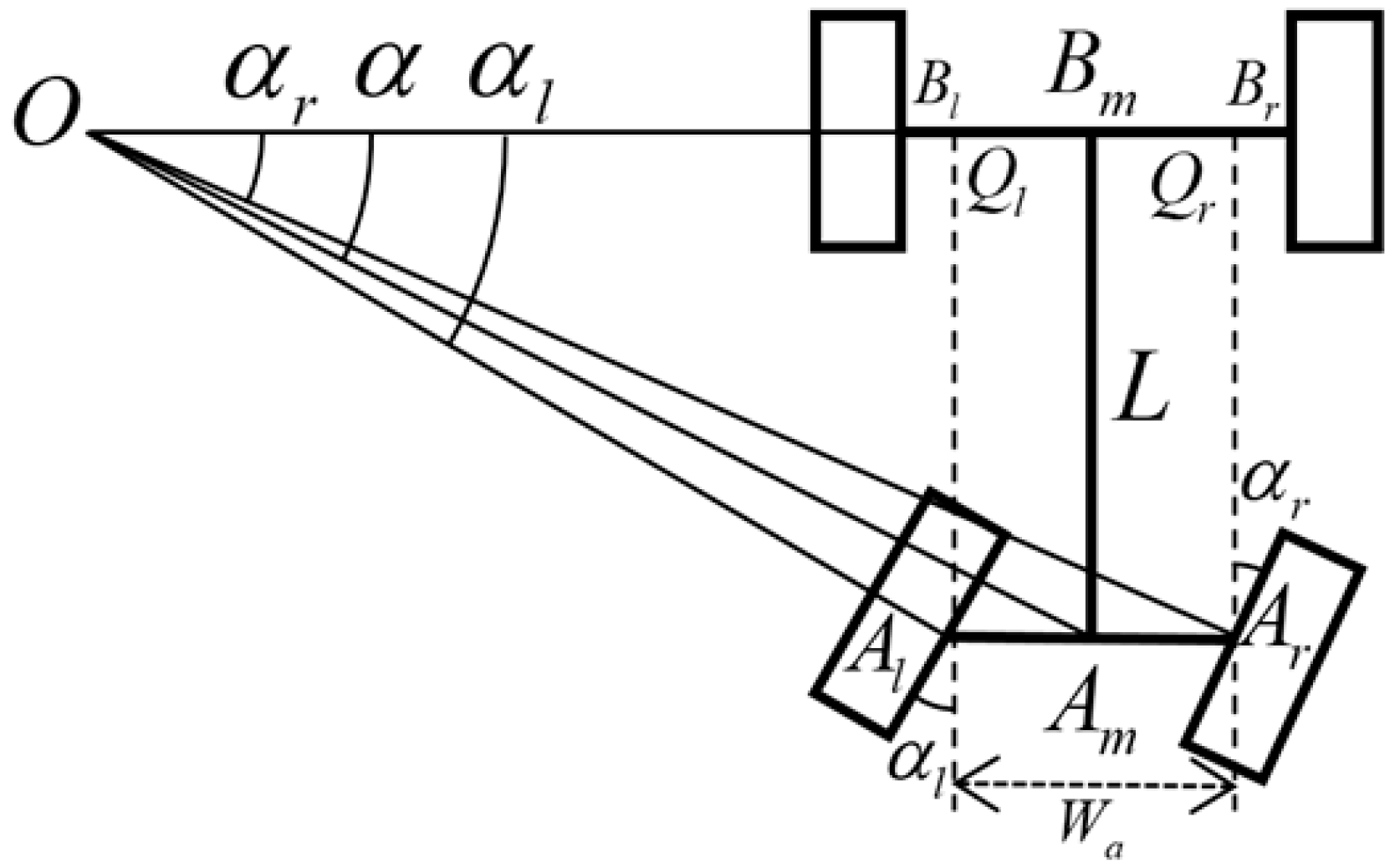
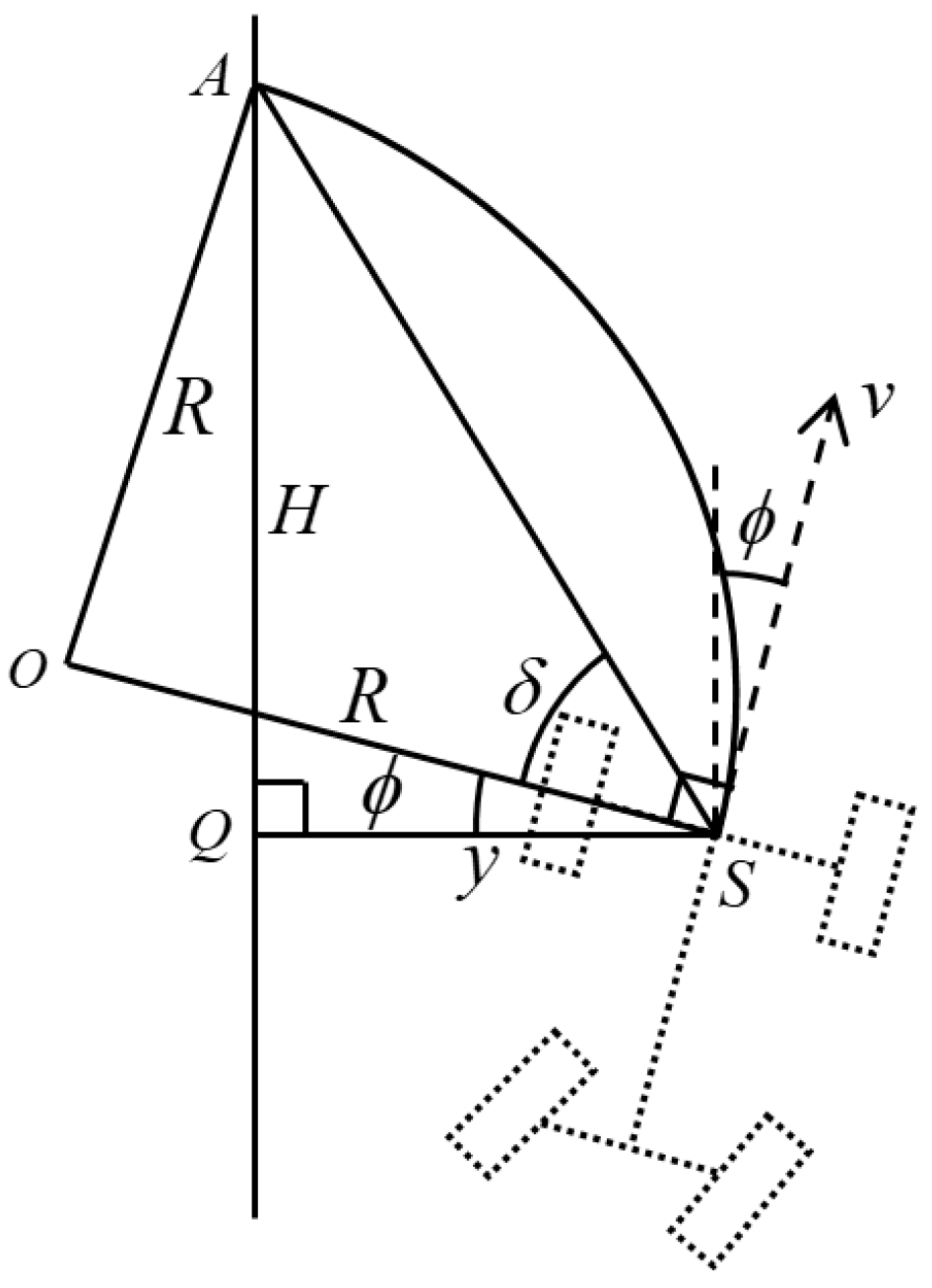
2.3. Look-Ahead Ackermann (LAA) Path Tracking Control
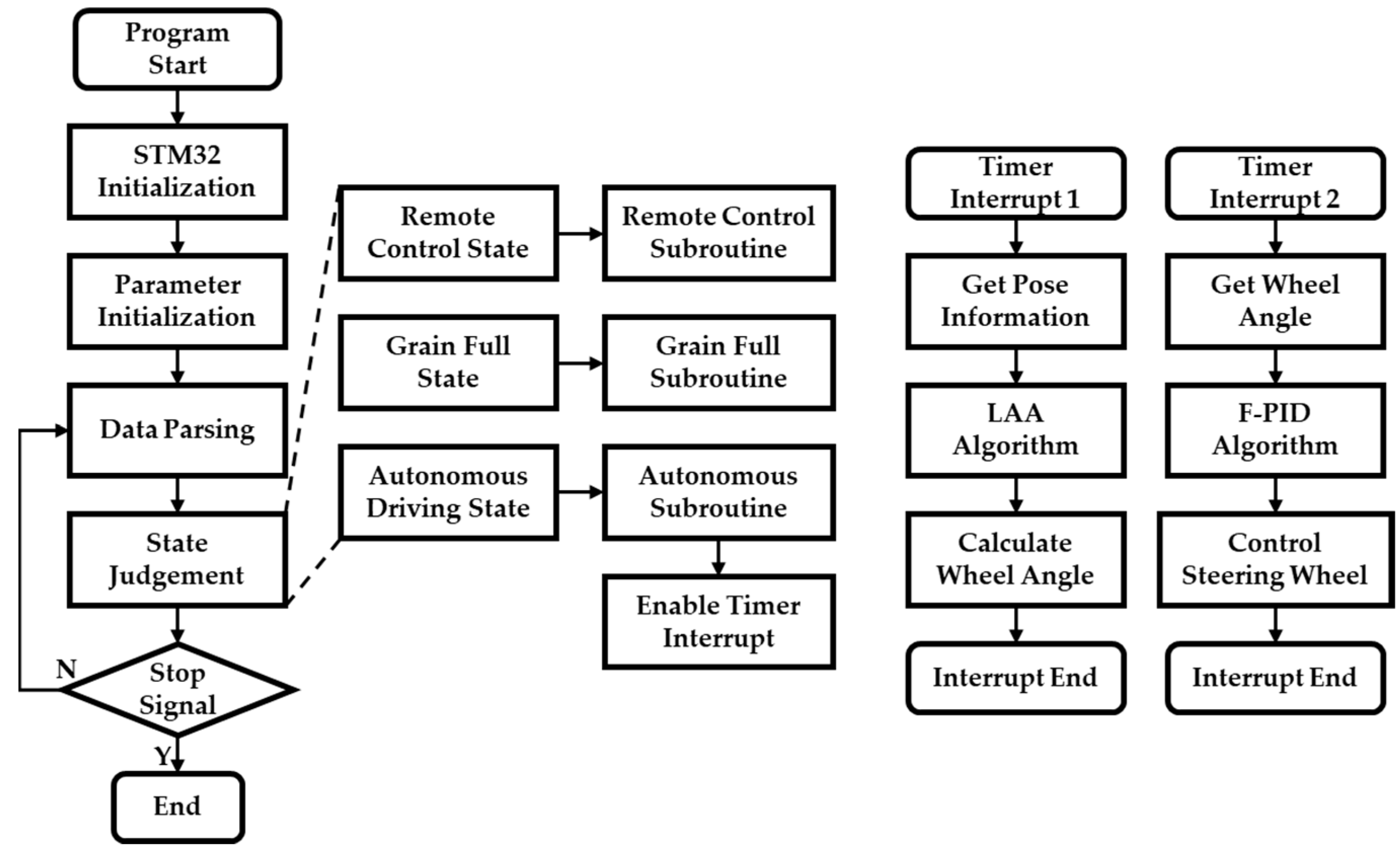
2.4. Realization Strategy of the Whole-Field Autonomous Driving Control
3. Experiments and Results
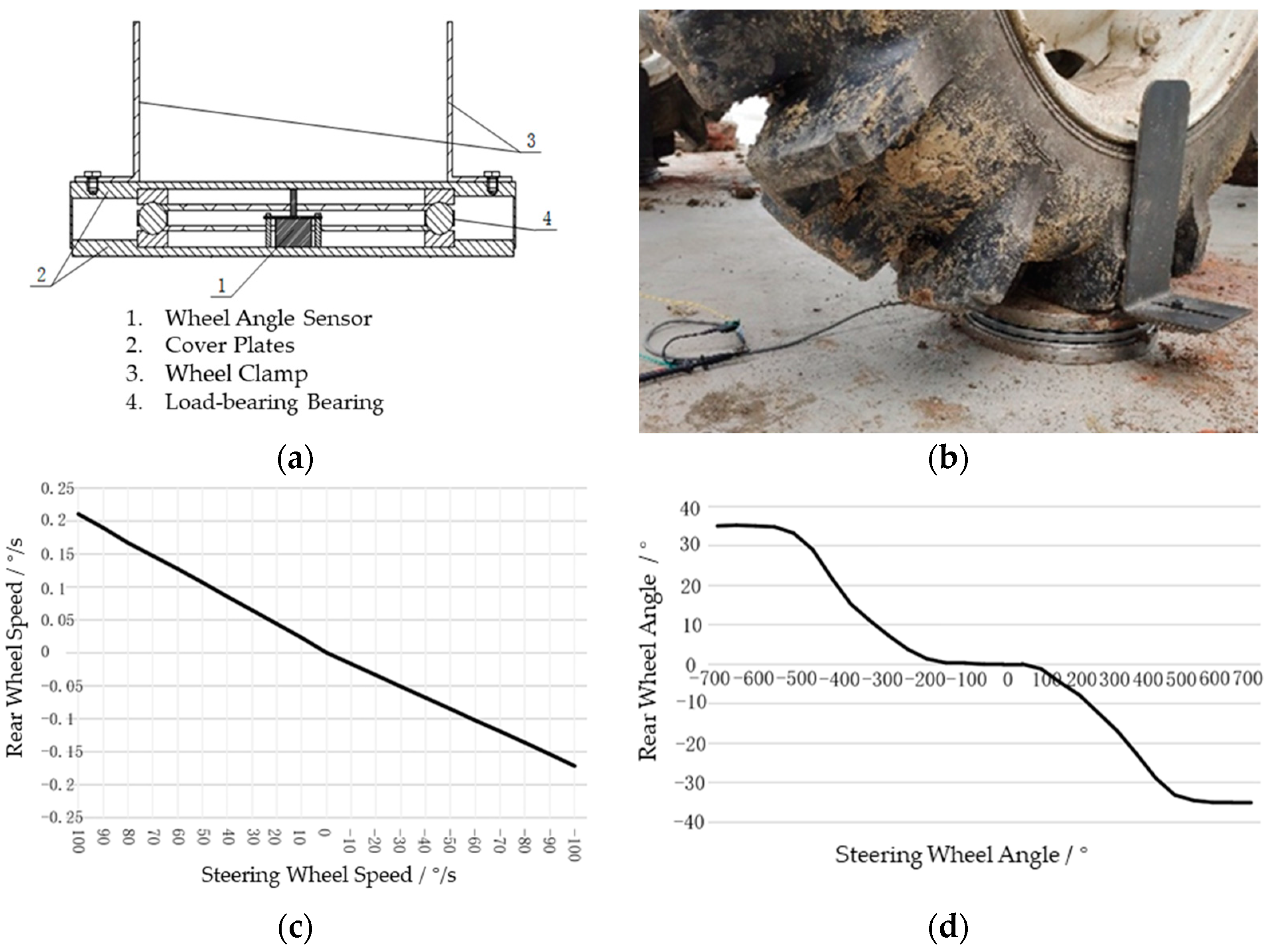
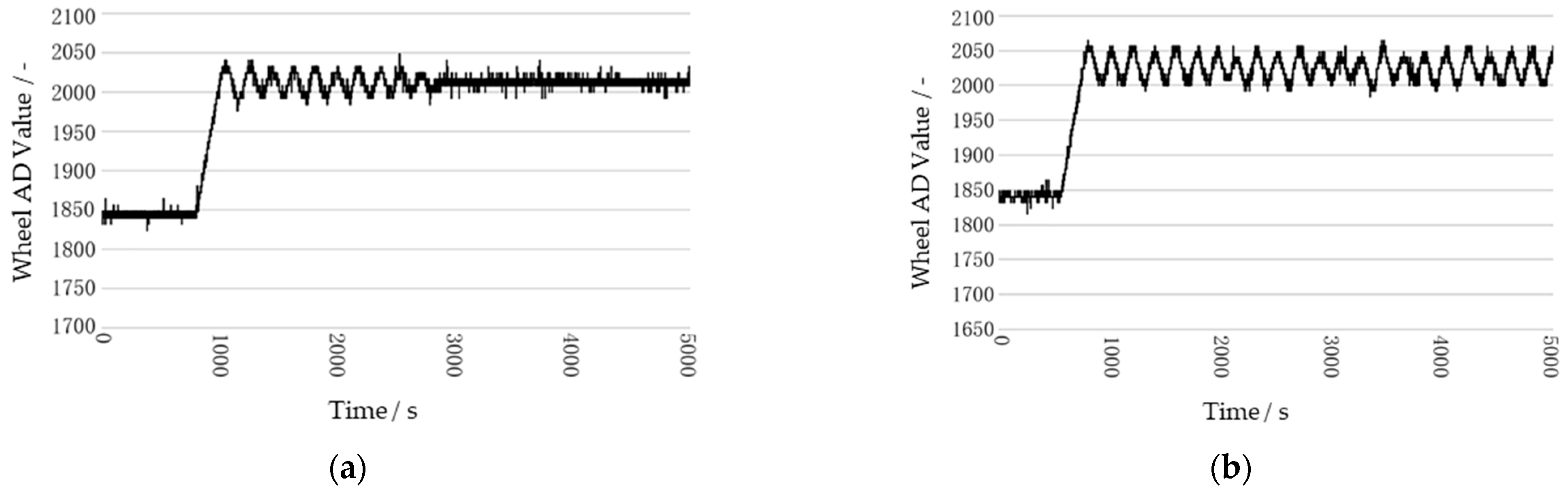
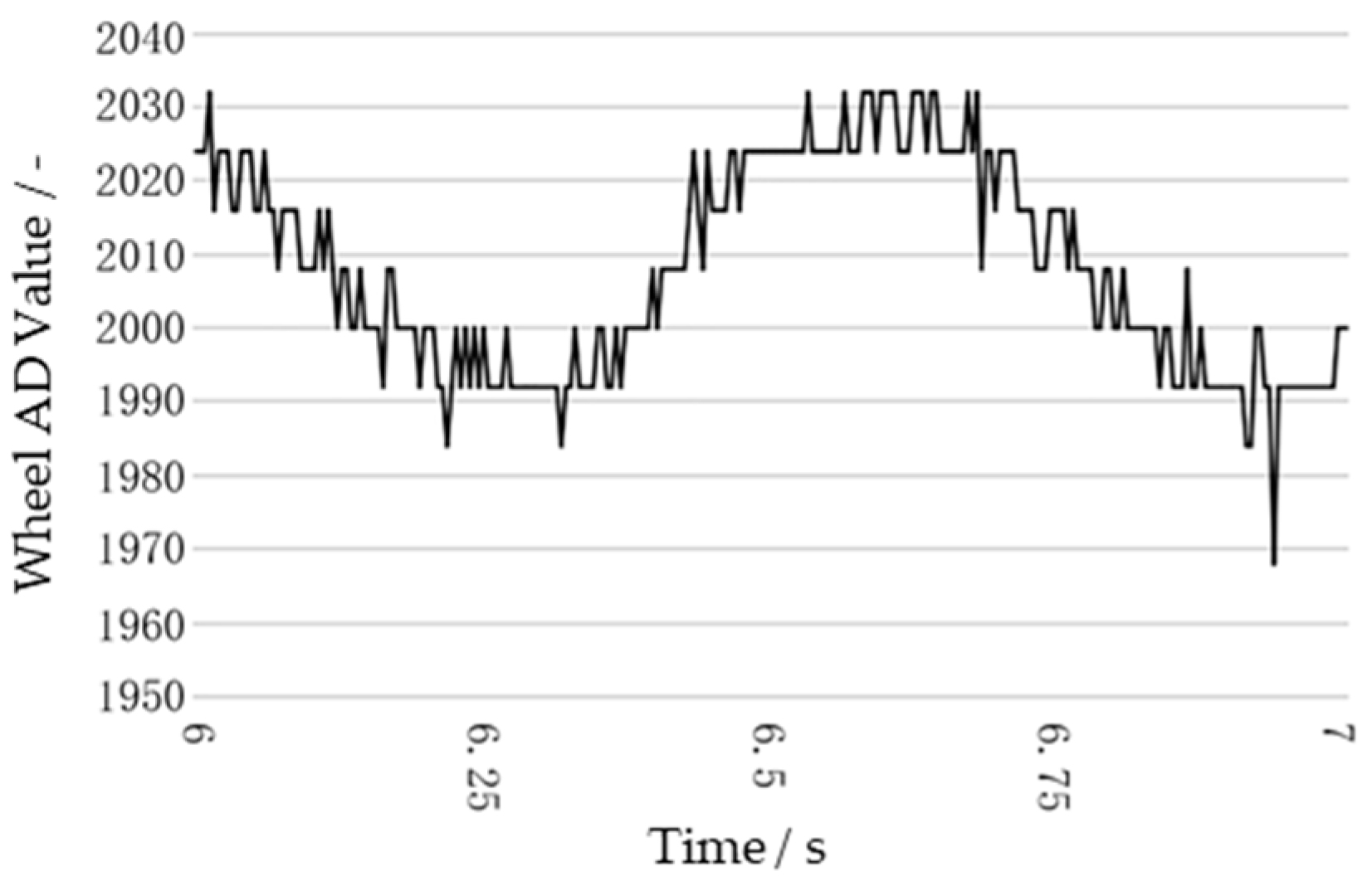
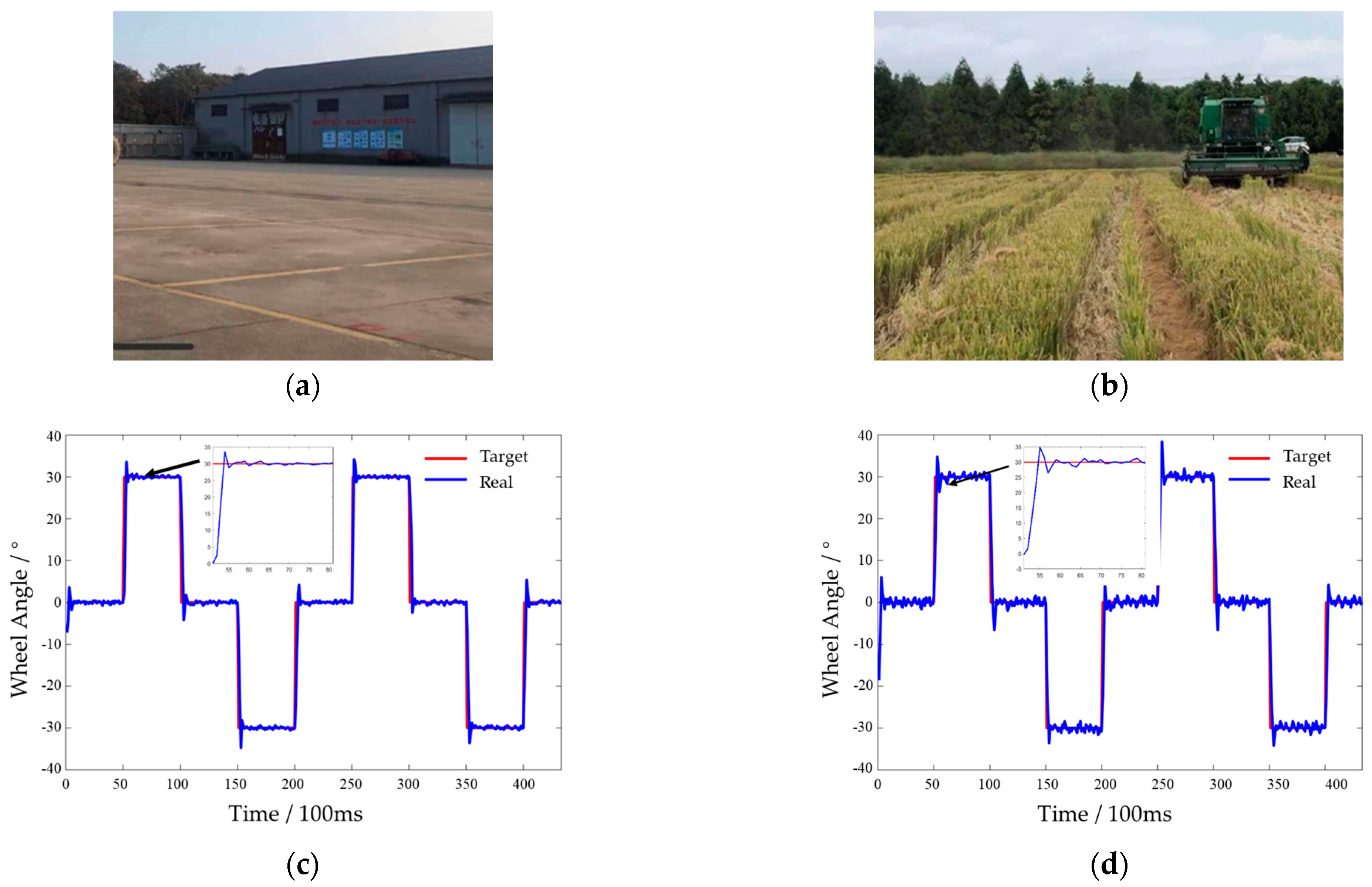
3.1. Performance Test of the Steering System
3.2. Field AB-Line Operation Experiment
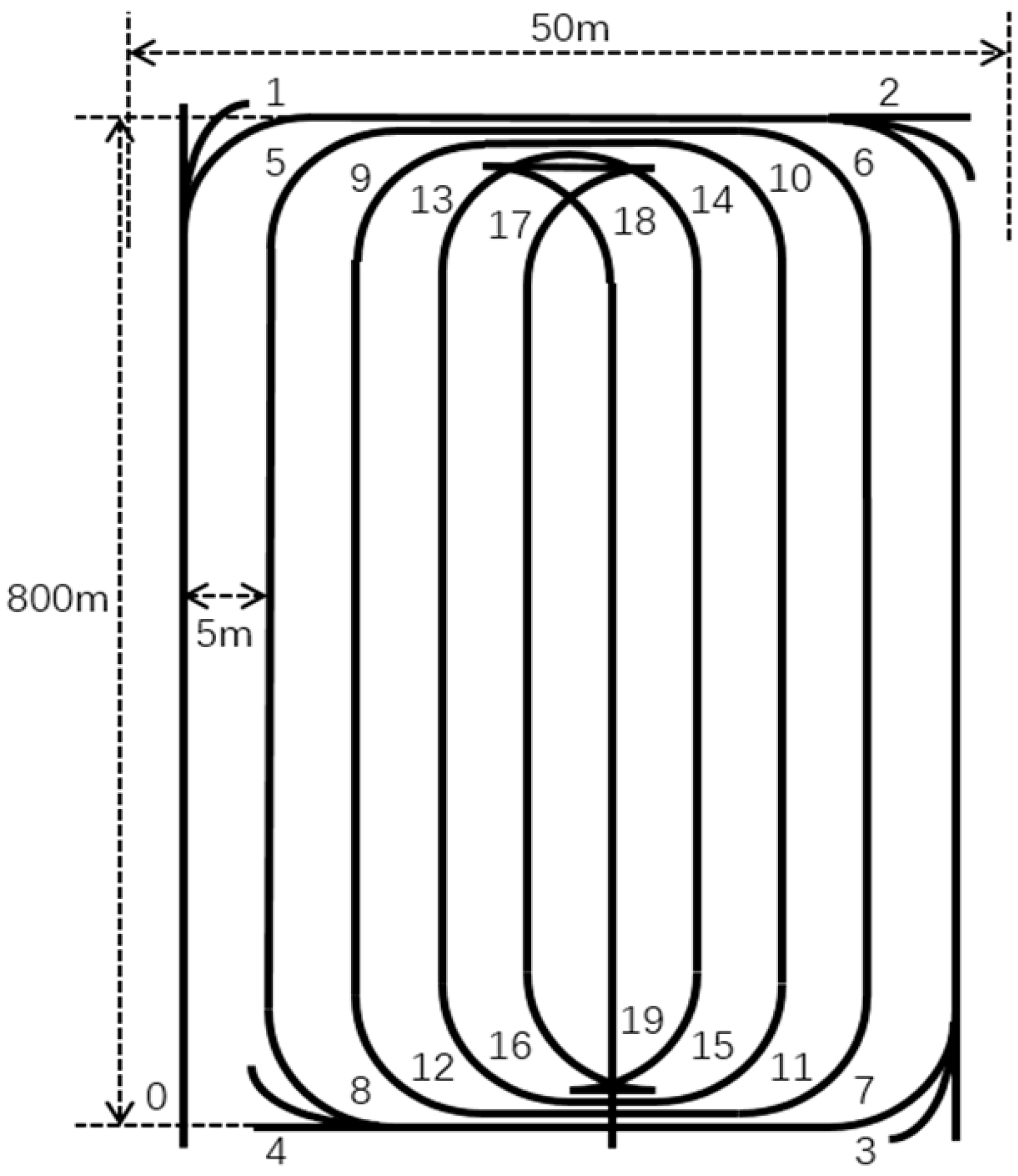
3.3. Complete “Loop” Field Operation Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- An, N.; Wei, W.; Qiao, L.; Zhang, F.; Christie, P.; Jiang, R.; Dobermann, A.; Goulding, K.W.T.; Fan, J.; Fan, M. Agronomic and Environmental Causes of Yield and Nitrogen Use Efficiency Gaps in Chinese Rice Farming Systems. Eur. J. Agron. 2018, 93, 40–49. [Google Scholar] [CrossRef]
- Li, D.; Nanseki, T.; Chomei, Y.; Kuang, J. A Review of Smart Agriculture and Production Practices in Japanese Large-Scale Rice Farming. J. Sci. Food Agric. 2023, 103, 1609–1620. [Google Scholar] [CrossRef] [PubMed]
- Qu, J.; Zhang, Z.; Qin, Z.; Guo, K.; Li, D. Applications of Autonomous Navigation Technologies for Unmanned Agricultural Tractors: A Review. Machines 2024, 12, 218. [Google Scholar] [CrossRef]
- Etezadi, H.; Eshkabilov, S. A Comprehensive Overview of Control Algorithms, Sensors, Actuators, and Communication Tools of Autonomous All-Terrain Vehicles in Agriculture. Agriculture 2024, 14, 163. [Google Scholar] [CrossRef]
- Zhang, Q. (Ed.) Precision Agriculture Technology for Crop Farming; Taylor & Francis: Abingdon, UK, 2016. [Google Scholar]
- Li, M.; Imou, K.; Wakabayashi, K.; Yokoyama, S. Review of Research on Agricultural Vehicle Autonomous Guidance. Int. J. Agric. Biol. Eng. 2009, 2, 1–16. [Google Scholar] [CrossRef]
- Soitinaho, R.; Oksanen, T. Local Navigation and Obstacle Avoidance for an Agricultural Tractor with Nonlinear Model Predictive Control. IEEE Trans. Control Syst. Technol. 2023, 31, 2043–2054. [Google Scholar] [CrossRef]
- O’Connor, M.; Bell, T.; Elkaim, G.; Parkinson, B. Automatic Steering of Farm Vehicles Using GPS. In Proceedings of the Third International Conference on Precision Agriculture, Minneapolis, MN, USA, 23–26 June 1996; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1996; pp. 767–777, ISBN 978-0-89118-257-3. [Google Scholar]
- Han, X.Z.; Kim, H.J.; Kim, J.Y.; Yi, S.Y.; Moon, H.C.; Kim, J.H.; Kim, Y.J. Path-Tracking Simulation and Field Tests for an Auto-Guidance Tillage Tractor for a Paddy Field. Comput. Electron. Agric. 2015, 112, 161–171. [Google Scholar] [CrossRef]
- Zhang, M.; Ji, Y.; Li, S.; Cao, R.; Xu, H.; Zhang, Z. Research Progress of Agricultural Machinery Navigation Technology. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2020, 51, 4. [Google Scholar]
- Ding, Y.; Xia, Z.; Peng, J.; Hu, Z. Design and experiment of the single-neuron PID navigation controller for a combine harvester. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2020, 36, 34–42. [Google Scholar]
- Ji, X.; Wei, X.; Wang, A.; Cui, B.; Song, Q. A Novel Composite Adaptive Terminal Sliding Mode Controller for Farm Vehicles Lateral Path Tracking Control. Nonlinear Dyn. 2022, 110, 2415–2428. [Google Scholar] [CrossRef]
- Kaizu, Y.; Imou, K. A Dual-Spectral Camera System for Paddy Rice Seedling Row Detection. Comput. Electron. Agric. 2008, 63, 49–56. [Google Scholar] [CrossRef]
- Patkar, V.; Mehendale, N. Autonomous Ground Vehicles: Technological Advancements, Implementation Challenges, and Future Directions. Int. J. Intell. Robot Appl. 2025, 1–38. [Google Scholar] [CrossRef]
- Benson, E.R.; Reid, J.F.; Zhang, Q. Machine Vision-Based Guidance System for Agricultural Grain Harvesters Using Cut-Edge Detection. Biosyst. Eng. 2003, 86, 389–398. [Google Scholar] [CrossRef]
- Noguchi, N.; Kise, M.; Ishii, K.; Terao, H. Field Automation Using Robot Tractor. In Proceedings of the 2002 Conference, Automation Technology for Off-Road Equipment, Chicago, IL, USA, 26–27 July 2002; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2002; p. 239. [Google Scholar]
- Nagasaka, Y.; Umeda, N.; Kanetai, Y.; Taniwaki, K.; Sasaki, Y. Autonomous Guidance for Rice Transplanting Using Global Positioning and Gyroscopes. Comput. Electron. Agric. 2004, 43, 223–234. [Google Scholar] [CrossRef]
- Nagasaka, Y.; Saito, H.; Tamaki, K.; Seki, M.; Kobayashi, K.; Taniwaki, K. An Autonomous Rice Transplanter Guided by Global Positioning System and Inertial Measurement Unit. J. Field Robot. 2009, 26, 537–548. [Google Scholar] [CrossRef]
- Zhu, F.; Chen, J.; Guan, Z.; Zhu, Y.; Shi, H.; Cheng, K. Development of a Combined Harvester Navigation Control System Based on Visual Simultaneous Localization and Mapping-Inertial Guidance Fusion. J. Agric. Eng. 2024, 55. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Lin, F.; Xu, H. Integrated Yaw and Rollover Stability Control of an Off-Road Vehicle with Mechanical Elastic Wheel. J. Vibroeng. 2019, 21, 450–471. [Google Scholar] [CrossRef]
- Wolf, P.; Ropertz, T.; Berns, K.; Thul, M.; Wetzel, P.; Vogt, A. Behavior-Based Control for Safe and Robust Navigation of an Unimog in Off-Road Environments. In Commercial Vehicle Technology 2018, Proceedings of the 5th Commercial Vehicle Technology Symposium-CVT 2018, Wiesbaden, Germany, 13–15 March 2018; Berns, K., Dressler, K., Fleischmann, P., Görges, D., Kalmar, R., Sauer, B., Stephan, N., Teutsch, R., Thul, M., Eds.; Springer Fachmedien: Wiesbaden, Germany, 2018; pp. 63–76. [Google Scholar]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive Backstepping Control of Tracked Robot Running Trajectory Based on Real-Time Slip Parameter Estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Chai, X.; Hu, J.; Ma, T.; Liu, P.; Shi, M.; Zhu, L.; Zhang, M.; Xu, L. Construction and Characteristic Analysis of Dynamic Stress Coupling Simulation Models for the Attitude-Adjustable Chassis of a Combine Harvester. Agronomy 2024, 14, 1874. [Google Scholar] [CrossRef]
- Chen, T.; Xu, L.; Ahn, H.S.; Lu, E.; Liu, Y.; Xu, R. Evaluation of Headland Turning Types of Adjacent Parallel Paths for Combine Harvesters. Biosyst. Eng. 2023, 233, 93–113. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive Disturbance Observer-Based Fixed Time Nonsingular Terminal Sliding Mode Control for Path-Tracking of Unmanned Agricultural Tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Lenain, R.; Thuilot, B.; Cariou, C.; Martinet, P. Adaptive and Predictive Path Tracking Control for Off-Road Mobile Robots. Eur. J. Control 2007, 13, 419–439. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, B.; Zhang, C.; Zhang, Y.; Shen, G. A Model-Free Adaptive Predictive Path-Tracking Controller with PID Terms for Tractors. Biosyst. Eng. 2024, 242, 38–49. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, Q. Feedforward-plus-Proportional-Integral-Derivative Controller for an off-Road Vehicle Electrohydraulic Steering System. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2003, 217, 375–382. [Google Scholar] [CrossRef]
- Imani, Z.; Forsythe, P.; Fard Fini, A.A.; Maghrebi, M.; Waller, T.S. Autopilot Drone in Construction: A Proof of Concept for Handling Lightweight Instruments and Materials. Results Eng. 2024, 23, 102498. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, X.; Liu, C.; Ge, J.; Cui, X.; Wang, F.; Wang, A.; Chen, W. Adaptive Path Tracking and Control System for Unmanned Crawler Harvesters in Paddy Fields. Comput. Electron. Agric. 2025, 230, 109878. [Google Scholar] [CrossRef]
- Jing, T.; Tang, Z.; Ding, Z.; Liang, Y.; Fang, M.; Wang, T. Paddy Soil Compaction Effect Undergoing Multi-Dimensional Dynamic Load of Combine Harvester Crawler. Agriculture 2024, 14, 202. [Google Scholar] [CrossRef]
- Hu, L.; Luo, X.; Zhang, Z.; Zhao, Z. Design of distributed navigation control system for rice transplanters based on controller area network. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2009, 25, 88–92. [Google Scholar]
- Sun, Y.; Cui, B.; Ji, F.; Wei, X.; Zhu, Y. The Full-Field Path Tracking of Agricultural Machinery Based on PSO-Enhanced Fuzzy Stanley Model. Appl. Sci. 2022, 12, 7683. [Google Scholar] [CrossRef]
- Guo, P. Development of Autonomous Navigation System for Crawler Combine. Master’s Thesis, Nanjing Agricultural University, Nanjing, China, 2017. [Google Scholar]
- Zhang, Y. Research on Automatic Driving and Working Control System of Unmanned Agriculture Machinery in Paddy Field. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2019. [Google Scholar]
- He, Y.; Zhou, J.; Sun, J.; Jia, H.; Liang, Z.; Awuah, E. An Adaptive Control System for Path Tracking of Crawler Combine Harvester Based on Paddy Ground Conditions Identification. Comput. Electron. Agric. 2023, 210, 107948. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, J.; Xu, Z.; Yuan, S.; Li, P.; Wang, J. Development Status and Trend of Agricultural Robot Technology. Int. J. Agric. Biol. Eng. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Li, X.; Lv, X.; Herbst, A.; Song, J.; Xu, T.; Qi, Y. Editorial: Precise Chemical Application Technology for Horticultural Crops. Front. Plant Sci. 2024, 15, 1413941. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, X.; Deng, Y.; Zang, C.; Ji, X.; Wang, A. Design and experiment of whole field path tracking algorithm for crawler harvester. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2023, 39, 36–45. [Google Scholar]
- Cui, B.; Wei, X.; Wu, S.; Xiao, J.; Chen, J.; Liao, W. Development of agricultural machinery self-driving software system based on dynamic path search. J. Agric. Mech. Res. 2022, 44, 228–232+238. [Google Scholar] [CrossRef]
- Lakkad, S. Modeling and Simulation of Steering Systems for Autonomous Vehicles. Master’s Thesis, The Florida State University, Tallahassee, FL, USA, 2004. [Google Scholar]
- Zhang, C.; Lam, H.-K.; Qiu, J.; Qi, P.; Chen, Q. Fuzzy-Model-Based Output Feedback Steering Control in Autonomous Driving Subject to Actuator Constraints. IEEE Trans. Fuzzy Syst. 2021, 29, 457–470. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems and Automation Society: Pittsburgh, PA, USA, 2006; ISBN 978-1-55617-942-6. [Google Scholar]
- Fotuhi, M.J.; Ben Hazem, Z.; Bingül, Z. Modelling and Torque Control of an Non-Linear Friction Inverted Pendulum Driven with a Rotary Series Elastic Actuator. In Proceedings of the 2019 3rd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 11–13 October 2019; pp. 1–6. [Google Scholar]




| Parameter | Value | Unit |
|---|---|---|
| Combine Dimensions (Length-Width-Height) | 9710-5800-3960 | mm |
| Combine Weight | 12,500 | kg |
| Front Wheel Track | 2820 | mm |
| Back Wheel Track | 2600 | mm |
| Wheelbase | 3717 | mm |
| Travel Speeds | Maximum driving: 24 Operating: 1.5–9.8 | km/h |
| Minimum Turning Radius | 9200 | mm |
| Cut Width | 5400 | mm |
| Grain Tank Capacity | 5500 | L |
| Parameter | Symbol |
|---|---|
| Electric Steering Wheel Speed | |
| Angular Velocity Compensate Coefficient | |
| Target Rear Wheel Angle | |
| F-PID Coefficients | |
| Rotation Angles of the Rear Wheels | |
| Rear Wheel Track | |
| Wheelbase | |
| Turning Radius | |
| Look-ahead Distance | |
| Lateral Deviation | |
| Heading Deviation | |
| LAA Auxiliary Angle | |
| Look-ahead Time | |
| Vehicle’s Velocity |
| Parameter | Value | Unit |
|---|---|---|
| Convergence Time (Smooth Concrete) | 1.5 | s |
| Overshoot (Smooth Concrete) | 13% | - |
| Convergence Time (Dry Stubble) | 2 | s |
| Overshoot (Dry Stubble) | 17% | - |
| Parameter | Value | Unit |
|---|---|---|
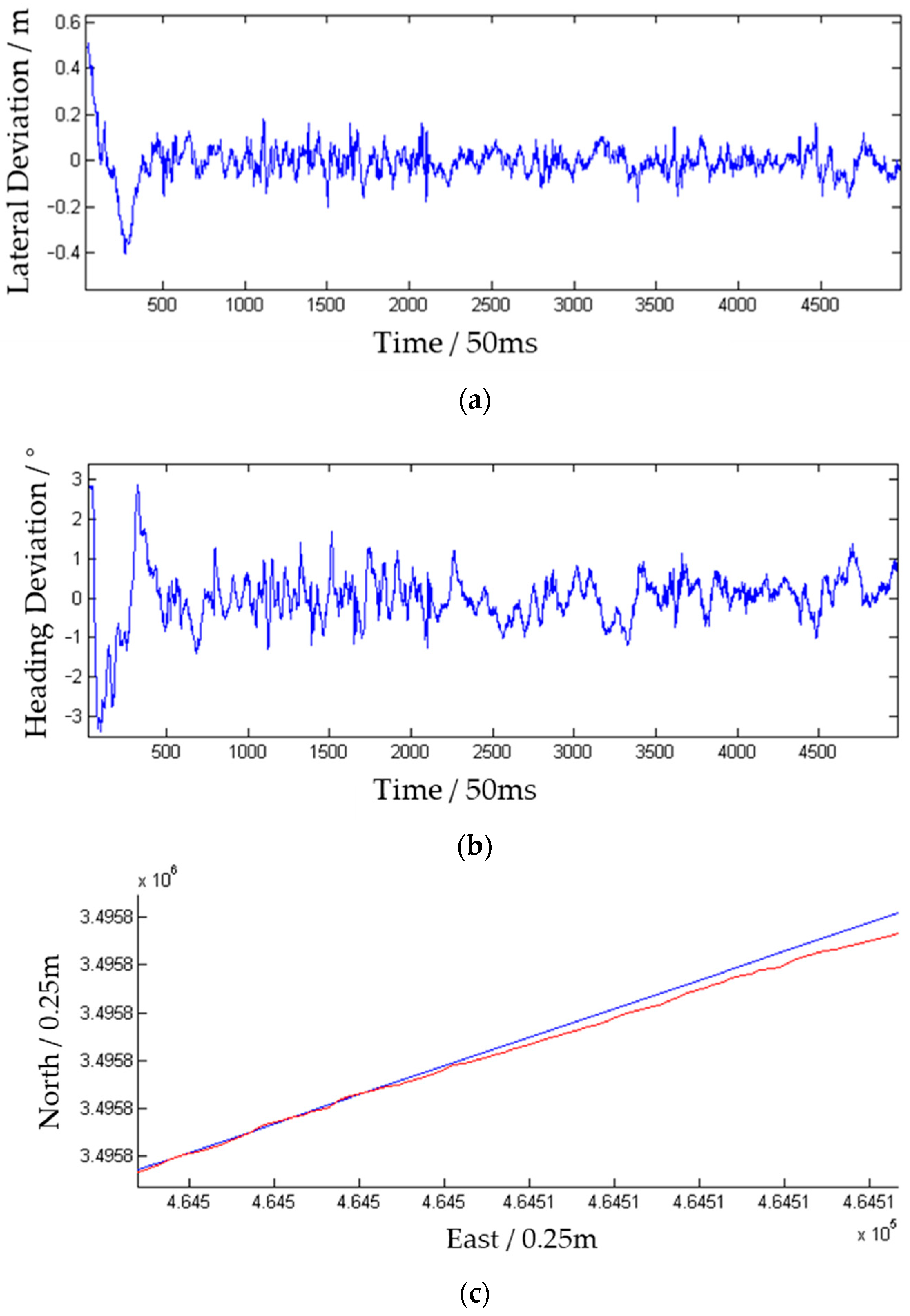
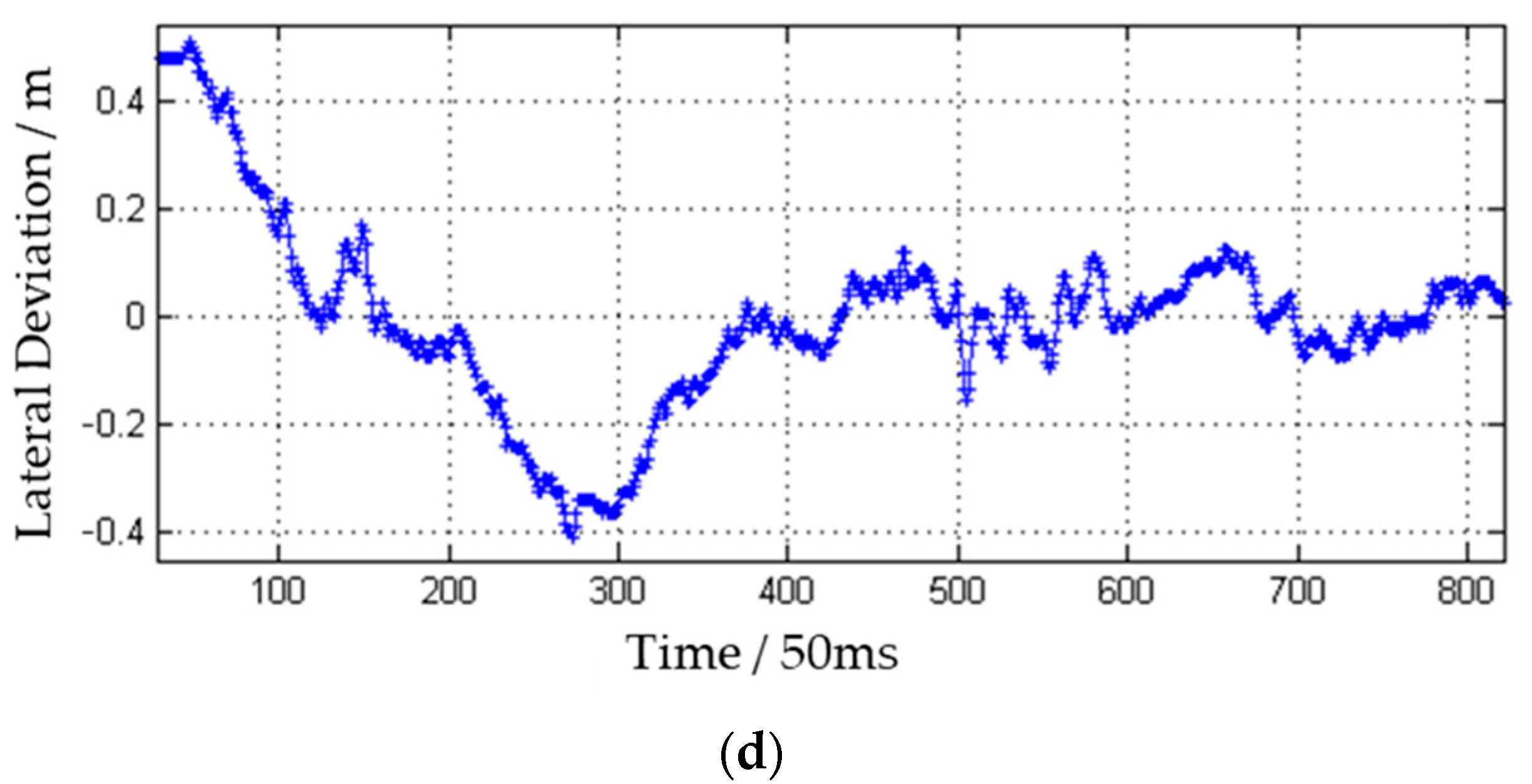
| Convergence Time (Set Initial Deviation and Speed) | 25 | s |
| Maximum Deviation (Steady-state) | 0.194 | m |
| Average Deviation (Steady-state) | 0.043 | m |
| Parameter | Value | Unit |
|---|---|---|
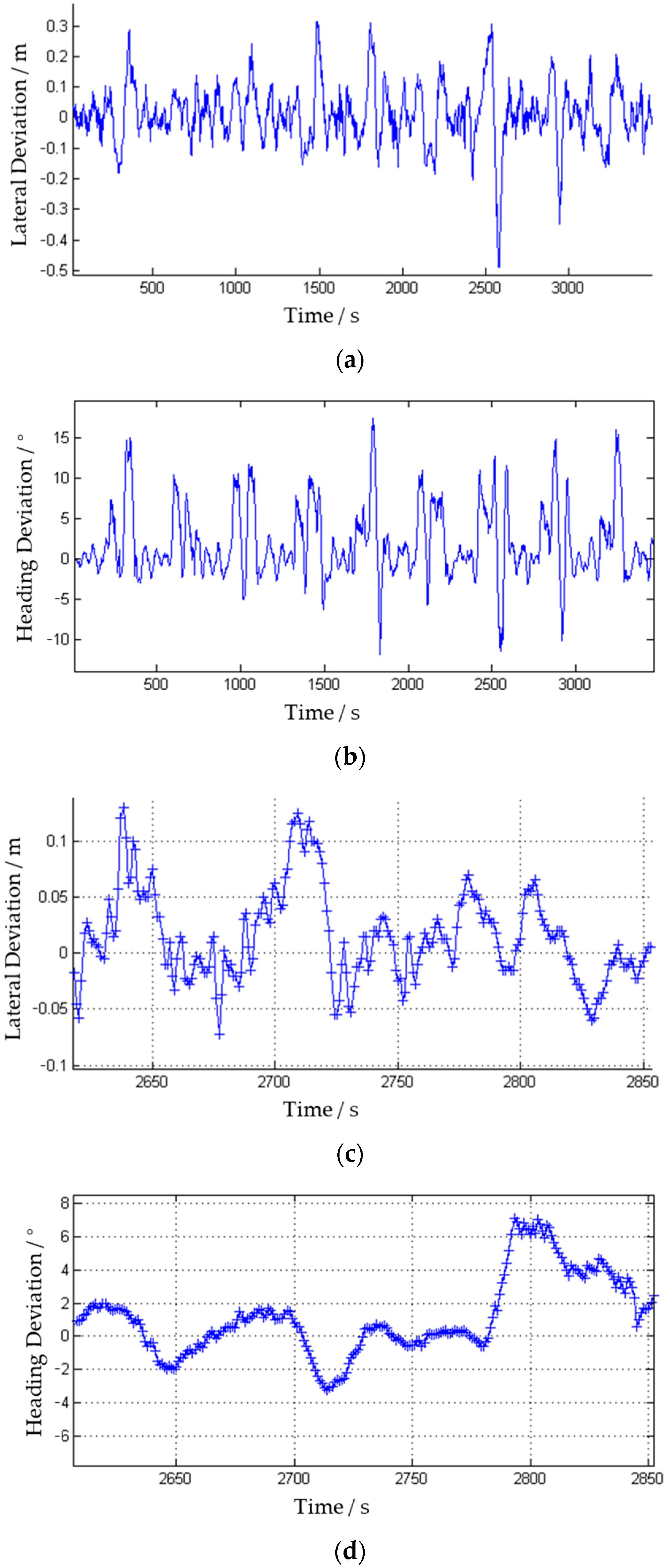
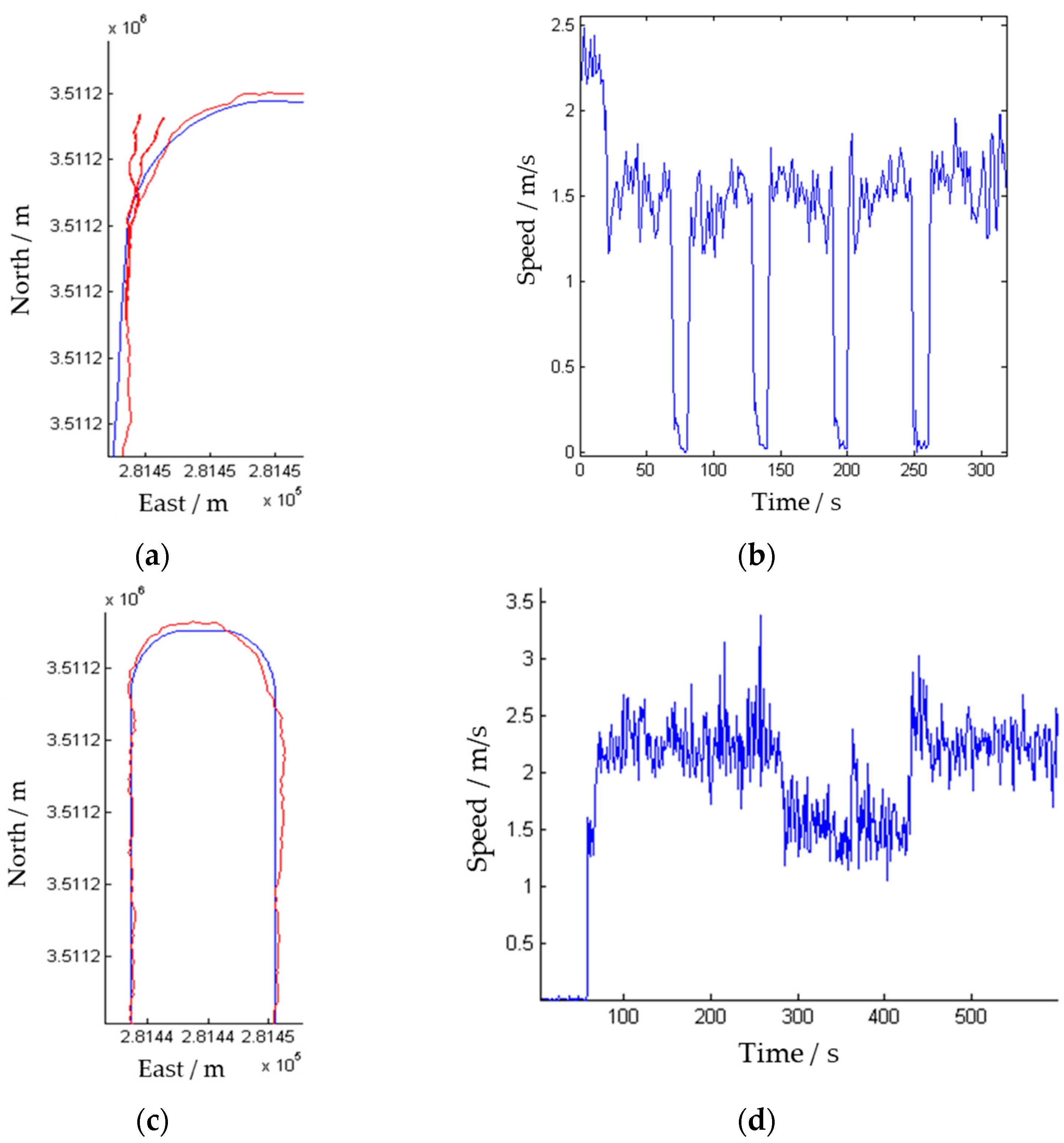
| Maximum Deviation (Steady-state) | 0.20 | m |
| Average Deviation (Steady-state) | 0.05 | m |
| Crop unharvesting rate (Whole Field) | 0.25‰ | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Liu, Q.; Xu, H.; Yang, Z.; Hu, X.; Song, Q.; Wei, X. Path Tracking Control of a Large Rear-Wheel–Steered Combine Harvester Using Feedforward PID and Look-Ahead Ackermann Algorithms. Agriculture 2025, 15, 676. https://doi.org/10.3390/agriculture15070676
Zhang S, Liu Q, Xu H, Yang Z, Hu X, Song Q, Wei X. Path Tracking Control of a Large Rear-Wheel–Steered Combine Harvester Using Feedforward PID and Look-Ahead Ackermann Algorithms. Agriculture. 2025; 15(7):676. https://doi.org/10.3390/agriculture15070676
Chicago/Turabian StyleZhang, Shaocen, Qingshan Liu, Haihui Xu, Zhang Yang, Xinyu Hu, Qi Song, and Xinhua Wei. 2025. "Path Tracking Control of a Large Rear-Wheel–Steered Combine Harvester Using Feedforward PID and Look-Ahead Ackermann Algorithms" Agriculture 15, no. 7: 676. https://doi.org/10.3390/agriculture15070676
APA StyleZhang, S., Liu, Q., Xu, H., Yang, Z., Hu, X., Song, Q., & Wei, X. (2025). Path Tracking Control of a Large Rear-Wheel–Steered Combine Harvester Using Feedforward PID and Look-Ahead Ackermann Algorithms. Agriculture, 15(7), 676. https://doi.org/10.3390/agriculture15070676





