Study on the Adsorption Mechanism of Spherical Particles near the Seed Metering Disk Surface by Narrow Elongated Suction Holes

Abstract

The long-edge characteristics of narrow elongated suction holes in air suction seed metering devices guide the alignment of multiple seeds during multiple-seed adsorption. This feature offers advantages in applications requiring seed singulation. However, research on the application of narrow elongated suction holes in air suction seed metering devices is still limited. To explore the applicability of such suction holes in seeding operations, we conducted single-factor experiments and Box–Behnken experiments. The single-factor experiments, based on computational fluid dynamics (CFD) simulations, analyzed the effects of suction hole width, length, vacuum pressure, and particle diameter on the suction force acting on a single spherical particle as it moved from the suction hole center to the outer region near the seed metering disk wall. Additionally, the Box–Behnken experiments were conducted using a dynamic–static combined adsorption measurement test platform, establishing a regression equation with suction hole width, particle diameter, and vacuum pressure as the experimental factors and the critical suction hole length for dual-particle adsorption as the response variable. The single-factor experiments indicated that suction hole width, length, vacuum pressure, and particle diameter significantly influenced the near-wall adsorption capacity of the suction hole. Analysis of the dual-particle adsorption experiments revealed that when the narrow elongated suction hole was in a vertical position, the lower particle in the adsorbed pair was more likely to detach. The critical adsorption characteristics of the narrow elongated suction hole enable dual-particle deduplication while ensuring continuous single-particle capture, thereby facilitating precision seeding.

1. Introduction

Study on the effects of narrow elongated suction holes on seeds near the seed metering disk surface, as well as their critical adsorption capacity for two seeds simultaneously, provides important guidance for applying such holes in air suction seed metering devices. Air suction seed metering technology offers strong adaptability to various seed types and causes minimal seed damage, making it suitable for seeding crops with significant shape variations [1,2]. It is widely applied in maize and soybean planting [3]. However, due to differences in seed morphology, metering disk suction holes frequently experience multiple-seed adsorption [4,5]. To ensure a high single-seed rate during sowing, excess adsorbed seeds must be removed from the suction holes [6]. Currently, leading enterprises and researchers primarily achieve seed singulation by designing specialized seed singulation mechanisms [7,8].

For example, Precision Planting in the United States and Maschio in Italy utilize a forced singulation method by disturbing seeds on both sides of the suction hole to remove multiple adsorbed seeds [9,10]. John Deere adopts a three-stage brush mechanism installed inside the seed metering disk, which reduces the intensity of forced seed singulation, balancing seed singulation efficiency with reduced seed breakage [11]. Yan Yuqian et al. [12] designed and optimized a four-stage seed singulation mechanism to address multiple-seed adsorption in small-seeded vegetable sowing, effectively reducing missed seed singulation events and improving seed metering quality. Ding Li et al. [13] developed a parametric model for the seed singulation mechanism of a specific air suction seed metering device, optimizing its parameters to enhance the seeding qualification index. Li Yuhuan et al. [14] designed a dual-sided seed singulation device to mitigate excessive seed singulation during high-speed sowing.

However, all these seed singulation mechanisms rely on forced methods, where the device intrudes into the suction hole area to forcibly scrape off excess seeds. This process can lead to seed bouncing, breakage, and clogging. Additionally, since seed morphology follows a normal distribution, a single set of singulation parameters cannot accommodate all seeds effectively.

In addition to seed cleaning mechanisms, excess seed adsorption can also be mitigated by adjusting the shape of the suction hole [15]. Previous studies have demonstrated that suction hole geometry influences the orientation and constraint of adsorbed seeds [16]. Jyotirmay Mahapatr et al. [17] developed a flexible hole seed tray to solve the problem of changes in seed shape, size, and direction, thereby improving the seed absorption capacity of the seed tray. Zhao Xueguan et al. [18] optimized the seed placement mechanism based on the effects of suction cone angle, suction hole edge distance, and hole spacing, achieving controlled maize seed orientation. Zhao Xuan [19] designed suction grooves in the metering device to constrain the adsorption posture of sunflower seeds, ensuring reliable single-seed adsorption. Chen Yulong et al. [20] modified the suction hole region of the metering disk by adding an inclined boss structure, altering the adsorption posture of flat seeds to address unstable seed filling performance. These studies highlight that modifying the interaction between suction holes and seeds significantly impacts sowing quality.

Ibrahim’s research suggested that when seeds fail to seal the pores, differences in seed size lead to the pores holding multiple seeds [21]. The elongated shape of narrow elongated suction holes creates a similarly elongated airflow pattern, causing multiple adsorbed seeds to align along the hole’s long axis. This suggests that modifying the long-axis characteristics of the suction hole can influence its seed-carrying capacity, enabling the removal of excess adsorbed seeds.

Seeds are constrained by airflow at the suction hole of the metering disk, resulting in different adsorption postures [5]. Under airflow influence, seeds experience suction forces from the suction hole [22,23], with the force direction perpendicular to the metering disk. Consequently, excess adsorbed seeds can only detach along the near-wall surface of the metering disk. Wang Yongjie et al. [24,25] studied the pressure gradient distribution around seeds and systematically analyzed factors influencing suction force. Using orthogonal experiments, they developed an initial suction force model for ellipsoidal seeds, achieving an error range within ±10% by combining the π theorem with a modified Murphy’s law. Wang Zhaoyang et al. [26] investigated the effects of circular suction holes and hole opening shapes on airflow fields and constructed a mathematical model of the adsorption domain for quasi-spherical seeds with circular holes. However, these studies primarily focused on circular suction holes and only considered scenarios where particles were directly above the suction hole. Research on the forces acting on seeds moving along the near-wall region of the metering disk remains limited. Analyzing seed forces near the wall can clarify the suction hole’s adsorption mechanism, ensure continuous single-seed adsorption, determine the critical conditions for dual-seed adsorption, and define the suction hole’s seed capture range. Therefore, understanding seed forces in the near-wall region of suction holes is equally important.

In summary, to investigate the force variations on a single standard spherical particle moving along the near-wall region of a metering disk, we conducted single-factor simulation experiments to analyze the effects of suction hole width, length, vacuum pressure, and particle diameter on suction force. Additionally, a dynamic–static combined adsorption measurement test platform was developed to examine the critical suction hole length required for dual-seed adsorption under gravity. A mathematical equation was established to describe the relationship between suction hole length and the critical dual-seed adsorption conditions for different seed diameters. Through theoretical analysis and quantitative modeling, this study further explored the adsorption characteristics of narrow elongated suction holes. By analyzing the forces acting on seeds near the metering disk surface, this research clarified the critical conditions for seed singulation in narrow elongated suction holes, providing a reference for innovative design and application in seed metering devices.

2. Principles and Analysis

2.1. Force Analysis of Seeds

During the operation of a seed metering device, multiple-seed adsorption frequently occurs. Figure 1 illustrates the force analysis of seeds captured by a narrow elongated suction hole. According to the Agricultural Machinery Design Manual, if friction is neglected, the primary forces acting on the seed include gravitational force G_s, adsorption force F_s, inertial force J_s, and the supporting force F_n exerted by the suction hole.

$$J_s=m_a{R}_s{{\omega }_s}^2,$$

(1)

where m_a is the seed mass, kg; R_s is the distance from the seed’s center of mass to the rotation center of the seed metering disk, m; ω_s is the angular velocity of the seed metering disk, rad/s.

Since the suction hole width is limited, it follows that H_s < d_a/2. The short edge of the suction hole contacts the particle at support point O_t, meaning the supporting force F_n from the seed metering disk passes through O_t. Therefore, for a single seed to achieve adsorption equilibrium, Equation (2) must be satisfied.

$$F_{s}sin{\theta }_a+F_{n}sin\left({\displaystyle \frac{\sqrt{{d_a}^2-4{H_s}^2}}{d_a}}\right)=T_s,$$

(2)

where F_s is the adsorption force, N; θ_a is the angle F_s between and the horizontal line, (°); T_s is the resultant force of gravity G_s and inertial force J_s, N; d_a is the particle diameter, m; H_s is the distance from the seed’s center of mass to the surface of the suction hole, m.

In the case of double-seed adsorption, seeds typically align along the long edge of the narrow elongated suction hole. When the long edge of the suction hole is positioned vertically, the seeds are stacked (as shown in Figure 1). The lower seed experiences additional force components due to the gravitational force and adsorption force from the upper seed, making it more prone to detachment. Experimental observations indicate that when the lower seed is about to detach from the suction hole, its center has already moved beyond the suction hole boundary, and the supporting force exerted by the seed metering disk is perpendicular to its surface. Therefore, for stable adsorption of two seeds, the forces acting on the lower seed must satisfy the conditions described in Equation (3).

$$F_{s}sin{\theta }_a+F_{n}sin\left({\displaystyle \frac{\sqrt{{d_a}^2-4{H_s}^2}}{d_a}}\right)=T_s$$

(3)

Among,

$$F_{m2}=-F_{m1}=F_{s1}sin{\theta }_{a1}+T_{s1}$$

(4)

2.2. Definitions

The software ANSYS Fluent 2022 (ANSYS, Canonsburg, PA, USA) is used to simulate airflow influenced by the suction hole and particles [27,28]. The SST k–ω turbulence model, which is well-established for analyzing near-wall flow behavior, is employed [29]. Based on CFD simulation principles, the flow field variations are obtained by solving the governing Equations (5)–(7).

The continuity equation is represented by Equation (5):

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla \cdot \left(\rho u\right)=0$$

(5)

The momentum equation is represented by Equation (6):

$$\rho \left({\displaystyle \frac{\partial u}{\partial t}}+\left(u\cdot \nabla \right)u\right)=-\nabla p+\mu {\nabla }^{2}u+F$$

(6)

The energy equation is expressed in Equation (7):

$$\rho c_p\left({\displaystyle \frac{\partial T}{\partial t}}+\left(u\cdot \nabla \right)T\right)=-\nabla \cdot \left(k\nabla T\right)+q,$$

(7)

where ρ is the fluid density, kg/m³; t is time, s; u is fluid velocity, m/s; P is pressure, Pa; µ is dynamic viscosity, Pa·s; F is the volumetric force acting on the fluid, N; c_p is the specific heat capacity, J/kg·K; T is temperature, K; k is the thermal conductivity, W/m·K; q is the heat source term, W.

The dynamic mesh model in ANSYS Fluent is used to simulate scenarios where boundary positions change over time. This model automatically updates the volume mesh positions at each time step according to new boundary locations. Thus, to use the dynamic mesh model, an initial mesh and a description of the movement in the designated region must be provided [30].

For boundaries undergoing movement, the integral form of the conservation equation for a general scalar Φ over a control volume V can be rewritten as Equation (8):

$${\displaystyle \frac{d}{d\mathrm{t}}}{\displaystyle {\int }_V\rho \varphi dV}+{\displaystyle {\int }_{\partial V}}\rho \varphi \left(\overrightarrow{u}-{\overrightarrow{u}}_g\right)\cdot dA={\displaystyle {\int }_{\partial V}\Gamma \nabla \varphi }\cdot dA+{\displaystyle {\int }_V{s}_{\varphi }dV},$$

(8)

where $\overrightarrow{u}$ is the flow velocity vector; ${\overrightarrow{u}}_g$ is the mesh velocity of the moving grid; $\Gamma$ is the diffusion coefficient; $s_{\varphi }$ is the source term; $\partial V$ is used to describe the boundary of the control volume.

The time derivative term in Equation (8) can be expressed using a first-order backward difference as shown in Equation (9):

$${\displaystyle \frac{d}{d\mathrm{t}}}{\displaystyle {\int }_V\rho \varphi dV}={\displaystyle \frac{{\left(\rho \varphi V\right)}^{n+1}-{\left(\rho \varphi V\right)}^n}{\Delta t}},$$

(9)

where n and n + 1 represent the current time and the next time step, respectively. The volume Vⁿ⁺¹ at the next time step is calculated using Equation (10):

$$V^{n+1}=V^n+{\displaystyle \frac{dV}{dt}}\Delta t,$$

(10)

where ${\displaystyle \frac{dV}{dt}}$ represents the time derivative of the volume of the control body.

To satisfy mesh conservation, the time derivative of the control volume is computed using Equation (11):

$${\displaystyle \frac{dV}{dt}}={\displaystyle {\int }_{\partial V}{\overrightarrow{u}}_g\cdot d\overrightarrow{A}={\displaystyle {\sum }_j^{n_f}{\overrightarrow{u}}_{g,j}\cdot {\overrightarrow{A}}_j}},$$

(11)

where $n_f$ represents the number of surfaces on the control volume; ${\overrightarrow{A}}_j$ represents the area vector of the j surface; ${\overrightarrow{u}}_{g,j}\cdot {\overrightarrow{A}}_j$ represents the dot product at each control volume surface, which can be calculated using Equation (12).

$${\overrightarrow{u}}_{g,j}\cdot {\overrightarrow{A}}_j={\displaystyle \frac{\delta V_j}{\Delta t}}$$

(12)

In the formula, $\delta V_j$ represents the volume change caused by the expansion of the control volume surface j during the entire time step $\Delta t$.

3. Experimental Design

3.1. Single-Seed Adsorption Experiment for Narrow Elongated Suction Holes

Ensuring consistent single-seed capture by the suction hole is critical for achieving a high single-seed rate during seeding [31]. Therefore, it was essential to study the adsorption force acting on seeds near the seed metering disk surface.

3.1.1. Simulation Model and Parameters

A simulation model, as shown in Figure 2, was established, with the simulation parameters listed in

Table 1. Simulation test parameter setting table.

Project	Parameters
Fluid density ρg (kg/m3)	1.225
Dynamic discosity μg (kg/m/s)	1.789 × 10−5
Atmospheric pressure P0 (Pa)	101.325
Pressure inlet (Pa)	Set value
Pressure outlet (Pa)	0

. To improve the accuracy of numerical calculations in CFD simulations, local mesh refinement was applied around the idealized model. Using the dynamic mesh function in ANSYS Fluent 2022, the motion of a particle near the seed metering disk surface was simulated along the x-/y-axes from the suction hole center (U point). A force monitor was employed to record the variation in adsorption force acting on the particle as it moved past the suction hole edge. To prevent negative volume formation in the mesh, a 0.1 mm gap was maintained between the particle surface and the suction hole surface.

The motion velocity and direction of the particle were controlled using a custom profile file. The particles moved uniformly at a speed of 5 mm/s along the x-/y-axes without rolling. The model adopted a tetrahedral mesh, with an overall size of 1 mm, and a refined mesh of 0.02 mm was applied at the suction hole and particle surface. To avoid errors caused by mesh density, a mesh independence test was conducted using an overall mesh of 0.01 mm, 0.05 mm, and the current mesh. The results showed that the maximum deviation between the current mesh and the 0.01 mm mesh was 0.43%, while the maximum deviation between the 0.01 mm and 0.05 mm meshes was 0.78%, indicating that the current mesh was reasonable.

3.1.2. Single-Factor Experiment Design

Barut’s research found that seed retention rate is affected by the shape, size, negative pressure, and rotation speed of the suction hole [32]. Therefore, the factors influencing the adsorption force on spherical seeds near the wall surface include suction hole width K_b, suction hole length K_l, vacuum pressure P, particle diameter d_a, and the relative position of the particle and suction hole. Single-factor experiments were conducted to explore the influence of these factors.

(1) Effect of the Suction Hole Width

To investigate the effect of the suction hole width on the adsorption force acting on particles near the wall surface, a single-factor experiment was designed, as shown in

Table 2. Experimental scheme on the effect of the suction hole width on the suction force experienced by particles.

Test Number	Kb	Kl	P	da	Moving Direction	Suction Force	Z-Axis Component	X-Axis Component	Y-Axis Component
1	1	7	7	7	X	Fs1	Fz1	Fx1	Fy1
2	2	7	7	7	X	Fs2	Fz2	Fx2	Fy2
3	3	7	7	7	X	Fs3	Fz3	Fx3	Fy3
4	1	7	7	7	Y	Fs4	Fz4	Fx4	Fy4
5	2	7	7	7	Y	Fs5	Fz5	Fx5	Fy5
6	3	7	7	7	Y	Fs6	Fz6	Fx6	Fy6

. The suction hole length K_l, vacuum pressure P, and particle diameter d_a were fixed, while the suction hole width K_b was set to 1, 2, and 3 mm. The particle movement (shown in Figure 2c, moving along the x-/y-axes of the suction hole) was analyzed.

(2) Effect of the Suction Hole Length

The long edge of the narrow elongated suction hole is a key feature influencing seed adsorption. A single-factor experiment was designed, as shown in

Table 3. Experimental scheme on the effect of the suction hole length on the suction force experienced by particles.

Test Number	Kb	Kl	P	da	Moving Direction	Suction Force	Z-Axis Component	X-Axis Component	Y-Axis Component
7	2	4	7	7	X	Fs7	Fz7	Fx7	Fy7
8	2	7	7	7	X	Fs8	Fz8	Fx8	Fy8
9	2	10	7	7	X	Fs9	Fz9	Fx9	Fy9
10	2	4	7	7	Y	Fs10	Fz10	Fx10	Fy10
11	2	7	7	7	Y	Fs11	Fz11	Fx11	Fy11
12	2	10	7	7	Y	Fs12	Fz12	Fx12	Fy12

, to study the effect of the suction hole length K_l on adsorption force. Under a vacuum pressure of 7 kPa and with a fixed suction hole width K_b of 2 mm, the adsorption force on a 7 mm diameter spherical particle was analyzed for the K_l values of 4, 7, and 10 mm. The particle movement (shown in Figure 2c, moving along the x-/y-axes of the suction hole) was analyzed.

(3) Effect of Vacuum Pressure

Vacuum pressure is a critical factor influencing adsorption capability. A single-factor experiment was designed, as shown in

Table 4. Experimental scheme on the effect of vacuum pressure on the suction force experienced by particles.

Test Number	Kb	Kl	P	da	Moving Direction	Suction Force	Z-Axis Component	X-Axis Component	Y-Axis Component
13	2	7	4	7	X	Fs13	Fz13	Fx13	Fy13
14	2	7	7	7	X	Fs14	Fz14	Fx14	Fy14
15	2	7	10	7	X	Fs15	Fz15	Fx15	Fy15
16	2	7	4	7	Y	Fs16	Fz16	Fx16	Fy16
17	2	7	7	7	Y	Fs17	Fz17	Fx17	Fy17
18	2	7	10	7	Y	Fs18	Fz18	Fx18	Fy18

, to analyze adsorption force and its components under vacuum pressures of 4, 7, and 10 kPa while keeping other parameters constant.

(4) Effect of Particle Diameter

To investigate the influence of particle size on adsorption force, a single-factor experiment was designed, as shown in

Table 5. Experimental scheme on the effect of particle diameter on the suction force experienced by particles.

Test Number	Kb	Kl	P	da	Moving Direction	Suction Force	Z-Axis Component	X-Axis Component	Y-Axis Component
19	2	7	7	4	X	Fs19	Fz19	Fx19	Fy19
20	2	7	7	7	X	Fs20	Fz20	Fx20	Fy20
21	2	7	7	10	X	Fs21	Fz21	Fx21	Fy21
22	2	7	7	4	Y	Fs22	Fz22	Fx22	Fy22
23	2	7	7	7	Y	Fs23	Fz23	Fx23	Fy23
24	2	7	7	10	Y	Fs24	Fz24	Fx24	Fy24

. The suction hole size and vacuum pressure P were fixed, while the particle diameter d_a varied (4, 7, and 10 mm).

3.2. Verification of Simulation Accuracy

To verify the accuracy of the simulation results, an adsorption force measurement test platform (as shown in Figure 3) was used for validation before conducting the simulation experiments. Actual adsorption force tests were performed using the suction hole and particle parameters listed in

Table 6. Suction model verification test parameters and results.

Test Number	Kb	Kl	P	da	Location	Fsc/N	Fs/N	y0/%
1	2	7	7	7	U	0.0538	0.0512	4.83
2	2	7	10	7	U	0.0795	0.073	8.18
3	2	7	7	10	U	0.0749	0.0706	5.74

. The measured adsorption force of the particles (F_sc) was compared with the simulated adsorption force (F_s) to analyze the relative error.

During the experiment, the position of the tested particles was adjusted using an electric lead screw controller under a set vacuum condition. A negative pressure fan provided a stable negative pressure airflow for the seed metering device. The adsorption force F_sc was sampled and recorded on a laptop via a force acquisition system. Each test group was repeated five times, and the average value was taken. The test platform, equipped with a force gauge, measured the force components exerted on the particles along the airflow direction.

3.3. Critical Adsorption Experiment for Double Seeds in Narrow Elongated Suction Holes

Based on the force analysis of particle adsorption states in Section 2.1, it is clear that for a vertically oriented narrow elongated suction hole, the lower seed is more likely to detach during multiple-seed adsorption. Therefore, to achieve seed deduplication by controlling the suction hole length, a critical adsorption experiment was designed to determine the minimum suction hole length required to adsorb two seeds under varying suction hole widths, particle diameters, and vacuum levels.

3.3.1. Experimental Methods and Equipment

Experimental observations show that seeds always detach from the suction hole along the seed metering disk’s wall surface (i.e., the near-wall region of the flow field). Combined with the force analysis, the supporting force from the seed metering disk along the suction hole direction interacts with the z-component of the suction force, preventing the seeds from detaching perpendicularly to the seed metering disk. The primary forces causing seed detachment from the suction hole are gravity and additional compressive forces acting on the seeds.

Based on the above analysis, a dynamic–static combined plate adsorption measurement test platform was constructed. As shown in Figure 4, the platform consisted of a seed metering base, a detachable A-type dynamic plate, a detachable B-type static plate, a stepper motor, a vacuum fan, an air pump, a high-speed camera, a laptop, and spherical nylon particles. The detachable A-type dynamic plate and the detachable B-type static plate together formed a narrow elongated suction hole (combined plate). The static B-type plate was fixed to the seed metering base and remained stationary, while the rotating A-type dynamic plate gradually shortened the suction hole length until the suction hole could no longer hold two seeds. The vacuum chamber formed by the combined plate and the seed metering base was connected to the vacuum fan, providing stable negative pressure airflow. Since the B-type static plate was designed with positioning slots, the long edge of the tested suction hole remained in a vertical orientation. The narrow elongated suction hole constrained the re-adsorbed seeds to align along its long edge. Using an L-PRI 1000 high-speed camera (AOS Technologies AG, Baden, Switzerland), the motion of the two seeds during the rotation of the A-type dynamic plate was recorded until the seeds detached from the suction hole. At that moment, the length of the suction hole was documented [33].

The motion principle of the dynamic–static combined plate adsorption measurement test platform is illustrated in Figure 5. The long hole in the B-type static plate remained fixed at the long edge of the narrow suction hole, while the A-type dynamic plate rotated around the center O_s, forming a narrow suction hole in combination with the static plate. The width of the U-shaped hole gradually narrowed along the rotation direction, shortening the length of the narrow elongated suction hole. To facilitate observation, size markers were placed at the edges of the U-shaped hole.

The experiment was conducted at the National Key Laboratory of Agricultural Equipment Technology, where external airflow and vibrations were minimized. The test objects were standard spherical nylon particles (Figure 6), manufactured using 3D additive manufacturing technology with a processing accuracy of 0.02 mm. The particles had smooth and flawless surfaces.

3.3.2. Experimental Plan for Double-Seed Adsorption

(1) Double-Seed Adsorption Experiment with Equal-Diameter Particles

To determine the critical suction hole length K_l^′ required to accommodate two seeds, a three-factor, three-level Box–Behnken experiment was designed using Design-Expert V8.0.6 (Stat-Ease, Minneapolis, MN, USA). The experimental factors were suction hole width K_b, particle diameter d_a, and vacuum level P, with K_l^′ as the experimental response variable. The factors and levels are listed in

Table 7. Test factors and levels.

Levels	Factor
	Kb/mm	da/mm	P/kPa
−1	1	5	4
0	2	7	7
1	3	9	10

. The experiment consisted of 17 test groups, as shown in

Table 8. Test plan and results.

Test Number	Factor			Index
	Kb/mm	da/mm	P/kPa	Kl′
1	2	7	7	4.79
2	3	7	4	5.61
3	1	5	7	4.
4	2	5	4	4.87
5	2	7	7	4.79
6	1	7	10	5.11
7	2	7	7	5.71
8	1	9	7	7.93
9	2	7	7	4.84
10	3	7	10	5.08
11	3	5	7	4.69
12	3	9	7	7.01
13	1	7	4	7.22
14	2	9	10	6.83
15	2	7	7	4.97
16	2	5	10	3.91
17	2	9	4	7.72

, including 12 factor analysis trials and 5 zero-point error estimations. Each test was repeated three times, and the average value was used as the final result.

(2) Double-Seed Adsorption Experiment with Unequal-Diameter Particles

In actual operation, the diameters of two simultaneously adsorbed seeds often vary. Therefore, an experiment was conducted to study the multiple-seed adsorption characteristics of particles with unequal diameters. Since re-adsorbed seeds align along the long edge, the force analysis in Figure 1 indicates that the lower seed experiences additional gravity and suction force components from the upper seed, making it more prone to detachment. To investigate whether a pattern exists for the critical suction hole length required for the simultaneous adsorption of unequal-diameter seeds, a full-factor experiment was conducted using the dynamic–static combined plate adsorption measurement test platform, as shown in

Table 9. Experimental scheme and results of double-seed adsorption of particles with unequal diameters.

Test Name	Upper Particle Diameter	Lower Particle Diameter	Mean Critical Hole Length	Standard Deviation
9-9	9	9	7.27	0.17
9-7	9	7	5.91	0.3
9-5	9	5	5.4	0.08
7-9	7	9	6.5	0.11
7-7	7	7	5.33	0.19
7-5	7	5	4.74	0.3
5-9	5	9	5.59	0.09
5-7	5	7	4.4	0.08
5-5	5	5	4.07	0.18

. The experimental method was the same as in the previous section, with each test repeated five times, and the mean and standard deviation were calculated. The experimental parameters included a suction hole width of 2 mm, a vacuum level of 7 kPa, and particle diameter and alignment order as experimental factors, with the required critical suction hole length for two seeds as the response variable.

4. Results and Analysis

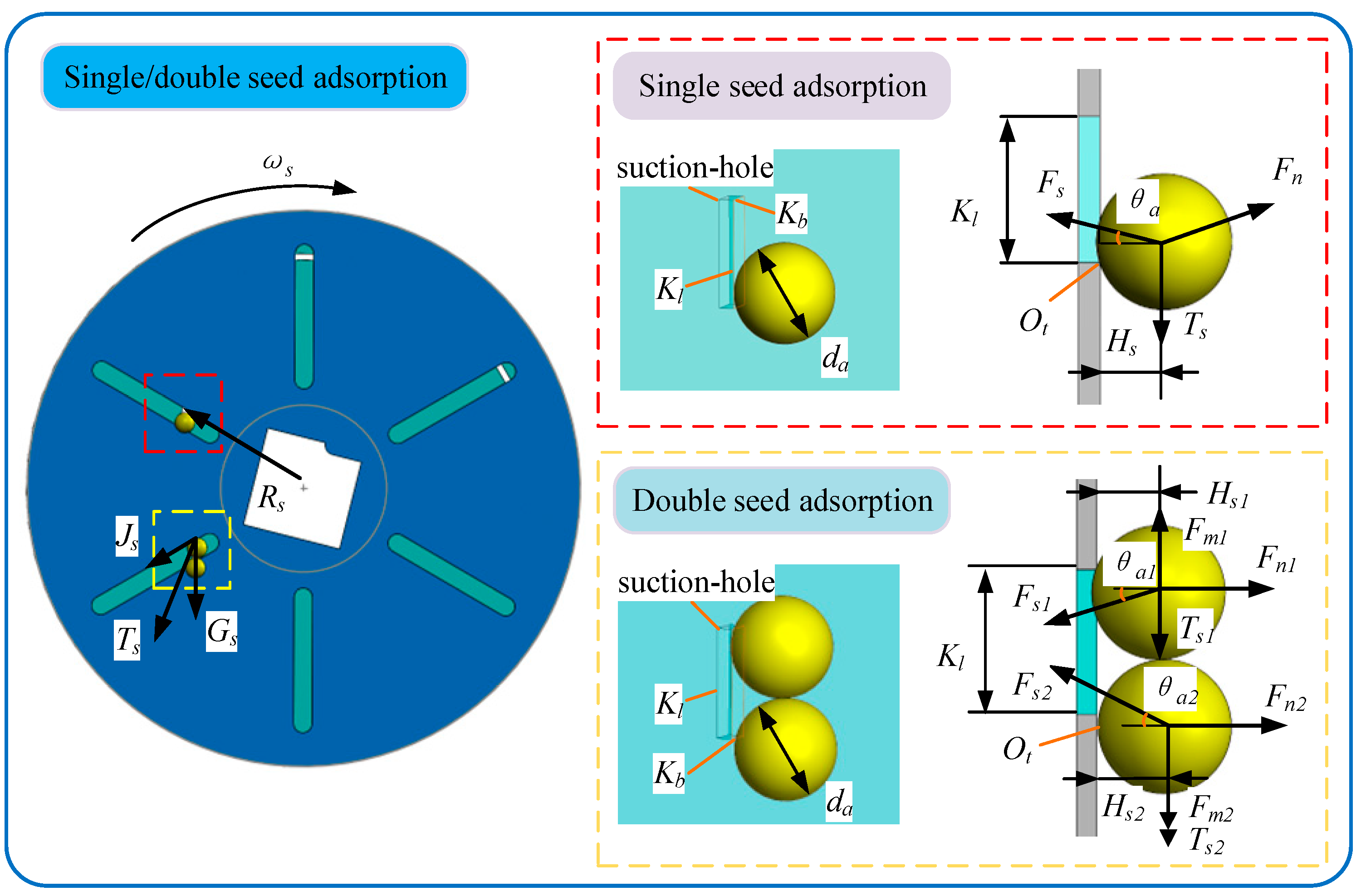
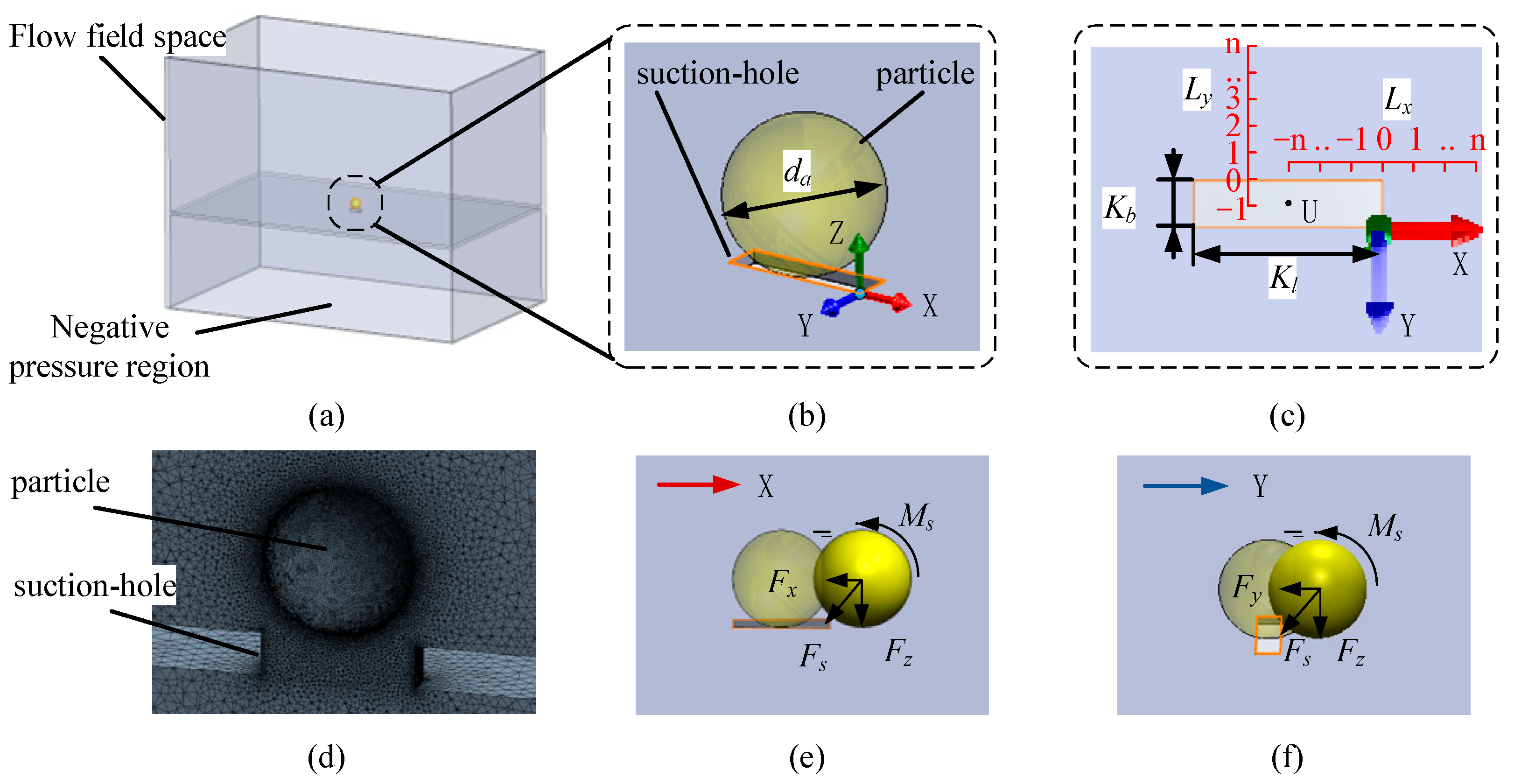
4.1. Study on the Single-Seed Adsorption Characteristics of Narrow Elongated Suction Holes

(1) Effect of the Suction Hole Width on the Adsorption Force Acting on Near-Wall Particles

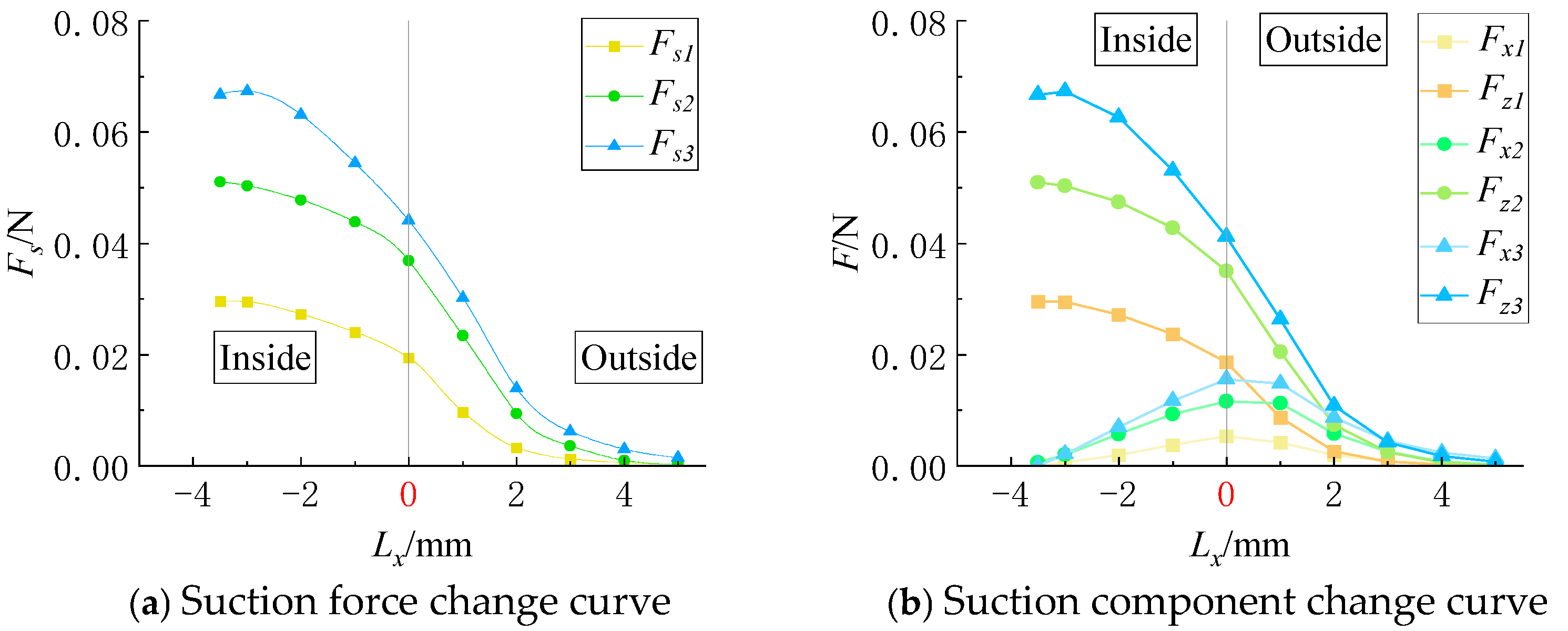
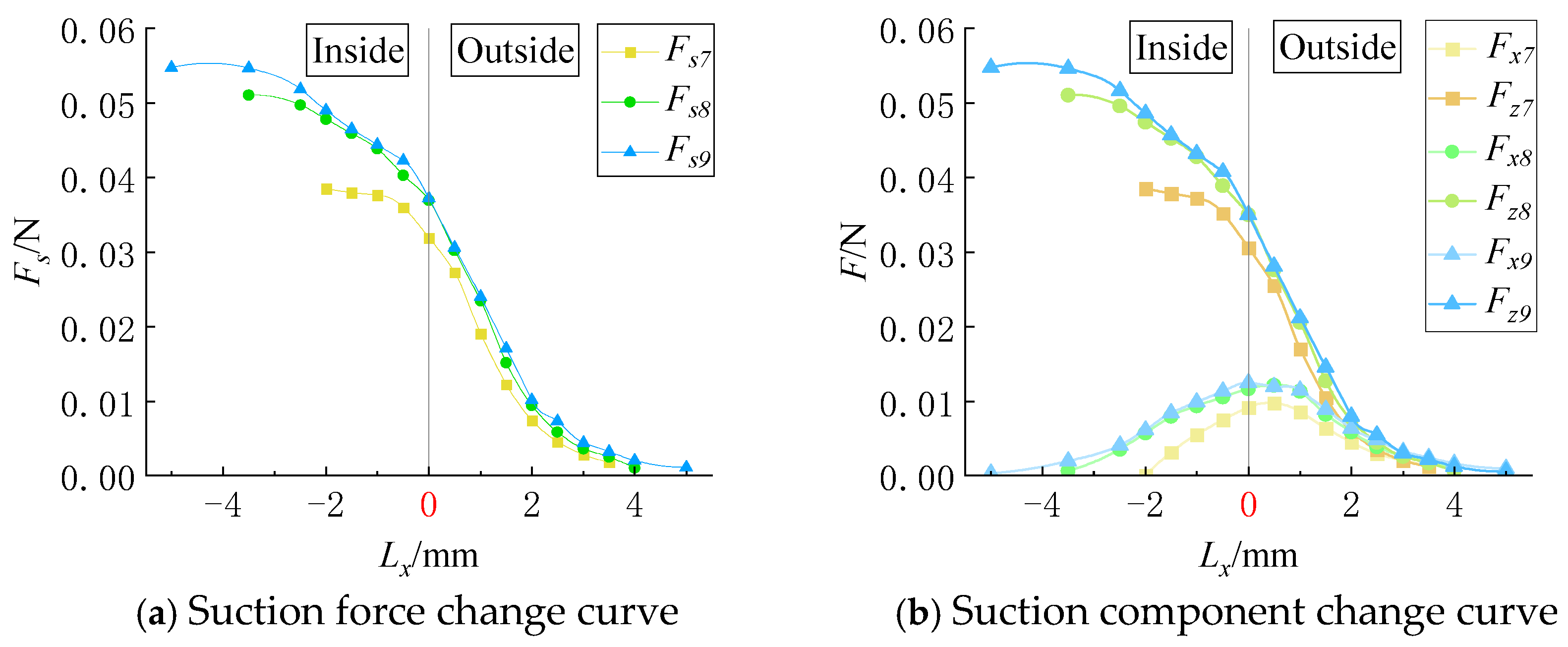
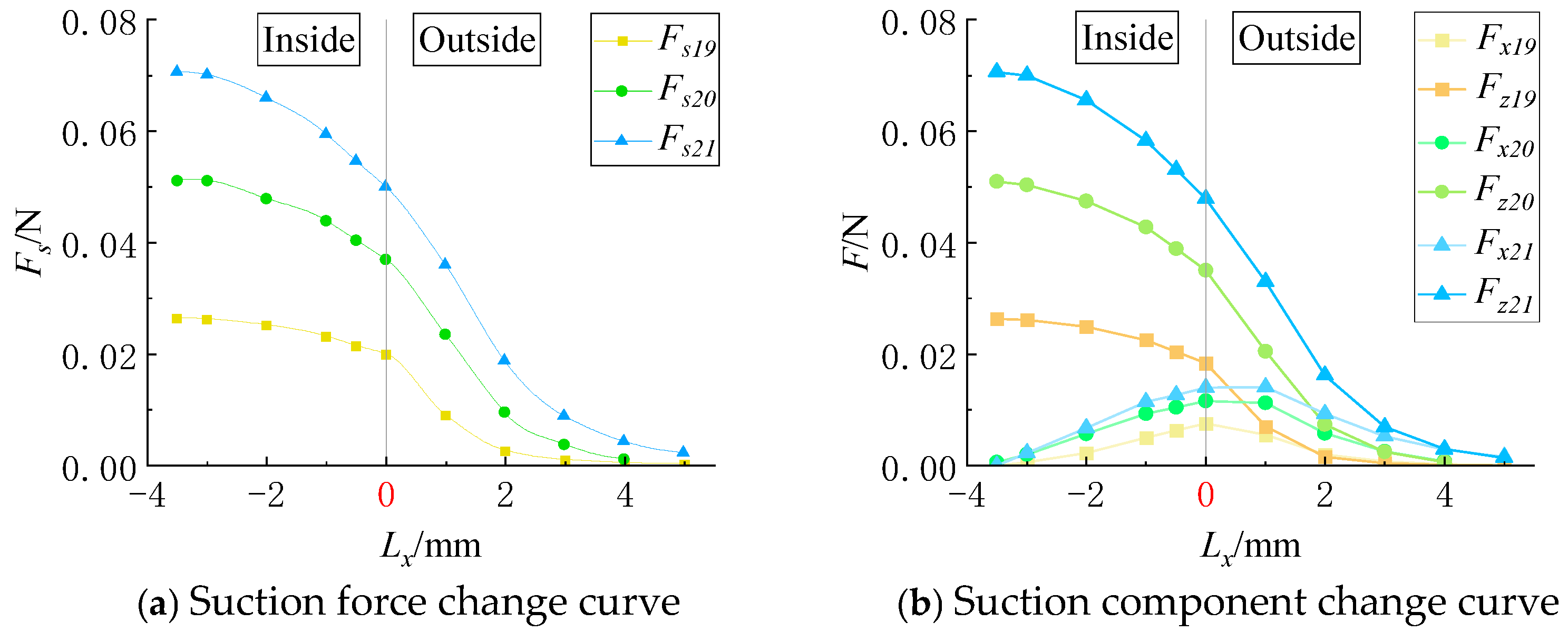
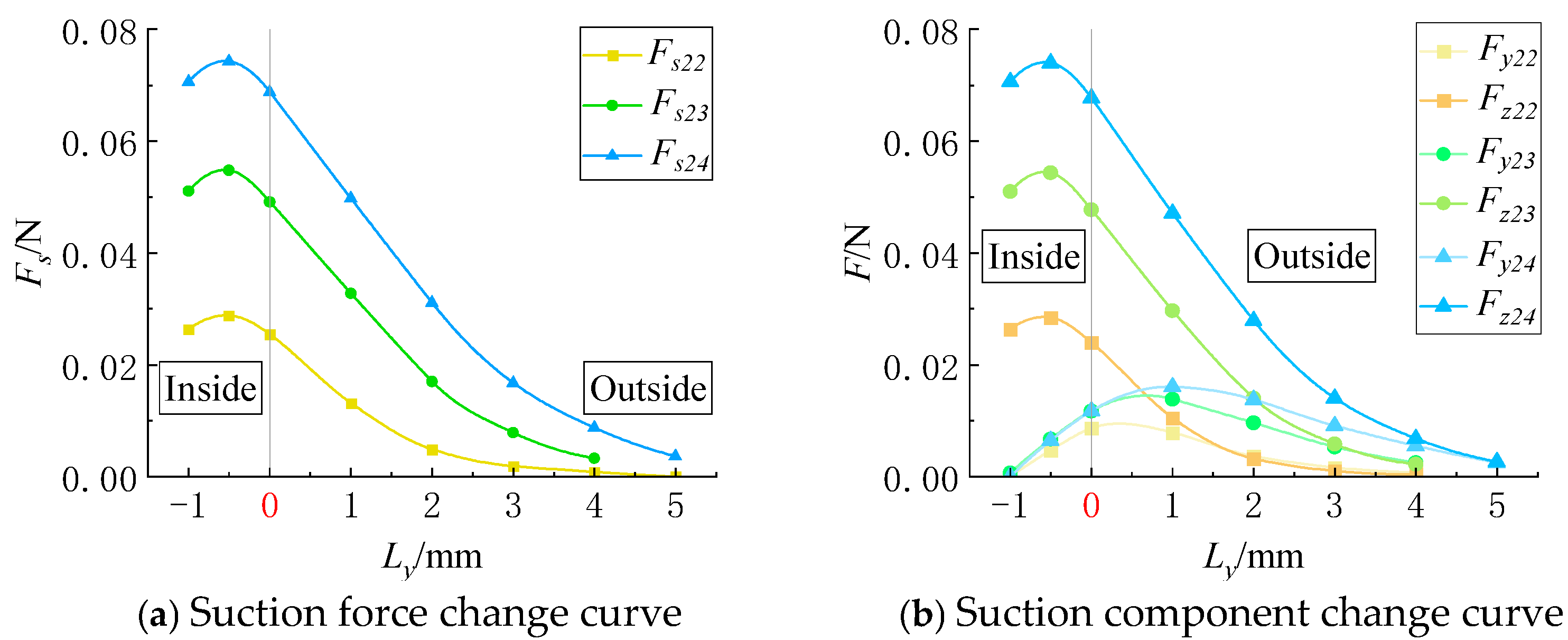
The force curves of the particles moving along the x-axis under different suction hole widths are shown in Figure 7, while those along the y-axis are shown in Figure 8.

When a particle moves along the long side of the suction hole (x-axis), the adsorption force F_s is significantly affected by K_b, as illustrated in Figure 7. An increase in K_b expands the suction hole area, thereby enhancing the adsorption force acting on the particle. Figure 7a shows that when K_b = 3 mm, the peak adsorption force is 1.32 times that at K_b = 2 mm, while at K_b = 2 mm, the peak adsorption force is 1.72 times that at K_b = 1 mm. This indicates that variations in K_b significantly affect the magnitude of the adsorption force. As the particle moves towards the suction hole edge (with L_x approaching 0), the adsorption force gradually decreases. At K_b = 3 mm, the adsorption force at the boundary of the long side (L_x = 0) is reduced by 34% compared to that at the hole center, while for K_b = 2 mm and K_b = 1 mm, the reduction is 27.7% and 34.24%, respectively. Outside the suction hole region, the adsorption force continues to decline at different rates for each width, with the decay rate slowing down when L_x exceeds 2 mm. The ranking of L_x values corresponding to zero adsorption force follows: 3 mm > 2 mm > 1 mm.

The flow field around the narrow elongated suction hole exhibits a semi-ellipsoidal shape. Due to symmetry, the y-component of the adsorption force (F_y) is approximately zero when the particle moves along the x-axis. Thus, the total adsorption force F_s can be decomposed into an x-axis component (F_x) and a z-axis component (F_z), as shown in Figure 7b. When the particle is at the suction hole center (U point), both F_x and F_y are nearly zero, making F_s equal to F_z. In Figure 7a,b, F_z closely follows F_s in both magnitude and trend, making further analysis of F_z unnecessary. However, as the particle moves away from the suction hole center, F_x increases, reaching its maximum between 0.5 mm and 1 mm, though its value remains significantly lower than F_z.

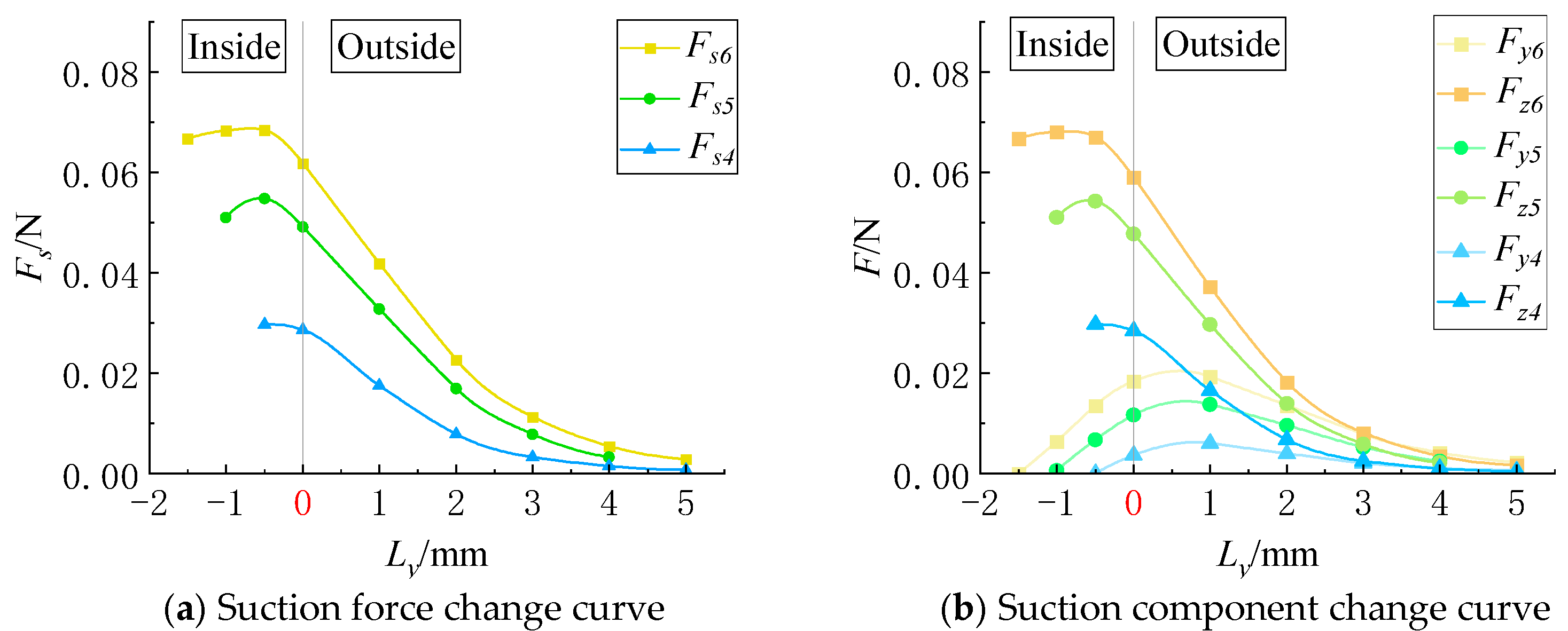
When the particle moves along the short side of the suction hole (y-axis), as shown in Figure 8, the adsorption force F_s varies slightly within the suction hole region. At K_b = 3 mm, the adsorption force at the short-side boundary (L_y = 0) decreases by 9.57% compared to its maximum value; for K_b = 2 mm and K_b = 1 mm, the reductions are 10.23% and 3.57%, respectively. When K_b = 1 mm, the particle moves over a short distance within the suction hole, resulting in minimal variation in F_s. For K_b = 2 mm and K_b = 3 mm, the F_s curve exhibits a slight initial increase, followed by a decrease. This phenomenon occurs because at the suction hole center (U point), the symmetrical flow field results in a near-zero y-axis force. As the particle moves, this symmetry is disrupted, increasing airflow differences on either side of the particle and causing a slight increase in F_s, with a peak at L_y = −0.5 mm. Outside the suction hole region, the force decay rate transitions from fast to slow, with the smallest suction force observed for the 1-mm-wide hole, which also reaches zero the fastest.

When the particle moves along the y-axis, the x-axis force (F_x) is negligible and thus not analyzed. The force decomposition in Figure 8b shows that F_z closely follows F_s. As the particle moves away from the symmetry center (U point), F_y increases before gradually decreasing beyond a certain distance, with the gradient of F_y varying significantly with K_b.

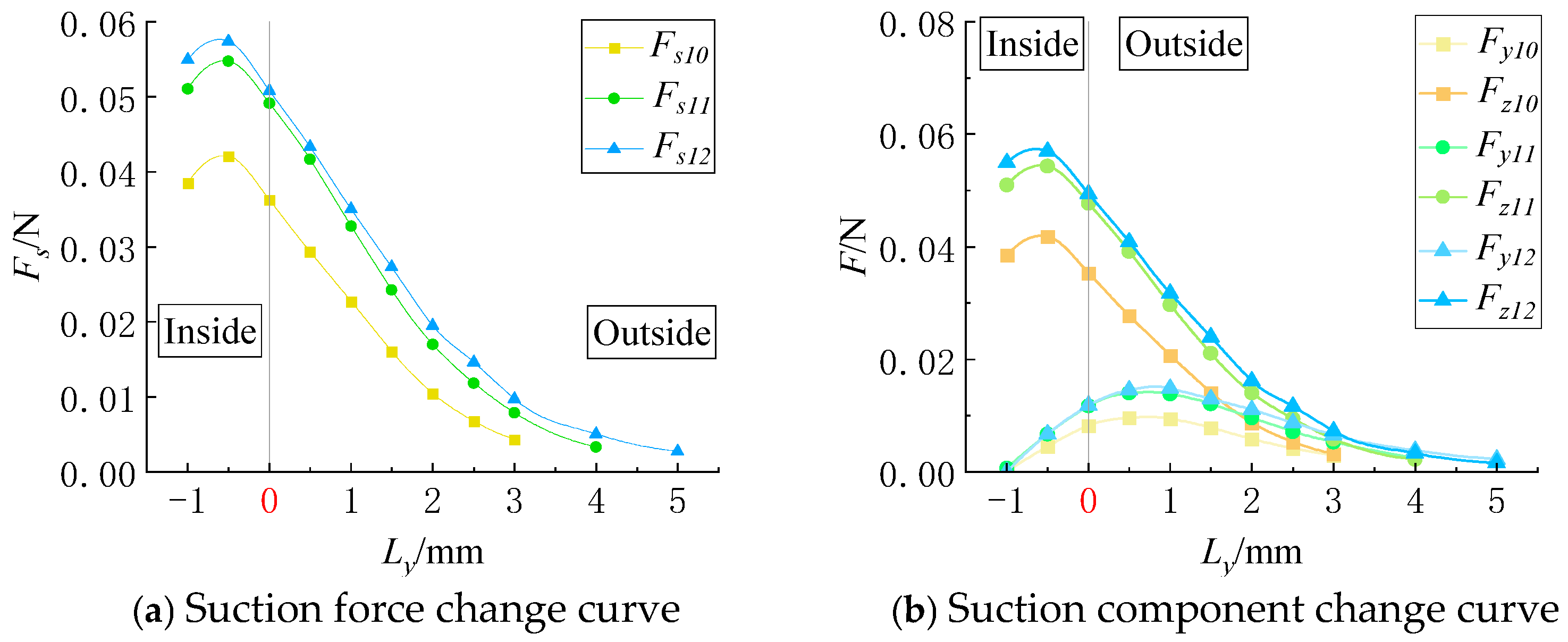
(2) Effect of the Suction Hole Length on the Adsorption Force Acting on Near-Wall Particles

The force curves for particle movement along the x-axis and y-axis under different suction hole lengths are shown in Figure 9 and Figure 10, respectively.

As shown in Figure 9, when the particle moves along the long side of the suction hole (x-axis), the adsorption force F_s varies significantly with K_l. The order of adsorption force magnitudes corresponds to the order of suction hole lengths. When K_l = 7 mm, the peak adsorption force is 1.33 times that at K_l = 4 mm, whereas at K_l = 10 mm, it is only 1.07 times that at K_l = 7 mm. This suggests that when K_l is smaller than d_a, its variations significantly influence F_s; however, beyond this threshold, further increasing K_l has little additional impact. Within the suction hole region, the adsorption force decreases as the particle moves toward the edge (with L_x approaching 0), but the decay rate is lower compared to that outside the suction hole region. At K_l = 10 mm, the adsorption force at L_x = 0 is reduced by 32.11% compared to that at the hole center; for K_l = 7 mm and K_l = 4 mm, the reductions are 27.7% and 17%, respectively. Outside the suction hole region, the adsorption forces on particles at the same relative positions are nearly identical across different K_l values.

The flow field around the narrow elongated suction hole exhibits a semi-ellipsoidal shape. Due to symmetry, the y-component of the adsorption force (F_y) remains nearly zero when the particle moves along the x-axis, allowing the force decomposition into F_x and F_Z (Figure 9b). As the particle moves from the suction hole center (U point) to the edge, F_x first increases and then decreases, peaking between 0.5 mm and 1 mm, while F_Z closely follows F_S.

As shown in Figure 10, when the particle moves along the short-edge direction of the suction hole (y-axis), the adsorption force F_S initially increases slightly within the suction hole region before decreasing. Specifically, when K_l is 10 mm, the adsorption force at the short-edge boundary (L_y = 0) decreases by 13.8% relative to the maximum adsorption force; when K_l is 7 mm, the reduction is 10.23%; and when K_l is 4 mm, the reduction is 11.44%. A shorter K_b results in smaller variations in adsorption force within the suction hole region.

Outside the suction hole region, the adsorption force acting on the particle at the same relative position varies depending on the suction hole length. This indicates that in the y-axis direction, a 4-mm-long suction hole has a smaller effective capture range for near-wall particles than a 7-mm-long suction hole, while a 10-mm-long suction hole captures near-wall particles within a slightly larger range than the 7-mm-long suction hole.

Since the x-axis adsorption force F_x was not analyzed in this section, only the force components F_z and F_s were considered, as illustrated in Figure 10b. The magnitudes and variations of F_z closely resemble those of F_s. As the particle moves away from the symmetric center of the flow field (U point), F_y begins to increase, reaching a peak after a certain distance from the suction hole before decreasing. The semi-ellipsoidal nature of the airflow field within the narrow elongated suction hole leads to a shorter decay distance for the adsorption force when the particle moves along the minor axis (y-axis) compared to when it moves along the major axis (x-axis).

(3) Influence of Vacuum Level on Adsorption Force Acting on Near-Wall Particles

Under different vacuum levels, the force curves for particle movement along the x-axis and y-axis are shown in Figure 11 and Figure 12, respectively.

As illustrated in Figure 11, when a particle moves along the long edge direction (x-axis) of the suction hole, the vacuum level P significantly influences the adsorption force. The trends in adsorption force under the three vacuum levels are highly similar, but the force magnitudes at the same position vary considerably. When P = 10 kPa, the peak adsorption force is 1.43 times that at P = 7 kPa, while at P = 7 kPa, it is 1.71 times that at P = 4 kPa. The adsorption force gradually decreases as the particle moves from the suction hole center to the boundary. Specifically, at P = 10 kPa, the adsorption force at the long-edge boundary decreases by 30.35% compared to the suction hole center; at P = 7 kPa, the reduction is 27.71%; and at P = 4 kPa, the reduction is 31.99%.

Outside the suction hole region, the force differences between the three vacuum levels gradually diminish. The force curve at P = 10 kPa exhibits the steepest decline, with the force approaching zero at a 4 mm distance from the short edge. At P = 4 kPa, the force curve declines the slowest, approaching zero at a 3 mm distance from the short edge.

Similar to the previous analysis, the adsorption force along the x-axis can be decomposed into F_x and F_z (Figure 11b). F_z closely resembles F_s in magnitude and variation trend. As the particle moves away from the suction hole center, F_x gradually increases, reaching a maximum between 0.5 mm and 1 mm. Since F_x is significantly smaller than F_z, the adsorption force in the z-axis plays a dominant role in restraining the particle within the suction hole.

When the particle moves along the short-edge direction (y-axis) of the suction hole, all three vacuum levels exhibit a slight increase in adsorption force F_s before decreasing (Figure 12a), with a larger increase at higher P values. Experimental results show that at P = 10 kPa, the adsorption force at the short-edge boundary decreases by 10.79% relative to the peak force; at P = 7 kPa, it decreases by 10.23%; and at P = 4 kPa, it decreases by 10.35%.

Outside the suction hole region, the adsorption force at the same L_y position is positively correlated with P, indicating that the particle capture capability of the suction hole along the y-axis follows the order 10 kPa > 7 kPa > 4 kPa.

As shown in Figure 12b, decomposing the adsorption force into F_y and F_z reveals that F_z closely matches F_s in magnitude and trend. When the particle moves away from the symmetric center of the flow field, F_y begins to increase, reaching a maximum after a certain distance from the suction hole before decreasing.

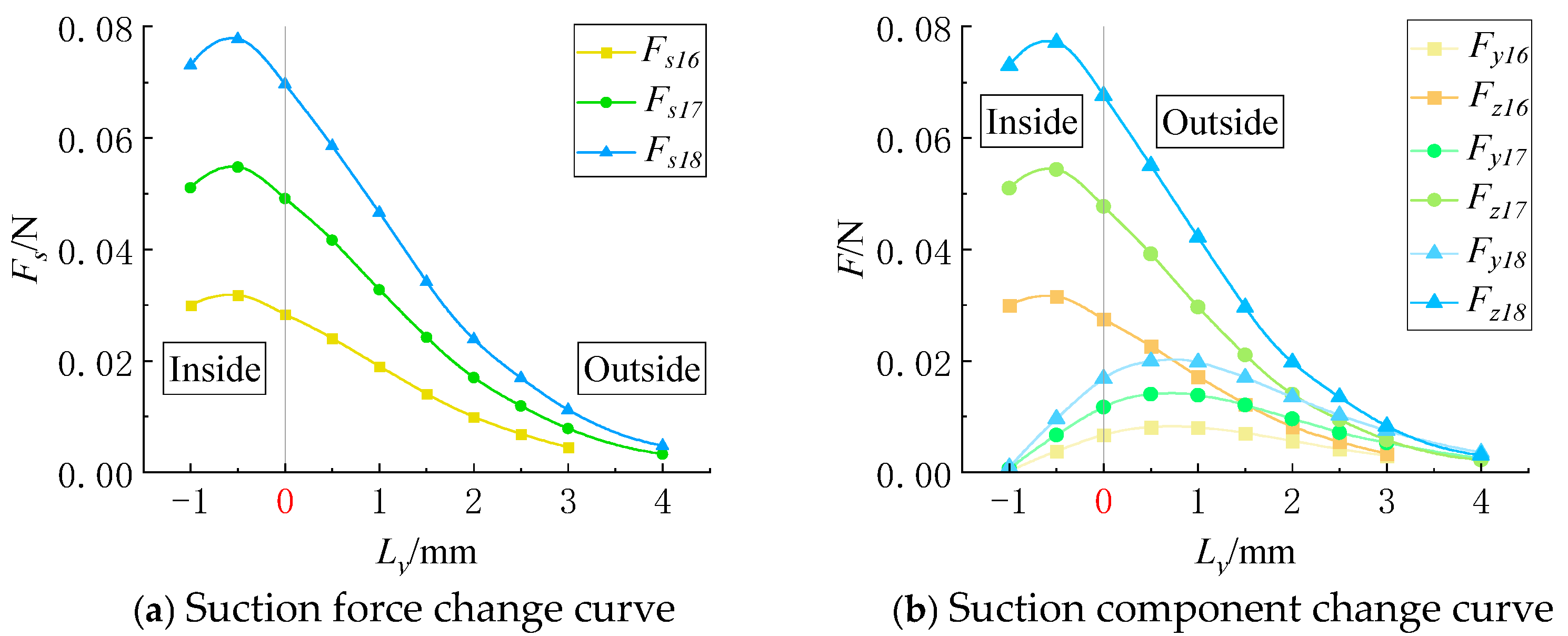
(4) Influence of Particle Diameter on the Suction Force Acting on Near-Wall Particles

The force curves for particles moving along the x-axis under different particle diameters are shown in Figure 13, while those for particles moving along the y-axis are presented in Figure 14.

As illustrated in Figure 13, the suction force F_s acting on a particle varies as it moves along the long edge of the suction hole (x-axis direction). Differences in particle diameter d_a result in significant variations in the suction force. When d_a = 10 mm, the peak suction force is 1.38 times that when d_a = 7 mm, while the peak suction force for d_a = 7 mm is 1.94 times that for d_a = 4 mm. As the particle moves from the center of the suction hole to its boundary, the suction force gradually decreases. Specifically, when d_a = 10 mm, the suction force at the boundary along the long edge is reduced by 22.67% compared to that at the center of the suction hole. For d_a = 7 mm, the reduction is 27.71%, while for d_a = 4 mm, it is 24.45%. When the particle moves outside the suction hole region, the rate of decrease in suction force slows down. The force curve for d_a = 10 mm shows the fastest decline, with the suction force approaching zero when the distance from the short edge L_x reaches 4.5 mm. The force curve for d_a = 4 mm shows the slowest decline; however, due to its lower force values, the suction force approaches zero when the distance from the short edge reaches 3 mm.

Similar to the previous analysis, the suction force F_s acting on a particle moving along the long edge of the suction hole (x-axis direction) could be decomposed into the x-component F_x and the z-component F_z (Figure 13b). The magnitude and trend of F_z closely resemble those of F_s and will not be discussed in detail. As the particle moves away from the center of the suction hole, F_x gradually increases, reaching its peak at a position 0.5–1 mm away.

For particle movement along the short edge of the suction hole (y-axis direction), the suction force experienced by particles of all three diameters exhibits a slight increase before decreasing within the suction hole region (Figure 14). Larger particle diameters correspond to greater increases in suction force. Experimental results show that when d_a = 10 mm, the suction force at the short-edge boundary (L_y = 0) decreases by 7.38% compared to its maximum value. For d_a = 7 mm, this reduction is 10.23%, and for d_a = 4 mm, it is 11.5%. Outside the suction hole region, larger-diameter particles experience the influence of suction force over a greater distance.

Decomposing the suction force into F_y and F_z, we found that the magnitude and trend of F_z are highly similar to those of F_s; they will not be discussed further. When a particle moves away from the symmetric center of the flow field, the value of F_y begins to increase, reaching a peak after a certain distance before starting to decrease.

(5) Flow Field Analysis

Experiments 2, 8, 14, and 20, as well as experiments 5, 11, 17, and 23, were repeated tests with identical parameters. Therefore, representative points were selected from the particle motion process, as shown in Figure 15, including U point (L_x = −3.5 mm, L_y = −1 mm), X₁ point (L_x = 0 mm), X₂ point (L_x = 2 mm), Y₁ point (L_y = 0 mm), and Y₂ point (L_y = 2 mm), to analyze the flow field state under the suction hole–particle interaction.

According to the velocity contour plots of the flow field, when the particle is at the suction hole center (U point), the airflow on both sides remains symmetrical, resulting in F_x and F_y being zero. As the particle moves along the x-/y-axes, the shape of the suction hole causes asymmetry in the front and rear flow fields, generating a force in the movement direction. However, the force component in the lateral direction remains zero due to the continued symmetry of the suction hole on both sides.

From the pressure distribution contour plots on the particle surface, it can be observed that the pressure gradient contour lines exhibit no distinct pattern, indicating a turbulent flow. Due to the influence of the suction hole boundary, the low-pressure region on the particle surface shifts along with the suction hole boundary. The conclusion that the suction hole shape affects the particle surface pressure distribution is consistent with the findings of previous research [24].

4.2. Adsorption Force Verification Results

As shown in Table 6, a comparison between the simulated adsorption force values and the actual adsorption force values under the same parameter conditions revealed that the relative error y₀ of the three test groups was less than 10%, indicating that the simulation model and parameter settings were reasonable and that the simulation results are reliable.

4.3. Study on the Critical Adsorption Behavior of Dual-Particle Adsorption

(1) Dual-Particle Adsorption Experiment with Equal-Diameter Particles

A multiple regression analysis was performed on the test results presented in Table 8, establishing a quadratic polynomial regression model with K_l^′ as the response variable and K_b, d_a, and P as the test factors. After removing nonsignificant terms, the optimized regression equation is presented in Equation (13):

$$K_l^{’}=13.11-3.25K_b-1.33d_a-0.45P+0.13K_{b}P+0.5{K_b}^2+0.15{d_a}^2$$

(13)

Analysis of variance (ANOVA) was conducted on the optimized model, as shown in

Table 10. ANOVA of the optimal regression model of critical suction length.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	22.64	6	3.77	30.95	<0.0001 **
Kb	0.83	1	0.83	6.78	0.0263 *
da	16.02	1	16.02	131.38	<0.0001 **
P	2.53	1	2.53	20.73	0.0011 **
KbP	0.61	1	0.61	5.04	0.0486 *
Kb2	1.07	1	1.07	8.81	0.0141 *
da2	1.43	1	1.43	11.76	0.0065 **
Residual	1.22	10	0.12
Lack of fit	0.6	6	0.1	0.65	0.6981
Pure error	0.62	4	0.15
Cor total	23.86	16

Note: * indicates a significant effect (0.01 < p < 0.05) and ** indicates a highly significant effect (p < 0.01).

. The results show that the p-value of the fitted model is significantly less than 0.01, while the lack-of-fit p-value is greater than 0.05. The coefficient of determination R² is 0.949, indicating that the optimized regression model is highly significant and well-fitted and, thus, reliable. The effects of d_a, P, and d_a² on the critical suction hole length are highly significant (p < 0.01), whereas the effects of K_b, K_b P, and K_b² on K_l^′ are significant (0.01 < p < 0.05).

To investigate the interaction between K_b and P, response surface plots were generated using Design-Expert V8.0.6, as shown in Figure 16.

When the particle diameter is at the central level (d_a = 7 mm), K_l^′ decreases with increasing P for a given K_b. When K_b = 1 mm, the reduction in K_l^′ with increasing P is more pronounced. When P < 7.5 kPa, K_l^′ decreases as K_b increases. However, when P > 7.5 kPa, K_l^′ first decreases and then increases with increasing K_b, though the variation is relatively small. This indicates that the interaction between P and K_b significantly affects K_l^′, with P having a greater impact. This conclusion is consistent with the influencing factors of pressure and velocity gradient explored by Wang Zhaoyang [26].

(2) Dual-Particle Adsorption Experiment with Unequal-Diameter Particles

Figure 17 shows the critical suction hole length required for dual-particle adsorption when the particles have unequal diameters. The results indicate that the critical suction hole length is always smaller than the distance between the centers of the two particles.

In the adsorption measurement tests conducted using a dynamic–static combination plate test platform, two test particles were adsorbed sequentially onto the suction hole. The data indicate that when the upper particle diameter remains constant, decreasing the diameter of the lower particle reduces the critical suction hole length required for dual-particle adsorption.

When the upper particle diameter is 9 mm, the suction hole length required to adsorb a lower particle of 9 mm is 1.23 times that required for a 7 mm particle and 1.35 times that for a 5 mm particle. Similarly, when the upper particle diameter is 7 mm, the suction hole length required to adsorb a lower 9 mm particle is 1.22 times that required for a 7 mm particle and 1.37 times that for a 5 mm particle. A similar trend is observed for an upper particle diameter of 5 mm.

When the lower particle diameter remains constant, decreasing the upper particle diameter also reduces the critical suction hole length. Additionally, when the lower particle diameter is larger than the upper particle diameter, the critical suction hole length required for multiple-seed adsorption increases. This is because larger particles, being heavier, are more prone to detachment from the suction hole.

5. Analysis and Discussion

5.1. Analysis and Discussion of the Single-Particle Adsorption Tests

In summary, within the suction hole region, the adsorption force acting on particles remains relatively strong. When a particle moves toward the edge of the suction hole, the adsorption force decreases slightly. However, once the particle moves outside the suction hole region, the adsorption force decreases more rapidly with increasing distance. The z-axis force component (F_z) is greater than the y-axis (F_y) or x-axis (F_x) components, and its magnitude and variation trend closely resemble those of the total adsorption force (F_s). This indicates that F_z plays a dominant role in capturing near-wall particles. This phenomenon occurs because when the relative boundary distance is between 0 and 3.5 mm, part of the particle still remains directly above the suction hole, experiencing the direct influence of airflow. By analyzing the flow field contour plots, it is evident that once the particle moves away from the suction hole center, the flow field in the movement direction loses its symmetry, and the airflow around the particle becomes asymmetric, resulting in the generation of F_y or F_x. This indicates that the adsorption force on the particle is a nonuniformly distributed force, which is the integral effect of airflow on the particle surface. The torque induced by the adsorption force is also a distributed moment. The distribution of pressure on the particle surface is influenced by the position and shape of the suction hole boundary.

Both particle diameter (d_a) and vacuum pressure (P) significantly influence the adsorption force F_s acting on the particle. However, as the seed diameter increases, its mass also increases. Therefore, the enhancement of adsorption capacity by increasing P is more effective than increasing d_a. Under identical test conditions, a comparison of F_s experienced by particles when L_x = L_y = 1.5 mm shows that particles moving along the y-axis experience greater F_s than those moving along the x-axis. This indicates that narrow elongated suction holes have a stronger adsorption retention capability in the short-edge direction and they are more effective at capturing near-wall particles located at an equal distance outside the suction hole boundary in the short-edge direction than in the long-edge direction. This characteristic suggests that controlling the suction hole length can be an effective strategy for regulating the critical multiple-seed adsorption of dual seeds.

5.2. Analysis and Discussion of the Dual-Particle Adsorption Tests

In summary, during dual-particle multiple-seed adsorption, standard spherical particles align along the long edge of the narrow elongated suction hole, resulting in a vertical arrangement. This vertical alignment causes the lower particle to detach more easily. Combined with the findings from single-particle adsorption tests, it is clear that the suction force acts over a longer range in the long-edge direction of the suction hole, which is beneficial for maintaining single-seed adsorption. The results of the Box–Behnken experimental design show that the factors influencing the critical suction hole length required for dual-particle adsorption, ranked by contribution, are particle diameter, vacuum pressure, and suction hole width. The regression model suggests that, based on the equivalent spherical diameter distribution of seeds, the critical suction hole length for dual-particle adsorption can be determined under specific suction hole width and vacuum pressure conditions. This conclusion is significant for the development of the precision seeding technology, where the shape characteristics of narrow elongated suction holes can be utilized to prevent dual-seed adsorption while maintaining single-seed adsorption.

The standard deviation of the critical suction hole length in Table 9 suggests that, even when repeating the same test, variations arise due to particle oscillation and interactions with the seed plate. Therefore, in practical operations, additional factors such as machine vibrations and seed plate rotation speed should be considered.

6. Conclusions

We conducted simulation analyses of single-particle adsorption near the seed metering disk using standard spherical particles, along with bench tests on the critical adsorption of dual-particle systems. The following conclusions can be drawn:

• The length, width, vacuum pressure, and particle diameter of the narrow elongated suction hole significantly influence the adsorption force acting on near-wall particles. However, once the suction hole length exceeds the particle diameter, further increases in length do not significantly affect the adsorption force.
• When the projection of a particle’s center on the seed metering disk lies outside the suction hole region, the particle still experiences adsorption forces. Within a certain distance from the suction hole boundary, the z-axis force component remains dominant compared to the x- and y-axis components. When a particle is positioned at the suction hole boundary, the maximum reduction in adsorption force compared to the center is approximately 30%.
• At the same distance from the suction hole boundary, particles moving in the short-edge direction (y-axis) experience greater adsorption forces than those moving in the long-edge direction (x-axis). Therefore, for the same narrow elongated suction hole, the ability to capture near-wall spherical particles outside the suction hole is weaker in the long-edge direction than in the short-edge direction. The unique seed-capturing ability of narrow elongated suction holes gives them a special advantage in breeding test seeders, where the seed population size is small and the seed differences are significant.
• During dual-particle adsorption, the lower particle experiences additional forces from the weight and partial adsorption force of the upper particle, making it more prone to detachment. A predictive model for the critical suction hole length required for dual-particle adsorption in narrow elongated suction holes was established. This model can predict the minimum suction hole length required for the simultaneous adsorption of two spherical seeds within the parameter ranges of 1 mm ≤ K_b ≤ 3 mm, 5 mm ≤ d_a ≤ 9 mm, and 4 kPa ≤ P ≤ 10 kPa.
• Narrow elongated suction holes capture seeds in an orderly manner along their long edge. When positioned vertically, the seeds at the lower part of the suction hole experience additional gravity and an adsorption force component from the seeds above. By applying an external force or adjusting the suction capacity, excess seeds positioned at the lower part can be removed, enabling seed singulation in narrow elongated suction holes. At present, our team has tried to apply it to the operation of breeding and sowing machinery with small seed quantity and large differences in seed appearance.