Safety Analysis of Agricultural Implement for Mulching and Soil Covering
Abstract
1. Introduction
2. Materials and Methods
2.1. Test System
2.2. Strain Measurement
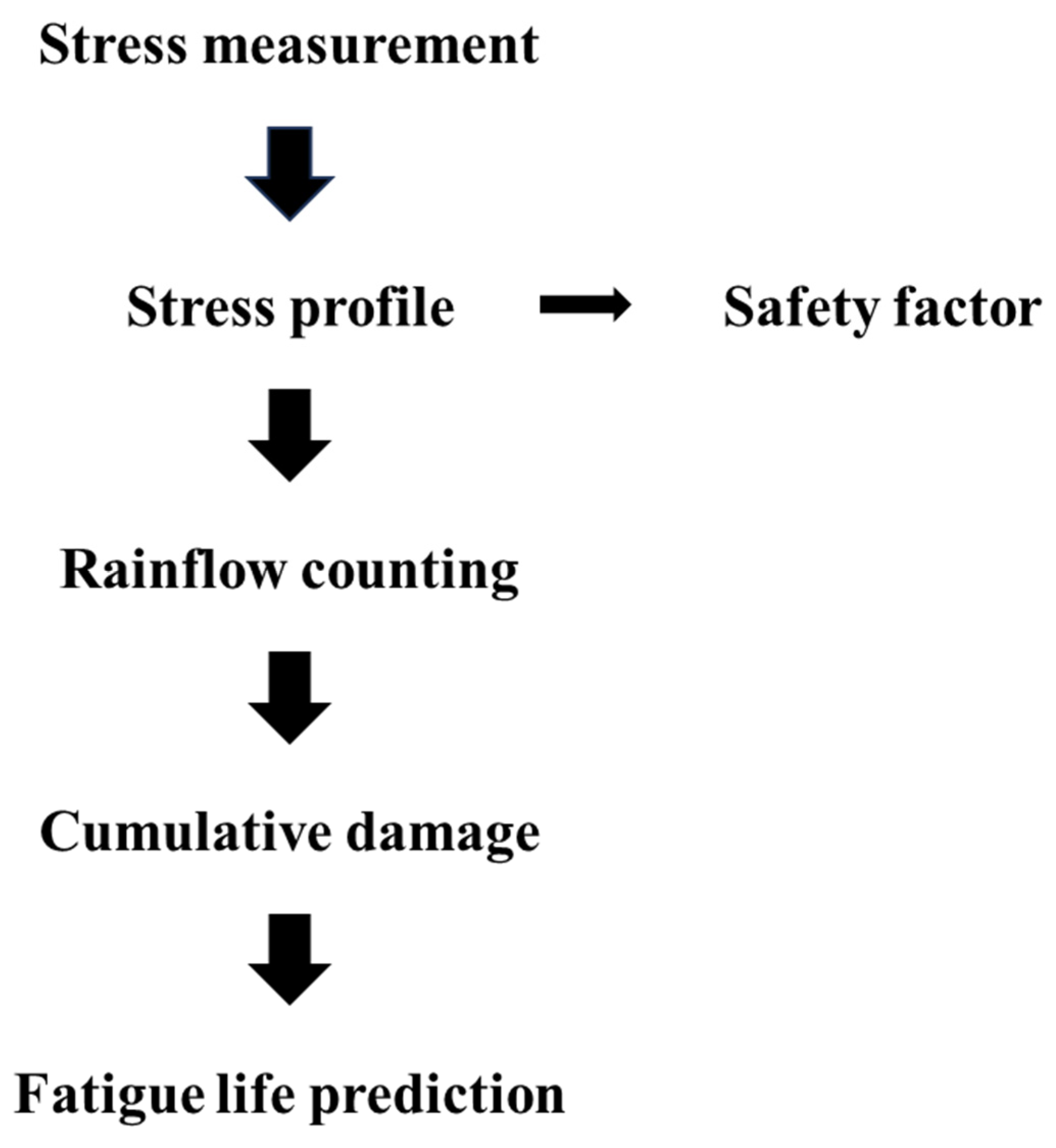
2.3. Safety Analysis
2.3.1. Converting Strain to Stress
2.3.2. Safety Factor
2.3.3. Fatigue Life Prediction
3. Results and Discussion
3.1. Stress Profile
3.2. Safety Factor
3.3. Fatigue Life Prediction
4. Conclusions
- When measuring stress at the strain gauge attachment points under various conditions, point #5 showed the highest average von Mises stress at 43.75 MPa. However, the maximum single von Mises stress during operation was observed at point #4, reaching 107.52 MPa. The average stress at points other than #4 and #5 was mostly measured below 10 MPa.
- The range of safety factors according to the maximum shear stress theory is from 1.65 to 16.54, while the range according to the strain energy theory is from 2.42 to 19.83. As the safety factors derived from the maximum shear stress theory were lower than those from the strain energy theory, it was confirmed that the maximum shear stress theory is a more conservative approach in mechanical design. Attachment points (#1, #2, #3) show safety factors significantly higher than the recommended values for their conditions and are thus considered safe. However, excessively high safety factors can lead to issues such as increased costs, increased weight, and reduced efficiency. Therefore, there is a need to redesign the safety factors to more appropriate levels.
- Analysis of the rainflow counting histogram and cumulative damage histogram revealed that most stress cycles are distributed in small stress ranges and low mean stresses. Large stress ranges and high mean stresses do not occur in many cycles. However, it was observed that these high-stress cycles, although few in number, cause significant damage.
- Calculation of predicted fatigue life values showed that the lowest calculated fatigue life was 14,575 h, which translates to approximately 607 years of use if operated all day, every day. Therefore, the developed implement is evaluated as safe in terms of safety factor and fatigue life analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, B.; Mishra, A.K.; Luo, B. Aging population, farm succession, and farmland usage: Evidence from rural China. Land Use Policy 2018, 77, 437–445. [Google Scholar] [CrossRef]
- Liu, J.; Fang, Y.; Wang, G.; Liu, B.; Wang, R. The aging of farmers and its challenges for labor-intensive agriculture in China: A perspective on farmland transfer plans for farmers’ retirement. J. Rural. Stud. 2023, 100, 103013. [Google Scholar] [CrossRef]
- Salzwedel, M. Labor Shortage Poses Safety Challenges for Growing Agritourism Industry. J. Agromed. 2023, 28, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Lee, R.; Mason, A. Fertility, Human Capital, and Economic Growth over the Demographic Transition. Eur. J. Popul./Rev. Eur. De Demogr. 2009, 26, 159–182. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Yoo, H.-j.; Shin, M.; Oh, J.; Shim, S.-B. Analysis of Overturning Stability of Small off-Road Vehicle. J. Biosyst. Eng. 2023, 48, 309–318. [Google Scholar] [CrossRef]
- Benos, L.; Bechar, A.; Bochtis, D. Safety and ergonomics in human-robot interactive agricultural operations. Biosyst. Eng. 2020, 200, 55–72. [Google Scholar] [CrossRef]
- Kumar, G.V.P.; Dewangan, K.N. Agricultural accidents in north eastern region of India. Saf. Sci. 2009, 47, 199–205. [Google Scholar] [CrossRef]
- Rondelli, V.; Casazza, C.; Martelli, R. Tractor rollover fatalities, analyzing accident scenario. J. Saf. Res. 2018, 67, 99–106. [Google Scholar] [CrossRef]
- Rautiainen, R.H.; Reynolds, S.J. Mortality and Morbidity in Agriculture in the United States. J. Agric. Saf. Health 2002, 8, 259–276. [Google Scholar] [CrossRef]
- Christensen, S.; Søgaard, H.T.; Kudsk, P.; Nørremark, M.; Lund, I.; Nadimi, E.S.; Jørgensen, R. Site-specific weed control technologies. Weed Res. 2009, 49, 233–241. [Google Scholar] [CrossRef]
- Namdeo, R.; Shrivastava, A.K.; Kumar, A.; Nandini, Y. Optimization of the performance parameters of the L-shaped rotary blade for the development of a plastic mulching machine. Pharma Innov. J. 2022, 11, 5944–5953. [Google Scholar]
- Balli, S.R.; Shetty, P.; Sajjan, S. Design and Development of Tractor Operated Plastic Mulch Laying Machine. J. Mech. Robot. 2020, 5, 16–19. [Google Scholar] [CrossRef]
- Khazimov, Z.M.; Bora, G.C.; Khazimov, K.M.; Khazimov, M.Z.; Ultanova, I.B.; Niyazbayev, A.K. Development of a dual action planting and mulching machine for vegetable seedlings. Eng. Agric. Environ. Food 2018, 11, 74–78. [Google Scholar] [CrossRef]
- Parmar, B.S.; Shrivastava, A.K.; Singh, S.K.; Patel, A.; Gajendra, S. Economic Analysis of Low-Cost Tractor Drawn Plastic Mulching Machine. Int. J. Environ. Clim. Change 2023, 13, 2401–2408. [Google Scholar] [CrossRef]
- Collins, J.A. Failure of Materials in Mechanical Design: Analysis, Prediction, Prevention; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Yu, T.; Xue, P. Chapter 4—Yield criteria. In Introduction to Engineering Plasticity; Yu, T., Xue, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 67–87. [Google Scholar] [CrossRef]
- Mises, R.v. Mechanik der festen Körper im plastisch-deformablen Zustand. Nachrichten Von Der Ges. Der Wiss. Zu Göttingen Math.-Phys. Kl. 1913, 1913, 582–592. Available online: http://eudml.org/doc/58894/ (accessed on 20 February 2001).
- Menacho-Mendoza, E.; Cedamanos-Cuenca, R.; Díaz-Suyo, A. Stress analysis and factor of safety in three dental implant systems by finite element analysis. Saudi Dent. J. 2022, 34, 579–584. [Google Scholar] [CrossRef]
- Henriques, B.; Carvalho, M.; Tavares, S.; de Castro, P. A comparison of safety factor values for Soderberg and DIN 743 fatigue analyses. U. Porto J. Eng. 2021, 7, 11–21. [Google Scholar] [CrossRef]
- Matvienko, Y.G. The simplified approach for estimating probabilistic safety factors in fracture mechanics. Eng. Fail. Anal. 2020, 117, 104814. [Google Scholar] [CrossRef]
- Al-Oqla, F.M.; Hayajneh, M.T. Stress failure interface of cellulosic composite beam for more reliable industrial design. Int. J. Interact. Des. Manuf. (IJIDeM) 2022, 16, 1727–1738. [Google Scholar] [CrossRef]
- Xi, L.; Songlin, Z. Changes in mechanical properties of vehicle components after strengthening under low-amplitude loads below the fatigue limit. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 847–855. [Google Scholar] [CrossRef]
- Wöllner, U.; Szlosarek, R.; Kröger, M. Fatigue behavior of agricultural rims under rotating bending load. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2143–2158. [Google Scholar] [CrossRef]
- Barna, R.A.; Popovych, P.V. Influence of Operating Media on the Fatigue Fracture of Steels for Elements of Agricultural Machines. Mater. Sci. 2014, 50, 377–380. [Google Scholar] [CrossRef]
- Chen, Z.; Long, K.; Zhang, C.; Yang, X.; Lu, F.; Wang, R.; Zhu, B.; Zhang, X. A fatigue-resistance topology optimization formulation for continua subject to general loads using rainflow counting. Struct. Multidiscip. Optim. 2023, 66, 210. [Google Scholar] [CrossRef]
- Wu, S.-D.; Shang, D.-G.; Liu, P.-C.; Hao, G.-C.; Hou, G.; Shi, F.-T.; Miao, B. Fatigue life prediction based on modified narrowband method under broadband random vibration loading. Int. J. Fatigue 2022, 159, 106832. [Google Scholar] [CrossRef]
- Abdullah, L.; Singh, S.S.K.; Abdullah, S.; Azman, A.H.; Ariffin, A.K. Fatigue reliability and hazard assessment of road load strain data for determining the fatigue life characteristics. Eng. Fail. Anal. 2021, 123, 105314. [Google Scholar] [CrossRef]
- Li, H.-W.-X.; Chelidze, D. Fatigue life estimation of structures under statistically and spectrally similar variable amplitude loading. Mech. Syst. Signal Process. 2021, 161, 107856. [Google Scholar] [CrossRef]
- Loew, S.; Obradovic, D.; Bottasso, C.L. Model predictive control of wind turbine fatigue via online rainflow-counting on stress history and prediction. J. Phys. Conf. Ser. 2020, 1618, 022041. [Google Scholar] [CrossRef]
- Eun-Jin, C.; Jin-Kyeong, L.; Min-Ho, J.; Min, A.C.; Jae-Hyun, K.; Seung-Je, H.; Jin-Hee, P.; Chang-Seop, S. Soil Characterization of the Field where Rice has been Cultivated during Five Years. J. Korean Soc. Manuf. Process Eng. 2021, 20, 8–13. [Google Scholar] [CrossRef]
- Juvinall, R.C.; Marshek, K.M. Fundamentals of Machine Component Design; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Palmgren, A. Die Lev/bensdauer von kugellagern. VDI. Z. 1924, 68, 339–341. [Google Scholar]
- Miner, M.A. Cumulative Damage in Fatigue. J. Appl. Mech. 2021, 12, A159–A164. [Google Scholar] [CrossRef]
- Vidosic, J. Machine Design Projects; Ronald Press: New York, NY, USA, 1957. [Google Scholar]




| Items | Specifications |
|---|---|
| Model | LT470D |
| Size (L × W × H) (mm) | 3655 × 1655 × 2328 |
| Weight (kg) | 2395 |
| Engine | Water cooled, 4 Cycle, Diesel |
| Engine displacement | 2505 |
| Power (ps/rpm) | 45/2600 |
| Driving system | 4WD |
| Items | Specifications |
|---|---|
| Model | Mulching and soil covering implement |
| Size (L × W × H) (mm) | 2240 × 2120 × 1140 |
| Weight (kg) | 796 |
| Mulching (line) | 2 |
| Soil covering (line) | 2 |
| Items | Specifications |
|---|---|
| Model | KFGS-1-350-D17-11 |
| Manufacturer/Nation | KYOWA/Japan |
| Gage factor | 2.11 ± 1.0% |
| Gage length (mm) | 1 |
| Gage resistance (Ω) | 350.0 ± 0.75 |
| Material | Mechanical Properties | Value |
|---|---|---|
| Stainless steel 400 | Young’s modulus (GPa) | 206 |
| Poisson’s ratio | 0.3 | |
| ) | 7800 | |
| Ultimate tensile strength (MPa) | 450 | |
| Yield strength (MPa) | 260 |
| Point | Engine Level | PTO Level | Maximum Shear Stress (MPa) | Von Mises Stress (MPa) | Safety Factor Based on Maximum Shear Stress | Safety Factor Based on von Mises Stress |
|---|---|---|---|---|---|---|
| #1 | 1 | 1 | 13.30 | 26.46 | 9.77 | 9.83 |
| 2 | 18.08 | 24.36 | 7.19 | 10.67 | ||
| 2 | 1 | 9.76 | 13.63 | 13.32 | 19.08 | |
| 2 | 22.03 | 30.01 | 5.90 | 8.66 | ||
| #2 | 1 | 1 | 8.71 | 19.60 | 14.93 | 13.27 |
| 2 | 13.89 | 21.10 | 9.36 | 12.32 | ||
| 2 | 1 | 10.74 | 13.11 | 12.10 | 19.83 | |
| 2 | 10.15 | 17.07 | 12.81 | 15.23 | ||
| #3 | 1 | 1 | 11.02 | 36.04 | 11.80 | 7.21 |
| 2 | 7.86 | 25.67 | 16.54 | 10.13 | ||
| 2 | 1 | 9.41 | 23.43 | 13.82 | 11.10 | |
| 2 | 15.86 | 36.19 | 8.20 | 7.18 | ||
| #4 | 1 | 1 | 54.60 | 101.00 | 2.38 | 2.57 |
| 2 | 78.81 | 107.52 | 1.65 | 2.42 | ||
| 2 | 1 | 44.31 | 60.27 | 2.93 | 4.31 | |
| 2 | 59.05 | 75.91 | 2.20 | 3.43 | ||
| #5 | 1 | 1 | 42.97 | 76.39 | 3.03 | 3.40 |
| 2 | 64.11 | 78.50 | 2.03 | 3.31 | ||
| 2 | 1 | 50.56 | 61.79 | 2.57 | 4.21 | |
| 2 | 68.58 | 84.49 | 1.90 | 3.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, I.-S.; Ji, S.-M.; Im, W.-T.; Shin, C.-S. Safety Analysis of Agricultural Implement for Mulching and Soil Covering. Agriculture 2025, 15, 632. https://doi.org/10.3390/agriculture15060632
Hwang I-S, Ji S-M, Im W-T, Shin C-S. Safety Analysis of Agricultural Implement for Mulching and Soil Covering. Agriculture. 2025; 15(6):632. https://doi.org/10.3390/agriculture15060632
Chicago/Turabian StyleHwang, In-Seok, Sung-Min Ji, Wan-Tae Im, and Chang-Seop Shin. 2025. "Safety Analysis of Agricultural Implement for Mulching and Soil Covering" Agriculture 15, no. 6: 632. https://doi.org/10.3390/agriculture15060632
APA StyleHwang, I.-S., Ji, S.-M., Im, W.-T., & Shin, C.-S. (2025). Safety Analysis of Agricultural Implement for Mulching and Soil Covering. Agriculture, 15(6), 632. https://doi.org/10.3390/agriculture15060632






