Evaluating Remote Sensing Resolutions and Machine Learning Methods for Biomass Yield Prediction in Northern Great Plains Pastures
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site Description
2.2. Data Acquisition
2.2.1. Ground Truth Biomass Data
2.2.2. Climate and Soil Data
2.2.3. Satellite Image Data
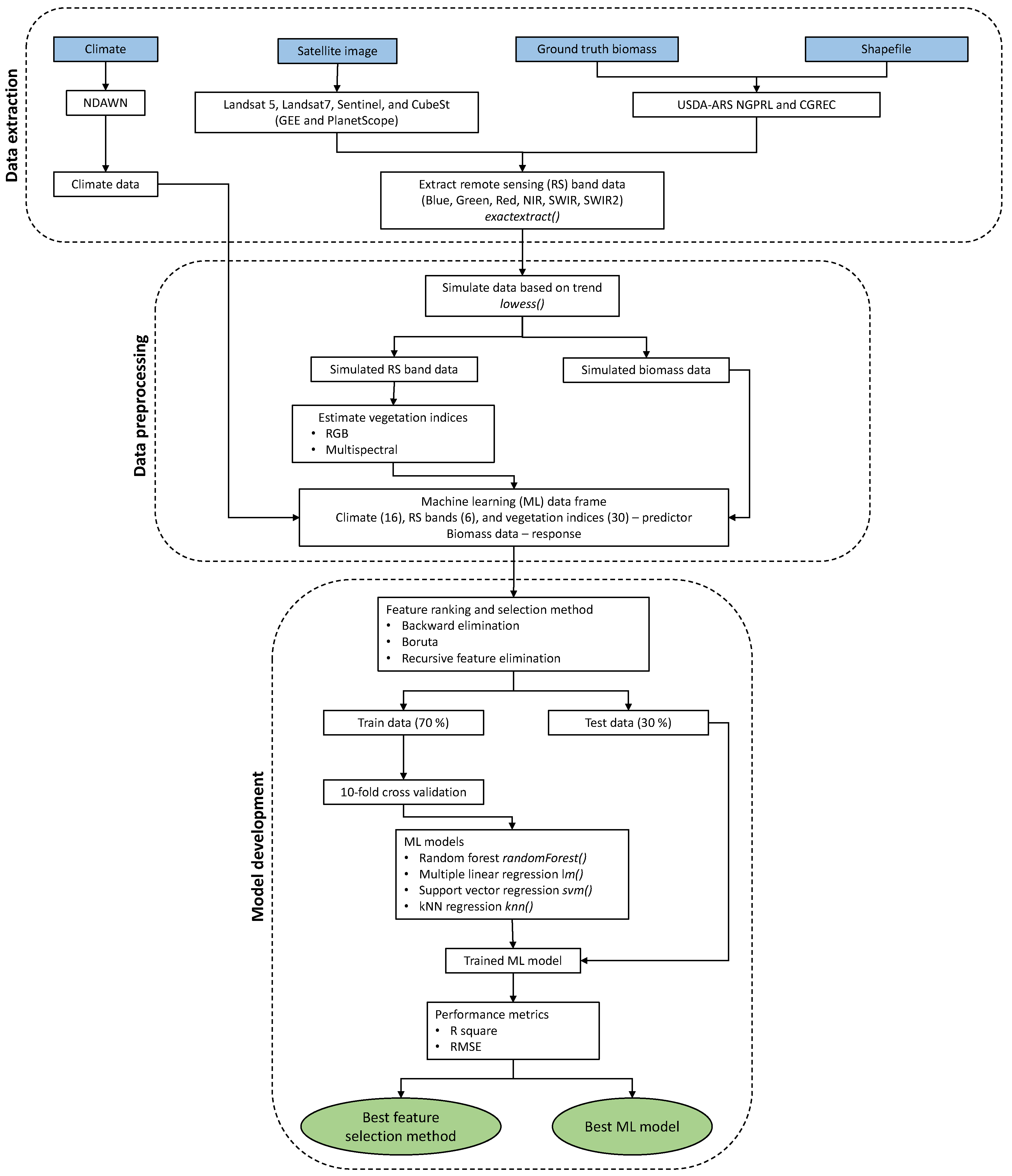
2.3. Data Processing
2.4. Estimation of Vegetation Indices
| Vegetation Index | Equation | Reference |
|---|---|---|
| Red chromatic coordinate (RCC) | [34] | |
| Green chromatic coordinate (GCC) | [34] | |
| Blue chromatic coordinate (BCC) | [34] | |
| Excess green (ExG ) | [34] | |
| Normalized excess green (ExG2) | [34] | |
| Excess red (ExR) | [35] | |
| Excess green minus excess red (ExGR) | [36] | |
| Green-red vegetation index (GRVI) | [37] | |
| Green-blue vegetation index (GBVI) | ||
| Blue red vegetation index (BRVI) | ||
| Greed-red ration (G/R) | [38] | |
| Green-red difference (G-R) | ||
| Blue-green difference (B-G) | ||
| Visible-band difference vegetation index (VDVI) | [39] | |
| Visible atmospherically resistant index (VARI) | [40] | |
| Modified green-red vegetation index (MGRVI) | [41] | |
| Colour index of vegetation (CIVE) | [42] | |
| Woebbecke index (WI) | [34] | |
| Coloration index (CI) | ||
| Normalized difference vegetation index (NDVI) | [43] | |
| Green normalized vegetation index (GNDVI) | [44] | |
| Soil-adjusted vegetation index (SAVI) | [45] | |
| Modified soil-adjusted vegetation index (MSAVI) | [46] | |
| Enhanced vegetation index (EVI) | [47] | |
| Normalized difference moisture index (NDMI) | [48] | |
| Green atmospherically resistant vegetation index (GARI) | [44] | |
| Simple ratio index (SR) | [49] | |
| Atmospherically resistant vegetation index (ARVI) | [50] | |
| Green chlorophyll index (GCI) | [51] | |
| Structure intensive pigment index (SIPI) | [52] |
2.4.1. Common RGB Bands
2.4.2. Multispectral
2.5. Modeling Approaches
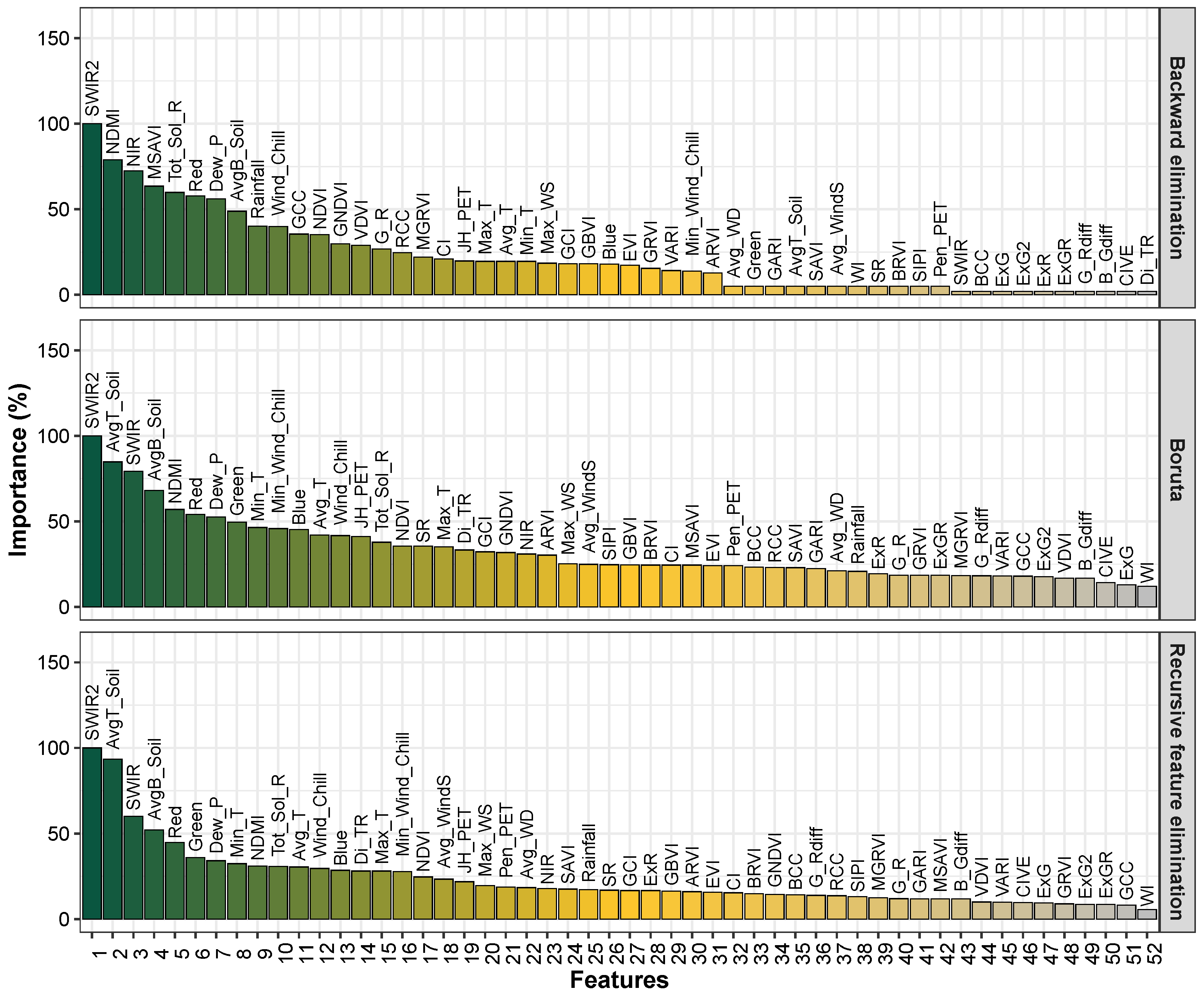
2.6. Feature Selection
2.6.1. Backward Elimination
2.6.2. Boruta
2.6.3. Recursive Feature Elimination
2.7. Linear and Machine Learning Prediction Models
2.7.1. Training, Validation, and Test Datasets
2.7.2. Multiple Linear Regression
2.7.3. Random Forest
2.7.4. Support Vector Regression
2.7.5. k-Nearest Neighbors
2.8. High-Performance Computing Resources Used
2.9. Model Performance Assessment
2.9.1. Hypertuning Parameters
2.9.2. Performance Metrics
3. Results and Discussion
3.1. Feature Ranking Results
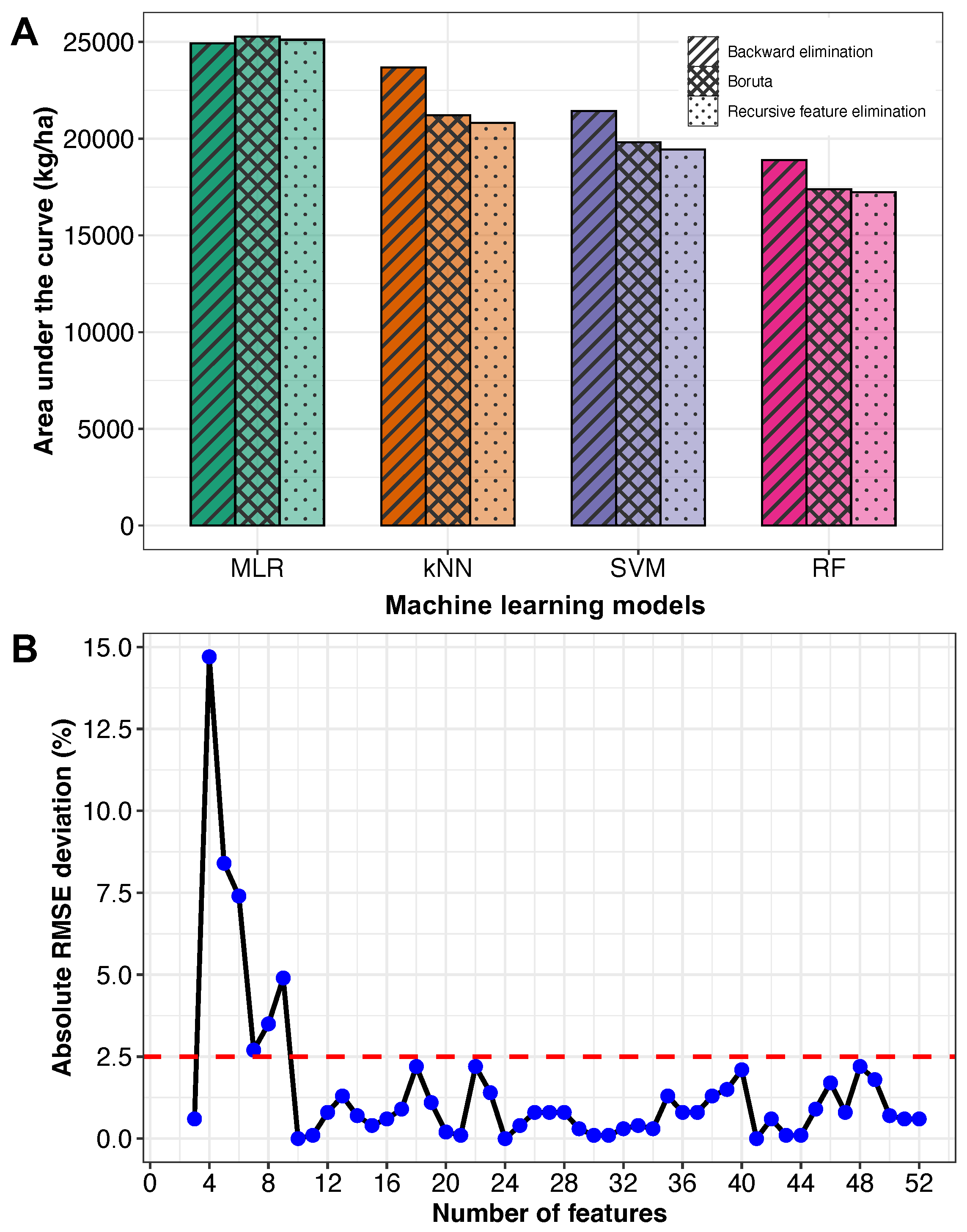
3.2. Feature Selection and Model Performance Comparison
3.2.1. Feature Selection Method Comparison
3.2.2. Machine Learning Models Comparison—Ranking
3.3. Application of the Developed Methodology and Model
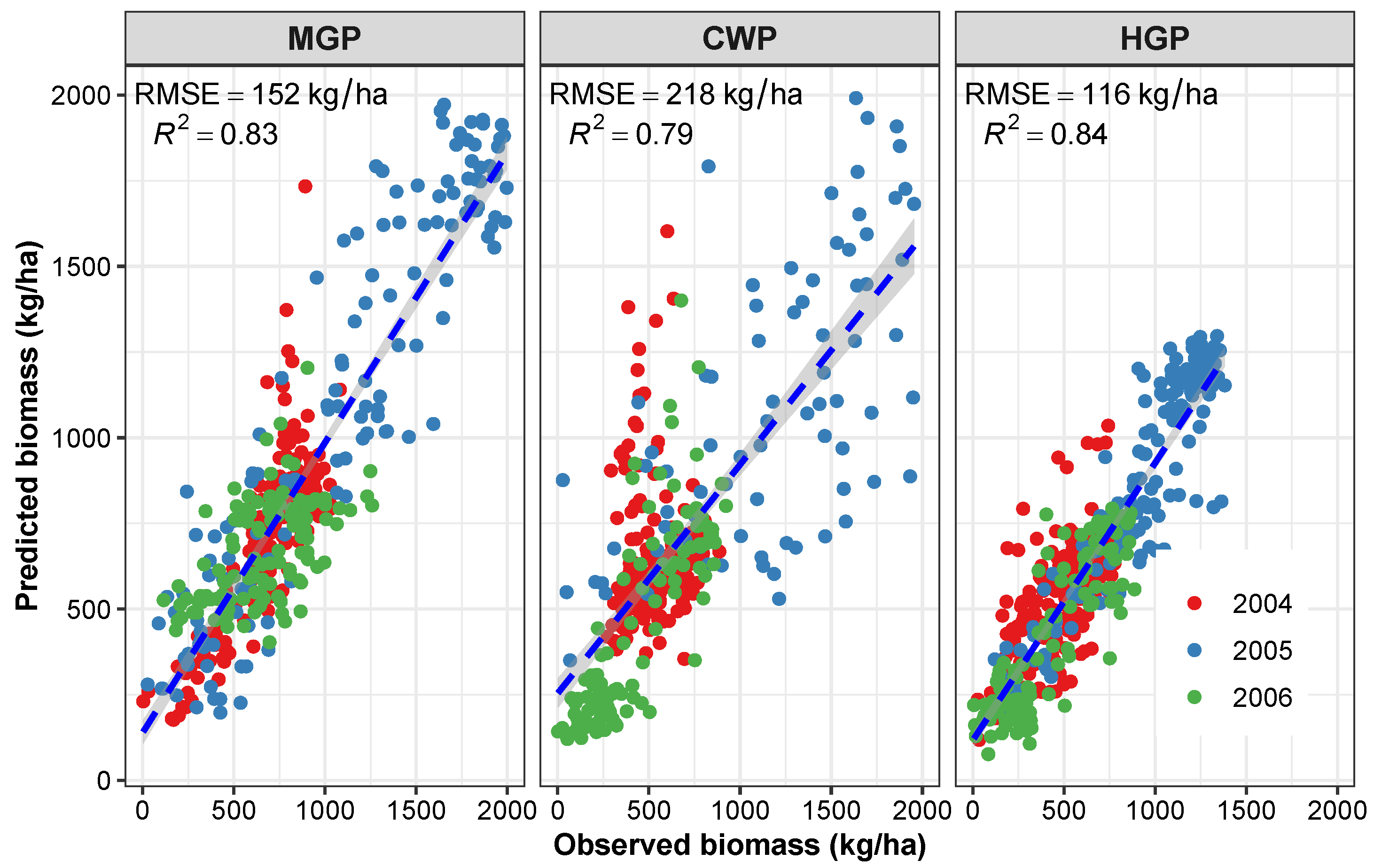
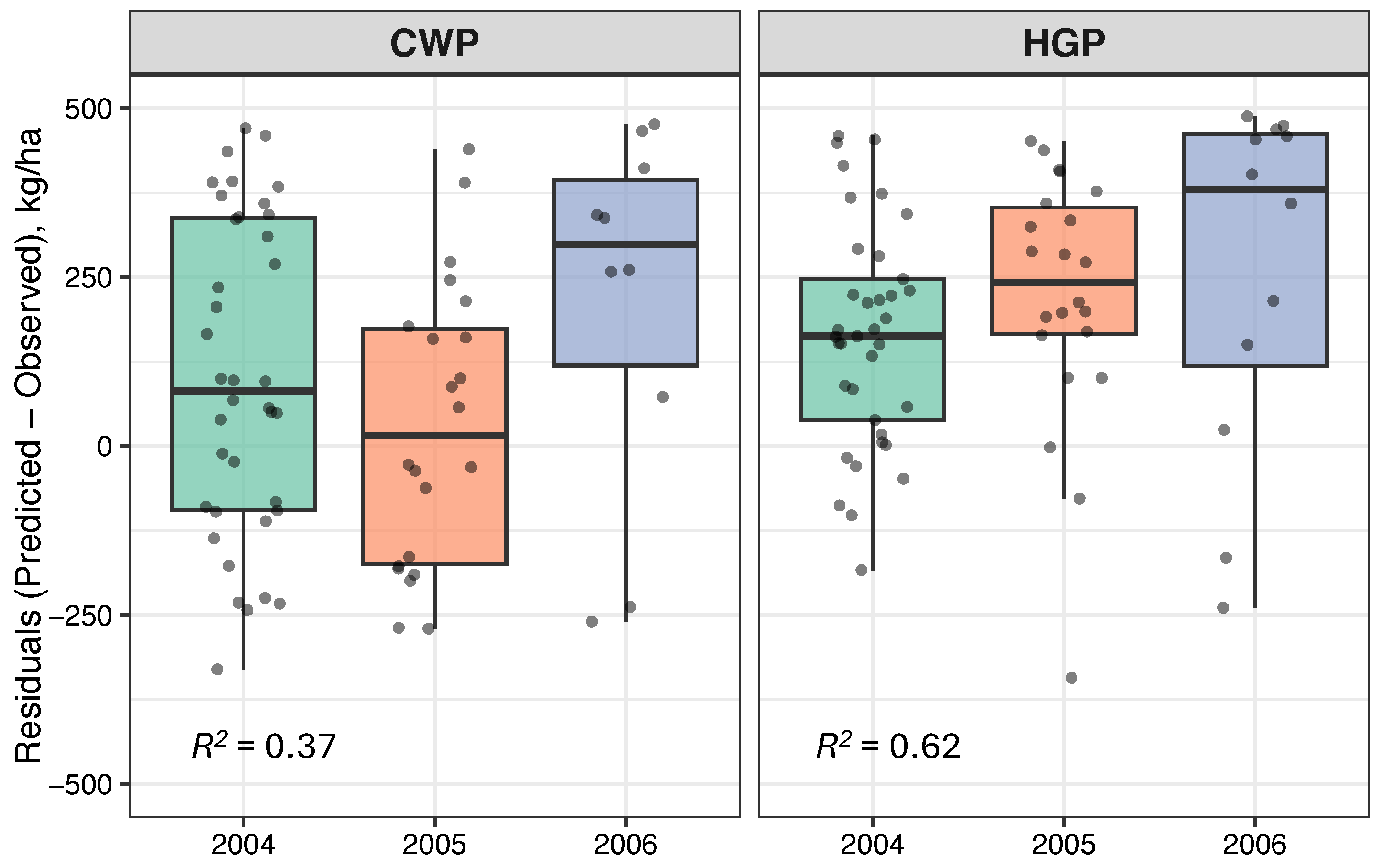
3.3.1. Application 1—Performance of the Developed Methodology in Other Pastures
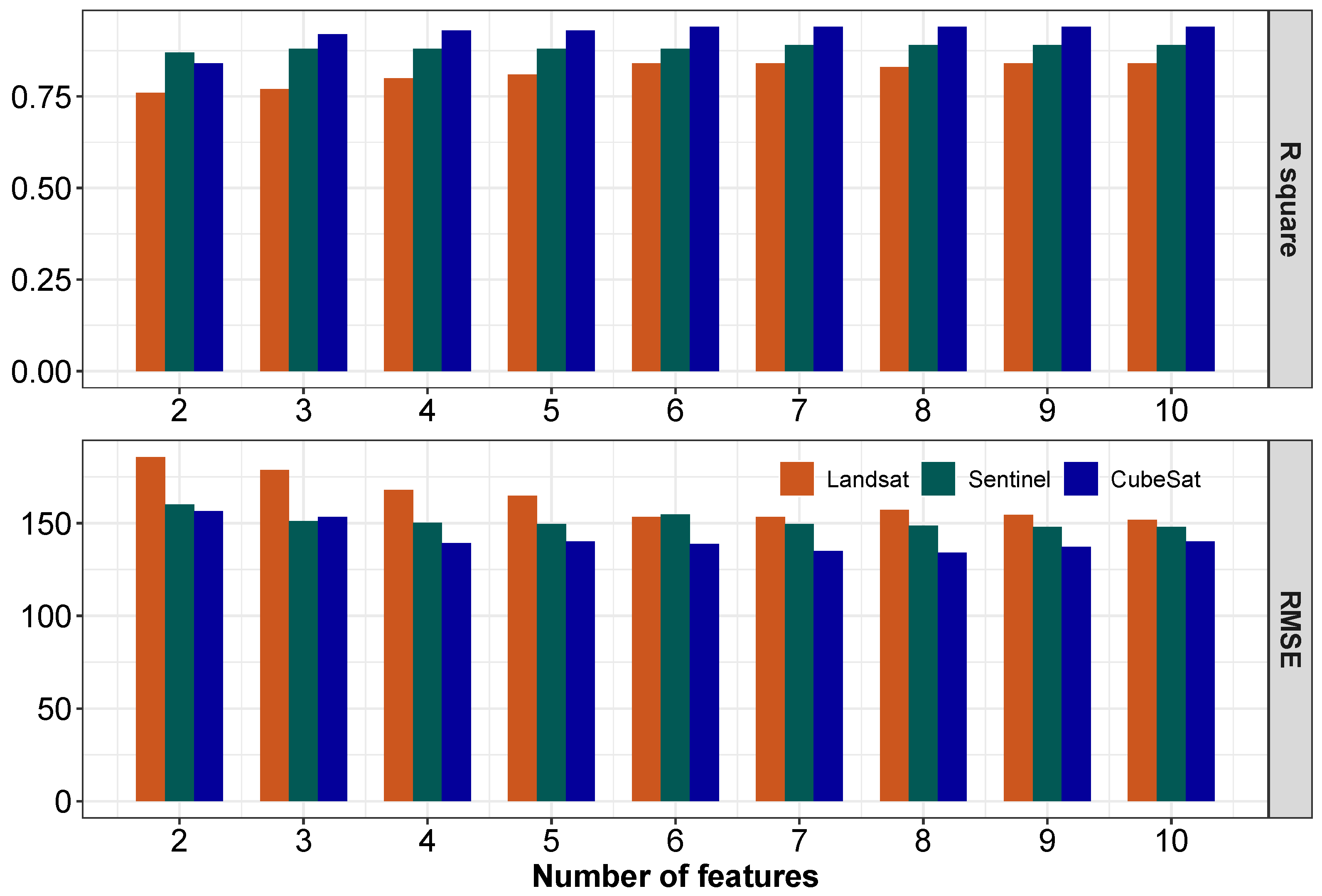
3.3.2. Application 2—Effect of Remote Sensing Platforms Resolution in Forage Prediction
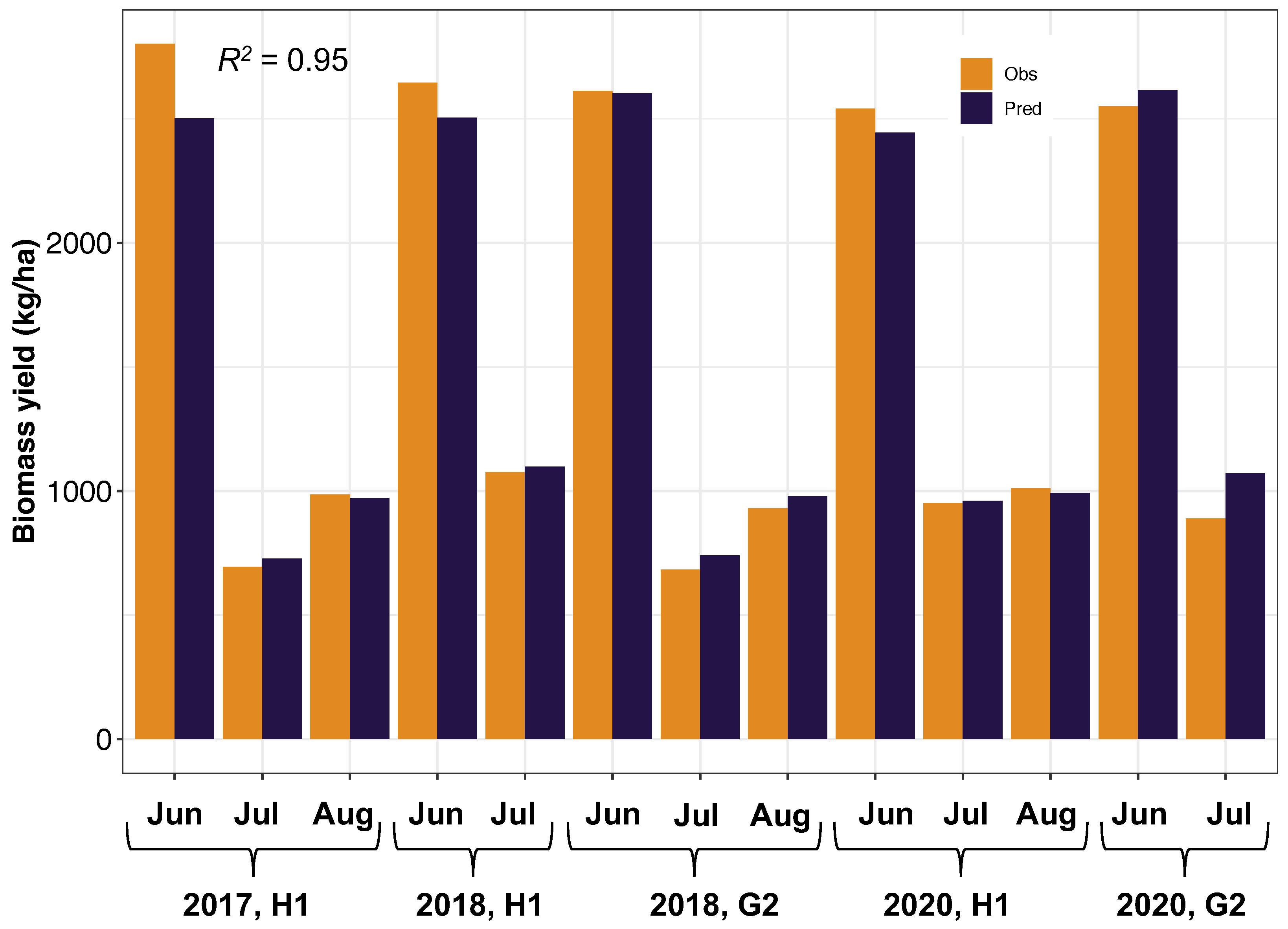
3.3.3. Application 3—Cultivated Hay Crop Alfalfa Yield Prediction with Developed Methodology Using CubeSat
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lupo, C.D.; Clay, D.E.; Benning, J.L.; Stone, J.J. Life-cycle assessment of the beef cattle production system for the Northern Great Plains, USA. J. Environ. Qual. 2013, 42, 1386–1394. [Google Scholar] [CrossRef] [PubMed]
- Ritz, K.E.; Heins, B.J.; Moon, R.; Sheaffer, C.; Weyers, S.L. Forage yield and nutritive value of cool-season and warm-season forages for grazing organic dairy cattle. Agronomy 2020, 10, 1963. [Google Scholar] [CrossRef]
- Portugal, T.B.; Szymczak, L.S.; de Moraes, A.; Fonseca, L.; Mezzalira, J.C.; Savian, J.V.; Zubieta, A.S.; Bremm, C.; de Faccio Carvalho, P.C.; Monteiro, A.L.G. Low-Intensity, high-frequency grazing strategy increases herbage production and beef cattle performance on sorghum pastures. Animals 2021, 12, 13. [Google Scholar] [CrossRef]
- Aparicio, N.; Villegas, D.; Casadesus, J.; Araus, J.L.; Royo, C. Spectral vegetation indices as nondestructive tools for determining durum wheat yield. Agron. J. 2000, 92, 83–91. [Google Scholar] [CrossRef]
- Lussem, U.; Bolten, A.; Gnyp, M.; Jasper, J.; Bareth, G. Evaluation of RGB-based vegetation indices from UAV imagery to estimate forage yield in grassland. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, 42, 1215–1219. [Google Scholar] [CrossRef]
- Ji, L.; Fan, K. Climate prediction of satellite-based spring Eurasian vegetation index (NDVI) using coupled singular value decomposition (SVD) patterns. Remote Sens. 2019, 11, 2123. [Google Scholar] [CrossRef]
- Gómez, D.; Salvador, P.; Sanz, J.; Casanova, J.L. New spectral indicator Potato Productivity Index based on Sentinel-2 data to improve potato yield prediction: A machine learning approach. Int. J. Remote Sens. 2021, 42, 3426–3444. [Google Scholar] [CrossRef]
- Safi, A.R.; Karimi, P.; Mul, M.; Chukalla, A.; de Fraiture, C. Translating open-source remote sensing data to crop water productivity improvement actions. Agric. Water Manag. 2022, 261, 107373. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Zhihui, W.; Jianbo, S.; Blackwell, M.; Haigang, L.; Bingqiang, Z.; Huimin, Y. Combined applications of nitrogen and phosphorus fertilizers with manure increase maize yield and nutrient uptake via stimulating root growth in a long-term experiment. Pedosphere 2016, 26, 62–73. [Google Scholar]
- Onwuka, B.; Mang, B. Effects of soil temperature on some soil properties and plant growth. Adv. Plants Agric. Res 2018, 8, 34. [Google Scholar] [CrossRef]
- Meng, L.; Liu, H.; L Ustin, S.; Zhang, X. Predicting maize yield at the plot scale of different fertilizer systems by multi-source data and machine learning methods. Remote Sens. 2021, 13, 3760. [Google Scholar] [CrossRef]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Subhashree, S.N.; Sunoj, S.; Hassanijalilian, O.; Igathinathane, C. Decoding Common Machine Learning Methods: Agricultural Application Case Studies Using Open Source Software. In Applied Intelligent Decision Making in Machine Learning; CRC Press: Boca Raton, FL, USA, 2020; pp. 21–52. [Google Scholar]
- Timsina, J.; Dutta, S.; Devkota, K.P.; Chakraborty, S.; Neupane, R.K.; Bishta, S.; Amgain, L.P.; Singh, V.K.; Islam, S.; Majumdar, K. Improved nutrient management in cereals using Nutrient Expert and machine learning tools: Productivity, profitability and nutrient use efficiency. Agric. Syst. 2021, 192, 103181. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Guzmán, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E.; Pote, J.W. An integrated SVR and crop model to estimate the impacts of irrigation on daily groundwater levels. Agric. Syst. 2018, 159, 248–259. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Gopal, P.M.; Bhargavi, R. Feature selection for yield prediction in Boruta algorithm. Int. J. Pure Appl. Math. 2018, 118, 139–144. [Google Scholar]
- Prasad, N.; Patel, N.; Danodia, A. Crop yield prediction in cotton for regional level using random forest approach. Spatial Inf. Res. 2021, 29, 195–206. [Google Scholar] [CrossRef]
- Gopal, M.P.S.; Bhargavi, R. Performance evaluation of best feature subsets for crop yield prediction using machine learning algorithms. Appl. Artif. Intell. 2019, 33, 621–642. [Google Scholar]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.; Madonsela, S.; Van De Kerchove, R.; Kaszta, Z.; Wolff, E. Monitoring grass nutrients and biomass as indicators of rangeland quality and quantity using random forest modelling and WorldView-2 data. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 43–54. [Google Scholar] [CrossRef]
- López-Calderón, M.J.; Estrada-Ávalos, J.; Rodríguez-Moreno, V.M.; Mauricio-Ruvalcaba, J.E.; Martínez-Sifuentes, A.R.; Delgado-Ramírez, G.; Miguel-Valle, E. Estimation of Total Nitrogen Content in Forage Maize (Zea mays L.) Using Spectral Indices: Analysis by Random Forest. Agriculture 2020, 10, 451. [Google Scholar] [CrossRef]
- Zimmer, S.N.; Schupp, E.W.; Boettinger, J.L.; Reeves, M.C.; Thacker, E.T. Considering spatiotemporal forage variability in rangeland inventory and monitoring. Rangeland Ecol. Manag. 2021, 79, 53–63. [Google Scholar] [CrossRef]
- Kuwata, K.; Shibasaki, R. Estimating corn yield in the United States with MODIS EVI and machine learning methods. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2016, 3, 131–136. [Google Scholar]
- Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. SPRS J. Photogramm. Remote Sens. 2020, 160, 124–135. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Z.; Cao, J.; Luo, Y.; Zhang, L.; Li, Z.; Zhang, J. Prediction of winter wheat yield based on multi-source data and machine learning in China. Remote Sens. 2020, 12, 236. [Google Scholar] [CrossRef]
- Ahamed, A.M.S.; Mahmood, N.T.; Hossain, N.; Kabir, M.T.; Das, K.; Rahman, F.; Rahman, R.M. Applying data mining techniques to predict annual yield of major crops and recommend planting different crops in different districts in Bangladesh. In Proceedings of the 2015 IEEE/ACIS 16th International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD); IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Liebig, M.; Kronberg, S.; Hendrickson, J.; Dong, X.; Gross, J. Carbon dioxide efflux from long-term grazing management systems in a semiarid region. Agric. Ecosyst. Environ. 2013, 164, 137–144. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote. Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Congedo, L. Semi-Automatic Classification Plugin: A Python tool for the download and processing of remote sensing images in QGIS. J. Open Source Softw. 2016, 6, 3172. [Google Scholar] [CrossRef]
- Foley, W.J.; McIlwee, A.; Lawler, I.; Aragones, L.; Woolnough, A.P.; Berding, N. Ecological applications of near infrared reflectance spectroscopy–a tool for rapid, cost-effective prediction of the composition of plant and animal tissues and aspects of animal performance. Oecologia 1998, 116, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Meyer, G.E.; Hindman, T.W.; Laksmi, K. Machine vision detection parameters for plant species identification. In Proceedings of the Precision Agriculture and Biological Quality International Society for Optics and Photonics, Boston, MA, USA, 3–4 November 1999; Volume 3543, pp. 327–335. [Google Scholar]
- Meyer, G.E.; Neto, J.C.; Jones, D.D.; Hindman, T.W. Intensified fuzzy clusters for classifying plant, soil, and residue regions of interest from color images. Comput. Electron. Agric. 2004, 42, 161–180. [Google Scholar] [CrossRef]
- Hunt, E.R.; Cavigelli, M.; Daughtry, C.S.; Mcmurtrey, J.E.; Walthall, C.L. Evaluation of digital photography from model aircraft for remote sensing of crop biomass and nitrogen status. Precis. Agric. 2005, 6, 359–378. [Google Scholar] [CrossRef]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D.C.; Merzlyak, M.N. Nondestructive estimation of anthocyanin content in grapevine leaves. Am. J. Enol. Vitic. 2009, 60, 87–92. [Google Scholar] [CrossRef]
- Xiaoqin, W.; Miaomiao, W.; Shaoqiang, W.; Yundong, W. Extraction of vegetation information from visible unmanned aerial vehicle images. Trans. Chin. Soc. Agric. Eng. 2015, 31. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Kataoka, T.; Kaneko, T.; Okamoto, H.; Hata, S. Crop growth estimation system using machine vision. Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan , 20–24 July 2003 , IEEE: Piscataway, NJ, USA, 2003; Volume 2, b1079–b1083. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Huete, A.; Liu, H.; Batchily, K.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
- Birth, G.S.; McVey, G.R. Measuring the color of growing turf with a reflectance spectrophotometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Venables, W.; Ripley, B. Modern Applied Statistics with S-PLUS; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Xu, L.; Zhang, W.J. Comparison of different methods for variable selection. Anal. Chim. Acta 2001, 446, 475–481. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Wang, Y.; Men, Z.; Liu, H. Regional soil organic matter mapping models based on the optimal time window, feature selection algorithm and Google Earth Engine. Soil Til. Res. 2022, 219, 105325. [Google Scholar] [CrossRef]
- Chen, Z.; Cheng, Q.; Duan, F.; Huang, X.; Xu, H.; Sui, R.; Li, Z. UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat. Agronomy 2022, 12, 202. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Kereszturi, G.; Yule, I. Integrating airborne hyperspectral, topographic, and soil data for estimating pasture quality using recursive feature elimination with random forest regression. Remote Sens. 2018, 10, 1117. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Shastry, A.; Sanjay, H.; Hegde, M. A parameter based ANFIS model for crop yield prediction. In Proceedings of the 2015 IEEE International Advance Computing Conference (IACC); IEEE: Piscataway, NJ, USA, 2015; pp. 253–257. [Google Scholar]
- Jiang, X.; Zou, B.; Feng, H.; Tang, J.; Tu, Y.; Zhao, X. Spatial distribution mapping of Hg contamination in subclass agricultural soils using GIS enhanced multiple linear regression. J. Geochem. Explor. 2019, 196, 1–7. [Google Scholar] [CrossRef]
- Chambers, J.; Hastie, T. Linear models. Chapter 4 of statistical models in S. In Wadsworth & Brooks/Cole; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 1992; pp. 96–138. [Google Scholar]
- Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. SPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Filippi, P.; Jones, E.J.; Wimalathunge, N.S.; Somarathna, P.D.; Pozza, L.E.; Ugbaje, S.U.; Jephcott, T.G.; Paterson, S.E.; Whelan, B.M.; Bishop, T.F. An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning. Precis. Agric. 2019, 20, 1015–1029. [Google Scholar] [CrossRef]
- Fawagreh, K.; Gaber, M.M.; Elyan, E. Random forests: From early developments to recent advancements. Syst. Sci. Control Eng. 2014, 2, 602–609. [Google Scholar] [CrossRef]
- Were, K.; Bui, D.T.; Dick, Ø.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Shafiee, S.; Lied, L.M.; Burud, I.; Dieseth, J.A.; Alsheikh, M.; Lillemo, M. Sequential forward selection and support vector regression in comparison to LASSO regression for spring wheat yield prediction based on UAV imagery. Comput. Electron. Agric. 2021, 183, 106036. [Google Scholar] [CrossRef]
- Gunn, S.R. Support vector machines for classification and regression. ISIS Tehc. Rep. 1998, 14, 5–16. [Google Scholar]
- Zhang, Z.; Flores, P.; Igathinathane, C.; L Naik, D.; Kiran, R.; Ransom, J.K. Wheat lodging detection from UAS imagery using machine learning algorithms. Remote Sens. 2020, 12, 1838. [Google Scholar] [CrossRef]
- Gonzalez-Sanchez, A.; Frausto-Solis, J.; Ojeda-Bustamante, W. Predictive ability of machine learning methods for massive crop yield prediction. Span. J. Agric. Res. 2014, 12, 313–328. [Google Scholar] [CrossRef]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data. Ecol. Modell. 2019, 406, 109–120. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Bhadra, S.; Maimaitiyiming, M.; Brown, D.R.; Sidike, P.; Fritschi, F.B. Field-scale crop yield prediction using multi-temporal WorldView-3 and PlanetScope satellite data and deep learning. SPRS J. Photogramm. Remote Sens. 2021, 174, 265–281. [Google Scholar] [CrossRef]
- Yang, C.; Anderson, G.L. Mapping grain sorghum yield variability using airborne digital videography. Precis. Agric. 2000, 2, 7–23. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Xu, X.; Yang, G.; Wang, J. Estimation of winter wheat biomass and yield by combining the aquacrop model and field hyperspectral data. Remote Sens. 2016, 8, 972. [Google Scholar] [CrossRef]
- El-Hendawy, S.E.; Hassan, W.M.; Al-Suhaibani, N.A.; Schmidhalter, U. Spectral assessment of drought tolerance indices and grain yield in advanced spring wheat lines grown under full and limited water irrigation. Agric. Water Manag. 2017, 182, 1–12. [Google Scholar] [CrossRef]
- Dong, W.; Li, C.; Hu, Q.; Pan, F.; Bhandari, J.; Sun, Z. Potential Evapotranspiration Reduction and Its Influence on Crop Yield in the North China Plain in 1961–2014. Adv. Meteorol. 2020, 2020, 3691421. [Google Scholar] [CrossRef]
- Kahimba, F.C.; Ranjan, R.S.; Froese, J.; Entz, M.; Nason, R. Cover crop effects on infiltration, soil temperature, and soil moisture distribution in the Canadian Prairies. Appl. Eng. Agric. 2008, 24, 321–333. [Google Scholar] [CrossRef]
- Kaspar, T.; Bland, W.L. Soil temperature and root growth. Soil Sci. 1992, 154, 290. [Google Scholar] [CrossRef]
- Mao, K.Z. Orthogonal forward selection and backward elimination algorithms for feature subset selection. IEEE Trans. Syst. Man, Cybern. Part (Cybernetics) 2004, 34, 629–634. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa yield prediction using UAV-based hyperspectral imagery and ensemble learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- John, A.; Ong, J.; Theobald, E.J.; Olden, J.D.; Tan, A.; HilleRisLambers, J. Detecting Montane Flowering Phenology with CubeSat Imagery. Remote Sens. 2020, 12, 2894. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Lim, J.; Kawamura, K.; Lee, H.J.; Yoshitoshi, R.; Kurokawa, Y.; Tsumiyama, Y.; Watanabe, N. Evaluating a hand-held crop-measuring device for estimating the herbage biomass, leaf area index and crude protein content in an Italian ryegrass field. Grassland Sci. 2015, 61, 101–108. [Google Scholar] [CrossRef]



| Remote Sensing Data (Satellite Platforms) | Climate Data (NDAWN) | |||||||
|---|---|---|---|---|---|---|---|---|
| No. | Parameter | Abbreviation | Availability | No. | Parameter | Abbreviation | ||
| Landsat | Sentinel | CubeSat | ||||||
| Surface Reflectance Bands: | Weather Variables: | |||||||
| 1 | Blue (0.45–0.52 m) | B | ✓ | ✓ | ✓ | 37 | Air temperature (minimum, °C) | Min_T |
| 2 | Green (0.52–0.60 m) | G | ✓ | ✓ | ✓ | 38 | Air temperature (average, °C) | Avg_T |
| 3 | Red (0.63–0.69 m) | R | ✓ | ✓ | ✓ | 39 | Air temperature (maximum, °C) | Max_T |
| 4 | Near-infrared (0.77–0.90 m) | NIR | ✓ | ✓ | ✓ | 40 | Air temperature (diurnal range, °C) | Di_TR |
| 5 | Short-wave infrared 1 (1.57–1.75 m) | SWIR1 | ✓ | ✓ | – | 41 | Bare soil temperature (°C) | AvgB_Soil |
| 6 | Short-wave infrared 2 (2.09–2.35 m) | SWIR2 | ✓ | ✓ | – | 42 | Turf soil temperature (°C) | AvgT_Soil |
| Color Vegetation Indices: | 43 | Wind speed (average, km/h) | Avg_WindS | |||||
| 7 | Red chromatic coordinate | RCC | ✓ | ✓ | ✓ | 44 | Wind speed (maximum, km/h) | Max_WS |
| 8 | Green chromatic coordinate | GCC | ✓ | ✓ | ✓ | 45 | Wind direction (average,°) | Avg_WD |
| 9 | Blue chromatic coordinate | BCC | ✓ | ✓ | ✓ | 46 | Total solar radiation (Ly) | Tot_Sol_R |
| 10 | Excess green | ExG | ✓ | ✓ | ✓ | 47 | Potential evapotranspiration (Penman, mm) | Pen_PT |
| 11 | Normalized excess green | ExG2 | ✓ | ✓ | ✓ | 48 | Potential evapotranspiration (Jensen-Haise, mm) | JH_PET |
| 12 | Excess red | ExR | ✓ | ✓ | ✓ | 49 | Total rainfall (mm) | Rainfall |
| 13 | Excess green minus excess red | ExGR | ✓ | ✓ | ✓ | 50 | Dew point (average, °C) | Dew_P |
| 14 | Green-red vegetation index (VI) | GRVI | ✓ | ✓ | ✓ | 51 | Wind chill (minimum, °C) | Min_Wind_Chill |
| 15 | Green-blue VI | GBVI | ✓ | ✓ | ✓ | 52 | Wind chill (average, °C) | Wind_Chill |
| 16 | Blue red VI | BRVI | ✓ | ✓ | ✓ | |||
| 17 | Green-red ratio | ✓ | ✓ | ✓ | ||||
| 18 | Green-red difference | ✓ | ✓ | ✓ | ||||
| 19 | Blue-green difference | ✓ | ✓ | ✓ | ||||
| 20 | Visible-band difference VI | VDVI | ✓ | ✓ | ✓ | |||
| 21 | Visible atmospherically resistant index | VARI | ✓ | ✓ | ✓ | |||
| 22 | Modified green-red VI | MGRVI | ✓ | ✓ | ✓ | |||
| 23 | Colour index of vegetation | CIVE | ✓ | ✓ | ✓ | |||
| 24 | Woebbecke index | WI | ✓ | ✓ | ✓ | |||
| 25 | Coloration index | CI | ✓ | ✓ | ✓ | |||
| Multispectral Vegetation Indices: | ||||||||
| 26 | Normalized difference VI | NDVI | ✓ | ✓ | ✓ | |||
| 27 | Green normalized VI | GNDVI | ✓ | ✓ | ✓ | |||
| 28 | Soil-adjusted VI | SAVI | ✓ | ✓ | ✓ | |||
| 29 | Modified soil-adjusted VI | MSAVI | ✓ | ✓ | ✓ | |||
| 30 | Enhanced VI | EVI | ✓ | ✓ | ✓ | |||
| 31 | Normalized difference moisture index | NDMI | ✓ | ✓ | – | |||
| 32 | Green atmospherically resistance VI | GARI | ✓ | ✓ | ✓ | |||
| 33 | Simple ratio index | SR | ✓ | ✓ | ✓ | |||
| 34 | Atmospherically resistant VI | ARVI | ✓ | ✓ | ✓ | |||
| 35 | Green chlorophyll index | GCI | ✓ | ✓ | ✓ | |||
| 36 | Structure intensive pigment index | (SIPI) | ✓ | ✓ | ✓ | |||
| Rank | Landsat | Sentinel | CubeSat |
|---|---|---|---|
| 1 | AvgT_Soil | AvgT_Soil | AvgT_Soil |
| 2 | Green | Di_TR | NIR |
| 3 | G_Rdiff | SWIR2 | GCI |
| 4 | SWIR2 | Tot_Sol_R | MSAVI |
| 5 | SWIR | Avg_WindS | GNDVI |
| 6 | AvgB_Soil | AvgB_Soil | SAVI |
| 7 | Blue | SWIR | AvgB_Soil |
| 8 | SIPI | Avg_WD | Blue |
| 9 | BCC | NDMI | RCC |
| 10 | Di_TR | JH_PET | NDVI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subhashree, S.N.; Igathinathane, C.; Hendrickson, J.; Archer, D.; Liebig, M.; Halvorson, J.; Kronberg, S.; Toledo, D.; Sedivec, K. Evaluating Remote Sensing Resolutions and Machine Learning Methods for Biomass Yield Prediction in Northern Great Plains Pastures. Agriculture 2025, 15, 505. https://doi.org/10.3390/agriculture15050505
Subhashree SN, Igathinathane C, Hendrickson J, Archer D, Liebig M, Halvorson J, Kronberg S, Toledo D, Sedivec K. Evaluating Remote Sensing Resolutions and Machine Learning Methods for Biomass Yield Prediction in Northern Great Plains Pastures. Agriculture. 2025; 15(5):505. https://doi.org/10.3390/agriculture15050505
Chicago/Turabian StyleSubhashree, Srinivasagan N., C. Igathinathane, John Hendrickson, David Archer, Mark Liebig, Jonathan Halvorson, Scott Kronberg, David Toledo, and Kevin Sedivec. 2025. "Evaluating Remote Sensing Resolutions and Machine Learning Methods for Biomass Yield Prediction in Northern Great Plains Pastures" Agriculture 15, no. 5: 505. https://doi.org/10.3390/agriculture15050505
APA StyleSubhashree, S. N., Igathinathane, C., Hendrickson, J., Archer, D., Liebig, M., Halvorson, J., Kronberg, S., Toledo, D., & Sedivec, K. (2025). Evaluating Remote Sensing Resolutions and Machine Learning Methods for Biomass Yield Prediction in Northern Great Plains Pastures. Agriculture, 15(5), 505. https://doi.org/10.3390/agriculture15050505








