Study on the Design and Performance of a Seed Discharger for Peanut Plot Breeding Based on the CFD-DEM Method
Abstract
1. Introduction
2. Materials and Methods
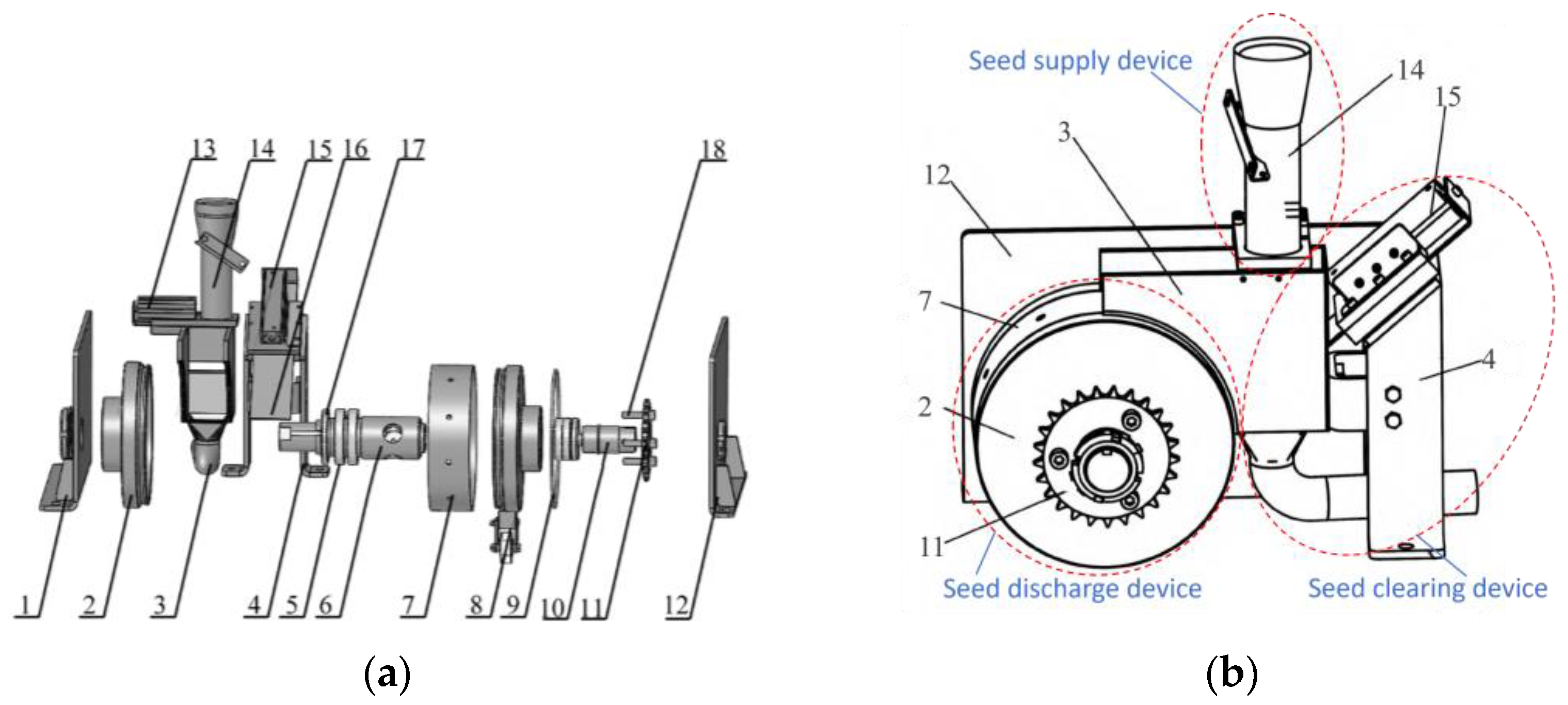
2.1. Composition and Working Principle of the Seed Discharger
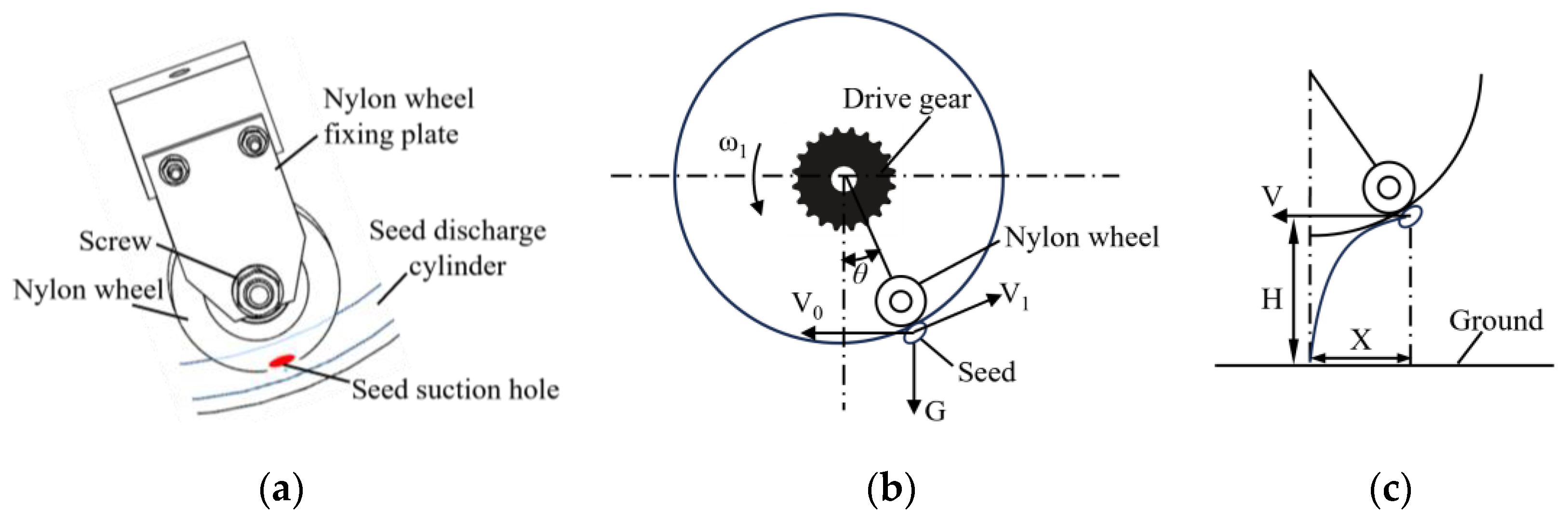
2.1.1. Composition of the Seed Discharger
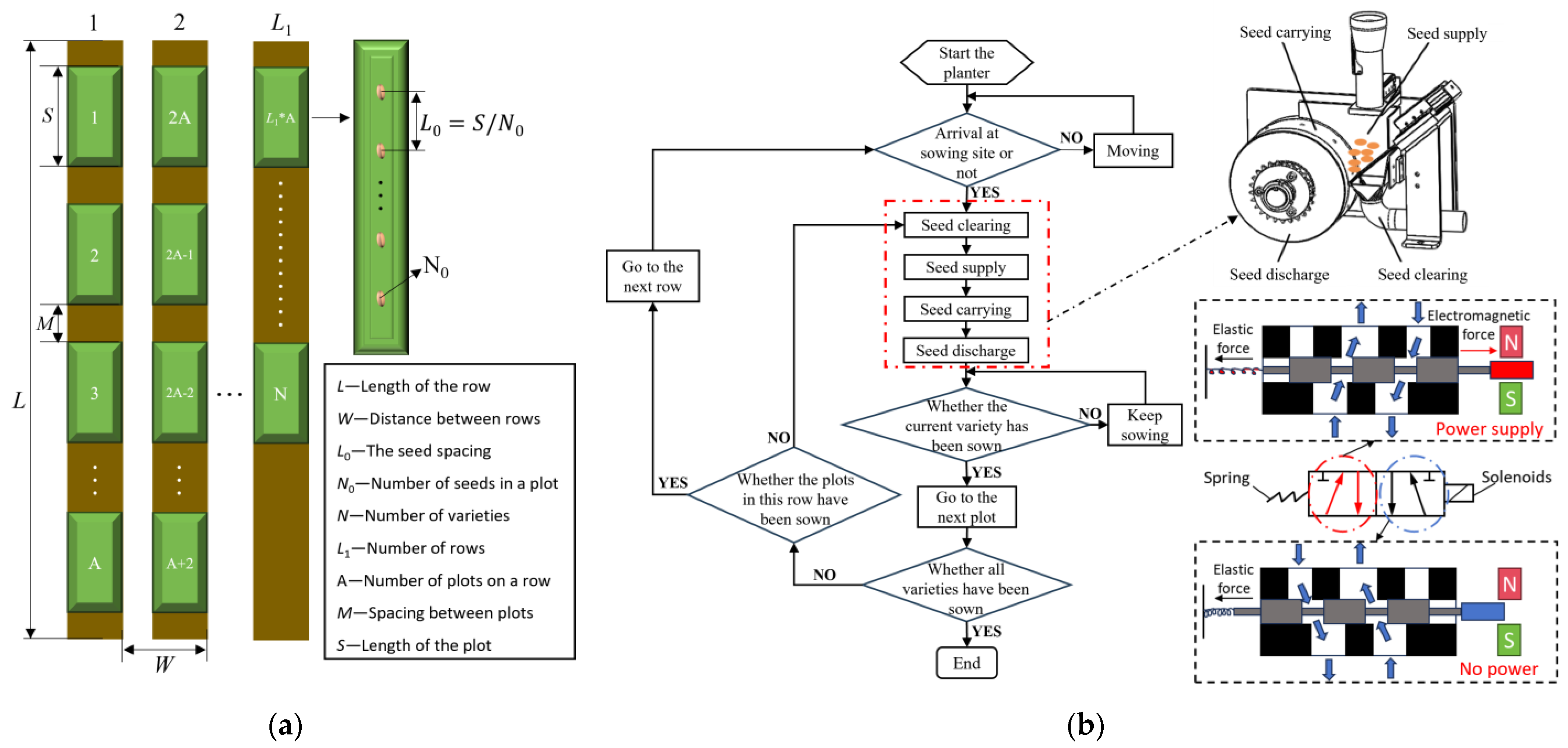
2.1.2. Working Principle of the Seed Discharger
2.2. Material Parameters of Peanut Seeds and Seed Discharger Materials
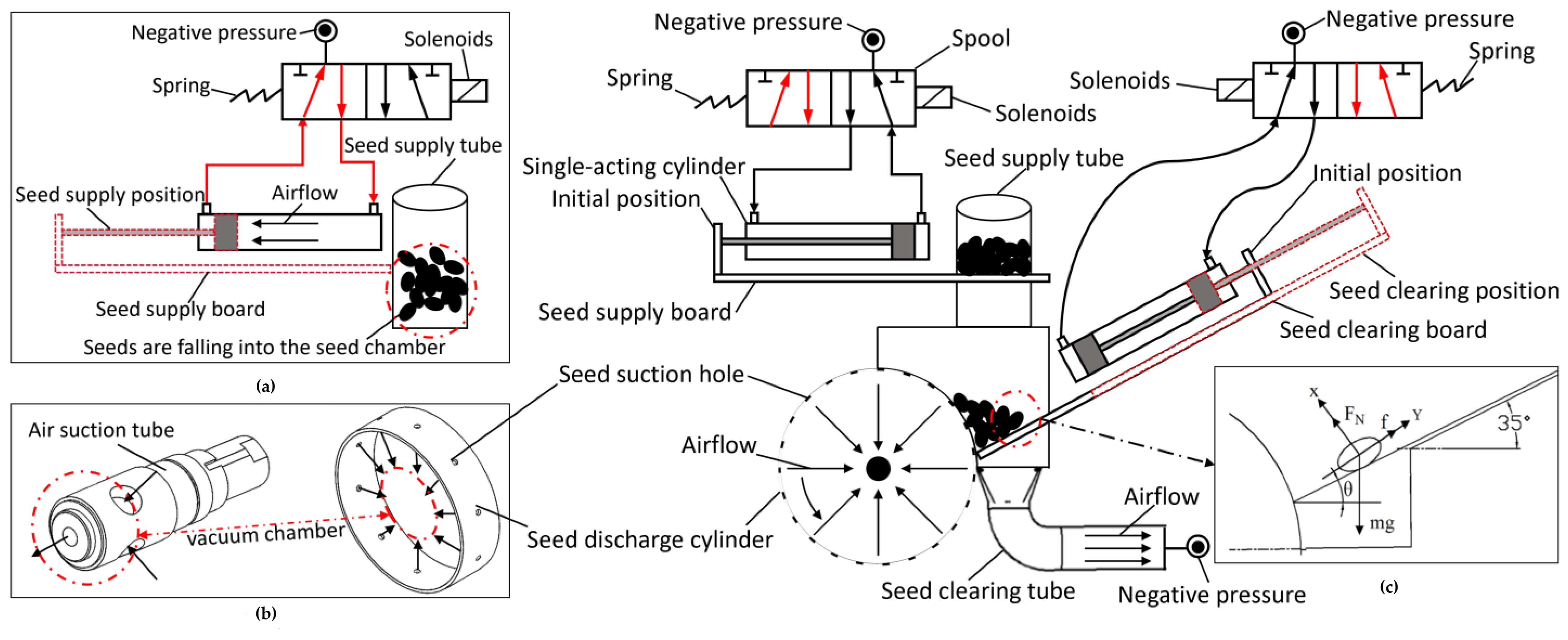
2.3. Design of Seed Supply and Clearing Devices
2.3.1. Principle of Operation of the Seed Supply and Clearing Device
2.3.2. Theoretical Analysis of the Seed Absorption Process
2.4. Design and Theoretical Analysis of Seed Discharge Device
Structural Design of the Seed Discharge Cylinder
2.5. Design of the Seed Discharge Device
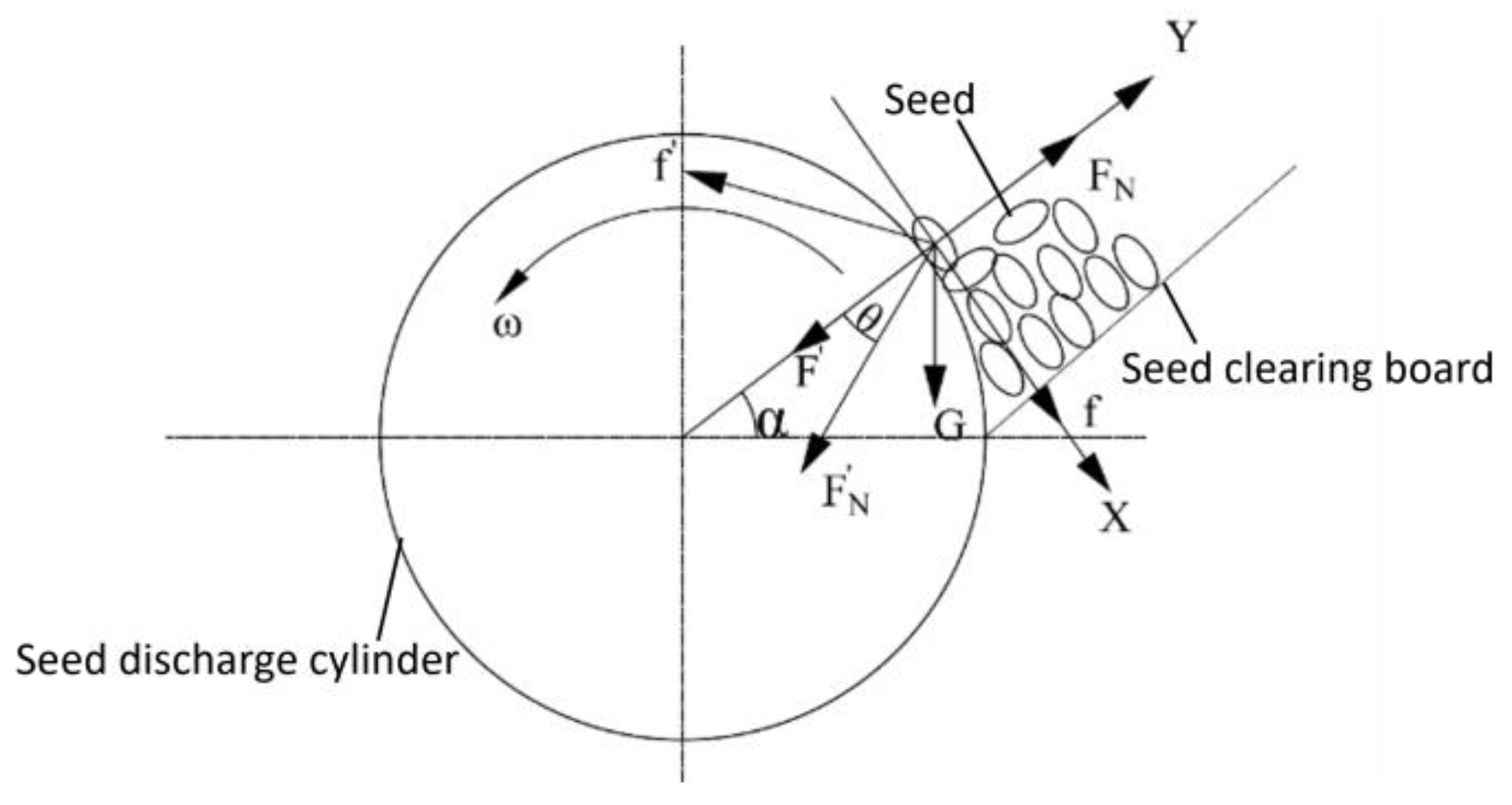
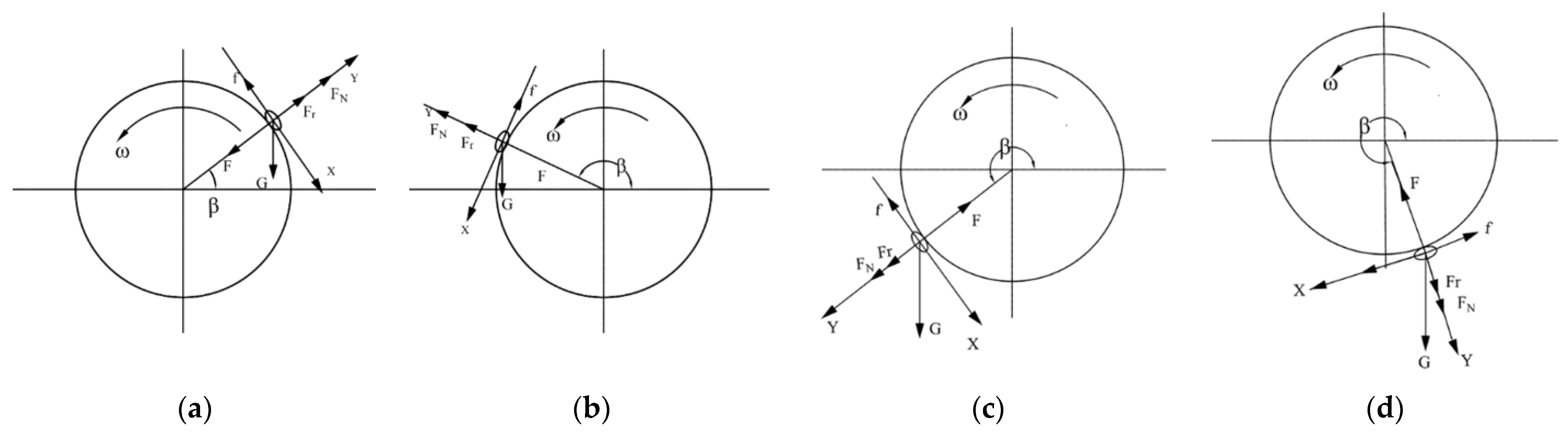
Analysis of the Seed Carrying Process
2.6. Determination of Key Structural Parameters Based on Fluent
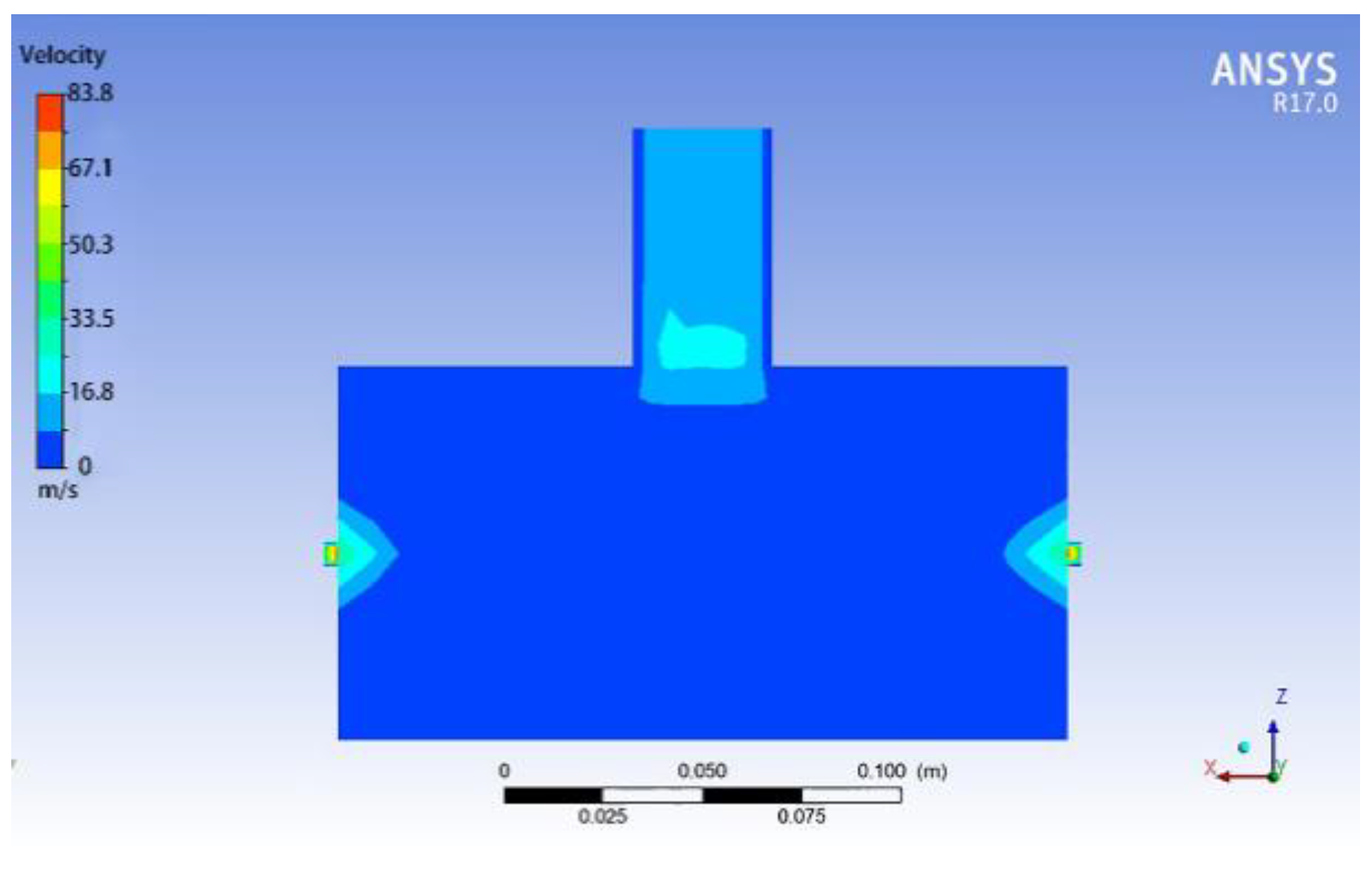
2.6.1. Simulation Model Building and Parameter Setting
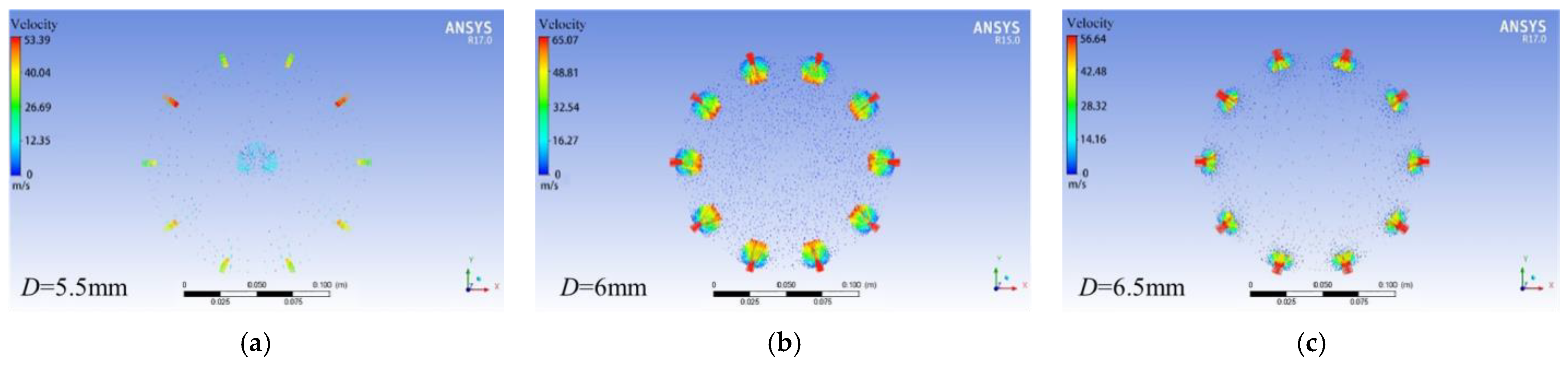
2.6.2. Simulation of Fluid Field with Different Seed Suction Hole Diameters
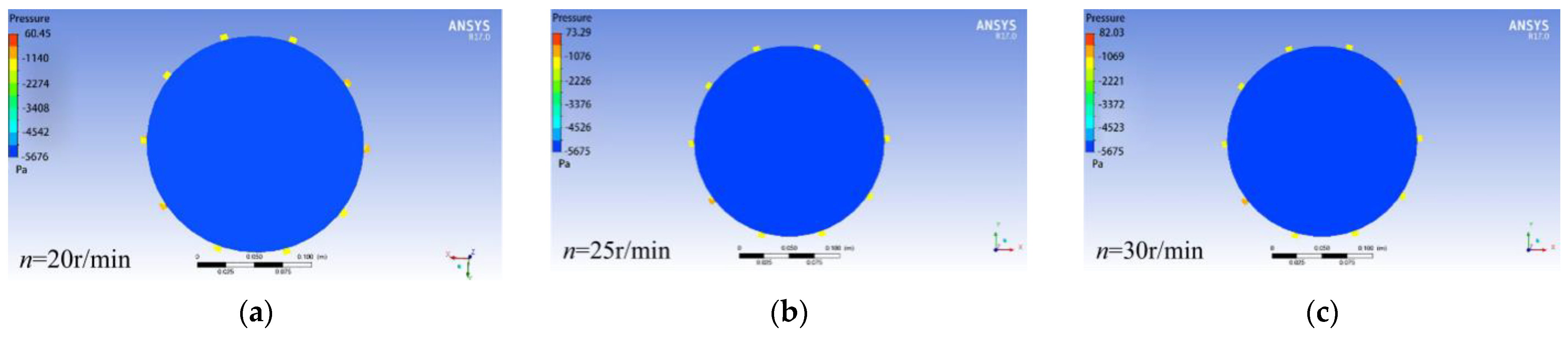
2.6.3. Simulation of Flow Field at Different Rotational Speeds of the Seed Discharge Cylinder
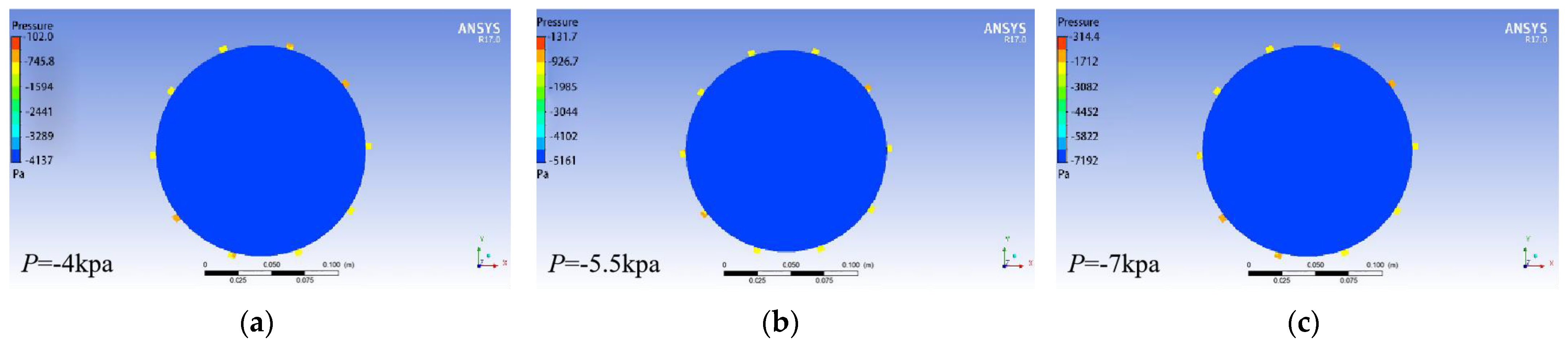
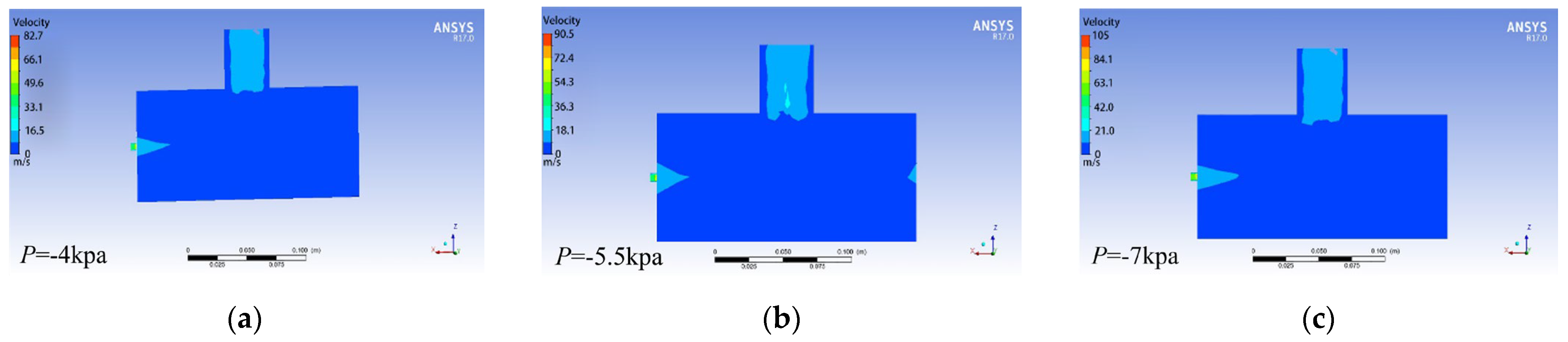
2.6.4. Simulation of the Flow Field with Different Negative Pressures
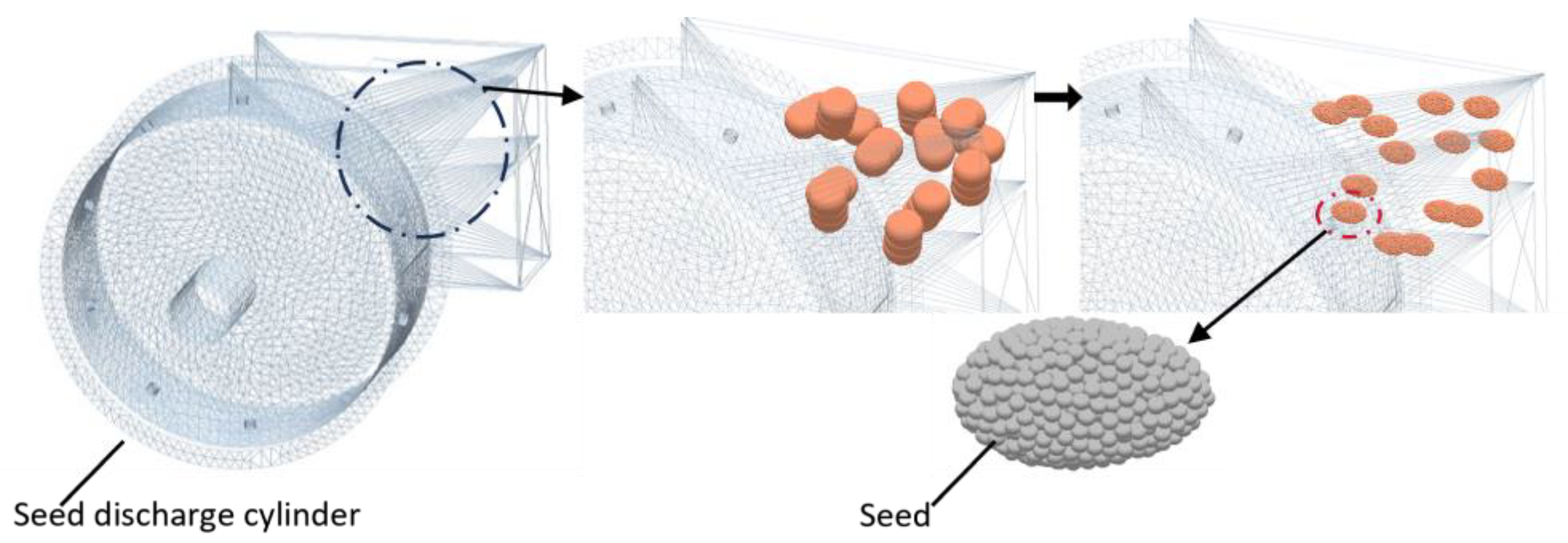
2.7. Coupling Simulation Based on CFD-DEM Method
2.7.1. Parameter Setting of the Simulation Model
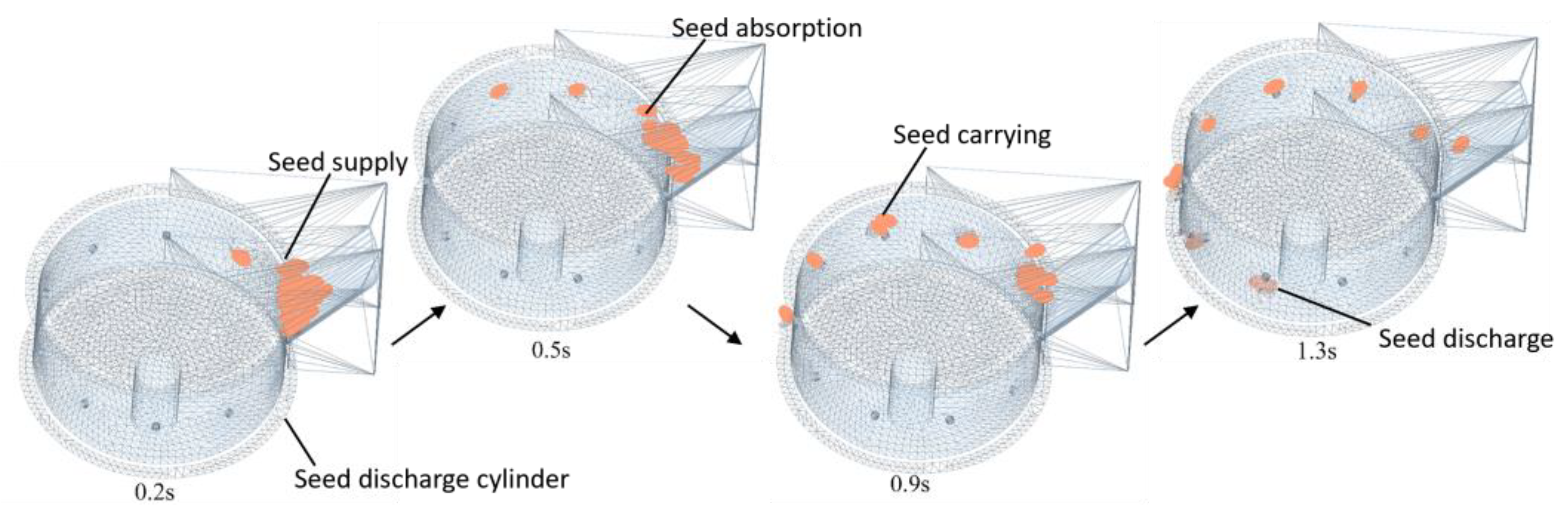
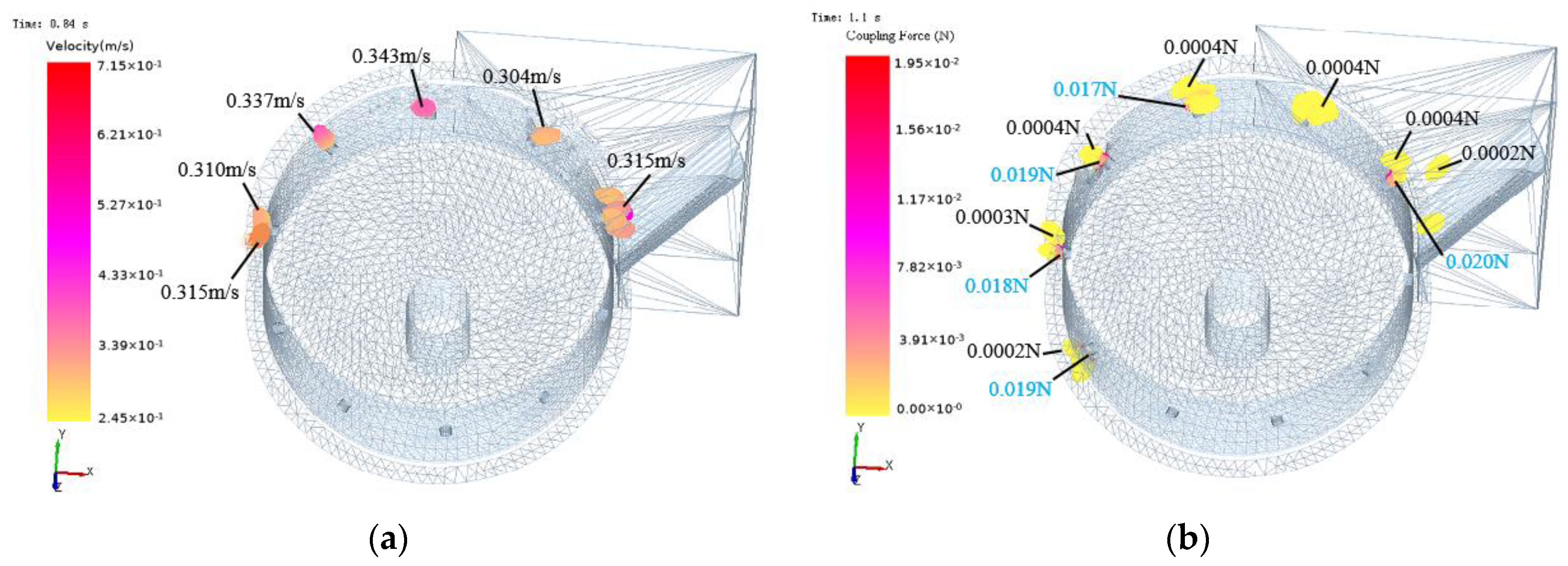
2.7.2. Simulation of Coupling and Results of the Seed Discharging Process
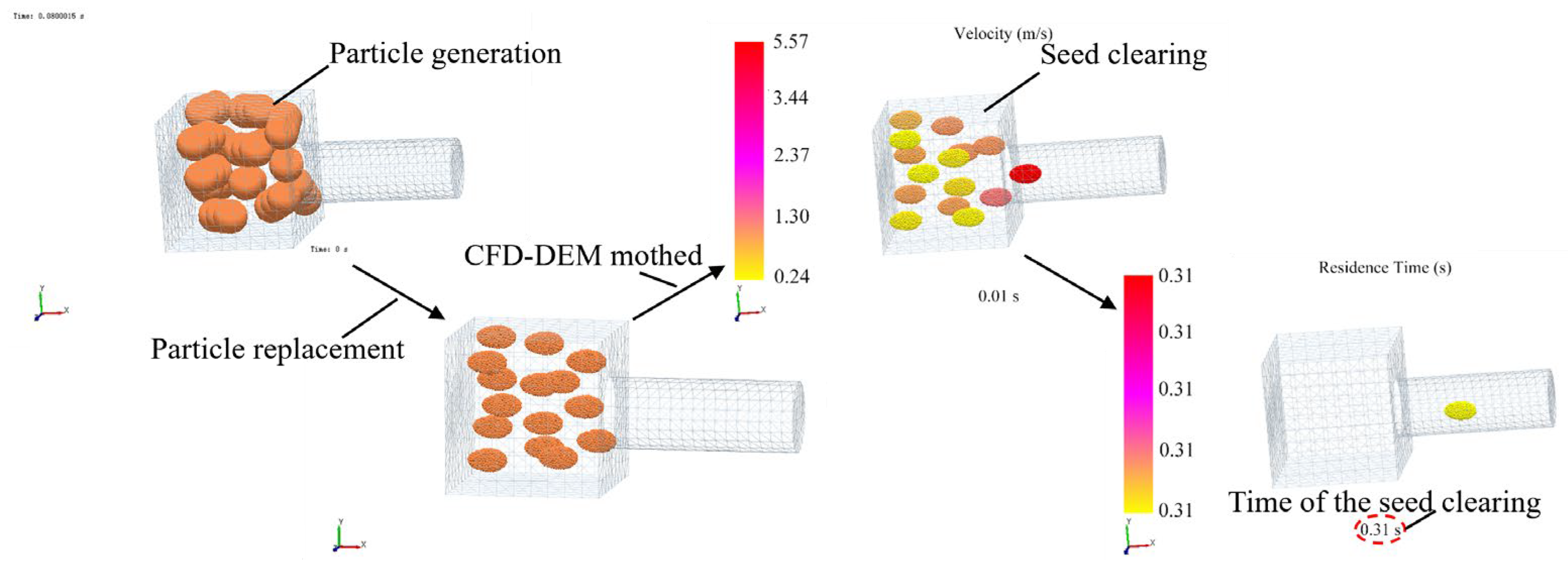
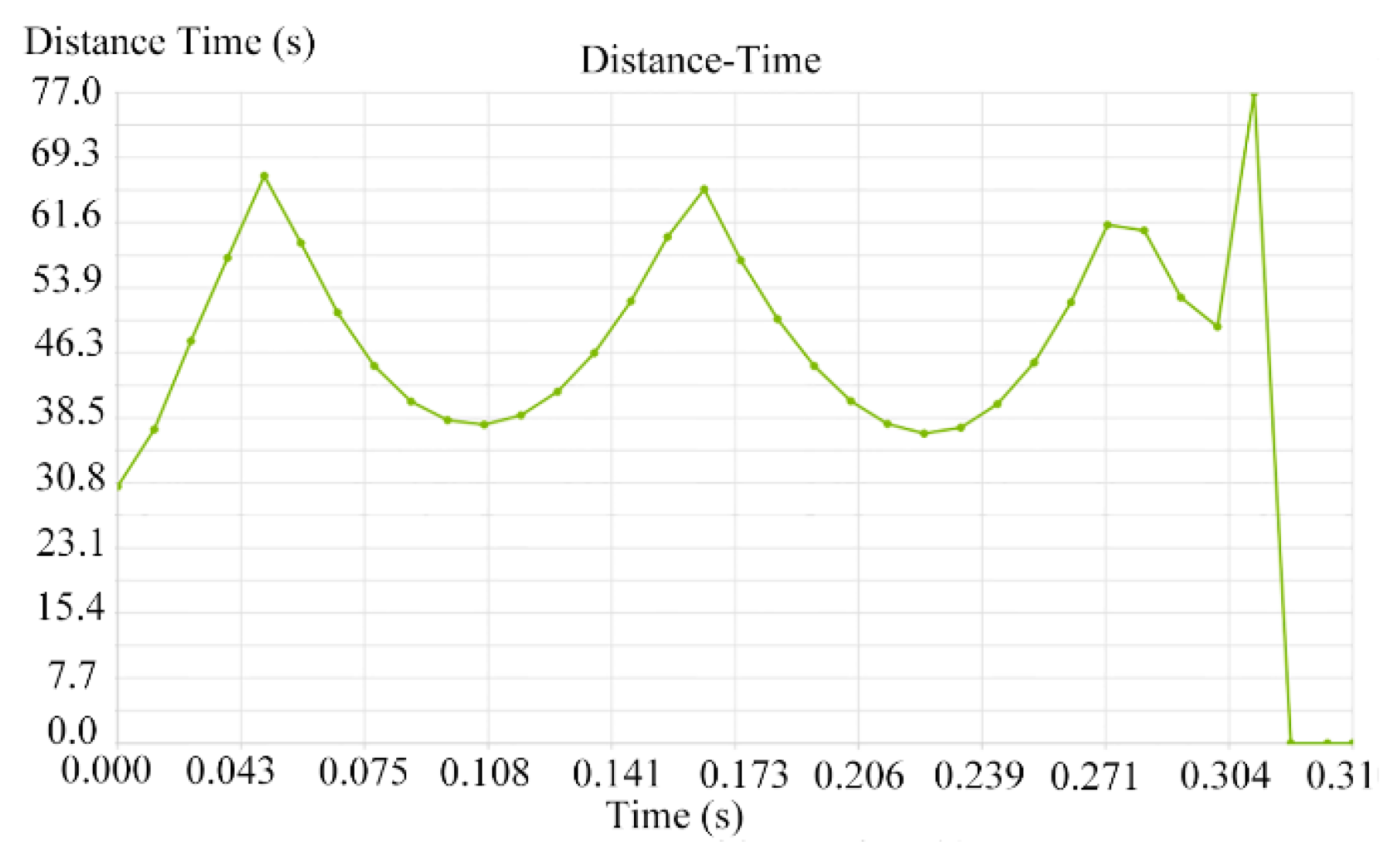
2.7.3. The Coupled Process of the Seed Clearing and Simulation Results
3. Results and Discussion
3.1. Bench Test Results and Discussion
3.1.1. Preparation and Method of the Test
3.1.2. Test Programmes and Results
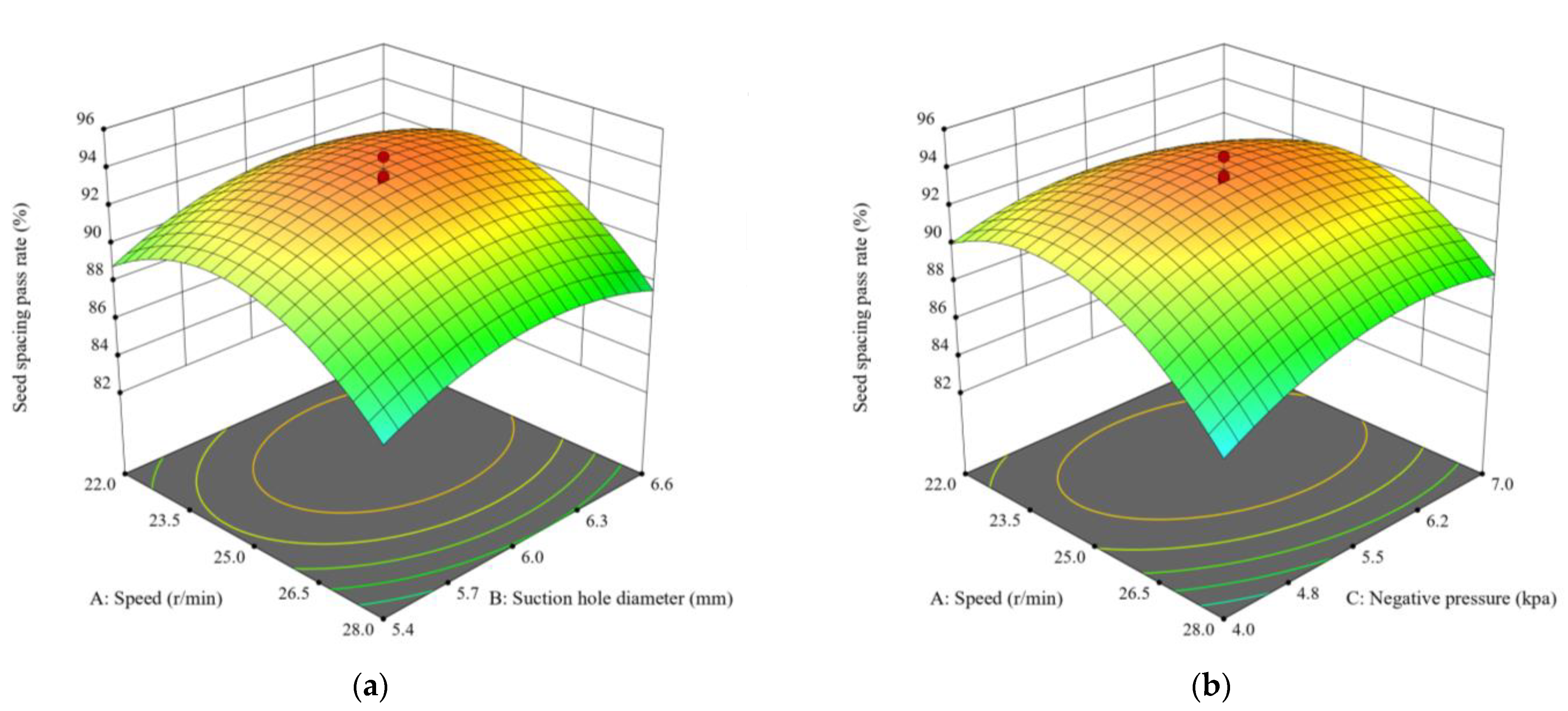
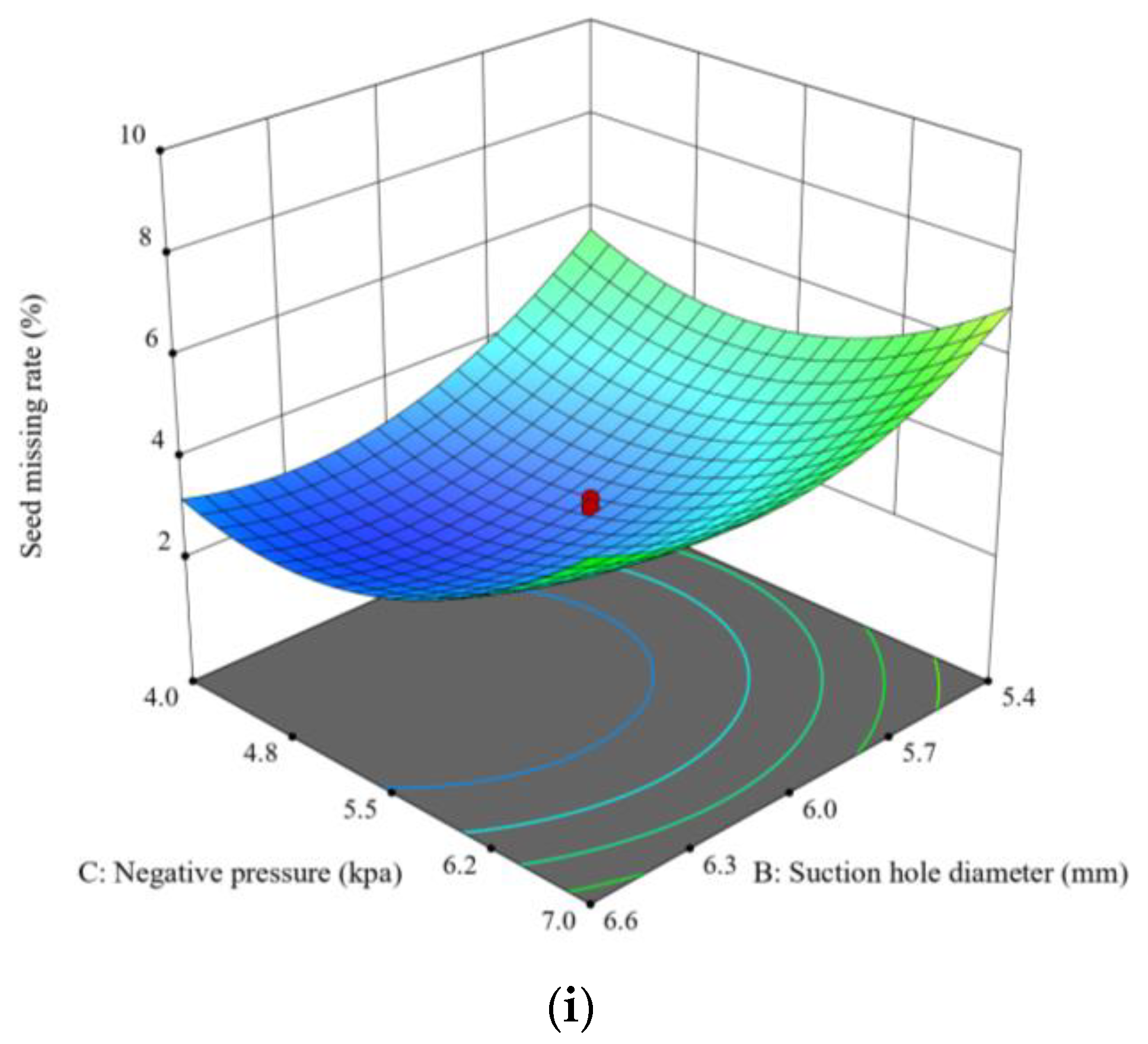
3.1.3. Analysis of the Test Results
3.1.4. Final Parameters of the Discharger
3.2. Field Trial Results and Discussion
4. Conclusions
- (1)
- Two single stroke cylinders were used for seed replacement and to avoid confusion between different varieties of seeds. The seed supply process was controlled by a seed supply cylinder with a stroke of 40 mm, and the seed-clearing process was controlled by a seed-clearing cylinder with a stroke of 70 mm. The installation angle of the plugging wheel was designed to be 27° and the inclination angle of the seed-clearing plate was designed to be 35°. The diameter of the seed discharge cylinder was designed to be 190 mm, and the number of seed suction holes was designed to be 10.
- (2)
- The flow field inside the seed discharger was analysed by Fluent R17.0 software. The rotation speed of the seed discharge cylinder was designed in the range of 20~30 r/min, the diameter of the seed suction hole was designed in the range of 5.5–6.5 mm, and the working negative pressure was designed in the range of 5.5–6.5 kPa. The simulation results of the CFD-DEM method showed that the adsorption force at the seed suction hole was about 0.02 N, and the seed clearing time was 0.31 s when the rotation speed of the seed discharge cylinder was 25 r/min, the diameter of the seed suction hole was 6 mm, and the working negative pressure was 5.5 kPa. The seed clearing time was 0.31 s, indicating that the seeds of the previous variety could be removed before moving to the next plot.
- (3)
- The developed seed discharger was installed on the test bench to carry out the central composite design experiment, and the test results were analysed and optimised with the help of Design-Expert 13 software. The final parameters of the seed discharger were obtained as follows: rotational speed of the seed cylinder was 25 r/min, the diameter of the seed suction hole was 6 mm, and the working negative pressure was −6 kPa. Finally, the seed discharger was tested in the field, and the results showed that the seed spacing pass rate was bigger than 90%, the multiple-seed rate was less than 6%, the seed missing rate was less than 4.5%, and the seed-clearing rate reached 100%, which meets the requirements of peanut plot breeding. Optimisation of the structure allows the seed discharger to meet the operating requirements with as little power consumption as possible.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Zhang, Y.; Yan, L.; Chen, Y.; Kang, Y.; Huai, D.; Wang, X.; Liu, K.; Jiang, H.; Lei, Y.; et al. Correlation and variability analysis of yield and quality related traits in different peanut varieties across various ecological zones of China. Oil Crop Sci. 2023, 8, 236–242. [Google Scholar] [CrossRef]
- Zhou, X.; Ren, X.; Luo, H.; Huang, L.; Liu, N.; Chen, W.; Lei, Y.; Liao, B.; Jiang, H. Safe conservation and utilization of peanut germplasm resources in the Oil Crops Middle-term Genebank of China. Oil Crop Sci. 2022, 7, 9–13. [Google Scholar] [CrossRef]
- Zhao, S.-C.; Lü, J.-L.; Xu, X.-P.; Lin, X.-M.; Luiz, M.R.; Qiu, S.-J.; Ciampitti, I.; He, P. Peanut yield, nutrient uptake and nutrient requirements in different regions of China. J. Integr. Agric. 2021, 20, 2502–2511. [Google Scholar] [CrossRef]
- Haro, R.J.; Carrega, W.C.; Otegui, M.E. Row spacing and growth habit in peanut crops: Effects on seed yield determination across environments. Field Crops Res. 2022, 275, 108363. [Google Scholar] [CrossRef]
- Zhao, J.; Lai, H.; Bi, C.; Zhao, M.; Liu, Y.; Li, X.; Yang, D. Effects of paclobutrazol application on plant architecture, lodging resistance, photosynthetic characteristics, and peanut yield at different single-seed precise sowing densities. Crop J. 2022, 11, 301–310. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Geng, Y.; Guo, F.; Li, X.-G.; Wan, S.-B. Research progress on the mechanism of improving peanut yield by single-seed precision sowing. J. Integr. Agric. 2020, 19, 1919–1927. [Google Scholar] [CrossRef]
- Qiu, Y.J.; Li, G.Q.; Zang, X.W.; Liu, J.; Hao, X.; Zhang, J.; Cui, Y.N.; Zhang, P.L.; Liu, B.; Liu, H.J. Research Hotspots and Trends of Groundnut (Arachis hypogaea L.) Breeding and Cultivation Based on Bibliometric Analysis. J. Peanut Sci. 2024, 53, 88–104. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Wang, C.H.; Xia, Y.L.; Mao, J.X.; Wang, Y.; Du, Q.; Yang, H.; You, Y. Evolution analysis of main traits of registered peanut varieties in China from 2020 to 2023. Chin. J. Oil Crop Sci. 2024, 46, 687–696. [Google Scholar] [CrossRef]
- Liao, J.H.; Cong, J.L.; You, Y.; Mao, J.X. Research progress of high-oleic acid peanut in China. Cereals Oils 2023, 36, 5–8. Available online: https://kns.cnki.net/kcms2/article/abstract?v=_bj0XFJq-767bRK6yLu8hKTwSGNotieJ0nJIu_ih1-fo6F3vLvwNuNI6zaqr_wUN0_6lqN8luc9210DrRn9E4Wzzqf3dZrSEwwGqpheC88nKTe_e0UYW-zn97px70NjR0nlqJZKg-YPePeX1Uc1FnqTOuBthUJFuSOP2PnXTAXfL0jv90j3eVCKSoq81RLeQbDs9356iN_NEIeKXlXsG9A==&uniplatform=NZKPT (accessed on 18 April 2023).
- De Almeida Moreira, B.R.; Marra, T.M.; da Silva, E.A.; de Brito Filho, A.L.; Júnior, M.R.B.; dos Santos, A.F.; da Silva, R.P.; Vellidis, G. Advancements in peanut mechanization: Implications for sustainable agriculture. Agric. Syst. 2024, 215, 103868. [Google Scholar] [CrossRef]
- Çiftçi, S.; Suna, G. Functional components of peanuts (Arachis hypogaea L.) and health benefits: A review. Future Foods 2022, 5, 100140. [Google Scholar] [CrossRef]
- Qi, B.B.; Cong, J.L.; Zeng, M.J.; Yan, Q.; Hu, R.; Wu, M.C.; Zhu, T. Experimental study on the effect of soaking treatment on peanut seed damage. J. Shihezi Univ. (Nat. Sci.) 2020, 38, 146–154. [Google Scholar] [CrossRef]
- Shang, S.Q.; Wu, X.F.; Yang, R.B.; Li, G.Y.; Yang, X.L. Research Status and Prospect of Plot-sowing Equipment and Technology. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar] [CrossRef]
- Ren, D.G.; Wang, D.W.; Li, M.X.; Li, X.; Ma, Z.J.; Dong, T.T.; Chang, X.L.; Ma, S.K.; Yu, H.L. Design and Experiment of Air Suction Seed Metering Device for Alfalfa Plot Breeding. J. Agric. Mech. Res. 2025, 47, 39–45. [Google Scholar] [CrossRef]
- Chang, X.L.; Shang, S.Q.; He, X.N.; Li, Y.T.; Liu, J.J.; Li, X.J.; Li, W.J.; Li, Q. Design and Test of Precision Planter for Peanut Community Breeding. J. Agric. Mech. Res. 2025, 7, 1–6. [Google Scholar] [CrossRef]
- Hao, J.J.; Qin, J.H.; Yang, S.H.; Ai, Q.H.; Ma, Z.K. Design and experiments of a precision sowing unit with the spoon clip for single peanut seed planting in plot. Trans. Chin. Soc. Agric. Eng. 2023, 39, 33–41. [Google Scholar] [CrossRef]
- Liu, B.; Wang, D.W.; Li, X.J.; He, X.N.; Yang, X.C.; Xun, G.S.; Liu, S.M.; Zhao, Z. Simulation and Experiment of Peanut Air Suction Seed Metering Device Based on DEM-CFD Coupling Method. J. Agric. Mech. Res. 2022, 44, 166–172. [Google Scholar] [CrossRef]
- Wang, W.W.; Song, L.Z.; Shi, W.B.; Wei, D.H.; Chen, Y.X.; Chen, L.Q. Design and Experiment of Air-suction Double-row Staggered Precision Seed Metering Device for Maize Dense Planting. Trans. Chin. Soc. Agric. Mach. 2024, 55, 53–63. [Google Scholar] [CrossRef]
- Li, C.; Zhang, D.X.; Yang, L.; Cui, T.; He, X.T.; Li, Z.M.; Dong, J.Q.; Xing, S.L.; Jiang, Y.Y.; Liang, J.Y. Research on a centrifugal high-speed precision seed metering device for maize with airflow-assisted seed filling and cleaning. Comput. Electron. Agric. 2024, 226, 109434. [Google Scholar] [CrossRef]
- Yu, Y.X.; Wang, Y.; Zhou, J.W.; Pan, Y.L. Design and Test of Combined Pumpkin Seed Attitude-constrained Directional Seed Metering Device. Trans. Chin. Soc. Agric. Mach. 2025, 55, 121–132+158. [Google Scholar] [CrossRef]
- Shang, Z.Q.; Zhang, K.F.; Yang, D.F.; Ma, Z.P. Simulation optimization of seed plate of air suction soybean seed-metering device based on DEM-CFD coupling. J. Chin. Agric. Mech. 2023, 44, 1–8. [Google Scholar] [CrossRef]
- Wang, G.W.; Xia, X.M.; Zhu, Q.H.; Yu, H.Y.; Huang, D.Y. Design and experiment of soybean high-speed precision vacuum seed metering with auxiliary filling structure based on DEM-CFD. J. Jilin Univ. (Eng. Technol. Ed.) 2022, 52, 1208–1221. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Zhang, D.X.; Cui, T.; Gao, Y.J. Design and Experiment of Seed Plate of Corn Air Suction Seed Metering Device Based on DEM-CFD. Trans. Chin. Soc. Agric. Mach. 2019, 50, 50–60. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Wu, D.H.; Li, D.Y.; Zhang, D.X.; Liu, S.R. Simulation and Experiment of Corn Air Suction Seed Metering Device Based on DEM-CFD Coupling Method. Trans. Chin. Soc. Agric. Mach. 2018, 49, 48–57. [Google Scholar] [CrossRef]
- GB/T 6973-2005; Testing Methods of Single Seed Drills (Precision Drills). Machinery Industry Publishing House: Beijing, China, 2005.
- JB/T51017-1999; Product Quality Classification of Precision Planters for Mid-Tillage Crops. Machinery Industry Publishing House: Beijing, China, 2000.
- JB/T 10293-2013; Specifications for Single Seed Drills (Precision Drills). Machinery Industry Publishing House: Beijing, China, 2013.






| Variable | Parameters | Unit |
|---|---|---|
| Mean length of peanut seeds | 19.23 | mm |
| Mean width of peanut seeds | 9.67 | mm |
| Mean thickness of peanut seeds | 8.50 | mm |
| Density of peanut seeds | 860 | kg·m−3 |
| Density of the seed discharger (stainless steel) | 7850 | kg·m−3 |
| Poisson’s ratio of peanut seeds | 0.25 | \ |
| Poisson’s ratio of the seed discharger | 0.33 | \ |
| Elastic modulus of peanut seeds | 6 × 107 | Pa |
| Elastic modulus of the seed discharger (stainless steel) | 2 × 1011 | Pa |
| The static friction coefficient between seed and seed | 0.50 | \ |
| The static friction coefficient between the seed and the seed discharger | 0.30 | \ |
| The dynamic friction coefficient between seed and seed | 0.04 | \ |
| The dynamic friction coefficient between the seed and the seed discharger | 0.05 | \ |
| Elastic collision recovery coefficient between seed and seed | 0.10 | \ |
| Elastic collision recovery coefficient between the seed and the seed discharger | 0.40 | \ |
| Performance | Performance Indicator | ||
|---|---|---|---|
| Seed Spacing ≤ 10 cm | Seed Spacing > 10~20 cm | Seed Spacing > 20~30 cm | |
| seed spacing pass rate | ≥60% | ≥75% | ≥80% |
| multiple-seed rate | ≤30% | ≤20% | ≤15% |
| seed missing rate | ≤15% | ≤10% | ≤8% |
| Code Value | Speed/r·min−1 | Suction Hole Diameter/mm | Negative Pressure/kPa |
|---|---|---|---|
| −r (−1.682) | 20 | 5 | −3 |
| −1 Level | 22 | 5.5 | −4 |
| 0 Level | 25 | 6 | −5.5 |
| +1 Level | 28 | 6.5 | −7 |
| +r (1.682) | 30 | 7 | −8 |
| Test Programmes | Test Factors | Test Indicators | ||||
|---|---|---|---|---|---|---|
| Speed X1/r·min−1 | Suction Hole Diameter X2/mm | Negative Pressure X3/kPa | Seed Spacing Pass Rate Q/% | Multiple-Seed Rate R/% | Seed Missing Rate M/% | |
| 1 | 22 | 5.5 | −4 | 88.6 | 5.6 | 7.8 |
| 2 | 28 | 5.5 | −4 | 83.2 | 11.5 | 5.3 |
| 3 | 22 | 6.5 | −4 | 89.5 | 3.6 | 6.9 |
| 4 | 28 | 6.5 | −4 | 84.1 | 12.7 | 2.2 |
| 5 | 22 | 5.5 | −7 | 87.2 | 4.2 | 8.6 |
| 6 | 28 | 5.5 | −7 | 85.6 | 5.3 | 9.1 |
| 7 | 22 | 6.5 | −7 | 89.3 | 2.2 | 8.5 |
| 8 | 28 | 6.5 | −7 | 86.7 | 5.6 | 7.7 |
| 9 | 20 | 6 | −5.5 | 85.5 | 4.3 | 9.2 |
| 10 | 30 | 6 | −5.5 | 82.8 | 10.1 | 7.1 |
| 11 | 25 | 5 | −5.5 | 86.8 | 5.7 | 8.5 |
| 12 | 25 | 7 | −5.5 | 90.3 | 5.1 | 4.6 |
| 13 | 25 | 6 | −3 | 87.3 | 6.5 | 6.2 |
| 14 | 25 | 6 | −8 | 90.2 | 2.1 | 7.7 |
| 15 | 25 | 6 | −5.5 | 94.6 | 2.4 | 3 |
| 16 | 25 | 6 | −5.5 | 93.4 | 3.9 | 2.6 |
| 17 | 25 | 6 | −5.5 | 92.5 | 5.2 | 2.3 |
| 18 | 25 | 6 | −5.5 | 92.8 | 5 | 3.2 |
| 19 | 25 | 6 | −5.5 | 92.9 | 4.1 | 3 |
| 20 | 25 | 6 | −5.5 | 93.6 | 3.6 | 2.8 |
| Indicator | Std. Dev. | Mean | C.V.% | R2 | Adjusted R2 | Predicted R2 | Adeq Precision |
|---|---|---|---|---|---|---|---|
| Seed spacing pass rate | 0.8933 | 88.84 | 1.01 | 0.9685 | 0.9401 | 0.8288 | 18.2962 |
| Multiple-seed rate | 0.9920 | 5.44 | 18.25 | 0.9375 | 0.8812 | 0.7269 | 14.3484 |
| Seed missing rate | 0.7633 | 5.81 | 13.13 | 0.9544 | 0.9133 | 0.6780 | 11.9932 |
| Source | Sum of Squares | df | F-Value | p-Value |
|---|---|---|---|---|
| Model | 245.11 | 9 | 34.13 | <0.0001 |
| X1-Speed | 27.96 | 1 | 35.03 | 0.0001 |
| X2-Suction hole diameter | 8.68 | 1 | 10.87 | 0.0080 |
| X3-Negative pressure | 5.02 | 1 | 6.29 | 0.0311 |
| X1X2 | 0.1250 | 1 | 0.1566 | 0.7006 |
| X1X3 | 5.44 | 1 | 6.82 | 0.0259 |
| X2X3 | 0.2450 | 1 | 0.3070 | 0.5917 |
| X12 | 150.86 | 1 | 189.03 | <0.0001 |
| X22 | 40.66 | 1 | 50.95 | <0.0001 |
| X32 | 37.31 | 1 | 46.75 | <0.0001 |
| Residual | 7.98 | 10 | ||
| Lack of Fit | 5.14 | 5 | 1.81 | 0.2653 |
| Pure Error | 2.84 | 5 | ||
| Cor Total | 253.09 | 19 |
| Source | Sum of Squares | df | F-Value | p-Value |
|---|---|---|---|---|
| Model | 147.60 | 9 | 16.67 | <0.0001 |
| X1-Speed | 62.67 | 1 | 63.68 | <0.0001 |
| X2-Suction hole diameter | 0.9016 | 1 | 0.9162 | 0.3610 |
| X3-Negative pressure | 40.44 | 1 | 41.09 | <0.0001 |
| X1X2 | 3.78 | 1 | 3.84 | 0.0784 |
| X1X3 | 13.78 | 1 | 14.00 | 0.0038 |
| X2X3 | 0.1012 | 1 | 0.1029 | 0.7550 |
| X12 | 22.43 | 1 | 22.80 | 0.0008 |
| X22 | 5.39 | 1 | 5.47 | 0.0414 |
| X32 | 0.7128 | 1 | 0.7243 | 0.4146 |
| Residual | 9.84 | 10 | ||
| Lack of Fit | 4.67 | 5 | 0.9022 | 0.5436 |
| Pure Error | 5.17 | 5 | ||
| Cor Total | 157.45 | 19 |
| Source | Sum of Squares | df | F-Value | p-Value |
|---|---|---|---|---|
| Model | 121.90 | 9 | 23.25 | <0.0001 |
| X1-Speed | 8.91 | 1 | 15.30 | 0.0029 |
| X2-Suction hole diameter | 10.65 | 1 | 18.28 | 0.0016 |
| X3-Negative pressure | 14.81 | 1 | 25.43 | 0.0005 |
| X1X2 | 1.53 | 1 | 2.63 | 0.1360 |
| X1X3 | 5.95 | 1 | 10.22 | 0.0096 |
| X2X3 | 0.7813 | 1 | 1.34 | 0.2738 |
| X12 | 45.98 | 1 | 78.93 | <0.0001 |
| X22 | 21.47 | 1 | 36.85 | 0.0001 |
| X32 | 26.73 | 1 | 45.89 | <0.0001 |
| Residual | 5.83 | 10 | ||
| Lack of Fit | 5.30 | 5 | 10.03 | 0.0522 |
| Pure Error | 0.5283 | 5 | ||
| Cor Total | 121.90 | 9 | 23.25 | <0.0001 |
| Programmes | Seed Spacing Pass Rate/% | Multiple-Seed Rate/% | Seed Missing Rate/% | Seed-Clearing Rate/% |
|---|---|---|---|---|
| Test 1 | 91.4 | 4.55 | 4.05 | 100 |
| Test 2 | 90.1 | 5.59 | 4.31 | 100 |
| Test 3 | 91.7 | 5.27 | 3.03 | 100 |
| Confidence interval | 91.0667 ± 2.111 | 5.1367 ± 1.323 | 3.7967 ± 1.681 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, D.; Chang, X.; Liu, B.; Yang, Y.; Li, M.; Wang, D.; Gao, Z. Study on the Design and Performance of a Seed Discharger for Peanut Plot Breeding Based on the CFD-DEM Method. Agriculture 2025, 15, 276. https://doi.org/10.3390/agriculture15030276
Ren D, Chang X, Liu B, Yang Y, Li M, Wang D, Gao Z. Study on the Design and Performance of a Seed Discharger for Peanut Plot Breeding Based on the CFD-DEM Method. Agriculture. 2025; 15(3):276. https://doi.org/10.3390/agriculture15030276
Chicago/Turabian StyleRen, Degang, Xueliang Chang, Bing Liu, Yangyang Yang, Mengzhu Li, Dongwei Wang, and Zenghui Gao. 2025. "Study on the Design and Performance of a Seed Discharger for Peanut Plot Breeding Based on the CFD-DEM Method" Agriculture 15, no. 3: 276. https://doi.org/10.3390/agriculture15030276
APA StyleRen, D., Chang, X., Liu, B., Yang, Y., Li, M., Wang, D., & Gao, Z. (2025). Study on the Design and Performance of a Seed Discharger for Peanut Plot Breeding Based on the CFD-DEM Method. Agriculture, 15(3), 276. https://doi.org/10.3390/agriculture15030276






