Assessing Reference Evapotranspiration Estimation Considering Irrigation Scheduling Intervals

Abstract

Accurate estimation of reference evapotranspiration (ET_o) is essential for irrigation planning in semi-arid Mediterranean regions. This study evaluated temperature-based and neural network models for estimating daily ET_o and its accumulated values over multiple timescales, using data from two lysimeter stations in Albacete and Badajoz, Spain. Model performance was assessed against the FAO56 PM equation and against lysimeter measurements to quantify the joint effect of benchmark choice and temporal aggregation. Under FAO56 PM benchmarking, RRMSE for temperature-based models in Albacete decreased from about 0.18 for daily ET_o to around 0.08 for monthly accumulated ET_o, while complex models achieved daily RRMSE near 0.06–0.07, and all models exhibited RRMSE below 0.08 at monthly and longer scales. When lysimeter ET_o was used as the benchmark, errors increased and became more variable in winter, with daily RRMSE often exceeding 0.22, indicating reduced lysimeter reliability under cold, calm conditions. Overall, extending the estimation interval from daily to multi-day periods markedly reduced errors and narrowed differences among models. These results show that, in the semi-arid Mediterranean environments studied, temperature-based models can provide operationally reliable estimates at irrigation-relevant timescales, while FAO56 PM offers a more robust primary benchmark than lysimeter measurements for winter irrigation planning.

1. Introduction

Accurate estimation of crop water requirements is crucial for the design and management of irrigation systems. When considering soil water balance, crop water requirements primarily depend on estimating crop evapotranspiration (ET_c). A widely adopted and straightforward method for estimating ET_c, initially proposed by [1], consists of multiplying a crop-specific coefficient (K_c), which accounts for the specific physiological and morphological traits, by the reference evapotranspiration (ET_o) for a grass surface [2]. ET_o represents the atmospheric demand for water by integrating soil evaporation and plant transpiration from a standardised reference surface. The FAO Penman–Monteith method (FAO56 PM) defines this reference surface as a hypothetical grass crop with specific characteristics, including a height of 0.12 m, a surface albedo of 0.23, and a constant surface resistance of 70 s m⁻¹ under standard conditions [2].

The FAO56 PM equation, regarded as the standard method for estimating ET_o, requires multiple meteorological inputs, including maximum and minimum air temperatures (T_max and T_min), solar radiation (R_s), air humidity, and wind speed (u₂). However, due to the frequent scarcity or unreliability of weather data in some regions, different simplified methods with reduced input requirements have been proposed. One of these variants is the temperature-based model proposed by the FAO, hereafter referred to as PMT, which relies primarily on temperature data, often the most recorded and, in many datasets, the only available variables [3]. Another widely used temperature-based model is the Hargreaves–Samani (HS) equation [4]. This method has become popular because of its simplicity and minimal data requirements. In this sense, the development of temperature-based methods for estimating ET_o is supported by several reasons. On the one hand, temperature, along with Rs, accounts for most of the variability in ET_o [5], and the daily temperature range can indirectly reflect other climatic factors such as humidity, cloud cover, and advection-related processes [6,7,8]. Moreover, temperature is the most widely monitored and easily measured meteorological variable, often recorded even in areas lacking complete weather datasets [9]. As a result, numerous simplified models using only temperature inputs have been proposed across diverse climates [10]. While many of these models aim to reproduce the results of the FAO56 PM method, they often lack its physical foundations [11]. For this reason, FAO recommends estimating any missing inputs and preserving the original formulation to maintain the integrity of the physical relationships between variables, an approach that is sometimes overlooked in practice [11].

Several studies have shown that both PMT and HS equations can provide accurate ET_o estimates, with relatively low errors when compared to the FAO56 PM reference method, e.g., [3,10,12,13]. Although these alternatives improve applicability in data-limited contexts, they often require local calibration or methodological adjustments to achieve acceptable accuracy [14,15]. Calibration procedures often rely on FAO56 PM estimates, typically involving the adjustment of a single average calibration coefficient per site. One of the main limitations of these calibrated models is their lack of transferability, as the calibration remains site-specific and cannot be applied to locations without prior local parameterisation. In most cases, the HS parameters are calibrated using the entire dataset from a given station, or even from a group of stations, resulting in a single set of factors per location. In contrast, only a limited number of studies have explored the monthly calibration of HS parameters, generally focusing on deriving monthly coefficients rather than examining the monthly performance of both calibrated and non-calibrated equations to determine whether seasonal trends justify such calibration [16]. Using a single correction factor for an entire station may not adequately address systematic biases occurring at shorter temporal scales. Therefore, applying a month-specific coefficient enables the model to capture seasonal variability more effectively, improving the accuracy of ET_o estimates and, consequently, crop irrigation requirements.

Alongside these empirical methods, data-driven techniques, particularly machine learning (ML) models, have become valuable alternatives for ET_o estimation when input data are limited. Among these, artificial neural networks (ANN) [17], support vector machines (SVM) [18,19], gene expression programming (GEP) [20,21], and random forest (RF) [22,23], among others, have been recognised for their efficiency in ET_o prediction using minimal input variables. Despite their strong predictive abilities, these methods do not inherently incorporate the physical principles underlying the FAO56 PM framework [11]. These models are trained with site-specific datasets, and their estimation accuracy typically decreases outside the training context, although it remains higher than that of temperature-based models. To simulate actual prediction conditions with limited or even absent climatic records, some studies assessed the generalisation ability of ML models using spatial k-fold validation, i.e., reserving the complete data set of a different independent station in each iteration for testing the models, e.g., [20]. Moreover, previously to model training, preliminary techniques such as clustering stations with similar climatic characteristics may help to enhance the transferability of models across regions [24].

Another experimental method to determine ET is the use of weighing lysimeters, which estimate water loss based on the components of the soil water balance within a controlled cultivation system [25]. In cases where the crop grown on the lysimeter surface meets the standard reference conditions, the recorded evapotranspiration can be regarded as ET_o [26]. However, despite their potential to provide highly accurate short-term ET_o measurements, both lysimeters and other advanced experimental tools, such as eddy covariance flux towers, present several limitations. These include high costs, complex installation and maintenance, the need for sufficient fetch, and intensive data processing requirements [27]. Moreover, the limited spatial extent of typical meteorological station plots may hinder these instruments from capturing representative surface conditions [28]. As a result, direct ET_o measurements are rarely available and/or fully reliable. In this context, some studies have assessed the calibration and/or validation of empirical and/or ML models against lysimeter-derived ET_o values instead of the FAO56 PM reference method, e.g., [16,29]. However, it is important to note that if the lysimeter system does not maintain the FAO standard reference crop conditions, this may lead to biased conclusions regarding model performance.

As evidenced in the literature, the calibration and validation of ET_o methods, such as empirical equations and ML models, have been extensively studied. However, most studies focus on achieving high accuracy in daily ET_o estimates, based on the premise that precise daily irrigation doses are necessary. Nonetheless, considering that the soil can act as a buffer for water availability, it may be more realistic to require accurate estimations only for accumulated ET values over extended periods, such as a week, a common timeframe used for scheduling and adjusting irrigation practices. Some studies have assessed the reliability of ET_o estimates over extended periods. For instance, although the HS equation has shown reasonable accuracy daily, Hargreaves et al. [30] noted that its performance improves when applied to 5-day or longer intervals. This is because short-term estimates tend to exhibit greater variability due to factors such as shifting weather fronts and fluctuations in wind speed and cloud cover. However, these results referred to averaged ET_o values, not to cumulated ones.

This paper has two main objectives. First, it evaluates the implications of using grass-reference lysimeter observations as benchmarks for assessing ET_o models, compared with the recommended practice of using FAO56 PM as the target. Second, it analyses the practical implications of daily ET_o model accuracy for irrigation scheduling by comparing the performance of different ET_o modelling approaches when evaluated on both daily and accumulated ET_o values at trial, weekly, fortnightly, monthly, and annual intervals. Daily and accumulated ET_o estimates were calculated for all models and timescales, using FAO56 PM estimates and lysimeter measurements as target values, to assess how discrepancies in daily ET_o propagate over time and may affect irrigation decision making at different intervals.

2. Materials and Methods

2.1. Data Set

This study used climate records collected from two lysimetric facilities in Spain: Las Tiesas, near Albacete in the Castilla-La Mancha region (39°03′ N, 2°05′ W; 695 m above sea level), and La Orden, near Badajoz in the Extremadura region of southwestern Spain (38°51′ N, 6°40′ W; 198 m above sea level) (Figure 1). For Las Tiesas, the data cover the period 2007 to 2015, excluding 2010, while for La Orden, it spans from January 2007 to December 2016, excluding 2013. Variables recorded include T_max, mean air temperature (T_mean), and T_min, u₂, maximum (RH_max) and minimum (RH_min) relative humidity, R_s, and ET_o. The study period was characterised by typical climatic conditions, without abrupt deviations or anomalies. Las Tiesas is located on the Eastern Mancha plateau and is subject to a semi-arid continental climate, characterised by pronounced seasonal variation, with mean temperatures ranging from 4.6 °C in January to 24.1 °C in July and an average annual precipitation of 314 mm. Conversely, La Orden experiences a Mediterranean climate with Atlantic influence, with milder winters and warmer summers, average temperatures of 9 °C in January and 26 °C in July, and an average annual rainfall of approximately 525 mm. According to the Köppen climate classification, Las Tiesas is cold semi-arid (BSk), whereas La Orden has a hot-summer Mediterranean climate (Csa). Thus, although both stations are located in Mediterranean-type semi-arid environments, they exhibit contrasting climatic regimes in terms of thermal and pluviometric conditions. Both stations meet the criteria for reference sites. Data quality control procedures were used to identify and remove outliers. Additional climatic information is available in [29].

2.1.1. ‘Las Tiesas’ Agricultural Research Facility

‘Las Tiesas’ research facility is representative of the 110,000 ha of irrigated farmland that characterises the Eastern Mancha area. Climate data were collected by an agrometeorological station installed within a 1.6 ha plot of tall fescue (Festuca arundinacea Schreb., cv. “Galatea”). Air temperature at 2 m was measured with a platinum resistance thermometer (sensor Pt 100 Ω, model MP100, Campbell Scientific, Logan, UT, USA), and relative humidity at 2 m with a Rotronic hygrometer (model C-80, Rotronic AG, Bassersdorf, Switzerland). Wind speed at 2 m was recorded with a cup anemometer (Switching Anemometer, model A100R, Vector Instruments Ltd., Rhyl, North Wales, UK). Net radiation (R_n) was obtained as the difference between net shortwave and net longwave radiation. Incoming and reflected shortwave radiation were measured with two pyranometers (model CM14, Kipp & Zonen B.V., Delft, The Netherlands), and longwave radiation with a pyrgeometer (model CG2, Kipp & Zonen B.V., Delft, The Netherlands). All sensors were connected to a CR10X datalogger (Campbell Scientific, Logan, UT, USA), which sampled at intervals shorter than 10 s. These high-frequency readings were subsequently averaged to derive hourly and daily climatic variables. Further details regarding the sensors and their specifications are available in [29].

A large precision weighing lysimeter was installed within the same grass reference plot, approximately 4 m from the agrometeorological station. The grass canopy was actively growing, uniformly maintained at 0.10–0.15 m, and ensured complete ground coverage. To preserve conditions close to the FAO reference standard [2,31], the plot was regularly irrigated using a fully underground 15 × 12.5 m sprinkler system that operated overnight to avoid peak evaporative demand. Frequent mowing and consistent irrigation ensured that the soil remained near field capacity and that the vegetation was kept in optimal condition. The lysimeter tank, with dimensions of 2.3 × 2.7 × 1.7 m (6.21 m² surface area) and weighing approximately 14.5 t, was embedded within this reference surface and managed under the same agronomic conditions as the surrounding plot to ensure representativeness. The weighing system was based on a set of beams and counterweights designed to balance the static load of the soil-filled tank, reducing the force applied to the weighing beam at a ratio of 1000:1. This force was transmitted to a steel load cell connected to a datalogger. The system was regularly calibrated with known weights, and the combined resolution of the load cell and logger allowed for the detection of mass variations as small as 0.250 kg, equivalent to 0.04 mm of water. The system recorded weight data every 15 min, based on measurements taken every second. Further technical details on the lysimeter design and operation are provided in [26,29]. Variations in lysimeter mass were used to determine ET_o. Irrigation periods were scheduled exclusively during nighttime hours and were excluded from the hourly ET_o calculations. Daily verification of lysimeter data was performed to detect and correct any potential anomalies. Data gaps were associated with rainfall events, instrument calibration and maintenance procedures, or soil disturbance within the lysimeter tank. Any records affected by such incidents were discarded and excluded from the analysis. Furthermore, quality assurance and quality control (QA/QC) protocols for lysimetric ET_o measurements were implemented following the guidelines proposed by [27,32].

2.1.2. ‘La Orden’ Agricultural Research Facility

‘La Orden’ agricultural research site is situated within the central area of the irrigated agrarian zone known as Vegas Bajas del Guadiana, which spans approximately 35,000 ha across 15 km of the lower Guadiana River basin. Data were collected from a 1.3 ha plot uniformly covered with grass (Festuca arundinacea Moench) and surrounded by other irrigated crops. Throughout the measurement period, the grass was regularly irrigated and mowed to preserve conditions similar to those of the standard reference crop. As a result, the soil was maintained close to field capacity, and the grass canopy was kept at a height between 0.10 and 0.15 m. Climate variables were monitored using an automated weather station positioned above the grass surface. Air temperature and relative humidity at 1.40 m were measured with a combined probe (sensor model HMP60, Campbell Scientific, Logan, UT, USA), and wind speed at 2 m with an anemometer (model 05103, Young, Traverse City, MI, USA). R_s at 1.70 m was measured directly with a CMP3 pyranometer (Kipp & Zonen, B.V., Delft, The Netherlands) [30]. High-frequency measurements were recorded by a CR10X datalogger (Campbell Scientific, Logan, UT, USA), and hourly mean values were obtained by averaging these records. R_n was estimated from measured Rs and meteorological variables using the FAO-56 radiation equations [2]. Further technical details regarding the sensors and instrumentation are provided in [29].

The weighing lysimeter, installed 10 m from the weather station, had tank dimensions of 2.67 × 2.25 × 1.5 m (surface area of 6 m²), as described by [33]. The tank was supported by a balance mechanism equipped with a counterweight system designed to compensate for its weight. This assembly was connected to a load cell with a nominal capacity of 10 kg and a sensitivity of 2 mV V⁻¹. Regular calibration using known weights was performed to ensure measurement accuracy. The combined sensitivity of the load cell and datalogger enabled detection of mass variations as small as 0.20 kg, equivalent to 0.033 mm of water. The sampling interval was 0.05 s, and average weight values were recorded every 5 min. Hourly ET_o rates were computed from successive weight changes in the lysimeter, and daily values were obtained by summing the hourly estimates. As with the ‘Las Tiesas’ facility, irrigation was performed exclusively at night, and any measurements corresponding to irrigation periods were excluded from the analysis. Only days without disturbances, such as irrigation, rainfall, mowing, or equipment malfunction, were included in the final dataset. QA/QC procedures for lysimetric ET_o measurements were also implemented.

2.2. Models Assessed and Input Combinations

Two input combinations with relevant differences in their estimation accuracy of daily ET_o values were assessed to evaluate eventual changes in their estimation accuracy for cumulated ET_o values, considering different intervals. Therefore, two widely used methods for estimating ET_o relying on a few input variables were evaluated: the HS equation [4] and the PMT version applied with missing data [2]. On the other hand, two feedforward neural networks with backpropagation were implemented, each using a different combination of climatic variables, namely: (i) T_max, T_min, and R_a (ANN3), i.e., relying on the same inputs as the HS and PMT equations; and (ii) T_max, T_min, RH_max, RH_min, u₂, and R_s (ANN6), i.e., relying on the complete set of inputs required by the FAO56 PM reference method. R_a was calculated according to [2] based on the site’s latitude. All models were applied at a daily time step. Daily climatic variables were derived from the subhourly observations recorded at each station.

2.2.1. Hargreaves-Samani Equation

As described by Hargreaves et al. [4], ET_o can be estimated using the following equation:

$${\mathrm{E}\mathrm{T}}_{\mathrm{o}}^{\mathrm{H}\mathrm{S}}=\mathrm{A}\mathrm{H}\mathrm{C}\cdot {\mathrm{R}}_{\mathrm{a}}\cdot \left({\mathrm{T}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}+17.8\right)\cdot \sqrt{\Delta \mathrm{T}}$$

(1)

where ET_o^HS represents the estimated reference evapotranspiration (mm day⁻¹); R_a is the extraterrestrial radiation (MJ m⁻² day⁻¹); T_mean is the mean daily air temperature (°C); ΔT is the daily temperature range (°C); and AHC is the adjusted Hargreaves coefficient. The latter is calculated as 0.0135 k_Rs/λ, where 0.0135 is a factor for conversion of units from the American to the International System; k_Rs is an empirical radiation adjustment coefficient (°C^−0.5); λ is the latent heat of vaporisation (2.45 MJ kg⁻¹). Equation (1) was developed based on the estimation of the R_s, rather than on its direct measurement, using the following approach:

$${\mathrm{R}}_{\mathrm{s}}={\mathrm{k}}_{\mathrm{R}\mathrm{s}}\cdot {\mathrm{R}}_{\mathrm{a}}\cdot \sqrt{\Delta \mathrm{T}}$$

(2)

An AHC equal to 0.0023 was proposed as a general reference value [2,4]. Further details on the development of the HS equation can be found in [30].

2.2.2. Temperature-Based FAO56 PM Equation for Estimating Missing Data (PMT)

Allen et al. [2] developed a methodology that enables the application of the FAO56 PM equation even when relative humidity, psychrometric observations and solar radiation inputs are unavailable. This approach estimates the dew point temperature (T_dew) from either T_min or T_mean and derives R_s based on ΔT. Vapour pressure deficit (VPD) is calculated by subtracting the actual vapour pressure (e_a) from the saturation vapour pressure (e_s), which is typically estimated as the average of the saturation pressures at T_max and T_min. The value of e_a can be estimated based on the mean relative humidity (RH_mean) using the following expression:

$${\mathrm{e}}_{\mathrm{a}}={\mathrm{e}}_{\mathrm{s}}\cdot {\displaystyle \frac{{\mathrm{RH}}_{\mathrm{mean}}}{100}}$$

(3)

In the absence of RH_mean data, e_a can be estimated by approximating T_dew to T_min, as recommended in [2], using the following expression:

$${\mathrm{e}}_{\mathrm{a}}={\mathrm{e}}^{\mathrm{o}}\left({\mathrm{T}}_{\min }\right)=0.611\cdot \exp \left({\displaystyle \frac{17.27\cdot {\mathrm{T}}_{\min }}{{\mathrm{T}}_{\min }+237.3}}\right)$$

(4)

2.2.3. ANN Models

This study considers feedforward neural networks trained by backpropagation, a widely applied configuration, commonly known as multilayer perceptrons. Neurons were configured according to [34]. Architectures with a single hidden layer and a variable number of neurons (1–25) were considered. The hyperbolic tangent sigmoid activation function was applied in the hidden layer, and a linear transfer function was used in the output layer. The networks were implemented in MATLAB (2025 release; MathWorks, Natick, MA, USA) and trained using the Levenberg–Marquardt algorithm with early stopping based on a validation subset comprising 30% of the training data. Mean square error (MSE) was used as the performance function. The main training parameters were kept constant for all ANN configurations. They were set as follows: maximum number of epochs 1000, performance goal 0, maximum validation failures 10, minimum performance gradient 1 × 10⁻⁶, initial μ (mu) 0.001, μ decrease factor 0.1, μ increase factor 10, maximum μ 1 × 10¹⁰, and no time limit on training.

The application of ANN models requires defining a data partition, i.e., the training, cross-validation, and test sets. Rather than adopting a conventional hold-out strategy, which may lead to partial conclusions due to the limited representativeness of a single train-test configuration, e.g., [20], an annual k-fold validation approach was implemented for ANN3 and ANN6. This methodology involved subsequent data partitioning, reserving each time a different year for testing, while the remaining years were used for training. This resulted in an 8-fold validation for Las Tiesas (Albacete) and a 9-fold validation for La Orden (Badajoz), requiring 8 and 9 train–test cycles, respectively, to systematically evaluate model performance across all available yearly data patterns. Such a temporally structured validation approach ensures a robust model assessment. Although more complex methods, such as bootstrap or leave-one-out cross-validation, the annual-fold validation used here provides a computationally efficient and temporally consistent alternative [29]. To further ensure robustness, each network configuration was trained 50 times with different random initialisations of weights, thereby mitigating the influence of random factors and enabling a reliable assessment of model performance variability.

2.3. Calibration Strategies

2.3.1. HS and PMT Equations

The application of the HS equation should be limited to the climatic conditions for which it has been locally calibrated, as recommended in [35]. In this context, the performance of both the original and calibrated versions of the HS equation has been extensively evaluated across a variety of climatic settings. However, providing a comprehensive review of those studies lies beyond the scope of this work. In contrast, the calibration of the PMT equation is less frequently performed, particularly when certain input variables are estimated rather than measured [16]. Nonetheless, in this study, PMT outputs were also calibrated to enable a more balanced comparison with the calibrated HS estimates.

In this study, calibration was performed by applying a linear correction that adjusted only the slope coefficient. For each station, monthly calibration was conducted by comparing the original ET_o estimates with the benchmark ET_o, as described in the following section. Specifically, the daily ratio of the estimated to benchmark ETo values was calculated to determine the slope adjustment for each month. The monthly average of these ratios was then computed to obtain a single calibration coefficient for each month and station. These monthly coefficients were subsequently applied to the original ET_o estimates, resulting in calibrated values that more accurately reflected the seasonal variability. These calibrated versions are hereafter referred to as HS_cal and PMT_cal, respectively. Unlike the more common approach in the literature, which applies a single calibration factor per station, the use of monthly coefficients in this work allows for a more accurate correction of seasonal biases in ET_o estimation [16]. Notably, only the ET_o equations themselves were calibrated in this study, while no calibration was applied to any of their input variables, such as R_s or RH_mean. This choice was based on several considerations. First, when certain inputs are unavailable and must be estimated using auxiliary empirical equations, the lack of observed data makes it unfeasible to calibrate parameters such as k_Rs. Second, consistent with this, the term non-calibrated, as used for the HS and PM equations in this study, refers to cases in which neither the ET_o equations nor the equations used to estimate missing inputs were adjusted. Third, calibrating input variables before calibrating the ET_o equation itself could affect the resulting parameter values of the ET_o models, potentially introducing inconsistencies. To ensure a fair comparison between calibrated and non-calibrated ET_o estimates, including the ANN models, as well as to assess their impact on irrigation water requirements, all calibrations in this study were strictly based on ET_o reference values, without any prior modification of input variables.

The entire dataset was used for both HS and PMT calibration and evaluation purposes. The development of calibration constants with generalisation capability lies beyond the scope of this study. So, it was not deemed necessary to divide the data into separate calibration and validation subsets for these equations. The use of independent test datasets is particularly relevant in the calibration of parametric models, where the resulting equations for the calibration constants should ideally be evaluated on data not involved in their estimation, or more complex approaches such as ANNs. Furthermore, previous studies (e.g., [36]) have noted that although local k-fold validation may provide a more robust evaluation of calibrated estimates, the performance differences are generally minimal when a sufficiently long time series is available. This effect becomes even less significant when the evaluation period is short (e.g., on a monthly basis).

2.3.2. Monthly ANN3 Models

In parallel with the calibration procedure applied to the HS and PMT equations, the ANN3 models were also assessed on a monthly basis, thus allowing a consistent comparison across approaches. For each station, the available dataset was split by month and year, and a specific ANN3 model was trained and tested independently for each monthly subset using a k-fold validation approach in which each year within a given month served once as the test set. This was translated into 96 ANN3 models (12 × 8) in Badajoz and into 108 ANN3 models (12 × 9) in Albacete. The training process followed the same structure described in previous sections, with a single hidden layer, a variable number of neurons (1–25), and 50 repetitions per architecture to select the best-performing model based on the lowest RRMSE. This monthly training approach enabled the identification of optimal ANN configurations for each month and year, thereby enhancing the models’ capacity to capture intra-annual ET_o variability. The resulting predictions from the best ANN3 models per month and station (hereafter referred to as ANN3_month) were then used to evaluate their performance against reference values, following the same criteria as for the HS and PMT equations.

2.4. Accumulated ET_o Estimation and Assessment

In order to evaluate the practical implications of ET_o estimation bearing in mind usual irrigation scheduling intervals, the accumulated values of ET_o were calculated for each model, both calibrated and non-calibrated, as well as for lysimeter-based measurements and the reference FAO56 PM equation. The accumulated ET_o was computed over five different time intervals: year, month, fortnight, week, and trial. These aggregation levels were selected to represent the potential decision-making periods used in irrigation planning and scheduling, ranging from broad estimations of total crop water consumption (annual) [37], and seasonal evaluations (monthly) [38], to more frequent operational intervals (fortnightly, weekly) [39], and even site-specific intensive intervals (trial-based) [40].

By integrating ET_o values over these periods, it was possible to examine the extent to which model calibration, input selection, and estimation method influence cumulative water demand estimations. This step is particularly relevant for quantifying the effect of model choice on irrigation scheduling accuracy, ensuring that comparisons between approaches are not limited to daily performance but extended to the time scales most relevant to agricultural water management. The accumulated ET_o for a given time interval and model was calculated as the sum of the daily ET_o values within that period. To ensure consistency and comparability across models, the same number of days with available data was used for all models within each time interval. This procedure was uniformly applied across all methods and time scales, enabling a fair assessment of cumulative estimates.

2.5. Benchmarking

The FAO56 PM equation was adopted as the reference method for model calibration and evaluation, given its widespread recommendation as the standard approach for estimating ET_o and validating empirical methods in the absence of direct measurements [2]. This equation is an adaptation of the original Penman-Monteith formulation for a standardised reference crop, clipped grass, 0.12 m in height, under fixed values of surface resistance, aerodynamic resistance, and albedo, as well as constant air density and latent heat of vaporisation [41]. The daily ET_o, expressed in mm day⁻¹, is computed as follows:

$$\mathrm{E}{\mathrm{T}}_{\mathrm{o}}^{\mathrm{P}\mathrm{M}}={\displaystyle \frac{0.408 \Delta \left({\mathrm{R}}_{\mathrm{n}}-\mathrm{G}\right)+\mathrm{\gamma }\frac{900}{{\mathrm{T}}_{\mathrm{mean}}+273}{\mathrm{u}}_2\left({\mathrm{e}}_{\mathrm{s}}-{\mathrm{e}}_{\mathrm{a}}\right)}{\Delta +\mathrm{\gamma }\left(1+0.34 {\mathrm{u}}_2\right)}}$$

(5)

where R_n is the net radiation at the crop surface (MJ m⁻² day⁻¹); G is the soil heat flux density (MJ m⁻² day⁻¹); T_mean is the mean daily air temperature at 2 m height (°C); γ is the psychrometric constant (kPa °C⁻¹); Δ is the slope of vapor pressure curve (kPa °C⁻¹); e_s is the saturation vapor pressure (kPa); e_a is the actual vapor pressure (kPa); and u₂ is the wind speed at 2 m height (m s⁻¹). For the daily time step considered in this study, soil heat flux was assumed to be negligible and therefore set to zero (G ≈ 0) in all FAO56 PM calculations, and all required parameters were computed using the equations proposed in FAO-56 guidelines [2].

To assess the effect of the benchmarks, all model results were compared with both lysimeter data and the reference FAO56 PM estimations. The FAO56 PM, widely recognised as the standard method for estimating ET_o, served as the primary reference for calibration and validation, according to [2], while lysimeter-based ET_o values were evaluated as an alternative baseline for model assessment and irrigation water requirement estimation. Thus, both FAO56 PM ET_o values and lysimeter measurements were used as targets for model training and testing.

Finally, a seasonal breakdown of the results was conducted to identify potential patterns across different seasons, given that ET_o values exhibit substantial fluctuations between winter and summer. This analysis aimed to determine whether model performance and calibration accuracy varied across seasons.

2.6. Performance Assessment

Several error metrics were computed to evaluate the predictive accuracy of the methods under study, following the approach described in [42]. Specifically, the mean absolute error (MAE), mean bias error (MBE), and relative root mean squared error (RRMSE) were calculated as expressed in Equations (6)–(8). In these expressions, x_i denotes the observed ET_o value and the predicted counterpart, while n represents the total number of observations within the ET_o dataset. The RRMSE is a dimensionless indicator, whereas MAE and MBE are expressed in units of mm per unit of time interval (e.g., mm day⁻¹).

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|x_i-\widehat{x_i}\right|$$

(6)

$$\mathrm{MBE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(\widehat{x_i}-x_i\right)$$

(7)

$$\mathrm{RRMSE}={\displaystyle \frac{1}{\overline{x}}}\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(x_i-\widehat{x_i}\right)}^2}$$

(8)

Additionally, the coefficient of determination (R²) was computed to evaluate the degree of correlation between observed and predicted ET_o values, based on the ratio of their respective standard deviations.

$${\mathrm{R}}^2={\left({\displaystyle \frac{\mathrm{c}\mathrm{o}\mathrm{v}\left({\mathrm{x}}_{\mathrm{i}},\widehat{{\mathrm{x}}_{\mathrm{i}}}\right)}{{\mathsf{\sigma }}_{{\mathrm{x}}_{\mathrm{i}}}\cdot {\mathsf{\sigma }}_{\widehat{{\mathrm{x}}_{\mathrm{i}}}}}}\right)}^2$$

(9)

The error metrics described were computed for both Albacete and Badajoz stations, considering daily and accumulated periods of ET_o estimates derived from the HS and PMT equations and the ANN models, in both calibrated and non-calibrated forms. In all cases, the reference values used for comparison corresponded to the benchmarks defined in the previous section.

3. Results

3.1. Model Performance Assessment Against FAO56 PM Targets

Table 1. Average performance indicators (MAE, RRMSE, MBE, R²) of calibrated and non-calibrated HS, PMT, and ANN models for estimating daily and accumulated reference evapotranspiration at different timescales in Albacete and Badajoz, using FAO56 PM targets.

Tested Model	Accumulated Timescale	Las Tiesas (Albacete)				La Orden (Badajoz)
		MAE (mm)	RRMSE (-)	MBE (mm)	R2 (-)	MAE (mm)	RRMSE (-)	MBE (mm)	R2 (-)
HS	Year	18.454	0.025	1.683	0.978	65.246	0.070	38.190	0.821
	Month	4.812	0.076	0.145	0.990	7.284	0.093	4.092	0.985
	Fortnight	2.957	0.095	0.090	0.984	3.953	0.101	2.034	0.981
	Week	1.767	0.116	0.036	0.976	2.219	0.113	1.011	0.969
	Trial	1.065	0.140	0.017	0.955	1.253	0.132	0.476	0.944
	Daily	0.572	0.179	0.007	0.887	0.608	0.155	0.191	0.849
HS_cal	Year	16.633	0.023	−3.310	0.981	52.459	0.057	2.211	0.828
	Month	3.541	0.060	−0.285	0.994	6.004	0.072	0.237	0.986
	Fortnight	2.620	0.082	−0.130	0.988	3.215	0.083	0.118	0.982
	Week	1.664	0.107	−0.070	0.979	1.934	0.099	0.059	0.972
	Trial	1.026	0.134	−0.034	0.959	1.130	0.123	0.028	0.948
	Daily	0.554	0.174	−0.014	0.892	0.575	0.149	0.011	0.858
PMT	Year	25.676	0.032	−16.231	0.978	63.635	0.066	29.201	0.811
	Month	5.301	0.084	−1.396	0.989	8.203	0.103	3.129	0.981
	Fortnight	3.188	0.099	−0.690	0.984	4.527	0.112	1.555	0.975
	Week	1.870	0.118	−0.345	0.976	2.463	0.126	0.773	0.960
	Trial	1.026	0.134	−0.034	0.959	1.130	0.123	0.028	0.948
	Daily	0.594	0.183	−0.069	0.884	0.666	0.168	0.143	0.817
PMT_cal	Year	16.879	0.024	−3.513	0.981	53.918	0.059	2.009	0.818
	Month	3.663	0.061	−0.302	0.994	6.408	0.077	0.215	0.984
	Fortnight	2.522	0.081	−0.138	0.988	3.423	0.090	0.107	0.979
	Week	1.594	0.104	−0.074	0.980	2.074	0.108	0.053	0.967
	Trial	1.008	0.132	−0.036	0.960	1.212	0.133	0.025	0.939
	Daily	0.559	0.176	−0.015	0.890	0.614	0.159	0.007	0.841
ANN3	Year	18.708	0.023	1.139	0.977	44.465	0.050	0.093	0.869
	Month	4.200	0.069	0.098	0.992	5.759	0.068	0.010	0.988
	Fortnight	2.711	0.085	0.020	0.987	2.865	0.068	0.044	0.988
	Week	1.596	0.104	0.025	0.980	1.772	0.087	0.002	0.978
	Trial	0.976	0.130	0.012	0.961	0.989	0.103	0.001	0.962
	Daily	0.518	0.164	0.005	0.905	0.493	0.126	0.000	0.894
ANN3_month	Year	17.631	0.022	0.272	0.979	39.642	0.046	0.818	0.893
	Month	4.089	0.066	0.023	0.992	5.069	0.060	0.088	0.990
	Fortnight	2.711	0.085	0.020	0.987	2.865	0.068	0.044	0.988
	Week	1.606	0.105	0.006	0.980	1.680	0.082	0.022	0.980
	Trial	0.992	0.133	0.003	0.960	0.943	0.099	0.010	0.965
	Daily	0.526	0.166	0.001	0.902	0.478	0.124	0.004	0.898
ANN6	Year	22.652	0.028	−0.954	0.964	25.528	0.029	−1.209	0.967
	Month	2.690	0.048	−0.082	0.996	3.180	0.042	−0.130	0.995
	Fortnight	1.482	0.052	−0.039	0.995	1.647	0.044	−0.064	0.995
	Week	0.796	0.057	−0.020	0.994	0.859	0.047	−0.032	0.994
	Trial	0.427	0.063	−0.010	0.991	0.431	0.052	−0.015	0.991
	Daily	0.204	0.070	−0.004	0.983	0.188	0.057	−0.006	0.978

presents the global performance indicators of the considered models, divided by timescale, at Albacete and Badajoz, using FAO56 PM estimations as benchmarks. In Albacete, all models showed a gradual decrease in RRMSE as the accumulation interval increased, indicating, as expected, that model accuracy improved when ET_o values were aggregated over longer timescales. For the HS model, RRMSE values ranged from 0.179 for daily ET_o to 0.025 for annual estimates, with 0.140 for trial, 0.116 for weekly, 0.095 for fortnightly, and 0.076 for monthly. The reduction between daily and weekly scales was 6.3%, followed by 4.0% from weekly to monthly, and 5.1% from monthly to annual, resulting in a total absolute decrease of approximately 15.4% across the entire range. The corresponding MAE values ranged from 0.57 mm day⁻¹ to 18.45 mm year⁻¹, with intermediate values of 1.07 mm (trial), 1.77 mm (week), 2.96 mm (fortnight), and 4.81 mm (month). Similarly, the PMT model displayed a very comparable pattern, with RRMSE values of 0.183 (daily), 0.134 (trial), 0.118 (week), 0.099 (fortnight), 0.084 (month), and 0.032 (annual). The decrease was more gradual, amounting to 6.5% from daily to weekly intervals, 3.5% from weekly to monthly intervals, and 5.2% from monthly to annual intervals, for a total reduction of roughly 15.1%. MAE values ranged from 0.59 mm day⁻¹ to 25.68 mm year⁻¹, with intermediate figures of 1.03 mm (trial), 1.87 mm (week), 3.19 mm (fortnight), and 5.30 mm (month). Conversely, the ANN6 model mainly differed in the magnitude of errors, which were substantially smaller across all timescales. RRMSE decreased from 0.070 at the daily scale to 0.063 (trial), 0.057 (week), 0.052 (fortnight), 0.048 (month), and 0.028 (annual). The reduction was therefore 1.3% from daily to weekly, 0.9% from weekly to monthly, and 2.0% from monthly to annual, leading to a total absolute decrease of 4.2%. The corresponding MAE values ranged from 0.20 mm day⁻¹ to 22.65 mm year⁻¹, with intermediate values of 0.43 mm (trial), 0.80 mm (week), 1.48 mm (fortnight), and 2.69 mm (month). Overall, all models showed a consistent pattern of decreasing error as the accumulation interval increased, indicating that daily discrepancies tend to diminish when ET_o is aggregated over multi-day or seasonal periods. Thus, even for the temperature-based models, the relative discrepancy with FAO56 PM becomes significantly smaller at weekly and longer timescales, while ANN6 displays more minor additional improvements with aggregation because its daily agreement with FAO56 PM is already high.

When comparing the models, differences were substantial at the daily scale (RRMSE = 0.179 and 0.183 for HS and PMT, respectively, versus 0.070 for ANN6), indicating that ANN6 achieved higher accuracy on this scale. However, at weekly and fortnightly intervals, the gap between temperature-based and data-driven models narrowed considerably (RRMSE approximately 0.10–0.12 for HS/PMT versus 0.05–0.06 for ANN6). At monthly to yearly scales, the differences became minimal, with all models showing RRMSE ≤ 0.08 and converging to values near 0.03–0.04 at the most extended periods. The calibrated versions of HS and PMT (HS_cal and PMT_cal) displayed the same decreasing trend, with RRMSE values ranging from 0.174 to 0.023 and from 0.176 to 0.024, respectively, across the daily-to-yearly spectrum. ANN3 and ANN3_month produced intermediate results, with RRMSE values ranging from 0.164 to 0.023 and from 0.166 to 0.022, respectively, consistent with the general pattern seen in the other models. Slight differences between calibrated and non-calibrated configurations suggest that variations due to calibration or ANN structure were minor compared to the effect of the accumulation interval. Furthermore, the highest R² values were observed for monthly accumulated ET_o across all models considered. These patterns reveal that model choice has a greater impact when daily ET_o is assessed, whereas differences between models diminish as ET_o is aggregated over weekly or more extended periods. The limited effect of calibration also implies that, under FAO56 PM benchmarking, the primary factor driving performance improvements is the timescale of ET_o aggregation rather than detailed adjustments of model parameters.

In Badajoz, similar results were observed. All models exhibited a steady decline in RRMSE with increasing accumulation intervals, following the same general trend observed in Albacete. For HS, RRMSE values were 0.155 for daily ET_o, 0.132 for trial, 0.113 for weekly, 0.101 for fortnightly, 0.093 for monthly, and 0.070 for annual estimations. The decrease between daily and weekly intervals was 4.2%, 2.0% from weekly to monthly and 2.3% from monthly to annual, amounting to an overall reduction of 8.5%. Corresponding MAE values ranged from 0.61 mm day⁻¹ to 65.25 mm year⁻¹. PMT followed a very similar pattern, with RRMSE values of 0.168 (daily), 0.133 (trial), 0.126 (weekly), 0.112 (fortnight), 0.103 (month), and 0.066 (annual), with an overall absolute reduction of 10.2%. MAE ranged from 0.67 mm day⁻¹ to 63.64 mm year⁻¹. Conversely, ANN6 maintained significantly lower errors, with RRMSE of 0.057 (daily), 0.052 (trial), 0.047 (weekly), 0.044 (fortnight), 0.042 (month), and 0.029 (annual). The reductions were 1.0% from daily to weekly, 0.5% from weekly to monthly, and 1.8% from monthly to annual, totalling 2.8% across the day-to-year spectrum. MAE values ranged from 0.19 mm day⁻¹ to 25.53 mm year⁻¹, with intermediate values of 0.43 mm (trial) and 0.86 mm (week).

Across models, differences remained evident at the daily scale (RRMSE = 0.155 and 0.168 for HS and PMT, respectively, versus 0.057 for ANN6), but, as in Albacete, these differences significantly diminished with increasing accumulation intervals. At weekly and fortnightly scales, RRMSE values were 0.11–0.13 for HS and PMT, compared to 0.05–0.06 for ANN6, while over monthly to annual intervals, all models converged to values below 0.08, with differences less than 0.03. HS_cal and PMT_cal showed nearly identical patterns, with RRMSE values ranging from 0.149 to 0.057 and from 0.159 to 0.059, respectively, across daily to annual scales. Similarly, ANN3 and ANN3_month produced intermediate results (0.126–0.050 and 0.124–0.046), displaying performance trends similar to those observed in Albacete. The fact that these patterns closely mirror those observed in Albacete suggests that the decrease in error with increasing accumulation interval is consistent across the two semi-arid Mediterranean locations analysed.

3.2. Performance of Models Against Lysimeter Targets

Table 2. Average performance indicators (MAE, RRMSE, MBE, R²) of calibrated and non-calibrated HS, PMT, and ANN models for estimating daily and accumulated reference evapotranspiration at different timescales in Albacete and Badajoz, using lysimeter measurements as targets.

Tested Model	Accumulated Timescale	Las Tiesas (Albacete)				La Orden (Badajoz)
		MAE (mm)	RRMSE (-)	MBE (mm)	R2 (-)	MAE (mm)	RRMSE (-)	MBE (mm)	R2 (-)
HS	Year	44.784	0.054	29.508	0.914	58.430	0.070	−46.748	0.879
	Month	6.756	0.115	2.538	0.981	9.808	0.131	−5.009	0.966
	Fortnight	4.060	0.132	1.297	0.974	5.443	0.154	−2.490	0.952
	Week	2.359	0.155	0.629	0.960	3.016	0.174	−1.237	0.930
	Trial	1.354	0.179	0.304	0.933	1.683	0.207	−0.583	0.879
	Daily	0.711	0.221	0.125	0.841	0.860	0.255	−0.234	0.706
HS_cal	Year	36.329	0.045	−6.702	0.921	33.933	0.049	1.620	0.881
	Month	5.257	0.092	−0.577	0.986	7.231	0.106	0.174	0.973
	Fortnight	4.060	0.110	−0.295	0.979	4.374	0.131	0.086	0.961
	Week	2.142	0.140	−0.143	0.965	2.540	0.154	0.043	0.940
	Trial	1.277	0.167	−0.069	0.939	1.506	0.190	0.020	0.892
	Daily	0.701	0.213	−0.028	0.848	0.792	0.243	0.008	0.725
PMT	Year	40.692	0.050	11.594	0.912	66.097	0.078	−55.737	0.879
	Month	7.142	0.118	0.997	0.980	10.995	0.144	−5.972	0.962
	Fortnight	4.274	0.133	0.510	0.973	6.104	0.168	−2.968	0.944
	Week	2.386	0.154	0.247	0.961	3.333	0.189	−1.475	0.919
	Trial	1.277	0.167	−0.069	0.939	1.506	0.190	0.020	0.892
	Daily	0.731	0.224	0.049	0.837	0.917	0.266	−0.282	0.686
PMT_cal	Year	37.790	0.047	−6.990	0.917	32.593	0.048	5.568	0.888
	Month	5.421	0.092	−0.601	0.986	7.276	0.110	0.597	0.971
	Fortnight	3.464	0.110	−0.307	0.979	4.511	0.136	0.297	0.957
	Week	2.101	0.137	−0.149	0.966	2.638	0.162	0.147	0.934
	Trial	1.264	0.165	−0.072	0.940	1.561	0.198	0.069	0.884
	Daily	0.706	0.215	−0.030	0.847	0.811	0.248	0.025	0.715
ANN3	Year	36.294	0.045	1.081	0.908	37.706	0.054	−0.608	0.853
	Month	5.684	0.099	0.093	0.984	8.092	0.119	−0.065	0.967
	Fortnight	3.584	0.115	−0.086	0.977	4.400	0.135	0.049	0.958
	Week	2.045	0.138	0.023	0.966	2.630	0.160	−0.016	0.936
	Trial	1.256	0.166	0.011	0.939	1.483	0.191	−0.008	0.891
	Daily	0.660	0.204	0.005	0.861	0.772	0.240	−0.003	0.730
ANN3_month	Year	30.835	0.042	−1.968	0.916	42.244	0.056	0.914	0.840
	Month	5.700	0.098	−0.169	0.984	7.543	0.110	0.098	0.971
	Fortnight	3.584	0.115	−0.086	0.977	4.400	0.135	0.049	0.958
	Week	2.098	0.140	−0.042	0.965	2.590	0.155	0.024	0.939
	Trial	1.274	0.168	−0.020	0.938	1.472	0.184	0.011	0.899
	Daily	0.673	0.207	−0.008	0.858	0.769	0.237	0.005	0.737
ANN6	Year	30.682	0.038	3.401	0.932	74.744	0.086	0.330	0.621
	Month	4.550	0.076	0.293	0.991	9.594	0.130	0.035	0.961
	Fortnight	2.765	0.084	0.149	0.988	5.510	0.151	0.018	0.948
	Week	1.580	0.100	0.073	0.982	2.970	0.164	0.009	0.932
	Trial	0.867	0.115	0.035	0.971	1.564	0.194	0.004	0.888
	Daily	0.459	0.144	0.114	0.935	0.898	0.258	−0.430	0.732

presents the global performance indicators of the considered models, split by timescale, for Albacete and Badajoz, using lysimeter measurements as the benchmark. In Albacete, all models exhibited higher RRMSE values when evaluated against lysimeter data than against FAO56 PM, yet the gradual improvement with more extended accumulation periods remained evident. For HS, RRMSE values dropped from 0.221 at the daily scale to 0.179 (trial), 0.155 (weekly), 0.132 (fortnightly), 0.115 (monthly), and 0.054 (annual). The reduction between daily and weekly periods was 6.6%, followed by 4.0% from weekly to monthly and 6.1% from monthly to annual, giving an overall decrease of 16.6%. MAE values ranged from 0.71 mm day⁻¹ to 44.78 mm year⁻¹. The PMT model followed a comparable progression, with RRMSE values of 0.224 (daily), 0.167 (trial), 0.154 (weekly), 0.133 (fortnight), 0.118 (month), and 0.050 (annual). The total reduction reached 17.4%, and MAE varied between 0.73 mm day⁻¹ and 40.69 mm year⁻¹. Conversely, ANN6 produced considerably lower errors at all timescales, with RRMSE decreasing from 0.144 (daily) to 0.115 (trial), 0.100 (week), 0.084 (fortnight), 0.076 (month), and 0.038 (annual). The corresponding decline was 10.6%, and MAE ranged from 0.46 mm day⁻¹ to 30.68 mm year⁻¹. Thus, although all models exhibited larger errors against lysimeter ET_o than against FAO56 PM, the progressive reduction in RRMSE with increasing accumulation interval remained evident, indicating that daily discrepancies were also attenuated when ET_o was aggregated over multi-day or seasonal periods under lysimeter benchmarking.

Regarding differences among models, the most considerable contrasts occurred at the daily scale (RRMSE of 0.221 and 0.224 for HS and PMT vs. 0.144 for ANN6), but decreased notably as the period lengthened. At weekly and fortnightly resolutions, RRMSE values ranged from 0.13 to 0.15 for HS and PMT and approximately 0.10 for ANN6, while at monthly and annual levels, all models presented values below 0.08. HS_cal and PMT_cal exhibited a very similar evolution (RRMSE of 0.213–0.045 and 0.215–0.047, respectively), whereas ANN3 and ANN3_month showed intermediate results (0.204–0.045 and 0.207–0.046).

In the case of Badajoz, the same overall pattern was observed. All models yielded higher RRMSE values under lysimeter benchmarking, although the decrease with increasing aggregation remained consistent. HS showed RRMSE values of 0.255 (daily), 0.207 (trial), 0.174 (weekly), 0.154 (fortnight), 0.131 (month), and 0.070 (annual). The reduction from daily to weekly was 8.1%, followed by 4.3% from weekly to monthly and 6.1% from monthly to annual, resulting in an overall decrease of 18.5%. MAE values varied between 0.86 mm day⁻¹ and 58.43 mm year⁻¹. PMT behaved in parallel, with RRMSE values of 0.266 (daily), 0.190 (trial), 0.189 (weekly), 0.168 (fortnight), 0.144 (month), and 0.078 (annual), corresponding to a total reduction of 18.8%. MAE ranged from 0.92 mm day⁻¹ to 66.10 mm year⁻¹. In contrast, ANN6 again showed more minor errors, with RRMSE values of 0.258 (daily), 0.194 (trial), 0.164 (weekly), 0.151 (fortnight), 0.130 (month), and 0.086 (annual). The total decrease was 17.2%, and MAE ranged from 0.90 mm day⁻¹ to 74.74 mm year⁻¹.

Between models, the most pronounced differences were again found at the daily and weekly levels (RRMSE ≈ 0.22–0.27 for HS/PMT vs. 0.26 for ANN6), whereas from fortnightly to annual periods, all models performed more similarly, with RRMSE ≤ 0.15 and converging towards 0.07–0.09 at the most extended intervals. HS_cal and PMT_cal maintained the same decreasing tendency (RRMSE = 0.243–0.048 and 0.248–0.050, respectively), while ANN3 and ANN3_month remained intermediate (0.240–0.047 and 0.237–0.046). Overall, slight differences were observed between calibrated and non-calibrated versions, and RRMSE variability among models diminished progressively with the length of the accumulation period. Compared with the FAO56 PM benchmark (Table 1), these daily and weekly RRMSE values show that ANN6 no longer exhibits a clear advantage over HS and PMT when the lysimeter is used as the reference, particularly in Badajoz. In addition, R² values were slightly higher in Albacete (up to 0.982) than in Badajoz (up to 0.940), confirming a more stable agreement between estimated and benchmark ET_o in the former site and suggesting that lysimeter-based targets were more affected by local variability at Badajoz.

3.3. Seasonal Variation of Model Performance Under FAO56 PM and Lysimeter Benchmarks

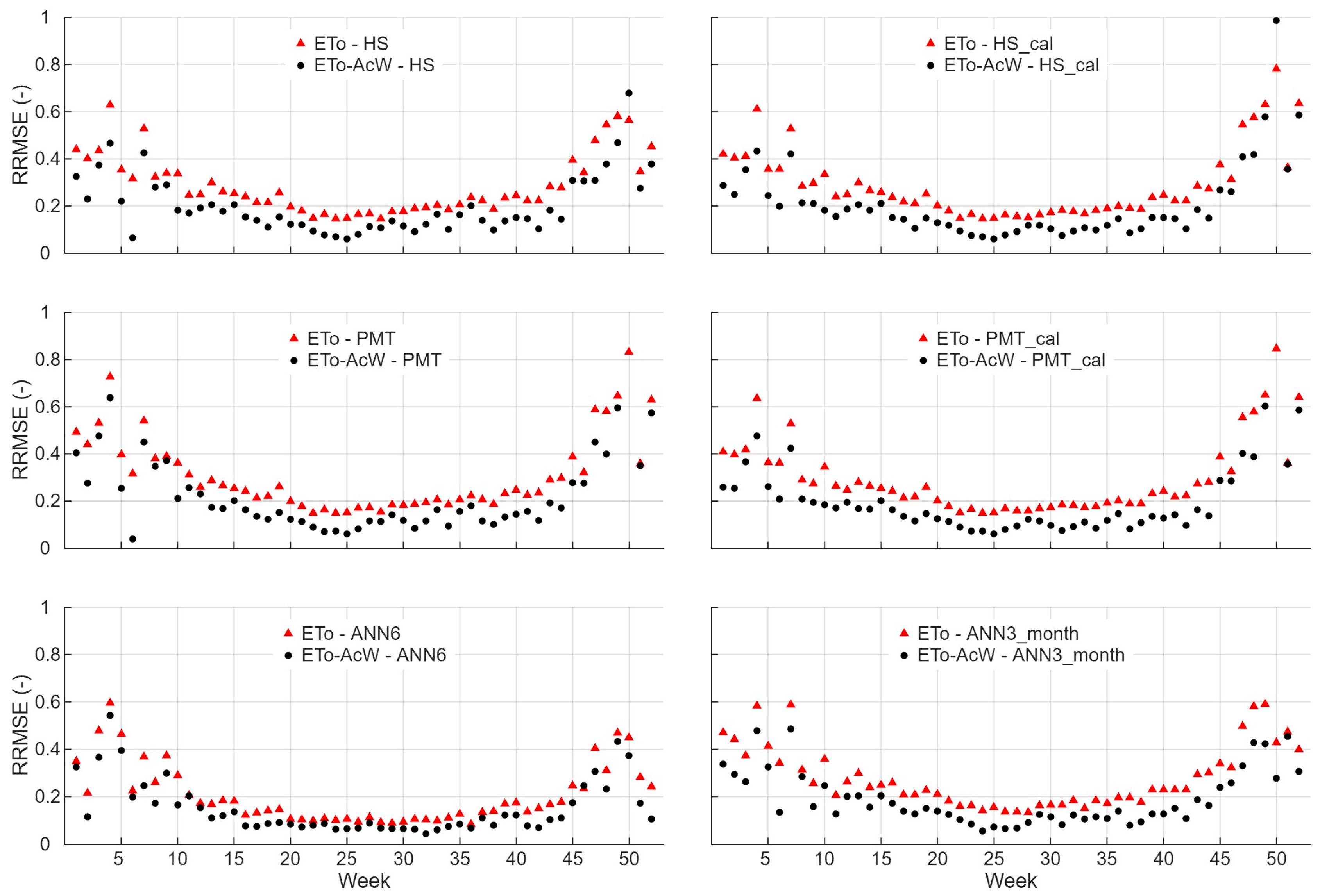
Figure 2 and Figure 3 show the weekly evolution of RRMSE for daily ET_o and weekly accumulated ET_o (ET_o-AcW) in Albacete and Badajoz, respectively, using FAO56 PM estimations as the benchmark.

As observed, the model accuracy varied throughout the year, with lower performance during the cooler weeks (November–January) and higher accuracy during the warmer period (June–August). In Albacete, daily ET_o RRMSE values for ANN6 ranged from 0.035 (week 26) to 0.180 (week 52), while in Badajoz, they ranged from 0.024 (week 30) to 0.174 (week 5). For ET_o-AcW, the corresponding ranges were 0.025 (week 26)–0.159 (week 52) in Albacete and 0.021 (week 30)–0.146 (week 49) in Badajoz. Among the temperature-based models, RRMSE values for ET_o-AcW ranged from 0.040 (week 34) to 0.483 (week 48) for HS, from 0.041 (week 25) to 0.635 (week 50) for PMT, and from 0.043 (week 25) to 0.594 (week 51) for ANN3_month in Albacete. In Badajoz, the ranges were 0.066–0.402 for HS (weeks 26 and 49, respectively), 0.071 (week 35)–0.613 (week 48) for PMT, and 0.031 (week 33)–0.594 (week 49) for ANN3_month. The most minor difference between daily and weekly RRMSE occurred around mid-summer (weeks 25–30), while the largest occurred in late autumn (weeks 48–52). Overall, the seasonal pattern was more pronounced for daily ET_o than for ET_o-AcW, indicating that model performance is strongly modulated by the annual cycle of atmospheric demand, with more stable behaviour during the peak evaporative season and enhanced sensitivity to synoptic variability during the colder weeks.

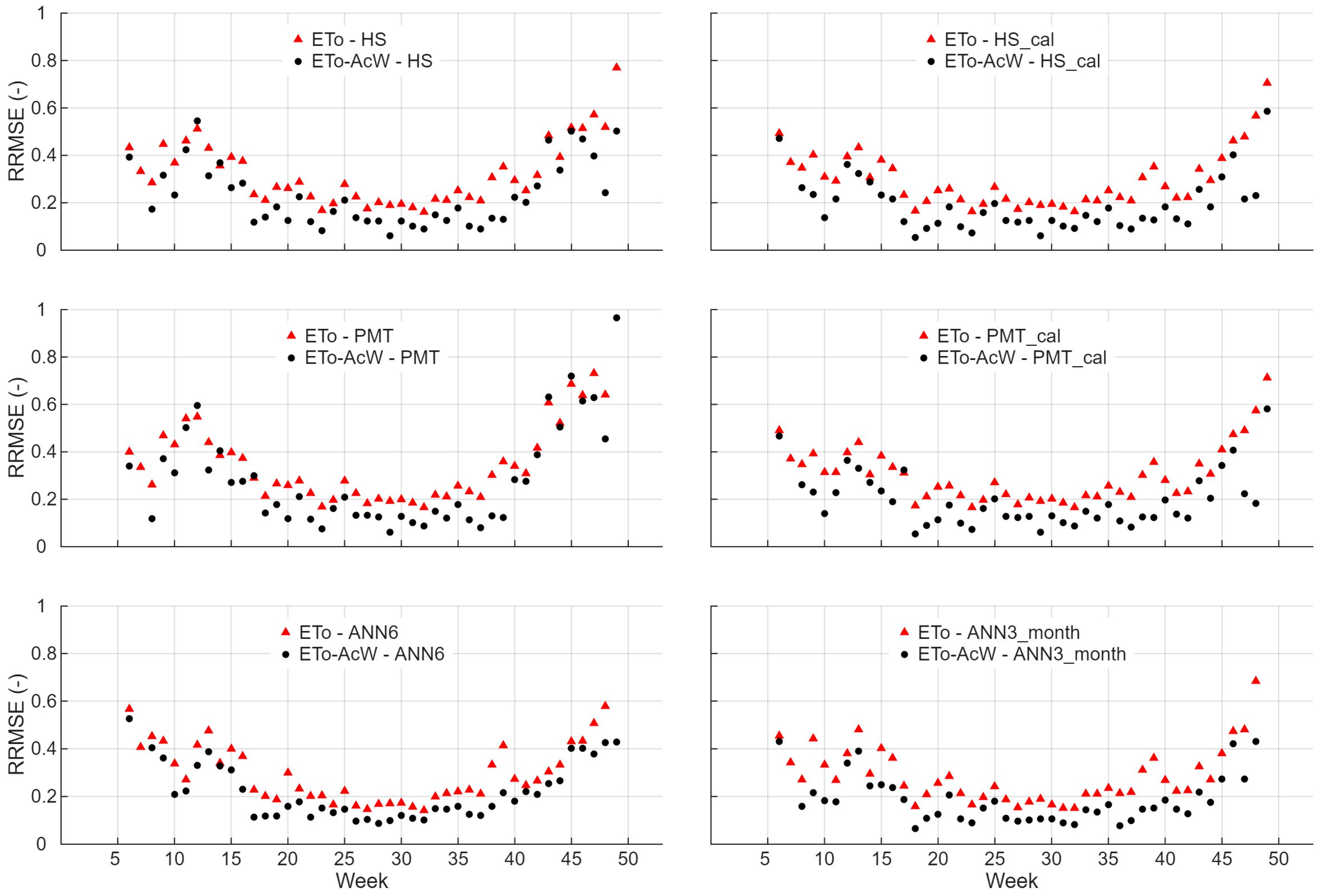
Figure 4 and Figure 5 show the same analysis using lysimeter measurements as benchmarks. In Albacete, daily ET_o RRMSE values presented a minimum of approximately 0.15 for both HS (week 24) and PMT (week 22) models, either calibrated or not. Maximum errors were 0.63 (week 4) for HS, 0.83 (week 50) for PMT, 0.59 (week 49) for ANN3_month, and 0.60 (week 4) for ANN6. The corresponding RRMSE ranges were 0.13–0.59 (weeks 28–49) for ANN3_month and 0.09–0.60 (weeks 36–4) for ANN6. The corresponding RRMSE ranges for ET_o-AcW were 0.04 (week 25)–0.99 (week 50) for HS_cal, 0.04 (week 6)–0.64 (week 4) for PMT, 0.06 (week 24)–0.48 (week 7) for ANN3_month, and 0.04 (week 32)–0.54 (week 4) for ANN6. In Badajoz, daily ET_o errors ranged from 0.16 (week 32) to 0.77 (week 49) for HS, 0.16 (week 32) to 0.73 (week 47) for PMT, 0.15 (week 32) to 0.68 (week 48) for ANN3_month, and 0.14 (week 32) to 0.58 (week 48) for ANN6. For ET_o-AcW, they varied between 0.06 (week 29)–0.55 (week 12) for HS, 0.06 (week 29)–0.97 (week 49) for PMT, 0.07 (week 18)–0.43 (week 6) for ANN3_month, and 0.09 (week 28)–0.53 (week 6) for ANN6. As in the FAO56 PM-based analysis, weekly accumulated estimates (ET_o-AcW) were consistently more accurate than daily estimates, except for certain winter weeks, when missing or sparse data led to occasional deviations. In some winter weeks, RRMSE peaks exceeded 1.00 for ET_o-AcW, reaching 1.09 in Albacete (HS_cal) and 1.34 in Badajoz (ANN3_month). Occasional peaks in daily ET_o were also observed, with maximum values of 2.94 for ANN3_month in Badajoz. These peaks occurred during periods of very low reference ET_o and reduced data availability, when small absolute discrepancies translate into significant relative errors. Overall, seasonal RRMSE patterns were consistent across sites and benchmarks, with higher variability and larger errors observed under the lysimeter reference than under FAO56 PM, particularly during the coldest part of the year, while differences among models diminished during summer.

In summary, across both sites and benchmarks, all models exhibited a consistent reduction in RRMSE and MAE as the accumulation interval increased from daily to trial, weekly, fortnightly, monthly, and annual scales (Table 1 and Table 2). Under FAO56 PM benchmarking, daily RRMSE ranged approximately between 0.06 and 0.18, whereas at monthly and annual scales, it was below 0.08 for all models at both sites, with ANN6 showing the lowest errors throughout. When lysimeter measurements were used as benchmarks, daily RRMSE values increased to approximately 0.14–0.27, while weekly values remained below about 0.18, and monthly and annual RRMSE rarely exceeded 0.15. The seasonal analysis (Figure 2, Figure 3, Figure 4 and Figure 5) further showed that errors were most significant and most variable during the coldest weeks of the year and smallest during summer, and that ET_o-AcW generally presented lower RRMSE than daily ET_o. Differences between temperature-based and ANN models were pronounced at the daily scale. Still, they became progressively smaller at weekly and longer intervals, so that at monthly and annual scales, the performance of all models converged within relatively narrow RRMSE ranges under both benchmarks.

4. Discussion

Our results show that model accuracy and dispersion highly depend on the chosen benchmark. Errors were systematically higher and more variable when lysimeter data were used, particularly during the coldest weeks of the year, whereas FAO56 PM produced lower and more stable values. This divergence suggests that the use of lysimeter measurements as a benchmark for assessing ET_o may reflect the influence of local environmental and operational factors. During winter, lysimeters can be affected by mechanical and microclimatic disturbances, such as frost, condensation, or the oasis and clothesline effects, which may alter the energy balance and induce anomalous fluxes. Their accuracy may also be influenced by restricted fetch and drainage dynamics, which are negligible under summer conditions but become significant in cold, calm periods [43,44]. Consequently, apparent model errors tend to increase when the lysimeter is used as the target, not necessarily because models perform worse, but because the benchmark itself becomes less representative of the standardised reference surface described in FAO56. These findings agree with [45]. From a benchmarking perspective, our results indicate that, under the semi-arid Mediterranean conditions analysed, FAO56 PM behaves as a physically consistent and operationally robust reference. In contrast, lysimeter-based ET_o should be interpreted as an experimental benchmark whose representativeness is more sensitive to local conditions. Nevertheless, lysimeters might remain a valuable tool for directly measuring evapotranspiration under real conditions, especially during well-controlled periods or for model calibration purposes. During the winter season, when water-demanding crops such as barley, wheat, rapeseed, or leafy vegetables are commonly cultivated, special care should be taken when interpreting lysimeter data for irrigation planning.

When lysimeter data were used, the period of increased model error extended roughly from weeks 1–12 and 40–52, in line with previous findings [16]. This broader high-error window indicates that non-calibrated models appeared to perform worse over a larger portion of the year when lysimeter data were used as the benchmark. However, this apparent degradation mainly reflects the greater sensitivity of lysimeter measurements under cold conditions, where limited reference availability and minor measurement errors disproportionately increase the overall error, particularly in Badajoz, where such conditions are more frequent. Thus, discrepancies between benchmarks are largely seasonal. FAO56 PM remains physically consistent throughout the year, while lysimeter measurements introduce additional variability in winter due to both environmental and operational factors. As a result, lysimeter observations can accentuate models’ tendency to under- or overestimate irrigation requirements, as reflected in higher MBE values. By contrast, FAO56 PM remains the widely recommended reference for ET_o estimation, since it is based on well-established physical principles and can be applied reliably whenever the required climatic data are available, unlike the constraints associated with lysimeter measurements, as also noted in [46]. Therefore, in the context of semi-arid Mediterranean climates similar to those of Albacete and Badajoz, FAO56 PM appears to be a more suitable primary benchmark for model evaluation and ET_o estimation. At the same time, lysimeter observations provide complementary experimental evidence, particularly useful for detecting departures between physically based estimates and actual evapotranspiration under specific site conditions.

Regarding the effect of the irrigation interval on ET_o accuracy, model errors decreased consistently with more extended accumulation periods across all benchmarks and stations, confirming that temporal aggregation smooths daily discrepancies. Extending the estimation period from daily to multi-day or weekly irrigation intervals resulted in substantial reductions in RRMSE across all models, particularly for HS and PMT, which exhibited the most significant daily errors. This behaviour reflects a compensation effect among day-to-day deviations, which tend to cancel each other out when aggregated, provided that positive and negative errors are approximately balanced over time. Therefore, differences among models progressively diminished at longer timescales, and by monthly or annual intervals, their performance became nearly equivalent. Similar findings on the influence of timescales were reported by [16], although their indicators were derived from daily estimates over a given period rather than from accumulated ET_o values. It is important to note that this compensation mainly affects the non-systematic component of the error. Systematic biases are only partially reduced and may still be reflected in MAE and MBE at longer timescales. Nevertheless, the systematic decrease in RRMSE and the relatively small MBE values observed at trial, weekly and fortnightly scales suggest that, under the semi-arid Mediterranean conditions considered here, a substantial fraction of daily errors tends to compensate in cumulative ET_o. This mechanism is likely to operate in other environments where daily deviations fluctuate around zero, and irrigation is scheduled over multi-day intervals. However, its magnitude should always be verified with local data. Conversely, in sites where simpler methods exhibit a persistent bias of the same sign, the scope for error compensation would be much more limited, and a marked reduction in error differences with aggregation should not be expected.

The practical implication is that trial, weekly, or fortnightly accumulated ET_o estimations provide a more realistic assessment framework for irrigation scheduling than daily values. Farmers usually plan irrigation in multi-day intervals, and the soil water buffer further mitigates daily fluctuations in evapotranspiration [11]. Therefore, evaluating model performance exclusively at the daily scale can exaggerate differences that are not operationally significant, especially when irrigation decisions are based on cumulative water requirements. In this context, temperature-based models applied in this study might provide sufficiently accurate results when data availability is limited, while the more complex ANN formulations, such as ANN6, confirm that, under complete datasets, physically based estimates can be closely reproduced without substantially improving at longer intervals. In this sense, ANN6 was not proposed as an operational model but instead used as a complex reference to contextualise the performance of temperature-based approaches. Since it relies on the same meteorological inputs as FAO56 PM, its practical relevance is limited, as the reference equation can be directly computed when full datasets are available. Overall, these findings confirm that benchmark selection and temporal aggregation are crucial sources of variability in ET_o model performance. At the same time, differences among modelling approaches are significantly reduced at operational timescales relevant to irrigation management, so that the principal added value of this study lies in quantifying how benchmark choice and aggregation interval affect the apparent adequacy of well-established empirical and ANN-based methods under semi-arid Mediterranean conditions.

The ability of temperature-based methods and reduced-input ANN configurations to provide reasonable accuracy in the study area can be partly explained by the climatic setting. In semi-arid Mediterranean climates, key drivers of ET_o, such as net radiation, vapour pressure deficit, and aerodynamic demand, exhibit strong seasonal and synoptic co-variability with air temperature, so that temperature and solar radiation alone can account for a significant fraction of ET_o variability [16]. As a result, T_max and T_min carry substantial information about the broader energy and moisture regime, which helps to explain the good performance of HS, PMT and the reduced-input ANN3 in our experiments, in line with previous work showing that reduced-input data-driven and empirical models can reach accuracies comparable to full-input formulations under similar Mediterranean conditions [29]. Furthermore, the inputs used in ANN3 (T_max, T_min and R_a) are not independent: R_a and the seasonal cycle of air temperature are tightly coupled in these environments, indirectly capturing much of the variability in R_s and R_n. While this reliance on correlation structures enhances model performance in the present semi-arid Mediterranean conditions, it also implies that the empirical relationships learned by these models may not be directly transferable to markedly different climatic regimes without retraining and additional validation.

Several limitations should be considered when interpreting these results. First, the analysis is based on long-term records from only two grass-reference lysimetric stations located in semi-arid Mediterranean environments: a cold semi-arid climate in Albacete and a hot-summer Mediterranean climate with Atlantic influence in Badajoz. Consequently, the quantitative indicators reported here are conditioned by these specific climatic and management conditions and by the quality and length of the available datasets. Second, the study does not include independent validation using reanalysis products or additional observational networks, so the robustness of the conclusions at regional scales cannot be assessed. These factors imply that the findings should be viewed as site-specific and primarily applicable to semi-arid Mediterranean environments with similar data availability. Nevertheless, the qualitative patterns identified are supported by physical reasoning and are expected to have a more general scope. In particular, the greater robustness of FAO56 PM as a benchmark compared with lysimeter targets in winter, the marked reduction in apparent model differences with increasing aggregation intervals, and the partial compensation of daily errors in cumulative ET_o reflect mechanisms that can, in principle, operate at other sites. Their expression will depend on the local bias pattern of the simpler methods: where daily deviations fluctuate around zero, a substantial reduction in error differences with aggregation is likely, whereas in locations with a persistent over- or underestimation pattern, the scope for error compensation will be more limited. Thus, while the magnitude of the error reduction remains site-specific and should be verified with local data, the conceptual framework and the role of daily bias patterns in shaping cumulative ET_o errors can be qualitatively extended to other networks, including those based solely on FAO P-M reference estimates.

5. Conclusions

This study evaluated the performance of temperature-based (HS and PMT) and neural network (ANN3 and ANN6) models for estimating daily ET_o and its accumulated values over different time intervals at two contrasting Mediterranean sites in southeastern and southwestern Spain. The analysis was conducted using both the FAO56 PM equation and lysimeter measurements as benchmarks, and across different temporal aggregation intervals relevant to irrigation and water planning management, ranging from trial to weekly, fortnightly, monthly, and annual periods, under the semi-arid Mediterranean conditions represented by these sites. As a result, increasing the estimation interval from daily to weekly or fortnightly periods markedly reduced model errors and narrowed differences among approaches, indicating that temporal aggregation compensates for daily fluctuations and yields a more realistic assessment for irrigation scheduling. Since irrigation is usually not scheduled daily but rather at intervals that may account for soil water buffering and operational constraints, evaluating models at these timescales provides a more realistic measure of their accuracy. This reinforces the need to assess models beyond daily estimates, as otherwise they may lead to misleading conclusions for irrigation planning and on-farm decision-making. Most of the practically relevant error reduction was already achieved at weekly and fortnightly scales, while systematic components of the error remained visible in MAE and MBE at longer timescales.

The results also demonstrated that benchmark selection and temporal aggregation are crucial factors that govern model performance variability. Errors were systematically higher and more dispersed when lysimeter data were used, particularly during winter, likely reflecting the influence of environmental and operational factors under cold and calm conditions. By contrast, FAO56 PM provided more stable and consistent reference values throughout the year, confirming its suitability as the standard method for evaluating ET_o models under semi-arid Mediterranean conditions. In this context, FAO56 PM emerges as a more suitable primary benchmark for model evaluation. In contrast, lysimeter-based ET_o should be regarded as an experimental reference that is extremely valuable for validating and refining physically based formulations, but whose representativeness is more sensitive to local site characteristics and to the strict fulfilment of FAO reference crop requirements.

Finally, under complete climatic datasets, ANN6 achieved the highest accuracy when compared with FAO56 PM. Still, its relevance is primarily methodological, as it relies on the same inputs as the reference equation and is therefore not intended as an operational alternative. Temperature-based models, such as HS, PMT, exhibited stable behaviour across sites and benchmarks, and their accuracy at multi-day scales was comparable to that of more complex neural network formulations. These findings indicate that simple models remain robust and operationally useful tools in data-scarce or heterogeneous conditions, particularly when irrigation is scheduled over multi-day intervals, and a substantial part of daily errors tends to compensate in cumulative ET_o. At the same time, FAO56 PM might be the most reliable alternative for reference evapotranspiration assessment when sufficient input data are available for its application. Lysimeter measurements, although subject to environmental variability, remain an essential component of experimental validation and contribute to refining physically based estimation approaches. The empirical relationships highlighted in this study are therefore best understood as site-specific and mainly relevant to semi-arid Mediterranean environments with similar climatic and management conditions. They are conditioned by the length and quality of the datasets available at the two experimental sites. The systematic decrease in model error observed at operational timescales indicates that, under these conditions, partial compensation of daily biases in cumulative ET_o is likely to occur, provided that daily deviations fluctuate approximately around zero. This behaviour should nevertheless be confirmed with local data before extrapolating to markedly different climatic regimes or to locations where simpler methods exhibit a persistent over- or underestimation pattern.