Dynamic Task Scheduling Optimisation Method for Hilly Orchard Rail Transport Systems

Abstract

Efficient scheduling of automated rail transportation in hilly orchards is critical for maintaining fruit freshness and ensuring timely market delivery. This study develops a dynamic scheduling method for multi-transporter orchard rail systems through mathematical modeling, reinforcement learning algorithms, and field validation. We formulated a comprehensive scheduling model and designed four distinct frameworks to address randomly arriving tasks. In the optimal framework (Framework 3, which was chosen due to its hybrid strategy combining periodic global planning and local task point adjustment), we compared six rule-based heuristic algorithms against three reinforcement learning approaches: centralized SAC, decentralized MARL-DQN, and conventional DQN. Additionally, two emergency response strategies were developed and evaluated. Simulation experiments demonstrated that Framework 3 maintained high load factors while reducing task completion times. The centralized SAC algorithm outperformed other methods, achieving 1533.71 ± 50.09 reward points compared to 863.67 ± 30.54 for rule-based heuristics, a 77.6% improvement. For emergency tasks, Strategy 2 achieved faster response times with minimal disruption to routine operations. Field trials on a 153 m physical track with four autonomous transporters validated the DQN algorithm, confirming good sim-to-real consistency. This research provides a practical solution for dynamic scheduling challenges in hilly orchards, offering measurable efficiency improvements over traditional methods.

1. Introduction

Hilly regions cover about two-thirds of China’s land area and are vital for agriculture [1]. Characterised by steep slopes and high elevations, these areas are predominantly used to cultivate economically significant crops such as fruit trees and tea plants [2]. However, the rugged terrain makes road construction difficult, preventing large tractors from reaching harvesting sites and posing significant challenges to agricultural transport. To address these challenges and improve the mechanisation of agriculture in hilly regions, various transport equipment suited for these terrains have recently been developed by researchers, among which the hilly orchard track transport system stands out [3,4]. This system features tracks laid along the agricultural sites, designed to be easily installed in complex environments and capable of accommodating multiple transporters simultaneously.

Currently, the operational management of these track systems predominantly relies on manual decision-making or rudimentary heuristic dispatching. Operators typically assign transporters based on visual observation of task accumulation at loading points, employing implicit heuristics such as ‘first-come-first-served’ or ‘nearest-task-first’ [5,6]. While these approaches are intuitive, they exhibit several critical limitations in practice: (1) they function reactively rather than anticipating task accumulation trends; (2) they fail to systematically optimize system-wide objectives such as load factor maximization; (3) they struggle to coordinate multiple transporters effectively on unidirectional tracks, leading to congestion; and (4) they lack established mechanisms for prioritizing emergency tasks. Consequently, these inefficiencies hinder the overall throughput of the system. The necessity for a more advanced solution arises from the inherent variability of fruit harvesting operations, where picking rates fluctuate depending on fruit ripeness, worker availability, and weather conditions [7,8]. In contrast to industrial settings defined by deterministic tasks, the exact timing and quantities of orchard transport tasks cannot be predetermined, rendering static scheduling methods inadequate. Instead, dynamic scheduling is required to adapt dispatch decisions based on real-time task accumulation and transporter status, thereby maintaining operational efficiency despite stochastic variability [9].

Research on agricultural machinery scheduling has primarily focused on flat agricultural fields [10], orchards [11], and greenhouse operations [12], but these models do not fully translate to the unique configuration of mountainous orchard track transport. Moreover, the operation of track transport systems during the harvest season encounters dynamically changing tasks, necessitating adaptable scheduling methods. While various strategies have been applied in general agricultural contexts, they largely rely on fixed-task assumptions that differ significantly from the dynamic environment of hilly orchards. The core challenges in this specific domain include unpredictable task arrival patterns during harvesting, real-time multi-transporter coordination on unidirectional tracks, and the critical need to balance system responsiveness with load factor optimization.

This study introduces an optimisation method for dynamic task scheduling in hilly orchard track transport systems. The scheduling concept for the orchard track system is inspired by the circular Rail-Guided Vehicle (RGV) systems used in industrial settings [13] and has been specifically adapted for transport tasks in hilly orchards. In automated warehouse environments, RGVs are utilised for material handling [14], and transport tasks are managed through the development of scheduling models and optimised algorithms [15]. However, these approaches are not entirely suitable for the transport dynamics in hilly orchards, which often involve multiple loading points and a single unloading point [16]. A dynamic scheduling model tailored to the features of the hilly orchard track transport system has been developed, utilising frameworks, algorithms, and strategies designed for this type of operation. The study addresses the extensive demands of dynamic transport task scheduling during the fruit harvesting season and can also handle urgent transport tasks effectively.

This paper pursues the following objectives and presents the corresponding conclusions:

• To develop a dynamic scheduling model for the circular track transport system. We establish a comprehensive mathematical model that effectively addresses load capacity optimization, task completion timing, and multi-agent coordination, demonstrating its suitability for the system’s operational constraints and dynamic task arrival patterns.
• To design and evaluate dynamic scheduling solutions. We propose four distinct frameworks with varying rescheduling strategies and decision scopes, along with multiple algorithms including rule-based heuristics and reinforcement learning (RL) approaches, namely Deep Q-Network (DQN), Multi-Agent DQN with Centralized Training and Decentralized Execution (MARL-DQN), and centralized Soft Actor–Critic (SAC). Through systematic evaluation, our results indicate that specific framework-algorithm combinations offer substantial performance advantages over traditional methods. Furthermore, we develop a proximity-based emergency response strategy that effectively minimizes operational disruptions when transporters encounter unexpected obstacles.
• To validate the proposed methods through a staged evaluation approach. Recognizing the practical constraints and safety considerations of simultaneously deploying multiple advanced RL algorithms on physical hardware, we conduct extensive simulation experiments complemented by real-world field trials. The field validation focuses on DQN as a representative RL baseline, confirming the practical applicability of RL-based scheduling control. Combined with the substantial performance advantages observed for SAC in simulation, these findings substantiate both the robustness of our framework and the promising deployment potential of advanced centralized RL controllers for real-world scheduling applications.

2. Related Work

2.1. Track Transportation Scheduling

Track transportation scheduling often employs advanced algorithms and systems [17] that outperform traditional manual methods in complex, variable environments. These technologies have shown significant potential in optimising resource allocation and enhancing transport efficiency across various contexts, including railway transport [18], urban track transport [19], industrial production [20], scenic areas [21], and mining operations [22]. Due to their robust load capacity and excellent climbing abilities, track transporters are specifically adapted for hilly orchards [23]. In this specific domain, the development of hardware and control systems has reached a mature stage domestically and internationally [6,24]. However, existing works predominantly focus on the mobility and automation of individual transporter units rather than fleet coordination. Unlike traditional battery-powered models that face downtime constraints, a sliding contact line-powered track transporter with unlimited range capabilities was developed in our previous work [24]. By eliminating the uncertainty of charging interruptions, this platform ensures continuous operation, thereby providing a stable physical foundation specifically suited for the high-throughput, multi-agent cooperative scheduling strategies explored in this study.

However, despite these hardware advancements, the operational management of current hilly orchard systems exhibits several critical limitations that constrain their practical effectiveness: (1) Manual scheduling dependence: Operators largely rely on visual observation and experiential judgment to dispatch transporters, resulting in suboptimal load factors and inconsistent decision quality across different personnel [6,24]. (2) Lack of dynamic adaptability: Existing control systems cannot automatically adjust dispatch decisions in response to variable harvest task arrivals, frequently leading to either premature departures with partial loads or excessive waiting times [25]. (3) Absence of systematic emergency response: When unexpected situations occur (e.g., equipment failures or urgent transport requests), there are no established protocols for rapid task reassignment, causing significant operational disruptions [26,27]. (4) Multi-transporter coordination challenges: Without centralized scheduling intelligence, multiple transporters operating simultaneously on unidirectional tracks frequently experience congestion at loading points and inefficient sequencing, reducing overall system throughput.

To address these specific bottlenecks, the transporter system in this study has been upgraded with an IoT-based scheduling framework. This integration enables the system to handle complex dynamic tasks and diverse transport needs while maintaining high operational efficiency, directly overcoming the limitations of traditional manual management.

2.2. Scheduling Algorithms

Existing scheduling algorithms for track transport systems can be generally categorized into three classes, each exhibiting distinct characteristics and limitations when applied to the specific context of hilly orchards:

(1)

Heuristic rule-based methods [28,29], including greedy algorithms [30] and simple priority dispatching, offer computational simplicity and ease of implementation. However, these approaches typically apply fixed decision logic regardless of the system state. They function reactively to immediate conditions rather than anticipating task accumulation trends and, in multi-transporter scenarios, often lack the mechanisms for global coordination needed to prevent congestion at high-demand loading points.

(2)

Metaheuristic optimization algorithms, such as chaos particle swarm optimization, genetic algorithms [31,32], ant colony optimization [33], differential evolution [34], and tabu search [35], possess global search capabilities that can identify near-optimal solutions. Nevertheless, a critical drawback of these methods is their requirement for complete task specification before optimization begins. This characteristic creates a fundamental incompatibility with dynamic harvesting operations where tasks arrive stochastically. Furthermore, their iterative nature often incurs computational overhead that precludes real-time decision-making.

(3)

Reinforcement learning (RL) approaches, including Q-learning [36] and Proximal Policy Optimization [37], have demonstrated the ability to learn adaptive policies through environmental interaction. While promising, existing RL applications predominantly target railway or warehouse systems characterized by bidirectional movement and deterministic demand patterns. The unique constraints of hilly orchards, such as the unidirectional closed-loop track, multi-loading-single-unloading topology, and stochastic arrivals, present distinct state-space challenges not adequately addressed by general-purpose RL formulations.

In the specific context of hilly orchards, our team previously established a static scheduling method [25], which successfully applied heuristic rule-based algorithms combined with a variable neighbourhood search genetic algorithm. This work provided a robust baseline for optimising transport efficiency when task sets are known a priori. However, actual harvesting operations involve stochastic task arrivals that cannot be fully predicted, creating a need to extend these static principles into a real-time framework.

Building upon the carpooling concepts introduced in [25], the current study advances the field by addressing these dynamic challenges through a four-pronged approach: (1) evolving the static model into a dynamic scheduling framework with four architectural options capable of responding to real-time task triggers; (2) moving beyond fixed heuristics by employing reinforcement learning algorithms (DQN, MARL-DQN, SAC) to learn adaptive policies from operational experience; (3) supplementing the scheduling logic with two specific emergency response strategies to handle emergency situations, a critical capability absent in static models; and (4) validating the proposed methods through both extensive simulations and physical field trials (detailed in Appendix D) to bridge the gap between theoretical algorithms and practical deployment.

3. Materials and Methods

3.1. Scenario Description

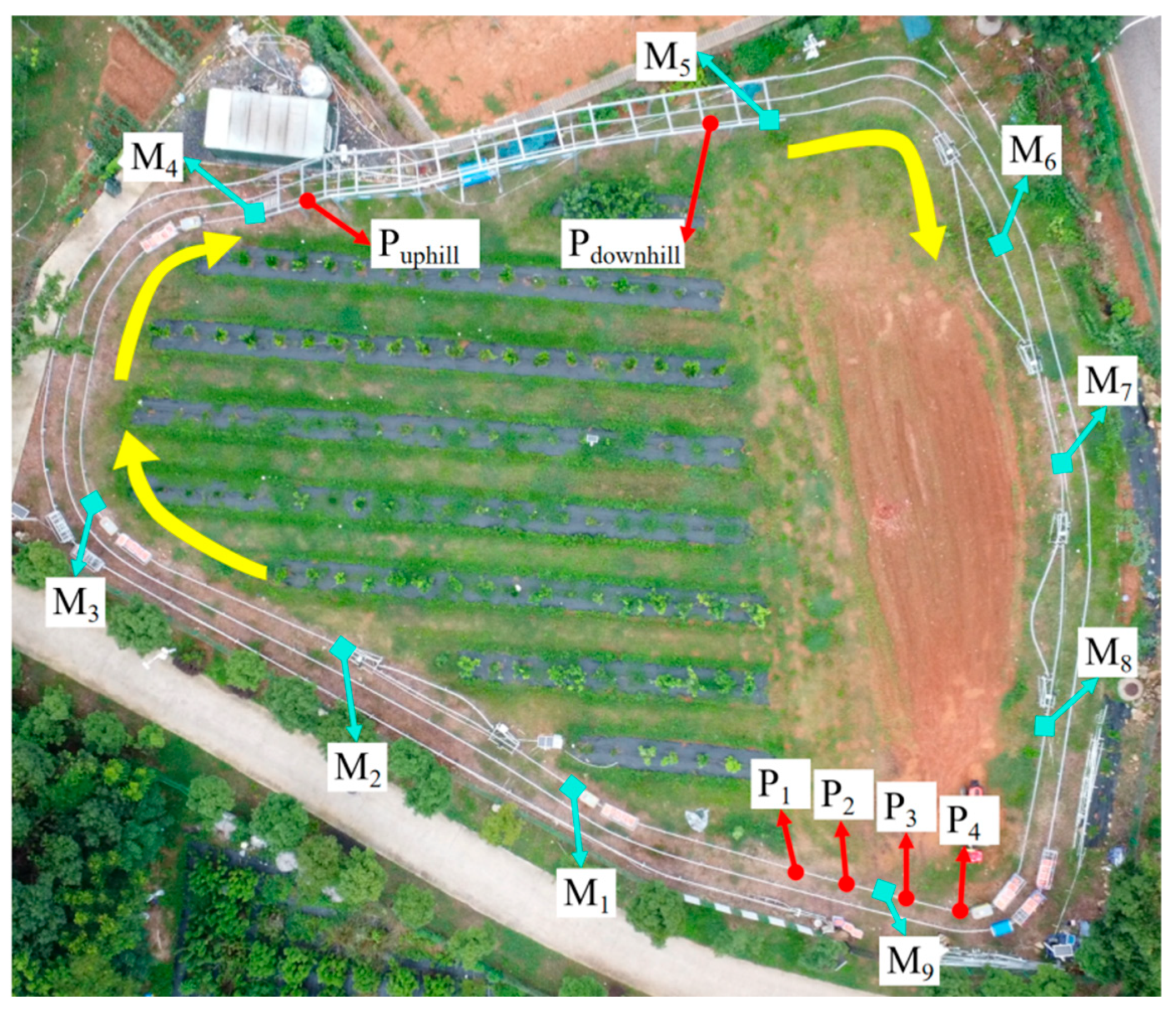
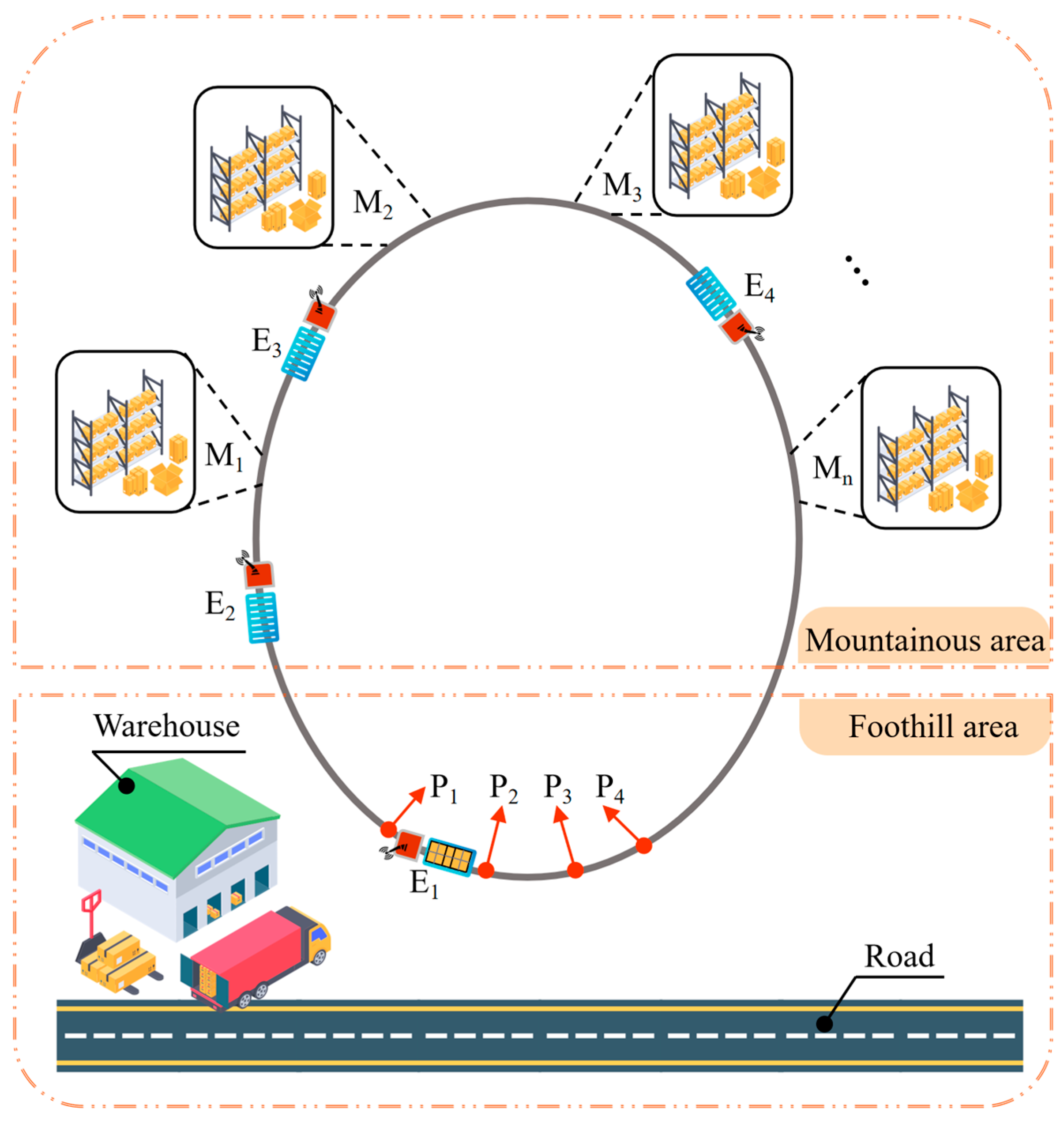
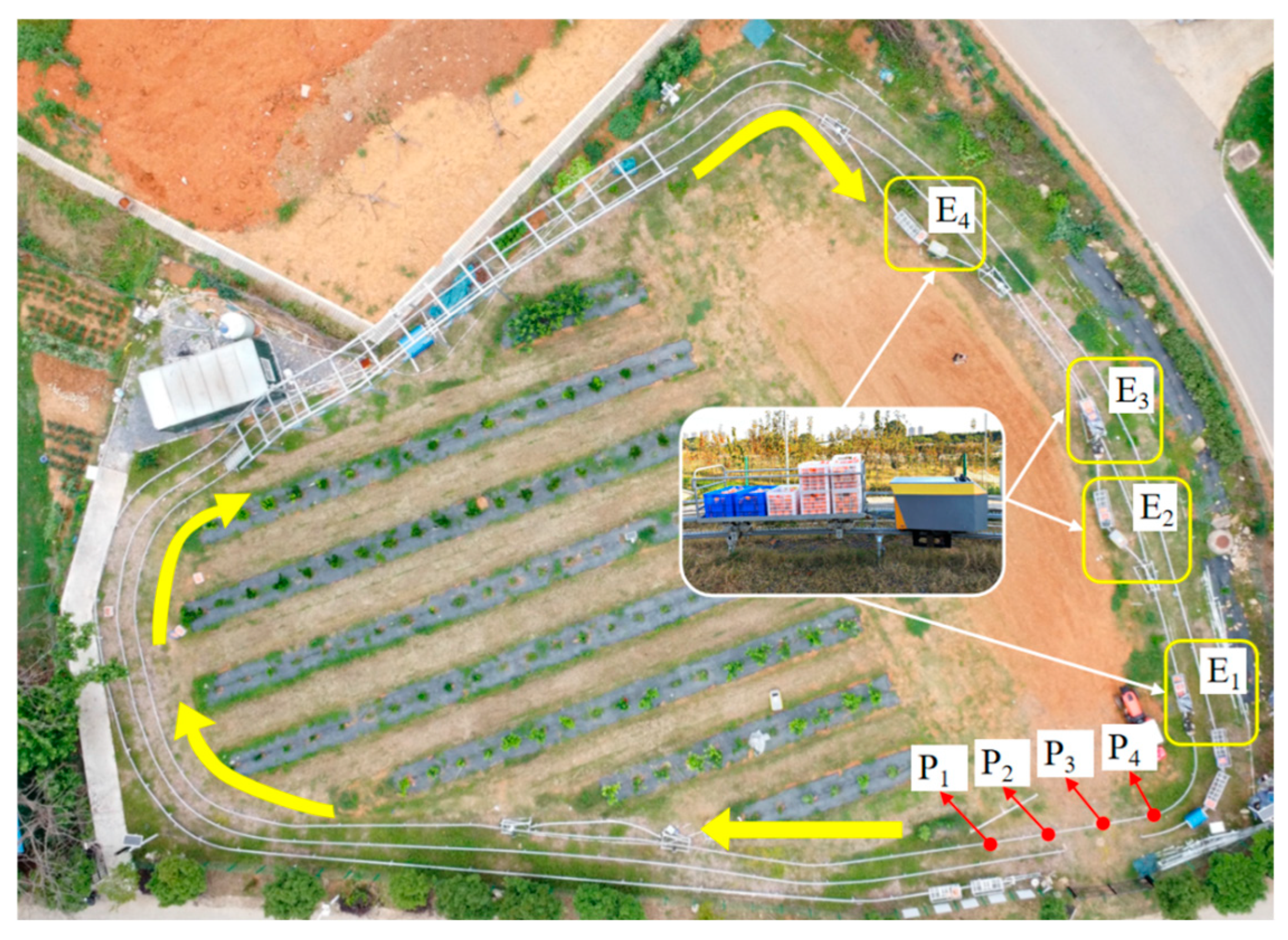
The hilly orchard rail transport system is well-suited to areas characterised by significant topographical variations and high transportation demands. It is utilised in the central and southern hilly orchards of China for the transportation of harvested fruits and agricultural equipment. Figure 1 presents a prototype of the hilly orchard rail transport system.

The focus of this paper is the fruit harvesting period, during which the proposed transport system integrates individual transporters into a unified scheduling network designed for high-efficiency orchard logistics. The system operates on several core principles to address the complex terrain. First, unlike battery-powered alternatives with limited range, the transporters utilize a sliding contact line power supply technology [24] to enable continuous operation without charging interruptions, which is critical for maintaining system-level throughput. Second, to ensure safety and simplify control, the system enforces a unidirectional clockwise flow on the closed-loop track. Crucially, this configuration facilitates an inter-vehicle collision avoidance mechanism, where transporters maintain safe separation distances based on their real-time on-track positions.

In terms of logistics, the layout is designed with multiple distributed loading points (M₁–M_n) converging to a single unloading station near the base, reflecting a typical ‘field-to-warehouse’ pattern where agricultural equipment is non-consumable and circulates between tasks. Furthermore, to enable intelligent coordination, each transporter is equipped with onboard controllers (Orange Pi 5 Pro, Shenzhen Xunlong Software Co., Ltd., Shenzhen, China), position sensors (JY-L8900 RFID Reader, Guangzhou Jianyong Information Technology Co., Ltd., Guangzhou, China), load cells (DYLY-102, Bengbu Dayang Sensor System Engineering Co., Ltd., Bengbu, China), and wireless modules (LTE Module Air780E, Shanghai AirM2M Communication Technology Co., Ltd., Shanghai, China) that report real-time status to a central server for dynamic task allocation. For specific mechanical designs of the transporters and detailed system-level field configurations, please refer to Reference [24] and Appendix D, respectively. The overall schematic layout is depicted in Figure 2.

The research was conducted through a series of targeted experimental sessions from May 2023 to October 2025. This extended period allowed for an iterative development process comprising two primary phases: (1) System Characterization (May–October 2023): Initial physical trials were performed to measure foundational operational parameters, including transporter speeds under varying loads and standard dwell times. These real-world measurements were essential for calibrating the simulation environment to ensure fidelity. (2) Algorithm Evolution and Hybrid Validation (2024–2025): This phase involved the parallel development of scheduling algorithms and their validation. We first established the simulation platform to train and comprehensively compare the proposed algorithm suite, including DQN, MARL-DQN, and SAC, using realistic task configurations (detailed in Section 4.1.1). Subsequently, intermittent field validation campaigns were conducted on the 153 m experimental track. In these trials, the DQN algorithm was deployed as the representative baseline to verify the feasibility of the RL-based control strategies and to validate the consistency between simulation predictions and physical system behavior, as detailed in Section 4.5 and Appendix D.

3.2. Model Assumptions and Formula Derivation

The basic prerequisites for completing transport tasks include the performance parameters of the transporters, operational environments, and task parameters. This paper is based on the actual operating conditions of hilly orchard track transport systems and considers constraints related to circular RGV systems. The following assumptions have been made:

• The initial spacing between each transporter equals the length of the transporter plus a minimum safety distance.
• The transporters operate unidirectionally on a closed track exclusively in a clockwise direction, without any allowance for reversing or overtaking; they are also sequentially numbered in descending order following the clockwise direction.
• The locations of the task points and the existing task quantities are known. Task points are numbered in a clockwise direction starting from the initial position, with higher numbers indicating longer travel times from the initial position.
• Transporters are assumed to travel at a constant speed throughout the journey, with a fixed maximum load capacity. Additionally, all transporters are of the same model with identical performance parameters.
• In simulations, the position of the transporter is indirectly calculated using time and operational parameters.
• Upon reaching any task point, transporters can immediately begin loading or unloading to ensure operational efficiency, with only one transporter allowed to operate at each task point at any time.
• The dwell time at each loading point is the same for all transporters, regardless of the load amount, meaning more loading activities will increase the duration needed to complete the tasks.
• During each transport cycle, each transporter can stop at multiple task points as per its maximum load capacity, but the total amount transported must not exceed this limit.
• If the distance between adjacent transporters falls below the minimum safety distance, the following transporter will stop moving.

The derivation of the total task completion time for the transport system is as follows:

Multiple loading points are set along the track, collectively defined as $M_{\mathrm{up}}=\left\{M_j\right|j=1, 2,\dots , n\}$, where n is the number of task points. There is only one storage point (unloading point), denoted as $M_{\mathrm{down}}$. The set of current task quantities required at each task point is denoted as $S_{\mathrm{task}}=\{M_j:tas{k}_j|M_1:tas{k}_1, M_2:tas{k}_2,\dots , M_n:tas{k}_n\}$. The set of transporters on the track is $S_{\mathrm{car}}=\left\{E_i\right|i=1, 2,\dots , c\}$, where c is the number of transporters. Each transporter’s load capacity is denoted as $n_{\mathrm{load}}$, in boxes. The smallest set of tasks generated is $S_{\mathrm{newtask}}=\left\{N_k\right|k=1, 2,\dots , num\}$, where num is the minimum number of tasks. The number of trips is denoted as $n_t$.

As shown in Equation (1), $T^t$ represents the time taken for c transporters to complete the t-th trip, as calculated in Equations (2)–(4). Assuming that c transporters work simultaneously and in parallel to complete tasks, the completion time $T^t$ for each trip is the maximum of the individual completion times $T_{C_i}^t$ for each transporter

$$T_{task}=min\sum _{t=1}^{n_t}{T}^t$$

(1)

$$T^t=max\left\{T_{C_1}^t,\dots ,T_{C_i}^t,\dots ,T_{C_c}^t\right\}$$

(2)

$$T_{C_i}^t=T_{response}(t, i)+T_{act}(t, i)$$

(3)

$$T_{act}=\sum _{n_1=1}^{n_{up}}{T}_{up}+\sum _{n_2=1}^{n_{down}}{T}_{down}+\sum _{n_3=1}^{n_{jam}}{T}_{jam}+\sum _{n_4=1}^{n_{walk}}{T}_{walk}$$

(4)

where $T_{\mathrm{response}}$ is the response time from task issuance to the transporter’s start of execution, measured in seconds; $T_{\mathrm{act}}$ represents the active time required to complete a trip task, also measured in seconds; $T_{\mathrm{up}}$ and $T_{\mathrm{down}}$ denote the loading and unloading times, respectively, with $T_{\mathrm{up}}$ measured in seconds and $n_{\mathrm{up}}$ indicating the number of loadings, and $T_{\mathrm{down}}$ is the unloading time in seconds, with $n_{\mathrm{down}}$ representing the number of unloadings, set as a constant of 1 for this study; $T_{\mathrm{jam}}$ describes the waiting time due to road congestion during task execution, in seconds, with $n_{\mathrm{jam}}$ counting the number of stops due to congestion; and $T_{\mathrm{walk}}$ refers to the travel time of the transporters during task execution, measured in seconds, with $n_{\mathrm{walk}}$ counting the number of travel instances.

3.3. Model Establishment

3.3.1. Description of Dynamic Events

In the hilly orchard track transport system, dynamic scheduling is a key strategy for addressing constantly changing tasks. Unlike static scheduling, it can respond in real time to dynamic and emergency tasks [38], significantly enhancing system flexibility and efficiency. The system mainly faces two types of dynamic events: task disturbances and resource disturbances [39]. Task disturbances involve the random arrival of tasks and the handling of urgent tasks. During the fruit harvest season, the timing and quantity of fruit arrivals vary dynamically, making static scheduling insufficient. Additionally, emergency transport tasks for agricultural equipment often take a higher priority, requiring the scheduling system to quickly reallocate resources. Resource disturbances include transporter malfunctions or track congestion. To prevent such issues, all transporters undergo thorough debugging before starting tasks. Therefore, this model primarily focuses on task disturbances. Dynamic scheduling must handle urgent tasks while ensuring the smooth transport of regular goods. The scheduling method should flexibly manage the random arrival of tasks and adjust in real time to accommodate emergencies, enabling the transport system to operate efficiently under various conditions.

3.3.2. Rescheduling Methods

In the hilly and mountainous orchard rail transport system, dynamic scheduling faces the challenge of managing tasks with multiple loading points and a single unloading point. New tasks are constantly generated during transport. Rescheduling is crucial for addressing these issues by clearly defining specific operational procedures, including application positions, strategies, and timing of the scheduling algorithm.

• Rescheduling Locations

Rescheduling should take place at designated spots where the transporter is stationary and its location is fixed. The transporter’s location varies significantly while moving but is more easily determined when stopped, especially at preset loading and unloading points. Before each task begins, the transporter is dispatched from its initial position, which also serves as the unloading and task assignment point. After receiving tasks at this initial position, the transporter proceeds to the targeted loading point to load cargo. This design considers targeted loading points as potential rescheduling locations, facilitating adjustments to the original scheduling plan based on environmental parameters. Thus, rescheduling locations include the initial position and any cargo loading points.

2.

Rescheduling Strategies

Rescheduling strategies are categorised into two types: event-driven and period-driven. Event-driven scheduling is initiated by specific events, such as the availability of a transporter at the initial position and the presence of pending tasks at a task point. Decisions to deploy transporters are based on the match between the number of tasks and the availability of transporters. Period-driven scheduling is conducted at set intervals, typically starting with the deployment of one transporter at the beginning of each period, followed by subsequent transporters dispatched at fixed intervals. During the first cycle, multiple transporters may be dispatched simultaneously. As tasks progress, subsequent rescheduling usually involves only one transporter, ensuring continuity and efficiency.

3.

Rescheduling Parameters

In dynamic scheduling, tasks arrive randomly, leading to a gradual increase in the quantity of tasks at each point. As the transporter moves from its initial position to the targeted loading points, the quantity of tasks continually changes. Therefore, it is important to determine two key parameters: the number of each loading point and the cargo quantity corresponding to each loading point. These parameters are essential components of the transporter’s scheduling plan. If rescheduling is limited to the initial position, the scheduling algorithm must establish all loading point numbers and their corresponding cargo quantities before departure. If rescheduling includes other task stop points, it is possible to plan future loading point numbers and cargo quantities in advance. For the current loading point, the cargo quantity may be adjusted based on specific conditions to optimise loading efficiency. Consequently, the main dynamic rescheduling parameters include the loading point numbers and their corresponding cargo quantities.

3.3.3. Establishing the Objective Function and Constraints

The primary challenge in dynamic scheduling is the uncertainty of task arrival times, which prevents ensuring that each transporter is always fully loaded. Therefore, while the load rate is an important performance indicator, it cannot serve as a constraint in dynamic scheduling but only as a target for optimisation. The formula to calculate the load rate, ω, is given by:

$$\omega =⌈{\displaystyle \frac{{task}_{all}}{n_{load}}}⌉/n_c$$

(5)

In this equation, $tas{k}_{\mathrm{all}}$ refers to the total task quantity at all points at the end of the tasks, measured in boxes; $n_{\mathrm{load}}$ is the load capacity of a single transporter, also in boxes; $n_c$ is the total number of transporters required to complete all tasks, counted in transporters. The ceiling brackets ⌈ ⌉ are used to round up the result of ${\displaystyle \frac{tas{k}_{all}}{n_{load}}}$ to the nearest higher integer, which determines the minimum number of transporters needed. $n_c$ represents the actual number of transporters used.

Dynamic scheduling is time-oriented and simulates the entire transport process. The total task completion time, $T_{\mathrm{task}}$, is determined by the time the last transporter returns to the initial position and is influenced by the number of loading operations, occurrences of congestion, and the departure time of the last transporter. Furthermore, dynamic scheduling allows for rescheduling of loading quantities at loading points to adapt to the arrival of new tasks and changes in existing task quantities. To minimise the instances of transporters stopping at loading points with no tasks, a performance metric n₀ is introduced to represent the minimum number of transporter visits to empty task points. This metric has direct practical significance, as each empty stop wastes energy, increases mechanical wear on the braking and starting systems, and extends overall task completion time, thereby reducing operational efficiency. Therefore, the objective function for dynamic scheduling considers the maximum load rate ω, the shortest total task completion time T_task, and the minimum visits to empty task points n₀.

These targets reflect the impact of rescheduling methods, scheduling algorithm performance, and the rate of task generation. The load rate is the most crucial performance indicator, followed by the total task completion time, and finally, the number of transporter visits to empty task points is considered when the first two metrics are comparable.

The objective function for the dynamic scheduling model is:

$$\min f_1={[-\omega T_{\mathrm{task}}{n}_0]}^{\mathrm{T}}$$

(6)

where ω is maximized (equivalently, −ω is minimized), T_task is minimized, and n₀ is minimized. The load rate is the most crucial performance indicator, followed by the total task completion time, and finally, the number of transporter visits to empty task points.

The constraints are as follows:

(1)

The task quantity at each point must be completed entirely but not redundantly.

(2)

In the actual system, the sequence of transporter positions cannot be altered; hence, in the simulated transport process, the arrival time of any transporter at any position cannot be earlier than those who started later.

3.4. Dynamic Scheduling Methodology

To effectively address the dynamic arrival of tasks within the hilly orchard environment, our methodology proceeds in two distinct stages. First, we establish an optimal foundational scheduling structure by conducting a comparative evaluation of several candidate frameworks. Second, operating within this selected structure, we perform an extensive comparative analysis to identify promising approaches for the decision-making algorithm for the problem at hand.

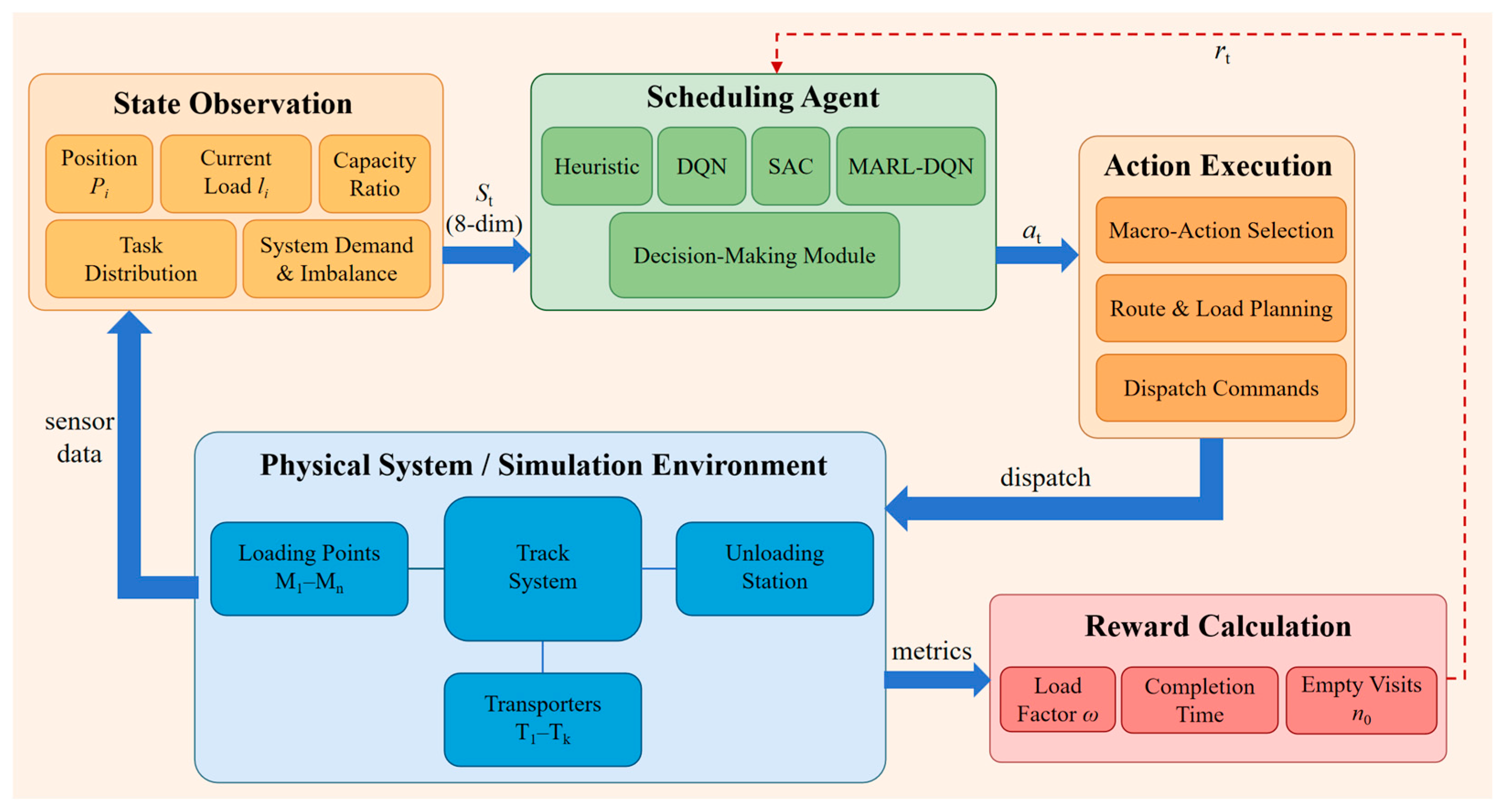
To provide a holistic view of the interaction between these stages, Figure 3 presents the system architecture of the proposed dynamic scheduling framework, illustrating the closed-loop data flow among five functional modules. The workflow initiates in the Physical System/Simulation Environment (Blue Block), which represents the hilly orchard track system and generates real-time sensor data. This raw data is aggregated by the State Observation (Yellow Block) module into a structured 8-dimensional state vector (S_t), encompassing key variables such as transporter position (P_i), current load (l_i), capacity ratio, and system-wide demand imbalance. Acting as the decision-making core, the Scheduling Agent (Green Block) receives this state input and selects an optimal policy using candidate algorithms (Heuristic, DQN, SAC, or MARL-DQN). The resulting policy decision is translated by the Action Execution (Orange Block) module into physical operations, handling macro-action selection, route planning, and dispatch command issuance. Finally, primarily during the training phase, the Reward Calculation (Red Block) module evaluates performance metrics, including load factor (ω), completion time, and empty visits (n₀), to generate a reward signal (r_t) that updates the agent’s policy, completing the feedback loop.

3.4.1. Framework Design

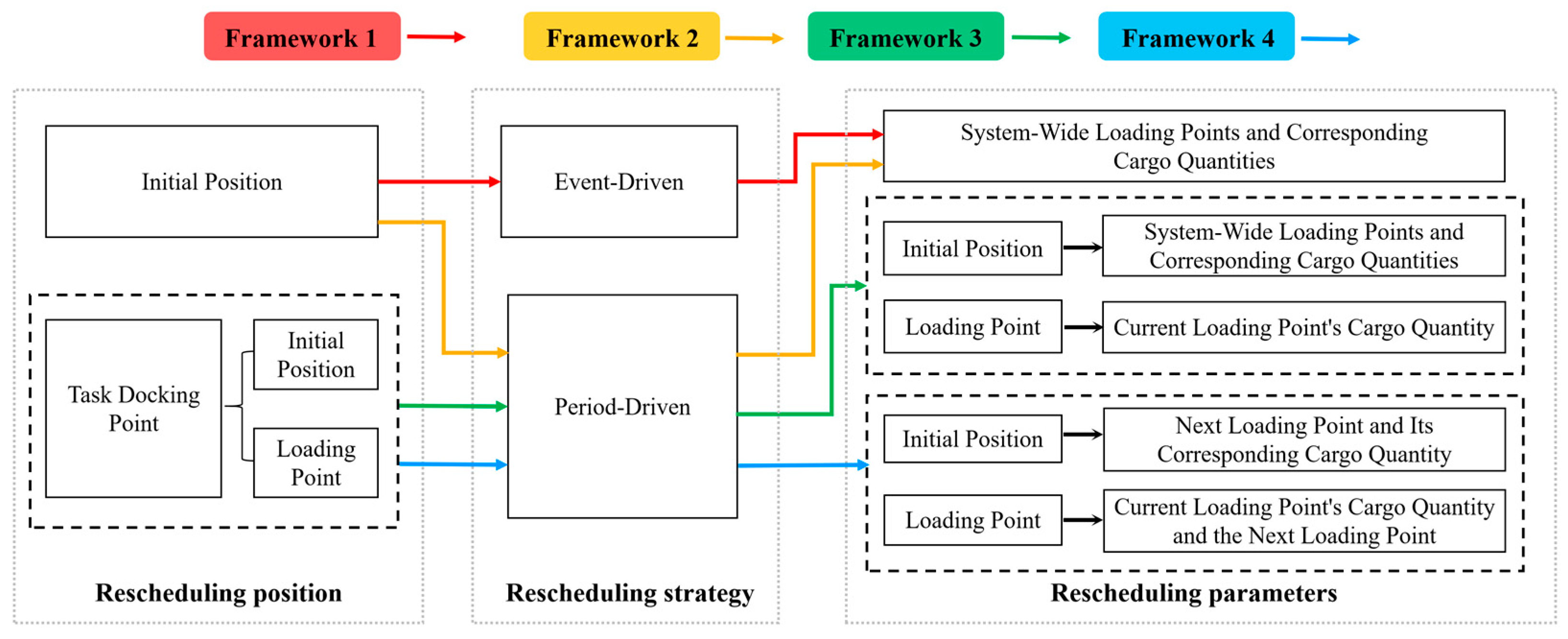
The proposed frameworks are each constructed from three core components: Rescheduling Position, Rescheduling Strategy, and Rescheduling Parameters. As illustrated in Figure 4, these frameworks are systematically differentiated across these three design dimensions. The diagram utilizes color-coded arrows to map the specific operational structure of each framework, visually highlighting the architectural differences through a feature-by-feature comparison detailed in

Table 1. Comparative analysis of the proposed scheduling frameworks.

Feature Dimension	Framework 1	Framework 2	Framework 3	Framework 4
	Event-Driven	Period-Driven Static	Period-Driven Hybrid	Period-Driven Sequential
1. Rescheduling Position	At the Initial Position only.	At the Initial Position only.	At each Task Docking Point (i.e., both Initial Position and Loading Points).	At each Task Docking Point (i.e., both Initial Position and Loading Points).
2. Rescheduling Strategy	Event-Driven: Triggered by transporter and task availability.	Period-Driven: Triggered by a fixed time interval.	Period-Driven: Same as Framework 2.	Period-Driven: Same as Framework 2.
3. Rescheduling Parameters	System-Wide: Determines all loading points and cargo quantities for the entire route at once.	System-Wide: Same as Framework 1.	Hybrid (System-Wide + Local): At Initial Position: Determines System-Wide loading points. At Loading Point: Adjusts the Current Loading Point’s cargo quantity.	Sequential (Local Only) At Initial Position: Determines only the Next Loading Point. At Loading Point: Adjusts the Current Point’s quantity and determines the Next Loading Point.
4. Core Design Philosophy	A simple, reactive model for immediate dispatch.	A structured model to regulate flow by making System-Wide plans periodically.	A balanced model that combines a System-Wide plan for stability with local adjustments for adaptability.	A highly flexible model that breaks the problem into a sequence of Next Loading Point decisions.
5. Hypothesized Outcome and Trade-Offs	Fast but Inefficient: Shortest delay, but at a high risk of poor load factors.	Efficient but Slow: High load factors due to System-Wide planning, but at a risk of longer task times.	The Optimal Balance: Hypothesized to combine the efficiency of a System-Wide plan with superior temporal performance.	Flexibility vs. Myopia Risk: The focus on the Next Loading Point creates a significant risk of poor system-level coordination and globally inefficient routes.

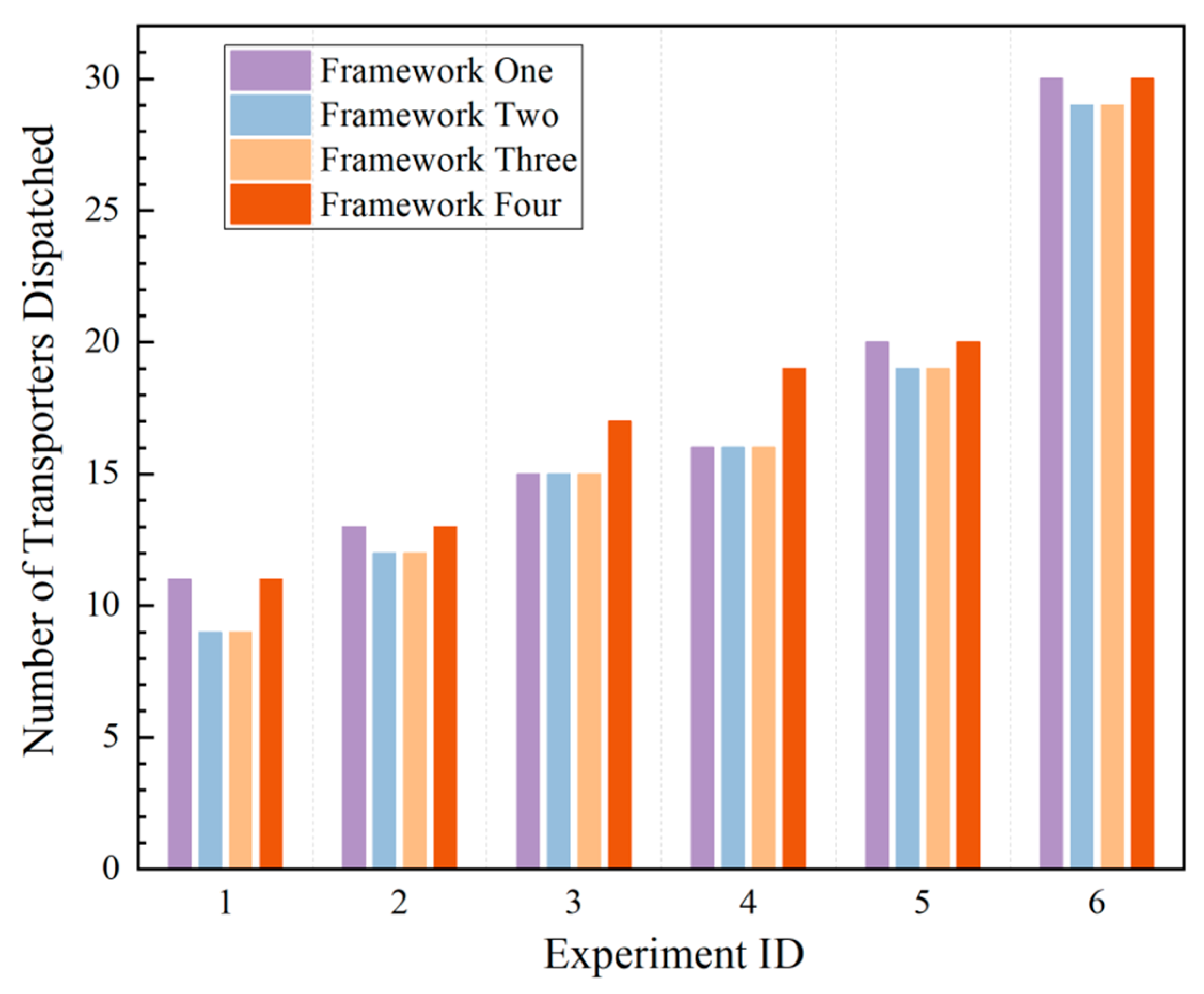
. For a complete technical breakdown of all four frameworks, including detailed flowcharts and corresponding pseudocode, please refer to Appendix A (Figure A1, Figure A2, Figure A3 and Figure A4 and Algorithms A1–A4, respectively). As will be quantitatively demonstrated in the experimental results (Section 4.2), preliminary analysis revealed that Framework 3 provides the optimal performance trade-off. Consequently, it was selected as the foundational platform for the in-depth algorithmic comparisons central to this study.

3.4.2. Action Space Design: A Heuristic Rule Set as Macro-Actions

To enable the reinforcement learning agents to focus on high-level strategic decision-making rather than low-level micro-operations, we designed a discrete action space composed of six heuristic rules. This “Macro-Action” design philosophy is a core component of our methodology. It abstracts the complex decision-making problem into a higher-level strategic choice: “Given the current system state, which scheduling policy is most efficient?” This approach not only significantly reduces the exploration difficulty for the learning algorithm but also serves as a powerful method for embedding domain knowledge into the RL framework.

These six heuristic rules are designed to encapsulate four distinct, widely applied priority concepts in scheduling, aiming to explore solutions from different dimensions:

• Position-based Priority (Rules 1–2): The core of these rules is route optimization. They make decisions based on the physical location of task points, such as prioritizing those farthest from or closest to the origin, intending to minimize the transporter’s total travel distance.
• Task Quantity-based Priority (Rules 3–4): These rules are a direct embodiment of a greedy strategy. They always prioritize task points with the largest current backlog of goods, representing the most intuitive policy for rapidly clearing system-wide tasks.
• Historical Fairness-based Priority (Rule 5): This rule introduces a temporal dimension. It prioritizes task points that have been visited least frequently, aiming to prevent the long-term neglect of certain points due to uneven resource allocation and thus improving overall system fairness and responsiveness.
• Future Trend-based Priority (Rule 6): This rule introduces a predictive perspective. It prioritizes serving “hot” task points with the highest average task generation rate, aiming to proactively manage and control task growth at its source to maintain long-term system stability.

By learning to dynamically combine and switch between these macro-actions, which represent different scheduling philosophies, the reinforcement learning agent is expected to discover a superior, adaptive high-level policy that surpasses any single fixed rule. The specific implementation steps for these six rules are detailed in Appendix B.

3.4.3. Comparative Algorithm Design: A Duel of Decision-Making Paradigms

Having established the optimal scheduling platform (Framework 3) and defined a common macro-action space, this study aims to systematically evaluate a core scientific question: which decision-making paradigm can most effectively learn and utilize this action space? To this end, we designed and implemented a comparative experimental framework encompassing four representative methodologies. This framework is intended to rigorously investigate the performance trade-offs of different computational intelligence paradigms in solving complex dynamic scheduling problems through empirical research.

• Heuristic Baseline

To establish a reliable performance benchmark for non-learning methods, we selected the “Prioritise by Task Quantity” rule from the set defined in Section 3.4.2. This rule represents a direct, traditional scheduling philosophy with extremely low computational cost. Its performance serves as a reference point to measure the effectiveness of all subsequent learning-based algorithms.

2.

Conventional Single-Agent Baseline: Deep Q-Network (DQN)

To introduce learning capabilities, we first implemented the classic DQN algorithm [40] as a conventional reinforcement learning baseline. In this configuration, the entire multi-transporter system is treated as a single macroscopic entity, controlled by one central DQN agent. This agent receives the global state of the entire system (detailed in Section 3.4.4) and selects one of the six macro-actions defined in Section 3.4.2. 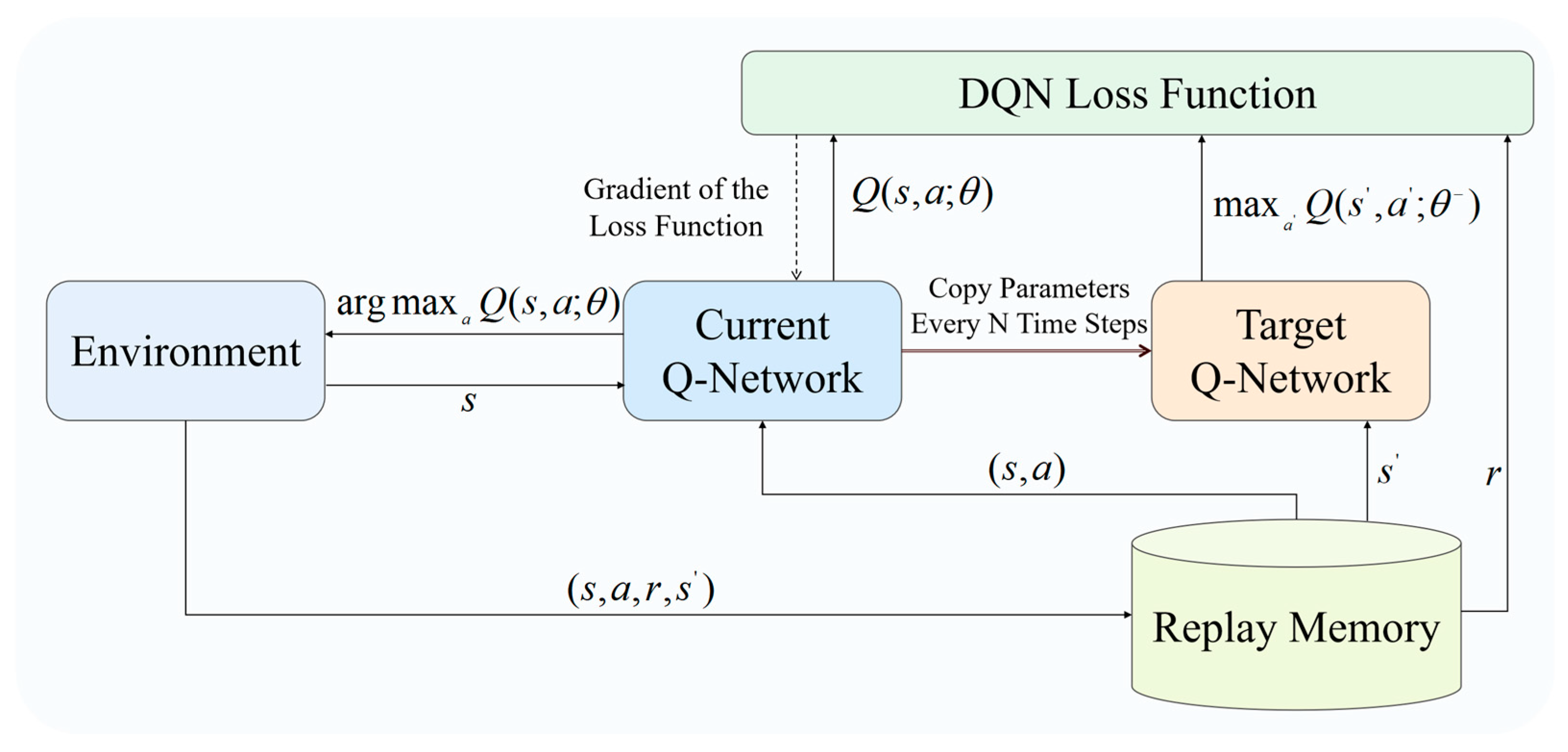Figure 5 illustrates the DQN architecture. The agent observes the environment state s, selects an action a via its Q-network, and the environment returns a reward r and a new state s’. This transition (s, a, r, s’) is stored in the experience replay memory. During training, batches are sampled from this memory to update the network parameters.

3.

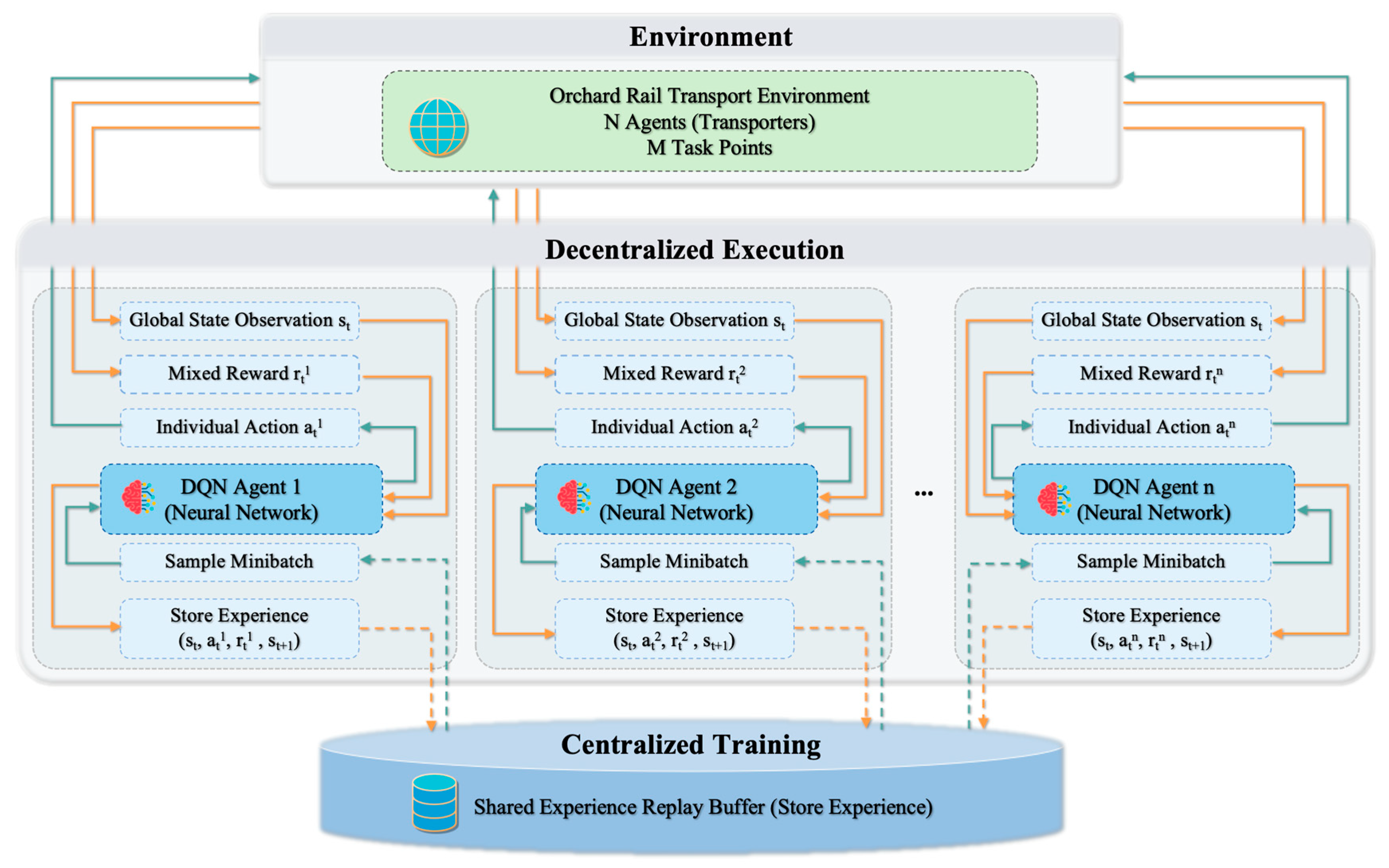
Decentralized Paradigm: Multi-Agent DQN (MARL-DQN)

To more realistically capture the operation of multiple transporters as independent decision-making units, we implemented a Multi-Agent Deep Q-Network (MARL-DQN) as the decentralized paradigm, illustrated in Figure 6. Unlike the conventional DQN, which amalgamates all vehicles into a single entity, MARL-DQN adopts the “Centralized Training with Decentralized Execution” (CTDE) framework. During the execution phase, each transporter is modeled as an individual DQN agent, selecting and executing actions based solely on its local observations and interacting independently with the environment. During the training phase, the experiences generated by all agents are aggregated into a shared replay buffer. Each agent then independently samples from this shared buffer to update its network parameters. This allows agents to learn from the collective experience of the system rather than from isolated individual trajectories, fostering a more cooperative policy without the burden of explicit communication. Furthermore, this design balances scalability with training stability and can, to some extent, mitigate the non-stationarity inherent in multi-agent learning.

4.

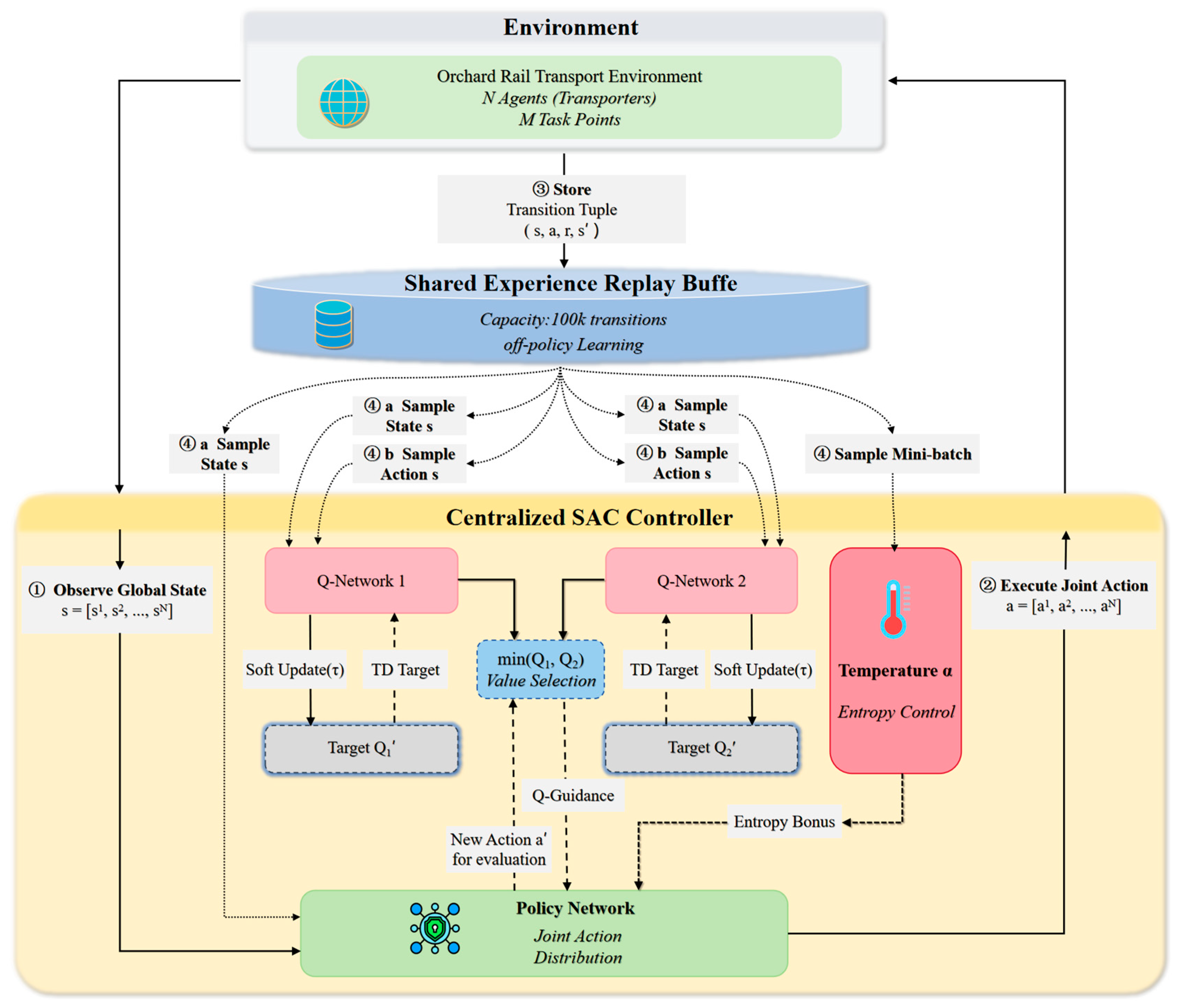
Centralized Paradigm: Soft Actor–Critic (SAC)

To explore the upper-performance bounds of a centralized control paradigm possessing complete global information and conducting top-level unified planning, we introduced the advanced Soft Actor–Critic (SAC) algorithm. As illustrated in Figure 7, which shows the centralized SAC controller architecture, the controller observes the global state and outputs a joint action via its policy network. The value networks (Q-Networks) evaluate the action, and exploration is promoted by maximizing an entropy-based reward. As a unified central controller, SAC’s operational mechanism is fundamentally different from the DQN family. It employs an Actor–Critic architecture and optimizes based on a maximum entropy framework. This framework, by maximizing policy stochasticity concurrently with reward maximization, dramatically enhances the algorithm’s exploration capabilities and robustness, which is key to its powerful performance. In this study, the SAC controller receives the global state and directly outputs the joint action decision for all transporters, representing a “globally optimal” planning approach for solving such highly coordinated problems.

3.4.4. Reinforcement Learning Formulation

Our scheduling problem is formulated as a distributed multi-agent reinforcement learning (MARL) framework where each of the N = 4 transporter agents learns an independent policy based on local observations. This decentralized design enables scalable real-time decision-making suitable for resource-constrained orchard environments.

• State Space

Each agent i observes an 8-dimensional state vector $s_i\in {\mathbb{R}}^8$ comprising: (1) vehicle-specific features (position, load, time progress), (2) task distribution at representative nodes (queues at nodes 1 and 4, cumulative system demand), and (3) global coordination signals (cumulative system demand, load imbalance indicator). This design prioritizes information density while retaining essential coordination information. All features are normalized to [−1, 1] to facilitate neural network training. Complete mathematical specifications are provided in Appendix C.1.

2.

Action Space

Each agent selects from a discrete action space ${\mathrm{A}}_i=\{a_0, a_1,\dots , a_k\}$ where a₀ represents waiting and a_k (k > 0) represents navigating to task node k. For our configuration with M = 8 task points, the action space is limited to the 6 most frequently accessed nodes, yielding $|{\mathrm{A}}_i| = 6$. All agents execute actions concurrently in a fully decentralized manner.

3.

Reward Function

The reward function encourages task completion while promoting operational efficiency:

$$r_i = \alpha ·r_i^{\mathrm{task}}+\beta ·r_i^{\mathrm{efficiency}}+\gamma ·r_i^{\mathrm{penalty}}$$

(7)

where $r_i^{\mathrm{task}}$ rewards loading/unloading operations (+10 each), $r_i^{\mathrm{efficiency}}$ incentivizes high load factors and penalizes empty travel, and $r_i^{\mathrm{penalty}}$ discourages idle time and invalid actions. Through sensitivity analysis, we determined optimal weights α = 1.0, β = 0.5, γ = −1.0. The ratio β/α = 0.5 balances task completion priority with efficiency optimization. Detailed component definitions are provided in Appendix C.2.

4.

Learning Objective

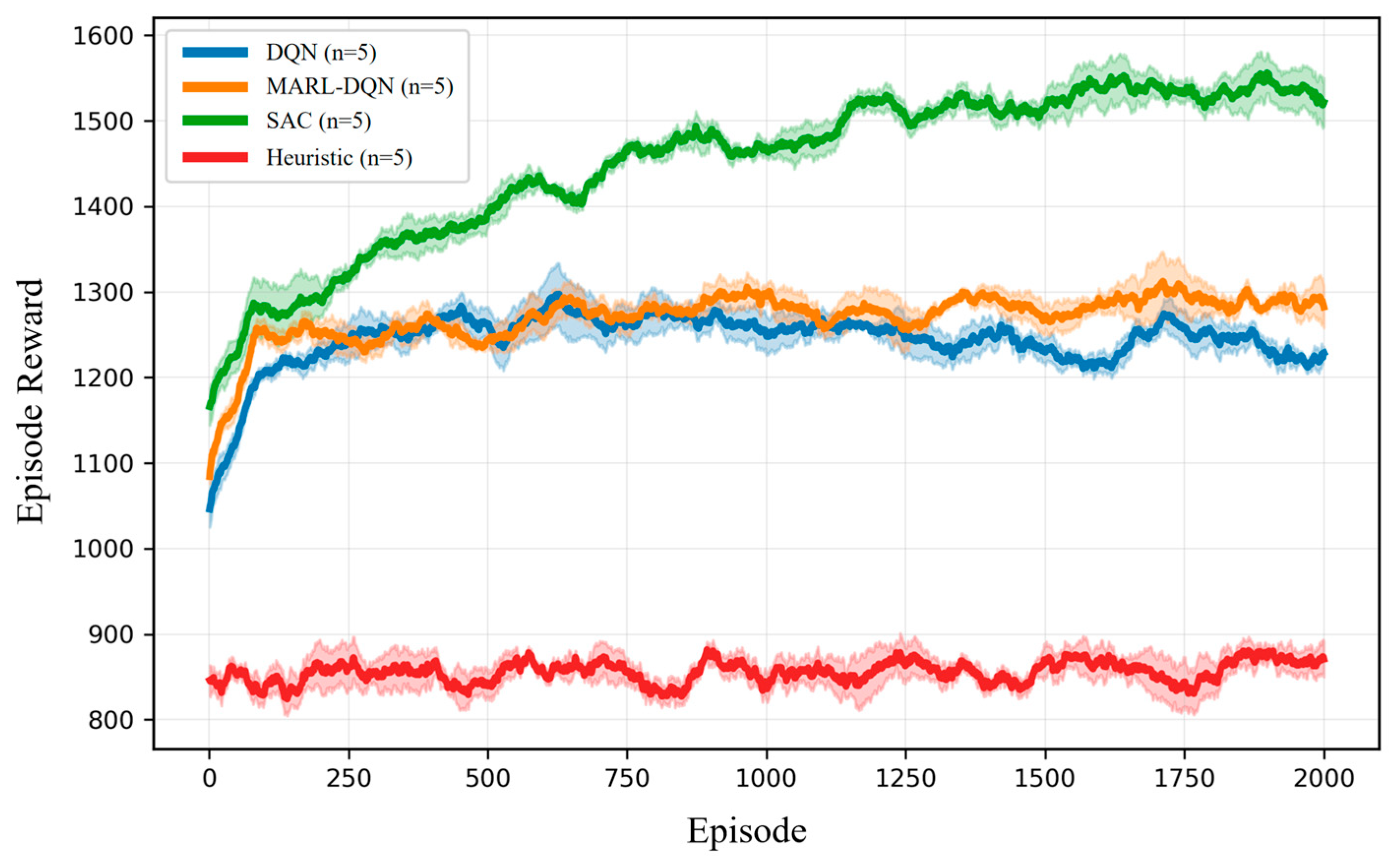
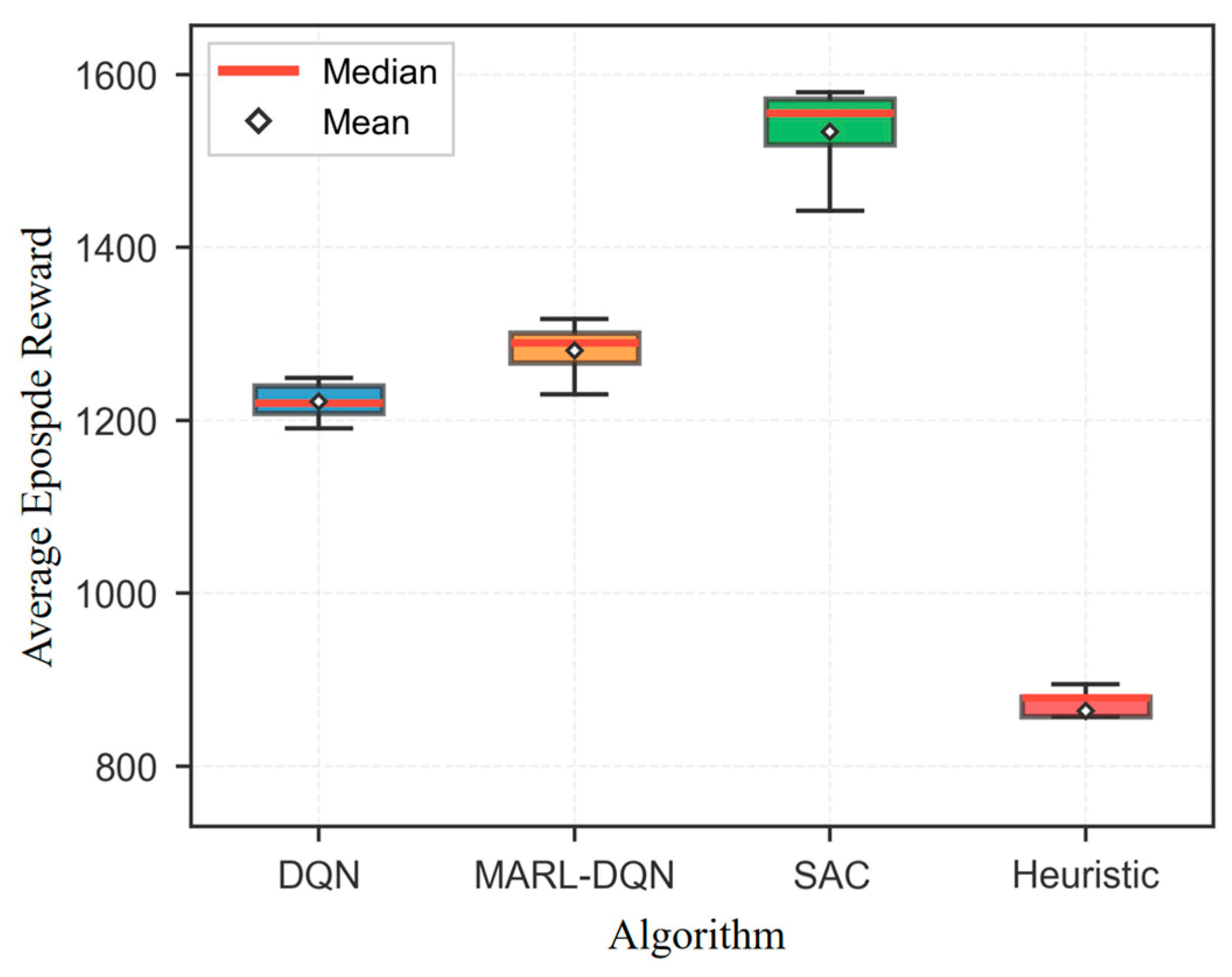
Each agent i learns a policy ${\pi }_i$ maximizing expected cumulative discounted reward $\mathrm{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_{i,t}\right]$ with discount factor γ = 0.95. Agents are trained over T_max = 3000 time steps per episode using deep reinforcement learning algorithms (DQN, SAC, MARL-DQN; see Section 3.4.3), typically converging within 1500–2000 episodes. While agents learn independently without explicit communication, coordination emerges implicitly through shared environment dynamics and global state signals.

3.4.5. Training Strategy and Hyperparameter Configuration

To ensure that all learning-based agents converge stably to their optimal performance within the complex scheduling environment, and to guarantee absolute fairness in the algorithmic comparison, we designed a standardized training pipeline. This pipeline incorporates both curriculum learning and systematic hyperparameter tuning.

• Training Acceleration Strategy: Curriculum Learning

Training an RL agent from scratch directly in the complex environment (e.g., 4 transporters and 8 task nodes) presents significant challenges, including the curse of dimensionality and sparse rewards, often making it difficult to learn an effective policy. To overcome this hurdle, we uniformly adopted a Curriculum Learning (CL) strategy for all learning-based algorithms (DQN, MARL-DQN, and SAC).

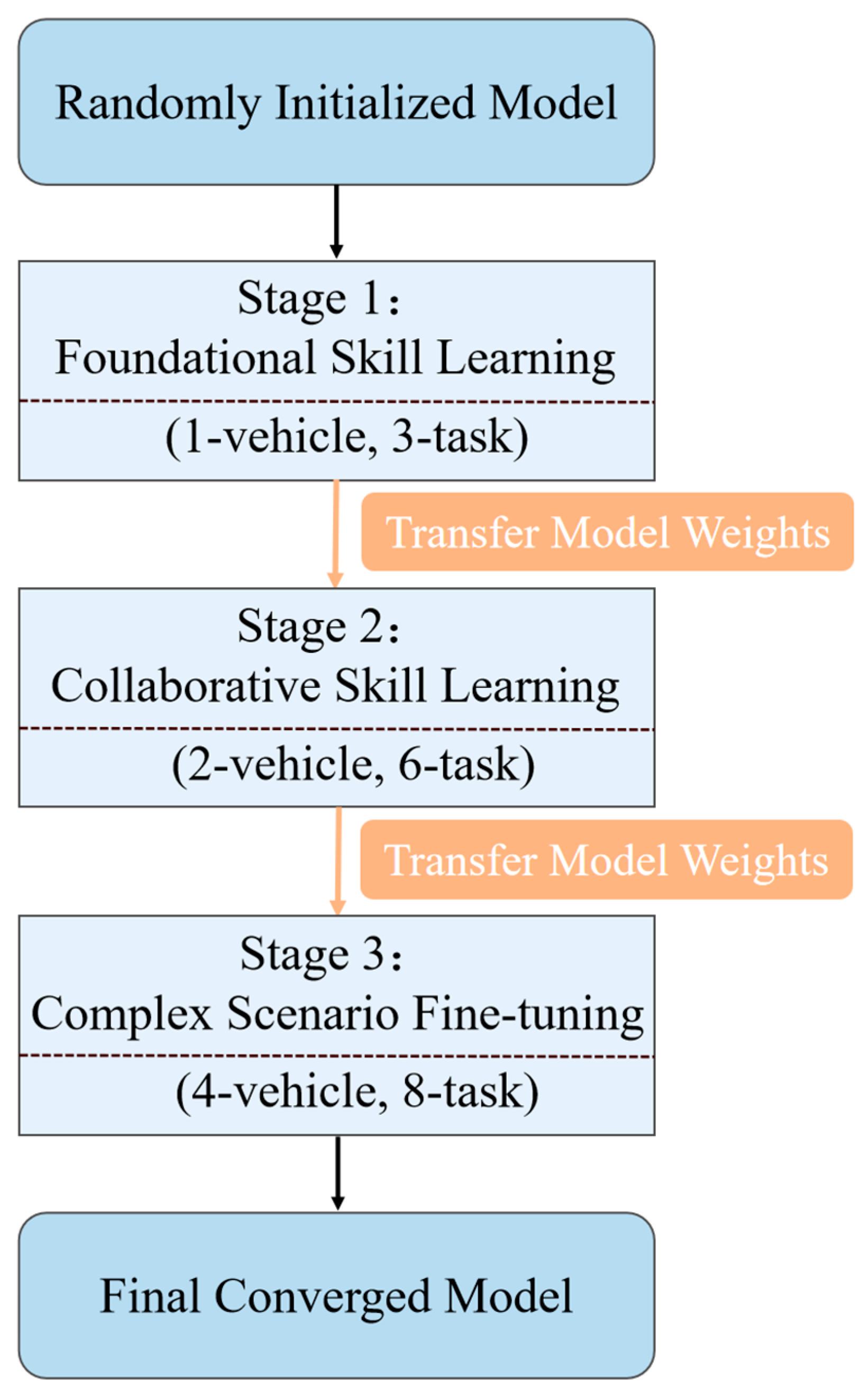
As illustrated in Figure 8, the core idea of curriculum learning is to decompose the complex learning objective into a sequence of sub-tasks with increasing difficulty. The agent first masters fundamental skills in a simple environment, and then, the learned knowledge (i.e., model weights) is transferred to a more complex environment for fine-tuning. The specific curriculum is set as follows:

• Phase 1: Basic Skills Learning (1-Transporter, 3-Task Nodes): The agent learns the fundamental logic of task selection and transport in the simplest setting.
• Phase 2: Collaborative Skills Learning (2-Transporters, 6-Task Nodes): The agent inherits the knowledge from the previous phase and begins to learn collaborative strategies between two agents.
• Phase 3: Complex Scenario Fine-Tuning (4-Transporters, 8-Task Nodes): The agent inherits the collaborative skills and performs final policy refinement in the complex environment that precisely matches our final testing scenario.

This “easy-to-hard” training paradigm significantly improves training stability and convergence speed, and it contributes to our ability to obtain high-performance policies in such a complex environment.

Figure 8. The Curriculum Learning (CL) training pipeline, showing the three-stage process with model weight transfer.

Figure 8. The Curriculum Learning (CL) training pipeline, showing the three-stage process with model weight transfer.

2.

Hyperparameter Configuration and Tuning

A fair algorithmic comparison is highly dependent on robust hyperparameter tuning. We employed a systematic methodology to determine the key hyperparameters.

Table 2. Hyperparameter configuration for reinforcement learning algorithms.

Categories	Parameter	DQN	MARL-DQN	SAC (Centralized)
Network Architecture	State Dimension (per agent)	8	8	8
	Number of Agents	1	4	4
	Action Dimension	6	6	6
	Hidden Layers	[64, 32, 16]	[64, 32, 16]	[64, 64]
Learning Parameters	Learning Rate	0.001	0.0001	0.0003 *
	Discount Factor (γ)	0.95	0.98	0.99
	Soft Update (τ)	–	0.005	0.005
	Entropy Temperature (α)	–	–	0.2
	Target Update Freq.	100	100	–
Exploration and Experience Replay	Initial Exploration (ϵ0)	0.9	0.9	–
	Minimum Exploration (ϵmin)	0.05	0.05	–
	Exploration Decay	0.9995	0.9990	–
	Memory Size	10,000	10,000	100,000
	Batch Size	2048	2048	2048

Note: * For SAC, Actor, Critic, and Alpha learning rates are identical (0.0003).

summarizes the final core hyperparameter configurations used for all learning-based algorithms in this study. These values were determined through a multi-stage process: first, we established initial parameter search ranges based on academic literature in related fields; second, we further narrowed the potential range of optimal parameters through preliminary exploratory experiments; finally, we conducted systematic hyperparameter tuning to identify robust parameter settings for our comparative evaluation. This process validated the robustness of our chosen parameters and supported fair comparisons across all algorithms.

State dimension represents the observation space for each individual agent. MARL-DQN employs distributed execution with 4 independent agents, each observing an 8-dimensional state vector. SAC uses centralized control over 4 agents, with each agent’s observation contributing to a global state representation. See Appendix C.1 for detailed state space formulation. Action dimension of 6 comprises one waiting action plus five task node navigation actions, adaptively simplified from the full 8-node environment to maintain tractable learning complexity while retaining sufficient decision-making flexibility.

3.5. Emergency Task Response Strategies

Having established a comprehensive methodology for regular dynamic tasks, this study further investigates the system’s response capabilities when confronted with high-priority, emergent events. Emergency tasks, such as the urgent transport of agricultural equipment, differ fundamentally from routine goods transport in their objectives and constraints. They primarily emphasize response timeliness and the minimization of disruption to regular operations. Accordingly, we first established a distinct mathematical model and set of optimization objectives specifically for this emergency task scenario. Subsequently, building upon our established optimal platform, Framework 3, we designed and proposed two distinct emergency response strategies (Strategy 1 and Strategy 2). The objective of this comparison is to explore how different scheduling logics affect overall system efficiency while ensuring the high priority of emergency tasks is met.

• Model Establishment

The priority of emergency tasks is higher than that of regular goods in events of random task arrivals, and these tasks cannot be combined with other tasks for carpooling transport. The set of emergency tasks is represented as $U_{\mathrm{task}}=\{[{\mathrm{t}}^u, M_j^u, M_{j^{\prime }}^u]|u=1, 2,\dots , n_u; j(j^{\prime })=1, 2,\dots , n; j\ne j^{\prime }\}$, where t^u is the time when the uth emergency task occurs. $M_j^u$ and $M_{j^{\prime }}^u$ are the loading and unloading points for this emergency task, respectively, and must not be the same task point. 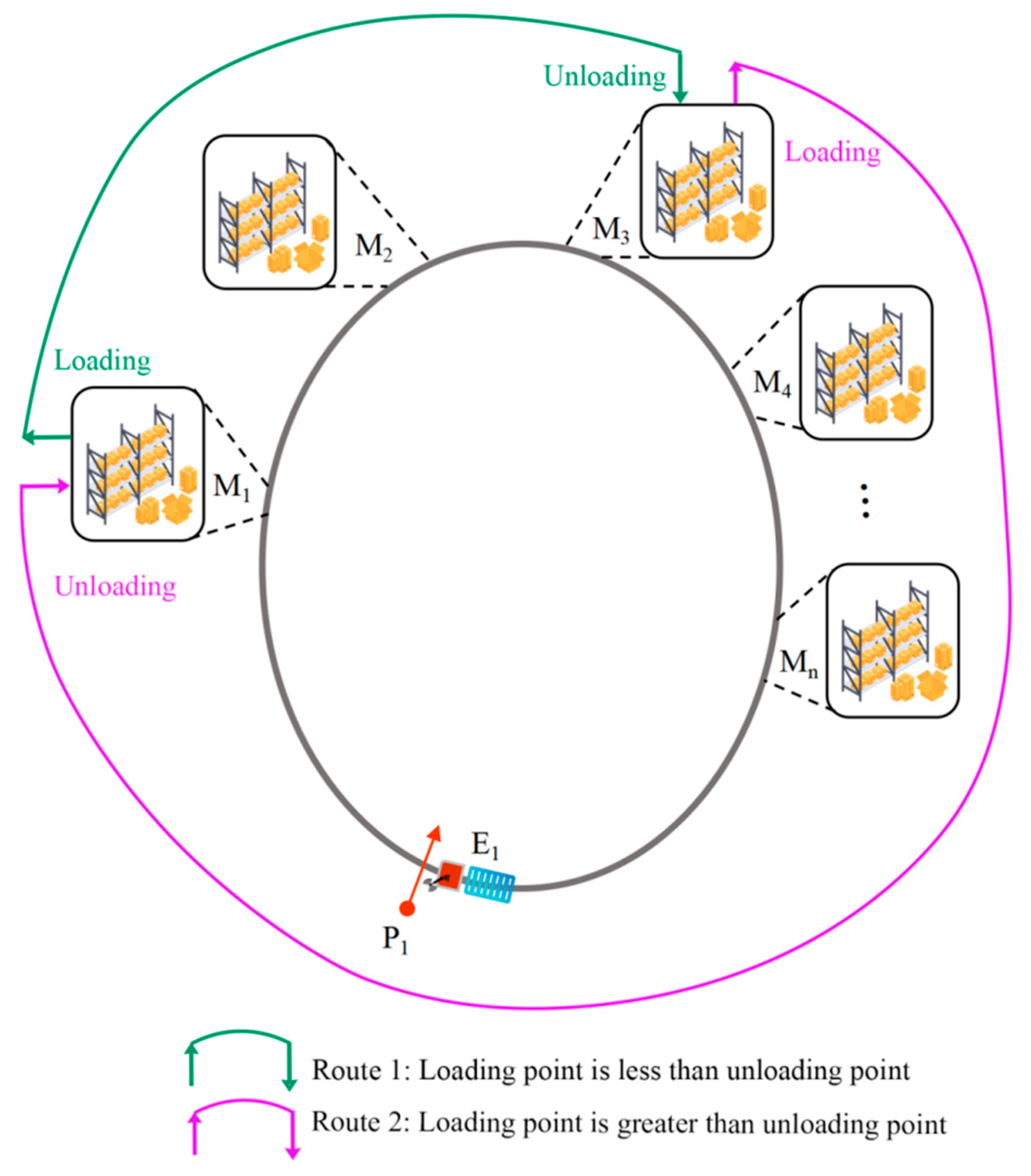$n_u$ is the total number of emergency tasks. As shown in Figure 9, if the loading point number $M_j^u$ is less than the unloading point number $M_{j^{\prime }}^u$, the task flow direction matches the direction of the transporter’s movement, as depicted by the green trajectory; the emergency task can be completed without passing through the initial position. Conversely, if the loading point number $M_j^u$ is greater than the unloading point number $M_{j^{\prime }}^u$, since the transporter can only move in one direction and cannot reverse, as illustrated by the purple trajectory, it must travel via the initial position after loading to reach the unloading point.

Transporting ordinary goods primarily focuses on devising a scheduling plan that enables transporters to reach full capacity at the fewest possible task points. In contrast, transporting emergency tasks emphasises the timing of the task, the start and end positions, and the status of each transporter. The goal is to determine the transporter number to complete emergency tasks as quickly as possible while minimising the impact on the originally planned transport of ordinary goods. The objective function $f_2$ for the dynamic scheduling model with randomly arriving emergency tasks is established as follows:

$$T_d={\displaystyle \frac{\sum _{u=1}^{n_u}\left(t_r^u-t^u\right)}{n_u}}$$

(8)

$$G_d=\left[\right({\omega }_a-{\omega }_y\left)\right(n_y-n_a\left)\right]$$

(9)

$$min{f}_2={\left[T_d{ G}_d\right]}^T$$

(10)

In the formula, $t_r^u$ represents the time when the system responds to the uth emergency task and assigns a transporter number. $T_d$ is the average difference between the system response time and the emergency task occurrence time, used to assess the response speed to emergency tasks. A smaller difference indicates a faster system response, with a zero difference signifying an immediate response. ${\omega }_a$ and $n_a$ represent the load rate and the number of rescheduling occurrences, respectively, when there are no emergency tasks and only ordinary goods arrive randomly. ${\omega }_y$ and $n_y$ represent the load rate and the number of rescheduling occurrences, respectively, under the same conditions of ordinary goods arriving randomly, but with emergency tasks present. $G_d$ is used to assess the impact of emergency tasks on the originally planned transport. Larger differences in $G_d$ indicate a greater negative impact on the transport of ordinary goods, with a zero difference indicating no impact.

The model assumptions and constraints are consistent with those under random task arrival events.

2.

Framework Design

The system primarily responds to random demands for ordinary goods before any emergency tasks arise. When an emergency task occurs, it is prioritised, and the transport of ordinary goods is either delayed or replanned. After the emergency task is completed, the system resumes responding to ordinary goods. Previously, in Section 3.4.1 “Framework Design”, four scheduling frameworks were proposed and tested with different rescheduling methods aimed at improvement. Experiments showed that Framework 3 was the most effective (see detailed analysis in Section 4.2). Based on Framework 3, two emergency task response strategies are proposed. The selection between these strategies depends on the operational tolerance for schedule adjustments. Strategy 1 (Initial-Position-Based Response) is applied when the system requires strict adherence to the pre-planned schedule. By restricting emergency dispatch to transporters at the initial position, it ensures zero additional rescheduling events for existing on-track tasks, making it suitable for scenarios where system stability is the absolute priority. In contrast, Strategy 2 (Proximity-Based Preemptive Response) is designated for scenarios where response timeliness is the primary objective. It employs a proximity-based logic to preempt the nearest eligible empty transporter; while this incurs a moderate increase in rescheduling events, our analysis demonstrates that this strategy achieves significantly faster response times without compromising the system’s core load efficiency.

• Strategy 1

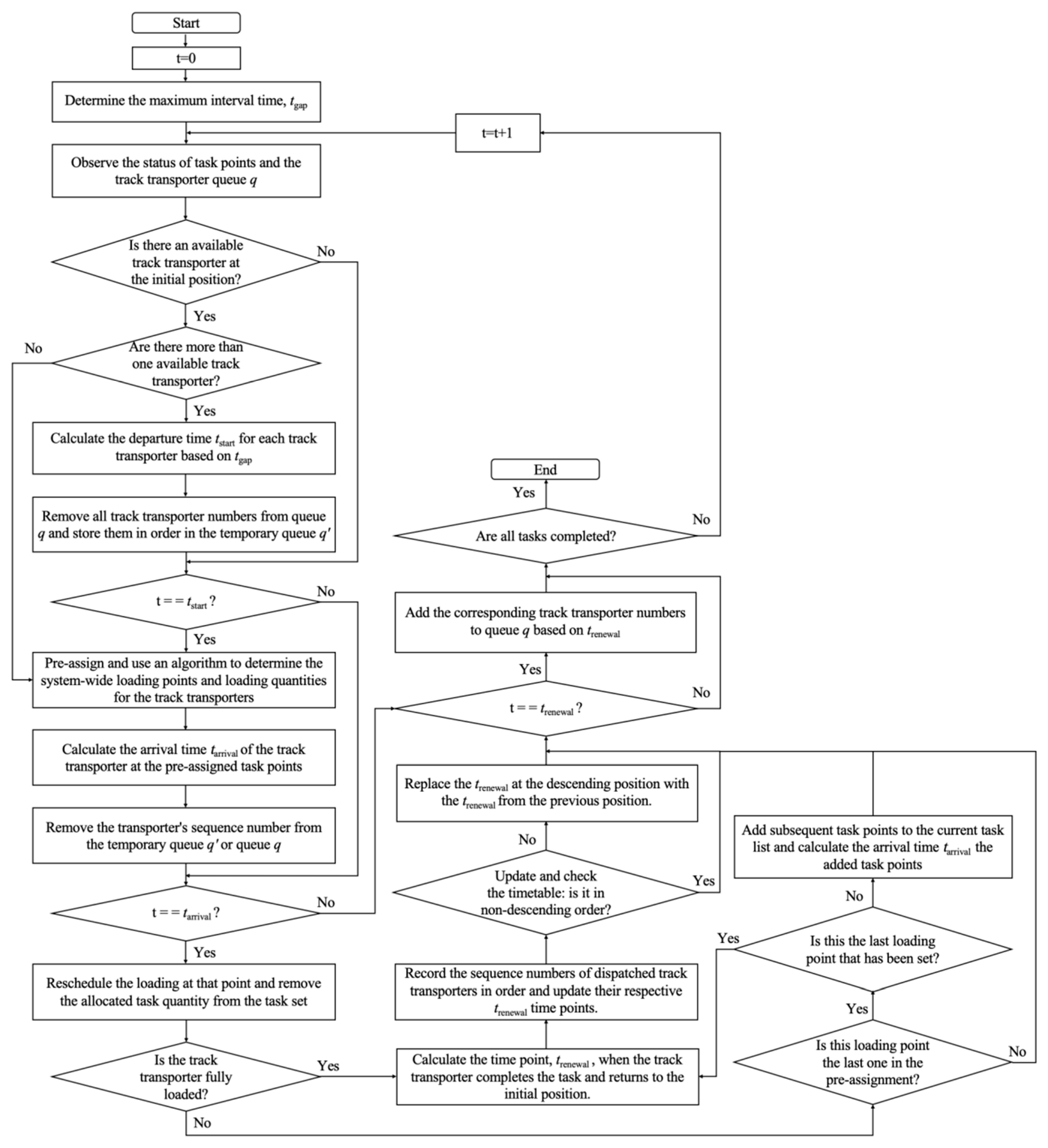
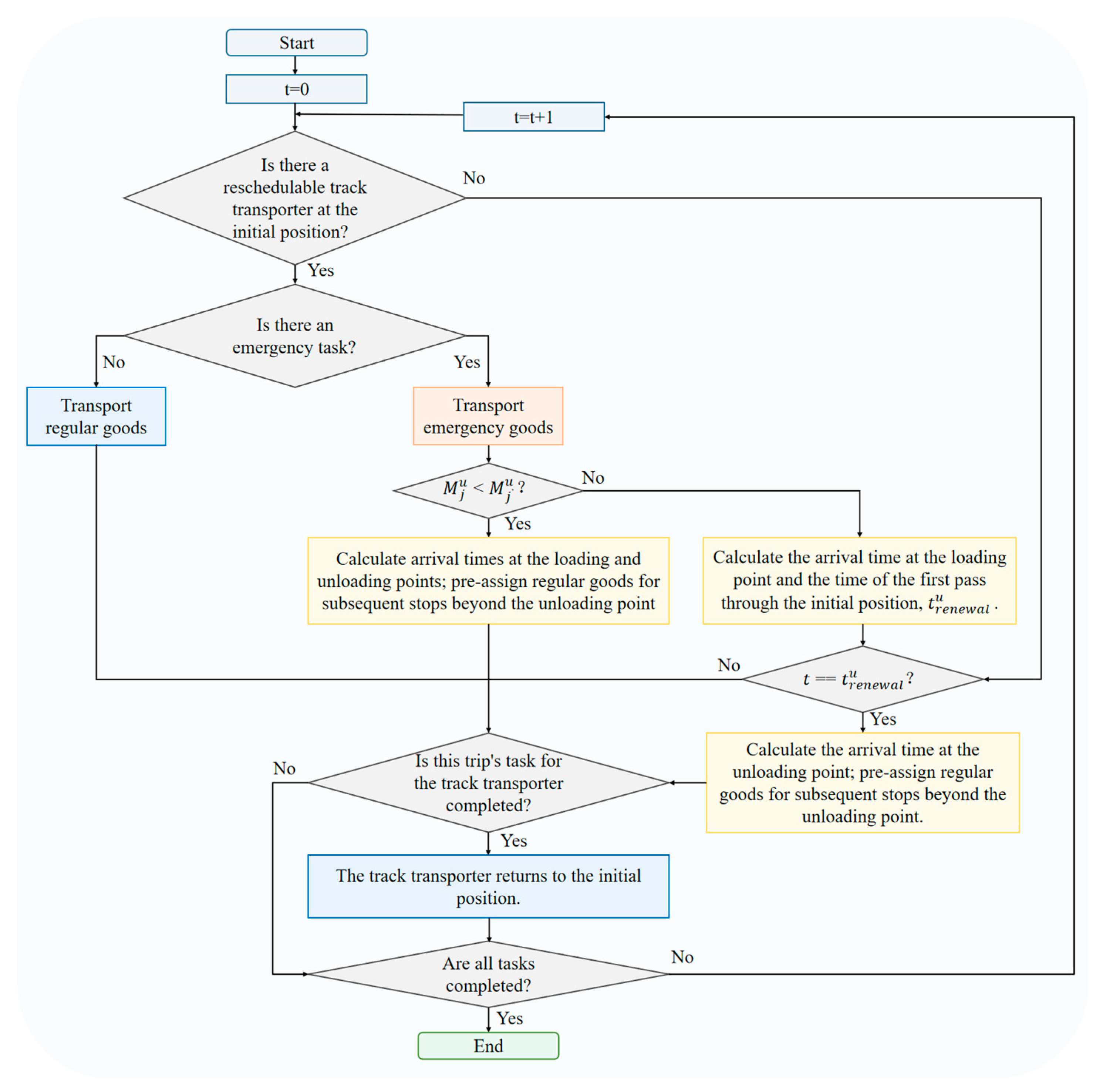
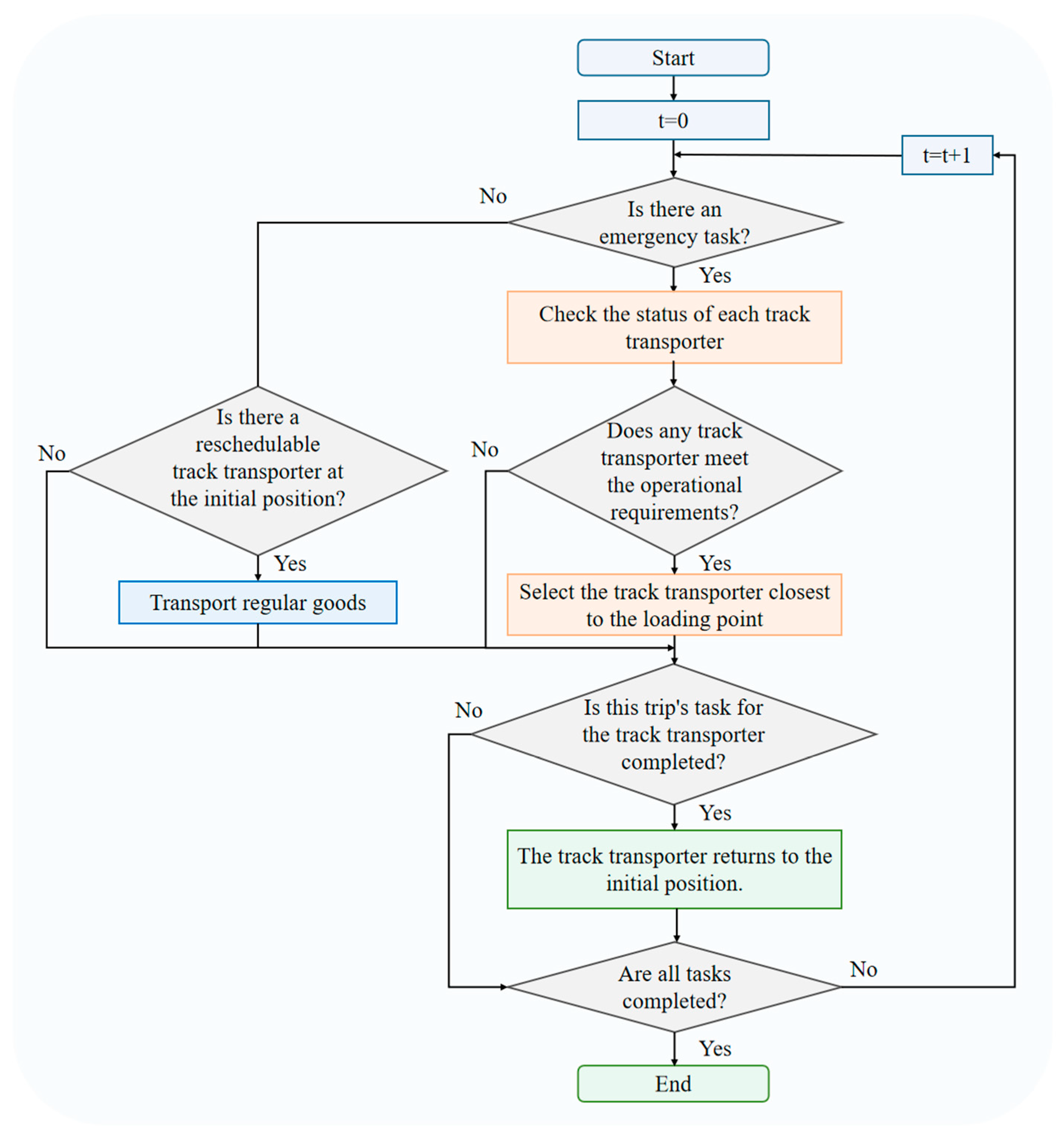
Strategy 1 responds to emergency tasks based on the periodic scheduling strategy of Framework 3. In Framework 3, the initial position is a key site for pre-allocating the system-wide loading points and quantities of regular goods. Adjustments to the actual loading quantities or additions of extra task points can be made at the target loading points. However, rescheduling at other locations is not permitted. Thus, Framework 3 ensures that transporters are assigned specific tasks before departing from the initial position. When an emergency task occurs, the first available transporter at the initial position can be used to prioritise the emergency task. After completing the emergency task, the transporter returns to the initial position to prepare for the next round of scheduling. If returning empty, the transporter may pass through the unloading point of the emergency task and subsequent task points to transport regular goods en route. The related algorithmic flowchart is detailed in Figure 10.

The specific steps are summarised as follows:

Step 1:

Initialise the Algorithm Parameters.

Step 2:

Regularly Update Both Ordinary and Emergency Tasks.

Step 3:

At the current time point t, if transporters are available at the initial position and no emergency tasks are present, transport ordinary goods and proceed to Step 5. If both emergency and ordinary tasks are present, the transporter prioritises the emergency task. If the loading point of the emergency task is less than the unloading point, calculate the arrival times to the emergency task’s loading and unloading points. Pre-allocate the unloading point and subsequent ordinary goods and then proceed to Step 5. If the loading point is greater than the unloading point, calculate the time to reach the emergency task’s loading point and the time ${\mathrm{t}}_{\mathrm{renewal}}^u$ for passing the initial position with emergency goods. If no transporters are available, proceed to Step 4.

Step 4:

If the current time point t equals ${\mathrm{t}}_{\mathrm{renewal}}^u$, the transporter passes the initial position. At this time, calculate the arrival time to the emergency task’s unloading point and pre-allocate the unloading point and subsequent ordinary goods. If t does not equal any ${\mathrm{t}}_{\mathrm{renewal}}^u$, proceed to Step 5.

Step 5:

If at the current time point t the transporter has completed its trip, it returns to the initial position ready for the next task. If the trip is not completed, proceed to Step 6.

Step 6:

Determine if all tasks are completed. If not, continue the scheduling, increment the time point t by 1, and return to Step 2. If all tasks are completed, the scheduling ends and the complete scheduling plan is output.

• Strategy 2

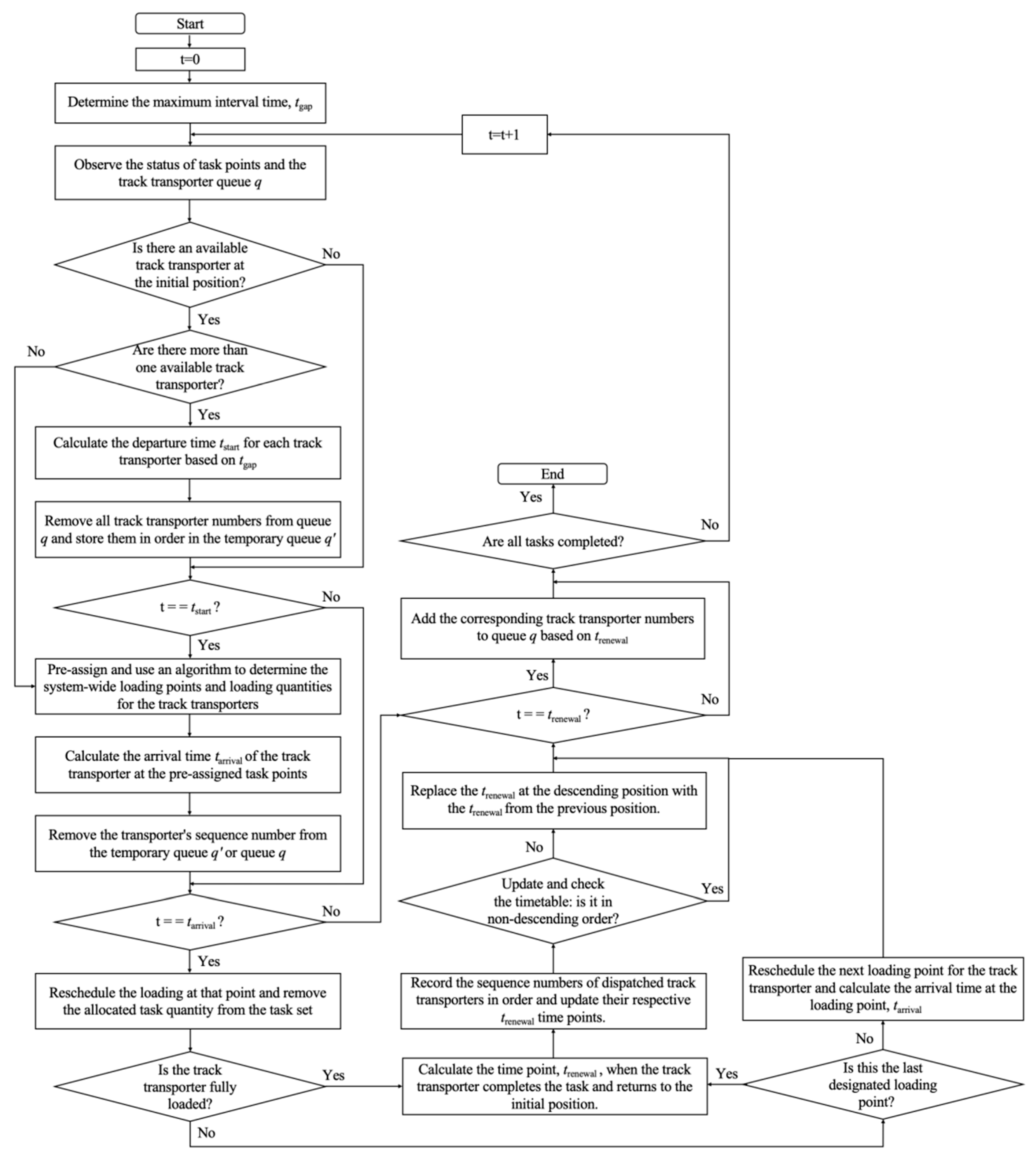
When an emergency task arises, transporters eligible to execute such tasks must meet the following criteria: they must be positioned before the target loading point and must not be carrying any regular goods. To respond to emergency tasks most rapidly, a proximity strategy will be employed, prioritising the nearest empty transporter to the target loading point.

Situation 1:

As described in Strategy 1, if there is an available empty transporter at the initial position ready for rescheduling, it will be prioritised for the emergency task. After completing the emergency task, the transporter can continue to carry regular goods if it passes other task points.

Situation 2:

If a transporter has been assigned a regular goods task but is still empty and appropriately located when the emergency task signal is received, its original regular goods task will be cancelled in favour of prioritising the emergency task. After completing the emergency task, the transporter will also execute subsequent regular goods tasks along the route.

Situation 3:

For transporters assigned to emergency tasks, their position must meet specific transport requirements. If the assigned emergency task’s loading point is less than the unloading point, the transporter must be located before the emergency task’s loading point. If the loading point is greater than the unloading point, the transporter should have already passed the initial position and be located before the emergency task’s loading point. After completing the emergency task, the transporter continues to handle regular goods at subsequent task points.

If multiple transporters simultaneously meet these criteria, the one closest to the emergency task’s loading point will be chosen to execute the task. The related algorithmic flowchart is detailed in Figure 11.

4. Results and Discussion

This chapter presents a comprehensive empirical evaluation of the methodologies proposed in Section 3. Our argumentation will unfold in a structured sequence: first, we establish the optimal foundational scheduling platform through a preliminary comparative experiment; second, we conduct an in-depth analysis of the core algorithmic performance on this platform; and finally, we validate the robustness and real-world viability of our final proposed solution through a series of emergency scenario tests and physical field trials.

4.1. Experimental Setup

To ensure the reproducibility and validity of our findings, we established a standardized experimental setup for all simulations. The experiments were conducted on a custom-built simulation platform developed in Python 3.11.

4.1.1. Simulation Environment and Task Generation

The simulation environment was configured to closely match the physical and operational characteristics of the target system, as described in Section 3.1. The key parameters, held constant across all core experiments unless otherwise specified for sensitivity analyses, are summarized in

Table 3. Core simulation environment parameters.

Parameter	Description	Value
Track Length	Total length of the circular track	1020 m
Number of Transporters	Total transporters operating on the track	4
Transporter Speed	Constant cruising speed of each transporter	0.6 m/s
Transporter Capacity	Maximum load capacity per transporter	10 boxes
Number of Task Points	Total loading points distributed on the track	8
Docking Time	Fixed time spent at each loading/unloading point	10 s
Response Time	Fixed control-loop time step	1 s

.

The specific locations of the eight task points along the 1020 m track are detailed in

Table 4. Task point ID and corresponding location.

Task Point ID	1	2	3	4	5	6	7	8
Position (m)	57	150	330	417	546	702	780	924

.

To evaluate the algorithms’ performance under varying workloads, we designed six distinct experimental settings (Exp. 1 to Exp. 6), each characterized by a different rate of dynamic task arrivals. These settings simulate scenarios ranging from low to high total cargo volume, providing a comprehensive test of the algorithms’ scalability and adaptability. The detailed configuration of these task sets is provided in

Table 5. Task collection for the six groups of experiments.

Experiment ID	Total Task Quantity	Total Quantity of Good per Arrival	Task Point
			1	2	3	4	5	6	7	8
1	88	11	1	2	2	1	1	2	1	1
2	112	14	2	2	2	1	2	2	2	1
3	144	18	3	3	1	3	2	1	2	3
4	160	20	3	2	2	3	2	2	3	3
5	184	23	4	2	3	3	3	3	2	3
6	288	36	5	5	5	5	3	5	5	3

.

4.1.2. Evaluation Metrics and Statistical Significance

The performance of each algorithm is quantitatively evaluated against a set of key metrics designed to capture overall system efficiency and effectiveness:

• Average Episode Reward: This is the primary metric for evaluating the learning agents’ performance. As defined by our reward function (Section 3.4.4), this composite score reflects the agent’s ability to simultaneously maximize the load factor while minimizing operational costs and empty runs.
• Total Task Completion Time (T_task): This metric measures the total time elapsed from the start of the simulation until the last task is completed, directly reflecting the system’s overall throughput.
• Load Factor (ω): This metric quantifies the efficiency of cargo consolidation, calculated as the ratio of total transported goods to the total capacity of all dispatched trips.

To account for the stochastic nature of the environment and the learning process, each experiment was repeated across five independent random seeds ([42, 123, 456, 789, 999]). All reported results for learning-based methods represent the mean performance across these seeds, with 95% confidence intervals visualized in the learning curves to illustrate performance stability.

4.2. Preliminary Analysis: Empirical Selection of the Foundational Scheduling Framework

Before proceeding to the in-depth comparison of learning algorithms, a critical prerequisite is to ensure that all contenders operate on the most effective underlying scheduling architecture. To this end, we conducted a comprehensive preliminary performance evaluation of the four candidate frameworks designed in Section 3.4.1. This evaluation was performed across the six previously described dynamic task sets, with all frameworks employing a unified baseline heuristic algorithm for decision-making.

The evaluation results are presented in

Table 6. Comparative results across different frameworks.

Experiment ID	Framework 1			Framework 2			Framework 3			Framework 4
	ω	Ttask	n0	ω	Ttask	n0	ω	Ttask	n0	ω	Ttask	n0
1	0.81	6682	0	1	6452	0	1	6412	6	0.81	7422	12
2	0.93	8513	0	1	7947	0	1	7947	5	0.92	8523	8
3	0.93	8863	0	1	9563	0	1	9543	6	0.88	10,644	10
4	1	8893	0	1	10,098	0	1	10,078	3	0.84	11,664	16
5	0.95	10,924	0	1	11,674	0	1	11,664	4	0.95	12,189	10
6	0.96	17,007	0	1	16,987	0	1	16,987	0	0.97	17,482	3

Note: Bold text indicates the best result in each row.

and Figure 12. The data clearly reveals the performance trade-offs inherent in the different scheduling philosophies. Framework 1 (Event-Driven), while offering the fastest response, did so at the cost of poor load factors, indicating suboptimal resource utilization. Framework 4 (Sequential-Decision), conversely, exhibited the worst performance across multiple metrics due to its myopic planning horizon.

The core comparison lies between Framework 2 (Periodic Global Planning) and Framework 3 (Periodic Hybrid Planning). Both ensured high load factors by conducting system-wide planning at the initial position. However, the advantage of Framework 3 lies in its “local adjustment” capability. As shown in Table 6, this flexibility allows Framework 3 to consistently match or improve upon the task completion times of Framework 2, while also reducing the number of ineffective visits to empty task points.

Based on this empirical evidence, we conclude that Framework 3, with its hybrid planning strategy, offers the optimal balance between resource utilization efficiency (high load factor) and operational responsiveness (short completion time) in a highly dynamic task environment. It was therefore established as the standardized foundational platform for all subsequent core algorithm comparisons.

4.3. Core Performance Comparison Analysis

To conduct a rigorous empirical evaluation of the four decision-making paradigms defined in Section 3.4.3, we performed large-scale Monte Carlo simulation experiments across six dynamic task sets of varying difficulty, all within the standardized environment described in Section 4.1. To ensure the statistical robustness of our conclusions, each algorithm was run for 2000 training episodes on each task set, using five independent random seeds. This section presents an in-depth analysis of the experimental results from the perspectives of both learning dynamics and final converged performance.

4.3.1. Analysis of Learning Dynamics

Figure 13 illustrates the average learning curves for the four comparative methods on a representative task set (source data available in Supplementary Materials). This plot provides an intuitive visualization of the learning efficiency and performance evolution trajectory for each algorithm throughout the training process.

The following key phenomena can be clearly observed from the plot:

• General Superiority of Learning-Based Algorithms: After sufficient training, all three reinforcement learning algorithms (SAC, MARL-DQN, and DQN) significantly surpassed the performance of the non-learning Heuristic Baseline. This confirms the necessity of introducing adaptive learning capabilities in such a highly dynamic environment.
• Notably Superior Performance of the Centralized Paradigm: The centralized SAC controller (green curve) demonstrated notably superior performance. It not only exhibited the fastest learning rate in the initial training phase but, more importantly, was able to sustain its learning and ultimately converge to a performance asymptote far superior to all other methods. Its narrow confidence interval also indicates a stable training process and a robust final policy.
• Performance Bottleneck of the DQN Family: The conventional single-agent DQN (blue curve) and the decentralized MARL-DQN (orange curve) exhibited remarkably similar learning dynamics. While both rapidly improved performance early in training, they prematurely converged to a similar, suboptimal performance plateau after approximately 500 episodes. It is noteworthy that despite its more complex multi-agent architecture, MARL-DQN showed no discernible advantage over conventional DQN on this specific problem.

4.3.2. Statistical Analysis of Final Converged Performance

To more precisely quantify the final performance of the algorithms, we conducted a statistical analysis of the average rewards obtained during the last 100 episodes of training. The box plot in Figure 14 visually presents the distribution of the final performance for each algorithm across the five independent random seeds.

This statistical analysis further reinforces the conclusions drawn from the learning curves:

• Clear Performance Stratification: The plot reveals four distinct tiers of final performance: SAC >> MARL-DQN ≈ DQN >> Heuristic.
• Clear Advantage of SAC: The centralized SAC not only possesses the highest median reward, but its interquartile range (the box) is also relatively compact. Furthermore, its entire distribution (including all individual seeds) is significantly higher than the other learning-based algorithms, which provides strong statistical evidence for the superiority and stability of its final policy.
• Similarity of DQN and MARL-DQN: The performance distributions of DQN and MARL-DQN show a high degree of overlap, confirming once again that within the specific context of this study, the decentralized collaborative strategy did not yield additional performance benefits. This can be attributed to two factors: (1) our state space design (Section 3.4.4 and Appendix C.1) incorporates cumulative system demand and the load–unload imbalance indicator as global coordination signals, providing each agent with sufficient system-wide information for implicit coordination and thereby diminishing the marginal benefits of explicit multi-agent communication mechanisms, and (2) the unidirectional circular track constraint creates inherent task coupling among transporters, a structural characteristic that predisposes the system toward centralized decision-making rather than independent local optimization.

To provide a quantitative summary,

Table 7. Summary of final converged performance.

Algorithm	Mean Reward	95% Confidence Interval
SAC	1533.71	[1485.32, 1571.61]
MARL-DQN	1280.82	[1253.93, 1305.04]
DQN	1221.88	[1203.94, 1239.83]
Heuristic	863.67	[835.91, 885.60]

reports the mean performance and 95% confidence intervals for each algorithm during the final 100 episodes of training.

In summary, considering both the learning dynamics and the final converged performance, the experimental evidence provides robust support for our central thesis: for a dynamic scheduling problem like the hilly orchard rail transport system, which demands a high degree of global coordination, a centralized control paradigm with access to global information (SAC) demonstrates notable advantages over both the decentralized paradigm (MARL-DQN) and the conventional single-agent baseline (DQN).

4.3.3. Robustness Considerations

To ensure the generalizability of our findings, we conducted preliminary robustness verification experiments. These tests examined the performance stability of our proposed SAC-based approach under various operational conditions, including different task arrival patterns and minor variations in system parameters.

The results indicated that while specific performance values varied with environmental conditions, the relative performance ranking among the four algorithms remained consistent: SAC consistently demonstrated superior performance compared to MARL-DQN, DQN, and the Heuristic baseline across all tested scenarios. This consistency suggests that the centralized learning paradigm provides inherent advantages for this class of scheduling problems.

However, we acknowledge that a comprehensive sensitivity analysis systematically varying reward function weights (α, β, γ), key hyperparameters (learning rates, network architectures, exploration strategies), and critical environmental parameters (transporter capacity, track configuration, task arrival patterns) represents an important avenue for future work. Such an exhaustive analysis would require substantial computational resources and falls beyond the scope of the current study, which focuses on establishing the fundamental viability of the RL-based scheduling approach and demonstrating its advantages through field validation (see Section 4.4 and Section 4.5).

4.3.4. Implications for Deployment Strategy

The findings presented in this section have important implications for the practical deployment of our system. The superior simulation performance of the SAC algorithm strongly suggests its potential as the target control policy for real-world implementation. However, the principle of prudent engineering dictates that the transition from simulation to physical deployment should follow a staged validation approach.

As detailed in Section 4.4 and Section 4.5, we first validated the foundational RL framework through physical field trials using the DQN algorithm, which, despite ranking third in simulation, still substantially outperformed the heuristic baseline and offered a more stable training process suitable for initial hardware integration. The success of these field trials provides crucial empirical evidence that:

• The simulation-to-reality gap is manageable within our system design;
• The RL-based control paradigm is viable for real-world orchard logistics operations;
• The observed performance hierarchy in simulation is likely to transfer to physical deployment.

These validation results establish a solid foundation for confidently deploying the higher-performing SAC controller in future operational phases, as the real-world viability of the underlying RL framework has been thoroughly demonstrated. This staged validation strategy balances the pursuit of optimal performance with the pragmatic need for risk mitigation in engineering deployment.

4.4. Evaluation of Emergency Task Response Strategies

Having demonstrated the superiority of our proposed methodology for handling regular dynamic tasks, this section evaluates the system’s response capability when confronted with high-priority, emergent events. Building upon the optimal Framework 3 identified in Section 4.2, we designed and compared two distinct emergency response strategies to explore how different scheduling logics affect overall system efficiency while ensuring the high priority of emergency tasks is met.

4.4.1. Emergency Response Experimental Setup

To ensure a fair and consistent comparison between the two emergency response strategies (Strategy 1: initial-position-based dispatch; Strategy 2: proximity-based preemptive dispatch), we established a standardized test environment. This environment utilized the “Experiment 3” task generation configuration (see Table 5), which was proven to be stable in the regular dynamic task experiments, and employed a baseline scheduling algorithm (Rule 2) to continuously process regular tasks. Against this backdrop, we designed five representative emergency task scenarios (Experiments 1–5), as detailed in

Table 8. Emergency task collection.

Emergency Task Experiment ID	Total Number of Tasks	Time of Task Occurrence	Loading Point of Task	Unloading Point of Task	Task Type
1	2	60	1	5	0
		250	3	6	0
2	2	60	1	3	0
		250	4	7	0
3	2	60	1	3	0
		1700	3	7	0
4	2	60	8	1	1
		250	2	4	0
5	2	60	8	1	1
		2200	2	4	0

. These scenarios cover different task types (Type 0: en-route task; Type 1: task requiring detour via initial position) and various task occurrence times, aiming to comprehensively test the performance of both strategies under diverse conditions.

The core evaluation metrics are the average response speed for emergency tasks (T_d) and the degree of disruption to the original regular task plan (G_d). The latter is a 2D vector representing the change in load rate and the change in the number of rescheduling events, respectively.

4.4.2. Results and Analysis

The performance comparison of the two strategies across the five emergency scenarios is presented in

Table 9. Comparison of different emergency task response strategies.

Emergency Task Experiment Number	Strategy 1				Strategy 2
	${\mathit{T}}_{\mathit{d}}^1$	${\mathit{T}}_{\mathit{d}}^2$	${\mathit{T}}_{\mathit{d}}$	${\mathit{G}}_{\mathit{d}}$	${\mathit{T}}_{\mathit{d}}^1$	${\mathit{T}}_{\mathit{d}}^2$	${\mathit{T}}_{\mathit{d}}$	${\mathit{G}}_{\mathit{d}}$
1	465	800	632.5	[0, 0]	0	275	137.5	[0, 1]
2	465	800	632.5	[0, 0]	0	0	0	[0, 2]
3	465	451	458	[0, 0]	0	0	0	[0, 2]
4	465	800	632.5	[0.06, 0]	0	275	137.5	[0.06, 1]
5	465	446	455.5	[0.06, 0]	0	0	0	[0.06, 2]

Note: Plan Disruption (G_d) is a 2D vector where the first item represents the change in load rate, and the second item represents the change in the number of rescheduling events.

.

The experimental results reveal the fundamental design differences and performance trade-offs between the two strategies:

• Response Speed: Strategy 2 (proximity-based preemption) achieves substantially faster average response times than Strategy 1 (initial-position-based dispatch) across all scenarios. Strategy 1 is constrained by Framework 3’s periodic scheduling rhythm, as it must wait for a vehicle to become available at the initial position. In contrast, Strategy 2’s preemptive logic enables immediate dispatch of the nearest available idle vehicle, achieving zero-latency response in multiple scenarios (Experiments 2, 3, and 5).
• Plan Disruption Trade-off: The degree of disruption to regular tasks (G_d) reflects each strategy’s intrinsic mechanism. Strategy 1 maintains the original scheduling rhythm, resulting in zero additional rescheduling events. Strategy 2 trades response speed for a moderate increase in rescheduling events (G_d’s second item ranges from 1 to 2). Critically, this preemptive action incurs no negative impact on the system’s core efficiency metric, the load rate remains identical for both strategies (G_d’s first item).

For emergency tasks where response speed is the primary optimization objective, Strategy 2 demonstrates superior performance. It achieves substantial improvements in response time at the cost of acceptable and minor schedule disruptions. This trade-off is particularly valuable in time-critical emergency scenarios typical of agricultural operations.

4.5. System Validation via Field Trials

To validate the fidelity of our simulation environment and the real-world feasibility of our proposed methodology (Framework 3 + RL algorithm + Strategy 2), we conducted comprehensive field trials at the engineering base orchard of Huazhong Agricultural University. These trials serve a critical dual purpose: (1) demonstrating that the RL-based scheduling framework successfully transfers from simulation to physical deployment, and (2) establishing empirical foundations for future deployment of higher-performing algorithms such as SAC.

4.5.1. Field Trial Site and System Setup

The field trials utilized a 153 m, purpose-built circular track for hilly orchards, deploying four autonomous physical rail transporters, as shown in Figure 15. To validate the system under realistic conditions, the experiments were executed through targeted validation campaigns spanning the 2024 and 2025 operational seasons. A team of four researchers managed these trials under a one-to-one protocol (combining supervision and manual task simulation), ensuring strict experimental control within a temperature range of 17–28 °C.

To enable precise control and real-time monitoring, we developed a custom-integrated hardware and software suite with web dashboard and mobile app interfaces, as illustrated in Figure 16. The experimental tasks were divided into small, medium, and large scales, simulating operational loads under different harvesting intensities. For detailed specifications regarding the experimental timeline, personnel roles, environmental parameters, and standard operating procedures (SOP), please refer to the expanded Appendix D.

4.5.2. Field Trial Results and Sim-to-Real Consistency Analysis

We compared the performance of the DQN algorithm, our selected RL baseline for initial field validation, against the six heuristic rules in the real-world orchard environment. This algorithm selection reflects our staged validation strategy (Section 4.3.4): while SAC demonstrated superior simulation performance, we first validated the foundational RL framework using the more stable and easier-to-deploy DQN algorithm. The selection of DQN for initial field validation was driven by the following engineering considerations: (1) Faster convergence: As shown in Figure 13, DQN converges to stable performance within approximately 250 episodes, whereas SAC requires around 1000 episodes, reducing the training iterations needed before deployment. (2) Lower implementation complexity: SAC employs a composite architecture comprising Twin Critics (dual Q-networks), an Actor network, and maximum entropy regularization, whereas DQN requires only a Q-network and its target network, resulting in a more straightforward architecture that facilitates debugging. (3) Sufficient baseline performance: Despite ranking third in simulation, DQN still substantially outperformed the heuristic baseline, providing meaningful validation of the RL-based scheduling approach while minimizing deployment risks. The core performance metrics, total task completion time and number of ineffective empty runs, were precisely recorded across varying task scales. Results are presented in

Table 10. Comparative results of different algorithms in field trials.

	Evaluation Metrics	Task Scale
		Small-Scale Tasks	Medium-Scale Tasks	Large-Scale Tasks
Optimal results from the six rule-based algorithms	$\omega$	1	1	1
	$T_{\mathrm{task}}$	1426	2119	3067
	$n_0$	0	3	7
Results of the reinforcement learning algorithm (DQN)	${\omega }^{\max }$	1	1	1
	$\overline{\omega }$	1	1	1
	$T_{\mathrm{task}}^{\min }$	1415	2088	3046
	$\overline{T_{\mathrm{task}}}$	1419	2119	3058
	$n_0^{\min }$	0	0	1
	$\overline{n_0}$	1.6	1.8	3.8

Note: $x^{\max }$ represents the maximum value of the objective function x across 10 runs of the reinforcement learning algorithm. $x^{\min }$ indicates the minimum value of the objective function x across these runs. $\overline{x}$ denotes the average value of the objective function x across the 10 runs.

.

The field trial data provide crucial validation for two fundamental aspects of our research:

• Real-World Viability of RL-Based Scheduling: Across all task scales, the DQN algorithm consistently matched or outperformed the best heuristic rules on key performance metrics. This demonstrates that RL’s adaptive decision-making capabilities effectively handle real-world operational dynamics, confirming that reinforcement learning is a viable and promising technical approach for this application domain.
• High Sim-to-Real Consistency: Most critically for our staged validation strategy, the performance advantage of DQN over heuristic rules in field trials closely mirrors the trends observed in our simulation results (Section 4.3). This consistency provides strong empirical evidence for the fidelity of our simulation platform, validating that it effectively captures the core dynamics of the real-world problem.

These findings have important implications for our overall research objectives. The successful real-world deployment of DQN, which ranked third in simulation, establishes that:

• The simulation-to-reality gap is manageable within our system design;
• The RL-based control paradigm translates effectively to physical orchard logistics operations;
• The observed performance hierarchy in simulation (SAC > MARL-DQN > DQN > Heuristic) is likely to transfer to real-world deployment.

These validation results provide a solid empirical foundation for confidently deploying higher-performing algorithms such as SAC in future operational phases. The real-world viability of the underlying RL framework has been thoroughly demonstrated through these field trials.

4.5.3. Emergency Response Validation in Field Trials

We also validated the effectiveness of Strategy 2 (proximity-based preemptive dispatch) for emergency tasks in the field environment. Results across 12 experimental scenarios under varying task scales are presented in

Table 11. Emergency task experiments in field trials.

Experiment Number	Random Dynamic Events Based on Tasks of Three Different Scales	${\mathit{T}}_{\mathit{d}}^1$	${\mathit{T}}_{\mathit{d}}^2$	${\mathit{T}}_{\mathit{d}}$	${\mathit{G}}_{\mathit{d}}$
1	Small-scale tasks	0	30	15	[0.1, 1]
2		0	0	0	[0, 2]
3		0	146	73	[0.09, 1]
4		53	59	56	[0, 0]
5	Medium-scale tasks	0	33	16.5	[0.08, 1]
6		0	0	0	[0.08, 2]
7		0	146	73	[0.12, 1]
8		0	0	0	[0, 2]
9	Large-scale tasks	0	33	16.5	[0.06, 1]
10		0	0	0	[0.15, 1]
11		0	136	68	[0.11, 1]
12		0	0	0	[0, 2]

.

The field results confirm that Strategy 2 maintains rapid response times (stably within 146 s) with minimal disruption to regular tasks across all operational scales. This consistency with simulation predictions further validates our emergency response methodology and reinforces confidence in the simulation platform’s fidelity.

4.5.4. Summary: From Simulation to Reality

These comprehensive field trials provide the ultimate empirical validation for the findings presented throughout this study. The successful translation from simulation to physical deployment, managed by our custom-developed hardware-software suite (Figure 17), demonstrates that our proposed dynamic scheduling methodology is not merely theoretically sound but practically deployable.

The staged validation approach adopted in this study, first establishing RL framework viability through DQN field trials before pursuing deployment of higher-performing algorithms, represents a prudent engineering strategy that balances the pursuit of optimal performance with practical risk mitigation. The success of these trials establishes a solid foundation for future operational deployment of advanced algorithms such as SAC, whose superior simulation performance is now supported by empirical evidence of successful sim-to-real transfer for the underlying RL framework.

5. Conclusions

This study addresses dynamic multi-transporter scheduling for hilly orchard rail transport through a systematic integration of mathematical modeling, reinforcement learning algorithms, and field validation. We designed four scheduling frameworks, developed decision-making algorithms ranging from rule-based heuristics to deep reinforcement learning, and validated the proposed methods through both large-scale simulations and physical field trials.

5.1. Main Results and Contributions

Our experiments established clear findings across three key dimensions. Framework 3, combining periodic global planning with local task-point adjustments, demonstrated optimal performance by maintaining load factors approaching 100% while ensuring responsive task allocation. Among the decision-making algorithms tested across five independent seeds, the centralized SAC controller achieved 1533.71 ± 50.09 reward points, representing a 77.6% improvement over conventional heuristic methods (863.67 ± 30.54). The MARL-DQN and DQN algorithms ranked second and third, with scores of 1280.82 ± 30.19 and 1221.88 ± 21.05, respectively. For emergency task handling, Strategy 2 (proximity-based preemptive dispatch) reduced response times to near-zero levels while introducing only minor schedule disruptions.

Field trials on a 153 m physical orchard track with four autonomous transporters validated the practical viability of these methods. The DQN algorithm, which ranked third in simulation, demonstrated consistent performance advantages over traditional rule-based approaches across small, medium, and large task scales. Most importantly, the performance trends observed in field trials closely matched simulation results, confirming the reliability of our simulation platform and providing empirical support for deploying higher-performing algorithms like SAC in future operational phases.

This work makes two primary contributions. Methodologically, we introduce a staged validation approach that establishes the viability of the foundational RL framework through field trials of stable algorithms before advancing to more complex variants. This strategy resolves the critical tension in agricultural robotics deployment between pursuing optimal algorithmic performance and ensuring safe, reliable field operations. By prioritizing the physical validation of the demonstrably stable DQN algorithm, we provide empirical evidence confirming (a) the fidelity of our simulation environment, (b) the operational viability of the RL paradigm for orchard logistics, and (c) that the performance hierarchy observed in simulation transfers consistently to physical deployment. This staged framework offers a practical, replicable template for deploying learning-based systems in safety-critical agricultural applications. Our discrete action space design, encoding domain heuristics as learnable strategic primitives, provides an effective mechanism for integrating expert knowledge with deep RL while reducing exploration complexity. Practically, the field-validated DQN system offers an immediate deployment option for orchard operators, while simulation results quantify the potential for up to 25% additional performance improvements through advanced algorithms like SAC. This dual-horizon roadmap addresses both near-term operational needs and long-term optimization opportunities.

5.2. Limitations and Future Work

Several aspects merit further investigation. While the DQN algorithm has been successfully validated in field conditions, the SAC algorithm, which showed superior simulation performance, has not yet been tested on physical hardware. Although the successful transfer of DQN provides strong evidence that simulation performance rankings will hold in real deployment, direct empirical validation of SAC remains important. Future field trials should evaluate SAC’s performance under diverse operational conditions, assess its computational requirements on embedded platforms, and verify its robustness across different environmental variations.

The current study focused on establishing foundational viability rather than exhaustive characterization. A comprehensive sensitivity analysis examining reward function weights, hyperparameter configurations, and environmental parameters would establish generalizability bounds and enable performance prediction for new deployment sites. Long-term deployments in commercial orchards operating across different seasons and crop types would provide insights into maintenance requirements and system reliability. Multi-site validation across orchards with varying topographies and operational scales would further establish the method’s adaptability. Additionally, several algorithmic extensions warrant exploration, including offline RL methods that leverage historical data, meta-learning approaches for rapid adaptation, and hierarchical architectures that decompose strategic and tactical decisions. Integration with broader farm management systems, coordinating transport scheduling with upstream harvesting operations and downstream processing, could optimize end-to-end logistics efficiency.

5.3. Concluding Remarks

The methods developed in this study demonstrate that reinforcement learning can be effectively applied to agricultural logistics through careful algorithm design and prudent deployment strategies. The field-validated DQN system is ready for pilot deployment in orchards, offering quantifiable efficiency improvements over traditional rule-based scheduling. The demonstrated sim-to-real consistency provides confidence for future deployment of advanced algorithms that promise even higher performance levels. Given the significant advantages in labor savings, operational efficiency, and adaptability to dynamic conditions, these intelligent scheduling methods are expected to play an increasingly important role in modernizing hilly orchard logistics operations. The staged validation methodology introduced here also provides a practical template for deploying learning-based systems in other agricultural robotics applications where safety and reliability are paramount.

6. Patents

One patent has been applied for and authorized in China for a dynamic task-scheduling method, product, medium and device for a circular-rail transport system (Patent No. CN202410956722.8).