Design and Experiment of a Variable-Rate Spraying System Based on RBFNN-SMC Control
Abstract
1. Introduction
2. Materials and Methods
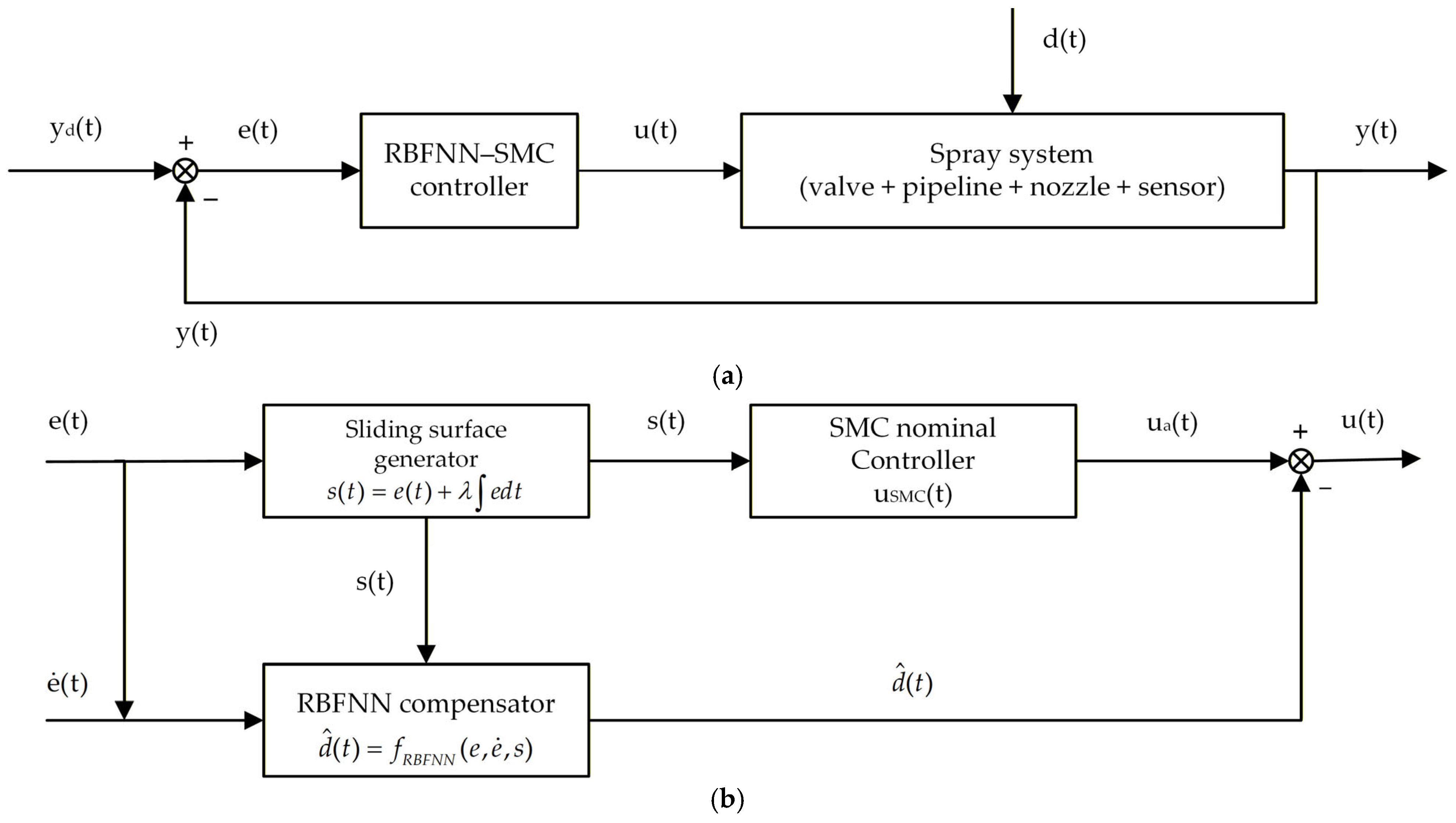
2.1. Variable-Spray Control System Architecture and Operational Principles
2.2. Design of the RBFNN-SCM
2.2.1. Modeling of Variable-Rate Application Control System
- GV(S) = Qv(s)/U(s) is the transfer function of the valve body;
- K1—the flow gain of the valve body, [L/min];
- T1—the time constant of the valve body, [s];
- s—complex frequency variable in the Laplace domain.
- Ga(S) = Qa(s)/U(s) is the transfer function of the electric actuator;
- K2—the gain of the actuator, [L/min];
- T2—the time constant of the actuator, [s];
- τ—the signal transmission delay time, [s].
- T—the time constant, [s];
- K0—the system gain, [L/min].
- u—the control input (PWM duty cycle signal);
- q(t)—flow rate contributions [L/min].
- Ts—The time constant obtained via the two-point method, [s];
- τs—The equivalent delay determined via the two-point method, [s];
- p1—the first response ratio point selected;
- p2—the second response ratio point selected;
- tp1—the arrival time of p1, [s];
- tp2—the arrival time of p2, [s].
2.2.2. Design of SMC
- e—the tracking error, [L/min];
- yd—the desired spray volume, [L/min];
- y—the actual spray volume, [L/min].
- s—sliding surface variable, [L/min];
- λ—sliding surface coefficient;
- f(x,t)—the aggregate of unmodeled dynamics, nonlinear characteristics, and external disturbances;
- b(x,t)—the control input gain.
- ueq—Equivalent Control.
- ua—actual control law;
- φ—the boundary layer thickness, [L/min];
- k—the switching gain;
- sat(⋅)—the saturation function.
2.2.3. Integration of RBFNN with SMC
- hi—hidden layer output;
- ci—the i-th RBF center;
- σi—the i-th RBF width.
- wi—output layer weights;
- b—output layer bias.
- Δwi—The incremental adjustment of the weight associated with the i-th output layer;
- η—learning rate;
- —sensitivity of the sliding surface to the control input u.
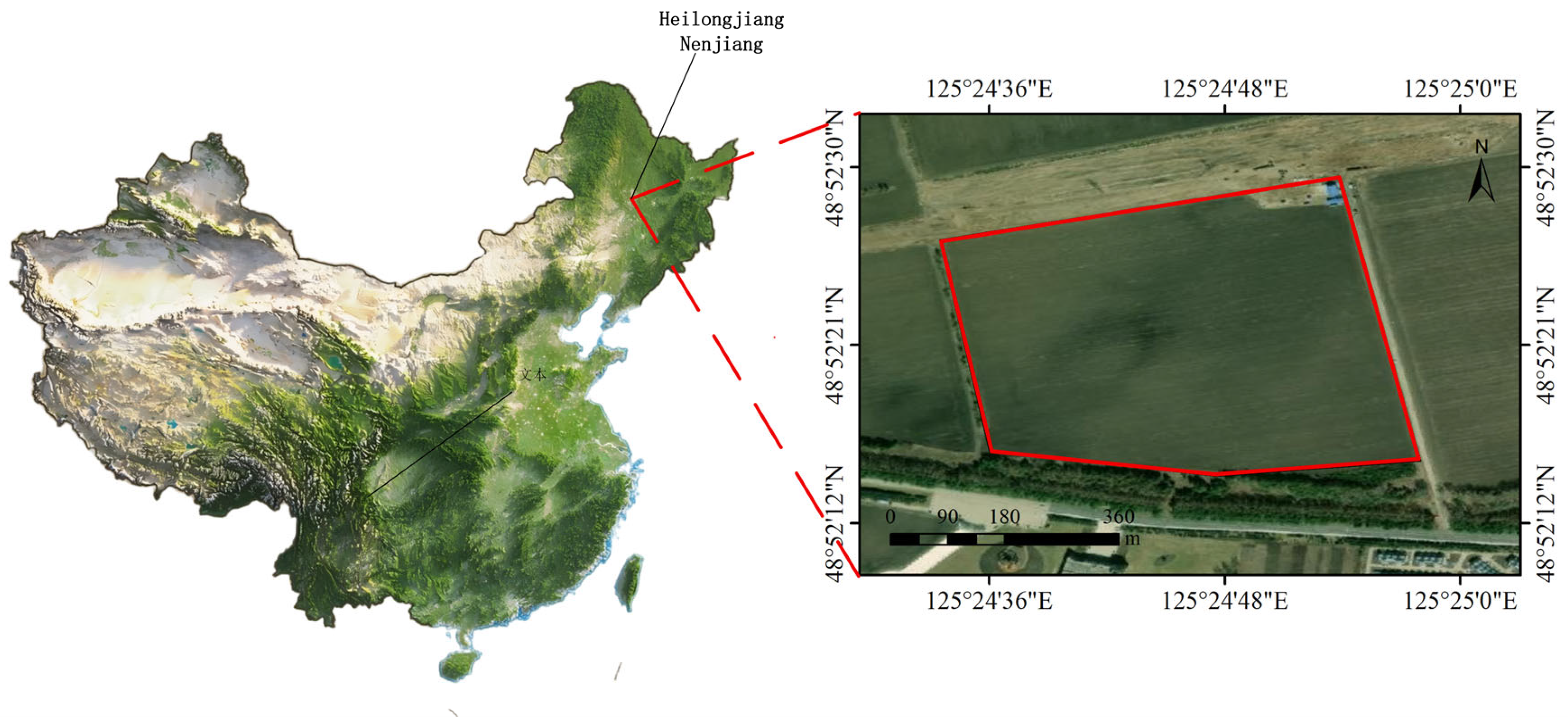
2.3. Experimental Design and Methodology
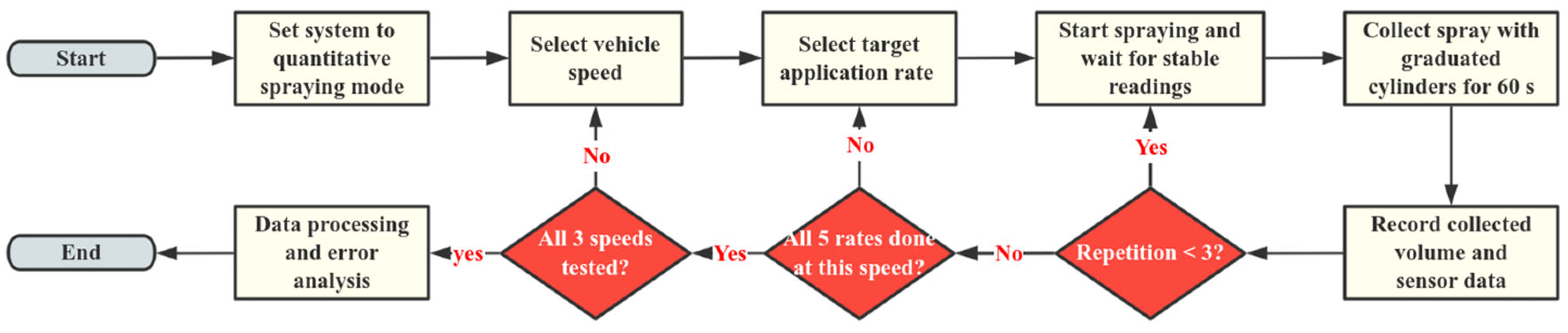
2.3.1. System Accuracy Verification Test
2.3.2. Field Efficacy Test of Pesticide Application
3. Results
3.1. Control System Simulation
3.2. Variable-Spray Experiment Results
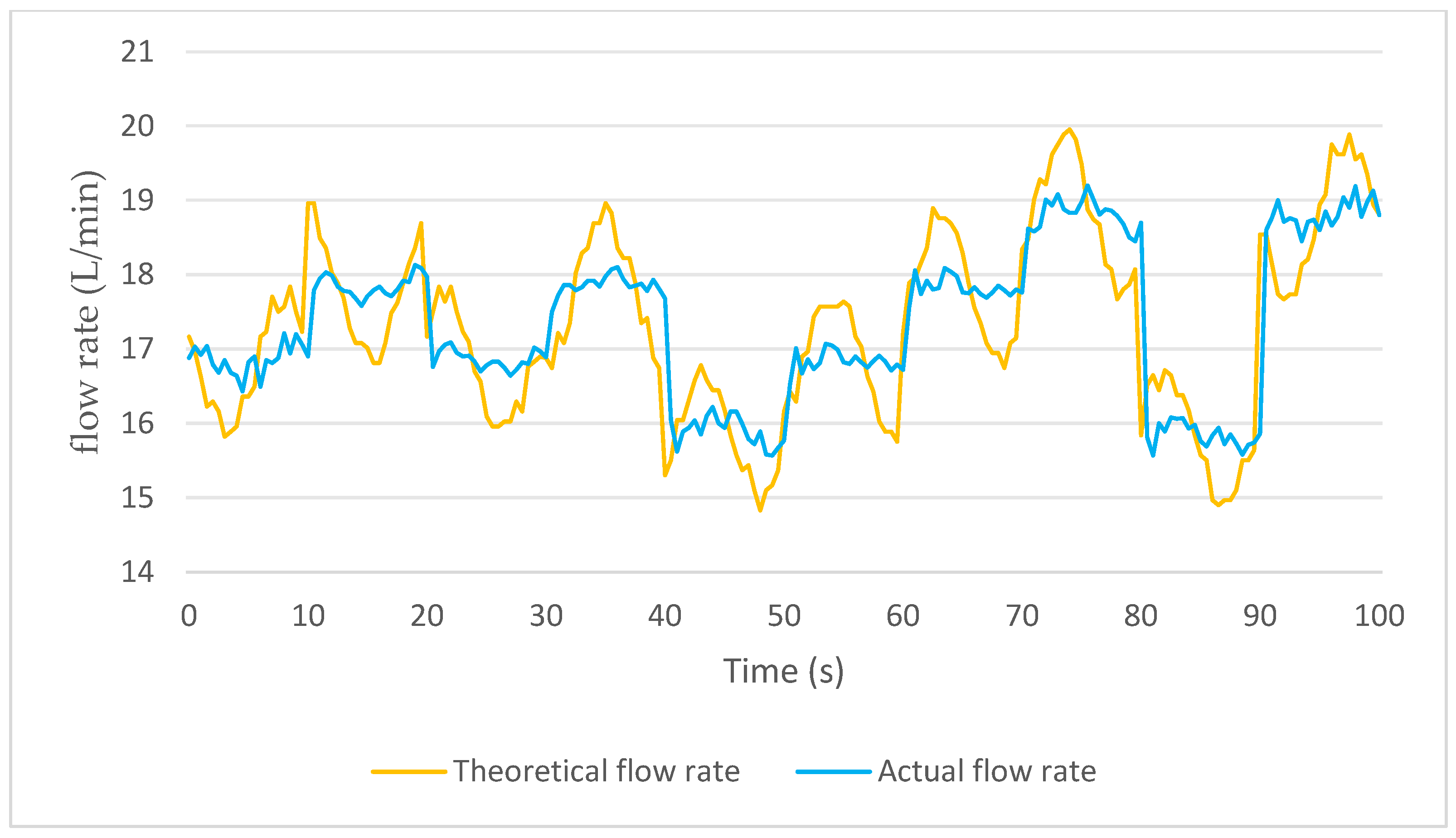
3.2.1. Analysis of System Accuracy Test Results
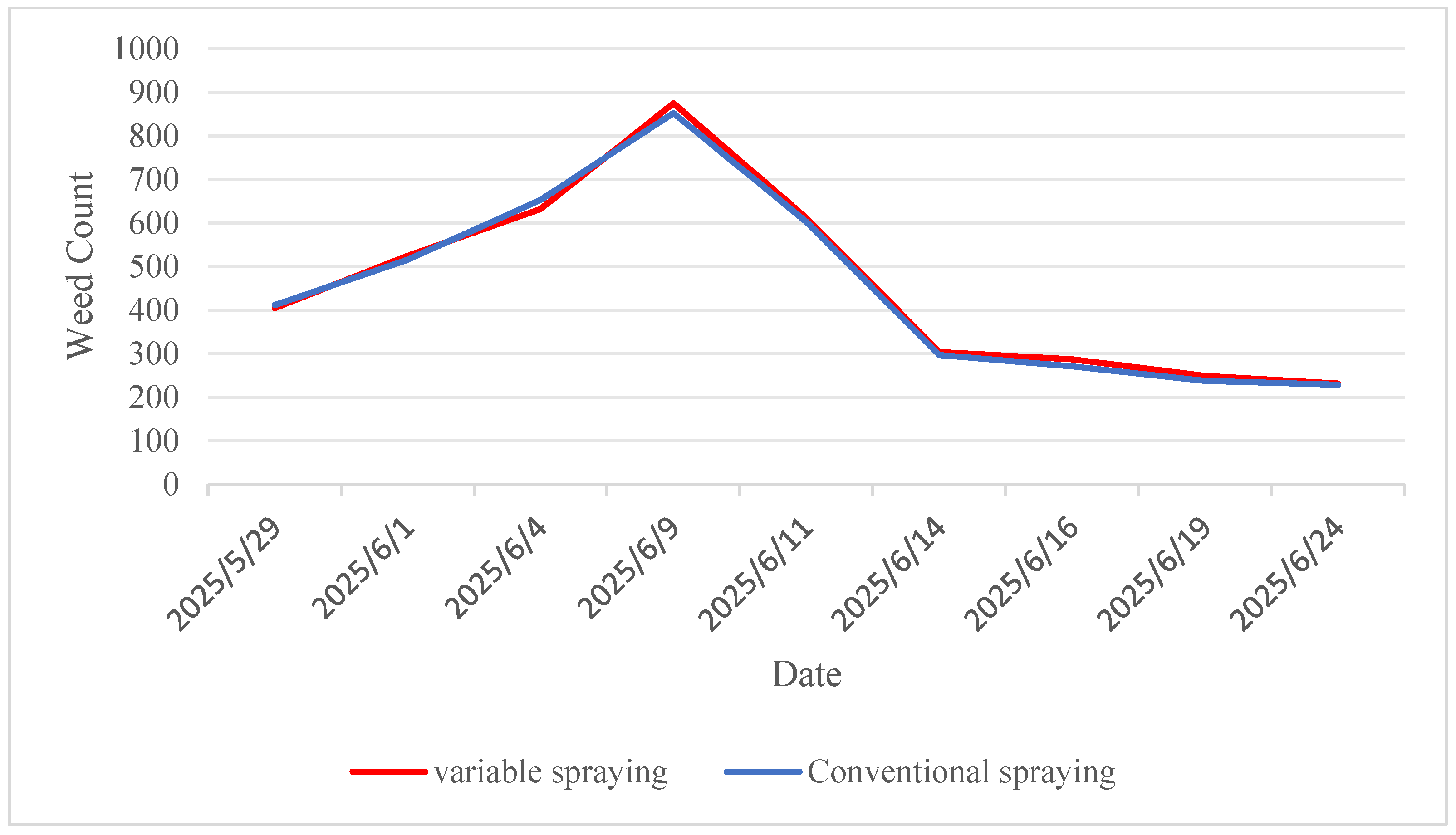
3.2.2. Analysis of Field Efficacy Test Results for Pesticide Application
4. Discussion
4.1. Control Performance and Comparison with Existing Approaches
4.2. Agronomic Efficacy, Economic, and Environmental Implications
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- He, X.K. Research status and development proposal of precision application technology and equipment in China. Smart Agric. 2020, 2, 133–146. [Google Scholar] [CrossRef]
- Yang, G.Y.; Kong, H.; Lan, Y.B.; Yin, L.L.; Han, X. Key technologies and application status of precise variable application. Agric. Technol. Equip. 2022, 1, 96–97. [Google Scholar] [CrossRef]
- Zhang, B.; Zhai, C.Y.; Li, H.Z.; Yang, S. Development Status Analysis of Precision Pesticide Application Techniques and Equipments. J. Agric. Mech. Res. 2016, 38, 1–5+28. [Google Scholar] [CrossRef]
- Campos, J.; Gallart, M.; Llop, J.; Ortega, P.; Salcedo, R.; Gil, E. On-farm evaluation of prescription map-based variable rate application of pesticides in vineyards. Agronomy 2020, 10, 102. [Google Scholar] [CrossRef]
- Hu, C.M.; Ru, Y.; Fang, S.P.; Rong, Z.F.; Zhou, H.P.; Yan, X.H.; Liu, M.G. Orchard variable rate spraying method and experimental study based on multidimensional prescription maps. Comput. Electron. Agric. 2025, 235, 110379. [Google Scholar] [CrossRef]
- Mariano, G.; Luis, E.; Manuel, P.; Juan, A.; Pablo, G. Autonomous systems for precise spraying–Evaluation of a robotised patch sprayer. Biosyst. Eng. 2016, 146, 165–182. [Google Scholar] [CrossRef]
- Ma, F.Y. Research on Variable Rate Application Control System Based on Prescription Map. Master’s Thesis, Jilin Agricultural University, Changchun, China, 2022. [Google Scholar]
- Liu, L.; Kong, F.X.; Yi, L.L.; Lan, Y.B.; Han, X.; Zhao, J.; Liu, J.; Lv, P.C.; Zhang, M.H. Design and Testing of a Variable Spray System Based on Pto Protocols. INMATEH-Agric. Eng. 2024, 73, 2. [Google Scholar] [CrossRef]
- Zhang, W.Z.; Liu, Z.Z. Experiment on variable rate spray with real-time mixing pesticide of 3WY-A3 sprayer. Trans. Chin. Soc. Agric. Eng. 2011, 27, 130–133. [Google Scholar] [CrossRef]
- Salcedo, R.; Zhu, H.; Ozkan, E.; Falchieri, D.; Zhang, Z.H.; Wei, Z.M. Reducing ground and airborne drift losses in young apple orchards with PWM-controlled spray systems. Comput. Electron. Agric. 2021, 189, 106389. [Google Scholar] [CrossRef]
- Wang, X.Y.; Hu, Z.X.; Li, X.Q.; Li, S.C.; Gai, J.X.; Wang, F.M. Design and Experiment of Multi-reflux Variable Spraying Control System. Trans. Chin. Soc. Agric. Mach. 2019, 50, 123–131. [Google Scholar] [CrossRef]
- Nasir, F.E.; Alam, M.S.; Tufail, M.; Khan, M.T. A novel pressure and flow control technique for variable-rate precision agricultural sprayer. In Proceedings of the 2021 International Conference on Robotics and Automation in Industry (ICRAI), Xian, China, 26 November 2021. [Google Scholar] [CrossRef]
- Cai, Y.J.; Wu, Z.D.; Gao, S.B.; Cui, C. Design and simulation of variable injection system based on PID control. Cereals Oils 2020, 33, 97–100. [Google Scholar]
- Padhiary, M.; Tikute, S.V.; Saha, D.; Barbhuiya, J.A.; Sethi, L.N. Development of an IOT-based semi-autonomous vehicle sprayer. Agric. Res. 2025, 14, 229–239. [Google Scholar] [CrossRef]
- Feng, Y.N.; Pei, L.; Chen, X.; Chen, X.B.; Liu, Y. A review of key technologies for variable application. J. Chin. Agric. Mech. 2021, 42, 65–71. [Google Scholar] [CrossRef]
- Grella, M.; Gioelli, F.; Marucco, P.; Zwertvaegher, I.; Mozzanini, E.; Mylonas, N.; Nuyttens, D.; Balsari, P. Field assessment of a pulse width modulation (PWM) spray system applying different spray volumes: Duty cycle and forward speed effects on vines spray coverage. Precis. Agric. 2022, 23, 219–252. [Google Scholar] [CrossRef]
- Butts, T.R.; Luck, J.D.; Fritz, B.K.; Hoffmann, W.C.; Kruger, G.R. Evaluation of spray pattern uniformity using three unique analyses as impacted by nozzle, pressure, and pulse-width modulation duty cycle. Pest Manag. Sci. 2019, 75, 1875–1886. [Google Scholar] [CrossRef]
- Fabula, J.; Sharda, A.; Luck, J.D.; Brokesh, E. Nozzle pressure uniformity and expected droplet size of a pulse width modulation (PWM) spray technology. Comput. Electron. Agric. 2021, 190, 106388. [Google Scholar] [CrossRef]
- Tang, R.P.; Tang, J.R.; Aridas, N.K.; Talip, M.S.A.; Luen, L.C. Research on RBF-PID hybrid drive control models for drone pesticide applications in tropical orchards. Geo-Spat. Inf. Sci. 2025, 1–18. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, J.; Zhang, C.; Zhou, H.P.; Jiang, X.S.; Yang, F.G.; Wang, Y. CFD analysis and RBFNN-based optimization of spraying system for a six-rotor unmanned aerial vehicle (UAV) sprayer. Crop Prot. 2023, 174, 106433. [Google Scholar] [CrossRef]
- Gao, Z.N.; Chen, Q.Y.; Hu, G.R.; Chen, C.; Li, C.L.; Chen, J. Design and Test of Self-Propelled Straddletype Lycium Barbarum L. Spraying machine. INMATEH-Agric. Eng. 2021, 65, 345–354. [Google Scholar] [CrossRef]
- Huyett, L.M.; Dassau, E.; Zisser, H.C.; Doyle, F.J. Design and Evaluation of a Robust PID Controller for a Fully Implantable Artificial Pancreas. Ind. Eng. Chem. Res. 2015, 54, 10311–10321. [Google Scholar] [CrossRef]
- Wang, X.T.; Zhao, Z.; Wang, Y.; Li, L. High Precision Control Method of Liquid Fertilizer Flow Based on Sliding Mode Technology. J. Agric. Mech. Res. 2023, 45, 8–14. [Google Scholar] [CrossRef]
- Sai, T.A.; Lee, H. Weight initialization on neural network for neuro pid controller-case study. In Proceedings of the 2018 International Conference on Information and Communication Technology Robotics (ICT-ROBOT), Xiamen, China, 27 January 2018. [Google Scholar] [CrossRef]
- GB/T 20183.3-2024; Equipment for Crop Protection—Spraying Equipment—Part 3: Test Method to Assess the Performance of Volume/Area Adjustment Systems. State Administration for Market Regulation, National Standardization Administration: Beijing, China, 2024.
- GB/T 17980.125-2004; Pesticide—Guidelines for the Field Efficacy Trials (II)—Part 125: Herbicides Against Weeds in Soybean. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China: Beijing, China, 2004.
- Li, P. Research on Drone Spraying Control System for Foliar Fertilization in Rice. Master’s Thesis, Heilongjiang Bayi Agricultural University, Daqing, China, 2023. [Google Scholar]
- Wen, H.J.; Ma, X.D.; Qin, C.J.; Chen, H.; Kang, H.Y. Research on path tracking of unmanned spray based on dual control strategy. Agriculture 2024, 14, 562. [Google Scholar] [CrossRef]
- Xu, W.H.; Cao, L.J.; Peng, B.Y.; Wang, L.; Gen, C.; Liu, Y.J. Adaptive nonsingular fast terminal sliding mode control of aerial manipulation based on nonlinear disturbance observer. Drones 2023, 7, 88. [Google Scholar] [CrossRef]
- Wen, H.; Liang, Z.X.; Zhou, H.X.; Li, X.Y.; Yao, B.H.; Mao, Z.H.; Lian, L. Adaptive sliding mode control for unknown uncertain non-linear systems with variable coefficients and disturbances. Commun. Nonlinear Sci. Numer. Simul. 2023, 121, 107225. [Google Scholar] [CrossRef]
- Sun, W.F.; Liu, H.Y.; Wang, R.T.; Fu, T.P.; Lu, J.Q.; Wang, F.L. Design and Experiment of PID Control Variable Application System Based on Neural Network Tuning. Trans. Chin. Soc. Agric. Mach. 2020, 51, 55–64+94. [Google Scholar] [CrossRef]

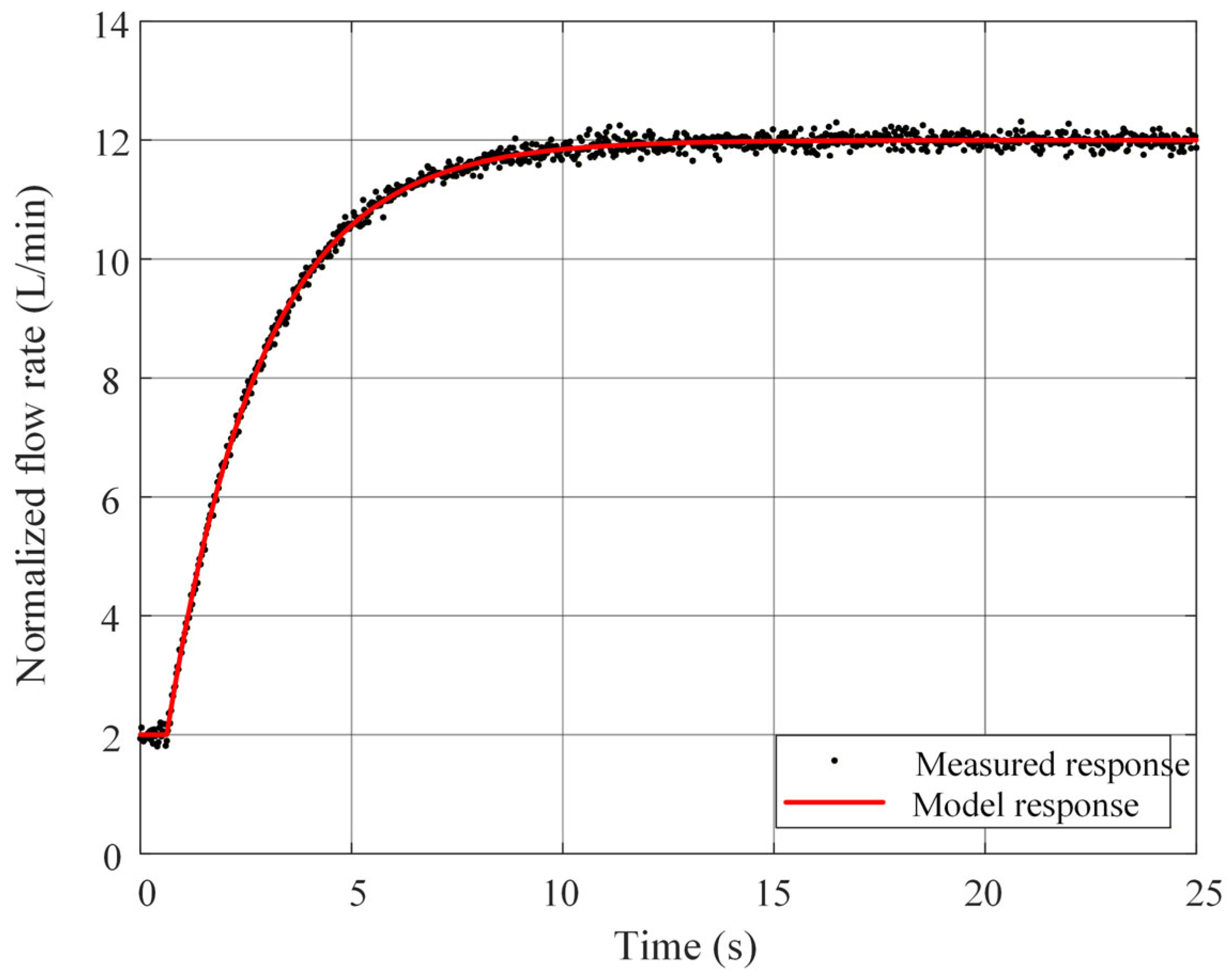


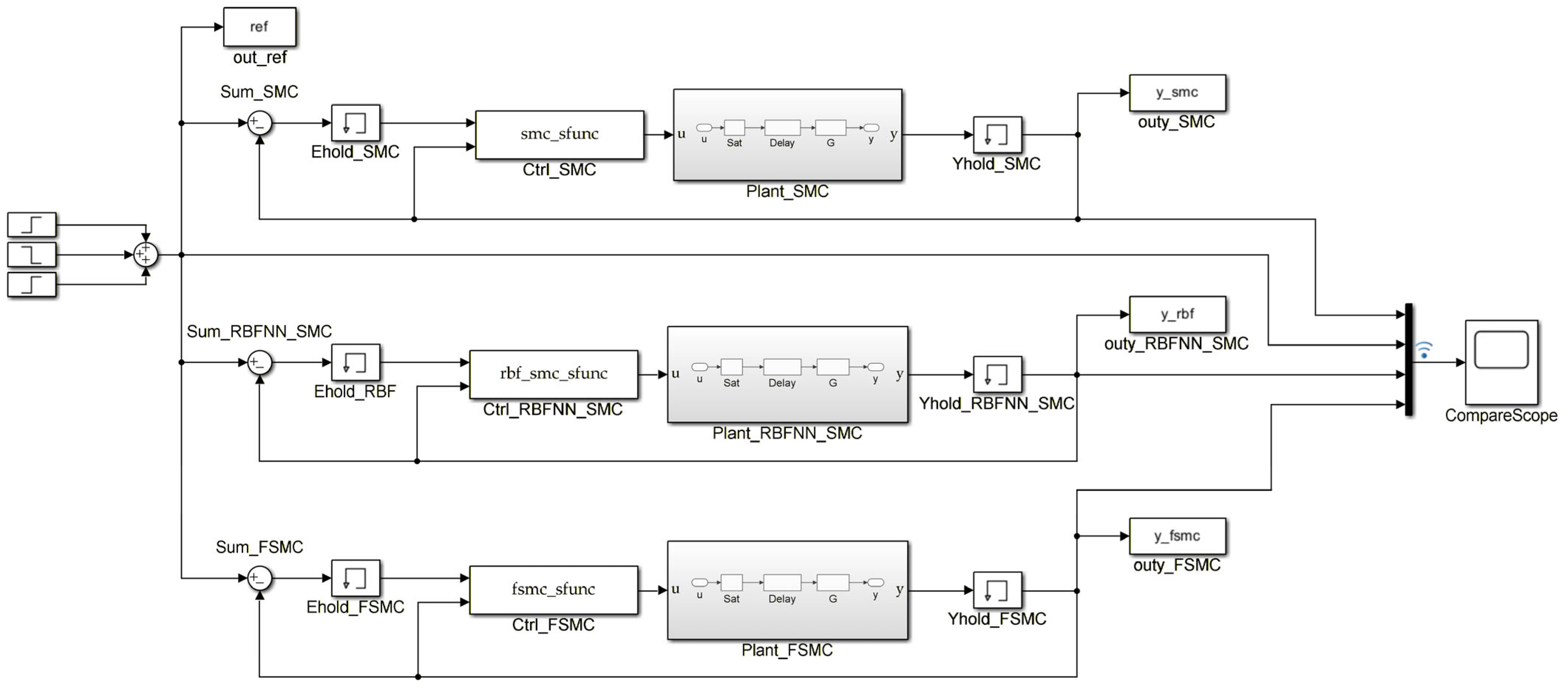
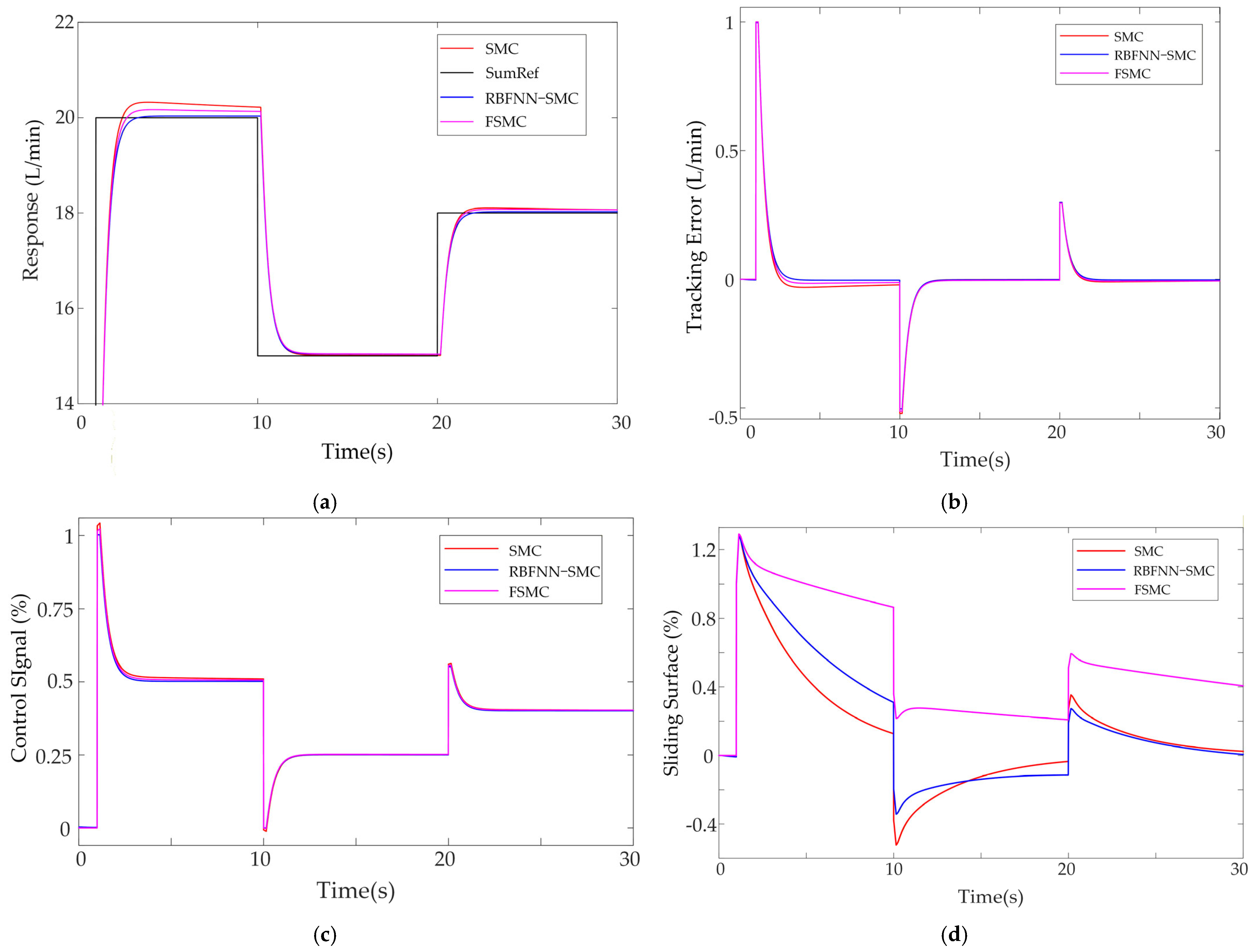
| Control Strategy | Average Overshoot (%) | Average Rise Time (s) | Average Steady-State Error (%) |
|---|---|---|---|
| Sliding Mode Control | 16.53 | 0.32 | 1.40 |
| Fuzzy Sliding Mode Control | 15.80 | 0.35 | 1.11 |
| Radial Basis Function Neural Network–Sliding Mode Control | 14.87 | 0.27 | 0.51 |
| Pesticide Application Levels Differential | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Average Adjustment Time (s, mean ± SD) | 0.12 ± 0.01 | 0.21 ± 0.01 | 0.3 ± 0.02 | 0.38 ± 0.02 |
| Times of Repetition | 3 | 3 | 3 | 3 |
| Theoretical Application Rate/ (L/h) | Speed/ (km/h) | Theoretical Flow Rate/ (L/min) | Measured Flow Rate/ (L/min, Mean ± SD, n = 3) | Absolute Error/ (L/min, Mean ± SD) | Relative Error/ (%, Mean ± SD) |
|---|---|---|---|---|---|
| 96 | 8 | 14.08 | 14.52 ± 0.28 | 0.44 ± 0.28 | 3.03 ± 1.98 |
| 9 | 15.84 | 15.37 ± 0.33 | 0.47 ± 0.33 | 3.06 ± 2.05 | |
| 10 | 17.60 | 17.13 ± 0.30 | 0.47 ± 0.30 | 2.74 ± 1.71 | |
| 102 | 8 | 14.96 | 15.34 ± 0.29 | 0.38 ± 0.29 | 2.47 ± 1.96 |
| 9 | 16.83 | 16.25 ± 0.23 | 0.58 ± 0.23 | 3.56 ± 1.36 | |
| 10 | 18.70 | 19.45 ± 0.43 | 0.75 ± 0.43 | 3.85 ± 2.28 | |
| 108 | 8 | 15.84 | 16.32 ± 0.19 | 0.48 ± 0.19 | 2.94 ± 1.21 |
| 9 | 17.82 | 18.43 ± 0.20 | 0.61 ± 0.20 | 3.31 ± 1.14 | |
| 10 | 19.80 | 19.53 ± 0.30 | 0.27 ± 0.30 | 1.38 ± 1.52 | |
| 114 | 8 | 16.72 | 17.23 ± 0.20 | 0.51 ± 0.20 | 2.95 ± 1.22 |
| 9 | 18.81 | 18.35 ± 0.23 | 0.46 ± 0.23 | 2.50 ± 1.21 | |
| 10 | 20.90 | 20.13 ± 0.30 | 0.77 ± 0.30 | 3.82 ± 1.43 | |
| 120 | 8 | 17.60 | 18.12 ± 0.29 | 0.52 ± 0.29 | 2.86 ± 1.63 |
| 9 | 19.80 | 19.34 ± 0.29 | 0.46 ± 0.29 | 2.37 ± 1.48 | |
| 10 | 22.00 | 21.44 ± 0.41 | 0.56 ± 0.41 | 2.61 ± 1.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Zhang, W.; Li, J.; Yu, C.; Qi, L.; Zhang, B. Design and Experiment of a Variable-Rate Spraying System Based on RBFNN-SMC Control. Agriculture 2025, 15, 2444. https://doi.org/10.3390/agriculture15232444
Zhao C, Zhang W, Li J, Yu C, Qi L, Zhang B. Design and Experiment of a Variable-Rate Spraying System Based on RBFNN-SMC Control. Agriculture. 2025; 15(23):2444. https://doi.org/10.3390/agriculture15232444
Chicago/Turabian StyleZhao, Chen, Wei Zhang, Jinyang Li, Chuntao Yu, Liqiang Qi, and Bo Zhang. 2025. "Design and Experiment of a Variable-Rate Spraying System Based on RBFNN-SMC Control" Agriculture 15, no. 23: 2444. https://doi.org/10.3390/agriculture15232444
APA StyleZhao, C., Zhang, W., Li, J., Yu, C., Qi, L., & Zhang, B. (2025). Design and Experiment of a Variable-Rate Spraying System Based on RBFNN-SMC Control. Agriculture, 15(23), 2444. https://doi.org/10.3390/agriculture15232444






