Next Article in Journal
Dual-Drive Window Control Method for Continuous Grain Drying Based on Water Potential Accumulation
Previous Article in Journal
Non-Destructive Quality Prediction of Fresh Goji Berries During Storage Using Dielectric Properties and ANN Modeling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agriculture
Volume 15
Issue 22
10.3390/agriculture15222354
agriculture-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Multi-Omics Annotation and Residual Split Strategy-Based Deep Learning Model for Efficient and Robust Genomic Prediction in Pigs

by
Jingnan Ma
1,
Zhenshuang Tang
2,
Haohao Zhang
3,
Yangfan Liu
1,
Xiong Xiong
1,
Xiaolei Liu
1,4,
Lilin Yin
1,4,* and
Minggang Lei
1,*
1
Key Laboratory of Agricultural Animal Genetics, Breeding and Reproduction, Ministry of Education & College of Animal Science and Technology, Huazhong Agricultural University, Wuhan 430070, China
2
Yazhouwan National Laboratory, Sanya 572024, China
3
School of Computer Science and Technology, Wuhan University of Technology, Wuhan 430070, China
4
Hubei Hongshan Laboratory, Wuhan 430070, China
*
Authors to whom correspondence should be addressed.
Agriculture 2025, 15(22), 2354; https://doi.org/10.3390/agriculture15222354
Submission received: 19 September 2025 / Revised: 27 October 2025 / Accepted: 10 November 2025 / Published: 13 November 2025
(This article belongs to the Special Issue Genomic Selection in Pigs: Precision Breeding and Trait Optimization)
Browse Figures
Versions Notes

Abstract

Genomic selection has become a widely adopted and effective breeding technology for modern genetic improvements in pigs. However, the core model currently used in genetic evaluation is primarily based on a linear mixed model, which accounts for only additive genetic effects. Non-additive effects and complex nonlinear interactions among genes or loci are often neglected, leaving substantial potential for improving the predictive ability of traits. To address this limitation, we here propose a Multi-omics Annotation and Residual Split strategy-based deep learning model (MARS). Through comprehensive comparisons and evaluations against various linear and nonlinear models across multiple pig traits, we demonstrate that the residual split indirect strategy effectively mitigates overfitting and underfitting issues commonly observed in deep learning models, thereby enhancing predictive accuracy for complex traits. Moreover, by incorporating multi-omics annotation information within a hierarchical feature selection procedure, our results show that it improves computational efficiency without significant sacrifices in prediction performance. It is foreseeable that our developed MARS would facilitate the application of artificial intelligence technology and the publicly available big omics data in the coming future of pig breeding.

1. Introduction

With the advancement of genomic sequencing technologies and bioinformatics, Meuwissen proposed genomic prediction(GP) [1]. This method utilizes high-density genetic markers spanning the entire genome to build a statistical model to estimate the Genomic Estimated Breeding Value (GEBV) of individuals. GP is now widely applied to early selection in breeding programs for livestock, poultry, plants, and aquatic species, as well as for the risk assessment of human diseases [2,3]. Currently, one of the most frequently used models in GP is Genomic Best Linear Unbiased Prediction (GBLUP) [4]. This approach offers advantages such as a relatively straightforward theoretical framework and high computational efficiency [5], leading to successful implementation in breeding improvements for multiple species. However, the GBLUP model has several limitations. Firstly, it inherently assumes that all markers contribute to the target trait and the effect size of each marker comes from normality with the same variance [6]. This assumption is often invalid for complex traits, because different genomic markers contribute variably to a trait’s genetic variance [7,8]. Secondly, the relationship between genotype and phenotype is not exclusively linear [9]. The GBLUP model struggles to capture complex nonlinear interactions between genes [10,11]. To overcome these limitations, it is imperative to develop new methodologies based on nonlinear models to enhance the accuracy of genomic prediction.
Recently, the rapid development of artificial intelligence models has extended machine learning (ML) and deep learning (DL) algorithms, renowned in the field of GP for their capability to powerfully fit nonlinear relationships [12,13,14]. DL has high flexibility and can model complex relationships between genotype and phenotype [15,16]. Crucially, this approach imposes no predefined assumptions about the specific nature of these relationships [17]. Instead, it autonomously learns underlying association patterns in a data-driven manner. This characteristic enables the inclusion of all genetic markers, including those with small effects, high correlations, or complex interactions [18]. Each marker has the opportunity to contribute to varying degrees of model fitting [19]. Yin developed the GP algorithm ‘KAML’ based on ML [20], which integrates multiple regression, cross-validation, grid search, and a binary algorithm to finely screen large-effect markers that contribute significantly to phenotype. It reduced the interference of noise SNPs on the model and improved its prediction performance. Ma developed DeepGS [21], a Convolutional Neural Network (CNN) architecture, which demonstrated superior prediction performance across multiple traits compared to rrBLUP and Multilayer Perceptron (MLP). Wang introduced DNNGP [22], a model applicable to diverse omics data for phenotype prediction. Compared to many ML/DL models, DNNGP exhibited robust prediction performance across four plant datasets. Collectively, these nonlinear statistical models demonstrate significant advantages in capturing non-additive genetic effects and complex high-dimensional data relationships [23,24], thereby offering a promising avenue for transcending the limitations of traditional linear models. However, rare studies systematically investigate the applicability of these models in pigs, which have various genetic backgrounds across different breeds and strains.
The dimensionality of genomic information is reasonably high, making it computationally expensive for ML/DL models; thus, dimensionality reduction before model fitting becomes essential [25]. However, current dimensionality reduction methods predominantly rely on the genomic data itself [26,27,28,29]. These approaches often overlook the underlying biological significance, which may result in the loss of valuable information and reduced efficiency in feature selection. As is well known, the genome is composed of multiple functional elements, including Quantitative Trait Locus (QTL), Open Chromatin Region (OCR), Footprint, Motif, etc. [30]. Annotation information typically covers various details, such as gene function, regulatory mechanisms, expression patterns, and interactions with other biomolecules. Genomic annotation characterizes the functional regions and properties of SNPs, enabling the assignment of biochemical functions to approximately 80% of the genome and facilitating the interpretation of phenotypic variation [30]. Annotations derived from multi-omics data offer several advantages: they not only reveal the contribution of genetic loci to the traits, but also provide reliable group information for dimensionality reduction, thereby helping to optimize feature selection strategies.
This research proposes a Multi-omics Annotation and Residual Split strategy-based deep learning model (MARS), which leverages multi-omics annotation information to construct an efficient hierarchical feature selection strategy, ensuring the maximum use of informative signals while reducing data dimensionality and improving computational efficiency. Subsequently, it employs residuals from a linear mixed model as phenotypes for deep learning algorithms. This two-step strategy enables the separate modeling of linear and nonlinear, and additive and interactive effects, thereby enhancing both the predictive performance for traits and the overall robustness of the model.

2. Materials and Methods

2.1. Pig Dataset

The pig dataset utilized in this study was from a published study [31]. The dataset comprises records for seven traits, including Back Fat thickness at 100 kg (BF), Loin Muscle Depth at 100 kg (LMD), Lean Meat Percentage at 100 kg (LMP), Time spent eating Per Day (TPD), Left Teat Number (LTN), Right Teat Number (RTN), and Total Teat Number (TTN). The raw dataset consisted of 2986 individual records and approximately 11.3 million single-nucleotide polymorphisms (SNPs), with an average sequencing depth of 0.73X. A quality control and processing pipeline was implemented: (1) initial quality control was performed using PLINK software (v1.9) [32], removing SNPs with a missing call rate > 0.05, removing SNPs with a minor allele frequency (MAF) < 0.1, and removing individuals with a missing call rate > 0.1, resulting in 2796 individuals and 9,922,023 SNPs retained; (2) linkage disequilibrium pruning was performed using PLINK software, with the window size set to 50, the sliding window step set to 1, and the LD coefficient (r2) threshold set to 0.5, resulting in 366,000 SNPs retained; (3) genotype imputation for missing loci was performed using Beagle software (v5.4) [33]; (4) secondary quality control was performed using PLINK software, removing SNPs with MAF < 0.05, resulting in 365,958 SNPs retained.

2.2. Multi-Omics Functional Annotation Information

The IFmut database annotated QTL, OCR, Nucleosome Free Region (NFR), Motif, Footprint, Transcription Factor Binding Site (TF binding Site), and H3K27ac Peak, covering 8 functional regulatory regions [34]. A functional confidence scoring system was established, and the scoring criteria are shown in Table 1.
Annotate and classify SNPs in pig datasets using the IFmut database. The specific steps are as follows: (1) obtain SNP annotation information from the database; (2) based on the SNP’s ID, locate its annotation information and obtain its category; (3) classify SNPs into 5 major categories; (4) classify SNPs that are not in the database into category 6 (rest).

2.3. Methods and Models

2.3.1. The Models Used for Comparisons

rrBLUP: This is a commonly used statistical method in GP, based on a mixed linear model framework. The basic idea is to estimate the parameters of high-dimensional genomic data through ridge regression. Therefore, it is good to achieve stable effect estimation in the presence of multicollinearity problems. It is mathematically equivalent to GBLUP, which assumes that all SNPs contribute minimally and equally to a trait, and follow the same normal distribution. This rough prior assumption is particularly suitable for complex quantitative traits controlled by a large number of small-effect SNPs.
Random forest (RF): This is an ensemble learning method that constructs multiple independent decision trees through Bagging and random feature selection [35], and derives the final prediction results through voting (for classification) or averaging (for regression). RF is particularly robust and relatively insensitive to noise. However, when dealing with large-scale data, further optimization is often required to address issues of computational efficiency and model interpretability.
Support Vector Regression (SVR): This is an extension of the Support Vector Machine for regression tasks. It seeks an optimal hyperplane in a high-dimensional feature space to minimize the error between predicted and true values [36]. The core idea of SVR lies in the ε -insensitive loss function, which ignores errors within a predefined margin ε and penalizes only those exceeding ε , thereby constructing a robust regression model. SVR can combine different kernel functions, such as linear kernel, Gaussian kernel, polynomial kernel, etc., to make it suitable for nonlinear regression tasks. We used the Gaussian kernel in this study.
LightGBM: This is an efficient distributed algorithm based on gradient-boosting decision trees (GBDT) [37], specifically designed for optimizing large-scale data and high-dimensional feature scenes. Compared to traditional GBDT, LightGBM employs histogram-based optimization and leaf-wise growth strategies, which substantially improve training speed and memory utilization. Its growth mode is vertical, meaning that at each iteration only the leaf node with the largest loss reduction is split, while other leaves remain unchanged, thereby reducing overall errors. To further improve computational efficiency, LightGBM introduces exclusive techniques such as gradient-based one-side sampling (GOSS), which retains instances with larger gradients while randomly sampling from smaller-gradient instances, thus reducing data size and complexity without sacrificing accuracy. Additionally, LightGBM supports feature parallelism, data parallelism, and bagging parallelism and leverages histogram-based algorithms to lower data storage costs. Together, these features enable LightGBM to efficiently train on large-scale datasets.
Multilayer Perceptron (MLP): This represents the fundamental form of neural networks. It learns feature representations by combining linear transformations with nonlinear activation functions and optimizes parameters through backpropagation and gradient descent. Each layer of neurons receives the outputs from the previous layer and extracts increasingly abstract features through weighted summation followed by nonlinear transformation. As shown in Figure 1, the MLP network used in this study consists of four fully connected layers (FC), the batch normalization layer (BatchNorm1d), Dropout layer, and Rectified Linear Unit (ReLU) layer.
The model is optimized using mean squared error (MSE) loss and trained with Adam for optimization, combined with an early stopping mechanism to ensure stability and predictive performance. The number of training epochs and the early stopping patience are treated as hyperparameters, which can be adjusted according to the characteristics of different traits.

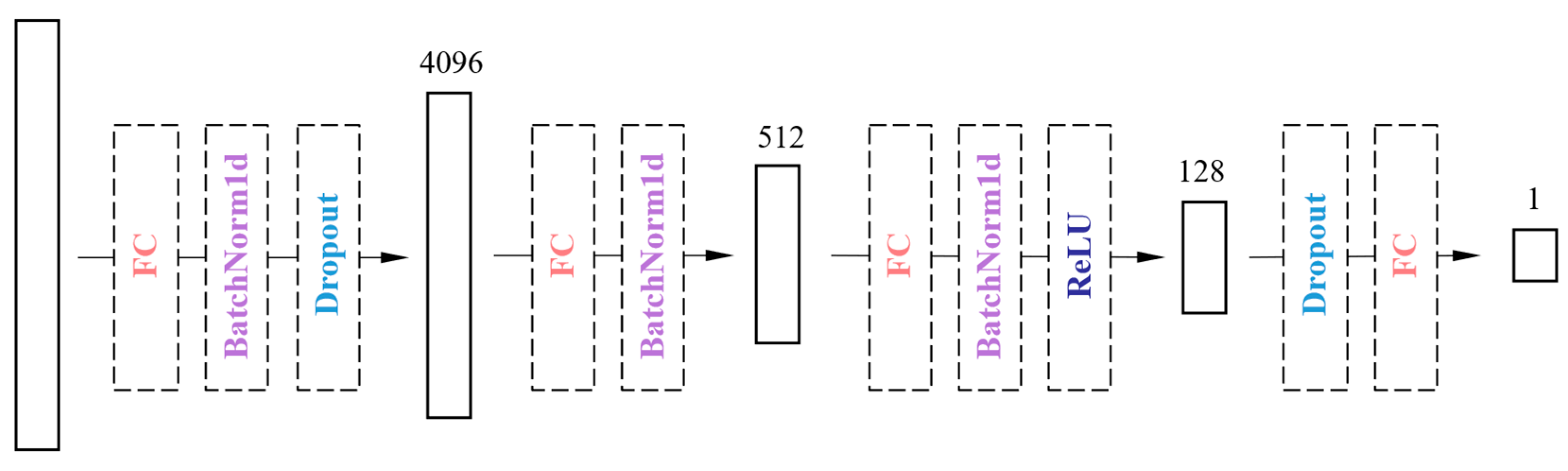
2.3.2. The Proposed Model ‘MARS’

The proposed MARS framework is a deep learning-based model that integrates multi-omics annotation with a residual split strategy to achieve efficient and robust prediction for complex traits. MARS consists of several core steps: deriving residuals from a general linear mixed model, performing multi-omics-based feature selection, fitting the deep learning model, and ultimately predicting the target traits of individuals. Firstly, we use the GBLUP model to calculate genomic estimated breeding values (GEBVs) and obtain the residuals. The equation form can be written as follows:
y = X b + Z g + e
where y represents the vector of phenotypic records; X b represents the index matrix and estimated coefficients for fixed effects; g represents the GEBVs of individuals, following a multivariate normal distribution of N 0 , G σ g 2 , where G represents the genomic relationship matrix and σ g 2 is the additive genetic variance; e is a vector of model residuals, following the independent and identity normal distribution N ( 0 , I σ e 2 ) ; and σ e 2 is the residual variance. The AIREML algorithm is used to estimate variance components σ g 2 and σ e 2 [38], then to calculate GEBVs and obtain the model residuals. We used the HiBLUP (v1.5.3) software to fit the GBLUP model [39].
In order to reduce the dimensionality of the input data for the downstream deep learning model while preserving as much valuable information as possible, we use multi-omics annotation information to classify genomic data. Splitting the genome into multiple biologically relevant subsets can reduce the interference of irrelevant features and enhance the biological relevance of feature selection. It can also effectively reduce the feature dimension of a single calculation. In the processing, when the number of SNPs in each category is less than or equal to 100, feature selection is not performed. And when the number of SNPs in each category is more than 100, feature selection is performed separately for each category using XGBoost. XGBoost is an optimized GB algorithm [40], which constructs a powerful prediction model by combining multiple weak tree learners. The information gain for each feature was calculated and recorded, because it reflects the changes in the objective function before and after feature splitting, and describes the contribution of this feature to model performance. If the gain of an SNP is greater than 0, it indicates that the split model of the SNP is better, so this SNP is included in the feature subset. After completing feature selection separately for each category, the selected SNP features are merged to form the final input for the subsequent deep learning model fitting.
To obtain stable and robust prediction performance, we constructed a new GP deep learning model based on the CNN framework, and its overall structure is shown in Figure 2. This model consists of an input layer, a convolutional block, fully connected layers, and an output layer.
The objective is to minimize prediction error and use mean square error as the loss function. MSE calculates the sum of squared errors between predicted and true values to measure the prediction performance of the model for continuous quantitative trait regression tasks. Parameter optimization adopts the Adam (Adaptive Moment Estimation) algorithm [41]. To prevent overfitting, an early-stopping mechanism is introduced during the training process. The training epochs and early-stopping epochs are hyperparameters, and corresponding adjustments are made for the fitting of different traits to ensure the optimal performance of the model in the task. The input of the CNN model is individual genotype data. The target output is as follows:
r = f θ X
where r   represents the residual prediction value calculated by the CNN, X represents the one-dimensional tensor of SNP, f θ represents the CNN model, and θ represents the model parameter.
Finally, the predicted values from the GBLUP and CNN models are combined to obtain the final phenotype predictions for all individuals on the target traits:
y ^ = g + r
where y ^ represents the final predicted phenotype value and g represents the estimated values from the GBLUP model.

2.3.3. Evaluation Methods and Indicators

The Pearson correlation coefficient (PCC) was used as an indicator to evaluate prediction ability. PCC measures the strength of the linear relationship between predicted and true phenotypes, with values closer to 1 indicating a stronger positive linear correlation. This study employed five-fold cross-validation. Specifically, the dataset was partitioned into five subsets; in each iteration, four subsets were used for model training and the remaining subset for testing. The PCC between predicted and true phenotypes was calculated on the testing set, and the process was repeated five times so that each subset served as the test set once. To further improve the reliability of the prediction performance evaluation, the five-fold cross-validation was repeated four times. The final result was obtained as the average across all repetitions. All computations in this study were conducted on a KunPeng 920 Kylin Linux server with 2.60 GHz HiSilicon 128 CPUs and 500 GB memory; the GPU is NVIDIA A100-PCIe with 40GB Video Memory and driver version NVIDIA SMI 510.85.02.

3. Results

3.1. Data Analysis

There are a total of seven traits in the pig dataset, and their descriptive statistical results are shown in Table 2. LMP has 2795 records, TPD has 2604 records, and all other traits have 2796 records. The median and mean of each trait are close, with a coefficient of variation ranging from 0.03 to 0.21.
After quality control and preprocessing, 365,958 SNPs remained. The genome-wide distribution of these SNPs was visualized using the rMVP package [42]. As shown in Figure 3, SNP markers are almost distributed across all chromosomes, with high coverage and representativeness. A few genomic regions have no SNPs because the low-coverage whole-genome sequencing strategy cannot fully capture the linkage disequilibrium (LD) across the whole genome, leading to unexpected imputation performance in certain regions.

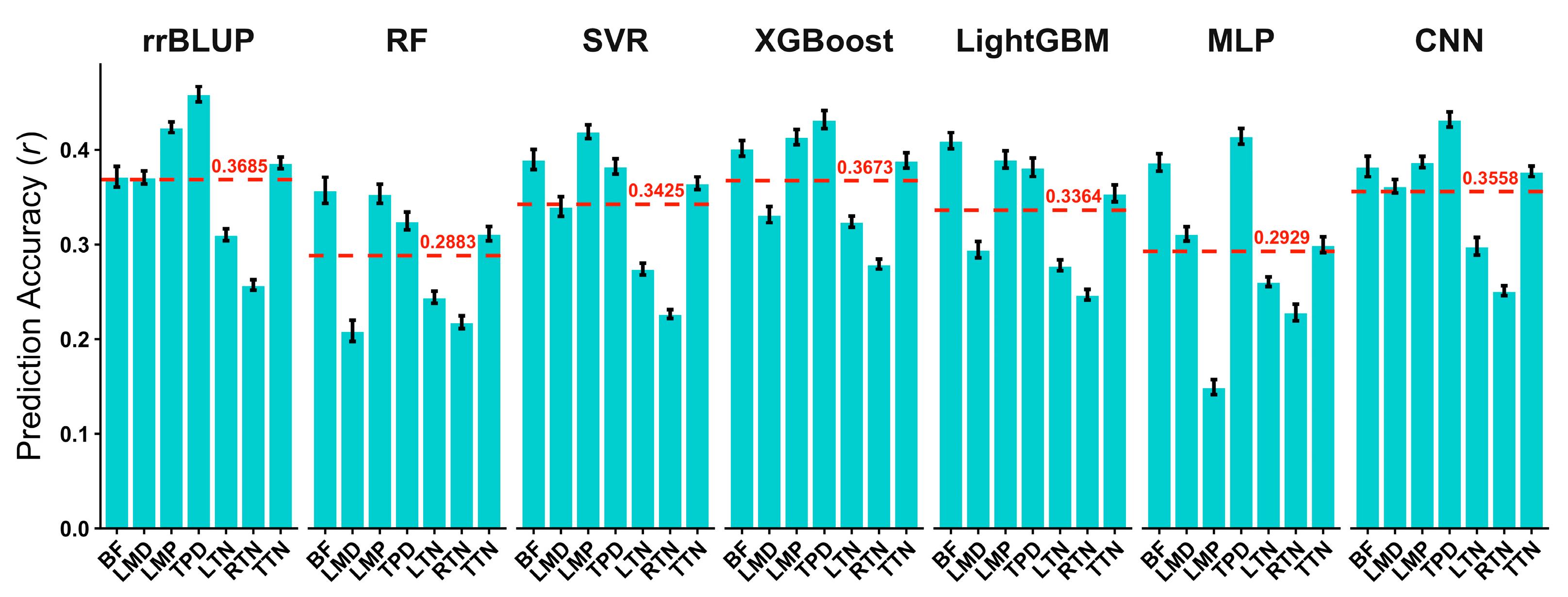
3.2. Comparison of Prediction Performances of Different Models

To investigate the predictive performance of commonly used ML/DL models on the traits of pigs, we first conducted systematic comparisons of seven algorithms, including the linear mixed model rrBLUP, and six nonlinear models: RF, SVR, XGBoost, LightGBM, MLP, and CNN. The results are summarized in Figure 4. Substantial differences were observed in the predictive performance of the seven algorithms across the seven traits. No single algorithm achieved the best performance on all traits, suggesting that the genetic complexity of these traits may exceed the analytical capacity of the current model. Among them, the rrBLUP exhibited a high PCC in most traits, with an average prediction accuracy of 0.3685, outperforming the other algorithms. XGBoost achieved the highest PCC on the traits related to nipple number, with an average PCC only 0.12% higher than rrBLUP. CNN performed comparably to rrBLUP across multiple traits, with an average PCC difference of only 1.27%. LightGBM outperformed rrBLUP on the BF trait, but its performance on other traits was relatively poor. By contrast, MLP displayed relatively low predictive ability, with a PCC of only 0.1493 for the trait of LMP. RF consistently showed the poorest performance among all models.
Based on the average PCC across all traits, the overall performance of the models can be ranked as follows: rrBLUP > XGBoost > CNN > SVR > LightGBM > MLP > RF. Therefore, these results indicate that, contrary to prior expectations regarding their potential in genomic prediction, the evaluated ML/DL models failed to surpass the traditional linear mixed model (rrBLUP) in predicting pig traits.

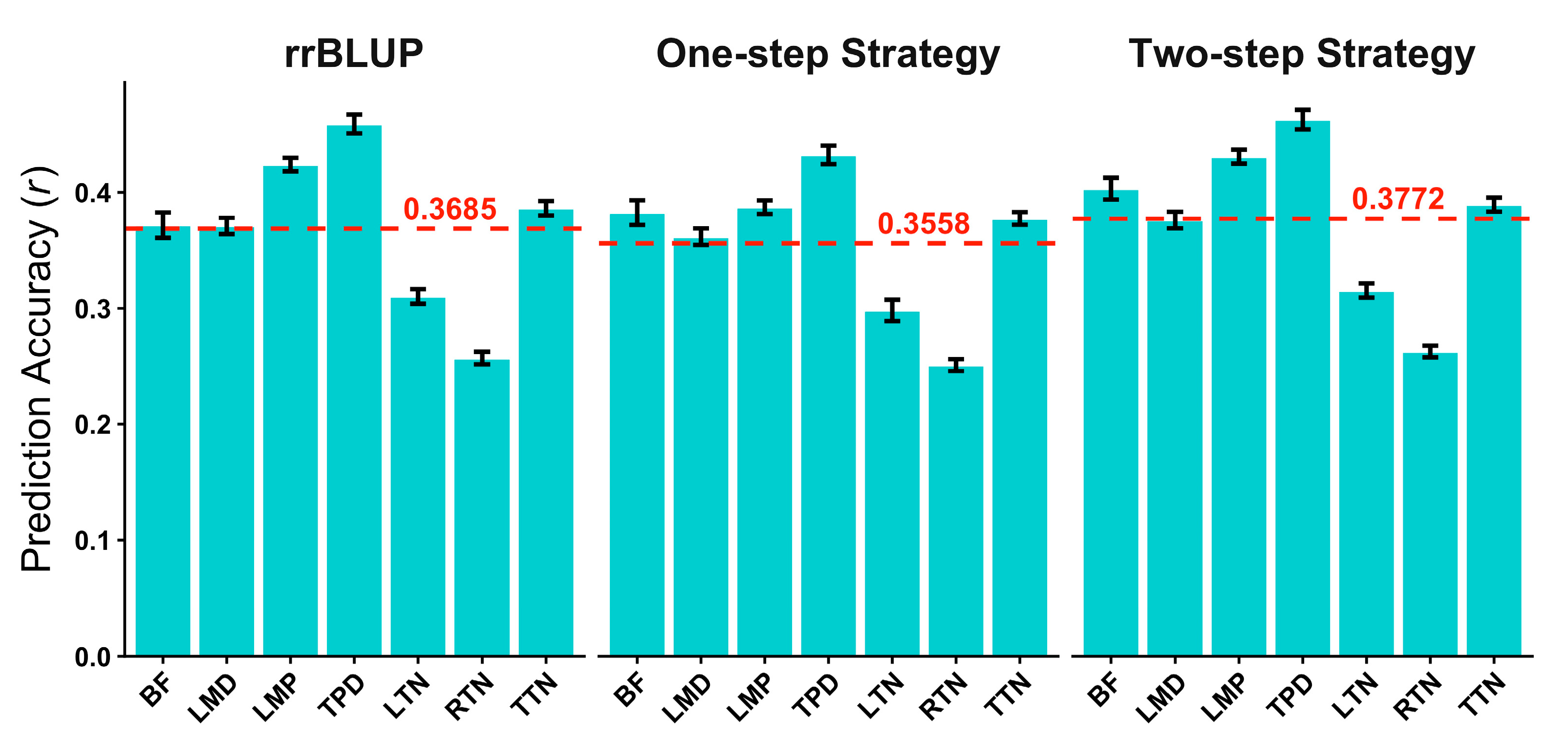
3.3. Effectiveness of Residual Split Strategy on Deep Learning Model

To enhance the predictive performance of deep learning models, we adopted a residual split strategy that separately models linear versus nonlinear and additive versus interactive effects. Specifically, the GBLUP model is first fitted to capture the linear additive components, after which the deep learning model is applied to the residuals together with the genotype. This approach reduces model complexity and helps to mitigate the overfitting and underfitting issues commonly encountered in deep learning models. For efficiency, we used the CNN model as a representative deep learning architecture to evaluate the residual split strategy; the results are summarized in Figure 5.
Interestingly, we found that the two-step strategy significantly outperformed both rrBLUP and the one-step strategy across all traits, with average PCC improvements of 0.87% and 2.14%, respectively. Compared with rrBLUP, the largest gain was observed for the BF trait, with an improvement of 3.15%. In comparison to the one-step strategy, the greatest improvement was achieved for the LMP trait, reaching 4.34%. These results suggest that the residual split strategy may be an effective and optimal approach to improve both the predictive ability and stability of deep learning models when applied to species with complex genetic architectures, such as pigs.

3.4. Multi-Omics Annotation-Based Hierarchical Feature Selection

Besides the predictive ability, the computational efficiency is also a bottleneck of deep learning models, particularly when applied to the rapidly increasing number of genome-wide markers generated by advances in sequencing technology. Consequently, feature selection has become a critical step for reducing computational burden before fitting deep learning models. Here, we leveraged the multi-omics annotation information as prior knowledge and proposed a hierarchical feature selection strategy to explore its applicability in genomic prediction.
According to the functional regulatory regions defined in the IFmut database for SNP annotation, we counted the number of SNPs covered within each annotation category; the results are summarized in Table 3. A single SNP may simultaneously occur in multiple regulatory regions and therefore be assigned to more than one annotation category. Among these, we found that the number of SNPs in the Matched Motif and Intersect Motif regions is relatively small (56 and 167, respectively), whereas the Enhancer Narrow Peak region contains the largest number of SNPs (62,506).
Since the annotation categories cannot fully reflect the significance of SNPs to the traits, we re-grouped the SNPs using the numerical grades provided in the IFmut dataset, as shown in Table 1. In this scheme, each SNP was assigned to only one category. From Table 4, we found that category five contained the highest number of SNPs, totaling 54,169 (14.8%). In contrast, the number of SNPs in category one and category two is relatively small, with only 45 (0.01%) and 68 (0.02%), respectively. The ‘rest’ category comprised 276,597 SNPs (75.6%), indicating that the majority of loci were either outside the top five annotations or belonged to unclassified variants.
We then conducted feature selection separately for each numerical grade category. The selected SNP features were merged to form the final input for the subsequent deep learning model fitting, i.e., CNN; the prediction performances are shown in Table 5. Integrated with the hierarchical feature selection strategy, we found that the two-step strategy-based CNN model has no significant difference in prediction accuracy compared to that with no feature selection, and the PCC of the TPD, RTN, and TTN traits slightly increased.
Simultaneously, we recorded the program running time, as shown in Table 6. It is worth noting that the average prediction time of the model decreased by 1.03 h (nearly tripling the computational efficiency) after adopting the hierarchical feature selection strategy. The time required for hierarchical feature selection is relatively stable and accounts for a considerable proportion of the total runtime. Nevertheless, it substantially accelerates model training efficiency. In summary, these results highlight the advantage of omics-annotation-based feature selection in reducing the computational complexity of deep learning models.

4. Discussion

The differences in predictive performance among different models in genome prediction essentially reflect their ability to analyze genetic structures and adapt to data features. Model selection is a core decision-making process in genome prediction research. This study evaluated the predictive ability of seven models on the traits of pigs, including rrBLUP, RF, SVR, XGBoost, LightGBM, MLP, and CNN. The average prediction performance of rrBLUP is still the highest, but no model can always perform best across all traits, and it is difficult to comprehensively capture complex genetic effects. This result is similar to that of previously published studies [43,44]. We believe that the inability of ML/DL models to outperform traditional models is primarily due to the limited sample size. Since ML/DL models attempt to capture highly complex statistical relationships among variables, insufficient data often prevents the models from converging effectively, resulting in suboptimal predictive performance [45]. Therefore, given the current population size of pigs, traditional models may still be more appropriate for genomic prediction than conventional ML/DL approaches.
In order to extend the applicability of deep learning models in species with various complexities of genetic architecture, this study adopts a two-step strategy, which first fits the GBLUP model to estimate individual GEBVs and calculate phenotype residuals. Subsequently, the residuals are fitted using a CNN model. Compared to using GBLUP or CNN alone, the two-step strategy has the following advantages: (1) GBLUP provides stable estimates of additive genetic effects. Its unbiasedness ensures the accuracy of baseline prediction for genome selection [46]. It is especially suitable for quantitative traits that are jointly affected by a large number of minor genes [47,48]. (2) By stripping the additive genetic effects (i.e., removing the mean and GEBV), the remaining residuals mainly include non-additive effects and environmental noise. It provides a more streamlined objective to the CNN model; thus, the CNN model can focus more on capturing this complex nonlinear information, avoiding the impact of noise and enhancing the modeling ability for non-additive and environmental effects [49]. (3) Due to the relatively low variance of phenotype residuals and the relatively stable noise, the parameter space of the CNN model during training is reduced, which makes it easier for the model to meet the early stopping condition. And it can quickly converge in fewer iterations, thereby shortening the model training time [50]. This residual split strategy fully utilizes the complementary advantages of GBLUP and CNN models and enables the final prediction model to accurately estimate additive genetic effects and identify complex non-additive effects, as well as gene interactions.
To further improve the capability of handling big data of deep learning models, we proposed a hierarchical feature selection strategy integrating multi-omics annotation information. It significantly shortens the model training time while maintaining the basic performance of prediction. The XGBoost selects SNPs that are correlated to traits, ensuring a certain level of prediction performance. A previous study found that the trait-associated regions identified by XGBoost overlapped with those of significantly associated loci detected by genome-wide association studies (GWAS) [51]. However, the omics-based annotation information currently used is general rather than trait-specific, which limits its ability to improve prediction performance. Future research should explore the use of trait-specific annotation data or the development of adaptive weighting algorithms to achieve more precise classification and enhanced predictive accuracy.

5. Conclusions

We evaluated the capability of multiple traditional deep learning models in predicting the economic traits of pigs and found that ML/DL models failed to surpass the traditional linear mixed model. Therefore, we proposed a Multi-omics Annotation and Residual Split strategy-based deep learning model (MARS), which leverages multi-omics annotation information to construct an efficient hierarchical feature selection strategy, ensuring the maximum use of informative signals while reducing data dimensionality and improving computational efficiency. Subsequently, it employs residuals from a linear mixed model as phenotypes for deep learning algorithms. This two-step strategy enables the separate modeling of linear and nonlinear, and additive and interactive effects, thereby enhancing both the predictive performance for traits and the overall robustness of the model. To make the proposed model more accessible for practical applications, we developed a user-friendly package, which is freely available to the public at https://github.com/jnanma/MARS. Meanwhile, it should be clarified that we have currently validated the improved predictive ability of MARS only for pig traits. It remains unclear whether MARS would perform equally well for traits in other species. Further investigations are required to demonstrate its applicability across different species.

6. Availability of Used Software Tools and Packages

PLINK: https://www.cog-genomics.org/plink/1.9 (accessed on 18 August 2024);
Beagle: https://faculty.washington.edu/browning/beagle/beagle.html (accessed on 10 October 2024);
rMVP: https://github.com/xiaolei-lab/rMVP (accessed on 1 August 2024);
HIBLUP: https://www.hiblup.com (accessed on 28 September 2024);
IFmut: http://www.ifmutants.com:8212/#/home (accessed on 12 May 2024);
The proposed model MARS of this study: https://github.com/jnanma/MARS.

Author Contributions

M.L. and L.Y. conceived the study. J.M. performed the experiments, developed the software, and wrote the raw manuscript. X.L. and X.X. provided professional suggestions and helped to edit and proofread the manuscript. Z.T., H.Z. and Y.L. assisted in the data analysis, software testing, and evaluation. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Science and Technology Major Project [2022ZD0115704-03], and the China Agriculture Research System of MOF and MARA [CARS-35].

Data Availability Statement

The original data presented in the study are openly available in GigaDB at https://gigadb.org/dataset/100894 (accessed on 18 August 2024).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
  2. Georges, M.; Charlier, C.; Hayes, B. Harnessing genomic information for livestock improvement. Nat. Rev. Genet. 2019, 20, 135–156. [Google Scholar]
  3. Chatterjee, N.; Shi, J.; García-Closas, M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 2016, 17, 392–406. [Google Scholar] [CrossRef]
  4. Xu, Y.; Ma, K.; Zhao, Y.; Wang, X.; Zhou, K.; Yu, G.; Li, C.; Li, P.; Yang, Z.; Xu, C. Genomic selection: A breakthrough technology in rice breeding. Crop J. 2021, 9, 669–677. [Google Scholar]
  5. Schaeffer, L. Strategy for applying genome-wide selection in dairy cattle. J. Anim. Breed. Genet. Genet. 2006, 123, 218–223. [Google Scholar]
  6. Lilin, Y.; Yunlong, M.; Tao, X.; Mengjin, Z.; Mei, Y.; Xinyun, L.; Xiaolei, L.; Shuhong, Z. The Progress and Prospect of Genomic Selection Models. Acta Vet. Zootech. Sin. 2019, 50, 233–242. [Google Scholar]
  7. Zuk, O.; Hechter, E.; Sunyaev, S.R.; Lander, E.S. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA 2012, 109, 1193–1198. [Google Scholar] [CrossRef]
  8. Lappalainen, T.; Li, Y.I.; Ramachandran, S.; Gusev, A. Genetic and molecular architecture of complex traits. Cell 2024, 187, 1059–1075. [Google Scholar] [CrossRef]
  9. Avasthi, P.; Celebi, F.M.; Hochstrasser, M.L.; Mets, D.G.; York, R. Harnessing genotype-phenotype nonlinearity to accelerate biological prediction. Arcadia Sci. 2023. [Google Scholar] [CrossRef]
  10. Costa-Neto, G.; Fritsche-Neto, R.; Crossa, J. Nonlinear kernels, dominance, and envirotyping data increase the accuracy of genome-based prediction in multi-environment trials. Heredity 2021, 126, 92–106. [Google Scholar] [CrossRef]
  11. Hay, E.H. Machine Learning for the Genomic Prediction of Growth Traits in a Composite Beef Cattle Population. Animals 2024, 14, 3014. [Google Scholar] [CrossRef]
  12. Zhu, W.; Li, W.; Zhang, H.; Li, L. Big data and artificial intelligence-aided crop breeding: Progress and prospects. J. Integr. Plant Biol. 2024, 67, 722–739. [Google Scholar] [CrossRef]
  13. Montesinos-López, O.A.; Montesinos-López, A.; Pérez-Rodríguez, P.; Barrón-López, J.A.; Martini, J.W.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A review of deep learning applications for genomic selection. BMC Genom. 2021, 22, 19. [Google Scholar] [CrossRef]
  14. Chafai, N.; Hayah, I.; Houaga, I.; Badaoui, B. A review of machine learning models applied to genomic prediction in animal breeding. Front. Genet. 2023, 14, 1150596. [Google Scholar] [CrossRef]
  15. Srivastava, S.; Lopez, B.I.; Kumar, H.; Jang, M.; Chai, H.-H.; Park, W.; Park, J.-E.; Lim, D. Prediction of Hanwoo Cattle Phenotypes from Genotypes Using Machine Learning Methods. Animals 2021, 11, 2066. [Google Scholar] [CrossRef]
  16. Shokor, F.; Croiseau, P.; Gangloff, H.; Saintilan, R.; Tribout, T.; Mary-Huard, T.; Cuyabano, B.C.D. Deep Learning and GBLUP Integration: An Approach that Identifies Nonlinear Genetic Relationships Between Traits. bioRxiv 2024. [Google Scholar] [CrossRef]
  17. An, B.; Liang, M.; Chang, T.; Duan, X.; Du, L.; Xu, L.; Zhang, L.; Gao, X.; Li, J.; Gao, H. KCRR: A nonlinear machine learning with a modified genomic similarity matrix improved the genomic prediction efficiency. Brief Bioinform 2021, 22, 132. [Google Scholar] [CrossRef]
  18. Pérez-Enciso, M.; Zingaretti, L.M. A guide on deep learning for complex trait genomic prediction. Genes 2019, 10, 553. [Google Scholar] [CrossRef]
  19. Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the bayesian alphabet for genomic selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef]
  20. Yin, L.; Zhang, H.; Zhou, X.; Yuan, X.; Zhao, S.; Li, X.; Liu, X. KAML: Improving genomic prediction accuracy of complex traits using machine learning determined parameters. Genome Biol. 2020, 21, 146. [Google Scholar] [CrossRef]
  21. Ma, W.; Qiu, Z.; Song, J.; Cheng, Q.; Ma, C. DeepGS: Predicting phenotypes from genotypes using Deep Learning. bioRxiv 2017. bioRxiv:241414. [Google Scholar]
  22. Wang, K.; Abid, M.A.; Rasheed, A.; Crossa, J.; Hearne, S.; Li, H. DNNGP, a deep neural network-based method for genomic prediction using multi-omics data in plants. Mol. Plant 2023, 16, 279–293. [Google Scholar] [CrossRef]
  23. e Silva, F.F.; Zambrano, M.F.B.; Varona, L.; Glória, L.S.; Lopes, P.S.; Silva, M.V.G.B.; Arbex, W.; Lázaro, S.F.; Resende, M.D.V.d.; Guimarães, S.E.F. Genome association study through nonlinear mixed models revealed new candidate genes for pig growth curves. Sci. Agric. 2017, 74, 1–7. [Google Scholar] [CrossRef]
  24. Xu, Y.; Liu, X.; Fu, J.; Wang, H.; Wang, J.; Huang, C.; Prasanna, B.M.; Olsen, M.S.; Wang, G.; Zhang, A. Enhancing genetic gain through genomic selection: From livestock to plants. Plant Commun. 2020, 1, 100005. [Google Scholar] [CrossRef] [PubMed]
  25. Romero, A.; Carrier, P.L.; Erraqabi, A.; Sylvain, T.; Auvolat, A.; Dejoie, E.; Legault, M.-A.; Dubé, M.-P.; Hussin, J.G.; Bengio, Y. Diet Networks: Thin Parameters for Fat Genomic. arXiv 2016, arXiv:1611.09340. [Google Scholar]
  26. Nani, J.P.; Rezende, F.M.; Peñagaricano, F. Predicting male fertility in dairy cattle using markers with large effect and functional annotation data. BMC Genom. 2019, 20, 258. [Google Scholar] [CrossRef]
  27. Edwards, S.M.; Sørensen, I.F.; Sarup, P.; Mackay, T.F.C.; Sørensen, P. Genomic Prediction for Quantitative Traits Is Improved by Mapping Variants to Gene Ontology Categories in Drosophila melanogaster. Genetics 2016, 203, 1871–1883. [Google Scholar] [CrossRef] [PubMed]
  28. Gao, N.; Martini, J.W.R.; Zhang, Z.; Yuan, X.; Zhang, H.; Simianer, H.; Li, J. Incorporating Gene Annotation into Genomic Prediction of Complex Phenotypes. Genetics 2017, 207, 489–501. [Google Scholar] [CrossRef] [PubMed]
  29. Speed, D.; Balding, D.J. MultiBLUP: Improved SNP-based prediction for complex traits. Genome Res. 2014, 24, 1550–1557. [Google Scholar] [CrossRef]
  30. Dunham, I.; Kundaje, A.; Aldred, S.F.; Collins, P.J.; Davis, C.A.; Doyle, F.; Epstein, C.B.; Frietze, S.; Harrow, J.; Kaul, R.; et al. An integrated encyclopedia of DNA elements in the human genome. Nature 2012, 489, 57–74. [Google Scholar] [CrossRef]
  31. Yang, R.; Guo, X.; Zhu, D.; Tan, C.; Bian, C.; Ren, J.; Huang, Z.; Zhao, Y.; Cai, G.; Liu, D.; et al. Accelerated deciphering of the genetic architecture of agricultural economic traits in pigs using a low-coverage whole-genome sequencing strategy. GigaScience 2021, 10, 048. [Google Scholar] [CrossRef]
  32. Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.W.; Daly, M.J.; et al. PLINK: A Tool Set for Whole-Genome Association and Population-Based Linkage Analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
  33. Ayres, D.L.; Darling, A.; Zwickl, D.J.; Beerli, P.; Holder, M.T.; Lewis, P.O.; Huelsenbeck, J.P.; Ronquist, F.; Swofford, D.L.; Cummings, M.P.; et al. BEAGLE: An Application Programming Interface and High-Performance Computing Library for Statistical Phylogenetics. Syst. Biol. 2012, 61, 170–173. [Google Scholar] [CrossRef]
  34. Ma, R.; Kuang, R.; Zhang, J.; Sun, J.; Xu, Y.; Zhou, X.; Han, Z.; Hu, M.; Wang, D.; Fu, Y.; et al. Annotation and assessment of functional variants in regulatory regions using epigenomic data in farm animals. bioRxiv 2024, 6, 578787. [Google Scholar] [CrossRef]
  35. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  36. Smola, A.J.; Schölkopf, B.J.S. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
  37. Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
  38. Gilmour, A.R.; Thompson, R.; Cullis, B.R. Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 1995, 51, 1440–1450. [Google Scholar] [CrossRef]
  39. Yin, L.; Zhang, H.; Tang, Z.; Yin, D.; Fu, Y.; Yuan, X.; Li, X.; Liu, X.; Zhao, S. HIBLUP: An integration of statistical models on the BLUP framework for efficient genetic evaluation using big genomic data. Nucleic Acids Res. 2023, 51, 3501–3512. [Google Scholar] [CrossRef]
  40. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
  41. Adam, K.D.B.J. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
  42. Yin, L.; Zhang, H.; Tang, Z.; Xu, J.; Yin, D.; Zhang, Z.; Yuan, X.; Zhu, M.; Zhao, S.; Li, X.; et al. rMVP: A Memory-efficient, Visualization-enhanced, and Parallel-accelerated Tool for Genome-wide Association Study. Genom. Proteom. Bioinform. 2021, 19, 619–628. [Google Scholar] [CrossRef] [PubMed]
  43. Montesinos-López, A.; Montesinos-López, O.A.; Gianola, D.; Crossa, J.; Hernández-Suárez, C.M. Multi-environment genomic prediction of plant traits using deep learners with dense architecture. G3 Genes Genomes Genet. 2018, 8, 3813–3828. [Google Scholar] [CrossRef]
  44. Wang, J.; Tiezzi, F.; Huang, Y.; Maltecca, C.; Jiang, J. Benchmarking of feed-forward neural network models for genomic prediction of quantitative traits in pigs. Front. Genet. 2025, 16, 1618891. [Google Scholar] [CrossRef]
  45. Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
  46. VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
  47. Goddard, M. Genomic selection: Prediction of accuracy and maximisation of long term response. Genetica 2009, 136, 245–257. [Google Scholar] [CrossRef] [PubMed]
  48. Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
  49. Töpner, K.; Rosa, G.J.M.; Gianola, D.; Schön, C.-C. Bayesian Networks Illustrate Genomic and Residual Trait Connections in Maize (Zea mays L.). G3 Genes|Genomes|Genet. 2017, 7, 2779–2789. [Google Scholar] [CrossRef] [PubMed]
  50. Yu, B.; Xie, L.; Wang, F. An improved deep convolutional neural network to predict airfoil lift coefficient. In Proceedings of the International Conference on Aerospace System Science and Engineering, Toronto, ON, Canada, 30 July–1 August 2019; pp. 275–286. [Google Scholar]
  51. Xiang, T.; Li, T.; Li, J.; Li, X.; Wang, J. Using machine learning to realize genetic site screening and genomic prediction of productive traits in pigs. FASEB J. 2023, 37, 22961. [Google Scholar] [CrossRef]
Agriculture 15 02354 g001
Figure 1. Model structure of MLP used in the study.
Figure 1. Model structure of MLP used in the study.
Agriculture 15 02354 g001
Agriculture 15 02354 g002
Figure 2. The detailed structure of the CNN model.
Figure 2. The detailed structure of the CNN model.
Agriculture 15 02354 g002
Agriculture 15 02354 g003
Figure 3. Marker density plot of genome-wide markers.
Figure 3. Marker density plot of genome-wide markers.
Agriculture 15 02354 g003
Agriculture 15 02354 g004
Figure 4. Comparison of prediction performances of one-step strategies for different models. The prediction accuracy is assessed using the Pearson correlation coefficient between the predicted value and the actual value. The accuracy in the figure is the mean values obtained from four repetitions of five-fold cross-validation. The red dashed lines represent the corresponding average values of different models on all traits.
Figure 4. Comparison of prediction performances of one-step strategies for different models. The prediction accuracy is assessed using the Pearson correlation coefficient between the predicted value and the actual value. The accuracy in the figure is the mean values obtained from four repetitions of five-fold cross-validation. The red dashed lines represent the corresponding average values of different models on all traits.
Agriculture 15 02354 g004
Agriculture 15 02354 g005
Figure 5. Comparison of prediction performances between one-step and two-step strategies. In the one-step strategy, the CNN model directly fits the phenotype with the genotype; in the two-step strategy, the GBLUP model is first fitted to the phenotype, and then the CNN model is applied to the residuals together with the genotype. The accuracy in the figure is the mean values obtained from four repetitions of five-fold cross-validation. The red dashed lines represent the corresponding average values of different models on all traits.
Figure 5. Comparison of prediction performances between one-step and two-step strategies. In the one-step strategy, the CNN model directly fits the phenotype with the genotype; in the two-step strategy, the GBLUP model is first fitted to the phenotype, and then the CNN model is applied to the residuals together with the genotype. The accuracy in the figure is the mean values obtained from four repetitions of five-fold cross-validation. The red dashed lines represent the corresponding average values of different models on all traits.
Agriculture 15 02354 g005
Table 1. Classification standard of SNP in the IFmut database.
Table 1. Classification standard of SNP in the IFmut database.
CategorySupporting Data
1aQTL + OCR + NFR + Motif + Footprint
1bOCR + NFR + Motif + Footprint
1cQTL + OCR + NFR + Footprint
1dOCR + NFR + Footprint
2aQTL + OCR + Motif + Footprint
2bOCR + Motif + Footprint
2cQTL + OCR + Footprint
2dOCR + Footprint
3aOCR + NFR
3bOCR/NFR + Motif
4OCR/NFR/Footprint + TF binding site
5H3K27ac peak
6rest
Table 2. Descriptive statistical analysis of each trait.
Table 2. Descriptive statistical analysis of each trait.
TraitsNumberMaxMinMedianMeanSDCV
BF279638.276.110.7410.992.260.21
LMD279659.45.24646.153.930.09
LMP279559.8947.1554.0154.021.580.03
TPD260493.091062.4962.969.990.16
LTN27969455.350.660.12
RTN27968455.370.640.12
TTN27961581110.731.070.10
Table 3. Number of SNPs in different annotation categories.
Table 3. Number of SNPs in different annotation categories.
Annotation CategoryNumber of Classified SNPs
QTL13,594
OCR19,122
NFR5493
Footprint1154
Matched Motif56
Intersect Motif167
Any motif6641
Enhancer39,750
Enhancer Narrow Peak62,506
Active promoter9262
Active promoter narrow peak19,852
Table 4. Number of SNPs in different categories.
Table 4. Number of SNPs in different categories.
CategoryNumber of Classified SNPs
145
268
3643
434,436
554,169
rest276,597
Total365,958
Table 5. Impact of hierarchical feature selection on prediction performances.
Table 5. Impact of hierarchical feature selection on prediction performances.
TraitsFeature Selection
NoYes
BF0.4032 (0.0094)0.3988 (0.0099)
LMD0.3760 (0.0072)0.3752 (0.0068)
LMP0.4307 (0.0060)0.4293 (0.0059)
TPD0.4626 (0.0084)0.4659 (0.0079)
LTN0.3153 (0.0061)0.3123 (0.0065)
RTN0.2629 (0.0050)0.2640 (0.0055)
TTN0.3895 (0.0061)0.3915 (0.0058)
Mean0.37720.3767
Note: the prediction accuracy is assessed using the Pearson correlation coefficient between the predicted value and the actual value. The accuracy in the table is the mean values obtained from four repetitions of five-fold cross-validation. The values in parentheses indicate the corresponding standard errors.
Table 6. Impact of hierarchical feature selection on prediction time.
Table 6. Impact of hierarchical feature selection on prediction time.
Traits/
Time (h)		CNN_Without_HFS 1CNN_with_HFS 2
Training Time 3HFS Time 4Total Time 5
BF7.741.490.291.78
LMD0.660.200.300.5
LMP1.660.130.340.47
TPD0.270.050.310.36
LTN0.620.160.350.51
RTN0.340.070.310.38
TTN0.270.040.320.36
Mean1.650.310.320.62
Note: CNN_without_HFS 1: training time of two-step strategy-based CNN model without feature selection. CNN_with_HFS 2: time of two-step strategy-based CNN model with hierarchical feature selection. Training time 3: time spent on training the CNN model. HFS time 4: time spent on hierarchical feature selection. Total time 5: sum of training time and HFS time.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ma, J.; Tang, Z.; Zhang, H.; Liu, Y.; Xiong, X.; Liu, X.; Yin, L.; Lei, M. Multi-Omics Annotation and Residual Split Strategy-Based Deep Learning Model for Efficient and Robust Genomic Prediction in Pigs. Agriculture 2025, 15, 2354. https://doi.org/10.3390/agriculture15222354

AMA Style

Ma J, Tang Z, Zhang H, Liu Y, Xiong X, Liu X, Yin L, Lei M. Multi-Omics Annotation and Residual Split Strategy-Based Deep Learning Model for Efficient and Robust Genomic Prediction in Pigs. Agriculture. 2025; 15(22):2354. https://doi.org/10.3390/agriculture15222354

Chicago/Turabian Style

Ma, Jingnan, Zhenshuang Tang, Haohao Zhang, Yangfan Liu, Xiong Xiong, Xiaolei Liu, Lilin Yin, and Minggang Lei. 2025. "Multi-Omics Annotation and Residual Split Strategy-Based Deep Learning Model for Efficient and Robust Genomic Prediction in Pigs" Agriculture 15, no. 22: 2354. https://doi.org/10.3390/agriculture15222354

APA Style

Ma, J., Tang, Z., Zhang, H., Liu, Y., Xiong, X., Liu, X., Yin, L., & Lei, M. (2025). Multi-Omics Annotation and Residual Split Strategy-Based Deep Learning Model for Efficient and Robust Genomic Prediction in Pigs. Agriculture, 15(22), 2354. https://doi.org/10.3390/agriculture15222354

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop