Abstract
This study proposes a data-efficient surrogate modeling approach for predicting hydrostatic transmission (HST) system efficiency in tractors using minimal data. Only 27 samples were selected from a dataset of 5092 measurements based on the minimum, mean, and maximum values of the input variables (input shaft speed, HST ratio, and load), which were used as the training data. A hybrid prediction model combining deep kernel learning and a residual radial basis function surrogate was developed with hyperparameters optimized via Bayesian optimization. For performance verification, the proposed model was compared with Neural Network (NN), Random Forest, XGBoost, Gaussian Process (GP), and Support Vector Regressor (SVR) models trained using 27 samples. As a result, the proposed model achieved the highest prediction accuracy (R2 = 0.93, MAPE = 5.94%, RMSE = 4.05). Process, SVM (Support Vector MA). These findings indicate that the proposed approach can be effectively used to predict the overall HST efficiency using minimal data, particularly in situations where experimental data collection is limited.
1. Introduction
Tractors are representative work machines designed to perform tasks such as traction, driving, and transport by mounting various pieces of equipment. They are widely used in various fields, including agriculture, construction, and forestry, and their demand has steadily increased [1]. Among the various components of a tractor, the transmission system plays a key role in determining its overall work efficiency, and therefore, it is of particular importance [2,3].
Among tractor transmissions, the hydrostatic transmission (HST) offers the advantages of continuous variable gear shifting, convenient forward and reverse operations, and reduced torsional shock [4,5]. However, as an HST comprises a hydraulic pump and a motor, it generally exhibits a lower overall system efficiency than mechanical transmissions [6,7]. Therefore, various approaches are required for improved HST efficiency.
To understand and improve the HST efficiency, it is essential to obtain detailed information on its operating characteristics and overall efficiency [8]. Previous studies have employed various approaches for HST efficiency, including purely physics models, physics models calibrated with experimental data, and machine learning (ML) models.
Previous studies primarily focused on the development of physics models for HST efficiency predictions. Kim et al. [9] mathematically formulated a dynamic model of a pump, which is a key HST component, and analyzed its operational characteristics under varying parameter conditions. Manring et al. [10] developed a mathematical model of an HST system by deriving a third-order state-space representation comprising a pump, hose, and motor assembly. Dasgupta [11] performed a geometric analysis to estimate leakage and constructed a physics model capable of analyzing the efficiency characteristics with respect to the pump swash plate angle and load using a bond-graph approach. As in previous studies, physics models do not require separate experimental datasets, making them valuable for use in the early stages of transmission design. However, their accuracy may be limited because the implementation of complex nonlinear equations often entails neglecting certain parameters that can significantly influence performance. Therefore, to improve the accuracy of a physics-based prediction model, it is necessary to develop the model using experimental data that reflect the specific characteristics of the target product.
Several studies have incorporated experimental data into model development to improve the accuracy of conventional physics models. Mandal et al. [12] and Pandey et al. [13] derived modified efficiency estimation equations from existing theoretical formulations by introducing loss coefficients, which were experimentally determined to enhance model accuracy. Similarly, Singh et al. [14] proposed efficiency equations based on a physics model to predict HST efficiency and analyze the steady-state performance, using the equation coefficients obtained experimentally. In such cases, a physics-based model using experimental data has the advantage of improving the physics-based model accuracy. However, a large amount of data is required for the parameterization and the definition of boundary conditions, and the process of constructing the mathematical formulations is time-consuming. Moreover, prediction accuracy can decrease due to trade-off errors among parameter calibration objectives, inaccurate specification of the model structure, or excessive simplification [15,16].
Meanwhile, ML-based models can learn the functional relationship between inputs and outputs without explicit equations. They are particularly advantageous for capturing and predicting complex nonlinear and interaction effects among the input variables, and their computational process is simpler than that of physics-based models [17]. ML is also well-suited for systems that are difficult to model physically or whose physical models are incomplete, and its application has been rapidly expanding in the field of fluid mechanics [18]. In particular, it is highly effective for modeling nonlinear systems such as HST [19]. Lu et al. developed a neural network (NN)–based predictive model to estimate the efficiency of a continuously variable hydromechanical transmission [20]. Their approach was designed to overcome the low accuracy and complexity associated with physics-based models and achieved a high prediction accuracy with an R2 of 0.948 under specific conditions. Similarly, Li et al. developed a NN model to predict the efficiency and output torque of a piston motor, which is a key component of an HST [21]. Their results demonstrated high accuracy, with the prediction errors remaining within 2% of the experimental measurements.
In previous studies, NN approaches have been primarily used for efficiency prediction. Although NNs can achieve high prediction accuracy when sufficiently large datasets are available, their performance significantly degrades when trained on small datasets. This is because a typical NN-based model lacks a prior structure that governs the input–output relationship and instead relies entirely on the learned weights. Consequently, it becomes highly dependent on a small amount of data, making it extremely prone to overfitting. Therefore, large amounts of data are required to achieve high prediction accuracy [22].
As acquiring experimental data for HSTs requires costly testing procedures, it is more efficient to develop predictive models that can achieve high accuracy with a limited number of experimental data.
Recently, ML has been increasingly applied to domains where acquiring large datasets is challenging. Among these methods, the Gaussian Process (GP) model is a nonparametric Bayesian regression method that can flexibly learn functional forms from data through kernel functions. In addition to prediction, it provides uncertainty estimates, allowing confidence intervals for prediction results to be easily obtained [23]. This enables kernel-based modeling even with a small number of samples, and its advantage is that the regression function form does not need to be predefined [23]. However, GP is not flexible enough when the data in different areas changes abruptly, and a single kernel function cannot fit effectively [24]. Deep Kernel Learning (DKL) proposes a novel approach that enables powerful and data-efficient representation learning by using a probabilistic neural network to map data points in the latent space to probability distributions, thereby allowing the GP to learn highly expressive kernels even from a small amount of labeled data [25]. In other words, by combining the flexibility of kernel-based nonparametric methods with the structural characteristics of deep neural networks, it can effectively capture the nonlinear structure of the input variables and is advantageous for prediction with a small amount of data [26]. This feature makes DKL particularly advantageous for developing predictive models when only a limited amount of training data is available [25,27].
In summary, conventional physics-based models suffer from low accuracy, whereas physics-based models combined with experiments and traditional ML methods require a large number of experiments. The development of a highly accurate prediction model using only a small amount of experimental data can effectively overcome these limitations. To overcome the limitations of previous studies on physics-based models, physics models calibrated with experimental data, and ML models, this paper proposes a predictive model that uses strategically selected minimal input datasets. This study enables high-efficiency control of the HST and can reduce fuel consumption in tractors. The main contributions of this paper can be summarized as follows:
- (1)
- The proposed predictive model was developed using DKL, which is advantageous when a limited number of training samples are available and is further enhanced by incorporating a residual Radial Basis Function (RBF) interpolator to compensate for residual errors.
- (2)
- For model training, the input datasets were constructed using the maximum, minimum, and mean values of the input variables. The input variables are the input shaft speed, HST ratio, and load, and the output variable is the overall efficiency.
- (3)
- Despite relying on minimal datasets, the proposed model is expected to provide stable and accurate HST efficiency predictions across the full operating range of agricultural tractors.
2. Materials and Methods
2.1. HST System
The specifications of the HST used in this study are listed in Figure 1. The piston pump displacement ranges from 0 to 42.4 cc/rev, whereas that of the piston motor is fixed at 42.4 cc/rev. Transmission is achieved by controlling the pump swash-plate angle. The pump swash-plate angle varies from 0° to ±18°, whereas the motor swash-plate angle is fixed at 18°. The pump swash-plate angle variation is controlled by the output of a pressure-proportional control valve. The maximum operating pressure is 340 ± 10 bar (@ 30 L/min).

Figure 1.
Specification of HST.
The HST system used in this study comprised a variable displacement pump, fixed displacement motor, electronic control valve for pump swash-plate angle adjustment, neutral control valve for maintaining vehicle standstill, and a maximum pressure relief valve to protect the HST system. A schematic of the HST system is shown in Figure 2. The pump shaft is driven by a tractor engine that allows oil to flow from low- to high-pressure lines. The pump swash-plate angle is regulated using an electronic control valve that adjusts the discharge flow rate accordingly. The discharged hydraulic flow passes through the hydraulic motor, generating rotational motion at the output shaft. Theoretically, no flow should be discharged from the pump without an electronic control valve. However, the tractor may move if an oil leak occurs. To prevent this, the neutral control valve directs the oil to the drain port and maintains a stationary tractor. To protect the HST system, if the pressure exceeds 340 bar, excess oil is discharged to maintain a maximum operating pressure of 340 bar.
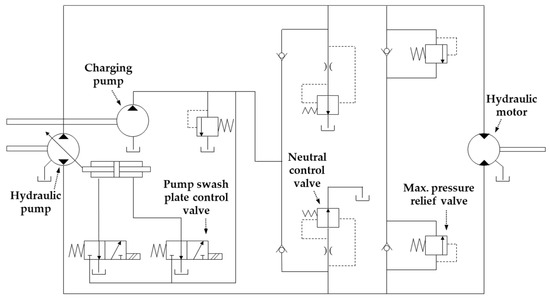
Figure 2.
Hydraulic circuit diagram of the HST used in this study.
As shown in Figure 2, the rotational power from the input shaft drives the pump, which discharges the hydraulic fluid that flows through the internal passages to rotate the motor and generate output power. However, part of the input power is lost before reaching the output shaft owing to various losses. Energy losses in HST systems can be primarily categorized into volumetric and mechanical losses. Volumetric losses occur owing to leakage within the pump, motor, and various valves, thereby reducing the effective flow rate delivered to the hydraulic motor. By contrast, mechanical losses primarily occur owing to friction in bearings and rotating parts, which reduces the torque transmission efficiency [28,29]. The overall efficiency of an HST system is determined as the product of its volumetric and mechanical efficiencies. This is expressed in Equations (1)–(3), where , and denote the volumetric, mechanical, and total efficiencies, respectively; and denote the pump input shaft speed and motor output shaft speed, respectively; and denote the input shaft torque to the pump and the output shaft torque from the motor, respectively; and is the HST ratio.
2.2. HST Test Bench
The test bench used to measure the HST efficiency was configured as shown in Figure 3. The input shaft motor simulates the function of the tractor engine and transmits power to the transmission input shaft. The power transmitted to the HST is measured using torque and rotational speed sensors installed on the input shaft. Similarly, the output power is measured at the output shaft using the corresponding torque and speed sensors.
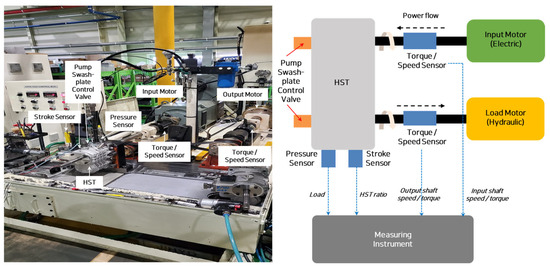
Figure 3.
HST test bench for experimental data acquisition.
The load is applied using a hydraulic swash-plate motor, and the loading level is controlled by adjusting the pressure difference between the inlet and outlet sides of the HST. The HST pump swash-plate angle is regulated using an electrohydraulic pressure-proportional valve, which is controlled using an external electronic controller.
The specifications of the bench components are as follows. The driving motor (K1379, Kosan Heavy Electric, Siheung, Republic of Korea) has a rated power of 150 kW and a maximum speed of 3600 rpm. The stroke sensor (TCL-20M, Showa Sokki, Nishihokima, Japan) was a linear variable differential transformer (LVDT) type sensor, with a displacement range of 5 to 50 mm, nonlinearity of ±0.5%, hysteresis of ±0.5%, and repeatability of ±0.3%. The torque sensor (1605-5K, Honeywell, Charlotte, NC, USA) incorporates an internal speed sensor. The sensor can measure torques up to 565 N·m, a nonlinearity of ±0.1%, hysteresis of ±0.1%, and repeatability of ±0.05%. The maximum measurable speed is 10,000 rpm. The pressure sensor (TPSA, Gefran, Provaglio d’Iseo, Italy) can measure a range of 0 to 600 bar and an accuracy of ±0.15% FS. The load motor (SH11C, SAM Hydraulik, Reggio Emilia, Italy) has a maximum pressure of 430 bar, a maximum speed of 5000 rpm, and a maximum torque capacity of 386 N·m.
The experimental data were measured by conducting tests using the HST test bench, as summarized in Table 1. The input shaft speed was set within the actual operating range of the tractor engine (1000–2600 rpm) in 200-rpm increments. The HST pump swash-plate angle was measured in the range of 10–100%, where the output shaft rotation was generated at intervals of 5%. The load pressure was varied from 50 to 340 bar, which corresponds to the relief valve setting for the maximum pressure, in 10-bar increments. All test conditions were configured to replicate the realistic input operating range of the HST system. The tests were conducted at room temperature (25 ± 2 °C). The oil viscosity grade was ISO VG 46, and the oil temperature was maintained at 50 ± 5 °C using a dedicated circulation cooling system. The oil viscosity grade and temperature were determined based on the Korean Industrial Standards (KS) “Test methods for electronically controlled oil hydraulic pumps” (KS B 6516:2021) [30].

Table 1.
Experimental input variable design.
2.3. Efficiency Prediction Model
The primary objective of this study was to develop a scientifically reliable and data-efficient model that can accurately predict the efficiency of a nonlinear HST system using only a minimum amount of experimental data. First, to use the minimum amount of experimental data, 27 data samples were extracted from an original dataset of 5092 points, which comprised the minimum, average, and maximum values of three key input variables (namely, input shaft speed, HST ratio, and load). The minimum, average, and maximum values of each variable were helpful for designing and conducting the experiments.
In this study, a novel hybrid method that integrates DKL for global trend modeling and a residual RBF interpolator for HST efficiency prediction is proposed. A detailed overview of the prediction model development process is shown in Figure 4.
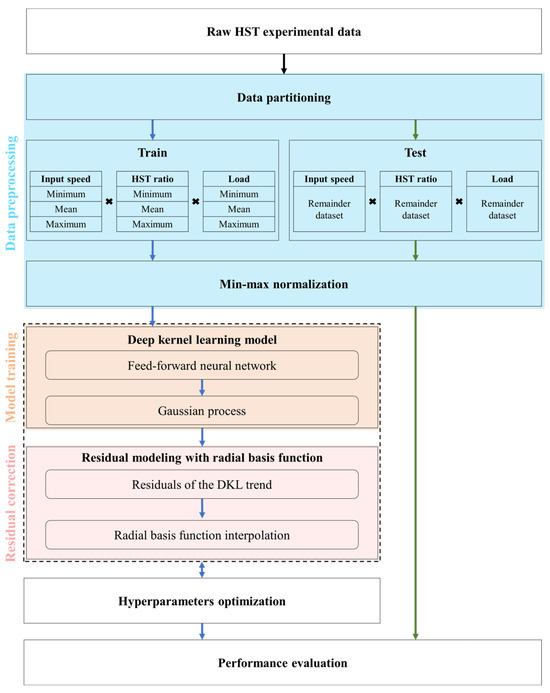
Figure 4.
Overall workflow of the proposed hybrid DKL with residual RBF Interpolator modeling framework for HST efficiency prediction.
2.3.1. Data Sampling from an Experimental Design Perspective
The purpose of this study is to develop an HST efficiency prediction model that achieves high accuracy even with a small number of samples. To accomplish this, it is essential to establish criteria for determining which data should be collected during the experimental design stage. In this study, the minimum, mean, and maximum values were used as these criteria. Combining the minimum, mean, and maximum values for each input feature (input speed, HST ratio, load) instead of random sampling provides a systematic and reproducible coverage of the entire operating range, which strengthens the efficiency predictions. By including the extreme low and high values of each factor (along with a central mean value), we ensure that the model is trained at the full boundaries of the HST’s working envelope, thereby capturing the broadest variability and avoiding any need to extrapolate beyond observed data [31].
In fact, deliberate maximum variation sampling—i.e., purposefully taking the extremes—has been shown to yield more representative and reliable results than purely random sampling [31,32]. The addition of a midpoint (mean) is a standard design-of-experiments practice to detect nonlinear or curvature effects in the response [33], since a third level allows one to identify any bending in the relationship between inputs and efficiency that would be missed by using only two extremes. Moreover, using fixed min–mean–max settings makes the procedure inherently reproducible: each HST has well-defined minimum and maximum operating limits (and a known typical mean). Therefore, these exact values can be reused by any researcher or model, ensuring consistent conditions across studies. In contrast, a random sample would introduce arbitrary variability and require a large number of trials (and careful seeding) to cover all conditions with the same confidence. Notably, this min–mean–max approach effectively constitutes a full three-level factorial design, which examines every combination of low, mid, and high values for the three factors. Such factorial designs are known to efficiently capture main effects and even interactions with relatively few experiments, all while maintaining high reproducibility [34].
2.3.2. Data Partitioning and Preprocessing
The available dataset was first divided into two subsets: a core set used for model training/optimization and the remaining set reserved for final testing (external validation). Each data instance comprises three input features (input shaft speed, HST ratio, and load) and one output response (efficiency). To ensure consistent scaling and avoid bias in favor of any features, all input features from both the core and remaining sets were normalized to the 0–1 range using a min-and-max scaler. This global normalization prevents scale differences from influencing the learning process and is a common best practice in NN training and GP regression [35]. Formally, for each feature , values were scaled as such that for all data points [36].
2.3.3. DKL Regression Model
We employed a DKL model to capture the primary trend in the data. DKL combines the expressive power of deep NNs with the nonparametric flexibility of GP regression [27,37]. In our implementation, a feed-forward NN , with two hidden layers (each of size , with rectified linear unit activations), serves as a trainable feature extractor that transforms the three-dimensional input into a latent feature vector. These learned features are fed into an exact GP regression model with a constant mean and an RBF covariance kernel. In essence, the NN defines a deep kernel, , whose parameters (the network weights) are learned via GP marginal likelihood maximization [37,38]. The GP covariance function is a squared-exponential (Gaussian) kernel operating on learned features, ensuring that the model can capture complex, nonlinear trends in the data [38].
During training, the DKL model parameters (network weights and GP hyperparameters, including the GP output noise variance) were optimized by maximizing the log marginal likelihood of the training data [39]. This corresponds to minimizing the negative log marginal likelihood loss, which has the following form [40]:
where is the negative log marginal likelihood loss, is the kernel matrix on training points, is the noise variance, is the vector of observed efficiencies, and is the identity matrix. The optimization was performed with the AdamW (adaptive gradient descent using a weight decay regularization) optimizer [41]. We incorporated an early stopping criterion to prevent overfitting. The training iterations were halted if did not improve for five consecutive epochs, thereby retaining the model state with the best log-likelihood [42]. This yields a trained DKL model that provides a trend prediction for any input . The GP predictive mean for a new input is given by [43]:
where denotes the vector of kernel evaluations between the embedded test input and all training points, is the covariance matrix, is the noise variance, and is the vector of observed outputs [43]. The kernel used in our implementation was the RBF kernel, and the GP was trained by maximizing the exact marginal log-likelihood using the AdamW optimizer.
2.3.4. Residual Modeling with the RBF Interpolator
Although the DKL GP captures the general trend, any systematic residual pattern not learned by the GP can be modeled using a flexible surrogate [44]. We propose a two-stage model in which the residuals of the DKL trend are fitted using an RBF interpolator. This approach is conceptually analogous to universal kriging, where one assumes −a deterministic trend plus a residual term [45]. Here, is provided by the DKL GP trend, and is modeled via RBF interpolation. In geostatistical terms, DKL acts as a drift/trend function, and the RBF interpolator accounts for the leftover spatially correlated structure in the errors [46].
After training the DKL, we computed the residuals on the core set for each training sample , . These residuals (along with their corresponding feature vectors ) were used to fit the RBF model . RBF interpolation constructs an approximating function as a weighted sum of radial basis kernels centered at the training points [47]. Specifically, the surrogate residual function takes the following form [48]:
where is a selected radial basis kernel and are weights determined by fitting the residuals (interpolation equations). We selected a thin-plate spline (TPS) as the radial basis kernel because of its smoothness. The TPS is a special case of a polyharmonic spline that provides an exact interpolator that minimizes bending energy [49]. In radial form, the TPS kernel is (in two dimensions, with a similar form generalized for higher dimensions) [50]. This kernel yields smooth interpolation surfaces and is well-suited for the smooth modeling of varying residual errors. We also included a smoothing parameter in the RBF interpolator (as is common in TPS regression [51]), which imposes a penalty on roughness to prevent overfitting to noise. In practice, controls a trade-off: for values up to the RBF passes exactly through all residual data points, whereas allows a smoother fit that does not exactly interpolate every residual [52]. The RBF interpolator was fitted by solving for weights such that for all core points, subject to the smoothing constraint [53].
The ensemble prediction of our two-stage model for a new normalized input was obtained by adding the GP trend and RBF residual terms as follows:
where represent the global trend predicted by DKL, and compensates for the residuals generated after DKL training, as formulated in (6). This implies that DKL provides a baseline estimate, and the residual RBF interpolator corrects it by adding localized adjustments based on the learned residual patterns. By construction, exactly reproduces the training outputs (if is small and the residual model interpolates) or provides a smooth approximation thereof (if is selected for smoothing). This two-stage modeling approach leverages the strengths of both global and local function approximators and is analogous to methods that combine a deterministic trend with a stochastic residual model in spatial statistics.
2.3.5. Hyperparameter Extraction via Bayesian Optimization
To improve the DKL performance with the residual interpolator model, the optimal hyperparameters were extracted via Bayesian optimization. The hyperparameters included the number of neurons, learning rate, weight decay, epoch value, and RBF smoothing parameter.
Internal leave-one-out cross-validation (LOOCV) on the core training set was used to evaluate each hyperparameter combination [54]. In LOOCV, the model was trained on training points and tested on a single held-out point, repeating this procedure for all points. Formally, if the core set indices are , with as the true value and as the model prediction for , when trained without the -th sample, the LOOCV root mean squared error (RMSE) is as follows [55]:
Bayesian optimization was configured to evaluate 25 hyperparameter sets, starting with seven randomly sampled points to broadly explore the space, followed by 18 iterative selections guided by the EI criterion [56]. This process identifies an optimal setting that minimizes the LOOCV error. The optimal hyperparameters were then fixed for the final model training. Notably, the optimal RBF smoothing λ was determined in this process, allowing the data to inform how much residual smoothing was needed. If the core data were noisy, a higher λ would be favored to avoid overfitting, whereas very clean systematic residuals would favor λ = 0 for exact interpolation [57].
Next, we present the criteria used to determine the search ranges for hyperparameter optimization.
Neuron Numbers
The hidden dimension refers to the number of units in the NN hidden layer (or the size of the learned feature embedded before the GP layer). In practice, DKL and related NN + GP models use a moderate number of hidden units (typically tens to a few hundreds) to balance expressiveness and overfitting. For example, Al-Shedivat et al. [58] trained GP-LSTM networks with hidden layer sizes ranging from 32 to 256 units. This indicates that a range of to units (such as 64 to 256 units) is a reasonable choice. Such a range is large enough to capture complex patterns, as seen in deep GP experiments that used approximately 128 units in hidden layers [59], but not large enough to overfit, given the typically smaller data regimes of GPs. Thus, 64–256 hidden units are scientifically sensible, aligning with successful DKL architectures in the literature.
Learning Rates
In both deep learning and DKL contexts, learning rates on a logarithmic scale between and (0.001–0.1) are commonly tested. Empirical studies often start with a small value, such as 0.001, for adaptive optimizers (e.g., Adam) or approximately 0.01 to 0.1 for stochastic gradient descent (SGD) without adaptivity [60,61]. For instance, one experiment varied the SGD learning rates from 0.05 to 0.2 and Adam rates from approximately 0.0005 to 0.0015, finding that tuning within the – range covers the best-performing values [61]. Likewise, guidelines for hyperparameter search frequently recommend exploring 0.001, 0.01, 0.1 (and values in between on a log-scale), as these values often yield good convergence [61]. This range is sufficiently broad to include fast initial learning (0.1) and more conservative rates (0.001) to refine the training. In summary, a learning rate within the 1 × –1 × range is well-supported in the literature as a starting point for DKL models, covering typical defaults (0.001 for Adam; 0.01–0.1 for SGD).
Weight Decay
Weight decay or L2 regularization helps prevent overfitting by penalizing large weights. In deep neural networks (including the neural feature extractor in DKL), weight decay values are usually quite small (on the order of 1−5 to 1−3), but can range up to 1−2 in some cases. Classic vision networks, for example, often use 5 × (0.0005) as the weight decay coefficient [61]. AlexNet’s original training used 0.0005 and found this “small amount of weight decay” crucial for learning [60]. Modern architectures, such as ResNet, typically use 1 × (0.0001) as the default L2 regularization strength [62]. These values fell well within –. Using a weight decay (e.g., ) can underfit a model; however, values in the range are consistently effective across many domains [60,62]. Therefore, a weight decay range of 1 × to 1 × is scientifically justified with common choices of approximately 5 × [60], or [62], for DKL’s neural network component to improve generalization.
RBF Smoothing
The RBF smoothing parameter typically refers to the length-scale or smoothing factor in the RBF kernel, or a regularization term that smooths the kernel/interpolation. In GP kernels, this governs how smooth or rapidly varying the functions can be. Empirically, useful values tend to be fairly small (allowing the GP to fit the data closely) but not zero. A common approach is to search over a log range from very small (e.g., ) up to approximately . In practice, previous studies have selected values in this range to balance fit and smoothness. For example, an experiment on two-sample testing set the RBF smoothing hyperparameter σ = 0.1 (i.e., ) as an appropriate choice [63]. This indicates that the upper end of the range is approximately 0.1 in at least one application. On the lower end, values approaching would make the RBF kernel nearly “exact-fitting” (almost no smoothing). Although specific works may not always report the smallest attempted value, the need to add a very small nugget/jitter to GPs (often ) suggests that is a sensible lower bound to consider for numerical stability and minimal smoothing. Indeed, using a non-zero smoothing can significantly improve model performance in some cases; one study reported that adding an RBF smoothing parameter (0.75 in their notation) improved accuracy by over 10% [64]. Generally, 0 < smoothing ≦ 0.1 is a safe range: near-zero for almost exact interpolation and up to 0.1 for modest smoothing. Empirical evidence thus supports RBF smoothing tuning from 1 × to 1 × , with specific optimal values depending on the noise level and smoothness of the target function [63].
Epochs
The epoch hyperparameter (number of full passes through the training data) typically ranges from a few tens to a few hundred in most deep-learning experiments, depending on the dataset size and model complexity. In the context of DKL or NN + GP training, researchers often report training on the order of tens of epochs, up to approximately 100 epochs for convergence. For instance, Ober and Rasmussen [65] trained deep GP models for only 20 epochs and achieved stable results by that point [59], suggesting that with smaller datasets or very powerful models, early stopping at approximately a few dozen epochs can suffice. By contrast, in a joint NN and multi-task GP model for a medical data task, the authors trained 100 epochs to reach convergence [66]. Similarly, many deep-learning setups (e.g., for image classification or regression on moderate-sized data) use epoch counts in the 50–100 range, sometimes with early stopping. Considering these practices, a range of approximately 20–100 epochs is a logical choice. It captures scenarios in which a model learns quickly in a few dozen epochs [59] as well as more complex or large-data scenarios requiring 100 epochs [66]. This range is well-supported by relevant literature.
2.4. Modeling Training and Validation
Using the selected hyperparameters, the DKL model was retrained on the entire core dataset (all available training samples) to maximize data utilization. The training procedure was the same as described previously (GP marginal likelihood maximization with early stopping to capture the best model). After this final training, we extracted the DKL’s predictions on the core set to compute the residuals one more time. A final TPS RBF surrogate, , was then fitted on the full set of core residuals using the previously optimized (smoothing parameter).
The remaining set (test data not observed during training or hyperparameter tuning) was evaluated. For each test input in the remainder of the set, the DKL model produces a trend prediction , and the RBF interpolator produces a residual correction , yielding the final prediction for efficiency.
To assess the predictive performance of the test set, we computed several standard regression metrics: the coefficient of determination (which measures the fraction of variance explained by the model), RMSE, and mean absolute percentage error (MAPE). These metrics are calculated as follows:
R2 represents the proportion of variance reduction in residuals relative to the total variance of the data. It indicates how well the model captures the overall trend of the dataset; the higher the R2; value, the greater the model’s explanatory power for the trend. The RMSE has the same unit as the dependent variable and intuitively presents the magnitude of the average prediction error. As the errors are squared, the RMSE is more sensitive to large deviations. The MAPE provides a relative error (%) that facilitates interpretation across different units or scales. It intuitively shows how much, on average, the predictions deviate in percentage terms, making it useful for multi-condition or multi-system comparisons using a consistent metric [67,68,69].
These metrics provide a comprehensive evaluation of the prediction accuracy, relative error, and goodness-of-fit. The results for the remaining set confirmed the effectiveness of the proposed DKL using the RBF approach, with a low RMSE and high , indicating that the model captured the underlying relationship well, and a low MAPE, indicating high predictive precision in percentage terms.
To compare the predictive performance of the models developed in this study, various previously reported prediction models were applied. First, tests were conducted using the NN method, which has been employed for efficient prediction in HST systems and related fields, as previously discussed. Additionally, the HST system is a nonlinear system, and the Random Forest and XGBoost methods, which are ensemble tree methods that are effective for nonlinear system prediction, were employed [70,71]. These tree-based models divide the input space of a decision tree into multiple regions and make predictions for each region. Through this hierarchical partitioning process, they can effectively approximate the complex interactions and nonlinearity between the input variables [70]. Additionally, prediction models commonly used for small datasets were also used for comparison. The GP model is a nonparametric Bayesian regression method that can flexibly learn functional forms from data using kernel functions. Besides predictions, it provides uncertainty estimates, allowing confidence intervals for the prediction results to be easily obtained [72]. This enables kernel-based modeling even with a small number of samples, and its flexibility lies in the fact that the regression function form does not need to be predefined [23]. The Support Vector Regression (SVR) model is a regression version of the SVM that can learn nonlinear relationships through kernel functions [73]. Furthermore, as SVR forms a model based only on support vectors without directly depending on the number of dimensions or the dimensionality of the feature space, it can achieve a relatively stable performance even in high-dimensional input spaces [74]. It has also been reported to exhibit good predictive performance, even with small datasets or noisy data [75]. In summary, the predictive accuracies of the NN, Random Forest, GP, and SVR models were compared with those of the proposed prediction model. All models were trained using 27 samples, and the test data used the remaining experimental data, excluding the 27 training samples. The hyperparameters of each prediction model were determined with reference to previous studies [24,76,77,78].
The proposed prediction model combines DKL with a residual RBF interpolator. This hybrid approach integrates two models, and it is necessary to verify whether it achieves higher accuracy than each individual model [79]. Therefore, the predictive accuracy of the three models was compared as follows: the model using DKL alone, the model using the residual RBF interpolator alone, and the hybrid model combining the DKL model with the residual RBF interpolator developed in this study.
3. Results
3.1. Experimental Data Measurement Using HST Test Bench
Figure 5a presents the efficiency data as a function of the input shaft speed measured at 200-rpm intervals from 1000 to 2600 rpm. Figure 5b shows the efficiency variation with respect to the HST ratio, measured at 5% intervals from 10% to 100%. Figure 5c presents the efficiency as a function of the load ranging from 50 to 340 bar at 10-bar intervals. From Figure 5, it can be confirmed that the experimental data aligned with the expected operating conditions. Additionally, the relationship between each input variable and the output (efficiency) exhibited very low linearity. The R2; between the input shaft speed and efficiency, HST ratio and efficiency, and load and efficiency were 0.006, 0.497, and 0.149, respectively, confirming that all input–output relationships were nonlinear.
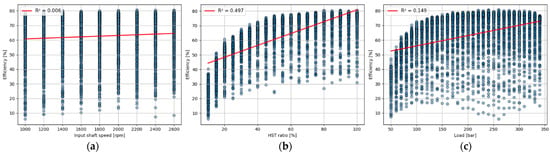
Figure 5.
Experimental data measured using HST test bench: (a) input shaft speed vs. efficiency; (b) HST ratio vs. efficiency; (c) load vs. efficiency.
The experimental data distribution is shown in Figure 6. As shown in Figure 6a, the input shaft speed was measured uniformly at 200 rpm intervals according to the experimental conditions. In Figure 6b, the HST ratio was measured from 10% to 100% in 5% increments. However, when the input shaft speed was 1000 rpm and the HST ratio was 10%, the maximum pressure was 260 bar; when the input shaft speed was 1200 rpm and the HST ratio was 10%, the maximum pressure was 270 bar; and when the input shaft speed was 1400 rpm and the HST ratio was 10%, the maximum pressure was 300 bar. Thus, it was not possible to apply a pressure of 340 bar. This is because when the pump discharge flow is insufficient, a high pressure cannot be generated.

Figure 6.
Distribution of experimental data by input variables: (a) input shaft speed; (b) HST ratio; (c) load; (d) efficiency.
As shown in Figure 6c, the load was measured from 50 to 340 bar in 10 bar increments. However, under conditions where the input shaft speed was 2600 rpm and the HST ratio exceeded 80%, the minimum achievable pressure was 60 bar. This was because the pump discharge flow was sufficiently high, and the internal resistance generated a minimum load pressure above the set lower limit of 50 bar. In addition, the number of samples above 260 bar was relatively small, because high pressures could not be generated under low HST ratio conditions. In Figure 6d, the distribution of the output variable (Efficiency) became denser as the efficiency increased, showing the highest concentration above 70%.
3.2. Results of Data Partitioning and Preprocessing
To minimize the number of experiments when constructing a prediction model for efficiency in nonlinear systems, a subset of the experimental data was selected using the minimum, maximum, and mean values of each input variable. As summarized in Table 2, the minimum, maximum, and average values were 1000, 2600, and 1800 rpm for the input shaft speed; 10.00%, 100.00%, and 55.56% for the HST ratio; and 50.00, 340.00, and 194.81 bar for the load, respectively. The HST efficiency ranged from a minimum of 8.41% to a maximum of 78.10%, with an average of 48.49%.

Table 2.
Statistical analysis results of experimental data.
Based on this statistical analysis, the 27 data points with values closest to these key statistics were extracted. The distributions of the 27 selected data points are shown in Figure 7. As shown in Figure 7a, the input shaft speed values corresponding to the minimum (1000 rpm), maximum (2600 rpm), and mean (1800 rpm) are selected at nine points. As shown in Figure 7b, the HST ratio values selected as the minimum are 10% and 15%, corresponding to six and three data points, respectively, whereas both the maximum and mean values were represented by nine data points each. The minimum values were chosen as 10% or 15% because, as mentioned earlier, some data points were impossible to measure in the 10% HST ratio region. For the load, as shown in Figure 7c, the minimum values (50 and 60 bar) are represented by nine and one data points, respectively, whereas the maximum value of 340 bar is represented by nine data points. The mean values were 190 and 200 bar, represented by six and three data points, respectively. The selection of 50 and 60 bar as the minimum values and 190 and 200 bar as the mean values was due to the inability to measure some data points at the minimum pressure condition of 50 bar, as described earlier. The output data corresponding to the selected results for each input variable are shown in Figure 7d. The efficiency data exhibits a high concentration in the region above 70%, with more than 10 data points within this range. Compared with the experimental data, the higher proportion of data above 70% was similar. However, it cannot be considered to be fully representative of the overall characteristics of the output data. This is because in this study, the training dataset was selected based on the input variables without considering the characteristics of the output variable.

Figure 7.
Distribution of sampling data by input variables: (a) input shaft speed; (b) HST ratio; (c) load; (d) efficiency.
3.3. Hyperparameter Extraction Through Bayesian Optimization
Bayesian optimization with a GP surrogate and an expected improvement acquisition function was used to tune the DKL using a residual RBF interpolator pipeline. The objective of this selection was to determine the LOOCV RMSE. Across the 25 evaluations, the objective values initially displayed the variability characteristic of random exploration, with scores between 3.683 and 4.226, and then progressed toward progressively lower incumbents (Figure 8), indicating a stable improvement in the surrogate-guided search. The minimum cross-validated error of 3.136 was reached in Evaluation 23, and the incumbent error remained unchanged thereafter, which indicates practical convergence and diminishing returns. Therefore, the optimization was terminated after 25 evaluations, consistent with the common stopping practice in GP-based Bayesian optimization when the best-so-far curve plateaus and additional queries are unlikely to yield material gains [80,81]. This trajectory indicates that the final setting was obtained by an efficient and well-behaved search rather than by exploiting the noise in a small sample.
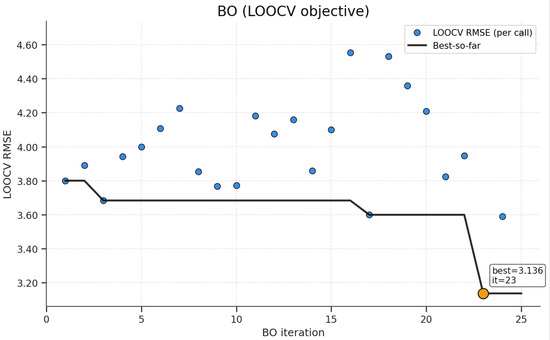
Figure 8.
Convergence plot of LOOCV RMSE.
The tuned hyperparameters are listed in Table 3. The selected hyperparameters for the model were as follows: the number of neurons was set to 64, the learning rate to 3.147 × 10−2, the weight decay to 7.749 × 10−5, the RBF smoothing factor to 9.100 × 10−6, and the number of training epochs to 59. These optimized hyperparameters were applied to the learning model, contributing to an improved prediction accuracy.

Table 3.
Hyperparameters optimization results.
3.4. Validation of Prediction Model
3.4.1. Accuracy Comparison with Commonly Used Prediction Models
For comparison with the proposed prediction model, the prediction accuracy of the NN, Random Forest, XGBoost, GP, and SVM models was analyzed. The results are presented in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 and Table 4.
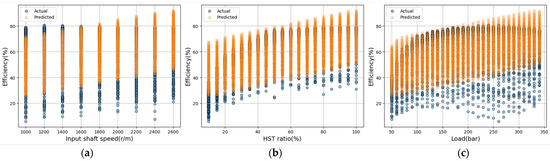
Figure 9.
Actual vs. predicted efficiency using the NN model; (a) input shaft speed; (b) HST ratio; (c) load.
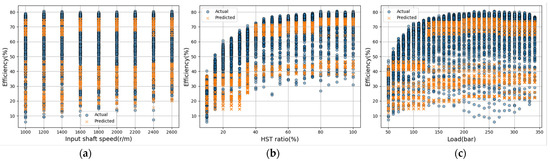
Figure 10.
Actual vs. predicted efficiency using the Random Forest model; (a) input shaft speed; (b) HST ratio; (c) load.
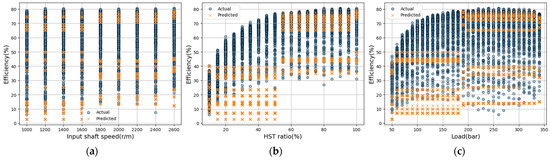
Figure 11.
Actual vs. predicted efficiency using XGBoost model; (a) input shaft speed; (b) HST ratio; (c) load.
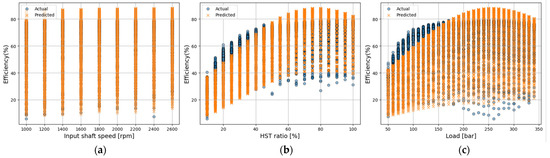
Figure 12.
Actual vs. predicted efficiency using GP model; (a) input shaft speed; (b) HST ratio; (c) load.
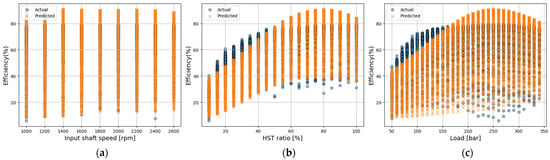
Figure 13.
Actual vs. predicted efficiency using SVM model; (a) input shaft speed; (b) HST ratio; (c) load.

Table 4.
Comparison between different prediction models trained on 27 samples.
The prediction accuracy of the NN model is shown in Figure 9. The performance evaluation results demonstrated that the NN model achieved a low coefficient of determination ( = 0.41) with a high MAPE of 19.57% and RMSE of 11.94%, indicating poor predictive accuracy. These results suggest that when a limited number of training samples is used, NN-based models exhibit very low accuracy. The NN model is highly data-dependent, and because it was trained with a limited number of samples, it was unable to capture the trends associated with rapid increases or decreases in the gradients.
The prediction accuracy of the Random Forest model is shown in Figure 10. The performance evaluation results were as follows: an of 0.11, MAPE of 19.59%, and RMSE of 14.70%, indicating poor predictive accuracy. This is because only 27 samples were used for the three input variables in the prediction process based on the decision tree, resulting in too few samples within each region after partitioning. The prediction accuracy of the XGBoost model is shown in Figure 11. The performance evaluation results were as follows: an of −2.25, MAPE of 33.35%, and RMSE of 28.11%, indicating poor predictive accuracy. This is because, similar to the Random Forest model, the decision-tree-based prediction process involves too few samples, resulting in an insufficient number of samples within each region. Consequently, when using a small number of samples, significant data overlap and a lack of diversity among trees lead to reduced prediction accuracy.
In general, XGBoost exhibits higher prediction performance than Random Forest when sufficient data are available. However, in this study, where the number of data points was extremely limited, the prediction accuracy of XGBoost drastically decreased. This is because XGBoost sequentially learns the residuals, which can lead to an overfitting problem. In contrast, Random Forest independently trains multiple trees and averages their results, which makes it less prone to overfitting and thus yields higher prediction accuracy than XGBoost [82]. Notably, the R2 value of the XGBoost model was −2.25, indicating that its prediction errors were even larger than those obtained by simply predicting the mean value. This suggests that, under the 27-sample training condition, the boosting algorithm progressively amplified noise components rather than capturing the actual physical trend. In this case, the model fit is poor as it fails to capture the trend [83].
As shown in Figure 12, the GP model achieved an R2 of 0.63, a MAPE of 14.53%, and an RMSE of 9.46, showing higher accuracy than the Random Forest and XGBoost models, but still relatively low overall accuracy. The GP model can make predictions within a smoothing function space based on changes in input variables. However, because of its tendency to rely on smooth interpolation between data points, its prediction performance decreases in regions where the data change abruptly or gradually, resulting in lower accuracy. The SVM model achieved an R2 of 0.54, a MAPE of 16.16%, and an RMSE of 10.57, as shown in Figure 13, indicating low accuracy. Because SVM performs predictions based on a single kernel function, it tends to produce relatively smooth predictions. Consequently, it cannot sufficiently reflect local sensitivity, where the output variable changes unevenly across input intervals, leading to reduced prediction accuracy.
3.4.2. DKL Only, Residual RBF Interpolator Only, DKL with Residual RBF Interpolator
The predictive accuracy of the proposed DKL model with the residual RBF interpolator was compared with that of each standalone model. The results are presented in Figure 14, Figure 15 and Figure 16 and Table 5. Figure 14 and Figure 15 show the predictive performance of the models using the DKL and residual RBF interpolator individually, respectively. Figure 14 shows the accuracy of the DKL-only model, which achieved an R2 of 0.83, MAPE of 9.26%, and RMSE of 6.20. Because of the characteristics of DKL, the overall trend can be predicted; however, in the high-efficiency region (above 70%), the kernel tends to smooth out nonlinear regions, resulting in lower prediction accuracy. Figure 15 shows the accuracy of the residual-RBF-interpolator-only model, which achieved an R2 = 0.71, MAPE = 12.34%, and RMSE = 8.31. As the RBF serves only to smoothly connect data points, it struggles to predict regions with abrupt or gradual variations, leading to reduced accuracy.
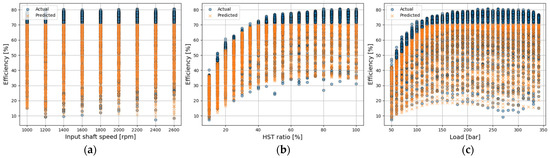
Figure 14.
Actual vs. predicted efficiency using the DKL-only model; (a) input shaft speed; (b) HST ratio; (c) load.
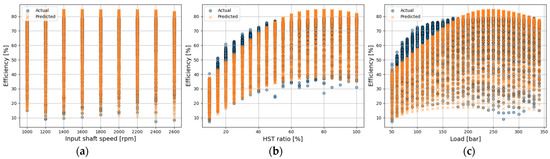
Figure 15.
Actual vs. predicted efficiency using the residual-RBF-interpolator-only model; (a) input shaft speed; (b) HST ratio; (c) load.
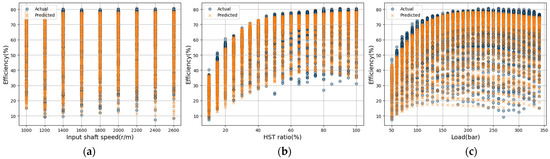
Figure 16.
Actual vs. predicted efficiency using the proposed DKL with residual RBF interpolator model; (a) input shaft speed; (b) HST ratio; (c) load.

Table 5.
Comparison between different prediction models trained on 27 samples (DKL-only, residual-RBF-interpolator-only, DKR with residual RBF interpolator).
The HST efficiency prediction results using the novel DKL with the residual RBF interpolator correction are shown in Figure 16. The validation results of the prediction model exhibited an of 0.93, MAPE of 5.94%, and RMSE of 4.05, indicating a relatively high prediction accuracy. By compensating for the residuals in the smoothed regions of the original DKL model through the residual RBF interpolator, the proposed model demonstrated higher accuracy than the DKL-only and residual-RBF-interpolator-only prediction models. However, the prediction accuracy was relatively low in regions where the efficiency of each input feature was high. In particular, the prediction error reached 7.49% for samples with efficiencies exceeding 70%, higher than the total average error of 5.94%. This can be interpreted as the result of the maximum value of the output variable (efficiency) when only a subset of the entire dataset is used. The maximum, minimum, and mean values of the input variables were selected. However, the maximum value of the output variable was not included. Consequently, the data points with efficiency values exceeding the maximum value represented in the training set may have been treated as noise.
4. Discussion
This study focused on developing a tractor HST system efficiency estimation model with the goal of maintaining high prediction accuracy even with a small amount of data. The model developed in this study combines DKL with a residual RBF interpolator. The proposed model demonstrated a higher prediction performance than the NN, Random Forest, XGBoost, GP, and SVM models. It also exhibited higher prediction performance than both the DKL model and the residual RBF interpolator individually.
First, the physical characteristics of the HST were compared with the experimental data, and the relationships between the physical characteristics and the prediction errors were analyzed as follows. As the input shaft speed increases, the influence of internal leakage flow decreases, resulting in an increase in volumetric efficiency [84]. However, as the input shaft speed increases, the mechanical efficiency decreases due to factors such as rotational friction and viscous friction losses in the rotating shaft [85]. The effect of input shaft speed on total efficiency is not clearly defined and may vary depending on the operating point. In other words, depending on the operating point, either volumetric efficiency or mechanical efficiency may become the dominant influencing factor; therefore, an increase in input shaft speed does not necessarily lead to a consistent increase or decrease in total efficiency [86]. For this reason, the efficiency in this study did not show a clear increasing or decreasing trend with respect to the input shaft speed.
As the HST ratio increases, similar to the input shaft speed, the effect of leakage flow diminishes, leading to an increase in volumetric efficiency [86]. In addition, as the HST ratio increases, the loss torque decreases, resulting in higher mechanical efficiency [87]. Consequently, the total efficiency increases as the HST ratio increases, which is consistent with the trends observed in this study. When the load increases, the flow through multiple leakage paths also increases, and the compressibility of the fluid rises, reducing the ratio of the actual effective flow to the theoretical discharge flow, thereby decreasing the volumetric efficiency [86]. However, as the load increases, the mechanical efficiency tends to increase because the viscous friction losses between relatively moving parts inside the pump decrease [86]. In this study, the increase in mechanical efficiency with higher load was greater than the decrease in volumetric efficiency, resulting in an overall increase in total efficiency.
The results of the prediction error analysis for the model developed in this study are shown in Figure 17. These results were analyzed from both physical and modeling perspectives as follows. As shown in Figure 17a, for the input shaft speed, the prediction accuracy was relatively lower in the low-speed region. In this region, the leakage flow is relatively large compared to the discharge flow. The errors are considered to result from discrepancies between the actual variation trend of the internal leakage flow and that predicted by the model.
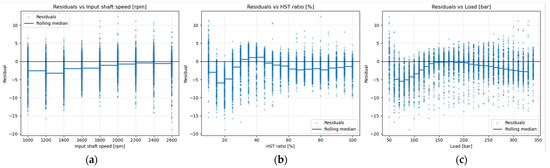
Figure 17.
The distribution of error of actual vs. predicted efficiency using DKL with residual RBF interpolator model; (a) input shaft speed vs. efficiency; (b) HST ratio vs. efficiency; (c) load vs. efficiency.
As shown in Figure 17b, for the HST ratio, relatively large errors were observed in the low range (below 40%). Similar to the case of the input shaft speed, this region also shows a relatively large leakage flow compared to the discharge flow. These errors are likewise attributed to differences between the actual internal leakage behavior and the trend predicted by the model. In contrast, in the region above 50%, the errors are mainly caused by the characteristics of the DKL model, which has difficulty predicting values beyond those used in the training process.
As shown in Figure 17c, for the load, errors occurring in the low-load region (below 150 bar) are mainly attributed to viscous friction losses, and these errors appear to arise from discrepancies between the actual trend of viscous friction losses and that predicted by the model. In the region above 200 bar, similar to the case of the HST ratio, the errors are considered to originate from the inherent limitation of the DKL model in predicting values beyond the range of training data.
As in the previous analysis, the prediction accuracy was relatively low in regions where the efficiency was high. This is considered to be a characteristic of the DKL model. This can be attributed to the fact that, when only a subset of the full dataset is used, the maximum value of the output variable (efficiency) cannot be fully represented. Consequently, values exceeding the maximum efficiency contained in the training data were regarded as noise by the model, making prediction difficult [88]. This issue can be addressed by including additional data samples corresponding to high-efficiency regions in the training set. However, in this study, representative data samples were selected based on easily applicable criteria, namely, the maximum, minimum, and mean values of the input variables; thus, these aspects were not considered.
Factors influencing HST efficiency were analyzed to identify additional input variables. In this study, the input shaft speed, HST ratio, and load were used as input variables. However, the oil temperature and viscosity characteristics can also influence the HST efficiency [89]. As the oil temperature increased, the viscosity decreased, leading to an increase in the leakage flow through the mechanical clearances and, consequently, a decrease in the volumetric efficiency. Conversely, when the temperature decreased, viscosity increased, resulting in greater frictional resistance and reduced mechanical efficiency [89]. In this study, the temperature condition was fixed at 50 ± 5 °C according to the Korean Agency for Technology and Standards (KS) “Test methods for electronically controlled oil hydraulic pumps.” This limitation arises from the time and cost constraints of the experimental process. Future work should include model training and validation, considering the efficiency characteristics under varying temperature conditions.
The prediction errors associated with the aforementioned physical characteristics, the characteristics of the DKL model, and the newly identified input variables can be used for feature engineering in future studies aimed at enhancing the accuracy of currently developed models. The experimental sample distribution can be adjusted by analyzing the physical characteristics and model prediction errors to improve the prediction accuracy. Furthermore, incorporating new input variables, such as oil temperature, can enhance the prediction accuracy under various operating conditions.
Furthermore, it is necessary to discuss the generalizability of the proposed prediction model. The proposed ML-based prediction model may yield different results if the HST structure varies; this generalizability issue has also been identified as a limitation in previous studies [90,91]. However, as discussed in prior research on data-driven models for predicting the characteristics of external gear pumps [92], artificial intelligence (AI)-based prediction methods primarily provide an architectural framework for modeling. Additional calibration experiments are required to apply such models to various types of systems or products. In other words, the prediction model developed in this study requires supplementary experimental data for extension to other products.
From this perspective, the fact that the proposed model required only 27 samples for training is a significant advantage. This implies that even with a small amount of experimental data, an accurate and efficient prediction model can be developed, indicating a high potential for generalization and ease of application to HST systems with different structural configurations.
Nevertheless, the proposed model is significant in that it achieves a predictive performance comparable to that of a model trained with 5092 data points using only 27 samples. The proposed prediction model can therefore be highly useful in industrial settings where information on HST efficiency is required but experimental resources are limited. Furthermore, the proposed approach has potential applicability beyond HST systems, extending to other types of transmissions or engines in which efficiency prediction plays a crucial role in powertrain components.
5. Conclusions
The main objective of this study was to develop an efficient predictive model for accurate HST system efficiency estimation using minimal experimental data. Based on the results, the main findings of this study can be summarized as follows:
- (1)
- A prediction model was developed for accurate HST efficiency estimation using 27 sets of experimental data. The model was constructed based on DKL, which is advantageous for prediction with limited datasets, and was further enhanced by integrating a residual RBF interpolator for error correction.
- (2)
- A minimal dataset was constructed by extracting samples, specifically the maximum, minimum, and mean values of each input variable (input shaft speed, HST ratio, and load). Consequently, 27 data points were selected from a full set of 5092 experimental samples.
- (3)
- Optimal hyperparameters were extracted to enhance the model’s prediction accuracy. Bayesian optimization was performed, and the neuron number, learning rate, weight decay, RBF smoothing, and epochs were determined.
- (4)
- The performance of the proposed DKL with the residual RBF interpolator model was validated. For this purpose, its predictive performance was compared with that of other existing models. The proposed model achieved a high prediction accuracy (= 0.93; MAPE = 5.94%; RMSE = 4.05), even with limited training data. These results showed higher prediction accuracy than the Neural NN (= 0.41; MAPE = 19.57%; RMSE = 11.94%), Random Forest (= 0.11; MAPE = 19.59%; RMSE = 14.70), XGBoost (= −2.25; MAPE = 39.35%; RMSE = 28.11), GP ( = 0.63; MAPE = 14.53%; RMSE = 9.46), SVR ( = 0.54; MAPE = 16.16%; RMSE = 10.57) models.
- (5)
- The proposed model was compared with the DKL-only and the residual-RBF interpolator-only models. The results show that the proposed model exhibited higher prediction accuracy than both the DKL-only model (= 0.83; MAPE = 9.26%; RMSE = 6.20) and the residual-RBF-interpolator-only model ( = 0.71; MAPE = 12.34%; RMSE = 8.31). Thus, it was confirmed that the combined model performed better than the individual models.
This study demonstrates that the HST efficiency can be predicted without relying on physical theories and can be particularly useful for efficiency estimation under conditions where the number of experimental trials is limited. Through this study, the number of experiments required to obtain the conventional HST efficiency map can be significantly reduced, thereby decreasing the time and effort needed for testing. In addition, by utilizing the derived efficiency map, high-efficiency control of the HST can be achieved, which in turn can reduce fuel consumption in agricultural tractors and alleviate the economic burden on farmers.
Author Contributions
Conceptualization, J.K.P. and J.H.M.; methodology, J.K.P., O.Y. and J.H.M.; software, J.K.P. and O.Y.; validation, J.K.P.; formal analysis, O.Y. and J.H.M.; investigation, J.W.L.; resources, J.W.L.; data curation, Y.C.; writing—original draft preparation, J.K.P. and O.Y.; writing—review and editing, J.K.P., O.Y. and J.H.M.; supervision, J.H.M.; project administration, J.K.P.; funding acquisition, J.K.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Foundation of Korea (NRF), Korea Government (MSIT), grant number NR058465 and this work was in part supported by Korea Institute of Industrial Technology as “Development of domestic technology for automatic transmission for tractors for autonomous agricultural work (kitech JA-25-0013)”.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from LS MTRON Ltd. and are available from the authors with the permission of LS MTRON Ltd.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HST | Hydrostatic transmission |
| HST ratio | Hydrostatic transmission pump swash-plate ratio (%) |
| Load | Hydrostatic transmission line pressure difference (bar) |
| NN | Neural network |
| DKL | Deep kernel learning |
| RBF | Radial basis function |
| GP | Gaussian process |
| RMSE | Root mean squared error |
| LOOCV | Leave-one-out cross-validation |
| MAPE | Mean absolute percentage error (%) |
References
- Kim, W.S.; Kim, Y.J.; Park, S.U.; Hong, S.J.; Kim, Y.S. Evaluation of PTO severness for 78kW-class tractor according to disk plow tillage and rotary tillage. J. Drive Control 2019, 16, 23–31. [Google Scholar] [CrossRef]
- Kim, W.S.; Kim, Y.J.; Kim, Y.S.; Baek, S.Y.; Baek, S.M.; Lee, D.H.; Nam, K.C.; Kim, T.B.; Lee, H.J. Development of control system for automated manual transmission of 45-kW agricultural tractor. Appl. Sci. 2020, 10, 2930. [Google Scholar] [CrossRef]
- Lukas, B.; Patrick, B.; Leon, S.; Markus, K. Enhanced efficiency prediction of an electrified off-highway vehicle transmission utilizing machine learning methods. Procedia Comput. Sci. 2021, 192, 417–426. [Google Scholar] [CrossRef]
- Park, Y.J.; Kim, S.C.; Kim, J.G. Analysis and verification of power transmission characteristics of the hydromechanical transmission for agricultural tractors. J. Mech. Sci. Technol. 2016, 30, 5063–5072. [Google Scholar] [CrossRef]
- Kim, D.M.; Kim, S.C.; Noh, D.K.; Jang, J.S. Jerk phenomenon of the hydrostatic transmission through the experiment and analysis. Int. J. Automot. Technol. 2015, 16, 783–790. [Google Scholar] [CrossRef]
- Ho, T.H.; Ahn, K.K. Modeling and simulation of hydrostatic transmission system with energy regeneration using hydraulic accumulator. J. Mech. Sci. Technol. 2010, 24, 1163–1175. [Google Scholar] [CrossRef]
- Jung, G.H. Gear train design of 8-speed automatic transmission for tractor. J. Drive Control 2013, 10, 30–36. [Google Scholar] [CrossRef][Green Version]
- Manring, N.D. Mapping the efficiency for a hydrostatic transmission. J. Dyn. Sys. Meas. Control 2016, 138, 031004. [Google Scholar] [CrossRef]
- Kim, S.D.; Cho, H.S.; Lee, C.O. A parameter sensitivity analysis for the dynamic model of a variable displacement axial piston pump. Proc. Inst. Mech. Eng. 1987, 201, 235–243. [Google Scholar] [CrossRef]
- Manring, N.D.; Luecke, G.R. Modeling and designing a hydrostatic transmission with a fixed-displacement motor. J. Dyn. Sys. Meas. Control 1998, 120, 45–49. [Google Scholar] [CrossRef]
- Dasgupta, K. Analysis of a hydrostatic transmission system using low speed high torque motor. Mech. Mach. Theory 2000, 35, 1481–1499. [Google Scholar] [CrossRef]
- Mandal, S.K.; Singh, A.K.; Verma, Y.; Dasgupta, K. Performance investigation of hydrostatic transmission system as a function of pump speed and load torque. J. Inst. Eng. India Ser. C 2012, 93, 187–193. [Google Scholar] [CrossRef]
- Pandey, A.K.; Vardhan, A.; Dasgupta, K. Theoretical and experimental studies of the steady-state performance of a primary and secondary-controlled closed-circuit hydrostatic drive. J. Process Mech. Eng. 2019, 233, 1024–1035. [Google Scholar] [CrossRef]
- Singh, V.P.; Pandey, A.K.; Dasgupta, K. Steady-state performance investigation of closed-circuit hydrostatic drive using variable displacement pump and variable displacement motor. J. Process Mech. Eng. 2020, 235, 249–258. [Google Scholar] [CrossRef]
- Wöhling, T.; Delgadillo, A.O.C.; Kraft, M.; Guthke, A. Comparing Physics-Based, Conceptual and Machine-Learning Models to Predict Groundwater Levels by BMA. Groundwater 2025, 63, 484–505. [Google Scholar] [CrossRef]
- Choi, D.; An, Y.; Lee, N.; Park, J.; Lee, J. Comparative Study of Physics-Based Modeling and Neural Network Approach to Predict Cooling in Vehicle Integrated Thermal Management System. Energies 2020, 13, 5301. [Google Scholar] [CrossRef]
- Gumiere, S.J.; Camporses, M.; Botto, A.; Lafond, J.A.; Paniconi, C.; Gallichand, J.M.; Rousseau, A.N. Machine Learning vs. Physics-Based Modeling for Real-Time Irrigation Management. Front. Water 2020, 2, 8. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, H.G.; Jang, J.H.; Park, S.D. An experimental study of the characteristics of hydrostatic transmission. Adv. Robot. 2015, 29, 939–946. [Google Scholar] [CrossRef]
- Lu, K.; Liu, M.; Lu, Z.; Shi, J.; Xing, P.; Wang, L. Research of transmission efficiency prediction of heavy-duty tractors HMCVT based on VMD and PSO-BP. Agriculture 2014, 14, 539. [Google Scholar] [CrossRef]
- Li, C.; Xia, Z.; Tang, Y. Prediction and dynamic simulation verification of output characteristics of radial piston motors based on neural networks. Machines 2024, 12, 491. [Google Scholar] [CrossRef]
- Hagiwara, K.; Fukumizu, K. Relation between Weight Size and Degree of Over-Fitting in Neural Network Regression. Neural Netw. 2008, 21, 377–386. [Google Scholar] [CrossRef]
- Baiz, A.A.; Ahmadi, H.; Shariatmadari, F.; Karimi Torshizi, M.A. A Gaussian Process Regression Model to Predict Energy Contents of Corn for Poultry. Poult. Sci. 2020, 99, 5838–5843. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, D.; Qian, W.; Liang, Y. Application of the gaussian process regression method based on a combined kernel function in engine performance prediction. ASC Omega 2022, 7, 41732–41743. [Google Scholar] [CrossRef]
- Mallick, A.; Dwivedi, C.; Kailkhura, B.; Joshi, G.; Han, T.Y. Deep kernels with probabilistic embeddings for small-data learning. arXiv 2021, arXiv:1910.05858. [Google Scholar] [CrossRef]
- Wilson, A.G.; Hu, Z.; Salakhutdinov, R.; Xing, E.P. Deep Kernel Learning. arXiv 2016, arXiv:1511.02222. [Google Scholar] [CrossRef]
- Singh, S.; Hernández-Lobato, J.M. Deep Kernel learning for reaction outcome prediction and optimization. Commun. Chem. 2024, 7, 136. [Google Scholar] [CrossRef]
- Costa, G.K.; Sepehri, N. Understanding overall efficiency of hydrostatic pumps and motors. Int. J. Fluid Power 2018, 19, 106–116. [Google Scholar] [CrossRef]
- Skorek, G. Study of losses and energy efficiency of hydrostatic drives with hydraulic cylinder. Pol. Marit. Res. 2018, 25, 114–129. [Google Scholar] [CrossRef]
- KS B 6516:2021; Test Methods for Electronically Controlled Oil Hydraulic Pumps. Korean Standards Association: Seoul, Republic of Korea, 2021.
- Van Hoeven, L.R.; Janssen, M.P.; Roes, K.C.; Koffijberg, H. Aiming for a representative sample: Simulating random versus purposive strategies for hospital selection. BMC Med. Res. Methodol. 2015, 15, 90. [Google Scholar] [CrossRef]
- Palinkas, L.A.; Horwitz, S.M.; Green, C.A.; Wisdom, J.P.; Duan, N.; Hoagwood, K. Purposeful sampling for qualitative data collection and analysis in mixed method implementation research. Adm. Policy Ment. Health Ment. Health Serv. Res. 2015, 42, 533–544. [Google Scholar] [CrossRef]
- Box, G.E.P.; Wilson, K.B. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–38. [Google Scholar] [CrossRef]
- Baker, T.B.; Smith, S.S.; Bolt, D.M.; Loh, W.Y.; Mermelstein, R.; Fiore, M.C.; Piper, M.E.; Collins, L.M. Implementing Clinical Research Using Factorial Designs: A Primer. Behav. Ther. 2017, 48, 567–580. [Google Scholar] [CrossRef]
- Mukangango, J.; Muyskens, A.; Priest, B.W. A robust approach to Gaussian process implementation. ASCMOAdv. Stat. Clim. Meteorol. Oceanogr. 2024, 10, 143–158. [Google Scholar] [CrossRef]
- Islam, M.J.; Ahmad, S.; Haque, F.; Reaz, M.B.I.; Bhuiyan, M.A.S.; Islam, M.R. Application of min-max normalization on subject-invariant EMG pattern recognition. IEEE Trans. Instrum. Meas. 2022, 71, 2521612. [Google Scholar] [CrossRef]
- Zinage, S.; Mondal, S.; Sarkar, S. Dkl-kan: Scalable deep kernel learning using kolmogorovarnold networks. arXiv 2024, arXiv:2407.21176. [Google Scholar] [CrossRef]
- Milsom, E.; Anson, B.; Aitchison, L. Convolutional deep kernel machines. arXiv 2023, arXiv:2309.09814. [Google Scholar] [CrossRef]
- Ament, S.; Santorella, E.; Eriksson, D.; Letham, B.; Balandat, M.; Bakshy, E. Robust Gaussian processes via relevance pursuit. Adv. Neural Inf. Process Syst. 2024, 37, 61700–61734. [Google Scholar]
- Wenger, J.; Wu, K.; Hennig, P.; Gardner, J.; Pleiss, G.; Cunningham, J.P. Computation-aware gaussian processes: Model selection and linear-time inference. Adv. Neural Inf. Process Syst. 2024, 37, 31316–31349. [Google Scholar]
- Wang, X.; Aitchison, L. How to set AdamW’s weight decay as you scale model and dataset size. arXiv 2024, arXiv:2405.13698. [Google Scholar] [CrossRef]
- Hussein, B.M.; Shareef, S.M. An empirical study on the correlation between early stopping patience and epochs in deep learning. In Proceedings of the ITM Web of Conferences, Erbil, Iraq, 20–21 May 2024; Volume 64, p. 01003. [Google Scholar] [CrossRef]
- Candido, A.; Debbio, L.D.; Giani, T.; Petrillo, G. Bayesian inference with Gaussian processes for the determination of parton distribution functions. Eur. Phys. J. C 2024, 84, 716. [Google Scholar] [CrossRef]
- Kapadia, H.; Feng, L.; Benner, P. Active-learning-driven surrogate modeling for efficient simulation of parametric nonlinear systems. Comput. Methods Appl. Mech. Eng. 2024, 419, 116657. [Google Scholar] [CrossRef]
- Franco-Villoria, M.; Ignaccolo, R. Universal, Residual, and External Drift Functional Kriging. In Geostatistical Functional Data Analysis; Mateu, J., Giraldo, R., Eds.; Wiley: Hoboken, NJ, USA, 2022; pp. 55–72. [Google Scholar]
- Nakamura, A.; Yamanaka, Y.; Nomura, R.; Moriguchi, S.; Terada, K. Radial basis function-based surrogate computational homogenization for elastoplastic composites at finite strain. Comput. Methods Appl. Mech. Eng. 2025, 436, 117708. [Google Scholar] [CrossRef]
- He, H.; Chen, Z.; He, C.; Ni, L.; Chen, G. A hierarchical updating method for finite element model of airbag buffer system under landing impact. Chin. J. Aeronaut 2015, 28, 1629–1639. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Pan, Z. Deep residual surrogate model. Inf. Sci. 2022, 605, 86–98. [Google Scholar] [CrossRef]
- de Gooijer, B.M.; Havinga, J.; Geijselaers, H.J.; van den Boogaard, A.H. Radial basis function interpolation of fields resulting from nonlinear simulations. Eng. Comput. 2024, 40, 129–145. [Google Scholar] [CrossRef]
- Poggio, T.; Girosi, F.; Jones, M. From regularization to radial, tensor and additive splines. In Proceedings of the 1993 International Conference on Neural Networks (IJCNN), Nagoya, Japan, 25-29 October 1993. [Google Scholar]
- Guo, Y.; Nath, P.; Mahadevan, S.; Witherell, P. Active learning for adaptive surrogate model improvement in high-dimensional problems. Struct. Multidiscip. Optim. 2024, 67, 122. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S.; Golunski, L. Two-stage variable-fidelity modeling of antennas with domain confinement. Sci. Rep. 2022, 12, 17275. [Google Scholar] [CrossRef]
- Ludot, A.; Snedker, T.H.; Kolios, A.; Bayati, I. Data-Driven Surrogate Models for Real-Time Fatigue Monitoring of Chain Mooring Lines in Floating Wind Turbines. Wind Energy Sci. 2025, 2025, 1–36. [Google Scholar] [CrossRef]
- Iyengar, G.; Lam, H.; Wang, T. Is cross-validation the gold standard to estimate out-of-sample model performance? Adv. Neural Inf. Process Syst. 2024, 37, 94736–94775. [Google Scholar] [CrossRef]
- Greber, K.E.; Topka Kłończyński, K.; Nicman, J.; Judzińska, B.; Jarzyńska, K.; Singh, Y.R.; Sawicki, W.; Puzyn, T.; Jagiello, K.; Ciura, K. Application of biomimetic chromatography and QSRR approach for characterizing organophosphate pesticides. Int. J. Mol. Sci. 2025, 26, 1855. [Google Scholar] [CrossRef]
- Sudhakar, A.; Sujatha, S.; Sathiya, M.; Sivaramakrishnan, A.; Subramanian, B.; Venkata, R.K. Bayesian Optimization for Hyperparameter Tuning in Healthcare for Diabetes Prediction. Informing Sci. 2025, 28, 8. [Google Scholar] [CrossRef]
- Cavieres, J.; Karkulik, M. Efficient estimation for a smoothing thin plate spline in a two-dimensional space. arXiv 2024, arXiv:2404.01902. [Google Scholar] [CrossRef]
- Al-Shedivat, M.; Wilson, A.G.; Saatchi, Y.; Hu, Z.; Xing, E.P. Learning scalable deep kernels with recurrent structure. J. Mach. Learn. Res. 2017, 18, 1–37. [Google Scholar]
- van der Lende, M.; Ferrao, J.L.; Müller-Hof, N. Evaluating Uncertainty in Deep Gaussian Processes. arXiv 2025, arXiv:2504.17719. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Yong, H.; Huang, J.; Hua, X.; Zhang, L. Gradient centralization: A new optimization technique for deep neural networks. arXiv 2020, arXiv:2004.01461. [Google Scholar] [CrossRef]
- Sun, X.; Wang, N.; Chen, C.Y.; Ni, J.; Agrawal, A.; Cui, X.; Venkataramani, S.; Maghraoui, K.E.; Srinivasan, V.; Gopalakrishnan, K. Ultra-low precision 4-bit training of deep neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 1796–1807. [Google Scholar]
- Issa, Z.; Horvath, B. Non-parametric online market regime detection and regime clustering for multidimensional and path-dependent data structures. arXiv 2023, arXiv:2306.15835. [Google Scholar] [CrossRef]
- Horňas, J.; Běhal, J.; Homola, P.; Doubrava, R.; Holzleitner, M.; Senck, S. A machine learning based approach with an augmented dataset for fatigue life prediction of additively manufactured Ti-6Al-4V samples. Eng. Fract. Mech. 2023, 293, 109709. [Google Scholar] [CrossRef]
- Ober, S.W.; Rasmussen, C.E.; van der Wilk, M. The Promises and Pitfalls of Deep Kernel Learning. arXiv 2021, arXiv:2102.12108. [Google Scholar] [CrossRef]
- Zhang, K.; Karanth, S.; Patel, B.; Murphy, R.; Jiang, X. Real-time prediction for mechanical ventilation in covid-19 patients using a multi-task gaussian process multi-objective self-attention network. arXiv 2021, arXiv:2102.01147. [Google Scholar] [CrossRef]
- Plevris, V.; Solorzano, G.; Bakas, N.P.; Seghier, M.E.A. Investigation of Performance Metrics in Regression Analysis and Machine Learning-Based Prediction Models. In Proceedings of the 8th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2022), Oslo, Norway, 5–9 June 2022. [Google Scholar]
- Botchkarev, A. Performance metrics (error measures) in machine learning regression, forecasting and prognostics: Properties and typology. arXiv 2018, arXiv:1809.03306. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Kern, C.; Klausch, T.; Kreuter, F. Tree-based Machine Learning Methods for Survey Research. Surv. Res. Methods 2019, 13, 73–93. [Google Scholar]
- Cao, J.; Tao, T. Using machine-learning models to understand nonlinear relationships between land use and travel. Transp. Res. Part D 2023, 123, 103930. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, X.; Mihaylova, L. Review of Recent Advances in Gaussian Process Regression Methods. arXiv 2022, arXiv:2409.08112. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Advances in Neural Information Processing Systems 1997, 28(7), 779–784. [Google Scholar]
- Rivas-Perea, P.; Cota-Ruiz, J.; Garcia Chaparro, D.; Perez Venzor, J.A.; Quezada Carreón, A.; Rosiles, J.G. Support vector machines for regression: A succinct review of large-scale and linear programming formulations. Int. J. Intell. Sci. 2013, 3, 5–14. [Google Scholar] [CrossRef]
- Bloch, G.; Lauer, F.; Colin, G.; Chamaillard, Y. Support vector regression from simulation data and few experimental samples. Inf. Sci. 2008, 178, 3813–3827. [Google Scholar] [CrossRef]
- Kaliappan, J.; Srinivasan, K.; Qaisar, S.M.; Sundararajan, K.; Chang, C.Y.; C, S. Performance evaluation of regression models for the prediction of the COVID-19 reproductive rate. Front. Public Health 2021, 9, 729795. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Li, C.; Zhou, J. Application of XGBoost model optimized by multi-algorithm ensemble in predicting FRP-concrete interfacial bond strength. Materials 2025, 18, 2868. [Google Scholar] [CrossRef]
- Yang, H.; Guo, S.; Xie, H.; Wen, J.; Wang, J. Evaluation of Machine Learning Models for Predicting Performance Metrics of Aero-Engine Combustors. Case Stud. Therm. Eng. 2025, 65, 105627. [Google Scholar] [CrossRef]
- Lee, J.; Cho, Y. National-Scale Electricity Peak Load Forecasting: Traditional, Machine Learning, or Hybrid Model? Energy 2022, 239, 122366. [Google Scholar] [CrossRef]
- Brunzema, P.; Jordahn, M.; Willes, J.; Trimpe, S.; Snoek, J.; Harrison, J. Bayesian Optimization via Continual Variational Last Layer Training. arXiv 2024, arXiv:2412.09477. [Google Scholar] [CrossRef]
- Cong, H.; Wang, B.; Wang, Z. A novel Gaussian process surrogate model with expected prediction error for optimization under constraints. Mathematics 2024, 12, 1115. [Google Scholar] [CrossRef]
- Cha, G.W.; Moon, H.J.; Kim, Y.C. Comparison of Random Forest and Gradient Boosting Machine Models for Predicting Demolition Waste Based on Small Datasets and Categorical Variables. Int. J. Environ. Res. Public Health 2021, 18, 8530. [Google Scholar] [CrossRef]
- Alexander, D.L.; Tropsha, A.; Winkler, D.A. Beware of R2: Simple, unambiguous assessment of the prediction accuracy of QSAR and QSPR models. J. Chem. Inf. Model. 2015, 55, 1316–1322. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hua, C.; Tong, C.; Zang, Y.; Ruan, J. Volumetric Efficiency in Motor-Driven Two-Dimensional Piston Pumps with Leakage and Reverse Flow under High Pressure. Sci. Rep. 2024, 14, 28963. [Google Scholar] [CrossRef]
- Huang, Y.; Ruan, J.; Zhang, C.; Ding, C.; Li, S. Research on the Mechanical Efficiency of High-Speed 2D Piston Pumps. Processes 2020, 8, 853. [Google Scholar] [CrossRef]
- Kauranne, H. Effect of Operating Parameters on Efficiency of Swash-Plate Type Axial Piston Pump. Energies 2022, 15, 4030. [Google Scholar] [CrossRef]
- Manring, N.D.; Mehta, V.S.; Nelson, B.E.; Graf, K.J.; Kuehn, J.L. Increasing the Power Density for Axial-Piston Swash-Plate Type Hydrostatic Machines. J. Mech. Des. 2013, 135, 071002. [Google Scholar] [CrossRef]
- Wang, Z.; Xing, W.; Kirby, R.; Zhe, S. Physics Informed Deep Kernel Learning. arXiv 2022, arXiv:2006.04976. [Google Scholar] [CrossRef]
- Inaguma, Y.; Yoshida, N. Mathematical Analysis of Influence of Oil Temperature on Efficiencies in Hydraulic Pumps for Automatic Transmissions. SAE Int. J. Passeng. Cars–Mech. Syst. 2013, 6, 786–797. [Google Scholar] [CrossRef]
- Gaugel, S.; Reichert, M. Industrial Transfer Learning for Multivariate Time Series Segmentation: A Case Study on Hydraulic Pump Testing Cycles. Sensors 2023, 23, 3636. [Google Scholar] [CrossRef]
- Orhan, N. Predicting deep well pump performance with machine learning methods during hydraulic head changes. Heliyon 2024, 10, e31505. [Google Scholar] [CrossRef]
- Peric, B.; Engler, M.; Schuler, M.; Gutshce, K.; Woias, P. Using Neural Networks as a Data-Driven Model to Predict the Behavior of External Gear Pumps. Processes 2024, 12, 526. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).