DEM-CFD Simulation of Organic–Inorganic Fertiliser Mixing-Spreading: Optimizing Inorganic Fertiliser Placement for Uniformity
Abstract
1. Introduction
2. Materials and Methods
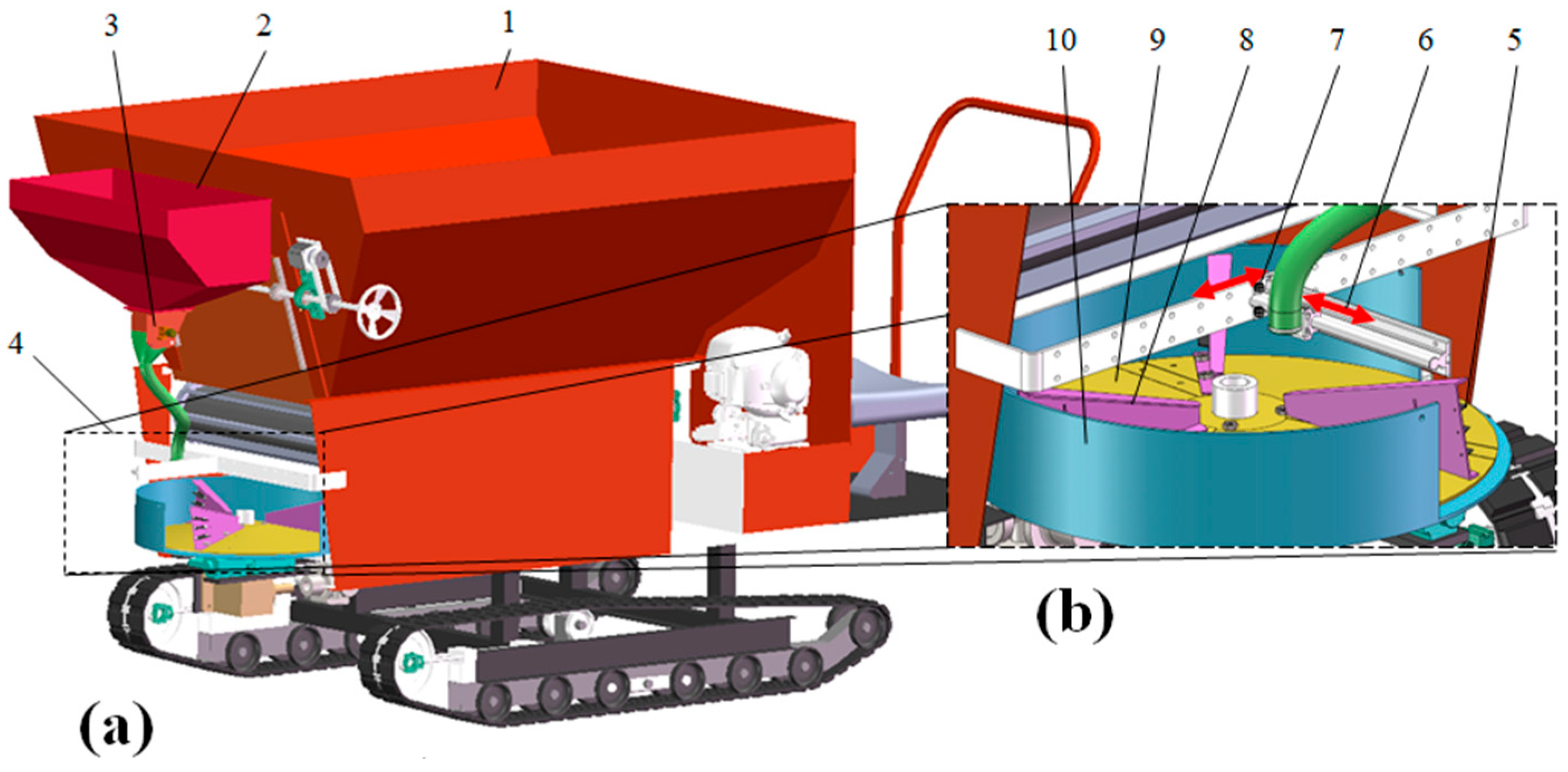
2.1. Structure and Principles of Inorganic and Organic Fertiliser Spreader
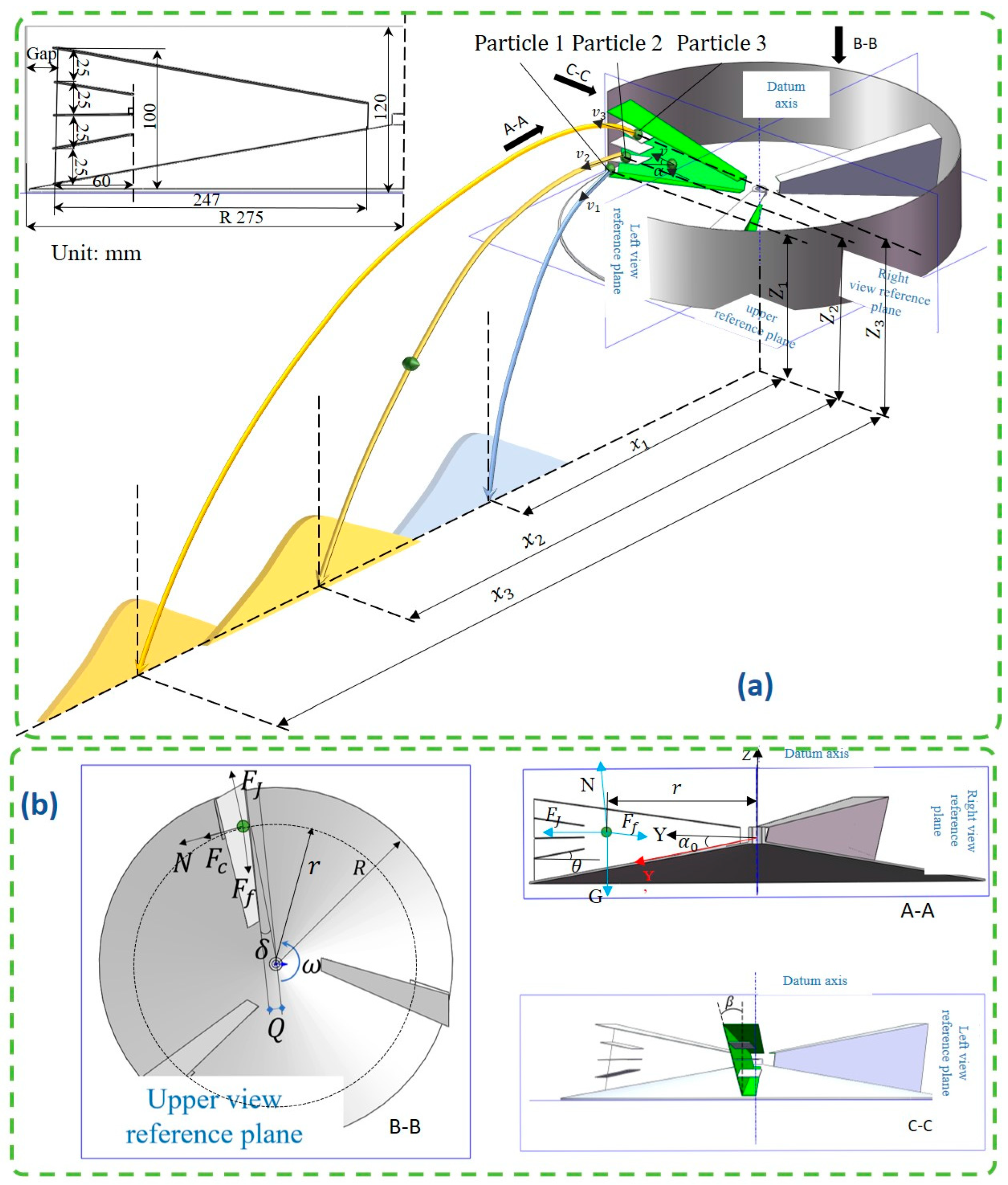
2.2. Analysis of the Movement of Particles on Disc
2.3. Analysis of Fertiliser Particle Motion in Air
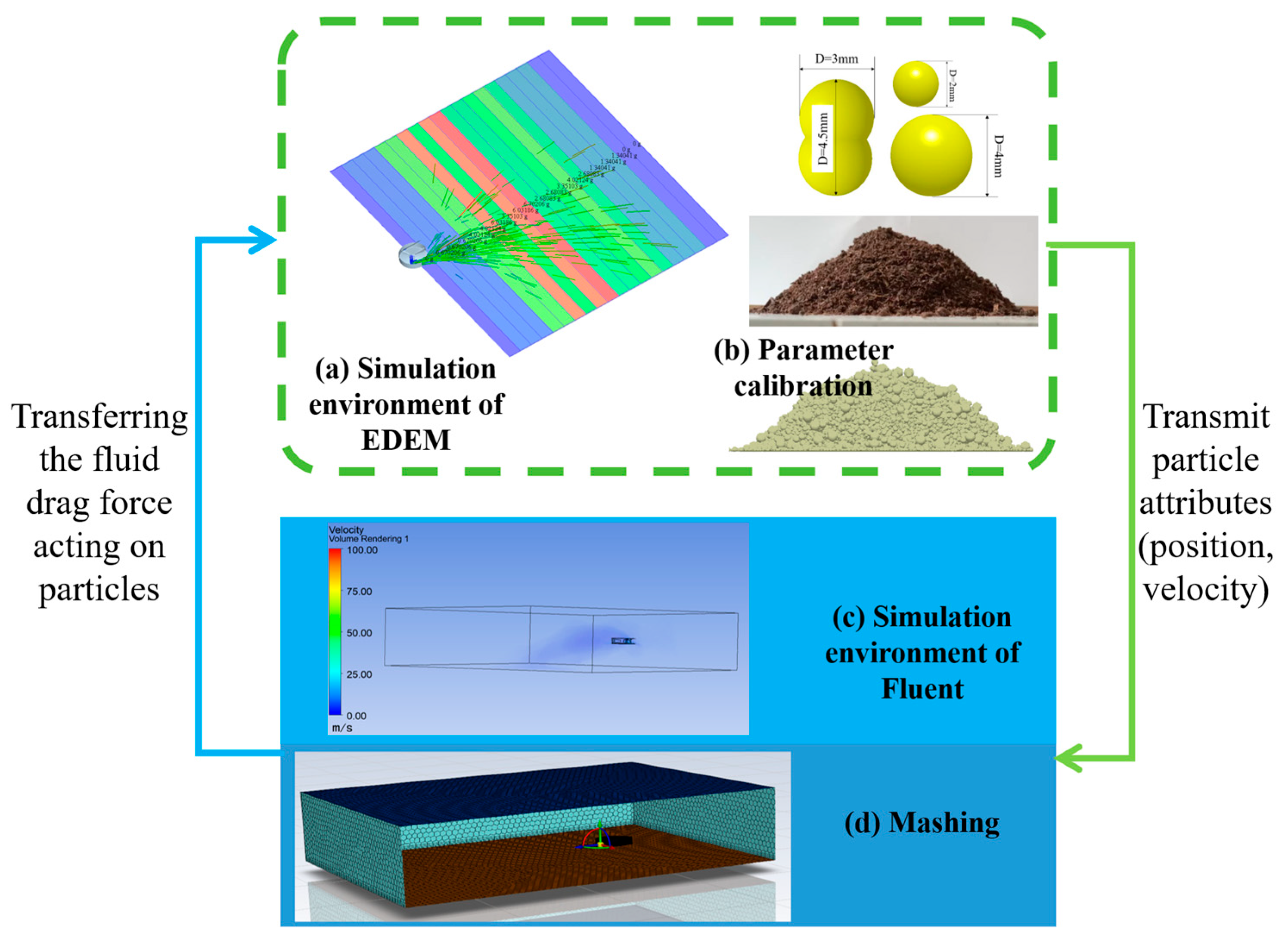
2.4. EDEM-Fluent Coupled Simulation Approach
2.4.1. Discrete Element Model Parameterisation
2.4.2. Simulation and Boundary Condition Settings
2.5. Methodology for Calculating Indicators
2.6. Simulation Experiment Design
2.6.1. One-Factor Simulation Experimental Design
2.6.2. Box–Behnken Fertiliser Drop Location Optimisation Test
2.7. Performance Test with Spreader
3. Results and Discussion
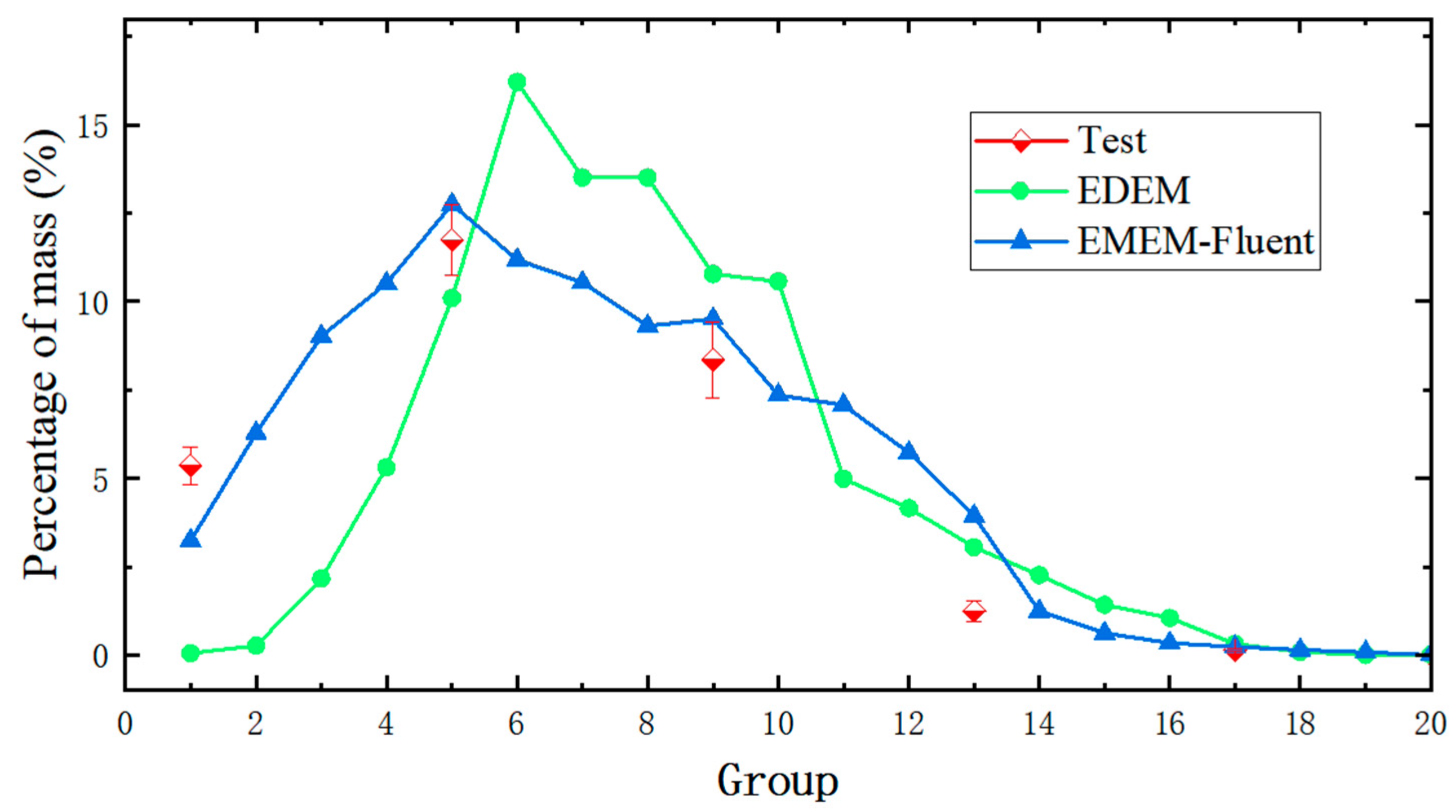
3.1. Model Validation Test Results
3.2. Results of the One-Way Test
3.2.1. Effect of Organic Fertiliser Flow Rate on Inorganic Fertiliser Uniformity
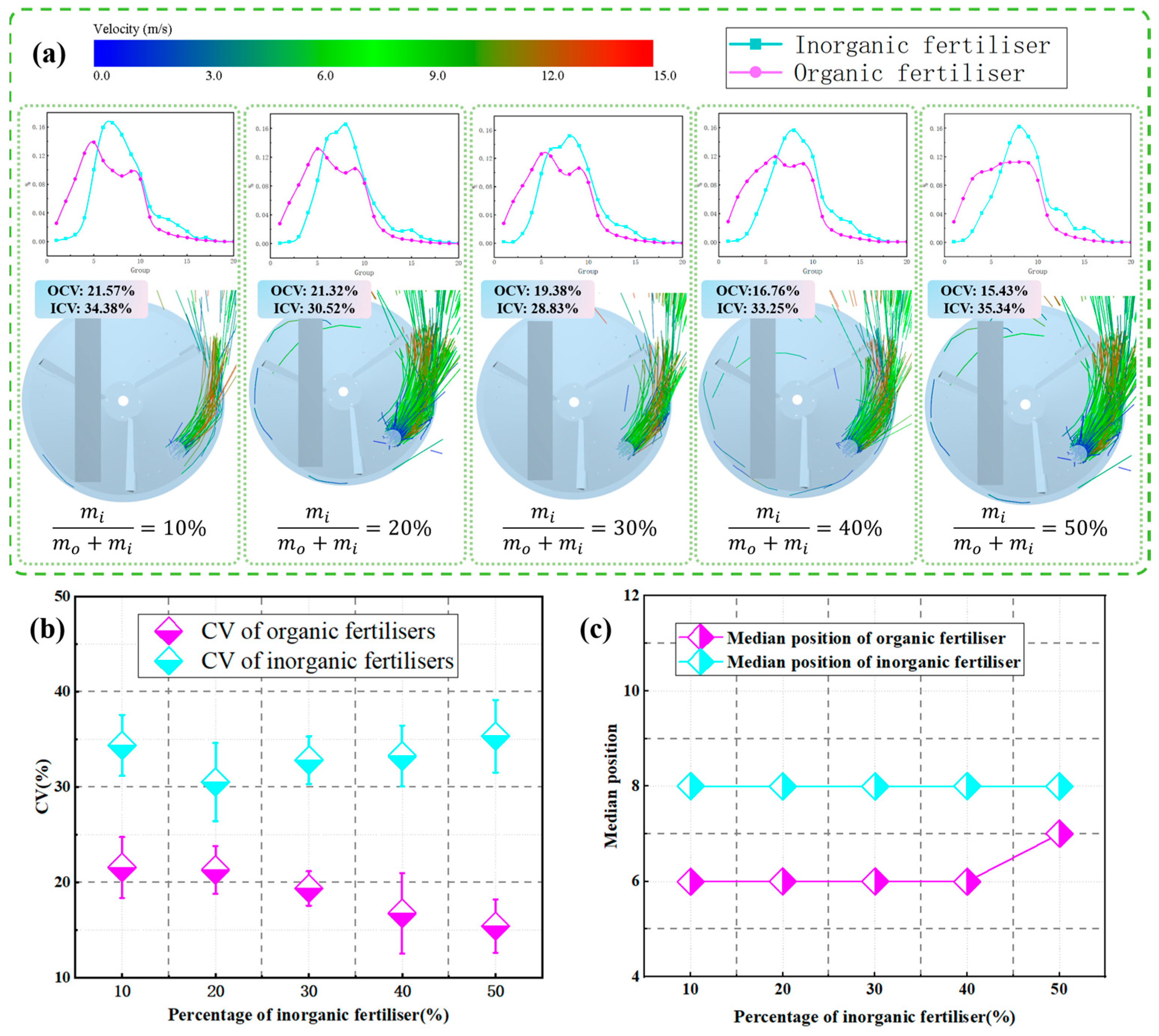
3.2.2. Effect of Inorganic Fertiliser Percentage on Inorganic Fertiliser Uniformity
3.2.3. Effect of Rotational Speed of Fertiliser Spreading Discs on the Uniformity of Inorganic Fertilisers
3.2.4. Effect of Inorganic Fertiliser Drop Location on Uniformity
3.2.5. Discussion on the Location of the Fertiliser Drop
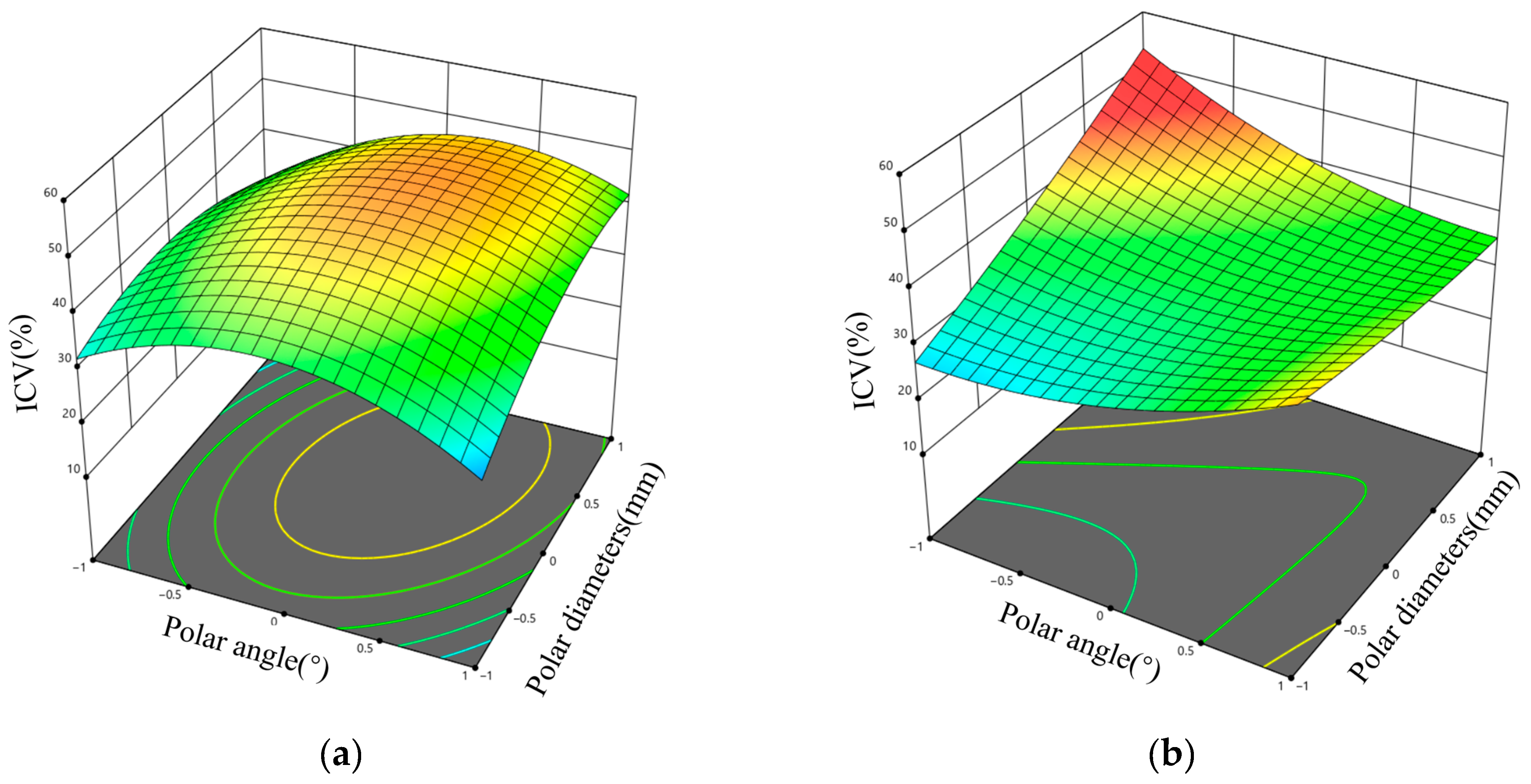
3.2.6. Optimisation Test Results
3.2.7. Validation of Optimal Parameter Combinations
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zhang, J.; Li, H.; Wang, Y.; Deng, J.; Wang, L. Multiple-year nitrous oxide emissions from a greenhouse vegetable field in China: Effects of nitrogen management. Sci. Total Environ. 2018, 616–617, 1139–1148. [Google Scholar] [CrossRef]
- Zhang, J.; Zhuang, M.; Shan, N.; Zhao, Q.; Li, H.; Wang, L. Substituting organic manure for compound fertiliser increases yield and decreases NH3 and N2O emissions in an intensive vegetable production systems. Sci. Total Environ. 2019, 670, 1184–1189. [Google Scholar] [CrossRef]
- Kang, Y.; Lee, J.; Chun, J.; Yun, Y.; Atef Hatamleh, A.; Al-Dosary, M.; Oh, T. Influence of individual and co-application of organic and inorganic fertilizer on NH3 volatilisation and soil quality. J. King Saud Univ. Sci. 2022, 34, 102068. [Google Scholar] [CrossRef]
- Cui, J.; Zhu, R.; Wang, X.; Xu, X.; Ai, C.; He, P.; Zhu, P. Effect of high soil C/N ratio and nitrogen limitation caused by the long·term combined organic–inorganic fertilisation on the soil microbial community structure and its dominated SOC decomlocation. structure and its dominated SOC decomlocation. J. Environ. Manag. 2022, 303, 114155. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, J.; Shahbaz, M.; Tang, H.; Liu, S.; Zhang, W.; Ge, T. Microorganisms maintain C:N stoichiometric balance by regulating the priming effect in long·term fertilised soils. Appl. Soil Ecol. 2021, 167, 104033. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Chen, B.; Zhong, J.; Fan, X.; Hewitt, A. Distribution uniformity improvement methods of a large discharge rate disc spreader for UAV fertiliser application. Comput. Electron. Agric. 2024, 220, 108928. [Google Scholar] [CrossRef]
- Abbou-ou-Cherif, E.M.; Piron, E.; Chateauneuf, A.; Miclet, D.; Lenain, R.; Koko, J. On-the-field simulation of fertiliser spreading: Part 2—Uniformity investigation. Comput. Electron. Agric. 2017, 141, 118–130. [Google Scholar] [CrossRef]
- Hu, J.; He, J.; Wang, Y.; Wu, Y.; Chen, C.; Ren, Z.; He, P. Design and study on lightweight organic fertiliser distributor. Comput. Electron. Agric. 2020, 169, 105149. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Q.; Li, H.; He, J.; Lu, C.; Xu, D.; Sun, M. Experimental research on a propeller blade fertiliser transport device based on a discrete element fertiliser block model. Comput. Electron. Agric. 2023, 208, 107781. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Q.; Xu, D.; Li, H.; He, J.; Lu, C. Design and experimental research on the counter roll differential speed solid organic fertiliser crusher based on DEM. Comput. Electron. Agric. 2023, 207, 107748. [Google Scholar] [CrossRef]
- Sun, X.; Niu, L.; Cai, M.; Liu, Z.; Wang, Z.; Wang, J. Particle motion analysis and performance investigation of a fertiliser discharge device with helical staggered groove wheel. Comput. Electron. Agric. 2023, 213, 108241. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G. Effects of control sequence optimisation on the performance of bivariate fertiliser applicator. Comput. Electron. Agric. 2022, 192, 106594. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Z.; Wang, X.; Odhiambo, M.O.; Ding, W. Motion analysis and system response of fertiliser feed apparatus for paddy Variable-Rate fertiliser spreader. Comput. Electron. Agric. 2018, 153, 239–247. [Google Scholar] [CrossRef]
- Yu, H.; Ding, Y.; Fu, X.; Liu, H.; Jin, M.; Yang, C.; Dou, X. A solid fertiliser and seed application rate measuring system for a seed-fertilizer drill machine. Comput. Electron. Agric. 2019, 162, 836–844. [Google Scholar] [CrossRef]
- Kömekçi, F.; Kömekçi, C.; Doğu, D.; Aykas, E. Effects of number of vanes, vane angle and disc peripheral speed on the distribution uniformity of twin-disc granular fertiliser broadcaster. Heliyon 2024, 10, e37922. [Google Scholar] [CrossRef]
- Xu, B.; Cui, Q.; Guo, L.; Hao, L. Design and parameter optimization of a combined rotor and lining plate crushing organic fertilizer spreader. Agronomy 2024, 14, 1732. [Google Scholar] [CrossRef]
- Li, A.; Jia, F.; Chu, Y.; Han, Y.; Li, H.; Sun, Z.; Ji, S.; Li, Z. Simulation of the movement of rice grains in a centrifugal huller by discrete element method and the influence of blade shape. Biosyst. Eng. 2023, 236, 54–70. [Google Scholar] [CrossRef]
- Guan, Z.; Mu, S.; Jiang, T.; Li, H.; Zhang, M.; Wu, C.; Jin, M. Development of centrifugal disc spreader on tracked combine harvester for rape undersowing rice based on DEM. Agriculture 2022, 12, 562. [Google Scholar] [CrossRef]
- Zhou, W.Q.; Lu, Q.; Wang, Y.; Tang, H.; Wang, J.W.; Wang, Y.J.; Sun, X.B. Evaluating the influence of double-channel inclined spreading blades on the effect of fertiliser granule spreading: DEM modelling and simulations. Biosyst. Eng. 2025, 257, 22. [Google Scholar] [CrossRef]
- Sharipov, G.M.; Heiß, A.; Eshkabilov, S.L.; Griepentrog, H.W.; Paraforos, D.S. Considering field topography in the model-based assessment of a centrifugal spreader’s variable rate application accuracy. Comput. Electron. Agric. 2023, 213, 108234. [Google Scholar] [CrossRef]
- Bivainis, V.; Jotautienė, E.; Lekavičienė, K.; Mieldažys, R.; Juodišius, G. Theoretical and experimental verification of organic granular fertiliser spreading. Agriculture 2023, 13, 1135. [Google Scholar] [CrossRef]
- Xie, Y.T.; Liu, H.X.; Shang, J.J.; Guo, L.F.; Zheng, G.X. Effect of Angle Between Center-Mounted Blades and Disc on Particle Trajectory Correction in Side-Throwing Centrifugal Spreaders. Agriculture 2025, 15, 32. [Google Scholar] [CrossRef]
- Villette, S.; Piron, E.; Miclet, D.; Martin, R.; Jones, G.; Paoli, J.-N.; Gée, C. How mass flow and rotational speed affect fertiliser centrifugal spreading: Potential interpretation in terms of the amount of fertiliser per vane. Biosyst. Eng. 2012, 111, 133–138. [Google Scholar] [CrossRef]
- Villette, S.; Cointault, F.; Piron, E.; Chopinet, B. Centrifugal Spreading: An Analytical Model for the Motion of Fertiliser Particles on a Spinning Disc. Biosyst. Eng. 2005, 92, 157–164. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, H.; Chen, X.; Liu, M.; Xiao, L.; Yu, J.; Huang, X. Design and experiment of centrifugal fertilizer spreading mechanism with double drop point feeding. Acta Agric. Univ. Jiangxiensis 2025, 47, 521–533. [Google Scholar] [CrossRef]
- Fan, C.; Liu, X.; Shi, J.; Shi, Y.; He, R. Structural analysis and optimal design of a centrifugal side-throw organic fertiliser spreader. Comput. Electron. Agric. 2025, 234, 110309. [Google Scholar] [CrossRef]
- Fan, C.; He, R.; Shi, Y.; He, L. Structure and operation mode of centrifugal side-throwing organic fertiliser spreader for greenhouses. Powder Technol. 2024, 438, 119457. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, G.; Li, J.; Wang, X.; Ding, L.; Wang, L. Analysis of jujube movement characteristics under positive and negative pressure airflow based on CFD-DEM. Comput. Electron. Agric. 2023, 210, 107902. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ooi, J.Y.; Ahmadian, H. Scaling of discrete element model parameters for cohesionless and cohesive solid. Powder Technol. 2016, 293, 130–137. [Google Scholar] [CrossRef]
- Yousefi, A.; Ng, T.-T. Dimensionless input parameters in discrete element modelling and assessment of scaling techniques. Comput. Geotech. 2017, 88, 164–173. [Google Scholar] [CrossRef]
- Yuan, F.; Yu, H.; Wang, L.; Shi, Y.; Wang, X.; Liu, H. Parameter calibration and systematic test of a discrete element model (DEM) for compound fertilizer particles in a mechanized variable-rate Application. Agronomy 2023, 13, 706. [Google Scholar] [CrossRef]
- Yuan, Q.; Xu, L.; Ma, S.; Niu, C.; Yan, C.; Zhao, S. The effect of paddle configurations on particle mixing in a soil-fertiliser continuous mixing device. Powder Technol. 2021, 391, 292–300. [Google Scholar] [CrossRef]
- Chu, K.; Chen, J.; Yu, A. Applicability of a coarse-grained CFD-DEM model on dense medium cyclone. Miner. Eng. 2016, 90, 43–54. [Google Scholar] [CrossRef]
- GB/T 25401-2010; Agricultural Machinery—Manure Spreaders—Environmental Protection—Requirements and Test Methods. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China: Beijing, China, 2010.
- NY/T4366-2023; Operating Quality of Fertilizer Spreader. Ministry of Agriculture and Rural Affairs of the People’s Republic of China: Beijing, China, 2023.
- GB/T 20346.1-2021; Equipment for Distributing Fertilizer-Part 1: Full Width Fertilizer Distributors. State Administration for Market Regulation, Standardization Administration of the People’s Republic of China: Beijing, China, 2021.

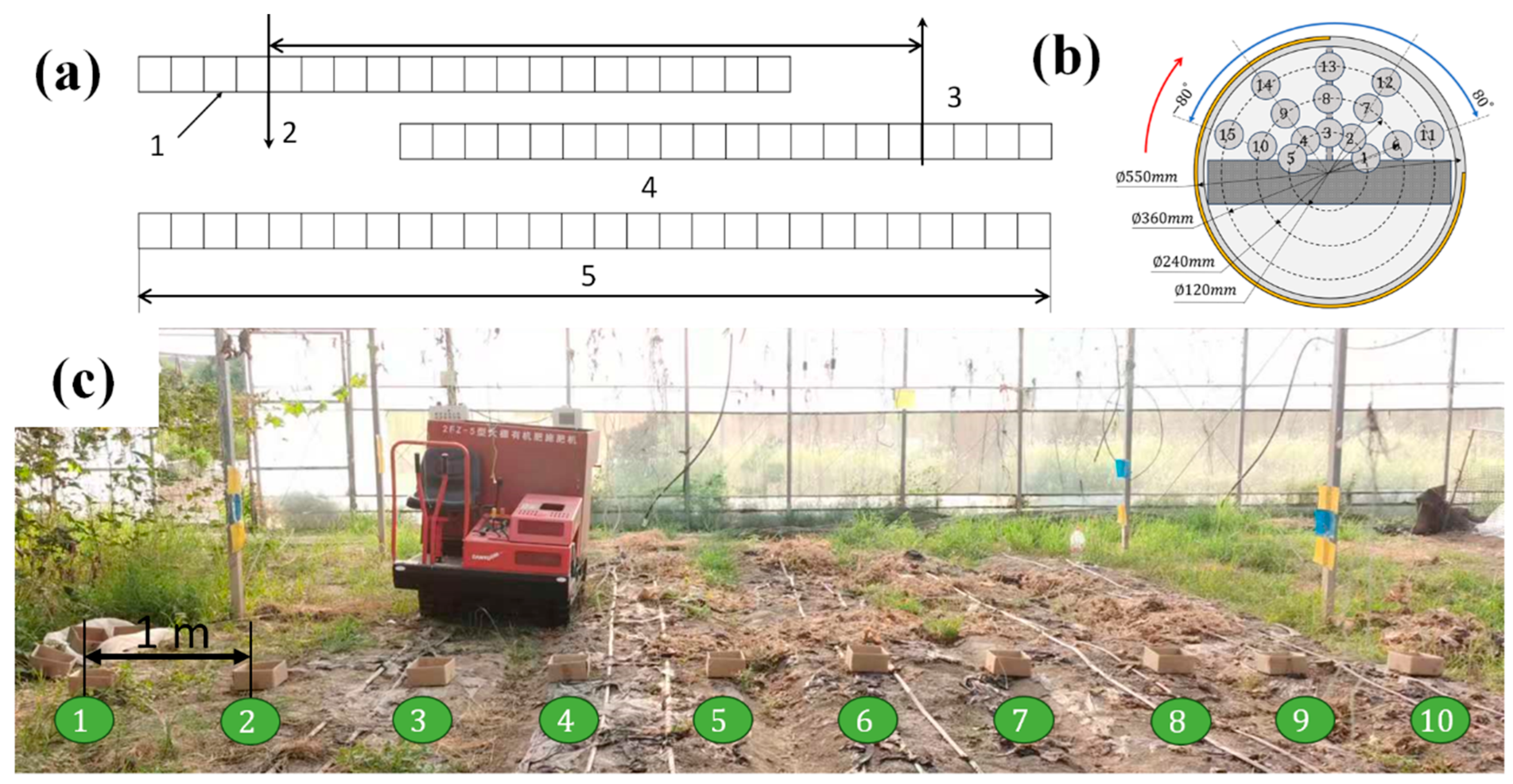

| Considerations | Organic Fertiliser |
|---|---|
| Organic fertiliser density (kg·) | 672 a |
| Water content (%) | 15–23 a |
| Particle size of Organic fertiliser (mm) | [0, 0.5):[0.5, 1):[1, 1.5): > 1.5 = 1:1:1:1 a |
| Organic fertiliser Poisson’s ratio | 0.25 b |
| Organic fertiliser shear modulus (Pa) | 1.25 × 107 b |
| Inorganic fertiliser density (kg·) | 1348 a |
| Particle size of Inorganic fertiliser (mm) | Length:Width:Height = 2.0:1.5:1.1 a |
| Inorganic fertiliser Poisson’s ratio | 0.24 b |
| Inorganic fertiliser shear modulus (Pa) | 1.15 × 107 b |
| Density of steel (kg·m−3) | 7861 a |
| Poisson’s ratio of steel | 0.3 b |
| Shear modulus of steel (Pa) | 7.9 × 1010 b |
| O-O restitution coefficient | 0.4 b |
| O-O static friction coefficient | 0.65 b |
| O-O rolling friction coefficient | 0.15 b |
| O-I restitution coefficient | 0.20 b |
| O-I static friction coefficient | 0.65 b |
| O-I rolling friction coefficient | 0.20 b |
| O-S restitution coefficient | 0.40 b |
| O-S static friction coefficient | 0.70 b |
| O-S rolling friction coefficient | 0.15 b |
| I-I restitution coefficient | 0.40 b |
| I-I static friction coefficient | 0.70 b |
| I-I rolling friction coefficient | 0.35 b |
| I-S restitution coefficient | 0.60 b |
| I-S static friction coefficient | 0.40 b |
| I-S rolling friction coefficient | 0.10 b |
| O-O JKR | 0.02 b |
| O-I JKR | 1 b |
| I-I JKR | 0.01 b |
| Number | Factor | Level | Conditions |
|---|---|---|---|
| 1–6 | Spreading disc speed/r·min−1 | 300, 400, 500, 600, 700 | Organic fertiliser mass flow rate 2625 g·s−1, Inorganic fertiliser mass flow rate 585 g·s−1, Fertiliser drop location: 7 |
| 7–13 | Organic fertiliser mass flow rate/g·s−1 | 875, 1312.5, 1750, 2187.5, 2625, 3262.5, 3500 | Inorganic fertiliser mass flow rate 585 g·s−1, speed: 400 r·min−1, fertiliser drop location: 7 |
| 14–19 | Percentage of inorganic fertiliser | 10%, 20%, 30%, 40%, 50% | Speed: 400 r·min−1, Fertiliser drop location: 7, Organic fertiliser flow + Inorganic fertiliser flow = 3210 g·s−1 |
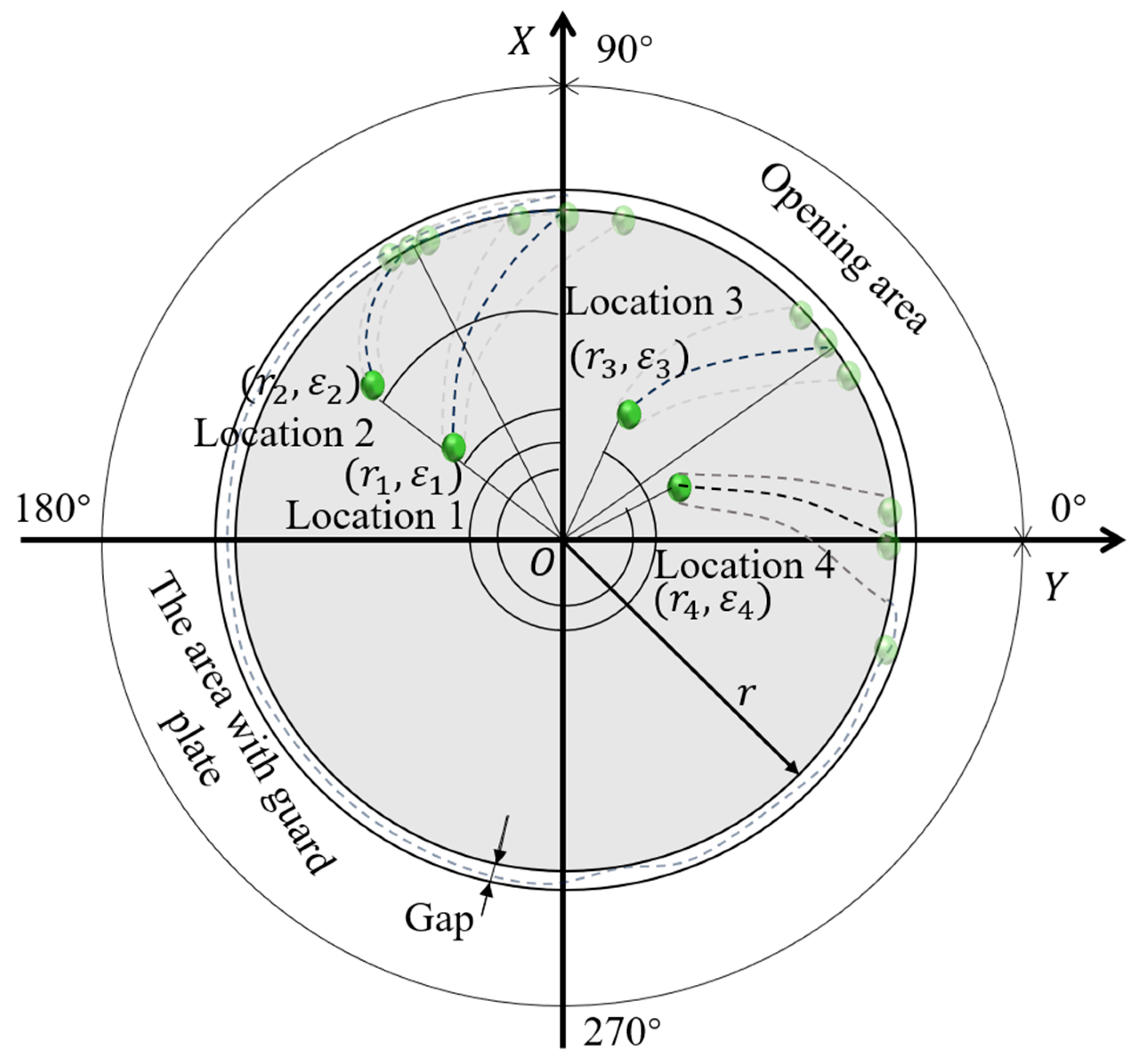
| 20–34 | Inorganic fertiliser drop location | Setting 15 fertiliser drop locations (Figure 6b) | Organic fertiliser mass flow rate 2287.5 g·s−1, Inorganic fertiliser mass flow rate 585 g·s−1, Speed: 400 r·min−1 |
| Level | Level | |||||
|---|---|---|---|---|---|---|
| −1 | 0 | 1 | −1 | 0 | 1 | |
| Spreading disc speed/r·min−1 | 300 | 500 | 700 | 300 | 500 | 700 |
| Organic fertiliser flow/g·s−1 | 875 | 2187.5 | 3500 | 875 | 2187.5 | 3500 |
| Polar angle/° | −80 | −40 | 0 | 0 | 40 | 80 |
| Polar diameter/mm | 60 | 120 | 180 | 60 | 120 | 180 |
| Number | A: Fertiliser Spreading Disc Speed (r·min−1) | B: Organic Fertiliser Flow (g·s−1) | C: Polar Angle (°) | D: Polar Diameter (mm) | ICVL (%) | ICVR (%) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | −1 | 0 | 29.50 | 33.41 |
| 2 | −1 | 0 | 0 | 1 | 41.36 | 37.72 |
| 3 | 0 | 0 | −1 | 1 | 36.54 | 36.91 |
| 4 | 0 | 0 | 0 | 0 | 52.64 | 31.92 |
| 5 | 0 | 1 | 0 | −1 | 32.28 | 25.67 |
| 6 | 1 | 0 | 1 | 0 | 34.16 | 37.84 |
| 7 | −1 | 0 | 1 | 0 | 31.19 | 38.29 |
| 8 | 1 | 1 | 0 | 0 | 29.76 | 31.73 |
| 9 | −1 | 0 | −1 | 0 | 38.73 | 30.50 |
| 10 | 0 | 1 | −1 | 0 | 24.83 | 37.15 |
| 11 | 0 | 0 | 0 | 0 | 52.28 | 31.57 |
| 12 | 0 | 1 | 1 | 0 | 37.99 | 32.33 |
| 13 | 0 | 0 | 0 | 0 | 51.29 | 32.56 |
| 14 | 0 | 0 | 0 | 0 | 53.12 | 32.39 |
| 15 | 0 | −1 | 1 | 0 | 24.43 | 42.33 |
| 16 | 0 | −1 | 0 | 1 | 41.09 | 30.41 |
| 17 | 0 | −1 | −1 | 0 | 42.52 | 23.89 |
| 18 | 0 | 0 | 0 | 0 | 51.14 | 32.77 |
| 19 | 1 | −1 | 0 | 0 | 31.46 | 30.77 |
| 20 | −1 | 1 | 0 | 0 | 30.93 | 30.79 |
| 21 | 0 | 1 | 0 | 1 | 40.85 | 35.48 |
| 22 | 0 | 0 | −1 | −1 | 40.54 | 25.70 |
| 23 | 0 | 0 | 1 | −1 | 26.28 | 41.04 |
| 24 | 0 | −1 | 0 | −1 | 38.30 | 34.35 |
| 25 | 1 | 0 | 0 | 1 | 36.90 | 31.20 |
| 26 | 0 | 0 | 1 | 1 | 37.74 | 32.02 |
| 27 | −1 | 0 | 0 | −1 | 38.95 | 28.31 |
| 28 | 1 | 0 | 0 | −1 | 31.49 | 33.59 |
| 29 | −1 | −1 | 0 | 0 | 35.82 | 33.88 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 1878.65 | 14 | 134.19 | 41.79 | <0.0001 |
| A-A | 46.85 | 1 | 46.85 | 14.59 | 0.0019 |
| B-B | 24.03 | 1 | 24.03 | 7.48 | 0.0161 |
| C-C | 36.3 | 1 | 36.3 | 11.3 | 0.0047 |
| D-D | 59.14 | 1 | 59.14 | 18.42 | 0.0007 |
| AB | 2.54 | 1 | 2.54 | 0.7922 | 0.3885 |
| AC | 37.21 | 1 | 37.21 | 11.59 | 0.0043 |
| AD | 2.25 | 1 | 2.25 | 0.7006 | 0.4166 |
| BC | 244.14 | 1 | 244.14 | 76.02 | <0.0001 |
| BD | 8.35 | 1 | 8.35 | 2.6 | 0.1291 |
| CD | 59.75 | 1 | 59.75 | 18.61 | 0.0007 |
| A2 | 585.5 | 1 | 585.5 | 182.32 | <0.0001 |
| B2 | 585.34 | 1 | 585.34 | 182.27 | <0.0001 |
| C2 | 678.27 | 1 | 678.27 | 211.21 | <0.0001 |
| D2 | 195.65 | 1 | 195.65 | 60.92 | <0.0001 |
| Residual | 44.96 | 14 | 3.21 | ||
| Lack of Fit | 42.02 | 10 | 4.2 | 5.71 | 0.0538 |
| Pure Error | 2.94 | 4 | 0.7355 | ||
| Cor Total | 1923.61 | 28 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 495.69 | 13 | 38.13 | 35.31 | <0.0001 |
| A-A | 0.0766 | 1 | 0.0766 | 0.0709 | 0.7937 |
| B-B | 0.5062 | 1 | 0.5062 | 0.4687 | 0.5040 |
| C-C | 109.65 | 1 | 109.65 | 101.54 | <0.0001 |
| D-D | 18.93 | 1 | 18.93 | 17.53 | 0.0008 |
| AB | 4.1 | 1 | 4.1 | 3.8 | 0.0704 |
| AC | 2.81 | 1 | 2.81 | 2.61 | 0.1273 |
| AD | 34.84 | 1 | 34.84 | 32.26 | <0.0001 |
| BC | 135.22 | 1 | 135.22 | 125.22 | <0.0001 |
| BD | 47.27 | 1 | 47.27 | 43.78 | <0.0001 |
| CD | 102.26 | 1 | 102.26 | 94.7 | <0.0001 |
| A2 | 1.92 | 1 | 1.92 | 1.77 | 0.2028 |
| B2 | 2.61 | 1 | 2.61 | 2.42 | 0.1408 |
| C2 | 32.77 | 1 | 32.77 | 30.35 | <0.0001 |
| D2 | 0.283 | 1 | 0.283 | 0.249 | 0.6255 |
| Residual | 16.2 | 15 | 1.08 | ||
| Lack of Fit | 15.24 | 11 | 1.39 | 5.79 | 0.0523 |
| Pure Error | 0.9579 | 4 | 0.2395 | ||
| Cor Total | 511.88 | 28 |
| Num | Target Value | Optimal Fertiliser Drop Location | Num of Box | OCV (%) | ICV (%) | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | = −0.47 | ; C = −0.8°; D = 70.2 mm | 3 to 8 | 16.45 | 19.34 | 17.38 | 28.93 | 0.93 | 9.59 |
| 2 | = −0.47 | ; C = −0.6°; D = 71.4 mm | 2 to 9 | 18.72 | 23.78 | 18.10 | 32.43 | −0.62 | 8.65 |
| 3 | = 0.47 | ; C = 12.96°; D = 60.36 mm | 3 to 8 | 14.39 | 21.45 | 15.62 | 38.17 | 1.23 | 16.72 |
| 4 | = 0.47 | ; C = −66.18°; D = 179.82 mm | 2 to 9 | 17.61 | 23.10 | 16.83 | 29.32 | −0.78 | 6.22 |
| Mean value | 16.79 | 21.92 | 16.98 | 32.21 | 0.19 | 10.29 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, C.; Shi, Y.; Sun, J.; He, R.; Xu, G.; Li, Y. DEM-CFD Simulation of Organic–Inorganic Fertiliser Mixing-Spreading: Optimizing Inorganic Fertiliser Placement for Uniformity. Agriculture 2025, 15, 2256. https://doi.org/10.3390/agriculture15212256
Fan C, Shi Y, Sun J, He R, Xu G, Li Y. DEM-CFD Simulation of Organic–Inorganic Fertiliser Mixing-Spreading: Optimizing Inorganic Fertiliser Placement for Uniformity. Agriculture. 2025; 15(21):2256. https://doi.org/10.3390/agriculture15212256
Chicago/Turabian StyleFan, Chengsai, Yinyan Shi, Jianfu Sun, Ruiyin He, Gaoming Xu, and Yinian Li. 2025. "DEM-CFD Simulation of Organic–Inorganic Fertiliser Mixing-Spreading: Optimizing Inorganic Fertiliser Placement for Uniformity" Agriculture 15, no. 21: 2256. https://doi.org/10.3390/agriculture15212256
APA StyleFan, C., Shi, Y., Sun, J., He, R., Xu, G., & Li, Y. (2025). DEM-CFD Simulation of Organic–Inorganic Fertiliser Mixing-Spreading: Optimizing Inorganic Fertiliser Placement for Uniformity. Agriculture, 15(21), 2256. https://doi.org/10.3390/agriculture15212256






