Abstract
Regions with insufficient resilience in their agriculture industry can usually be exposed to threats of unstable supply of food and agricultural products. Therefore, agricultural resilience is important for regional development and welfare. To support the development of agricultural resilience, proper policies and incentives need to be implemented. To achieve this, the first step is to appropriately evaluate the regional agricultural resilience levels. In this study, a novel agricultural resilience evaluation method was developed based on hybrid weighting approaches and dynamic CoCoSo (i.e., Combined Compromise Solution). The method can capture the temporal change in resilience levels, integrate richer information, and provide more robust output. To confirm its effectiveness, the method was applied to the evaluation of regional agricultural resilience in 21 cities of Sichuan province in China across five years. Over a recent five-year period, the annual average levels of agricultural resilience in Sichuan have increased, although this trend became less significant in more recent years. Also, the resilience levels among cities are diverse, and some cities have experienced significant changes of resilience across years. When considering temporal effects integrating five years, Liangshanzhou city ranks the first and Bazhong city ranks the last in terms of their resilience levels, but such results can depend on CoCoSo parameters and time weight parameters, with the latter having more significant influence. This study can contribute to the existing literature by providing new methodological tools for agricultural resilience research and regional management studies. Also, this study can help identify cities with different agricultural resilience levels and dynamics, informing practitioners’ new perspectives for agricultural policy evaluation as well as business strategy planning.
1. Introduction
Agriculture is vitally important for economic growth and social welfare, and agricultural and food security have now become a key focus worldwide [1]. The robustness and stability of agricultural product supply can not only enable people’s quality of life but also support the realization of sustainable development goals (SDGs) proposed by the United Nations, such as SDG 2 (i.e., Zero Hunger).
In China, due to its high population, agriculture is of great importance to social and economic development. Each year, multiple policies have been implemented to support and enhance the security of the agricultural industry. For example, China unveiled the 2025 “No. 1 central document” recently. As one of the most important policy documents in China each year, the document in 2025 has pointed out the necessity of enhancing the sustainable supply capability of food and other key agricultural products [2]. The “plan to accelerate building up the strength in agriculture for the period from 2024 to 2035” was recently unveiled by the Communist Party of China Central Committee and the State Council, also explicitly emphasizing the importance of the stable and secure supply of food and agricultural products [3].
Sichuan is one of the provinces with the largest population in China. The province is located in southwestern China and has 21 cities. According to the China Statistical Yearbook 2024 [4], the population of Sichuan province has reached around 83.68 million, ranking in the top five provinces in terms of population size in China. Therefore, the regional agricultural security in Sichuan significantly determines regional development and welfare.
To enhance regional agricultural security, one of the most effective approaches is to strengthen agricultural resilience. Agricultural resilience, according to the existing literature, can be defined as the ability of agricultural systems to resist and recover from shocks and damage [5,6]. Specifically, the shocks and damage here, adapting the definition of resilience developed by the Food and Agricultural Organization (FAO) of the United Nations, can be considered as the threats that impact agriculture, nutrition, food security and food safety [7]. In recent years, due to the occurrence of extreme weather and natural disasters, as well as varied uncertain factors, the importance of agricultural resilience has attracted more attention in both academic and industrial communities. To enhance agricultural resilience, the first step is to properly evaluate the resilience level of agricultural systems, as it drives the policy and incentives to be better implemented to develop its resilience.
In the existing literature, multiple explorations have been conducted for agricultural resilience. Different topics have been covered, such as identifying the factors influencing agricultural resilience [8], developing evaluation approaches to measure the resilience levels [5], and comparing and ranking regions in terms of their agricultural resilience [9]. However, the published studies revealed research gaps that need to be addressed. First, the evaluation of agricultural resilience normally adopted a static perspective, with little focus on dynamic evaluation. This can potentially fail to catch the impact of temporal effects on resilience evaluation, delivering inappropriate or even inaccurate messages to policy makers. Second, the evaluation approaches were normally developed based on widely used methods (e.g., spatial regression, machine learning, etc.), but their robustness may not be fully examined and secured, potentially undermining the validity of study findings. Finally, the research scope of the studies on agricultural resilience normally adopted a national level perspective, with few applying a province-wide or region-wide scope. As agricultural industry in different provinces can present diverse structures and properties, examining agricultural resilience only from a national level may hinder the capture of unique features of regional agricultural industry.
Therefore, to properly address the above research gaps and inform practitioners and policy makers, this study aims to investigate the following research questions:
- (1)
- How can the agricultural resilience of cities in Sichuan province be evaluated dynamically?
- (2)
- What are the patterns of agricultural resilience of cities in Sichuan province in the past five years?
To address the research questions, this paper developed a hybrid weighting dynamic CoCoSo approach to examine the agricultural resilience levels across the 21 cities of Sichuan province. Through developing an agricultural resilience evaluation index system, the resilience of each city was examined and compared based on the data from Sichuan statistical yearbooks 2020 to 2024, and the policy and managerial implications were generated based on the evaluation results. By doing this, we believe this paper can contribute to the academic and practical implications:
- Academically speaking, this study introduced a novel and robust dynamic evaluation method which can capture rich information for agricultural resilience evaluation. This can enrich the analytical tools for agricultural risk and resilience management. Also, the findings can provide a theoretical basis for future studies of Sichuan province and other close regions in relevant topics (e.g., regional food safety study, regional economy, or regional risk prevention research).
- Practically speaking, this study can enable the policy makers to longitudinally evaluate the outcomes of agricultural policy, further supporting policy makers to design and implement more effective agricultural policy and incentives. In addition, local agricultural companies can benefit from the proposed method to upgrade their decision-making software to make more strategically appropriate plans.
2. Literature Review
This study concerns two streams of literature review, namely agricultural resilience development and resilience level evaluation.
2.1. Agricultural Resilience Development
Existing literature has examined resilience development under multiple factors. The first category is the resilience development under natural factors, such as extreme weather, climate change, natural disasters, or pandemics. For example, Rezvi et al. [8] indicated that climate change can be a key factor that poses negative effects to crop production and agricultural food security. To mitigate such effects and enhance agricultural resilience, the authors proposed the solution of developing tolerant and biofortified rice varieties. Zeng et al. [10] revealed that extreme weather events can do harm to the stability and robustness of the agricultural economy. They also mentioned that agricultural insurance can be an effective tool to mitigate negative consequences of these events. By using agricultural insurance, the ability to resist extreme weather consequences in agriculture can be enhanced, increasing its resilience. Lioutas et al. [11] discussed how agriculture can improve its ability to cope with major disasters based on the experience from the COVID-19 pandemic. They discussed the practices drawn by Canadian and American governments, and proposed that to promote agricultural resilience, policies should support the development of crisis management plans and enhance farmers’ ability to resist external disturbance.
Another category is resilience development under economic and technological factors, such as industrial and market structures or technological advancement and digitalization. For example, Zhou et al. [12] analyzed agricultural resilience from an economic perspective. Using panel data of provinces in China, they found that the integration of rural industries can significantly contribute to agricultural economic resilience, and such effect can vary in different regions. Xue et al. [13] examined how a digital economy can impact agricultural industry. Their findings claimed that a digital economy can positively contribute to the agricultural development resilience.
The third category is resilience development under social factors, such as population and labor structures. For example, Zhang et al. [14] applied the spatial autoregressive model and the generalized moment method to measure the effect of an aging rural workforce on agricultural economic resilience. Using the Chinese agricultural industry as the research context, they found that an aging rural workforce significantly reduced agricultural economic resilience. Han et al. [15] analyzed the panel data of China to identify the effect of population from the agricultural economy perspective. They also found negative impacts posed by population aging in risk resilience of the agricultural economy.
The above literature indicated that there have been rich explorations in agricultural resilience development, and many of them were conducted in China. However, the explorations seem to prefer to adopt national level investigation, with few focusing on provincial level and regionally specific properties in agriculture industry.
2.2. Agricultural Resilience Evaluation
The second stream of the literature is the agricultural resilience evaluation, and three topics can be identified in this stream. First, the existing literature of this stream explored the construction of an agricultural resilience index system, where multiple indicators have been considered to obtain an inclusive evaluation. For example, Lin et al. [6] developed an analysis index system of agricultural resilience by considering the resistance recovery capacity, adaptive regulatory capacity, and innovation and transformation capacity. Using this system, the authors examined the evolutionary pattern of Chinese agricultural resilience. Qiao et al. [5] developed an agricultural resilience index system from both resistance and reconstructive power perspectives. The system considered five dimensions of agricultural resilience, including production resilience, ecological resilience, economic resilience, adaptability, and transformation and innovation capabilities. Luo et al. [16] examined the cropland resilience evaluation, and they developed an index system incorporating resistance, adaptation, and innovation dimensions with 18 sub-factors.
The second direction is the methods proposed for agricultural resilience evaluation. For example, Yang et al. [17] adopted machine learning techniques such as random forest to measure the agri-economy resilience and explore its influential factors. Chao et al. [18] used the entropy method to calculate the agri-economy resilience index and analyze the effect of agricultural production agglomeration by applying the Spatial Durbin model, kernel density estimation, and threshold regression. In the literature, the MCDM methods are also applied to the agricultural resilience evaluation. For example, Xue et al. [13] applied entropy-TOPSIS (i.e., Technique for Order Preference by Similarity to Ideal Solution) method to measure the levels of agricultural development resilience and the digital economy, further exploring their relationship. Also, Kertolli et al. [19] measured the resilience of the water–energy–food–ecosystem nexus of the Fès–Meknès region in Morocco to help farmers adapt to climate change, and the SAW (i.e., simple additive weighting) method was used to prioritize innovative strategies for adaption.
Finally, the third direction is the practical applications of agricultural resilience evaluation, in which the evaluation results are used to support decision-making (e.g., policy design and business strategy planning). For example, Robert et al. [20] evaluated the economic vulnerability and resilience of agriculture in England and Wales based on individual farm business data, supporting the decision-making and strategy planning for sustainable agricultural promotion. Qiao et al. [5] measured the agricultural resilience levels of each province in China, finding that the overall levels of agricultural resilience in China are still relatively low and presenting regional difference. The findings therefore can inform the necessity of customized policies for different regions. Chen et al. [21] used the fuzzy analytic hierarchy process and entropy methods to evaluate the resilience to drought of Huaibei plain, and their results supported the design of proper policy and emergency plans in agriculture.
The above literature revealed that multiple studies have been conducted in agricultural resilience evaluation, and different methods were adopted. However, compared with the widely used methods (i.e., statistical inference/regression or machine learning models), the MCDM methods seem less popular, with dynamic MCDM attracting even fewer academic attentions in agricultural resilience evaluation.
2.3. Research Gap Identification
Based on the above literature review, the following research gaps can be identified. On the one hand, although rich studies have been conducted to explore the factors and evaluation of agricultural resilience, the majority of them adopted a national level and were lacking in more specific investigation (i.e., provincial level). As suggested by the above literature [5] that significant difference can exist among different regions, lacking in such a view may hinder the way of appropriate and tailored policy design for specific provinces. On the other hand, although multiple methods have been developed to evaluate the agricultural resilience level, the MCDM method, especially its dynamic variations, has rarely been used. This makes the current research fail to benefit from the robustness of MCDMs as well as their ability to capture dynamic information in alternative evaluations.
Therefore, to address the above research gaps, this paper aims to develop a dynamic hybrid weighting CoCoSo method and apply it to evaluating agricultural resilience in Sichuan province. Through this, this paper is expected to contribute to the methodological innovation in agricultural resilience studies, as well as to the support of policy design and strategy planning for regional policy-makers and agricultural companies.
3. Materials and Methods
Having identified the research gaps from the literature, this study attempts to address them by following the methodological flows in Figure 1. The proposed method is based on the CoCoSo model which is a widely used and robust algorithm in MCDM [22]. The extension of this algorithm made by this paper enables its objective evaluation using dynamic data. The R (version 4.4.2) was used for programming. Specifically, there are four main steps to achieve this extension, namely MCDM formation, hybrid weight, dynamic CoCoSo calculation and sensitivity analysis.
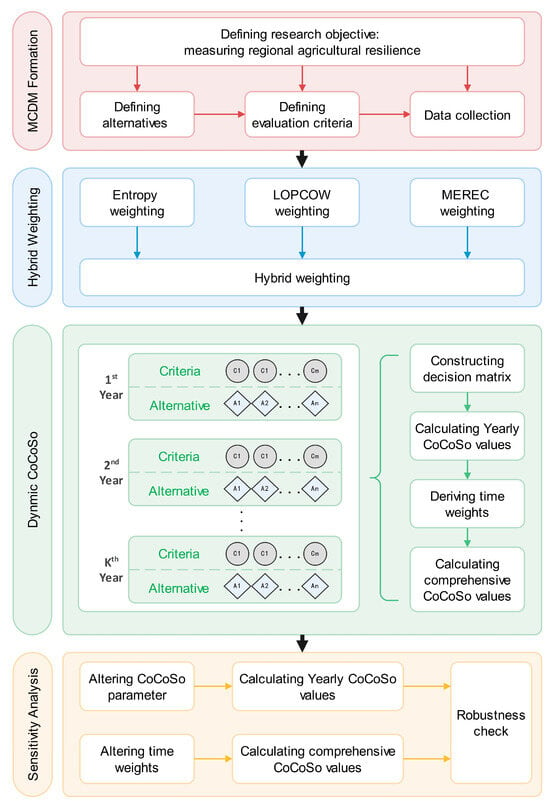
Figure 1.
Methodological flows.
3.1. MCDM Formation
The first step of this study is to form the MCDM problem. To properly construct the MCDM problem, the alternatives should be decided. To obtain a thorough evaluation of agricultural resilience in Sichuan, all cities in the province were taken into account. Specifically, Table 1 summarizes the 21 cities in Sichuan which are the alternatives in the model.

Table 1.
Cities in Sichuan province.
After constructing the alternatives, the evaluation index system should be developed. Multiple indicators should be included in the evaluation index to obtain a comprehensive and accurate evaluation of agricultural resilience. After thoroughly reviewing the previous literature related to agricultural resilience (i.e., [5,16,21,23,24,25]) as well as carefully considering the data accessibility (e.g., statistical data of cities in Sichuan province), the index system with ten indicators are developed in Table 2.

Table 2.
Index system for agricultural resilience.
Finally, the data for MCDM were collected. To capture the changes of the agricultural resilience across years, this paper adopted a novel dynamic perspective for resilience evaluation. This means the indicator data needed to be collected by multiple years, which is different from the classical static MCDM models. To achieve a thorough evaluation, consistent with the previous literature [26], we collected the data of five years for each indicator by cities from the Sichuan Statistical Yearbooks published from 2020 to 2024 [27] to ensure the dynamic CoCoSo could be conducted to comprehensively evaluate the cities’ agricultural resilience levels. Due to the time delay, what should be noted is that the published year means the data covering the last year. For example, statistical yearbook 2022 represents the data covering from the beginning of 2021 to the end of 2021 (i.e., the beginning of 2022). Also, the Sichuan Statistical Yearbook 2020–2024 is the most recent 5-year available data that we could collect when conducting this study.
Based on the data collected, the decision array can be developed as , where is the time dimension which is five (i.e., 2020 to 2024), while and are the number of alternatives (i.e., 21) and indicators (i.e., 10). Specifically, it is formulated as follows, and is the element of , with , , and .
3.2. Hybrid Weights
After constructing the MCDM problem, the second step is to determine the relative importance of each indicator in the index system. This needs to weigh indicators. To obtain appropriate weights, this study conducted a hybrid weighting approach integrating entropy, MEREC (i.e., method based on the removal effects of criteria), and LOPCOW (i.e., logarithmic percentage change-driven objective weighting) weights. The justification of adopting hybrid weights is that three weighting approaches can extract indicator information from different perspectives (see following mathematical formulae for details), expecting to contribute to a more appropriate decision-making in greater possibility.
3.2.1. Entropy Method
The first way of weighting is the Entropy method, which is one of the most frequently used weighting method (e.g., [28]). Compared with the previous literature, as this paper considers the dynamics of agricultural resilience, the effects of multi-period need to be considered in the weight generation. Based on the entropy method, the weight of the indicator () is derived as . The specific steps of entropy method are presented in Appendix A.1.1.
3.2.2. MEREC Method
The second way of weighting is the MEREC method. It was developed in [29]. To fit the dynamic evaluation in the modelling, the approach is also adapted to enable temporal effects. Based on the MEREC method, the weight of indicator () is derived as . The specific steps of MEREC method are presented in Appendix A.1.2.
3.2.3. LOPCOW Method
The third way of weighting is the LOPCOW method, which was developed in [30]. To fit the dynamic evaluation in the modelling, the approach is also adapted to enable temporal effects. Based on the LOPCOW method, the weight of indicator () is derived as . The specific steps of LOPCOW method are presented in Appendix A.1.3.
3.2.4. Hybrid Weighting Process
After obtaining the weights of indicators by using entropy, MEREC, and LOPCOW methods individually (i.e., , , and ), the hybrid indicator weights are constructed to achieve a holistic indicator weighting. In this study, the geometric mean formula is used to obtain the hybrid weights, with a similar means of observation in the previous literature (e.g., [31]):
According to the previous literature, the hybrid weights can reduce the possible bias induced from single weighting methods [32]. Also, using hybrid weights can contribute to obtaining diverse information from different features [33]. Therefore, in this study, the hybrid weights can integrate the information captured by the individual methods, expectedly resulting in more informative and robust weights of dynamic agricultural resilience for each indicator.
The formulation of hybrid weights reflects the economic implications for indicators: the larger weights represent the bigger impacts on the agricultural resilience from certain indicators. In other words, policy makers should pay more attention to the indicators with larger weights when designing and implementing policies (e.g., subsidies or public budget planning).
3.3. Dynamic CoCoSo
Having derived the weights from the above methods, we next apply the dynamic CoCoSo to comprehensively evaluate the regional agricultural resilience. Specifically, based on the weights derived from the hybrid processes, the CoCoSo is used to calculate the agricultural resilience levels for the cities. CoCoSo was developed in [22], and the justification of using CoCoSo rather than other methods such as TOPSIS, ARAS (i.e., additive ratio assessment) or WASPAS (i.e., weighted aggregated sum product assessment) is because of its superiority in robustness in evaluating alternatives. Specifically, the robustness and reliability of CoCoSo are secured from its unique combination of three compromised score functions [34]. Benefiting from such a mathematical structure, the regional agricultural resilience considering temporal effects can be better examined under dynamic changes.
As the weights have considered temporal effects, the model is essentially a dynamic CoCoSo model. Specifically, by extending previous literature, the dynamic CoCoSo value can be derived as (, ). To interpret the meaning of , it represents the agricultural resilience level of each city by year. For example, means the resilience level of the third city in 1st year. More specifically, it means the resilience level of PZH (see Table 1) in 2020 (as 2020 is the first year the data were collected). Also, the property of mathematical models determines higher implies a higher agricultural resilience level.
First, the is normalized to based on the following formula with as the element of :
Second, the weighted sum and the power weighted sum of each alternative under indicators are calculated as follows [22]:
Third, the three appraisal scores are derived as follows [35]:
The here indicates the relative importance between and . Supported by the previous literature [22], is set to 0.5. The rationale to adopt this baseline value is to assume a neutral decision maker who has equal preference on both values. In the sensitivity analysis below, the effect of different values of will be analyzed.
Fourth, the CoCoSo values for each city by year can be derived as follows [35]
Finally, as the existence of the temporal effect, the levels of agricultural resilience in different years may have varied importance. This leads to the consideration of time weights for resilience levels each year. Notating as the time weights with , the dynamic CoCoSo values for comprehensive evaluation of the city’s agricultural resilience level can be derived as follows [36]:
To interpret the meaning of , it represents the comprehensive measurement of the agricultural resilience level of city () across five years. For example, means the agricultural resilience level of ZG (see Table 1) integrating the temporal effect of data of five years.
According to the previous literature (e.g., [36,37]), to appropriately derive the , the widely used nonlinear optimization approach is applied where satisfies the following relationship:
The value of ranges from 0 to 1, and it indicates the relative importance attached to the more recent data [36]. The lower the is, the more relative importance of recent data is considered by the decision maker. For example, if is 0.1, it means the extreme importance attached to the recent data. On the contrary, if is 0.9, the recent data is of low importance. The mathematical property of the above nonlinear programming also indicates that if is 0.5, the data across different time periods will have equal importance. Therefore, it can be justified that the adoption of this way of determining time weights can enable the decision-makers to flexibly adjust the relative importance of recent data, better fitting the practices and informing policy making. For more information about this way of determining time weights, we refer interested readers to [36] for details. Supported by the previous literature of dynamic MCDM [36,37], the is set to 0.2 in this study to give higher weights to the more recent data. The rationale is that the old data close to 2019 may be affected more by the COVID-19 pandemic. Considering the effects of the COVID-19 pandemic have gradually diminished, less consideration should be given to the old data to achieve a fairer evaluation. However, the robustness of results subject to different will be tested in the sensitivity analysis below.
3.4. Sensitivity Analysis
When calculating the results of dynamic CoCoSo, the results of the evaluation of agricultural resilience of cities in Sichuan essentially depend on two parameters, i.e., for CoCoSo calculation, and for time weight calculation. Therefore, it is necessary to alter the parameters and check result sensitivity, which can better inform the policy makers and local agricultural enterprises in their decision-making to enhance the regional agricultural resilience.
3.5. Method Summary
The above Section 3.1, Section 3.2, Section 3.3 and Section 3.4 have depicted the method flows of this study. To sum up, this study first forms the MCDM problem (identifying alternatives and criteria), then calculates criterion weights (using entropy, MEREC, and LOPCOW) and derives hybrid weights (using geometric mean) and calculates dynamic CoCoSo values (by integrating CoCoSo and time weights) and finally conducts sensitivity analysis (by altering and ). In the following section, the results of each step are presented.
4. Results
Based on the methods in Section 3, the agricultural resilience levels of each city are reported in this section.
4.1. Results for Agricultural Resilience Evaluation
First, to evaluate the resilience levels, the raw data of the index system developed in Table 2 were collected from the Sichuan statistical yearbook published in 2020 to 2024. The data are presented in Appendix A, Table A1.
Based on the data, the entropy weights, MEREC weights, and LOPCOW weights are derived individually, and the hybrid weighs are calculated based on Equation (2). The weighting result is presented in Table 3.

Table 3.
Indicator weights by hybrid methods.
By applying the above weights to CoCoSo model, the values of regional agricultural resilience levels can be derived by year. Figure 2 presents the results, and several insights can be identified. First, the average resilience level among all cities each year shows an increasing trend. This increasing trend of average resilience level is consistent with the previous studies of national agricultural resilience [38], as well as studies focusing on the resilience in other provinces [39]. More specifically, in Sichuan province, this increasing trend seems the most significant from 2020 to 2021 and less significant in the more recent years. Also, the relative ranks of cities in terms of their agricultural resilience levels keep dynamically changing. For example, from 2020 to 2021, CD ranked first but fell out of the top three after 2021. Another city, YB, did not show in the top three group until 2022, and remains in the group afterwards. What should be noticed is LSZ city that has always ranked in the top three since 2020 and has become the first place since 2022. This may suggest that LSZ is the city that possibly has the most sustained agricultural resilience. Finally, the city with the least resilience levels has been BZ since 2021, and SN city has ranked the second to the last since 2021. The information indicates that both cities are in low agricultural resilience and need more attention from the local government.
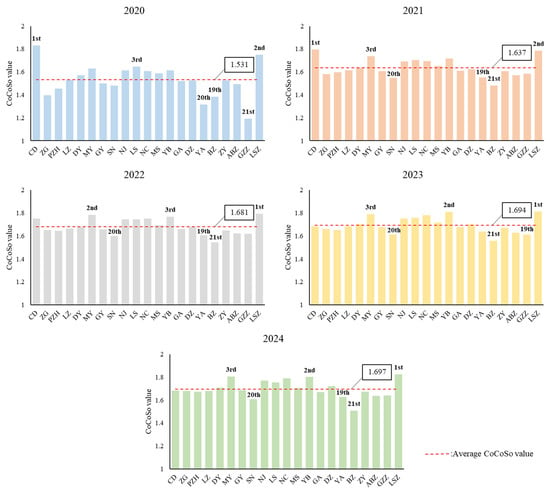
Figure 2.
CoCoSo values for regional agricultural resilience levels by city each year.
The above results indicate the changes of cities’ agricultural resilience by year. To comprehensively consider the resilience levels across all years, the time weights are considered to consolidate the levels. By solving the Formula (11) with , the weights (i.e., ) that can be found for the years from 2020 to 2024 are approximately {0.029, 0.060, 0.124, 0.256, 0.531}. Applying the weights to Equation (10), the comprehensive evaluation considering the time effects (i.e., ) was derived. Figure 3 visualizes the results. When considering all periods together, the city with the highest agricultural resilience level is LSZ, followed by MY city. The CD city, reaching the first places in 2020–2021, falls out of the top three place under the dynamic evaluation. This essentially confirms the observation in the above that LSZ is the city that has the most sustained and strongest agricultural resilience. Overall, the results suggest that development of agricultural resilience level may not be fully balanced among cities, consistent with the previous agricultural resilience literature focusing on other provinces [39]. Such regional diversity in agricultural resilience was also identified by studies focusing on places outside China like OECD countries [40]. Therefore, the finding here essentially advocates that diverse policies may need to be considered for improving agricultural resilience in different regions.
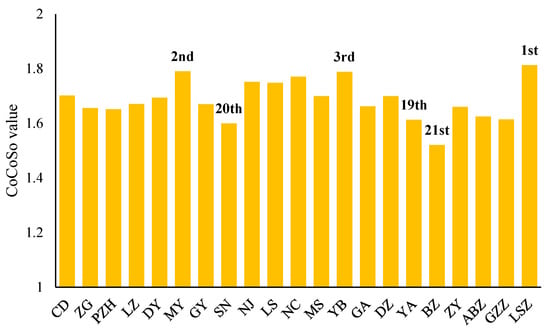
Figure 3.
CoCoSo evaluation of agricultural resilience considering time effects.
4.2. Sensitivity Analysis for Agricultural Resilience Evaluation
Having obtained the results from the dynamic CoCoSo, it is necessary to check the result robustness of dynamic CoCoSo results, and the following two sensitivity tests were conducted. First, consistent with the previous literature [41], the for CoCoSo calculation alters from 0.1 to 0.9 to check the robustness of the results. In practice, the change in reflects different decision makers’ preference of using a weighted sum model (i.e., ) or using a weighted product model (i.e., ) [22]. If τ = 0.9, it represents the decision maker prefers weighted sum model much more than weighted product model, with = 0.1 means the opposite. The special case lies at = 0.5 [35], representing both models are treated equally. As the change in might cause the change in the data scale and make the absolute CoCoSo values not compatible, the rank values under each value of are used in sensitivity analysis to expectedly lead to a fairer comparison [41]. Figure 4 presents the ranks of each city based on their agricultural resilience levels based on the comprehensive CoCoSo considering time effects (i.e., ). Although Figure 4 indicates some cities like CD, MS, and GA can have varied ranks under different , the maximal rank difference is only two. The figure shows that the original results are generally robust, as the top three cities with highest resilience levels are always LSZ, MY, and YB, and the bottom three cities with lowest resilience levels are always YA, SN, and BZ. This confirms the results in Figure 3.
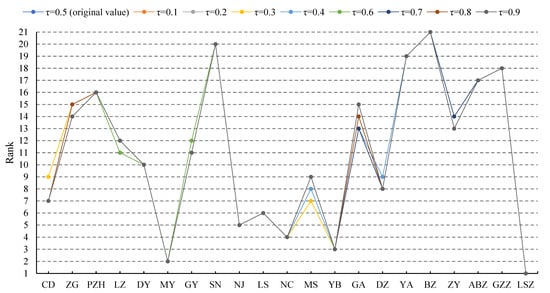
Figure 4.
Sensitivity analysis of τ by ranks.
Apart from the parameter , it is also necessary to consider the different relative importance of recent data. Therefore, the for dynamic CoCoSo calculation alters as 0.1, 0.3, 0.5, 0.7, 0.9 to check the sensitivity of the results. The higher the is, the higher importance is attached to the long-term data. In practice, if = 0.1, it means the decision-makers or policy makers treat the recent data as much more important than the old data for decision-making (e.g., agricultural business strategy planning) or policy making (agricultural policy design). On the other hand, = 0.9 means the opposite, representing that decision-makers or policy makers consider old data more strongly when designing and implementing the agricultural business strategies or policies. The special case lies at = 0.5, and it represents all periods being treated equally. Consistent with the sensitivity analysis above, the city ranks under each value of are used for a fairer comparison. Figure 5 visualizes the results of sensitivity analysis of . It can be seen that the results present diverse ranks under different values. First, for cities ranking in the first three places, the LSZ is always in the party. MY and YB can rank in the top three together if is relatively low (such as = 0.1, 0.2 or 0.3), while CD and LS can enter the top three group if is sufficiently high (such as = 0.9). In addition, the cities located in the bottom three places also change depending on . Apart from BZ which almost always ranks in last place, the SN can be categorized in the last three if is relatively low (such as = 0.1, 0.2 or 0.3). In contrast, YA city can also fall into the last three group except = 0.3. Some other significant cases whose ranks are largely influenced by can be ZG, SN, and GZZ cities. Specifically, depending on , ZG’s rank can vary from 13 to 18 while SN’s rank can vary from 16 to 20. For GZZ, it can be the least one with high (such as = 0.9
or 0.7) but obtains higher rank if gets lower. This essentially indicates that the different
importance attached to the recent data can significantly vary the comprehensive
evaluation of cities’ agricultural resilience levels, informing decision-makers
carefully assigning the value of .
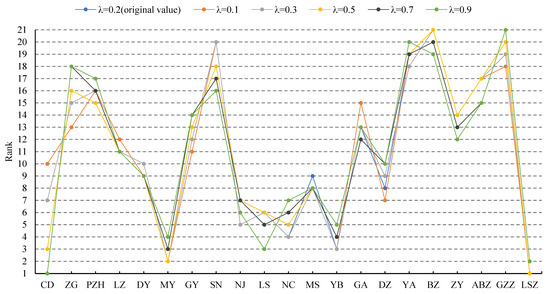
Figure 5.
Sensitivity analysis of λ by ranks.
4.3. Results Summary
To better summarize the results of Section 4.1 and Section 4.2, this section reveals key findings:
- The average annual agricultural resilience levels of Sichuan province keep increasing, although such increasing trend has become less significant in more recent years.
- The agricultural resilience levels among cities are diverse, and the resilience of some cities have experienced significant change across years.
- When considering temporal effects integrating five years, LSZ is the city with the highest resilience level, and BZ is the city with the lowest resilience (when τ = 0.5 and λ = 0.2).
- The CoCoSo parameter (i.e., τ) has little effect on agricultural resilience measurements, while the time weight parameter (i.e., λ) can pose result variations when evaluating resilience levels.
5. Discussion
Based on the above results, several insights can be interpreted for supporting decision making for policy makers and local agricultural companies.
First, the results reflected from Figure 2 depict the longitudinal changes of agricultural resilience levels. Specifically, the annual average resilience level of Sichuan province keeps increasing in the five years, although this trend turns smaller in more recent years. This essentially suggests that the policies and actions implemented to enhance agricultural resilience in the five years in Sichuan worked generally well. However, it should also be noticed that this is possibly due to twofold reasons that make increasing effects become less significant. On the one hand, it could be the case that the currently implemented policies or actions have already exhausted the improvement potential of agricultural resilience in Sichuan province, leaving little space for future increase. If this is the case, it probably calls for new policies to implement and actions to take to obtain more significant increase for provincial agricultural resilience. For example, new risk prevention initiatives can be promoted in province wise to activate new directions for resilience increase, such as organic fertilizer applications and financial incentives for farmers [19]. Also, targeted irrigation improvements can be conducted, and digital agriculture technologies can be invested in, such as agricultural big data analytics, digital twins, and sensors.
On the other hand, it is also possible that there are new norms in the provincial agriculture industry in recent years, diminishing the effects of policies implemented for resilience enhancement. For example, the extreme weather becomes more frequent, which undermines the effectiveness of the agricultural system and brings higher risks and disruptions to agricultural production. Under such a case, additional actions may be needed to adapt to the new norm, so that a sustained increase can be maintained. For example, climate adaptation programs can be implemented like soil and water conservation [19], and the government public budget expenditures can be increased to adapt to new norms in the agriculture industry.
Apart from the provincial level, the city level results also give insights for agricultural resilience development. Results indicate that some cities always have relatively high resilience in their agricultural industry (e.g., LSZ), while some always have low resilience (e.g., BZ). Although such a rank can be related to the city’s own natural resources as well as the capacity and development levels of agriculture industry, it could also be possible that the policies and actions taken by the cities with higher resilience could be more effective in resilience enhancement. Therefore, it is worth comparing the policies implemented in cities with high and low resilience levels and promoting the suitable policies/actions to the agricultural industry of cities with low resilience levels.
Finally, the results also indicate the importance of decision-making processes in agricultural resilience evaluation, especially the decision-makers’ attitudes towards the more recent data. The results in Figure 5 indicate that the relative importance attached to the more recent data can pose influence of measuring levels of agricultural resilience among different cities. This directly leads to the evaluation of the performance and effectiveness of policies and actions taken by certain cities. Therefore, the processes in evaluation decision-making should be carefully designed and conducted. Suggested by the previous literature [36,37], to improve the efficiency and accuracy in this perspective, multiple decision-makers with relevant background in agriculture should form groups to design the evaluation processes together after thorough discussion.
6. Conclusions
This study evaluated the regional agricultural resilience levels. A novel dynamic CoCoSo model with hybrid weighting methods was proposed for evaluation purposes. Using 21 cities of Sichuan province in China as research objects, the agricultural resilience levels of the cities were comprehensively evaluated, and the dynamics of resilience across five years were examined. The results indicated several insights. First, the average agricultural resilience of Sichuan province has kept increasing since 2020, but the increase trend has been less significant in the more recent years. Also, among 21 cities, LSZ city seems to be the one with the strongest and most sustained agricultural resilience, while BZ city is the one with the lowest agricultural resilience. Finally, the evaluated agricultural resilience levels for some cities can change significantly under different relative importance attached to the more recent data, calling for the decision-makers to carefully design their evaluation protocols.
We believe this study has both theoretical and practical implications. Academically speaking, this study can contribute to the existing agricultural management research. To the best of our knowledge, this is the first paper applying dynamic CoCoSo with hybrid weights to agricultural resilience evaluation in Sichuan. In this study, the dynamic information of resilience captured as well as the comprehensive evaluation enabled by the method can therefore confirm its potential for agricultural management, providing new analytical tools for future agricultural resilience research. Also, the method offers flexible decision-making mechanisms to adapt different importance attached to the more recent data for agricultural resilience measurement, building a basis for future exploration on risk and disruption management in regional agriculture and relevant directions.
Practically, this study can inform policy makers and local agricultural companies for better decision-making. For example, the index system developed in this study, together with the method proposed, can become a useful tool for policy makers to evaluate the effectiveness of agricultural policies, supporting the opportunities for policy design or update. Also, the ways this study collects and analyzes data can inform practitioners (e.g., software engineers, information system managers, etc.) in agricultural companies to update their management and decision support systems. By utilizing these methods, agricultural practitioners can expectedly capture more improvement opportunities.
However, we also acknowledge there are limitations of this study, thus offering chances for future research. First, as this study only considers Sichuan province, the evaluation indicators, as well as the evaluation results, can be regionally specific. Due to data availability issues, some important indicators such as soil quality, water stress, land degradation, and biodiversity were not able to be included. In other words, the generalization of the index systems and results should be further validated in other regions [21,25]. Therefore, one of the interesting research directions in the future can be utilizing our method in other regions using various data to test its effectiveness and triangulate the findings. To achieve this, data adjustments and contextual considerations should be covered. For example, new indicators, such as soil quality, water stress, land degradation, and biodiversity can be added for examining resilience in other regions using our model once such data are available. Also, due to the properties of the data, the method and our analysis framework are limited to objective and quantitative data. However, as it is common that in agricultural MCDM research, some data are often fuzzy and subjective, and personal judgments can be applied in the decision-making process [42,43]. This leads future research to consider adding qualitative data into our framework. For example, future research can construct a fuzzy dynamic CoCoSo with hybrid weights, or even mixed data dynamic CoCoSo (e.g., integrating fuzzy and real numbers) to capture more information within the resilience evaluation. Finally, it could be interesting to extend the developed method to other industries, such as automotive or logistics, to check its effectiveness in resilience evaluation under different contexts.
Author Contributions
Conceptualization, S.H., M.T. and H.C.; methodology, S.H. and M.T.; software, S.H.; validation, S.H. and K.L.; formal analysis, S.H. and K.L.; investigation, S.H. and K.L.; resources, H.C.; data curation, K.L.; writing—original draft preparation, S.H. and H.C.; writing—review and editing, S.H., M.T. and H.C.; visualization, S.H.; project administration, M.T. and H.C.; funding acquisition, S.H., M.T. and H.C. All authors have read and agreed to the published version of the manuscript.
Funding
The first author was supported by Sichuan Key Research Bases for Humanities and Social Sciences in Universities Research Centre for Water Transport Economics (grant number SYJJ2023A01). The third author was supported by National Social Science Fund of China (grant number 24XGL028). The fourth author was supported by Chengdu Philosophy and Social Research Base-Chengdu Park Urban Demonstration Area Construction Research Center (grant number GYCS2022-YB003) and Special Funding Project for Academic Research of the 2024 Fiscal Year under the “14th Five-Year Plan” for Philosophy and Social Sciences of Sichuan Province (grant number SC24E003).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data supporting the conclusion of this study are presented in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Weighting Methods
Appendix A.1.1. Entropy Method
First, the is
normalized to based on the following formula with as the element of :
Second, the is calculated as follows:
Third, the entropy of each indicator is calculated, with the parameter as the number of all alternatives (i.e., = 5 21 = 105):
Finally, the entropy weights of each indicator, , is calculated as follows:
Appendix A.1.2. MEREC Method
First, the is normalized to based on the following formula with as the element of :
Second, the overall performance of each alternative by year, , is calculated as follows:
Third, the performance of each alternative by year after removing certain indicator , is calculated as follows:
Fourth, the summation of the total deviation of each indicator, , is calculated as follows:
Finally, the MEREC weights for each indicator are calculated by applying the following relationship:
Appendix A.1.3. LOPCOW Method
First, the is normalized to based on the following formula with as the element of :
Second, the percentage value of each indicator, , is calculated as follows where is the standard deviation of values under each indicator:
Finally, the weight of each indicator by LOPCOW is derived:
Appendix A.2. Data
The data based on the index system (i.e., Table 2) for regional agricultural resilience evaluation are in Table A1. The data contain ten indicators for 21 cities in Sichuan with time periods across five years (i.e., 2020 to 2024). The numbers after the name of the city indicate the specific year. For example, ZG2021 means the data of ZG city in 2021.

Table A1.
Raw data for regional agricultural resilience indicators.
Table A1.
Raw data for regional agricultural resilience indicators.
| City by Year | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
|---|---|---|---|---|---|---|---|---|---|---|
| CD2020 | 0.506939 | 0.563115 | 0.373827 | 0.150373 | 0.023161 | 1003.343 | 6.058585 | 24,357.09 | 17,572.1 | 1,125,457 |
| ZG2020 | 0.274302 | 0.312839 | 0.573883 | 0.433405 | 0.023878 | 324.2333 | 3.324244 | 17,276.54 | 14,271.19 | 219,824 |
| PZH2020 | 0.57906 | 0.979105 | 0.47786 | 0.236687 | 0.035461 | 140.1198 | 4.869357 | 18,351.87 | 13,383.66 | 141,786 |
| LZ2020 | 0.287312 | 0.432391 | 0.582776 | 0.450514 | 0.018996 | 357.1778 | 2.231948 | 16,531.47 | 12,774.62 | 542,006 |
| DY2020 | 0.328465 | 0.4072 | 0.671782 | 0.50801 | 0.03567 | 406.3268 | 3.363584 | 18,248.73 | 14,538.17 | 284,063 |
| MY2020 | 0.331584 | 0.514284 | 0.642078 | 0.433694 | 0.029672 | 504.4739 | 3.559609 | 17,734.57 | 13,991.71 | 512,035 |
| GY2020 | 0.187649 | 0.577042 | 0.746903 | 0.527817 | 0.019339 | 272.044 | 2.263275 | 13,127.36 | 11,020.6 | 545,244 |
| SN2020 | 0.340974 | 0.330459 | 0.714325 | 0.393101 | 0.032009 | 309.9816 | 2.921912 | 16,358.1 | 13,789.54 | 359,919 |
| NJ2020 | 0.280088 | 0.490257 | 0.7244 | 0.4183 | 0.022552 | 377.323 | 4.663952 | 16,450.23 | 13,007.62 | 300,627 |
| LS2020 | 0.413446 | 0.787047 | 0.620453 | 0.350097 | 0.023392 | 385.9616 | 3.309696 | 16,727.95 | 13,724.19 | 548,329 |
| NC2020 | 0.258116 | 0.337956 | 0.708737 | 0.425469 | 0.022955 | 656.0281 | 3.519983 | 15,027.21 | 12,022.54 | 706,477 |
| MS2020 | 0.538572 | 0.692802 | 0.650891 | 0.365058 | 0.035907 | 333.1927 | 2.475084 | 18,177.29 | 14,800.64 | 327,988 |
| YB2020 | 0.317056 | 0.427591 | 0.621328 | 0.458869 | 0.012695 | 450.8414 | 2.095788 | 16,999.23 | 13,418.44 | 655,813 |
| GA2020 | 0.259927 | 0.607983 | 0.745423 | 0.392234 | 0.024659 | 331.6753 | 2.086064 | 16,444.98 | 12,522.87 | 486,481 |
| DZ2020 | 0.226432 | 0.341582 | 0.662618 | 0.482547 | 0.025251 | 551.4275 | 2.194959 | 15,504.2 | 11,535.51 | 764,290 |
| YA2020 | 0.461797 | 1.41545 | 0.556209 | 0.234494 | 0.041097 | 193.4038 | 2.748444 | 14,585.56 | 12,189.13 | 142,393 |
| BZ2020 | 0.180312 | 0.372042 | 0.72046 | 0.522394 | 0.022708 | 214.3556 | 1.738295 | 13,231.54 | 11,089.67 | 480,083 |
| ZY2020 | 0.221612 | 0.352914 | 0.835476 | 0.485456 | 0.009664 | 261.792 | 1.627004 | 17,592.5 | 13,323.81 | 310,414 |
| ABZ2020 | 0.360051 | 1.006597 | 0.718889 | 0.175471 | 0.013919 | 115.0571 | 2.387051 | 14,252.14 | 12,861.52 | 654,424 |
| GZZ2020 | 0.432077 | 1.091248 | 0.828624 | 0.206609 | 0.003174 | 100.3635 | 1.409919 | 12,807.81 | 9388.539 | 991,955 |
| LSZ2020 | 0.249621 | 0.479897 | 0.789226 | 0.461927 | 0.017218 | 600.2257 | 2.241951 | 13,906.78 | 10,327.37 | 2,470,088 |
| CD2021 | 0.508431 | 0.56925 | 0.33171 | 0.149937 | 0.021777 | 1071.945 | 4.089632 | 26,431.74 | 18,500.95 | 1,201,524 |
| ZG2021 | 0.272072 | 0.317916 | 0.617999 | 0.443043 | 0.021748 | 374.8134 | 4.844221 | 18,787.89 | 14,742.05 | 268,816 |
| PZH2021 | 0.615686 | 0.986346 | 0.467593 | 0.239352 | 0.029263 | 148.848 | 4.924289 | 19,938.25 | 14,293.19 | 185,823 |
| LZ2021 | 0.284239 | 0.429889 | 0.601772 | 0.455897 | 0.017903 | 430.2896 | 3.049584 | 18,035.25 | 13,630.58 | 582,466 |
| DY2021 | 0.324619 | 0.40663 | 0.649752 | 0.513714 | 0.034256 | 460.3089 | 4.17913 | 19,790.32 | 14,761.57 | 324,608 |
| MY2021 | 0.328392 | 0.518523 | 0.634059 | 0.437358 | 0.027953 | 631.148 | 4.83916 | 19,303.43 | 15,038.29 | 576,083 |
| GY2021 | 0.184883 | 0.575049 | 0.726263 | 0.536767 | 0.017861 | 336.5695 | 3.623666 | 14,367.11 | 12,083.37 | 605,437 |
| SN2021 | 0.339312 | 0.335086 | 0.694962 | 0.401552 | 0.03098 | 363.1067 | 3.494956 | 17,814.5 | 14,771.72 | 420,378 |
| NJ2021 | 0.277819 | 0.503303 | 0.719359 | 0.424551 | 0.020449 | 422.9692 | 5.462147 | 17,918.42 | 14,076.29 | 336,686 |
| LS2021 | 0.404897 | 0.771356 | 0.60977 | 0.354986 | 0.022188 | 436.6401 | 4.205388 | 18,174.69 | 14,836.65 | 506,026 |
| NC2021 | 0.2542 | 0.335242 | 0.705825 | 0.433257 | 0.021084 | 763.9239 | 4.200365 | 16,431.4 | 13,075.13 | 832,648 |
| MS2021 | 0.534059 | 0.693657 | 0.608836 | 0.36826 | 0.034135 | 380.4231 | 3.195125 | 19,730.13 | 15,314.05 | 428,390 |
| YB2021 | 0.314411 | 0.422004 | 0.616878 | 0.46341 | 0.01215 | 563.7472 | 3.225707 | 18,568.89 | 14,605.64 | 752,123 |
| GA2021 | 0.258373 | 0.611898 | 0.75417 | 0.39749 | 0.023125 | 384.4388 | 3.2675 | 17,867.27 | 13,539.06 | 469,848 |
| DZ2021 | 0.236509 | 0.339766 | 0.638634 | 0.489237 | 0.022108 | 636.0389 | 3.177444 | 16,876.15 | 12,495.93 | 803,732 |
| YA2021 | 0.458933 | 1.415356 | 0.536697 | 0.237012 | 0.038155 | 237.6164 | 4.598304 | 15,889.94 | 13,211.62 | 181,304 |
| BZ2021 | 0.174846 | 0.364475 | 0.708597 | 0.529453 | 0.020842 | 291.1581 | 2.551561 | 14,428.71 | 12,023.28 | 621,154 |
| ZY2021 | 0.221942 | 0.354502 | 0.809088 | 0.490142 | 0.00949 | 318.2045 | 2.808968 | 19,075.99 | 13,705.01 | 307,181 |
| ABZ2021 | 0.393027 | 0.99161 | 0.717949 | 0.17836 | 0.013126 | 142.2087 | 3.260628 | 15,539.04 | 12,162.18 | 737,790 |
| GZZ2021 | 0.457231 | 1.08584 | 0.82965 | 0.212396 | 0.003025 | 123.2873 | 1.785746 | 13,966.64 | 9867.617 | 890,742 |
| LSZ2021 | 0.251612 | 0.480367 | 0.772463 | 0.463255 | 0.016144 | 698.7156 | 2.765006 | 15,232.37 | 11,288.79 | 2,024,651 |
| CD2022 | 0.408366 | 0.572858 | 0.321167 | 0.148163 | 0.021242 | 942.6124 | 3.66971 | 29,126.33 | 20,459.94 | 1,227,997 |
| ZG2022 | 0.291736 | 0.318794 | 0.640985 | 0.451677 | 0.020998 | 392.9342 | 5.222533 | 20,693.86 | 16,266.32 | 277,968 |
| PZH2022 | 0.607537 | 0.961184 | 0.476279 | 0.244592 | 0.028416 | 159.5456 | 5.281489 | 21,979.14 | 15,688.46 | 177,928 |
| LZ2022 | 0.282083 | 0.429629 | 0.602131 | 0.464906 | 0.017174 | 444.853 | 3.240191 | 20,008.24 | 15,225.35 | 616,560 |
| DY2022 | 0.319175 | 0.403308 | 0.629096 | 0.522803 | 0.033424 | 475.2248 | 4.418722 | 21,858.32 | 16,390.64 | 336,286 |
| MY2022 | 0.32759 | 0.527846 | 0.633397 | 0.44627 | 0.027065 | 641.2822 | 5.088874 | 21,339.53 | 16,623.55 | 574,983 |
| GY2022 | 0.18384 | 0.57591 | 0.722561 | 0.546486 | 0.016968 | 358.7886 | 3.975185 | 15,925.12 | 13,309.14 | 592,615 |
| SN2022 | 0.333598 | 0.340261 | 0.698546 | 0.410634 | 0.029429 | 367.1668 | 3.653375 | 19,726.62 | 16,238.53 | 437,085 |
| NJ2022 | 0.274314 | 0.506123 | 0.723573 | 0.433335 | 0.019032 | 434.9058 | 5.823245 | 19,819.39 | 15,544.5 | 354,612 |
| LS2022 | 0.397352 | 0.767672 | 0.611175 | 0.361948 | 0.021311 | 437.8487 | 4.327208 | 20,042.99 | 16,557.72 | 510,632 |
| NC2022 | 0.254255 | 0.336342 | 0.713206 | 0.44365 | 0.020206 | 787.4623 | 4.446577 | 18,246.56 | 14,655.62 | 842,710 |
| MS2022 | 0.531848 | 0.691349 | 0.609692 | 0.37453 | 0.033477 | 391.8993 | 3.367526 | 21,771.45 | 16,959.66 | 407,445 |
| YB2022 | 0.318398 | 0.422225 | 0.623978 | 0.471883 | 0.011611 | 583.4159 | 3.387747 | 20,591.14 | 16,302.12 | 763,828 |
| GA2022 | 0.268681 | 0.607837 | 0.754413 | 0.405389 | 0.021964 | 397.0713 | 3.43698 | 19,751.6 | 15,003.66 | 474,982 |
| DZ2022 | 0.232913 | 0.341658 | 0.633338 | 0.499495 | 0.021101 | 665.2611 | 3.391562 | 18,637.51 | 13,893.35 | 856,300 |
| YA2022 | 0.452625 | 1.400642 | 0.537451 | 0.241422 | 0.03688 | 247.2839 | 4.900683 | 17,579.88 | 14,691.11 | 207,003 |
| BZ2022 | 0.177725 | 0.363477 | 0.7099 | 0.541509 | 0.019795 | 314.8797 | 2.844336 | 15,962.13 | 13,346.19 | 630,112 |
| ZY2022 | 0.221337 | 0.358497 | 0.82428 | 0.499094 | 0.011474 | 324.6032 | 3.017587 | 21,022.69 | 15,034.5 | 324,676 |
| ABZ2022 | 0.398465 | 0.990348 | 0.729097 | 0.182743 | 0.012659 | 153.2017 | 3.728885 | 17,161.35 | 13,199.3 | 695,979 |
| GZZ2022 | 0.453096 | 1.089342 | 0.802198 | 0.213455 | 0.00299 | 120.5172 | 1.835338 | 15,379.48 | 10,783.96 | 998,664 |
| LSZ2022 | 0.254224 | 0.48271 | 0.771874 | 0.465921 | 0.015932 | 742.5621 | 2.961238 | 16,807.83 | 12,443.51 | 1,584,416 |
| CD2023 | 0.375769 | 0.575358 | 0.311721 | 0.144431 | 0.020642 | 950.4171 | 3.614473 | 30,931.11 | 21,195.64 | 1,246,105 |
| ZG2023 | 0.293587 | 0.316706 | 0.639783 | 0.447086 | 0.020122 | 408.8582 | 4.943816 | 21,976.1 | 17,081.75 | 278,331 |
| PZH2023 | 0.579061 | 0.963366 | 0.478017 | 0.243445 | 0.027725 | 172.3233 | 5.050382 | 23,364.15 | 16,357.25 | 181,420 |
| LZ2023 | 0.2862 | 0.424858 | 0.600635 | 0.456996 | 0.01643 | 464.1492 | 3.222455 | 21,348.46 | 15,851.83 | 634,320 |
| DY2023 | 0.317022 | 0.397233 | 0.62642 | 0.517971 | 0.032274 | 498.1186 | 4.345364 | 23,192.32 | 17,415.89 | 352,976 |
| MY2023 | 0.318942 | 0.526646 | 0.631349 | 0.439118 | 0.025986 | 648.3117 | 4.785598 | 22,726.18 | 17,345.82 | 583,873 |
| GY2023 | 0.183446 | 0.573677 | 0.721597 | 0.539694 | 0.01632 | 385.3789 | 3.981957 | 16,881.23 | 14,058.88 | 577,700 |
| SN2023 | 0.326776 | 0.34331 | 0.697799 | 0.408061 | 0.028353 | 367.1592 | 3.402094 | 20,986.27 | 17,100.78 | 463,771 |
| NJ2023 | 0.26894 | 0.506617 | 0.720551 | 0.424599 | 0.018189 | 457.7679 | 5.560485 | 20,995.68 | 16,236.7 | 347,104 |
| LS2023 | 0.389449 | 0.765411 | 0.61603 | 0.354748 | 0.020674 | 449.8108 | 4.178904 | 21,338.98 | 17,344.39 | 514,623 |
| NC2023 | 0.259362 | 0.339549 | 0.711685 | 0.440837 | 0.019697 | 830.8139 | 4.470316 | 19,468.94 | 15,501.75 | 819,587 |
| MS2023 | 0.521275 | 0.683155 | 0.608092 | 0.370438 | 0.032498 | 411.782 | 3.365315 | 23,098.87 | 17,731.25 | 443,823 |
| YB2023 | 0.317534 | 0.426807 | 0.623268 | 0.458467 | 0.011167 | 646.2158 | 3.543478 | 21,845.55 | 17,205.58 | 840,985 |
| GA2023 | 0.26484 | 0.605401 | 0.759511 | 0.399817 | 0.020894 | 401.874 | 3.252302 | 20,963.9 | 15,898.63 | 499,818 |
| DZ2023 | 0.232201 | 0.340429 | 0.634445 | 0.495823 | 0.020265 | 698.0941 | 3.347971 | 19,905.78 | 14,646.42 | 856,301 |
| YA2023 | 0.44433 | 1.379628 | 0.537294 | 0.239999 | 0.035582 | 264.6207 | 4.875467 | 18,793.73 | 15,797.9 | 239,944 |
| BZ2023 | 0.174136 | 0.360049 | 0.709273 | 0.534386 | 0.019112 | 345.5546 | 2.858801 | 16,966.96 | 14,169.81 | 635,478 |
| ZY2023 | 0.217586 | 0.355351 | 0.831032 | 0.486122 | 0.011263 | 359.4847 | 3.185459 | 22,326.26 | 15,701.84 | 315,232 |
| ABZ2023 | 0.391618 | 0.942808 | 0.730726 | 0.182115 | 0.011937 | 159.2392 | 3.652916 | 18,260.52 | 13,886 | 686,401 |
| GZZ2023 | 0.4185 | 1.028249 | 0.803294 | 0.211384 | 0.002731 | 127.4596 | 1.92464 | 16,362.69 | 11,349.83 | 887,000 |
| LSZ2023 | 0.248278 | 0.48071 | 0.741621 | 0.455248 | 0.015469 | 812.3198 | 3.060438 | 17,949.8 | 13,066.11 | 1,565,648 |
| CD2024 | 0.398042 | 0.612805 | 0.302653 | 0.145125 | 0.021417 | 957.762 | 3.868002 | 30,088.6 | 21,163.71 | 1,372,916 |
| ZG2024 | 0.292645 | 0.325266 | 0.638168 | 0.458972 | 0.019768 | 417.1546 | 5.440209 | 20,573.53 | 15,900.74 | 314,018 |
| PZH2024 | 0.604467 | 0.96652 | 0.477976 | 0.244829 | 0.027456 | 176.3121 | 5.39401 | 22,977.95 | 15,911.68 | 196,556 |
| LZ2024 | 0.286826 | 0.438411 | 0.597969 | 0.468574 | 0.016208 | 470.2071 | 3.384366 | 20,015.54 | 14,845.91 | 649,168 |
| DY2024 | 0.316436 | 0.398951 | 0.622617 | 0.534287 | 0.031796 | 508.4059 | 4.719236 | 21,898.72 | 16,281.38 | 382,598 |
| MY2024 | 0.320361 | 0.539408 | 0.628234 | 0.448838 | 0.025713 | 656.2364 | 5.229981 | 21,620.81 | 16,438.27 | 662,394 |
| GY2024 | 0.185513 | 0.572812 | 0.720467 | 0.555712 | 0.01591 | 386.017 | 4.270995 | 17,191.88 | 12,712.75 | 608,027 |
| SN2024 | 0.340244 | 0.360678 | 0.697253 | 0.418919 | 0.028234 | 365.9757 | 3.606322 | 19,958.73 | 14,863.29 | 478,647 |
| NJ2024 | 0.266122 | 0.507778 | 0.719829 | 0.439235 | 0.017682 | 462.9293 | 5.962911 | 20,098.79 | 15,624.98 | 404,343 |
| LS2024 | 0.399536 | 0.802518 | 0.614671 | 0.363639 | 0.021055 | 458.8082 | 4.517216 | 20,366.58 | 15,200 | 532,724 |
| NC2024 | 0.257194 | 0.347864 | 0.710306 | 0.454035 | 0.019309 | 835.829 | 4.62573 | 18,960 | 14,694 | 886,825 |
| MS2024 | 0.516101 | 0.682368 | 0.606805 | 0.377752 | 0.031946 | 411.8193 | 3.576595 | 21,688.8 | 15,613 | 502,419 |
| YB2024 | 0.31294 | 0.441074 | 0.6221 | 0.473996 | 0.010864 | 657.1534 | 3.741714 | 20,452.59 | 15,431.14 | 855,043 |
| GA2024 | 0.260245 | 0.60488 | 0.757772 | 0.410788 | 0.020083 | 401.2889 | 3.417655 | 19,811.98 | 14,444.84 | 517,435 |
| DZ2024 | 0.232557 | 0.348398 | 0.633636 | 0.51045 | 0.019872 | 707.752 | 3.519454 | 19,435.1 | 14,396.82 | 964,881 |
| YA2024 | 0.441754 | 1.376257 | 0.536069 | 0.242513 | 0.035181 | 270.2676 | 5.155786 | 18,500.72 | 13,293.64 | 262,914 |
| BZ2024 | 0.172136 | 0.35964 | 0.708918 | 0.550035 | 0.018676 | 350.376 | 3.002153 | 17,246.87 | 14,454.99 | 666,613 |
| ZY2024 | 0.216072 | 0.363574 | 0.831067 | 0.507107 | 0.011084 | 362.6616 | 3.403843 | 20,923.6 | 14,565.83 | 339,636 |
| ABZ2024 | 0.382947 | 0.876942 | 0.732441 | 0.18394 | 0.011518 | 172.0071 | 4.069421 | 18,140.91 | 13,530.16 | 713,236 |
| GZZ2024 | 0.412654 | 0.999425 | 0.804189 | 0.212265 | 0.002607 | 130.8422 | 2.05196 | 16,917.81 | 12,568.04 | 940,013 |
| LSZ2024 | 0.246432 | 0.484105 | 0.740201 | 0.460623 | 0.015272 | 817.9504 | 3.286181 | 17,685.77 | 13,086.62 | 1,570,320 |
References
- Li, Y.; Narayanan, M.; Shi, X.; Chen, X.; Li, Z.; Ma, Y. Biofilms formation in plant growth-promoting bacteria for alleviating agro-environmental stress. Sci. Total Environ. 2024, 907, 167774. [Google Scholar] [CrossRef]
- The Central Committee of the Communist Party of China and the State Council of the People’s Republic of China. Opinions of the CPC Central Committee and the State Council on Further Deepening Rural Reforms and Taking Solid Steps to Advance All-around Rural Revitalization. Available online: https://www.gov.cn/zhengce/202502/content_7005158.htm (accessed on 21 September 2025).
- The Central Committee of the Communist Party of China and the State Council of the People’s Republic of China. A Plan to Accelerate Building Up Its Strength in Agriculture for the Period from 2024 to 2035. Available online: https://www.gov.cn/zhengce/202504/content_7017469.htm (accessed on 21 September 2025).
- National Bureau of Statistics of China. China Statistical Yearbook 2024. Available online: https://www.stats.gov.cn/sj/ndsj/2024/indexeh.htm (accessed on 21 September 2025).
- Qiao, G.; Chen, F.; Xu, C.; Li, Y.; Zhang, D. Study with agricultural system resilience and Agro-ecological efficiency synergistic evolutionary in China. Food Energy Secur. 2024, 13, e514. [Google Scholar]
- Lin, S.; Zhang, H.; Wong, C.U.I. Spatiotemporal dynamics of agricultural resilience in China: A multidimensional assessment framework and analysis of systemic driving mechanisms. GeoJournal 2025, 90, 158. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. The State of Food Security and Nutrition in the World 2025. Available online: https://www.fao.org/agrifood-economics/publications/detail/en/c/1740904/ (accessed on 24 October 2025).
- Rezvi, H.U.A.; Tahjib-Ul-Arif, M.; Azim, M.A.; Tumpa, T.A.; Tipu, M.M.H.; Najnine, F.; Dawood, M.F.A.; Skalicky, M.; Brestič, M. Rice and food security: Climate change implications and the future prospects for nutritional security. Food Energy Secur. 2023, 12, e430. [Google Scholar]
- Chen, X.; Wang, H.; Zhu, X.; Zhang, X. Spatial-temporal characteristics of agricultural economic resilience and spatial spillover effects of driving factors: Evidence from provincial panel data in China. Front. Environ. Sci. 2025, 13, 1437018. [Google Scholar] [CrossRef]
- Zeng, X.; Lu, H.; Qi, H.; Ji, L. Does extreme weather affect the resilience of agricultural economies? Analysis based on agricultural insurance. Front. Environ. Sci. 2025, 13, 1551030. [Google Scholar] [CrossRef]
- Lioutas, E.D.; Charatsari, C. Enhancing the ability of agriculture to cope with major crises or disasters: What the experience of COVID-19 teaches us. Agric. Syst. 2021, 187, 103023. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, H.; Bai, Q.; Liu, L.; Li, G.; Shen, Q. Can the Integration of Rural Industries Help Strengthen China’s Agricultural Economic Resilience? Agriculture 2023, 13, 1813. [Google Scholar] [CrossRef]
- Xue, X.; Gao, J.; Xu, S. The impact and mechanism of digital economy on agricultural development resilience: Evidence from China. Front. Sustain. Food Syst. 2025, 9, 1574461. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Quan, T. Strengthening or Weakening: The Impact of an Aging Rural Workforce on Agricultural Economic Resilience in China. Agriculture 2023, 13, 1436. [Google Scholar] [CrossRef]
- Han, P.; Liu, H.; Chen, Y. Aging, financial coverage, and agricultural economic resilience: Nonlinear dynamics and thresholds. Financ. Res. Lett. 2025, 82, 107518. [Google Scholar] [CrossRef]
- Luo, L.; Nie, Q.; Jiang, Y.; Luo, F.; Wei, J.; Cui, Y. Spatiotemporal Dynamics and Spatial Spillover Effects of Resilience in China’s Agricultural Economy. Agriculture 2024, 14, 1522. [Google Scholar] [CrossRef]
- Yang, C.; Liu, W.; Zhou, J. The Role of Digital Finance in Shaping Agricultural Economic Resilience: Evidence from Machine Learning. Agriculture 2024, 14, 1834. [Google Scholar] [CrossRef]
- Chao, R.K.; Li, J.S. The impact of agricultural production agglomeration on agricultural economic resilience: Based on spatial spillover and threshold effect test. Front. Sustain. Food Syst. 2024, 8, 1464732. [Google Scholar] [CrossRef]
- Kertolli, E.; Prosperi, P.; Harbouze, R.; Moussadek, R.; Echchgadda, G.; Belhouchette, H. The water–energy–food–ecosystem nexus in North Africa dryland farming: A multi-criteria analysis of climate-resilient innovations in Morocco. Agric. Food Econ. 2024, 12, 34. [Google Scholar] [CrossRef]
- Robert, B.; Mauro, V.; Julie, U. Economic resilience of agriculture in England and Wales: A spatial analysis. J. Maps 2022, 18, 70–78. [Google Scholar] [CrossRef]
- Chen, M.; Ning, S.; Cui, Y.; Jin, J.; Zhou, Y.; Wu, C. Quantitative assessment and diagnosis for regional agricultural drought resilience based on set pair analysis and connection entropy. Entropy 2019, 21, 373. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Qun, W.; Ranran, C.; Jingsuo, L.; Khan, N. Toward a sustainable agricultural system in China: Exploring the nexus between agricultural science and technology innovation, agricultural resilience and fiscal policies supporting agriculture. Front. Sustain. Food Syst. 2024, 8, 1390014. [Google Scholar] [CrossRef]
- Luo, L.; Li, Y.; Ma, W.; Rong, J.; Wei, J.; Cui, Y.; Qu, T. Temporal–Spatial Dynamics and Collaborative Effects of Cropland Resilience in China. Land 2025, 14, 108. [Google Scholar] [CrossRef]
- Li, W.; Guo, J.; Tang, Y.; Zhang, P. Resilience of agricultural development in China’s major grain-producing areas under the double security goals of “grain ecology”. Environ. Sci. Pollut. Res. 2024, 31, 5881–5895. [Google Scholar] [CrossRef]
- Yi, P.; Dong, Q.; Li, W. Evaluation of city sustainability using the deviation maximization method. Sustain. Cities Soc. 2019, 50, 101529. [Google Scholar] [CrossRef]
- Sichuan Provincial Bureau of Statistics. Sichuan Statistical Yearbook. Available online: https://tjj.sc.gov.cn/scstjj/c112132/pic_list.shtml (accessed on 10 September 2025).
- Huang, W.; Shuai, B.; Sun, Y.; Wang, Y.; Antwi, E. Using entropy-TOPSIS method to evaluate urban rail transit system operation performance: The China case. Transp. Res. Part A Policy Pract. 2018, 111, 292–303. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of objective weights using a new method based on the removal effects of criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. A novel LOPCOW-DOBI multi-criteria sustainability performance assessment methodology: An application in developing country banking sector. Omega 2022, 112, 102690. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Lu, J. Assessment of long and short-term flood risk using the multi-criteria analysis model with the AHP-Entropy method in Poyang Lake basin. Int. J. Disaster Risk Reduct. 2022, 75, 102968. [Google Scholar] [CrossRef]
- Chen, C.H. A novel multi-criteria decision-making model for building material supplier selection based on entropy-AHP weighted TOPSIS. Entropy 2020, 22, 259. [Google Scholar] [CrossRef] [PubMed]
- Zafar, S.; Alamgir, Z.; Rehman, M.H. An effective blockchain evaluation system based on entropy-CRITIC weight method and MCDM techniques. Peer-to-Peer Netw. Appl. 2021, 14, 3110–3123. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Ecer, F.; Pamucar, D.; Karamaşa, Ç. Comparative assessment of social sustainability performance: Integrated data-driven weighting system and CoCoSo model. Sustain. Cities Soc. 2021, 71, 102975. [Google Scholar] [CrossRef]
- Huang, S.; Cheng, H.; Luo, M. Comparative study on barriers of supply chain management MOOCs in China: Online review analysis with a novel TOPSIS-CoCoSo approach. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 1793–1811. [Google Scholar] [CrossRef]
- Long, R.; Li, H.; Wu, M.; Li, W. Dynamic evaluation of the green development level of China’s coal-resource-based cities using the TOPSIS method. Resour. Policy 2021, 74, 102415. [Google Scholar] [CrossRef]
- Guo, J.H. The efficiency evaluation of low carbon economic performance based on dynamic TOPSIS method. J. Interdiscip. Math. 2017, 20, 231–241. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, P.; Guo, J. How does agricultural resilience in China vary by region? Ecol. Indic. 2025, 174, 113513. [Google Scholar] [CrossRef]
- Tao, T.; Ma, L.; Wang, X.; Wu, S.; Shi, Z.; Cui, X. Resilience or efficiency? Strategic options for sustainable development of agricultural systems in ecologically fragile areas of China. Sci. Total Environ. 2023, 881, 163411. [Google Scholar] [CrossRef] [PubMed]
- Barel-Shaked, S.; Buda, E. Charting resilience: A typology of food self-sufficiency in OECD nations. Agric. Food Secur. 2025, 14, 19. [Google Scholar] [CrossRef]
- Huang, S.; Cheng, H.; Tan, M.; Tang, Z.; Teng, C. Evaluating Regional Potentials of Agricultural E-Commerce Development Using a Novel MEREC Heronian-CoCoSo Approach. Agriculture 2024, 14, 1338. [Google Scholar] [CrossRef]
- Yazdani, M.; Torkayesh, A.E.; Chatterjee, P.; Fallahpour, A.; Montero-Simo, M.J.; Araque-Padilla, R.A.; Wong, K.Y. A fuzzy group decision-making model to measure resiliency in a food supply chain: A case study in Spain. Socio-Econ. Plan. Sci. 2022, 82, 101257. [Google Scholar] [CrossRef]
- Zandi, P.; Rahmani, M.; Khanian, M.; Mosavi, A. Agricultural risk management using fuzzy TOPSIS analytical hierarchy process (AHP) and failure mode and effects analysis (FMEA). Agriculture 2020, 10, 504. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).