1. Introduction
Global cherry production, including both sweet (
Prunus avium L.) and sour (
Prunus cerasus L.) varieties, amounts to approximately 2.4 million tons. Türkiye ranks first worldwide with a production of about 627,000 tons, accounting for 26% of the total cherry production [
1]. Cherries, which have a wide distribution area in the world, are commercially produced in countries such as Türkiye, the USA, Iran and Italy. In Türkiye, cherries also have a wide production area, and the number of cherry trees is increasing day by day. Türkiye, which is among the leading countries in cherry production, is also one of the major exporters of cherries. Cherry production in Türkiye mainly takes place in Kemalpaşa (Izmir), Manisa, Akşehir (Konya), Sultandağı (Afyon), Uluborlu (Isparta), Hanaz (Denizli) and recently in the Hadim and Taşkent (Konya) regions [
2]. The variety produced and exported is the 0900 Ziraat cherry variety. This variety has become one of the most important cherries in the world due to its hard and sweet flesh, large and crack-resistant fruit, long green stem and resistance to transportation and storage, and is known as the ‘Turkish Cherry’ in Europe [
3,
4,
5].
There are important diseases and pests that limit cherry production. Among these pests, the cherry fruit fly
Rhagoletis cerasi L. (Diptera: Tephritidae) has an important role. There are important criteria for deciding on the chemical control of this pest. Among these criteria, the flowering of cherries and the timing of fruit set and ripening are of particular importance. In agricultural control technical guidelines, the period when cherry fruit begins to turn pink is an important criterion in deciding on control measures. Important pomological changes such as fruit coloration, which is an important criterion in cherry fruit fly control, play significant roles in the pest’s infestation of the fruit. Female
Rhagoletis sp. individuals show specific responses to volatile compounds secreted from hosts and visual sources. The degree of this response is directly dependent on the host’s characteristics [
6,
7,
8,
9,
10]. These characteristics of the hosts vary greatly depending on the species and varieties.
In addition, these different pomological characteristics of cherry fruits vary according to the changes in soil conditions and meteorological data where the varieties are grown. Among the different property values that are important for fruit pomology, weight, width, length, fruit height, stem length, fruit hardness, fruit seed weight, water-soluble solids (WSSs), NaOH and fruit acidity amounts are important criteria. These criteria vary depending on the stage of cherry ripening, and this variation is significant for understanding the degree of damage caused by species that are directly harmful to the fruit, as well as the agricultural control strategy, based on the pomological differences in the fruit. Optimizing data collection at the initial stage of pest-induced damage is essential for accurately quantifying damage severity in relation to fruit composition. For the purpose of evaluating the effects of three distinct insecticides (malathion, cypermethrin and azadirachtin) used in five different cherry coloring periods on the number of
R. cerasi, it has been determined that the control success was the highest in the second cherry coloring period [
11].
According to the study conducted, insecticide applications during the second phe-nological coloration period of cherry were found to be the most effective, resulting in the lowest rates of worm-infested fruits [
11]. This finding confirms the earlier literature indicating that the cherry fly causes the most damage during this stage. Therefore, the algorithms used in fruit coloration-based pest control strategies are generally built around the second coloration period, as this stage marks the onset of egg-laying activity and a critical rise in the population density of the cherry fruit fly.
Therefore, the algorithms used in fruit coloration-based pest control strategies are generally built around the second coloration period, as this stage marks the beginning of egg-laying activity and a critical increase in the population density of the cherry fruit fly.
Various optimization-based methods have been proposed for classification rule mining, each employing distinct strategies with varying levels of success. Among these, evolutionary-based crisp rule learning algorithms represent a diverse set of approaches built upon evolutionary learning structures. By combining the complementary features of these methods, researchers have developed various hybrid classification algorithms that aim to enhance model performance. For example, hybrid models may integrate the fast learning capability and rule diversity of Michigan-based algorithms, the comprehensive rule set optimization of Pittsburgh-based algorithms and the structural flexibility of genetic programming. Such combinations are designed to exploit the strengths of individual approaches while mitigating their limitations, leading to improved classification accuracy, model interpretability and computational efficiency. The basic hybrid algorithm approaches are as follows:
1.1. Michigan-Based Genetic Algorithms
Within the Michigan approach, each individual is associated with only one classification rule. In this approach, while the evolutionary process improves individual rules, the final classifier is obtained as a combination of the best rules in the population. Since the interaction between rules is provided indirectly in this structure, diversity is more easily preserved. This method provides a fast learning ability, especially in large and highly diverse datasets [
12].
1.2. Pittsburgh-Based Genetic Algorithms
According to the Pittsburgh approach, every individual corresponds to a complete rule set. In the evolutionary process, each individual of the population is a classifier and these classifiers are optimized with goals such as accuracy and simplicity. Since the agreement between the rules is directly evaluated, a higher classification performance can be achieved; however, the search space is larger and this can increase the computational cost [
13].
1.3. Genetic Programming for Rule Learning
Genetic programming (GP) is an evolutionary computational technique in which rules are represented in tree structures. GP is particularly effective in learning complex combinations of rule conditions. The structure of the rule is optimized by evolving it into a tree, which allows the creation of explainable and flexible models. GP can optimize both classification accuracy and rule simplicity [
14].
In this study, the second pomological period, in which the fruit pest is frequently seen, was prioritized, and two periods were taken as the second pomological period and the others, with the dataset was divided into two groups accordingly. The second pomological period in the dataset was accepted as class 1 and the remaining pomological periods were accepted as class 0. In line with this assumption, three different evolutionary artificial intelligence classification algorithms were used to find the classification rules that indicate which class the new fruit samples belong to. In addition, two different fitness functions were applied to all three algorithms and the results were compared. According to the classification rules found by the algorithms, determining which class the new fruit sample belongs to and finding the fruits that will coincide with the second pomological period can be used as an auxiliary element by experts in the field in the fight against the pest.
In this study, the following methodological steps were followed while working on the algorithms:
- ▪
Data preprocessing and cleaning.
- ▪
Dividing the dataset into training (80%) and testing (20%).
- ▪
Training evolutionary calculation-based classification algorithms (CORE, DMEL, OCEC).
- ▪
Calculating fitness values for each algorithm.
- ▪
Evaluating the performance of the algorithms using a test dataset.
- ▪
Calculating accuracy, recall, precision and F1-Score metrics.
- ▪
Analyzing the rules produced by the algorithms.
- ▪
Visual comparison of the performances of the algorithms.
The contributions of this study to the literature are listed below:
The dataset collected within the study is new and unique with high widespread impact and output.
The application of the methods in this field is important in terms of pioneering various future studies in this field.
The use of explainable artificial intelligence applications is innovative for the focused problem.
The use of optimization-based classification models for this problem is a new and original approach.
To our knowledge, this is the first time that these algorithms have been used in the context of automatically identifying important criteria and relevant ranges for pest control.
This study is structured as follows:
Section 1 presents background information on the cherry fruit fly and cherry production, as well as an overview of optimization-based classification techniques used to extract classification rules.
Section 2 presents how the cherry samples were collected is explained and the algorithms chosen designed to discover classification rules are examined in detail. In addition, the dataset utilized in this study is described in detail.
Section 3 presents a comparative analysis of the results produced by the algorithms, supported by various visualizations. The outcomes of this study, including the classification rules identified by each algorithm, are summarized in tabular format.
Section 4 presents the results obtained with different algorithmic approaches, interprets these findings, highlights the interpretability advantages of the methods compared with black-box algorithms, and points to directions for future research.
2. Materials and Methods
2.1. Collection and Analysis of Cherry Fruit Samples
Sweet (
Prunus avium L.) cherry samples were taken from Elazig Province, Harput 1 and Harput 2, Baskil 1 and Baskil 2 during different coloration periods (
Figure 1), kept in the refrigerator and then sent to Malatya Fruit Research Institute for analysis (
Figure 2). For each cherry variety and each coloration stage, fruits were collected from 10 different trees. From each tree, 25 fruits were taken from four different orientations, resulting in 100 fruits per tree. Accordingly, a total of 1000 fruits were collected per coloration stage for each variety. Fruit samples were collected at five distinct coloration stages, ranging from the initial white stage to full red ripeness. Sampling was conducted separately for each stage, at intervals of approximately 15–20 days. The entire data collection process spanned from the end of March to the end of June, covering the full ripening period of the cherries.
In the studied region, the dominant commercially cultivated variety, which provides a 95% yield of 0900 Ziraat cherry variety, exhibits coloration criteria consistent with other varieties. However, the Dalbastı cherry is found in Malatya Province, and its fruit shape is different but its coloration is similar to other varieties. Because this cherry variety is not widely cultivated, the study was conducted on the dominant variety. In these analyses, the weight, width, length, fruit height, stem length, fruit hardness, fruit seed weight, water-soluble dry matter content (WDSM), NaOH and fruit acidity amounts of the fruits were analyzed according to each location and the analysis results obtained were used in classification. At the same time, this analysis aims to determine the coloration period of the cherries by looking at various numerical parameters, regardless of the presence of fruit flies. For the purposes of this study, Python version 3.13.3 was utilized to implement a classification system and to produce various graphical outputs for data visualization.
During the development of the fruit coloration scale, fruits at each coloration stage were photographed using an Olympus SZX 7 stereomicroscope equipped with an Olympus SC50 camera (Olympus Corporation, Tokyo, Japan). Efforts were made to match identical colors on the same tree and within the same phenological stage. Color separation was carried out multiple times with the assistance of several observers, ensuring that fruits with identical color tones were consistently assigned to the same color scale. Additionally, fruits corresponding to the same color scale were photographed using a Canon 550D camera (Canon Corporation, Tokyo, Japan), transferred to a digital environment and used to generate the final color scales.
2.2. Implementation of Algorithms
In this study, three different classification methods based on evolutionary algorithms were adapted and compared to a unique pomological dataset: CORE (Coevolutionary Rule Extractor), DMEL (Data Mining by Evolutionary Learning) and OCEC (Organizational Coevolutionary Algorithm for Classification) [
15,
16,
17]. All three methods focus on the rule-based classification problem and use different evolutionary strategies and structures. By examining their potential applicability to cherry fruit classification, different issues were highlighted such as dataset imbalance, high-dimensional visual features and the need for interpretable rules for agricultural decision support. Compared with conventional classifiers, these evolutionary rule-based methods are particularly advantageous in scenarios that require both accurate prediction and human-interpretable rules. This study emphasizes the following:
CORE allows the coevolution of individual rules and rule sets, which enhances diversity and prevents premature convergence.
DMEL introduces dynamic element learning, providing flexibility and adaptability in constructing rule sets.
OCEC leverages organization-based clustering to discover informative and compact rules in a bottom-up manner.
By outlining these points, this study highlights the novelty of its approach, its advantages over traditional classification techniques and its relevance to cherry fruit classification where interpretability, adaptability and robustness are crucial.
2.2.1. CORE Algorithm
The CORE algorithm has a coevolutionary structure that simultaneously evolves the rules and the rule set. By combining the advantages of the Michigan and Pittsburgh approaches, it allows for the optimization of both the individual rules and the intra-cluster interaction [
17]. The cooperation of the two populations in the coevolutionary process aims to increase the agreement between the rules and improve the classification accuracy. In CORE, the population diversity is preserved and unnecessary rules are eliminated by the token competition method.
Unlike traditional methods, this algorithm produces more meaningful and comprehensive results by coevolving candidate rules and rule sets in two collaborative populations simultaneously, rather than in separate stages [
17].
CORE is primarily distinguished by its dual population structure, in which rules and rule sets evolve simultaneously. This architecture effectively reduces the search space and facilitates the generation of rules with a superior classification performance [
17]. The reCORE algorithm based on this structure aims to increase understandability while preserving the simplicity of the rules and it shows a classification performance that can compete with rule-based algorithms such as Ridor and JRip [
18].
In a comprehensive review of the genetic-based machine learning literature, it was emphasized that CORE works with a penalized fitness function that minimizes false positives and applies different crossover strategies according to nominal/numeric attributes [
17].
The coevolutionary architecture of CORE has inspired not only rule-based systems but also models that aim to improve the robustness of decision trees. For example, the CoEvoRDT algorithm proposed in 2023 coevolved two populations representing decision trees and corrupted features to produce decision trees that are optimized according to the minimax regret criterion [
19]. This shows the applicability of the architecture of the CORE algorithm to different classification models.
Finally, in another study in 2024, the future directions of coevolutionary algorithms were discussed and the OMNIREP and SAFE algorithms were developed by extending the basic principles of CORE-like systems. These systems provide more flexible and adaptive coevolutionary learning models by enabling the evolution of representation encoding and objective functions, respectively [
20].
CORE Algorithm’s Genetic Structure and Coding
The CORE algorithm uses two collaborative population methods:
Main population: In accordance with the Michigan approach, each chromosome corresponds to a single classification rule.
Supporting populations: Each chromosome represents a rule set comprising multiple rules, in accordance with the Pittsburgh approach.
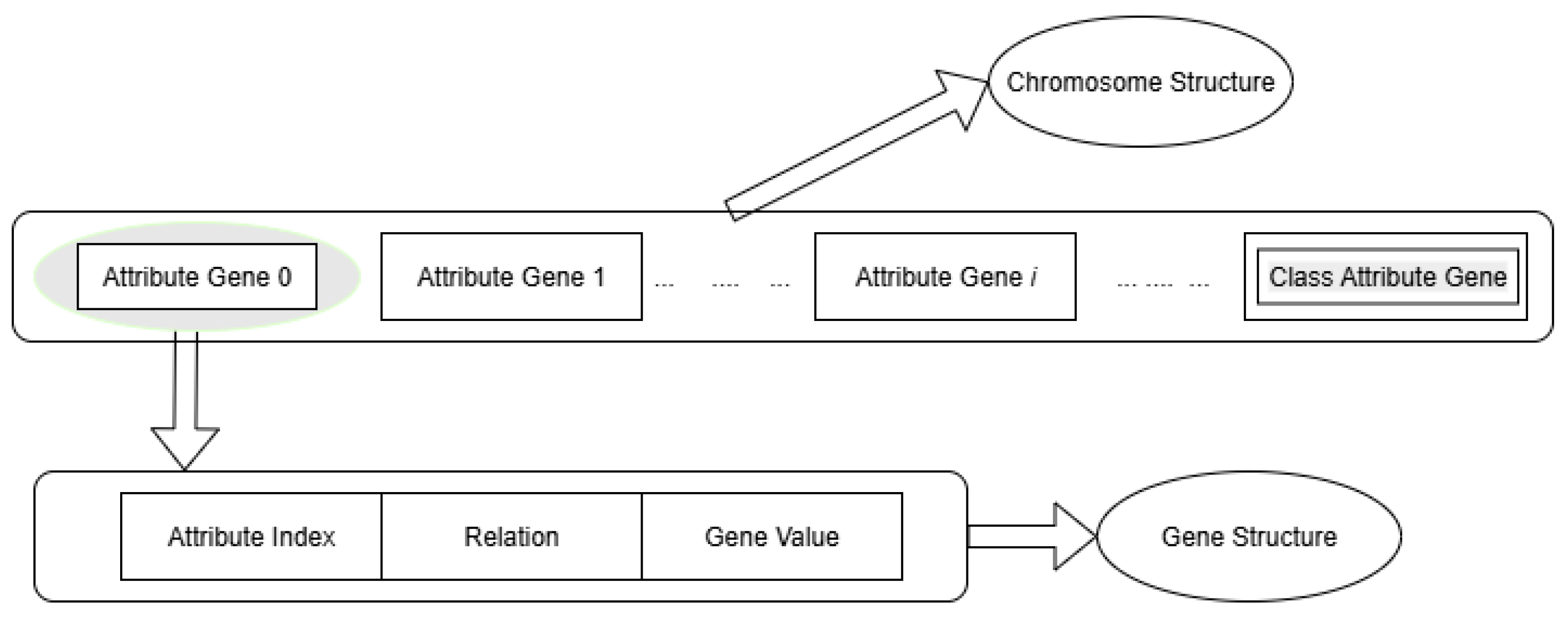
Chromosomes are designed with a variable length to support nominal and numeric attributes. Numerical values are normalized into the range [0, 1]. The gene structure consists of three fields: attribute index, relation (>, <, =, etc.) and value.
Evolutionary Process
Selection: Tournament selection.
Crossover: Classic one-point or multi-point crossover.
Mutation: Small random changes at the gene level.
Token competition: Niching method to maintain population diversity.
Regeneration: Random reproduction of low-fitness individuals.
Algorithm Features
Rule-based classification approach.
Flexible structure that allows overlapping rules.
Genetic algorithm-based search strategy.
Fitness function that balances accuracy and coverage.
Tournament selection, crossover, and mutation operators.
CORE Algorithm Pseudocode
Initialize main population with random Michigan-style chromosomes.
Initialize co-populations with random co-chromosomes (rule sets).
Repeat until termination condition:
Apply token competition among rules to capture training instances.
Update adjusted fitness values based on tokens captured.
Apply crossover and mutation on chromosomes:
- -
One-point crossover at chromosome level.
- -
Bit-string or real-coded crossover at gene level.
- -
Mutation only on the value field of genes.
Mutate co-chromosomes (rule sets) to maintain diversity.
Regenerate weak chromosomes with probability p to ensure exploration.
Update the pool of best rules from token competition.
Output final pool of best rules as the rule set classifier.
The CORE framework employs a dual population design: a Michigan-style main population where each chromosome encodes a single classification rule, and Pittsburgh-style co-populations where each co-chromosome encodes a set of rules. Each gene within a Michigan chromosome is composed of three fields: the attribute index, the relation operator (e.g., =, <, >, in) and the corresponding value. Decoding a chromosome produces an IF–THEN rule, while co-chromosomes yield ordered rule sets with a default class. In
Figure 3 the represantation of each attribute in the dataset as a gene can be seen in the chromosome structure.
Crossover operators are implemented at both chromosome and gene levels. At the chromosome level, a one-point crossover may exchange sequences of genes between parents, while at the gene level, bit-string crossover is used for nominal attributes and real-coded blending for numeric attributes. Mutation occurs only in the value field, while gene insertion/deletion operations allow dynamic rule length. Diversity is further maintained via a regeneration mechanism.
Labeling and competition are governed by a token competition mechanism. Each data instance is treated as a token. Rules compete for tokens based on matching antecedents and correct classification, with ties resolved by fitness. This ensures niche preservation and the balanced coverage of the instance space.
2.2.2. DMEL Algorithm
The DMEL algorithm has been developed specifically for applications where each classification decision is given with a probability estimation. In the evolutionary process, probabilistically derived first-order rules are initially generated, from which more complex rule sets are then derived. The prominent features of DMEL are the evaluation of the estimated probabilities and the selection of rules based on an interestingness measure. Chromosome fitness is calculated based on the probability of the data being correctly classified by the rules. It is especially characterized by its ability to work with missing data [
15]. The population is not initially created randomly; the rules are derived from statistically significant relationships.
Although traditional decision tree-based algorithms (C4.5 [
21], SLIQ [
22], RainForest [
23]) give successful results in classification accuracy, they are insufficient for the probabilistic reliability of the obtained classes [
15]. On the other hand, methods such as logistic regression and artificial neural networks are capable of generating classification probabilities; however, these techniques produce models that lack explainability and are difficult to interpret [
24,
25]. The DMEL algorithm was developed to fill this gap and provides both symbolic rule-based modeling and produces probability values of the predictions [
15].
The unique aspect of DMEL is that it offers a learning structure in which rules are developed evolutionarily. The algorithm initially generates meaningful first-order rules through a probabilistic inductive method called APACS (Attribute Pattern Analysis and Classification System) [
26] and works through a filtering process in which these rules are evaluated with objective criteria such as information gain and weight of evidence [
15]. In the next stage, these first-order rules are transformed into higher-order rules by evolutionary algorithms, where chromosomes consist of genes, each of which represents a rule. Fitness values for each chromosome are computed by assessing the likelihood that its constituent rules accurately predict the attribute values of a record [
15].
DMEL overcomes the limitations of traditional Michigan and Pittsburgh genetic algorithm approaches and is based on the Pittsburgh approach, which represents the entire rule set in a chromosome; thus, it can provide more efficient solutions to multiple classification problems [
27,
28]. In addition, the double crossover- (crossover-1 and crossover-2) and hill-climbing-based mutation operators that are implemented in the algorithm both preserve structural diversity and increase solution quality [
15]. Another remarkable feature of the algorithm is that it can successfully work in datasets containing missing data; in this respect, it exhibits a superior performance in applications where missing records are common, such as telecommunications [
15].
The DMEL algorithm is particularly effective in problems such as churn prediction, where not only the classification but also the ranking of each individual according to probabilistic risk is critical. In experimental studies on a subscriber dataset of 100,000 records from a real telecommunications operator, it has been shown that DMEL produces more accurate predictions than both decision tree-based C4.5 and neural network models and can predict customer churn with higher accuracy [
15]. In addition, evaluations made with lift curves show that DMEL can predict the maximum number of churns with limited resources (e.g., only 5% customer segment), and thus it offers high added value for call center strategies [
15].
DMEL Algorithm’s Genetic Structure and Coding
The DMEL algorithm creates the rules by increasing them incrementally:
First generation: First-degree (single conditional) rules are generated by the probabilistic induction (APACS) technique.
Subsequent generations: More complex rules are created by combining previously discovered lower-order rules.
Each chromosome contains more than one rule (genes). The rule structure is as follows:
DMEL Evolutionary Process
Selection: Roulette wheel.
Crossover: Two-point crossover that respects rule boundaries.
Mutation: Bit-level mutation.
Recoding: In each generation, irrelevant or low relevance rules are eliminated.
Algorithm Features
Dynamic rule structure and multi-expression learning.
Hierarchical rule organization.
Genetic programming-like approach.
Separate rule sets for each class.
Compact and interpretable rule sets.
DMEL Algorithm Pseudocode
Initialize chromosomes with first-order rules (alleles).
Expand element pool with higher-order candidate rules.
Repeat until convergence:
Evaluate chromosome fitness via likelihood-based scoring.
Apply crossover:
- -
Crossover-1: swap rules across boundaries.
- -
Crossover-2: intra-rule mixing of components.
Apply mutation via hill-climbing replacement:
- -
Temporarily substitute allele with candidate pool element.
- -
Retain the best performing element.
Update ranking of rules using lift and weight of evidence.
Return the final rule set for classification.
The DMEL algorithm encodes entire rule sets within a single chromosome. Each chromosome contains a collection of elements (alleles), which dynamically expand as new candidate rules are induced. A decoding procedure evaluates all alleles sequentially, with fitness defined probabilistically in terms of the likelihood of correct classification.
Two distinct crossover operators are employed: crossover-1, which exchanges rule segments across boundaries, and crossover-2, which performs intra-rule mixing. Mutation in DMEL follows a hill-climbing strategy: an allele is temporarily replaced with candidate elements from a pool, and the best replacement is retained. This controlled local improvement prevents disruptive random changes.
Conflict resolution during labeling relies on likelihood-based aggregation. Multiple matching rules vote according to their weight of evidence, with predictions based on cumulative likelihood scores.
2.2.3. OCEC Algorithm
The OCEC algorithm is an evolutionary classification model based on organizational structures. It is a new evolutionary algorithm for classification problems, inspired by the interaction processes between individuals in human societies [
16]. Instead of traditional individual-based evolutionary algorithms, it is based on the evolution of sets of instances (organizations). It employs a bottom-up search mechanism and ultimately generates meaningful and generalizable classification rules upon completion of the evolutionary process. OCEC is characterized by its scalability and low computational cost, especially for high-dimensional data. In addition, thanks to its ability to naturally handle multi-class problems, it can learn different classes simultaneously. Unlike the random rule generation seen in classical evolutionary algorithms, OCEC aims to directly derive meaningful rules from examples. The attribute importance levels are dynamically updated throughout the evolutionary process, guiding the rule generation. As this method operates on observational sample groups, it demonstrates a high capacity for generalization [
16].
The primary distinction of OCEC lies in its operation on groups of samples, referred to as ‘organizations’, rather than on individual instances. Each organization consists of samples with the same class label and is evolutionarily optimized by three specific evolutionary operations (migration, exchange and merge) [
16]. The fitness of organizations is evaluated according to two criteria: the number of samples contained within each organization and the quantity of relevant attributes. Useful attributes are those attributes for which individuals belonging to the same class have common values and are meaningful for rule extraction. In this process, the concept of attribute significance is defined and updated in each generation and used as a guide in evolutionary operations [
16].
The process of rule extraction is performed by constructing IF–THEN rule structures from useful attributes of organizations. These rules are then listed by relative support metrics and the redundant ones are eliminated. Thus, both meaningful and fewer rules are obtained [
16].
OCEC’s ability to handle multi-class classification problems naturally is an important feature that distinguishes it from other evolutionary AI-based methods. This is achieved by handling the organizations belonging to each class as separate populations. In addition, the goal is not to create rules during the evolutionary process of organizations, but only to optimize sample sets; rules are extracted only at the final stage. This approach produces more consistent and highly accurate rules compared with classical methods [
16].
The performance of OCEC is tested on the UCI dataset and multiplexer problems. The results demonstrate that OCEC attains a superior classification accuracy and reduced computational cost compared with established algorithms in the literature, including G-Net [
29] and JoinGA [
30]. Notably, for the 20-bit and 37-bit multiplexer problems, OCEC achieved nearly 100% accuracy by the conclusion of the evolutionary process, simultaneously generating a minimal number of rules with maximal generality [
16]. Additionally, within the context of radar target recognition, a key real-world application, in terms of accuracy, OCEC has outperformed well-established techniques, including artificial neural networks (ANNs) and support vector machines (SVMs) [
31].
OCEC Algorithm’s Sub-Based Search Strategy
OCEC follows a different way to generate rules from examples:
Examples are first divided into organizations (clusters) based on similar attribute values.
Organizations are clusters of examples belonging to similar classes.
Each organization follows an evolutionary process and eventually rules are derived from it.
Population and Evolutionary Operators
Population units are “organizations”; therefore, evolutionary operations are performed on a sample-by-sample basis rather than on a traditional individual basis.
Three specific evolutionary operators are used:
Merge: Brings similar organizations together.
Split: If the fit is low, the organization is split into two.
Cross-organization exchange: Genes are exchanged between similar organizations.
OCEC Algorithm’s Fitness Function
The fitness of organizations is based on two main criteria:
Number of members: Organizations with more examples are stronger.
Number of useful attributes: It ensures that the rules are meaningful. However, excessive detail can reduce generalization ability, so a balance is achieved.
Attribute significance levels are learned evolutionarily by the algorithm and used in the creation of rules.
Algorithm Features
Organization-based rule structure.
Rules that allow overlaps between classes.
Conditions with different operators (<, >, ≤, ≥, between).
Adaptive fitness evaluation.
Hierarchical evolutionary strategy.
OCEC Algorithm Pseudocode
Initialize organizations by grouping similar class instances.
Repeat until termination:
Select two parent organizations.
Apply one operator:
- -
Merge: combine organizations.
- -
Split: partition an organization.
- -
Exchange: swap members between organizations.
Update attribute significance.
Evaluate fitness of new organizations.
Select fittest organizations for next generation.
Extract rules from organizations using relative support (RS).
Rank and prune redundant rules.
Classify instances using match value (MV) with RS tie-breaking.
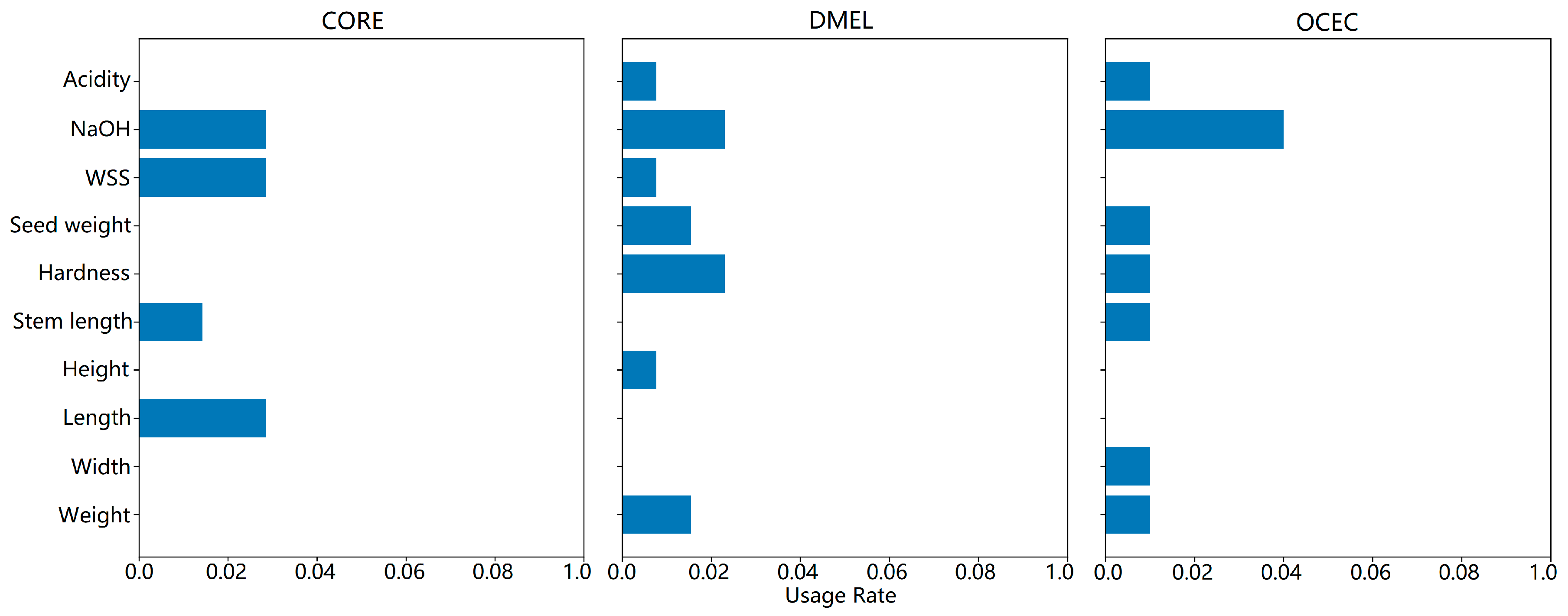
Table 1 shows the comparison of the CORE, DMEL and OCEC classification algorithms according to various criteria.
2.3. Dataset
In this study, a dataset containing pomological data on cherry variety is used. The dataset contains various attribute values of cherry variety and is used for classification purposes.
Table 2 shows the characteristics of the dataset and numbers of each feature used by the algorithms to find classification rules.
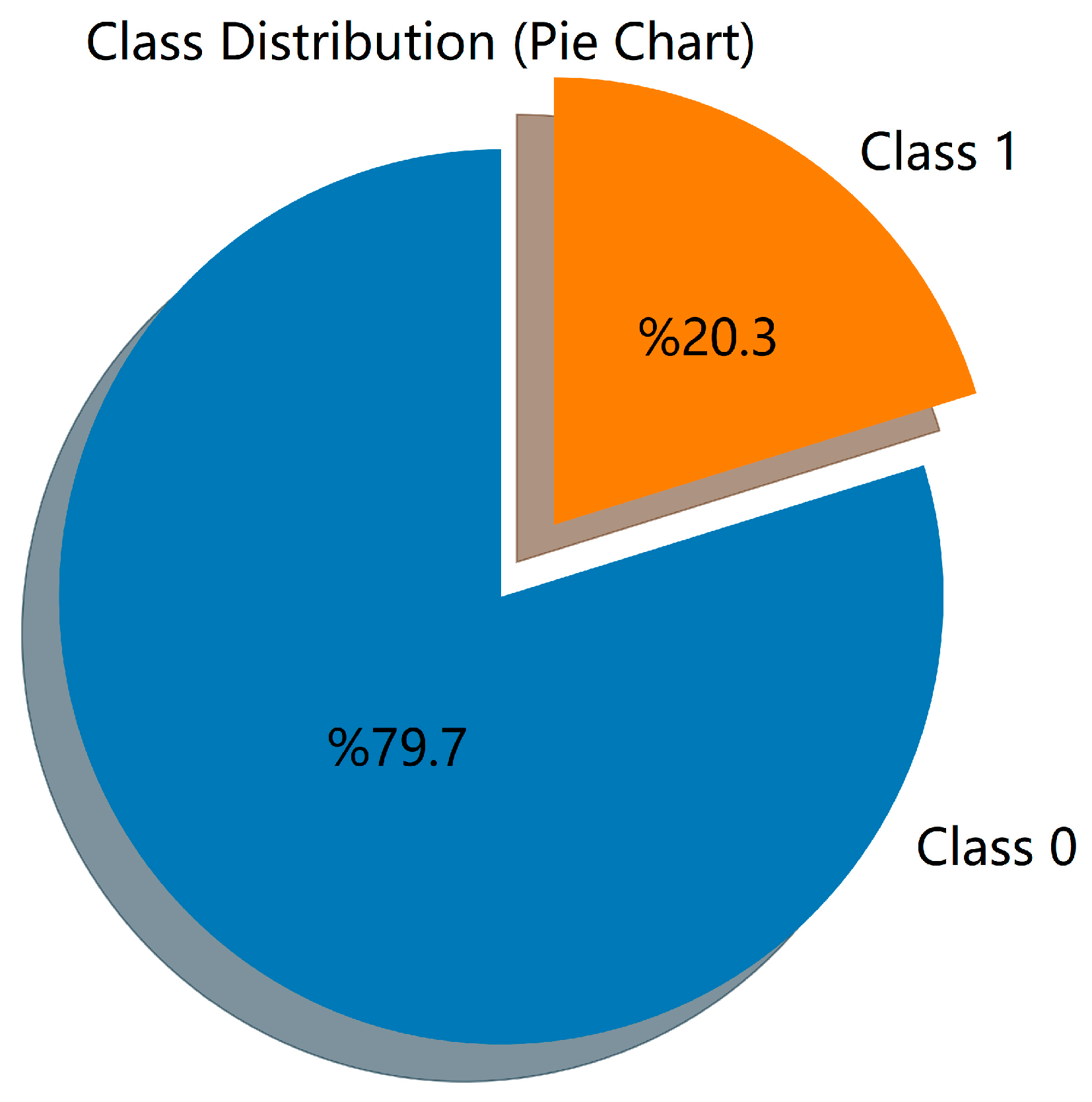
The distribution of examples belonging to class 0 and class 1 in the dataset used is presented in
Figure 4 in the form of a pie chart. As can be seen from
Figure 4, approximately 80% of the total dataset consists of class 0 data and approximately 20% consists of class 1 data.
2.4. Methodological Steps Used by the Algorithms
The following methodological steps are followed in this study:
Data preprocessing and cleaning.
Dividing the dataset into training (80%) and testing (20%) sets.
Training evolutionary computation-based classification algorithms (CORE, DMEL, OCEC).
Calculating fitness values for each algorithm.
Evaluating the performance of algorithms by using the test dataset.
Calculating accuracy, recall, precision and F1-Score metrics.
Analyzing the rules generated by the algorithms.
Visually comparing the performance of the algorithms.
2.5. Algorithms’ Parameters
The following parameter values in
Table 3 are used when creating each of the three evolutionary algorithms.
Two different fitness functions have been developed for the optimization methods adapted to the classification model focused on the problem, as shown in Equations (1) and (2). In this study, coverage is defined as the proportion of instances in the dataset that are covered by a given rule, i.e., the ratio of the number of instances satisfying the antecedent of the rule to the total number of instances in the dataset. This measure reflects the generality of a rule.
Rule complexity is quantified by the number of conditions that are the antecedent of the rule. A rule with one condition is a first-order rule, while a rule with k conditions is a k-th (“k” denotes the total number of rules that are utilized by the classification model for decision-making) order rule. To avoid excessive specialization, a penalty term is included in the fitness function.
The term max_condition_number denotes the maximum allowable number of conditions in a rule, predefined as a parameter of the algorithm. Normalizing rule complexity by this value ensures comparability across rules of different lengths and datasets.
4. Conclusions and Discussion
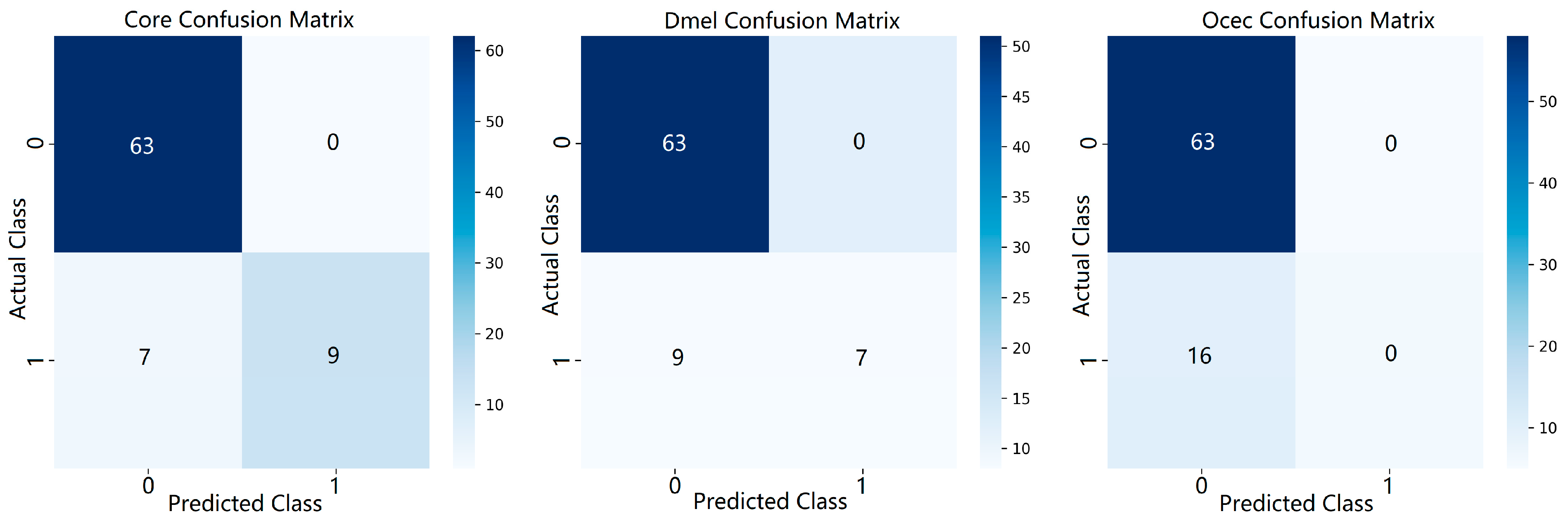
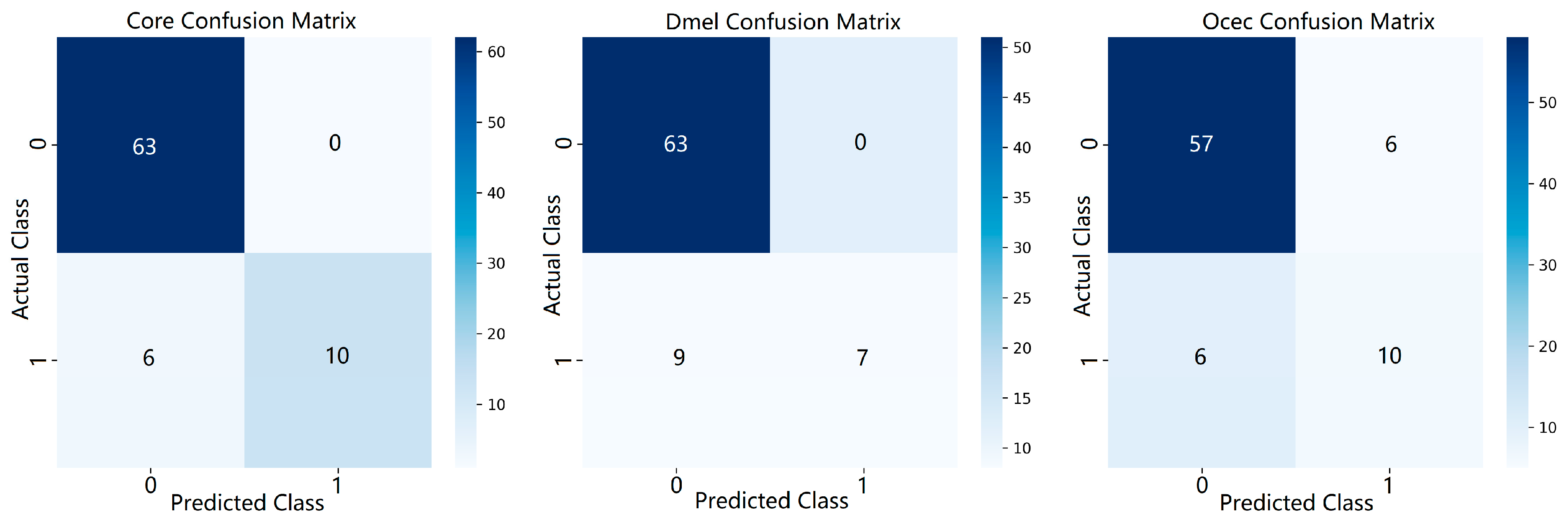
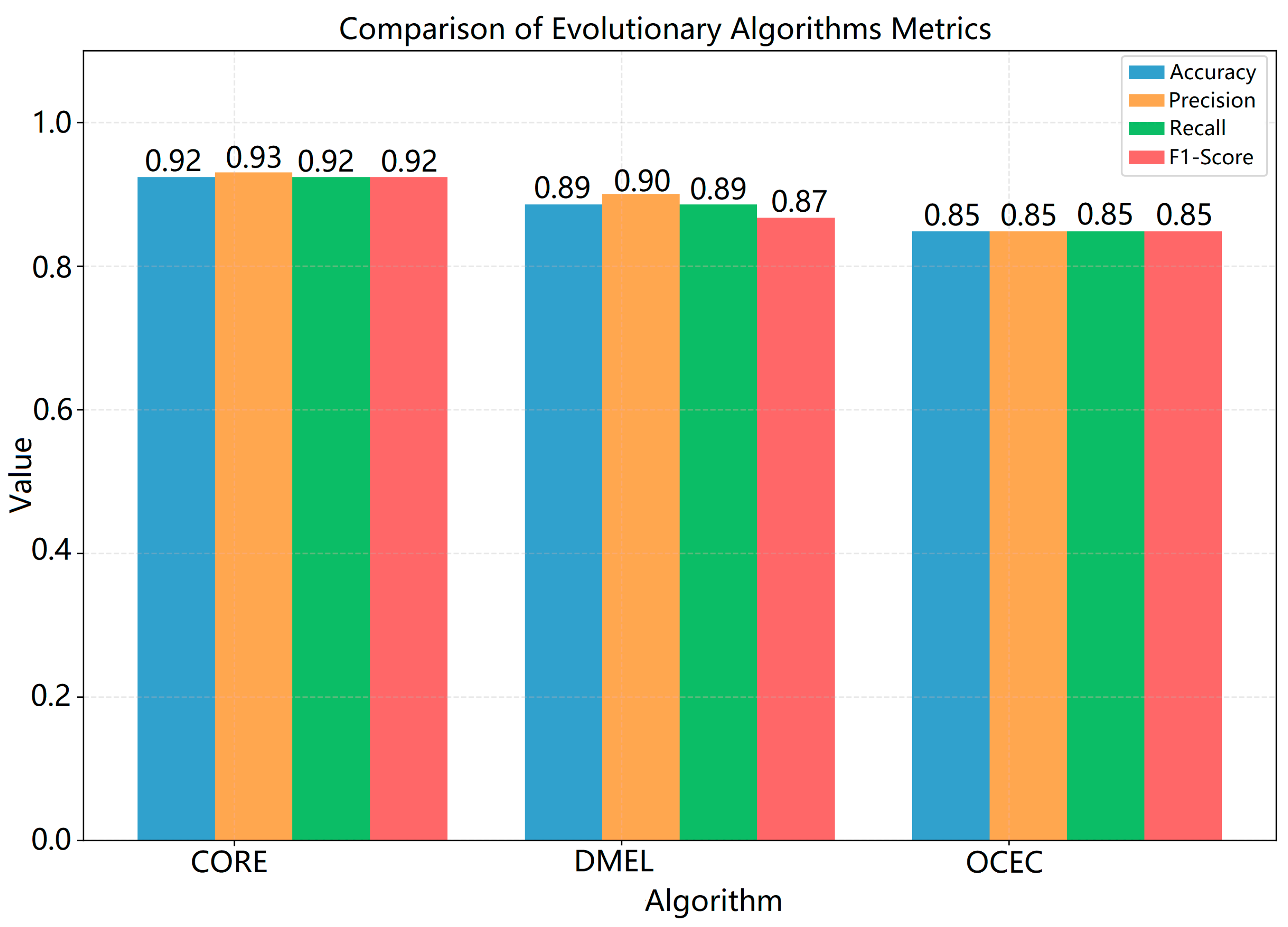
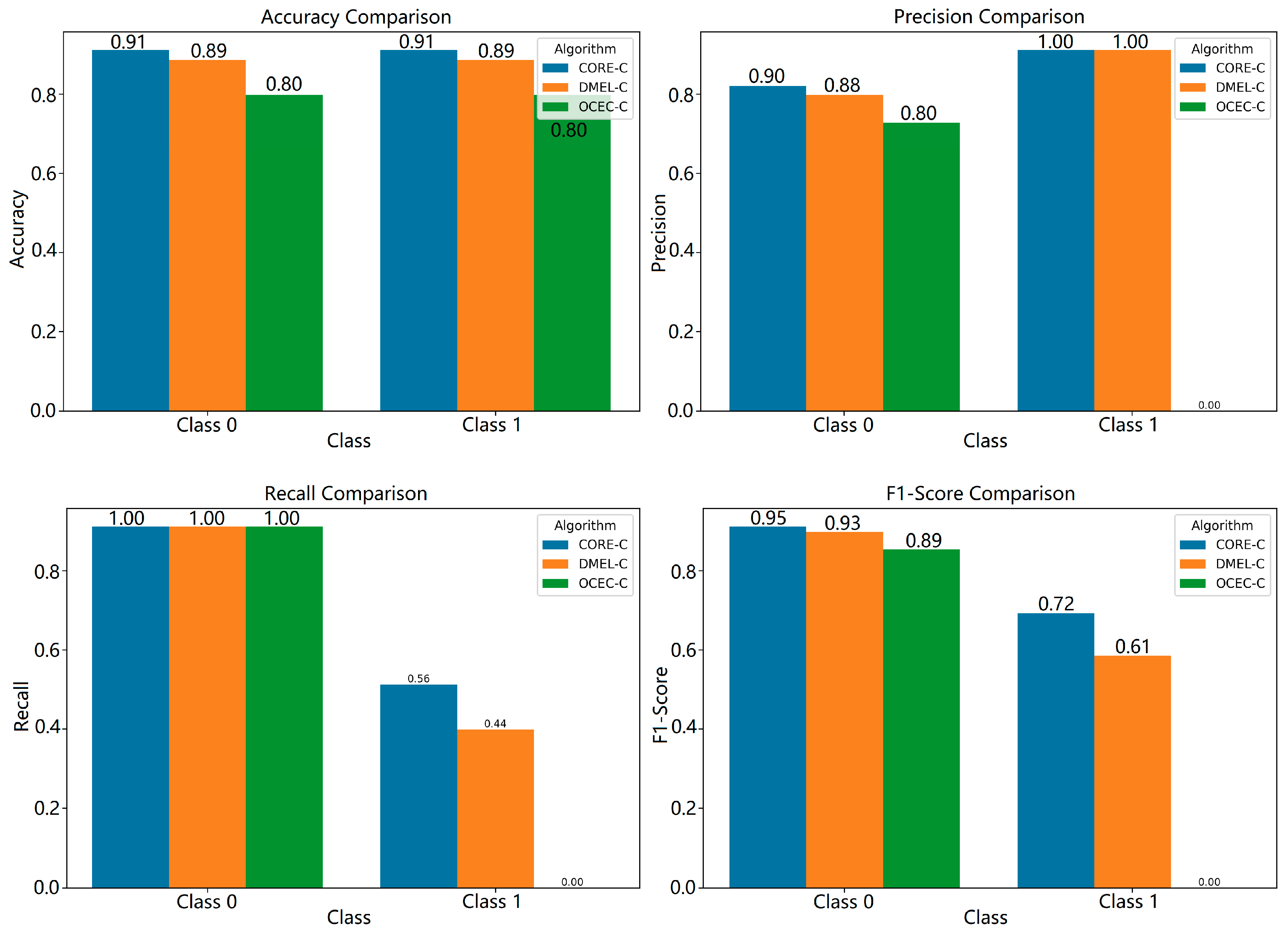
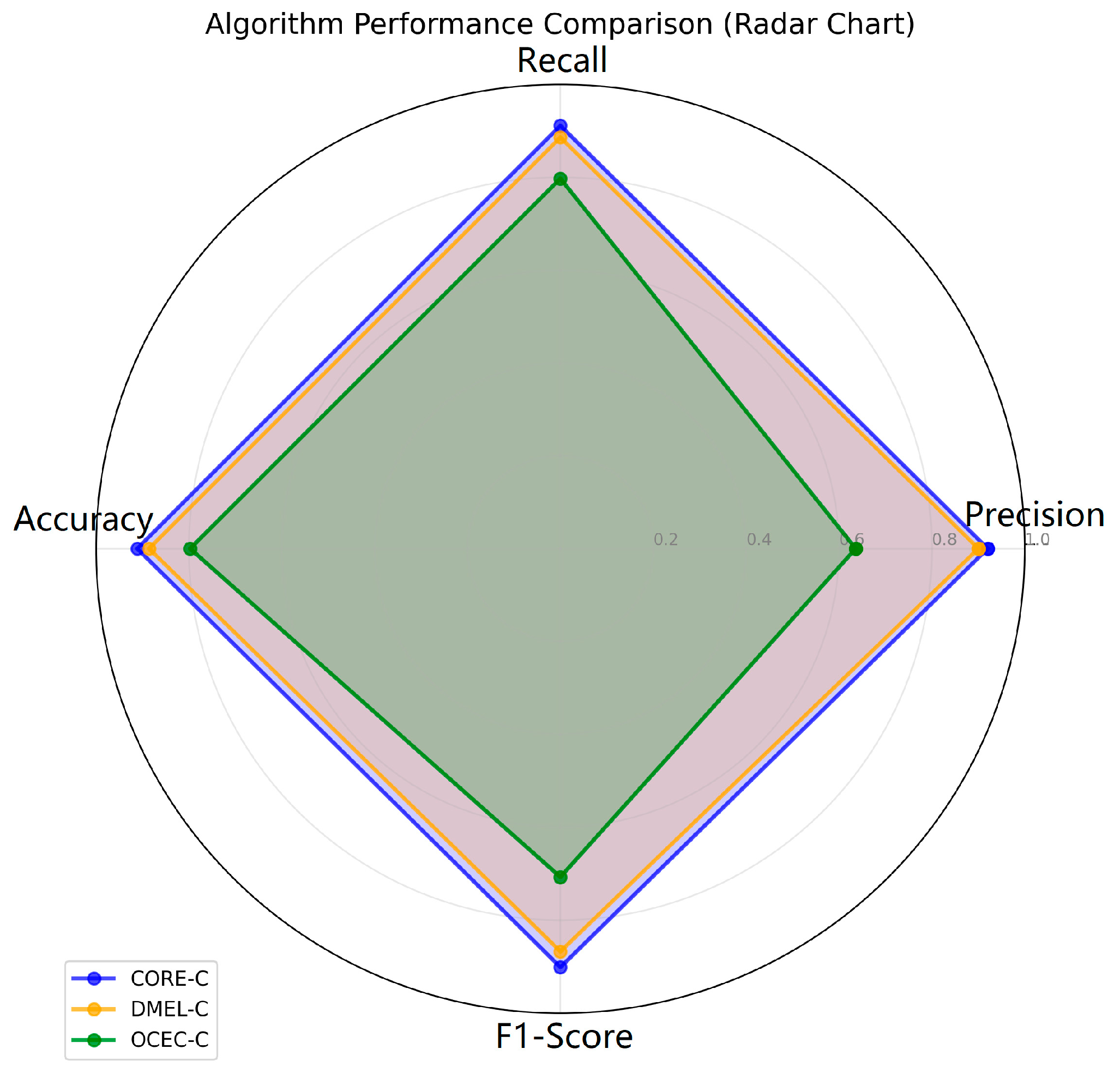
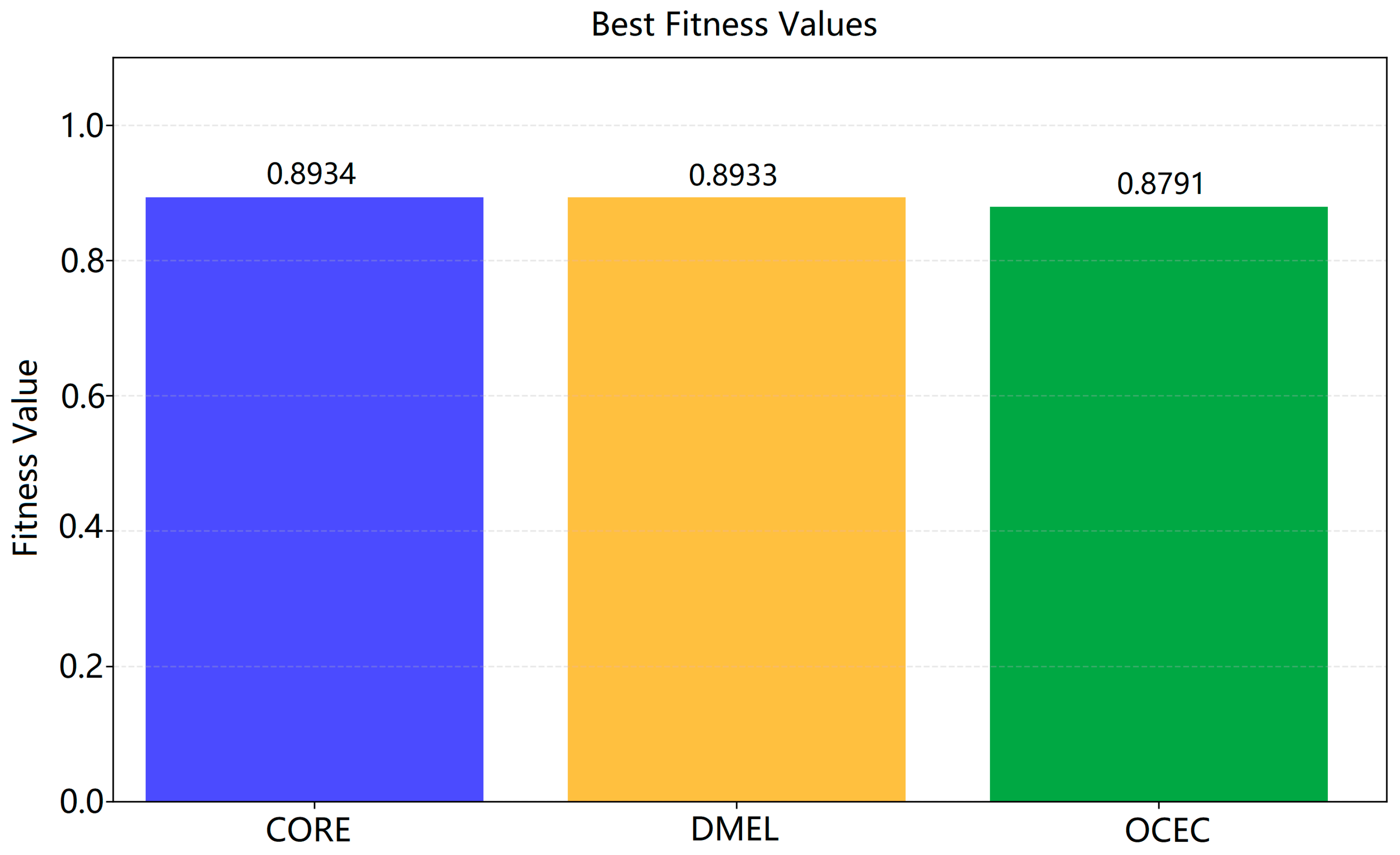
In this study, three different evolutionary classification algorithms (CORE, DMEL and OCEC) were evaluated for various classification problems regarding original pomological data under equal conditions. The datasets used consist of originally collected pomological datasets. In this study 80% of the dataset was selected as training data and 20% as test data. Since the number of pest occurrences is higher during the second pomological period, the dataset was divided into two classes for the second pomological period and the others. The comparison of the algorithms is based on metrics such as accuracy, sensitivity, precision and F1-Score. The results show that the CORE algorithm performs the best with a precision value of 0.9203.
When the rules produced by the evolutionary algorithms are analyzed, it is seen that these rules use the value ranges of the attributes effectively and present the classification decisions in an explainable way. In this study, the predictive task addressed by all three evolutionary algorithms (CORE, DMEL and OCEC) is the classification of cherries into their phenological ripening classes. That is, given a set of attribute values describing the cherries (e.g., weight, length, fruit height, stem length, fruit hardness, fruit seed weight or other relevant phenological indicators), the algorithms generate IF–THEN rules that map these input features to discrete phenological ripening stages. While CORE produces comprehensible rule sets by coevolving rules and rule sets concurrently, DMEL extends the process by providing, in addition to the class label, an estimate of the likelihood associated with each classification. OCEC, on the other hand, adopts a bottom-up organizational coevolutionary strategy, extracting rules from groups of similar examples to enhance robustness and avoid meaningless rules. In all three cases, the ultimate prediction is the phenological class of cherries during the ripening phase, thereby enabling the explainable and accurate classification of the ripening process.
The creation of classification rules for all three algorithms constitutes the strength of these algorithms in terms of explainability. In particular, the interpretability of the rules created by the algorithms provides a great advantage over classical black-box algorithms. As the rules created by the algorithms are in IF–THEN format, they provide a structure that experts can easily understand and evaluate. When the general classification performance of the algorithms is analyzed, it is seen that they generally perform classification with a high level of accuracy. Since the artificial intelligence algorithms used in this study make classifications based on rule extraction, it also adds value to the study in terms of interpretability.
These results show that different evolutionary strategies offer various advantages in data mining and that method selection is important according to the application context. In future studies, the parameter adjustments of the algorithms can be examined in more detail and can be tested on larger datasets. In addition, different fitness functions and operators can be tried to improve the quality of the rules.
For the management of pest populations, the findings of a previous study indicate that the second phenological fruit coloration period is the stage during which the cherry fly (
Rhagoletis cerasi L.) reaches its highest reproductive population levels [
11]. Compared with the other coloration periods (1, 3, 4 and 5), this second period demonstrates distinct fruit trait criteria, as identified through rule associations within three different classification algorithms. These findings can be integrated into farmer decision support systems as a predictive and early warning tool based on fruit coloration. Among the three classification algorithms, the simplest inference can be made using the CORE algorithm, while both the DIMEL and OCEC algorithms also provide rule-based predictions specifically related to the second fruit coloration period.
For instance, if the NaOH value of the fruit is equal to or greater than 9.45, the fruit likely belongs to coloration periods 1, 3, 4 or 5. This type of analysis is not costly and can be easily performed in local laboratories or monitored in real time through in-field sensors, enabling the identification of whether a fruit belongs to the second phenological period. Furthermore, when pomological characteristics specific to the second period are considered, fruits with a berry weight less than 5.47 g and a firmness value between 1.94 and 3.71 kgf/cm2 (×105 Pa) can be associated with the peak egg-laying activity of the cherry fly. Among these, berry weight offers the most practical measurement method for farmers.
These evaluation metrics are specifically applicable to the 0900 Ziraat cherry variety, which holds significant importance in export markets, but can also be adapted for use in other cherry cultivars on an international scale.