On Improving the Performance of Kalman Filter in Denoising Oil Palm Hyperspectral Data
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
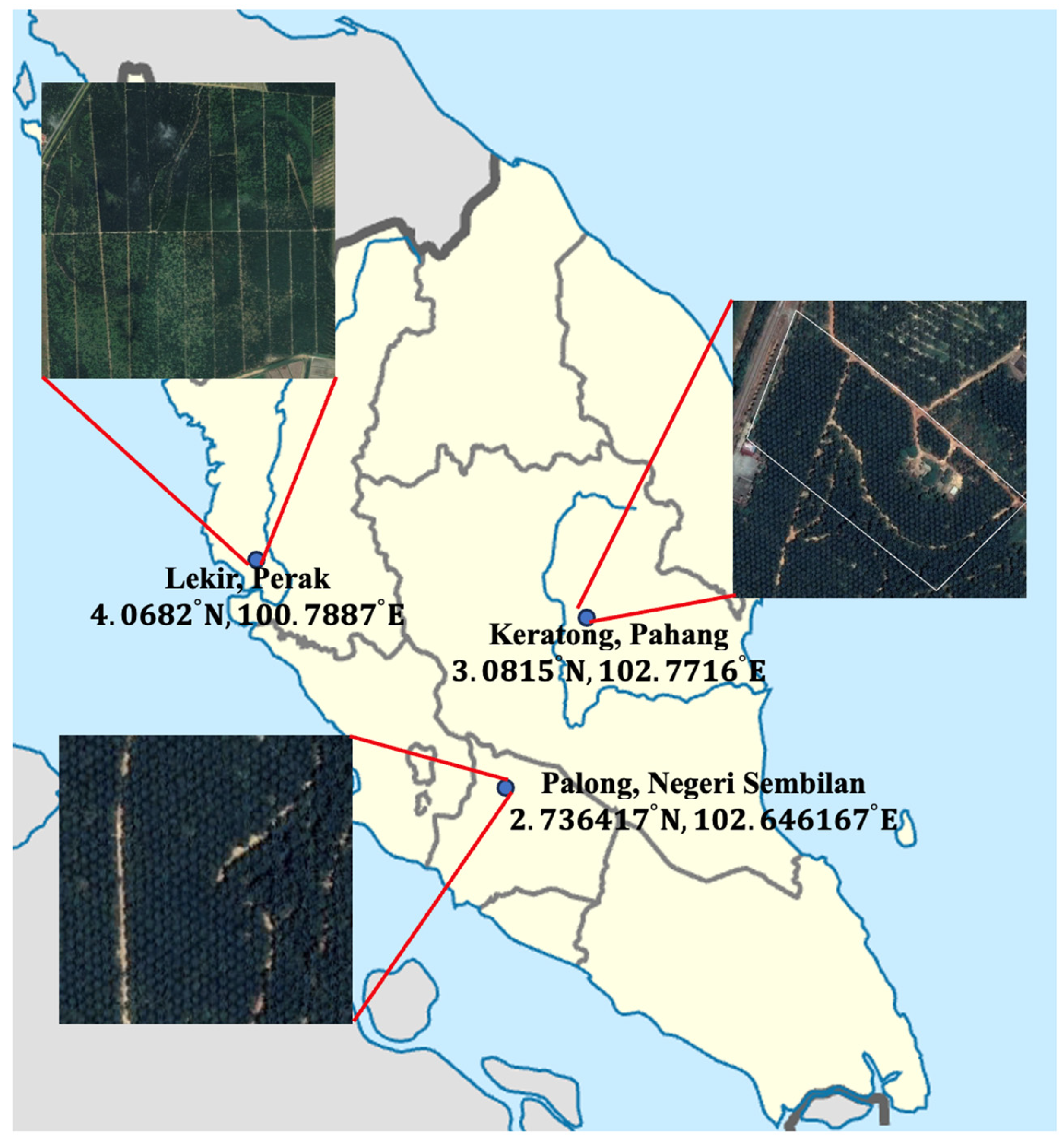
3.1. Database
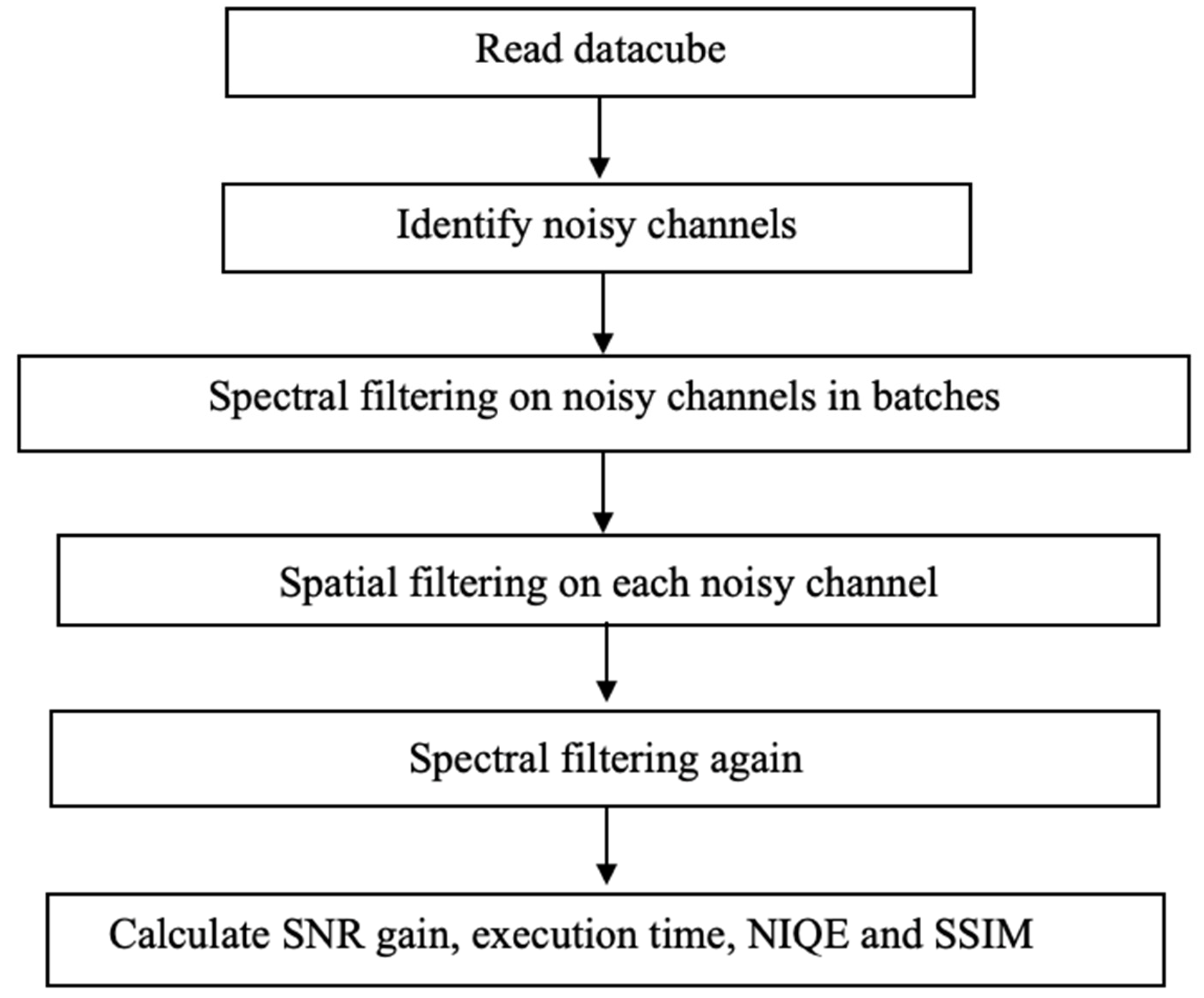
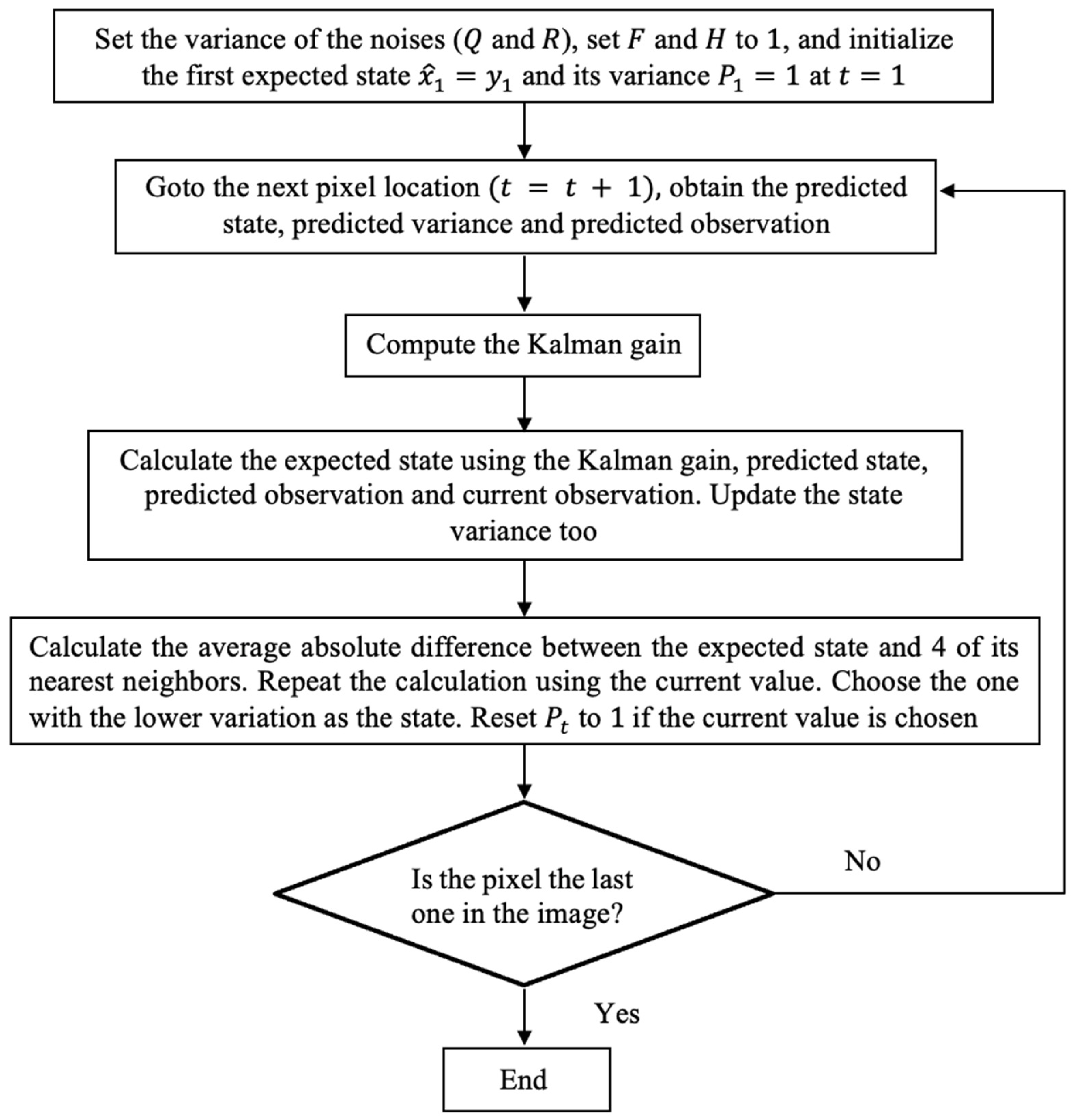
3.2. Approach
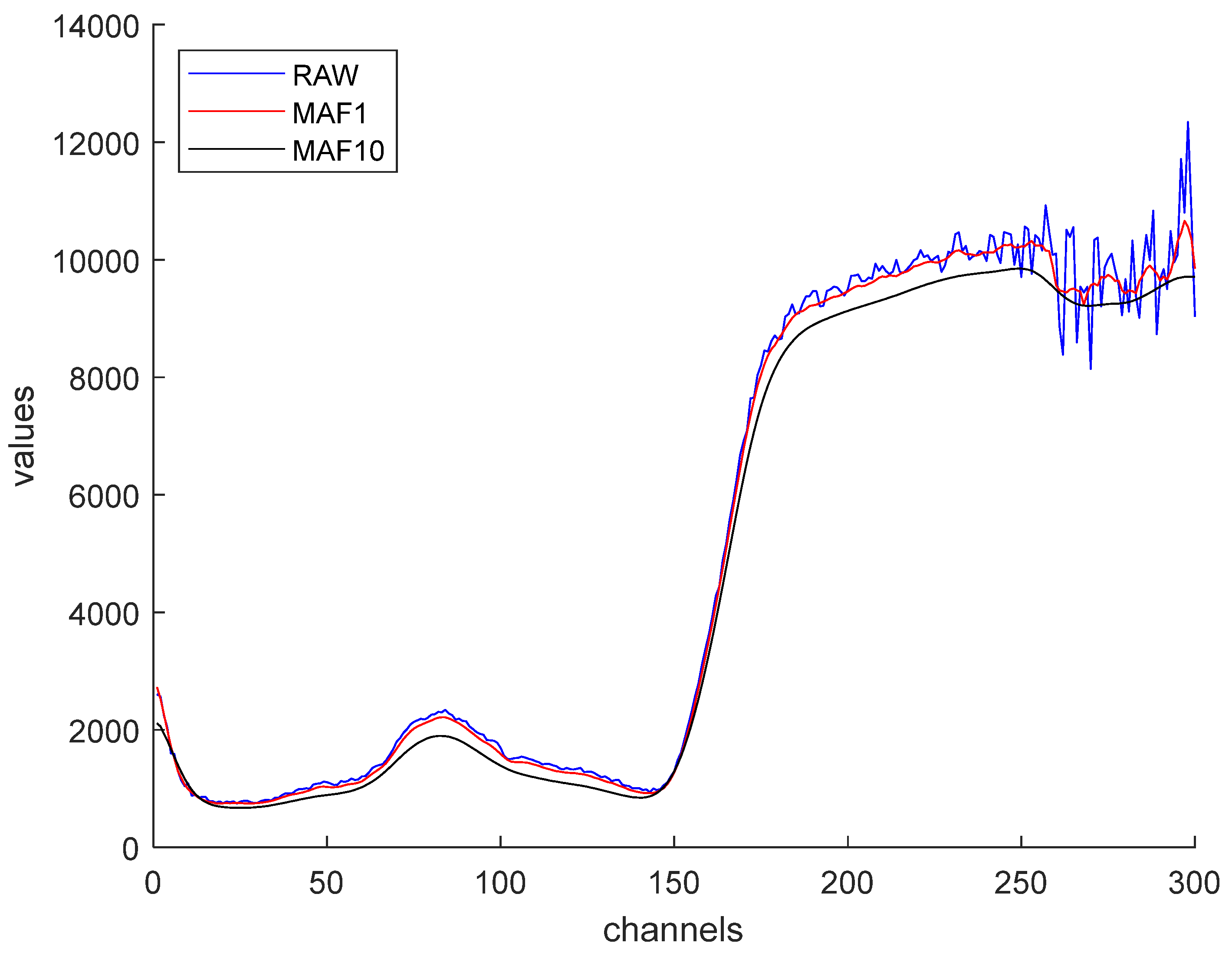
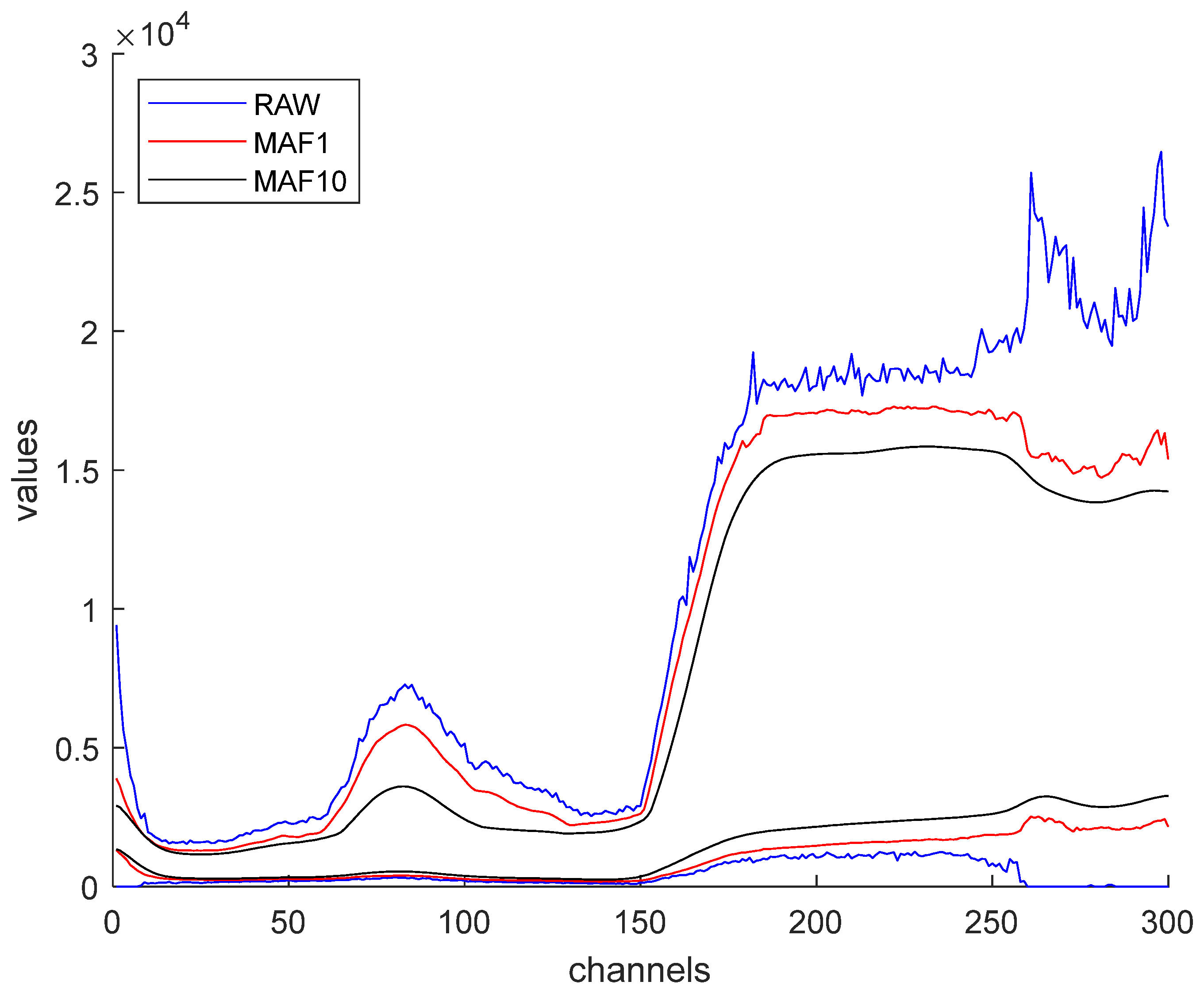
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| KF | Kalman Filter |
| EKF | Extended Kalman Filter |
| KS | Kalman Smoother |
| EKS | Extended Kalman Smoother |
| MAF | Moving Average Filter |
| SNR | Signal-to-Noise Ratio |
| NIQE | Naturalness Image Quality Evaluator |
| SSIM | Structural Similarity Index Measure |
| UAV | Unmanned Aerial Vehicle |
| PCA | Principal Component Analysis |
| BM4D | Block Matching 4-Dimensions |
| LRMR | Low-rank Matrix Recovery |
| HSI | Hue, Saturation and Intensity |
| CNN | Convolution Neural Network |
| NN | Neural Network |
| FT | Fourier Transform |
| LiDAR | Light Detection and Ranging |
| LFF | Local Fitness Function |
| KFWB | Kalman Filter with Break |
References
- Izzuddin, M.A.; Seman Idris, A.; Nisfariza, M.N.; Nordiana, A.A.; Shafri, H.Z.M.; Ezzati, B. The development of spectral indices for early detection of Ganoderma disease in oil palm seedlings. Int. J. Remote Sens. 2017, 38, 6505–6527. [Google Scholar] [CrossRef]
- Chang, C.I. Hyperspectral Data Processing: Algorithm, Design and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2013; p. 196. [Google Scholar]
- Atkinson, I.; Kamalabadi, F.; Jones, D.L. Wavelet-based hyperspectral image estimation. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; Volume 2, pp. 743–745. [Google Scholar] [CrossRef]
- Zelinski, A.; Goyal, V. Denoising hyperspectral imagery and recovering junk bands using wavelets and sparse approximation. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 387–390. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2010, 49, 973–980. [Google Scholar] [CrossRef]
- Chen, G.; Bui, T.D.; Quach, K.G.; Qian, S.E. Denoising hyperspectral imagery using principal component analysis and block-matching 4D filtering. Can. J. Remote Sens. 2014, 40, 60–66. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4729–4743. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Chen, B.; Zhong, S.; Tian, Y. Hyperspectral image restoration: Where does the low-rank property exist. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6869–6884. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5174–5189. [Google Scholar] [CrossRef]
- Maffei, A.; Haut, J.M.; Paoletti, M.E.; Plaza, J.; Bruzzone, L.; Plaza, A. A single model CNN for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2516–2529. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 667–682. [Google Scholar] [CrossRef]
- Pan, E.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. SQAD: Spatial-spectral quasi-attention recurrent network for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5524814. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, X.; Liu, D.; Xu, F.; Wang, Y.; Lin, L.; Yuan, Q. A hyperspectral image denoising method based on land cover spectral autocorrelation. Int. J. Appl. Earth Obs. Geoinf. 2023, 123, 103481. [Google Scholar] [CrossRef]
- Karami, A.; Heylen, R.; Scheunders, P. Denoising of hyperspectral images using shearlet transform and fully constrained least squares unmixing. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, J.; He, W.; Shen, H.; Zhang, L. Double low-rank matrix decomposition for hyperspectral image denoising and destriping. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5502619. [Google Scholar] [CrossRef]
- Torun, O.; Yuksel, S.E.; Erdem, E.; Imamoglu, N.; Erdem, A. Hyperspectral image denoising via self-modulating convolutional neural networks. Signal Process. 2024, 214, 109248. [Google Scholar] [CrossRef]
- Ertürk, A. Sparse unmixing based denoising for hyperspectral images. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7006–7009. [Google Scholar] [CrossRef]
- Ibrahim, I.; AlRowaily, M.H.; Arof, H.; Abu Talip, M.S. Performance Comparison of Selected Filters in Fast Denoising of Oil Palm Hyperspectral Data. Appl. Sci. 2024, 14, 2076–3417. [Google Scholar] [CrossRef]
- Bai, J.; Niu, Z.; Wang, L. A theoretical demonstration on the independence of distance and incidence angle effects for small-footprint hyperspectral LiDAR: Basic physical concepts. Remote Sens. Environ. 2024, 315, 114452. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006; p. 270. ISBN 9780470045343. [Google Scholar]






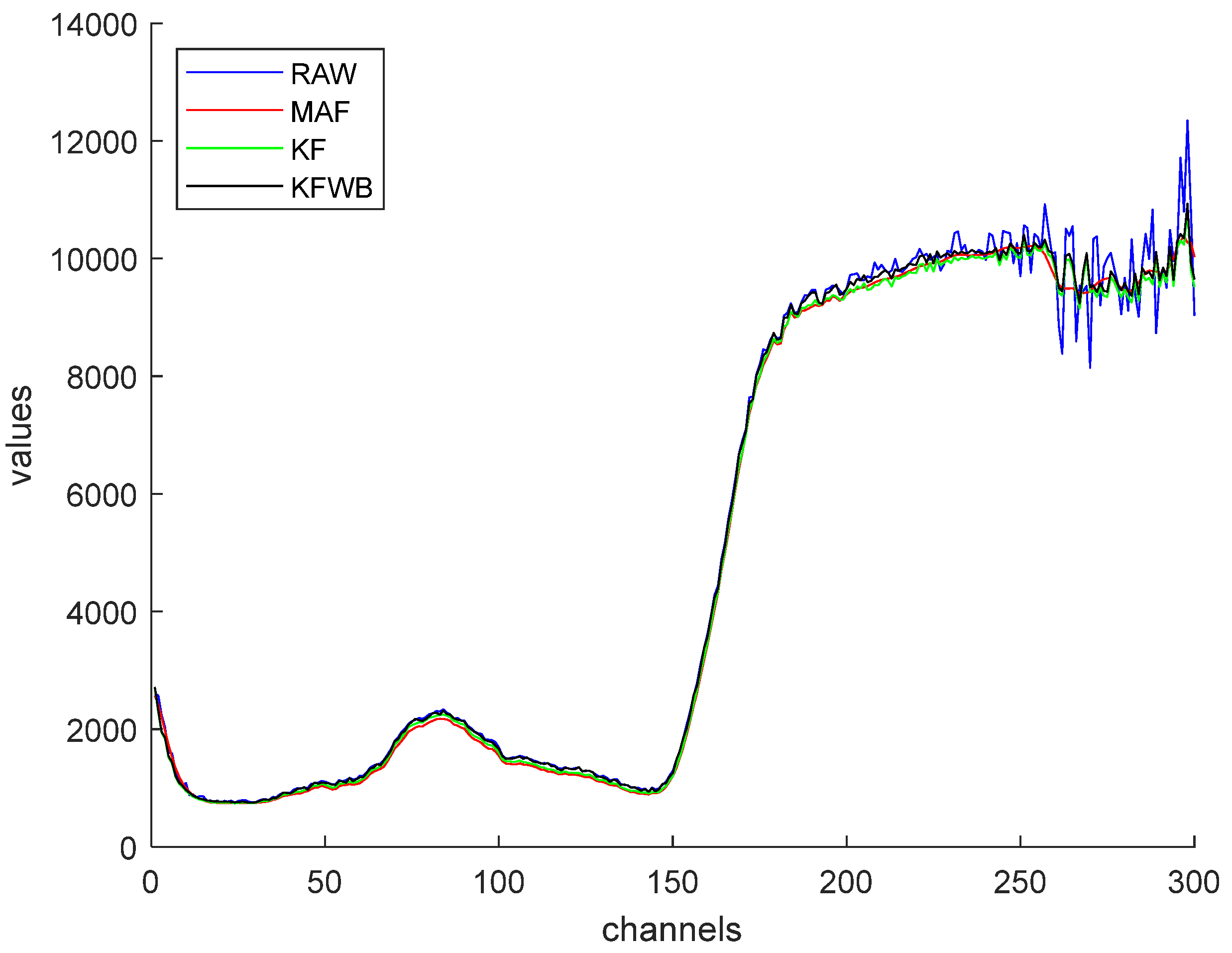
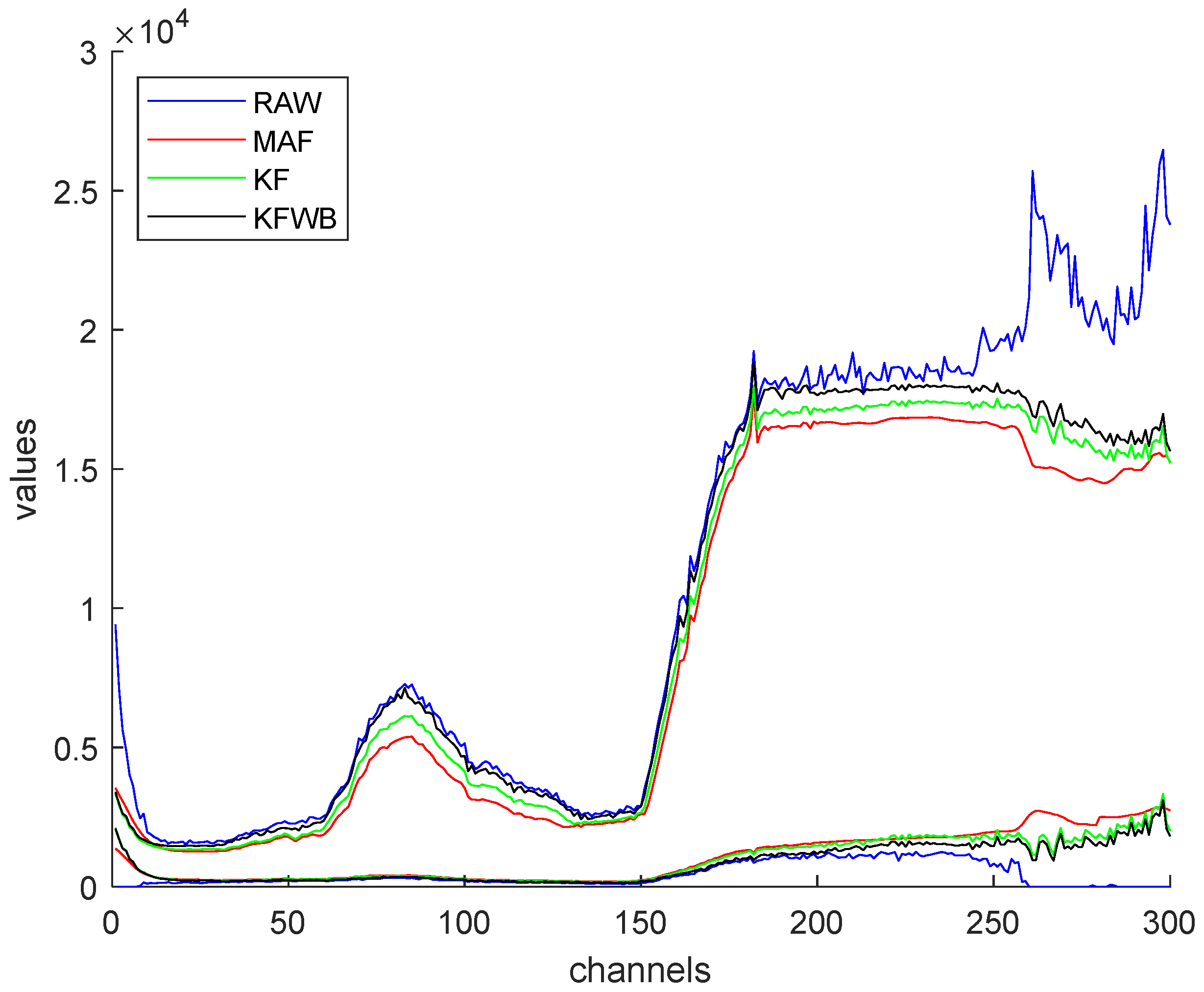
| Filter | KF | EKF | KS | EKS | MAF |
|---|---|---|---|---|---|
| SNR Gain | 18.1 dB | 18.1 dB | 18.1 dB | 18.1 dB | 16 dB |
| Execution Time | 0.19 s | 0.2 s | 0.2 s | 0.21 s | 0.19 s |
| NIQE | 10.5 | 10.5 | 10.5 | 10.5 | 8.5 |
| SSIM | 0.42 | 0.42 | 0.42 | 0.41 | 0.24 |
| Filter | KF | EKF | KS | EKS | MAF |
|---|---|---|---|---|---|
| SNR Gain | 7.3 dB | 7.3 dB | 7.4 dB | 7.4 dB | 6.0 dB |
| Execution Time | 0.18 s | 0.19 s | 0.2 s | 0.21 s | 0.18 s |
| NIQE | 9.5 | 9.5 | 9.45 | 9.45 | 9.0 |
| SSIM | 0.27 | 0.27 | 0.26 | 0.26 | 0.14 |
| Channels | First Four Group | Last Four Group | ||||
|---|---|---|---|---|---|---|
| Filter | MAF | KF | KFWB | MAF | KF | KFWB |
| SNR Gain | 16 dB | 18 dB | 18 dB | 6 dB | 7.4 dB | 7.5 dB |
| Ex. Time | 0.2 s | 0.19 s | 0.2 s | 0.2 s | 0.18 s | 0.2 s |
| NIQE | 8.5 | 10.5 | 10.5 | 9.1 | 9.5 | 9.6 |
| SSIM | 0.24 | 0.42 | 0.42 | 0.14 | 0.27 | 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, I.; Arof, H.; Anuar, M.I.; Abu Talip, M.S. On Improving the Performance of Kalman Filter in Denoising Oil Palm Hyperspectral Data. Agriculture 2025, 15, 2149. https://doi.org/10.3390/agriculture15202149
Ibrahim I, Arof H, Anuar MI, Abu Talip MS. On Improving the Performance of Kalman Filter in Denoising Oil Palm Hyperspectral Data. Agriculture. 2025; 15(20):2149. https://doi.org/10.3390/agriculture15202149
Chicago/Turabian StyleIbrahim, Imanurfatiehah, Hamzah Arof, Mohd Izzuddin Anuar, and Mohamad Sofian Abu Talip. 2025. "On Improving the Performance of Kalman Filter in Denoising Oil Palm Hyperspectral Data" Agriculture 15, no. 20: 2149. https://doi.org/10.3390/agriculture15202149
APA StyleIbrahim, I., Arof, H., Anuar, M. I., & Abu Talip, M. S. (2025). On Improving the Performance of Kalman Filter in Denoising Oil Palm Hyperspectral Data. Agriculture, 15(20), 2149. https://doi.org/10.3390/agriculture15202149






