Design and Experiment of Drying Equipment for Alfalfa Bales
Abstract
1. Introduction
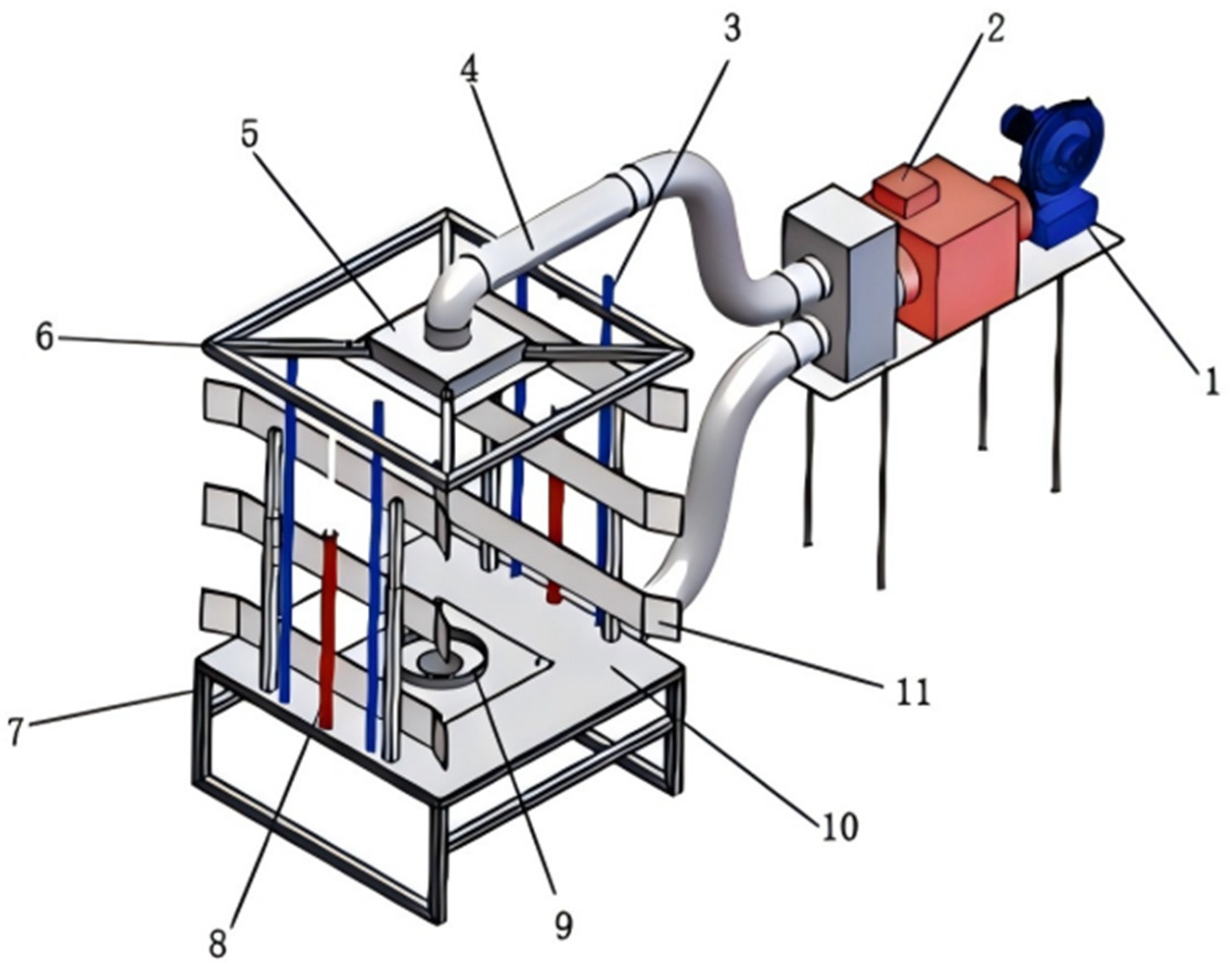
2. Overall Structure and Working Principle
2.1. Overall Structure
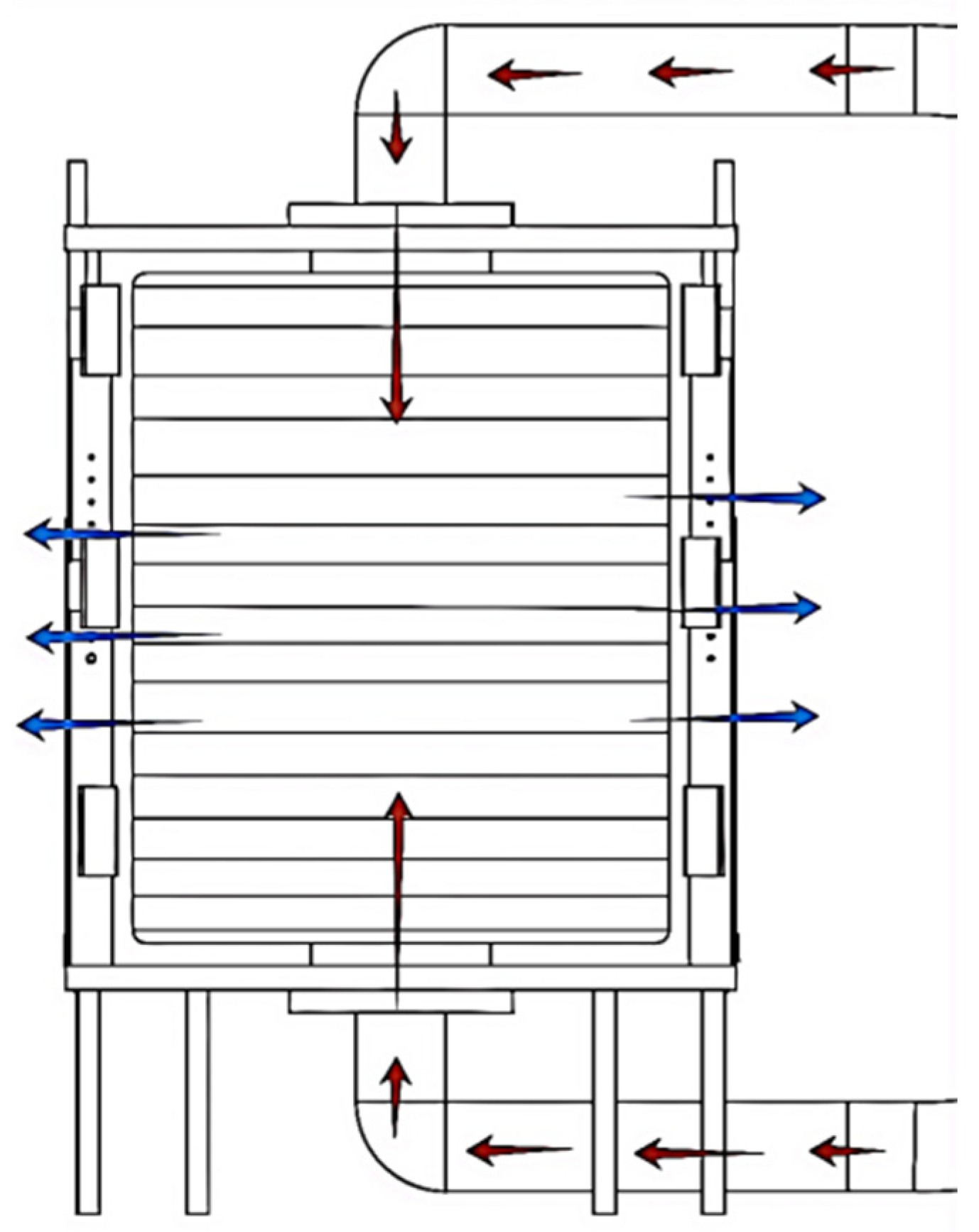
2.2. Working Principle
3. Simulation Analysis of Drying Process of Alfalfa Round Grass Bale
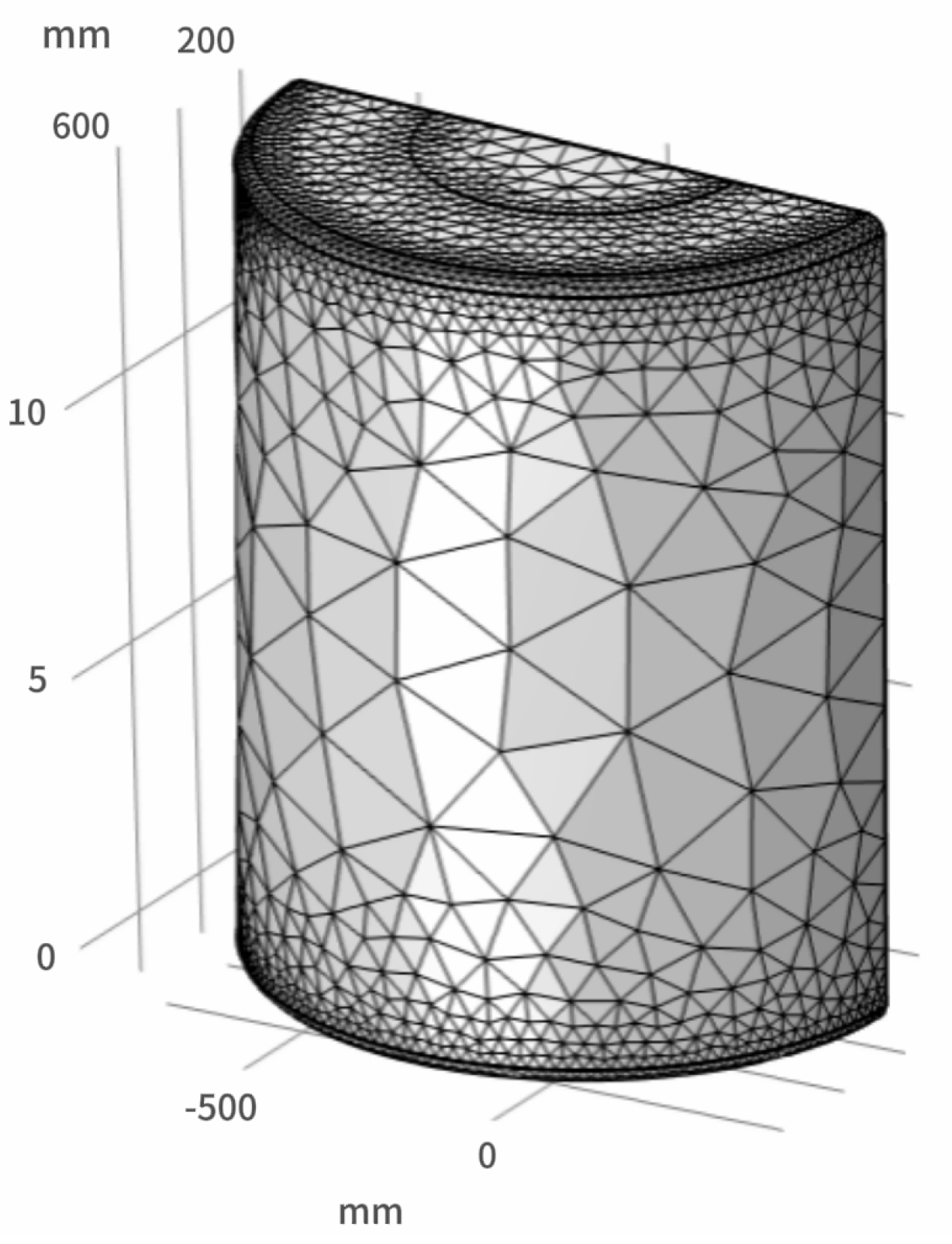
3.1. Mathematical Model Establishment and Boundary Condition Setting
3.2. Simulation Analysis
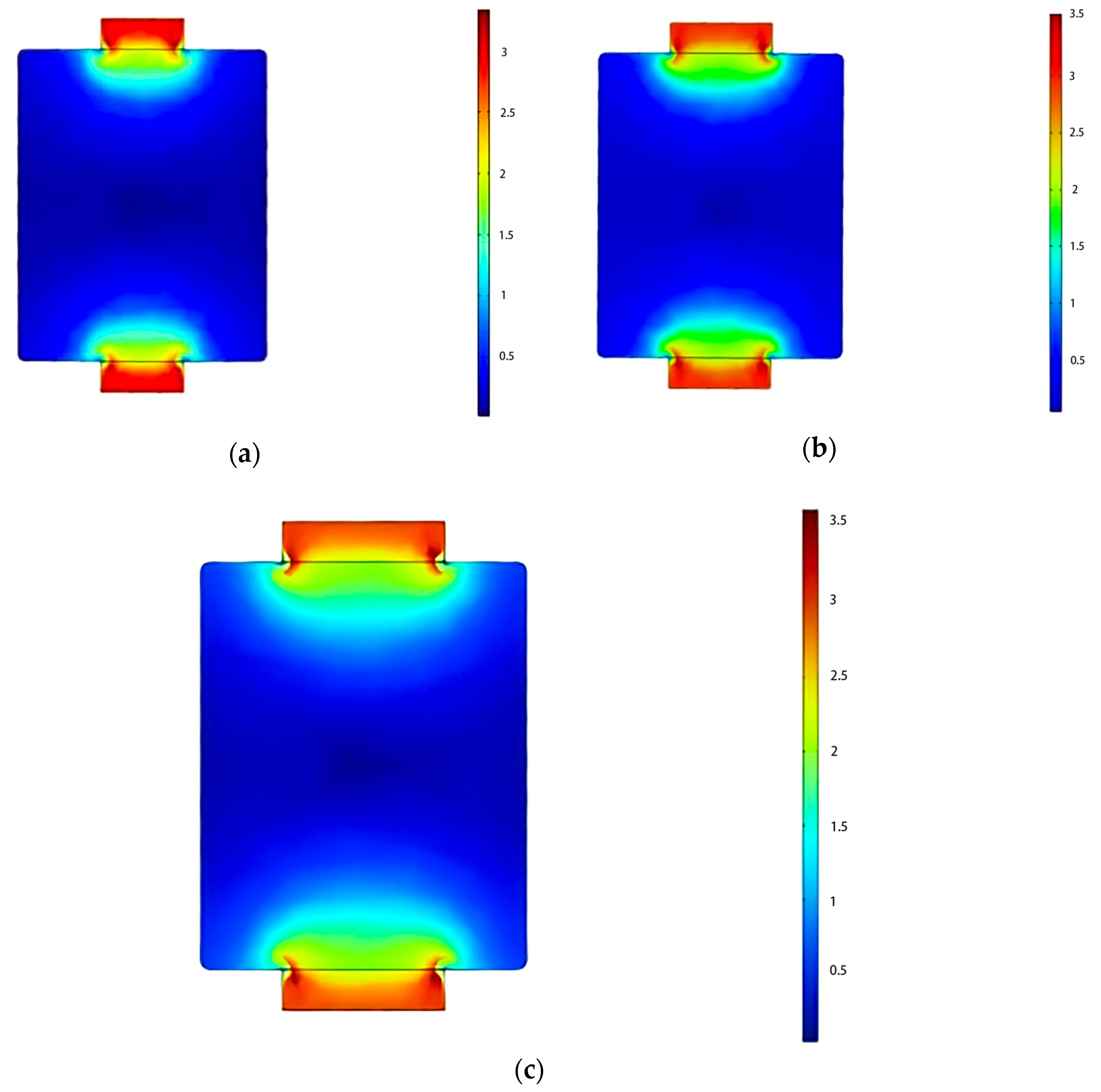
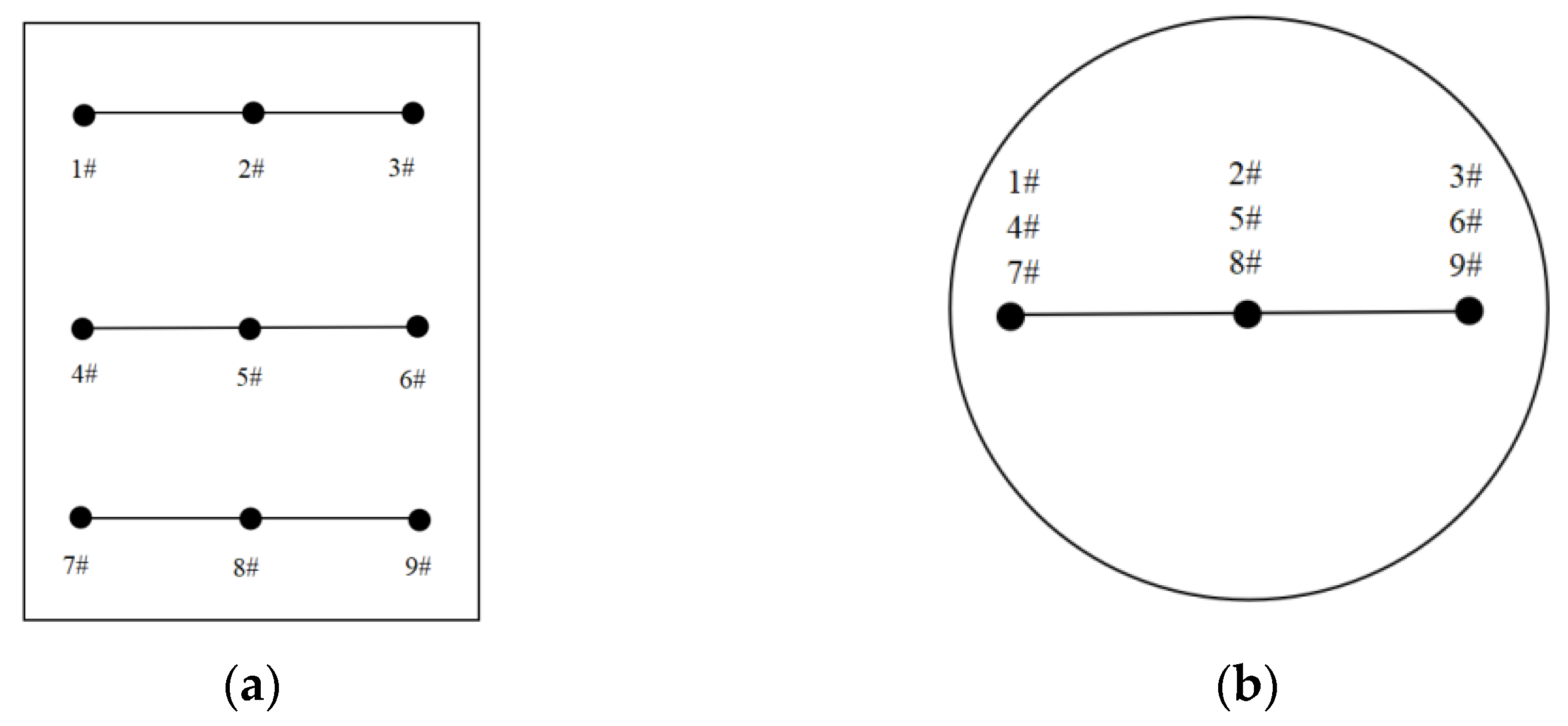
3.2.1. Wind Speed Field Simulation Analysis
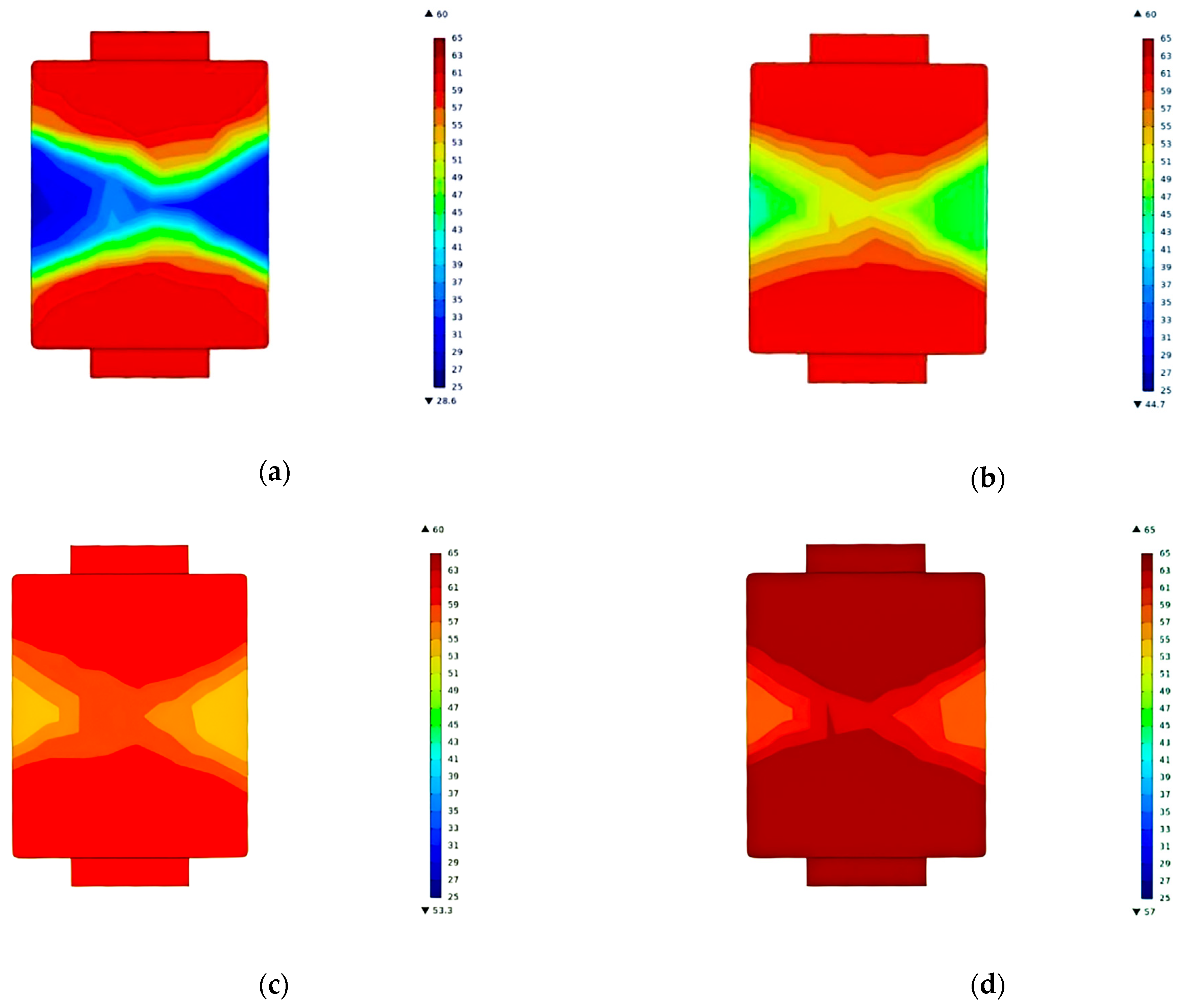
3.2.2. Temperature Field Simulation Analysis
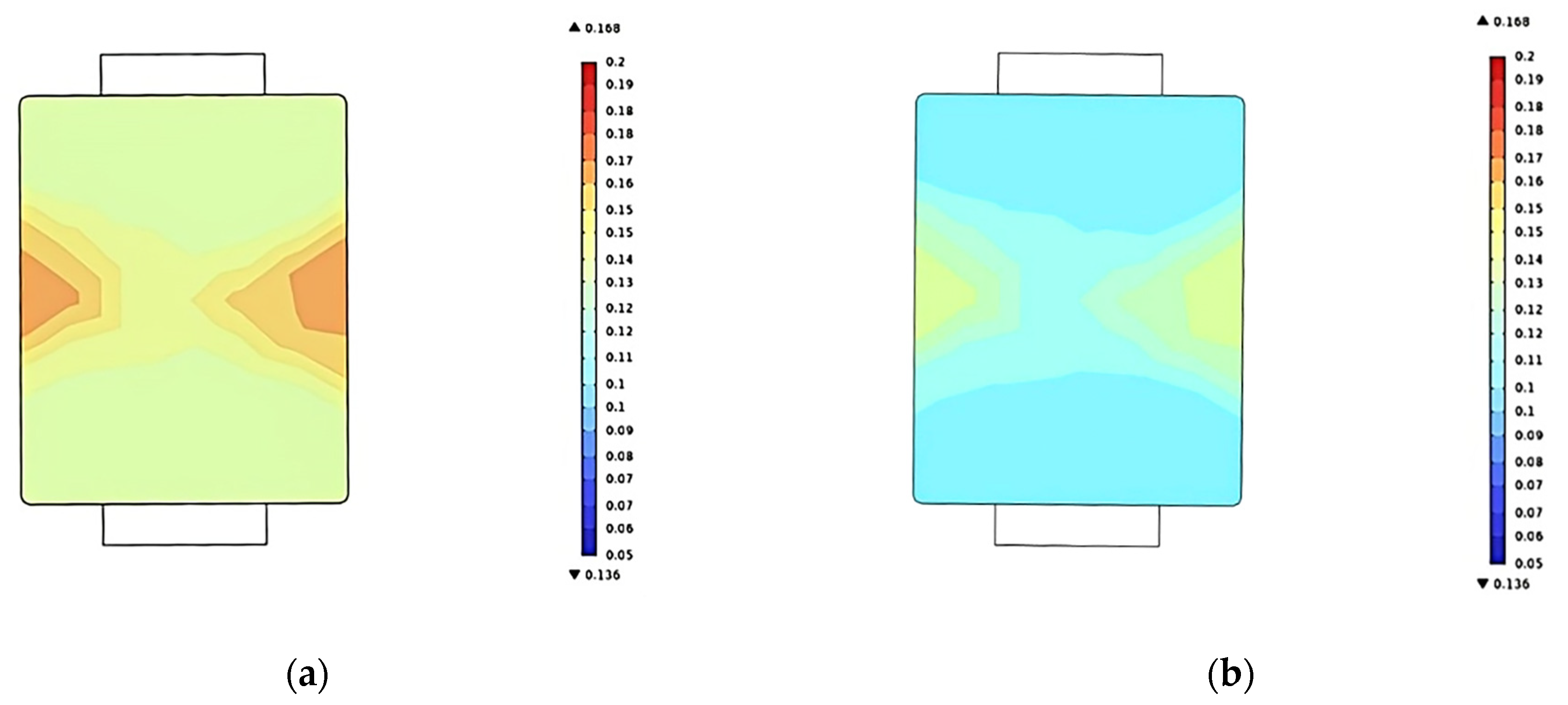
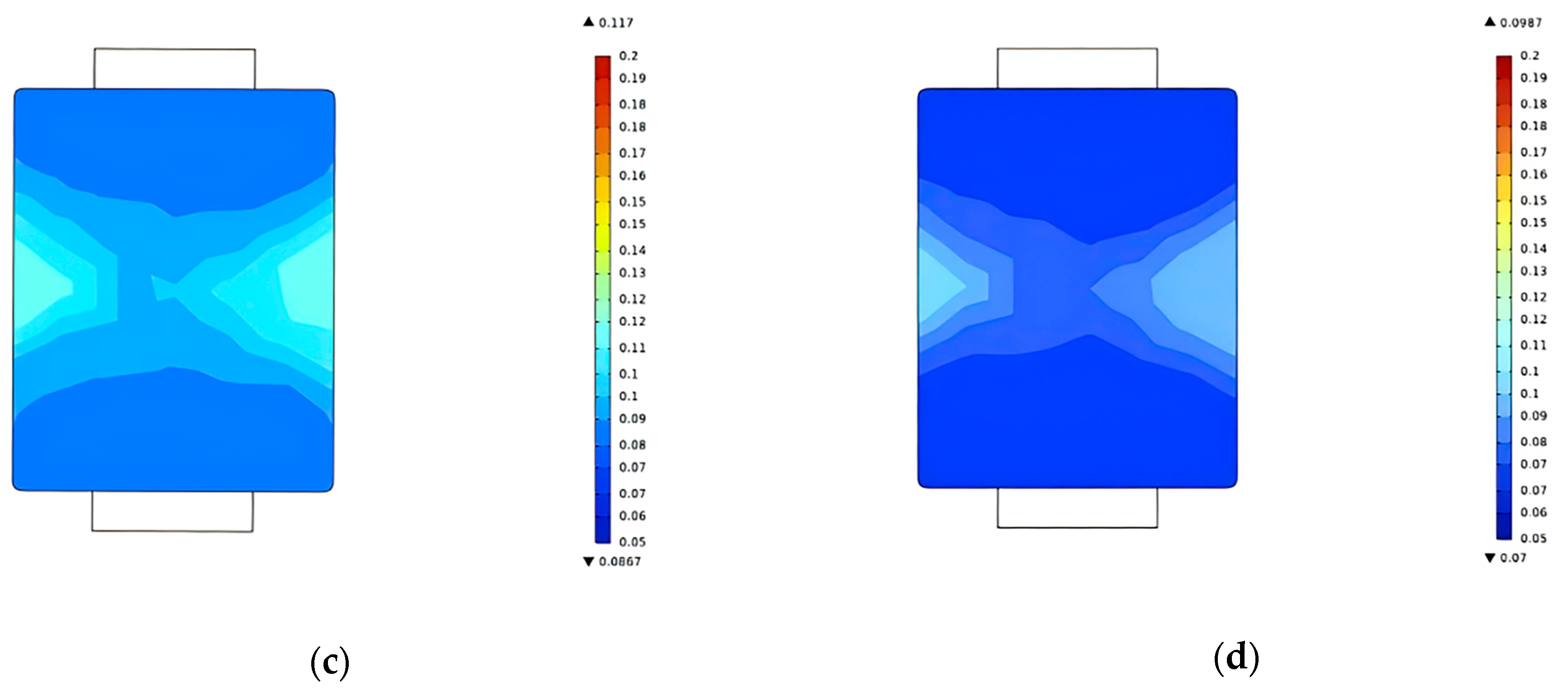
3.2.3. Humidity Field Simulation Analysis
3.3. Results Analysis
4. Materials and Methods
4.1. Test Methods
4.2. Effect of Experimental Factors on Drying Characteristics of Round Bale
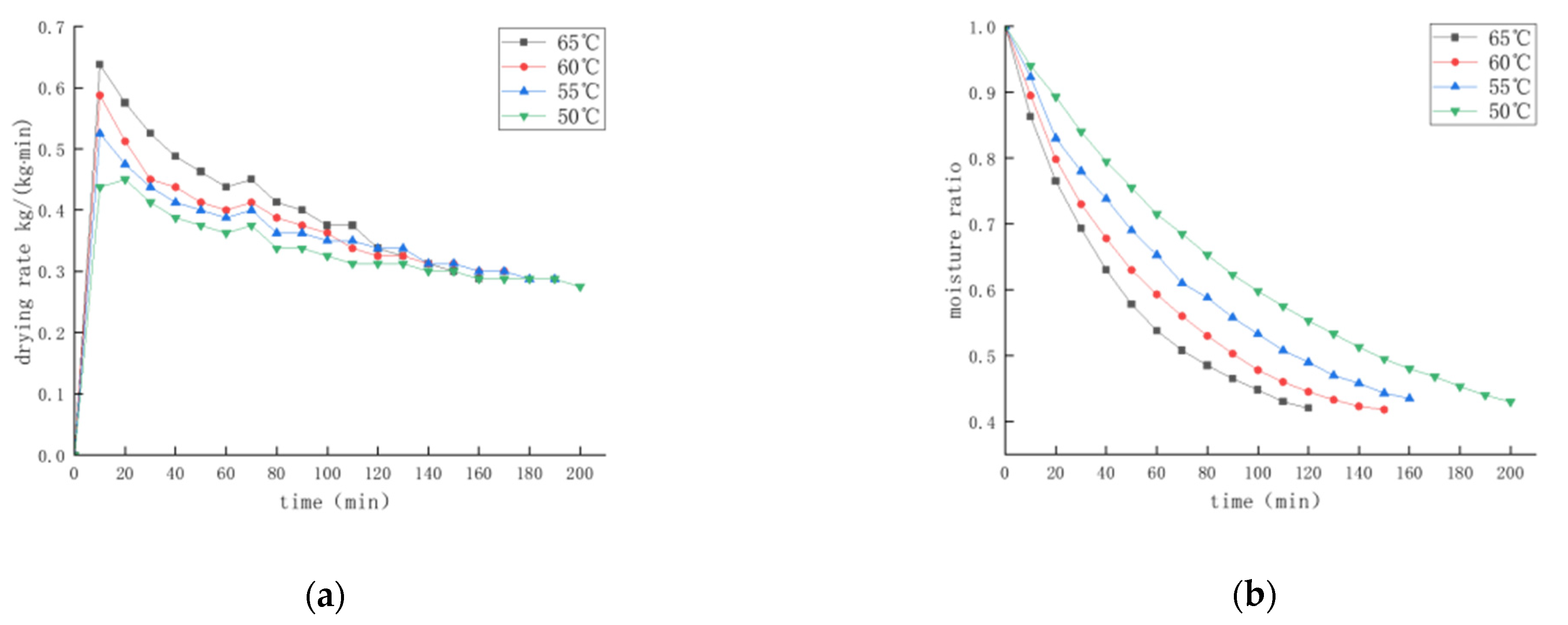
4.2.1. Effect of Hot Air Temperature on Drying Characteristics of Round Bale
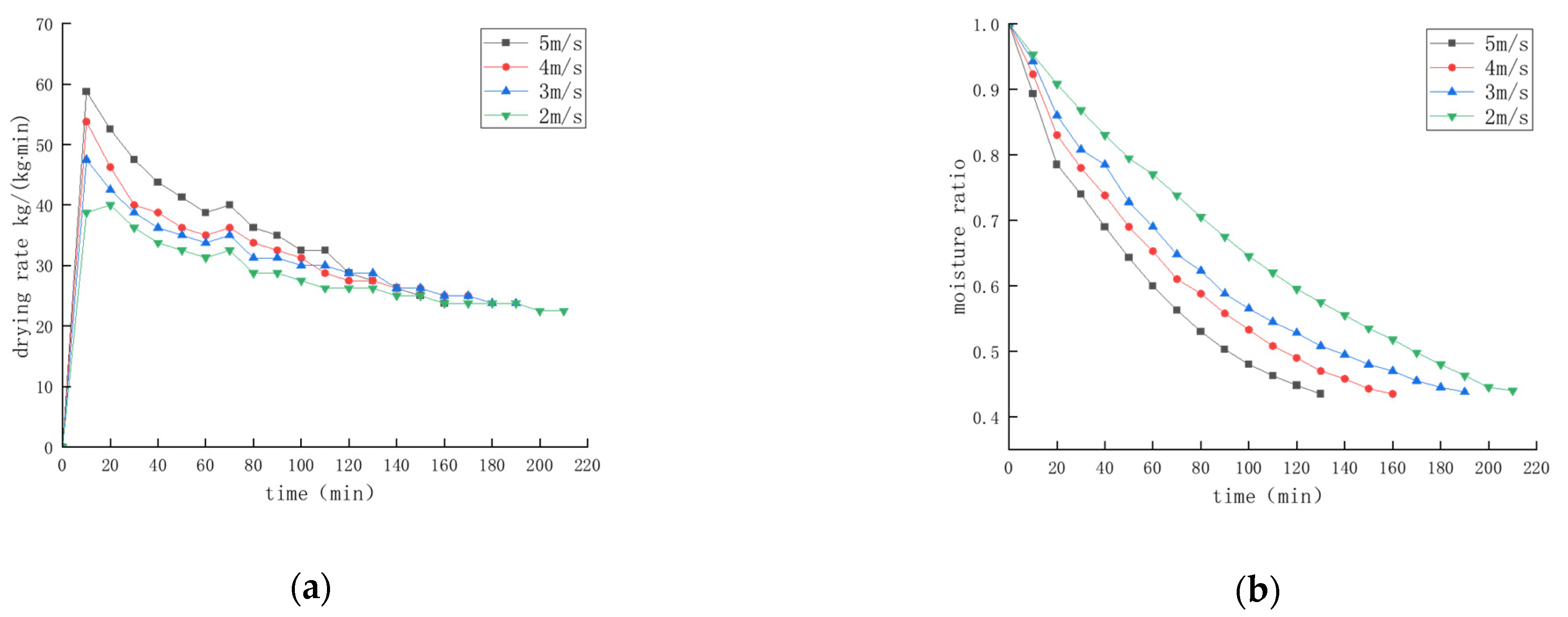
4.2.2. Effect of Hot Air Speed on Drying Characteristics of Round Bales
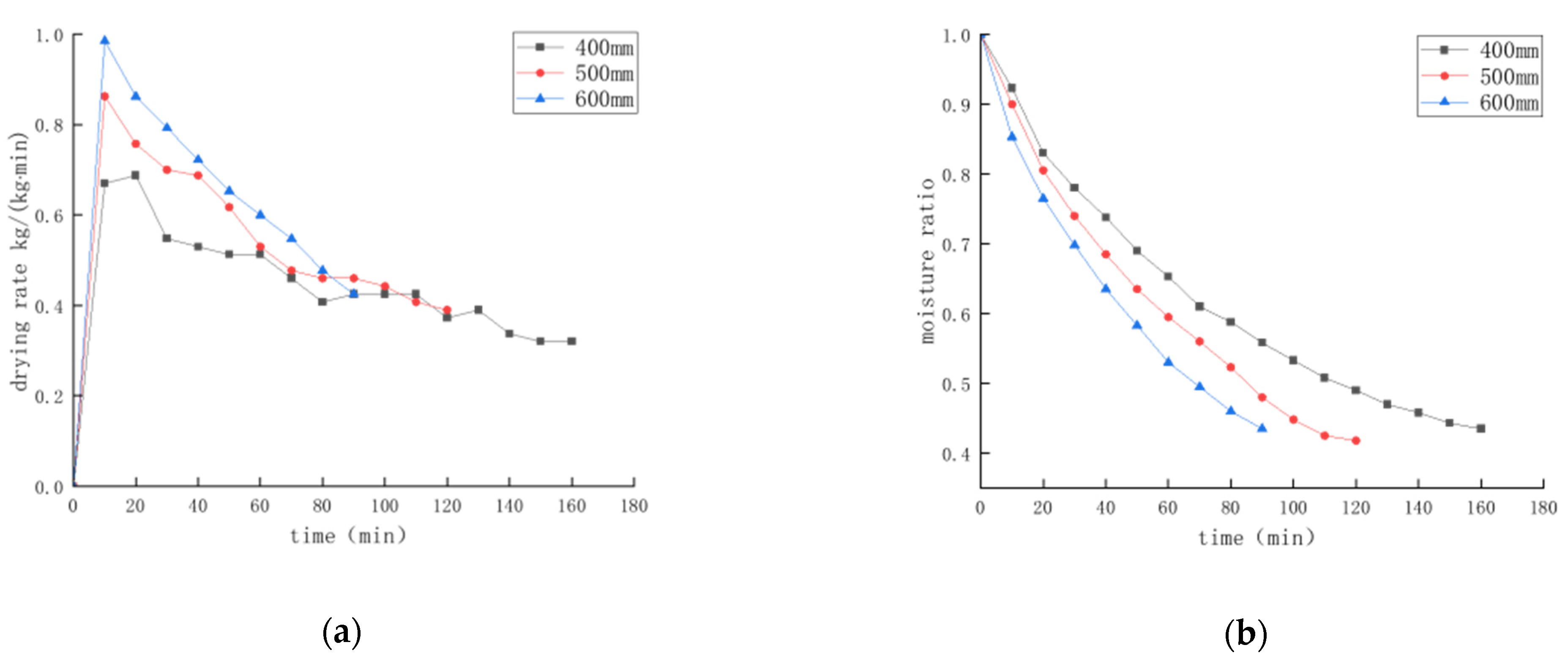
4.2.3. Effect of Air Duct Opening Diameter on Drying Characteristics of Round Bale
4.3. Response Surface Testing and Analysis
4.3.1. Response Surface Test Design Scheme
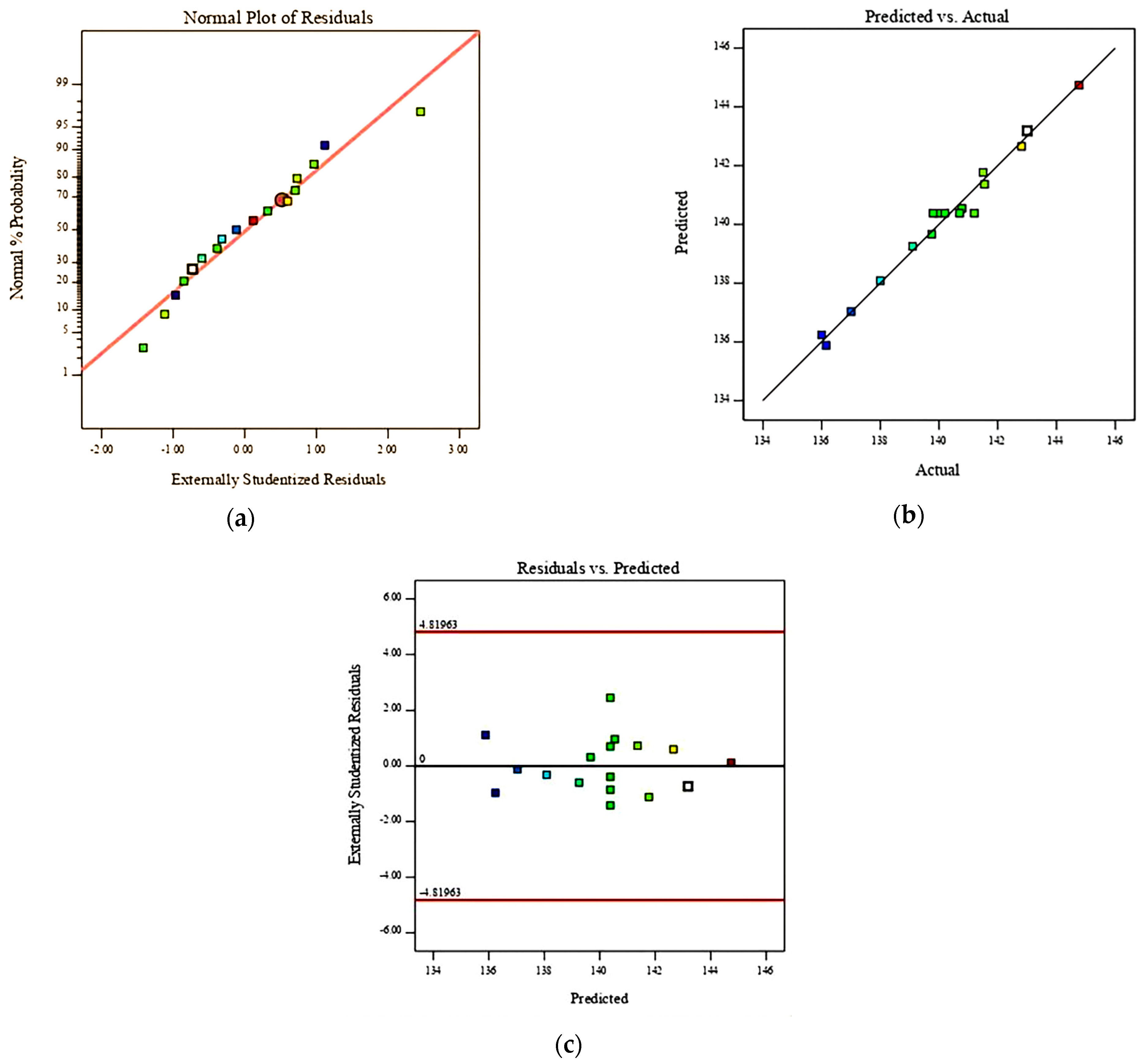
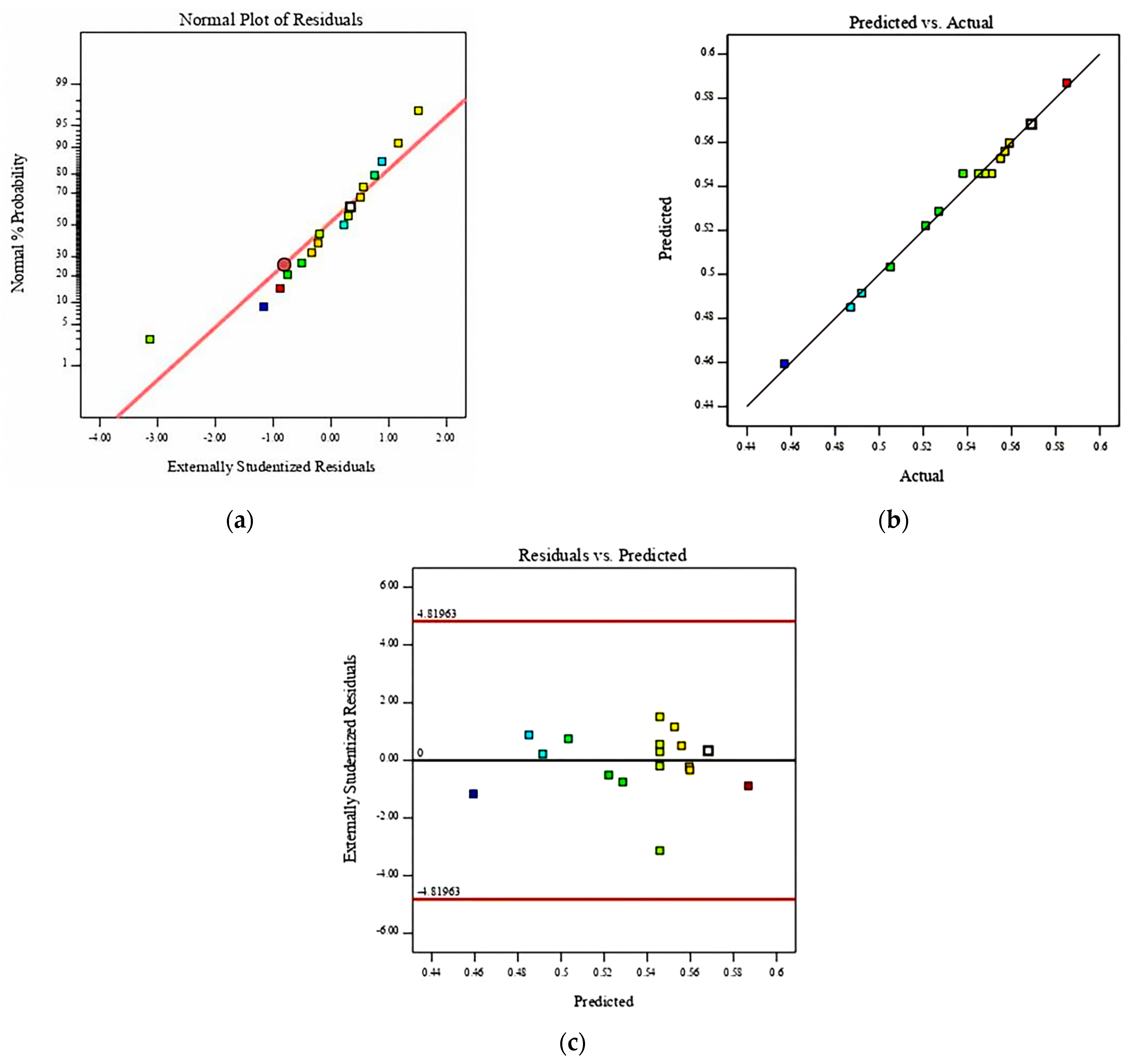
4.3.2. Establishment and Analysis of Regression Equation
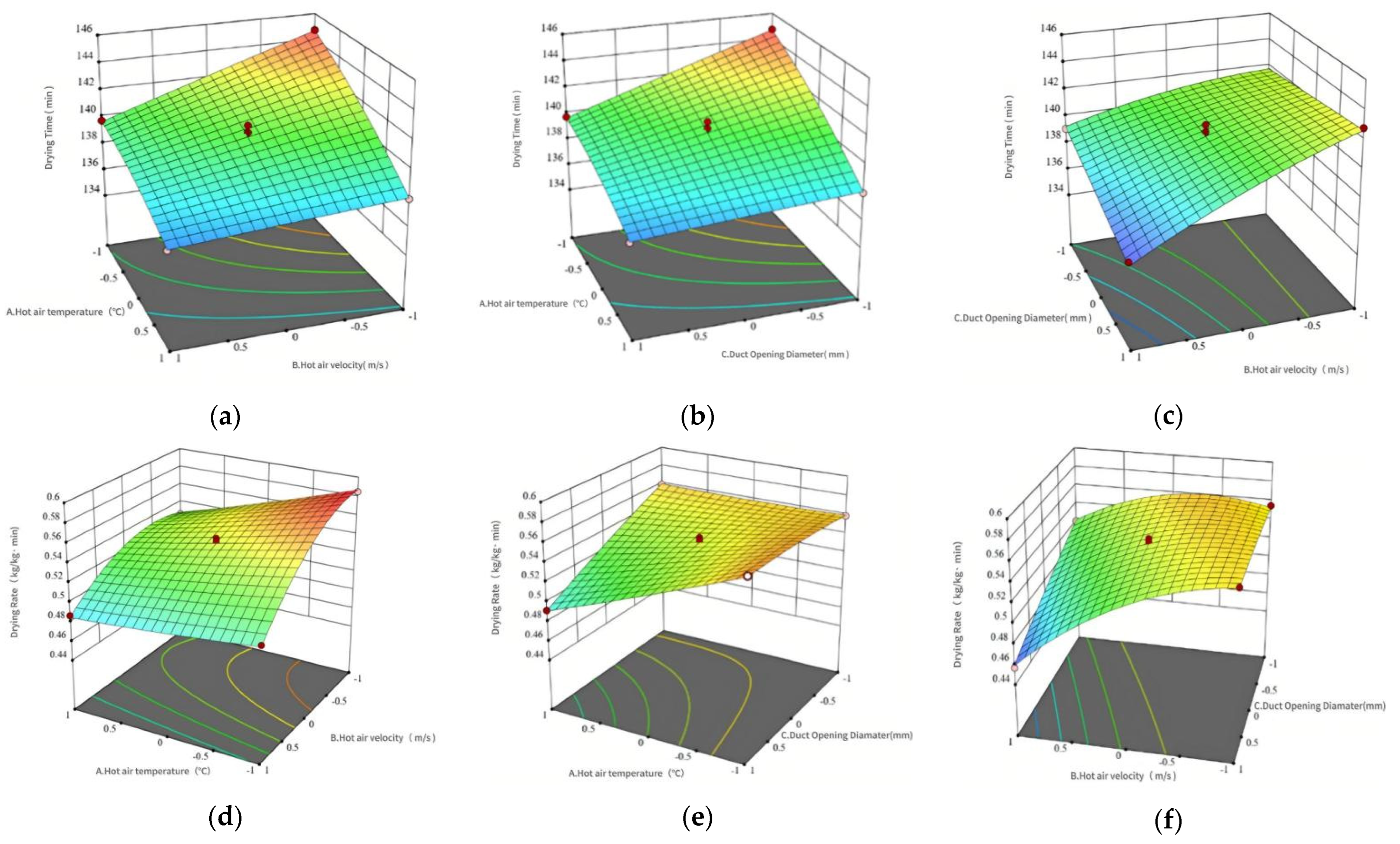
4.4. Interactive Response Surface Analysis and Optimal Process Parameter Verification
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nguyen, M.H.; Nguyen, T.L. The Influence of Drying Mode on the Drying Time of Anchovy Fish in a Hybrid Infrared-Convective Dryer: Drying Time Correlation and Taguchi Analysis. Appl. Eng. Lett. 2023, 8, 167–174. [Google Scholar] [CrossRef]
- Li, M.; Geng, Z.; Zhang, X.; Yang, X.; Zhang, Q. Establishment and application of a simulation model for infrared radiation combined with hot air intermittent drying of jujube slices. LWT 2025, 215, 117280. [Google Scholar] [CrossRef]
- Chen, P.; Xiong, Z.; Xu, J.; Liu, M. Simulation and parameter optimization of high moisture rice drying on combine harvester before threshing. Comput. Electron. Agric. 2023, 215, 108451. [Google Scholar] [CrossRef]
- Cheng, W.; Bian, H.; Shi, H.; Xun, F. Experimental and numerical modelling of desiccation shrinkage process of kaolin clays. Sci. Rep. 2025, 15, 20905. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Yi, K.; Chen, J. Characterization of temperature, moisture and stress distribution in corn drying process based on numerical simulation. J. Food Meas. Charact. 2025, 19, 6179–6191. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, W.; Pan, Z.; Yang, Z.; Li, J.; Yao, Z.; Qi, Y. Drying characteristics and numerical simulation of tissue paper. Nord. Pulp Pap. Res. J. 2025, 40, 345–356. [Google Scholar] [CrossRef]
- Li, B.; Feng, S.; He, Q.; Zhu, Y.; Hu, Z.; Jiang, Y.; Su, L. Numerical simulation of rice drying process in a deep bed under an angular air duct. J. Food Process Eng. 2023, 46, e14438. [Google Scholar] [CrossRef]
- Akal, D.; Kahveci, K.; Akyol, U.; Cihan, A. Drying kinetics of cotton based yarn bobbins in a pressurized hot-air convective dryer. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 294–308. [Google Scholar] [CrossRef]
- Park, S.; Kim, W. Improving drying performance of porous media by controlling surface pore size in convective drying. Int. J. Multiph. Flow 2025, 191, 105301. [Google Scholar] [CrossRef]
- Oliveira, D.P.D.; Coradi, P.C.; Leal, M.M.; Dolianitis, B.M.; Zabot, G.L.; Lopes, A.M. Drying and Storing Grains and Cereals: A Flow Approach in Porous Media and Applications. Food Rev. Int. 2025, 41, 1013–1049. [Google Scholar] [CrossRef]
- Ahmad, F.; Talbi, M.; Prat, M.; Tsotsas, E.; Kharaghani, A. Non-local equilibrium continuum modeling of partially saturated drying porous media: Comparison with pore network simulations. Chem. Eng. Sci. 2020, 228, 115957. [Google Scholar] [CrossRef]
- Meng, Z.; Cui, X.; Liu, Y.; Du, C.; Hu, R.; Wang, S.; Wang, F. Effect of electrohydrodynamics on hot air drying characteristics of fruits and vegetables. Sustain. Energy Technol. Assess. 2022, 53, 102716. [Google Scholar] [CrossRef]
- Zhang, W.P.; Yang, X.H.; Mujumdar, A.; Ju, H.Y.; Xiao, H.W. The influence mechanism and control strategy of relative humidity on hot air drying of fruits and vegetables: A review. Dry. Technol. 2022, 40, 2217–2234. [Google Scholar] [CrossRef]
- Feng, C.; Guo, H.; Xu, M.; Zhou, Y.; Lai, H.; Yan, Z.; Zhou, L.; Hu, J.; Li, J.; Xiong, Y. Effects of Hot Air Drying and Vacuum Drying on Thin-Layer Drying Kinetics and Quality Changes of Essential Oil of the Fruits of Evodia rutaecarpa (Juss.) Benth. J. Essent. Oil Bear. Plants 2022, 25, 910–923. [Google Scholar] [CrossRef]
- Chen, P.; Fan, M.; Zhu, W.; Liu, Y.; Jiang, M.; Wang, Y.; Wang, X. Numerical simulation of hot air drying of wheat grain piles based on CFD-DEM and experimental research. Dry. Technol. 2024, 42, 199–211. [Google Scholar] [CrossRef]
- Sun, D.; Hu, R.; Wang, P.; Yu, B. Integrated simulation method construction and process optimization for hot air drying of shiitake mushrooms. LWT 2024, 206, 116577. [Google Scholar] [CrossRef]
- Román, F.D.; Hensel, O. Numerical simulations and experimental measurements on the distribution of air and drying of round hay bales. Biosyst. Eng. 2014, 122, 1–15. [Google Scholar] [CrossRef]
- Du, J.; Liu, C. Experimental Study on Drying Characteristics of Alfalfa Hay Bales Using Hot Air Convection. Appl. Sci. 2025, 15, 3921. [Google Scholar] [CrossRef]
- Weller, S.; Florentine, S.; Sillitoe, J.; Grech, C.; McLaren, D.; Chauhan, B.S.; Li, M. Detecting the Seeds of Nassella neesiana in Large Round Hay Bales, by Means of Non-Destructive Core Sampling. PLoS ONE 2017, 10, e0137343. [Google Scholar] [CrossRef] [PubMed]
- Beck, A.P.; Beck, R.M.; Hubbell, D.; Hess, T.; Foote, A.P.; Gadberry, S.; Kegley, B.B. 234 Can We Use Moderate Quality Round Bale Bermudagrass Silage to Stretch Wheat pasture? J. Anim. Sci. 2023, 101, 160–161. [Google Scholar] [CrossRef]
- Janez, B. An Analysis of the Process of Drying Fresh Bales. Teh. Vjesn. 2019, 26, 1714–1719. [Google Scholar] [CrossRef]
- Gao, X.; Xuan, C.; Tang, Z.; Hong, B.; Ma, Y.; Qian, S. A dynamic drying process: Mathematical modeling and energy consumption optimization of alfalfa bales using hot air drying. Renew. Energy 2025, 246, 122961. [Google Scholar] [CrossRef]
- Dario, F. Mathematical Modelling of Rotary Drum Dryers for Alfalfa Drying Process Control. Inventions 2023, 8, 11. [Google Scholar] [CrossRef]
- Romano, G.; Nagle, M.; Müller, J. Two-parameter Lorentzian distribution for monitoring physical parameters of golden colored fruits during drying by application of laser light in the Vis/NIR spectrum. Innov. Food Sci. Emerg. Technol. 2016, 33, 498–505. [Google Scholar] [CrossRef]
- Lukas, E.; Ilon, J. A mass, momentum, and energy conservative dynamical low-rank scheme for the Vlasov equation. J. Comput. Phys. 2021, 443, 110495. [Google Scholar] [CrossRef]
- Hajiketabi, M.; Abbasbandy, S. A Fictitious Time Lie-Group Integrator for the Brinkman–Forchheimer Momentum Equation Modeling Flow of Fully Developed Forced Convection. Comput. Math. Math. Phys. 2022, 62, 1527–1538. [Google Scholar] [CrossRef]
- Kamruzzaman, M. Modified transport equation for the turbulent kinetic energy dissipation of the grid turbulence in the transition period of decay. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 78. [Google Scholar] [CrossRef]
- Juncu, G.; Nicola, A.; Popa, C.; Stroila, E. Preconditioned Conjugate Gradient and Multigrid Methods for Numerical Solution of Multicomponent Mass Transfer Equations I. Diffusion-Reaction Equations. Numer. Heat Transf. Part A Appl. 2014, 66, 1268–1296. [Google Scholar] [CrossRef]
- Serhat, S.T.; Erdoğan, K.; Hailu, A.F.; Karacabey, E. A novel drying system—Simultaneous use of ohmic heating with convectional air drying: System design and detailed examination using CFD. Innov. Food Sci. Emerg. Technol. 2021, 72, 102727. [Google Scholar] [CrossRef]
- Khan, I.H.; Batuwatta-Gamage, C.P.; Karim, M.A.; Gu, Y. Fundamental Understanding of Heat and Mass Transfer Processes for Physics-Informed Machine Learning-Based Drying Modelling. Energies 2022, 15, 9347. [Google Scholar] [CrossRef]
- Su, L.; Yang, X.; Wang, Q.; Qin, X.; Zhou, B.; Shan, Y. Functional Extremum Solution and Parameter Estimation for One-Dimensional Vertical Infiltration using the Brooks–Corey Model. Soil Sci. Soc. Am. J. 2018, 82, 1319–1332. [Google Scholar] [CrossRef]
- Wang, N.; Yu, J.; Tahmasebi, A.; Han, Y.; Lucas, J.; Wall, T.; Jiang, Y. Experimental Study on Microwave Pyrolysis of an Indonesian Low-Rank Coal. Energy Fuels 2013, 28, 254–263. [Google Scholar] [CrossRef]


| Serial Number | Project | Unit | Technical Index |
|---|---|---|---|
| 1 | power conditioning | V/Hz | 380/50 |
| 2 | heating power | kW | 75.5 |
| 3 | temperature range | °C | 20–100 |
| 4 | diameter of air duct opening | mm | 400–600 |
| 5 | wind speed adjustment | m/s | 1–6 |
| 6 | temperature sensor accuracy | °C | ±0.5 °C |
| Parameter | Numerical Value |
|---|---|
| porosity/% | 39.22% |
| 0.571 | |
| 150 | |
| 840 |
| Experimental Factors | Test Index | ||
|---|---|---|---|
| Hot Blast Temperature (°C) | Hot Wind Speed (m/s) | Diameter of Air Duct Opening (mm) | Coefficient of Wind Speed Non-Uniformity |
| 50 | 3 | 400 | 40.7% |
| 500 | 35.4% | ||
| 600 | 28.9% | ||
| Check Point | Scheme A (m/s) | Scheme B (m/s) | Scheme C (m/s) |
|---|---|---|---|
| 1# | 1.5 | 1.3 | 1.7 |
| 2# | 1.9 | 2.1 | 2.3 |
| 3# | 1.4 | 1.3 | 1.6 |
| 4# | 0.5 | 0.8 | 0.9 |
| 5# | 0.7 | 0.9 | 0.9 |
| 6# | 0.6 | 0.5 | 0.7 |
| 7# | 1.4 | 1.2 | 1.6 |
| 8# | 2.0 | 2.2 | 2.4 |
| 9# | 1.3 | 1.5 | 1.6 |
| Coefficient of Wind Speed Non-Uniformity in Each Layer | Scheme A (%) | Scheme B (%) | Scheme C (%) |
|---|---|---|---|
| First layer wind speed non-uniformity coefficient | 31.1 | 27.9 | 25.2 |
| Second layer wind speed non-uniformity coefficient | 58.3 | 49.4 | 38.0 |
| Third layer wind speed non-uniformity coefficient | 32.7 | 28.8 | 23.5 |
| Experimental Factors | Test Index | ||
|---|---|---|---|
| Hot Blast Temperature (°C) | Hot Wind Speed (m/s) | Diameter of Air Duct Opening (mm) | Coefficient of Temperature Heterogeneity |
| 50 | 2 | 600 | 48.03% |
| 3 | 26.33% | ||
| 4 | 11.5% | ||
| 5 | 5.77% | ||
| Coefficient of Heterogeneity of Each Layer | Scheme A (%) | Scheme B (%) | Scheme C (%) | Scheme D (%) |
|---|---|---|---|---|
| Coefficient of first-layer temperature non-uniformity | 27.7 | 18.0 | 5.6 | 2.1 |
| Coefficient of temperature non-uniformity in the second layer | 80.1 | 41.1 | 20.7 | 11.5 |
| Coefficient of third-layer temperature non-uniformity | 36.3 | 19.9 | 8.2 | 3.7 |
| Experimental Factors | Test Index | ||
|---|---|---|---|
| Hot Blast Temperature (°C) | Hot Wind Speed (m/s) | Diameter of Air Duct Opening (mm) | Wet Velocity Non-uniformity Coefficient |
| 50 | 2 | 600 | 48.03% |
| 3 | 26.33% | ||
| 4 | 11.5% | ||
| 5 | 5.77% | ||
| Coefficient of Heterogeneity for Each Layer | Scheme A (%) | Scheme B (%) | Scheme C (%) | Scheme D (%) |
|---|---|---|---|---|
| Coefficient of humidity non-uniformity in the first layer | 13.9 | 11.3 | 9.9 | 3.9 |
| Coefficient of moisture non-uniformity in the second layer | 25.2 | 28.1 | 13.7 | 5.2 |
| Coefficient of moisture non-uniformity in the third layer | 20.6 | 19.6 | 14.6 | 4.6 |
| Hot Blast Temperature (%) | Dehumidification Capacity (kg) | Energy Consumption Value (kW·h) | SMER Value (kg/kW·h) |
|---|---|---|---|
| 50 | 74.84 | 40.80 | 1.83 |
| 55 | 74.84 | 45.00 | 1.66 |
| 60 | 74.84 | 56.00 | 1.34 |
| 65 | 74.84 | 71.00 | 1.05 |
| Hot Wind Speed (m/s) | Dehumidification Capacity (kg) | Energy Consumption Value (kW·h) | SMER Value (kg/kW·h) |
|---|---|---|---|
| 2 | 74.84 | 48.5 | 1.54 |
| 3 | 74.84 | 44.0 | 1.70 |
| 4 | 74.84 | 39.5 | 1.90 |
| 5 | 74.84 | 33.5 | 2.23 |
| Diameter of Air Duct Opening (mm) | Dehumidification Capacity (kg) | Energy Consumption Value (kW·h) | SMER Value (kg/kW·h) |
|---|---|---|---|
| 400 | 74.84 | 72.5 | 1.03 |
| 500 | 74.84 | 50.0 | 1.50 |
| 600 | 74.84 | 38.5 | 1.94 |
| Test Number | Factor Level | Evaluation Indicators | |||
|---|---|---|---|---|---|
| Hot Wind Speed | Hot Air Temperature | Air Duct Opening Diameter | Drying Time (min) | Drying Speed (m/s) | |
| 1 | −1 | −1 | 0 | 144.77 | 0.585 |
| 2 | 1 | −1 | 0 | 139.75 | 0.527 |
| 3 | −1 | 1 | 0 | 138 | 0.505 |
| 4 | 1 | 1 | 0 | 137 | 0.487 |
| 5 | −1 | 0 | −1 | 140.78 | 0.559 |
| 6 | 1 | 0 | −1 | 141.55 | 0.559 |
| 7 | −1 | 0 | 1 | 143 | 0.569 |
| 8 | 1 | 0 | 1 | 136 | 0.492 |
| 9 | 0 | −1 | −1 | 141.5 | 0.555 |
| 10 | 0 | 1 | −1 | 139.1 | 0.521 |
| 11 | 0 | −1 | 1 | 142.81 | 0.557 |
| 12 | 0 | 1 | 1 | 136.15 | 0.457 |
| 13 | 0 | 0 | 0 | 140 | 0.551 |
| 14 | 0 | 0 | 0 | 140.7 | 0.547 |
| 15 | 0 | 0 | 0 | 139.8 | 0.548 |
| 16 | 0 | 0 | 0 | 140.2 | 0.538 |
| 17 | 0 | 0 | 0 | 141.2 | 0.545 |
| Source of Mutation | Square Sum | Degree of Freedom | Mean Square | F Value | p Value |
|---|---|---|---|---|---|
| Model | 89.62404 | 9 | 9.958226 | 41.56746 | <0.0001 *** |
| X1 | 43.15205 | 1 | 43.15205 | 180.1245 | <0.0001 *** |
| X2 | 18.75781 | 1 | 18.75781 | 78.29854 | <0.0001 *** |
| X3 | 3.087613 | 1 | 3.087613 | 12.88826 | 0.0088 ** |
| X1X2 | 4.0401 | 1 | 4.0401 | 16.86412 | 0.0045 ** |
| X2X3 | 4.5369 | 1 | 4.5369 | 18.93785 | 0.0033 ** |
| X1X3 | 15.09323 | 1 | 15.09323 | 63.00188 | <0.0001 *** |
| X12 | 0.935059 | 1 | 0.935059 | 3.903108 | 0.088752 (ns) |
| X22 | 0.00348 | 1 | 0.00348 | 0.014527 | 0.907451 (ns) |
| X32 | 0.00148 | 1 | 0.00148 | 0.006179 | 0.939546 (ns) |
| Residual | 1.676975 | 7 | 0.239568 | ||
| Lack of Fit | 0.388975 | 3 | 0.129658 | 0.402666 | 0.759591 (ns) |
| Pure Error | 1.288 | 4 | 0.322 | ||
| Sum | 91.30101 | 16 |
| Source of Mutation | Square Sum | Degree of Freedom | Mean Square | F Value | p Value |
|---|---|---|---|---|---|
| Model | 0.017642 | 9 | 0.00196 | 111.9643 | <0.0001 *** |
| X1 | 0.008065 | 1 | 0.008065 | 460.6406 | <0.0001 *** |
| X2 | 0.002926 | 1 | 0.002926 | 167.1389 | <0.0001 *** |
| X3 | 0.00177 | 1 | 0.00177 | 101.1087 | <0.0001 *** |
| X1X2 | 0.0004 | 1 | 0.0004 | 22.84782 | 0.0020 ** |
| X2X3 | 0.001089 | 1 | 0.001089 | 62.20318 | <0.0001 *** |
| X1X3 | 0.001482 | 1 | 0.001482 | 84.66544 | <0.0001 *** |
| X12 | 0.001861 | 1 | 0.001861 | 106.3147 | 0.566938 (ns) |
| X22 | 6.32 × 10−6 | 1 | 6.32 × 10−6 | 0.360905 | <0.0001 *** |
| X32 | 2.18 × 10−5 | 1 | 2.18 × 10−5 | 1.244755 | 0.0030 ** |
| Residual | 0.000123 | 7 | 1.75 × 10−5 | ||
| Lack of Fit | 2.78 × 10−5 | 3 | 9.25 × 10−6 | 0.390295 | 0.767219 (ns) |
| Pure Error | 9.48 × 10−5 | 4 | 2.37 × 10−5 | ||
| sum | 0.017764 | 16 |
| Hot Blast Temperature (°C) | Hot Wind Speed (m/s) | Diameter of Air Duct Opening (mm) | Drying Time (min) | Dry Rate (kg/kg·min) | |
|---|---|---|---|---|---|
| Optimize parameters | 60 | 5 | 600 | 119.3 | 0.62 |
| Test verification | 60 | 5 | 600 | 122 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Sun, Z.; Chen, Z. Design and Experiment of Drying Equipment for Alfalfa Bales. Agriculture 2025, 15, 2000. https://doi.org/10.3390/agriculture15192000
Du J, Sun Z, Chen Z. Design and Experiment of Drying Equipment for Alfalfa Bales. Agriculture. 2025; 15(19):2000. https://doi.org/10.3390/agriculture15192000
Chicago/Turabian StyleDu, Jianqiang, Zhiwen Sun, and Zeqi Chen. 2025. "Design and Experiment of Drying Equipment for Alfalfa Bales" Agriculture 15, no. 19: 2000. https://doi.org/10.3390/agriculture15192000
APA StyleDu, J., Sun, Z., & Chen, Z. (2025). Design and Experiment of Drying Equipment for Alfalfa Bales. Agriculture, 15(19), 2000. https://doi.org/10.3390/agriculture15192000





