Trajectory Tracking Control of an Orchard Robot Based on Improved Integral Sliding Mode Algorithm
Abstract
1. Introduction
2. Materials and Methods
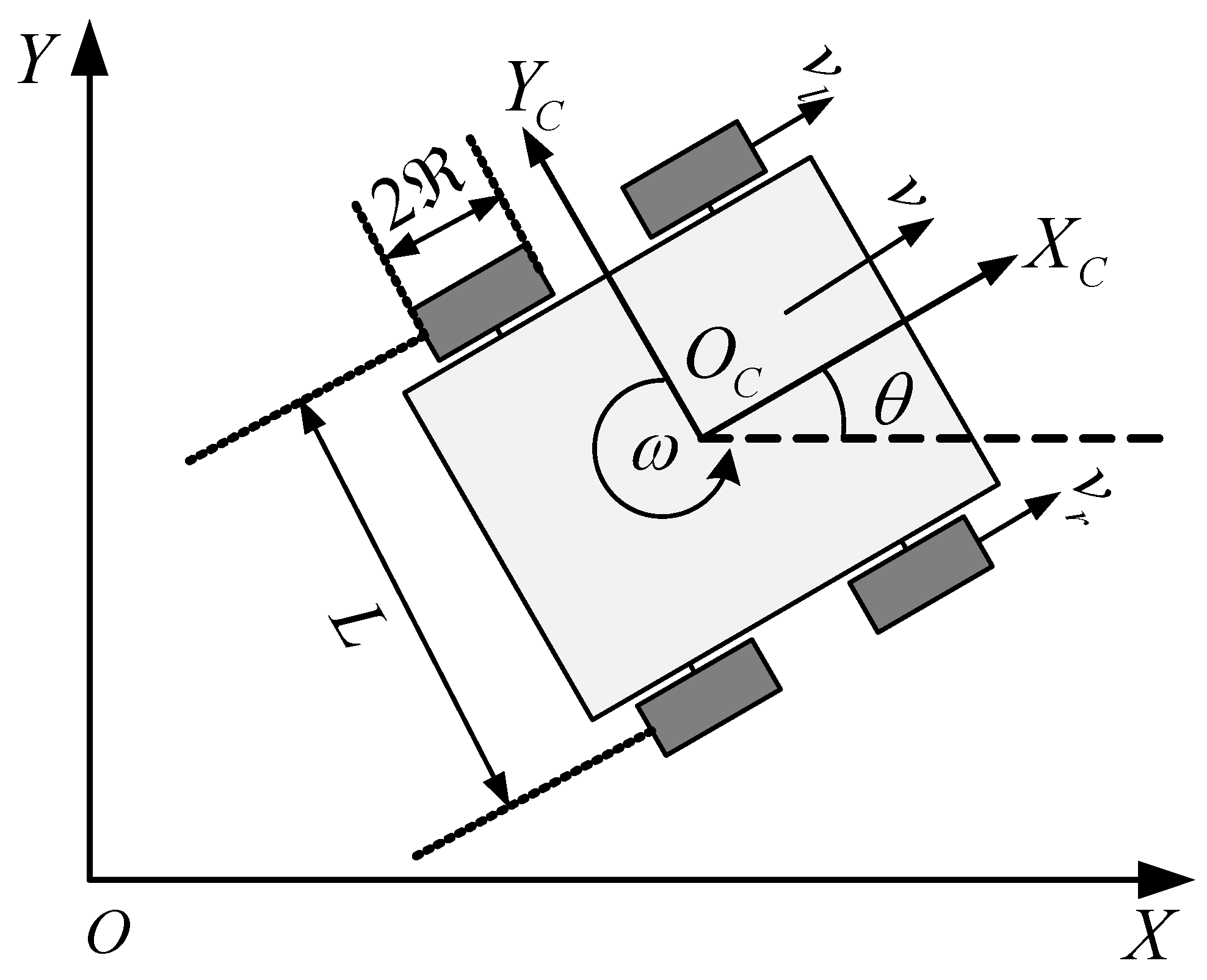
2.1. Kinematic Model Construction
2.2. Dual-Loop Trajectory Tracking Control
- (1)
- The inner-loop attitude tracking is sensitive to external disturbances, necessitating attention to the anti-disturbance performance during the tracking process.
- (2)
- The outer-loop position error has no upper bound, requiring consideration of the stability of the convergence rate when the orchard mobile robot is far from the target trajectory. Once it approaches the target trajectory, the position error should converge rapidly within a finite time.
- (3)
- To avoid control oscillations and response delays, the convergence rate of the inner-loop system must be significantly faster than that of the outer loop, and the output of the outer loop must ensure continuity.
2.3. Design of the Trajectory Tracking Controller
- (1)
- The sliding mode variable for outer-loop position tracking control is as follows:
- (2)
- The sliding mode variable for inner-loop attitude tracking control is as follows:
2.4. Design of the Reaching Law
- (1)
- Existence condition validation
- (2)
- Reaching condition validation
2.5. Stability Analysis
3. Results and Discussion
3.1. Simulation Results of the Control System
3.2. Comparative Analysis of Results with Different Control Methods
4. Conclusions
- (1)
- Comparative simulations across reaching laws and sliding mode controller variants indicate that the Improved DPRL-TVITSMC achieves faster convergence and higher accuracy in complex trajectory tracking tasks, reducing both tracking error and chattering.
- (2)
- For an external disturbance acting in the inner loop, the simulations yield , and the upper bound on the tracking error derived from the stability analysis satisfies .
- (3)
- A preset detour trajectory demonstrates that the proposed tracking controller enables the orchard mobile robot to follow the detour effectively; settles within 0.01 rad after 0.17 s, settles within 0.01 m within 1.23 s, and settles within 0.01 m after 1.04 s. These results highlight favorable rapidity, accuracy, and robustness.
- (1)
- The present study considers only idealized simulation scenarios and representative disturbances, and lacks hardware experiments on a real orchard robot. As future work, we will build a physical platform and conduct comparative experiments to verify the controller’s robustness and portability under uneven terrain and external disturbances.
- (2)
- To assess the robustness margins and reproducibility of the control strategy, subsequent experiments will report key implementation details—including the chassis and actuation scheme, sensor types and mounting poses, computing hardware and real-time system, terrain conditions, and path settings—and will evaluate the algorithm’s adaptability in non-ideal scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| R | RMSE_x1 | RMSE_x2 |
|---|---|---|
| 50 | 0.007 | 0.041 |
| 100 | 0.004 | 0.035 |
| 200 | 0.002 | 0.04 |
| 500 | 0.001 | 0.057 |
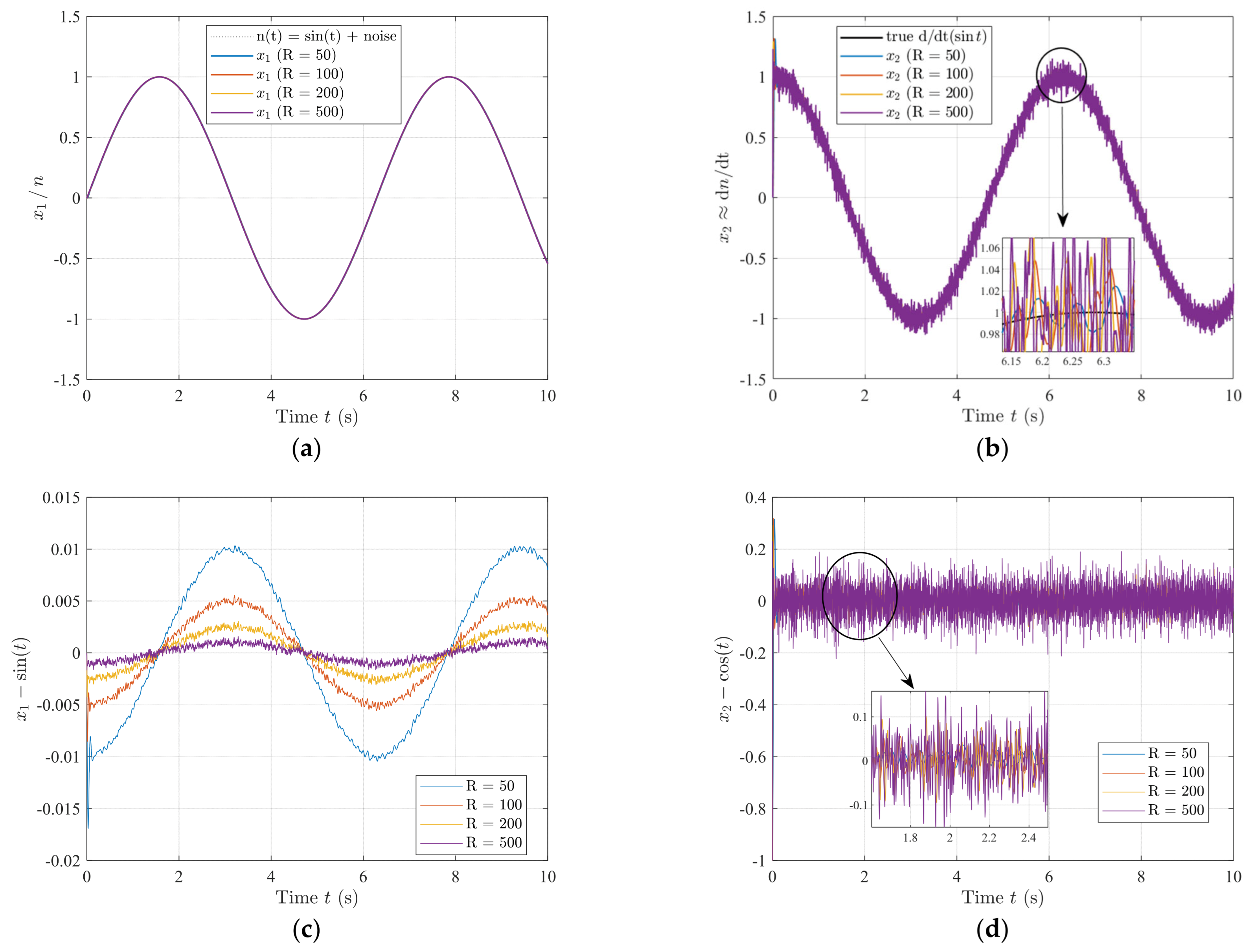
Appendix B
Appendix B.1
| Sample Size | ERL-TVITSMC | PRL-TVITSMC | DRL-TVITSMC | Improved DPRL-TVITSMC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | |
| 1 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 2 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 3 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 4 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 5 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 6 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 7 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 8 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 9 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 10 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 11 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 12 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 13 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 14 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| 15 | 0.8274 | 0.8245 | 0.3833 | 1.009 | 0.8948 | 2.808 | 0.8648 | 0.8452 | 0.6234 | 0.7629 | 0.7698 | 0.2754 |
| Sample Size | ERL-TVITSMC | PRL-TVITSMC | DRL-TVITSMC | Improved DPRL-TVITSMC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | |
| 1 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 2 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 3 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 4 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 5 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 6 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 7 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 8 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 9 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 10 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 11 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 12 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 13 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 14 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| 15 | 0.0675 | 0.0297 | 0.2321 | 0.1302 | 0.0429 | 1.034 | 0.0763 | 0.0333 | 0.2686 | 0.0484 | 0.0229 | 0.1545 |
| Sample Size | Improved DPRL-SMC | Improved DPRL-ISMC | Improved DPRL-TSMC | Improved DPRL-TVITSMC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | |
| 1 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 2 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 3 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 4 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 5 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 6 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 7 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 8 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 9 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 10 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 11 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 12 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 13 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 14 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| 15 | 3.362 | 4.205 | 2.942 | 1.265 | 0.8502 | 1.293 | 0.8948 | 0.7714 | 0.5837 | 0.7629 | 0.7698 | 0.2754 |
| Sample Size | Improved DPRL-SMC | Improved DPRL-ISMC | Improved DPRL-TSMC | Improved DPRL-TVITSMC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | IAE | ISE | ITAE | |
| 1 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 2 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 3 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 4 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 5 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 6 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 7 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 8 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 9 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 10 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 11 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 12 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 13 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 14 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| 15 | 0.1927 | 0.1042 | 0.2089 | 0.0926 | 0.0445 | 0.5954 | 0.1576 | 0.0442 | 2.873 | 0.0484 | 0.0229 | 0.1545 |
| Sample Size | ERL-TVITSMC | PRL-TVITSMC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 2 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 3 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 4 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 5 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 6 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 7 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 8 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 9 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 10 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 11 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 12 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 13 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 14 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| 15 | 1.617 | 0.740 | 0.231 | 1.855 | 1.821 | 0.231 | 3.160 | 0.797 | 0.462 | 6.201 | 6.332 | 0.477 |
| Sample size | DRL-TVITSMC | Improved DPRL-TVITSMC | ||||||||||
| 1 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 2 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 3 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 4 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 5 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 6 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 7 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 8 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 9 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 10 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 11 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 12 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 13 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 14 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 15 | 1.960 | 0.753 | 0.255 | 2.583 | 2.532 | 0.255 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| Sample Size | Improved DPRL-SMC | Improved DPRL-ISMC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 2 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 3 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 4 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 5 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 6 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 7 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 8 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 9 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 10 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 11 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 12 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 13 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 14 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| 15 | 1.441 | 3.051 | 0.641 | 1.441 | 3.051 | 0.641 | 1.818 | 3.591 | 0.204 | 1.220 | 3.023 | 0.204 |
| Sample size | Improved DPRL-ITSMC | Improved DPRL-TVITSMC | ||||||||||
| 1 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 2 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 3 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 4 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 5 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 6 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 7 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 8 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 9 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 10 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 11 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 12 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 13 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
| 14 | 1.273 | 3.065 | 0.204 | 1.256 | 3.051 | 0.204 | 0.966 | 0.753 | 0.144 | 0.975 | 0.966 | 0.144 |
Appendix B.2
| Comparison | Metric | Mean | Std | CI95_Lower | CI95_Upper | t | dt | sig |
|---|---|---|---|---|---|---|---|---|
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | IAE | −0.065 | −0.065 | −0.065 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | IAE | −0.246 | −0.246 | −0.246 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | IAE | −0.102 | −0.102 | −0.102 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | ISE | −0.055 | −0.055 | −0.055 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | ISE | −0.125 | −0.125 | −0.125 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | ISE | −0.075 | −0.075 | −0.075 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | ITAE | −0.108 | −0.108 | −0.108 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | ITAE | −2.533 | −2.533 | −2.533 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | ITAE | −0.348 | −0.348 | −0.348 | 14 | *** |
| Comparison | Metric | Mean | Std | CI95_Lower | CI95_Upper | t | dt | sig |
|---|---|---|---|---|---|---|---|---|
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | IAE | −0.019 | −0.019 | −0.019 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | IAE | −0.082 | −0.082 | −0.082 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | IAE | −0.028 | −0.028 | −0.028 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | ISE | −0.007 | −0.007 | −0.007 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | ISE | −0.020 | −0.020 | −0.020 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | ISE | −0.010 | −0.010 | −0.010 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | ITAE | −0.078 | −0.078 | −0.078 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | ITAE | −0.880 | −0.880 | −0.880 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | ITAE | −0.114 | −0.114 | −0.114 | 14 | *** |
| Comparison | Metric | Mean | Std | CI95_Lower | CI95_Upper | t | dt | sig |
|---|---|---|---|---|---|---|---|---|
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | xe | −0.652 | −0.652 | −0.652 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | xe | −2.194 | −2.194 | −2.194 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | xe | −0.994 | −0.994 | −0.994 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | ye | 0.012 | 0.012 | 0.012 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | ye | −0.045 | −0.045 | −0.045 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | ye | 0.000 | 0.000 | 0.000 | 14 | n.s. | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | θe | −0.087 | −0.087 | −0.087 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | θe | −0.317 | −0.317 | −0.317 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | θe | −0.110 | −0.110 | −0.110 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | s1 | −0.880 | −0.880 | −0.880 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | s1 | −5.226 | −5.226 | −5.226 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | s1 | −1.608 | −1.608 | −1.608 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | s2 | −0.855 | −0.855 | −0.855 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | s2 | −5.367 | −5.367 | −5.367 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | s2 | −1.566 | −1.566 | −1.566 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. ERL-TVITSMC | s3 | −0.087 | −0.087 | −0.087 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. PRL-TVITSMC | s3 | −0.332 | −0.332 | −0.332 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. DRL-TVITSMC | s3 | −0.110 | −0.110 | −0.110 | 14 | *** |
| Comparison | Metric | Mean | Std | CI95_Lower | CI95_Upper | t | dt | sig |
|---|---|---|---|---|---|---|---|---|
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | IAE | −2.599 | −2.599 | −2.599 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | IAE | −0.502 | −0.502 | −0.502 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-TSMC | IAE | −0.132 | −0.132 | −0.132 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | ISE | −3.435 | −3.435 | −3.435 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | ISE | −0.080 | −0.080 | −0.080 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-TSMC | ISE | −0.002 | −0.002 | −0.002 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | ITAE | −2.667 | −2.667 | −2.667 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | ITAE | −1.018 | −1.018 | −1.018 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-TSMC | ITAE | −0.308 | −0.308 | −0.308 | 14 | *** |
| Comparison | Metric | Mean | Std | CI95_Lower | CI95_Upper | t | dt | sig |
|---|---|---|---|---|---|---|---|---|
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | IAE | −0.144 | −0.144 | −0.144 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | IAE | −0.044 | −0.044 | −0.044 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-TSMC | IAE | −0.109 | −0.109 | −0.109 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | ISE | −0.081 | −0.081 | −0.081 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | ISE | −0.022 | −0.022 | −0.022 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-TSMC | ISE | −0.021 | −0.021 | −0.021 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | ITAE | −0.054 | −0.054 | −0.054 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | ITAE | −0.441 | −0.441 | −0.441 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-TSMC | ITAE | −2.719 | −2.719 | −2.719 | 14 | *** |
| Comparison | Metric | Mean | Std | CI95_Lower | CI95_Upper | t | dt | sig |
|---|---|---|---|---|---|---|---|---|
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | xe | −0.473 | −0.473 | −0.473 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | xe | −0.850 | −0.850 | −0.850 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ITSMC | xe | −0.305 | −0.305 | −0.305 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | ye | −2.306 | −2.306 | −2.306 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | ye | −2.847 | −2.847 | −2.847 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ITSMC | ye | −2.321 | −2.321 | −2.321 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | θe | −0.492 | −0.492 | −0.492 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | θe | −0.055 | −0.055 | −0.055 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ITSMC | θe | −0.055 | −0.055 | −0.055 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | s1 | −0.473 | −0.473 | −0.473 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | s1 | −0.252 | −0.252 | −0.252 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ITSMC | s1 | −0.288 | −0.288 | −0.288 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | s2 | −2.082 | −2.082 | −2.082 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | s2 | −2.055 | −2.055 | −2.055 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ITSMC | s2 | −2.082 | −2.082 | −2.082 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-SMC | s3 | −0.492 | −0.492 | −0.492 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ISMC | s3 | −0.055 | −0.055 | −0.055 | 14 | *** | ||
| Improved DPRL-TVITSMC vs. Improved DPRL-ITSMC | s3 | −0.055 | −0.055 | −0.055 | 14 | *** |
References
- Liu, L.; Yang, F.; Liu, X.; Du, Y.; Li, X.; Li, G.; Chen, D.; Zhu, Z.; Song, Z. A review of the current status and common key technologies for agricultural field robots. Comput. Electron. Agric. 2024, 227, 109630. [Google Scholar] [CrossRef]
- Yuan, J.; Huang, Z. Intelligent Agricultural Machinery and Robots: Embracing Technological Advancements for a Sustainable and Highly Efficient Agricultural Future. Agriculture 2024, 14, 2150. [Google Scholar] [CrossRef]
- Ma, Z.; Yin, C.; Du, X.; Zhao, L.; Lin, L.; Zhang, G.; Wu, C. Rice row tracking control of crawler tractor based on the satellite and visual integrated navigation. Comput. Electron. Agric. 2022, 197, 106935. [Google Scholar] [CrossRef]
- Liu, C.; Gong, L.; Yuan, J.; Li, Y. Current Status and Development Trends of Agricultural Robots. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2022, 53, 1–22+55. [Google Scholar] [CrossRef]
- Seol, J.; Park, Y.; Pak, J.; Jo, Y.; Lee, G.; Kim, Y.; Ju, C.; Hong, A.; Son, H.I. Human-Centered Robotic System for Agricultural Applications: Design, Development, and Field Evaluation. Agriculture 2024, 14, 1985. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, P.; Fang, Z.; Zheng, S.; Guo, Z.; Xing, D. Trajectory Tracking Control of the Wheeled Mobile Robot based on the Curve Tracking Algorithm. J. Phys. Conf. Ser. 2023, 2419, 012106. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, S.; Wei, J.; Qin, F. Improved biological neural network approach for path planning of differential drive agricultural robots with arbitrary shape. Comput. Electron. Agric. 2024, 216, 108525. [Google Scholar] [CrossRef]
- Zhao, X.; Lu, E.; Tang, Z.; Luo, C.; Xu, L.; Wang, H. Trajectory prediction method for agricultural tracked robots based on slip parameter estimation. Comput. Electron. Agric. 2024, 222, 109057. [Google Scholar] [CrossRef]
- Song, Y.; Xue, J.; Zhang, T.; Sun, X.; Sun, H.; Gao, W.; Chen, Q. Path tracking control of crawler tractor based on adaptive adjustment of lookahead distance using sparrow search algorithm. Comput. Electron. Agric. 2025, 234, 110219. [Google Scholar] [CrossRef]
- Wei, P.; Peng, C.; Lu, W.; Zhu, Y.; Vougioukas, S.; Fei, Z.; Ge, Z. Efficient and Safe Trajectory Planning for Autonomous Agricultural Vehicle Headland Turning in Cluttered Orchard Environments. IEEE Robot. Autom. Lett. 2025, 10, 2574–2581. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Xie, J.; Wang, X.; Liu, H.; Li, J.; Wang, P.; Yang, X. Path planning and tracking control of orchard wheel mower based on BL-ACO and GO-SMC. Comput. Electron. Agric. 2025, 228, 109696. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Shen, S.; Li, J.; Chen, Y.; Lv, J. Fuzzy Extended State Observer-Based Sliding Mode Control for an Agricultural Unmanned Helicopter. Agriculture 2025, 15, 306. [Google Scholar] [CrossRef]
- Xie, P.; Che, Y.; Liu, Z.; Wang, G. Research on Vibration Reduction Performance of Electromagnetic Active Seat Suspension Based on Sliding Mode Control. Sensors 2022, 22, 5916. [Google Scholar] [CrossRef]
- Incremona, G.P.; Rubagotti, M.; Tanelli, M.; Ferrara, A. A General Framework for Switched and Variable Gain Higher Order Sliding Mode Control. IEEE Trans. Autom. Control 2021, 66, 1718–1724. [Google Scholar] [CrossRef]
- Abrazeh, S.; Parvaresh, A.; Mohseni, S.R.; Zeitouni, M.J.; Gheisarnejad, M.; Khooban, M.H. Nonsingular Terminal Sliding Mode Control With Ultra-Local Model and Single Input Interval Type-2 Fuzzy Logic Control for Pitch Control of Wind Turbines. IEEE/CAA J. Autom. Sin. 2021, 8, 690–700. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X.; Li, S. Fast Fixed-Time Nonsingular Terminal Sliding Mode Control and Its Application to Chaos Suppression in Power System. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 151–155. [Google Scholar] [CrossRef]
- Kim, H.; Son, J.; Lee, J. A High-Speed Sliding-Mode Observer for the Sensorless Speed Control of a PMSM. IEEE Trans. Ind. Electron. 2011, 58, 4069–4077. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Gao, J.; Wang, Y.; Yan, L. An Improved Delay-Suppressed Sliding-Mode Observer for Sensorless Vector-Controlled PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5913–5923. [Google Scholar] [CrossRef]
- Lu, X.; Lin, H.; Feng, Y.; Han, J. Soft switching sliding mode observer for PMSM sensorless control. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2015, 30, 106–113. [Google Scholar]
- Zhang, H.X.; Fan, J.S.; Meng, F.; Huang, J.F. A new double power reaching law for sliding mode control. Control. Decis. 2013, 28, 289–293. [Google Scholar]
- Kang, Z.; Yu, H.; Li, C. Variable-parameter double-power reaching law sliding mode control method. Automatika 2020, 61, 345–351. [Google Scholar] [CrossRef]
- Wen, H.; Ma, X.; Qin, C.; Chen, H.; Kang, H. Research on Path Tracking of Unmanned Spray Based on Dual Control Strategy. Agriculture 2024, 14, 562. [Google Scholar] [CrossRef]
- Shamshiri, R.R.; Navas, E.; Dworak, V.; Auat Cheein, F.A.; Weltzien, C. A modular sensing system with CANBUS communication for assisted navigation of an agricultural mobile robot. Comput. Electron. Agric. 2024, 223, 109112. [Google Scholar] [CrossRef]
- Song, L.; Huang, J.; Liang, Q.; Nie, L.; Liang, X.; Zhu, J. Trajectory Tracking Strategy for Sliding Mode Control With Double Closed-Loop for Lawn Mowing Robot Based on ESO. IEEE Access 2023, 11, 1867–1882. [Google Scholar] [CrossRef]
- Yao, M.; Xiao, X.; Tian, Y.; Cui, H. A fast terminal sliding mode control scheme with time-varying sliding mode surfaces. J. Frankl. Inst. 2021, 358, 5386–5407. [Google Scholar] [CrossRef]











| Parameters | Sliding Surface | ||
|---|---|---|---|
| k11 | 0.2 | 0.2 | 1 |
| k12 | 0.2 | 0.2 | 5 |
| Parameters | Sliding Surface | ||
|---|---|---|---|
| k21 | 0.3 | 0.2 | 1.5 |
| α21 | 0.5 | 0.5 | 0.5 |
| Parameters | Sliding Surface | ||
|---|---|---|---|
| k31 | 0.2 | 0.2 | 2 |
| k32 | 0.2 | 0.2 | 2 |
| α31 | 0.1 | 0.1 | 0.2 |
| β31 | 1.1 | 1.1 | 1.2 |
| Parameters | Sliding Surface | ||
|---|---|---|---|
| k41 | 0.2 | 0.2 | 1 |
| k42 | 0.2 | 0.2 | 5 |
| k43 | 0.2 | 0.2 | 2 |
| α41 | 0.1 | 0.1 | 0.2 |
| k44 | 0.2 | 0.2 | 2 |
| β41 | 1.1 | 1.1 | 1.2 |
| Control Method | IAE/m | ISE/m | ITAE/m |
|---|---|---|---|
| ERL-TVITSMC | 0.8274 | 0.8245 | 0.3833 |
| PRL-TVITSMC | 1.009 | 0.8948 | 2.808 |
| DPRL-TVITSMC | 0.8648 | 0.8452 | 0.6234 |
| Improved DPRL-TVITSMC | 0.7629 | 0.7698 | 0.2754 |
| Control Method | IAE/rad | ISE/rad | ITAE/rad |
|---|---|---|---|
| ERL-TVITSMC | 0.0675 | 0.0297 | 0.2321 |
| PRL-TVITSMC | 0.1302 | 0.0429 | 1.034 |
| DPRL-TVITSMC | 0.0763 | 0.0333 | 0.2686 |
| Improved DPRL-TVITSMC | 0.0484 | 0.0229 | 0.1545 |
| Sliding Mode Controller | Equation |
|---|---|
| Improved DPRL-SMC | |
| Improved DPRL-ISMC | |
| Improved DPRL-ITSMC |
| Control Method | IAE/m | ISE/m | ITAE/m |
|---|---|---|---|
| Improved DPRL-SMC | 3.362 | 4.205 | 2.904 |
| Improved DPRL-ISMC | 1.265 | 0.8502 | 1.293 |
| Improved DPRL-TSMC | 0.8948 | 0.7714 | 0.5837 |
| Improved DPRL-TVITSMC | 0.7629 | 0.7698 | 0.2754 |
| Control Method | IAE/rad | ISE/rad | ITAE/rad |
|---|---|---|---|
| Improved DPRL-SMC | 0.1927 | 0.1042 | 0.2089 |
| Improved DPRL-ISMC | 0.0926 | 0.0445 | 0.5954 |
| Improved DPRL-TSMC | 0.1576 | 0.0442 | 2.873 |
| Improved DPRL-TVITSMC | 0.0484 | 0.0229 | 0.1545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Pu, D.; He, X.; Song, L.; Yang, S.X.; Ma, W.; Shi, H. Trajectory Tracking Control of an Orchard Robot Based on Improved Integral Sliding Mode Algorithm. Agriculture 2025, 15, 1881. https://doi.org/10.3390/agriculture15171881
Luo Y, Pu D, He X, Song L, Yang SX, Ma W, Shi H. Trajectory Tracking Control of an Orchard Robot Based on Improved Integral Sliding Mode Algorithm. Agriculture. 2025; 15(17):1881. https://doi.org/10.3390/agriculture15171881
Chicago/Turabian StyleLuo, Yu, Dekui Pu, Xiaoli He, Lepeng Song, Simon X. Yang, Weihong Ma, and Hanwen Shi. 2025. "Trajectory Tracking Control of an Orchard Robot Based on Improved Integral Sliding Mode Algorithm" Agriculture 15, no. 17: 1881. https://doi.org/10.3390/agriculture15171881
APA StyleLuo, Y., Pu, D., He, X., Song, L., Yang, S. X., Ma, W., & Shi, H. (2025). Trajectory Tracking Control of an Orchard Robot Based on Improved Integral Sliding Mode Algorithm. Agriculture, 15(17), 1881. https://doi.org/10.3390/agriculture15171881








