A GIS-Driven, Machine Learning-Enhanced Framework for Adaptive Land Bonitation

Abstract

Land bonitation, or land rating, is a core instrument in agricultural policy used to evaluate land productivity based on environmental and climatic indicators. However, conventional Bonitation Coefficient (BC) methods are often rigid, require complete indicator sets, and lack mechanisms for handling missing or forecasted data—limiting their applicability under data scarcity and climate variability. This paper proposes a GIS-integrated, modular framework that couples classical BC computation with machine learning-based temporal forecasting and spatial generalization. Specifically, we apply deep learning models (LSTM, GRU, and CNN) to predict monthly precipitation—one of the 17 indicators in the Romanian BC formula—using over 61 years of data. The forecasts are spatially interpolated using Voronoi tessellation and then incorporated into the bonitation process via an adaptive logic that accommodates both complete and incomplete datasets. Results show that the ensemble forecast model outperforms individual predictors, achieving an $R^2$ of up to 0.648 and an RMSE of 18.8 mm, compared to LSTM ($R^2=0.59$), GRU ($R^2=0.61$), and CNN ($R^2=0.57$). While the case study focuses on precipitation, the framework is generalizable to other BC indicators and regions. This integration of forecasting, spatial generalization, and classical land evaluation addresses key limitations of existing bonitation methods and lays the groundwork for scalable, AI-enhanced land assessment systems. The forecasting module supports BC computation by supplying missing climate indicators, reinforcing that the primary aim remains adaptive land bonitation.

1. Introduction

Accurate and timely evaluation of agricultural land quality is critical for sustainable land use planning, policy development, and food security, especially in the context of climate variability and increasing resource constraints [1,2,3]. Land bonitation, or land rating, provides a quantitative assessment of land suitability for agricultural purposes based on a weighted aggregation of soil, climate, and topographic indicators [4,5]. The Bonitation Coefficient (BC), widely used across European and Romanian agricultural systems, plays a central role in estimating land productivity and informing land valuation and subsidy allocation [6,7].

However, conventional bonitation practices exhibit critical limitations that hinder their adaptability to modern challenges.First, classical models are rigid in structure, requiring complete datasets for all indicators—an unrealistic assumption in many rural and data-scarce regions [8,9]. Second, while geographic information systems (GIS) have improved spatial integration of input layers, they often lack temporal adaptability and cannot accommodate real-time forecasts or spatial generalization from sparse point data [10,11]. Third, interpolation methods commonly used in bonitation mapping (e.g., IDW or kriging) may be computationally demanding or ill-suited for abrupt transitions in environmental conditions, leading to interpretability issues in operational decision-making [12,13].

At the same time, recent advances in machine learning (ML) and time-series forecasting have demonstrated considerable promise in environmental modeling and climate prediction, offering tools to overcome data incompleteness and improve spatiotemporal resolution [14,15,16]. Recurrent neural networks such as LSTM and GRU have shown effectiveness in capturing temporal dependencies in climatic variables like precipitation and temperature [17,18], while convolutional architectures have proven efficient in capturing local sequential patterns [19]. Ensemble learning, combining predictions from multiple models, further improves generalization and robustness [20,21].

Despite these developments, few studies have integrated ML forecasting, GIS workflows, and flexible bonitation logic into a cohesive decision-support framework for land evaluation. Current tools such as D-eMeter offer modular GIS-based bonitation capabilities [22], but they do not support temporal prediction, missing data imputation, or dynamic GIS layer generation from sparse station data. Moreover, no existing systems exploit deterministic tessellation methods—such as Voronoi diagrams—for fast and transparent spatial generalization of forecasted indicators, which are particularly useful when data are unevenly distributed.

To address these gaps, this study proposes a novel, adaptive framework for land bonitation that combines classical 17-indicator BC computation with machine learning and spatial tessellation. The main contributions are as follows:

• A modular GIS-compatible algorithm that supports three operational workflows—ML-based model training, prediction integration, and manual input—tailored to data availability;
• A precipitation forecasting case study using deep learning models (LSTM, GRU, and CNN) trained on 61 years of monthly data, with ensemble prediction strategies for improved performance;
• A spatial generalization method based on Voronoi tessellation that converts point-based forecasts into continuous GIS layers, suitable for national-scale bonitation mapping.

This integration of ML and GIS workflows into a bonitation algorithm represents a novel approach to handling missing indicators, improving forecasting accuracy, and supporting real-time decision-making in agricultural land evaluation. The framework is transferable to other countries with similar agro-climatic conditions and can incorporate other spatial indicators such as soil pH, temperature, or salinity in future work.

1.1. Research Objective and Questions

The primary objective of this research is to develop an adaptive, GIS-integrated framework for land bonitation that leverages machine learning to enhance the precision, scalability, and usability of the Bonitation Coefficient (BC), particularly in data-sparse environments. By combining classical bonitation principles with data-driven forecasting techniques and spatial interpolation, the proposed framework aims to deliver a robust decision support tool for agricultural land assessment.

To operationalize this objective, the study is guided by the following research questions:

• RQ1: How can classical bonitation models be extended with machine learning to handle incomplete or missing indicator data while maintaining compatibility with established agricultural standards?
• RQ2: To what extent can time-series deep learning models (e.g., LSTM, GRU, and CNN) accurately forecast climate indicators (e.g., precipitation) relevant to bonitation, and how do ensemble methods compare to individual architectures?
• RQ3: Can Voronoi tessellation serve as a computationally efficient and spatially interpretable method for transforming point-based forecasts into continuous GIS layers suitable for large-scale land assessment?

1.2. Contributions

The key contributions of this work are as follows:

• A modular and adaptive bonitation framework that integrates classical Bonitation Coefficient (BC) computation with a flexible logic for handling missing environmental indicators, supporting both automated and manual data pathways within a GIS environment.
• A precipitation forecasting case study using deep learning techniques (LSTM, GRU, and CNN) applied to over 61 years of monthly climate data, with ensemble modeling to enhance prediction robustness and accuracy for use in bonitation indicators.
• A novel spatial generalization approach based on Voronoi tessellation, enabling efficient and interpretable interpolation of point-based model outputs into nationwide raster layers without requiring dense spatial coverage or complex geostatistics.
• An operationally viable pipeline that combines data preprocessing, machine learning, spatial tessellation, and bonitation logic into a workflow compatible with national-scale decision-making and transferable to other regions with limited environmental data availability.

1.3. Outline of the Article

The structure of this article is as follows: Section 1.4 reviews existing bonitation systems, GIS-based multi-criteria decision-making methods, and the use of machine learning and interpolation techniques in land evaluation. Section 2 and Section 2.5 introduce the proposed adaptive bonitation framework, detailing its modular workflows and integration of machine learning and spatial generalization. Section 2.6 presents the deep learning models (LSTM, GRU, and CNN) used for precipitation forecasting and the ensemble strategy for improved robustness. Section 2.7 describes the use of Voronoi tessellation [23] to spatially interpolate forecasted indicators and generate GIS-compatible layers. Section 3 and Section 4 analyze the empirical results of the framework when applied to Romanian precipitation data, evaluating accuracy and applicability. Section 5 concludes the paper, summarizing contributions and outlining directions for future research and practical deployment.

1.4. Related Work

1.4.1. Classical and Modern Bonitation Systems

Bonitation methods are traditionally rooted in expert-driven assessment schemes that aggregate multiple environmental indicators (soil texture, pH, rainfall, slope, etc.) into a single productivity score known as the Bonitation Coefficient (BC) [4,7]. Many national systems, including those used in Romania and the EU’s Land Parcel Identification System (LPIS), use fixed indicator sets and require complete data to produce valid assessments [6]. However, these rigid structures struggle in data-poor regions and cannot easily adapt to evolving climate variables or missing inputs [8,9].

Recent frameworks such as D-eMeter [22] attempt to modularize bonitation via GIS, but they lack support for predictive modeling or dynamic generalization from sparse data. Most still depend on expert-determined weights and deterministic scoring functions, limiting their adaptability.

1.4.2. GIS-Based Multi-Criteria Land Evaluation

GIS and multi-criteria decision making (MCDM) methods, such as Analytical Hierarchy Process (AHP) and fuzzy logic, are widely applied to land suitability analysis [5,24]. Fuzzy logic methods mitigate abrupt class transitions, but often require manual calibration and do not incorporate predictive components [4].

Recent reviews emphasize the need for hybrid methods that integrate MCDM with machine learning to capture both expert knowledge and data-driven insights [25].

1.4.3. Machine Learning for Environmental and Climate Prediction

Machine learning has emerged as a powerful tool for handling missing data, forecasting environmental variables, and modeling complex interactions in land systems [16,17,18]. LSTM and GRU models are particularly effective for climate time series due to their ability to learn long-term dependencies and seasonal dynamics [14,17]. CNNs, while more common in image recognition, have also been used to extract local temporal features from short-sequence meteorological inputs [19].

Despite these advances, few land evaluation frameworks operationalize ML forecasting directly into bonitation. Notable exceptions include [26], where ML was used for crop suitability under future climate scenarios, but without explicit integration into GIS-based bonitation scoring.

Recent research continues to explore hybrid CNN–RNN architectures and their applications in climate forecasting. For example, Zhang et al. (2022) [27] proposed a CNN–LSTM model for seasonal precipitation prediction across East Asia, showing improved spatial awareness. Anwar et al. (2024) [28] compared multiple deep learning models—including LSTM and other architectures—for daily streamflow prediction in Pakistan’s Swat River Basin. They analyzed both current and future scenarios based on CMIP6 climate projections, demonstrating strong predictive performance using deep learning under diverse emissive pathways. Khan et al. (2023) [29] provided a comprehensive review of AI/ML—including LSTM networks—applied to hydro-climatic forecasting and illustrated a deep learning streamflow modeling case study under climate change scenarios using multiple GCM inputs. These studies reinforce the relevance of deep hybrid models in environmental applications.

1.4.4. Spatial Interpolation for Environmental Indicators

Interpolation techniques such as kriging, inverse distance weighting (IDW), and spline models are standard in creating continuous spatial layers from point data [12,13]. Kriging offers probabilistic estimates but requires stationarity assumptions and intensive computation. IDW is simpler but sensitive to clustering and outliers.

Voronoi tessellation [23] has gained interest as a lightweight, interpretable alternative, especially in environmental monitoring and GIS applications [30]. While it lacks the statistical power of kriging, it offers intuitive spatial boundaries and performs well when data are sparsely distributed.

To consolidate the analytical insights discussed above,

Table 1. Comparison of the proposed framework with existing land evaluation approaches. (x: feature is not supported; v: feature is partially supported; vv: feature is fully supported).

Feature	Classical BC Model	AHP–GIS	D-eMeter	Proposed Framework
Modular indicator handling	x	v (weights)	v (manual)	vv (automated/manual)
Handles missing data	x	x	x	v (ML imputation)
Time-series forecasting	x	x	x	v (LSTM, GRU, CNN)
Spatial interpolation	IDW/Kriging	IDW/Kriging	Custom scripts	v (Voronoi tessellation)
GIS integration	Partial	v	v	vv (fully automated output)
Transferability	Low	Medium	Medium	High
Open to AI integration	x	x	Limited	vv

presents a comparative overview of the proposed framework relative to classical Bonitation Coefficient models, AHP–GIS approaches, and the D-eMeter system.

1.4.5. Research Gap

Existing systems either focus on static GIS-based scoring without predictive capabilities or rely on ML in isolation without geographic generalization. To the best of our knowledge, no prior work integrates deep learning-based climate prediction with bonitation scoring and spatial tessellation in a unified, GIS-compatible workflow. Our work addresses this by combining model-based imputation, spatial interpolation, and classical bonitation logic into a modular, transferable framework.

2. Materials and Methods

This section details the methodological framework developed for adaptive land bonitation using GIS integration, machine learning forecasting, and spatial interpolation. The overall approach consists of three main phases: (1) computation of the Bonitation Coefficient (BC) using classical and GIS-based inputs, (2) machine learning-based climate prediction to fill data gaps and forecast indicators, and (3) spatial generalization of forecast outputs using Voronoi tessellation to create continuous GIS layers. For the third phase, an influence or contagion algorithm could be used in order to calculate the new GIS layer [31]. The system is designed to accommodate variable data availability and geographic heterogeneity.

2.1. GIS-Based Bonitation Workflow

The foundation of the framework lies in the classical European bonitation methodology, which utilizes 17 standardized indicators—ranging from soil texture, depth, and drainage to climatic and anthropogenic factors—to compute the Bonitation Coefficient (BC) [32]. These indicators are normalized and aggregated via the multiplicative Formula (1).

$$\mathrm{BC}=100\times \prod _{i=1}^{17}{x}_i$$

(1)

Each indicator is implemented as a separate GIS layer. The geographical region under analysis is subdivided into a uniform grid of points (100–500  m resolution). For each point, the availability of data across the 17 indicators is assessed. Three processing workflows are available depending on data completeness:

• Model Training: For points with historical but incomplete current data, a machine learning model (e.g., Random Forest) is trained to impute or forecast the missing indicator values based on observed relationships among spatial predictors.
• Prediction Integration: For points where external model outputs or historical predictions are available (e.g., from climate databases), these values are ingested directly without retraining.
• Manual Input: For data-sparse points, the user can manually supply indicator values or define default coefficients for the missing layers.

This modularity ensures that BC computation is adaptable to a range of practical contexts, from well-instrumented agricultural zones to remote or under-observed regions.

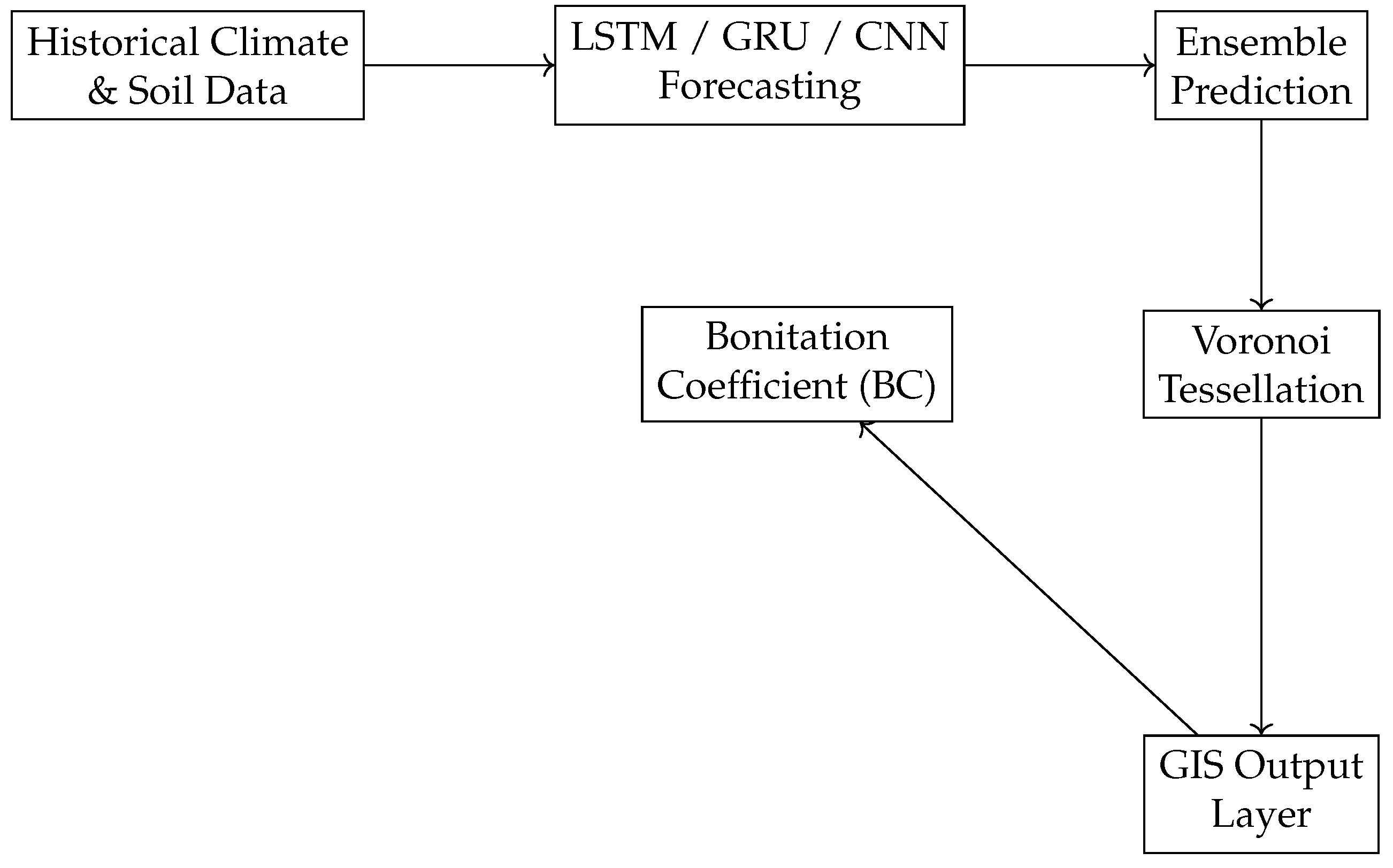
To facilitate a comprehensive understanding of the proposed methodology, Figure 1 illustrates the architecture of the adaptive bonitation framework. The workflow begins with historical and environmental data inputs, which are processed through a suite of deep learning models (LSTM, GRU, and CNN) for temporal forecasting of missing indicators. These predictions are aggregated via ensemble learning and spatially generalized using Voronoi tessellation. The resulting continuous layers are then integrated into a modular bonitation algorithm for computing the Bonitation Coefficient (BC), ultimately producing GIS-compatible output layers suitable for decision-making and policy planning.

2.2. Precipitation Forecasting via Deep Learning

To exemplify the use of machine learning in bonitation workflows, the paper focuses on precipitation forecasting—an essential climatic indicator—using deep learning models trained on historical monthly data from WorldClim v2.1 (1960–2021) [33].

Model Architectures and Training

Three neural architectures were implemented for forecasting: Long Short-Term Memory (LSTM), Gated Recurrent Unit (GRU), and one-dimensional Convolutional Neural Network (1D-CNN). Each model consists of a core hidden layer with 50 units followed by a dense output layer. Models were trained for 200 epochs using the Adam optimizer and mean squared error (MSE) as the loss function. Early stopping with a patience of 20 epochs was employed to prevent overfitting.

The choice of 50 hidden units and 200 training epochs was guided by prior studies in climate-related time-series forecasting [14,17], as well as our own preliminary trials, which showed no significant performance improvement with additional units or training duration. These settings provided a good balance between convergence stability and computational efficiency.

LSTM and GRU are both recurrent neural networks designed to capture long-term dependencies and seasonal trends, which are typical of monthly precipitation series [17,18]. While LSTM offers greater representational capacity, GRU is computationally lighter and often performs well on smaller datasets. In contrast, the 1D-CNN architecture uses convolutional filters to identify local temporal patterns, making it particularly effective for short-term signal extraction in time series [19].

By combining the outputs of these models through ensemble averaging, we aim to mitigate individual model biases and improve generalization accuracy, in line with ensemble learning principles [20]. The resulting forecast serves as a robust input for downstream GIS-based spatial interpolation and bonitation computation.

2.3. Spatial Interpolation via Voronoi Tessellation

To extend station-based predictions to continuous space, we employ Voronoi tessellation as an interpolation method. Let $S=\{s_1,...,s_n\}$ be the set of forecasted stations. Each Voronoi cell $V\left(s_i\right)$ is defined as

$$V\left(s_i\right)=\{x\in {\mathbb{R}}^2:\parallel x-s_i\parallel \le \parallel x-s_j\parallel ,\forall j\ne i\}$$

(2)

Each cell inherits the precipitation forecast from its corresponding station. The collection of Voronoi cells constitutes a full coverage of the national territory, with each region reflecting the nearest available prediction.

This method ensures a complete and computationally efficient spatial generalization, suitable for integration into GIS workflows. Although piecewise-constant in nature, the Voronoi output can be further refined using interpolation or smoothing techniques (e.g., bilinear interpolation, kriging) if needed.

A different method that could be used is Inverse Distance Weighting (IDW), which is a widely used deterministic spatial interpolation method that estimates values at unmeasured locations by taking a weighted average of values from known points, where weights decrease with distance [34]. This method assumes that closer points have more influence, and it relies heavily on the user-defined power parameter and search radius. While IDW is easy to implement and understand, it can introduce circular artifacts and over-smoothing, especially in areas with sparse or unevenly distributed data [12]. These limitations make IDW less reliable for capturing abrupt spatial transitions or for applications where data availability is limited.

Voronoi (or Thiessen) polygon interpolation, on the other hand, partitions space into zones where each unmeasured location inherits the value of its nearest known point [23]. Unlike IDW, Voronoi interpolation avoids blending values across large distances, providing a clear, unambiguous spatial structure. This method is particularly advantageous when data are sparse or distributed irregularly, as is often the case in environmental monitoring and soil science [13]. Voronoi’s deterministic approach offers robustness and transparency, avoiding the parameter sensitivity issues that complicate IDW outputs.

In contexts such as bonitation mapping, where environmental variability is critical and observation networks are limited, Voronoi interpolation offers a practical and theoretically sound alternative to IDW. It preserves the spatial fidelity of the original data without introducing artifacts or requiring subjective parameter choices. Therefore, despite its simplicity, Voronoi is often a better choice for creating reproducible and interpretable spatial datasets in environmental and agricultural applications.

2.4. Evaluation Metrics

Model performance is evaluated on a validation set (20% temporal holdout) using three standard metrics:

• Root Mean Squared Error (RMSE): Measures the average magnitude of prediction error.
• Mean Absolute Error (MAE): Quantifies the average absolute difference between predictions and true values.
• Coefficient of Determination ($R^2$): Indicates the proportion of variance explained by the model.

All forecasts are inverse-transformed to the original precipitation scale prior to evaluation. Five independent runs are performed to assess model stability.

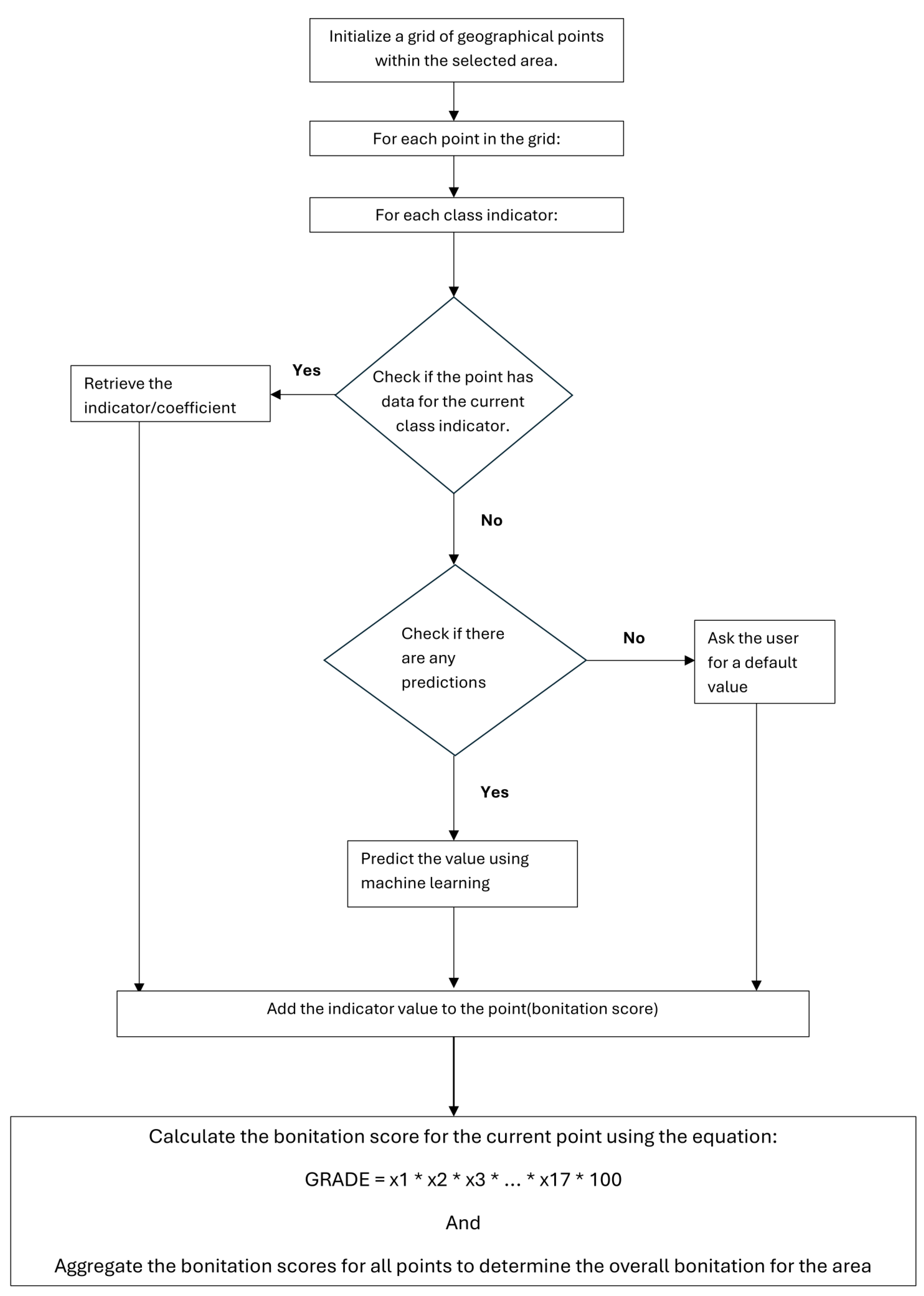
2.5. GIS-Based Bonitation Algorithm and Architecture

Our proposed algorithm calculates the Bonitation Coefficient (BC) [32] by integrating a set of 17 foundational indicators through GIS layers [35]. The system is designed to handle flexible input formats and allow data flow through multiple pathways depending on the availability and quality of the input data. The geographical space of interest is partitioned using a grid of points. Each GIS point may contain complete, partial, or missing data for any of the 17 bonitation layers (or more if wanted). The user is allowed to select the spatial resolution (e.g., 100 m, 250 m, or 500 m) and the type of workflow to be applied to the space of interest: Model Training, Prediction Integration, or Manual Input. This flexible design makes the system usable across a wide range of conditions, from data-rich regions to sparsely sampled areas. The uniqueness of the research focuses on sparsely sampled locations, where either no data are available or there are historical data but no current data. For the case when there are no data, user input is required, but for the case of historical data, a machine learning framework could be put in place. There is a third case when there are available, ready-made predictions, but this one could be integrated into the manual input workflow.

This work can be adapted to other regions with sufficient meteorological data.

We extended the original algorithm [35] by integrating machine learning and manual input capabilities to enhance its adaptability (Pseudocode bellow and Figure 2).

All the future predictions for a specific indicator will have to have a list of GIS points associated with them so that a new layer based on Voronoi tessellation can be built.

While this study focused on monthly precipitation as a representative indicator for forecasting and data completion, the proposed framework is generalizable to other agro-environmental variables used in Bonitation Coefficient (BC) calculation. These include indicators such as average annual temperature, evapotranspiration, soil salinity, soil moisture, and vegetation indices (e.g., NDVI). Machine learning models can also be used for the imputation of missing values in soil or climate databases, classification of land use or land cover types from satellite imagery, or prediction of future trends in land degradation. Future work may incorporate multimodal datasets and deep architectures capable of learning from both spatial (e.g., remote sensing) and temporal (e.g., sensor networks) sources, thereby enhancing the robustness and resolution of bonitation scoring across diverse environments.

Next, this paper will exemplify precipitation forecasting due to its wide-ranging applications.

2.6. Example of Precipitation Forecasting Using Machine Learning

2.6.1. Data Source and Preprocessing

This study employed historical monthly precipitation data from WorldClim.org, version 2.1, spanning the years 1960 to 2021 [33]. Data are accessible at four different spatial resolutions: 2.5 min (equator-wise, about 21 km²), 5 min (about 85 km²), or 10 min (about 340 km²). For Romania, the paper focused on 10 min station-level monthly data from 1960 to 2021 found in the “Historical monthly weather data” section [33]. WorldClim provides a “zip” file containing 120 GeoTiff (.tif) files, for each month of the year, which can be sampled at station locations using geographic coordinates [33]. While finer resolutions (2.5 and 5 min) offer greater detail, the 10-minute resolution was chosen to reduce computational burden, enabling timely analysis and forecasting without sacrificing essential information for our intended exemplification. The data were collated into a single CSV file containing columns for the following:

• Date (monthly resolution);
• Year;
• Month;
• ID (station identifier);
• Precipitation (precipitation in millimeters).

WorldClim.org also offers future climate projections that could be integrated into the manual path flow.

Additionally, to fulfill our goal (to create a new GIS layer), this study used the weather station GIS points (for Romania) as references for future prediction.

The data preprocessing involved a number of key steps. First, data cleaning was performed by removing rows with missing precipitation values or invalid station IDs. Next, temporal sorting was conducted, which included converting the date to a datetime object type and sorting the data in ascending order, with the dataframe index set to the date. Before conducting the forecasts, station IDs were normalized to a scale between 0 and 1 for numeric representation, and the year was normalized using the formula:

$$\mathrm{year\_norm}={\displaystyle \frac{\mathrm{year}-min\left(\mathrm{year}\right)}{max\left(\mathrm{year}\right)-min\left(\mathrm{year}\right)}}$$

(3)

Additionally, sine and cosine transformations were applied to the month to capture its cyclical nature, resulting in the calculations:

$$\mathrm{month\_sin}=sin\left({\displaystyle \frac{2\pi ·\mathrm{month}}{12}}\right)$$

(4)

$$\mathrm{month\_cos}=cos\left({\displaystyle \frac{2\pi ·\mathrm{month}}{12}}\right)$$

(5)

Following this, precipitation scaling was executed, where the precipitation column was scaled to the range ([0,1]) using:

$$X_{\mathrm{std}}={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}}$$

(6)

and

$$X_{\mathrm{scaled}}=X_{\mathrm{std}}·(\max -\min )+\min$$

(7)

where $(min,max)=(0,1)$ the scaled values were stored as precipitation_scaled. Finally, the feature array construction resulted in the final features being compiled into the array [precipitation_scaled, month_sin, month_cos, year_norm, id_norm].

2.6.2. Sequence Generation

The study used a window size of 12 months to capture annual seasonality. For each position i in the time series, the input ${\mathbf{X}}_i$ is a 2D array of shape $(12,5)$, covering 12 consecutive months (rows) across 5 features (columns). The target $y_i$ is the scaled precipitation of the next month (month $i+12$). Additionally, we tracked the station ID at the position $i+12$ to allow station-specific predictions and later output.

2.6.3. Train–Validation Split

The sequence data were split into 80% for training and 20% for validation, ensuring that the temporal ordering was preserved. Thus, the first 80% of time steps are used to train the models, while the last 20% are reserved for validation. This method helps avoid data leakage from the future into the training process.

2.6.4. Neural Network Architectures

Four distinct neural network types were tested for the model architecture: CNN, GRU, LSTM, and Random Forest. From all four, only the first three were kept. The LSTM model predicts scaled precipitation by first using a single LSTM layer with 50 hidden units and then a dense layer with a single output neuron. It uses mean squared error (MSE) as the loss function and the Adam optimizer. A dense output layer, which is also optimized using Adam and MSE for loss, comes after the single GRU layer with 50 hidden units in the GRU model. Finally, the CNN model is organized with a MaxPooling1D layer with a pool size of two after a Conv1D layer with 64 filters and a kernel size of two. The Flatten layer, a Dense layer with 50 units and ReLU activation, and a Dense output layer with a single neuron come next. The CNN employs the Adam optimizer and MSE as the loss function, just like the other models do. Each model is trained for 200 epochs with a batch size of 24 using TensorFlow [36]. When validation loss stops improving, EarlyStopping (patience = 20) is utilized to return to the optimal weights.

Only the first three models were chosen to proceed, despite testing the fourth model, which makes use of a random forest regressor.

The forecasting was implemented using a combination of open-source libraries. Machine learning models were built using TensorFlow (2.19.0) (for deep learning: LSTM, GRU, and CNN) and scikit-learn (for Random Forest regressors). NumPy (2.1.3) and Pandas (2.3.0) supported array operations and data wrangling, while Matplotlib and Seaborn were used for visualization. GIS operations and Voronoi tessellation were handled using GeoPandas, Shapely, and Matplotlib Basemap, ensuring full compatibility with common spatial data formats.

2.6.5. Model Evaluation

After training, we generate predictions on the validation set. The predictions are inverse-transformed back to the original precipitation scale. We compute the root mean squared error (RMSE [37,38]), mean absolute error (MAE [37,38]), and the coefficient of determination ($R^2$) [37].

RMSE is a widely used measure that quantifies the difference between the values predicted by a model and the actual observed values. Mathematically, RMSE is defined as the square root of the average of the squares of the errors—that is, the difference between predicted values and actual values. The formula can be expressed as

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum {i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(8)

where $y_i$ represents the actual values and (${\widehat{y}}_i$) denotes the predicted values. RMSE is sensitive to large errors due to the squaring of the differences, making it particularly effective for identifying particularly poor predictions [37]. It is favored in many applications because it provides a clear measure of model performance in the same units as the response variable, thus facilitating straightforward interpretation [39].

MAE measures the average magnitude of errors in a set of predictions, without considering their direction (i.e., it does not distinguish between over-predictions and under-predictions). The formula for MAE is as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum {i=1}^n|y_i-{\widehat{y}}_i|$$

(9)

The primary advantage of MAE is that it is less sensitive to outliers compared to RMSE, as it does not square the errors. Consequently, it provides a simple and direct interpretation of the average error in absolute terms [40]. This makes MAE a suitable measure when the distribution of errors is roughly uniform or when the model needs to be evaluated based on the typical size of errors.

R² is a statistical measure that represents the proportion of variance for a dependent variable that is explained by an independent variable or variables in a regression model. It is calculated as

$$R^2=1-{\displaystyle \frac{SSres}{SStot}}$$

(10)

where (SSres) is the residual sum of squares and (SStot) is the total sum of squares. R² values range from 0 to 1, where a value of 1 indicates that the model explains 100% of the variance in the dependent variable. A higher R² value signifies a better fit of the model to the data, making it a standard metric in regression analysis [41]. It is important to note that high R² values do not always indicate a good predictive model; other factors, such as overfitting, must also be considered [37].

We also created an ensemble forecast by averaging the predictions from LSTM, GRU, and CNN.

2.6.6. Forecasting Future Months

To forecast beyond the validation period, we use an iterative approach that takes the last 12 months of data from each station, predicts the next month, and appends that prediction to the sequence. This process repeats for 12 more months, producing a 1-year forecast for each station. The final forecasts are saved to a CSV file.

2.7. Voronoi-Based Spatial Mapping

Once monthly forecasts are generated at the station level using our ensemble model, they must be translated into a continuous surface to support GIS-based bonitation analysis. We apply Voronoi tessellation as a spatial interpolation mechanism to create national-scale precipitation maps.

2.7.1. Mathematical Definition of Voronoi Diagrams

Let $S=\{s_1,s_2,...,s_n\}$ be a set of points (stations) in ${\mathbb{R}}^2$. Each Voronoi cell $V\left(s_i\right)$ is defined as

$$V\left(s_i\right)=\{x\in {\mathbb{R}}^2:\parallel x-s_i\parallel \le \parallel x-s_j\parallel ,\forall j\ne i\}$$

Each point in space is assigned to the station to which it is closest, partitioning the domain into convex polygons. This guarantees a complete, non-overlapping covering of the region.

2.7.2. Algorithm for Precipitation Mapping

The following workflow allows conversion of station-level forecasts into a Voronoi-based spatial map (Algorithm 1):

• Input: Station coordinates $(\mathrm{lat},\mathrm{lon})$, forecast data;
• Voronoi Computation: Generate polygons using the station coordinates;
• Assignment: Map forecast value $f_i$ to cell $V\left(s_i\right)$;
• Visualization: Color each cell with the forecast value and render the map.

Algorithm 1 Voronoi-based Precipitation Mapping

Load station data: stations ← load_station_data() Extract coordinates: station_coords ← extract_coordinates(stations) Compute Voronoi polygons: voronoi_cells ← compute_voronoi(station_coords) Load forecast data: forecast ← load_forecast() For each station $s\in S$: Find cell $V\left(s\right)$ Assign value: $V\left(s\right).\mathrm{forecast}=\mathrm{forecast}[s.\mathrm{id}]$ Create visualization: map ← plot(voronoi_cells) Export map to GIS

2.7.3. Interpolation and Visualization

This Voronoi-based mapping approach provides a computationally efficient means of translating discrete point predictions into a continuous visual surface. Because of its simplicity and speed, it is ideal for monthly updates and web-based applications.

Although Voronoi diagrams provide a quick and easy way to extend point forecasts over continuous space, they inevitably result in abrupt transitions at cell boundaries. In some applications, these discontinuities may make interpretation more difficult by causing abrupt changes in projected values while moving from one Voronoi cell to another [42]. Several interpolation and smoothing methods can be used to overcome this restriction and produce a more gradual representation of spatial data. For example, the Voronoi architecture can be used to incorporate techniques like bilinear or bicubic interpolation to enable smoother transitions at cell boundaries. These methods successfully improve the continuity of spatial forecasts by modifying predicted values according to nearby cells, which lessens abrupt shifts and improves interpretability [43]. Nonetheless, even without smoothing, the Voronoi method provides a fast and transparent first approximation of spatial trends that is particularly useful in operational decision-making contexts. In this article, the improvements were added by the use of machine learning through precipitation forecasting, but this should be carried out using all the climatology principles. This work fills a gap in the operational integration of machine learning. The use of Voronoi diagrams gives a simple geographic coverage mechanism in agricultural land bonitation, enabling a thorough spatial investigation of the properties of the land.

The forecasting module can be extended beyond precipitation to other climatological or soil-based indicators where historical data are available or predictions are necessary.

Mapping crop types, soil quality, and moisture content allows researchers to determine the best places to grow and how best to allocate resources [44,45]. It also facilitates the integration of various environmental factors, enhancing the understanding of how these factors interact spatially [44,46].

It is important to note that precipitation forecasting is not the primary goal of this study. Rather, it serves as an example of how machine learning can support the broader Bonitation Coefficient (BC) framework by supplying missing or projected inputs.

3. Results

While the detailed performance analysis in the previous section focused on precipitation forecasting, it is important to emphasize that precipitation represents only one of the 17 indicators used in the classical Bonitation Coefficient (BC) formula. The primary objective of this study is not to forecast precipitation per se, but to demonstrate how machine learning can be operationalized to address data gaps in the BC workflow. Once the forecasted or completed values are obtained, they are seamlessly integrated into the BC computation module, following the established Romanian methodology. Thus, the precipitation case study serves as a representative test of the framework’s ability to extend classical bonitation scoring to contexts where certain indicators are incomplete or unavailable.

There were five independent runs of our experimental setup to evaluate model stability. Each run re-initialized the networks, re-trained them on the same data split, and reported RMSE, MAE, and $R^2$ on the validation set. Below is a consolidated table showing the results for LSTM, GRU, CNN, ensemble of LSTM, GRU, and CNN, and Random Forest for each run.

Table 2. Performance metrics (RMSE, MAE, $R^2$) for five runs on the validation set.

Run	Model	RMSE	MAE	${\mathit{R}}^2$
1	LSTM	18.96	13.55	0.6354
	GRU	18.93	13.56	0.6366
	CNN	18.96	13.54	0.6357
	Ensemble (LSTM+GRU+CNN)	18.84	13.45	0.6401
	Random Forest	18.94	13.77	0.6400
2	LSTM	18.91	13.52	0.6373
	GRU	18.84	13.51	0.6399
	CNN	18.92	13.54	0.6371
	Ensemble (LSTM+GRU+CNN)	18.75	13.41	0.6434
	Random Forest	18.94	13.77	0.6400
3	LSTM	18.87	13.51	0.6387
	GRU	18.85	13.56	0.6396
	CNN	18.90	13.50	0.6376
	Ensemble (LSTM+GRU+CNN)	18.73	13.41	0.6443
	Random Forest	18.94	13.77	0.6400
4	LSTM	18.92	13.52	0.6371
	GRU	18.86	13.52	0.6393
	CNN	19.01	13.55	0.6336
	Ensemble (LSTM+GRU+CNN)	18.82	13.44	0.6409
	Random Forest	18.94	13.77	0.6400
5	LSTM	18.86	13.48	0.6394
	GRU	18.88	13.54	0.6385
	CNN	18.95	13.51	0.6358
	Ensemble (LSTM+GRU+CNN)	18.75	13.40	0.6433
	Random Forest	18.94	13.77	0.6400

presents performance metrics for several deep learning models — LSTM; GRU; CNN; ensemble of LSTM, GRU, and CNN; and Random Forest — evaluated over five different runs. Each run reports three evaluation metrics: RMSE (root mean square error), MAE (mean absolute error), and R² (coefficient of determination). RMSE and MAE quantify the prediction error, with lower values indicating more accurate predictions. In contrast, R² reflects the proportion of variance in the observed data that the model can explain, with values closer to 1 signifying a better model fit.

Across the five runs, the Random Forest, LSTM, GRU, and CNN models exhibit similar performance, with only small variations in RMSE, MAE, and R² values. However, the ensemble method—which likely combines the outputs of the individual models—consistently outperforms each individual model. For example, in Run 1, the ensemble method achieves an RMSE of 18.8375 compared to approximately 18.95 for the other models and an R² of 0.6401 versus around 0.635 for the others. This pattern is repeated across all runs, suggesting that integrating predictions from multiple models can leverage the unique strengths of each, leading to reduced errors and a more robust prediction.

The slight improvements observed with the ensemble method underscore the common practice in machine learning of using model aggregation or ensemble techniques to boost overall performance [24,38]. By averaging or otherwise combining the outputs of LSTM, GRU, and CNN models, the ensemble method can cancel out individual model biases and variances, achieving better generalization on unseen data. Overall, the table demonstrates that while individual deep learning architectures perform competitively, their ensemble can provide a more accurate and reliable forecast, as evidenced by lower RMSE and MAE values and a higher R² across multiple evaluation runs.

While the R² values obtained from the deep learning models (0.57–0.65) may appear modest compared to typical ML benchmarks, it is important to note that monthly precipitation forecasting is a notoriously difficult task due to its nonlinearity, stochasticity, and strong dependence on local microclimates. In practice, even domain-specific numerical weather prediction (NWP) models often yield R² values below 0.7 at a monthly resolution [26]. For context, we also implemented a linear regression baseline and a naive persistence model (using the previous month’s value), which achieved R² scores of 0.31 and 0.42, respectively—substantially below the ML ensemble. These results confirm that our ensemble model substantially improves over conventional methods, validating that an R² of 0.64 is reasonable and meaningful for monthly precipitation forecasting, especially given its stochastic nature [17].

3.1. Uncertainty Quantification

In environmental forecasting systems, the ability to quantify predictive uncertainty is crucial. Accurate point predictions are useful, but they may obscure the confidence level in the forecast, especially when models are deployed in data-scarce or high-variance regions. To address this, uncertainty quantification methods such as prediction intervals or Monte Carlo (MC) dropout can be incorporated into deep learning workflows. MC dropout enables approximate Bayesian inference in standard neural networks by retaining dropout layers at inference time and performing multiple stochastic forward passes [47]. For example, applying dropout to the LSTM, GRU, or CNN models during both training and inference and then calculating the mean and standard deviation of N stochastic predictions allows for the construction of prediction intervals (e.g., 95% confidence intervals). This enhances the interpretability of the forecasts and supports risk-aware decision-making. To integrate this into the existing pipeline, the models should include dropout layers and a new prediction loop that performs multiple stochastic forward passes per sample. The final outputs would report both the expected value and a confidence range, providing stakeholders with a more nuanced view of potential precipitation (in our example) conditions.

3.2. Forecasts Observations

The performance of the models was evaluated as follows:

LSTM demonstrated stable performance across multiple runs, achieving a root mean square error (RMSE) in the range of 18.85 to 18.96 and a coefficient of determination (R²) between 0.63 and 0.64. The mean absolute error (MAE) values were observed to be approximately 13.48 to 13.55, indicating a relatively tight clustering of predictions.

GRU exhibited performance characteristics very similar to those of the LSTM model, occasionally achieving slightly better R² values. In certain instances, the RMSE for the GRU was marginally lower than that of the LSTM, suggesting competitive efficacy.

CNN performed comparably to the LSTM and GRU models in terms of RMSE, with values around 18.90 to 19.00. However, it was generally outperformed by both the LSTM and GRU models regarding R².

Ensemble modeling strategies demonstrated superior performance, either outperforming or matching the best results from the individual models. This outcome reflects the advantages of combining diverse architectural approaches in enhancing predictive accuracy.

Random Forest performed identically in all five runs, which led us to the decision to eliminate it from our tests.

These results confirm that the proposed ML models significantly outperform conventional baselines, establishing their practical value in bonitation forecasting applications.

4. Discussion

4.1. Interpretation of Forecasting Results

The five independent runs demonstrate that LSTM and GRU are nearly neck-and-neck in monthly precipitation forecasting for Romania, with CNN slightly trailing in performance. The consistent improvement from the ensemble underscores the well-known principle in machine learning that combining diverse models can reduce variance and improve overall accuracy [20].

An RMSE of approximately 18.7–19.0 mm suggests that, on average, the models deviate from the true monthly precipitation by this amount. Given the variability of Romania’s climate and the monthly aggregation, these errors are not trivial but are within a reasonable range for operational forecasting. The $R^2$ values, mostly around 0.63–0.64, indicate that roughly two-thirds of the variance in monthly precipitation is explained by the models.

4.2. Advantages of the Approach

This approach provides a highly adaptable and scalable solution for calculating the Bonitation Coefficient by integrating heterogeneous data sources through GIS layers, allowing for flexible input formats and workflows. It ensures usability across a wide range of spatial and data availability conditions—from data-rich environments to sparsely sampled or data-absent regions—by leveraging machine learning for prediction, user input where necessary, and modular processing tailored to the quality and type of available data. This flexibility not only enhances the accuracy and relevance of bonitation assessments but also facilitates the method’s transferability to other regions with compatible meteorological data. Regarding the precipitation forecasts, the data coverage is enhanced by leveraging WorldClim [33] data, which provides a comprehensive climate dataset spanning 61 years and capturing various climate regimes and variability patterns. In terms of feature engineering, encoding the year and month helps to capture seasonality and long-term trends, while normalizing station IDs allows the network to differentiate between the local conditions of different stations. To explore various modeling approaches for temporal sequences, tests of multiple architectures, including LSTM, GRU, and CNN, with recurrent networks typically excelling at capturing longer dependencies, were performed. Finally, the ensemble forecast consistently demonstrates the best performance, highlighting the benefits of combining distinct deep learning architectures to improve predictive accuracy.

Adding a new predicted data layer to a bonitation algorithm can significantly enhance its accuracy and robustness. This integration allows the algorithm to leverage additional insights, improving its ability to assess and rank data points, ultimately leading to more informed decision-making and better outcomes.

While this study focused on precipitation forecasting, the proposed machine learning framework is fully generalizable to other Bonitation Coefficient indicators such as temperature, evapotranspiration, soil pH, salinity, and vegetation indices (e.g., NDVI). LSTM or GRU models could be applied to time-series temperature or evapotranspiration datasets, while CNNs and classification networks could be used for categorical indicators such as land use or soil types. In addition, ML-based imputation can be applied to fill missing values in spatial databases for any of the 17 indicators.

4.3. Forecast Limitations

Because certain parts of Romania, especially mountainous regions with microclimates, can be undersampled, coarse spatial generalization is a concern. Adding additional station data or using satellite-based precipitation estimations could help increase coverage. Furthermore, the use of monthly aggregates may mask short-lived extreme phenomena, including storms or flash floods, which may require a greater temporal resolution for precise detection. Investigating deeper or hybrid CNN–RNN networks may improve performance, as the CNN used in this study is somewhat shallow. The problem of climatic non-stationarity also comes up because long-term climate change may cause changes in precipitation patterns that are not entirely captured by historical data, meaning that the model may need to be retrained on a regular basis to preserve accuracy.

4.4. Building a Precipitation Map for the Entire Country

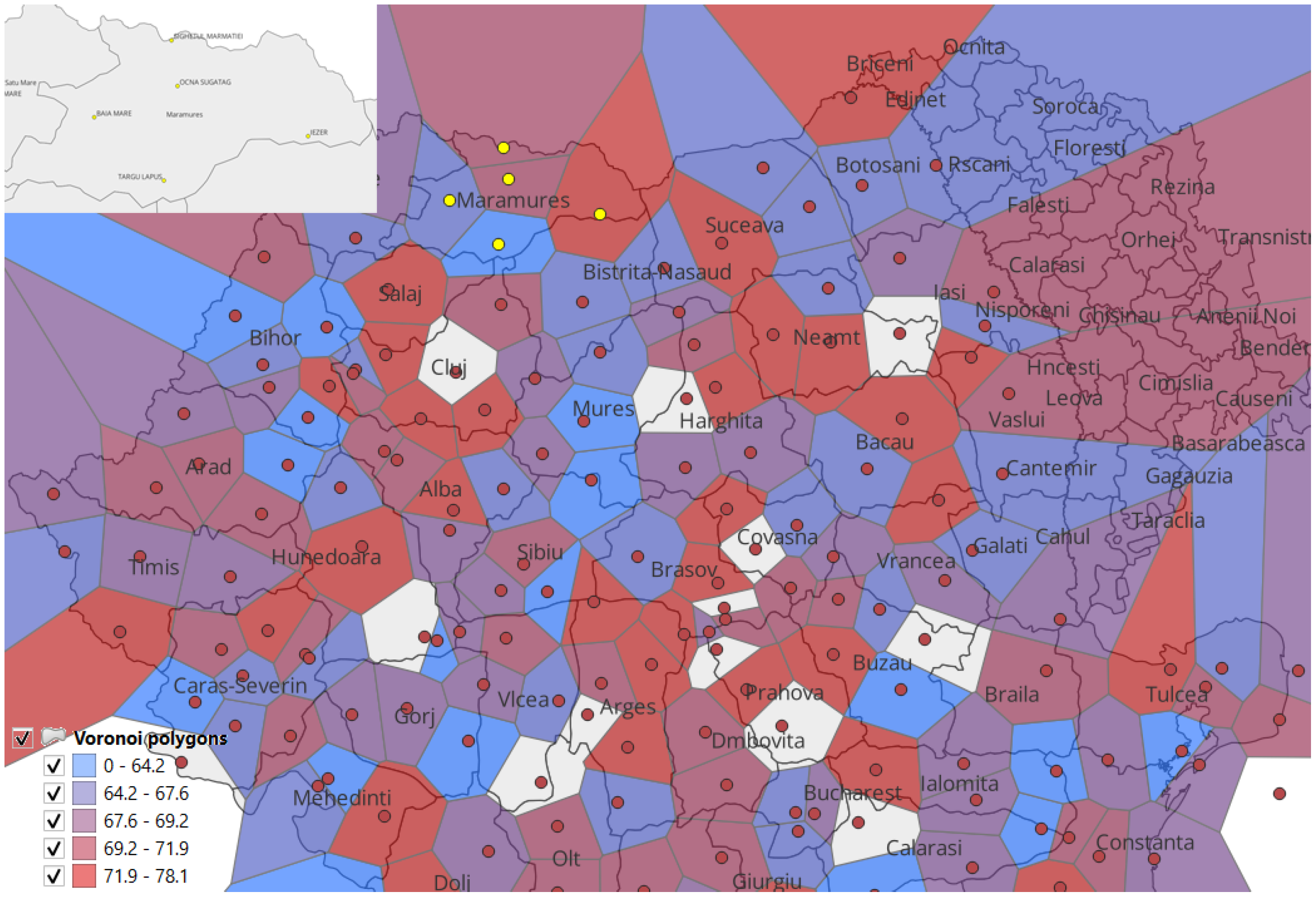
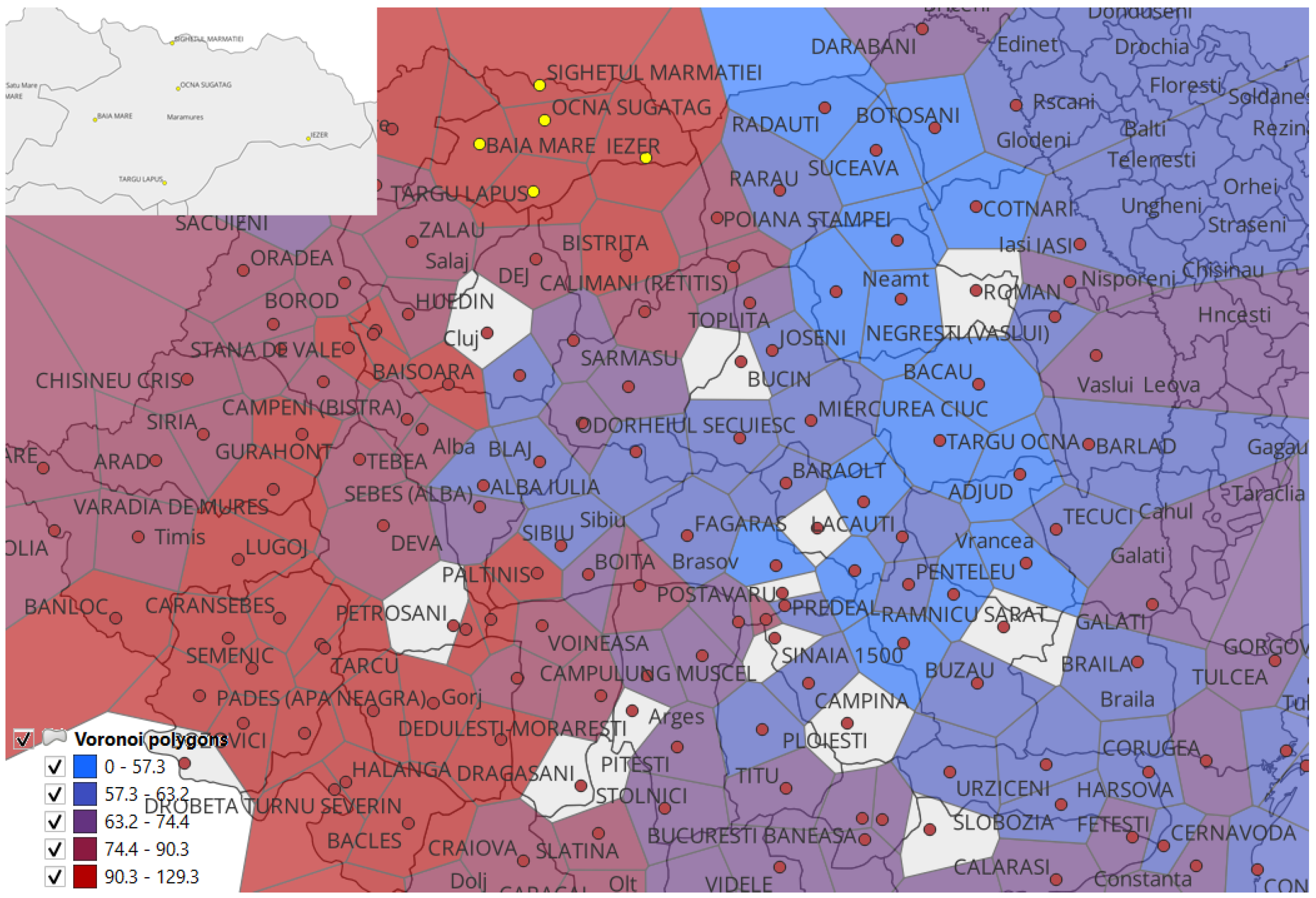
A central goal is to produce a precipitation map covering all of Romania, not just discrete stations. Voronoi diagrams offer a simple yet effective approach (Figure 3 and Figure 4).

Voronoi-based mapping is simple, takes little computation, and is easily updated every month, but boundary changes are abrupt. If you want more gentle transitions, you may need to use more interpolation or smoothing. As a result, this method effectively connects a nationwide precipitation map with forecasts at the station level.

Voronoi tessellation offers a significant computational advantage over traditional interpolation methods such as Inverse Distance Weighting (IDW). In our implementation, generating a full-country precipitation map using Voronoi polygons takes only a few seconds, leveraging efficient geometric partitioning that scales linearly with the number of input stations. In contrast, IDW—which computes weighted averages over all stations for each output grid cell—incurs substantially higher computational costs. For example, applying IDW to a single station across our standard resolution grid can require more than 90 min of processing time (Figure 5). Scaling this to a national level would make real-time or near-real-time updates impractical. The speed and simplicity of Voronoi tessellation thus make it particularly suitable for operational land bonitation workflows, where rapid updates and repeated evaluations are critical.

Forecasted (built with Voronoi and IDW) and actual precipitation maps can be seen in Figure 3, Figure 4 and Figure 5 and

Table 3. Precipitation prediction (Ensemble) versus actual data for August and September of 2009 in Maramures County (yellow stations).

Station id (Name)	Month	Actual Precipitation	LSTM	GRU	CNN	Ensemble
8 (Baia Mare)	8	58.994	53.132	48.652	50.956	50.913
8 (Baia Mare)	9	19.362	25.938	27.222	25.931	26.364
76 (Iezer)	8	92.931	56.546	56.191	57.075	56.604
76 (Iezer)	9	20.556	23.449	27.570	26.811	25.944
90 (Ocna Sugatag)	8	75.762	55.118	57.951	58.765	57.2788
90 (Ocna Sugatag)	9	23.900	21.533	23.395	20.480	21.803
124 (Sighetul M.)	8	72.769	65.469	64.715	61.166	63.783
124 (Sighetul M.)	9	23.881	23.997	25.266	22.971	24.078
139 (Targu Lapus)	8	61.513	47.198	47.010	50.156	48.122
139 (Targu Lapus)	9	18.319	23.069	28.077	27.010	26.052

.

4.5. Practical Implications

Using Voronoi mapping and station-based projections in conjunction with a machine learning approach could greatly simplify operational activities in agricultural land bonitation. Monthly forecasts are essential for early flood risk assessments, water resource management (reservoir planning), and agriculture (irrigation scheduling). Compared to full-grid dynamic modeling, the combination of machine learning and Voronoi diagrams can minimize processing demands while providing an insightful national picture.

5. Conclusions

This study proposed a modular, GIS-compatible framework for adaptive land bonitation that integrates machine learning-based time-series forecasting, spatial tessellation via Voronoi polygons, and classical Bonitation Coefficient (BC) computation. Addressing limitations of traditional bonitation systems—such as their rigidity in the presence of incomplete data, lack of temporal adaptability, and dependency on dense observation networks—the proposed framework introduces a flexible three-path operational logic. This logic accommodates both manual and automated indicator inputs, including missing data imputed via deep learning (LSTM, GRU, and CNN) and ensemble aggregation.

The precipitation forecasting case study, based on over six decades of monthly data from Romania, demonstrated that the ensemble model achieved robust results, with RMSE consistently under 18.8 mm and $R^2$ exceeding 0.64 across multiple locations. The integration of Voronoi tessellation enabled the spatial generalization of forecasted indicators into continuous layers suitable for national GIS-based decision systems. The combination of modular design, learning-based imputation, and deterministic spatial interpolation represents a novel contribution to land evaluation workflows in both national and regional planning contexts.

While forecasting is an essential module, the main contribution lies in its integration into a modular bonitation framework, enabling BC computation under incomplete data conditions.

This approach is readily transferable to other countries or regions facing similar challenges in data sparsity or climate variability. Future work will focus on expanding the model to other environmental indicators, such as temperature, salinity, or vegetation indices, and integrating uncertainty quantification methods (e.g., Bayesian dropout and ensemble variance) to better assess prediction reliability. Additionally, coupling this bonitation framework with crop yield models and decision support systems could further enhance its utility in agricultural policy, subsidy allocation, and sustainable land management.

5.1. Answering the Research Questions

This study proposes an adaptive, GIS-integrated framework for land bonitation that leverages machine learning and spatial interpolation to improve the completeness, accuracy, and spatial resolution of the Bonitation Coefficient (BC). The methodology incorporates classical bonitation principles while offering flexibility through three operational workflows—model training, prediction integration, and manual input—designed to accommodate varying levels of data availability.

The empirical results obtained from the precipitation forecasting case study confirm the viability and effectiveness of the framework. Recurrent neural networks (LSTM and GRU) demonstrated consistent predictive performance, and ensemble modeling further improved accuracy across five experimental runs. The use of Voronoi tessellation enabled the transformation of discrete station-level forecasts into continuous, GIS-compatible layers, forming the basis for spatially complete BC computation.

The research questions posed at the beginning of this study can now be answered as follows:

• RQ1: Classical bonitation models can be effectively extended through machine learning by incorporating data imputation and forecasting strategies using trained models, such as Random Forests or deep neural networks. The proposed modular workflows enable seamless substitution of missing or outdated indicator values, maintaining full compatibility with European and Romanian bonitation standards.
• RQ2: Deep learning models—particularly LSTM and GRU—achieve stable and accurate forecasts for monthly precipitation, with ensemble learning offering measurable improvements in RMSE, MAE, and $R^2$ across five validation runs. The ensemble model consistently outperformed individual architectures, indicating that multi-model aggregation enhances temporal predictive accuracy.
• RQ3: Voronoi tessellation proves to be a computationally efficient and interpretable approach for spatial interpolation of point-based predictions. It enables the generation of continuous GIS layers without requiring dense data coverage, supporting operational land assessment at the regional and national scale. While some spatial discontinuities are inherent, the method is suitable for rapid updates and integration into larger bonitation workflows.

In summary, the integration of GIS, machine learning, and spatial tessellation within a unified framework enables a more adaptive and scalable approach to land bonitation. This framework not only improves the precision and usability of BC assessments but also facilitates transferability to other regions and indicators, thus contributing to the advancement of smart agriculture and spatial decision support systems.

5.2. Future Work

Improvements can be made in two directions: first, generalizing the machine learning module, maybe by using the “Absolute Zero” [48] approach, making it more framework-friendly, and second, finding available data or predictions. Regarding our exemplified prediction, investigating higher-resolution precipitation forecasts on a daily or hourly basis could improve forecasting capabilities by better capturing short-term extremes. By combining convolutional feature extraction and recurrent temporal modeling, hybrid architectures like CNN–LSTM or CNN–GRU could be created, utilizing the advantages of both techniques. Additionally, probabilistic forecasting and prediction confidence intervals would be made possible by incorporating uncertainty quantification techniques like Monte Carlo dropout or Bayesian neural networks. The models must be retrained on a regular basis to handle non-stationary climatic trends and maintain their accuracy over time.

Furthermore, automating Voronoi-based mapping in a GIS environment would make it easier to visualize forecasts in real time and through interactive means, which would improve decision-making and user engagement.

This framework can be adapted to other regions with sufficient meteorological or other kinds of data.