Neural Network-Based SLAM/GNSS Fusion Localization Algorithm for Agricultural Robots in Orchard GNSS-Degraded or Denied Environments
Abstract
1. Introduction
2. Materials and Methods
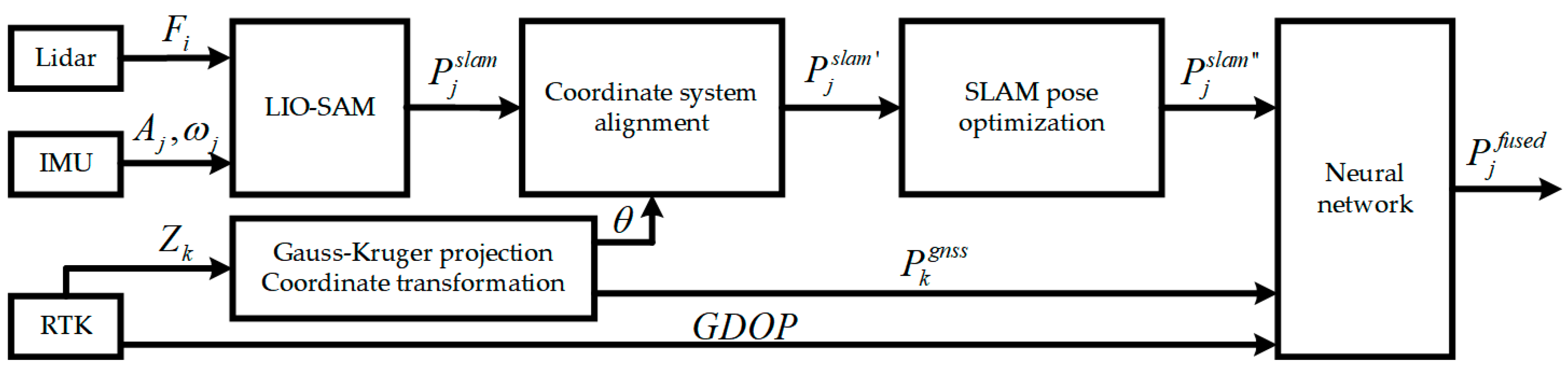
2.1. Algorithm Framework
2.2. SLAM/GNSS Fusion Localization Algorithm
2.2.1. LiDAR-Inertial Odometry
2.2.2. Coordinate System Alignment
2.2.3. SLAM Pose Optimization
2.2.4. Neural Network-Based Dynamic Weight Adjustment
| Algorithm 1. The pseudocode for the neural network-based dynamic weight adjustment algorithm. |
| Input: M, , , , , , , GDOP Output: , , ,
|
2.3. Robotic Platform Experiments
2.3.1. Experimental Platform
2.3.2. Experimental Protocol
2.4. Orchard Experiments
2.4.1. Experimental Platform
2.4.2. Experimental Protocol
3. Results and Discussion
3.1. Analysis of Neural Network Model Training Results
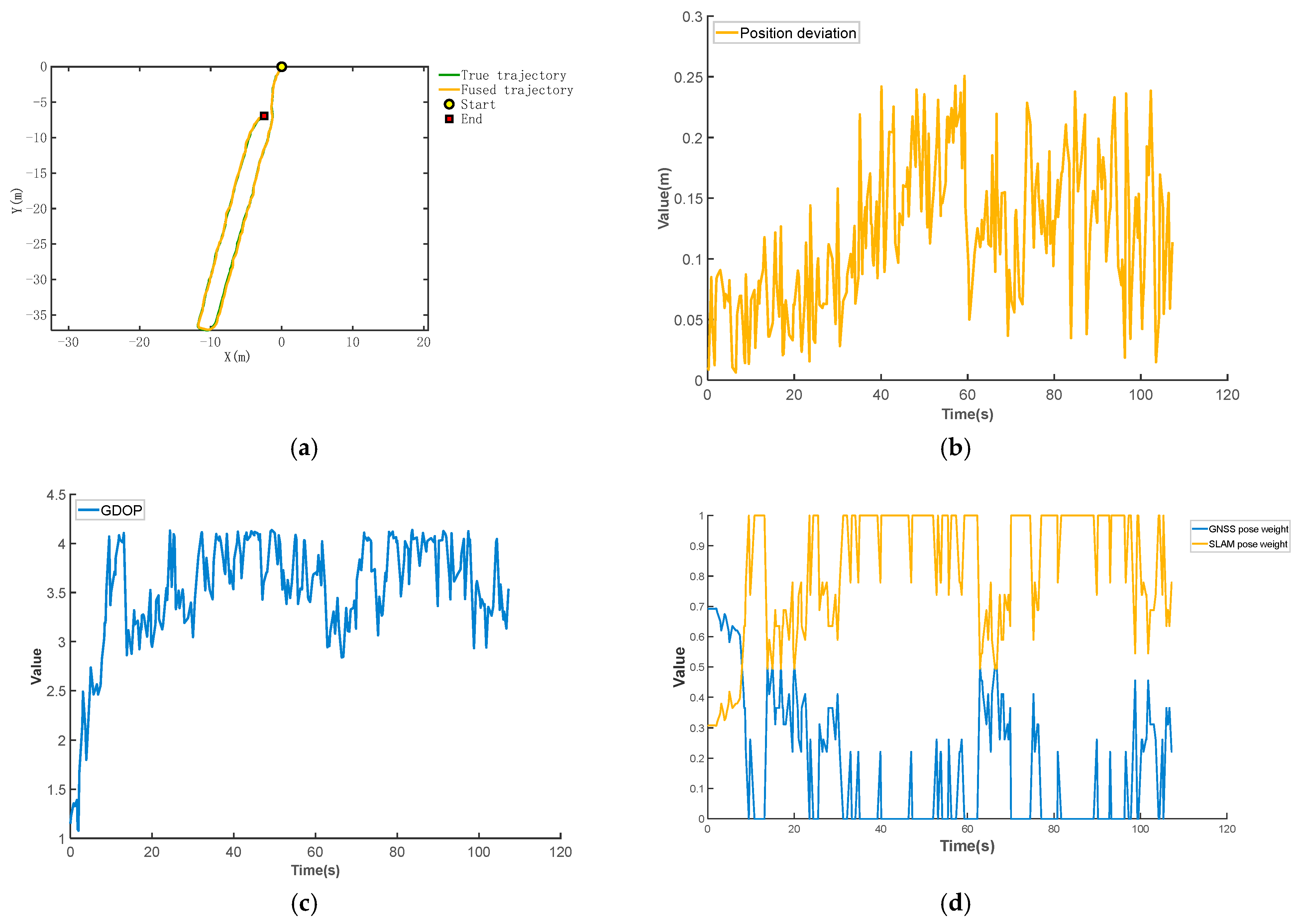
3.2. Analysis of Robotic Platform Experimental Results
3.3. Analysis of Orchard Experimental Results
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, X.W.; Hu, L.; He, J.; Zhang, Z.G.; Zhou, Z.Y.; Zhang, W.Y.; Liao, J.; Huang, P.K. Key Technologies and Practice of Unmanned Farm in China. Trans. Chin. Soc. Agric. Eng. 2024, 40, 1–16. [Google Scholar] [CrossRef]
- Liu, J.Z.; Jiang, Y.X. Industrialization Trends and Multi-arm Technology Direction of Harvesting Robots. Trans. Chin. Soc. Agric. Mach. 2024, 55, 1–17. [Google Scholar] [CrossRef]
- Sun, Z.Q.; Tang, S.Y.; Luo, X.F.; Dong, J.W.; Xu, N. Research and Application Status of Path Planning for Agricultural Inspection Robots. Agric. Equip. Veh. Eng. 2025, 63, 18–24. [Google Scholar] [CrossRef]
- Wang, N.; Han, Y.X.; Wang, Y.X.; Wang, T.H.; Zhang, M.; Li, H. Research Progress of Agricultural Robot Full Coverage Operation Planning. Trans. Chin. Soc. Agric. Mach. 2022, 53, 1–19. [Google Scholar] [CrossRef]
- Zhang, M.; Ji, Y.H.; Li, S.C.; Cao, R.Y.; Xu, H.Z.; Zhang, Z.Q. Research Progress of Agricultural Machinery Navigation Technology. Trans. Chin. Soc. Agric. Mach. 2020, 51, 1–18. [Google Scholar] [CrossRef]
- Xu, T.; Zhou, Z.Q. Current Status and Trends of Agricultural Robotics Development. Agric. Equip. Technol. 2024, 2025, 51. [Google Scholar]
- Chen, Y.; Zhang, T.M.; Sun, D.Z.; Peng, X.D.; Liao, Y.Y. Design and experiment of locating system for facilities agricultural vehicle based on wireless sensor network. Trans. Chin. Soc. Agric. Eng. 2015, 31, 190–197. [Google Scholar] [CrossRef]
- Ma, Q.; Tang, G.Y.; Fu, Z.Y.; Deng, H.G.; Fan, J.N.; Wu, C.C. Research progress on autonomous agricultural machinery technology and automatic parking methods in China. Trans. Chin. Soc. Agric. Eng. 2025, 41, 15–27. [Google Scholar] [CrossRef]
- Liu, C.L.; Gong, L.; Yuan, J.; Li, Y.M. Development Trends of Agricultural Robots. Trans. Chin. Soc. Agric. Mach. 2022, 53, 1–22, 55. [Google Scholar] [CrossRef]
- Liu, Z.P.; Zhang, Z.G.; Luo, X.W.; Wang, H.; Huang, P.K.; Zhang, J. Design of automatic navigation operation system for Lovol ZP9500 high clearance boom sprayer based on GNSS. Trans. Chin. Soc. Agric. Eng. 2018, 34, 15–21. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Luo, X.W.; Zhao, Z.X.; Huang, P.S. Trajectory Tracking Control Method Based on Kalman Filter and Pure Pursuit Model for Agricultural Vehicle. Trans. Chin. Soc. Agric. Mach. 2009, 40, 6–12. [Google Scholar]
- Ding, Y.C.; He, Z.B.; Xia, Z.Z.; Peng, J.Y.; Wu, T.H. Design of navigation immune controller of small crawler-type rape seeder. Trans. Chin. Soc. Agric. Eng. 2019, 35, 12–20. [Google Scholar] [CrossRef]
- Li, Q.T.; Liu, B. Design and Path Planning of Agricultural Machinery Automatic Navigation System Based on GNSS. Test. Meas. Technol. 2024, 38, 256–263. [Google Scholar] [CrossRef]
- Hu, J.T.; Gao, L.; Bai, X.P.; Li, T.C.; Liu, X.G. Review of research on automatic guidance of agricultural vehicles. Trans. Chin. Soc. Agric. Eng. 2015, 31, 1–10. [Google Scholar] [CrossRef]
- Ji, C.Y.; Zhou, J. Current Situation of Navigation Technologies for Agricultural Machinery. Trans. Chin. Soc. Agric. Mach. 2014, 45, 44–54. [Google Scholar] [CrossRef]
- Luo, X.W.; Liao, J.; Hu, L.; Zhou, Z.Y.; Zhang, Z.G.; Zang, Y.; Wang, P.; He, J. Research progress of intelligent agricultural machinery and practice of unmanned farm in China. J. South China Agric. Univ. 2021, 42, 8–17. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Z.W.; Xu, Z.S.; Huang, Z.D.; Jing, J.S.; Niu, R.X. Inter-rows Navigation Method of Greenhouse Robot Based on Fusion of Camera and LiDAR. Trans. Chin. Soc. Agric. Mach. 2023, 54, 32–40. [Google Scholar] [CrossRef]
- Yousuf, S.; Kadri, M.B. Information Fusion of GPS, INS and Odometer Sensors for Improving Localization Accuracy of Mobile Robots in Indoor and Outdoor Applications. Robotica 2021, 39, 250–276. [Google Scholar] [CrossRef]
- Yin, X.; Wang, Y.X.; Chen, Y.L.; Jin, C.Q.; Du, J. Development of autonomous navigation controller for agricultural vehicles. Int. J. Agric. Biol. Eng. 2020, 13, 70–76. [Google Scholar] [CrossRef]
- He, Y.; Huang, Z.Y.; Yang, N.Y.; Li, X.Y.; Wang, Y.W.; Feng, X.P. Research Progress and Prospects of Key Navigation Technologies for Facility Agricultural Robots. Smart Agric. 2024, 6, 1–19. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, J.; Pan, D.; Zhao, L.J.; Li, M.S. Localization Method for Agricultural Robots Based on Fusion of LiDAR and IMU. Smart Agric. 2024, 6, 94–106. [Google Scholar] [CrossRef]
- Jin, B.; Li, J.X.; Zhu, D.K.; Guo, J.; Su, B.F. GPS/INS navigation based on adaptive finite impulse response-Kalman filter algorithm. Trans. Chin. Soc. Agric. Eng. 2019, 35, 75–81. [Google Scholar] [CrossRef]
- Cao, J.J.; Fang, J.C.; Sheng, W.; Bai, H.X. Adaptive neural network prediction feedback for MEMS-SINS during GPS outage. J. Astronaut. 2009, 30, 2231–2236, 2264. [Google Scholar] [CrossRef]
- Shen, C.; Zhang, Y.; Tang, J.; Cao, H.; Liu, J. Dual-optimization for a MEMS-INS/GPS system during GPS outages based on the cubature Kalman filter and neural networks. Mech. Syst. Signal Process. 2019, 133, 106222. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Hao, L.L.; Huang, S.J.; Zhu, S.Y. A New Study of Neural Network Aided GPS/MEMS-INS Integrated Navigation. J. Geomat. Sci. Technol. 2014, 31, 336–341. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Wang, J.; Zhang, Z.G.; He, J.; Hu, L.; Luo, X.W. Self-calibrating Variable Structure Kalman Filter for Tractor Navigation during BDS Outages. Trans. Chin. Soc. Agric. Mach. 2020, 51, 18–27. [Google Scholar] [CrossRef]
- Wei, Y.F.; Li, Q.L.; Sun, Y.T.; Sun, Y.J.; Hou, J.L. Research on Orchard Robot Navigation System Based on GNSS and Lidar. J. Agric. Mech. Res. 2023, 45, 55–61+69. [Google Scholar] [CrossRef]
- Hu, L.; Wang, Z.M.; Wang, P.; HE, J.; Jiao, J.K.; Wang, C.Y.; Li, M.J. Agricultural robot positioning system based on laser sensing. Trans. Chin. Soc. Agric. Eng. 2023, 39, 1–7. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar] [CrossRef]
- Liu, H.; Pan, G.S.; Huang, F.X.; Wang, X.; Gao, W. LiDAR-IMU-RTK fusion SLAM method for large-scale environment. J. Chin. Inert. Technol. 2024, 32, 866–873. [Google Scholar] [CrossRef]
- Jiang, L.; Xu, B.; Husnain, N.; Wang, Q. Overview of Agricultural Machinery Automation Technology for Sustainable Agriculture. Agronomy 2025, 15, 1471. [Google Scholar] [CrossRef]
- Tateno, K.; Tombari, F.; Laina, I.; Navab, N. CNN-SLAM: Real-Time Dense Monocular SLAM with Learned Depth Prediction. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Feng, M.; Hu, S.; Ang, M.; Lee, G.H. 2D3D-MatchNet: Learning to Match Keypoints Across 2D Image and 3D Point Cloud. arXiv 2019, arXiv:1904.09742. [Google Scholar] [CrossRef]










| Symbol | Meaning |
|---|---|
| The point cloud data from LiDAR | |
| The acceleration from IMU | |
| The angular velocity from IMU | |
| The positioning orientation data from the dual antennas | |
| The initial RTK heading angle | |
| The observed pose in the GNSS coordinate system | |
| The observed pose in the SLAM coordinate system | |
| The SLAM pose after preprocessing of coordinate system alignment | |
| The optimized SLAM pose | |
| The fused pose | |
| i, j, k | The time-series markers of the LiDAR, IMU, and RTK |
| Parameters | Value |
|---|---|
| ) | 1023 × 778 × 400 |
| 130 | |
| ) | 1.5 |
| 0 | |
| Max Gradeability/° | 30 |
| 560 |
| Experiment NO. | |||||
|---|---|---|---|---|---|
| 1 | 0.07 | 0.03 | 0.07 | 0.11 | 0.60 |
| 2 | 0.07 | 0.04 | 0.07 | 0.10 | 0.54 |
| 3 | 0.06 | 0.04 | 0.05 | 0.08 | 0.58 |
| Average | 0.07 | 0.04 | 0.06 | 0.10 | 0.57 |
| Experiment NO. | |||||
|---|---|---|---|---|---|
| 1 | 0.12 | 0.06 | 0.12 | 0.13 | 0.67 |
| 2 | 0.11 | 0.05 | 0.10 | 0.15 | 0.53 |
| 3 | 0.12 | 0.07 | 0.11 | 0.14 | 0.46 |
| Average | 0.12 | 0.06 | 0.11 | 0.14 | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wang, J.; Chen, Y.; Hu, L.; Li, Z.; Xie, F.; He, J.; Wang, P. Neural Network-Based SLAM/GNSS Fusion Localization Algorithm for Agricultural Robots in Orchard GNSS-Degraded or Denied Environments. Agriculture 2025, 15, 1612. https://doi.org/10.3390/agriculture15151612
Zhou H, Wang J, Chen Y, Hu L, Li Z, Xie F, He J, Wang P. Neural Network-Based SLAM/GNSS Fusion Localization Algorithm for Agricultural Robots in Orchard GNSS-Degraded or Denied Environments. Agriculture. 2025; 15(15):1612. https://doi.org/10.3390/agriculture15151612
Chicago/Turabian StyleZhou, Huixiang, Jingting Wang, Yuqi Chen, Lian Hu, Zihao Li, Fuming Xie, Jie He, and Pei Wang. 2025. "Neural Network-Based SLAM/GNSS Fusion Localization Algorithm for Agricultural Robots in Orchard GNSS-Degraded or Denied Environments" Agriculture 15, no. 15: 1612. https://doi.org/10.3390/agriculture15151612
APA StyleZhou, H., Wang, J., Chen, Y., Hu, L., Li, Z., Xie, F., He, J., & Wang, P. (2025). Neural Network-Based SLAM/GNSS Fusion Localization Algorithm for Agricultural Robots in Orchard GNSS-Degraded or Denied Environments. Agriculture, 15(15), 1612. https://doi.org/10.3390/agriculture15151612







