An Optimized Multi-Stage Framework for Soil Organic Carbon Estimation in Citrus Orchards Based on FTIR Spectroscopy and Hybrid Machine Learning Integration
Abstract
1. Introduction
2. Materials and Methods
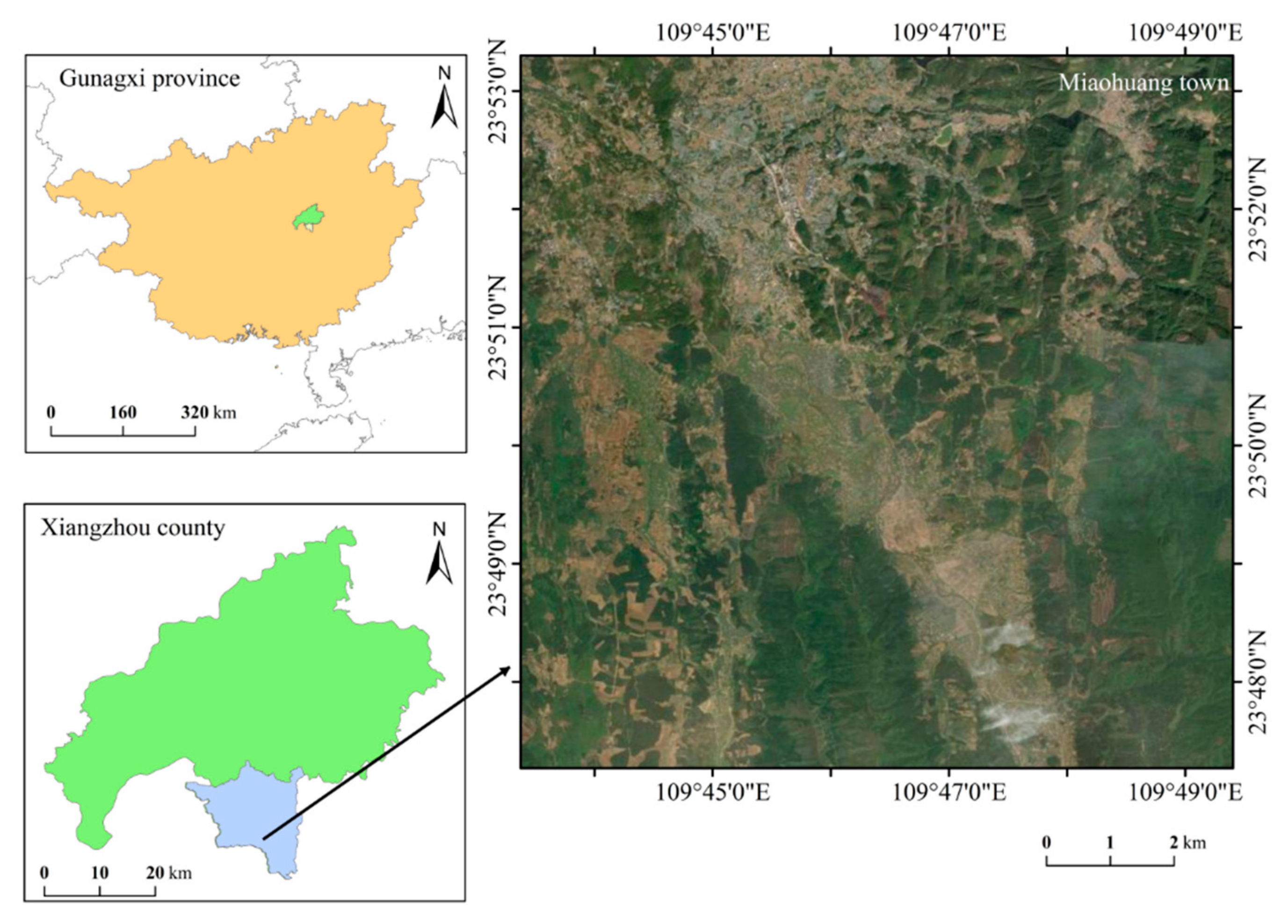
2.1. Overview of the Study Area
2.2. Soil Sample Collection
2.3. Division of Calibration and Prediction Datasets
2.4. Soil Spectral Data Preprocessing
2.5. Feature Spectral Selection for Soil Organic Carbon Content
2.6. Model Construction and Accuracy Validation
3. Results
3.1. Descriptive Statistical Features of Soil Organic Carbon Content in Citrus Soil
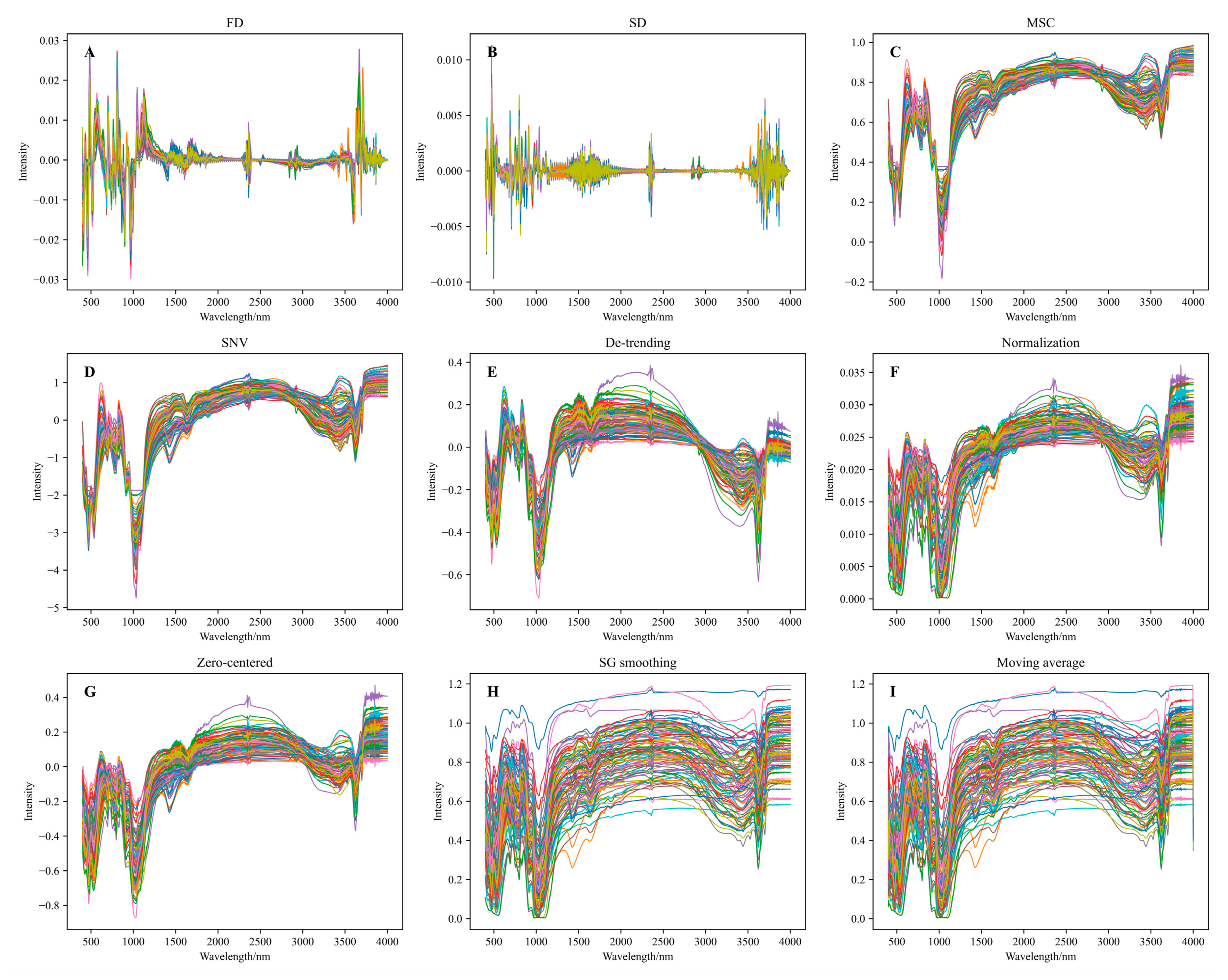
3.2. Soil Spectral Preprocessing and Method Selection for Citrus Soil
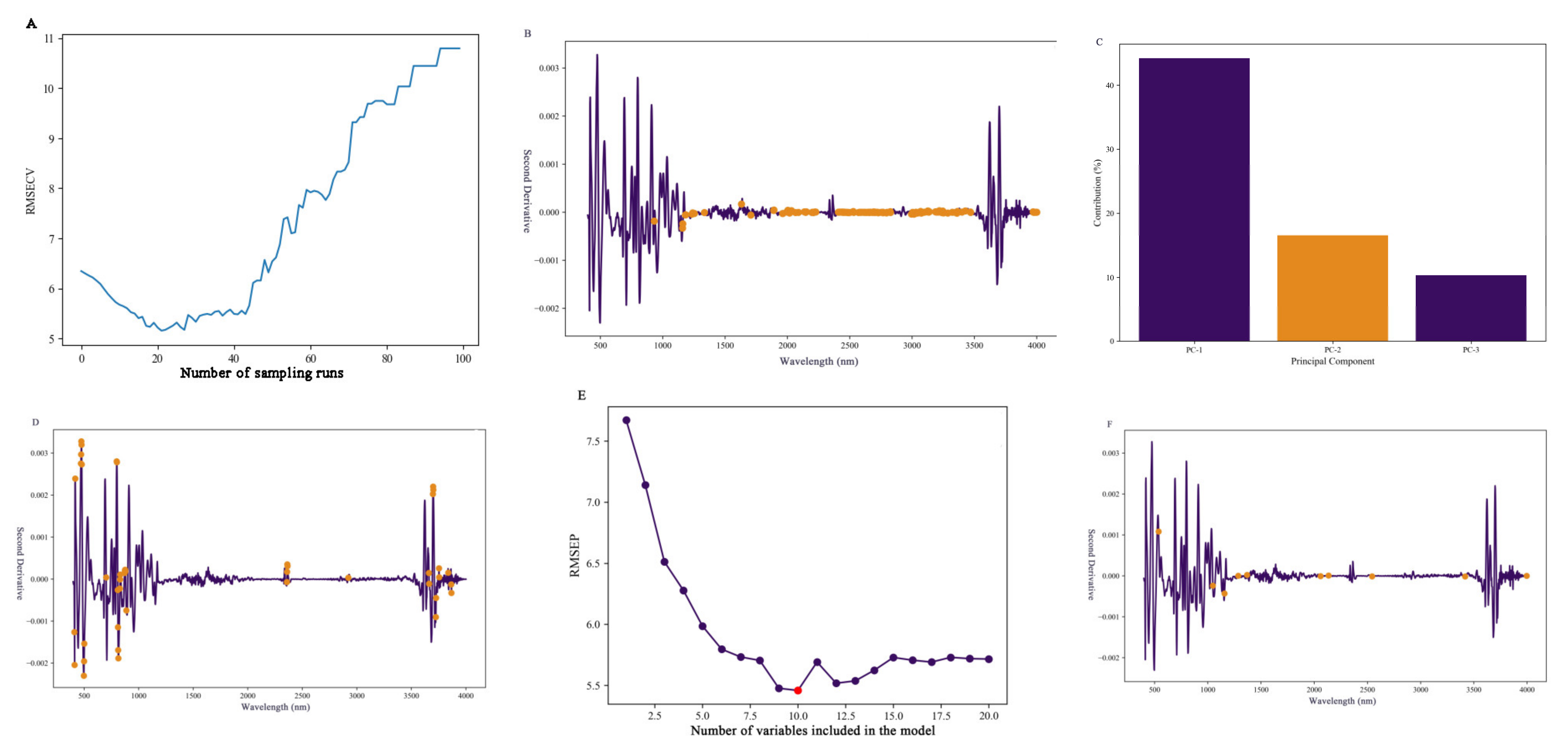
3.3. Selection of Spectral Feature Bands and Optimization of Methods for Citrus Soil
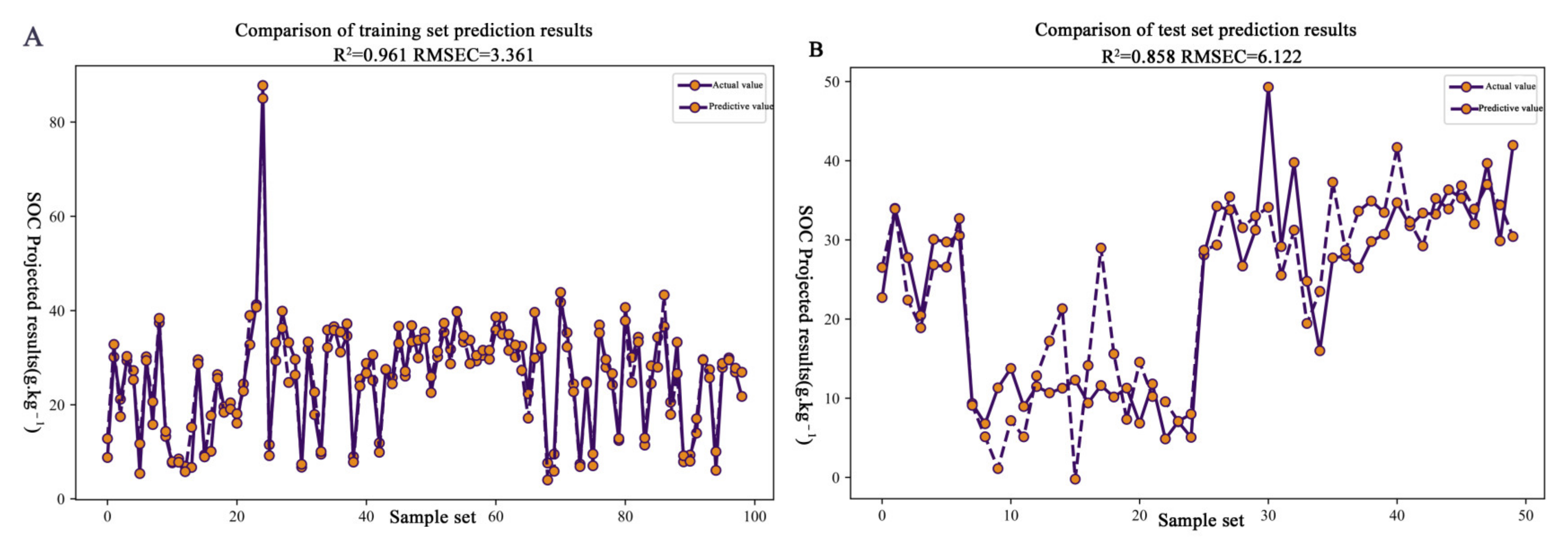
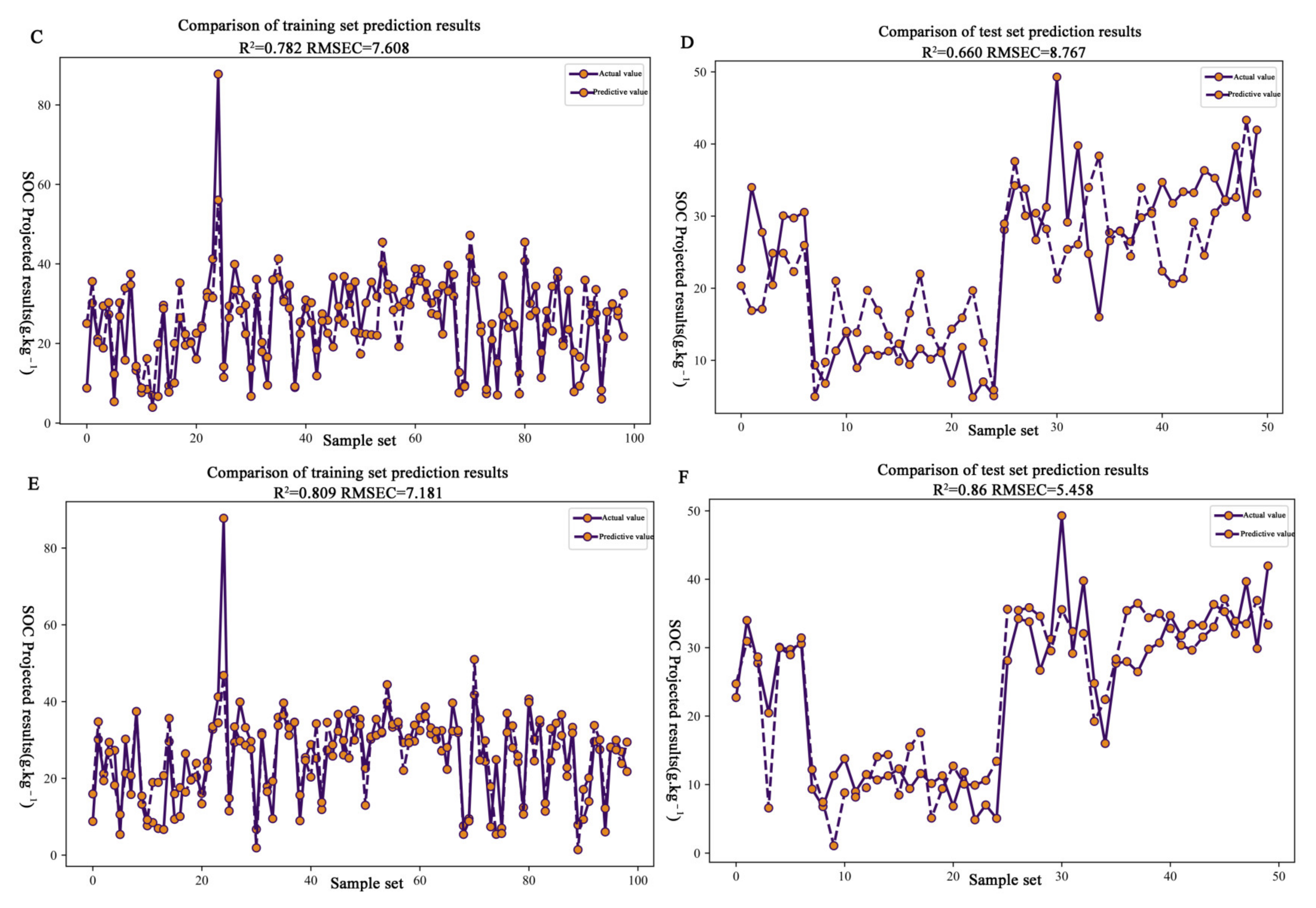
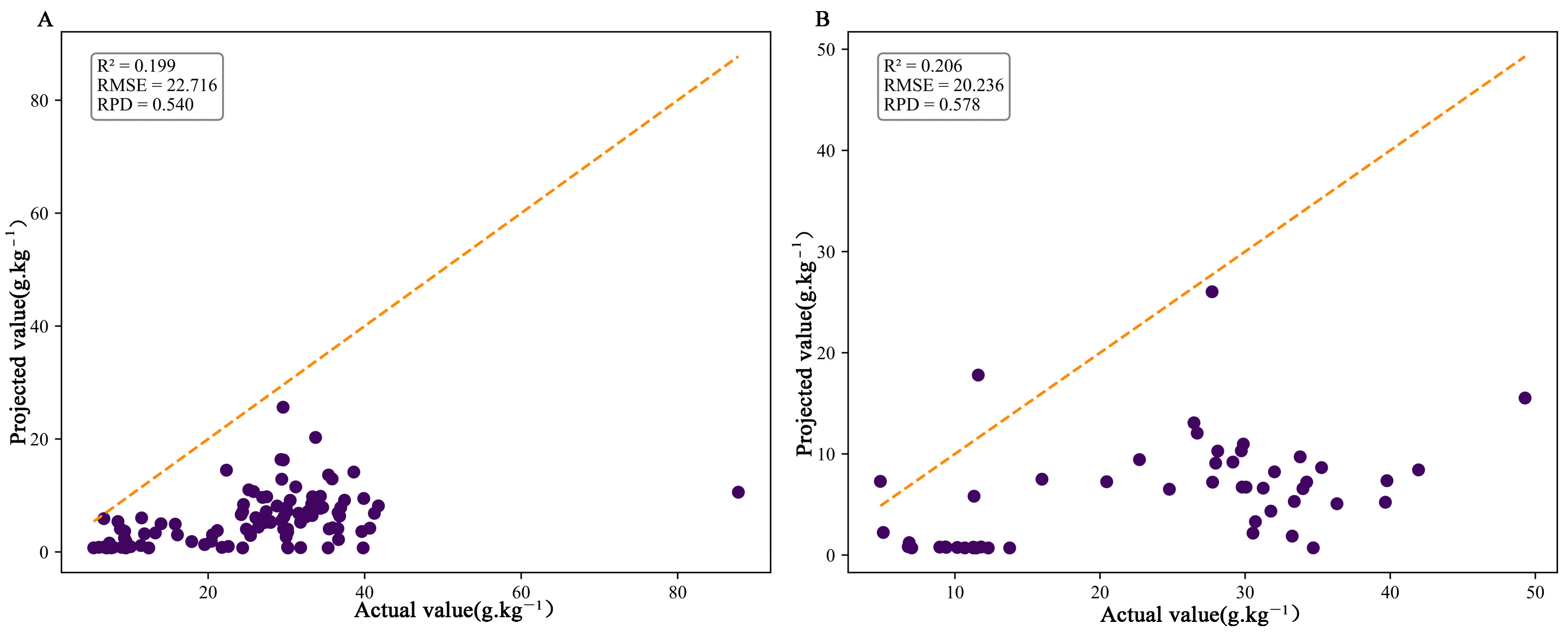
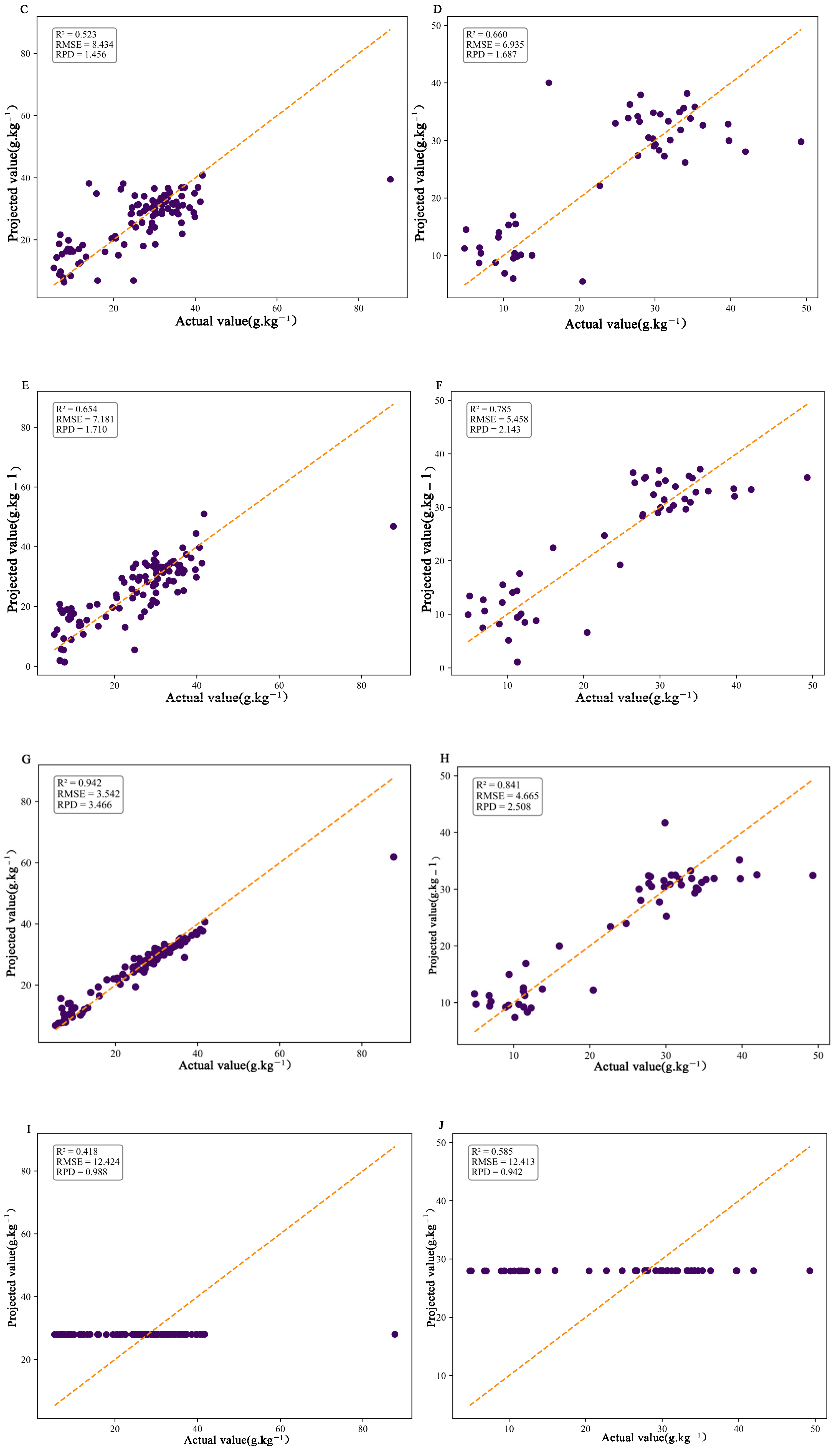
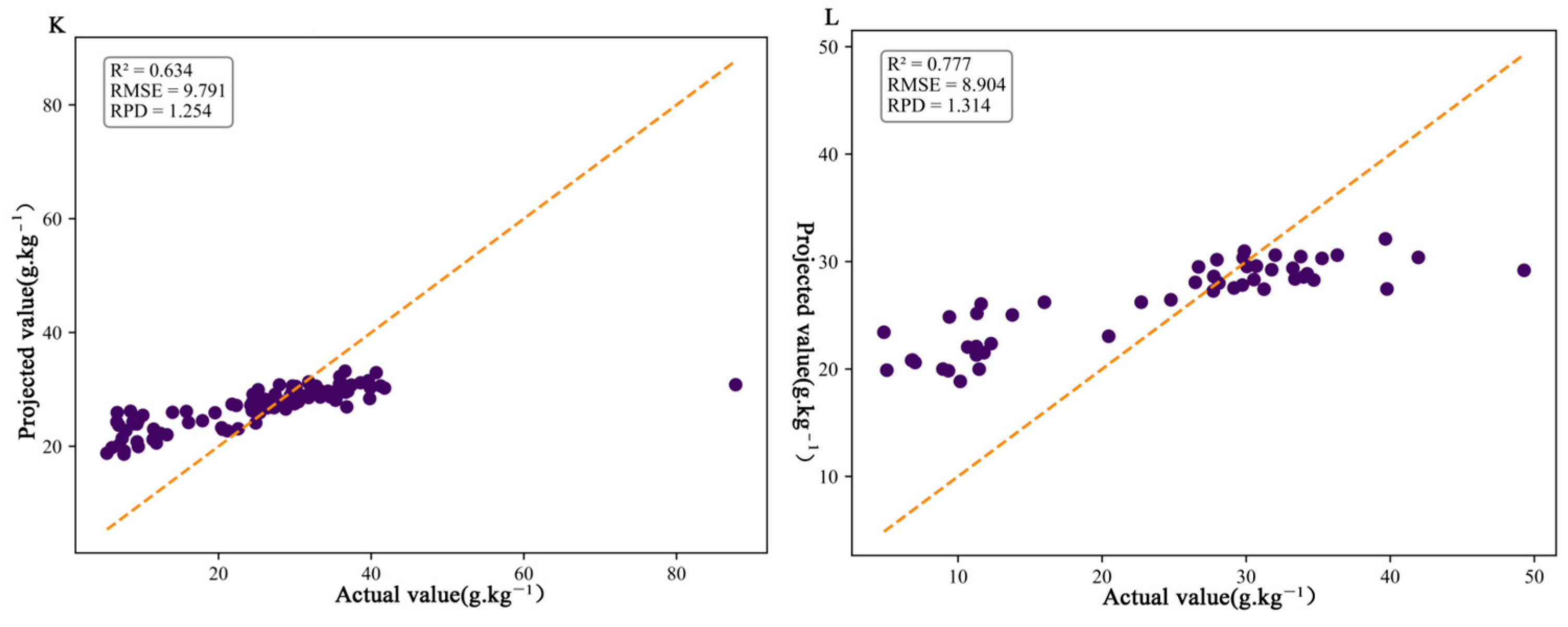
3.4. Establishment and Validation of the Estimation Model for Organic Matter Content in Citrus Soil
4. Discussion
4.1. Effects of Different Spectral Transformations on Modeling Accuracy
4.2. Influence of Spectral Feature Band Selection on Modeling Accuracy
4.3. Comparison of Modeling Methods for SOC Estimation (PLSR, PCR, RF, SVR, SVR-GWO, and BPNN)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Interpretation of SPA-Selected Features

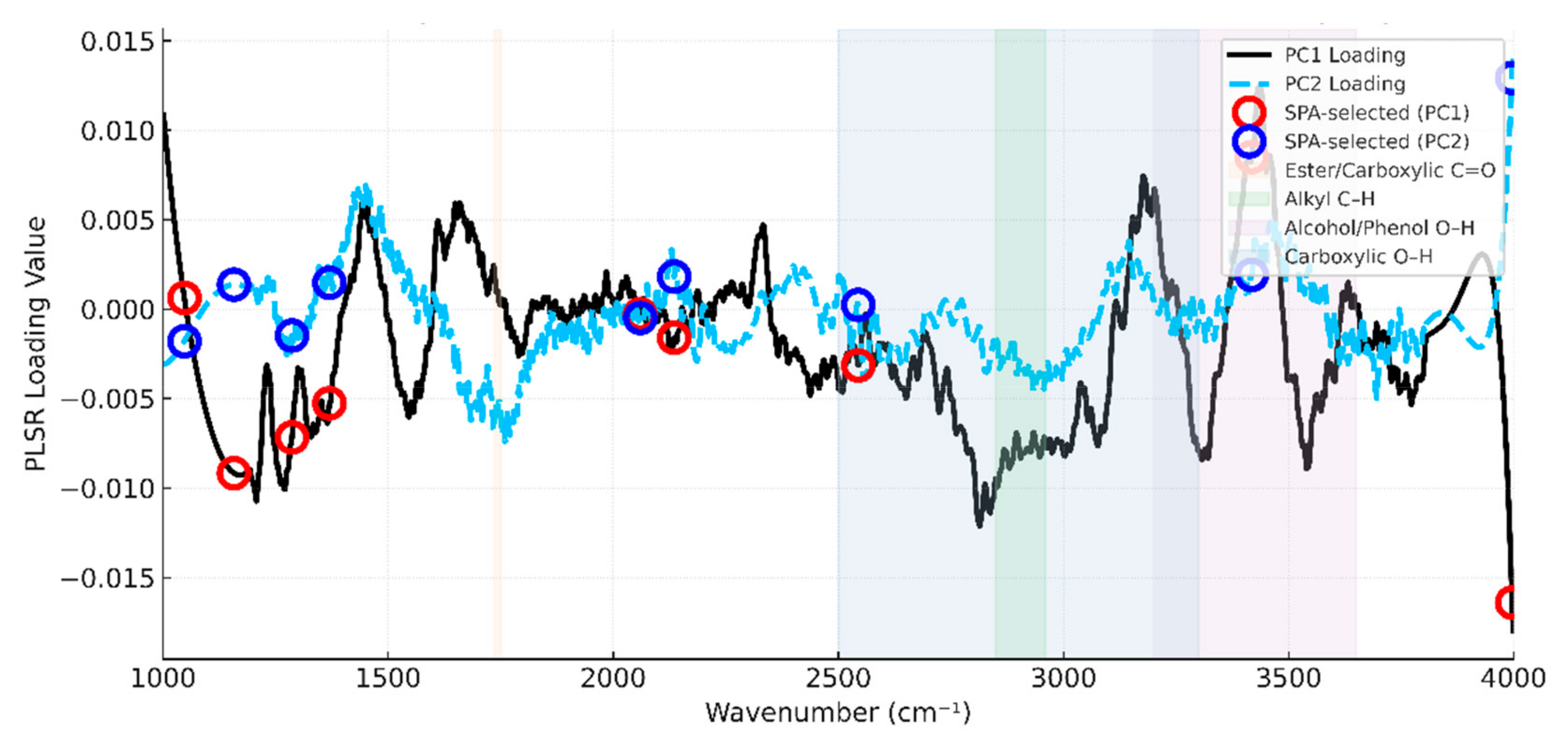
| SPA Wavenumber (cm−1) | Assigned Functional Group | IR Region (cm−1) | Chemical Relevance |
|---|---|---|---|
| 1047.35 | C–O stretch (ester/ether) | 1000–1300 | Relevant (SOM signature) |
| 538.14 | Possible halide (C–Br) | 500–600 | Low relevance |
| 3417.86 | O–H stretch (phenol/alcohol) | 3200–3600 | Relevant (hydroxyl) |
| 1286.52 | C–O stretch (ester) | 1200–1300 | Relevant (ester components) |
| 1157.29 | C–O stretch (alcohol) | 1100–1200 | Relevant (alcohol indicators) |
| 1369.46 | CH3 bend (alkyl) | 1350–1400 | Relevant (alkyl side chains) |
| 3996.51 | Instrument edge/noise | >3800 | Ignore (out of range) |
| 2135.2 | C≡C or C≡N stretch (alkyne/nitrile) | 2100–2260 | Possible trace group |
| 2544.11 | O–H broad tail (carboxylic acid) | 2500–3300 | Relevant (acidic region) |
| 2059.98 | Weak signal/uncertain | 2000–2100 | Uncertain |
References
- Gao, G.; Li, G.; Liu, M.; Liu, J.; Ma, S.; Li, D.; Liang, X.; Wu, M.; Li, Z. Microbial Carbon Metabolic Activity and Bacterial Cross-Profile Network in Paddy Soils of Different Fertility. Appl. Soil Ecol. 2024, 195, 105233. [Google Scholar] [CrossRef]
- Trivedi, P.; Singh, B.P.; Singh, B.K. Soil Carbon. In Soil Carbon Storage; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–28. ISBN 978-0-12-812766-7. [Google Scholar]
- Dusenge, M.E.; Duarte, A.G.; Way, D.A. Plant Carbon Metabolism and Climate Change: Elevated CO2 and Temperature Impacts on Photosynthesis, Photorespiration and Respiration. New Phytol. 2019, 221, 32–49. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; An, S.; Liang, C.; Liu, Y.; Kuzyakov, Y. Microbial Necromass as the Source of Soil Organic Carbon in Global Ecosystems. Soil Biol. Biochem. 2021, 162, 108422. [Google Scholar] [CrossRef]
- Zhao, H.; Dong, Z.; Liu, B.; Xiong, H.; Guo, C.; Lakshmanan, P.; Wang, X.; Chen, X.; Shi, X.; Zhang, F.; et al. Can Citrus Production in China Become Carbon-Neutral? A Historical Retrospect and Prospect. Agric. Ecosyst. Environ. 2023, 348, 108412. [Google Scholar] [CrossRef]
- Yun, S.-M.; Kim, C.-S.; Lee, J.-J.; Chung, J.-S. Application of ATR-FTIR Spectroscopy for Analysis of Salt Stress in Brussels Sprouts. Metabolites 2024, 14, 470. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, X.; Wu, W. Application of Fourier Transform Infrared (FTIR) Spectroscopy in Sample Preparation: Material Characterization and Mechanism Investigation. Adv. Sample Prep. 2024, 11, 100122. [Google Scholar] [CrossRef]
- Buja, I.; Sabella, E.; Monteduro, A.G.; Chiriacò, M.S.; De Bellis, L.; Luvisi, A.; Maruccio, G. Advances in Plant Disease Detection and Monitoring: From Traditional Assays to In-Field Diagnostics. Sensors 2021, 21, 2129. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.; Pu, R.; Gonzalez-Moreno, P.; Yuan, L.; Wu, K.; Huang, W. Monitoring Plant Diseases and Pests through Remote Sensing Technology: A Review. Comput. Electron. Agric. 2019, 165, 104943. [Google Scholar] [CrossRef]
- Muneer, M.A.; Afridi, M.S.; Saddique, M.A.B.; Chen, X.; Nisa, Z.U.; Yan, X.; Farooq, I.; Munir, M.Z.; Yang, W.; Ji, B.; et al. Nutrient Stress Signals: Elucidating the Morphological, Physiological, and Molecular Responses of Fruit Trees to Macronutrient Deficiency and Their Management Strategies. Sci. Hortic. 2024, 329, 112985. [Google Scholar] [CrossRef]
- Margenot, A.J.; Parikh, S.J.; Calderón, F.J. Fourier-transform Infrared Spectroscopy for Soil Organic Matter Analysis. Soil Sci. Soc. Amer. J. 2023, 87, 1503–1528. [Google Scholar] [CrossRef]
- Li, X.; McCarty, G.W. Use of Principal Components for Scaling Up Topographic Models to Map Soil Redistribution and Organic Carbon. JoVE 2018, 140, 58189. [Google Scholar] [CrossRef]
- Bian, Z.; Guo, X.; Wang, S.; Zhuang, Q.; Jin, X.; Wang, Q.; Jia, S. Applying Statistical Methods to Map Soil Organic Carbon of Agricultural Lands in Northeastern Coastal Areas of China. Arch. Agron. Soil Sci. 2020, 66, 532–544. [Google Scholar] [CrossRef]
- Das, B.; Chakraborty, D.; Singh, V.K.; Das, D.; Sahoo, R.N.; Aggarwal, P.; Murgaokar, D.; Mondal, B.P. Partial Least Squares Regression-Based Machine Learning Models for Soil Organic Carbon Prediction Using Visible–Near Infrared Spectroscopy. Geoderma Reg. 2023, 33, e00628. [Google Scholar] [CrossRef]
- Emadi, M.; Taghizadeh-Mehrjardi, R.; Cherati, A.; Danesh, M.; Mosavi, A.; Scholten, T. Predicting and Mapping of Soil Organic Carbon Using Machine Learning Algorithms in Northern Iran. Remote. Sens. 2020, 12, 2234. [Google Scholar] [CrossRef]
- Li, Y.; Yao, G.; Li, S.; Dong, X. Predicting and Mapping of Soil Organic Matter with Machine Learning in the Black Soil Region of the Southern Northeast Plain of China. Agronomy 2025, 15, 533. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Zhu, X. Soil Organic Carbon Estimation Using Remote Sensing Data-Driven Machine Learning. PeerJ 2024, 12, e17836. [Google Scholar] [CrossRef]
- Meng, W. Risk Perception and Influencing Factors of Citrus Growers. Master’s Thesis, Guangxi University, Nanning, China, 2023. (In Chinese) [Google Scholar] [CrossRef]
- Qi, Z. Hyperspectral Inversion Method for Estimating Orchard Soil Organic Carbon Content. Master’s Thesis, Shandong Agricultural University, Taian, China, 2023. (In Chinese). [Google Scholar]
- Yang, D.; Hu, J. A Detection Method of Oil Content for Maize Kernels Based on CARS Feature Selection and Deep Sparse Autoencoder Feature Extraction. Ind. Crops Prod. 2024, 222, 119464. [Google Scholar] [CrossRef]
- Liu, K.; Chen, X.; Li, L.; Chen, H.; Ruan, X.; Liu, W. A Consensus Successive Projections Algorithm—Multiple Linear Regression Method for Analyzing near Infrared Spectra. Anal. Chim. Acta 2015, 858, 16–23. [Google Scholar] [CrossRef]
- Ma, J.; Yuan, Y. Dimension Reduction of Image Deep Feature Using PCA. J. Vis. Commun. Image Represent. 2019, 63, 102578. [Google Scholar] [CrossRef]
- Malgady, R.G.; Krebs, D.E. Understanding Correlation Coefficients and Regression. Phys. Ther. 1986, 66, 110–120. [Google Scholar] [CrossRef]
- Williams, P.C.; Sobering, D.C. Comparison of Commercial near Infrared Transmittance and Reflectance Instruments for Analysis of Whole Grains and Seeds. J. Near Infrared Spectrosc. 1993, 1, 25–32. [Google Scholar] [CrossRef]
- Zheng, J.Y.; Zhao, J.S.; Shi, Z.H.; Wang, L. Soil aggregates are key factors that regulate erosion-related carbon loss in citrus orchards of southern China: Bare land vs. grass-covered land. Agric. Ecosyst. Environ. 2021, 309, 107254. [Google Scholar] [CrossRef]
- Yao, X.; Yu, K.; Deng, Y.; Liu, J.; Lai, Z. Spatial variability of soil organic carbon and total nitrogen in the hilly red soil region of Southern China. J. For. Res. 2020, 31, 2385–2394. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A Review of Feature Selection Techniques in Bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Wang, J.; Ge, X. Prediction of Soil Organic Matter in Northwestern China Using Fractional-Order Derivative Spectroscopy and Modified Normalized Difference Indices. CATENA 2020, 185, 104257. [Google Scholar] [CrossRef]
- Lee, L.C.; Liong, C.-Y.; Jemain, A.A. A Contemporary Review on Data Preprocessing (DP) Practice Strategy in ATR-FTIR Spectrum. Chemom. Intell. Lab. Syst. 2017, 163, 64–75. [Google Scholar] [CrossRef]
- Jiao, Y.; Li, Z.; Chen, X.; Fei, S. Preprocessing Methods for Near-infrared Spectrum Calibration. J. Chemom. 2020, 34, e3306. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Saberioon, M.M.; Kozák, J.; Vašát, R.; Němeček, K. Comparing Different Data Preprocessing Methods for Monitoring Soil Heavy Metals Based on Soil Spectral Features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, Z.; Huang, J.; Leng, G.; Xu, W.; Wang, Y.; Xie, Z.; Yang, J. Enhancing Soil Texture Classification with Multivariate Scattering Correction and Residual Neural Networks Using Visible Near-Infrared Spectra. J. Environ. Manag. 2024, 352, 120094. [Google Scholar] [CrossRef]
- Brunet, D.; Barthès, B.G.; Chotte, J.-L.; Feller, C. Determination of Carbon and Nitrogen Contents in Alfisols, Oxisols and Ultisols from Africa and Brazil Using NIRS Analysis: Effects of Sample Grinding and Set Heterogeneity. Geoderma 2007, 139, 106–117. [Google Scholar] [CrossRef]
- Heil, K.; Schmidhalter, U. An Evaluation of Different NIR-Spectral Pre-Treatments to Derive the Soil Parameters C and N of a Humus-Clay-Rich Soil. Sensors 2021, 21, 1423. [Google Scholar] [CrossRef] [PubMed]
- Rosin, N.A.; Dalmolin, R.S.D.; Horst-Heinen, T.Z.; Moura-Bueno, J.M.; Silva-Sangoi, D.V.D.; Silva, L.S.D. Diffuse Reflectance Spectroscopy for Estimating Soil Organic Carbon and Making Nitrogen Recommendations. Sci. Agric. 2021, 78, e20190246. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Z.; Ji, C.; Hao, Y.; Liang, Z.; Yan, X.; Qiao, X.; Feng, M.; Xiao, L.; Song, X.; et al. Efficient Prediction of SOC and Aggregate OC Components by Continuous Wavelet Transform Spectra under Different Feature Selection Methods. Comput. Electron. Agric. 2024, 217, 108550. [Google Scholar] [CrossRef]
- Salem, N.; Hussein, S. Data Dimensional Reduction and Principal Components Analysis. Procedia Comput. Sci. 2019, 163, 292–299. [Google Scholar] [CrossRef]
- Liu, J.; Han, J.; Zhang, Y.; Wang, H.; Kong, H.; Shi, L. Prediction of Soil Organic Carbon with Different Parent Materials Development Using Visible-near Infrared Spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 204, 33–39. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Phil. Trans. R. Soc. A. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Tang, G.; Huang, Y.; Tian, K.; Song, X.; Yan, H.; Hu, J.; Xiong, Y.; Min, S. A New Spectral Variable Selection Pattern Using Competitive Adaptive Reweighted Sampling Combined with Successive Projections Algorithm. Analyst 2014, 139, 4894. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key Wavelengths Screening Using Competitive Adaptive Reweighted Sampling Method for Multivariate Calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Galvão, R.K.H.; Araújo, M.C.U.; Fragoso, W.D.; Silva, E.C.; José, G.E.; Soares, S.F.C.; Paiva, H.M. A Variable Elimination Method to Improve the Parsimony of MLR Models Using the Successive Projections Algorithm. Chemom. Intell. Lab. Syst. 2008, 92, 83–91. [Google Scholar] [CrossRef]
- Ayna, C.O.; Mdrafi, R.; Du, Q.; Gurbuz, A.C. Learning-Based Optimization of Hyperspectral Band Selection for Classification. Remote Sens. 2023, 15, 4460. [Google Scholar] [CrossRef]
- Zheng, Z.; Liu, Y.; He, M.; Chen, D.; Sun, L.; Zhu, F. Effective Band Selection of Hyperspectral Image by an Attention Mechanism-Based Convolutional Network. RSC Adv. 2022, 12, 8750–8759. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, R.; Liu, D. Downscaling MODIS Spectral Bands Using Deep Learning. GIScience Remote Sens. 2021, 58, 1300–1315. [Google Scholar] [CrossRef]
- Barra, I.; Haefele, S.M.; Sakrabani, R.; Kebede, F. Soil Spectroscopy with the Use of Chemometrics, Machine Learning and Pre-Processing Techniques in Soil Diagnosis: Recent Advances–A Review. TrAC Trends Anal. Chem. 2021, 135, 116166. [Google Scholar] [CrossRef]
- Cai, H.; Zhou, L.; Shi, Z.; Ji, W.; Luo, D.; Peng, J.; Feng, C. Hyperspectral Inversion of Soil Organic Matter in Southern Xinjiang Jujube Orchards Using the CARS-BPNN Model. Spectrosc. Spectr. Anal. 2023, 43, 2568–2573. [Google Scholar]
- Wijewardane, N.K.; Ge, Y.; Wills, S.; Loecke, T. Prediction of Soil Carbon in the Conterminous United States: Visible and Near Infrared Reflectance Spectroscopy Analysis of the Rapid Carbon Assessment Project. Soil Sci. Soc. Amer. J. 2016, 80, 973–982. [Google Scholar] [CrossRef]
- Engelen, S.; Hubert, M.; Vanden Branden, K.; Verboven, S. Robust PCR and Robust PLSR: A Comparative Study. In Theory and Applications of Recent Robust Methods; Hubert, M., Pison, G., Struyf, A., Van Aelst, S., Eds.; Birkhäuser Basel: Basel, Switzerland, 2004; pp. 105–117. ISBN 978-3-0348-9636-8. [Google Scholar]
- Were, K.; Bui, D.T.; Dick, Ø.B.; Singh, B.R. A Comparative Assessment of Support Vector Regression, Artificial Neural Networks, and Random Forests for Predicting and Mapping Soil Organic Carbon Stocks across an Afromontane Landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Karray, E.; Elmannai, H.; Toumi, E.; Hedi Gharbia, M.; Meshoul, S.; Aichi, H.; Ben Rabah, Z. Evaluating the Potentials of PLSR and SVR Models for Soil Properties Prediction Using Field Imaging, Laboratory VNIR Spectroscopy and Their Combination. Comput. Model. Eng. Sci. 2023, 136, 1399–1425. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Xiao, C.; Zhao, X.; Shi, Y.; Yang, H.; Liu, Z.; Li, S. Study on Prediction Model of Soil Cadmium Content, Moisture Content Correction Based on GWO-SVR. Acta Opt. Sin. 2020, 40, 1030002. (In Chinese) [Google Scholar] [CrossRef]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost Tree-Based Ensemble Classification and Spectral Band Selection for Ecotope Mapping Using Airborne Hyperspectral Imagery. Remote Sens. Environ. 2008, 112, 2999–3011. (In Chinese) [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A. Comparison between Random Forests, Artificial Neural Networks and Gradient Boosted Machines Methods of On-Line Vis-NIR Spectroscopy Measurements of Soil Total Nitrogen and Total Carbon. Sensors 2017, 17, 2428. [Google Scholar] [CrossRef]
- Goh, A.T.C. Back-Propagation Neural Networks for Modeling Complex Systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Schuetzke, J.; Szymanski, N.J.; Reischl, M. Validating Neural Networks for Spectroscopic Classification on a Universal Synthetic Dataset. NPJ Comput. Mater. 2023, 9, 100. [Google Scholar] [CrossRef]
| Dataset | Number of Samples | Minimum (g/kg) | Maximum (g/kg) | Mean (g/kg) | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Total Samples | 149 | 4.86 | 87.75 | 24.91 | 12.09 | 0.49 |
| Calibration Set | 99 | 5.38 | 87.75 | 25.63 | 12.28 | 0.48 |
| Validation Set | 50 | 4.86 | 49.29 | 23.46 | 11.70 | 0.50 |
| Method | R2c | RMSEC | RPDC | R2p | RMSEP | RPDP |
|---|---|---|---|---|---|---|
| FD | 0.77 | 5.852 | 2.098 | 0.821 | 4.905 | 2.385 |
| SD | 0.886 | 4.129 | 2.973 | 0.765 | 5.617 | 2.082 |
| MSC | 0.66 | 7.127 | 1.723 | 0.734 | 5.971 | 1.959 |
| SNV | 0.695 | 6.741 | 1.821 | 0.774 | 5.51 | 2.123 |
| De-trending | 0.623 | 7.503 | 1.636 | 0.667 | 6.681 | 1.751 |
| Normalization | 0.59 | 7.819 | 1.57 | 0.674 | 6.611 | 1.769 |
| Zero-centered | 0.588 | 7.839 | 1.566 | 0.689 | 6.455 | 1.812 |
| SG smoothing | 0.534 | 8.334 | 1.473 | 0.624 | 7.104 | 1.646 |
| Moving average | 0.534 | 8.334 | 1.473 | 0.624 | 7.101 | 1.647 |
| Filtering Method | The Number of Variables | Calibration Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | R2 | RMSE | RPD | ||
| CARS | 152 | 0.96 | 3.36 | 4.08 | 0.86 | 6.12 | 1.89 |
| PCA | 23 | 0.78 | 7.61 | 1.61 | 0.66 | 8.77 | 1.32 |
| SPA | 10 | 0.81 | 7.18 | 1.7 | 0.89 | 5.46 | 2.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Mo, X.; Yu, S.; Wu, S.; Chen, H.; Qin, Y.; Zeng, Z. An Optimized Multi-Stage Framework for Soil Organic Carbon Estimation in Citrus Orchards Based on FTIR Spectroscopy and Hybrid Machine Learning Integration. Agriculture 2025, 15, 1417. https://doi.org/10.3390/agriculture15131417
Wei Y, Mo X, Yu S, Wu S, Chen H, Qin Y, Zeng Z. An Optimized Multi-Stage Framework for Soil Organic Carbon Estimation in Citrus Orchards Based on FTIR Spectroscopy and Hybrid Machine Learning Integration. Agriculture. 2025; 15(13):1417. https://doi.org/10.3390/agriculture15131417
Chicago/Turabian StyleWei, Yingying, Xiaoxiang Mo, Shengxin Yu, Saisai Wu, He Chen, Yuanyuan Qin, and Zhikang Zeng. 2025. "An Optimized Multi-Stage Framework for Soil Organic Carbon Estimation in Citrus Orchards Based on FTIR Spectroscopy and Hybrid Machine Learning Integration" Agriculture 15, no. 13: 1417. https://doi.org/10.3390/agriculture15131417
APA StyleWei, Y., Mo, X., Yu, S., Wu, S., Chen, H., Qin, Y., & Zeng, Z. (2025). An Optimized Multi-Stage Framework for Soil Organic Carbon Estimation in Citrus Orchards Based on FTIR Spectroscopy and Hybrid Machine Learning Integration. Agriculture, 15(13), 1417. https://doi.org/10.3390/agriculture15131417






