Evaluating Sustainability of Water–Energy–Food–Ecosystems Nexus in Water-Scarce Regions via Coupled Simulation Model
Abstract
1. Introduction
2. Methodology
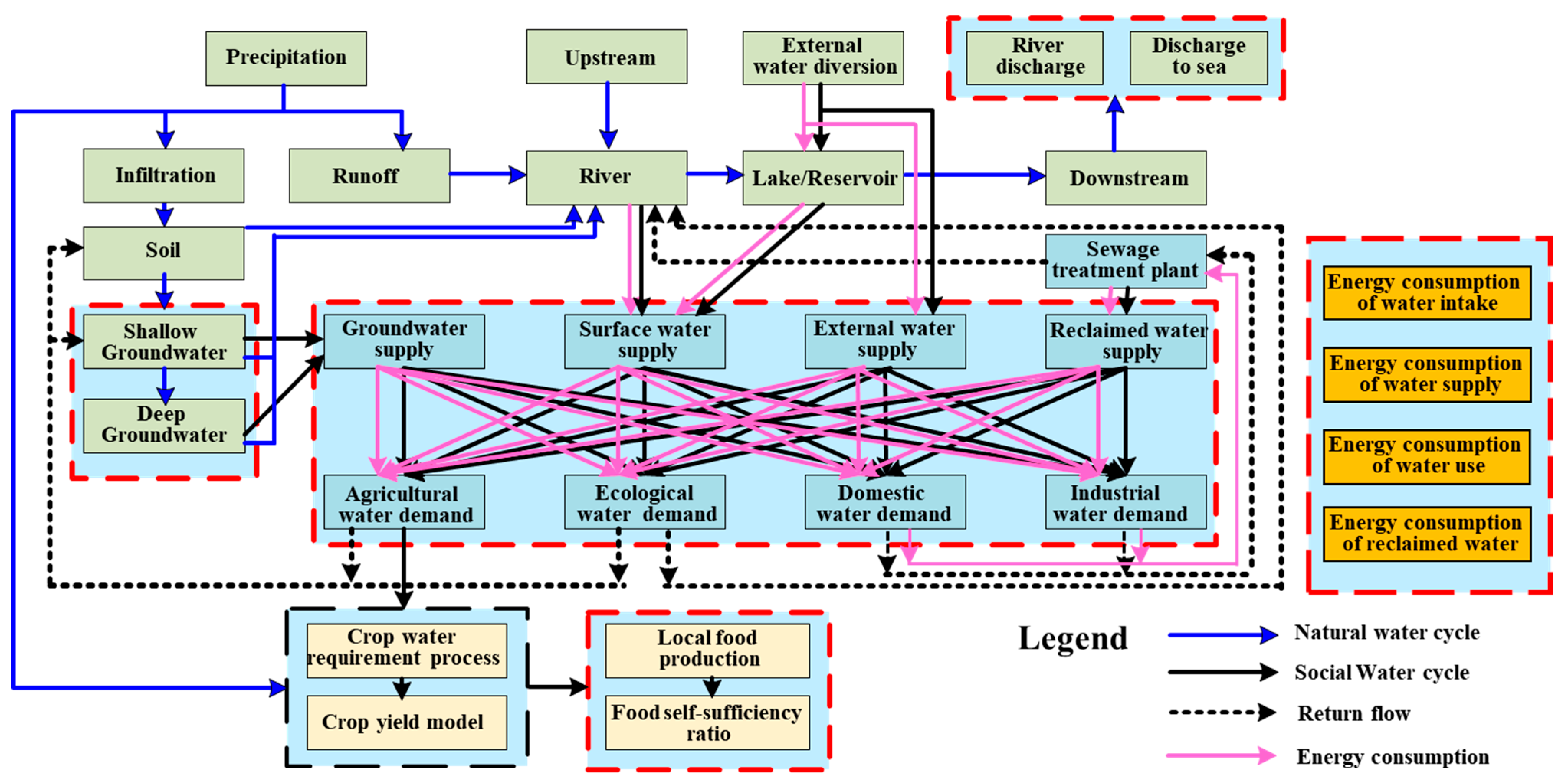
2.1. CSM-WEFE Architecture
2.2. Major Modules of CSM-WEFE
2.2.1. Natural Water Cycle
2.2.2. Social Water Cycle
- (1)
- Water resource allocation
- (2)
- Reclaimed water simulation
2.2.3. Food Production Simulation
2.2.4. Energy Consumption for the Social Water Cycle
- (1)
- Energy consumption for water intake
- (2)
- Energy consumption for water supply
- (3)
- Energy consumption for water use
- (4)
- Energy consumption for reclaimed water treatment
2.3. WEFE Subsystem Evaluation Indicators
2.4. Coordinated Sustainable Development Evaluation Method
2.4.1. Reliability Index
2.4.2. Equilibrium Index
2.4.3. Coupling Coordination Degree Index
2.4.4. Coordinated Sustainable Development Index
3. Study Area and Data Sources
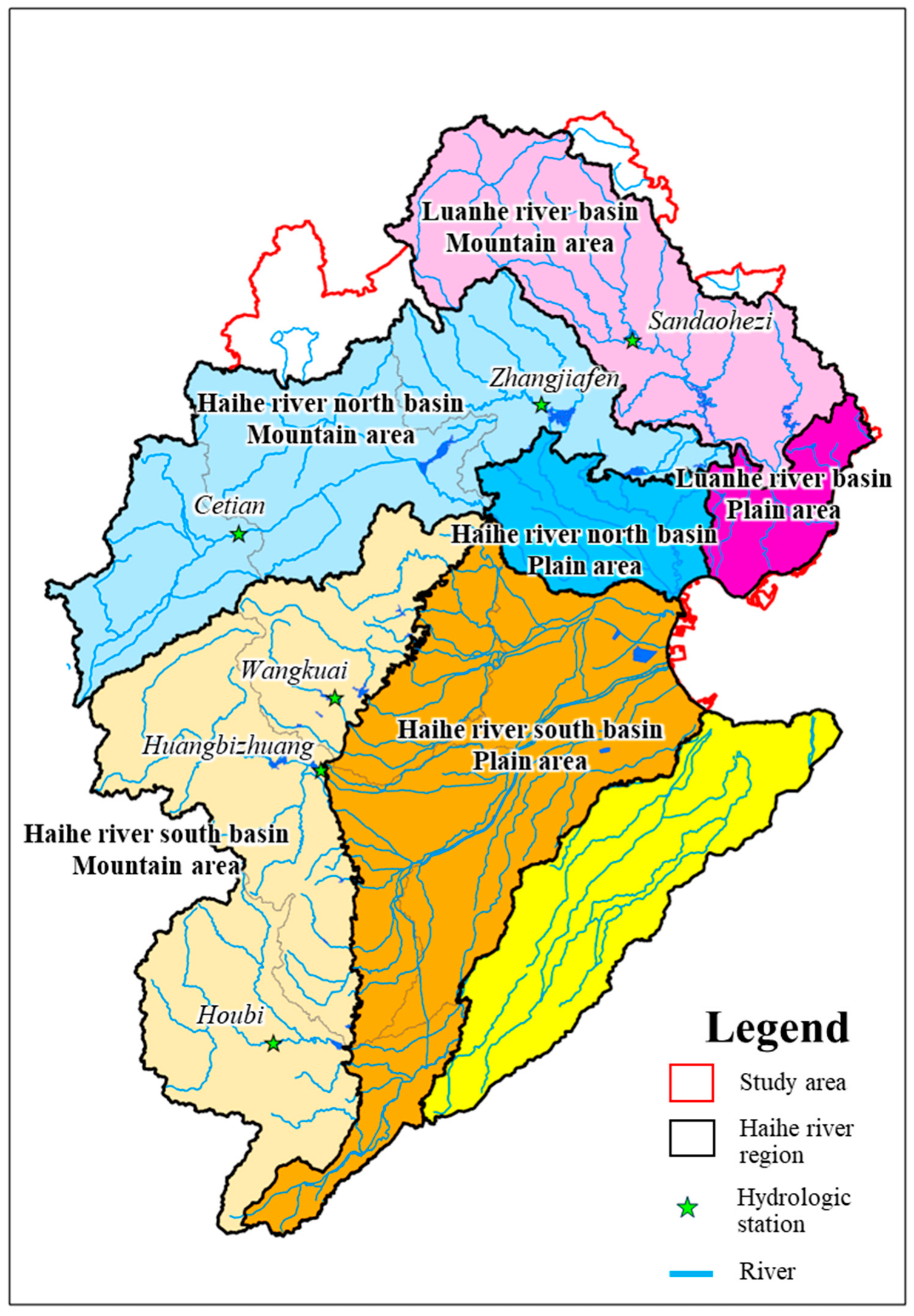
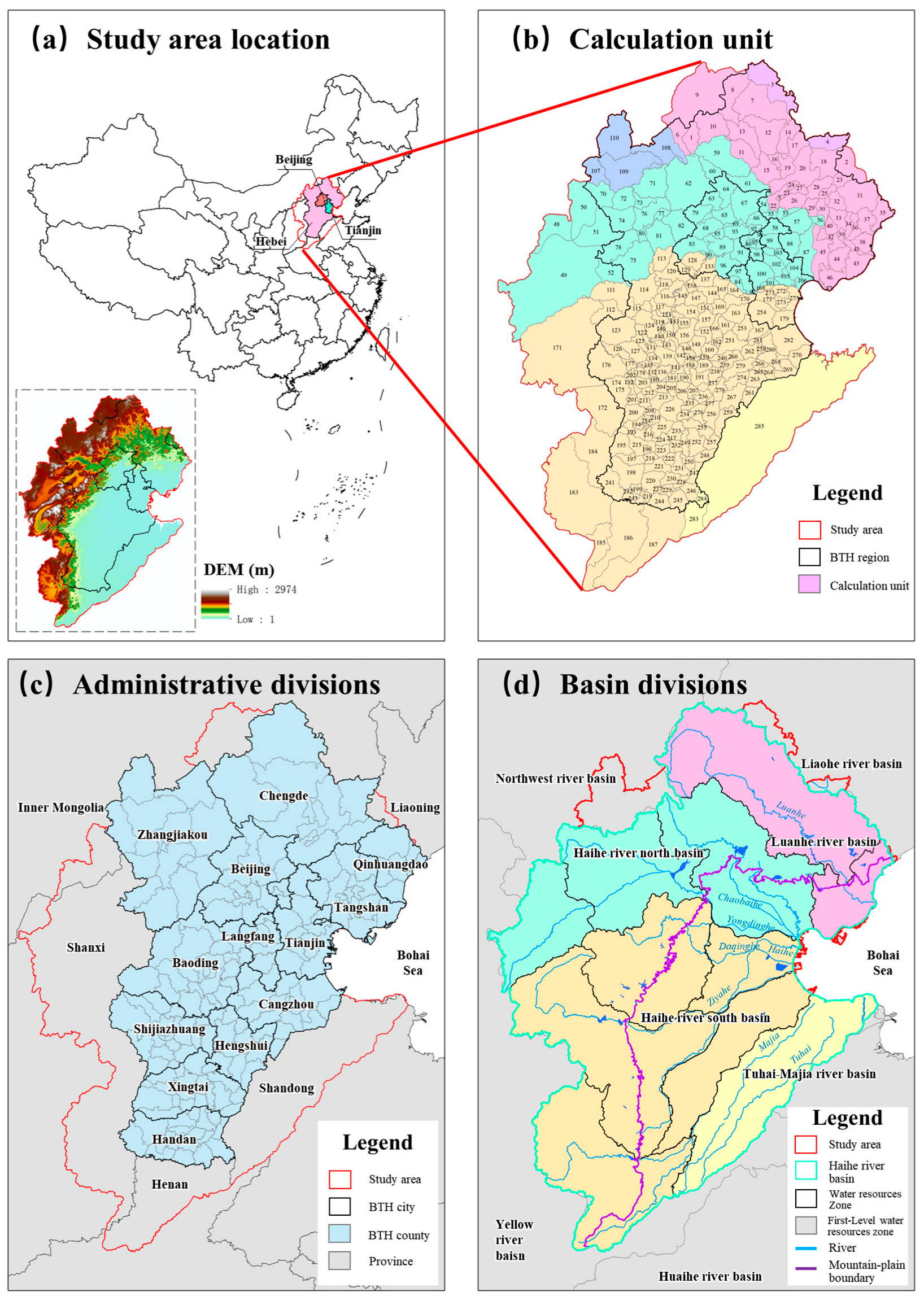
3.1. Study Area
3.2. Data Sources
3.3. Scenario Setting
4. Results
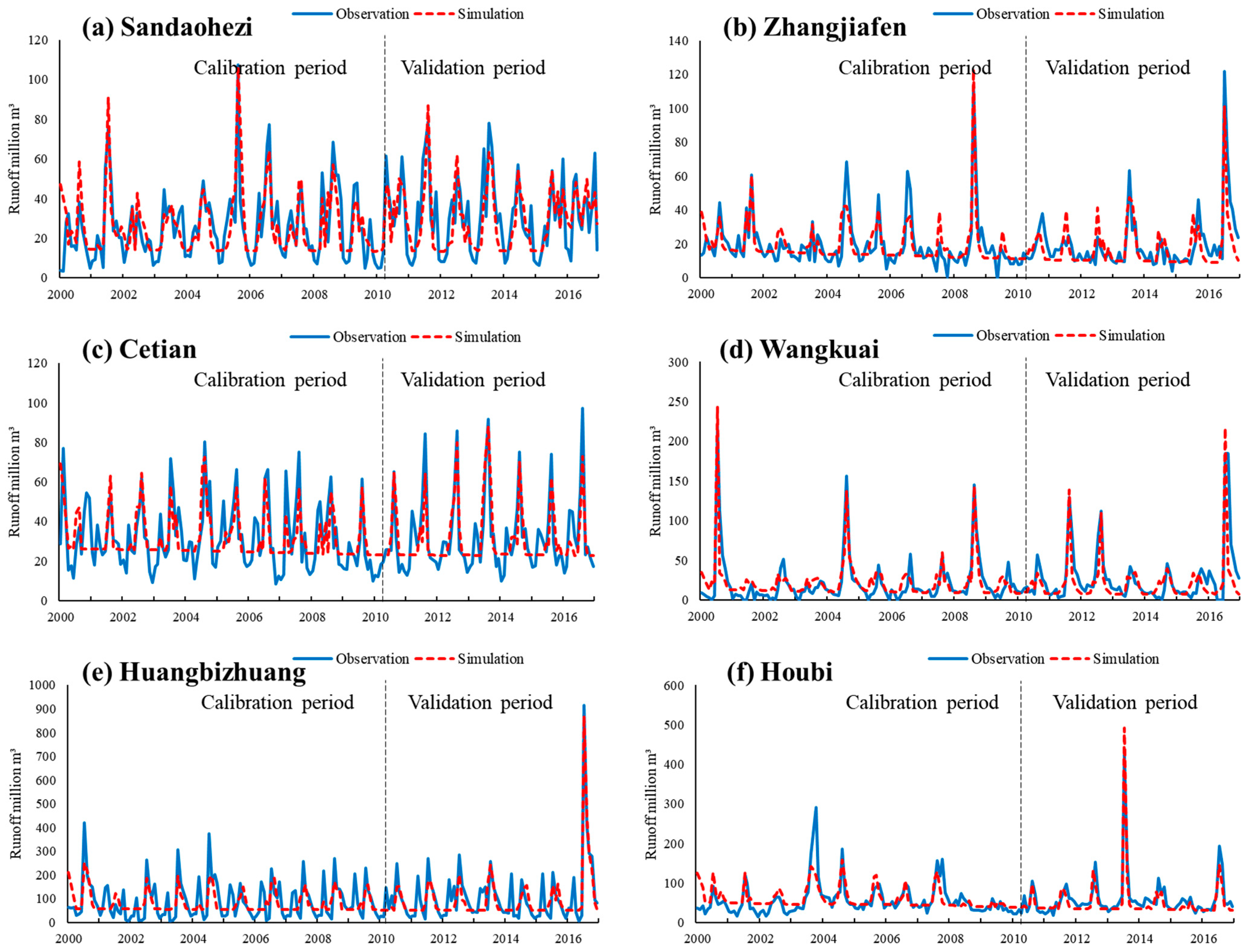
4.1. Evaluation of CSM-WEFE Simulation Performance
4.2. Baseline Scenario Simulation and Evaluation
4.2.1. Coupled Simulation Results of the Current WEFE System
4.2.2. Evaluation of the Current Coordinated Sustainable Development
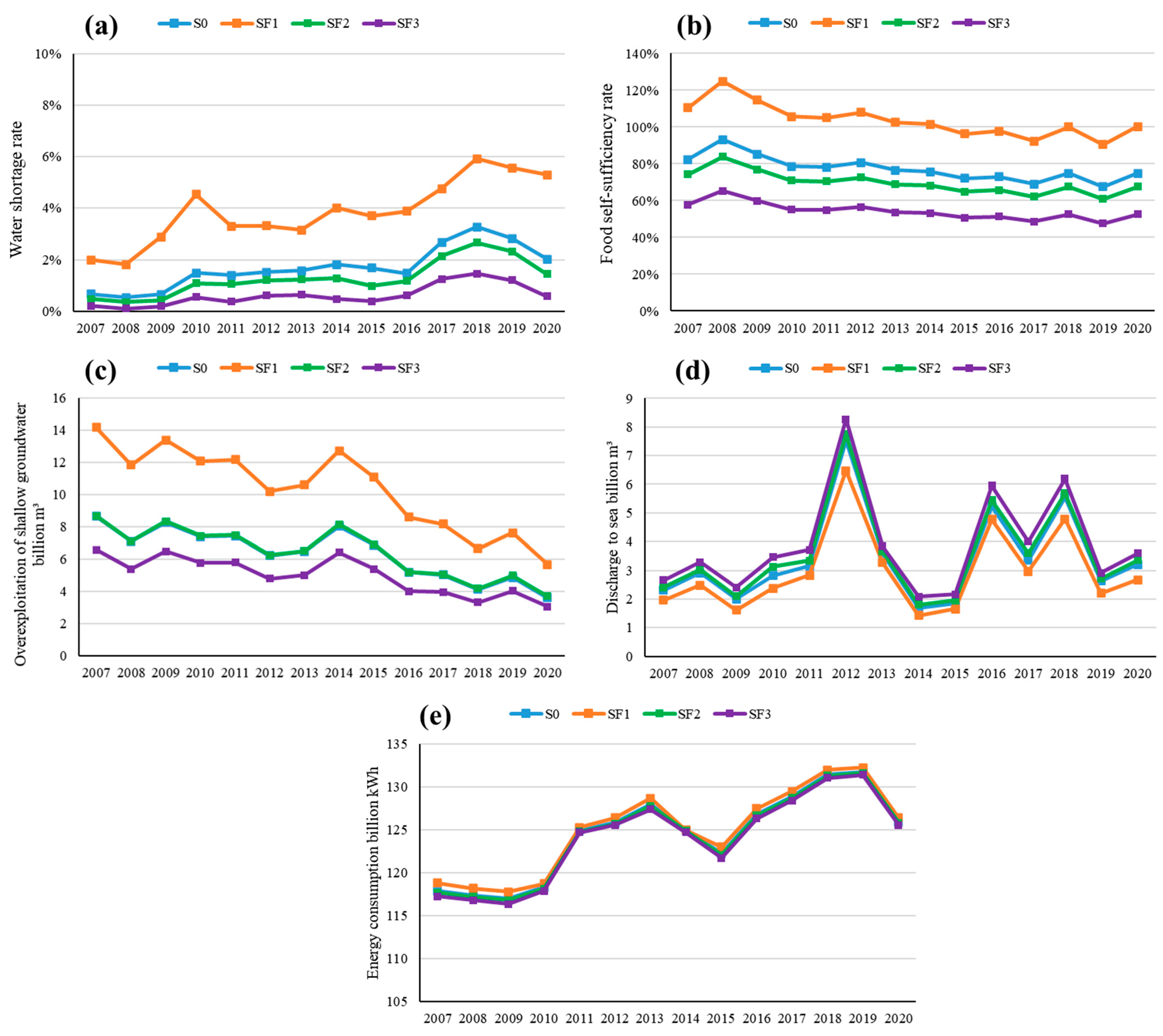
4.3. Food Security Scenarios Simulation and Evaluation
4.3.1. Coupled Simulation Results of the WEFE System Under Food Security Scenarios
4.3.2. Evaluation of Coordinated Sustainable Development Under Food Security Scenarios
4.4. Ecological Restoration Scenario Simulation and Evaluation
4.4.1. Coupled Simulation Results of the WEFE System Under Ecological Restoration Scenarios
4.4.2. Evaluation of Coordinated Sustainable Development Under Ecological Restoration Scenarios
5. Discussion
5.1. Correlation Analysis of Different Evaluation Indices
5.2. Trade-Off Between Food Security and Ecological Restoration of the WEFE System
5.3. Limitations and Model Applicability
6. Conclusions
6.1. Summary of Key Findings
- (1)
- This study develops a coupled simulation model of water–energy–food–ecosystems (CSM-WEFE) which consists of a natural water cycle module, a social water cycle module, a food production module, and an energy consumption module. This model allows for the dynamic simulation and feedback of key elements across WEFE subsystems. The model was validated with high accuracy using runoff, water resources, water allocation, river discharge into the sea, and food production outputs.
- (2)
- Based on the outputs of the CSM-WEFE, three performance indices, i.e., REL, CCD, and EQU, were designed, and a coordinated sustainability development index (CSD) was further developed to distinguish the differences in WEFE system development across scenarios, addressing the inconsistency in evaluation standards in traditional indicator-based methods. The multi-year average CSD of the BTH region under the current condition was found to be 0.523, indicating that the overall WEFE system remains in a sustainable development state.
- (3)
- The results reveal that enhancing food security targets tends to intensify groundwater overextraction and ecological degradation, thereby weakening WEFE system coordination. Conversely, restricting groundwater overextraction can improve ecological conditions but significantly increases water scarcity and reduces food self-sufficiency. Under the current water-use pattern, agricultural water demand is met primarily through overextraction of groundwater and encroachment on ecological water requirements. Even with the full operation of SNWDP-MR, the region still faces a 16.4% water shortage. Coordinated development under different scenarios is constrained by the trade-off between food security and ecological restoration, with the CSD ranging between 0.510 and 0.538 across scenarios.
6.2. Policy Implications
- (1)
- Promote zonal food self-sufficiency targets and coordinate agricultural land retirement for water reallocation.
- (2)
- Enhance the water-saving potential of irrigation districts to promote efficient agricultural development.
- (3)
- Optimize the allocation mechanism of the SNWDP to enable coordinated ecological replenishment, agricultural reallocation, and urban reuse.
- (4)
- Establish coordinated surface–groundwater management to enhance ecological restoration feasibility.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WEFE | Water–Energy–Food–Ecosystems |
| CSM-WEFE | Coupled Simulation Model of the WEFE |
| BTH | Beijing–Tianjin–Hebei |
| BJ | Beijing |
| TJ | Tianjin |
| HB | Hebei |
| LR | Luanhe River Basin |
| HRN | Haihe River North Basin |
| HRS | Haihe River South Basin |
| SNWDP | South-to-North Water Diversion Project |
| GWAS | General Water Allocation and Simulation for Management System |
| Energy Consumption for Surface Water Intake | |
| Energy Consumption for Groundwater Extraction | |
| Energy Consumption for Water Production | |
| Energy Consumption for Water Distribution | |
| Energy Consumption for Domestic Water Use | |
| Energy Consumption for Industrial Water Use | |
| Energy Consumption for Reclaimed Water Treatment | |
| Total Energy Consumption of the Social Water Cycle | |
| Water Shortage Rate | |
| Food Self-Sufficiency Rate | |
| REL | Reliability index |
| EQU | Equilibrium index |
| CCD | Coupling Coordination Degree index |
| CD | Coordination Degree |
| CE | Comprehensive Evaluation |
| CSD | Coordinated Sustainable Development index |
| Relative Error | |
| Coefficient of Determination | |
| Nash–Sutcliffe Efficiency | |
| Root Mean Square Error |
Appendix A
| Subsystem | Indicator | Attribute | Subsystem | Indicator | Attribute |
|---|---|---|---|---|---|
| Water | Water shortage rate | Negative | Food | Agricultural water use | Negative |
| Equilibrium | Positive | Food self-sufficiency rate | Positive | ||
| Domestic and industrial water use | Positive | Food production | Positive | ||
| Energy | EC for water intake and supply | Negative | Ecology | Groundwater overextraction | Negative |
| EC for water use | Negative | Ecology water use | Positive | ||
| EC for reclaimed water treatment | Negative | Reclaimed water usage | Positive |
| Evaluation Method | Formula |
|---|---|
| Relative error | |
| Correlation coefficient | |
| Nash–Sutcliffe efficiency coefficient | |
| Root mean square error |

References
- Qin, J.X.; Duan, W.L.; Chen, Y.N.; Dukhovny, V.A.; Sorokin, D.; Li, Y.P.; Wang, X.X. Comprehensive evaluation and sustainable development of water-energy-food-ecology systems in Central Asia. Renew. Sust. Energ. Rev. 2022, 157, 112061. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Bijl, D.L.; Bogaart, P.; Stehfest, E.; Biemans, H.; Dekker, S.C.; Doelman, J.C.; Gernaat, D.; Harmsen, M. Integrated scenarios to support analysis of the food-energy-water nexus. Nat. Sustain. 2019, 2, 1132–1141. [Google Scholar] [CrossRef]
- He, C.Y.; Liu, Z.F.; Wu, J.G.; Pan, X.H.; Fang, Z.H.; Li, J.W.; Bryan, B.A. Future global urban water scarcity and potential solutions. Nat. Commun. 2021, 12, 4667. [Google Scholar] [CrossRef]
- Newell, J.P.; Goldstein, B.; Foster, A. A 40-year review of food-energy-water nexus literature and its application to the urban scale. Environ. Res. Lett. 2019, 14, 073003. [Google Scholar] [CrossRef]
- Endo, A.; Tsurita, I.; Burnett, K.; Orencio, P.M. A review of the current state of research on the water, energy, and food nexus. J. Hydrol.-Reg. Stud. 2017, 11, 20–30. [Google Scholar] [CrossRef]
- Zhang, J.; Campana, P.E.; Yao, T.; Zhang, Y.; Lundblad, A.; Melton, F.; Yan, J. The water-food-energy nexus optimization approach to combat agricultural drought: A case study in the United States. Appl. Energy 2018, 227, 449–464. [Google Scholar] [CrossRef]
- Liu, P.W.; Famiglietti, J.S.; Purdy, A.J.; Adams, K.H.; McEvoy, A.L.; Reager, J.T.; Bindlish, R.; Wiese, D.N.; David, C.H.; Rodell, M. Groundwater depletion in California’s Central Valley accelerates during megadrought. Nat. Commun. 2022, 13, 7825. [Google Scholar] [CrossRef]
- Bostic, D.; Mendez-Barrientos, L.; Pauloo, R.; Dobbin, K.; Macclements, V. Thousands of domestic and public supply wells face failure despite groundwater sustainability reform in California’s Central Valley. Sci. Rep. 2023, 13, 14797. [Google Scholar] [CrossRef]
- Amjath-Babu, T.S.; Sharma, B.; Brouwer, R.; Rasul, G.; Wahid, S.M.; Neupane, N.; Bhattarai, U.; Sieber, S. Integrated modelling of the impacts of hydropower projects on the water-food-energy nexus in a transboundary Himalayan river basin. Appl. Energy 2019, 239, 494–503. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wei, J.Y.; Shan, W.B.; Zhao, J.S. Modeling the water-energy-food-environment nexus and transboundary cooperation opportunity in the Brahmaputra River Basin. J. Hydrol.-Reg. Stud. 2023, 49, 101497. [Google Scholar] [CrossRef]
- Basheer, M.; Wheeler, K.G.; Ribbe, L.; Majdalawi, M.; Abdo, G.; Zagona, E.A. Quantifying and evaluating the impacts of cooperation in transboundary river basins on the Water-Energy-Food nexus: The Blue Nile Basin. Sci. Total Environ. 2018, 630, 1309–1323. [Google Scholar] [CrossRef]
- Yu, Y.; Bo, Y.; Castelletti, A.; Dumas, P.; Gao, J.; Cai, X.; Liu, J.; Kahil, T.; Wada, Y.; Hu, S. Transboundary cooperation in infrastructure operation generates economic and environmental co-benefits in the Lancang-Mekong River Basin. Nature Water 2024, 2, 589–601. [Google Scholar] [CrossRef]
- Wang, S.S.; Yang, J.Y.; Wang, A.L.; Liu, T.F.; Du, S.B.; Liang, S.T. Coordinated analysis and evaluation of water-energy-food coupling: A case study of the Yellow River basin in Shandong Province, China. Ecol. Indic. 2023, 148, 110138. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Zhao, Y.; Li, H.H.; Zhu, Y.N.; He, G.H.; Xu, Y.R.; Shang, Y.Z. A copula-based security risk evaluation and probability calculation for water-energy-food nexus. Sci. Total Environ. 2023, 856, 159236. [Google Scholar] [CrossRef] [PubMed]
- Yin, D.Y.; Yu, H.C.; Shi, Y.Y.; Zhao, M.Y.; Zhang, J.; Li, X.S. Matching supply and demand for ecosystem services in the Yellow River Basin, China: A perspective of the water-energy-food nexus. J. Clean. Prod. 2023, 384, 135469. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Su, X.L.; Singh, V.P.; Wu, H.J.; Niu, J.P.; Wu, L.Z.; Chu, J.D. Improving synergy of the water-agriculture-ecology system in arid areas using a novel co-optimization model. Agric. Water Manag. 2025, 312, 109408. [Google Scholar] [CrossRef]
- Chen, J.X.; Wu, H.; Zhang, C.L.; Guo, P.; Huo, Z.L. An inexact bi-level multi-objective modeling approach for managing agricultural water-food-carbon-land-ecology-nutrition nexus in an arid area. J. Hydrol. 2023, 621, 129556. [Google Scholar] [CrossRef]
- Ding, T.H.; Chen, J.F. Evaluation and obstacle factors of coordination development of regional water-energy-food-ecology system under green development: A case study of Yangtze River Economic Belt, China. Stoch. Environ. Res. Risk Assess. 2022, 36, 2477–2493. [Google Scholar] [CrossRef]
- Liu, L.M.; Wang, C.B.; Chen, J.F. Simulation of regional green development policies under the nexus of water-energy-food-ecology: A case study of the Yangtze River economic Belt. Ecol. Indic. 2025, 173, 113364. [Google Scholar] [CrossRef]
- Lv, Y.X.; Li, Y.; Zhang, Z.X.; Luo, S.M.; Feng, X.; Chen, X.D. Spatio-temporal evolution pattern and obstacle factors of water-energy-food nexus coupling coordination in the Yangtze river economic belt. J. Clean. Prod. 2024, 444, 141229. [Google Scholar] [CrossRef]
- Conway, D.; van Garderen, E.A.; Deryng, D.; Dorling, S.; Krueger, T.; Landman, W.; Lankford, B.; Lebek, K.; Osborn, T.; Ringler, C.; et al. Climate and southern Africa’s water-energy-food nexus. Nat. Clim. Change 2015, 5, 837–846. [Google Scholar] [CrossRef]
- Botai, J.O.; Botai, C.M.; Ncongwane, K.P.; Mpandeli, S.; Nhamo, L.; Masinde, M.; Adeola, A.M.; Mengistu, M.G.; Tazvinga, H.; Murambadoro, M.D.; et al. A Review of the Water-Energy-Food Nexus Research in Africa. Sustainability 2021, 13, 1762. [Google Scholar] [CrossRef]
- Kalvani, S.R.; Celico, F. The Water-Energy-Food Nexus in European Countries: A Review and Future Perspectives. Sustainability 2023, 15, 4960. [Google Scholar] [CrossRef]
- Saladini, F.; Betti, G.; Ferragina, E.; Bouraoui, F.; Cupertino, S.; Canitano, G.; Gigliotti, M.; Autino, A.; Pulselli, F.M.; Riccaboni, A.; et al. Linking the water-energy-food nexus and sustainable development indicators for the Mediterranean region. Ecol. Indic. 2018, 91, 689–697. [Google Scholar] [CrossRef]
- Karatayev, M.; Rivotti, P.; Mourão, Z.S.; Konadu, D.D.; Shah, N.; Clarke, M. The water-energy-food nexus in Kazakhstan: Challenges and opportunities. Energy Procedia 2017, 125, 63–70. [Google Scholar] [CrossRef]
- Sadeghi, S.H.; Moghadam, E.S.; Delavar, M.; Zarghami, M. Application of water-energy-food nexus approach for designating optimal agricultural management pattern at a watershed scale. Agric. Water Manag. 2020, 233, 106071. [Google Scholar] [CrossRef]
- Dalla Fontana, M.; de Araújo Moreira, F.; Di Giulio, G.M.; Malheiros, T.F. The water-energy-food nexus research in the Brazilian context: What are we missing? Environ. Sci. Policy 2020, 112, 172–180. [Google Scholar] [CrossRef]
- Del Borghi, A.; Tacchino, V.; Moreschi, L.; Matarazzo, A.; Gallo, M.; Vazquez, D.A. Environmental assessment of vegetable crops towards the water-energy-food nexus: A combination of precision agriculture and life cycle assessment. Ecol. Indic. 2022, 140, 109015. [Google Scholar] [CrossRef]
- Armengot, L.; Beltrán, M.J.; Schneider, M.; Simón, X.; Pérez-Neira, D. Food-energy-water nexus of different cacao production systems from a LCA approach. J. Clean. Prod. 2021, 304, 126941. [Google Scholar] [CrossRef]
- Tabatabaie, S.M.H.; Murthy, G.S. Development of an input-output model for food-energy-water nexus in the pacific northwest, USA. Resour. Conserv. Recycl. 2021, 168, 105267. [Google Scholar] [CrossRef]
- Deng, H.-M.; Wang, C.; Cai, W.-J.; Liu, Y.; Zhang, L.-X. Managing the water-energy-food nexus in China by adjusting critical final demands and supply chains: An input-output analysis. Sci. Total Environ. 2020, 720, 137635. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Zhang, X.; Peng, H.; Skitmore, M.; Bai, X.; Zheng, Z. The energy-food-water nexus: Water footprint of Henan-Hubei-Hunan in China. Renew. Sustain. Energy Rev. 2021, 135, 110417. [Google Scholar] [CrossRef]
- Yue, Q.; Guo, P. Managing agricultural water-energy-food-environment nexus considering water footprint and carbon footprint under uncertainty. Agric. Water Manag. 2021, 252, 106899. [Google Scholar] [CrossRef]
- Wang, Y.R.; Song, J.X.; Zhang, X.X.; Sun, H.T.; Bai, H.F. Coupling coordination evaluation of water-energy-food and poverty in the Yellow River Basin, China. J. Hydrol. 2022, 614, 128461. [Google Scholar] [CrossRef]
- Zhang, L.; Kong, L.J.; Ji, X.Y.; Ren, Y.H.; Lin, C.; Lu, Z.H. Developing a quantitative framework for watershed sustainable development: The ecology-water energy food (E-WEF) approach. Ecol. Indic. 2025, 172, 113291. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, B.; Han, J.; Zhao, Y.; Cao, Y.; Yao, J.; Shi, L. Evaluation of the Coupling Coordination and Sustainable Development of Water–Energy–Land–Food System on a 40-Year Scale: A Case Study of Hebei, China. Land 2024, 13, 1089. [Google Scholar] [CrossRef]
- Chang, H.Y.; Cao, Y.Q.; Zhao, Y.; He, G.H.; Wang, Q.M.; Yao, J.Q.; Ren, H.; Yang, H.C.; Hong, Z. Competitive and synergic evolution of the water-food-ecology system: A case study of the Beijing-Tianjin-Hebei region, China. Sci. Total Environ. 2024, 923, 14. [Google Scholar] [CrossRef]
- Sun, C.Z.; Hao, S. Research on the competitive and synergistic evolution of the water-energy-food system in China. J. Clean. Prod. 2022, 365, 171509. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Li, Y.P.; Huang, G.H.; Ma, Y. A copula-based stochastic fractional programming method for optimizing water-food-energy nexus system under uncertainty in the Aral Sea basin. J. Clean. Prod. 2021, 292, 126037. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Wang, Y.Y.; Ma, X.J.; Bo, H.; Luo, J. Supply-demand risk assessment and multi-scenario simulation of regional water-energy-food nexus: A case study of the Beijing-Tianjin-Hebei region. Resour. Conserv. Recycl. 2021, 174, 105799. [Google Scholar] [CrossRef]
- Kamrani, K.; Roozbahani, A.; Shahdany, S.M.H. Using Bayesian networks to evaluate how agricultural water distribution systems handle the water-food-energy nexus. Agric. Water Manag. 2020, 239, 106265. [Google Scholar] [CrossRef]
- Momblanch, A.; Papadimitriou, L.; Jain, S.K.; Kulkarni, A.; Ojha, C.S.P.; Adeloye, A.J.; Holman, I.P. Untangling the water-food-energy-environment nexus for global change adaptation in a complex Himalayan water resource system. Sci. Total Environ. 2019, 655, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.L.; Ren, L. Simulating and assessing the effects of seasonal fallow schemes on the water-food-energy nexus in a shallow groundwater-fed plain of the Haihe River basin of China. J. Hydrol. 2021, 595, 125992. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.N.; Wei, T.T.; Wang, Y.K.; Liu, Y.J.; Xu, L.G.; He, J.Q.; Wang, X.J. A quantitative analysis framework for analyzing impacts of climate change on water-food-energy-ecosystem nexus in irrigation areas based on WEAP-MODFLOW. J. Clean. Prod. 2024, 470, 143315. [Google Scholar] [CrossRef]
- Liu, Y.J.; Jiang, Y.A.; Xu, C.; Lyu, J.Y.; Su, Z.H. A quantitative analysis framework for water-food-energy nexus in an agricultural watershed using WEAP-MODFLOW. Sustain. Prod. Consump. 2022, 31, 693–706. [Google Scholar] [CrossRef]
- Wang, X.K.; Dong, Z.C.; Susnik, J. System dynamics modelling to simulate regional water-energy-food nexus combined with the society-economy-environment system in Hunan Province, China. Sci. Total Environ. 2023, 863, 160993. [Google Scholar] [CrossRef]
- Howells, M.; Hermann, S.; Welsch, M.; Bazilian, M.; Segerström, R.; Alfstad, T.; Gielen, D.; Rogner, H.; Fischer, G.; Van Velthuizen, H. Integrated analysis of climate change, land-use, energy and water strategies. Nat. Clim. Change 2013, 3, 621–626. [Google Scholar] [CrossRef]
- Karnib, A. Bridging Science and Policy in Water-Energy-Food Nexus: Using the Q-Nexus Model for Informing Policy Making. Water Resour. Manag. 2018, 32, 4895–4909. [Google Scholar] [CrossRef]
- Imasiku, K.; Ntagwirumugara, E. An impact analysis of population growth on energy-water-food-land nexus for ecological sustainable development in Rwanda. Food Energy Secur. 2020, 9, e185. [Google Scholar] [CrossRef]
- Martinez-Hernandez, E.; Leach, M.; Yang, A.D. Understanding water-energy-food and ecosystem interactions using the nexus simulation tool NexSym. Appl. Energy 2017, 206, 1009–1021. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Q.M.; Jiang, S.; Zhai, J.Q.; Wang, J.H.; He, G.H.; Li, H.H.; Zhang, Y.; Wang, L.Z.; Zhu, Y.N. Irrigation water and energy saving in well irrigation district from a water -energy nexus perspective. J. Clean. Prod. 2020, 267, 122058. [Google Scholar] [CrossRef]
- Wang, L.H.; Jia, B.H.; Xie, Z.H.; Wang, B.; Liu, S.; Li, R.C.; Liu, B.; Wang, Y.; Chen, S. Impact of groundwater extraction on hydrological process over the Beijing-Tianjin-Hebei region, China. J. Hydrol. 2022, 609, 127689. [Google Scholar] [CrossRef]
- Kattel, G.; Reeves, J.; Western, A.; Zhang, W.J.; Jing, W.; McGowan, S.; Cuo, L.; Scales, P.; Dowling, K.; He, Q.; et al. Healthy waterways and ecologically sustainable cities in Beijing-Tianjin-Hebei urban agglomeration (northern China): Challenges and future directions. Wiley Interdiscip. Rev.-Water 2021, 8, e1500. [Google Scholar] [CrossRef]
- Luo, J.M.; Zhang, H.M.; Qi, Y.Q.; Pei, H.W.; Shen, Y.J. Balancing water and food by optimizing the planting structure in the Beijing-Tianjin-Hebei region, China. Agric. Water Manag. 2022, 262, 107326. [Google Scholar] [CrossRef]
- Sang, X.; Wang, H.; Wang, J.; Zhao, Y.; Zhou, Z. Water resources comprehensive allocation and simulation model (WAS), part I. Theory and development. J. Hydraul. Eng 2018, 49, 1451–1459. [Google Scholar]
- Chang, H.; Sang, X.; He, G.; Wang, Q.; Jiang, S.; He, F.; Li, H.; Zhao, Y. Research and Application of the Mutual Feedback Mechanism of a Regional Natural-Social Dualistic Water Cycle: A Case Study in Beijing–Tianjin–Hebei, China. Water 2022, 14, 3227. [Google Scholar] [CrossRef]
- Yan, Z.; Zhou, Z.; Liu, J.; Wen, T.; Sang, X.; Zhang, F. Multiobjective optimal operation of reservoirs based on water supply, power generation, and river ecosystem with a new water resource allocation model. J. Water Resour. Plan. Manag. 2020, 146, 05020024. [Google Scholar] [CrossRef]
- Rao, N.; Sarma, P.; Chander, S. A simple dated water-production function for use in irrigated agriculture. Agric. Water Manag. 1988, 13, 25–32. [Google Scholar] [CrossRef]
- Stewart, J.I.; Hagan, R.; Pruitt, W.; Danielson, R.; Franklin, W.; Hanks, R.; Riley, J.; Jackson, E. Optimizing Crop Production Through Control of Water and Salinity Levels in the Soil; Merrill-Cazier Library: Logan, UT, USA, 1977. [Google Scholar]
- Kuznietsov, P.M.; Biedunkova, O.O.; Yaroschuk, O.V.; Pryshchepa, A.M.; Antonyuk, O.O. Analysis of the Impact of Water Use and Consumption for a Nuclear Power Plant on Alterations in the Hydrological and Temperature Regimes of a River: A Case Study. IOP Conf. Ser. Earth Environ. Sci. 2024, 1415, 012100. [Google Scholar] [CrossRef]












| Model | Feature | Limitation | Improvements of CSM-WEFE |
|---|---|---|---|
| Indicator-based models (e.g., coupling coordination degree, copula functions) | Utilization of statistical data and composite indices to assess system coordination and sustainability. | Difficult to establish standardized evaluation criteria; scenario comparisons across regions are not directly comparable; results are sensitive to subjective weighting schemes. | Integrates three objective performance indices—reliability (REL), coupling coordination degree (CCD), and equilibrium (EQU)—and develops a unified coordinated sustainable development index (CSD) to enable consistent scenario-based comparisons. |
| System dynamics models | Simulation of feedback loops and time delays among subsystems using causal loop diagrams. | High-level abstraction oversimplifies the underlying physical processes; limited ability to capture spatial heterogeneity. | CSM-WEFE embeds physically based modules for natural and social water cycles, agricultural production, and energy feedback, enhancing simulation accuracy and spatial resolution. |
| Coupled process-based models (e.g., WEAP, SWAT, MODFLOW) | Linking mature models to quantify key processes across the water–food–energy–ecology nexus. | Coupling complexity; high data requirements; and challenging model calibration and validation. | Employs a modular architecture to reduce integration complexity, while achieving dynamic coupling of core processes; validated against multi-source observations to ensure simulation accuracy. |
| Integrated nexus models (e.g., CLEWS, MuSIASEM, NexSym) | Capturing cross-sectoral linkages through optimization or simulation across systems. | Frequent focus on macro-scale energy–economic interactions, with limited representation of regional water constraints and ecological dynamics. | Anchored in the regional water cycle, CSM-WEFE integrates ecological water needs and food production feedback, addressing ecological–security trade-offs under water scarcity conditions. |
| Scenario | Scenario Condition | |
|---|---|---|
| Baseline | S0 | Current situation |
| Food security | SF1 | Irrigated area: 6.6 million ha |
| Average annual agricultural water demand: 22.8 billion m3 | ||
| SF2 | Irrigated area: 4.88 million ha | |
| Average annual agricultural water demand: 14.6 billion m3 | ||
| SF3 | Irrigated area: 3.42 million ha | |
| Average annual agricultural water demand: 10.2 billion m3 | ||
| Ecological restoration | SE1 | Balance of groundwater intake and recharge |
| SE2 | Extends SE1 | |
| Available water supply of SNWDP-MR: 4.95 billion m3 | ||
| SE3 | Extends SE2 | |
| The amount of discharge to sea shall not be less than 4.05 billion m3 | ||
| Hydrological Station | Basin | Calibration Period 2000~2010 | Validation Period 2011~2016 | ||||
|---|---|---|---|---|---|---|---|
| Sandaohezi | LR | 1.70% | 0.692 | 0.684 | 4.20% | 0.621 | 0.613 |
| Zhangjiafen | HRN | −0.50% | 0.71 | 0.709 | 9.50% | 0.694 | 0.682 |
| Cetian | HRN | −0.80% | 0.636 | 0.632 | 2.80% | 0.705 | 0.703 |
| Wangkuai | HRS | −9.70% | 0.772 | 0.763 | 14.80% | 0.618 | 0.605 |
| Huangbizhuang | HRS | 8.70% | 0.619 | 0.608 | 10.80% | 0.776 | 0.766 |
| Houbi | HRS | 2.80% | 0.71 | 0.707 | 13.80% | 0.899 | 0.761 |
| Water Resources | LR Mountain | LR Plain | HRN Mountain | HRN Plain | HRS Mountain | HRS Plain | |
|---|---|---|---|---|---|---|---|
| Surface water resources | 0.783 | 0.939 | 0.883 | 0.905 | 0.783 | 0.748 | |
| 5.799 | 2.689 | 2.144 | 2.208 | 9.553 | 5.363 | ||
| Groundwater | 0.572 | 0.807 | 0.680 | 0.797 | 0.662 | 0.796 | |
| 4.624 | 2.648 | 5.114 | 2.035 | 11.395 | 7.466 | ||
| City | |||
|---|---|---|---|
| Beijing | 0.1% | 0.999 | 0.047 |
| Tianjin | 2.8% | 0.922 | 0.968 |
| Shijiazhuang | 0.8% | 0.990 | 0.362 |
| Tangshan | 1.0% | 0.984 | 0.351 |
| Qinhuangdao | 0.4% | 0.995 | 0.050 |
| Handan | 1.0% | 0.959 | 0.279 |
| Xingtai | 1.7% | 0.993 | 0.380 |
| Baoding | 1.0% | 0.971 | 0.602 |
| Zhangjiakou | 0.3% | 0.998 | 0.047 |
| Chengde | 0.7% | 0.984 | 0.113 |
| Cangzhou | 4.6% | 0.778 | 0.821 |
| Langfang | 1.8% | 0.900 | 0.248 |
| Hengshui | 1.5% | 0.966 | 0.309 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Zhao, Y.; Cao, Y.; He, G.; Wang, Q.; Liu, R.; Ren, H.; Yao, J.; Li, W. Evaluating Sustainability of Water–Energy–Food–Ecosystems Nexus in Water-Scarce Regions via Coupled Simulation Model. Agriculture 2025, 15, 1271. https://doi.org/10.3390/agriculture15121271
Chang H, Zhao Y, Cao Y, He G, Wang Q, Liu R, Ren H, Yao J, Li W. Evaluating Sustainability of Water–Energy–Food–Ecosystems Nexus in Water-Scarce Regions via Coupled Simulation Model. Agriculture. 2025; 15(12):1271. https://doi.org/10.3390/agriculture15121271
Chicago/Turabian StyleChang, Huanyu, Yong Zhao, Yongqiang Cao, Guohua He, Qingming Wang, Rong Liu, He Ren, Jiaqi Yao, and Wei Li. 2025. "Evaluating Sustainability of Water–Energy–Food–Ecosystems Nexus in Water-Scarce Regions via Coupled Simulation Model" Agriculture 15, no. 12: 1271. https://doi.org/10.3390/agriculture15121271
APA StyleChang, H., Zhao, Y., Cao, Y., He, G., Wang, Q., Liu, R., Ren, H., Yao, J., & Li, W. (2025). Evaluating Sustainability of Water–Energy–Food–Ecosystems Nexus in Water-Scarce Regions via Coupled Simulation Model. Agriculture, 15(12), 1271. https://doi.org/10.3390/agriculture15121271










