Inversion of SPAD Values of Pear Leaves at Different Growth Stages Based on Machine Learning and Sentinel-2 Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
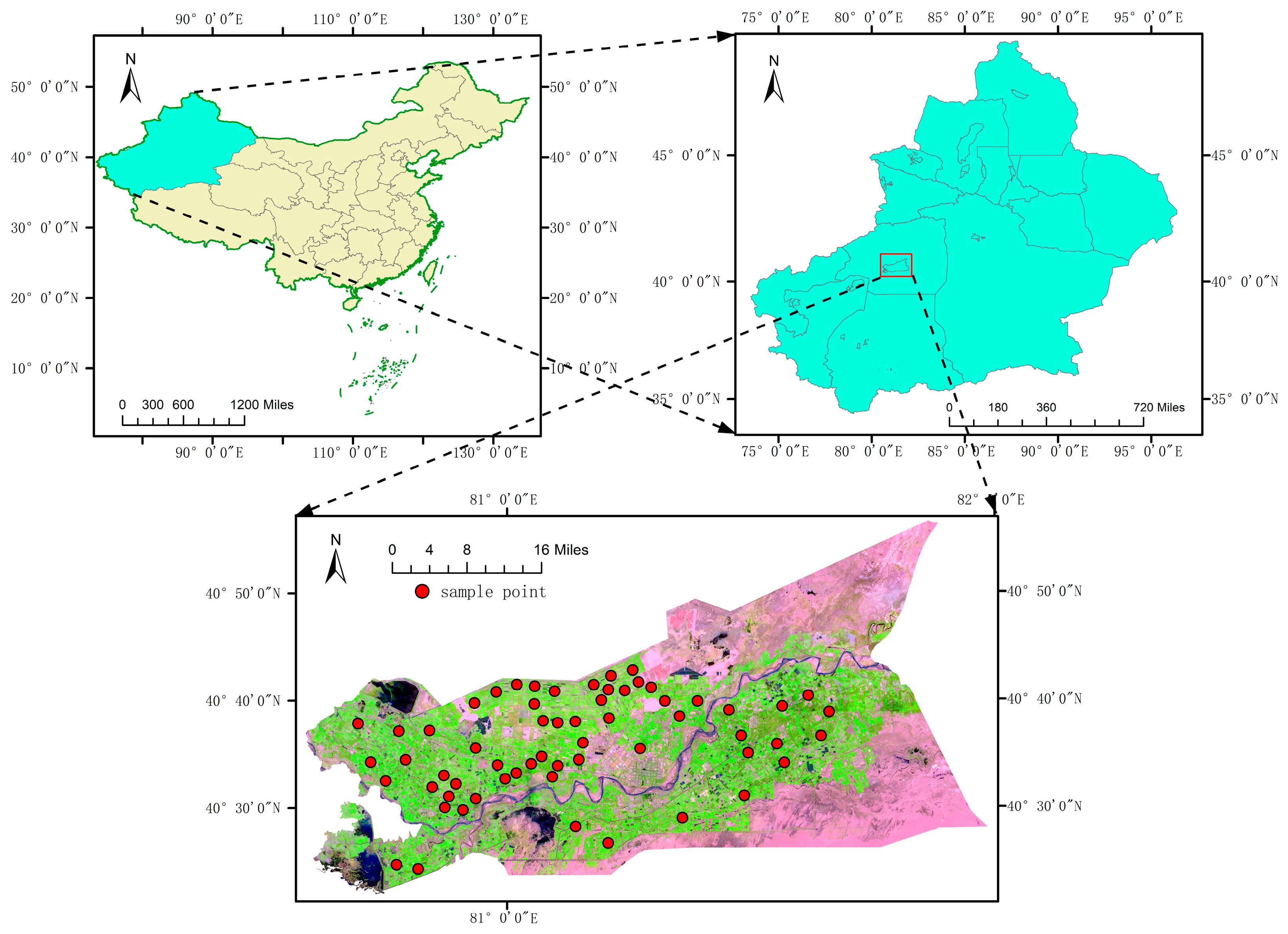
2.1. Overview of the Study Area
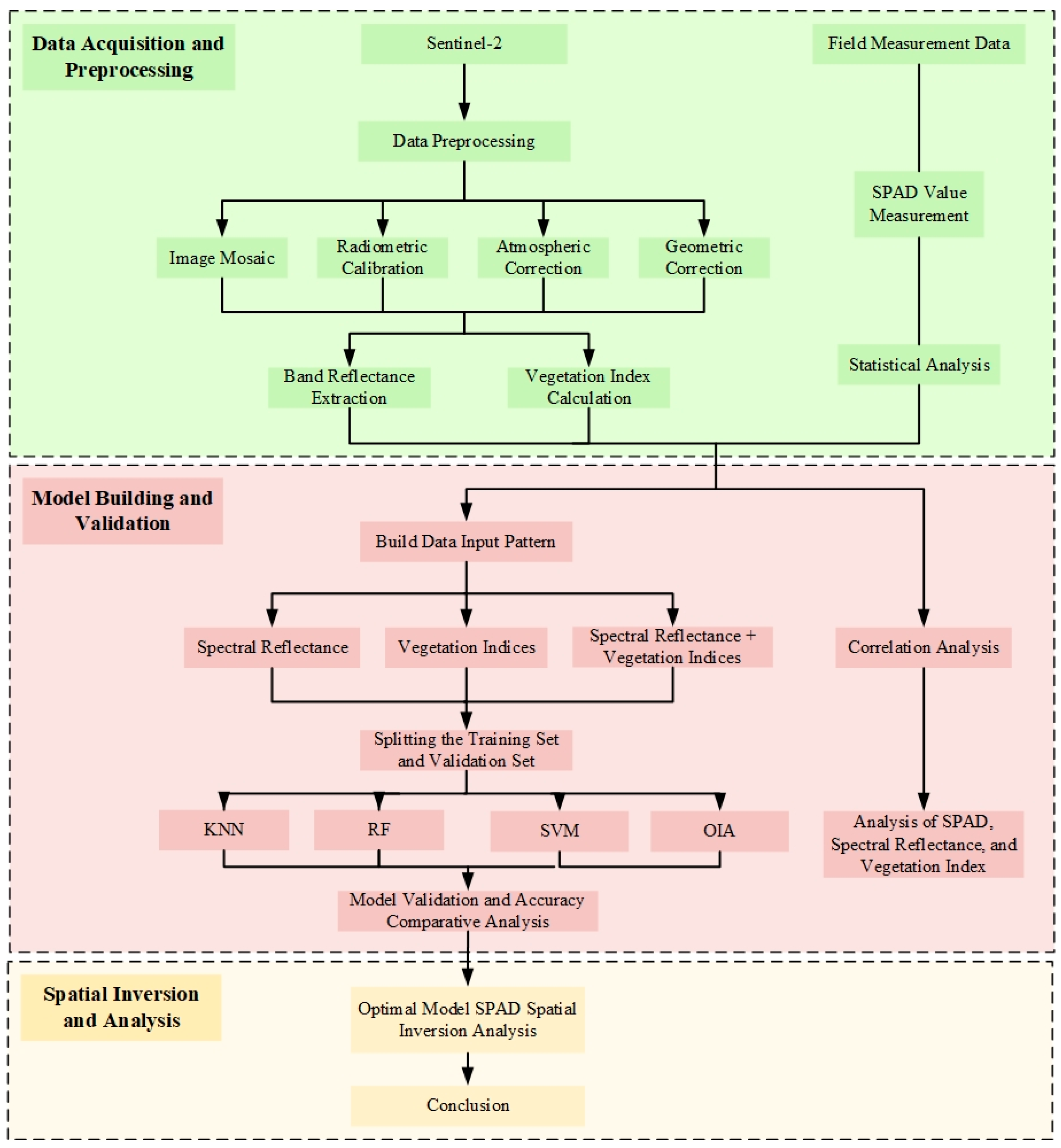
2.2. Data Acquisition and Processing
2.2.1. Remote Sensing Image Acquisition and Pre-Processing
2.2.2. Ground-Truthing Data Acquisition
2.2.3. Vegetation Indices Selection and Calculation
2.3. Model Construction and Evaluation
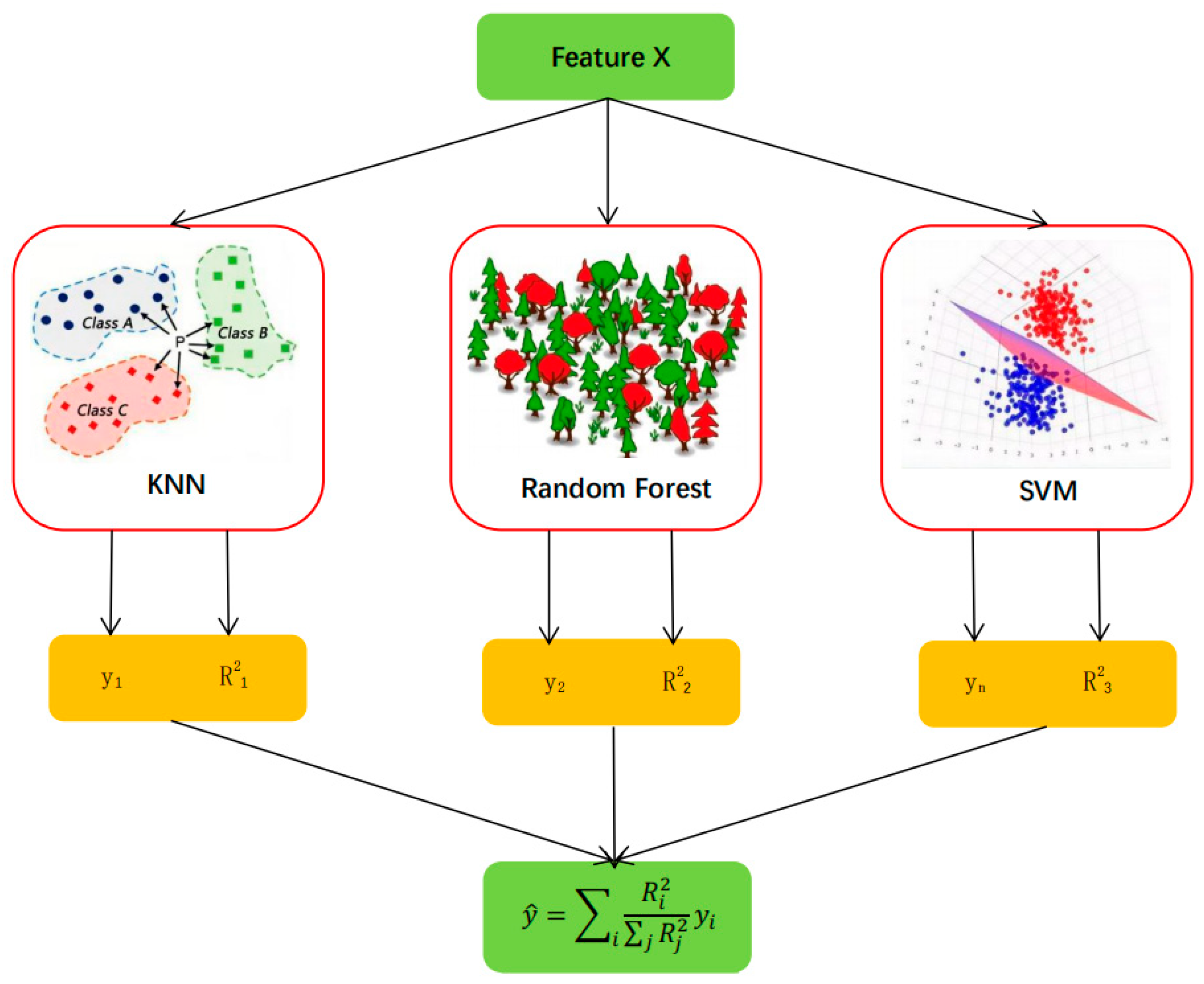
2.3.1. Model Construction Method
2.3.2. Evaluation of Model Accuracy
3. Results
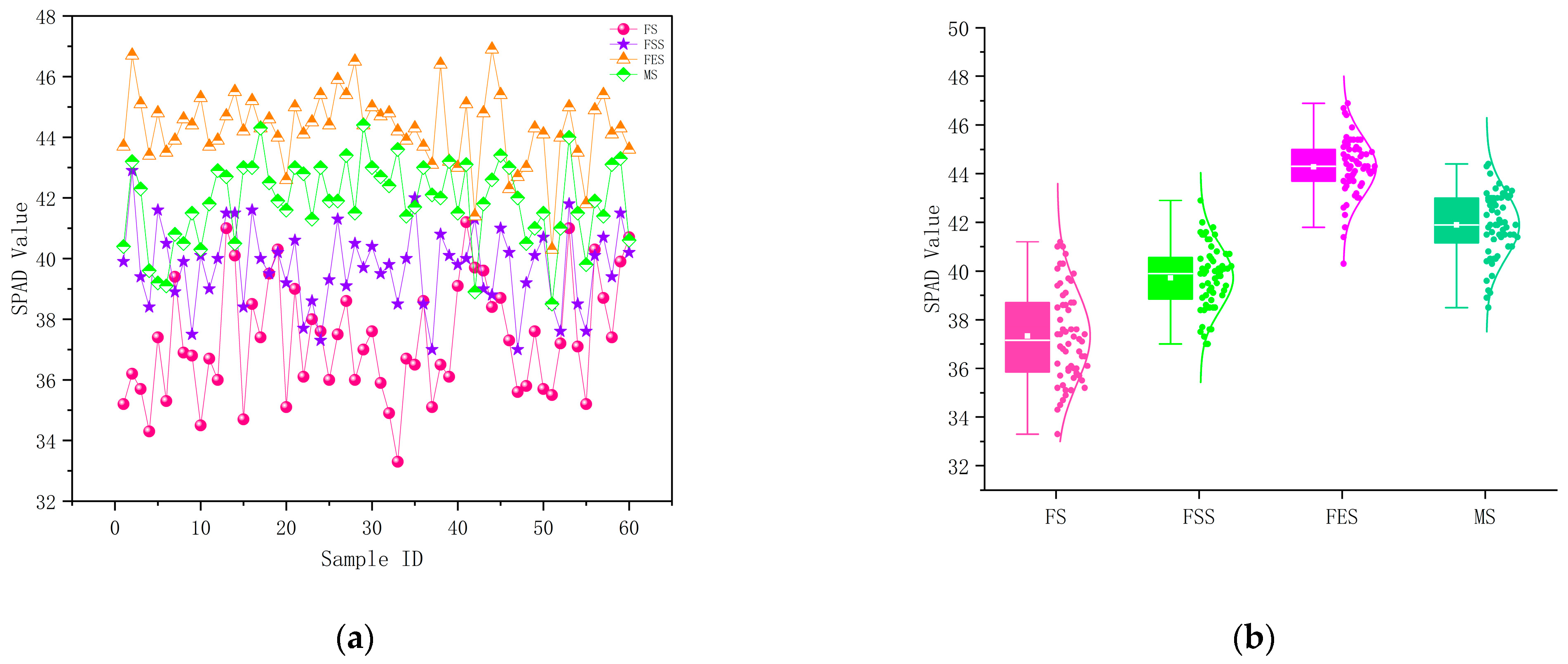
3.1. Variation Characteristics of SPAD Values of Pear Tree Leaves
3.2. Analysis of SPAD Values and Spectral Reflectance Characteristics
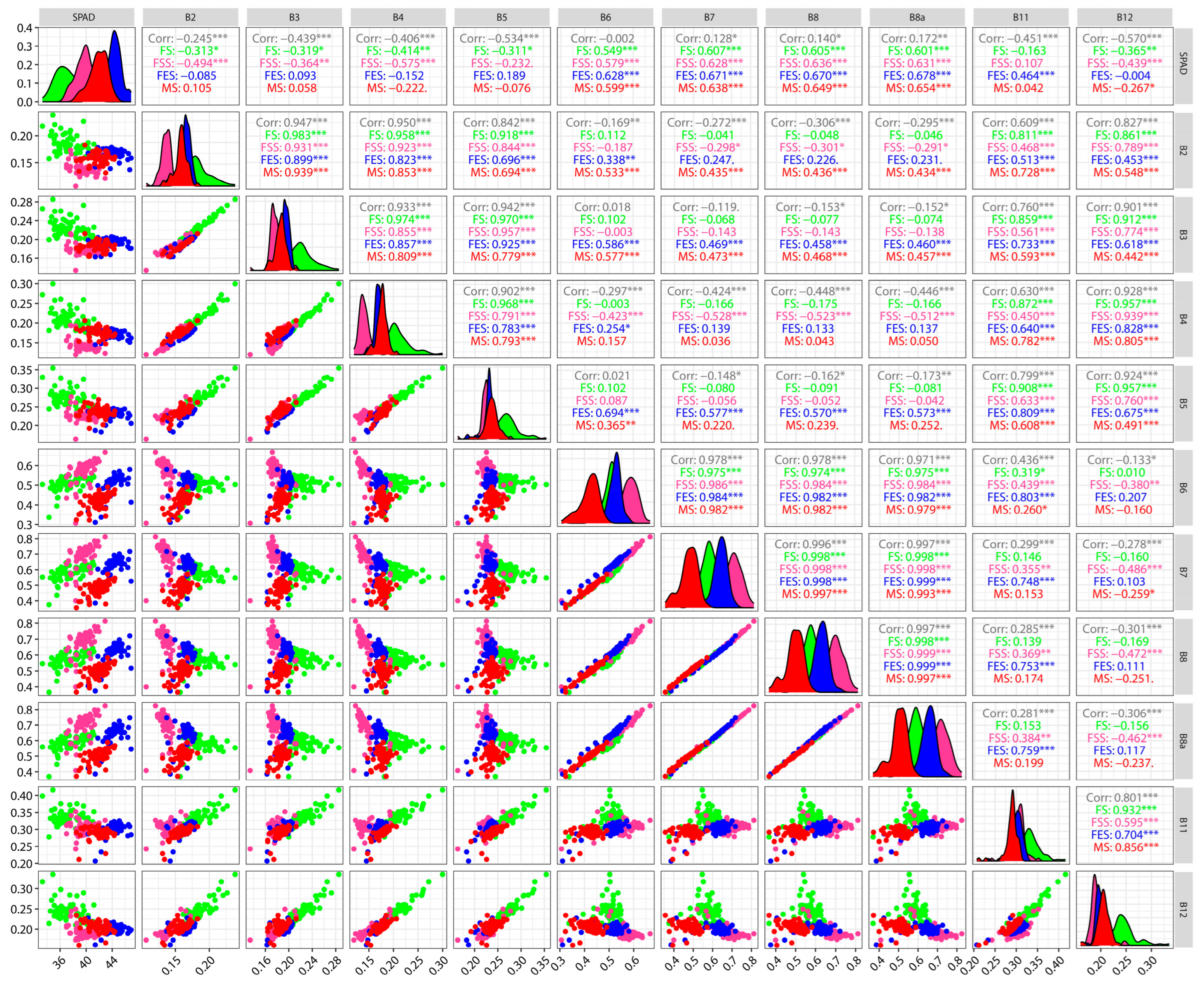
3.3. Correlation Analysis Between Spectral Reflectance and SPAD Values
3.4. Correlation Analysis Between Vegetation Indices and SPAD Values
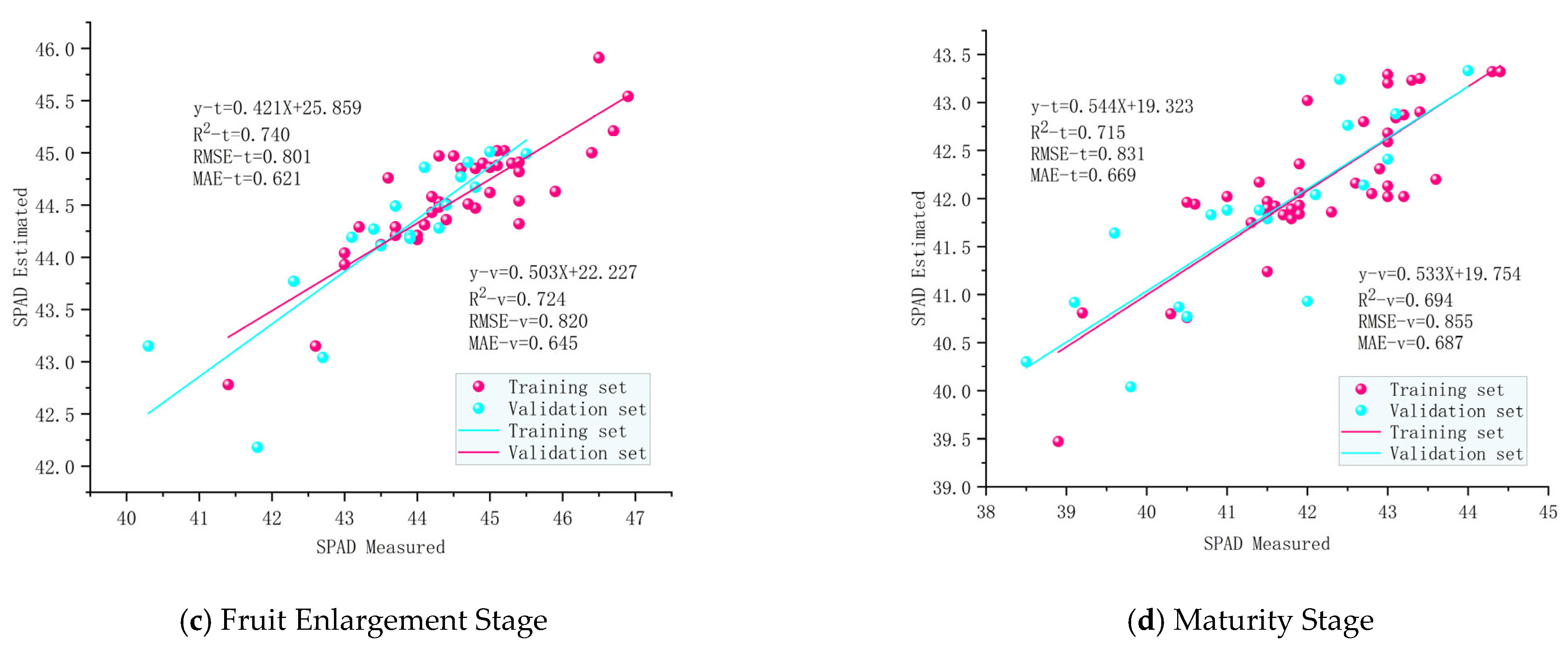
3.5. Inversion Model Results and Analysis for SPAD Values of Pear Tree Leaves
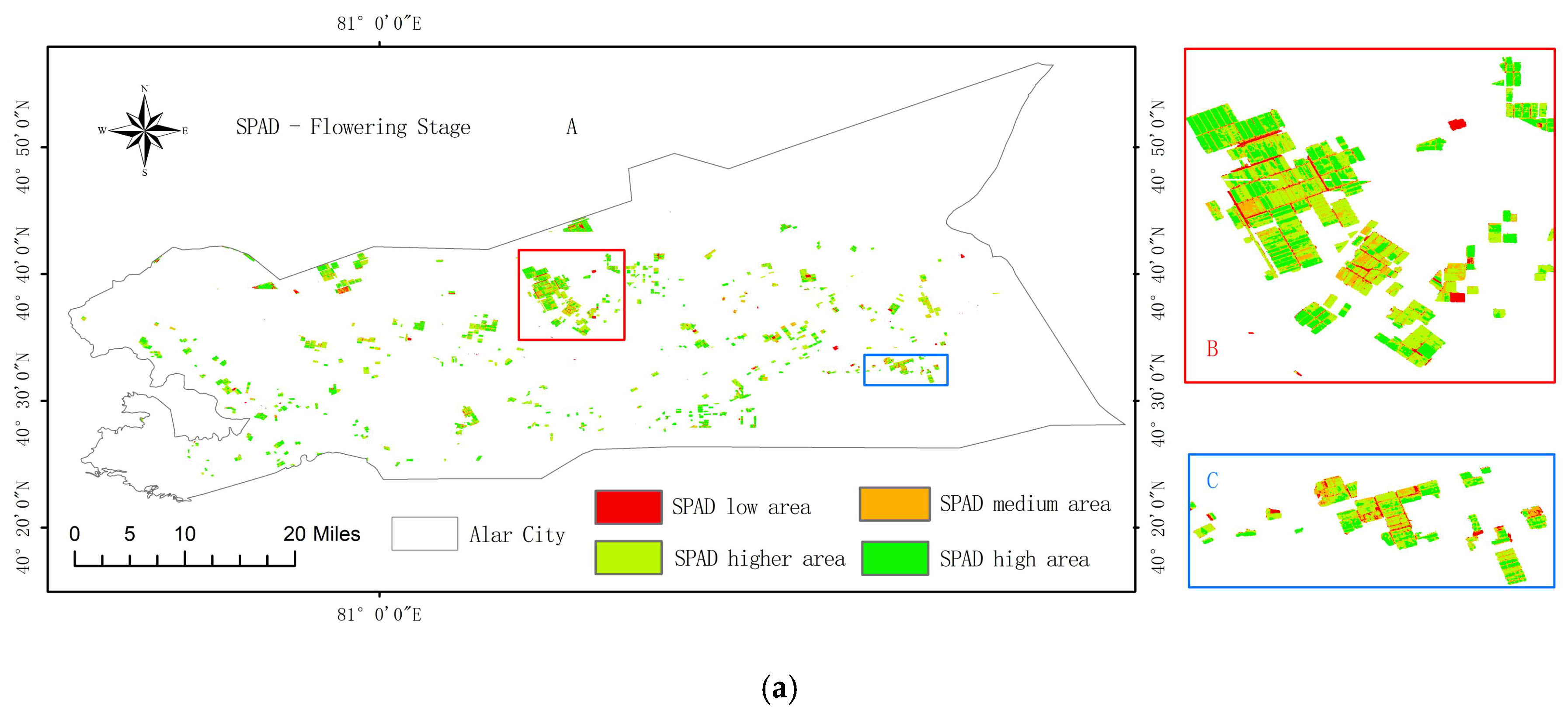
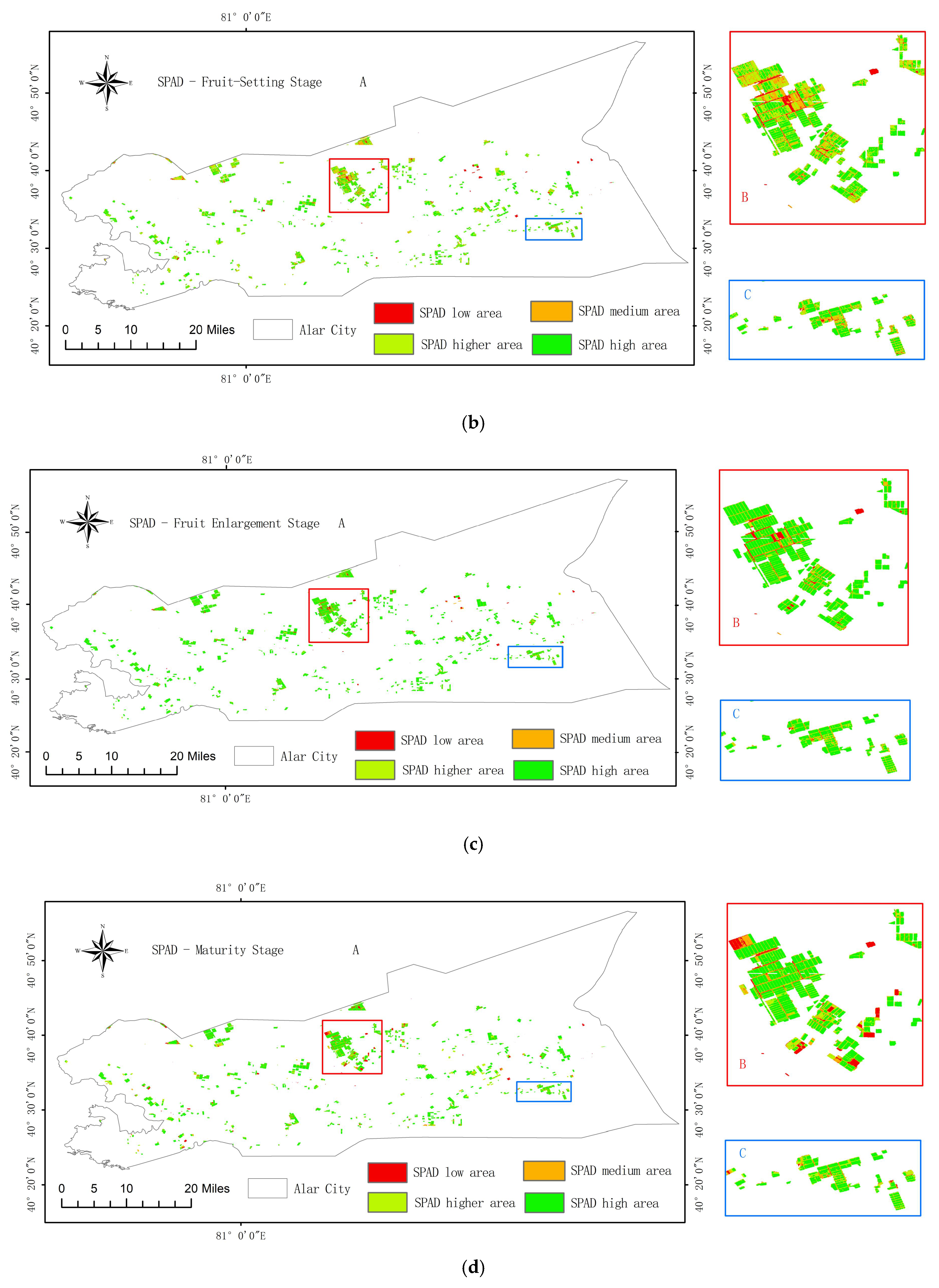
3.6. Temporal and Spatial Distribution Characteristics of Pear Tree Leaf SPAD Values Based on the Optimal Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Taha, M.F.; Mao, H.; Zhang, Z.; Elmasry, G.; Awad, M.A.; Abdalla, A.; Mousa, S.; Elwakeel, A.E.; Elsherbiny, O. Emerging Technologies for Precision Crop Management Towards Agriculture 5.0: A Comprehensive Overview. Agriculture 2025, 15, 582. [Google Scholar] [CrossRef]
- Torres-Quezada, E.; Fuentes-Peñailillo, F.; Gutter, K.; Rondón, F.; Marmolejos, J.M.; Maurer, W.; Bisono, A. Remote Sensing and Soil Moisture Sensors for Irrigation Management in Avocado Orchards: A Practical Approach for Water Stress Assessment in Remote Agricultural Areas. Remote Sens. 2025, 17, 708. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, G.; Lang, K.; Su, B.; Chen, X.; Xi, X.; Zhang, H. Integrated Satellite, Unmanned Aerial Vehicle (UAV) and Ground Inversion of the SPAD of Winter Wheat in the Reviving Stage. Sensors 2019, 19, 1485. [Google Scholar] [CrossRef]
- Dinish, U.S.; Teng, M.T.J.; Xinhui, V.T.; Dev, K.; Tan, J.J.; Koh, S.S.; Urano, D.; Olivo, M. Miniaturized Vis-NIR handheld spectrometer for non-invasive pigment quantification in agritech applications. Sci. Rep. 2023, 13, 9524. [Google Scholar] [CrossRef]
- Ma, W.; Han, W.; Zhang, H.; Cui, X.; Zhai, X.; Zhang, L.; Shao, G.; Niu, Y.; Huang, S. UAV multispectral remote sensing for the estimation of SPAD values at various growth stages of maize under different irrigation levels. Comput. Electron. Agric. 2024, 227, 109566. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Zhang, Y. The applicability of empirical vegetation indices for determining leaf chlorophyll content over different leaf and canopy structures. Ecol. Complex. 2014, 17, 119–130. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Noland, T.L.; Mohammed, G.H.; Sampson, P.H. Scaling-up and model inversion methods with narrowband optical indices for chlorophyll content estimation in closed forest canopies with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1491–1507. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Chen, M.; Xiao, F.; Wang, Z.; Feng, Q.; Ban, X.; Zhou, Y.; Hu, Z. An Improved QAA-Based Method for Monitoring Water Clarity of Honghu Lake Using Landsat TM, ETM+ and OLI Data. Remote Sens. 2022, 14, 3798. [Google Scholar] [CrossRef]
- Kumar, P.; Dobriyal, M.; Kale, A.; Pandey, A.K. Temporal dynamics change of land use/land cover in Jhansi district of Uttar Pradesh over past 20 years using LANDSAT TM, ETM+ and OLI sensors. Remote Sens. Appl. Soc. Environ. 2021, 23, 100579. [Google Scholar] [CrossRef]
- Men, Y.; Liu, Y.; Ma, Y.; Wong, K.P.; Tsou, J.Y.; Zhang, Y. Remote Sensing Monitoring of Green Tide Disaster Using MODIS and GF-1 Data: A Case Study in the Yellow Sea. J. Mar. Sci. Eng. 2023, 11, 2212. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, X.; Chen, A.; Guo, J.; Xing, X.; Yang, D.; Xu, B.; Lan, X.; Yang, X. A spatio-temporal fusion strategy for improving the estimation accuracy of the aboveground biomass in grassland based on GF-1 and MODIS. Ecol. Indic. 2023, 157, 111276. [Google Scholar] [CrossRef]
- Ali, M.; Ali, T.; Gawai, R.; Dronjak, L.; Elaksher, A. The Analysis of Land Use and Climate Change Impacts on Lake Victoria Basin Using Multi-Source Remote Sensing Data and Google Earth Engine (GEE). Remote Sens. 2024, 16, 4810. [Google Scholar] [CrossRef]
- Xu, K.; Hou, Y.; Sun, W.; Chen, D.; Lv, D.; Xing, J.; Yang, R. A Detection Method for Sweet Potato Leaf Spot Disease and Leaf-Eating Pests. Agriculture 2025, 15, 503. [Google Scholar] [CrossRef]
- Li, H.; Han, Z.; Wang, H. Using HJ-1 CCD and MODIS Fusion Data to Invert HJ-1 NBAR for Time Series Analysis, a Case Study in the Mountain Valley of North China. Appl. Sci. 2022, 12, 12233. [Google Scholar] [CrossRef]
- Qiao, K.; Zhu, W.; Xie, Z.; Wu, S.; Li, S. New three red-edge vegetation index (VI3RE) for crop seasonal LAI prediction using Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2024, 130, 103894. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Han, X.; Huang, X.; Yang, J. Evaluation of Spectral Bandwidth and Position on Leaf Chlorophyll Content Estimation Using Vegetation Indices. Photogramm. Rec. 2025, 40, e12532. [Google Scholar] [CrossRef]
- Zhen, J.; Jiang, X.; Xu, Y.; Miao, J.; Zhao, D.; Wang, J.; Wang, J.; Wu, G. Mapping leaf chlorophyll content of mangrove forests with Sentinel-2 images of four periods. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102387. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y.; Zhang, Y.; Shang, J. Review of Remote Sensing Applications in Grassland Monitoring. Remote Sens. 2022, 14, 2903. [Google Scholar] [CrossRef]
- Fang, S.; Wu, Z.; Wu, S.; Chen, Z.; Shen, W.; Mao, Z. Enhancing Water depth inversion accuracy in turbid coastal environments using random forest and coordinate attention mechanisms. Front. Mar. Sci. 2024, 11, 1471695. [Google Scholar] [CrossRef]
- Yu, F.; Bai, J.; Fang, J.; Guo, S.; Zhu, S.; Xu, T. Integration of a parameter combination discriminator improves the accuracy of chlorophyll inversion from spectral imaging of rice. Agric. Commun. 2024, 2, 100055. [Google Scholar] [CrossRef]
- Cui, B.; Zhao, Q.-j.; Huang, W.-j.; Song, X.-y.; Ye, H.-c.; Zhou, X.-f. Leaf chlorophyll content retrieval of wheat by simulated RapidEye, Sentinel-2 and EnMAP data. J. Integr. Agric. 2019, 18, 1230–1245. [Google Scholar] [CrossRef]
- Qian, B.; Ye, H.; Huang, W.; Xie, Q.; Pan, Y.; Xing, N.; Ren, Y.; Guo, A.; Jiao, Q.; Lan, Y. A sentinel-2-based triangular vegetation index for chlorophyll content estimation. Agric. For. Meteorol. 2022, 322, 109000. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; Van den Brande, M.M.M. Using Sentinel-2 Data for Retrieving LAI and Leaf and Canopy Chlorophyll Content of a Potato Crop. Remote Sens. 2017, 9, 405. [Google Scholar] [CrossRef]
- Garofalo, S.P.; Modugno, A.F.; De Carolis, G.; Sanitate, N.; Negash Tesemma, M.; Scarascia-Mugnozza, G.; Tekle Tegegne, Y.; Campi, P. Explainable Artificial Intelligence to Predict the Water Status of Cotton (Gossypium hirsutum L., 1763) from Sentinel-2 Images in the Mediterranean Area. Plants 2024, 13, 3325. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.M.; Zhang, X.; Yan, Y.; Zhu, J.; Zheng, H.; Zhou, K.; Yao, X.; Tian, Y.; Zhu, Y.; et al. Improved estimation of leaf chlorophyll content of row crops from canopy reflectance spectra through minimizing canopy structural effects and optimizing off-noon observation time. Remote Sens. Environ. 2020, 248, 111985. [Google Scholar] [CrossRef]
- Beckmann, D.; Spyrakos, E.; Hunter, P.; Jones, I. Widespread phytoplankton monitoring in small lakes: A case study comparing satellite imagery from planet SuperDoves and ESA sentinel-2. Front. Remote Sens. 2025, 6, 1549119. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Lopez-Sanchez, J.M.; Bhattacharya, A.; McNairn, H.; Rao, Y.S.; Ramana, K.V. Assessment of rice growth conditions in a semi-arid region of India using the Generalized Radar Vegetation Index derived from RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2020, 237, 111561. [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Zhang, Y.; Yin, Q.; Wang, W.; Zhou, G.; Huo, Z. Combining Texture, Color, and Vegetation Index from Unmanned Aerial Vehicle Multispectral Images to Estimate Winter Wheat Leaf Area Index during the Vegetative Growth Stage. Remote Sens. 2023, 15, 5715. [Google Scholar] [CrossRef]
- Yang, X.; Gao, F.; Yuan, H.; Cao, X. Integrated UAV and Satellite Multi-Spectral for Agricultural Drought Monitoring of Winter Wheat in the Seedling Stage. Sensors 2024, 24, 5715. [Google Scholar] [CrossRef]
- Tam, N.H.; Loi, N.V.; Tuan, H.H. Establishing Models for Predicting Above-Ground Carbon Stock Based on Sentinel-2 Imagery for Evergreen Broadleaf Forests in South Central Coastal Ecoregion, Vietnam. Forests 2025, 16, 686. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Kiangala, S.K.; Wang, Z. An effective adaptive customization framework for small manufacturing plants using extreme gradient boosting-XGBoost and random forest ensemble learning algorithms in an Industry 4.0 environment. Mach. Learn. Appl. 2021, 4, 100024. [Google Scholar] [CrossRef]
- Piccialli, V.; Sciandrone, M. Nonlinear optimization and support vector machines. Ann. Oper. Res. 2022, 314, 15–47. [Google Scholar] [CrossRef]
- Amri, M.; Abbes, Z.; Trabelsi, I.; Ghanem, M.E.; Mentag, R.; Kharrat, M. Chlorophyll content and fluorescence as physiological parameters for monitoring Orobanche foetida Poir. infection in faba bean. PLoS ONE 2021, 16, e0241527. [Google Scholar] [CrossRef]
- Li, Q.; Cui, J.; Jiang, W.; Jiao, Q.; Gong, L.; Zhang, J.; Shen, X. Monitoring of the Fire in Muli County on March 28, 2020, based on high temporal-spatial resolution remote sensing techniques. Nat. Hazards Res. 2021, 1, 20–31. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, H.; Huang, T.; Wu, Y.; Guo, B.; Liu, Z.; Luo, H.; Tang, J.; Zhou, H.; Wang, L.; et al. Improved random forest algorithms for increasing the accuracy of forest aboveground biomass estimation using Sentinel-2 imagery. Ecol. Indic. 2024, 159, 111752. [Google Scholar] [CrossRef]
- Cao, Y.; Li, G.L.; Luo, Y.K.; Pan, Q.; Zhang, S.Y. Monitoring of sugar beet growth indicators using wide-dynamic-range vegetation index (WDRVI) derived from UAV multispectral images. Comput. Electron. Agric. 2020, 171, 105331. [Google Scholar] [CrossRef]
- Wu, J.; Bai, T.; Li, X. Inverting Chlorophyll Content in Jujube Leaves Using a Back-Propagation Neural Network–Random Forest–Ridge Regression Algorithm with Combined Hyperspectral Data and Image Color Channels. Agronomy 2024, 14, 140. [Google Scholar] [CrossRef]
- Mistele, B.; Schmidhalter, U. Tractor-Based Quadrilateral Spectral Reflectance Measurements to Detect Biomass and Total Aerial Nitrogen in Winter Wheat. Agron. J. 2010, 102, 499–506. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- An, G.; Xing, M.; He, B.; Liao, C.; Huang, X.; Shang, J.; Kang, H. Using Machine Learning for Estimating Rice Chlorophyll Content from In Situ Hyperspectral Data. Remote Sens. 2020, 12, 3104. [Google Scholar] [CrossRef]
- Zhang, M.; Su, W.; Fu, Y.; Zhu, D.; Xue, J.-H.; Huang, J.; Wang, W.; Wu, J.; Yao, C. Super-resolution enhancement of Sentinel-2 image for retrieving LAI and chlorophyll content of summer corn. Eur. J. Agron. 2019, 111, 125938. [Google Scholar] [CrossRef]



| Vegetation Index | Calculation Formula | Reference |
|---|---|---|
| [29] | ||
| [29] | ||
| [30] | ||
| [30] | ||
| [29] | ||
| [30] | ||
| [29] | ||
| [30] | ||
| [31] | ||
| [32] |
| Correlation Coefficient | Relevant Intensity |
|---|---|
| 0.0–0.2 | Very weak correlation or no correlation |
| 0.2–0.4 | Weak correlation |
| 0.4–0.6 | Moderately relevant |
| 0.6–0.8 | Strong correlation |
| 0.8–1.0 | Highly relevant |
| Growth Period | Sample Size | SPAD Minimum Value | SPAD Maximum Value | SPAD Average Value | Standard Deviation | Coefficient of Variation |
| Flowering Stage | 60 | 33.3 | 41.2 | 37.3 | 2.13 | 5.36% |
| Fruit-Setting Stage | 60 | 37 | 42.9 | 39.9 | 1.42 | 3.56% |
| Fruit Enlargement Stage | 60 | 40.3 | 46.9 | 44.3 | 1.57 | 3.52% |
| Maturity Stage | 60 | 38.5 | 44.4 | 41.9 | 1.52 | 3.65% |
| Model | Data Set | Spectral Reflectance | Vegetation Indices | Spectral Reflectance + Vegetation Indices | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | ||
| KNN | Training Set | 0.596 | 0.039 | 1.195 | 0.993 | 0.631 | 0.035 | 1.096 | 0.939 | 0.650 | 0.037 | 1.079 | 0.863 |
| Validation Set | 0.571 | 0.042 | 1.210 | 1.079 | 0.618 | 0.038 | 1.103 | 0.954 | 0.637 | 0.042 | 1.093 | 0.876 | |
| RF | Training Set | 0.624 | 0.035 | 1.109 | 0.954 | 0.645 | 0.032 | 1.080 | 0.869 | 0.669 | 0.032 | 0.995 | 0.776 |
| Validation Set | 0.597 | 0.038 | 1.148 | 0.993 | 0.632 | 0.034 | 1.101 | 0.940 | 0.650 | 0.035 | 1.085 | 0.867 | |
| SVM | Training Set | 0.605 | 0.034 | 1.125 | 0.970 | 0.634 | 0.030 | 1.093 | 0.963 | 0.658 | 0.033 | 1.060 | 0.863 |
| Validation Set | 0.591 | 0.040 | 1.157 | 1.041 | 0.626 | 0.035 | 1.110 | 0.956 | 0.646 | 0.037 | 1.087 | 0.875 | |
| OIA | Training Set | 0.38 | 0.035 | 1.101 | 0.939 | 0.652 | 0.029 | 1.069 | 0.871 | 0.675 | 0.027 | 0.985 | 0.764 |
| Validation Set | 0.615 | 0.031 | 1.110 | 0.953 | 0.638 | 0.031 | 1.107 | 0.942 | 0.663 | 0.028 | 0.995 | 0.774 | |
| Model | Data Set | Spectral Reflectance | Vegetation Indices | Spectral Reflectance + Vegetation Indices | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | ||
| KNN | Training Set | 0.616 | 0.035 | 1.105 | 0.966 | 0.647 | 0.040 | 1.078 | 0.861 | 0.657 | 0.027 | 1.065 | 0.867 |
| Validation Set | 0.608 | 0.038 | 1.120 | 0.967 | 0.630 | 0.039 | 1.102 | 0.944 | 0.646 | 0.029 | 1.078 | 0.870 | |
| RF | Training Set | 0.644 | 0.032 | 1.076 | 0.874 | 0.658 | 0.035 | 1.062 | 0.861 | 0.674 | 0.025 | 0.981 | 0.760 |
| Validation Set | 0.632 | 0.036 | 1.097 | 0.944 | 0.646 | 0.037 | 1.081 | 0.863 | 0.663 | 0.026 | 0.995 | 0.786 | |
| SVM | Training Set | 0.633 | 0.039 | 1.094 | 0.940 | 0.647 | 0.034 | 1.075 | 0.869 | 0.665 | 0.025 | 0.991 | 0.780 |
| Validation Set | 0.621 | 0.042 | 1.101 | 0.948 | 0.635 | 0.041 | 1.095 | 0.966 | 0.650 | 0.028 | 1.076 | 0.858 | |
| OIA | Training Set | 0.653 | 0.027 | 1.076 | 0.851 | 0.678 | 0.028 | 0.977 | 0.752 | 0.709 | 0.021 | 0.840 | 0.673 |
| Validation Set | 0.645 | 0.029 | 1.089 | 0.877 | 0.657 | 0.030 | 1.062 | 0.861 | 0.685 | 0.024 | 0.901 | 0.702 | |
| Model | Data Set | Spectral Reflectance | Vegetation Indices | Spectral Reflectance + Vegetation Indices | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | ||
| KNN | Training Set | 0.645 | 0.033 | 1.077 | 0.871 | 0.656 | 0.030 | 1.067 | 0.870 | 0.678 | 0.021 | 0.976 | 0.751 |
| Validation Set | 0.627 | 0.036 | 1.110 | 0.956 | 0.638 | 0.032 | 1.110 | 0.928 | 0.654 | 0.025 | 1.067 | 0.848 | |
| RF | Training Set | 0.654 | 0.031 | 1.067 | 0.864 | 0.669 | 0.029 | 0.985 | 0.771 | 0.684 | 0.019 | 0.899 | 0.701 |
| Validation Set | 0.643 | 0.033 | 1.095 | 0.876 | 0.658 | 0.033 | 1.057 | 0.859 | 0.669 | 0.020 | 0.982 | 0.758 | |
| SVM | Training Set | 0.649 | 0.035 | 1.081 | 0.856 | 0.659 | 0.028 | 1.060 | 0.861 | 0.676 | 0.022 | 0.980 | 0.757 |
| Validation Set | 0.637 | 0.033 | 1.110 | 0.925 | 0.642 | 0.031 | 1.093 | 0.884 | 0.658 | 0.026 | 1.061 | 0.863 | |
| OIA | Training Set | 0.684 | 0.026 | 0.904 | 0.705 | 0.704 | 0.026 | 0.843 | 0.675 | 0.740 | 0.016 | 0.801 | 0.621 |
| Validation Set | 0.663 | 0.030 | 1.013 | 0.787 | 0.688 | 0.028 | 0.897 | 0.701 | 0.724 | 0.018 | 0.820 | 0.645 | |
| Model | Data Set | Spectral Reflectance | Vegetation Indices | Spectral Reflectance + Vegetation Indices | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | R2 | STD | RMSE | MAE | ||
| KNN | Training Set | 0.631 | 0.038 | 1.094 | 0.941 | 0.649 | 0.034 | 1.080 | 0.858 | 0.664 | 0.025 | 1.024 | 0.791 |
| Validation Set | 0.622 | 0.039 | 1.100 | 0.961 | 0.634 | 0.037 | 1.097 | 0.943 | 0.646 | 0.028 | 1.073 | 0.867 | |
| RF | Training Set | 0.651 | 0.033 | 1.080 | 0.849 | 0.659 | 0.031 | 1.062 | 0.865 | 0.675 | 0.024 | 0.977 | 0.760 |
| Validation Set | 0.637 | 0.035 | 1.112 | 0.928 | 0.643 | 0.033 | 1.090 | 0.887 | 0.664 | 0.026 | 1.018 | 0.792 | |
| SVM | Training Set | 0.641 | 0.034 | 1.094 | 0.922 | 0.652 | 0.029 | 1.073 | 0.850 | 0.665 | 0.025 | 1.010 | 0.787 |
| Validation Set | 0.632 | 0.036 | 1.097 | 0.945 | 0.637 | 0.032 | 1.108 | 0.922 | 0.654 | 0.027 | 1.070 | 0.846 | |
| OIA | Training Set | 0.671 | 0.029 | 0.980 | 0.751 | 0.695 | 0.029 | 0.852 | 0.660 | 0.715 | 0.020 | 0.831 | 0.669 |
| Validation Set | 0.660 | 0.030 | 1.008 | 0.779 | 0.674 | 0.029 | 0.982 | 0.761 | 0.694 | 0.021 | 0.855 | 0.687 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, N.; Xie, Q.; Qin, Y.; Wang, Q.; Lv, S.; Zhang, X.; Li, X. Inversion of SPAD Values of Pear Leaves at Different Growth Stages Based on Machine Learning and Sentinel-2 Remote Sensing Data. Agriculture 2025, 15, 1264. https://doi.org/10.3390/agriculture15121264
Yan N, Xie Q, Qin Y, Wang Q, Lv S, Zhang X, Li X. Inversion of SPAD Values of Pear Leaves at Different Growth Stages Based on Machine Learning and Sentinel-2 Remote Sensing Data. Agriculture. 2025; 15(12):1264. https://doi.org/10.3390/agriculture15121264
Chicago/Turabian StyleYan, Ning, Qu Xie, Yasen Qin, Qi Wang, Sumin Lv, Xuedong Zhang, and Xu Li. 2025. "Inversion of SPAD Values of Pear Leaves at Different Growth Stages Based on Machine Learning and Sentinel-2 Remote Sensing Data" Agriculture 15, no. 12: 1264. https://doi.org/10.3390/agriculture15121264
APA StyleYan, N., Xie, Q., Qin, Y., Wang, Q., Lv, S., Zhang, X., & Li, X. (2025). Inversion of SPAD Values of Pear Leaves at Different Growth Stages Based on Machine Learning and Sentinel-2 Remote Sensing Data. Agriculture, 15(12), 1264. https://doi.org/10.3390/agriculture15121264






