Abstract
The agricultural sector is one of the most significant sectors of the global economy, yet it is concurrently a highly energy-intensive industry. The issue of optimizing field operations in terms of energy consumption is therefore a key consideration for sustainable agriculture, and the solution to this issue leads to both environmental and financial benefits. The aim of this study was to estimate energy consumption during soil cultivation using geophysical scanning data and machine learning (ML) algorithms. This included determining the optimal set of independent variables and the most suitable ML method. Soil parameters such as electrical conductivity, magnetic susceptibility, and soil reflectance in infrared spectra were mapped using data from Geonics EM-38 and Veris 3100 scanners. These data, along with soil texture, served as inputs for predicting fuel consumption and field productivity. Three machine learning algorithms were tested: support vector machines (SVMs), multilayer perceptron (MLP), and radial basis function (RBF) neural networks. Among these, SVM achieved the best performance, showing a MAPE of 4% and a strong correlation (R = 0.97) between predicted and actual productivity values. For fuel consumption, the optimal method was MLP (MAPE = 4% and R = 0.63). The findings demonstrate the viability of geophysical scanning and machine learning for accurately predicting energy use in tillage operations. This approach supports more sustainable agriculture by enabling optimized fuel use and reducing environmental impact through data-driven field management. Further research is needed to obtain training data for different soil parameters and agrotechnical treatments in order to develop more universal models.
1. Introduction
Although it is a primarily reliant industry globally and a cornerstone of human survival, agriculture is also one of the most energy-intensive industries. Soil cultivation, a fundamental activity in crop production, consumes substantial amounts of energy, primarily through the operation of heavy machinery, impacting productivity and environmental sustainability [1]. According to Upadhyay and Raghubanshi [2], energy use in modern agriculture impacts agricultural sustainability and is ultimately very unsustainable. Therefore, knowing and managing agricultural energy use is vital for preserving agriculture’s long-term sustainability and competitiveness [3]. Accurately predicting energy requirements during soil cultivation is essential to optimize machinery efficiency, reduce fuel consumption, and promote sustainable farming practices [4].
Over the past few decades, agriculture has been heavily reliant on fossil fuels [1] and estimating energy inputs in agriculture entails examining the energy inputs required in various farming operations and processes [5,6]. It is broadly divided into direct and indirect consumption. Direct energy consumption includes energy used in agricultural production processes, including electricity, refined petroleum products, natural gas-based fuels, and wood chips [5,7]. In contrast, indirect energy inputs include energy used for producing fertilizers, pesticides, farm machinery, seeding, and feed [8,9]. Although direct energy consumption constitutes less than 50% of total energy consumption in the agricultural sector, optimizing this consumption is an integral component of sustainable agriculture [8,10]. Tillage, seeding and planting, fertilization and pesticide, irrigation, and harvesting are the key agricultural energy-consuming activities [4,11]. This research is focused on energy consumption relating to soil tillage. Energy consumption during tillage varies and is significantly influenced by soil texture and compaction, farm machinery efficiency, tillage method, and moisture content [4,7,11,12]. Understanding the energy inputs in these tasks is critical for optimizing farming techniques and lowering environmental footprints.
Traditional methods for estimating energy consumption rely on empirical models, laboratory tests, or field trials that measure draft force and traction efficiency [13]. While these methods provide useful insights, they are often time-consuming, labor-intensive, and inefficient, and may not capture the spatial variability of soil properties, leading to increased operational costs and energy waste [4]. As a result, there is a growing demand for innovative methods that can provide precise, real-time estimates of energy requirements while accounting for soil heterogeneity. Recent advancements in sensing technologies, such as Veris systems, Claas Telematics, and electromagnetic induction (EMI), offer innovative approaches to understanding and predicting energy consumption [14,15,16]. These technologies provide real-time, high-resolution data on soil characteristics such as soil compaction, moisture content, and subsurface structure, directly impacting the energy required for mechanical operations [17,18]. This enables a shift from generalized energy estimates to site-specific predictions [15].
In recent years, there has been an observable rise in the utilization of geophysical data within the agricultural sector. The data can be sourced from various devices, including scanners, which utilize electrode-based electrical resistivity tomography (ERT) and electromagnetic induction for measurement purposes. EMI is a technique used to measure the soil’s response to electromagnetic fields, thus determining its electrical conductivity, while ERT measures a soil’s response to induced current, hence resistivity. Apparent electrical conductivity (ECa), defined as the current flow in the soil, is proportional to the total dissolved solids in the soil [19] and is frequently used to characterize field variability for application in precision agriculture [20,21]. The factors influencing soil ECa are soil moisture content, texture, porosity, salinity level, bulk density, organic matter, and temperature [22,23,24]. The scanners employed in agriculture, including the Geonics EM-38 and Veris 3100, are proficient in measuring a range of parameters in addition to ECa. The Geonics EM-38 scanner is also used to measure magnetic susceptibility (MS), defined by Schenck [25] as a physical property that characterizes a material’s response to an external magnetic field. MS measurement is necessary to establish characteristics, contributing variables, and methods of soil development. In agriculture, the primary function of MS measurement is the identification of soil contamination by heavy metals [26]. However, it has been demonstrated in previous studies that the use of MS measured in the soil profile in conjunction with ECa improves the efficacy of models for estimating soil compaction based on soil electrical parameters [27]. The Veris 3100 scanner is armed with an optical sensor capable of measurements in the red light and infrared bands. Depending on variables, including settling times, soil preparation techniques, and pertinent soil properties, the infrared methodology can efficiently examine the distribution of soil particle sizes [28].
The acquisition of large amounts of data, including in real time, is becoming increasingly straightforward. Contemporary agricultural machinery is equipped with a plethora of sensors, with data being collected via the perception of the Internet of Things (IoT). However, the crux of the matter lies not in the acquisition of data but rather in its effective processing to yield actionable information useful to agricultural practice. The employment of machine learning (ML) is advantageous in this context, as it facilitates the development of highly accurate predictive and classification models through data analysis. The utilization of such models is manifold, encompassing applications such as yield prediction [29], crop quality assessment [30,31], optimization of the storage process for fruit and vegetables [32], and support for vision systems in agricultural robots [33]. These methods are also employed in the context of energy consumption estimation in the agricultural sector. Research on this topic is mainly concerned with energy consumption prediction from historical or energy-related data [10,34,35]. However, there is a lack of publications in the contemporary literature concerning the prediction of the energy consumption required to perform agrotechnical operations based on geophysical data. The use of scanning technologies for energy estimation is not only a step toward precision agriculture but a means to achieve sustainability goals. Precise energy predictions have the potential to assist farmers in optimizing machinery utilization, reducing fuel consumption, and minimizing greenhouse gas emissions. Furthermore, these technologies can enable site-specific soil management, allowing for targeted interventions that enhance soil health and productivity while reducing unnecessary energy expenditures.
Previous research has shown that soil compaction can be predicted based on geophysical parameters such as soil electrical conductivity and magnetic susceptibility [27]. As soil compaction has a significant impact on energy consumption, this study aimed to investigate how to estimate energy usage during soil cultivation, indicated by fuel consumption and productivity, by combining geophysical data with ML. To this end, a research hypothesis was formulated, stating that it is possible to predict energy consumption through the use of ML combined with scanning methods popular in agriculture. Using cutting-edge technologies, it bridges the gap between conventional approaches to energy consumption estimation and the demand for accurate, scalable, cost-effective, and machinery-efficient forecasts. The prevailing methodologies employed for the purpose of predicting energy consumption in agricultural operations are characterized by a reliance on predefined equations and fixed parameters that delineate physical processes, machinery specifications, and operational settings. This renders the models susceptible to inaccuracies in parameter estimation, which can result in substantial prediction errors. Consequently, there is an increasing necessity for more flexible, data-driven approaches that are capable of modeling nonlinear relationships and adapting to complex, evolving agricultural environments. The integration of machine learning with geophysical data represents a promising approach within this context. The study’s goal is to ascertain the two aspects of the development of predictive models. Firstly, the optimal ML method and its hyperparameters must be identified. Secondly, the most suitable set of independent variables for the models must be determined.
2. Materials and Methods
The process of generating machine learning models for energy consumption approximation was broken into two primary phases: gathering and evaluating data for model training, then executing the model training, and assessing the outcomes to determine the best options, as shown in the flowchart in Figure 1.
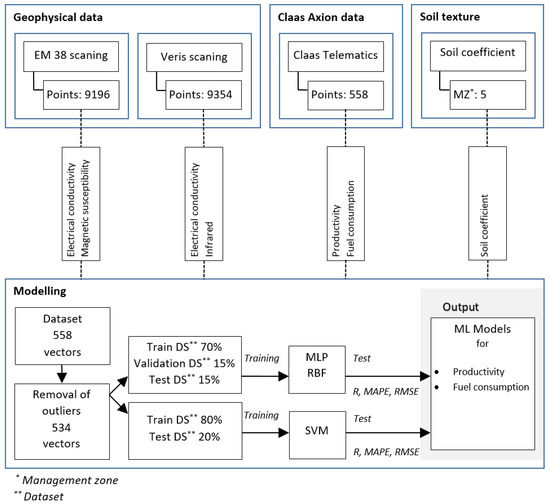
Figure 1.
A flowchart illustrating the research process, encompassing data collection and ML modeling.
2.1. Study Area
Field measurements were conducted in Brest county, Opolskie Voivodeship, Poland, with GNSS coordinates 50°39′41.55″ N/17°21′34.23″ E. The study area is located in one of the warmest climatic regions of Poland—the Wrocław climatic district. The climate is temperate with oceanic characteristics. The average annual temperature is approximately 8.5 °C, with annual precipitation ranging between 500 and 600 mm. Snow cover persists for about 50–60 days per year, and the growing season lasts around 225 days. The predominant winds are from the west and northwest. Approximately 80% of the area is covered by soils classified as protected for agricultural use (classes I–IVa). Clay soils are predominant in the region.
Within a plot of land of approximately 100 ha, a study site of 10 ha was designated for measurements (Figure 2). In 2022, after harvesting the main crop (spring barley), shallow post-harvest cultivation with a disk harrow was carried out, mustard catch crop sown and chemically eradicated in autumn 2022. No agrotechnical treatments were carried out on the plot before the 2023 survey. The main crop in 2023 on the surveyed plot was maize for grain.
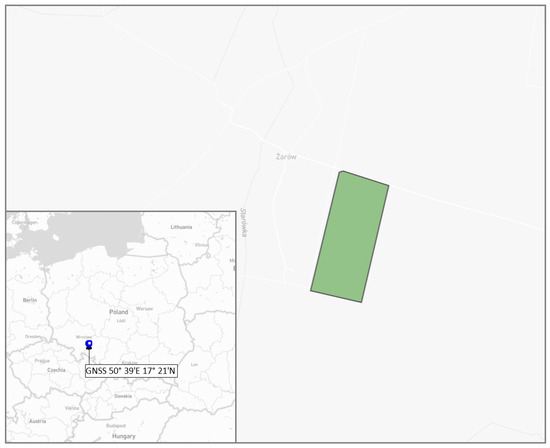
Figure 2.
The location of the study area and the study plot (green).
2.2. Sensor Data Acquisition
Using galvanic contact resistivity (GCR) and electromagnetic induction (EMI) techniques, soil geophysical parameters were measured at the same location. Geophysical measurements were carried out at 0.2 m using the Veris 3100 GCR sensor (Veris Technologies, Inc., Salina, KS, USA; VERIS-EC) as a contact scanner and Geonics EM-38 (Geonics Limited, Mississauga, ON, Canada) as a non-contact sensor scanner at a depth of 0.5 m. The two instruments were pulled by a gator separately, ensuring electrical measurements from scanners without electrical conductivity signal interruptions (Figure 3). The scanner surveys were conducted in an independent manner, with two distinct runs. Initially, the Veris 3100 scanner was utilized for scanning, followed by the EM-38 scanner being connected to the quad, resulting in another run along the delineated lines. A data logging station was mounted on the gator for the entire measurement period, recording data of the measured parameters.

Figure 3.
Gator during measurements. A Veris scanner is mounted on the rear of the vehicle and a soil sampling device is on the front.
The Veris 3100 soil scanner is a device that records four important soil properties in a single operation. In this electrode-based system, sensors are rolled across the fields to create direct contact with the soil. It is a three-sensor system measuring ECa, organic matter content, altitude, and acidity (pH) in the rooting zone. It also measures soil reflectance (IR) using its optical sensor in infrared spectra by directing IR light onto the soil as it moves across a field. The Veris 3100 used in this study to record measurements consists of 2 pairs of rolling colter disks, giving an electrical conductivity reading every second. To obtain ECa values, one pair of disk electrodes generates current into the soil, and the voltage change across the other pair of disk electrodes is monitored. A Global Navigation Satellite System (GNSS) receiver fitted on the Veris unit tracks the location of each soil electrical conductivity measurement site in the field. In the present study, the Veris 3100 scanner was utilized to measure two parameters: electrical conductivity and soil reflectance.
The Geonics EM-38 EMI conductivity meter is a portable field device used in measuring soil electrical conductivity and magnetic susceptibility in the rooting zone. It is appropriate for large-scale soil conductivity measurements because of its high speed and accuracy. It creates an initial electromagnetic field by ejecting small horizontal electrical currents in the soil, generating a secondary electromagnetic field. It features a built-in receiver coil that detects both fields, and the percentage of these is the measurement of ECa shown in units of mS·m−1. It is pulled on a non-conductive plastic material to prevent signal interruption and is assisted by a GPS receiver that tracks the location of each measurement site in the field. The present study involved the measurement of two parameters using the EM-38 scanner: electrical conductivity and magnetic susceptibility.
On the experimental plot, parallel lines were drawn along its longest edge at a distance of 10 m. For the first pass, GPS coordinates from the beginning to the end of the line were recorded and entered into the quad’s automatic guidance system (see Figure 4A).
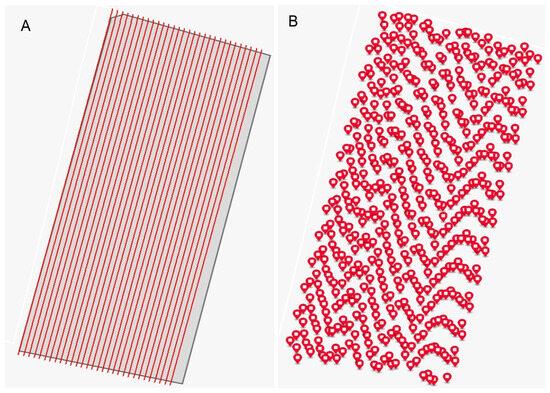
Figure 4.
(A) A schematic of the parallel lines along which the quad with scanners moved; (B) distribution of the measurement points from the Claas Axion 960TT.
Subsequently, the scanners were connected to the quad’s automatic guidance system, which received the coordinates of the drawn lines. The quad’s velocity was 2.5 m·s−1. Depending on the scanner settings, measurements were made every 3 m for the Veris 3100 and every 10 m for the EM-38.
2.3. The Layout of the Field Measurements of Energy Consumption
The Claas Axion 960TT (CLAAS, Paderborn, Germany) is primarily designed for heavy-duty agricultural tasks such as tillage, enhancing traction. Its Terra Trac system improves traction while protecting soil structure, making it ideal for large-scale and precision farming. It is equipped with a Global Navigation Satellite System (GNSS) receiver that tracks the location of each measurement point on the field. The tractor’s stability and adaptability across various terrains ensure reliable performance.
Claas Telematics is an advanced system designed to optimize efficiency and monitor the performance of agricultural machinery. It allows real-time data collection, analysis, and remote access to machine operations, including fuel consumption, working hours, and GPS-based field mapping. When mounted on a tractor for tillage, it collects real-time data such as fuel consumption, engine load, working speed, and GPS-based field position. Figure 4B shows the locations of the measurement points. It records tillage patterns, covered areas, and operational efficiency.
After the scan, cultivation was carried out to a depth of 0.25 m. Tillage was carried out with a Claas Axion 960TT semi-truck tractor and a Horsch Tiger 5 AS (HORSCH Maschinen GmbH, Schwandorf, Germany). After the tests, the nearest points of the EM-38 and Veris 3100 scanners were assigned to each recorded tractor point using the least squares method for further analysis.
The Horsch Tiger 5 AS is a robust cultivator engineered for intensive soil cultivation and capable of operating at depths of up to 35 cm. Its four-bar frame design features a tine spacing of 23 cm and a frame height of 85 cm, ensuring thorough mixing of crop residues across the entire working depth. The Horsch Tiger 5 AS also provides a variety of packer options to achieve optimal soil consolidation. With a working width of 4.7 m, a transport height of 3.3 m, and a transport width of 3 m, it requires a power input of 185 kW. It efficiently enhances soil aeration, integrates agricultural residues, and breaks up compacted soil layers. For high-intensity soil cultivation, the Axion 960TT and Tiger 5 AS work well together to provide effective, deep tillage with minimal soil disturbance. In this study, fuel consumption and productivity are the two parameters utilized as energy consumption indicators. Fuel consumption (dm3∙h−1) was measured using a flow meter equipped on the tractor. The parameters needed for calculating the tractor’s productivity were measured and recorded by the radar it is equipped with. The working width of the aggregate was measured to be 5 m; however, an overlap of 0.3 m was assumed to avoid uncultivated areas. Therefore, the assumed actual aggregate width was 4.7 m. Productivity was determined by the following equation:
where Prod is productivity (ha·h−1), V is the actual speed (km·h−1), and s is the actual aggregate width (m).
The fuel consumption of the tractor was recalculated to express this parameter in (dm3·ha−1):
where FC is fuel consumption (dm3·ha−1), FCTR is fuel consumption measured by tractor (dm3·h−1), and Prod is productivity (ha·h−1).
2.4. Soil Sampling
The establishment of five management zones (MZ) was facilitated by a proprietary algorithm, devised by the surveying enterprise, which drew upon the findings derived from the EM-38 scanner. Consequently, a reduced number of soil samples were collected to evaluate the moisture content and texture of the soil. Five soil samples, one from each MZ, weighing one kilogram, were randomly taken at depths varying from 0 to 30 cm and put in an airtight plastic bag with a label. Using a mortar and pestle, soil samples were ground after being air-dried for two days at 26 °C and then oven-dried for twenty-four hours at 105 °C. To ascertain the soil texture of the samples, Prószyński’s method [36] was used. Based on the results, the soil coefficient (SCoef) was calculated using the Prószyński method according to the following equation:
Using a penetrometer (Eijkelkamp Soil &Water, Giesbeek, The Netherlands), soil moisture was approximated at 27%.
2.5. Machine Learning Modeling Pipeline
Three ML techniques were utilized to model the relationship between the geophysical data, combined with soil properties, fuel consumption, and productivity. These methods included two types of artificial neural networks (ANNs)—multilayer perceptron (MLP) and radial basis function (RBF)—as well as support vector machines (SVMs). These methods are frequently employed in the development of regression models in agriculture, often yielding highly accurate results. Neural networks are inspired by the biological nervous system, where the fundamental unit, an artificial neuron, computes a weighted sum of inputs and applies an activation function to generate an output. ANNs have a layered architecture and do not require explicit programming; instead, they learn from a training dataset. After training, the model is evaluated on a separate test set to determine its generalization capability. Defining the network structure, particularly the number of neurons in the hidden layer, is a crucial step before training.
SVM operates based on support vectors—data points that define the optimal solution. In classification tasks, it identifies a hyperplane that separates different data groups, while in regression tasks, it finds a function that best represents the data. Support vectors play a key role in shaping the hyperplane or regression function. This study employed epsilon-insensitive support vector machine (ε-SVM) regression, which aims to find a function where deviations from target values do not exceed ε for each training data point. The Gaussian radial basis function kernel was selected due to its effectiveness in capturing nonlinear patterns in the data.
The dataset comprised 534 data vectors following the removal of outliers using Interquartile Range method. The data vector incorporated independent variables, namely electrical conductivity and magnetic susceptibility measured by Geonics EM-38 scanner (ECa_EM and MS_EM), electrical conductivity, and soil reflectance in infrared spectra measured by Veris 3100 (ECa_Veris and IR), and soil coefficient (SCoef), as well as independent variables, namely productivity and fuel consumption. The development of two distinct models for fuel consumption and productivity as predicted parameters was undertaken in this study. Furthermore, different combinations of input parameters were tested, according to the five scenarios presented in Table 1.

Table 1.
Input parameters in training scenarios. Parameter indicated by “√” was used as independent variable.
The experimental dataset was divided into subsets depending on the ML method. For ANNs, the data was divided into train, validation, and test subsets in a ratio of 70:15:15, with the train and validation subsets being used during the model training stage and the test set being used to assess whether model overfitting had occurred. For SVM models, the data were split into train and test sets in a ratio of 80:20. The optimization of model parameters was conducted through a grid search approach. For ANNs, the optimal number of neurons in the hidden layer was identified. Based on our previous research, a range of the number of neurons in the hidden layer from 10 to 50 was assumed. For MLP networks, an additional evaluation of diverse neuron activation functions in the hidden and output layers was undertaken, encompassing linear, sigmoid, hyperbolic tangent, and exponential types. The optimal parameters of the MLP and RBF models were adjusted after training 20,000 different network configurations with randomly determined initial values of synaptic weights. For the SVM models, the hyperparameters C (inverse regularization parameter), ε, and γ (RBF kernel width) were subject to fine-tuning, with model evaluation being conducted through the utilization of ten-fold cross-validation. Based on preliminary research, the following ranges of hyperparameters were used: C from 1 to 10, ε from 0.1 to 0.5, and γ from 0.1 to 0.5. The MLP, RBF, and SVM machine learning models were developed using Statistica v. 13 (TIBCO Software Inc., Tulsa, OK, USA).
The accuracy of the models was assessed based on three error metrics: the correlation coefficient R between target and predicted values, the mean absolute percentage error (MAPE), and the Root Mean Square Error (RMSE). The calculation of these metrics is described in Equations (4)–(6).
where Ytar is the absolute target value, is the mean target value, Ypred is the absolute predicted value, is the mean predicted value, and n is the number of vectors in a dataset.
2.6. Statistical Analysis
To evaluate the performance differences among the regression models, a 10-fold cross-validation procedure was applied. For each model and performance metric (MAPE, RMSE, R), the results from all folds were collected. Prior to conducting statistical tests, the normality of the distribution was assessed using the Shapiro–Wilk test, and homogeneity of variances was verified using Levene’s test. If the assumptions of normality and equal variances were satisfied, a one-way ANOVA was performed to determine statistically significant differences between models. In instances where these assumptions were violated, the non-parametric Kruskal–Wallis test was employed as an alternative. The significance level was set at p < 0.05 for all statistical comparisons.
3. Results
3.1. Soil Texture
Soil texture is a summation of sand, silt, and clay content proportions. It is a stable characteristic that significantly influences soil behavior. It is critical for plant growth and soil management. A survey conducted using the Geonics EM-38 scanner delineated five management zones, indicating areas of variation in soil texture. Samples of soil from each MZ were collected for laboratory analysis to ascertain the amount of sand, silt, and clay. Based on the USDA soil textural triangle, the percentage distribution of silt, sand, and clay content for each soil sample revealed that the experimental fields’ soil texture was silty loam. According to the analysis, every sample had between 3 and 7% clay, 58 and 83% silt, and 10 and 39% sand contents, classifying all soil samples as silty loam. In light of the findings, the calculation of soil coefficient values was undertaken, with the results ranging from 0.92 to 1.54. The research was conducted in a field characterized by minimal variability in soil texture. However, it should be noted that soil texture has been demonstrated to influence the working resistance of the tools [37], thus rendering the omission of this factor unjustified, despite the minor variations observed in the field.
3.2. Geophysical Parameters
Soil sensors vary by measurement type, depth, contact method, and data resolution. The variability of the geophysical parameters measured with the Geonics EM-38 and Veris 3100 scanners in the designated study field is exhibited in Figure 5 and Figure 6.
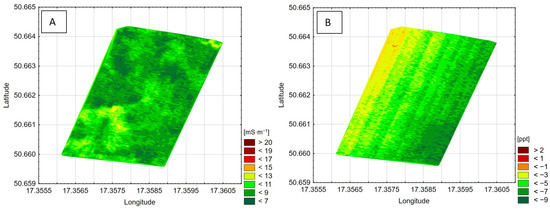
Figure 5.
(A) A map showing the spatial variability of electrical conductivity, as measured by the Geonics EM-38 scanner; (B) a map showing the spatial variability of magnetic susceptibility, as measured by the Geonics EM-38 scanner. Green = low value; yellow = moderate value; and red = high value of presented parameters.
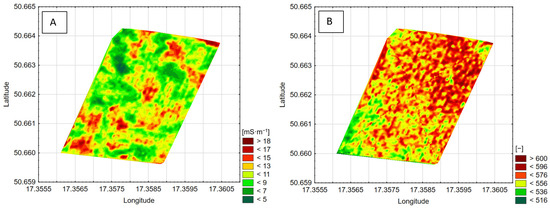
Figure 6.
(A) A map showing the spatial variability of electrical conductivity, as measured by the Veris 3100 scanner; (B) a map showing the spatial variability of soil reflectance, as measured by the Veris 3100 scanner. Green = low value; yellow = moderate value; and red = high value of presented parameters.
The map presented in Figure 5 illustrates spatial variations in soil electrical properties based on electromagnetic induction (EMI) in-phase measurements collected using EM-38. The dominant green and pockets of yellow regions represent low to moderate levels of apparent soil electrical conductivity (Figure 5A) and magnetic susceptibility (Figure 5B), indicating relatively uniform soil conditions across much of the field. However, distinct orange and red hotspots suggest stronger in-phase responses (Figure 5B). These localized anomalies highlight areas where soil structure may be denser or more variable.
Figure 6 illustrates spatial distributions of soil electrical properties, with Figure 6A showing apparent electrical conductivity and Figure 6B displaying infrared values measured with Veris 3100. In Figure 6A, the majority of the field is dominated by low to moderate electrical conductivity levels (green and yellow colors) with frequent scattered pockets of high electrical conductivity indicated in orange and red. Conversely, Figure 6B displays a more uniform dominance of moderate to high soil reflectance (yellow and red colors) with fewer localized low-value patches of low soil reflectance (orange color). While electrical conductivity (Figure 6A) shows more variation and potential zones of lower conductivity, the infrared response (Figure 6B) suggests a consistently higher soil reflectance.
3.3. Energy Consumption
Agricultural machinery efficiency, which is the ability of farming equipment to perform tasks effectively with minimal energy, time, and cost, measures how well machinery converts fuel into productive outputs (plowed fields). The evaluative factors include productivity and fuel consumption.
Figure 7 illustrates spatial distributions of tractor parameters across the same agricultural plot. Figure 7A represents productivity, while Figure 7B displays fuel consumption. In Figure 7A, the region shaded in red indicates zones of high productivity, while small patches of yellow and green near the edges suggest areas with lower productivity. In Figure 7B, the majority of the field is green and yellow, signifying low to moderate energy usage, with pockets of orange and red indicating higher energy usage.
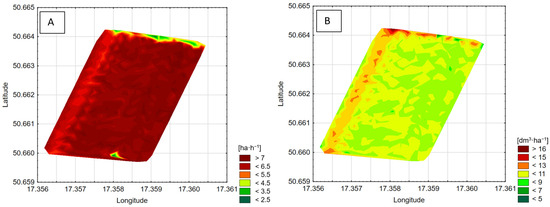
Figure 7.
Spatial variability of indicators of energy consumption: (A) productivity; (B) fuel consumption. Green = low value; yellow = moderate value; and red = high value of presented parameters.
3.4. Machine Learning Models
The inputs into the models include independent variables, namely electrical conductivity and magnetic susceptibility measured by the Geonics EM-38 scanner, electrical conductivity and soil reflectance in infrared spectra measured by the Veris 3100, and soil coefficient. Pearson’s correlation coefficient was calculated to verify the linear relationship between the explanatory variables. The results are detailed in Table 2.

Table 2.
Correlation coefficients between explanatory variables.
The data presented in Table 2 generally indicate low correlations between the independent variables. Only some of the correlations are statistically significant at p < 0.05. These include the correlations between the electrical parameters measured using the Geonics EM-38 scanner (ECa and MS) and the electrical conductivity measured using the Veris 3100 scanner, as well as the correlation between magnetic susceptibility and soil reflectance. The highest value recorded was for the correlation between ECa_EM and ECa_Veris (R = 0.7). Given that both parameters are related to soil electrical conductivity, yet are measured by different methods, the observed correlation is not unexpected. However, the value of the correlation coefficient indicates that both parameters can be considered as input variables in models.
MLP, RBF, and SVM are the three types of machine learning techniques used to develop a model of relationships between the geophysical data, combined with soil texture, fuel consumption, and productivity. For each scenario presented in Table 1, a new model was built for each dependent variable. Table 3 and Table 4 describe the properties of the three best models for fuel consumption and productivity.

Table 3.
Error metrics of best ML models developed for fuel consumption as dependent variable.

Table 4.
Error metrics of best ML models developed for productivity as dependent variable.
For fuel consumption, the best model was produced by an MLP neural network for scenario 4 with an R-value of 0.63 and RMSE of 0.55 for the test dataset and input combination of electrical conductivity and magnetic susceptibility measured using the Geonics EM-38 scanner, combined with electrical conductivity and soil reflectance measured using the Veris 3100 scanner. Slightly lower accuracy was obtained with the use of RBF neural network for the input vector described in scenario 4 (R = 0.62 and RMSE = 0.56), and with the use of the MLP neural network for the input parameters described in scenario 3 (R = 0.62 and RMSE = 0.56). All models had a low MAPE of 4%. Models of high accuracy, proved by the strong correlation between target and predicted values for the test dataset, were developed for productivity. The optimal model was produced by the SVM algorithm with three input parameters, namely electrical conductivity and magnetic susceptibility measured using the Geonics EM-38 scanner, and electrical conductivity measured using the Veris 3100 scanner. This model can be regarded as accurate and useful in real-life applications, as evidenced by the R-value, which approaches 1, RMSE = 0.54, and the low MAPE of 4% for the test dataset. The SVM model for scenario 4 achieved an R-value of 0.68, an RMSE of 0.34, and a MAPE of 4%. The RBF model achieved an R-value of 0.68, an RMSE of 0.28, and a MAPE of 3%. Figure 8 represents predicted values versus target values for the best models for fuel consumption (A) and productivity (B). The plots show the results of the test dataset.
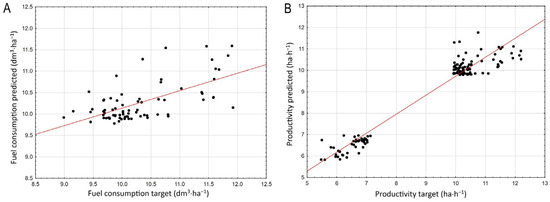
Figure 8.
Predicted values versus measured values of (A) fuel consumption and (B) productivity for best models.
Table 5 and Table 6 present the pair-wise comparisons of the models, with Kruskal–Wallis test being utilized to assess the statistical significance of differences in their performance (the data were found to be non-homogeneous in terms of variance). A series of statistical tests was conducted, with each test focusing on a distinct error metric, namely R, RMSE, and MAPE. For each model pair, the p-value was calculated. The findings indicate that, with regard to fuel consumption, none of the pair-wise comparisons resulted in statistically significant differences in performance, as all p-values exceed the established significance threshold (p < 0.05). A statistically significant discrepancy in the RMSE was identified between the SVM model for scenario 3 and the RBF model in terms of productivity. In other cases, pair-wise comparisons resulted in non-statistically significant differences in performance.

Table 5.
Statistical test results for comparisons of models of fuel consumption.

Table 6.
Statistical test results for comparisons of models of fuel productivity.
4. Discussion
Estimating energy usage in soil cultivation has been a growing research focus area, particularly with advancements in precision agricultural technologies. Several studies have explored approaches, including empirical modeling, mechanical sensor-based methods, and remote sensing techniques, to forecast energy consumption. However, integrating geophysical data with machine learning models to predict energy consumption during soil cultivation seems very promising as it considers the variability of the soil and time–cost–environmental effects. It addresses the gap between traditional energy consumption estimation methods and the need for cost-effectiveness, scalability, and accurate predictions using advanced technologies. Our findings support earlier research [38], which proved that geophysical data in combination with ML techniques enables the prediction of soil compaction, an important factor influencing energy consumption during agricultural operations. For both dependent variables, which we used as indicators of energy consumption (fuel consumption and productivity), the best models were produced by scenarios that used both electrical conductivity and magnetic susceptibility as inputs. More accurate models were obtained for productivity using the SVM algorithm and fuel consumption using the MLP algorithm. Therefore, it can be stated that the accuracy of the models indicated by the MAPE of 4% is appropriate for practical applications in estimating energy consumption. This is especially noticeable in the productivity context, where a very high R-value is correlated with a low MAPE. The superior performance of SVM relative to models based on neural networks may be attributable to the relatively modest size of the training dataset. SVM has been demonstrated to generate more accurate regression models in comparison to neural networks, including MLP and RBF, particularly in scenarios where the quantity of training data is restricted. In contrast to neural networks, which frequently necessitate extensive hyperparameter tuning and substantial datasets for effective generalization, SVMs demonstrate reduced sensitivity to the curse of dimensionality and exhibit robust performance in high-dimensional or sparse feature spaces [39]. Furthermore, SVM regression models employ a subset of the training data as support vectors, a feature that renders them more data-efficient and less prone to sensitivity to noise. This, in turn, results in improved generalization performance in small-sample scenarios.
Integrating geophysical data with machine learning methodologies facilitates the development of highly accurate predictive models for specific soil properties. Karim et al. [40] demonstrate that LiDAR sensors provide rapid and accurate data, including the ability to provide precise real-time data for field mapping, a critical factor influencing precision agriculture. This method reduces the need for extensive field sampling and allows for real-time decision-making—a major advantage over traditional mechanical approaches. Diaz-Gonzalez et al. [41] combined remote sensing data with ML algorithms to estimate soil quality in agricultural systems at local and regional scales. Their findings align with research supporting the use of SVM and ANN in precision agriculture. Similarly, Basso and Antle [42] demonstrated that integrating unmanned aerial vehicle-based multispectral imaging with AI-driven energy models improved the accuracy of productivity predictions, as AI-based approaches better capture complex interactions. Liu et al. [43] used Partial Least Squares Regression (PLSR), Random Forest (RF), SVM, and Gaussian Process Regression (GPR) in predicting soil water content. In their findings, the GPR model had the best prediction performance (R2 ≥ 0.95). Liu et al. [44], in their study to predict soil nutrients, proposed a sensor array optimization method based on the dynamic feature importance of the RF-Pearson correlation coefficient to identify the optimal sensor combinations for soil nutrients. SVM, RF, MLP, and MLP-RF models were applied to predict the soil nutrients. According to their findings, the MLP-RF model outperforms other models, with a coefficient of determination of 0.94. In researching the potential of utilizing land surface temperature data from MODIS satellites to estimate maximum air temperature across India, Joy et al. [45] employed extreme gradient boosting (XGBoost), ANN, a generalized additive model, and multiple linear regression models. From their results, XGBoost outperformed the other techniques, achieving the lowest RMSE and R² values of 1.79 °C and 0.90, respectively. In their study to provide an accurate classification of soil texture classes by assessing the capabilities of environmental covariates from Landsat 8 OLI Science products and a digital elevation model, Kaya et al. [46] employed Decision Tree (DT), RF, and SVM algorithms. The best of the three machine learning models for soil texture classification was RF, with an overall accuracy of 0.63 according to the accuracy evaluation. Deng et al. [47] aimed to improve the measurement accuracy and application range of low-frequency capacitance moisture sensors by correcting the relationship between low-frequency capacitance and moisture through the detection of soil conductivity. They utilized three modified models: logistic, exponential, and polynomial. The results showed that the Maximum Absolute Measurement Error (MAME) and Mean Absolute Error (MAE) of the logistic model were below 3.55% and 2.50%, respectively, which satisfy most agricultural production requirements for soil moisture detection. Waqas et al. [48] reviewed the use of machine learning and deep learning for crop selection, land monitoring and management, water, soil, and nutrient management, weed control, as well as harvest and post-harvest practices. They found that machine learning and deep learning facilitate the analysis of complex datasets, enabling data-driven decision-making, reducing reliance on subjective expertise, and improving farm management strategies. The authors noted that advancements in these technologies present significant opportunities to enhance agricultural productivity, sustainability, and resilience.
The utilization of ML algorithms has been demonstrated to facilitate the prediction of energy consumption within the agricultural sector. Trejo-Perea et al. [49] utilized MLP to forecast energy consumption in greenhouses, with the prediction model incorporating temperature, hour, relative humidity, and load as key variables. The ANN model developed in this research study demonstrated superior performance in comparison to the regression model, achieving a mean absolute percentage error (MAPE) of less than 6% and an R-value greater than 0.9. Ceylan [50] employed ML methods, including SVM and GPR, to forecast agricultural energy consumption in Turkey. The study utilized population data, combined with gross domestic product share of agriculture, agricultural value-added, and total arable land, as independent variables. The authors developed a GPR model of high accuracy, with a MAPE of 7% and an R-value of 0.97 for the test dataset. In their study, Sharma et al. [51] used statistical and ML methodologies, namely RF and LSTM, to estimate the seasonal peak demand for electricity consumption in the agricultural sector in India. The models were based on time series data. In that study, statistical methodologies generated more precise models.
It is also noteworthy that contemporary research continues to utilize statistical methodologies and mechanistic models to predict energy consumption in the agricultural sector [52,53]. The models presented in this thesis are not without their limitations. The utilization of data-driven models is constrained to the circumstances delineated in the data itself. The research was conducted in a single field, characterized by minimal variability in soil moisture and soil texture at the time of treatment with a specific aggregate. Consequently, the models obtained cannot be utilized under conditions that differ from those of the experiment that provided the training data. In order to obtain more universal models, it is planned that training data will be acquired under a variety of soil conditions and for different agrotechnical treatments.
5. Conclusions
This study establishes electrical parameter-based management as a crucial element of modern agricultural practices, contributing to economic viability and environmental sustainability. While traditional approaches rely on empirical models and field measurements, which are labor-intensive, costly, and prone to errors, modern scanning technologies like the Geonics EM-38 and Veris 3100 provide high-resolution data on soil texture, electrical properties, and spectral indices essential for optimizing resource use, reducing costs and time, and minimizing environmental impacts. The most accurate models were obtained using soil electrical parameters (electrical conductivity and magnetic susceptibility) measured with a Geonics EM-38 scanner, along with electrical conductivity and soil reflectance measured using a Veris 3100 scanner. The models demonstrating high accuracy (MAPE of 3–4%) were produced using the RBF, SVM, and MLP algorithms for productivity and fuel consumption as indicators of energy consumption. The results indicate that employing Geonics EM-38 and Veris 3100 scanners, combined with machine learning, predicts energy use with adequate accuracy for precision agriculture.
Integrating scanning techniques with machine learning-driven analysis enables real-time soil assessment, facilitating adaptive strategies such as variable-depth plowing to reduce fuel consumption and mechanical wear. Based on rapid scanning methods used in soil variability mapping, it is possible to obtain valuable information about soil condition variability, which directly affects draft forces, power requirements, and fuel consumption. This enables more accurate determination of the power needed to operate specific tractor-mounted agricultural implements of given widths and helps assess whether a particular tractor can efficiently work with a chosen implement on a given field. Additionally, this information can support optimal tractor ballasting, for example, by selecting the appropriate front ballast weight to ensure sufficient traction while minimizing soil compaction.
Author Contributions
Conceptualization, J.T.M. and K.P.; methodology, J.T.M., K.P., K.S.P. and T.W.; software, J.T.M., K.P. and K.S.P.; validation, J.T.M. and K.P.; formal analysis, J.T.M. and K.P.; investigation, J.T.M., K.P. and K.S.P.; resources, J.T.M. and K.P.; data curation, J.T.M., K.P. and K.S.P.; writing—original draft preparation, J.T.M.; writing—review and editing, K.P., K.S.P. and T.W.; visualization, J.T.M. and K.S.P.; supervision, K.P. and K.S.P.; funding acquisition, J.T.M. and K.P. All authors have read and agreed to the published version of the manuscript.
Funding
The article is part of a PhD dissertation titled “Prediction of energy consumption during soil cultivation based on scanning methods,” which was prepared during the Doctoral School at the Wrocław University of Environmental and Life Sciences. The APC is co-funded by Wrocław University of Environmental and Life Sciences.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest. The funder had no role in the design of the study; collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ECa | Soil electrical conductivity |
| MS | Magnetic susceptibility |
| IR | Soil reflectance in infrared spectra |
| MLP | Multilayer perceptron |
| RBF | Radial basis function neural network |
| SVM | Support vector machine |
| ML | Machine learning |
| EMI | Electromagnetic induction |
| R | Correlation coefficient |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
References
- Ozbek, F.S. Estimating the Direct Energy Use in Agriculture: A Case Study for Turkey. Bull. Univ. Agric. Sci. Vet. Med. Cluj-Napoca Agric. 2015, 72, 467–473. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Upadhyay, S.; Raghubanshi, A.S. Determinants of Soil Carbon Dynamics in Urban Ecosystems. In Urban Ecology: Emerging Patterns and Social-Ecological Systems; Elsevier: Amsterdam, The Netherlands, 2020; pp. 299–314. [Google Scholar] [CrossRef]
- Lemes, D.L.; Jacques, M.M.; Sousa, N.B.; Bernardon, D.P.; Sperandio, M.; Silva, J.A.; Chiara, L.M.; Wolter, M. Estimation of Electrical Energy Consumption in Irrigated Rice Crops in Southern Brazil. Energies 2023, 16, 6742. [Google Scholar] [CrossRef]
- Paris, B.; Vandorou, F.; Balafoutis, A.T.; Vaiopoulos, K.; Kyriakarakos, G.; Manolakos, D.; Papadakis, G. Energy Use in Open-Field Agriculture in the EU: A Critical Review Recommending Energy Efficiency Measures and Renewable Energy Sources Adoption. Renew. Sustain. Energy Rev. 2022, 158, 112098. [Google Scholar] [CrossRef]
- Ozkan, B.; Kurklu, A.; Akcaoz, H. An Input–Output Energy Analysis in Greenhouse Vegetable Production: A Case Study for Antalya Region of Turkey. Biomass Bioenergy 2004, 26, 89–95. [Google Scholar] [CrossRef]
- Alipour, A.; Veisi, H.; Darijani, F.; Mirbagheri, B.; Behbahani, A.G. Study and Determination of Energy Consumption to Produce Conventional Rice of the Guilan Province. Res. Agric. Eng. 2012, 58, 99–106. [Google Scholar] [CrossRef]
- Woods, J.; Williams, A.; Hughes, J.K.; Black, M.; Murphy, R. Energy and the Food System. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 2991–3006. [Google Scholar] [CrossRef]
- Baptista, F.J.; Silva, L.; de Visser, C.; Gołaszewski, J.; Meyer-Aurich, A.; Briassoulis, D.; Mikkola, H.; Murcho, D. Energy Efficiency in Agriculture. In Proceedings of the Título del Trabajo a Presentar en el XV Congreso Nacional de Ingeniería Mecánica, Santander, Spain, 10–13 June 2013. [Google Scholar]
- Pelletier, N.; Audsley, E.; Brodt, S.; Garnett, T.; Henriksson, P.; Kendall, A.; Kramer, K.J.; Murphy, D.; Nemecek, T.; Troell, M. Energy Intensity of Agriculture and Food Systems. Annu. Rev. Environ. Resour. 2011, 36, 233–246. [Google Scholar] [CrossRef]
- Sharafi, S.; Kazemi, A.; Amiri, Z. Estimating Energy Consumption and GHG Emissions in Crop Production: A Machine Learning Approach. J. Clean. Prod. 2023, 408, 137242. [Google Scholar] [CrossRef]
- Elsoragaby, S.; Yahya, A.; Mahadi, M.R.; Nawi, N.M.; Mairghany, M. Energy Utilization in Major Crop Cultivation. Energy 2019, 173, 1285–1303. [Google Scholar] [CrossRef]
- Chen, K.H.; Cheng, J.C.; Lee, J.M.; Li, L.Y.; Peng, S.Y. Energy Efficiency: Indicator, Estimation, and a New Idea. Sustainability 2020, 12, 4944. [Google Scholar] [CrossRef]
- Moitzi, G.; Haas, M.; Wagentristl, H.; Boxberger, J.; Gronauer, A. Energy Consumption in Cultivating and Ploughing with Traction Improvement System and Consideration of the Rear Furrow Wheel-Load in Ploughing. Soil Tillage Res. 2013, 134, 56–60. [Google Scholar] [CrossRef]
- Thongnim, P.; Yuvanatemiya, V.; Srinil, P. Smart Agriculture: Transforming Agriculture with Technology. In Methods and Applications for Modeling and Simulation of Complex Systems; Communications in Computer and Information Science; Springer: Singapore, 2024; Volume 1911, pp. 362–376. [Google Scholar] [CrossRef]
- Mat Su, A.S.; Adamchuk, V.I. Temporal and Operation-Induced Instability of Apparent Soil Electrical Conductivity Measurements. Front. Soil Sci. 2023, 3, 1137731. [Google Scholar] [CrossRef]
- Vijayakumar, S.; Chatterjee, D.; Subramanian, E.; Ramesh, K.; Saravanane, P. Efficient Management of Energy in Agriculture. In Handbook of Energy Management in Agriculture; Springer: Singapore, 2023; pp. 355–382. [Google Scholar] [CrossRef]
- Pradipta, A.; Soupios, P.; Kourgialas, N.; Doula, M.; Dokou, Z.; Makkawi, M.; Alfarhan, M.; Tawabini, B.; Kirmizakis, P.; Yassin, M. Remote Sensing, Geophysics, and Modeling to Support Precision Agriculture—Part 1: Soil Applications. Water 2022, 14, 1158. [Google Scholar] [CrossRef]
- Hemmat, A.; Adamchuk, V.I. Sensor Systems for Measuring Soil Compaction: Review and Analysis. Comput. Electron. Agric. 2008, 63, 89–103. [Google Scholar] [CrossRef]
- Klein, K.A.; Carlos Santamarina, J. Electrical Conductivity in Soils: Underlying Phenomena. J. Environ. Eng. Geophys. 2012, 8, 263–273. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Application of Soil Electrical Conductivity to Precision Agriculture. Agron. J. 2003, 95, 455–471. [Google Scholar] [CrossRef]
- Adviento-Borbe, M.A.A.; Doran, J.W.; Drijber, R.A.; Dobermann, A. Soil Electrical Conductivity and Water Content Affect Nitrous Oxide and Carbon Dioxide Emissions in Intensively Managed Soils. J. Environ. Qual. 2006, 35, 1999–2010. [Google Scholar] [CrossRef]
- Johnson, C.K.; Doran, J.W.; Duke, H.R.; Wienhold, B.J.; Eskridge, K.M.; Shanahan, J.F. Field-Scale Electrical Conductivity Mapping for Delineating Soil Condition. Soil Sci. Soc. Am. J. 2001, 65, 1829–1837. [Google Scholar] [CrossRef]
- Othaman, N.N.C.; Isa, M.N.M.; Ismail, R.C.; Ahmad, M.I.; Hui, C.K. Factors That Affect Soil Electrical Conductivity (EC) Based System for Smart Farming Application. AIP Conf. Proc. 2020, 2203, 020055. [Google Scholar] [CrossRef]
- Lund, E.D. Soil Electrical Conductivity. In Soil Science Step-by-Step Field Analysis; Soil Science Society of America: Madison, WI, USA, 2015; pp. 137–146. [Google Scholar] [CrossRef]
- Schenck, J.F. The Role of Magnetic Susceptibility in Magnetic Resonance Imaging: MRI Magnetic Compatibility of the First and Second Kinds. Med. Phys. 1996, 23, 815–850. [Google Scholar] [CrossRef]
- Zawadzki, J.; Fabijańczyk, P.; Magiera, T.; Rachwał, M. Geostatistical Microscale Study of Magnetic Susceptibility in Soil Profile and Magnetic Indicators of Potential Soil Pollution. Water Air Soil Pollut. 2015, 226, 142. [Google Scholar] [CrossRef] [PubMed]
- Pentoś, K.; Pieczarka, K.; Serwata, K. The Relationship between Soil Electrical Parameters and Compaction of Sandy Clay Loam Soil. Agriculture 2021, 11, 114. [Google Scholar] [CrossRef]
- Parent, E.J.; Parent, S.É.; Parent, L.E. Determining Soil Particle-Size Distribution from Infrared Spectra Using Machine Learning Predictions: Methodology and Modeling. PLoS ONE 2021, 16, e0233242. [Google Scholar] [CrossRef] [PubMed]
- Kurek, J.; Niedbała, G.; Wojciechowski, T.; Świderski, B.; Antoniuk, I.; Piekutowska, M.; Kruk, M.; Bobran, K. Prediction of Potato (Solanum tuberosum L.) Yield Based on Machine Learning Methods. Agriculture 2023, 13, 2259. [Google Scholar] [CrossRef]
- He, J.; Ren, Y.; Li, W.; Fu, W. YOLOv11-RCDWD: A New Efficient Model for Detecting Maize Leaf Diseases Based on the Improved YOLOv11. Appl. Sci. 2025, 15, 4535. [Google Scholar] [CrossRef]
- Cao, X.; Zhong, P.; Huang, Y.; Huang, M.; Huang, Z.; Zou, T.; Xing, H. Research on Lightweight Algorithm Model for Precise Recognition and Detection of Outdoor Strawberries Based on Improved YOLOv5n. Agriculture 2025, 15, 90. [Google Scholar] [CrossRef]
- Kuźniar, P.; Pentoś, K.; Gorzelany, J. Evaluation of the Use of Machine Learning to Predict Selected Mechanical Properties of Red Currant Fruit (Ribes rubrum L.) Ozonized during Storage. Agriculture 2023, 13, 2125. [Google Scholar] [CrossRef]
- Saleem, M.H.; Potgieter, J.; Arif, K.M. Automation in Agriculture by Machine and Deep Learning Techniques: A Review of Recent Developments. Prec. Agric. 2021, 22, 2053–2091. [Google Scholar] [CrossRef]
- Corchado, J.M.; Kollias, S.; Taheri, J.; Venkatesan, S.; Lim, J.; Ko, H.; Cho, Y. A Machine Learning Based Model for Energy Usage Peak Prediction in Smart Farms. Electronics 2022, 11, 218. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Fakhrzad, M.B.; Gharaat, S.; Jahangiri, M.; Dhanraj, J.A.; Band, S.S.; Issakhov, A.; Mosavi, A. Machine Learning for Prediction of Energy in Wheat Production. Agriculture 2020, 10, 517. [Google Scholar] [CrossRef]
- Ryżak, M.; Bartmiński, P.; Bieganowski, A. Methods for determining the granulometric distribution of mineral soils. Acta Agrophysica 2009, 175, 1–84. (In Polish) [Google Scholar]
- Oduma, O.; Oluka, S.I.; Eze, P.C. Effect of soil physical properties on performance of agricultural field machineries in the tropical region of Nigeria. Agric. Eng. Int. CIGR J. 2018, 20, 25–31. [Google Scholar]
- Pentoś, K.; Mbah, J.T.; Pieczarka, K.; Niedbała, G.; Wojciechowski, T. Evaluation of Multiple Linear Regression and Machine Learning Approaches to Predict Soil Compaction and Shear Stress Based on Electrical Parameters. Appl. Sci. 2022, 12, 8791. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Karim, M.R.; Reza, M.N.; Jin, H.; Haque, M.A.; Lee, K.H.; Sung, J.; Chung, S.O. Application of LiDAR Sensors for Crop and Working Environment Recognition in Agriculture: A Review. Remote Sens. 2024, 16, 4623. [Google Scholar] [CrossRef]
- Diaz-Gonzalez, F.A.; Vuelvas, J.; Correa, C.A.; Vallejo, V.E.; Patino, D. Machine Learning and Remote Sensing Techniques Applied to Estimate Soil Indicators—Review. Ecol. Indic. 2022, 135, 108517. [Google Scholar] [CrossRef]
- Basso, B.; Antle, J. Digital Agriculture to Design Sustainable Agricultural Systems. Nat. Sustain. 2020, 3, 254–256. [Google Scholar] [CrossRef]
- Liu, G.; Tian, S.; Xu, G.; Zhang, C.; Cai, M. Combination of Effective Color Information and Machine Learning for Rapid Prediction of Soil Water Content. J. Rock Mech. Geotech. Eng. 2023, 15, 2441–2457. [Google Scholar] [CrossRef]
- Liu, S.; Chen, X.; Xia, X.; Jin, Y.; Wang, G.; Jia, H.; Huang, D. Electronic Sensing Combined with Machine Learning Models for Predicting Soil Nutrient Content. Comput. Electron. Agric. 2024, 221, 108947. [Google Scholar] [CrossRef]
- Joy, A.; Satheesan, K.; Paul, A. High-Resolution Maximum Air Temperature Estimation over India from MODIS Data Using Machine Learning. Remote Sens. Appl. 2025, 37, 101463. [Google Scholar] [CrossRef]
- Kaya, F.; Başayiğit, L.; Keshavarzi, A.; Francaviglia, R. Digital Mapping for Soil Texture Class Prediction in Northwestern Türkiye by Different Machine Learning Algorithms. Geoderma Reg. 2022, 31, e00584. [Google Scholar] [CrossRef]
- Deng, X.; Gu, H.; Yang, L.; Lyu, H.; Cheng, Y.; Pan, L.; Fu, Z.; Cui, L.; Zhang, L. A Method of Electrical Conductivity Compensation in a Low-Cost Soil Moisture Sensing Measurement Based on Capacitance. Measurement 2020, 150, 107052. [Google Scholar] [CrossRef]
- Waqas, M.; Naseem, A.; Humphries, U.W.; Hlaing, P.T.; Dechpichai, P.; Wangwongchai, A. Applications of Machine Learning and Deep Learning in Agriculture: A Comprehensive Review. Green Technol. Sustain. 2025, 3, 100199. [Google Scholar] [CrossRef]
- Trejo-Perea, M.; Herrera-Ruiz, G.; Rios-Moreno, J.; Miranda, R.C.; Rivas-Araiza, E. Greenhouse Energy Consumption Prediction Using Neural Networks Models. Int. J. Agric. Biol. 2009, 11, 1–6. [Google Scholar]
- Ceylan, Z. Assessment of Agricultural Energy Consumption of Turkey by MLR and Bayesian Optimized SVR and GPR Models. J. Forecast. 2020, 39, 944–956. [Google Scholar] [CrossRef]
- Sharma, M.; Mittal, N.; Mishra, A.; Gupta, A. Machine Learning-Based Electricity Load Forecast for the Agriculture Sector. Int. J. Softw. Innov. 2003, 11, 1–21. [Google Scholar] [CrossRef]
- Almaliki, S.; Alimardani, R.; Omid, M. Fuel Consumption Models of MF285 Tractor under Various Field Conditions. Agric. Eng. Int. CIGR J. 2016, 18, 147–158. [Google Scholar]
- Kim, S.J.; Jang, M.K.; Hwang, S.J.; Lee, W.S.; Nam, J.S. Development of a Prediction Model for Specific Fuel Consumption in Rotary Tillage Based on Actual Operation. Agriculture 2024, 14, 1993. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).