Abstract
The application of drones has contributed to automated herbicide spraying in the context of precision agriculture. Although drone technology is mature, the widespread application of agricultural drones and their numerous advantages still demand improvements in battery endurance during flight missions in agricultural operations. This issue has been addressed by optimizing the path planning to minimize the time of the route and, therefore, the energy consumption. In this direction, a novel framework for autonomous drone-based herbicide applications that integrates deep learning-based semantic segmentation and coverage path optimization is proposed. The methodology involves computer vision for path planning optimization. First, semantic segmentation is performed using a DeepLab v3+ convolutional neural network to identify and classify regions containing weeds based on aerial imagery. Then, a coverage path planning strategy is applied to generate efficient spray routes over each weed-infested area, represented as convex polygons, while accounting for the drone’s refueling constraints. The results demonstrate the effectiveness of the proposed approach for optimizing coverage paths in weed-infested sugarcane fields. By integrating semantic segmentation with clustering and path optimization techniques, it was possible to accurately localize weed patches and compute an efficient trajectory for UAV navigation. The GA-based solution to the Traveling Salesman Problem With Refueling (TSPWR) yielded a near-optimal visitation sequence that minimizes the energy demand. The total coverage path ensured complete inspection of the weed-infected areas, thereby enhancing operational efficiency. For the sugar crop considered in this contribution, the time to cover the area was reduced by 66.3% using the proposed approach because only the weed-infested area was considered for herbicide spraying. Validation of the proposed methodology using real-world agricultural datasets shows promising results in the context of precision agriculture to improve the efficiency of herbicide or fertilizer application in terms of herbicide waste reduction, lower operational costs, better crop health, and sustainability.
1. Introduction
The application of drones has contributed to several agricultural tasks, such as crop mapping, real-time monitoring, automated herbicide spraying, and yield prediction in the context of precision agriculture [1]. Despite the widespread application of agricultural drones and their numerous advantages, several challenges to improving agricultural drone technology must be faced. Agricultural drones have sensors and devices such as diverse cameras and spraying systems. These drones are used for crop monitoring, herbicide and fertilizer spraying, and irrigation management [2]. Agricultural drones help farmers optimize resources, improve efficiency, and enhance overall crop yields by collecting and analyzing real-time data.
Although drone technology is mature, it still requires improvements in battery endurance during flight missions. This condition increases the operational cost and the risk of mission failure in agricultural operations. This issue has been addressed by optimizing the path planning to minimize the time of the route and, therefore, the energy consumption [3]. In this direction, computer vision has been incorporated into drone operations to optimize drone paths based on imagery of the environment [4].
Computer vision has emerged as a key technology in precision agriculture that permits monitoring and decision-making based on aerial and ground-based imagery. This technology has been applied to a wide range of tasks, including crop type classification, plant counting, disease detection, and weed mapping [5]. These capabilities improve efficiency, reduce chemical usage, and increase overall productivity. Moreover, research into agricultural drones has demonstrated the need to integrate computational vision technology into agricultural automation systems to enhance their performance [6].
However, traditional image classification techniques—typically based on pixel-level features or shallow machine learning models—often struggle in dense or complex agricultural environments. Deep learning methods based on convolutional neural networks have emerged as an alternative to overcome these issues in the context of pixel-wise classification methods for precision agriculture applications [7]. Deep convolutional neural networks (DCNNs) have been applied for weeds and crops discrimination based on imagery; the following architectures have been tested: (1) U-Net Model; (2) SegNet; (3) FCN (FCN-32s, FCN-16s, FCN-8s); (4) DepLabV3+ [8]. A discussion of the application of deep learning technology in weed detection using unmanned aerial vehicle (UAV) platforms is presented in [9]. A systematic review of applications of weed management in precision agriculture was presented and novel deep learning approaches were discussed for weed identification in [10]. These advancements highlight the growing importance of deep learning-based semantic segmentation as a robust solution for accurate and scalable weed and crop classification in complex agricultural scenarios.
A key challenge is planning UAV missions to maximize the flight time in large environments, given flight-time limitations, such as battery endurance. In this direction, deep learning methods using semantic segmentation have been applied for path planning of UAV missions. An online planning algorithm was proposed to adapt the UAV paths to obtain high-resolution semantic segmentation in areas with fine details based on the incoming images in [11]. A methodology was proposed that uses orchard segmentation and path planning based on UAV images to plan the path of the entire orchard to assist agricultural robots in tasks such as herbicide spraying and fruit harvesting in [12]. A strategy for semantics-aware autonomous exploration and inspection path planning of UAVs was also proposed in [13]. A convolutional neural network (CNN)-based model was designed to enhance obstacle classification for agricultural robots in [14]. The studies reported in [11,12,13,14] demonstrate the integration of semantic segmentation into UAV path planning; however, further research is needed to incorporate this approach into comprehensive mission optimization strategies for agricultural drones.
Coverage path planning (CPP) consists of planning a path to cover an entire target environment, generally defined as a determined area; this path should include the UAV motion constraints. Cabreira et al. [15] presented a survey about the coverage path planning of UAVs that details the main concepts and approaches reported in the literature. A key subject studied in CPP is path optimization to minimize the path time and energy consumption [16]. In this direction, the optimal coverage path planning in a cluttered environment was obtained with limited onboard energy in [3]. Coverage path planning for surveying disjoint areas was proposed by optimizing the visiting order and the flight lines orientation in [17]. The global optimization of UAV coverage path planning based on a genetic algorithm was also carried out in [18]. Torres et al. [19] proposed improvements in the coverage path planning based on geometrical definitions and the constraints of covered areas [19]. As an alternative to the coverage path optimization approach, multiple UAVs were used to cover large areas in agricultural applications in [20]. In addition, coverage path planning has been widely applied to UAV mission planning in precision agriculture for aerial spraying [21,22] and crop monitoring [20,23,24].
Despite notable advances in integrating semantic segmentation and optimizing coverage path planning (CPP) for UAV missions, there remains a significant gap in developing unified mission planning frameworks that simultaneously leverage semantic information, address agricultural mission-specific needs (such as weed treatment), and incorporate operational constraints like limited battery endurance and the necessity for multiple refueling operations.
This study aims to develop a comprehensive framework for autonomous drone-based herbicide application that integrates deep learning-based semantic segmentation, automated extraction of target treatment areas, and optimization of a refueling-aware coverage path. The proposed system combines semantic segmentation of crop images using DeepLab v3+, polygon extraction from detected weed regions, and planning of an optimized coverage path that takes into account drone constraints and battery limitations.
The main contributions of this work are summarized as follows:
- 1.
- Coverage path planning with refueling constraints: Design of an off-line coverage path planning strategy that includes the following: (i) Sweep direction optimization based on a custom cost function that considers both drone velocity and yaw dynamics; (ii) Integration of the Traveling Salesman Problem with Refueling (TSPWR), solved using a metaheuristic approach based on genetic algorithms to obtain the total trajectory over a crop field.
- 2.
- Mission optimization: Enhancement of herbicide or fertilizer application efficiency through the integration of semantic perception and refueling-aware path optimization.
- 3.
- A comprehensive framework is developed for autonomous drone-based herbicide application that integrates deep learning-based semantic segmentation and coverage path optimization. In addition, the feasibility and effectiveness in precision agricultural scenarios of the proposed method, using real-world agricultural datasets, is demonstrated.
The paper is organized into four sections. Section 2 presents the methods applied to the present approach that encompass semantic segmentation and optimization of the coverage path. Section 3 presents the numerical results of the application of semantic segmentation for weed detection and the optimization of the total coverage path. Finally, Section 4 presents the conclusions and future work.
2. Materials and Methods
This section outlines the methodology developed to integrate computer vision for path planning optimization. The case study conducted in the present research study to validate the proposed methodology considers the unmanned aerial systems imagery of a sugar cane plantation in northern Brazil, captured as a single UAV-acquired sugarcane field orthomosaic according to [25]. Additional information about the imagery experimental acquisition is described in Section 3.1. First, semantic segmentation is performed using a DeepLab v3+ convolutional neural network to identify and classify regions containing weeds based on aerial imagery. Second, a coverage path planning strategy is applied to generate efficient spray routes over each weed-infested area, represented as convex polygons, while accounting for the drone’s refueling constraints. The following subsections detail the implementation of each stage.
2.1. Semantic Segmentation Using DeepLab v3+
Semantic segmentation is a pixel-level image classification algorithm that assigns a class label to each individual pixel in an image [26]. In the context of precision agriculture, the semantic segmentation technique enables the automated identification and mapping of different components in crop fields, such as distinguishing weeds from crop rows and background regions. Deep convolutional neural networks (DCNNs) have shown superior performance in semantic segmentation tasks due to their ability to learn hierarchical features from raw image data.
Among the state-of-the-art [27,28] CNN-based architectures for semantic segmentation, DeepLab v3+ stands out for its accuracy and robustness in capturing contextual information at multiple scales. The model using DepLab v3+ could precisely extract weeds compared to other classifiers [29]. It extends the original DeepLab series by incorporating an encoder-decoder structure that enhances boundary delineation (see Figure 1a). The encoder leverages atrous spatial pyramid pooling (ASPP) to extract multi-scale features while preserving spatial resolution, and the decoder refines the segmentation results, especially around object boundaries.
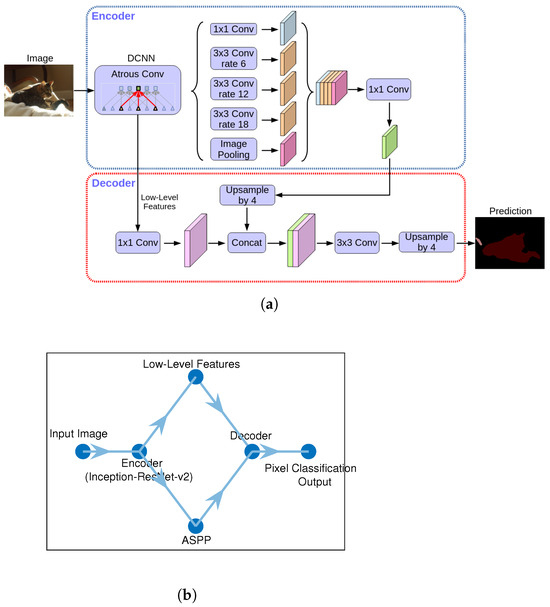
Figure 1.
DeepLabV3+ architecture: (a) DeepLabV3+ architecture in [29]. (b) Simplified DeepLabV3+ implemented in this contribution.
For this study, the Inception-ResNet-v2 network was used as the backbone for the DeepLab v3+ model. The DeepLab v3+ model has exhibited acceptable performance for weeds and crops discrimination from imagery [8]. This architecture combines the strengths of inception modules—efficient multi-scale feature extraction—and residual connections that facilitate the training of deeper networks by addressing vanishing gradient problems. This combination makes it well suited for complex image classification tasks, such as those encountered in field conditions. Moreover, a simplified diagram of the DeepLabv3+ architecture is presented in Figure 1b. The input image is first processed by the encoder, based on the Inception-ResNet-v2 backbone, which extracts high-level semantic features. In parallel, low-level features from earlier encoder layers are preserved to help refine object boundaries. The extracted high-level features pass through the atrous spatial pyramid pooling (ASPP) module, which captures multi-scale contextual information. These features are then combined with the low-level features in the decoder to produce a refined segmentation map. Finally, the pixel classification layer outputs the semantic segmentation for each pixel in the input image.
2.2. Coverage Path Planning of a Convex Polygon with Refueling
An agricultural spraying mission is an operation performed by a drone that applies herbicides, pesticides or fertilizers to crops. In the context of the present study, the drone’s configuration is defined as with and , are coordinates over the north-east-down (NED) frame and the orientation with respect to the east axis. Moreover, and v represent the drone’s angular velocity (yaw rate) and linear velocity in a straight line.
Convex polygons can commonly describe the area that the drone should cover with the following characteristics for a spraying mission: (i) the covered area is commonly specified by a small number of vertices, and (ii) there are no obstacles above a determined height [16]. By considering these two assumptions, the covered area is defined as a convex polygon with vertices ; thus, with for .
The agricultural spraying mission consists of a drone flying over the polygon area. The coverage path () is defined by a series of waypoints to cover the polygon with a back-and-forth pattern (BFP) [30], thus . The BFP consists of straight parallel segments that lie from the polygon edges in denominated rows to ensure complete coverage of a polygon area. At the end of each row, the drone executes a turning maneuver to align with the next row; thus, the flight direction has opposite directions considering contiguous rows. For example, the BFP defines a path from east to west and from west to east. Once the area is covered, the drone lands or returns to a base station for battery replacement.
The coverage path planning proposed in this contribution (see Algorithm 1) aims to minimize the execution time considering the refuel (return to take-off position for battery replacement). The algorithm performs coverage path planning (CPP) for a convex polygon while considering an endurance constraint (see Figure 2). It begins by initializing the cost parameters and computing the rotated bounding box of based on a given sweep direction (orientation of the rows). The coverage path is generated row-by-row, alternating between left-to-right and right-to-left directions. For each row, the algorithm determines the intersection points with the polygon and appends the valid segments to the total path ; thus, waypoints for each row are determined and . The cost function is evaluated at each step, and if the partial cost exceeds the maximum allowable endurance , the drone returns to the home position (take-off), increments the number of returns to take-off position , and resets . This process continues until the entire area is covered, after which the algorithm returns the total cost function c, the computed path , and the number of returns .
| Algorithm 1 Coverage path with refueling (CPWR). |
|
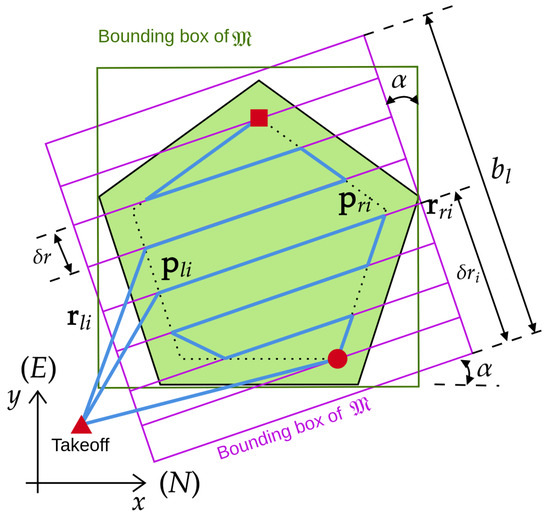
Figure 2.
Coverage path planning with refueling (CPWR): path (–), path start (•), path finish (▪).
The cost function to evaluate the path execution time considers the time sum for all waypoints () that is presented in Equation (1).
with and being two consecutive waypoints. is the time that the drone takes to displace and orient for two consecutive waypoints. v and are the drone’s linear velocity and angular velocity, respectively. It is worth mentioning that the cost function of Equation (1) also includes the return time that will depend on the distance of the actual drone’s position to the take-off position (see Figure 2 and line 15 of Algorithm 1).
The goal is to determine the optimal sweep direction for a convex polygon , which directly affects the efficiency of the coverage path within the region. A sweep direction defines the orientation of parallel lines along which the back-and-forth coverage path is executed. Since different sweep angles result in varying numbers of turns and path lengths due to the geometry of the polygon, it is important to select the direction that minimizes the total cost of coverage. This cost, denoted by (in Equation (1)), is a function of the total time, number of turns, and the vehicle’s kinematic parameters, such as the linear and angular velocities. To find , a set of candidate angles is evaluated, and for each angle, a path is computed and its associated cost is calculated. The angle that yields the minimum cost is then selected as the optimal sweep direction for that polygon according to Equation (2).
for . It is worth stating that was computed based on the coverage path with refueling in Algorithm 1.
2.3. Total Coverage Path for Several Polygons
The proposed approach aims to determine the total coverage path of the infested areas where the weed is present. These areas are defined as convex polygons. The total path needs to cover all polygons using an efficient coverage path to visit them optimally, subject to endurance constraints, to minimize the total flight time or energy. Consequently, the present approach consists of three main stages: (i) determination of the convex polygons of infested areas, (ii) determination of the optimal sequence for the polygons to be visited, and (iii) determination of the total coverage path for the convex polygons.
(i) Determination of the convex polygons of infested areas: The weed position over the considered area was previously defined by the semantic segmentation of the crop image, i.e., the Cartesian coordinates where the weed is present. The present operation defines the separate areas containing the weed by obtaining their corresponding convex polygons that limit the infested areas. For the present study, the separation and grouping of weed location into separate sets is carried out by applying Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [31]; every obtained set corresponds to a cluster. Then, the convex hull for every cluster is applied, i.e., a convex polygon that contains every clustered weed area. Finally, this step defines the convex polygons and their corresponding centroids where , and is the total number of polygons.
(ii) Determining the optimal sequence for visiting polygons: The definition of the total coverage path consists of determining the optimal order in which the drone should visit the polygons, considering the refueling constraints defined by the drone’s endurance. Thus, this problem derives from the well-known traveling salesman problem with refueling (TSPWR) [32], a combinatorial optimization problem. TSPWR considers the traveling salesman problem (TSP) with refueling decisions, i.e., the drone battery capacity limitation should be taken into account to define the path for visiting all the polygon’s centroids once to minimize the travel time (the total time between two refueling points never exceeds the battery capacity). If the drone exceeds the battery capacity, the drone should return to the home-position (depot) to charge the battery. is the fuel remaining upon arrival at node i.
The following variables are defined for the mathematical formulation of this problem. The vector of nodes corresponds to the numbering of the centroids of the polygon, where node 0 is the take-off position (depot); corresponds to the time taken to travel from node i to j. is the battery capacity defined in time units; : 1 if the vehicle travels from node i to j; 0 otherwise.
The TSPWR optimization problem consists of minimizing the travel time of Equation (3) subject to the following constraints: (a) each node is visited exactly once (Equations (4) and (5)), (b) the departure is equal to arrival that is node zero (take-off position) Equation (6), (c) battery capacity bounds (7), and (d) battery charge at take-off position node (8).
Subject to:
The TSPWR of Equations (3)–(8) is a complex combinatorial optimization problem, and several approaches have been used to solve this problem: reinforcement learning [32]; the heuristics, Variable Neighborhood Descent and Variable Neighborhood Search (VNS) [33]; metaheuristic methods (ant colony optimization [34] and simulated annealing [35]); and the mixed integer linear programming model [36]. In the present contribution, the genetic algorithm (GA), a metaheuristics method, was selected because it is scalable to large problems, can easily be included in new constraints, and has global search capabilities. However, special attention is paid to its weak characteristics, such as parameter sensitivity and no optimal solution [34]. In addition, the nearest neighbor (NN) is used as a baseline to evaluate GA solutions.
Initially, the centroids of the polygons to be visited are treated as nodes in the TSPWR according to Algorithm 2. Two methods were implemented to find the path: the nearest neighbor (NN) and a genetic algorithm (GA). In the NN method, the drone always visits the closest point within the flight endurance limit, returning to the home position when necessary to charge the battery. The GA evolves populations of paths represented by the set of the nodes vector . Using tournament selection, ordered crossover, mutations, and reintroduction of diversity, with evaluation based on penalties for paths that exceed flight endurance, the GA is used to improve candidate solutions over the execution of generations g. Finally, the optimal order of the nodes that minimizes the path time is obtained, after executing the maximum number of generations without changes in the best solution, as the stop criterion.
(iii) Total coverage path for convex polygons: Once the optimal order to visit the polygons is found , the total path that includes the coverage of the path is determined using the CPWR of Algorithm 1. Consequently, the total coverage path for a set of convex polygons , each requiring coverage via a back-and-forth sweeping motion. The path must begin and end at a take-off location (home position), subject to refueling constraints. The objective is to compute a sequence of waypoints representing the complete coverage path, which starts and ends at a take-off location , while minimizing the total coverage cost under a maximum flight endurance constraint. For each polygon visited in order , the approach is composed of two main steps:
| Algorithm 2 Genetic algorithm (GA) for the traveling salesman problem with refueling constraint (TSPWR). |
|
Step 1 Optimal sweep direction: determine the optimal sweep direction by minimizing the coverage cost:
Step 2 Constructing the total coverage path: the corresponding coverage path :
where each is a sequence of waypoints covering using the selected sweep direction , possibly with intermediate returns to take-off to satisfy flight endurance constraints: (i) the cost of the polygon path is defined as , and it should be less than the battery charge autonomy (refueling constraint); thus, , or insert return to , and (ii) coverage paths must be concatenated in the order given by (connectivity constraint). The proposed approach is implemented in Algorithm 3.
Algorithm 3 describes the complete procedure for computing the total coverage path of a set of convex polygons using three different coverage path methods of the convex polygons and two alternatives to solve the traveling salesman problem (TSPWR) that define the visiting order of the polygons. The coverage path strategy considers two alternative approaches in the literature to compare the proposed (CPWR) (using Equation (2) based on Algorithm 1). These approaches are the line sweep direction (LSD) [19] and the Boustrophedon cellular decomposition (BCD) [30]. Moreover, the TSPWR was solved using the nearest neighbor or the genetic algorithm. The algorithm begins at a predefined take-off location and iteratively computes the coverage path for each polygon in the sequence . Each coverage path is computed based on the selected method and ensures compliance with the endurance constraint by returning to the take-off position when necessary. The total coverage path is constructed by concatenating the individual paths and logging all returns to the take-off position (depot). The final output includes the complete trajectory , total operational cost , and number of returns for refueling .
| Algorithm 3 Computation of total coverage path for multiple convex polygons. |
|
2.4. Approach for Coverage Path Optimization in Weed-Infested Areas
The proposed approach to optimize the drone’s operation for herbicide spraying in a sugarcane crop is presented in Figure 3. The proposed approach involves using a convolutional neural network to obtain information about the weed (Section 2.1). Then, the solution of an optimization problem is required to obtain the coverage path of the drone (Section 2.3 and Section 2.2). The integration of the aforementioned methods is presented in the flowchart of Figure 3.
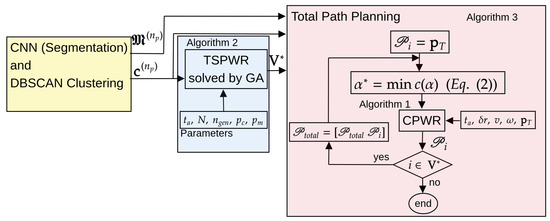
Figure 3.
Flowchart of the proposed approach: coverage path optimization in weed-infested areas.
Initially, a convolutional neural network is used to obtain the weed location in the sugarcane crop. Then, clustering is applied to obtain the definition of the convex polygons that bound the infested areas; the convex polygons are defined by the vertices and centroids . The drone should cover these areas.
Then, the TSPWR is solved using the GA in Algorithm 2 to obtain the optimal sequence for visiting the polygons .
Finally, the total coverage path () is computed using the method described in Algorithm 3 to obtain the total path. The obtention of each infested area’s coverage paths demands applying the coverage path with refueling (CPWR) described in Algorithm 1.
The numerical simulations were performed on a personal computer equipped with an Intel® Core™ i7 processor (2.9 GHz), 16 GB of RAM, and a 64-bit Ubuntu 20.4 operating system. The code was developed and executed using MATLAB R2024a. This computational setup ensures sufficient processing power and memory to efficiently handle the matrix operations and iterative procedures required by the numerical method.
3. Results
This section presents the numerical results of the application of semantic segmentation for weed detection in the sugarcane crop of Section 2.1, analysis of the coverage path with refueling (CPWR) of Section 2.2, and the obtention of the total coverage path of Section 2.3.
3.1. Semantic Segmentation for Weed Detection in Sugarcane Fields
Experimental results showed that the DepLab v3+ segmentation model for crop/weed discrimination could extract weeds more precisely than other classifiers based on the U-Net Model, SegNet, and FCN deep learning methods [8]. Thus, a DeepLab v3+ architecture [29] in MATLAB using the Inception-ResNet-v2 backbone was implemented to perform semantic segmentation on the sugarcane crop images presented in [25]. The dataset consisted of RGB images of the sugarcane crop (see Figure 4a) and their corresponding pixel-wise annotations (see Figure 4b), where each pixel was labeled as croprow (green), weed (yellow), or background (red). According to [25], the image was acquired using a fixed-wing UAV from Horus Aeronaves (https://drones.horusaeronaves.com/droneshow2020), equipped with a Canon G9X RGB visible light camera. The UAV operated at an altitude between 125 and 200 m, providing a spatial resolution of approximately 5 cm per pixel.
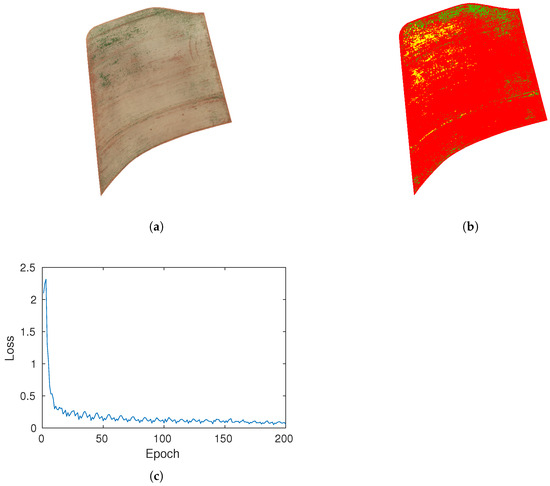
Figure 4.
Images of the sugarcane crop: (a) Original image. (b) Pixel-wise annotations. (c) Loss function.
Images and labels were loaded using the imageDatastore and pixelLabelDatastore functionalities, respectively. The dataset was randomly partitioned into training (80%) and testing (20%) subsets. All images were resized to pixels to conform to the input size required by the DeepLab v3+ network.
Data prepossessing and augmentation were applied through custom transformation functions, and image–label pairs were combined using the combine function. The combine function was then used to merge the imageDatastore (containing the input images) and the pixelLabelDatastore (containing the ground truth masks) into a single datastore. This combined datastore ensures that any transformation applied to an image is synchronously applied to its corresponding label, maintaining data consistency during training. The training was conducted with the Adam optimizer using a mini-batch size of 20, an initial learning rate of , and a total of 20 epochs. The cross-entropy loss function was applied to network training (see Figure 4c), and training progress was monitored and saved. The model progressively learned to fit the data because the training loss decreased steadily over the epochs. The observed rapid drop in loss during the initial epochs indicates convergence toward a stable solution.
In the evaluation procedure of Figure 5, each image in the test dataset (imdsTest) (see Figure 5a) is processed sequentially to allow a visual comparison between the ground truth labels (see Figure 5b) and the predictions generated by a trained semantic segmentation network (see Figure 5c). For each image, the corresponding label mask is read from the pixel label datastore (pxdsTest) and converted into an RGB representation using a predefined colormap, then displayed. The original RGB image is also read, resized to 299 × 299 pixels (the expected input size of the DeepLab v3+ network), and displayed. This resized image is passed through the segmentation network (net), which returns a categorical prediction for each pixel (C). The predicted segmentation mask is then converted into an RGB image using the same colormap and visualized. This process allows a qualitative assessment of the network’s pixel-wise classification accuracy by enabling side-by-side visual comparison of the ground truth and predicted masks across the defined classes: croprow, weed, and background.
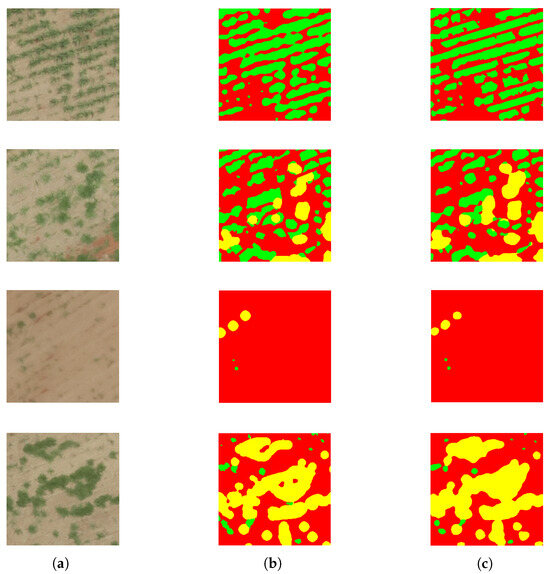
Figure 5.
Assessment of semantic segmentation: (a) RGB images, (b) pixel-wise annotations, and (c) predicted segmentation masks.
The trained network was then used to segment the entire test dataset, and performance metrics were computed using MATLAB’s evaluateSemanticSegmentation function, which provides class-wise accuracy, intersection-over-union (IoU), and a normalized confusion matrix. The evaluation was conducted on 50 test images, and the results indicate that the network achieved a global accuracy of 95.91%, reflecting the overall proportion of correctly classified pixels. The mean class accuracy was 88.30%, indicating a high average performance across all classes. The mean IoU, which measures the overlap between the predicted and true regions, was 75.07%, and the weighted IoU was 92.92%, showing strong performance even when accounting for class imbalance. Furthermore, the network obtained a mean Boundary F1 (BF) score of 80.02%, demonstrating reliable segmentation quality at the boundary of the object. These results suggest that the model generalizes the test data well and is capable of accurately segmenting the key semantic classes in the dataset. It is worth noting that the network evaluation was conducted on a relatively small test set comprising only 50 test images. While the results provide preliminary insights into the network’s performance, this sample size may not be sufficient to fully capture the variability of real-world scenarios.
A normalized confusion matrix was plotted to visually assess the classification performance. Each cell in the matrix was color-coded and annotated with percentage values to indicate the proportion of correct and incorrect predictions between the three classes (see Figure 6).
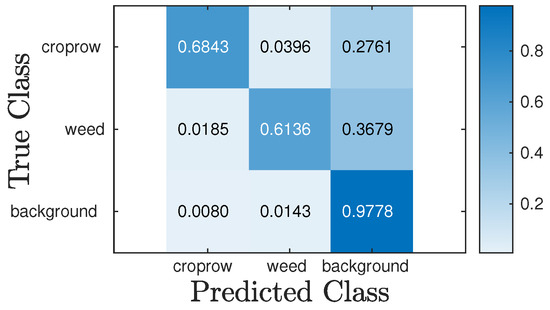
Figure 6.
Confusion matrix of DeepLab v3+ classification for sugarcane crop dataset.
3.2. Coverage Path Planning Approach
For the present section, the following parameters were considered for the definition of the path: v = 4.7 m/s, = 5 m, = 0.7854 rad/s, and = 500 s. These parameters were selected according to the average operational characteristics of the available agricultural multirotor drones [37]. This section initially presents an analysis of the coverage path with the refueling approach (CPWR) and then a numerical analysis to illustrate the incantation of the total coverage path, considering several convex polygons to be covered.
3.2.1. Analysis of the Coverage Path with Refueling (CPWR)
The objective of the present study is to assess its characteristics: the sweep direction () and number of returns to take-off position () as a function of the parameters that define the coverage path, i.e., evaluating how the battery charge endurance and the drone’s angular velocity affect the resulting coverage path of the convex polygon considering the refueling.
Initially, an analysis of the convex polygon coverage path in Figure 7a by minimizing the cost according to Equation (2) is carried out. For the present analysis, = 4.7 m, v = 5 m/s, = 900 s, and the take-off position is (−70, 10) m. In addition, the impact of the input parameters defined as intervals—endurance = (540, 930) s and drone angular velocity = (0.17, 1.57) rad/s—are evaluated for the resulting coverage path . Thus, the coverage path obtained in Figure 7a has one return to home ( = 1) and sweep direction = 0.40 rad assuming = 0.5468 rad/s and = 566 s.
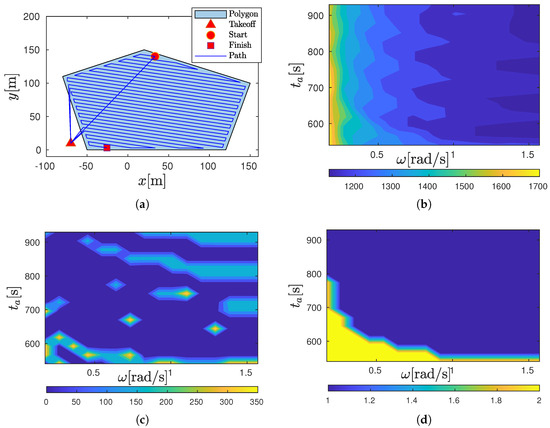
Figure 7.
Coverage path analysis: (a) Coverage path and polygon. (b) Path cost (c) as a function of and . (c) Sweep direction () as a function of and . (d) Number of return to take-off position () as a function of and .
Initially, the path cost (c) (obtained by using Equation (1)) is presented in Figure 7b. The resulting cost (c) indicates that the small angular velocities imply an increase in the path time. Moreover, endurance () does not significantly affect the cost, and the endurance variation does not increase the time required to complete the path. The sweep direction () obtained as a function of and is presented in Figure 7c. The definitions of angular velocity and endurance do not exhibit a specific trend on the sweep direction (). Thus, the sweep direction does not depend only on the polygon geometry but on the inputs of and for each specific case of the analysis to minimize the path time. Finally, the number of returns to take-off () (see Figure 7d) obtained shows that increasing the angular velocity and endurance does not require the return to be performed for battery replacement during the execution of the path.
Table 1 presents the outputs of the coverage path obtained for two different convex polygons to minimize the execution time according to Equation (2). The coverage path for Polygon 1 (Figure 7a and Figure 8a) shows that a slight variation in the drone’s angular velocity has a significant effect on the coverage path characteristics, i.e. the sweep direction is adjusted to minimize the path execution time to compensate for the increment in the number of return to take-off positions (). Moreover, a slight difference in the sweep direction was observed compared to the approach presented by [19]. Regarding the cover path of Polygon 2 (Figure 8c), a small increment in the drone’s endurance (from 566 s to 900 s) produces an additional return to take-off position and also modifies the sweep direction. Moreover, greater endurance implies a reduction in the path time execution. Moreover, one can also observe that the modification of the take-off position also modifies the characteristics of the coverage path because the sweep direction is adjusted to minimize the time path (see Figure 8b,d). Thus, one can observe that depending on the take-off position, the start and finish are switched; this implies that the sweep direction increment is rad. Finally, the coverage path with refueling (CPWR) is compared to the approach proposed in [19] that only considers the geometry of the convex polygons. One can observe that the results using both approaches agree with these two approaches for these case studies.

Table 1.
Coverage path outputs.
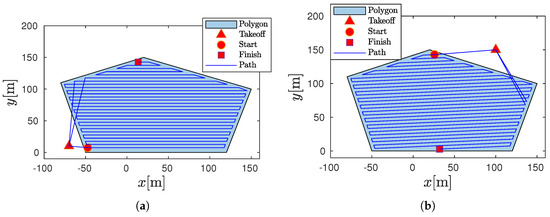
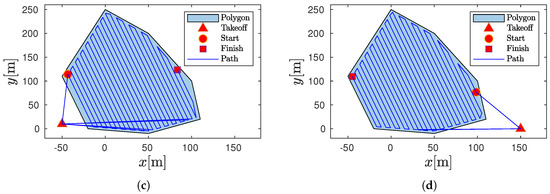
Figure 8.
Coverage path: (a) Polygon 1. (b) Polygon 1 with a different take-off position. (c) Polygon 2. (d) Polygon 2 with a different take-off position.
3.2.2. Total Coverage Path for Several Polygons
The present section presents a case study to illustrate the numerical procedure that computes the total coverage path using the method presented in Section 2.3.
Initially, a simulation environment illustrating the wedding location was obtained as a set of randomly distributed points over a rectangular area of 400 m × 350 m. The Cartesian points representing the weeds are presented in Figure 9a.
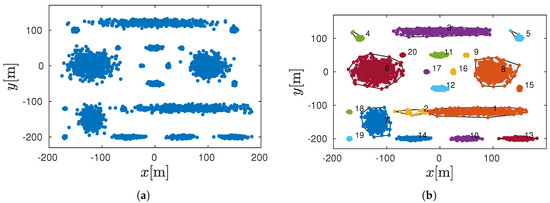
Figure 9.
Simulation environment and clustering: (a) Simulation environment. (b) Clusters (from to ) and their corresponding and polygons obtained from clustering.
The clustering using the DBSCAN algorithm was applied taking into account the neighborhood search radius and the minimum number of neighbors = 50 according to the MATLAB function dbscan based on [31]. As presented in Figure 9, the DBSCAN algorithm classifies the dataset of weed location into 20 different clusters. The corresponding convex polygon was then obtained for every set of clustered points; thus, the set of the polygons obtained corresponds to with . The corresponding centroids of the convex polygons were also computed; thus, .
Then, the optimal sequence for visiting the polygons is determined by solving the TSPWR of Equation (3) by using two algorithms: the nearest neighbor (NN) and the genetic algorithm (GA) presented in Algorithm 2.
As an introductory case study, this problem was solved considering the first fifteen polygons. Thus, = 15 and = 500 s. The centroids of the polygons and the route that defines the optimal sequence are presented in Figure 10. The optimal sequence obtained by the NN algorithm is = [0 14 2 12 9 11 15 5 4 10 13 0 7 1 0 3 8 0 6 0] (see Figure 10a). Then, the GA was applied with the following parameters: population N = 20, maximum number of generations without changing = 200, crossover probability = 0.7, and mutation probability = 0.3. These parameters were determined through a trial-and-error process. Several preliminary tests were conducted to assess the impact of different parameter values on the convergence speed and solution quality. The chosen parameter configuration represents a compromise between the computational cost and solution robustness, ensuring stable performance across different runs. Although a formal hyperparameter optimization was not performed, the selected values were sufficient to achieve reliable and satisfactory results for the problem addressed. The optimal sequence obtained by the GA algorithm is =[ 0 7 14 2 12 1 10 0 13 15 8 5 9 11 0 3 4 0 6 0] (see Figure 10b). For this case study, the sequence obtained defines the path, considering the return to take-off position (3 and 2 returns for NN and GA, respectively). In addition, GA exhibits a sense of an organized sequence (see Figure 10b) compared with the NN sequences (see Figure 10a) that demands returning to nodes located in regions that were previously visited).
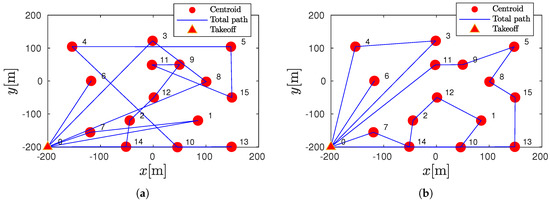
Figure 10.
Optimal sequence for visiting polygons for = 15: (a) Nearest neighbor (NN). (b) Genetic algorithm (GA)).
For the GA, the evolution of the fitness function over the generations is presented in Figure 11a. Thus, the GA stops after the execution of 144 generations. This case study’s computational time obtained with the NN algorithm (0.0101 s) is smaller than for GA (0.8002 s). Moreover, the optimal sequence obtained with GA resulted in a lower cost (c = 1424.9219 s) than the cost obtained using NN (c = 1671.9977 s).
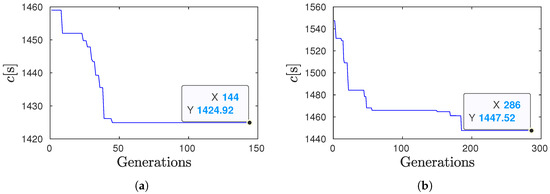
Figure 11.
Fitness function along the generations for the genetic algorithm (GA): (a) = 15. (b) = 20.
The GA was also computed for the twenty polygons ( = 20) of the simulation environment in Figure 9b. The obtained evolution of the fitness function along the generations by solving the GA for TSPWR is presented in Figure 11b. For this case study, the computational time obtained using the GA (2.2101 s) is greater than the NN algorithm (0.0013). Nevertheless, the cost associated with the optimal sequence obtained by the GA (c = 1447.5186 s) is smaller than the cost obtained from the NN algorithm (c = 1704.4278 s).
The TSPWR optimization problem of the present case study (Figure 9) was also solved considering four different sets of polygons shown in Figure 9b as described in Table 2. Thus, the first case study considers the first five polygons ( = 5); then, the first ten polygons ( = 10); then, the first fifteen ( = 15); finally, all twenty polygons were considered ( = 20) (see Table 2). For all cases, the GA obtained sequences for visiting the polygons at a lower cost than the NN algorithm. Nevertheless, the computational time was higher using GA than the NN algorithm. Therefore, it is observed that a compromise exists between the cost performance results in c and the computational time. For the present case study, the computational cost is not a limitation to minimize the time execution of the path.

Table 2.
Coverage path outputs.
Finally, the total coverage paths for the first fifteen polygons () of the simulation environment presented in Figure 9 were also computed using Algorithm 3 considering the take-off position = (−200, −200) m. The order of the sequence for the polygons visiting was previously computed using GA; thus, = [0 7 14 2 12 1 10 13 15 8 5 9 11 3 4 6 0].
The seep direction for the coverage path of each polygon was computed using three methods to compare the proposed CPWR in Section 2.2 with the approaches previously presented in [19,30]. Finally, the total coverage path was computed based on the expression of Equation (9) (see Figure 12). One can observe that the worst result in terms of the path time was obtained using the BCD to the coverage path (c = 3514.4 s and 7 returns to take-off for battery charge). Moreover, the proposed approach using CPWR resulted in the best performance regarding the other approaches (c = 2600.8 s and 5 returns to take-off for battery charge; see Figure 12b). On the other hand, the best result was obtained by applying the CPRW for the coverage path (c = 2401.4 s and 4 returns to take-off for battery charge; see Figure 12c). In addition, an intermediate result was obtained with the approach proposed in [19] (c = 2920.0 s and 5 returns to take-off for battery charge; see Figure 12b).
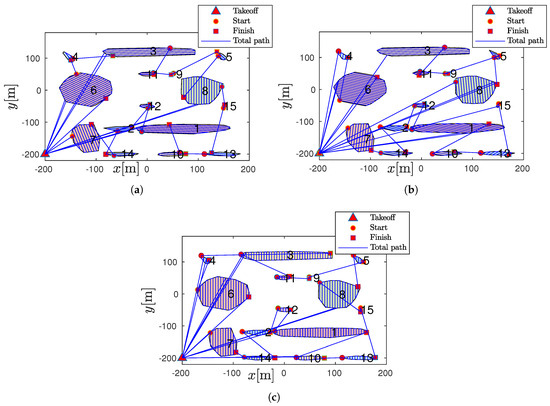
Figure 12.
Total path using genetic algorithm (GA): (a) Coverage path with refueling (CPWR). (b) Line sweep direction (LSD) [19]. (c) Boustrophedon cellular decomposition (BCD) [30].
The total path was also computed considering different numbers of polygons for the simulation environment of Figure 9 as presented in Table 2. The results show that the method proposed in the present contribution (CPWR) obtained better results for all the evaluated cases (see Table 2) than the method previously presented in the literature. This improvement minimizes the execution time of the path (c). Consequently, it minimizes the times the drone must return for battery changing due to CPWR adjusting the sweep direction to minimize path execution for every polynomial considering the refueling constraints. However, the CPWR significantly increases the computation time for all cases; this condition is not prohibitive for the present application since the computation time for 20 polygons is insignificant.
3.3. Coverage Path Optimization in Weed-Infested Areas
This section aims to illustrate the overall approach to obtain the optimal coverage path based on analysis of the sugarcane crop according to the procedures presented in Section 2.4.
Initially, the DeepLab v3+ architecture was implemented to perform semantic segmentation on the sugarcane crop images presented to detect the location of the weed in the image of the sugarcane crop according to the results presented in Section 3.1 (see Figure 13a). Then, the location of the weed within the sugarcane crop based on the image of Section 3.1 was obtained to establish the dataset to be analyzed (see Figure 13b). The dataset was then clustered using the DBSCAN algorithm. For the present application, the following parameters were selected = 8 and = 50. Thus, nineteen different convex polygons representing weed-infested areas were obtained according to Figure 13c.
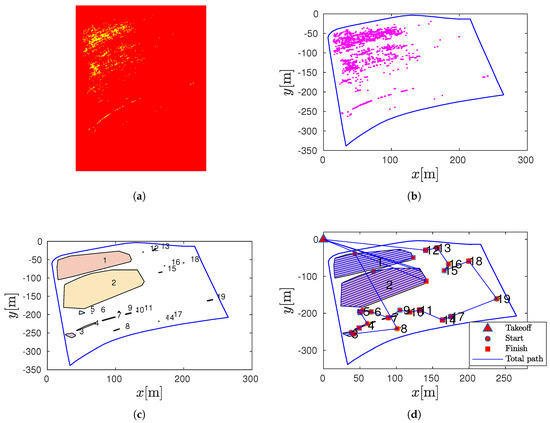
Figure 13.
Coverage path: (a) Weed detection in the image of the sugarcane crop. (b) Weed borders from the image. (c) Polygon of the infested areas. (d) Total coverage path of the infested areas.
The optimization of the TSPWR (of Equation (3)) to determine the optimal order in which convex polygons should be visited was then solved using the GA of Algorithm 3. The parameters considered for the GA were as follows: ta = 500 s, N = 360, = 200, = 0.7, and = 0.3. The optimal sequence obtained by the GA was = [0 12 13 18 16 15 19 17 14 11 10 9 7 8 3 4 5 6 2 1 0].
Finally, the total path () was obtained by applying Algorithm 3 (Figure 13d). The total time path obtained was c = 796.4795 s. This path only requires one return to the take-off position for the battery charge ( = 1). Moreover, the computation time required to obtain the coverage path was = 28.2429 s.
For the sugar crop considered in this contribution, the time to cover the total area was 1200.78. Thus, the present approach was reduced by 66.3% because only the weed-infested area was considered for herbicide spraying. The results presented in this section demonstrate the effectiveness of the proposed approach for optimizing the coverage paths in weed-infested sugarcane fields. By integrating semantic segmentation with clustering and path optimization techniques, it was possible to accurately localize weed patches and compute an efficient trajectory for UAV navigation. The GA-based solution to the TSPWR problem yielded a near-optimal visitation sequence that minimizes the energy demand. The total coverage path ensured complete inspection of the weed-infected areas, thereby enhancing operational efficiency.
3.4. Key Strengths and Limitations of the Proposed Method
The proposed framework offers several key strengths that contribute to advancing precision agriculture through autonomous drone-based herbicide spraying. One of the main strengths is integrating a deep learning-based semantic segmentation model (DeepLab v3+) with an efficient path-planning strategy. This approach enables the detection of weed-infested regions and the optimization of coverage paths while accounting for UAV battery limitations, resulting in decreased operational time, reduced herbicide usage, and lower environmental impact. Furthermore, the formulation of the path planning considering refueling solved using genetic algorithms demonstrates the capacity to handle practical UAV limitations in agricultural settings.
The proposed method also has some limitations. First, the semantic segmentation model has a limited performance because of the small training and test image set. This issue reduces the robustness subject to field conditions. Second, the current method depends on RGB images that may be insufficient to effectively differentiate crops from weeds subject to variable lighting conditions or different stages of plant development. The inclusion of multispectral or thermal imagery could enhance the robustness of detection. These limitations should be addressed in future work to enhance the proposed framework’s scalability and robustness for extending the proposed framework to more diverse crops and larger fields.
4. Conclusions
The present contribution proposed a framework for autonomous drone-based herbicide application that integrated deep learning-based semantic segmentation, automated extraction of target treatment areas, and optimization of a refueling-aware coverage path. The proposed system combines semantic segmentation of crop images using DeepLab v3+, polygon extraction from detected weed regions, and planning of an optimized coverage path that takes into account battery limitations.
The proposed methodology demonstrated the effectiveness of the proposed approach for optimizing coverage paths in weed-infested sugarcane fields by using semantic segmentation using the DeepLab v3+ architecture to successfully detect weed-infested areas over a sugarcane crop field based on DBSCAN clustering and convex hull algorithms. Then, this information was used for the proposed path optimization, minimizing the time path based on the traveling salesman problem with refueling solved using genetic algorithms. The obtained path showed better results compared to approaches previously proposed in the literature.
The validation of the proposed methodology using real-world agricultural datasets shows promising results in the context of precision agriculture to improve the efficiency of herbicide or fertilizer application in terms of herbicide waste reduction, lower operational costs, better crop health and sustainability. The results provide preliminary insights into the network’s performance that may not be sufficient to capture the variability of real-world scenarios fully. Despite the promising results, the proposed approach has several limitations that should be addressed in future work. First, establishing a reliable dataset for training the convolutional neural network requires extensive data collection in agricultural fields, along with expert-based classification of weed and crop regions. Second, the computational demands of processing high-resolution images and executing the full segmentation and path planning pipeline pose challenges for real-time applications in the field. Finally, the approach depends on the availability of high-quality aerial images, which requires additional data collection flights using UAVs equipped with suitable cameras.
Future work will focus on increasing the training and test image set for the semantic segmentation model to obtain robust performance aiming at application in real-world scenarios. Another direction will be the integration of additional sensors, such as multispectral and thermal cameras, to enhance the accuracy of weed detection and broaden the range of agricultural applications.
Funding
This research received no external funding.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
Symbols and Abbreviations
The following list of symbols and abbreviations are used in this manuscript.
| List of Symbols | |
| c | Cost function: time path |
| Sweep direction | |
| Flight endurance: the total time a drone | |
| can remain airborne on a single battery charge | |
| Drone’s angular velocity (yaw rate) | |
| v | Drone’s linear velocity in a straight line |
| Take-off position | |
| Row spacing | |
| Times of return-to-home take-off position (depot) | |
| Convex polygon of the weed-infested area | |
| Centroid of the polygon | |
| Partial cost function | |
| Bounding box limit | |
| Current row | |
| for the i-th row line | |
| Total coverage path | |
| , Waypoints of a single row | |
| Total number of waypoints | |
| Total number of polygons | |
| N | Population size |
| Number of generations | |
| Crossover probability | |
| Mutation probability | |
| Optimal sequence for visiting the polygons | |
| Time to compute the total coverage path | |
| Time to compute the TSPWR problem | |
| Abbreviations | |
| CPP | Coverage Path Planning |
| UAV | Unmanned Aerial Vehicle |
| TSPWR | Traveling Salesman Problem With Refueling |
| GA | Genetic Algorithm |
| NN | Nearest Neighbor |
References
- Mogili, U.R.; Deepak, B. Review on application of drone systems in precision agriculture. Procedia Comput. Sci. 2018, 133, 502–509. [Google Scholar] [CrossRef]
- Hafeez, A.; Husain, M.A.; Singh, S.; Chauhan, A.; Khan, M.T.; Kumar, N.; Chauhan, A.; Soni, S. Implementation of drone technology for farm monitoring & pesticide spraying: A review. Inf. Process. Agric. 2023, 10, 192–203. [Google Scholar]
- Bouzid, Y.; Bestaoui, Y.; Siguerdidjane, H. Quadrotor-UAV optimal coverage path planning in cluttered environment with a limited onboard energy. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 979–984. [Google Scholar] [CrossRef]
- Akshya, J.; Neelamegam, G.; Sureshkumar, C.; Nithya, V.; Kadry, S. Enhancing UAV path planning efficiency through adamoptimized deep neural networks for area coverage missions. Procedia Comput. Sci. 2024, 235, 2–11. [Google Scholar]
- Tian, H.; Wang, T.; Liu, Y.; Qiao, X.; Li, Y. Computer vision technology in agricultural automation—A review. Inf. Process. Agric. 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Latif, G.; Alghazo, J.; Maheswar, R.; Vijayakumar, V.; Butt, M. Deep learning based intelligence cognitive vision drone for automatic plant diseases identification and spraying. J. Intell. Fuzzy Syst. 2020, 39, 8103–8114. [Google Scholar] [CrossRef]
- Fawakherji, M.; Youssef, A.; Bloisi, D.; Pretto, A.; Nardi, D. Crop and weeds classification for precision agriculture using context-independent pixel-wise segmentation. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; IEEE: New York, NY, USA, 2019; pp. 146–152. [Google Scholar]
- Hashemi-Beni, L.; Gebrehiwot, A.; Karimoddini, A.; Shahbazi, A.; Dorbu, F. Deep Convolutional Neural Networks for Weeds and Crops Discrimination From UAS Imagery. Front. Remote. Sens. 2022, 3, 755939. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, F.; Zhang, Q.; Wang, M.; Yu, J.; Tan, Y. Advancements of UAV and deep learning technologies for weed management in Farmland. Agronomy 2024, 14, 494. [Google Scholar] [CrossRef]
- Rai, N.; Zhang, Y.; Ram, B.G.; Schumacher, L.; Yellavajjala, R.K.; Bajwa, S.; Sun, X. Applications of deep learning in precision weed management: A review. Comput. Electron. Agric. 2023, 206, 107698. [Google Scholar] [CrossRef]
- Stache, F.; Westheider, J.; Magistri, F.; Stachniss, C.; Popović, M. Adaptive path planning for UAVs for multi-resolution semantic segmentation. Robot. Auton. Syst. 2023, 159, 104288. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, R.; Chen, L.; Zhang, L.; Zhang, H.; Zhao, C. Semantic segmentation and path planning for orchards based on UAV images. Comput. Electron. Agric. 2022, 200, 107222. [Google Scholar] [CrossRef]
- Dharmadhikari, M.; Alexis, K. Semantics-aware exploration and inspection path planning. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: New York, NY, USA, 2023; pp. 3360–3367. [Google Scholar]
- Syed, T.N.; Zhou, J.; Lakhiar, I.A.; Marinello, F.; Gemechu, T.T.; Rottok, L.T.; Jiang, Z. Enhancing Autonomous Orchard Navigation: A Real-Time Convolutional Neural Network-Based Obstacle Classification System for Distinguishing ‘Real’ and ‘Fake’ Obstacles in Agricultural Robotics. Agriculture 2025, 15, 827. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Brisolara, L.B.; Ferreira, P.R., Jr. Survey on Coverage Path Planning with Unmanned Aerial Vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Di Franco, C.; Buttazzo, G. Coverage path planning for UAVs photogrammetry with energy and resolution constraints. J. Intell. Robot. Syst. 2016, 83, 445–462. [Google Scholar] [CrossRef]
- Vasquez-Gomez, J.I.; Herrera-Lozada, J.C.; Olguin-Carbajal, M. Coverage Path Planning for Surveying Disjoint Areas. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 899–904. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, Z.; Lian, Y.; Chen, L.; An, Q.; Wang, L.; Ma, B. Global Optimization of UAV Area Coverage Path Planning Based on Good Point Set and Genetic Algorithm. Aerospace 2022, 9, 86. [Google Scholar] [CrossRef]
- Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction. Expert Syst. Appl. 2016, 55, 441–451. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Yakunin, K.; Aubakirov, M.; Assanov, I.; Kuchin, Y.; Symagulov, A.; Levashenko, V.; Zaitseva, E.; Sokolov, D.; Amirgaliyev, Y. Coverage path planning optimization of heterogeneous UAVs group for precision agriculture. IEEE Access 2023, 11, 5789–5803. [Google Scholar] [CrossRef]
- Huang, J.; Du, B.; Zhang, Y.; Quan, Q.; Wang, B.; Mu, L. A pesticide spraying mission allocation and path planning with multicopters. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2277–2291. [Google Scholar] [CrossRef]
- Gao, H.; Ma, X. Multiple chromosomes particle swarm optimization-based coverage path planning for complex surfaces spray painting. Int. J. Adv. Robot. Syst. 2024, 21, 17298806241238980. [Google Scholar] [CrossRef]
- Menon, B.K.; Deshpande, T.; Pal, A.; Kothandaraman, S. Critical regions identification and coverage using optimal drone flight path planning for precision agriculture. Results Eng. 2025, 25, 104081. [Google Scholar] [CrossRef]
- Mansur, H.; Gadhwal, M.; Abon, J.E.; Flippo, D. Mapping for Autonomous Navigation of Agricultural Robots through Crop Rows Using UAV. Agriculture 2025, 15, 882. [Google Scholar] [CrossRef]
- Monteiro, A.; von Wangenheim, A. Orthomosaic Dataset of RGB Aerial Images for Weed Mapping. 2019. Available online: https://lapix.ufsc.br/weed-mapping-sugar-cane/ (accessed on 7 June 2025).
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Yao, C.; Lv, D.; Li, H.; Fu, J.; Li, C.; Gao, X.; Hong, D. A real-time crop lodging recognition method for combine harvesters based on machine vision and modified DeepLab V3+. Smart Agric. Technol. 2025, 11, 100926. [Google Scholar] [CrossRef]
- Chai, T.; Xiao, Z.; Shen, X.; Liu, Q.; Li, N.; Guan, T.; Tian, J. TransDeep: Transformer-integrated DeepLabV3+ for image semantic segmentation. IEEE Access 2025, 13, 6277–6291. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of 15th European Conference, Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Choset, H.; Pignon, P. Coverage Path Planning: The Boustrophedon Cellular Decomposition. In Field and Service Robotics; Zelinsky, A., Ed.; Springer: London, UK, 1998; pp. 203–209. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Ottoni, A.L.; Nepomuceno, E.G.; Oliveira, M.S.d.; Oliveira, D.C.d. Reinforcement learning for the traveling salesman problem with refueling. Complex Intell. Syst. 2022, 8, 2001–2015. [Google Scholar] [CrossRef]
- Levy, D.; Sundar, K.; Rathinam, S. Heuristics for routing heterogeneous unmanned vehicles with fuel constraints. Math. Probl. Eng. 2014, 2014, 131450. [Google Scholar] [CrossRef]
- Zhang, T.J.; Yang, Y.K.; Wang, B.H.; Li, Z.; Shen, H.X.; Li, H.N. Optimal scheduling for location geosynchronous satellites refueling problem. Acta Astronaut. 2019, 163, 264–271. [Google Scholar] [CrossRef]
- Suzuki, Y. A dual-objective metaheuristic approach to solve practical pollution routing problem. Int. J. Prod. Econ. 2016, 176, 143–153. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A. The pollution traveling salesman problem with refueling. Comput. Oper. Res. 2024, 167, 106661. [Google Scholar] [CrossRef]
- Marinello, F.; Pezzuolo, A.; Chiumenti, A.; Sartori, L. Technical analysis of unmanned aerial vehicles (drones) for agricultural applications. Eng. Rural. Dev. 2016, 15, 870–875. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).