Spatial–Temporal Variability of Soybean Yield Using Separable Covariance Structure
Abstract
1. Introduction
2. Materials and Methods
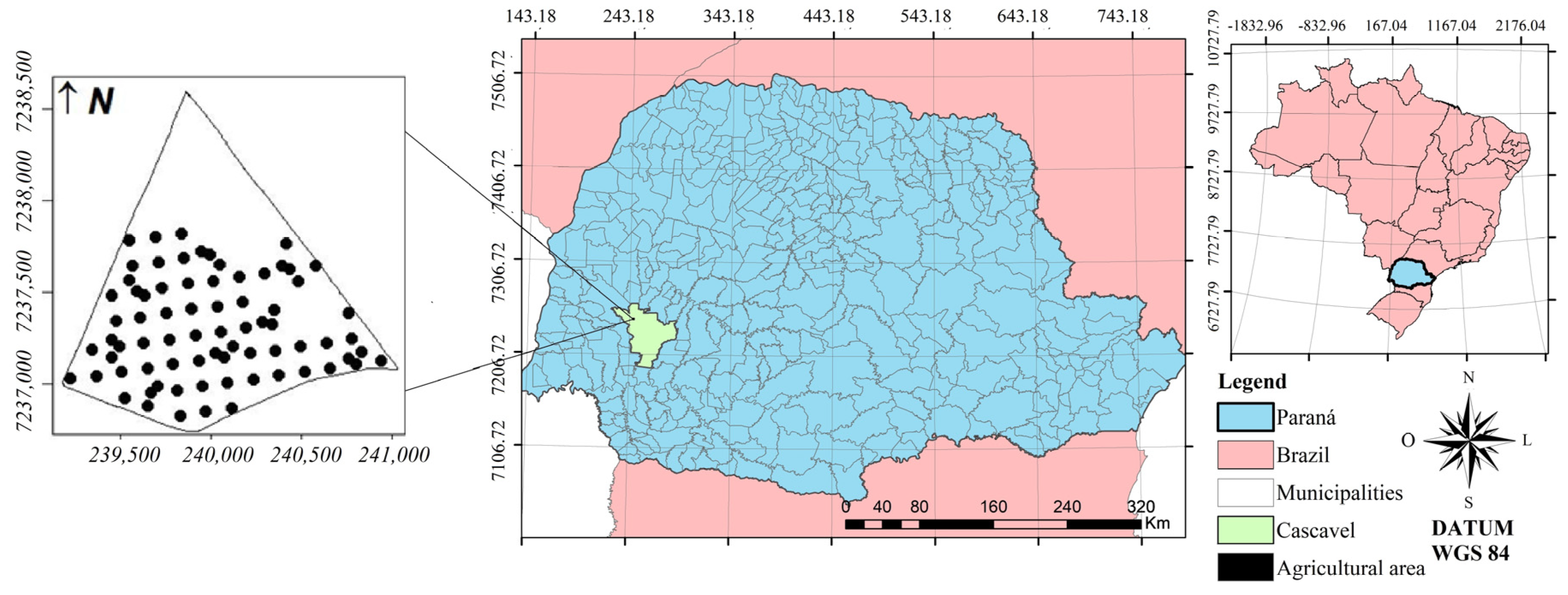
2.1. Description of Agricultural Area
2.2. Methodology: Spatiotemporal Analysis
2.3. Gaussian Linear Spatial Model with Multiple Independent Repetitions
2.4. Linear Spatiotemporal Model
2.5. Spatiotemporal Covariance Models with Separable Covariance Structure
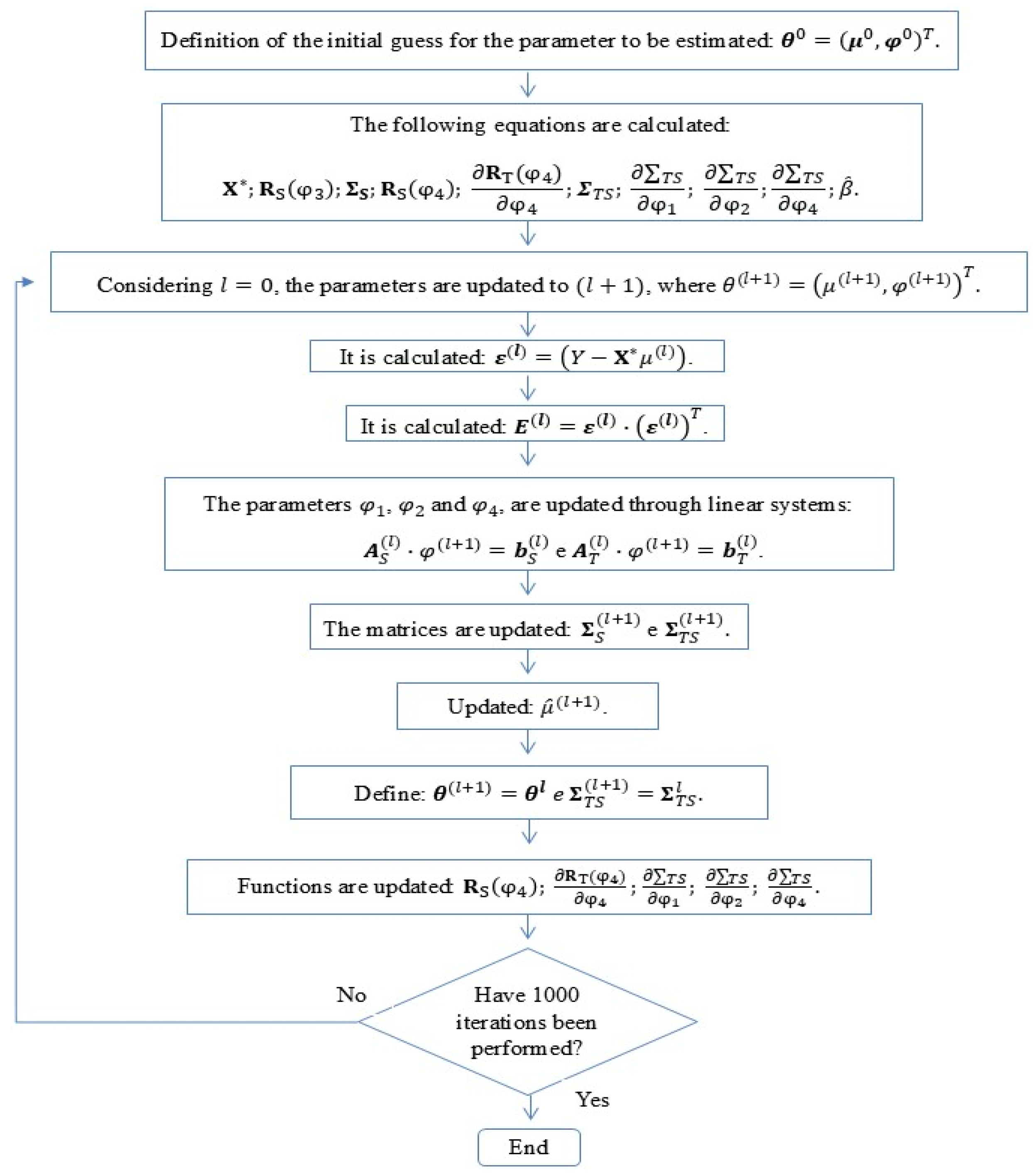
2.6. Estimation Methods
2.6.1. Identifiability of the Model
2.6.2. The Estimation of Parameters by Maximum Likelihood for the Separable Model
2.6.3. Asymptotic Standard Errors
2.6.4. Model Validation Criteria
2.6.5. Comparison of Thematic Maps
3. Results
3.1. Descriptive Analysis of Soybean Yields
3.2. Spatio Temporal Analyses
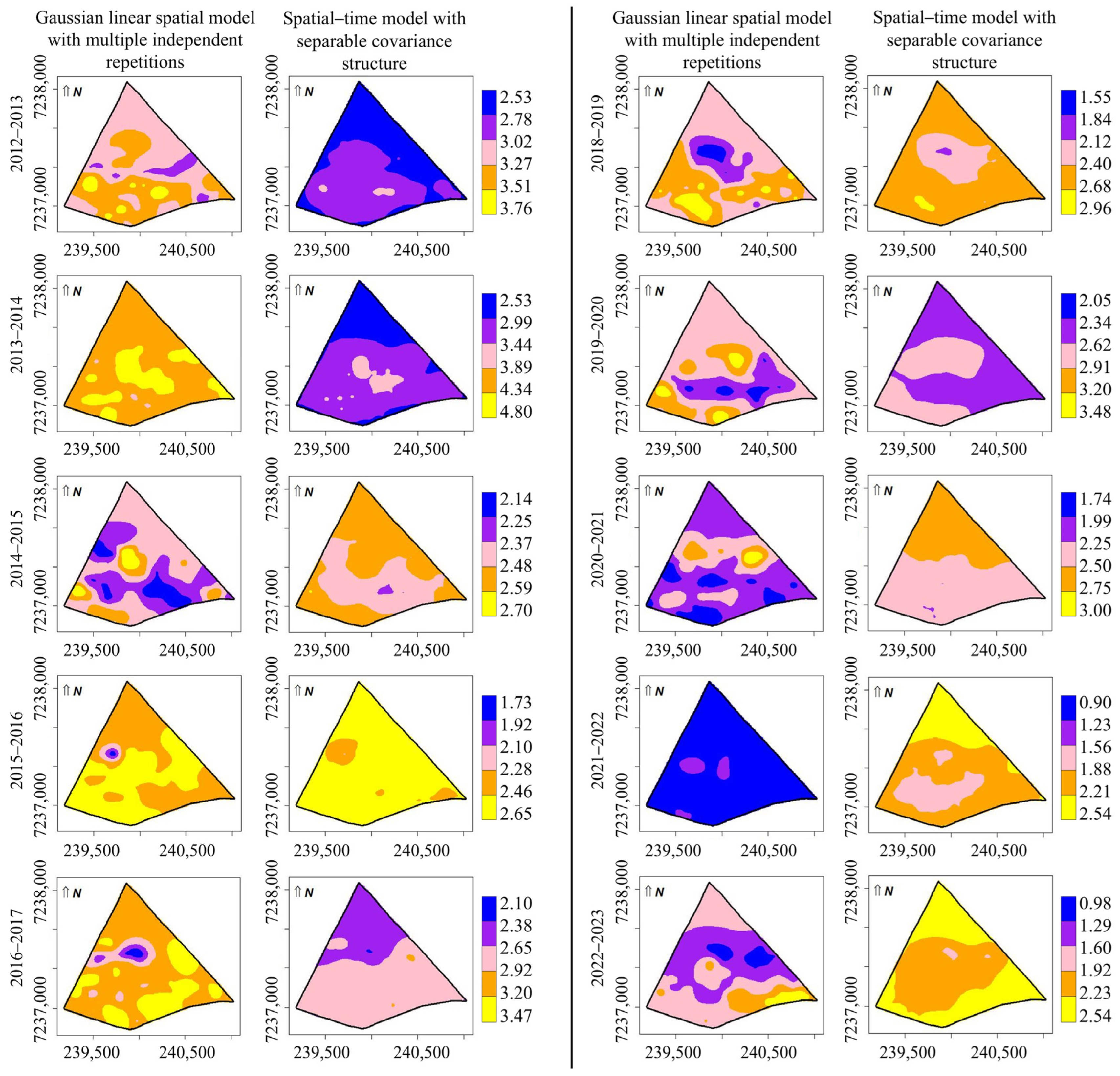
3.3. Gaussian Linear Spatial Model Analysis with Multiple Independent Repetitions (, Considering and
3.4. Model with Separable Covariance Structure (, Considering and
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PA | precision agriculture |
| LEE | Space Statistics Laboratory |
| LEA | Applied Statistics Laboratory |
| UTM | Universal Transverse Mercator |
| GA | Global Accuracy |
| Kp | Kappa |
| Kpw | weighted Kappa |
| CV | Coefficient of variation |
| rp | Pearson’s linear correlation coefficient |
References
- Lima, V.A.; Dos Santos, I.C. Atividades de inovação em agricultura de precisão no Brasil e o longo caminho para o ODS 2. Rev. Electrónica Mens. 2019, 3, 1–15. [Google Scholar]
- Barbosa, D.P.; Bottega, E.L.; Valente, D.S.M.; Santos, N.T.; Guimarães, W.D.; Ferreira, M.D.P. Influence geometric anisotropy in management zones delineation. Rev. Ciênc. Agron. 2019, 50, 543–551. [Google Scholar]
- Noetzold, R.; Da Silva, L.M.; Schoninger, E.L.; Tomé, P.C.D.T.; Alves, M.C. Variabilidade espacial e temporal de atributos químicos do solo durante cinco safras. Rev. Bras. Geom. 2018, 6, 328–345. [Google Scholar] [CrossRef]
- Ortega, R.A.; Santibanez, O.A. Determination of management zones in corn (Zea mays L.) based on soil fertility. Comput. Electron. Agric. 2007, 58, 49–59. [Google Scholar] [CrossRef]
- Cressie, N. Comment on “an approach to statistical spatial-temporal modeling of meteorological fields” by m. s. handcock and j. r. wallis. J. Am. Stat. Assoc. 1994, 89, 379–382. [Google Scholar]
- Goodall, C.; Mardia, K.V. Challenges in multivariate spatio-temporal modeling. In Proceedings of the XVII-th International Biometric Conference, Hamilton, ON, Canada, 8–12 August 1994; Volume 39, pp. 1–17. [Google Scholar]
- Cressie, N.; Shi, T.; Kang, E.L. Fixed rank filtering for spatio-temporal data. J. Comput. Graph. Stat. 2010, 19, 724–745. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; John Wiley & Sons: Hoboken, NJ, USA, 2011; p. 585. [Google Scholar]
- De Bastiani, F.; Galea, M.; Cysneiros, A.H.M.A.; Uribe-Opazo, M.A. Gaussian spatial linear models with repetitions: An application to soybean productivity. Spat. Stat. 2017, 21, 319–335. [Google Scholar] [CrossRef]
- Zhuo, Z.; Xing, A.; Li, Y.; Huang, Y.; Nie, C. Spatio-temporal variability and the factors influencing soil-available heavy metal micronutrients in different agricultural sub-catchments. Sustainability 2019, 11, 5912. [Google Scholar]
- Yang, H.; Song, X.; Zhao, Y.; Wang, W.; Cheng, Z.; Zhang, Q.; Cheng, D. Temporal and spatial variations of soil C, N contents and C: N stoichiometry in the major grain-producing region of the North China Plain. PLoS ONE 2021, 16, e0253160. [Google Scholar]
- Saavedra-Nievas, J.C.; Nicolis, O.; Galea, M.; Ibacache-Pulgar, G. Influence diagnostics in gaussian spatial–temporal linear models with separable covariance. Environ. Ecol. Stat. 2023, 30, 131–155. [Google Scholar]
- Santos, H.G.; Jacomine, P.T.; Anjos, L.H.C.; Oliveira, V.A.; Lumbreras, J.F.; Coelho, M.R.; Araujo Filho, J.O.; Oliveira, J.B.; Cunha, T.J.F. Brazilian Soil Classification System, 5th ed.; Embrapa: Brasília, Brazil, 2018. [Google Scholar]
- Aparecido, L.; Rolim, G.S.; Richetti, J.; Souza, P.S.; Johann, J.A. Köppen, Thornthwaite and Camargo climate classifications for climatic zoning in the State of Paraná, Brazil. Ciênc Agrotecnologia 2016, 40, 405–417. [Google Scholar] [CrossRef]
- Chipeta, M.G.; Terlouw, D.J.; Phiri, K.S.; Diggle, P.J. Inhibitory geostatistical designs for spatial prediction taking account of uncertain covariance structure. Environmetrics 2017, 28, e2425. [Google Scholar] [CrossRef]
- Maltauro, T.C.; Guedes, L.P.C.; Uribe-Opazo, M.A.; Canton, L.E.D. Spatial multivariate optimization for a sampling redesign with a reduced sample size of soil chemical properties. Rev. Bras. Ciênc. Solo 2023, 47, e0220072. [Google Scholar] [CrossRef]
- Arruda, M.R.; Moreira, A.; Pereira, J.C.R. Amostragem e Cuidados na Coleta de Solo Para Fins de Fertilidade; Embrapa Amazônia Ocidental Manaus: Itacoatiara, Brazil, 2014. [Google Scholar]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Mardia, K.V.; Marshall, R.J. Maximum likelihood estimation of models for residual covariance in spatial regression. Biometrika 1984, 71, 135–146. [Google Scholar] [CrossRef]
- Uribe-Opazo, M.A.; Borssoi, J.A.; Galea, M. Influence diagnostics in Gaussian spatial linear models. J. Appl. Stat. 2012, 39, 615–630. [Google Scholar] [CrossRef]
- Uribe-Opazo, M.A.; Dalposso, G.H.; Galea, M.; Johann, J.A.; De Bastiani, F.; Moyano, E.N.C.; Grzegozewski, D.M. Spatial variability of wheat yield using the gaussian spatial linear model. Aust. J. Crop Sci. 2023, 17, 179–189. [Google Scholar] [CrossRef]
- De Bastiani, F.; Cysneiros, A.H.M.A.; Uribe-Opazo, M.A.; Galea, M. Influence diagnostics in elliptical spatial linear models. Sociedad de Estadística e Investigación Operativa. TEST 2015, 24, 322–340. [Google Scholar] [CrossRef]
- Silva, A.S.; Ribeiro Jr, P.J. Modelos gaussianos geoestatísticos espaço-temporais e aplicações. Rev. Mat. Estat. 2000, 20, 1–10. [Google Scholar]
- Finkenstadt, B.; Held, L.; Isham, V. Statistical Methods for Spatio-Temporal Systems, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2006; p. 286. [Google Scholar]
- Gneiting, T.; Genton, M.G.; Guttorp, P. Geostatistical space-time models, stationarity, separability, and full symmetry. Monogr. Stat. App. Probab. 2006, 107, 151. [Google Scholar]
- Matérn, B. Spatial Variation, 2nd ed.; Lecture Notes in Statistics; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Diggle, P.J.; Giorgi, E. Model-Based Geostatistics for Global Public Health: Methods and Applications, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2019; p. 274. [Google Scholar]
- Cappello, C.; De Iaco, S.; Posa, D. Testing the type of non-separability and some classes of space-time covariance function models. Stoch Environ. Res Risk. Assess 2018, 32, 17–35. [Google Scholar] [CrossRef]
- Uribe-Opazo, M.A.; De Bastiani, F.; Galea, M.; Schemmer, R.C.; Assumpção, R.A.B. Influence diagnostics on a reparameterized t-Student spatial linear model. Spat. Stat. 2021, 41, 100481. [Google Scholar] [CrossRef]
- Zhang, H. Inconsistent estimation and asymptotically equal interpolations in model-based geostatistics. J. Am. Stat. Assoc. 2004, 99, 250–261. [Google Scholar] [CrossRef]
- Zhang, H.; Zimmerman, D.L. Hybrid estimation of semivariogram parameters. Math. Geol. 2007, 39, 247–260. [Google Scholar] [CrossRef]
- Zhang, H.; El-Shaarawi, A. On spatial skew-gaussian processes and applications. Environmetrics 2010, 21, 33–47. [Google Scholar] [CrossRef]
- Stein, M.L. (Ed.) Interpolation of Spatial Data: Some Theory for Kriging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Lange, K.L.; Little, R.J.A.; Taylor, J.M.G. Robust statistical modeling using the t distribution. J Am Stat Assoc 1989, 84, 881–896. [Google Scholar] [CrossRef]
- Mitchell, A.F.S. The information matrix, skewness tensor and α-connections for the general multivariate elliptic distribution. Ann. Inst. Stat. Math. 1989, 41, 289–304. [Google Scholar] [CrossRef]
- Landim, P.M.B. Sobre Geoestatística e mapas. Terra E Didat. 2006, 2, 19–33. [Google Scholar] [CrossRef]
- Anderson, J.F.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; Government Print Office: Alexandria, VA, USA, 2001. [Google Scholar]
- Krippendorff, K. Content Analysis: An Introduction to Its Methodology, 2nd ed.; Sage Publications Ltd.: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 5 January 2024).
- CONAB—Companhia Nacional de Abastecimento. Séries Históricas: Soja Brasil—Safras 1976/1977 a 2024/2025. Available online: https://www.conab.gov.br/info-agro/safras/serie-historica-das-safras?start=30 (accessed on 5 January 2025).
- Dalposso, G.H.; Uribe-Opazo, M.A.; De Oliveira, M.P. Comparison between Matheron and Genton semivariance function estimators in spatial modeling of soybean yield. Aust. J. Crop Sci. 2022, 16, 916–921. [Google Scholar] [CrossRef]
- Gasparin, P.P.; da Silva, E.M.; Becker, W.R.; Paludo, A.; Guedes, L.P.C.; Johann, J.A. Agroclimatic and spectral regionalization for soybean in different agricultural settings in the state of Paraná, Brazil. J. Agric. Sci. 2024, 162, 291–306. [Google Scholar] [CrossRef]
- Pimentel-Gomes, F.; Garcia, C.H. Estatística Aplicada a Experimentos Agronômicos e Florestais; FEALQ: Piracicaba, Brazil, 2002. [Google Scholar]
- Callegari-Jacques, S.M. Bioestatística: Princípios e Aplicações; Artmed: Porto Alegre, Brasil, 2003. [Google Scholar]
- Wikle, C.K.; Zammit-Mangion, A.; Cressie, N. Spatio-Temporal Statistics with R; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2019; p. 380. [Google Scholar]

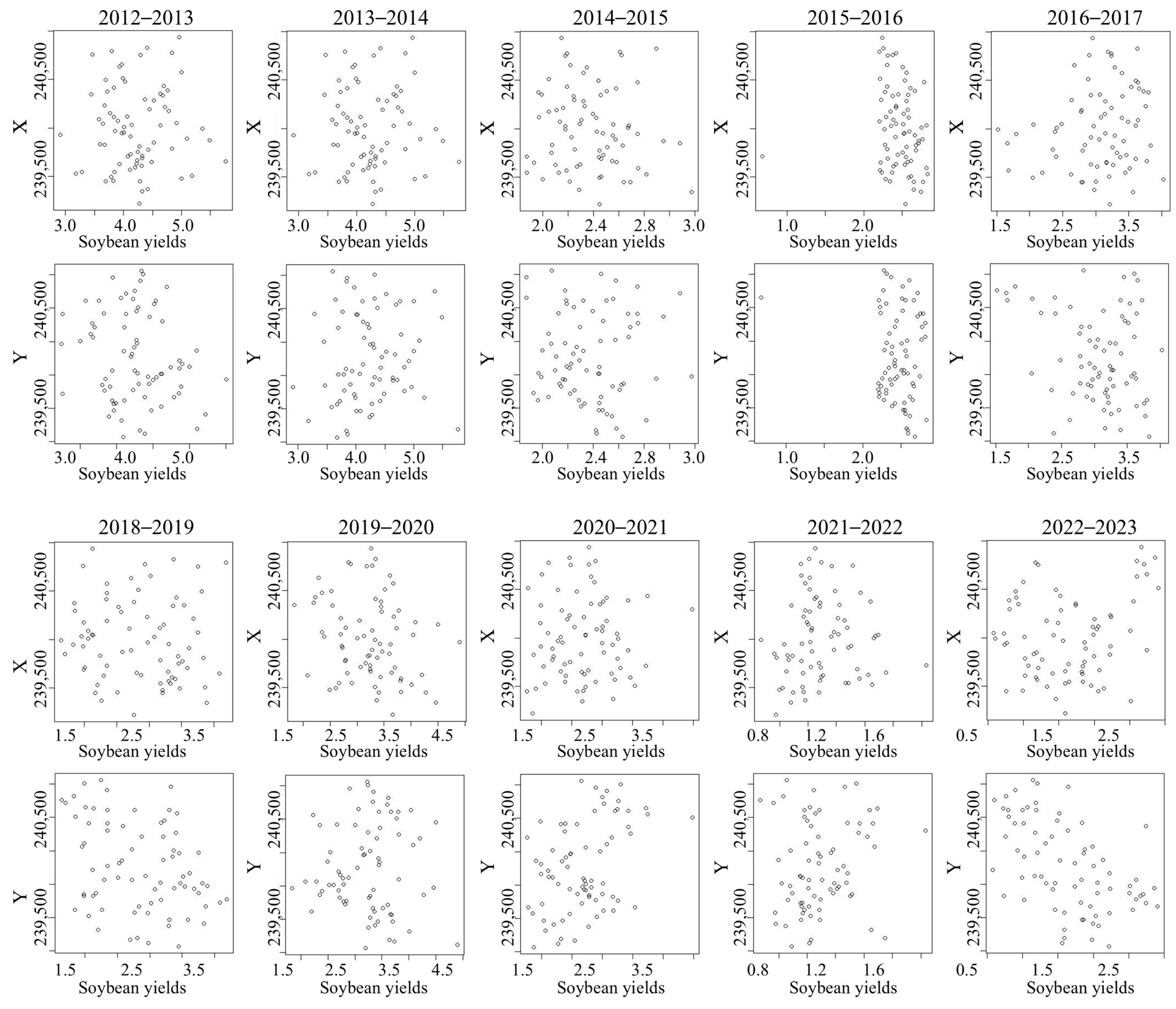
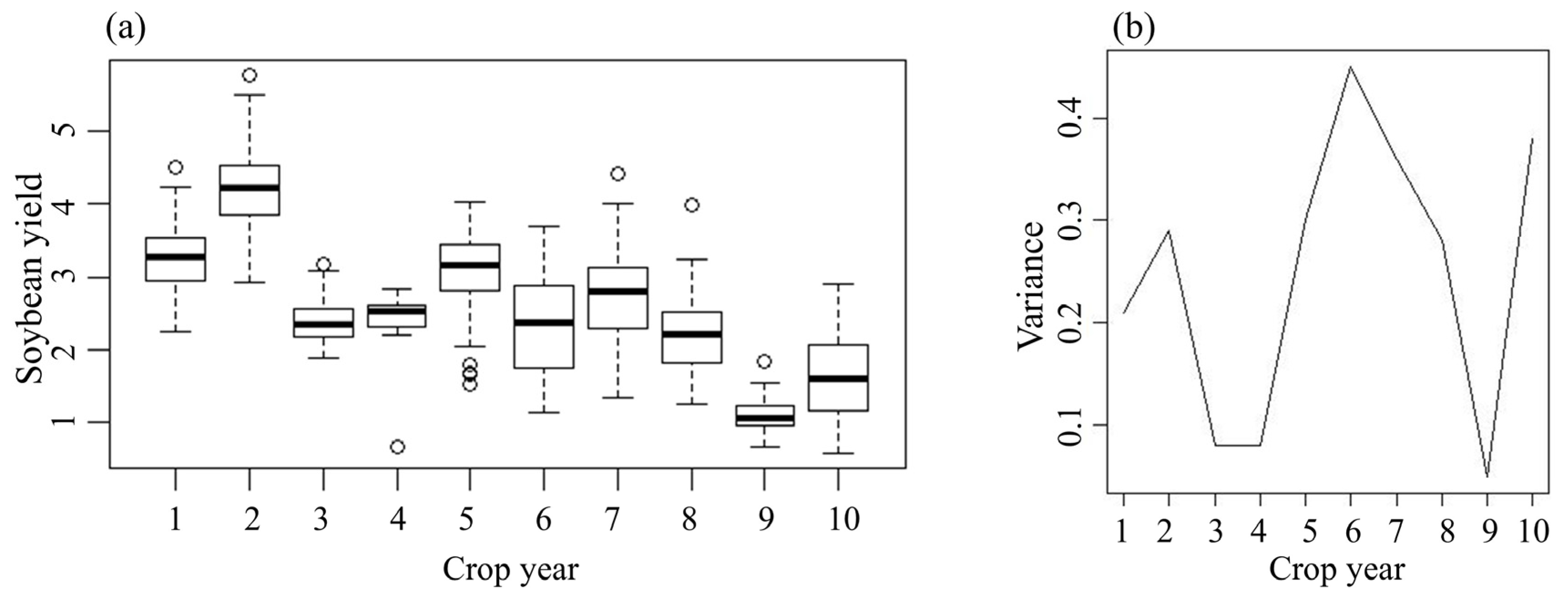
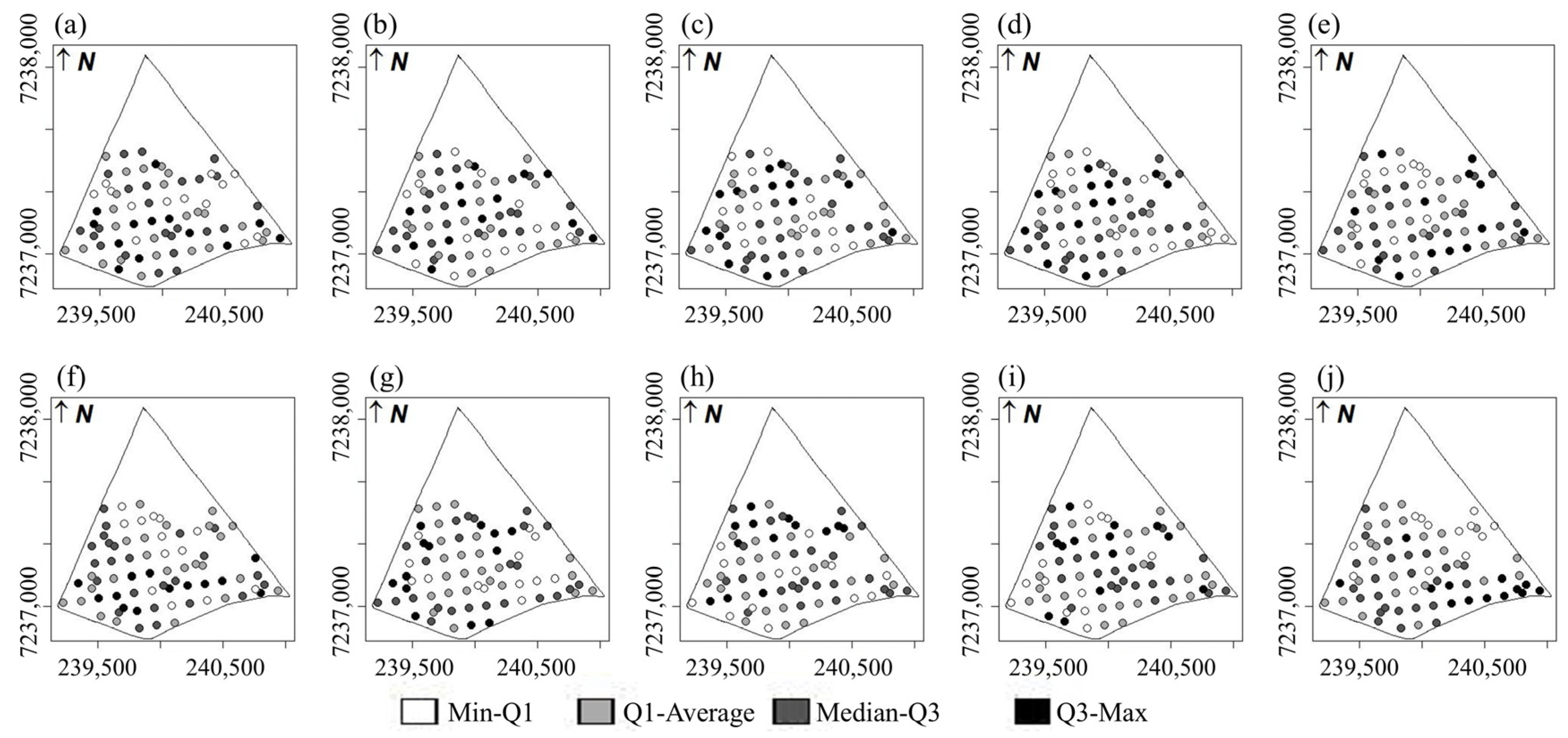
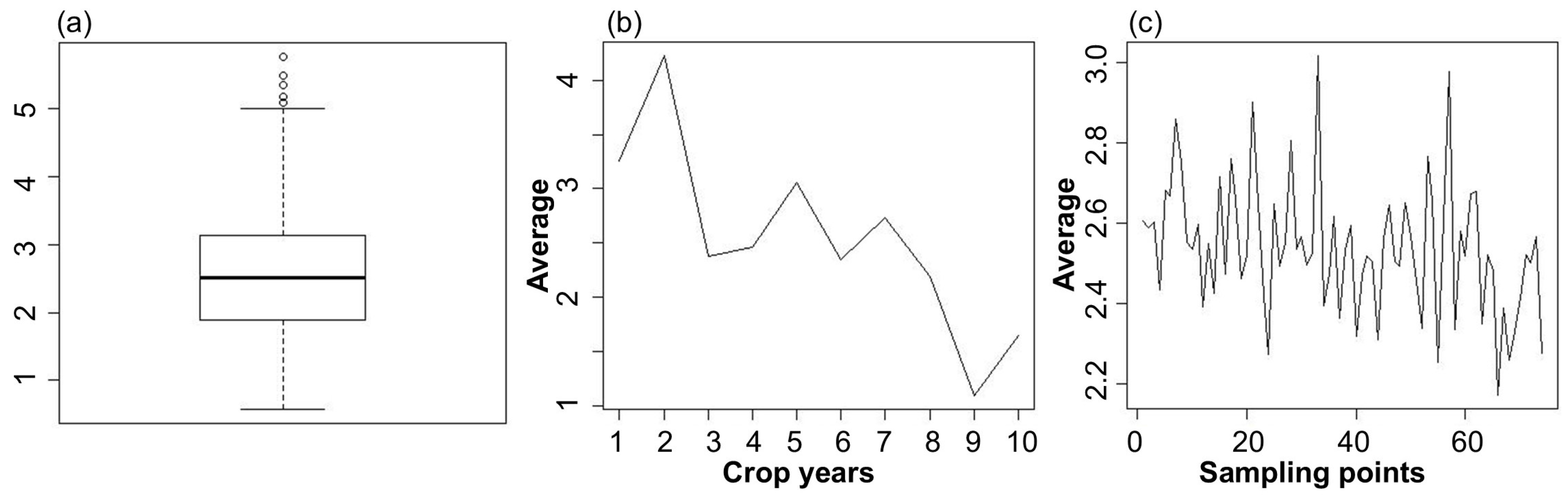
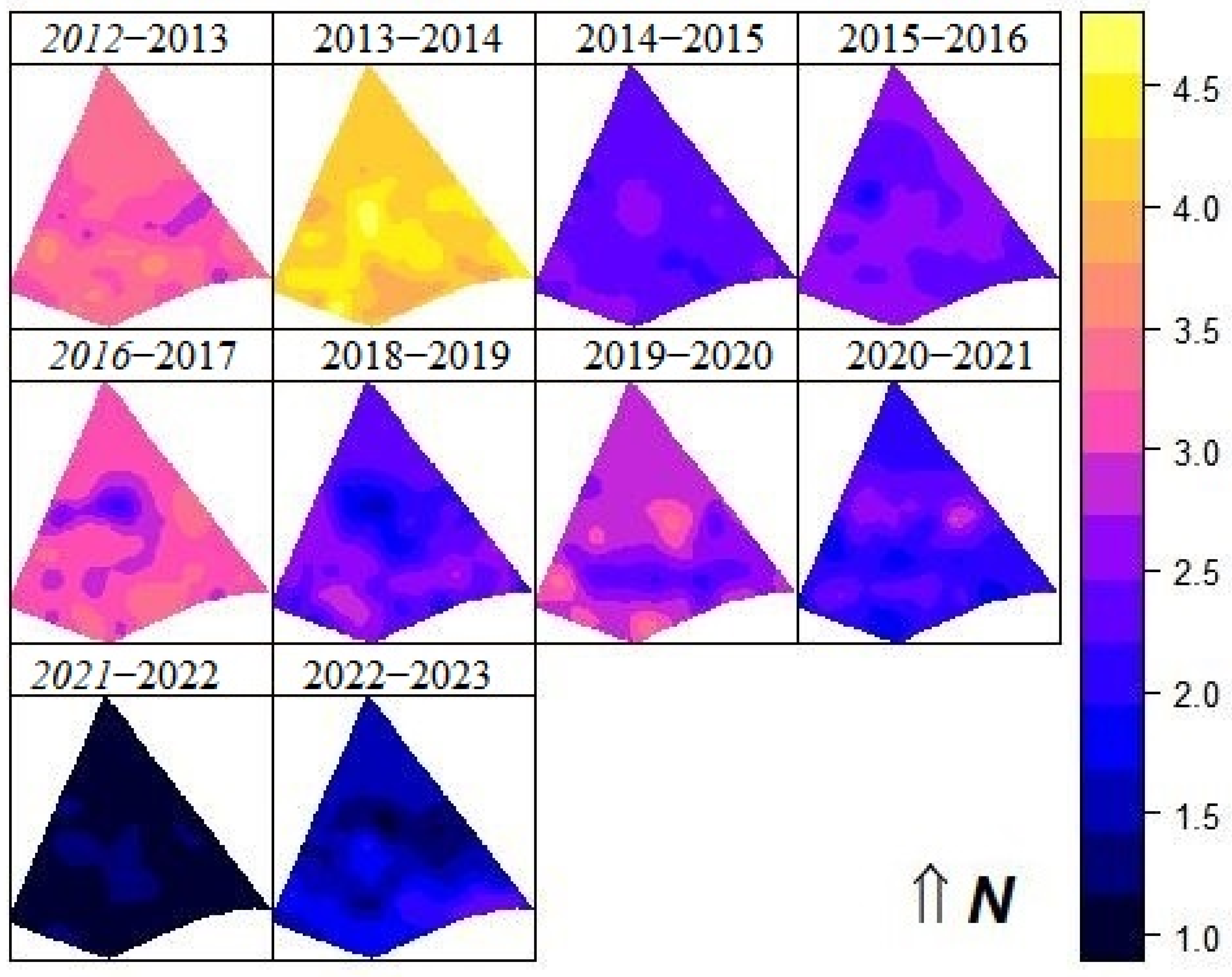
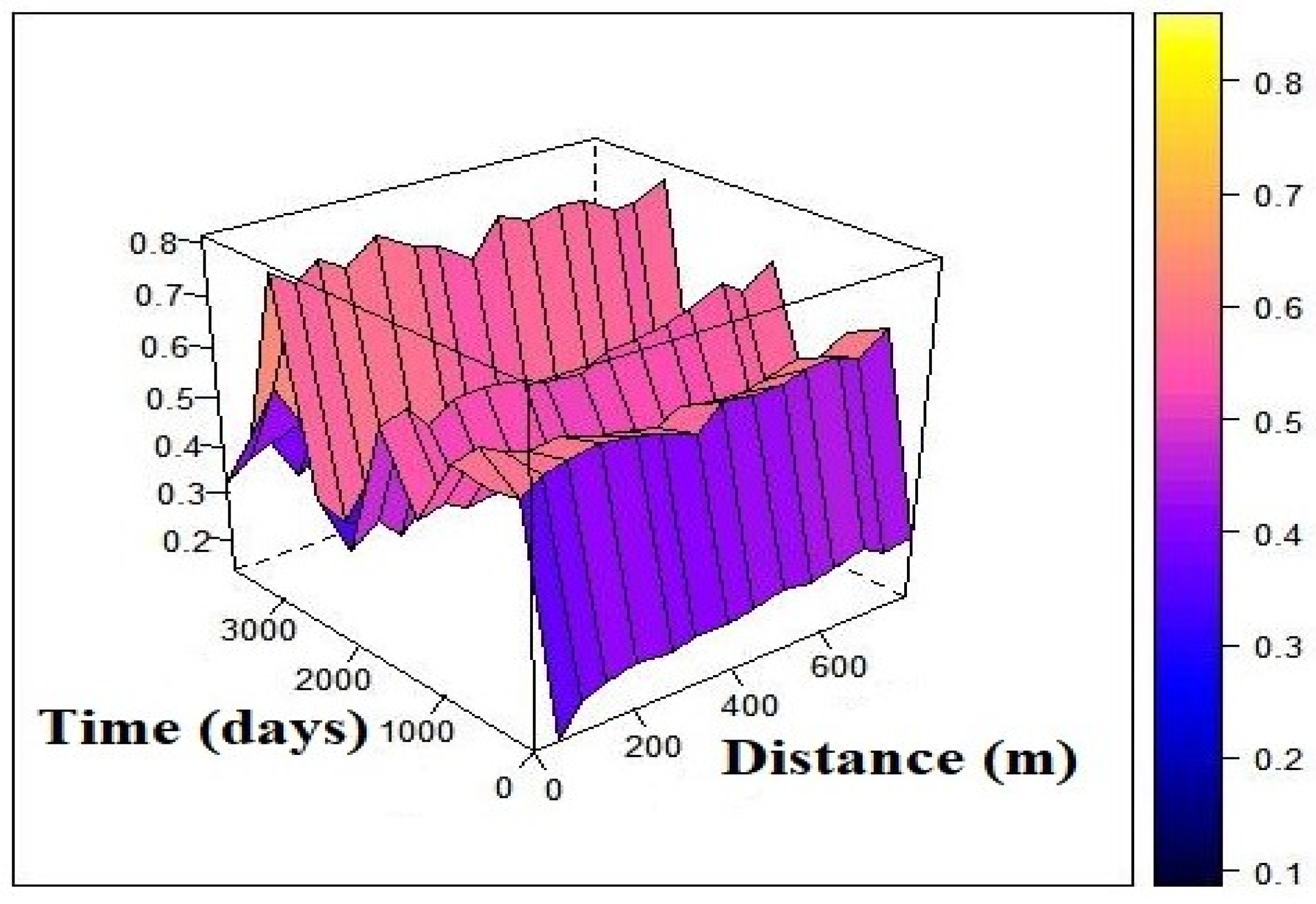
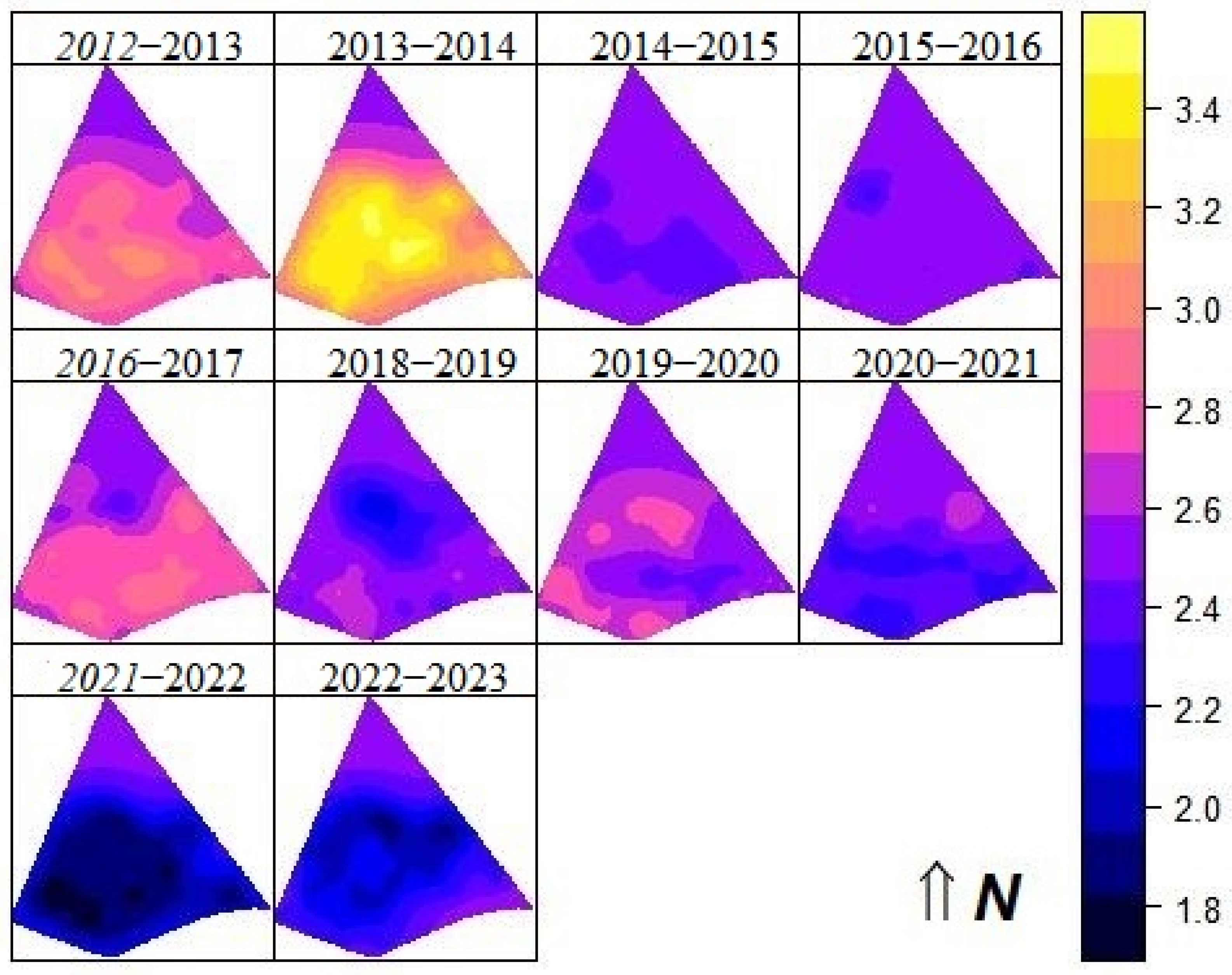
| Crop Year | Min. | Average | Max. | S.D | Var. | C.V (%) | Coef. X rp | Coef. Y rp | I Moran (p-Value) |
|---|---|---|---|---|---|---|---|---|---|
| 2012–2013 | 2.24 | 3.26 | 4.51 | 0.46 | 0.21 | 14.20 | −0.10 (0.37) | −0.19 (0.11) | 0.36 |
| 2013–2014 | 2.91 | 4.23 | 5.77 | 0.54 | 0.29 | 12.81 | 0.01 (0.90) | 0.09 (0.45) | 0.71 |
| 2014–2015 | 1.87 | 2.38 | 3.18 | 0.28 | 0.08 | 11.76 | −0.09 (0.43) | −0.02 (0.87) | 0.11 |
| 2015–2016 | 0.67 | 2.46 | 2.83 | 0.28 | 0.08 | 11.21 | −0.13 (0.26) | −0.15 (0.20) | 0.05 |
| 2016–2017 | 1.52 | 3.06 | 4.03 | 0.55 | 0.30 | 17.91 | 0.17 (0.16) | −0.26 (0.03 *) | 0.00 |
| 2018–2019 | 1.14 | 2.34 | 3.69 | 0.67 | 0.45 | 28.56 | −0.07 (0.55) | −0.30 (0.004 *) | 0.00 |
| 2019–2020 | 1.34 | 2.73 | 4.40 | 0.60 | 0.36 | 21.96 | −0.22 (0.06) | 0.01 (0.99) | 0.00 |
| 2020–2021 | 1.26 | 2.18 | 3.99 | 0.53 | 0.28 | 24.28 | 0.03 (0.77) | 0.41 (0.0003 *) | 0.00 |
| 2021–2022 | 0.67 | 1.09 | 1.83 | 0.22 | 0.05 | 19.79 | 0.06 (0.61) | 0.15 (0.20) | 0.02 |
| 2022–2023 | 0.58 | 1.65 | 2.91 | 0.62 | 0.38 | 37.60 | 0.22 (0.06) | −0.53 (0.000001 *) | 0.00 |
| Crop Year | 2012–2013 | 2013–2014 | 2014–2015 | 2015–2016 | 2016–2017 | 2018–2019 | 2019–2020 | 2020–2021 | 2021–2022 | 2022–2023 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2012–2013 | 1.00 | 0.29 | −0.16 | −0.12 | −0.05 | 0.19 | −0.08 | −0.15 | −0.07 | 0.09 |
| 2013–2014 | 0.29 | 1.00 | −0.07 | −0.04 | 0.00 | 0.01 | 0.01 | 0.14 | −0.13 | −0.02 |
| 2014–2015 | −0.16 | 0.07 | 1.00 | 0.59 | 0.02 | −0.07 | 0.38 | −0.05 | 0.06 | −0.01 |
| 2015–2016 | −0.12 | −0.04 | 0.59 | 1.00 | 0.17 | 0.04 | 0.17 | −0.26 | 0.12 | −0.05 |
| 2016–2017 | −0.05 | 0.00 | 0.02 | 0.17 | 1.00 | 0.28 | −0.20 | −0.13 | 0.15 | 0.39 |
| 2018–2019 | 0.19 | 0.01 | −0.07 | 0.04 | 0.28 | 1.00 | −0.17 | −0.25 | −0.12 | 0.30 |
| 2019–2020 | −0.08 | 0.01 | 0.38 | 0.17 | −0.20 | −0.17 | 1.00 | −0.05 | −0.08 | −0.08 |
| 2020–2021 | −0.15 | 0.14 | −0.05 | −0.26 | −0.13 | −0.25 | −0.05 | 1.00 | 0.03 | −0.25 |
| 2021–2022 | −0.07 | −0.13 | 0.06 | 0.12 | 0.15 | −0.12 | −0.08 | 0.03 | 1.00 | −0.07 |
| 2022–2023 | 0.09 | −0.02 | −0.01 | −0.05 | 0.39 | 0.30 | −0.08 | −0.25 | −0.07 | 1.00 |
| Statistics | nT | Min. | Average | Max. | S.D | Var. | C.V (%) | Coef. X (rp) | p-Value | Coef. Y (rp) | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall soybean yield | 740 | 0.58 | 2.54 | 5.77 | 0.96 | 0.92 | 37.83 | −0.01 NS | 0.94 | −0.05 NS | 0.14 |
| 2.5357 (0.0343) | 0.3142 (0.2405) | 0.2526 (0.2439) | 74.5948 (52.8771) | 298.2691 |
| 2.5310 (0.0607) | 0.5088 (0.4445) | 0.0048 (0.0005) | 0.4924 (0.0529) |
| RMSE | 2012–2013 | 2013–2014 | 2014–2015 | 2015–2016 | 2016–2017 | 2018–2019 | 2019–2020 | 2020–2021 | 2021–2022 | 2022–2023 |
| 0.5590 | 1.0427 | 0.2494 | 0.2353 | 0.5366 | 0.5621 | 0.2574 | 0.2329 | 0.8359 | 0.6877 |
| Crop Years/Index | GA | Kp | Kpw |
|---|---|---|---|
| 2012–2013 | 0.0131 | −0.0299 | 0.0880 |
| 2013–2014 | 0.0000 | −0.0006 | 0.0290 |
| 2014–2015 | 0.1702 | −0.1043 | 0.3238 |
| 2015–2016 | 0.5180 | 0.1087 | 0.2571 |
| 2016–2017 | 0.0639 | −0.0124 | 0.1453 |
| 2018–2019 | 0.4001 | 0.0798 | 0.4499 |
| 2019–2020 | 0.3981 | 0.0886 | 0.4230 |
| 2020–2021 | 0.1471 | −0.0208 | 0.1694 |
| 2021–2022 | 0.0000 | −0.2500 | 0.0006 |
| 2022–2023 | 0.0350 | −0.0301 | 0.1061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maltauro, T.C.; Uribe-Opazo, M.A.; Guedes, L.P.C.; Galea, M.; Nicolis, O. Spatial–Temporal Variability of Soybean Yield Using Separable Covariance Structure. Agriculture 2025, 15, 1199. https://doi.org/10.3390/agriculture15111199
Maltauro TC, Uribe-Opazo MA, Guedes LPC, Galea M, Nicolis O. Spatial–Temporal Variability of Soybean Yield Using Separable Covariance Structure. Agriculture. 2025; 15(11):1199. https://doi.org/10.3390/agriculture15111199
Chicago/Turabian StyleMaltauro, Tamara Cantú, Miguel Angel Uribe-Opazo, Luciana Pagliosa Carvalho Guedes, Manuel Galea, and Orietta Nicolis. 2025. "Spatial–Temporal Variability of Soybean Yield Using Separable Covariance Structure" Agriculture 15, no. 11: 1199. https://doi.org/10.3390/agriculture15111199
APA StyleMaltauro, T. C., Uribe-Opazo, M. A., Guedes, L. P. C., Galea, M., & Nicolis, O. (2025). Spatial–Temporal Variability of Soybean Yield Using Separable Covariance Structure. Agriculture, 15(11), 1199. https://doi.org/10.3390/agriculture15111199







