Abstract
To address the challenge of accurate apple harvesting by orchard robots, which is hindered by dynamic changes in apple position due to wind interference and branch swaying, this study proposes an optimized prediction algorithm based on an integration of the extended Kalman filter (EKF) and an improved particle filter (IPF), built upon initial apple detection and recognition using YOLOv8. The algorithm first employs spatial partitioning according to the cyclical motion patterns of apples to constrain the prediction results. Subsequently, it optimizes the rationality of particle weights within the particle filter (PF) and reduces its computational resource consumption by implementing historical position weighting and an adaptive particle number strategy. Finally, an adaptive error correction mechanism dynamically adjusts the respective weights of the EKF and IPF components, continuously enhancing the algorithm’s prediction accuracy. Experimental results demonstrate that, compared to the classic unscented Kalman filter (UKF) and unscented particle filter (UPF), the proposed EK-IPF algorithm reduces the mean absolute error (MAE) by 22.25% and 10.89%, respectively, and the root mean square error (RMSE) by 23.70% and 13.25%, respectively, indicating a significant improvement in overall prediction accuracy. This research provides technical support for dynamic apple trajectory prediction in orchard environments.
1. Introduction
Against the backdrop of advancing agricultural intelligence globally, fruit harvesting robots have emerged as a critical solution to mitigate labor shortages [1]. Conventional harvesting robots predominantly rely on static visual localization techniques. However, under disturbances from natural wind fields, fruits such as apples exhibit nonlinear, stochastic motion characteristics. This leads to positioning deviations by the robotic arm due to system latency, consequently impacting the harvesting success rate. Consequently, achieving real-time trajectory prediction for dynamically moving fruits has become a central challenge in enhancing the environmental adaptability of harvesting robots [2,3,4,5].
When addressing the problem of predicting the trajectory of moving fruits, mainstream approaches are generally categorized into two types: deep learning-based prediction and filter-based prediction [6]. Although deep learning demonstrates excellent performance in numerous time-series prediction tasks, its application to predicting the motion trajectories of objects like apples, characterized by small amplitudes and significant stochasticity, requires extensive trajectory data for training. This requirement is not only costly but also results in poor generalization capabilities across different scenarios [7,8]. Therefore, for the specific task of predicting apple motion trajectories, this study opted for filter-based prediction methods.
The Kalman filter (KF), as a classic recursive filter, is widely used for estimating the motion states of targets [9,10,11]. For example, Guo D’s team achieved rapid localization and tracking of multiple target vehicles by combining the Deepsort tracking network with the Kalman filter [12]. Wang’s team proposed a method for predicting fruit positions by leveraging the speed of adjacent fruits using the Kalman filter [13]. Liu’s team employed a fully convolutional network (FCN) to segment each frame into fruit and non-fruit pixels and predicted the new position of the target bounding box in the next frame using a Kanade–Lucas–Tomasi (KLT) tracker corrected by the Kalman filter [14].
However, the methods of Guo D’s team and Liu’s team rely on deep neural networks, where prediction accuracy is heavily influenced by the pre-trained models. Wang’s team’s prediction is limited to scenarios with slight oscillations and struggles to accurately forecast random nonlinear motion. Traditional Kalman filters assume a linear system model, which restricts their effectiveness in predicting nonlinear fruit motion [15].
To address nonlinear dynamics, several advanced filtering techniques have been developed. The extended Kalman filter (EKF) was introduced for state estimation in nonlinear systems [16,17,18], with applications ranging from space robotics to agricultural automation. For example, Zhang et al. utilized a continuous-discrete EKF for experiments involving a space robot grasping unknown moving objects [19]. However, the EKF algorithm still suffers from issues such as Taylor expansion truncation errors and sensitivity to the initial state [20,21,22]. In the agricultural domain, Prakash et al. demonstrated that conventional filtering approaches, including standard Kalman filters, perform poorly when handling nonlinear fruit motion under field conditions [23]. Their robust visual servoing system for cucumber harvesting revealed that motion blur from wind-induced fruit movement significantly degrades detection accuracy.
Similarly, the unscented Kalman filter (UKF) represents another approach to nonlinear state estimation that avoids the linearization issues of EKF. Research teams have applied UKF to diverse prediction tasks including drone flight trajectories [24], 3D ball trajectory prediction [25], and dynamic servo grasping [26]. While UKF shows improvements over EKF in certain scenarios, it still faces challenges with highly nonlinear and stochastic movements.
The particle filter (PF) offers a fundamentally different approach for nonlinear system prediction by simulating the posterior probability distribution using a set of particles [27]. For instance, Gong et al. employed an accelerated geometric particle filter based on color images for robotic arm tracking of randomly moving objects [28]. Tao et al. proposed a geometric particle filter robot dynamic grasping method using the affine group as state particles [29]. While these methods demonstrate PF’s flexibility in handling complex nonlinear dynamics, they also reveal the drawbacks of traditional PF, including irrational weight distribution and high computational complexity [30]. Several researchers have attempted to optimize particle filters for various tracking applications. In particle filtering for visual tracking, Zhao et al. [31] introduced a remarkable local resampling (RLR) strategy that uses double thresholds (weight and distance) to extract high-confidence local particles, effectively filtering out noise while requiring fewer particles. Their approach identified two key particle groups: those with maximum weight plus nearby high-weighted particles, and optimal local particles that assist tracking during occlusions. Complementarily, Li et al. [32] proposed a dynamic particle filter (DPF) framework that adaptively controls particle numbers based on scenario complexity, using context regressors with few particles for general scenarios and switching to target classifiers with many particles for challenging situations like occlusion and out-of-view events. Their particle number decision measure (PNDM) automatically determines when to switch between these approaches. However, these optimizations have not been specifically adapted to the unique challenges of predicting wind-induced oscillatory motion of hanging fruits in agricultural contexts, where specialized mechanisms for handling the periodic yet stochastic nature of fruit movements on branches are required.
Spatial constraints and partitioning techniques have demonstrated significant value in enhancing filtering performance across various tracking applications. Recent research has explored different approaches to incorporate spatial information into tracking algorithms. For example, Yılmaz and Bayram [33] proposed a particle filter-based method wherein particle weights are updated using a logistic function based on measurement wedges and particle positions, showing excellent performance in aerial tracking of moving targets. They integrated a bounded measurement model with particle filtering and combined it with a doubling strategy to determine subsequent measurement locations, thereby avoiding an arbitrarily large number of measurements. Similarly, Kumar and Mondal [34] noted in their review that incorporating various constraints and spatial information can significantly improve tracking performance, particularly in complex environments. They analyzed the performance of various recursive filtering methods, such as EKF, UKF, and PF under bounded constraint conditions. However, these approaches have not been specifically adapted to tracking objects exhibiting pendulum-like motions within physically constrained spaces, such as fruits on branches experiencing wind-induced oscillations.
Among the various filtering algorithms, this study opts to combine the EKF and PF algorithms. Compared to the UKF and UPF algorithms, the EKF linearizes the nonlinear system using Jacobian matrices. While ensuring nonlinear prediction capability, it offers lower computational complexity, better aligning with the high real-time requirements of agricultural scenarios. Furthermore, EKF and PF possess complementary strengths: EKF maintains high accuracy when dealing with mild nonlinearities, whereas PF excels at handling strong nonlinearities. Their combination is well-suited for predicting the motion of apples under wind disturbance.
Hybrid filtering techniques that combine complementary strengths of different filtering methods have shown promising results across various domains. Badar et al. proposed a Rao–Blackwellized particle filter using a noise-adaptive Kalman filter for fully mixing state-space models, which effectively handles unknown time-varying measurement variances by embedding a variational Bayesian adaptive Kalman filter within a particle filtering framework [35]. Their Monte Carlo variational Bayesian (MCVB) filter demonstrated improved numerical stability and performance in mobile robot tracking experiments. For wireless sensor networks, Peng et al. developed an improved snake optimization-based extended Kalman filter (ISO-EKF) that dynamically adjusts filter parameters in real time to adapt to the current motion state of mobile targets [36]. Their approach significantly reduced position root mean square error by 52% and 41% compared to standard optimization-EKF and EKF algorithms, respectively. In maritime applications, Yuan et al. employed an extended Kalman particle filter (EKPF) algorithm for parameter identification in vessel rudder permanent magnet synchronous motors [37]. By integrating an EKF with particle filtering, they addressed particle degeneracy issues while maintaining computational efficiency, demonstrating robust parameter identification under various operating conditions including sudden changes in resistance and inductance. These hybrid approaches highlight the effectiveness of combining filtering techniques for complex nonlinear systems, though they have not been specifically optimized for predicting the oscillatory motion patterns of fruits under wind disturbance in agricultural settings. Our proposed EK-IPF approach builds upon these foundations by introducing specialized mechanisms designed specifically for apple trajectory prediction in orchard environments.
Based on this analysis of existing approaches and their limitations, this paper proposes an optimized prediction algorithm integrating the extended Kalman filter and an improved particle filter (EK-IPF) for dynamic trajectory prediction. Unlike previous approaches that merely combine existing filtering algorithms, the present work makes several novel contributions: (1) a spatial partitioning method specifically designed for the periodic motion characteristics of apples under wind disturbance, which constrains prediction results to physically plausible regions; (2) a historical position weighting mechanism that learns from past trajectory patterns to optimize particle distribution, particularly enhancing prediction during direction changes; (3) an adaptive particle number strategy that dynamically balances computational efficiency and prediction accuracy; and (4) an adaptive error correction mechanism that continuously optimizes the fusion weights between EKF and IPF based on real-time performance. This comprehensive approach is specifically designed to address the unique challenges of apple trajectory prediction in orchard environments, demonstrating significant improvements over traditional filter-based prediction methods.
2. Materials and Methods
2.1. Data Collection
The research content of this paper focuses on predicting the dynamic trajectory of apples under wind influence in an orchard environment. A RealSense D415 depth camera was used to capture the movement trajectory data of apples swaying in the wind, with a resolution of 640 × 480 pixels and a shooting distance of 1 m. To avoid confusion caused by overlapping apples during coordinate detection, the identified objects were limited to single apples on individual branches.
The data collection was conducted in an apple orchard in Zhengzhou, Henan Province, China, from August to October 2024 during the apple ripening period. Data were collected under various wind conditions (light breeze, moderate wind, and strong wind) to ensure comprehensive coverage of possible motion patterns. A total of 100 sets of complete apple motion trajectories were recorded, with each set containing continuous motion data for at least 10 s. The sampling frequency was set at 5 Hz (one position record every 0.2 s) to ensure that critical position changes were not missed during rapid movements.
First, the YOLOv8 detection algorithm was employed to identify the target apple. Subsequently, the camera was used to obtain the planar XY coordinates of the apple relative to the camera lens, along with the Z-coordinate data derived from depth information, as illustrated in Figure 1. Leveraging the ROS topic publishing mechanism, the coordinate data for each frame were broadcast in real time via the “/XYZ” topic published by YOLO. A trajectory recording program was then initiated to subscribe to and receive the data from the “/XYZ” topic, automatically storing the trajectory data in an Excel spreadsheet format.

Figure 1.
Schematic diagram of deep information acquisition.
The hardware configuration of the experimental platform consists of an i7-9750H processor, an NVIDIA RTX 3050 graphics card (NVIDIA, Shenzhen, China), and 16 GB DDR4 memory (Lenovo, Shenzhen, China), while the software environment is based on the Ubuntu 20.04 LTS system and the ROS Noetic framework.
2.2. EK-IPF Optimized Prediction Algorithm
Figure 2 shows the flowchart of the EK-IPF algorithm. The EK-IPF algorithm first constrains the prediction results through spatial partitioning to make them more consistent with the true motion state of apples. Simultaneously, it incorporates a historical position weighting mechanism and an adaptive particle number mechanism to optimize particle distribution and enhance the rationality of particle weights. Additionally, the EK-IPF algorithm introduces an adaptive error correction mechanism, which dynamically adjusts the prediction weights of the extended Kalman filter and particle filter based on real-time state estimation errors. This algorithm aims to combine the strengths of both filtering prediction methods and improve the accuracy and robustness of predicting the nonlinear motion state of apples by introducing the aforementioned optimization mechanisms.
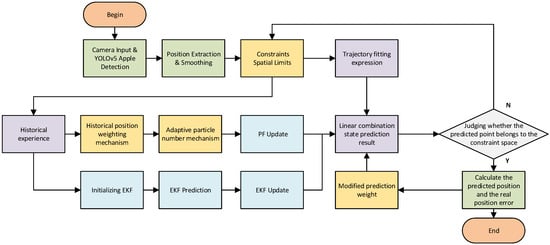
Figure 2.
Flowchart of the adaptive EKF-PF fusion algorithm for apple trajectory prediction. The algorithm combines extended Kalman filter (EKF) and particle filter (PF) with dynamic model selection to achieve accurate prediction of complex motion patterns.
2.2.1. Spatial Partitioning and Constraints
In orchard environments, the motion trajectories of apples disturbed by wind exhibit significant spatial locality characteristics. Their movement patterns can be decomposed into a composite motion of vertical oscillations and horizontal swings around an equilibrium position.
To better describe the motion characteristics of apples, this paper adopts a dynamic partitioning method to create two distinct subspaces—vertical subspace and horizontal subspace—corresponding to the up-down and left-right movements of apples, respectively. Figure 3 illustrates these subspaces, where spheres of the same color represent predicted points moving in the same direction. The yellow sphere denotes the equilibrium position, and the blue cylinder represents the constrained region for future predicted points. When a predicted point deviates from the blue cylinder’s restricted area, it indicates that the point does not align with the possible motion trajectory of an apple in the real environment. Therefore, such points are deemed unreliable and should be discarded to avoid interference with subsequent predictions.

Figure 3.
(a) Schematic of the vertical subspace, (b) Schematic of the horizontal subspace.
By employing the spatial partitioning and constraints method, the prediction accuracy of the filtering algorithm is improved through the construction of prioritized prediction regions. A constrained space is defined, with its calculation formula as
In the equation, represents the spatial constraint range, describing the distance from point to the equilibrium position of the apple’s motion; denotes the maximum allowable distance from the equilibrium position.
Based on the spatial coordinate data changes during the apple’s motion cycle, its swinging velocity and amplitude can be calculated, thereby constructing a subspace corresponding to the motion pattern. This subspace encompasses all historical positional coordinates of the apple’s swinging within the cycle.
Using the historically observed points farthest from both ends of the equilibrium position, linear extensions along these directions equivalent to the distance covered in 1 s of motion are added as an additional constraint space. This ensures potential motion trajectories are not overlooked.
The establishment of the constraint space is essential. Without constraints on predictions, abnormal observation points caused by factors such as camera shake or collisions during observation can introduce significant deviations in subsequent predictions, causing the results to persistently diverge from reality. By defining spatial range constraints for predicted points, outliers that markedly deviate from the object’s normal motion patterns can be effectively identified and automatically excluded. This approach not only prevents abnormal points from negatively impacting subsequent predictions but also enhances the accuracy and reliability of the forecasts.
2.2.2. Extended Kalman Filter
The extended Kalman filter (EKF) predicts the current state using a nonlinear state transition equation based on the system’s dynamic model and prior state estimates. Its calculation formula is as follows:
where is the state vector at the current time step; is the nonlinear state transition function; is the control input; and is the process noise.
The core of the EKF algorithm lies in performing a Taylor expansion around the current state estimate to achieve local linearization of the dynamic system. The algorithm constructs the Jacobian matrix by computing the first-order partial derivatives of the system and observation equations, thereby enabling continuous iterative optimization of state estimation in nonlinear environments.
However, the EKF algorithm has some significant drawbacks. First, it linearizes nonlinear functions through Taylor expansion, typically retaining only the first-order terms while neglecting higher-order terms. This approach can lead to substantial errors when the system exhibits strong nonlinearity. Second, the EKF algorithm is highly sensitive to the selection of initial state estimates and initial covariance matrices. Inaccurate initial values can directly affect the filter’s convergence speed and estimation accuracy.
2.3. Improved Particle Filtering
2.3.1. Particle Filter
Particle filter (PF) is a recursive state estimation method based on Bayesian theory, which approximates the posterior probability distribution using a set of particles. It is particularly suitable for state estimation in nonlinear dynamic systems. Compared to traditional filtering methods (such as Kalman filter and extended Kalman filter), PF demonstrates greater flexibility and adaptability when handling complex nonlinear systems.
However, the PF algorithm also has certain limitations. For instance, in practical applications, issues such as unreasonable weight distribution may arise, manifesting as chaotic particle weight allocation, low particle utilization, and a reduction in effective particle count. Additionally, the performance of the PF algorithm is influenced by the number of particles—an excessive number of particles can degrade computational real-time performance.
2.3.2. Historical Position Weighting
To enhance the predictive capability of particle filtering for motion trajectories in dynamic environments, particularly for events such as abrupt direction changes, this paper optimizes particle filtering using a historical position weighting method. This approach leverages the swinging trajectory patterns of apples on branches, taking into account the constraints imposed by the fruit stem on the apple’s swinging range, thereby refining the weight distribution of particles. Although the specific X, Y, and Z coordinates of the apple continuously vary, its motion trajectory exhibits certain regularities. By employing the historical position weighting method, the weight distribution of particles can be increased during direction-changing phases, making the particle weights better aligned with the predictive requirements of the actual motion trajectory.
Figure 4 illustrates the schematic of the historical position weighting mechanism. Using this mechanism, the initially uniformly distributed particle weights can be adjusted by learning from past instances of abrupt direction changes, assigning higher weights during direction-changing phases. This method improves the predictive ability for future direction variations, thereby more accurately reflecting the actual motion state of the apple.
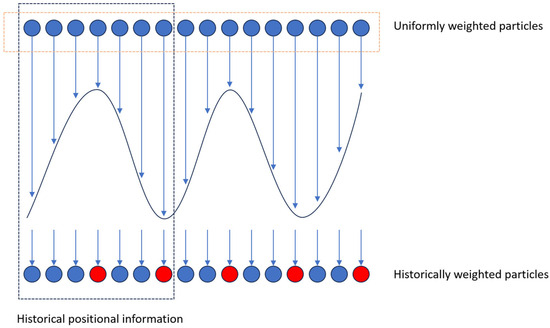
Figure 4.
Historical location weighting schematic.
Define a historical position set , calculated as
where each historical position contains position coordinates, directional information, and temporal information, expressed as
In the equation, is the position vector; is the movement direction; and is the time.
The historical weight function is calculated as
where is the spatial weight coefficient; is the directional weight coefficient; and is the temporal decay factor, calculated as
The particle filter update equation incorporating the historical weighting mechanism is calculated as
In the equation, is the weight of the -th particle at time − 1; is the observation noise parameter; is the observed value at time ; is the predicted value computed from the particle state via the observation model; and is a tuning coefficient used to control the degree of influence of historical weighting on the current particle weight.
2.3.3. Adaptive Particle Number
The prediction accuracy of particle filtering highly depends on the number of particles. While more particles generally improve prediction accuracy, they also significantly increase computational overhead. To balance prediction accuracy and computational cost, this paper introduces an adaptive particle number mechanism. The core idea of this mechanism is to dynamically adjust the number of particles based on the uncertainty of the system state and the trend of motion changes, thereby optimizing the utilization of particle resources.
Specifically, during critical phases where a sudden change in the target’s direction is anticipated, the number of particles is increased to enhance prediction accuracy. Conversely, when the future motion direction of the target is predicted to be stable, the number of particles is reduced to save computational resources.
Figure 5 illustrates the schematic diagram of the adaptive particle number principle. In the figure, larger circles represent a greater number of particles. The number of particles increases during direction mutations, as indicated by the yellow spheres, while it gradually decreases during trend-aligned motion processes, represented by smaller green spheres.

Figure 5.
Schematic diagram of adaptive particle number.
The calculation formula for the particle quantity update function is
The effective sample size is calculated using the following formula:
where is the effective sample size; represents the sum of the squared weights of all particles.
The effective sample size, , provides a way to quantify the diversity of the current particle set. A higher value indicates a more uniform distribution of particles in the state space, which contributes to improved estimation accuracy. Based on this metric, the effective sample size can be monitored during the application of the particle filter algorithm.
The State Uncertainty Index (SUI) at time step , denoted as , is calculated using the formula
where is the position variance, is the velocity variance, is the acceleration variance, and , , are weighting coefficients.
The adaptive particle number adjustment function is calculated using the formula
where represents the absolute difference between the current velocity and the velocity at the previous time step; represents the change in distance between the current position and the position at the previous time step; and , , are the weighting coefficients corresponding to the velocity change, distance change, and state uncertainty, respectively.
By considering the velocity change , the distance change , and the state uncertainty index , the number of particles can be dynamically adjusted. When uncertainty is high, the number of particles is increased to improve estimation accuracy; when uncertainty is low, the number of particles is reduced to save computational resources.
2.4. Prediction Algorithm
This paper adopts an optimized prediction algorithm that combines state prediction based on the extended Kalman filter (EKF) with probability prediction based on the particle filter (PF). Figure 6 illustrates the operational ranges of the PF and EKF algorithms. Among them, the PF algorithm excels in handling nonlinear motion scenarios with stochastic variations, such as abrupt directional changes. The EKF algorithm addresses nonlinear motion by locally linearizing the nonlinear model, providing high reliability and accuracy when the target’s directional change is minor and the motion trend is relatively deterministic. Therefore, during phases wherein the motion trend is clear and stable, the prediction weight of the EKF algorithm is increased while the number of particles in the PF algorithm is reduced. Conversely, during abrupt directional changes, the prediction weight of the PF algorithm is enhanced. Leveraging the respective strengths of both algorithms helps improve the prediction accuracy of the nonlinear trajectory of apples.
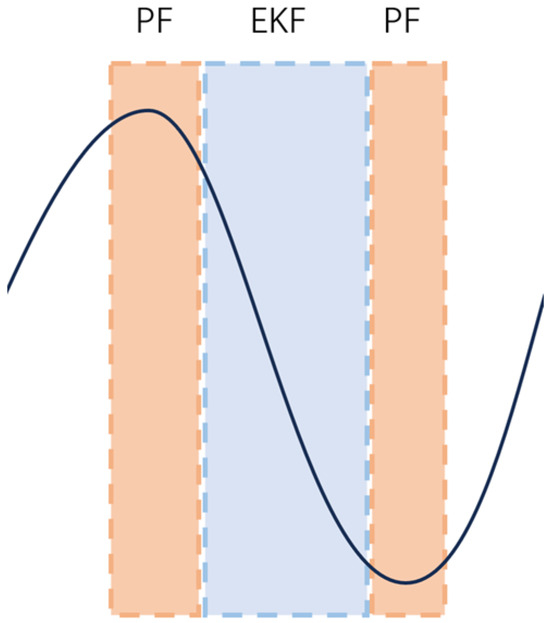
Figure 6.
Schematic diagram of the working range of particle filtering and extended Kalman filtering.
The dynamics model of apple oscillation is described by the following equation:
where the acceleration, is the velocity, is the position, is the equilibrium position, is the damping ratio, is the natural frequency, is the apple mass, and is the wind disturbance.
The natural frequencies for different directions are calculated as
for horizontal ( and ) directions, and
for vertical () direction, where is gravitational acceleration, is effective stem length, and k is stem axial stiffness.
The discrete implementation of the model with 0.2 s sampling interval is
where is the state vector at time , is the state transition matrix, is the process noise input matrix, and is the process noise from wind.
The calculation formula for the state propagation prediction function based on EKF is
where represents the predicted state value at time , based on the posterior state estimate at time − 1.
The calculation formula for predicting future states through particle swarm evolution is
where is the particle weight, is the particle state, and is the number of particles.
Each spatial dimension is predicted independently, and the results are fitted with a curve. The calculation formula is
The results of the two prediction methods are combined linearly using the calculation formula
where is the PF prediction result, is the EKF prediction result, and and are the weighting coefficients.
2.5. Adaptive Error Correction
Traditional extended Kalman filter (EKF) and particle filter (PF) frameworks face issues such as cumulative prediction bias and state estimation drift when dealing with complex nonlinear motion systems. To address this problem, this paper introduces an adaptive error correction mechanism based on multidimensional decomposition. This mechanism achieves dynamic correction of predicted trajectories through systematic error analysis and dynamic correction strategies, ultimately influencing the dynamic adjustment of prediction weights in both the EKF and PF frameworks.
In three-dimensional Euclidean space, the prediction error vector is decomposed into three orthogonal components, calculated as follows:
Define the spatiotemporal error integral operator such that the error correction not only considers the current error but also accounts for the error trend over a past period. The calculation formula is
In the equation, is the time-varying weight function; is the time decay coefficient; is the integration time window.
The weight update equations and are calculated as follows:
In the equation, represents the error integral of the result predicted by the EKF; denotes the error integral of the result predicted by the PF.
The calculation formula for the adaptive update rate function is
In the equation, represents the magnitude of the error vector at time , and denotes the error threshold.
When is relatively large and is relatively small, it indicates that the prediction error of the EKF is greater than that of the PF, causing to approach 1. Based on Equations (24) and (25), it can be inferred that is negative. According to Equations (22) and (23), this results in being smaller than , while increases, signifying an elevated weight of the PF in the prediction.
When the prediction error of the EKF is small, its weight increases accordingly. Conversely, when the prediction error of the PF is small, its weight increases accordingly, always ensuring + = 1.
In practical applications, during the initial prediction phase, the system adaptively reduces the prediction weight α of the EKF due to its sensitivity to initial motion values, while simultaneously increasing the prediction weight of the PF. During directional transition phases, because the particle filter exhibits higher flexibility in predicting directional changes, the system raises the prediction weight of the PF. Subsequently, the system dynamically adjusts the weights of the two filtering algorithms based on real-time error analysis to ensure continuous optimization of prediction accuracy.
3. Results
3.1. Simulation Experiment of the EK-IPF Algorithm
To validate the performance of the EK-IPF algorithm in predicting the dynamic trajectory of apples, a simulation prediction experiment was conducted based on 100 sets of collected apple movement trajectories.
Each trajectory in the dataset was divided into two parts: the first 2 s (10 data points) were used as training samples for algorithm initialization, while the remaining trajectory data were used for testing and performance evaluation. This division ensures that at least one complete motion cycle is captured in the training data, allowing the algorithm to learn the basic motion patterns before making predictions.
The dataset includes apple trajectories under different wind conditions: 40 trajectories under light breeze (wind speed < 2 m/s), 40 trajectories under moderate wind (wind speed 2–5 m/s), and 20 trajectories under strong wind (wind speed > 5 m/s). This distribution allows us to evaluate algorithm performance across various environmental conditions commonly encountered in orchard settings. For each trajectory, we recorded the three-dimensional coordinates at 5 Hz (every 0.2 s), resulting in approximately 100–500 data points per trajectory depending on the total recording duration.
To comprehensively evaluate prediction performance, this study employed two complementary error metrics: mean absolute error (MAE) and root mean square error (RMSE). The selection of these metrics was based on their specific relevance to apple harvesting application scenarios.
MAE was chosen as the core metric for assessing overall prediction accuracy, as it directly represents the average distance error between predicted and actual apple positions. Lower MAE values indicate more precise localization capability, which is crucial for delicate operations such as fruit grasping where damage must be avoided.
RMSE was adopted as a supplementary metric due to its squared term characteristic that assigns greater weight to larger errors. This property makes RMSE particularly suitable for harvesting scenarios—occasional significant prediction errors may lead to complete harvesting failure or equipment damage. By simultaneously monitoring both MAE and RMSE, the algorithm’s routine precision can be evaluated through MAE, while its robustness against occasional large deviations can be examined through RMSE.
This study conducted experiments using the EK-IPF algorithm, the unscented particle filter (UPF) algorithm, and the unscented Kalman filter (UKF) algorithm, respectively. The experimental design involved a one-time-step prediction, and the results are illustrated in Figure 7.


Figure 7.
Comparison of the results of three prediction algorithms in one set of simulation experiments.
A comparison of the X-axis trajectory predictions in Figure 7 reveals that both the UKF and UPF algorithms perform well when predicting trajectories with strong regularity. However, in the Y-axis and Z-axis dimensions, where motion patterns are less predictable, the sensitivity of these two algorithms to directional changes significantly decreases, leading to larger prediction errors during turning phases.
This limitation arises because, although the UKF and UPF algorithms employ unscented transformation and importance sampling to approximate nonlinearity, their inherent mechanisms exhibit lag when handling rapid and drastic changes in motion direction, with relatively low utilization of historical information. The performance of the UKF algorithm heavily relies on the precise characterization of state distributions. When the system exhibits strong nonlinearity, the limited number of Sigma points used to capture the full characteristics of the state distribution introduces constraints. Similarly, the performance of the UPF algorithm is limited by the quality of the proposal distribution, particularly during abrupt motion changes. If the proposal distribution fails to accurately reflect the true state-space distribution, prediction accuracy deteriorates.
In contrast, the EK-IPF algorithm overcomes these shortcomings by incorporating an adaptive particle count and a historical position weighting mechanism. The adaptive particle count increases the number of particles during turning phases to describe motion states more finely, while the historical position weighting leverages past information to estimate the current state more accurately, thereby enhancing the algorithm’s adaptability to rapid directional changes.
From the comparison of error variations over time among the algorithms in Figure 8, it is evident that the EK-IPF algorithm proposed in this study achieves the smallest error in predicting the dynamic trajectory of apples. By employing spatial partitioning and constraint methods, the EK-IPF algorithm effectively prevents abnormal abrupt changes in prediction points, thereby ensuring that the prediction error does not exhibit significant fluctuations.
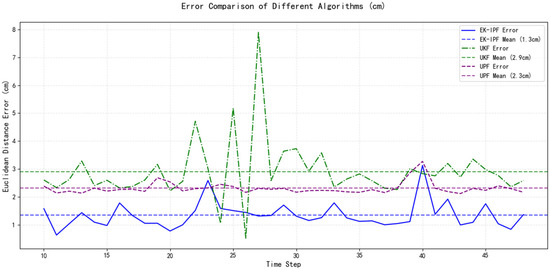
Figure 8.
Schematic diagram of the Euclidean distance error of the three algorithms changing over time.
From the MAE and RMSE error metrics over time shown in Figure 9 and Figure 10, it can be analytically concluded that the apple’s trajectory undergoes turning maneuvers at the 13th and 23rd time steps. The turning phase presents significant challenges for prediction algorithms. Both UKF and UPF algorithms demonstrate notably higher errors than the EK-IPF algorithm during non-turning phases, as they fail to incorporate physical constraints and optimizations that account for the realistic motion of apples affected by wind.
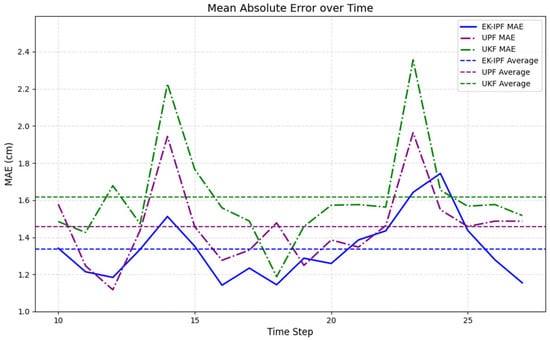
Figure 9.
Schematic diagram of the MAE (mean absolute error) of the three algorithms changing over time.
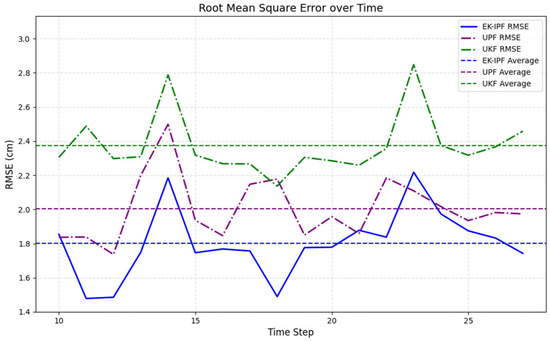
Figure 10.
Schematic diagram of the RMSE (root mean square error) of the three algorithms changing over time.
Table 1 presents the average results of 100 simulation experiments. Compared to the UKF and UPF algorithms, the EK-IPF algorithm reduces the MAE by 29.50% and 17.33%, and the RMSE by 29.07% and 18.50%, respectively. The data indicate that the EK-IPF algorithm outperforms the UKF and UPF algorithms in addressing the problem of apple trajectory prediction in orchard environments.

Table 1.
Compare experimental results.
The superior performance of the EK-IPF algorithm can be attributed to several key factors. First, the spatial partitioning and constraint mechanism effectively prevents prediction points from deviating significantly from the physically possible motion space of apples, ensuring that predictions remain within realistic boundaries even under complex motion patterns. This is particularly important in real orchard environments where external disturbances like sudden gusts of wind might otherwise cause traditional algorithms to produce physically implausible predictions.
Second, the historical position weighting mechanism significantly enhances the algorithm’s ability to predict direction changes by learning from past trajectory patterns. This is crucial for apple harvesting robots, as accurately predicting turning points in apple motion trajectories allows the robot to anticipate directional changes and adjust its harvesting strategy accordingly, rather than simply reacting to observed movements.
Third, the adaptive particle number strategy optimizes computational resource allocation, increasing the number of particles during critical motion phases (such as direction changes) while reducing them during stable motion periods. This not only improves prediction accuracy at critical moments but also ensures computational efficiency, which is essential for real-time applications in agricultural robotics with limited onboard computing resources.
Finally, the adaptive error correction mechanism continuously optimizes the fusion weights between EKF and IPF based on their real-time performance, effectively leveraging the complementary strengths of both algorithms.
3.2. Ablation Experiment of the EK-IPF Algorithm
To comprehensively evaluate the performance improvements brought by the respective optimization mechanisms in the proposed EK-IPF algorithm—including adaptive particle count, historical position weighting, spatial partitioning constraints, and adaptive error correction—an ablation experiment was designed for the EK-IPF algorithm. The following experimental results represent the average values obtained from repeated tests on 100 sets of apple trajectory datasets.
To eliminate the influence of varying particle counts on particle filter performance, the number of particles in the particle filter was uniformly set to 1100 in Table 2. According to the data in Table 2, the fusion of the extended Kalman filter and particle filter achieved significantly better results than either single filtering algorithm.

Table 2.
Ablation experiment results.
Based on the fusion filtering algorithm, the addition of a historical position weighting mechanism reduces the MAE by 33.80% and RMSE by 17.82% compared to the fusion algorithm.
After incorporating an adaptive error correction mechanism into the fusion filtering algorithm, the MAE decreases by 17.63% and RMSE by 23.83% relative to the fusion algorithm.
When a spatial partitioning and constraint mechanism is added to the fusion filtering algorithm, the MAE is reduced by 3.01% and RMSE by 14.93% compared to the fusion algorithm.
The experimental results demonstrate that the primary role of the spatial partitioning and constraint mechanism is to restrict prediction outcomes, avoiding unreasonable prediction points and improving prediction stability, which is reflected in the greater reduction in RMSE compared to MAE. The historical position weighting mechanism, by continuously learning directional mutation events in historical trajectories and rationally adjusting particle distribution, achieves better optimization for long-term trajectory prediction, as evidenced by its greatest impact on reducing MAE.
To verify the effectiveness of the adaptive particle number mechanism, performance comparison experiments were conducted under different particle number metrics based on the fusion filtering algorithm incorporating historical position weighting, adaptive error correction, spatial partitioning, and constraint optimization mechanisms. The results are shown in Table 3.

Table 3.
Performance comparison before and after adding adaptive particle number mechanism.
As seen in Table 3, when the number of particles is below 100, the error is relatively large due to insufficient particles, making it difficult to achieve optimal particle filter performance. As the number of particles gradually increases from 100 to 400, the prediction error shows a significant downward trend. When the number of particles exceeds 400, the reduction in error slows noticeably. After the number of particles surpasses 1100, the decrease becomes negligible, indicating that 1100 particles can adequately meet the accuracy requirements of the current particle filter.
After introducing the adaptive particle number mechanism, both MAE and RMSE error metrics decrease to varying degrees across different particle number configurations, demonstrating that the required number of particles can be effectively reduced while maintaining the same error performance. As the number of particles increases, the benefits of the adaptive mechanism gradually diminish, particularly when the particle count reaches 1100 or higher, where improvements are marginal. The experimental results indicate that the adaptive particle number mechanism can reduce the required number of particles while maintaining prediction accuracy, thereby lowering computational overhead.
The adaptive particle number mechanism merits particular attention from an implementation perspective. Experimental results demonstrate that this mechanism reduces the required number of particles by approximately 40% while maintaining equivalent prediction accuracy. This efficiency translates to significant computational savings in resource-constrained embedded systems typically deployed in agricultural robotics applications, potentially facilitating broader adoption of advanced prediction algorithms in practical field operations.
3.3. Experiment in Outdoor Scenes
The actual field experiment involved directly applying the prediction algorithm in an outdoor environment to mark the predicted point position for the next second in the frame. The EK-IPF, UPF, and UKF algorithms were run simultaneously in a multi-threaded manner, yielding the prediction results shown in Figure 11 below. The focus of Figure 11 below is on the critical stage of the apple’s direction change during movement.

Figure 11.
The actual prediction results of different algorithms, where the red bounding boxes and white dots represent the true position of the apple at this moment, the green bounding boxes and green dots represent the predicted position at this moment using the EK-IPF algorithm, the yellow bounding boxes and yellow dots represent the predicted position at this moment using the UPF algorithm, and the blue bounding boxes and blue dots represent the predicted position at this moment using the UKF algorithm.
As clearly illustrated in the figure, the predicted point positions obtained by the EK-IPF algorithm proposed in this study are closer to the actual positions of the apples, particularly in the first row of five images where directional changes are pronounced. The EK-IPF algorithm demonstrates faster responsiveness to state variations in direction.
In Figure 11, the real-time actual position of the apple is obtained by detecting the apple with YOLOv8 and combining it with the RealSense D415 depth camera. The experiment was conducted 100 times outdoors, accounting for different apple vibration frequencies. During the algorithm’s operation, the YOLO detection combined with the prediction program achieves a frame rate of 20 to 25 FPS, demonstrating good real-time performance. Figure 12 presents a comparison of the average error metrics for all experiments conducted in outdoor environments using three prediction algorithms. The performance advantage of EK-IPF over UPF is as follows: in terms of MAE, EK-IPF reduces the error by 10.89% compared to UPF, and in terms of RMSE, EK-IPF reduces the error by 13.25% compared to UPF. The performance advantage of EK-IPF over UKF is as follows: in terms of MAE, EK-IPF reduces the error by 22.25% compared to UKF, and in terms of RMSE, EK-IPF reduces the error by 23.70% compared to UKF. Based on the comprehensive evaluation, it is evident that EK-IPF outperforms all other tested filtering prediction algorithms.
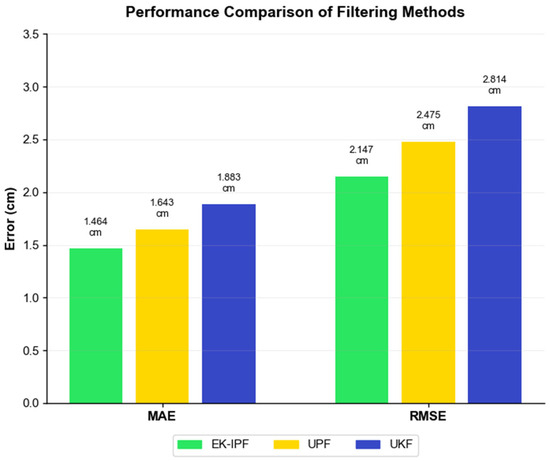
Figure 12.
Comparative chart of the average prediction error metrics from 100 sets of outdoor experiments. In the chart, the green bars represent the error metric data of the EK-IPF algorithm, the yellow bars represent the error metric data of the UPF algorithm, and the blue bars represent the error metric data of the UKF algorithm.
The outdoor experiments validated the superior performance of the EK-IPF algorithm in real-world conditions, demonstrating its practical value for apple harvesting robotics. However, several important challenges and limitations were observed during the experiments that merit discussion and indicate directions for future research.
The current algorithm primarily relies on visual information from depth cameras and the accuracy of apple recognition using YOLOv8. When apples are partially occluded by leaves or affected by strong lighting conditions leading to inaccurate recognition, the prediction accuracy can be significantly compromised. Future research should focus on enhancing the robustness of apple recognition under various environmental conditions.
Additionally, the existing implementation treats each apple as an independent entity without considering potential correlations between the movements of adjacent apples on the same branch. In reality, apples on the same branch often exhibit coordinated movement patterns due to their physical connection. Future work could explore modeling these correlations to further improve prediction accuracy, perhaps through techniques such as grouped particle filtering or graph-based motion models.
4. Conclusions
This study proposes an integrated approach for real-time trajectory prediction of apples in orchard environments. The method combines the YOLOv8 model for apple detection with a fusion algorithm integrating the extended Kalman filter and improved particle filter (EKF-IPF), constructing a YOLOv8-EKF-IPF framework capable of achieving accurate dynamic apple trajectory prediction in variable orchard conditions. The main research contents of this paper are as follows:
- (1)
- Ablation experiments verified the effectiveness of historical position weighting, spatial partitioning and constraints, and the adaptive error correction optimization mechanism in reducing prediction errors. The adaptive particle number optimization mechanism was also validated to effectively reduce the required number of particles while maintaining prediction accuracy.
- (2)
- Simulation experiments demonstrated the superiority of the proposed EK-IPF algorithm. Compared to the unscented Kalman filter algorithm and the unscented particle filter algorithm, the EK-IPF algorithm reduces the MAE by 29.50% and 17.33%, and the RMSE by 29.07% and 18.50%, respectively. Real-world experimental results show that, compared to the unscented Kalman filter and unscented particle filter algorithms, the EK-IPF algorithm reduced the MAE by 22.25% and 10.89%, and the RMSE by 23.70% and 13.25%, respectively. The real-world experiments confirmed the feasibility of the EK-IPF algorithm, providing technical support for dynamic trajectory prediction of apples in orchard environments.
Beyond the technical advances described above, this study carries broader significance for agricultural robotics. Precise, real-time prediction of fruit motion tackles one of the main obstacles that still limit the effectiveness of harvesting robots in commercial orchards. By allowing robots to anticipate where a fruit will be—rather than simply reacting to where it was observed a moment earlier—our approach moves robotic picking closer to the success rates achieved by skilled human workers and could accelerate the adoption of automated solutions in the face of chronic labor shortages.
Equally important is the method’s computational efficiency. The adaptive-particle strategy trims the number of particles whenever full resolution is unnecessary, cutting CPU load without compromising accuracy. As a result, advanced trajectory prediction can run on inexpensive embedded hardware, lowering the entry barrier for small and medium-sized farms and helping to democratize access to sophisticated harvesting technology.
Although the present work concentrates on apples, the underlying ideas are widely transferable. The EK-IPF framework, together with spatial partitioning and historical-position weighting, can be adapted to fruits and vegetables that show similar wind-induced oscillations—such as pears, peaches, or tomatoes—and even to other agricultural tasks that require motion prediction; for example, livestock tracking or crop-flow monitoring during mechanical harvesting.
Several promising research directions remain. First, integrating the predictor into a complete harvesting robot will allow us to measure its impact on actual pick rate under different field conditions. Second, transfer-learning techniques could be explored so that the model can be re-trained for new crops with only a small amount of additional data. Finally, supplementing the vision system with environmental sensors—such as local wind speed and direction—may further improve accuracy, especially under gusty conditions.
Author Contributions
Conceptualization, J.N. and J.Z.; methodology, Z.L. and S.W.; software, Z.L.; validation, Z.L., S.W., and J.H.; formal analysis, J.H. and S.W.; investigation, Z.L., S.W., and J.H.; resources, Z.L.; data curation, Z.L. and S.W.; writing—original draft preparation, Z.L.; writing—review and editing, J.N. and J.Z.; visualization, Z.L. and J.H.; supervision, J.N. and J.Z.; project administration, J.N.; funding acquisition, J.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Henan Province Key Research and Development Special Project under Grant No. 231111112700, Training Plan for Young Backbone Teachers in Colleges and Universities in Henan Province under Grant No. 2021GGJS077, and North China University of Water Resources and Electric Power Young Backbone Teacher Training Project under Grant No. 2021-125-4.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Z.; Igathinathane, C.; Li, J. Technology progress in mechanical harvest of fresh market apples. Comput. Electron. Agric. 2020, 175, 105606. [Google Scholar] [CrossRef]
- Yan, B.; Fan, P.; Lei, X.; Liu, Z.; Yang, F. A Real-Time Apple Targets Detection Method for Picking Robot Based on Improved YOLOv5. Remote Sens. 2021, 13, 1619. [Google Scholar] [CrossRef]
- Zhuang, M.; Li, G.; Ding, K. Obstacle avoidance path planning for apple picking robotic arm incorporating artificial potential field and A* algorithm. IEEE Access 2023, 11, 100070–100082. [Google Scholar] [CrossRef]
- Zhang, K.; Lammers, K.; Chu, P. System design and control of an apple harvesting robot. Mechatronics 2021, 79, 102644. [Google Scholar] [CrossRef]
- Chen, M.; Chen, Z.; Luo, L. Dynamic visual servo control methods for continuous operation of a fruit harvesting robot working throughout an orchard. Comput. Electron. Agric. 2024, 219, 108774. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, Y.; Lian, J. Apple harvesting robot under information technology: A review. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420925310. [Google Scholar] [CrossRef]
- Quan, R.; Zhu, L.; Wu, Y. Holistic LSTM for pedestrian trajectory prediction. IEEE Trans. Image Process. 2021, 30, 3229–3239. [Google Scholar] [CrossRef]
- Xie, G.; Shangguan, A.; Fei, R. Motion trajectory prediction based on a CNN-LSTM sequential model. Sci. China Inf. Sci. 2020, 63, 212207. [Google Scholar] [CrossRef]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Aghili, F. Fault-tolerant and adaptive visual servoing for capturing moving objects. IEEE/ASME Trans. Mechatron. 2021, 27, 1773–1783. [Google Scholar] [CrossRef]
- Wu, J.; Jin, Z.; Liu, A. A survey of learning-based control of robotic visual servoing systems. J. Frankl. Inst. 2022, 359, 556–577. [Google Scholar] [CrossRef]
- Guo, D.; Li, Z.; Shuai, H.; Zhou, F. Multi-Target Vehicle Tracking Algorithm Based on Improved DeepSORT. Sensors 2024, 24, 7014. [Google Scholar] [CrossRef]
- Wang, Z.; Walsh, K.; Koirala, A. Mango fruit load estimation using a video based MangoYOLO—Kalman filter—Hungarian algorithm method. Sensors 2019, 19, 2742. [Google Scholar] [CrossRef]
- Liu, X. Robust Fruit Counting: Combining Deep Learning, Tracking, and Structure from Motion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Madhukar, P.S.; Prasad, L.B. State Estimation using Extended Kalman Filter and Unscented Kalman Filter. In Proceedings of the International Conference on Emerging Trends in Communication, Control and Computing (ICONC3), Lakshmangarh, India, 21–22 February 2020. [Google Scholar]
- Awasthi, V.; Raj, K. A comparison of Kalman filter and extended Kalman filter in State estimation. Int. J. Electron. Eng. 2011, 3, 67–71. [Google Scholar]
- Zhang, G.; Yin, J.; Deng, P.; Sun, Y.; Zhou, L.; Zhang, K. Achieving Adaptive Visual Multi-Object Tracking with Unscented Kalman Filter. Sensors 2022, 22, 9106. [Google Scholar] [CrossRef]
- Deng, Y.; Hou, X.; Li, B. A highly powerful calibration method for robotic smoothing system calibration via using adaptive residual extended Kalman filter. Robot. Comput.-Integr. Manuf. 2024, 86, 102660. [Google Scholar] [CrossRef]
- Zhang, T.; Shi, P.; Yang, Y. Continuous-discrete extended Kalman filter based parameter identification method for space robots in postcapture. Nonlinear Dyn. 2024, 112, 21205–21225. [Google Scholar] [CrossRef]
- Bi, Y.; Ji, Y. Parameter estimation of fractional-order Hammerstein state space system based on the extended Kalman filter. Int. J. Adapt. Control Signal Process. 2023, 37, 1827–1846. [Google Scholar] [CrossRef]
- Maksymova, S.; Abu-Jassar, A.; Gurin, D. Comparative Analysis of methods for Predicting the Trajectory of Object Movement in a Collaborative Robot-Manipulator Working Area. Multidiscip. J. Sci. Technol. 2024, 4, 38–48. [Google Scholar]
- Bai, Y.; Yan, B.; Zhou, C. State of art on state estimation: Kalman filter driven by machine learning. Annu. Rev. Control 2023, 56, 100909. [Google Scholar] [CrossRef]
- Prakash, J.; Patwardhan, S.C.; Shah, S.L. State estimation and nonlinear predictive control of autonomous hybrid system using derivative free state estimators. J. Process Control 2010, 20, 787–799. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, Z.; Zhang, A. UAV trajectory prediction based on flight state recognition. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2629–2641. [Google Scholar] [CrossRef]
- Chiang, H.T.; Tseng, B.Y.; Chen, J.L. Trajectory analysis in UKF: Predicting table tennis ball flight parameters. IT Prof. 2024, 26, 65–72. [Google Scholar] [CrossRef]
- Gao, J.; Liang, X.; Chen, Y. Hierarchical image-based visual serving of underwater vehicle manipulator systems based on model predictive control and active disturbance rejection control. Ocean Eng. 2021, 229, 108814. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Zheng, H. Battery remaining useful life prediction using improved mutated particle filter. Energy Storage 2021, 3, e218. [Google Scholar] [CrossRef]
- Gong, Z.Y.; Qiu, C.R.; Tao, B. Tracking and grasping of moving target based on accelerated geometric particle filter on colored image. Sci. China Technol. Sci. 2021, 64, 755–766. [Google Scholar] [CrossRef]
- Tao, Y.; Ren, F.; Gao, H. A robot dynamic target grasping method based on affine group improved gaussian resampling particle filter. Appl. Sci. 2021, 11, 10270. [Google Scholar] [CrossRef]
- Elfring, J.; Torta, E.; van de Molengraft, R. Particle filters: A hands-on tutorial. Sensors 2021, 21, 438. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, T.; Liu, F. Remarkable local resampling based on particle filter for visual tracking. Multimed. Tools Appl. 2017, 76, 835–860. [Google Scholar] [CrossRef]
- Li, S.; Zhao, S.; Cheng, B. Dynamic particle filter framework for robust object tracking. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 3735–3748. [Google Scholar] [CrossRef]
- Yılmaz, M.K.; Bayram, H. Particle filter-based aerial tracking for moving targets. J. Field Robot. 2023, 40, 368–392. [Google Scholar] [CrossRef]
- Kumar, M.; Mondal, S. Recent developments on target tracking problems: A review. Ocean Eng. 2021, 236, 109558. [Google Scholar] [CrossRef]
- Badar, T.; Särkkä, S.; Zhao, Z. Rao–Blackwellized Particle Filter Using Noise Adaptive Kalman Filter for Fully Mixing State-Space Models. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6972–6982. [Google Scholar] [CrossRef]
- Peng, D.; Xie, K.; Liu, M. WSN Mobile Target Tracking Based on Improved Snake-Extended Kalman Filtering Algorithm. J. Beijing Inst. Technol. 2024, 33, 28–40. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, T.; Bai, J. Parameter Identification of Maritime Vessel Rudder PMSM Based on Extended Kalman Particle Filter Algorithm. J. Mar. Sci. Eng. 2024, 12, 1095. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).