Abstract
Wild chrysanthemum stems are cluttered and their flowers are dense, which makes them difficult to pick. In order to solve this problem, in this study, we designed a kind of opposed roller picking device. It was designed based on an analysis of the mechanical characteristics involved in the picking of wild chrysanthemum. The design focused on an opposed drum picking mechanism. Taking the critical post-collision acceleration as the evaluation metric, a theoretical analysis was conducted on the post-collision motion behaviors of wild chrysanthemum and the roller bow tooth. This study found that the primary factors affecting the picking process are the roller rotational speed, the feeding speed, and the impact angle. Furthermore, simulation experiments confirmed that when the roller rotational speed was 3.73 rad/s and the clamping chain moved at 1.3 m/s, the wild chrysanthemum picking platform achieved a picking efficiency of 87.72%, thereby meeting the corresponding requirements for wild chrysanthemum harvesting. Through bench tests, it was found that, when the roller gap was 100 mm, the roller bow tooth bending angle was 56°, and the feeding rate was 2.1 kg/s, the clean picking rate reached 95.9%, thereby meeting the requirements for wild chrysanthemum harvesting. The development of an opposite roller-type wild chrysanthemum-picking device can provide technical support for the development of wild chrysanthemum picking equipment.
1. Introduction
Chrysanthemum indicum L. is an important medicinal material with flowers as the primary raw material. It is a key ingredient in medicines such as Ganmaoling, and its market demand is substantial [1,2,3]. Due to the intertwined stems and irregular distribution of flowers on wild chrysanthemums, mechanical harvesting is difficult. Currently, manual labor or cutting and drying machines are used to cut the stems, followed by manual flower picking. At present, wild chrysanthemum harvesting primarily relies on manual labor or the use of swathers to cut the stems, followed by manual flower picking. The harvesting efficiency is extremely low, at only about 0.01 mu/person/day. Based on an estimated labor cost of approximately 100 RMB per person per day, harvesting 1 mu of wild chrysanthemum requires around 100 workdays, resulting in a labor cost as high as 10,000 RMB per mu. In contrast, the efficiency and cost advantages of mechanized operations are readily apparent. Such high labor input not only significantly raises the production cost per unit area, but also consumes substantial human resources, leading to severe productivity losses. This, in turn, limits the economic viability of wild chrysanthemum cultivation and represents a major bottleneck hindering its large-scale promotion and industrial development. Therefore, developing specialized harvesting devices for wild chrysanthemums is significant for the growth of the wild chrysanthemum industry [3,4].
Scholars both domestically and internationally have conducted a series of studies on flower harvesting devices, designing various types based on different harvesting principles [5,6,7]. These are mainly divided into two categories: “flower-striking” and “flower-combing”.
“Flower striking” devices are characterized by high efficiency and high flower picking rates, such as the PT-30 hop harvesting and cleaning combined operation machine produced by the Chimailexter-Weihua Cooperation [8]. This method uses multiple strikes to harvest hops, and the flowers are subjected to greater force. It is primarily suitable for flowers with a higher hardness, such as hops.
“Flower combing” devices have advantages like lower breakage rates and lower impurity content, such as the chrysanthemum harvesting machinery developed by Hanna Brabandt in Germany [9], which uses a comb-tooth mechanism for flower harvesting. This method, however, is not suitable for dense foliage conditions. Italian researchers have developed three self-propelled comb-tooth harvesters that operate at a fixed height and brush through the crop, each differing in its flower-detachment mechanism. Field tests in Italy have reported that these comb-tooth harvesters incur roughly 63% flower loss, with nearly 45% of lost blooms measuring under 10 mm in diameter.
Compared with the aforementioned flowers, wild chrysanthemums have dense branches and an irregular flower distribution, making simple “flower striking” or “flower combing” unsuitable for mechanical harvesting of wild chrysanthemums. Therefore, it is necessary to develop specialized harvesting devices tailored to the characteristics of wild chrysanthemums plants. In 2009, Zhai Dapeng et al. [10] invented a hand-held chrysanthemum picker that employs a cutting mechanism to shear multiple flower-bearing stems simultaneously, primarily targeting the Tagetes erecta market. As a small-scale mechanical aid, it not only substantially increases throughput compared with manual picking, but also reduces picker exposure to trace toxins in the flowers, mitigating symptoms such as dizziness and chest tightness. However, its shearing approach proves less effective when applied to wild chrysanthemum plants, which bear numerous, densely clustered blooms that require more comprehensive detachment methods.
In response to the mechanized harvesting needs of wild chrysanthemums, this paper proposes an opposite roller-type wild chrysanthemum-picking scheme based on the physical characteristics of the wild chrysanthemum plants and designs the harvesting device. This study employs theoretical analysis, simulation calculations, and bench tests to identify the main parameters affecting flower-picking performance, determine the structural parameters of the harvesting device, and verify the flower-picking performance through bench tests, with the aim of achieving mechanized harvesting of wild chrysanthemums and improving harvesting efficiency.
2. Materials and Methods
2.1. Overall Structure and Working Principle
The structure of the picking device designed in this paper is shown in Figure 1.
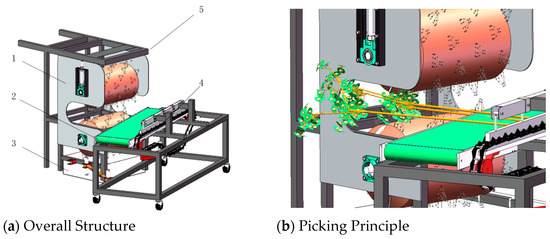
Figure 1.
Structure diagram of roller-type wild chrysanthemum-picking device. 1. Roller 2. Conveyor belt 3. Flower collection box 4. Clamping mechanism 5. Frame.
The device mainly consists of a roller, conveyor belt, clamping mechanism, frame, etc. Among these, the core components of the flower-picking mechanism are the picking roller, motor, sliding bearing seat, and so on. The picking roller is the key part that determines the picking performance of the device. Its main structure includes the picking bow teeth, guide plate, and drum, as shown in Figure 2.
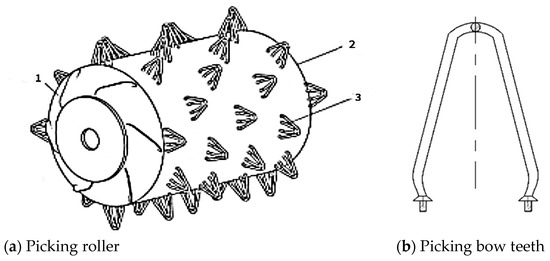
Figure 2.
Schematic diagram of picking bow tooth structure 1. Guide plate 2. Roller 3. Harvesting tooth.
The flower stem of wild chrysanthemums is clamped by the clamping device and driven by a motor through the driving wheel. This drives the wild chrysanthemums to be fed transversely into the two picking rollers. The conveyor device at the front end of the clamping mechanism provides support, preventing the wild chrysanthemums from tilting downward during the picking process and blocking the picking rollers. The densely clustered flowers at the upper parts of wild chrysanthemums are fed into the picking gap of the two picking rollers. The motors drive the rollers to rotate relative to each other, which strike and brush the flower clusters, thereby achieving flower picking.
2.2. Harvesting Characteristics of Wild Chrysanthemums
This study was conducted on 2-year-old Chrysanthemum indicum L. from the Bai Ta Village wild chrysanthemum planting base in Qian County, Xianyang City, Shaanxi Province. The plant structure is shown in Figure 3, which mainly includes the flower stalk, flower axis, small branch stems, and large branch stems. The physical parameters of different parts of the plant were measured, and the results are shown in Table 1.

Figure 3.
Growth diagram of Chrysanthemum indicum in the field.

Table 1.
Basic physical parameters of Chrysanthemum indicum.
The maximum shear force and rupture force of each part of wild chrysanthemums are the main factors affecting the flower picking performance. As shown in Figure 4, the mechanical parameters of wild chrysanthemums were measured using a universal material testing machine (model DDL10, with an accuracy of 0.015%). During the experiment, the rupture and shear tests were carried out at a speed of 20 mm/min. Ten random samples were selected for each group, and the average maximum shear force and rupture force of each part were recorded, as shown in Table 2.

Figure 4.
Mechanical parameter determination test.

Table 2.
Mechanical parameters of different parts of Chrysanthemum indicum.
2.3. Dynamics Analysis of the Picking Process
Wild chrysanthemum flowers are harvested under the impact and combined actions of the flower-picking roller. The interaction between the flower stem and the bow teeth is a non-normal collision. The basic collision model is shown in Figure 5. A dynamic analysis of the collision process reveals that:
where m1 and m2 are masses of the bow teeth and flower stem, v1 and v2 are the velocities of the bow teeth and flower stem before the collision (m/s), u1 and u2 are the velocities of the bow teeth and flower stem after the collision (m/s), and K is the coefficient of restitution.
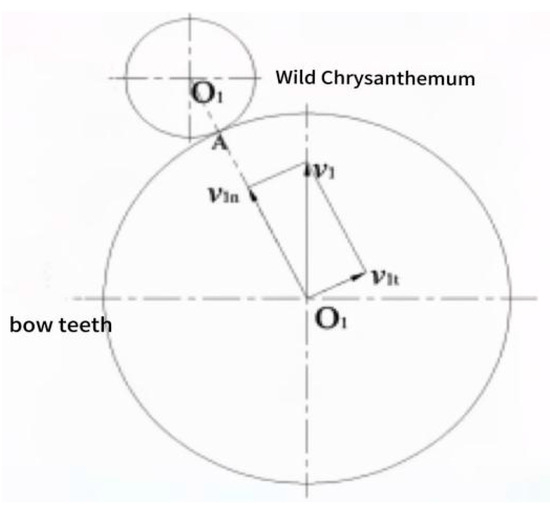
Figure 5.
Non-positive collision between the flower stem of the wild chrysanthemum and the bow teeth.
Assuming that the flower stem of wild chrysanthemum is initially at rest (v2 = 0) and that the mass of the flower stem relative to the bow teeth is negligible (m1 + m2 ≈ m1), Equation (1) can be simplified to:
This implies that, after the collision, the velocity of the bow teeth remains unchanged, while the flower stem attains a certain velocity. When the wild chrysanthemum flower stem and the bow teeth undergo a non-normal collision, a certain collision angle is generated, i.e., when the two normal lines O1O2 and V1 are not collinear:
where vln is the component of u1 in the O1O2 direction, N is the roller speed, rpm, D is the roller diameter, mm, and α is the collision angle, rad.
Thus, the velocity of wild chrysanthemum after collision is:
Assuming that the critical velocity for damage to wild chrysanthemum flowers is u0, the critical roller speed can be determined as:
A flower stem is fed into the holding device through its root (semi-feeding); thus, the collision angle α is controllable. By utilizing the uniform combing rule, the optimal combing distance P can control the collision angle α [11].
When the flower of the wild chrysanthemum comes into contact with the generatrix of the bow teeth cylinder (Figure 6a), a frontal collision occurs. Generally, during the picking process, it is rare for α = 0° to happen. The majority of collisions occur at a certain angle β relative to this plane, as shown in Figure 6b.
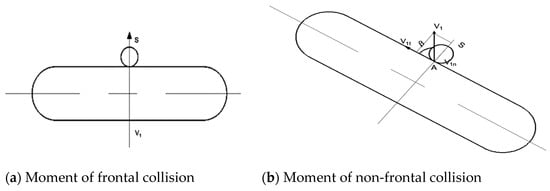
Figure 6.
Moment of frontal collision.
When the bow teeth undergo a non-normal collision, literature reviews indicate that, to determine the optimal collision angle, the tangential velocity of the bow teeth should ideally approach the critical velocity v0 [12,13]. Therefore:
Equation (6) indicates that when the bow teeth are inclined, the critical speed of the roller for causing collision damage increases as the angle β decreases. When the front segment of the bow teeth collides with the wild chrysanthemum, the normal line O1O2 forms an angle γ with the velocity v1, as shown in Figure 7:
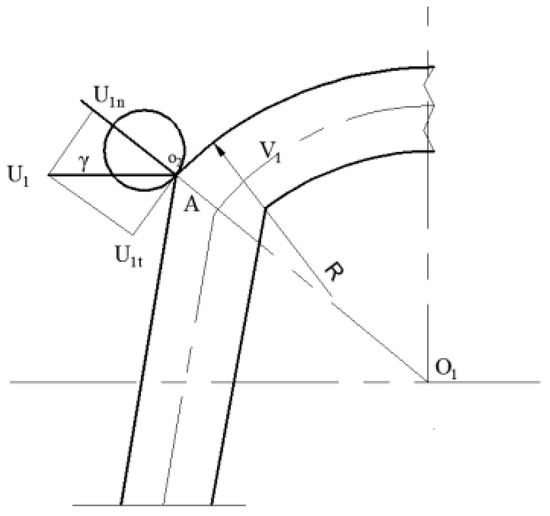
Figure 7.
Schematic after non-frontal collision.
Using the same method, the velocity vb of the flower stem after the collision can be obtained:
When the front part of the bow teeth collides with the wild chrysanthemum, frontal collisions are rare. Most collisions involve the bow teeth’s front end (B) and the horizontal section (A) with the flower stem, resulting in non-normal collision angles α, β, and γ, as shown in Figure 8:
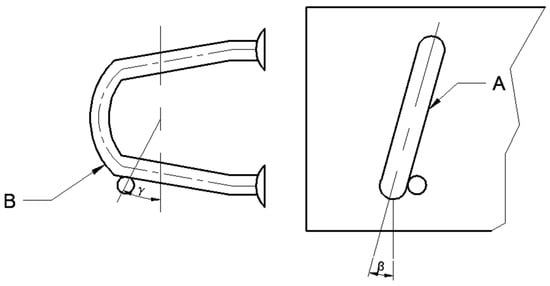
Figure 8.
Non-orthogonal collision moments on the X and Y planes.
Thus, the velocity of a flower stem after the collision can be expressed as:
During the striking process, the bow teeth on the flower picking roller are in motion, while the flowers are stationary. Due to the relative motion, the flowers can also be considered as moving while the bow teeth are stationary, equivalent to the flowers striking the stationary bow teeth at a certain velocity. According to the law of conservation of energy:
where mh is the mass of a single wild chrysanthemum flower (approximately 0.58 g), v is the instantaneous linear velocity of the bow teeth, FJ is the pulling force of the flower receptacle, and SH is the diameter of the flower receptacle.
Let FJ1 = 8 N and SH = 1.0 mm; then, the linear velocity v1 is:
Thus, when the bow teeth impact the flower receptacle at a linear velocity of 5.25 m/s, the flower stem is just broken once.
Let FJ2 = 5 N and SH = 1.0 mm; then, the linear velocity v2 is:
Thus, when the bow teeth impact the flower receptacle at a linear velocity of 7.3 m/s, the flower stem is just broken at the flower stalk.
When the small branch stem of a wild chrysanthemum strikes the bow teeth on the roller at velocity vx, and assuming that the small branch stem carries nh flowers, ny leaves, each flower weighing mh grams, each leaf weighing my grams, and other stems weighing mz grams, the total mass of the wild chrysanthemum small stem is mx grams:
Let nh = 12, ny = 8, mh = 0.3 my = 1 and mz = 5; then, mx = 16.6.
When the breaking force of the small branch stem is FJx = 150 N and the cross-sectional area is SX = 2.5 mm, the minimum linear velocity of the picking bow teeth when the wild chrysanthemum small stem is just broken once is:
Analysis indicates that using mechanical striking and combing methods to harvest the wild chrysanthemums essentially relies on the pulling force to separate the flowers from the stems. During this process, when the instantaneous velocity of the bow teeth on the drum is less than 4.15 m/s, multiple strikes are needed to detach the flower, and as the number of strikes increases, the flower’s shedding phenomenon worsens, leading to a higher breakage rate. When the instantaneous velocity is greater than 5.25 m/s but less than 7.42 m/s, the flowers can be picked in one strike, though most are broken at the middle of the flower stalk. Therefore, the optimal picking speed of the bow teeth lies between 4.15 m/s and 7.42 m/s, corresponding to a drum speed of 2.45 rad/s to 3.96 rad/s.
2.4. Structure Design of Picking Roller
The shape, number, and arrangement of the picking bow teeth, and the roller speed are key factors influencing the flower picking performance. Among these, the roller speed is affected by the agricultural practices for wild chrysanthemum harvesting, the clamping and feeding speed, and other factors. The structure of the picking bow teeth is shown in Figure 5. A rational design of the upper bending strip angle is crucial for reducing flower stem and flower branch entanglement, as well as minimizing flower damage. The reasonable arrangement of the picking bow teeth helps to increase the flower-picking efficiency, decrease flower branch entanglement with the roller, and increase the picking performance.
Based on the current manual picking methods and the agricultural requirements for wild chrysanthemum, combined with the structure of domestic and international drum-type flower picking devices, a bow tooth structure was selected. The tooth spacing is small, the top arc of the tooth is small (31–48°), and the wire diameter is relatively thin (5 mm) [14,15], which provide excellent performance for impact-based flower picking, as shown in Figure 5.
2.5. Simulation Experiment
2.5.1. Simulation Model Establishment
A simulation analysis of picking performance was conducted by integrating ADAMS and ANSYS 2022 R1. The ADAMS/Flex module was used to import the modal neutral file (mnf) generated by meshing the flexible flower stem in ANSYS.
The physical parameters of wild chrysanthemum were obtained through experimental measurements: the Poisson’s ratio was 0.3, and the density was 625.8 kg/m3. During operation, when the tine reaches its lowest point and comes into contact with the flower, the rotational speed and striking action of the roller impart a certain acceleration to the wild chrysanthemum on the striking tines, enabling it to quickly fall into the collection box below.
In the mechanical harvesting of wild chrysanthemum using a striking method, the primary picking force acts on the flower receptacle area and is predominantly a tensile (breaking) force. In the ADAMS simulation environment, the collision process was modeled using a contact function.
Material stiffness depends entirely on the properties of the specific material and is considered a qualitative value. As the tines in this case were made of rigid material, the force exponent was set between 2 and 3. The damping coefficient was set to a value c ≥ 0, typically between 0.1% and 1% of the stiffness value. When fully defining the penetration depth for damping, the requirement d ≥ 0 must be satisfied [16,17].
Accordingly, the simulation parameters were set as follows:
k = 2855 N/mm, c = 0.570 N·s/mm, e = 1.1, d = 0.1 mm.
Due to geographical differences, different wild chrysanthemum varieties exhibit varying characteristics. This study focused on a two-year-old ellipsoidal variety of wild chrysanthemum from the northwest region. The required physical parameters for simulation, obtained from prior physical experiments are shown in Table 3.

Table 3.
Physical parameters of wild chrysanthemum flower stems.
Since rigid models in ADAMS do not deform under force, simulating collisions with them can result in significant errors. Therefore, the discrete beam method was adopted, where the wild chrysanthemum stem was divided into two segments. The diameters of each segment were adjusted to ensure that the geometry of the discrete beam closely approximated that of the actual stem.
A wild chrysanthemum stem model was created in SolidWorks 2021 and imported into the finite element analysis software ANSYS for meshing, with a mesh resolution of 2 mm. The element type selected was Solid186, with an element length of 10 mm. The modal neutral file (mnf) generated from this was then imported into ADAMS using the Flex module [18,19,20].
The modal neutral file was exported with the default damping ratio. In ADAMS, a rigid tine model was created, and the mnf file output from ANSYS was imported to generate a flexible wild chrysanthemum stem model. The stem was analyzed as two separate elements, as shown in Figure 9.
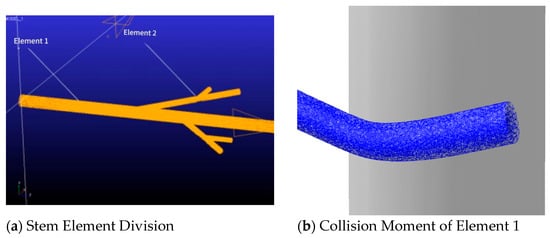
Figure 9.
ADAMS collision mode.
2.5.2. Simulation Analysis of Collision Process
The X-axis represents the oscillation of the flower stem under the impact of the picking teeth. Flower stem unit 1, being struck at the upper part of the teeth (Figure 10), experiences greater oscillation due to the impact at both ends of the picking teeth. Flower stem unit 2, however, is not located at the center of the impact zone (Figure 11) and shifts in one direction due to the influence of flower stem unit 1. By comparing the velocity and acceleration profiles of the different units, it can be observed that unit 1, which undergoes direct collision, shows a smoother change in velocity during the collision process compared with unit 2, which experiences non-direct collision. This reduces the impact on the flower cluster and the impurity rate.

Figure 10.
Kinematic curves of flower stem unit 1.
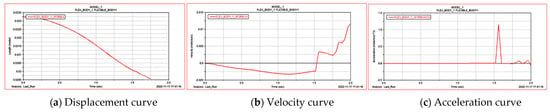
Figure 11.
Kinematic curves of flower stem unit 2.
From the analysis, it can be concluded that the critical acceleration after the collision is mainly determined by the applied drum speed and the feeding speed of the wild chrysanthemums. The critical acceleration generated by the collision can be used to determine the impact force at that location (when the impact force exceeds the maximum shear force at the flower stem, the wild chrysanthemums are picked). Therefore, to meet the required picking efficiency, it is necessary to analyze and optimize the motion parameters of the picking platform.
2.5.3. Experiment of the Influence of Motion Parameters on Flower Picking Performance
From the mechanical analysis of the collision process, it can be concluded that the kinematic parameters of the roller determine the success of the picking process. The simulation analyzes the main parameters during the collision process: roller speed, feeding speed, and collision angle [21]. The connections between different parts are relatively fragile, and when the wild chrysanthemum is on the flower stem, the relationship between the maximum acceleration and impact force can be described by Equation (14):
where F is the flower stem impact force (N), a is the maximum acceleration (m/s2), and m is the mass of the flowers on the stem unit (kg).
To achieve the flower picking process through impact, the maximum acceleration must exceed the critical acceleration, meaning that the impact force must be greater than the maximum shear force of the wild chrysanthemum flower stem [22]. To obtain the optimal impact force, a three-factor, three-level experiment was conducted using the following motion parameters for the simulation: the critical drum speed, feeding speed, and collision angle.
In the simulation process, the roller’s applied rotational speed, the feeding speed imposed on the flower stem, and the collision angle were identified as the main factors influencing the magnitude of the critical acceleration, that is, the tensile (breaking) force. According to the kinematic analysis in Section 2.3, the roller rotational speed was set at three levels within the range of 2.4475 r/s to 3.9632 r/s; the feeding speed, which must exceed 0.05 m/s and maintain a roller speed ratio greater than 1, was set at three levels within the range of 0.05 m/s to 3.4 m/s; and the collision deviation angle, ranging from 0° to 90°, was also set at three levels.
The experimental factors and coding were derived through Design Expert 12.0, as shown in Table 4.

Table 4.
Test factors and coding of the motion parameters on flower picking performance.
The experimental design and results are presented in Table 5.

Table 5.
Trial protocol and results of the motion parameters on flower picking performance.
The above results were fitted using a second-order regression model in Design-Expert 12 software, with the critical acceleration taken as the response variable.
An analysis of variance (ANOVA) was conducted on the critical acceleration. The results indicated that the regression model for critical acceleration was statistically significant (p < 0.05), with factors A, B, AB, A2, and B2 having significant effects on the response value (p < 0.05), while the other factors were not significant. The lack-of-fit p-value was greater than 0.05, indicating that no significant lack of fit existed in the regression model.
2.5.4. Validation Test
After parameter optimization, the motion parameters for the wild chrysanthemum picking platform were set to a roller rotational speed of 3.73 rad/s and a clamping chain speed of 1.3 m/s. The test results showed that the optimized wild chrysanthemum picking platform achieved a picking cleanliness rate of 87.72%, meeting the relevant harvesting requirements for wild chrysanthemum. Based on these parameters, further bench tests will be conducted to obtain a complete set of parameter selections.
2.6. Bench Test
To verify the feasibility of the simulation data for the wild chrysanthemum-picking device, and to identify and solve potential issues, the bench test aimed to validate the optimal roller speed and clamping conveyor belt speed determined during the simulation-based flower picking process [23]. The goal is to achieve maximum flower collection while minimizing damage, and based on the issues encountered during the picking process, improvements will be suggested to provide optimization data for the development of the wild chrysanthemum-picking device. The test setup and process are shown in Figure 12.


Figure 12.
Wild chrysanthemum-picking device workbench.
The test was conducted at the 2-year-old wild chrysanthemum demonstration plantation base in Bai Ta Village, Qian County, Shaanxi Province. The focus of this test was to examine the picking efficiency [24], which is the primary indicator for the wild chrysanthemum-picking device.
The flower-picking efficiency is calculated using the following formula:
where Wz is the total mass of flowers on the stem before the test (g), and Wc is the total mass of flowers picked (g).
Using Design-Expert 12 software, a three-factor, three-level orthogonal spiral combination experiment was conducted with the picking gap x1, roller bow tooth bending angle x2, and feeding rate x3 as experimental factors, and the picking cleanliness rate R as the experimental index, under conditions of a roller rotational speed of 3.73 rad/s and a clamping chain speed of 1.3 m/s. A total of 17 experimental groups were designed, with each group tested five times, and the sum of the five trials taken as the result for that group. The coding scheme for the experimental factors is shown in Table 6, and the experimental plan and results are provided in Table 7.

Table 6.
Test factors and coding.

Table 7.
Trial protocol and results.
Using Design-Expert 12.0, the data results from Section 2.6 were fitted with a second-order regression equation, yielding a polynomial regression model with the picking cleanliness rate of wild chrysanthemum flowers as the response function and the factor levels as the independent variables.
A lack-of-fit test was conducted on the regression equation.
3. Results and Discussion
3.1. Effects of Harvesting Characteristics of Wild Chrysanthemums
The analysis of the mechanical properties of the different parts of wild chrysanthemums shows that the flower stalk, which supports the flower, is relatively fragile. Both the shear force and rupture force are smaller than those of the flower axis and small branch stems. In the rupture force test of the flower stalk, the breaking point was found to be at the junction between the flower receptacle and the flower stalk, which means that the weakest point of the flower stalk is at the connection between the flower receptacle and the stalk. The rupture force and maximum shear force of the flower stalk, flower axis, and small branch stem showed an increasing trend. Therefore, flower picking can be achieved using pulling and shearing forces, and controlling the appropriate rupture and shear forces can effectively avoid other parts being torn off or pulled out by the roots during the picking process.
3.2. Effects of Motion Parameters on Flower Picking Performance
The results from Section 2.5.3 were fitted using a second-order regression model in Design-Expert 12 software, yielding a polynomial regression equation with the critical acceleration as the response variable and the coded values of each factor as the independent variables.
where X1 represents factor A and X2 represents factor B.
An analysis of variance (ANOVA) was conducted on the critical acceleration, as shown in Table 8. The results indicated that the regression model for critical acceleration was statistically significant (p < 0.05), with factors A, B, AB, A2, and B2 having significant effects on the response value (p < 0.05), while the other factors were not significant. The lack-of-fit p-value was greater than 0.05, indicating that no significant lack of fit existed in the regression model.

Table 8.
Critical acceleration analysis of variance.
To more clearly analyze the interaction effects of different experimental factors on the critical acceleration as the experimental index, a response surface analysis of the simulation results was conducted using Design-Expert 12.0, as shown in Figure 13.
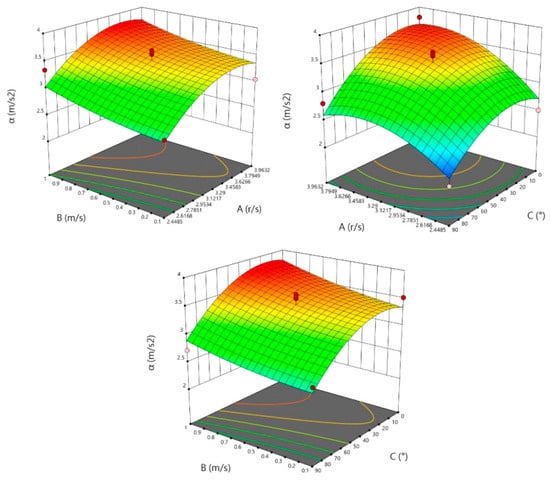
Figure 13.
Response surface of various factors affecting critical acceleration.
The critical acceleration y was optimized using Design-Expert 12 software, with the optimization objective function expressed as:
The optimal combination was determined to be a roller rotational speed of 3.8941 r/s and a feeding speed of 0.54 m/s. The corresponding maximum acceleration, as shown in Figure 14, was 3.524 m/s2.
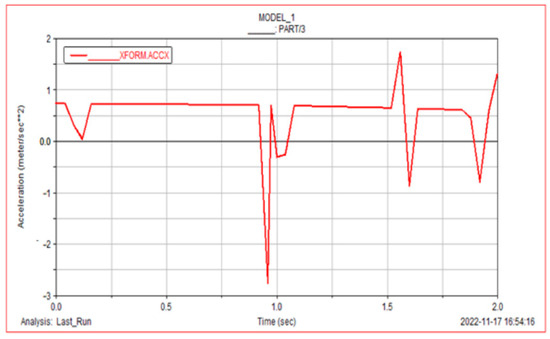
Figure 14.
Optimization of acceleration curve.
From Equation (17), it can be concluded that the optimal critical acceleration is 3.85 m/s2. Under this optimal acceleration, the maximum shear force of the flower stem would be 58.50 N, which was much greater than the maximum shear forces of each part in Table 2. This meets the flower-picking conditions, and subsequent bench tests will use this speed and feeding rate.
3.3. Effects of Bench Test
3.3.1. Analysis of Test Results
Using Design-Expert 12.0 software, a quadratic regression fitting equation was applied to the data from 2.6, resulting in a polynomial regression equation (Equation (18)), with flower-picking efficiency as the response function and the factor levels as independent variables:
The variance analysis of the net removal rate is shown in Table 9. The influence of each experimental factor on the net removal rate was significant for the whole model (0.01 < p < 0.05). The effect of C on the removal rate was very significant (p < 0.01). A, C2 had a significant effect on the removal rate, and A2 had a significant effect on the removal rate. The other experimental factors had no significant effect on the removal rate (p > 0.1).

Table 9.
Variance analysis.
The lack-of-fit test for the above regression equation gives a p-value of 0.188 (p > 0.1), which is not significant. This indicates that there are no other major factors affecting the experiment. The relationship between the experimental indicators and the factors is significantly quadratic, and the analysis results are reasonable.
3.3.2. Response Surface Analysis
The significant interactions between the bow tooth bending angle, feeding rate, and flower picking gap and their corresponding surface plots for picking efficiency are shown in Figure 15.
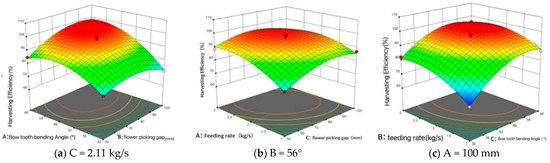
Figure 15.
Response surface lot.
For the flower picking rate R, during operation on the workbench, with a given drum speed and feeding speed, the feeding rate was the main factor influencing the picking rate.
To obtain the optimal operational parameters for the harvesting device’s performance, the Design Expert 12.0 software was used to perform objective optimization based on the regression model described above. According to the operational requirements and conditions of the picking device, the constraint function is given by Equation (19):
Through bench tests, it was verified that when the flower picking gap was 100 mm, the bending angle of the picking teeth was 56°, and the feeding rate was 2.1 kg/s, the picking rate achieved was 95.9%. The counter-rotating drum flower picking device thus met the design requirements.
4. Conclusions
- (1)
- In response to the challenges of high labor demands and low efficiency associated with the manual harvesting of wild chrysanthemum in China, and the absence of dedicated mechanized harvesting equipment, an opposed roller picking device was designed, tailored to meet the specific agronomic requirements of wild chrysanthemum harvesting.
- (2)
- The key components of the opposed roller picking device for wild chrysanthemum were analyzed to ensure full-range harvesting coverage during the picking process, and the optimal harvesting tines were selected. To enhance the picking efficiency during the collision between the flowers and the tines on the rollers, the roller arrangement was carefully designed, and the motion dynamics during the collision process were analyzed. It was determined that the primary factors influencing the picking performance were the roller rotational speed, feeding speed, and collision angle. Based on these factors, a regression orthogonal experiment was designed using critical acceleration as the experimental index to establish a regression model. Under optimal collision force conditions, the feeding speed was determined to be 1.3 m/s, and the roller rotational speed was 3.73 rad/s.
- (3)
- A regression orthogonal experiment was conducted using the picking gap, roller bow tooth bending angle, and feeding rate as experimental factors, with the flower picking cleanliness rate as the experimental index. A regression model was established to describe the relationship between the experimental index and the influencing factors, thereby identifying the optimal range of experimental parameters. Bench tests further verified that, when the picking gap was set to 100 mm, the roller bow tooth bending angle to 56°, and the feeding rate to 2.1 kg/s, the picking rate reached 95.9%, effectively meeting the design requirements.
Author Contributions
Conceptualization, Y.B.; methodology, Y.B.; software, S.L.; validation, Z.L.; formal analysis, Z.M.; investigation, S.L.; resources, Z.L. and Z.M.; data curation, Y.B.; writing original draft preparation, Y.B.; writing review and editing, Z.L.; visualization, Y.B.; supervision, Y.H.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China youth Science Foundation project (No. 32101629), the Key Research and Development Program of Shaanxi Province, China (No. 2022NY-227), and the China Postdoctoral Science Foundation project (No.2021M692657).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All relevant data are clearly mentioned within the article and are publicly available in appropriate data repositories.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yuan, H.; Lai, Z.; Guan, Y.; Zhang, Y.; Huang, Y. Pharmacology study of active constituents from chrysanthemum indicum. Chin. Arch. Tradit. Chin. Med. 2018, 36, 651–653. (In Chinese) [Google Scholar]
- Song, Y.; Xu, L.; Miu, J.; Xiao, P. Research progress in chrysanthemum indicum. Mod. Chin. Med. 2020, 22, 1751–1756, 1762. (In Chinese) [Google Scholar]
- Liu, S. Design and Experimental Study of Drum Type Wild Chrysanthemum Picking Device. Master’s Thesis, Northwest A&F University, Xianyang, China, 2023. (In Chinese). [Google Scholar]
- Wang, T. Design and Experimental Study of Stem Cutter for Wild Chrysanthemum. Master’s Thesis, Northwest A&F University, Xianyang, China, 2023. (In Chinese). [Google Scholar]
- Wang, R.; Yu, H.; Chen, A.; Li, A.; Gao, L.; Zheng, Z. Design and Test of Pneumatic Flipping Comb-type Chrysanthemum Picking Device. Trans. Chin. Soc. Agric. Mach. 2022, 53, 184–193. (In Chinese) [Google Scholar]
- Wang, R.; Zheng, Z.; Lu, X.; Cui, B.; Gao, L. Design and Test of Comb-teeth Reciprocating Chrysanthemum morifolium Picking Device. Trans. Chin. Soc. Agric. Mach. 2019, 50, 73–79, 97. (In Chinese) [Google Scholar]
- Ji, C.; Zhang, C.; Gu, B.; Fu, H.; Xie, D.; Guo, J. Design and experiment of shear-sucting mountain chrysanthemum picking machine. Trans. Chin. Soc. Agric. Mach. 2017, 48, 137–145. (In Chinese) [Google Scholar]
- Beier, K.; Ehlert, D. Methods for evaluation of picking performance of chamomile (Matricaria recutita L.) harvesters. J. Appl. Res. Med. Aromat. Plants 2014, 1, e1–e7. [Google Scholar]
- Kumhála, F.; Kavka, M.; Prošek, V. Capacitive throughput unit applied to stationary hop picking machine. Comput. Electron. Agric. 2013, 95, 92–97. [Google Scholar] [CrossRef]
- Zhai, D.; Zhai, W.; Zhai, Z. Hand-held Chrysanthemum Picker. CN201216069U, 8 April 2009. [Google Scholar]
- Cui, T.; Liu, J.; Zhang, D.; Shi, D. Flexible body simulation for corn stem based on ANSYS and ADAMS. Trans. Chin. Soc. Agric. Mach. 2012, 43 (Suppl. S1), 112–115. (In Chinese) [Google Scholar]
- Wang, F.; Li, F.; Zhang, P.; Zhang, L.; Wang, H. Design and experiment of double roller dried pepper pedicel removal device. Trans. Chin. Soc. Agric. Mach. 2024, 55, 191–199. (In Chinese) [Google Scholar]
- Lan, W. Research and experiment on harvesting straw during threshing before cutting. Fujian Agric. Mach. 1998, 39–43. (In Chinese) [Google Scholar]
- Pu, M.; Wu, J. Study on flexible sugarcane modeling based on ADAMS Software. J. Syst. Simul. 2009, 21, 1930–1932. (In Chinese) [Google Scholar]
- Sun, C.; Hu, C.; Hou, Q.; Pan, Z. Simulation of mechanical thinning flower actuator based on ADAMS. J. Agric. Mech. Res. 2015, 37, 70–73. (In Chinese) [Google Scholar]
- Chen, J. A Pilot Study About the Main Parameters of Hop Picking Machine. Master’s Thesis, Xin Jiang Agricultural University, Urumqi, China, 2011. (In Chinese). [Google Scholar]
- Zeng, H. Research on Hop’s Machine Pickability. Master’s Thesis, Xin Jiang Agricultural University, Urumqi, China, 2000. (In Chinese). [Google Scholar]
- Ehlert, D.; Adamek, R.; Giebel, A.; Horn, H.-J. Influence of comb parameters on picking properties for chamomile flowers (Matricaria recutita). Ind. Crops Prod. 2011, 33, 242–247. [Google Scholar] [CrossRef]
- Franke, R.; Schilcher, H. Relevance and Use of Chamomile (Matricaria recutita L.). Proceedings of the First International Symposium on Chamomile Research, Development and Production. Acta Hortic. 2007, 749, 29–43. [Google Scholar] [CrossRef]
- Lai, Q.; Yu, Q.; Dong, J. Dynamic analysis of rotary tiller gearbox based on EDEM, ADAMS and ANSYS. J. Intell. Fuzzy Syst. 2018, 36, 1153–1160. [Google Scholar] [CrossRef]
- Du, H.W.; Han, Z.Z. Design of Sweet Potato Vine Chopping and Returning Machine. Appl. Mech. Mater. 2014, 3064, 538. [Google Scholar] [CrossRef]
- Bajema, R.G.M.; Hyde, K. Peterson. Instrumentation design for dynamic axial compression of cylindrical tissue samples. Trans. ASAE 1998, 41, 747. [Google Scholar] [CrossRef]
- Derafshi, M.H. Design and Construction of a Pneumatic-thermal Machine for Controlling Colorado Potato Beetle (Leptinotarsa decemlineata). J. Appl. Sci. 2006, 6, 919–925. [Google Scholar]
- El Masry, G.; Cubero, S.; Molto, E.; Blasco, J. In-line sorting of irregular potatoes by using automated computer-based machine vision system. J. Food Eng. 2012, 112, 60–68. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).