Author Contributions
Conceptualization, M.L., X.H. and X.W.; data curation, G.Z. and J.L.; formal analysis, X.P.; funding acquisition, X.H. and X.W.; investigation, K.G.; methodology, X.H. and X.W.; project administration, X.H.; resources, X.W.; software, M.L., G.Z., X.P. and K.G.; supervision, X.W. and J.L.; validation, M.L.; writing—original draft, M.L.; writing—review and editing, M.L. and J.L. All authors have read and agreed to the published version of the manuscript.
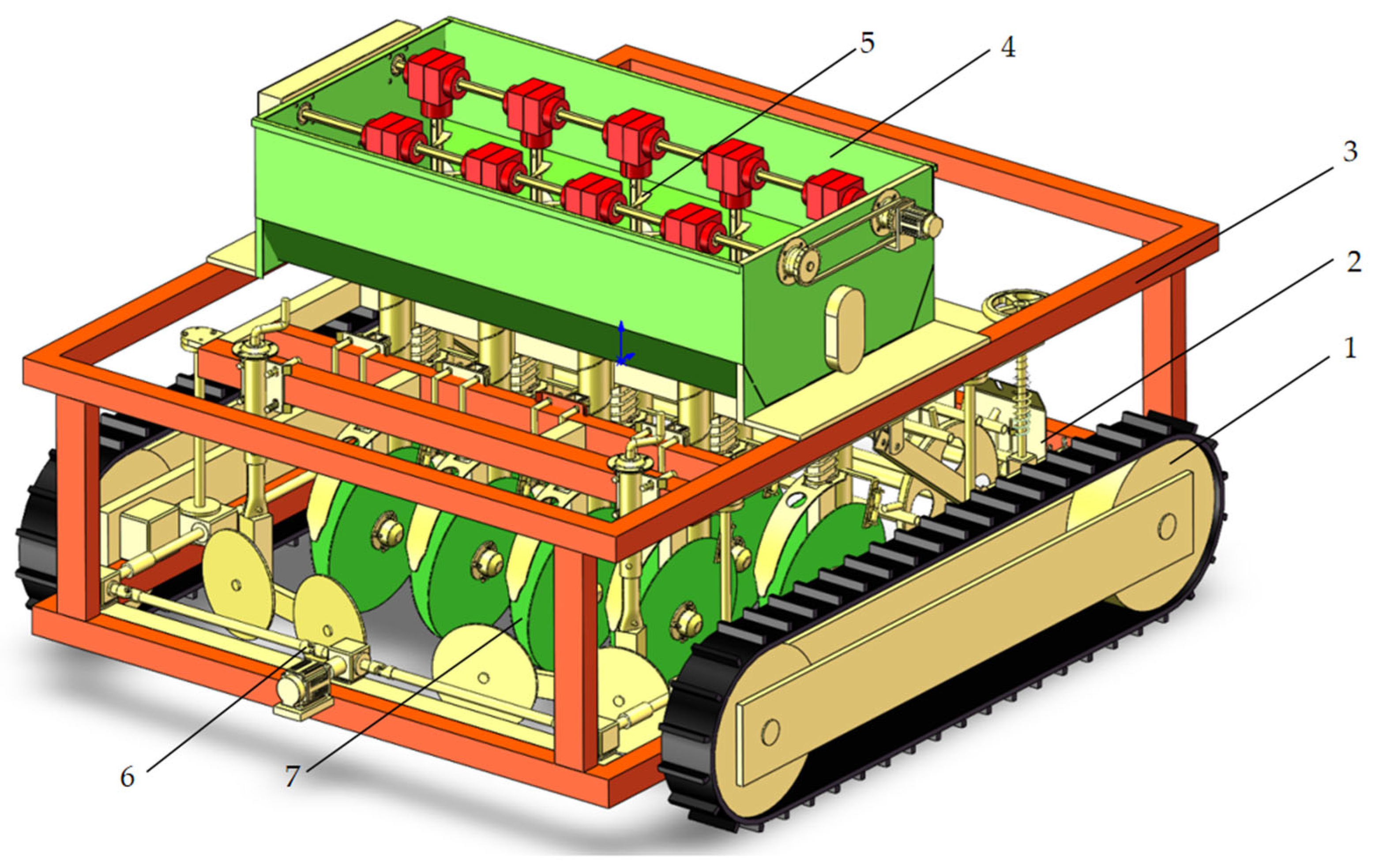
Figure 1.
Design drawings of morel mushroom seeder: 1, crawler chassis; 2, soil-covering module; 3, mobile chassis; 4, seeding module; 5, spiral seeding device; 6, four-corner lifting mechanism; and 7, trenching module.
Figure 1.
Design drawings of morel mushroom seeder: 1, crawler chassis; 2, soil-covering module; 3, mobile chassis; 4, seeding module; 5, spiral seeding device; 6, four-corner lifting mechanism; and 7, trenching module.
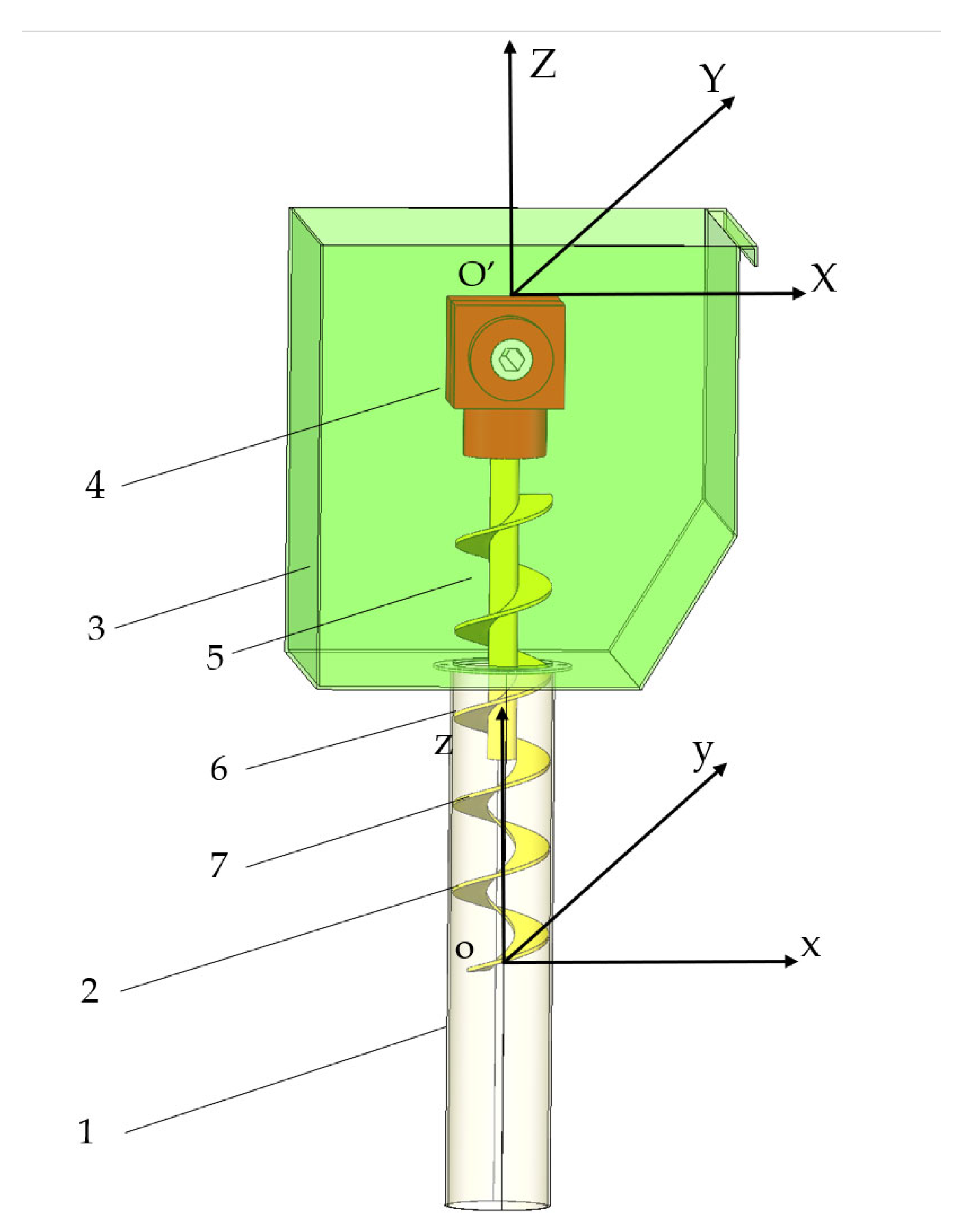
Figure 2.
Spiral seeding device and coordinate system establishment: 1, seeding tube; 2, spiral components; 3, seed box; 4, bevel gear steering device; 5, seed filling stage; 6, transport stage; and 7, dispersing stage.
Figure 2.
Spiral seeding device and coordinate system establishment: 1, seeding tube; 2, spiral components; 3, seed box; 4, bevel gear steering device; 5, seed filling stage; 6, transport stage; and 7, dispersing stage.
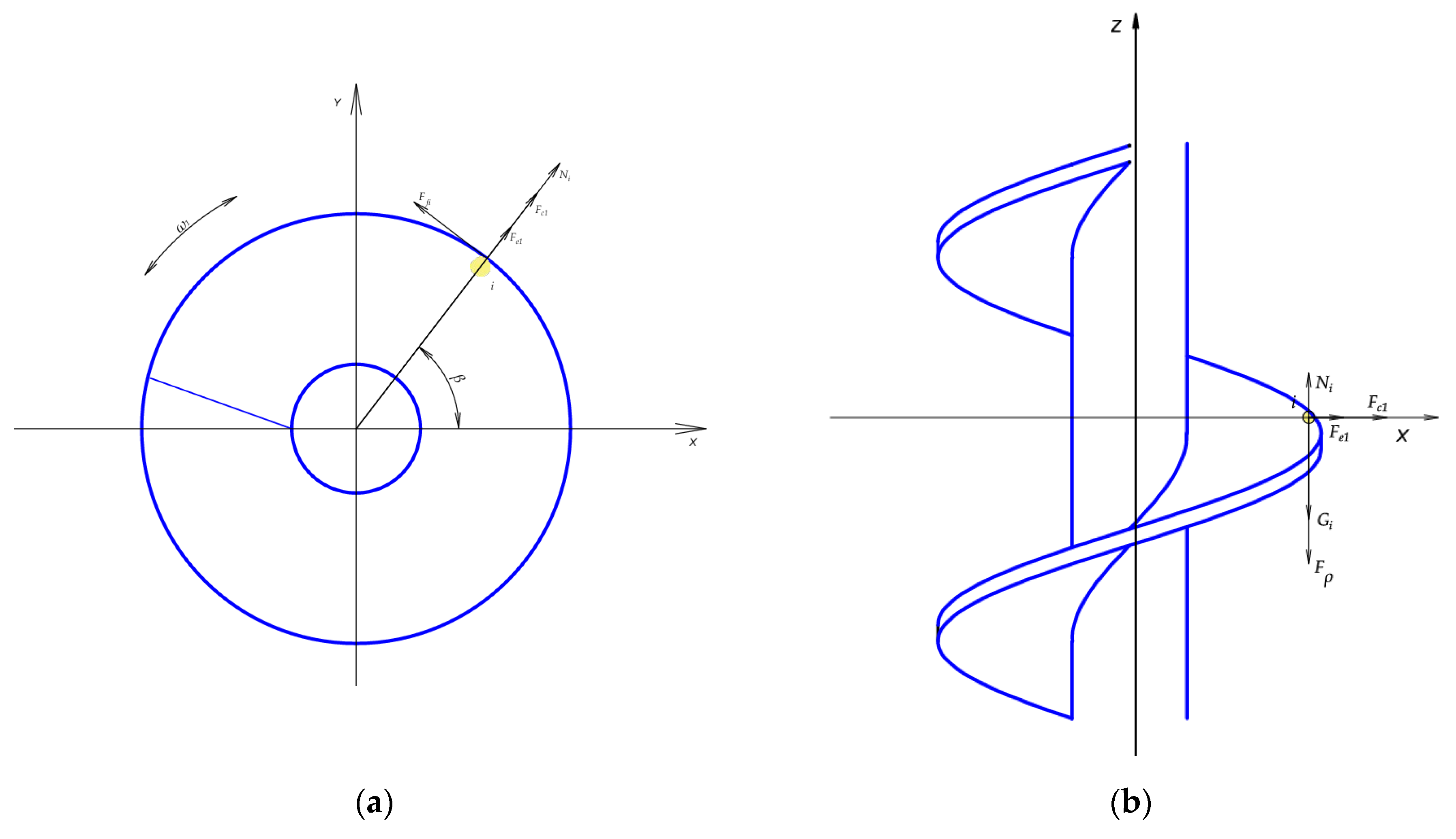
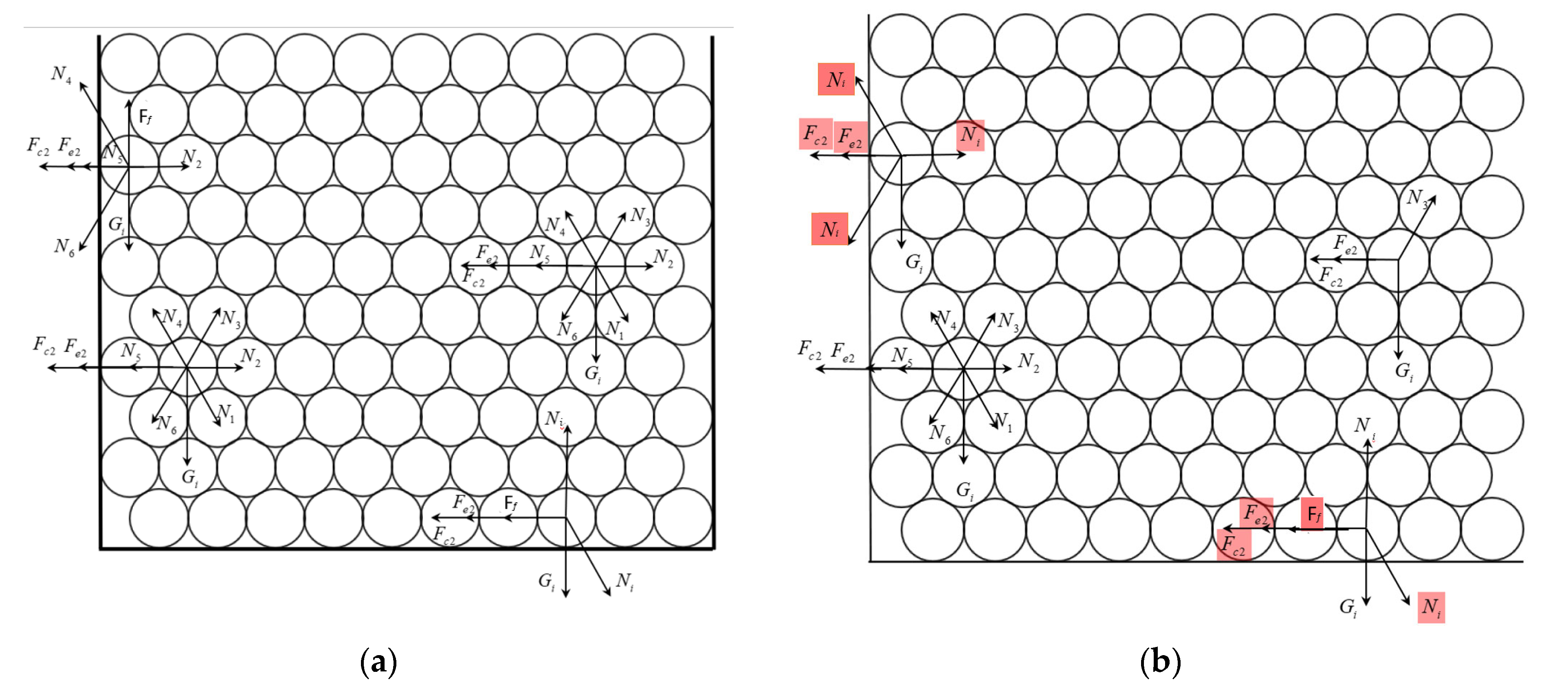
Figure 3.
Initial force analysis of seed particles: (a) XO’Y plane and (b) XO’Z plane.
Figure 3.
Initial force analysis of seed particles: (a) XO’Y plane and (b) XO’Z plane.
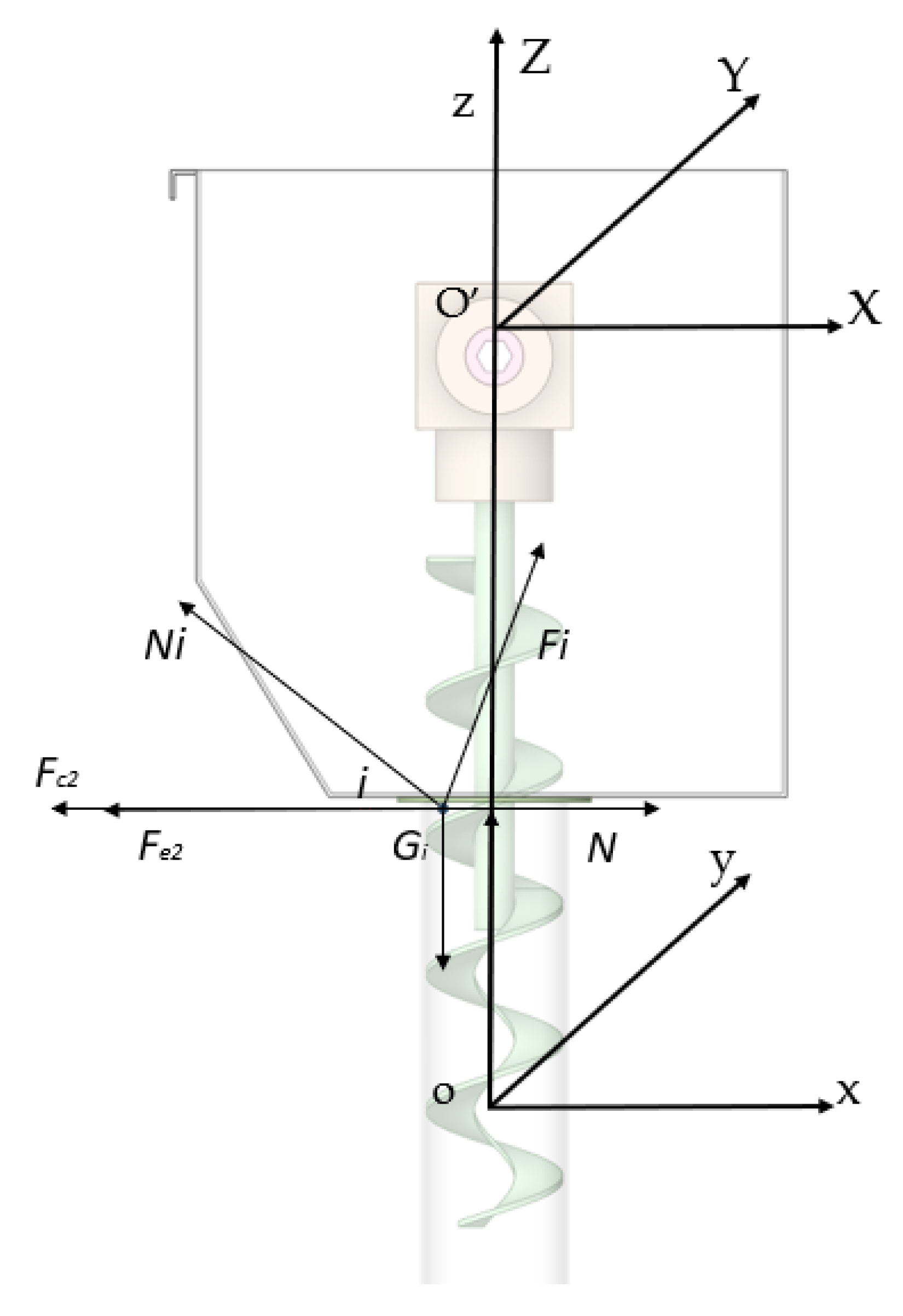
Figure 4.
Force analysis in reference coordinate system.
Figure 4.
Force analysis in reference coordinate system.
Figure 5.
Force analysis of seed particles at the instant of sliding: (a) Y direction and (b) Z direction.
Figure 5.
Force analysis of seed particles at the instant of sliding: (a) Y direction and (b) Z direction.
Figure 6.
Force diagram of the dispersing stage: (a) having inner wall support and (b) losing side wall support.
Figure 6.
Force diagram of the dispersing stage: (a) having inner wall support and (b) losing side wall support.
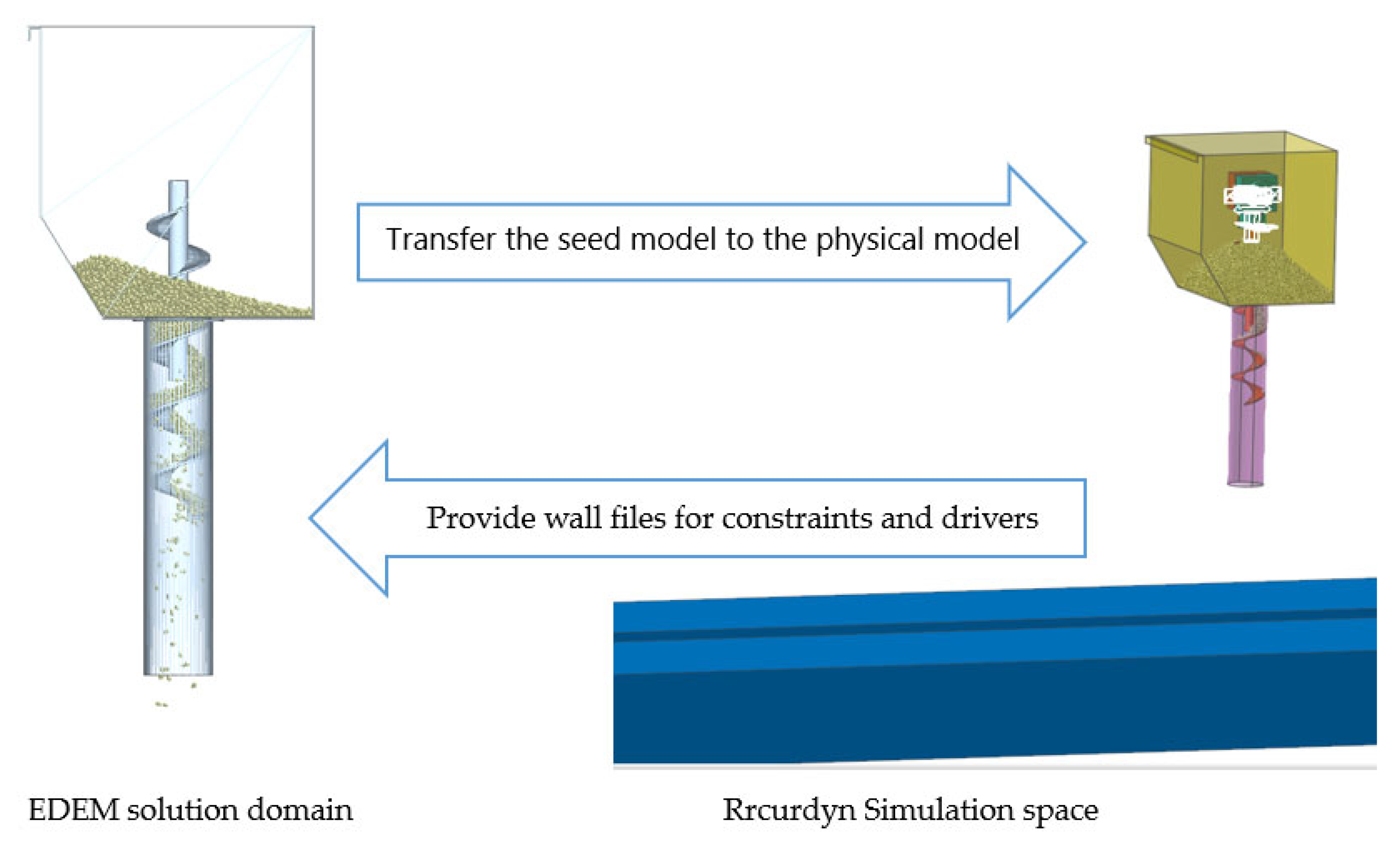
Figure 7.
Joint simulation model.
Figure 7.
Joint simulation model.
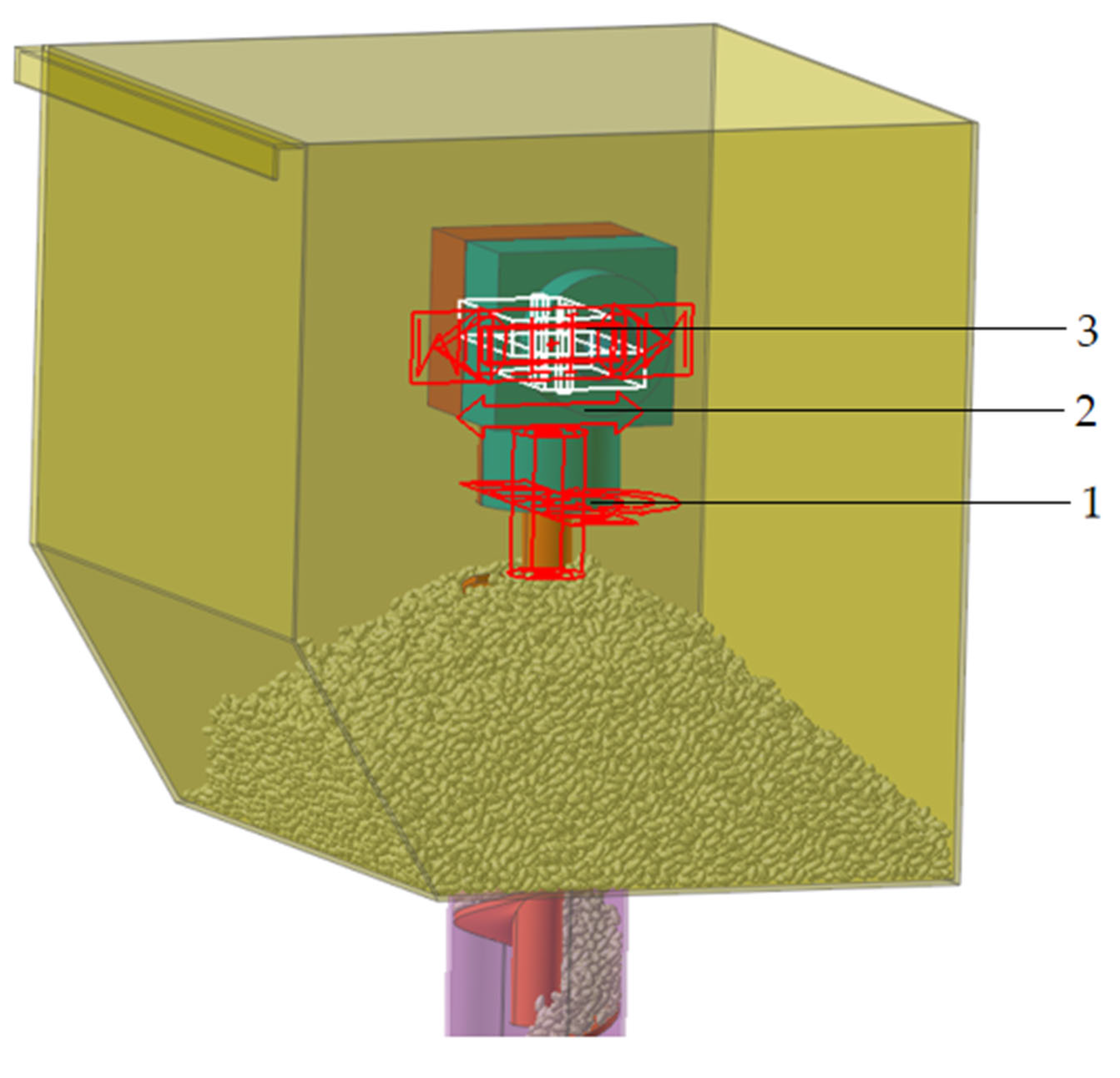
Figure 8.
Constraints and driving settings of EDEM–RecurDyn coupled simulation: 1, rotational Joint; 2, translational Joint; and 3, fixed joint.
Figure 8.
Constraints and driving settings of EDEM–RecurDyn coupled simulation: 1, rotational Joint; 2, translational Joint; and 3, fixed joint.
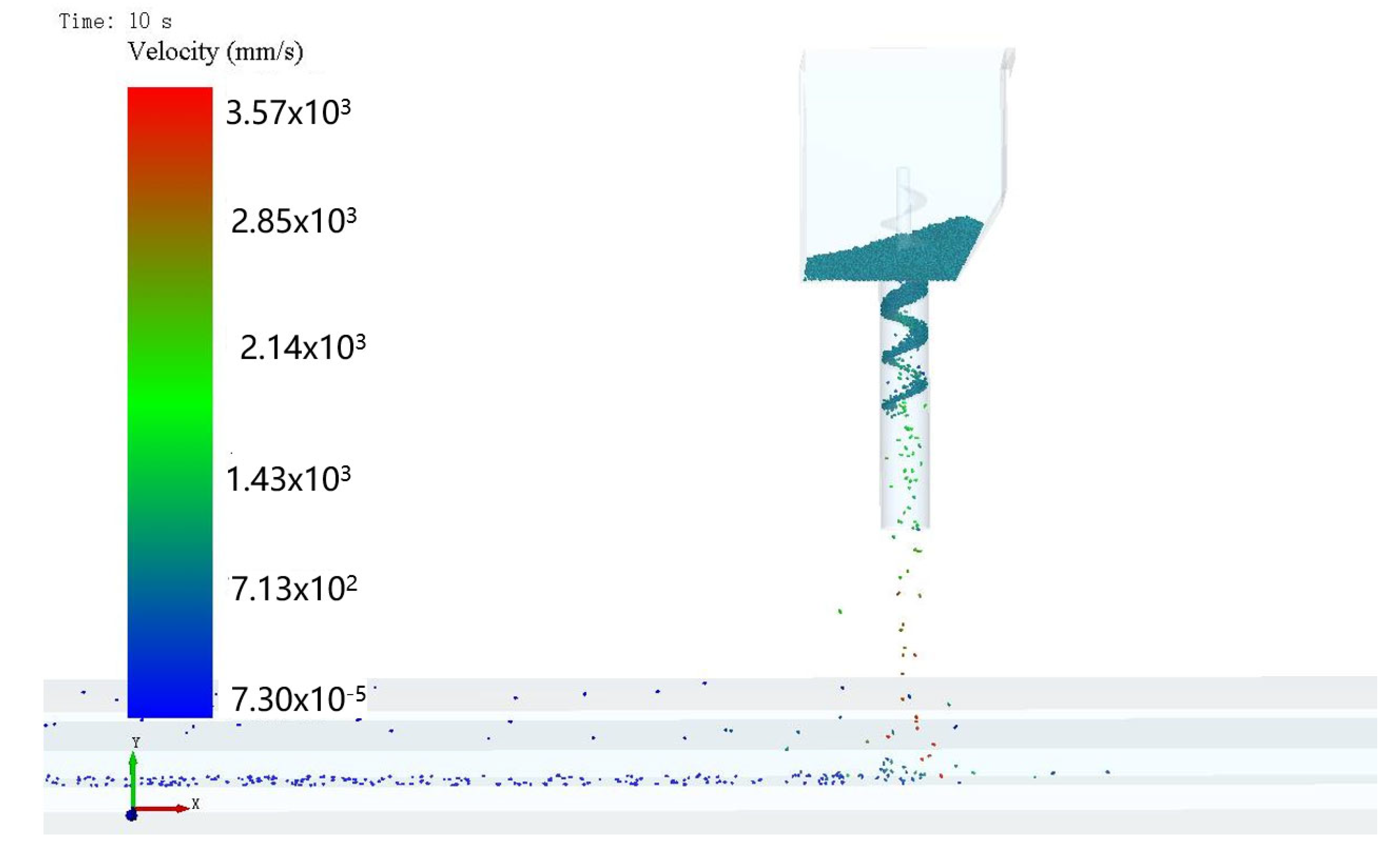
Figure 9.
Coupled DEM-MBD approach is adopted for the analysis.
Figure 9.
Coupled DEM-MBD approach is adopted for the analysis.
Figure 10.
Interval statistics diagram: (a) interval statistics for pitch 56 mm, (b) interval statistics for pitch 63 mm, and (c) interval statistics for pitch 70 mm. The red color in the picture is the projection of the seed box.
Figure 10.
Interval statistics diagram: (a) interval statistics for pitch 56 mm, (b) interval statistics for pitch 63 mm, and (c) interval statistics for pitch 70 mm. The red color in the picture is the projection of the seed box.
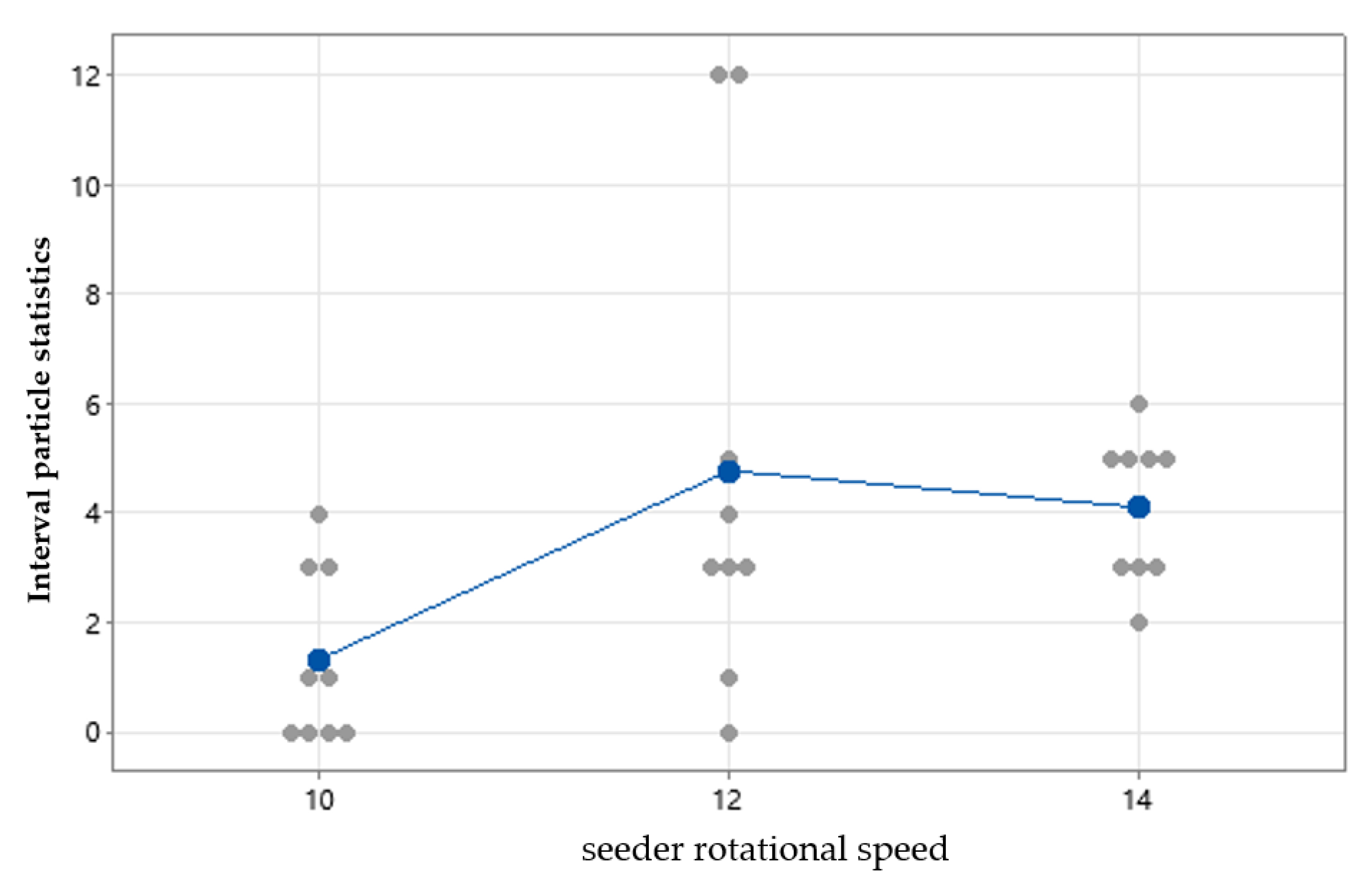
Figure 11.
Single-value of interval particle statistics fluctuate as the rotational speed of the planter increases.
Figure 11.
Single-value of interval particle statistics fluctuate as the rotational speed of the planter increases.
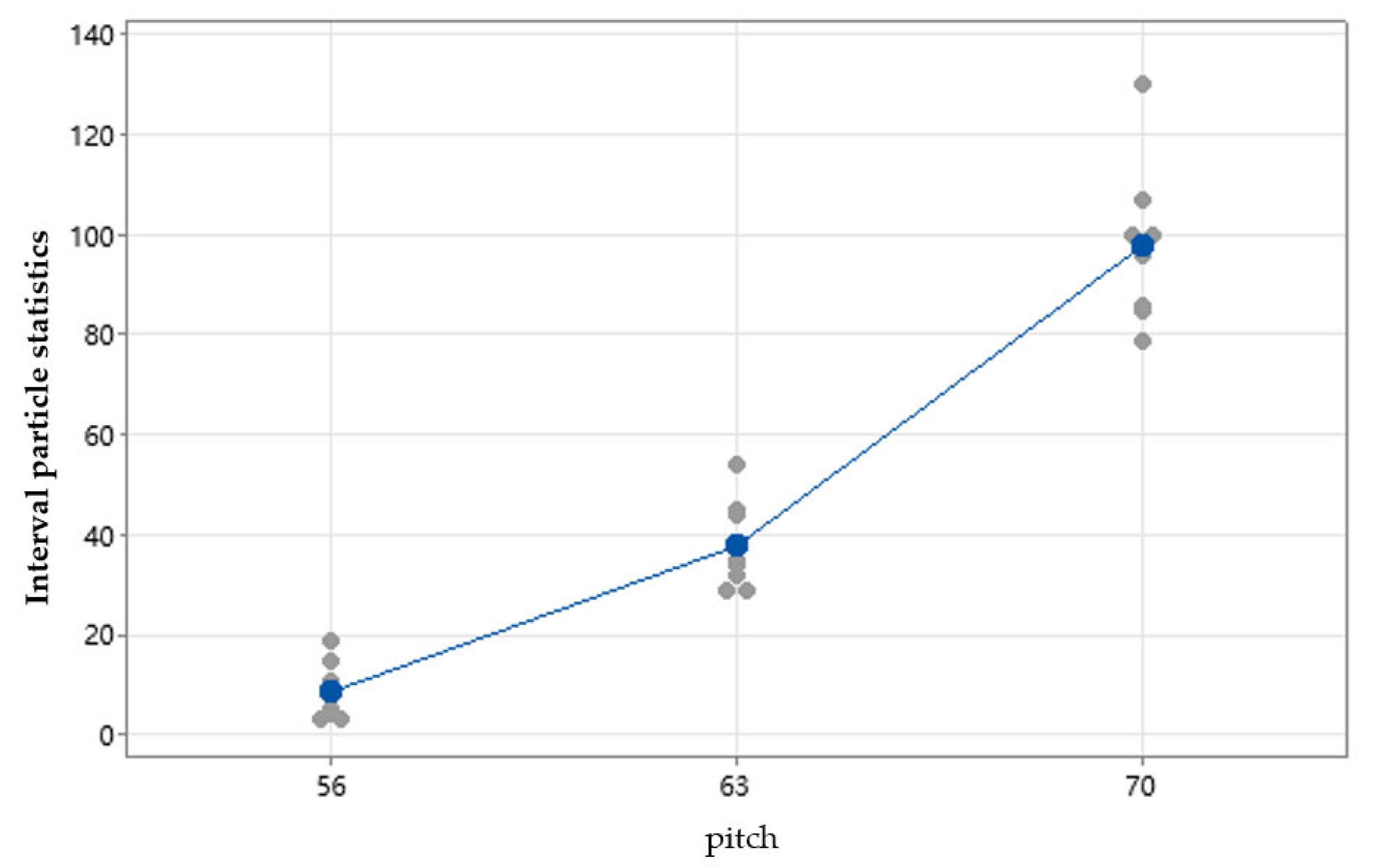
Figure 12.
Single-value plot of interval particle statistics and grouping with the increase in pitch.
Figure 12.
Single-value plot of interval particle statistics and grouping with the increase in pitch.
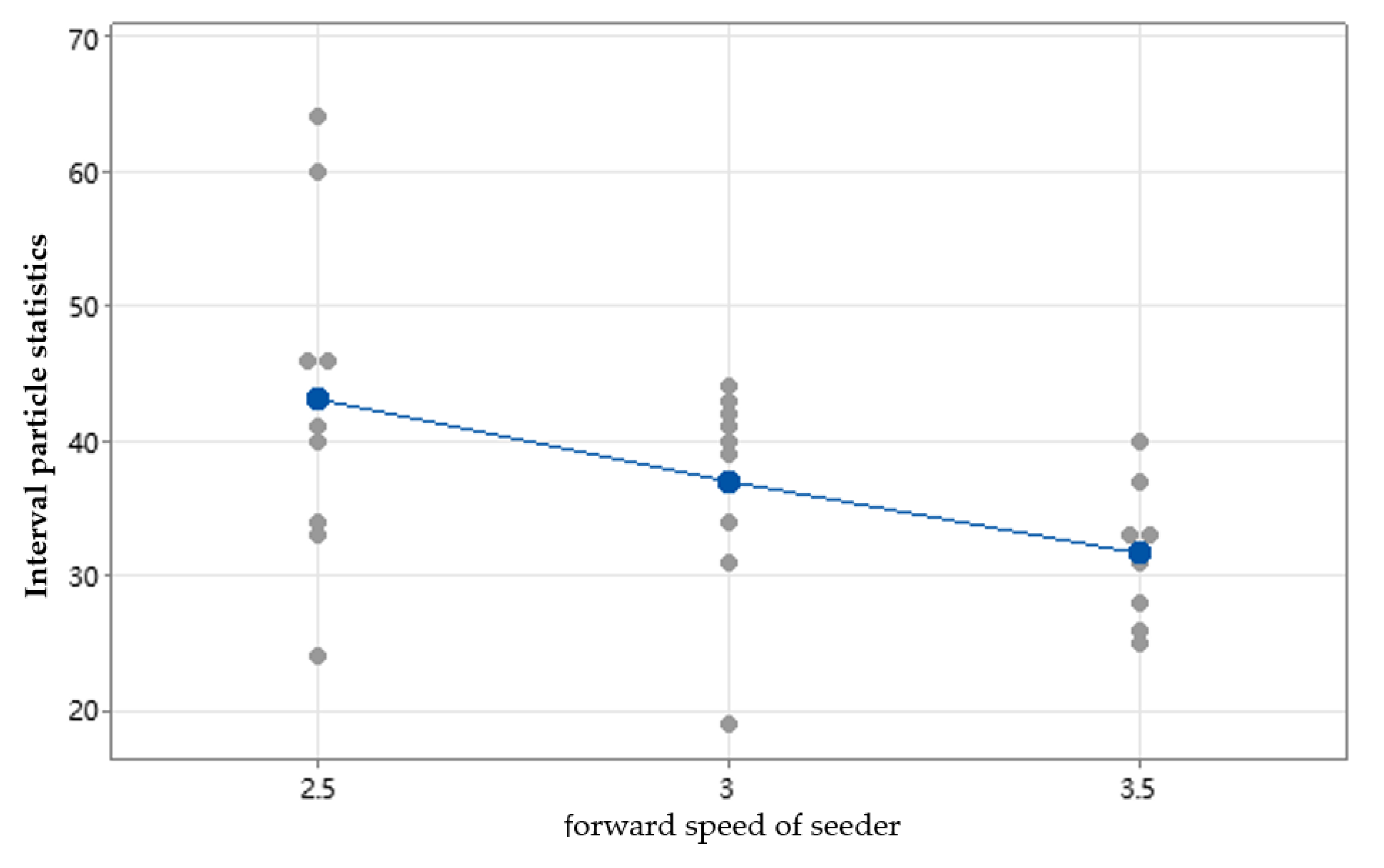
Figure 13.
Single-value plot of interval particle statistics and grouping with increasing forward speed of the seeder.
Figure 13.
Single-value plot of interval particle statistics and grouping with increasing forward speed of the seeder.
Figure 14.
Prototype of morel mushroom seeder: 1, seeding module; 2, GPS; 3, seeder power unit; 4, seed collection cloth; 5, crawler chassis; 6, soil-covering module; 7, trenching module; 8, chassis drive motor; 9, seeding tube; 10, four-corner lifting mechanism; 11, sowing positions; and 12, spiral components.
Figure 14.
Prototype of morel mushroom seeder: 1, seeding module; 2, GPS; 3, seeder power unit; 4, seed collection cloth; 5, crawler chassis; 6, soil-covering module; 7, trenching module; 8, chassis drive motor; 9, seeding tube; 10, four-corner lifting mechanism; 11, sowing positions; and 12, spiral components.
Figure 15.
Trials of seeding with a morel mushroom seeder: 1, morel mushroom seeds; 2, seeding furrow; and 3, tape measure.
Figure 15.
Trials of seeding with a morel mushroom seeder: 1, morel mushroom seeds; 2, seeding furrow; and 3, tape measure.
Figure 16.
Response surface plots and contour plots of AB against composite scores: (a) response surfaces to composite scores and (b) contour plots were examined.
Figure 16.
Response surface plots and contour plots of AB against composite scores: (a) response surfaces to composite scores and (b) contour plots were examined.
Figure 17.
Response surface plots and contour plots of AC against composite scores: (a) main view of the test area and (b) side view of test area.
Figure 17.
Response surface plots and contour plots of AC against composite scores: (a) main view of the test area and (b) side view of test area.
Figure 18.
Response surface plots and contour plots of BC to composite scores.
Figure 18.
Response surface plots and contour plots of BC to composite scores.
Table 1.
Simulation parameters of discrete element.
Table 1.
Simulation parameters of discrete element.
| Parameters | Mean Value |
|---|
| Seed size (mm × mm × mm) | 7.33 × 4.51 × 4.43 |
| Seed density (kg/m3) | 400 |
| Seed Poisson’s ratio | 0.34 |
| Seed shear modulus (Pa) | 1.23 × 106 |
| Steel density (kg/m3) | 7865 |
| Steel Poisson’s ratio | 0.3 |
| Steel shear modulus (Pa) | 7.90 × 1010 |
| Seed-to-seed static friction coefficient | 0.4 |
| Seed-to-seed kinetic friction coefficient | 0.45 |
| Seed-to-steel static friction coefficient | 0.4 |
| Seed-to-steel kinetic friction coefficient | 0.6 |
Table 2.
Experimental factors and codes.
Table 2.
Experimental factors and codes.
| Code | Factors |
|---|
| Pitch (mm) | Rotational Speed (r/min) | Forward Speed (km/h) |
|---|
| 1 | 56 | 10 | 2.5 |
| 2 | 63 | 12 | 3 |
| 3 | 70 | 14 | 3.5 |
Table 3.
Statistical information on the number of seeds.
Table 3.
Statistical information on the number of seeds.
| Partition | Pitch (mm)–Forward Speed (mm/s)–Rotational Speed (r/s) |
|---|
| 56-694-02 | 56-694-0167 | 56-694-0234 | 56-833-0167 | 63-694-02 | 63-833-02 | 63-833-0167 | 63-974-02 | 70-694-02 | 70-833-0167 | 70-833-0234 | 70-833-02 |
|---|
| 1 | 4 | 0 | 5 | 9 | 40 | 19 | 29 | 28 | 81 | 107 | 85 | 92 |
| 2 | 12 | 3 | 3 | 8 | 34 | 34 | 29 | 25 | 86 | 85 | 78 | 91 |
| 3 | 12 | 0 | 5 | 11 | 33 | 31 | 34 | 31 | 87 | 86 | 69 | 85 |
| 4 | 3 | 1 | 6 | 5 | 41 | 43 | 38 | 37 | 102 | 96 | 100 | 106 |
| 5 | 0 | 4 | 5 | 3 | 46 | 42 | 45 | 26 | 88 | 130 | 97 | 86 |
| 6 | 3 | 3 | 3 | 3 | 46 | 40 | 35 | 33 | 87 | 100 | 93 | 114 |
| 7 | 1 | 0 | 2 | 4 | 60 | 41 | 54 | 32 | 107 | 79 | 106 | 107 |
| 8 | 5 | 1 | 5 | 19 | 64 | 44 | 44 | 33 | 100 | 100 | 91 | 90 |
| 9 | 3 | 0 | 3 | 15 | 24 | 39 | 32 | 40 | 102 | 98 | 94 | 74 |
| Uniformity Coefficient | 29.57 | 18.59 | 66.82 | 34.37 | 70.40 | 78.46 | 77.78 | 84.53 | 90.00 | 84.71 | 87.38 | 86.50 |
Table 4.
Results of the experiment.
Table 4.
Results of the experiment.
| Run Sequence | Forward Speed (km/h) | Pitch (mm) | Spiral Speed (r/min) | Interval Seed Mean |
|---|
| 1 | 2.5 | 56 | 12 | 2.50 |
| 2 | 2.5 | 63 | 12 | 43.11 |
| 3 | 2.5 | 56 | 10 | 1.33 |
| 4 | 3.5 | 63 | 12 | 31.67 |
| 5 | 2.5 | 56 | 14 | 4.11 |
| 10 | 3.0 | 56 | 10 | 8.56 |
| 11 | 3.0 | 70 | 14 | 90.33 |
| 14 | 3.0 | 63 | 12 | 37.00 |
| 18 | 2.5 | 70 | 12 | 93.33 |
| 23 | 3.0 | 70 | 10 | 97.89 |
Table 5.
Analysis of variance.
Table 5.
Analysis of variance.
| Source | df | Adj SS | Adj MS | F-Value | p-Value |
|---|
| Model | 6 | 13,813.5 | 2302.26 | 50.91 | 0.001 |
| Linear | 3 | 5365.7 | 1788.56 | 39.55 | 0.002 |
| Forward speed | 1 | 216.6 | 216.58 | 4.79 | 0.094 |
| Pitch | 1 | 4009.6 | 4009.61 | 88.67 | 0.001 |
| Spiral speed | 1 | 154.1 | 154.05 | 3.41 | 0.139 |
| 2-Factor interaction | 3 | 141.5 | 47.15 | 1.04 | 0.465 |
| Forward speed
×
pitch | 1 | 61.3 | 61.31 | 1.36 | 0.309 |
| Speed × spiral speed | 1 | 139.3 | 139.34 | 3.08 | 0.154 |
| Pitch
×
spiral speed | 1 | 96.0 | 96.04 | 2.12 | 0.219 |
| Error | 4 | 180.9 | 45.22 | | |
| Total | 10 | 13,994.4 | | | |
Table 6.
Summary of calculation results.
Table 6.
Summary of calculation results.
| Partition | 56-694-02 | 56-694-0167 | 56-694-0234 | 56-833-0167 | 63-694-02 | 63-833-02 | 63-833-0167 | 63-974-02 | 70-694-02 | 70-833-0167 | 70-833-0234 | 70-833-02 |
|---|
| Uniformity coefficient (%) | 29.57 | 18.59 | 66.81 | 34.37 | 70.40 | 78.46 | 77.78 | 84.53 | 90.00 | 84.72 | 87.38 | 86.49 |
Table 7.
Evaluation index.
Table 7.
Evaluation index.
| Interval Classification | Assessment of Sowing Performance | |
|---|
| 0.9 × N0 ≤ N0 ≤ 1.1 × N0 | 100% | Excellent |
| 1.1 × N0 < N0 ≤ 1.2 × N0, 0.8 × N0 ≤ N0 < 0.9 × N0 | 90% | |
| 1.2 × N0 < N0 ≤ 1.3 × N0, 0.7 × N0 ≤ N0 < 0.8 × N0 | 80% | |
| 1.3 × N0 < N0 ≤ 1.4 × N0, 0.6 × N0 ≤ N0 < 0.7 × N0 | 70% | Qualified |
| 1.4 × N0 < N0 ≤ 1.5 × N0, 0.5 × N0 ≤ N0 < 0.6 × N0 | 60% | |
| 1.5 × N0 < N0 ≤ 1.6 × N0, 0.4 × N0 ≤ N0 < 0.5 × N0 | 50% | |
| 1.6 × N0 < N0 ≤ 1.7 × N0, 0.3 × N0 ≤ N0 < 0.4 × N0 | 40% | |
| 1.7 × N0 < N0 ≤ 1.8 × N0, 0.2 × N0 ≤ N0 < 0.3 × N0 | 30% | |
| 1.8 × N0 < N0 ≤ 1.9 × N0, 0.1 × N0 ≤ N0 < 0.2 × N0 | 20% | |
| 1.9 × N0 < N0, N0 < 0.1 × N0 | 10% | Poor |
Table 8.
Comprehensive evaluation results.
Table 8.
Comprehensive evaluation results.
| Parameter Settings | Uniformity Index (%) | Evaluation Index (%) | Comprehensive Evaluation Index (%) |
|---|
| 56-694-02 | 29.57 | 10 | 19.79 |
| 56-694-0167 | 18.59 | 10 | 14.29 |
| 56-694-0234 | 66.81 | 20 | 43.41 |
| 56-833-0167 | 34.37 | 30 | 32.19 |
| 63-694-02 | 70.40 | 60 | 65.20 |
| 63-833-02 | 78.46 | 80 | 79.23 |
| 63-833-0167 | 77.78 | 80 | 78.89 |
| 63-974-02 | 84.52 | 100 | 92.26 |
| 70-694-02 | 90.01 | 10 | 50.00 |
| 70-833-0167 | 84.72 | 10 | 47.36 |
Table 9.
Optimal parameter values.
Table 9.
Optimal parameter values.
| | Forward Speed (km/h) | Helical Pitch (mm) | Rotation Speed (r/min) |
|---|
| Optimal Parameters | 3.5 | 63 | 12 |
Table 10.
Response surface analysis experimental design.
Table 10.
Response surface analysis experimental design.
| Factors | Levels |
|---|
| −1 | 0 | 1 |
|---|
| A—Pitch(mm) | 56 | 63 | 70 |
| B—Rotational speed(r/min) | 10 | 12 | 14 |
| C—Forward speed(km/h) | 2.5 | 3 | 3.5 |
Table 11.
Response surface optimization integrated scoring test design and results.
Table 11.
Response surface optimization integrated scoring test design and results.
| Test Number | A—Pitch | B—Spiral Speed | C—Forward Speed | Y1—Uniformity Index | Y2—Amount | Y—Comprehensive Evaluation Index |
|---|
| 1 | 56 | 10 | 3 | 90.06 | 47 | 81.86 |
| 2 | 70 | 10 | 3 | 42.58 | 49 | 63.6 |
| 3 | 56 | 14 | 3 | 43.65 | 73 | 73.63 |
| 4 | 70 | 14 | 3 | 62.85 | 84 | 85.74 |
| 5 | 56 | 12 | 2.5 | 48.56 | 70 | 74.4 |
| 6 | 70 | 12 | 2.5 | 66.65 | 48 | 72.86 |
| 7 | 56 | 12 | 3.5 | 78.96 | 73 | 87.8 |
| 8 | 70 | 12 | 3.5 | 75.48 | 65 | 83.2 |
| 9 | 63 | 10 | 2.5 | 62.39 | 52 | 72.75 |
| 10 | 63 | 14 | 2.5 | 66.39 | 125 | 75.56 |
| 11 | 63 | 10 | 3.5 | 72.85 | 102 | 87.35 |
| 12 | 63 | 14 | 3.5 | 82.52 | 101 | 91.63 |
| 13 | 63 | 12 | 3 | 91.25 | 112 | 90.73 |
| 14 | 63 | 12 | 3 | 87.65 | 110 | 90.09 |
| 15 | 63 | 12 | 3 | 92.41 | 114 | 90.4 |
| 16 | 63 | 12 | 3 | 89.63 | 106 | 92.48 |
| 17 | 63 | 12 | 3 | 88.74 | 105 | 92.53 |
Table 12.
Results of the analysis of regression coefficients.
Table 12.
Results of the analysis of regression coefficients.
| Source | Adj SS | d f | Adj MS | F-Value | p-Value | Significance |
|---|
| Model | 1253.67 | 9 | 139.30 | 56.34 | <0.0001 | ** |
| A—Pitch | 18.88 | 1 | 18.88 | 7.64 | 0.0280 | * |
| B—Rotationalspeed | 55.13 | 1 | 55.13 | 22.30 | 0.0022 | ** |
| C—Forward speed | 370.06 | 1 | 370.06 | 149.67 | <0.0001 | ** |
| AB | 230.58 | 1 | 230.58 | 93.26 | <0.0001 | ** |
| AC | 2.34 | 1 | 2.34 | 0.95 | 0.3629 | |
| BC | 0.54 | 1 | 0.54 | 0.22 | 0.6544 | |
| A2 | 314.90 | 1 | 314.90 | 127.36 | <0.0001 | ** |
| B2 | 171.95 | 1 | 171.95 | 69.55 | <0.0001 | ** |
| C2 | 38.73 | 1 | 38.73 | 15.67 | 0.0055 | ** |
| Residual | 17.31 | 7 | 2.47 | | | |
| Lack of fit | 11.82 | 3 | 3.94 | 2.87 | 0.1673 | ns |
| Error | 5.49 | 4 | 1.37 | | | |
| Total | 1270.98 | 16 | | | | |
Table 13.
Results of correlation analysis.
Table 13.
Results of correlation analysis.
| Projects | Value | Projects | Value |
|---|
| Standard | 1.57 | Model coefficients (R2) | 0.99 |
| Mean value | 82.74 | Calibration decision factor (R2Adj) | 0.97 |
| Coefficient of variation/% | 1.90 | Predicted coefficient of decision (R2Pre) | 0.84 |
| Sum of squares of errors in forecasts | 197.65 | Relative accuracy | 22.52 |