Early Yield Prediction of Oilseed Rape Using UAV-Based Hyperspectral Imaging Combined with Machine Learning Algorithms

Abstract

Oilseed rape yield critically reflects varietal superiority. Rapid field-scale estimation enables efficient high-throughput breeding. This study evaluates unmanned aerial vehicle (UAV) hyperspectral imagery’s potential for yield prediction at the pod stage by utilizing wavelength selection and vegetation indices. Meanwhile, optimized feature selection algorithms identified effective wavelengths (EWs) and vegetation indices (VIs) for yield estimation. The optimal yield estimation models based on EWs and VIs were established, respectively, by using multiple linear regression (MLR), partial least squares regression (PLSR), extreme learning machine (ELM), and a least squares support vector machine (LS-SVM). The main results were as follows: (i) The yield prediction of oilseed rape using EWs showed better prediction and robustness compared to the full-spectral model. In particular, the competitive adaptive reweighted sampling–extreme learning machine (CARS-ELM) model (R_pre = 0.8122, RMSE_P = 170.4 kg/hm²) achieved the best prediction performance. (ii) The ELM model (R_pre = 0.7674 and RMSE_P = 187.6 kg/hm²), using 14 combined VIs, showed excellent performance. These results indicate that the remote sensing image data obtained from the UAV hyperspectral remote sensing system can be used to enable the high-throughput acquisition of oilseed rape yield information in the field. This study provides technical guidance for the crop yield estimation and high-throughput detection of breeding information.

1. Introduction

Oilseed rape (Brassica napus L.) belongs to the cruciferous family (Brassicaceae). It stands as one of the most extensively cultivated oilseed crops globally, with its primary growing regions encompassing Europe, Canada, China, India, Australia, and other countries [1,2]. Until now, oilseed rape is a vital source of forage crops, oil crops, and energy crops. It has great economic benefits and occupies over 40% of China’s total production of oil crops [3,4]. Rapeseed oil, produced from oilseed rape, is a good source of healthy fats and fat-soluble vitamins. So, it is considered a beneficial and affordable edible vegetable oil. In addition, the remaining “cake” after rapeseed oil extraction can also be used as a high-protein animal feed. There are also other potentials in various sectors such as renewable vehicle fuel, environmentally friendly lubricating oil, and raw materials in the chemical industry. Due to its great importance, the research on phenotypic information and the physiological process of winter oilseed rape has attracted growing attention. Most research focuses on guiding oilseed rape producers to be more efficient in planting, breeding, harvesting, and marketing.

Among the numerous studies on crop yield, it is of great significance to enable accurate early prediction for farmers [5]. The traditional method of yield estimation is to establish an approximate relationship between the crop yield and agronomic factors or climate factors after manual field surveys and statistical analysis [6,7]. However, with large-scale commercial oilseed rape breeding and the rapid soaring collaboration of breeding materials in recent years, these conventional methods are cumbersome and time-consuming, and the data’s consistency and timeliness can scarcely be guaranteed. The low-altitude remote sensing platform combined with an unmanned aerial vehicle (UAV) and remote sensing technology, as a versatile, flexible, and low-cost tool, can provide spatial and phenotypic information of field crops because of its high spatial and temporal resolution [8,9]. As a result, UAV-based low-altitude remote sensing is deemed a useful and crucial technology in agriculture with strong suitability and adaptability to complex farmland environments [10].

The past decade has seen an exponential increase in research and the application of UAVs in precision agriculture. The rapid development of UAVs marks the arrival of a new era of remote sensing [5]. UAV-based low-altitude remote sensing has many advantages. It is efficient in acquiring both phenotypic and image information in a real-time manner. In this sense, it is suitable for both qualitative and quantitative research concerning different phenotypic information [11,12]. Therefore, it has been widely applied for the analysis of physiological characteristics, disease diagnosis, insect and pest inspection, and the prediction of chlorophyll content, biomass, drought stress sensitivity, the leaf area index, and yield [5]. Crop structure can be influenced by physiological characteristic differences, leading to the corresponding changes in the crops’ spectral features, such as light absorption, reflection, and transmission. To a certain extent, they can reflect a crop’s phenotypic information, covering nutrient abundant deficiency, growth differences, the degree of plant diseases or pest invasion, etc. This is also the theoretical basis for why spectral imaging sensors enable the representation of the phenotypic information of crops [13,14].

Many researchers have been reported to build predictive models of crop yield by using UAV-based RGB and multispectral cameras [15,16,17], and they have coincidentally confirmed the feasibility of using UAV combined with image sensors for yield prediction. The future development of UAV remote sensing applications should be approached to improve the accuracy and adaptability of the prediction model [18]. The UAV hyperspectral remote sensing system is advantageous as it integrates image and spectral information into one system, and it has gradually grown into the cutting-edge technology in the current remote sensing field due to its high spatial and spectral resolution. However, the research on the estimation of crop yield based on the hyperspectral remote sensing system of micro and small UAVs is rare and inadequate. Therefore, this work aimed to explore the feasibility of a UAV remote sensing platform equipped with a UHD185 hyperspectral imager (Cubert GmbH, ULM, Baden-Wurttemberg, Germany) to predict the yield of oilseed rape at the pod information stage. The specific studies are as follows: (1) Compared the effects of various pretreatment methods on spectral features and selected the optimal spectral pretreatment method. (2) Compared the predictive performance of linear and non-linear models constructed based on eight feature wavelength extraction methods to determine the yield of oilseed rape systematically. (3) Obtained the optimal vegetation indices (VIs) suitable for rape yield estimation and investigated the internal relationship and correlation between rape yield and different VIs. (4) Developed the most desirable model to predict oilseed rape yield and acquired the most relevant spectral bands as well as VIs which are used as inputs of models. This work will provide vital guidance for future work in the high-throughput detection of crop breeding and yield estimation.

2. Materials and Methods

2.1. Experimental Location and Crop Husbandry

This work was carried out at the agricultural research station of Zhejiang University, Hangzhou, China (30°18′26″ N, 120°4′29″ E). The entire experiment process was conducted over the rapeseed growing season. The main procedures of the experiment included sowing seeds in a fertile sandy loam seedbed in early October to ensure healthy growth, cautiously transferring the plants to the experimental field in November, and finally harvesting the oilseed rape in May of the following year. The area and row spacing of each row in the experimental field are 24.4 m × 1.4 m and 0.3 m, respectively. Each row has 10 plots, and the area of each plot is 2.4 m × 1.4 m. Some rows do not actually plant rape due to the setting of protection channels. After removing these plots, there are approximately 420 sample plots in total. The fertilizers used in the experiment were calcium superphosphate (Ca(H₂PO₄)₂·H₂O), urea (CO(NH₂)₂), and potassium chloride (KCl). All plots were supplied with identical levels of phosphorus (P) and potassium (K), specifically 60 kg/hm² of P and 150 kg/hm² of K, to ensure adequate nutrition for rapeseed growth. To study the effect of nitrogen on rapeseed growth, different nitrogen concentrations were applied to rapeseed. Based on the normal growth demand of 150 kg/hm², their concentrations should be correspondingly 0, 75, 150, and 225 kg/hm², which were marked as N0, N1, N2, and N3, respectively. Once the rapeseed matured, all transplanted plants within the trial field were harvested using hand scythes and transported to the laboratory. To determine crop yield, the total weight of the harvested rapeseed from each plot was divided by the plot’s area, with the result expressed in kg/hm ². Due to human factors, the rapeseed yield data of some sample plots in the yield measurement and calculation process are missing. Finally, 373 rapeseed sample data with complete yield calculations are obtained.

2.2. Hyperspectral Imaging Data Acquisition

The UHD185(Cubert GmbH, Ulm, Baden-Württemberg, Germany) UAV hyperspectral remote sensing system consisted of a six-rotor UAV (Figure 1a), a UHD185 imaging spectrometer (Figure 1b), a ground control system, and a radiometric calibration system. The weight of the UAV was 4.2 kg, and the endurance time was 15–20 min. UHD185 is a frame-synchronous imaging spectrometer with 125 spectral channels in the 450–950 nm range. The UHD185 imager could simultaneously obtain a 12-bit (4096 DN) hyperspectral image in the dynamic range of 50 × 50 pixels and a grayscale image of 1000 × 1000 pixels. The acquired spectral image data were stored in an inner microcomputer.

The acquisition of hyperspectral images of rape at the pod formation stage was carried out using the UHD185 UAV hyperspectral remote sensing system. This experiment adopted the time-delay shooting method. The entire process was controlled by the POKINE Z software (EXTRA Computer GmbH, Sachsenhausen, Germany). During image collection, the UAV was kept at the 50 m flight altitude, the forward overlap stayed in the range of 40–70%, and the lateral overlap was more than 30%. Meanwhile, the hyperspectral imager worked downward vertically to obtain images with a 23 mm focal length at a fixed 1 ms sampling interval.

2.3. Data Processing

The overall procedure for predicting oilseed rape yield from UAV hyperspectral data, as depicted in Figure 2, involved several sequential steps beginning with data acquisition and preparation. Initially, raw hyperspectral image cubes and associated panchromatic images captured by the UAV system underwent image fusion to integrate spatial and spectral details. Crucially, radiometric calibration was then performed to convert sensor digital numbers into physically meaningful spectral reflectance values, followed by image stitching using Agisoft Photoscan (version 1.2.6, AgiSoft LLC, St. Petersburg, Russia) to assemble the individual calibrated captures into a complete hyperspectral orthophoto mosaic of the experimental field. Following the creation of the orthophoto, the extracted spectral reflectance data required preprocessing to minimize noise and environmental interference. A comparative analysis of various methods, including smoothing (MAS and SG), scatter correction (MSC and SNV), derivatives (1-Der and 2-Der), and wavelet transform (WT), was conducted using PLSR models. This evaluation identified WT as the optimal technique for enhancing data quality before further analysis.

Subsequently, two primary pathways were explored to extract the most relevant spectral features for yield prediction and reduce data dimensionality. The first pathway focused on selecting a subset of effective wavelengths (EWs) directly from the preprocessed spectra using algorithms like SPA, GAPLS, UVE, CARS, and others. The second pathway involved calculating various established and derived vegetation indices (VIs) and selecting the best ones through correlation analysis and ANOVA with the measured yield data. Finally, using either the selected EWs or the chosen combination of VIs as input features, the dataset was split into calibration and prediction sets. Four machine learning models (MLR, PLSR, ELM, and LS-SVM) were trained on the calibration data, and their predictive performance was rigorously evaluated using the independent prediction set to identify the most accurate and robust model for estimating oilseed rape yield. This comprehensive workflow ensured systematic data refinement and comparative model assessment [19,20].

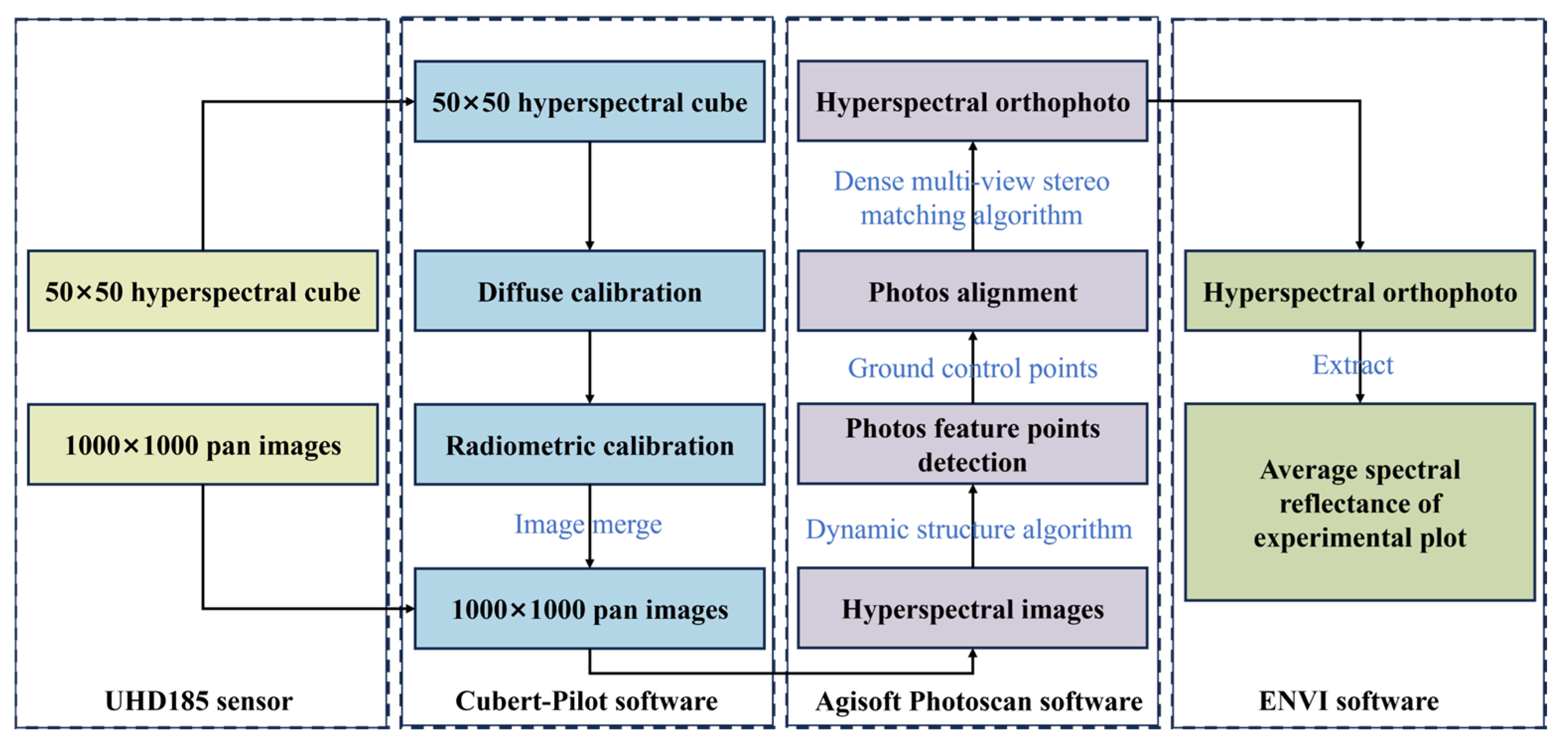
2.3.1. Hyperspectral Remote Sensing Image Processing

Processing the hyperspectral imagery acquired by the UAV system was a critical multi-step procedure essential for generating accurate spectral data for yield analysis, as illustrated in the workflow diagram (Figure 3). Given that individual remote sensing images captured by the UAV typically cover only a small area, image stitching is a key technology to create a complete spectral map of the entire experimental field from numerous overlapping frames. The process began with the raw data from the UHD185 sensor, which simultaneously captures lower-resolution (50 × 50 pixel) hyperspectral cubes and higher-resolution (1000 × 1000 pixel) panchromatic images. Initial processing, which was performed using the Cubert-Pilot software (Cubert GmbH, Ulm, Baden-Württemberg, Germany), involved fusing each hyperspectral cube with its corresponding panchromatic image. This step, often referred to as pansharpening, significantly enhanced the spatial resolution of the hyperspectral data to match that of the panchromatic image while also incorporating radiometric calibration based on diffuse calibration data to convert raw digital numbers into reflectance values.

Following the fusion and calibration of individual image pairs, the Agisoft Photoscan software was employed to mosaic these multiple overlapping high-resolution hyperspectral images into a single, continuous representation of the test field. Leveraging the rich point cloud information derived primarily from the panchromatic component of the fused images, along with ground control points for accurate georeferencing, Agisoft Photoscan performed photo alignment and applied dense multi-view stereo matching algorithms. This resulted in the generation of a comprehensive, 125-band hyperspectral digital orthophoto covering the 450–950 nm spectral range with a 4 nm sampling interval. A quality check using quick stitching in Photoscan was advisable after each flight to ensure data integrity and arrange re-flights if necessary due to poor stitching or missing imagery. Finally, to obtain the spectral information relevant to each experimental plot, the ENVI (version 4.6, ITT, Visual Information Solutions, Boulder, CO, USA) software was used.

2.3.2. Radiation Calibration

As the basis of remote sensing quantification, the radiometric calibration of UAV remote sensing images is necessary, i.e., converting the digital number (DN) values of images obtained by spectral image sensors into spectral reflectance with actual physical meaning. Therefore, radiometric calibration using black and white plates was needed before data collection using the UHD185 UAV hyperspectral remote sensing system, which enabled the calibration of the spectral reflectance for the target area to obtain more accurate spectral reflectance data. The radiation calibration was carried out using the following equation:

$${\mathit{Ref}}_{\mathit{target}}={\displaystyle \frac{{DN}_{target}-{DN}_{dark}}{{DN}_{panel}-{DN}_{dark}}}\times {\mathit{Ref}}_{\mathit{panel}}$$

(1)

where

DN_dark represents the systematic error of the hyperspectral imager;

DN_target represents the DN values of the target;

DN_panel represents the standard reference plate in the original hyperspectral image;

Ref_target represents the reflectance of the target;

Ref_panel represents the standard reference plate.

2.3.3. Spectral Preprocessing

To reduce the impact of external disturbances and improve the reliability and accuracy of the model, it is essential to apply spectral preprocessing. There were several preprocessing methods used: (1) Savitzky–Golay smoothing (SG) [21] and moving average smoothing (MAS) were performed to reduce the influence of noise. (2) A standard normalized variate (SNV) was used to correct the scattered noise interference [22]. (3) Multiplicative scatter correction (MSC) was applied to alleviate the interference caused by the scattering effect [23]. (4) A de-trending algorithm was employed in conjunction with SNV [22]. (5) A differential analysis algorithm including the first derivative (1-Der) and second derivative (2-Der) was implemented to reduce the influence of background interference or baseline drift [24]. (6) Wavelet transform (WT) was used for spectral data compression and smoothing processes in spectral analysis [25].

2.3.4. Wavelength Variable Selection

Data redundancy or collinearity is likely to result in an inferior model. Therefore, the selection of the optimal wavelengths is desired to trim the obtained spectral data, and it can save stored space and shorten data processing time. It is beneficial for reducing computational complexity and enhancing predictive ability, and the result can be used to develop online or portable multispectral devices [26].

In this study, multiple spectral variable selection algorithms were used. As a feed-forward variable selection method for multivariate calibration, successive projection algorithms (SPAs) can significantly decrease the number of variables, thereby increasing the speed and efficiency of modelling [26,27,28]. By calculating straightforward projections in a vector space, the SPA chose the wavelength variable, which has the lowest correlation and redundancy, as well as the largest projection vector. A weighted regression coefficient (BW) method is used to select the optimal wavelength recognized with a larger absolute value of BW, which is regarded as having a greater impact on the prediction result [29,30]. Genetic algorithm partial least squares (GAPLS), as one of the most effective variable selection algorithms, has been widely used in effective variable selection [31]. The genetic algorithm (GA) excels in global exploration and remains unencumbered by the premise of a restricted solution domain. For some discrete, multi-polar, and high-dimensional problems, the GA can still find solutions to these problems that are globally optimal, even in the presence of noise. In 1996, Centner et al. proposed a variable selection method named the uninformative variable elimination (UVE) algorithm. The UVE can eliminate wavelength variables which contribute little to the establishment of the PLS regression model and retain wavelengths which contain useful information. Thus, we can decrease the number of variables, reduce computation time and model complexity, and improve accuracy by using the SPA algorithm [32,33]. Derivative transformation can highlight useful information in the spectrum, weaken background interference, and improve spectral resolution. Different peaks and troughs tend to contain useful information. In this sense, this work selected feature wavelengths located at the major peaks and troughs of the second derivative (2-Der) spectra. Competitive adaptive reweighted sampling (CARS) is a feature variable selection method based on the regression coefficients of the least square model. After the PLS regression model is established using Monte Carlo sampling, adaptive weighted sampling can get rid of the corresponding wavelength ranges whose regression coefficient weight in the PLS model is relatively less than others but retain the rest of the wavelength ranges and take them as a new subset. Then, based on the new subset, the selection will be executed again. After several repeated cycle calculations, when they have the smallest root mean square error for the PLS model, the rest wavelength ranges will be selected as a combination [34]. The random frog (RF) algorithm is a variable selection method based on an iterative and reversible jumping Markov chain Monte Carlo method [35]. RF chooses the best combination of feature wavelength by repetitively screening variable subsets.

2.3.5. Vegetation Indices

The 53 common VIs and 6 other VIs are listed in Table S1 of the Supplementary Materials. These common VIs are divided into three categories: the characteristic index, the soil line vegetation index, and the atmospheric adaptability index. The latter two are mainly used to remove soil and atmospheric effects. The characteristic index is correlated with the epoxidation state of the lutein cycle, chlorophyll a + b concentration, the blue/green/red ratio index, carotenoid concentration, and the canopy structure [36]. The lutein pigment index mainly refers to the photochemical reflectance index (Pri570 and Pri515). When the wavelength is 515 nm, the calculated photochemical reflectance index will hardly suffer from the inference of the structure. Chlorophyll a + b concentration is mainly correlated with the Zarco-Tejada–Miller index (ZM), Vogelmann red edge index 1 (VOG1), Vogelmann red edge index 2 (VOG2), the chlorophyll absorption ratio index (CARI), the transformed chlorophyll absorption ratio index (TCARI), and the TCARI/optimized soil-adjusted vegetation index (OSAVI). The blue/green/red ratio index mainly includes the greenness index (R550/R670), the blue/green pigment index, the blue/red pigment index, and the Lichtenthaler index. Vegetation indices were associated with carotenoid concentration, which includes R520/R500, R515/R570, and R515/R670. The canopy structure index, including the normalized difference vegetation index (NDVI), the simple ratio (SR), the modified simple ratio (MSR), OSAVI, the triangular vegetation index (TVI), modified triangular vegetation index 1 (MTVI1), and other VIs, can be used to evaluate the changes in canopy structure caused by various biotic and abiotic stress.

2.3.6. Machine Learning Algorithms

Artificial intelligence techniques play indispensable roles in the hyperspectral remote sensing of UAVs at low latitudes, especially for image segmentation, ground object classification, and phenotypic index modelling and prediction [37,38]. There are multiple machine learning algorithms used in this work, namely multiple linear regression (MLR), partial least squares regression (PLSR), extreme learning machine (ELM), and a least squares support vector machine (LS-SVM).

MLR aims to establish a linear relationship between the spectral data and the measured indicators (e.g., physiological and biochemical indicators) [26,39]. Partial least squares (PLS) project the original variable to the orthogonal dimension to produce the principal component or principal factor which is also known as the latent variable (LV). LV carries the peak information content and optimal covariance linking spectral data and physical and chemical index readings, enabling it to account for the vast majority of the principal variable information, so PLS is frequently employed for feature extraction [26,29]. In this study, PLSR derived from PLS was used to solve quantitative regression problems. ELM suits well in the generalization of feed-forward neural networks, as it can select input weights and hidden layer deviations randomly during model development and overcome overfitting and local minimum problems effectively in the process of training [40,41]. A support vector machine (SVM) is a suitable modelling method when dealing with a small number of samples [42,43]. The LS-SVM can be used to obtain support vectors using a set of linear equations and can solve multivariate analysis problems, which are both linear and non-linear [26].

2.3.7. Model Evaluation

The correlation coefficient (R), with values closer to 1 indicating stronger predictive power, reflects the linear relationship between predicted and observed values. The root mean square error (RMSE) quantifies the standard deviation of the prediction errors, calculated as the difference between the reference and predicted values. Therefore, a smaller RMSE closer to 0 reveals a smaller prediction error, and the model performs better. In this work, we adopted R and RMSE as evaluation indicators, which were used to evaluate the performance of the model. The R and RMSE were calculated using the following equations:

$$R={\displaystyle \frac{\sum _{i=1}^n(\widehat{y_i}-\overline{\widehat{y}})(y_i-\overline{y})}{\sqrt{\sum _{i=1}^n{(\widehat{y_i}-\overline{\widehat{y}})}^2{(y_i-\overline{y})}^2}}}$$

(2)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{\mathrm{n}-1}}·\sum _{i=1}^n{(y_i-\widehat{y_i})}^2}$$

(3)

where

$y_i$ represents the ith sample’s reference value;

$\widehat{y_i}$ represents the $i$th sample’s predicted value;

$\overline{y}$ represents the averaged reference value;

$\overline{\widehat{y}}$ represents the averaged predicted value;

$n$ is the number of samples.

3. Results and Analysis

3.1. Investigating Yield Metrics and Spectral Attributes in Oilseed Rape Treatment

3.1.1. Descriptive Statistics of Measured Yield

Table 1. Statistics of the measured yield values of oilseed rape under different nitrogen gradients using standard methods.

Sample Sets	Number	Minimum (kg/hm2)	Maximum (kg/hm2)	Mean (kg/hm2)	Median (kg/hm2)	Standard Deviation (SD)	Coefficient of Variation (%)	Kurtosis	Skewness
Calibration	248	2217.3	3586.3	2942.68	2977.70	274.23	9.31	−0.41	−0.37
Prediction	125	2217.3	3526.8	2947.24	3023.80	292.97	9.94	−0.20	−0.53

presents a statistical overview of the yield data collected for field-grown oilseed rape across varying nitrogen levels. For the 373 samples, yields varied from 2217.3 to 3586.3 kg/hm². In this experiment, we randomly split all samples into a calibration set and a prediction set in a 2:1 ratio. The calibration set (248 samples) was used to establish a stable and reliable prediction model and evaluate the model objectively. The prediction set (125 samples) served primarily to evaluate the effectiveness of the developed model. As shown in Table 1, the calibration set had a mean yield of 2942.68 kg/hm² and a median yield of 2977.70 kg/hm², while the prediction set had a mean of 2947.24 kg/hm² and a median of 3023.80 kg/hm². The closeness of the mean and median values within each set, along with the negative skewness values (−0.37 for calibration, −0.53 for prediction), indicates a slight negative skew in the yield distributions for both groups. This suggests a tendency for yields to cluster towards the higher end of the observed range, with fewer instances of very low yields pulling the mean slightly below the median. Furthermore, the kurtosis values (−0.41 and −0.20, respectively) are negative, indicating platykurtic distributions, which are somewhat flatter than a normal distribution and possess fewer extreme outlier yields. The yield of different oilseed rape plots showed noticeable variation, as evidenced by the standard deviations (274.23 and 292.97 kg/hm ² for the calibration and prediction sets, respectively). Moreover, the sample groups, comprising the calibration and prediction groups, exhibited a considerable span of yield figures (see Table 1). The coefficients of variation (CV) were 9.31% for the calibration set and 9.94% for the prediction set, signifying moderate and comparable relative variability within both sample groups. These characteristics, including the range and distribution of yields, were conducive to establishing a robust quantitative prediction model and providing a reliable basis for its validation.

3.1.2. The Effect of Different Pretreatment Methods on the Yield Prediction of Oilseed Rape

Due to the complex environment of farmland, there are many influencing factors during the flight of the UAV, making the collected image and spectral data prone to interference information, such as noise, background, and stray light. This interference information is highly likely to cause a reduction in the accuracy and stability of the quantitative prediction model. In this study, eight spectral analysis methods (MAS, SG, SNV, MSC, standard normalized variable detrending (SNV-Detrending), 1-Der, 2-Der, and WT) were used to preprocess hyperspectral data. Therein, the wavelet basis functions and decomposition scale for WT preprocessing were db7 and 2, respectively. For different pre-processed spectral and raw spectral data, yield estimation models for oilseed rape were developed based on the PLSR algorithm. At the same time, we used the leave-one-out method of cross-validation (CV) to ascertain the optimal number of LVs needed to evaluate the effectiveness of different methods and select the optimal preprocessing method for subsequent studies.

The results of PLSR analysis models under different spectral pretreatments are shown in

Table 2. The comparison of different pretreatment methods based on PLSR for the yield prediction of oilseed rape.

Preprocessing Method	Models	LVs	Calibration		Prediction
			Rcal	RMSEC	Rpre	RMSEP
-	PLSR	4	0.7771	172.3	0.7770	183.8
MAS	PLSR	4	0.7750	173.0	0.7733	207.4
SG	PLSR	4	0.7768	172.4	0.7771	183.8
MSC	PLSR	5	0.7178	190.5	0.6365	225.5
SNV	PLSR	9	0.7182	190.4	0.6384	225.1
SNV-Detrending	PLSR	9	0.7141	191.6	0.6122	231.5
1-Der	PLSR	5	0.7144	191.5	0.6722	216.1
2-Der	PLSR	2	0.6430	209.6	0.5026	257.1
WT	PLSR	4	0.7767	172.4	0.7775	183.6

. Compared with the raw spectral curves, the five preprocessing methods, MAS, SG, MSC, SNV, and WT, maintained the trend of the raw spectral curves based on the smoothed spectral noise. The MSC, SNV, and SNV-Detrending reinforced the differences between the spectral curves from different perspectives. It can be seen from Table 2 that there was a certain effect of different spectral preprocessing methods for oilseed rape yield prediction. But R_cal and R_pre were not enhanced or reduced significantly; i.e., the model performance obtained by different preprocessing methods was not significantly different. Among them, the WT model achieved optimal prediction performance for the calibration set and the prediction set, with higher R_cal and R_pre and lower RMSE_C and RMSE_P. Therefore, the UAV hyperspectral data were chosen to be analyzed using wavelet transform processed spectral data.

3.1.3. Analysis of Spectral Features

The spectral profile of the canopy of oilseed rape is shown in Figure 4. While the precise positions and sizes of the peaks and troughs exhibited specificity, the broad tendency of the spectral response patterns aligned with that of other vegetations, including tobacco [27], maize [44], and tomato [28]. Prominent peaks were observed at wavelengths of 560, 760, and 890 nm, while the primary troughs were found in proximity to 480 and 680 nm, respectively. The peaks and troughs were caused by chlorophyll absorption in the plant leaves around 560 nm and 680 nm. The peak change was related to water absorption around 760 nm and 890 nm, and the spectral reflectance was dramatically increased by the red-edge effect from 680 to 760 nm [45].

As shown in Figure 4b, the average spectral patterns of oilseed rape canopies exhibited considerable uniformity across varying nitrogen levels. Nevertheless, within the 750–1000 nm wavelength region, the spectral profiles showed visually distinct patterns, and the reflectivity of profiles associated with higher nitrogen fertilization was elevated compared to that from oilseed rape treated with lower nitrogen fertilization. The difference might be affected by oilseed rape pods (intercellular space and cell arrangement) and the canopy structure (such as oilseed rape leaf inclination, the leaf area index, and biomass) [46]. In the range of 900–950 nm, the curves were not perfect and the reflectance decreased faster, which may be related to the imaging method and the construction of the instrument itself. Therefore, we chose to maintain all the spectral bands for subsequent analysis to select the optimal effective wavelengths (EWs) and VIs.

3.2. Feature Wavelength Selection and Comparison

Hyperspectral data are highly inter-wavelength correlated and exist with information redundancy, which can cause the instability of convergence and complex computation and be time-consuming in multivariate prediction models. Using EWs can simplify models, reduce computational complexity, improve the predictive power of models, and facilitate more stable model output [45]. Therefore, selecting appropriate EWs for oilseed rape yield prediction was necessary. In this study, eight methods (SPA, GAPLS, UVE, a combination of UVE and SPA (UVE-SPA), BW, 2-Der, CARS, and RF) were used to reduce the dimensionality of the full-spectrum data to select the optimal EWs. Figure 5 and Figure 6 show the process of the selection of EWs using SPA and GAPLS.

Different feature wavelength selection methods selected the EWs according to different principles, and the selection results are presented in

Table 3. The selected EWs for yield prediction using different wavelength selection algorithms.

Algorithms	(No.)	Selected EWs (nm)
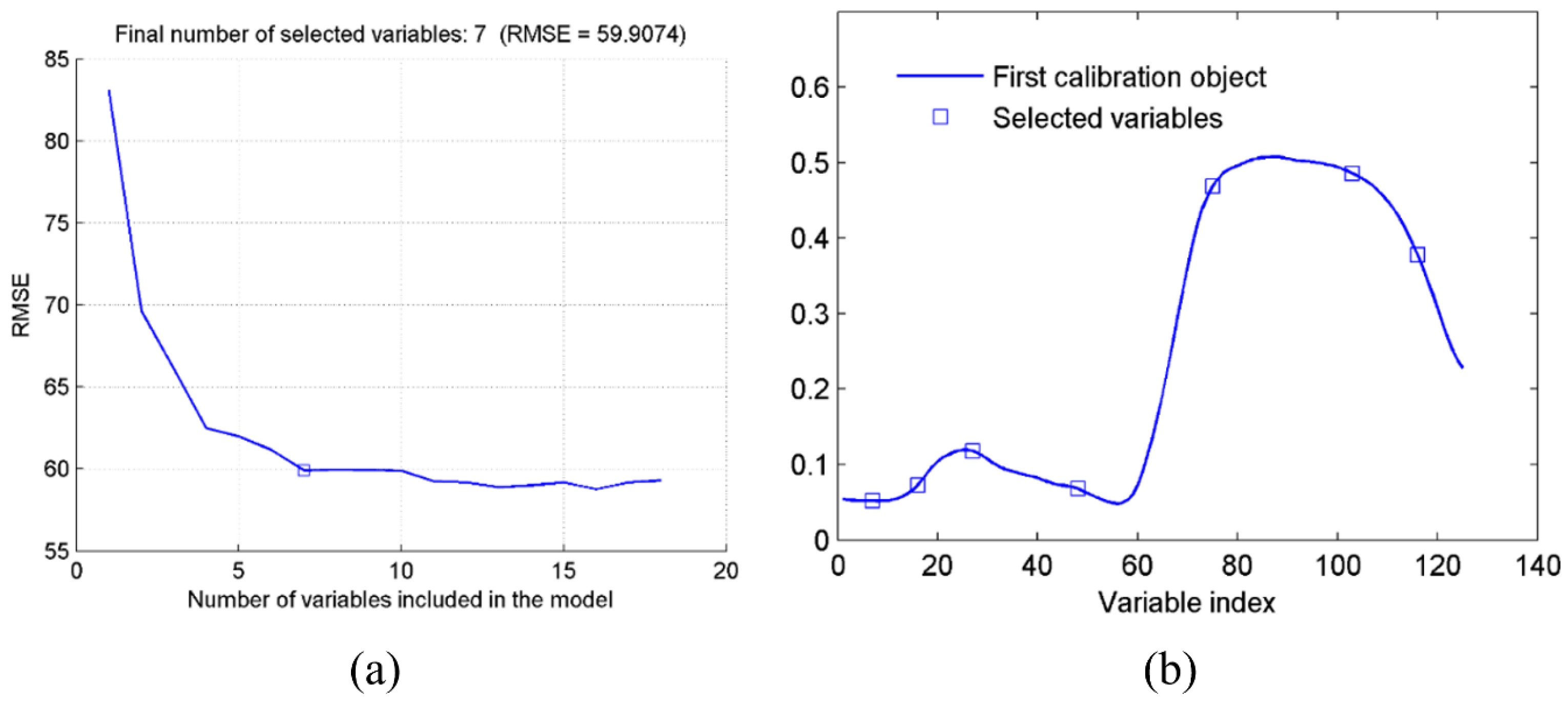
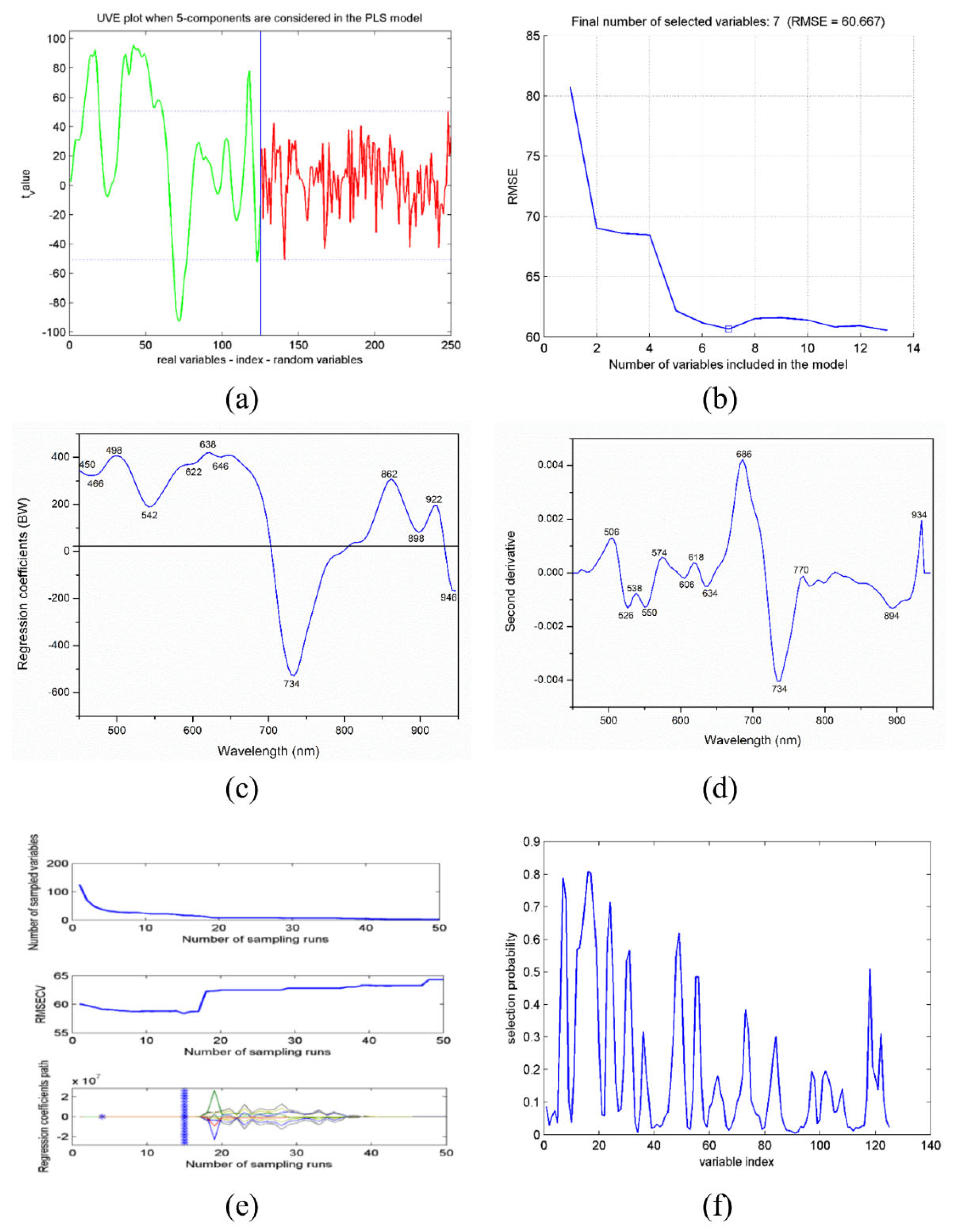
SPA	7	858, 474, 746, 638, 510, 554, and 910
GAPLS	32	918, 514, 922, 934, 518, 510, 914, 938, 542, 930, 738, 734, 926, 538, 858, 546, 730, 742, 862, 782, 474, 778, 854, 470, 786, 942, 698, 478, 534, 702, 506, and 746
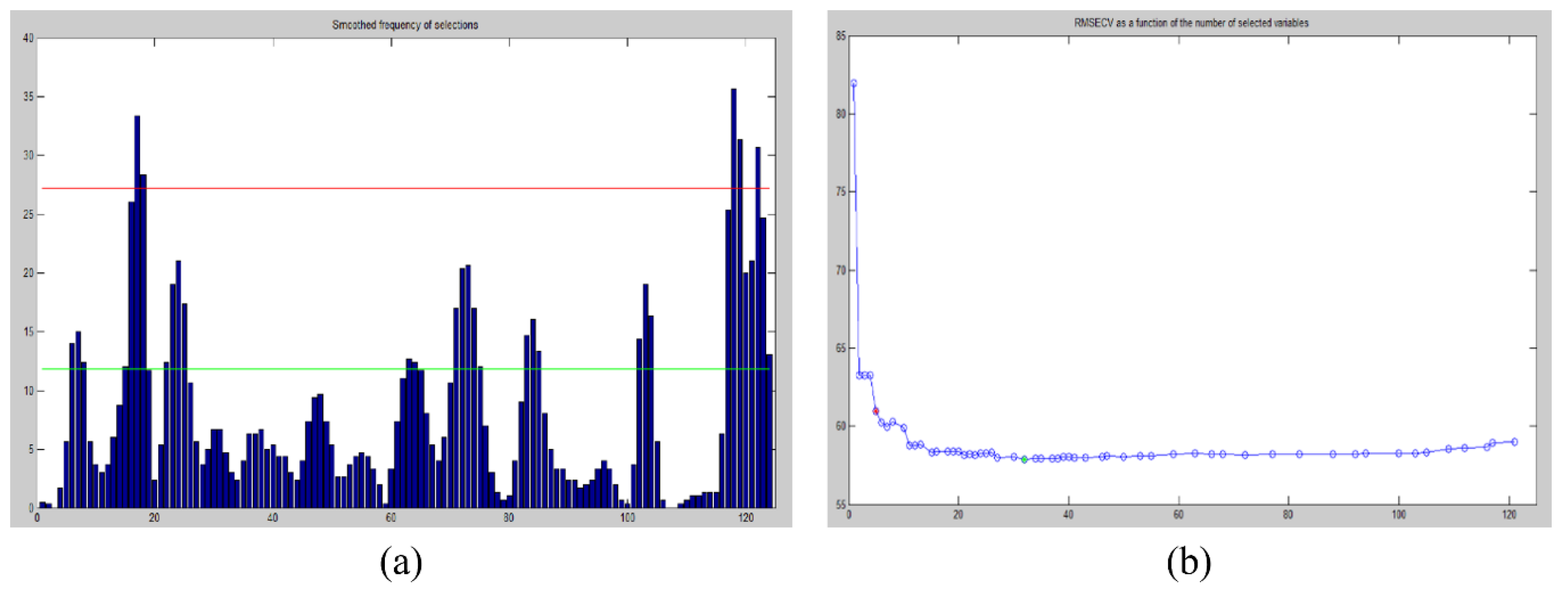
UVE	52	486–522, 582–754, 914–922, and 938
UVE-SPA	7	730, 494, 486, 650, 914, 754, and 938
BW	12	450, 466, 498, 542, 622, 638, 646, 734, 862, 898, 922, and 946
2-Der	13	506, 526, 538, 550, 574, 606, 618, 634, 686, 734, 770, 894, and 934
CARS	8	478, 498, 506, 542, 598, 914, 918, and 922
RF	29	510, 514, 474, 478, 506, 542, 518, 502, 642, 538, 498, 522, 494, 570, 638, 566, 918, 546, 666, 670, 646, 470, 738, 742, 590, 574, 634, 934, and 782

. Figure 7a shows the stability of each wavelength variable based on the UVE analysis. The wavelength variable and the random variable were located on the left and right sides, respectively. The two horizontal lines were the lower and upper limits of the maximum absolute value of the stable value in the random variable matrix. For the UVE algorithm, variables whose stability was inside the cutoff line were considered uninformative and eliminated. Finally, we picked 52 wavelength variables from 125 raw variables, which means that 58.4% of the wavelength variables were eliminated. Although the modelling variables were reduced by UVE analysis, the number of sensitive wavelengths was still large. To solve this problem, a combination of UVE and SPA was used for the selection of EWs. The EWs selected using SPA were ranked based on importance. The EWs selected using GA and RF were ranked according to the frequency or probability of variable selection, with the wavelengths ranked ahead being more important and selected frequently. In contrast, the EWs selected using 2-Der are selected based on the peaks and valleys of the second-order derivatives. Similarly, the EWs were selected using BW based on the peaks and troughs of the weighted regression coefficients of the PLSR algorithm. For the CARS method, Monte Carlo and adaptive weighted multiple sampling were used to select the EWs according to the wavelength corresponding to the subset with the lowest root mean square error in the PLSR algorithm.

As can be seen from Table 3, the number of wavelengths was reduced by more than 90% after the UVE-SPA or SPA treatment. It could effectively simplify the model and decrease the computational complexity. In contrast, the GA, CARS, and RF selected a larger number of EWs and contained more information, which would make the model more stable in the training phase. As a whole, the EWs selected were mainly related to photosynthetic capacity (495–680 nm), the red inflexion point (680–780 nm), plant water status (900–980 nm), etc. The EWs chosen around 450 nm and 550 nm may be associated with the absorption of anthocyanins [27]. Moreover, chlorophyll a and chlorophyll b had feature peaks at 675 nm and 620 nm, respectively, which can explain to some extent the EWs in this vicinity. At 700–750 nm, the wavelengths selected were associated with the red-edge index, etc. Labelling the shape of the red to near-infrared transition can indicate signs of canopy stress and senescence.

3.3. The Yield Prediction of Oilseed Rape Based on the Effective Wavelength

Using EWs and the full spectra as input variables, respectively, we constructed regression analysis models for the yield of oilseed rape based on the MLR, PLSR, ELM, and LS-SVM algorithms. The prediction results and the settings of model parameters are presented in

Table 4. The full spectra and the selected EWs for yield prediction using different machine learning algorithms.

Wavelength Selection Algorithms	EWs	Models	LVs/(γ, σ2)/ Hidden Neurons	Calibration		Prediction
				Rcal	RMSEC	Rpre	RMSEP
-	125	PLSR	4	0.7767	172.4	0.7775	183.6
-	125	MLR	-	0.8988	140.1	0.6588	247.2
-	125	LS-SVM	(76.4, 5.6 × 103)	0.8012	163.9	0.7703	186.1
-	125	ELM	48	0.8221	155.8	0.8019	175.2
SPA	7	PLSR	4	0.7760	172.6	0.7787	183.2
SPA	7	MLR	-	0.7805	171.1	0.7919	179.0
SPA	7	LS-SVM	(127.0, 392.1)	0.7894	168.0	0.7783	183.2
SPA	7	ELM	20	0.7963	165.5	0.8056	173.1
GAPLS	32	PLSR	4	0.7803	171.1	0.7824	181.9
GAPLS	32	MLR	-	0.7999	164.3	0.7846	181.0
GAPLS	32	LS-SVM	(6.4 × 103, 3.6 × 104)	0.7893	168.1	0.7888	179.4
GAPLS	32	ELM	39	0.8100	160.5	0.8060	172.9
UVE	52	PLSR	4	0.7793	171.5	0.7803	182.6
UVE	52	MLR	-	0.8459	147.3	0.7037	214.0
UVE	52	LS-SVM	(347.2, 2.7 × 103)	0.8006	164.0	0.7464	194.4
UVE	52	ELM	47	0.8281	153.4	0.7888	180.2
UVE-SPA	7	PLSR	4	0.7756	172.8	0.7773	183.8
UVE-SPA	7	MLR	-	0.7816	170.7	0.7858	180.6
UVE-SPA	7	LS-SVM	(9.4 × 103, 5.1 × 103)	0.7895	168.0	0.7881	179.7
UVE-SPA	7	ELM	29	0.8069	161.7	0.8050	173.4
BW	12	PLSR	4	0.7798	171.7	0.7750	184.5
BW	12	MLR	-	0.7853	169.8	0.7707	186.1
BW	12	LS-SVM	(2.2 × 103, 5.3 × 103)	0.7914	167.3	0.7798	182.7
BW	12	ELM	31	0.8101	160.5	0.7980	176.0
2-Der	13	PLSR	4	0.7705	174.5	0.7694	186.5
2-Der	13	MLR	-	0.7810	170.9	0.7594	189.9
2-Der	13	LS-SVM	(44.5, 279.1)	0.7916	167.3	0.7453	194.6
2-Der	13	ELM	8	0.7734	173.5	0.7879	179.9
CARS	8	PLSR	4	0.7750	173.0	0.7853	180.8
CARS	8	MLR	-	0.7844	169.8	0.7979	176.0
CARS	8	LS-SVM	(381.5, 333.1)	0.7952	166.0	0.7737	184.9
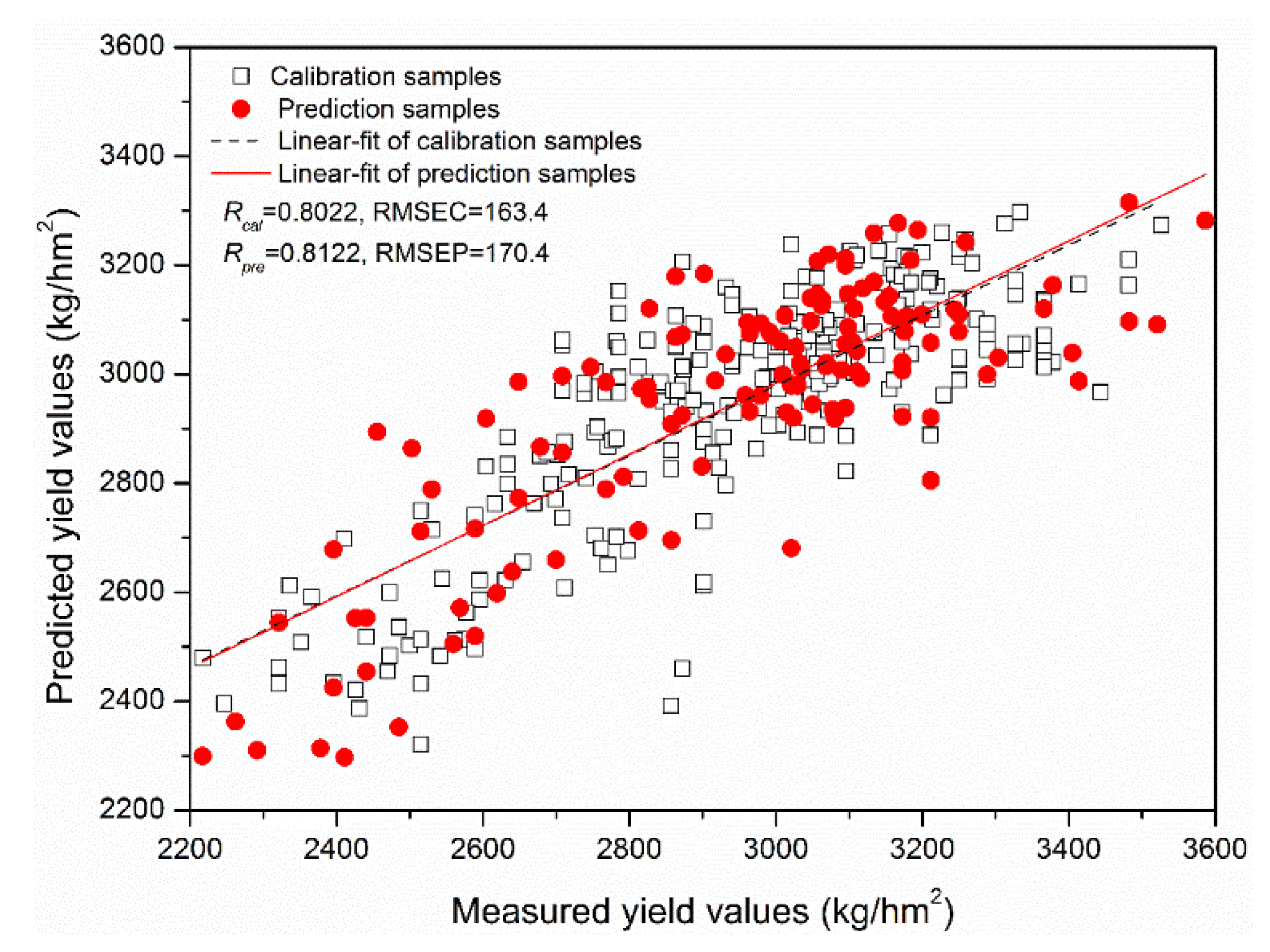
CARS	8	ELM	21	0.8022	163.4	0.8122	170.3
RF	29	PLSR	4	0.7792	171.5	0.7906	179.0
RF	29	MLR	-	0.8136	160.5	0.7743	186.2
RF	29	LS-SVM	(2.1 × 103, 2.8 × 103)	0.8078	161.4	0.7746	184.6
RF	29	ELM	39	0.8224	155.7	0.8018	175.0

Note: number of LVs for PLSR, (γ, σ²) for LS-SVM, number of hidden neurons for ELM.

. In the regression analysis model built using the full spectra, the PLSR, LS-SVM, and ELM models achieved good prediction performance, with R_cal and R_pre greater than 0.77. In particular, the ELM model performed the best, with R_cal and R_pre greater than 0.8. In the regression analysis model established based on the EWs selected using SPA, GAPLS, UVE-SPA, BW, CARS, and RF, the PLSR, MLR, LS-SVM, and ELM models all obtained well-prediction results, with R_cal and R_pre greater than 0.77, while the regression analysis models developed using UVE and 2-Der had the next-best prediction performance. Among them, the ELM prediction models established using UVE-SPA, CARS, and RF performed better, with R_cal and R_pre greater than 0.8. In general, the optimal prediction model was CARS-ELM, with R_cal and R_pre values of 0.8022 and 0.8122 and RMSE_C and RMSE_P values of 163.4 kg/hm² and 170.4 kg/hm², respectively, as shown in Figure 8.

In summary, the models using EWs with key information showed better robustness and performance than the models using full spectra. Among them, four feature band selection methods (GAPLS, CARS, RF, and UVE-SPA) showed better performances, and the ELM regression analysis model had better prediction. Employing diverse machine learning methodologies grounded in distinct principles, regression analyses were conducted on the datasets by examining them through varied lenses. From these analyses, the selection of a suitable regression modelling approach would prove advantageous for realizing oilseed rape yield prediction.

3.4. Optimal Narrow-Band Vegetation Index Selection and Analysis

In this study, we calculated different VIs and investigated the intrinsic link and correlation connecting oilseed rape yield and diverse VIs to identify the optimal VIs for estimating oilseed rape yield. For any two spectral bands (reflectance spectra and first-order derivative spectra), colour mapping of the absolute values of correlation coefficients between NDSI(_Rλ1, _Rλ2), RSI(_Rλ1, _Rλ2), DSI(_Rλ1, _Rλ2), SAVI(_Rλ1, _Rλ2), NDSI(_Dλ1, _Dλ2), RSI(_Dλ1, _Dλ2), and oilseed rape yield was plotted simultaneously to determine the optimal band combination for oilseed rape yield prediction. The calculation results for all combinations are shown in Figure 9. In the two-dimensional plot, the intersection points of each pair of bands corresponded to the absolute value of the correlation coefficient R between the VI and yield. The vegetation index was calculated using reflectance under this pair of bands, with redder-coloured points representing larger R and bluer representing smaller R. The most effective band combination and wavelength range for predicting field-based oilseed rape yield can be derived from the correlation coefficient plot.

For the vegetation index reflectance spectra NDSI(_Rλ1, _Rλ2) and RSI(_Rλ1, _Rλ2), the optimal correlation band combinations with the yield of oilseed rape were 550 nm and 582 nm, exhibiting absolute correlation coefficient values of 0.5493 and 0.5507, respectively. For the NDSI(_Dλ1, _Dλ2) of first-order derivatives, the best correlation band combinations were 522 nm and 650 nm, with a maximum absolute correlation coefficient value of 0.4943. As for the RSI(_Dλ1, _Dλ2) of first-order derivatives, R_max = 0.5042, and the band combinations were 522 nm and 654 nm. The optimal band combinations obtained from DSI(_Rλ1, _Rλ2) and SAVI(_Rλ1, _Rλ2) were (670 nm, 710 nm) and (622 nm, 666 nm), and the highest absolute values of correlation coefficients were 0.5960 and 0.5356, respectively. Finally, we obtained six optimal VIs based on these isopotential maps, which are NDSI(_550,582), RSI(_550,582), NDSI(_D522,D650), RSI(_D522,D654), DSI(_670,710), and SAVI(_622,666).

Due to the limitation of the band range, except for the 6 narrow-band VIs mentioned above, 53 VIs were used for correlation analysis and one-way analysis of variance (ANOVA) with the yield of oilseed rape. These outcomes are presented in Tables S2 and S3 in the Supplementary Materials. While the correlation analysis ranking did not perfectly align with the ANOVA-based order, the overall outcomes showed resemblance, and vegetation indices with higher F values tended to be associated with stronger correlation coefficients. Drawing from the aforementioned analytical findings and with model parsimony in subsequent phases in mind, we chose nine VIs (|R| > 0.5) as inputs to the machine learning model, namely CRI1, CRI2, TCARI, CARI, TCARI/OSAVI, RVSI, TVI, MTVI1, and PRI₅₁₂.

3.5. The Yield Prediction of Oilseed Rape Based on the Vegetation Index

Based on the correlation coefficient isopotential plots of narrow-band VIs and the results of the correlation analysis and ANOVA for other VIs, we selected 14 VIs with absolute values of correlation coefficients greater than 0.5 to establish the yield estimation model, namely NDSI(₅₅₀, ₅₈₂), RSI(₅₅₀, ₅₈₂), NDSI(_D522, _D650), RSI(_D522, _D654), DSI(₆₇₀, ₇₁₀), SAVI(₆₂₂, ₆₆₆), CRI1, CRI2, TCARI, CARI, TCARI/OSAVI, RVSI, TVI, MTVI1, and PRI₅₁₂.

Using the combination of VIs (CRI1 with a linear fitting equation of y = −463.4x + 5569 (|R| = 0.7405, RMSE = 188.6 kg/hm²)) as the input, we established regression-based prediction models developed using a range of machine learning algorithms (PLSR, MLR, LS-SVM, and ELM), and the model parameters were configured in line with the specifications outlined earlier (see Table 4). The predicted results for the oilseed rape yield model derived from the optimal combination of VIs are presented in

Table 5. Vegetation index combinations for yield prediction across various machine learning algorithms.

(No.)	Models	LVs/(γ, σ2)/ Hidden Neurons	Calibration		Prediction
			Rcal	RMSEC	Rpre	RMSEP
14	PLSR	2	0.7605	177.7	0.7736	185.4
14	MLR	-	0.7813	170.8	0.7670	187.4
14	LS-SVM	(0.80, 72.2)	0.7952	166.3	0.7493	193.5
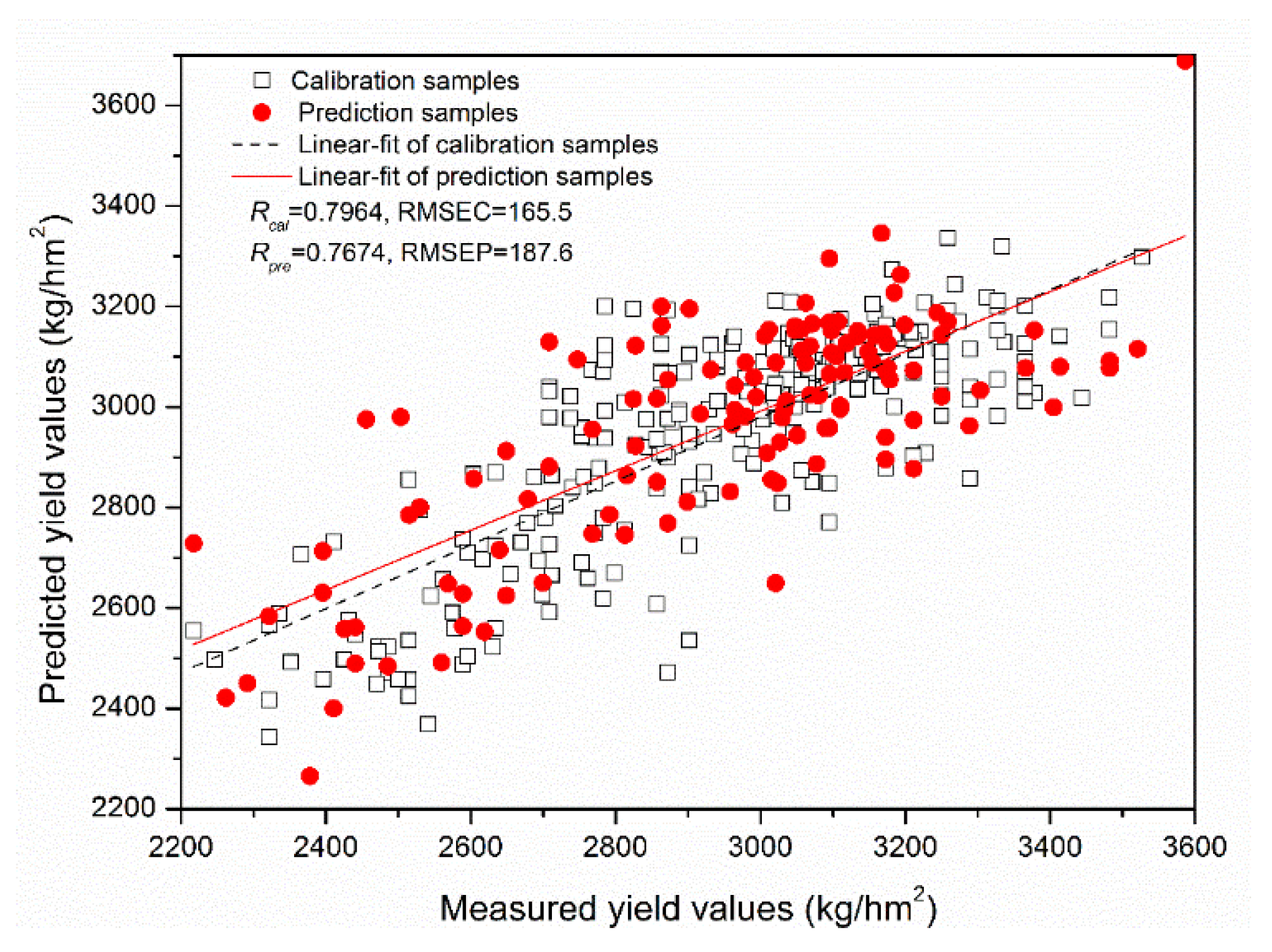
14	ELM	27	0.7964	165.5	0.7674	187.6

Note: parameters and abbreviations are shown in Table 4.

.

During the establishment of the regression model based on combining VIs, the PLSR, MLR, LS-SVM, and ELM models showed better prediction, with R_cal and R_pre greater than 0.74, and the PLSR achieved excellent predictive performance with R_pre up to 0.7736 and an RMSE_P value of 185.4 kg/hm². However, when combining the results of the calibration set and the prediction set, the ELM performed the best, with R_cal and R_pre values of 0.7964 and 0.7674 and RMSE_C and RMSE_P values of 165.5 kg/hm² and 187.6 kg/hm², respectively, as shown in Figure 10. Overall, the predictive models constructed based on the combined VIs predicted better than single VIs. The results show that fusing multiple VIs was more beneficial to constructing highly accurate and general yield prediction models, which can effectively promote the application of UAV remote sensing in the yield estimation of oilseed rape. Moreover, the performance of non-linear models (ELM and LS-SVM) was mostly better than that of linear models (MLR and PLSR) in the machine learning algorithms used.

4. Discussion

The yield estimation model for oilseed rape was developed based on raw spectra and different preprocessing spectral data. We evaluated the effects of different spectral pre-processing methods systematically (MAS, SG, SNV, MSC, SNV-Detrending, 1-Der,2-Der, and WT) on the spectral characteristics. Considering the performance of the model on the calibration and test sets, we concluded that WT was the optimal preprocessing method. The experimental results indicated that, compared with the raw spectral data, there was no significant difference in the prediction performance between the prediction models constructed based on different preprocessing methods (Table 2), but most of the noise and interference information in the raw spectral data could be effectively removed by using spectral preprocessing (Figure 4a,b). This phenomenon may be caused by the fact that the hyperspectral data still have highly tabulated redundancy or covariance after spectral preprocessing. The spectral data still contained a large amount of invalid information which was not relevant to the prediction of the yield of oilseed rape. Therefore, it is necessary to preprocess the spectral data and carry out feature analysis and extraction further.

To construct a yield estimation model for oilseed rape, we evaluated the effectiveness of eight wavelength selection methods (SPA, GAPLS, UVE, UVE-SPA, BW, 2-Der, CARS, and RF) for the extraction of EWs. In this context, effectiveness refers to the ability of the method to identify a subset of wavelengths that allows for the construction of simpler predictive models using fewer input variables. Based on the results of R and RMSE, the predictive performance is comparable to the models constructed using the full spectrum, thus successfully reducing the data dimensionality while preserving or enhancing the predictive power. As shown in Table 3, the characteristic wavelength variables were effectively reduced after wavelength selection. Compared to using full spectra, the regression analysis models using the EWs could achieve excellent predictions even with a significant reduction in the model input variables (Table 4). In addition, the prediction performance of the non-linear models was better than that of linear models. The results showed that it is feasible to select EWs containing key information by using wavelength selection algorithms and establish a quantitative analysis model based on EWs to achieve the yield prediction of oilseed rape.

To develop yield estimation models for oilseed rape based on VIs, we explored the intrinsic link and correlation between the oilseed rape yield and different VIs. Compared to the model prediction results based on single VIs and combined VIs (Table 5), we found that the prediction models based on combined VIs outperformed single VIs in terms of accuracy and stability. Here, accuracy is mainly measured by the R and RMSE between the model predictions and the measured rapeseed yield. As shown in Table 5, the ELM model using the combination of VIs obtained higher R values and lower RMSE values. Moreover, for the prediction models built by individual VIs, the prediction accuracy of the models was low, and there were significant differences in the fitted equations between the different sample sets. This may be caused by the fact that the model had fewer input feature variables, which affects the stability of the model. The research results indicated that fusing multiple VIs was more beneficial to constructing yield prediction models with high accuracy and generality.

The early prediction of crop yield relies heavily on obtaining the best spectral, spatial, and temporal signatures of yield by using appropriate platforms, sensors, and analytical methods. UAV low-altitude remote sensing technology with the advantages of low cost, high flexibility, high resolution, and easy operation provides a new strategy for the early prediction of crop yields at the field scale. We successfully achieved the early yield prediction of oilseed rape using a UAV remote sensing platform equipped with the UHD185 hyperspectral imaging system. Compared with existing international research, Yu et al. [17] collected large-scale soybean breeding trial multispectral images using drones and employed random forests to measure crop geometric features to improve soybean yield estimation, achieving a result of r = 0.82. Rajveer et al. [18] used machine learning regression models to predict corn and soybean yields in Ohio based on weather parameters, with R² values of 0.73 for corn and 0.64 for soybeans. Hassan et al. [15] explained significant variations in biomass and grain yield through UAV-NDVI by utilizing vegetation indices related to yield and physiological traits. In conjunction with this study, it is suggested that future research utilizing canopy spectral information from UAV hyperspectral remote sensing, along with optimized EWs and VIs, can establish a quantitative analysis model for canola yield, providing technical support for yield prediction at the field scale.

However, we have encountered several limitations. Firstly, this study is mainly based on the hyperspectral remote sensing images of rapeseed at the angular fruiting stage. In the future, we will try to use hyperspectral remote sensing images of other growth periods of oilseed rape to explore the feasibility of early yield prediction of oilseed rape. Second, this study mainly used the spectral features of hyperspectral images to predict oilseed rape yield, but the image information of hyperspectral images was not fully utilized. In future research, we will continue to expand the number and type of samples, combine cutting-edge data mining methods such as deep learning to resolve the spectral image features of UAV low-altitude remote sensing, construct more robust crop yield prediction models, and provide technical support for the high-throughput acquisition of crop yield estimation and breeding information.

5. Conclusions

In this study, we focus on the early prediction of crop yield. Using the canopy spectrum of oilseed rape at the pod information stage acquired by the UAV hyperspectral remote sensing system, we conducted a series of studies about the yield prediction of oilseed rape at the field scale. Using the preferred EWs and VIs, a quantitative analytical model of rapeseed yield was established. We evaluated the effects of various spectral preprocessing algorithms: EW selection algorithms and optimal VIs on the prediction performance of the yield of oilseed rape. The following conclusions were obtained: (1) Compared with using the full spectral band, the estimation model constructed with EWs containing key information had good prediction effects and robustness. (2) The integration of the multi-vegetation index was more conducive to the construction of a yield prediction model with high accuracy and strong versatility. In subsequent studies, we will focus on the early prediction of the yield of oilseed rape based on time-series hyperspectral images to construct more accurate and versatile crop yield prediction models to provide technical support for the high-throughput acquisition of the yield estimation of oilseed rape and breeding information.