Abstract
When investigating precision pest management strategies for fruit farmlands with complex geometries and restrictive boundaries, this study proposes an enhanced coverage optimization methodology for agricultural drones based on an enhanced Black-winged Kite Algorithm (BKA). Initially, the task area is segmented using the Segment Anything Model (SAM) based on deep learning, and an environmental map is created through gridding. Subsequently, by proposing coverage task cost functions, flight safety cost functions, and path length cost functions, the coverage challenge in complex-shaped areas is redefined as a challenge involving multiple constraints. To optimize this problem, we introduce a DWBKA that incorporates a Dynamic Position Balancing strategy and a modified Whale Random Walk strategy, thereby enhancing its global search capability and avoiding local optima traps. Finally, comparative experiments are conducted in six distinct scenarios of fruit farms, juxtaposing the DWBKA with the initially developed version and the BL-DQN. The results of this comparative analysis unequivocally demonstrate that the DWBKA achieves superior performance metrics, excelling in coverage rate, repeated coverage rate, path length, and computational time. When compared with extant coverage methodologies for complex shapes, the proposed DWBKA method exhibits marked performance enhancements in coverage tasks. This underscores its potential to significantly elevate the efficiency and precision of drone coverage in complex farm settings.
1. Introduction
Fruits, as a vital source of nutrition for humans [1,2,3,4], play a significant role in ensuring global economic stability and food safety [5,6,7]. The quality and yield of fruits are directly impacted by pests and diseases [8,9,10,11], which can lead to substantial economic losses [12,13,14,15]. Traditional methods of pest and disease control, such as manual pesticide spraying and mechanical spraying, are fraught with limitations. For instance, manual spraying is labor-intensive and inefficient [16,17], particularly in large-scale orchards, while mechanical spraying is restricted in complex terrains [18] and tall fruit trees [19,20], often resulting in pesticide waste [21] and environmental pollution [22,23,24]. Therefore, exploring more efficient, precise, and environmentally friendly pest and disease control technologies is of paramount importance.
The rapid advancement of Unmanned Aerial Vehicle (UAV) technology has introduced new possibilities for pest and disease control. Drones offer several advantages, including high mobility [25], efficient operation [26], and precise pesticide application [27]. They can rapidly reach the target areas in fruit farms, as well as accurately locate [28] and spray pesticides on affected regions, thereby enhancing pesticide utilization and mitigating environmental pollution [29,30,31]. Furthermore, drones equipped with various sensors can monitor plant growth [32,33,34] and pest and disease occurrences [35,36,37] in real time, providing early warnings [38] and precise control measures [39]. However, to fully leverage the potential of drones in pest and disease control, optimizing their flight paths for efficient and uniform pesticide application is essential.
Coverage Path Planning (CPP) focuses on generating paths that enable drones or other agents to traverse all points within a given area and meet specific coverage requirements [40]. As an important branch of path planning, CPP has garnered some research interest in agricultural drones. For instance, Huang et al. [41] proposed an autonomous task allocation and decision-making method for multi-quadrotor drones in agricultural activities, utilizing sequential quadratic programming to solve the optimal task allocation problem and validating their approach through simulations and flight tests. Nanavati et al. [42] introduced a data-driven optimal path planning framework for uniform pesticide application by drones, which relies on Gaussian kernel neural networks to design the spraying model and is verified through simulations and experiments using DJI AGRAS-T10 drones. Li et al. [43] addressed agricultural UAV spray coverage optimization through their methodology that integrates topological mapping algorithms to enhance path planning in concave regions, establishing a dual-objective fitness function that simultaneously minimizes flight distance and maximizes coverage redundancy. This optimization challenge was subsequently resolved through genetic algorithm-driven determination of optimal heading angles for coverage missions. Li and their team [44] introduced a framework for coverage path planning across multiple regions to fertilize precisely, which employs an improved Deep Q-Network (DQN) algorithm combined with LSTM and dueling network structures to enhance path planning efficiency and coverage quality. Fu et al. [45] devised a path-planning framework for agricultural drones based on the BL-DQN algorithm by amalgamating the Bidirectional Long Short-Term Memory structure with the DQN, with the objective of tackling the inefficacy inherent in traditional spraying methodologies.
The exploration of CPP for agricultural drones remains in its nascent stage, but CPP has been more extensively applied to other types of agricultural machinery. A CPP method for mobile robots in agriculture was suggested [46], utilizing tree exploration to identify potential solutions and similarity checks to select the optimal solution, aiming to maximize coverage area and minimize overlap and travel time while considering multiple entrances and complex field shapes. Wang et al. [47] developed an enhanced path planning and task allocation method for agricultural machinery operations in smart farms, combining Dijkstra’s algorithm with priority queues and three coverage methods, as well as an improved ant colony algorithm based on overall working paths, effectively addressing efficiency and resource waste issues in smart farm construction. Research has also been conducted on complete coverage path planning methods for agricultural vehicles with curvature constraints, involving field decomposition, path planning, and traversal order optimization to achieve smooth and efficient coverage, thereby laying the foundation for precision agriculture applications [48]. Zhang et al. [49] studied comprehensive coverage path planning for tracked lawn mowers in orchard environments, proposing an enhanced method based on the A* search algorithm, which was validated through simulations on the MATLAB 2020b platform and field trials for reliability and practicality.
Swarm intelligence algorithms, known for their adaptability, low computational complexity, and straightforward implementation [50,51], have been extensively applied in drone path planning. Chai et al. [52] integrated multi-population strategies, adaptive strategies, and interactive mutation strategies to balance exploration and exploitation capabilities, thereby increasing the number of feasible solutions for drone trajectory optimization in intricate situations. Jiang et al. [53] addressed the need for three-dimensional path planning of drones in complex environments by proposing a flight path generation and collision avoidance algorithm framework that combines an improved Grey Wolf Optimizer and partially observable Markov decision processes. Gupta and Verma [54] incorporated Coyote Optimization Algorithm and Particle Swarm Optimization, which was used for estimating drone flyable paths and smoothing them with cubic B-spline curves. Hu et al. [55] aimed to improve the Honey Badger Algorithm for drone path planning by introducing Bernoulli displacement mapping, piecewise optimal decreasing neighborhood strategies, and horizontal crossover strategies to enhance exploration and exploitation capabilities, thereby optimizing drone path selection in complex environments. Chen et al. [56] proposed an improved Pollen Dispersal Algorithm, analyzing and adjusting the global equations of FPA, introducing neighborhood global learning mechanisms and population reconstruction mechanisms to address drone path planning problems.
As a novel swarm intelligence algorithm launched in 2024, the Black-winged Kite Algorithm (BKA) [57], demonstrates significant potential in path planning. However, like other swarm intelligence optimization algorithms, the BKA experiences a disparity between its local exploitation and global exploration capabilities, which can lead to local optima, weak global exploitation, and insufficient obstacle avoidance in complex environments. To address these issues in the BKA, we propose an enhanced Black-winged Kite Algorithm (DWBKA) incorporating a Dynamic Position Balancing strategy and a modified Whale Random Walk strategy. The primary contributions of this work include the following:
- Utilizing the deep learning SAM model to segment the task area in fruit farms and creating an environmental map via gridding;
- Designing a new objective function by constructing the coverage task cost functions, the flight safety cost function, and the path length cost function, thereby restructuring the drone coverage issue as an optimizing problem with multi-constraints;
- Proposing a DWBKA that incorporates a Dynamic Position Balancing strategy and a modified Whale Random Walk mechanism to avoid local optima traps and augment its global search capability;
- Developing a drone coverage approach anchored in the DWBKA algorithm to plan near-optimal pesticide spraying flight paths in complex fruit farm environments.
The subsequent sections of this work are organized in this order: Section 2 elaborates the establishment of environmental maps, the formulation of the objective function for drone coverage path planning, the Black-winged Kite Algorithm, and its enhancements. Section 3 delineates the design of experiments, analysis of results, and discussion of limitations. Section 4 summarizes the research findings and outlines future work.
2. Materials and Methodology
2.1. Study Area Description
This research focuses on Meihekou City, situated in the southeast of Jilin Province in northeastern China. Located in the transitional zone between the Songliao Plain and the Changbai Mountains, the city lies at the foot of the Changbai Mountains, in the upper reaches of the Huifa River. The geographical coordinates extend from 42°08′ to 43°02′ north latitude and from 125°15′ to 126°03′ east longitude. The region experiences a temperate continental monsoon climate characterized by distinct seasons, concurrent rainfall and heat, moderate precipitation, significant diurnal temperature variations, an annual frost-free period of 137–145 days, and an effective accumulated temperature of 2920.5 °C, making it highly suitable for the growth of high-quality fruit trees. Meihekou City currently has over 200 hectares of fruit tree plantations, with 70 hectares being productive. The primary varieties include apples, pears, plums, and apricots.
2.2. Grid-Based Planning Area
The remote sensing image of the giant fruit farm in Meihekou City was obtained using the Google Earth platform, as shown in Figure 1. Six specific regions were selected for analysis, and the Segment Anything Model (SAM) was employed to meticulously divide the fruit farm area into task area and non-task area, with the detailed process shown in Figure 2.

Figure 1.
Giant fruit farm in Meihekou City.
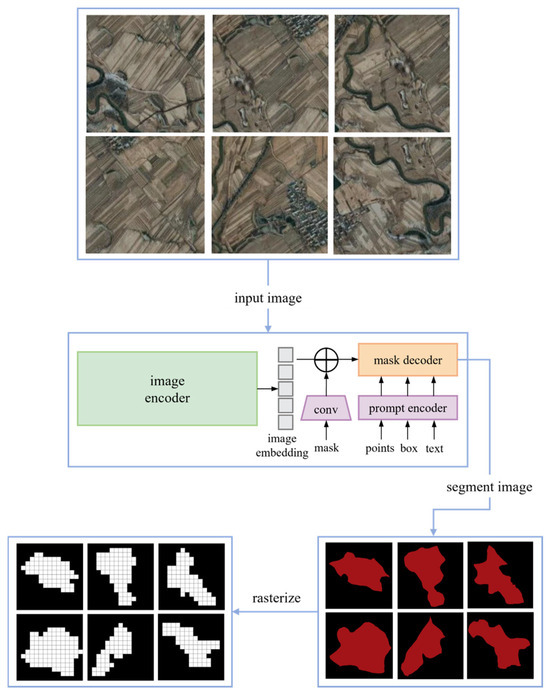
Figure 2.
Workflow for task map creation.
In addition, the research utilized a grid map method to partition the setting into a 15 × 15 grid, which was stored and manipulated with a matrix of 1 s and 0 s. Here, 1 indicates obstacle grids (non-task area), whereas 0 signifies free grids (task area). In the environmental model, obstacle grids are denoted by black grids (also referred to as no-fly grids), whereas free grids are indicated by white grids (also known as feasible grid points).
To facilitate implementation, the research employed both serial numbers and a rectangular coordinate system to distinguish grid positions. Specifically, every grid was allocated a unique serial number and its corresponding location within the rectangular coordinate system. The conversion rule between the coordinate position of each grid and its corresponding serial number pi is illustrated in Equation (1).
Here, denotes the modulo operation, represents the integer division, is the number of grids along the axis, and is the number of grids along the axis. For instance, in Figure 3, the grid with serial number 119 corresponds to the rectangular coordinates (13.5, 7.5).
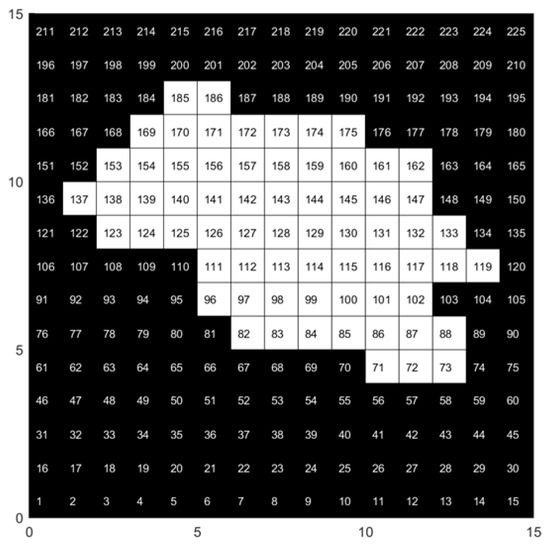
Figure 3.
Space environment model (white grids represent the task area, and black grids represent the non-task area).
2.3. Mathematical Model of Drone Coverage Path Planning
Figure 4 illustrates the flight path of the drone. After the grid network modeling, the drone can move in eight directions around the adjacent grids, as shown in Figure 4a. If there are no obstacles in the drone’s flight path, the drone can fly further, as shown in Figure 4b. If the drone collides with an obstacle during its operation, the path is considered infeasible, as shown in Figure 4c. If the drone moves from point A to point B and encounters an obstacle but does not collide with it throughout the process, the path is considered a feasible one, as shown in Figure 4d. The drone’s working path is a set of connecting lines formed by sequentially passing through a group of characteristic points of the target spraying shape under the premise of a feasible path.
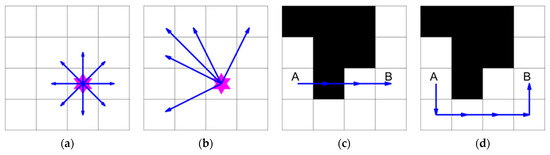
Figure 4.
Flight path of the drone: (a) flight path; (b) flight path without obstacles; (c) incorrect path; (d) correct path.
2.3.1. Representation of Flight Paths
This study conducted path planning experiments based on the aforementioned grid environment. Within this environment, the obstacle grids are denoted by the set , while the free grids are represented by the set . The elements within the sets and are indicated using a serial number method. When employing the swarm intelligence optimization algorithm presented in this study for optimization, each path is represented as an individual within the population, with each individual being characterized by a node serial number . Consequently, a path with m nodes, optimized by the path planning algorithm and originating from the specified starting point , can be expressed as shown below:
where represents the -th node traversed by the path.
2.3.2. Construction of the Objective Function
After establishing the relevant environmental data, to identify an ideal path that meets the requirements on the map, it is necessary to create an objective function (fitness function) that incorporates constraints and retains solutions that satisfy this function. This section considers constructing the fitness function from three aspects: UAV flight safety, coverage task, and path length.
- Flight Safety Cost Function
When designing the fitness function, it is essential to fully ensure the safety of the planned UAV flight path, that is, to prevent the UAV from colliding with any obstacles during path execution. Therefore, considering flight safety, this study constructs the fitness function , which is used to determine whether any path point is out of bounds or whether the line connecting it to the previous path point crosses an obstacle. When the path point is feasible, the return value is 0; otherwise, a larger number is returned, set here as 1000. The specific definition is as follows:
The flight safety function for the entire path is obtained by summing between each pair of nodes using the following equation:
where denotes the aggregate quantity of nodes along the path.
- 2.
- Coverage Task Cost Function
The coverage task is the core objective of UAV CPP problem, aiming to maximize the covered area while minimizing the proportion of repeated coverage. Therefore, this study designs a function to determine whether a path point during UAV flight is within the task area. If the UAV reaches the area for the first time, the element is removed from the coverage task set , and returns a value of 1. If the UAV reaches the area repeatedly and the element is no longer in the set , returns a value of 0.
The coverage task function is defined by subtracting the sum of between adjacent nodes from the total number of coverage task grids , as shown in the following equation:
From Equation (6), it is evident that the more the UAV completes the coverage task area, the lower the value of the .
- 3.
- Path Length Cost Function
The primary optimization objective is to reduce the total path length, which is a critical metric for evaluating the quality of a path. The calculation of the path length is based on the Euclidean distance between each pair of adjacent nodes along the path. In particular, the total path length can be expressed as follows:
Here, and represent the coordinates of two contiguous nodes and along the path. The objective function is employed to assess path quality, with lower values corresponding to shorter paths.
- 4.
- Overall Function for CPP
During the selection of the ideal path, the drone is required to account for flight safety cost, coverage task cost, and path length cost to ultimately plan a safe and efficient optimal path. The ultimate cost function for drone CPP is formulated by the following:
Here, denotes the weight coefficient corresponding to the -th function, and , , and are set to 1, 100, and 1, respectively. The optimizing tasks and restrictions of the drone path planning issue are incorporated into the cost function that establishes the prerequisites for the ensuing experiments in the study, which utilize swarm intelligence optimization algorithms to address the agricultural drone CPP challenges.
2.4. Black-Winged Kite Algorithm
The Black-winged Kite Algorithm (BKA) is a novel swarm intelligence algorithm that Wang et al. developed by observing the attacking and migrating behaviors of the black-winged kite. This algorithm combines the Leader tactic with the Cauchy mutation process to search for a wide range of appropriate convergent solutions.
2.4.1. Population Initialization
Initially, a matrix is generated to randomly allocate the positions of all black-winged kites. The initial locations of the black-winged kites are uniformly distributed by applying the following equation:
Here, is an integer between 1 and , where signifies the quantity of feasible solutions, namely, the population number of the black-winged kites. denotes the location of the -th black-winged kite. A random vector is generated inside [0, 1]. and indicate the upper and bottom limits of locations of black-winged kites, respectively.
During initialization, the individual exhibiting the most superior fitness value within the population is designated as the initial cohort’s leader , reflecting the ideal position of the group. The calculation for is as follows:
Here, represents the best value of fitness within the population, which is exemplified by the minimum value in this context.
2.4.2. Attack Behavior
Inhabiting the grassland ecosystems, black-winged kites hunt insects and small mammals. While airborne, they modify the angles of their tails and wings to adapt wind velocity, hover silently to monitor their targets, and subsequently execute a rapid dive to initiate an attack. This behavior can be characterized by two states: hovering in the air and diving towards the prey. The position update is as follows:
Here, and represent the locations of the -th dimension of the -th black-winged kite individual at the -th and -th iteration, respectively. A random variable is generated between 0 and 1. The value of the constant is set at 0.9. Equation (13) defines , whereby signifies the current iteration and indicates the maximum iterations.
2.4.3. Migration Behavior
The migration behavior is led by the leader. When the fitness score of the current individual surpasses that of a randomly selected individual, the leader will continue to lead the group towards the destination. In contrast, once the fitness score of the present individual is inferior to that of the randomly chosen individual, the leader will abdicate leadership and integrate into the migratory group. The specific description is provided by the subsequent equation:
Here, represents the leading scorer (current optimal solution) in the -th dimension of the black-winged kite at the -th iteration. ) denotes the Cauchy mutation. indicates the fitness score of the current individual, and signifies the fitness score of a randomly selected black-winged kite member from the population.
2.5. Enhancement of Algorithm
2.5.1. Dynamic Position Balancing Strategy
From Equation (12), it can be observed that the BKA incorporates an exponentially decaying function that modulates the length of the search step for each individual. Although this approach progressively diminishes the step length as iterations increase, thereby enhancing local exploitation capability, it may lead to the algorithm being ensnared in local extremum or converging too slowly. To raise the optimization performance and convergence speed of the BKA, this study introduces a Dynamic Position Balancing strategy to perturb and update the positions of black-winged kite individuals during their hovering process. When , the position update formula for the Dynamic Position Balancing strategy of the black-winged kite is as follows:
Here, represents the midpoint among positions of the current individual , the best individual , and the random individual ; is a randomly generated crossover operator vector with the same length as , containing only 0 or 1, where 1 indicates retaining part of the position of and 0 indicates abandoning part of the position of ; is the random candidate individual position in the current iteration; is a distance adaptation factor used to control the distance between the current black-winged kite and the leading black-winged kite , which is defined as follows:
Here, is a randomly generated number following a Gaussian distribution, is a randomly produced number within the range of 0 to 1, and is a coefficient related to the iteration. This study employs the Dynamic Position Balancing strategy in the first one-third of the maximum iterations of the algorithm; thus, .
2.5.2. Modified Whale Random Walk Strategy
During the migration process, black-winged kites tend to move towards the leader based on their relative positions. However, this approach can lead to the leader misleading the entire population, resulting in the algorithm becoming trapped in local optima. To boost the algorithm’s capacity to evade local extremum and improve global search capabilities, this study introduces a modified Whale Random Walk strategy motivated by the random walk patterns of whales.
Within the random walk strategy, the key to controlling the random walk of black-winged kite individuals lies in the fitness value. When the current individual’s fitness value is superior to the fitness value of a randomly chosen individual, the black-winged kite individual performs a global exploration update of its position. Unlike the original algorithm, the black-winged kite individual no longer moves toward the leading individual but instead moves toward a randomly selected candidate individual in the population. This shift helps the black-winged kite individual move away from its original position, thereby escaping local extremum. The mathematical representation of the modified Whale Random Walk mechanism is presented below:
Here, is a vector of the same length as randomly generated from a normal distribution. represents a random candidate solution in the current iteration with a fitness value better than that of the current individual . is an integer randomly selected from 1 or 2.
2.6. Flow of the Proposed Path Planning Method
To summarize, the algorithm for agricultural UAV coverage path planning, which enhances the Black-winged Kite method (DWBKA) through the Dynamic Position Balancing mechanism and modified Whale Random Walk strategy, is delineated below, and the flowchart is depicted in Figure 5:
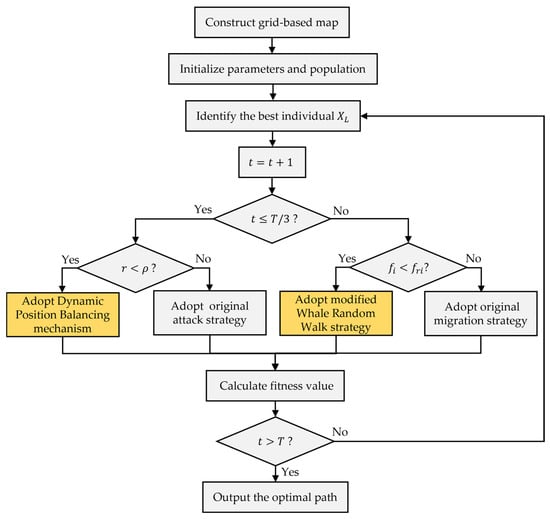
Figure 5.
Flowchart of the proposed path planning method.
- Step 1: The algorithm commences by constructing an environmental map using the grid-based method. The starting point of the UAV, the set of obstacle grids , the set of free grids , the set of coverage tasks , and the total number of coverage task grids are initialized;
- Step 2: The fundamental parameters of BKA population are initialized. These include the population size , the iteration counter , the maximum iterations , and the initial positions of all individuals inside the solution space;
- Step 3: Iterations begin. The fitness values of all individuals in the population are calculated, and the best individual is identified;
- Step 4: The iteration counter is incremented (). If , advance to Step 5. If not, continue to Step 6;
- Step 5: Attack behavior. A number is produced randomly in the range of 0 to 1. If , the original attack strategy (Equation (12)) is employed to modify the individual’s position. Otherwise, the Dynamic Position Balancing mechanism (Equation (16)) is used to update the individual’s position;
- Step 6: Migration behavior. The current individual’s fitness value is computed. If is inferior to a randomly chosen individual’s fitness value , the original migration strategy (Equation (14)) is used to modify the individual’s position. Otherwise, the modified Whale Random Walk strategy (Equation (19)) is employed to update the individual’s position;
- Step 7: The best individual position (optimal solution) and its fitness value are calculated according to Equation (8);
- Step 8: The algorithm undergoes verification of its termination condition. If the iteration counter is more than , proceed to Step 9. Otherwise, return to Step 3;
- Step 9: The algorithm concludes by outputting the value of fitness and the solution of optimum (optimal path).
3. Results and Discussion
3.1. Settings for Experiments
Delving into prior research on coverage optimization for agricultural drones, it becomes apparent that the works referenced in [41,42,44,58] fail to adequately account for boundary constraints and obstacle avoidance. These studies predominantly applied algorithmic frameworks to regular polygonal geometries or cross-regional coverage targets while neglecting resource utilization efficiency and the potential for hazardous incidents involving drones in non-operational zones. Notably, reference [58] employed conventional neural network architectures, whereas references [44,45] implemented more sophisticated deep reinforcement learning paradigms. Empirical evidence from reference [45] demonstrated that the BL-DQN algorithm achieved superior performance in terms of the coverage rate, duplicate coverage reduction, and path planning efficiency when benchmarked against conventional DQN and Depth-First Search algorithms. Against this backdrop, the present study conducts a comparative analysis of the proposed DWBKA algorithm with the original BKA algorithm and the BL-DQN algorithm.
In consideration of the fact that enhanced algorithms typically exhibit superior performance, the experiments were expanded to incorporate three well-established swarm intelligence optimization algorithms and their respective improved variants. These include the Whale Optimization Algorithm (WOA), Harris Hawk Optimization (HHO), and Grey Wolf Optimizer (GWO). The enhanced versions utilized in this study are as follows: the WOA with Random Spare and Double Adaptive Weight (RDWOA) [59], the HHO with a Cauchy Distribution Inverse Cumulative function and Tangent Flight operator (CTHHO) [60], and the GWO with a Dimension Learning-based Hunting strategy (DGWO) [61].
To ensure fairness, all experiments were performed on a computer system running Windows 11 equipped with 16 GB of memory and an AMD Ryzen R7 6800H CPU @ 3.20 GHz, using MATLAB R2024b for programming. To maintain consistency, the maximum iterations for the BKA and its improved version were set to 500, as well as the maximum training episodes for BL-DQN. Additionally, the population size for BKA and improved versions was set to 30, while the hyperparameters for BL-DQN can be referenced from Fu et al.’s work [45].
In this research, the performance of three distinct algorithms in the realm of path planning was assessed through the application of four specific indicators: coverage rate, repeated coverage rate, path length, and computation time.
The coverage rate refers to the proportion of the actual area covered by the drone within a given region to the total area, as shown in Equation (20):
Here, signifies the aggregate count of nodes constituting the path; denotes the -th node (grid) on the path; is the coverage task set, where repeated nodes are marked as 0 and non-repeated nodes as 1, as detailed in Equation (4); and represents the aggregate quantity of grids in the coverage task.
The repeated coverage rate is determined by the fraction of the area repeatedly traversed by the UAV during coverage to the actual covered area, as shown in Equation (21):
The path length refers to the cumulative distance of the UAV’s flight trajectory generated by the path planning algorithm, as illustrated in Equation (22):
The coordinates and correspond to the positions of the current node and the next node on the planned path, respectively. The conversion between node and its coordinates is referenced in Equation (1).
The computation time is determined by the duration from the initiation of the path planning algorithm to the generation of the final path, which is contingent upon reaching the maximum iterations or training episodes.
3.2. Results
The path planning results of various algorithms in different environments are presented in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. In these visualizations, the light blue squares represent the task area, the white squares indicate non-task areas, the yellow squares denote the starting point, and the regions enclosed by red frames highlight the repeated paths. It is evident that the suggested DWBKA exhibits substantial superiority in comparison with alternative algorithms with regard to task coverage rate, path repetition, and path length. The path planning results indicate that the paths generated by the DWBKA are more direct and smoother. Conversely, the BKA algorithm and other swarm intelligence algorithms generated more turns and detours in these environments, suggesting their limited problem-solving capability in path planning and higher likelihood of falling into local optima. Moreover, BL-DQN was unable to fulfill the requirements for complete regional coverage tasks, mainly because it requires extensive training to handle complex task scenarios, and insufficient training limits its performance.
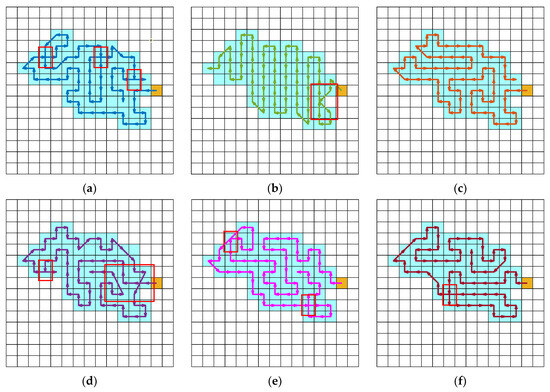
Figure 6.
Path planning results in Scenario 1 (red boxes indicate repeated paths): (a) BKA; (b) BL-DQN; (c) DWBKA; (d) RDWOA; (e) CTHHO; (f) DGWO.
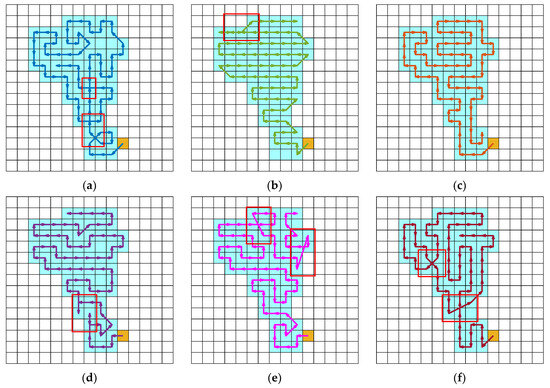
Figure 7.
Path planning results in Scenario 2 (red boxes indicate repeated paths): (a) BKA; (b) BL-DQN; (c) DWBKA; (d) RDWOA; (e) CTHHO; (f) DGWO.
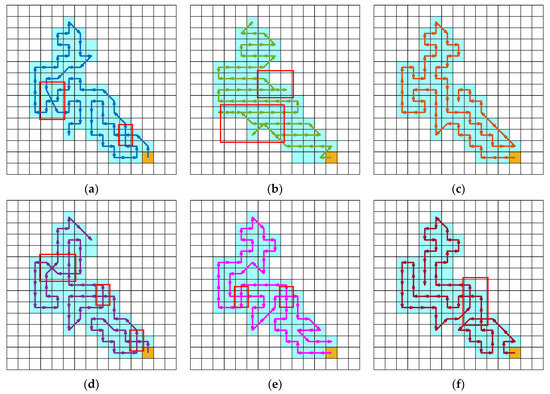
Figure 8.
Path planning results in Scenario 3 (red boxes indicate repeated paths): (a) BKA; (b) BL-DQN; (c) DWBKA; (d) RDWOA; (e) CTHHO; (f) DGWO.

Figure 9.
Path planning results in Scenario 4 (red boxes indicate repeated paths): (a) BKA; (b) BL-DQN; (c) DWBKA; (d) RDWOA; (e) CTHHO; (f) DGWO.
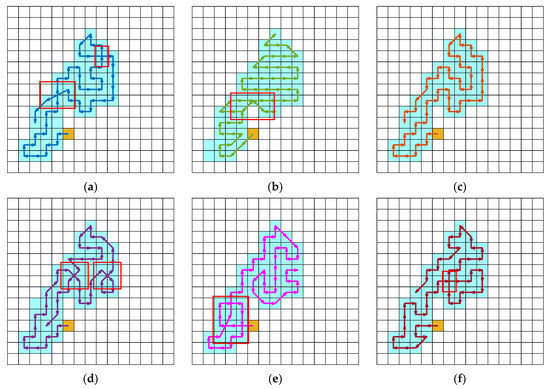
Figure 10.
Path planning results in Scenario 5 (red boxes indicate repeated paths): (a) BKA; (b) BL-DQN; (c) DWBKA; (d) RDWOA; (e) CTHHO; (f) DGWO.
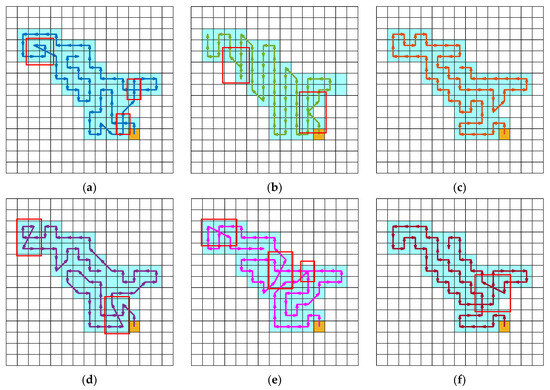
Figure 11.
Path planning results in Scenario 6 (red boxes indicate repeated paths): (a) BKA; (b) BL-DQN; (c) DWBKA; (d) RDWOA; (e) CTHHO; (f) DGWO.
To provide a quantitative evaluation of the three algorithms previously mentioned, the research measured the coverage rate, repetition rate, path length, and computation time for each method to complete the work area coverage process. The findings of the analysis, displayed in Table 1, clearly indicate that the developed DWBKA surpassed all other algorithms across all maps. Specifically, in all test scenarios, the suggested approach attained 100% coverage with the minimal rate of path repetition and the shortest path lengths. In terms of coverage rate, DWBKA was 1.52–2.82% higher than BKA and 1.52–4.00% higher than BL-DQN. Regarding the repetition rate, the improved algorithm reduced it by 2.90–8.33% compared to RDWOA and by 3.08–9.28% compared to CTHHO. In terms of path length, the proposed algorithm reduced it by 1.22–4.35% compared to DGWO and by 2.42–10.13% compared to BL-DQN. Regarding computation time, the proposed method reduced it by 48.97–51.90% compared to BKA and by 88.40–93.20% compared to BL-DQN. These findings indicate that DWBKA can devise more rational routes across various complicated situations, consequently showcasing superior capacity for path optimization.

Table 1.
Comparison of the experimental results.
Figure 12 presents the convergence curves of the path planning for the DWBKA and other swarm intelligence algorithms in different environments. The convergence curve serves as a visual representation of the algorithm’s precision in obtaining the final solution, with a decreasing amplitude indicating enhanced exploration capability and the ability to avoid localized optimal values. The ability of an algorithm to avoid localized optimal values somewhat reflects its performance in handling complicated tasks. Moreover, the iteration step at which the population of the algorithm stabilizes at the ultimate location can be discerned from the convergence curve. From the convergence patterns presented.
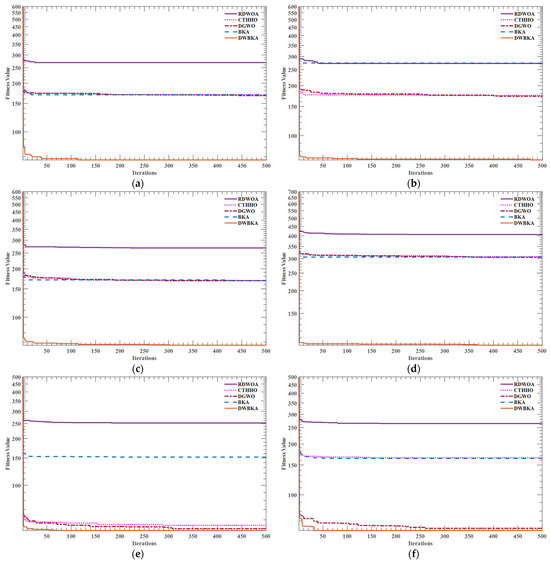
Figure 12.
Path planning convergence curves in different scenarios: (a) Scenario 1; (b) Scenario 2; (c) Scenario 3; (d) Scenario 4; (e) Scenario 5; (f) Scenario 6.
As shown in Figure 12. it is evident that in these six grid map scenarios, DWBKA consistently achieved better results than its counterparts. Notably, DWBKA maintained a faster convergence speed and improved solution accuracy in these scenarios. In contrast, BKA exhibited a relatively slower convergence speed and more fluctuations during the iteration process.
To substantiate the generalized applicability of the proposed method, the DWBKA was employed for irregular polygon coverage tasks and systematically benchmarked against the optimization framework documented in Reference [43]. As demonstrated in Figure 13, the proposed method achieved near-complete coverage fidelity while ensuring strict UAV confinement within target boundaries. Comparative analysis with reference [43] (Figure 14, yellow circles indicating initiation points) reveals pathological deviations beyond the polygonal perimeters in Scenarios 1–5.
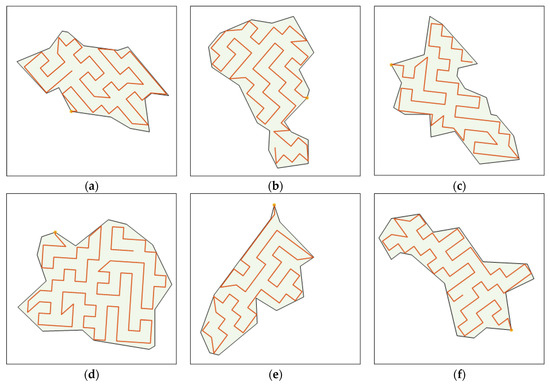
Figure 13.
Results of our method in polygonal scenes: (a) Scenario 1; (b) Scenario 2; (c) Scenario 3; (d) Scenario 4; (e) Scenario 5; (f) Scenario 6.
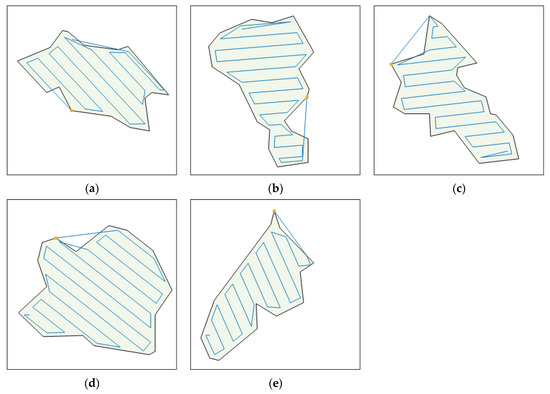
Figure 14.
Results of the other complex-shaped area CPP method in polygonal scenes: (a) Scenario 1; (b) Scenario 2; (c) Scenario 3; (d) Scenario 4; (e) Scenario 5.
Notably, the proposed methodology successfully maintained full spatial compliance throughout all test configurations. The suboptimal performance of reference [43] stems from its experimental paradigms, which predominantly employed convex pentagons/hexagons and regular mono-notched polygons, whereas the current fitness function demonstrated imperfect adaptability when confronted with irregular polygons featuring multiple concave features. Particularly in Scenario 6, the referenced method failed to generate viable solutions (thus omitted from the presentation) due to inherent limitations in directional adaptability—its core optimization mechanism of unidirectional scanning patterns becomes fundamentally inoperative in geometrically complex, multi-indentation polygons.
But the BL-DQN architecture encountered implementation failure when applied to the different mapping scenarios, which was fundamentally due to the absence of predefined drone movement direction parameters and compatible grid-based mapping infrastructures. The BL-DQN framework, rooted in conventional Deep Q-Network architecture, achieves Q-value convergence through reliance on a finite action set. However, the intrinsic contradiction between the continuous motion degrees of freedom inherent to UAVs in physical space and the discrete action repertoire remains inadequately reconciled within this framework. As the action space dimensionality expands from the standard octa-directional configuration to angular-directional continuity required in practical implementations, the Q-network’s parameter optimization confronts an escalating dimensionality curse. Furthermore, the rigid discretization inherent to conventional grid-based environmental representations induces irreversible information loss during spatial encoding, thereby precipitating a state representation crisis. Of particular concern is the fixed-resolution grid system’s inability to accommodate agricultural cartographic uncertainties, ultimately inducing an amplification effect on positional inaccuracies through Q-function propagation.
In summary, DWBKA demonstrated significant advantages over the BKA algorithm in terms of coverage rate, repetition rate, path length, computation time, and convergence speed. These results highlight the effectiveness and robustness of DWBKA in agricultural drone path planning, thereby proving its adaptability and potential in complex environments.
3.3. Discussion
The DWBKA algorithm outperformed the traditional BKA and BL-DQN algorithms in terms of the coverage rate, repetition rate, path length, and computation time. This indicates that the DWBKA can efficiently complete coverage tasks while improving the quality of planned paths and maintaining low computational complexity. Consequently, this enables UAVs to execute pesticide spraying missions with diminished energy expenditure, thereby mitigating pesticide waste and environmental contamination.
The algorithm’s enhanced efficacy is predominantly attributable to two key mechanisms: the Dynamic Position Balancing mechanism and the modified Whale Random Walk strategy. The Dynamic Position Balancing mechanism significantly augments the global exploration capabilities of BKA, facilitating the rapid identification of near-optimal solutions during the initial stages of algorithmic iteration. This is manifest in the convergence plot as a precipitous decline in solution quality metrics. In contrast, the modified Whale Random Walk strategy bolsters the local exploration prowess of the BKA, aiding the algorithm in extricating itself from local optima traps during the latter stages of iteration. This results in a more gradual and refined approach to the optimal solution, as depicted in the convergence plot. Furthermore, the original algorithm’s concurrent execution of both attack and migration strategies within a single iteration incurs substantial time overhead and resource inefficiency. The revised version, however, executes these strategies sequentially, focusing computational resources on one behavior per iteration. This streamlined approach not only enhances the algorithm’s solution-finding efficiency but also reduces computational time to approximately half that of the original algorithm.
In order to more comprehensively elucidate the optimization capabilities of the proposed algorithm, this investigation undertook a localized empirical validation utilizing a quadcopter drone, specifically the DJI Matrice 350. The UAV was configured with a sampling frequency of 64 Hz and an initial flight altitude of 3 m. The UAV and the resultant flight trajectory are visually represented in Figure 15 and Figure 16, wherein the blue polygon demarcates the mission area, while the green and red lines respectively delineate the ideal and actual flight trajectories.

Figure 15.
DJI quadcopter drone.
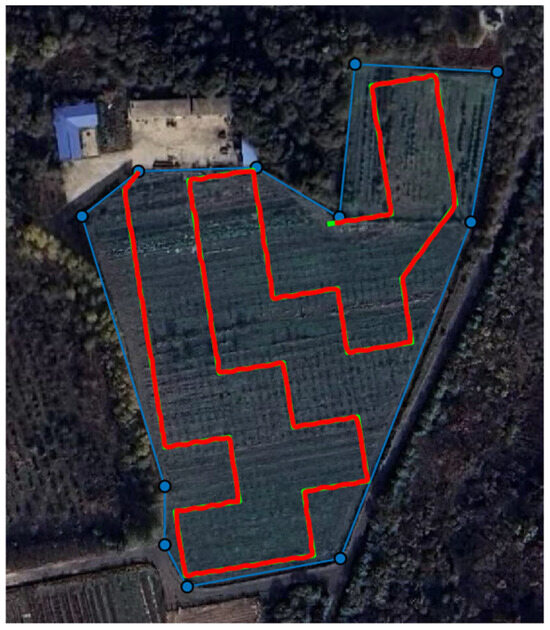
Figure 16.
The UAV CPP result in a small area (the green and red lines respectively represent the ideal and actual flight trajectories).
Furthermore, this study meticulously documented the UAV’s displacement and velocity data across the X, Y, and Z axes, as depicted in Figure 17. Figure 16 and Figure 17 reveal that the UAV’s flight displacement response exhibits a high degree of congruence with the planned trajectory, thereby affirming the algorithm’s efficacy in enabling the UAV to execute the planned path with remarkable precision in real-world conditions.
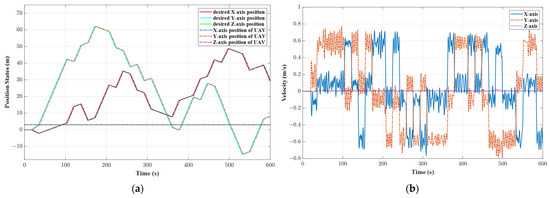
Figure 17.
UAV flight log data: (a) position states; (b) velocity.
In recent years, the field of UAV trajectory research has witnessed a plethora of novel advancements. With regard to large-scale navigation and energy consumption, Li et al. [62] refined the beetle antenna search algorithm to alleviate the constraints imposed by battery limitations on UAV round-trip times during rescue and disaster relief missions; Bhuiyan et al. [63] developed a hybrid approach incorporating greedy heuristics and genetic algorithms to minimize fleet size, battery replacement frequency, and overall energy consumption; Porcelli et al. [64] leveraged mobile ground battery replacement stations to accelerate UAV battery replacement processes and mitigate energy wastage. In the domain of advanced sensor utilization, Yu et al. [65] employed LiDAR technology to construct detailed maps of UAV flight environments; Seoane et al. [66] utilized LiDAR sensors to detect birds of various sizes, thereby enabling UAVs to avoid mid-air collisions; Xu [67] focused on UAV patrol trajectory planning and proposed an obstacle avoidance strategy that integrates machine vision with multi-sensor data fusion. When it comes to dynamic scenarios, Niu et al. [68] combined perturbation fluid dynamics systems with artificial neural networks to develop a real-time dynamic trajectory planning method for UAVs; Du et al. [69] considered the influence of wind speed and direction on the flight status of logistics UAVs and proposed a dynamic trajectory optimization method that integrates large-scale neighborhood search algorithms with genetic algorithms; Wang et al. [70] adopted a bi-level planning strategy to enhance the D* algorithm, facilitating dynamic collaborative trajectory planning for multiple UAVs in complex environments. In the context of multi-UAV formation flight, Kuyffer et al. [71] optimized UAV package delivery routes and swarm configurations using ant colony optimization-based V-shaped algorithms; Wang et al. [72] established a mathematical model incorporating constraints such as flight distance, collision threat, and trajectory stability to address the trajectory planning problem of UAV formations in mountainous forest monitoring missions; Poudel and Moh [64] employed actor-critic multi-agent reinforcement learning to handle dynamic environmental elements in heterogeneous UAVs and tasks.
Reflecting on the research trends that have emerged and evolved over the course of the past several years, the current study has meticulously examined these trends and, based on its comprehensive analysis, has pinpointed several areas within the relevant field that could clearly benefit from more in-depth and extensive investigation in order to further advance our understanding and knowledge:
- In planning the drone’s flight path, this study primarily focused on static threat factors and did not consider sudden situations or unknown local information, such as flocks of birds in the air or wind direction changes, which prevent real-time flight path planning. Adjusting the algorithm to accommodate different real-time factors will be a key focus in future work [73,74].
- Although this study has proposed a CPP algorithm for a single drone, the need for multi-agent collaborative work is becoming increasingly evident with the development of multi-drone systems. Future research can explore collaborative path planning algorithms for multiple drones to enhance overall system efficiency and collaborative performance [75,76].
4. Conclusions and Future Work
In the quest to explore pest and disease control methods for farms with complex shapes and restricted boundaries, an enhanced Black-winged Kite Algorithm (DWBKA) was utilized in this study to develop an agricultural drone coverage optimization method. This innovative approach utilizes the deep learning Segment Anything Model (SAM) to precisely segment the task area and employs gridding technology to construct a detailed environmental map, thereby providing a robust and accurate information base for drone path planning. Within this framework, by defining the coverage task cost function, the flight safety cost functions, and the path length cost functions, the coverage challenge in complex-shaped areas is reformulated as a complex optimization challenge with multi-constraints. The DWBKA, integrating a Dynamic Position Balancing mechanism and a modified Whale Random Walk approach, substantially boosts its global search capacity and effectively circumvents the pitfalls of local optima. During the experimental phase, DWBKA demonstrated exceptionally notable performance. It achieved 100% task coverage and demonstrated a remarkable improvement in computational efficiency: the total computation time was approximately half that of the Black-winged Kite Algorithm and less than one-tenth that of the BL-DQN. These results strongly demonstrate the significant improvement in computational efficiency achieved by DWBKA. Moreover, DWBKA also exhibited excellent performance in reducing redundant actions. In comparison to the Black-winged Kite Algorithm, the overall repetitive rate of coverage decreased by 5.69%; relative to the BL-DQN, it diminished by 5.10%. These data clearly indicate that DWBKA outperformed other algorithms in key indicators, such as the coverage rate, repeated coverage rate, path length, and computation time. The proposed method not only exhibits superior performance compared to other coverage methods for complex areas but also validates the high efficiency and superiority of the DWBKA in complex farm coverage tasks.
Subsequent study endeavors will concentrate on incorporating real-time information on the environment, including avian flocks in the air and meteorological conditions, into path planning problem to formulate algorithms that are adaptable to dynamic environments. Additionally, path planning for coordinating multiple drone fleets will be explored, considering task allocation, with the goal of applying the proposed algorithm to multi-agricultural drones to further augment the efficacy and sophistication of precision agriculture.
Author Contributions
Conceptualization, J.L. and S.F.; methodology, J.L., S.F. and W.Z.; software, W.Z. and H.F.; investigation, S.F. and W.Z.; resources, W.Z. and H.F.; validation, W.Z. and X.F.; data curation, H.F. and Z.L.; writing—original draft preparation, S.F.; writing—review and editing, J.L.; supervision, J.L. and X.F.; funding acquisition, J.L.; project administration, X.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jilin Province Science and Technology Development Plan Project, grant number 20240302092GX; Scientific Research Project of the Jilin Provincial Department of Education, grant number JJKH20250574BS; Demonstration Project for the Construction of a Provincial-Level Modern Agricultural Industry Technology System, grant number JLARS-2025-010216; Ginseng Soil Improvement Technology Development Project in Jingyu County, Baishan City, Jilin Province, grant number 20250017; and Science and Technology Project of the Jilin Provincial Department of Agriculture and Rural Affairs, grant number 2024PG1204.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| BKA | Black-winged Kite Algorithm |
| SAM | Segment Anything Model |
| DWBKA | BKA with Dynamic Position Balancing and modified Whale Random Walk |
| BL-DQN | Deep Q-Network with Bidirectional Long Short-Term Memory |
| UAV | Unmanned Aerial Vehicle |
| CPP | Coverage Path Planning |
| DQN | Deep Q-Network |
| WOA | Whale Optimization Algorithm |
| HHO | Harris Hawk Optimization |
| GWO | Grey Wolf Optimizer |
| RDWOA | WOA with Random Spare and Double Adaptive Weight |
| CTHHO | HHO with Cauchy Distribution Inverse Cumulative and Tangent Flight |
| DGWO | GWO with Dimension Learning-based Hunting |
References
- Jaramillo-Vivanco, T.; Balslev, H.; Montúfar, R.; Cámara, R.M.; Giampieri, F.; Battino, M.; Cámara, M.; Alvarez-Suarez, J.M. Three Amazonian palms as underestimated and little-known sources of nutrients, bioactive compounds and edible insects. Food Chem. 2022, 372, 131273. [Google Scholar] [CrossRef] [PubMed]
- Araujo, N.M.P.; Arruda, H.S.; Marques, D.R.P.; Oliveira, W.Q.; Pereira, G.A.; Pastore, G.M. Functional and nutritional properties of selected Amazon fruits: A review. Food Res. Int. 2021, 147, 110520. [Google Scholar] [CrossRef]
- Perera, S.; Silva, A.B.G.; Amarathunga, Y.; De Silva, S.; Jayatissa, R.; Gamage, A.; Merah, O.; Madhujith, T. Nutritional Composition and Antioxidant Activity of Selected Underutilized Fruits Grown in Sri Lanka. Agronomy 2022, 12, 1073. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Y.; Wang, S.; Zhao, X. Legume cover with optimal nitrogen management and nitrification inhibitor enhanced net ecosystem economic benefits of peach orchard. Sci. Total Environ. 2023, 873, 162141. [Google Scholar] [CrossRef] [PubMed]
- Afsharpour, P.; Zoughi, T.; Deypir, M.; Zoqi, M.J. Robust deep learning method for fruit decay detection and plant identification: Enhancing food security and quality control. Front. Plant Sci. 2024, 15, 1366395. [Google Scholar] [CrossRef]
- Mashilo, J.; Shimelis, H.; Contreras-Soto, R.I.; Ngwepe, R.M. A meta-analysis on rootstock-induced effects in grafted watermelon (Citrullus lanatus var. lanatus). Sci. Hortic. 2023, 319, 112158. [Google Scholar] [CrossRef]
- Wakchaure, G.C.; Minhas, P.S.; Kumar, S.; Mane, P.; Kumar, P.S.; Rane, J.; Pathak, H. Long-term response of dragon fruit (Hylocereus undatus) to transformed rooting zone of a shallow soil improving yield, storage quality and profitability in a drought prone semi-arid agro-ecosystem. Saudi J. Biol. Sci. 2023, 30, 103497. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, X.; Wang, J.; Wei, B.; Zhou, Q.; Cheng, S.; Sun, Y.; Li, B. Slight water loss affects the quality of ‘Longcheng 2’ kiwiberry fruit infected with gray mold disease. Sci. Hortic. 2024, 328, 112932. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Shan, X.; Wang, H.; Duan, Y. Bioactivities evaluation of an endophytic bacterial strain Bacillus tequilensis QNF2 inhibiting apple ring rot caused by Botryosphaeria dothidea on postharvest apple fruits. Food Microbiol. 2024, 123, 104590. [Google Scholar] [CrossRef]
- Ding, J.; Liu, C.; Huang, P.; Zhang, Y.; Hu, X.; Li, H.; Liu, Y.; Chen, L.; Liu, Y.; Qin, W. Effects of thymol concentration on postharvest diseases and quality of blueberry fruit. Food Chem. 2023, 402, 134227. [Google Scholar] [CrossRef]
- He, Z.; Abeywickrama, P.D.; Wu, L.; Zhou, Y.; Zhang, W.; Yan, J.; Shang, Q.; Zhou, Y.; Li, S. Diversity of Cytospora Species Associated with Trunk Diseases of Prunus persica (Peach) in Northern China. J. Fungi 2024, 10, 843. [Google Scholar] [CrossRef] [PubMed]
- Ning, M.; Guo, Q.; Guo, P.; Cui, Y.; Wang, K.; Du, G.; Wang, Z.; Yuan, Y.; Yue, T. Biocontrol activity of Kluyveromyces marxianus YG-4 against Penicillium expansum LPH9 on apples. Int. J. Food Microbiol. 2025, 427, 110943. [Google Scholar] [CrossRef]
- Winkler, A.; Bauer, S.; Jung, J.; Kleinhenz, B.; Racca, P. SIMKEF—A decision support system to predict the infestation probability of Drosophila suzukii. Crop Prot. 2024, 185, 106858. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Luo, D.; Ba, L. Advances in the Understanding of Postharvest Physiological Changes and the Storage and Preservation of Pitaya. Foods 2024, 13, 1307. [Google Scholar] [CrossRef]
- Acevedo, C.M.D.; Niño, D.D.C.; Gómez, J.K.C. Sensory Perception Systems and Machine Learning Methods for Pesticide Detection in Fruits. Appl. Sci. 2024, 14, 8074. [Google Scholar] [CrossRef]
- Gu, D.; Zhang, J.; Ding, Y.; Wang, Y.; Yang, J.; Shi, G.; Li, B.; Zhao, J. Design and Analysis of an Electric Integrated Work Vehicle for Corn Intertillage Fertilization and Pesticide Spraying. Appl. Sci. 2024, 14, 11356. [Google Scholar] [CrossRef]
- Araaf, R.T.; Minn, A.; Ahamed, T. Coffee Leaf Rust Disease Detection and Implementation of an Edge Device for Pruning Infected Leaves via Deep Learning Algorithms. Sensors 2024, 24, 8018. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, P. A Three-Dimensional Coverage Path Planning Method for Robots for Farmland with Complex Hilly Terrain. Appl. Sci. 2024, 14, 11231. [Google Scholar] [CrossRef]
- Liu, H.; Zeng, X.; Shen, Y.; Xu, J.; Khan, Z. A Single-Stage Navigation Path Extraction Network for agricultural robots in orchards. Comput. Electron. Agric. 2025, 229, 109687. [Google Scholar] [CrossRef]
- Shan, C.; Wang, G.; Wang, H.; Wu, L.; Song, C.; Hussain, M.; Wang, H.; Lan, Y. Assessing the efficiency of UAV for pesticide application in disease management of peanut crop. Pest Manag. Sci. 2024, 80, 4505–4515. [Google Scholar] [CrossRef]
- Shi, N.; Chen, Z.; Li, H.; Hua, H.; Xu, T.; Ye, J. Development and assessment of a novel single-drive variable angle spraying machine. Sci. Rep. 2024, 14, 31264. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, D.; Xue, X.; Xiahou, B.; Dai, Q.; Song, S. A Novel Approach to Enhancing Pesticide Spraying Effectiveness on Citrus Leaves: Adjusting Soil Moisture Content to Improve Leaf Wettability. Agronomy 2024, 14, 3065. [Google Scholar] [CrossRef]
- Marco, F.L.; Sabino, C.; Tuti, G.S.; Luisetto, I.; Petritoli, E.; Pecora, A.; Maiolo, L.; Đurović-Pejčev, R.; Đorđević, T.; Tomašević, A. Electronic nose for pesticides detection: A first realization. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 403–407. [Google Scholar]
- Kong, C.; Ren, L.; Zhang, T.; Sun, Y.; Chang, Z. Rapid identification of pesticides in soil by bionic sniffing sensing system with unknown category detection function. Comput. Electron. Agric. 2024, 217, 108667. [Google Scholar] [CrossRef]
- Chen, H.; Wu, K.; Lin, H.; Zhou, H.; Zhou, Z.; Mai, Y.; Shi, L.; Zhang, M.; Ma, Z.; Lin, P.; et al. A real-time vision guidance method for autonomous longan picking by the UAV. Comput. Electron. Agric. 2025, 229, 109735. [Google Scholar] [CrossRef]
- Chen, P.; Lan, Y.; Huang, X.; Qi, H.; Wang, G.; Wang, J.; Wang, L.; Xiao, H. Droplet Deposition and Control of Planthoppers of Different Nozzles in Two-Stage Rice with a Quadrotor Unmanned Aerial Vehicle. Agronomy 2020, 10, 303. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Kim, S.-H.; Eun, H.-R.; Kim, S.-M.; Jeong, M.-J.; Baek, J.-W.; Lee, Y.-H.; Noh, H.H.; Shin, Y. Enhancement of Tricyclazole Analysis Efficiency in Rice Samples Using an Improved QuEChERS and Its Application in Residue: A Study from Unmanned Arial Spraying. Appl. Sci. 2024, 14, 5607. [Google Scholar] [CrossRef]
- Fang, X.; Li, X.; Xie, L. Angle-displacement rigidity theory with application to distributed network localization. IEEE Trans. Autom. Control 2020, 66, 2574–2587. [Google Scholar] [CrossRef]
- Eun, H.R.; Kim, S.H.; Lee, Y.H.; Kim, S.M.; Lee, Y.J.; Jung, H.Y.; Min, Y.G.; Noh, H.H.; Shin, Y. Comparison of off-target pesticide drift in paddy fields from unmanned aerial vehicle spraying using cellulose deposition sampler. Ecotox. Environ. Safe. 2024, 285, 117075. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Ijaz, S.; Shi, Y.; Khan, Y.A.; Khodaverdian, M.; Javaid, U. Robust adaptive control law design for enhanced stability of agriculture UAV used for pesticide spraying. Aerosp. Sci. Technol. 2024, 155, 109676. [Google Scholar] [CrossRef]
- Jiang, J.; Ji, H.; Zhou, G.; Pan, R.; Zhao, L.; Duan, Z.; Liu, X.; Yin, J.; Duan, Y.; Ma, Y.; et al. Non-destructive monitoring of tea plant growth through UAV spectral imagery and meteorological data using machine learning and parameter optimization algorithms. Comput. Electron. Agric. 2025, 229, 109795. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Zhang, H.; Zhang, B.; Zhang, J.; Hu, X.; Du, X.; Cai, J.; Jia, W.; Wu, C. UAV-Based Multispectral Winter Wheat Growth Monitoring with Adaptive Weight Allocation. Agriculture 2024, 14, 1900. [Google Scholar] [CrossRef]
- Ruwanpathirana, P.P.; Sakai, K.; Jayasinghe, G.Y.; Nakandakari, T.; Yuge, K.; Wijekoon, W.M.C.J.; Priyankara, A.C.P.; Samaraweera, M.D.S.; Madushanka, P.L.A. Evaluation of Sugarcane Crop Growth Monitoring Using Vegetation Indices Derived from RGB-Based UAV Images and Machine Learning Models. Agronomy 2024, 14, 2059. [Google Scholar] [CrossRef]
- Shi, X.; Du, Y.; Liu, X.; Liu, C.; Hou, Q.; Chen, L.; Yong, R.; Ma, J.; Yang, D.; Yuan, H.; et al. Optimizing UAV spray parameters to improve precise control of tobacco pests at different growth stages. Pest Manag. Sci. 2024, 80, 5809–5819. [Google Scholar] [CrossRef]
- Guo, H.; Cheng, Y.; Liu, J.; Wang, Z. Low-cost and precise traditional Chinese medicinal tree pest and disease monitoring using UAV RGB image only. Sci Rep 2024, 14, 25562. [Google Scholar] [CrossRef]
- Joshi, P.; Sandhu, K.S.; Dhillon, G.S.; Chen, J.; Bohara, K. Detection and monitoring wheat diseases using unmanned aerial vehicles (UAVs). Comput. Electron. Agric. 2024, 224, 109158. [Google Scholar] [CrossRef]
- Bozzini, A.; Brugnaro, S.; Morgante, G.; Santoiemma, G.; Deganutti, L.; Finozzi, V.; Battisti, A.; Faccoli, M. Drone-based early detection of bark beetle infested spruce trees differs in endemic and epidemic populations. Front. For. Glob. Change 2024, 7, 1385687. [Google Scholar] [CrossRef]
- Anam, I.; Arafat, N.; Hafiz, M.S.; Jim, J.R.; Kabir, M.M.; Mridha, M.F. A systematic review of UAV and AI integration for targeted disease detection, weed management, and pest control in precision agriculture. Smart Agric. Technol. 2024, 9, 100647. [Google Scholar] [CrossRef]
- Wang, L.; Zhuang, X.; Zhang, W.; Cheng, J.; Zhang, T. Coverage Path Planning for UAVs: An Energy-Efficient Method in Convex and Non-Convex Mixed Regions. Drones 2024, 8, 776. [Google Scholar] [CrossRef]
- Huang, J.; Luo, Y.; Quan, Q.; Wang, B.; Xue, X.; Zhang, Y. An autonomous task assignment and decision-making method for coverage path planning of multiple pesticide spraying UAVs. Comput. Electron. Agric. 2023, 212, 108128. [Google Scholar] [CrossRef]
- Nanavati, R.V.; Meng, Y.; Coombes, M.; Liu, C. Generalized data-driven optimal path planning framework for uniform coverage missions using crop spraying UAVs. Precis. Agric. 2023, 24, 1497–1525. [Google Scholar] [CrossRef]
- Li, J.; Sheng, H.; Zhang, J.; Zhang, H. Coverage Path Planning Method for Agricultural Spraying UAV in Arbitrary Polygon Area. Aerospace 2023, 10, 755. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Ren, J.; Yu, W.; Wang, G.; Ding, P.; Wang, J.; Zhang, X. A Multi-Area Task Path-Planning Algorithm for Agricultural Drones Based on Improved Double Deep Q-Learning Net. Agriculture 2024, 14, 1294. [Google Scholar] [CrossRef]
- Fu, H.; Li, Z.; Zhang, W.; Feng, Y.; Zhu, L.; Fang, X.; Li, J. Research on Path Planning of Agricultural UAV Based on Improved Deep Reinforcement Learning. Agronomy 2024, 14, 2669. [Google Scholar] [CrossRef]
- Arab, D.P.; Spisser, M.; Essert, C. Complete coverage path planning for wheeled agricultural robots. J. Field Robot. 2023, 40, 1460–1503. [Google Scholar] [CrossRef]
- Wang, N.; Yang, X.; Wang, T.; Xiao, J.; Zhang, M.; Wang, H.; Li, H. Collaborative path planning and task allocation for multiple agricultural machines. Comput. Electron. Agric. 2023, 213, 108218. [Google Scholar] [CrossRef]
- Höffmann, M.; Patel, S.; Büskens, C. Optimal Coverage Path Planning for Agricultural Vehicles with Curvature Constraints. Agriculture 2023, 13, 2112. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X.; Wang, L.; Jin, L.; Wang, S. A Path Planning System for Orchard Mower Based on Improved A* Algorithm. Agronomy 2024, 14, 391. [Google Scholar] [CrossRef]
- Tang, C.; Li, W.; Han, T.; Yu, L.; Cui, T. Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning. Biomimetics 2024, 9, 552. [Google Scholar] [CrossRef]
- Warnakulasooriya, K.; Segev, A. Comparative analysis of accuracy and computational complexity across 21 swarm intelligence algorithms. Evol. Intell. 2024, 18, 18. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, Z.; Xiao, J.; Yan, L.; Qu, B.; Wen, P.; Wang, H.; Zhou, Y.; Sun, H. Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment. Aerosp. Sci. Technol. 2022, 121, 107287. [Google Scholar] [CrossRef]
- Jiang, W.; Lyu, Y.; Li, Y.; Guo, Y.; Zhang, W. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aerosp. Sci. Technol. 2022, 121. [Google Scholar] [CrossRef]
- Gupta, H.; Verma, O.P. A novel hybrid Coyote–Particle Swarm Optimization Algorithm for three-dimensional constrained trajectory planning of Unmanned Aerial Vehicle. Appl. Soft. Comput. 2023, 147, 110776. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Wei, G. SaCHBA_PDN: Modified honey badger algorithm with multi-strategy for UAV path planning. Expert Syst. Appl. 2023, 223, 119941. [Google Scholar] [CrossRef]
- Chen, Y.; Pi, D.; Xu, Y. Neighborhood Global Learning based Flower Pollination Algorithm and its Application to Unmanned Aerial Vehicle Path Planning. Expert Syst. Appl. 2020, 170, 114505. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.c.; Hu, X.X.; Qiu, L.; Zang, H.f. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 53. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Yakunin, K.; Aubakirov, M.; Assanov, I.; Kuchin, Y.; Symagulov, A.; Levashenko, V.; Zaitseva, E.; Sokolov, D.; Amirgaliyev, Y. Coverage Path Planning Optimization of Heterogeneous UAVs Group for Precision Agriculture. IEEE Access 2023, 11, 5789–5803. [Google Scholar] [CrossRef]
- Chen, H.; Yang, C.; Heidari, A.A.; Zhao, X. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl. 2020, 154, 113018. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.S.; Li, X.D.; Zhang, M.; Hao, W.K. Harris Hawk Optimization Algorithm Based on Cauchy Distribution Inverse Cumulative Function and Tangent Flight Operator. Appl. Intell. 2022, 52, 1–28. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Li, J.; Xiong, Y.; She, J.; Yu, A. Optimal path planning for unmanned aerial vehicles with multiple round-trip flights in coverage tasks. Robot. Auton. Syst. 2025, 189, 104970. [Google Scholar] [CrossRef]
- Bhuiyan, T.H.; Walker, V.; Roni, M.; Ahmed, I. Aerial drone fleet deployment optimization with endogenous battery replacements for direct delivery of time-sensitive products. Expert Syst. Appl. 2024, 252, 124172. [Google Scholar] [CrossRef]
- Porcelli, L.; Ficco, M.; D’Angelo, G.; Palmieri, F. Context-aware coverage path planning for a swarm of UAVs using mobile ground stations for battery-swapping. Soft Comput. 2025, 29, 1–21. [Google Scholar] [CrossRef]
- Yu, X.; Luo, Y.; Liu, Y. A novel adaptive two-stage approach to dynamic optimal path planning of UAV in 3-D unknown environments. Multimed. Tools Appl. 2022, 82, 18761–18779. [Google Scholar] [CrossRef]
- Seoane, P.; Aldao, E.; López, F.V.; Jorge, H.G. Assessment of LiDAR-Based Sensing Technologies in Bird–Drone Collision Scenarios. Drones 2024, 9, 13. [Google Scholar] [CrossRef]
- Xu, C. UAV patrol path planning based on machine vision and multi-sensor fusion. Open Comput. Sci. 2023, 13, 20220276. [Google Scholar]
- Niu, Y.; Yan, X.; Wang, Y.; Niu, Y. 3D real-time dynamic path planning for UAV based on improved interfered fluid dynamical system and artificial neural network. Adv. Eng. Inform. 2024, 59, 102306. [Google Scholar] [CrossRef]
- Du, P.; Shi, Y.; Cao, H.; Garg, S.; Alrashoud, M.; Shukla, P.K. AI-Enabled Trajectory Optimization of Logistics UAVs With Wind Impacts in Smart Cities. IEEE Trans. Consum. Electron. 2024, 70, 3885–3897. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, H.; Nie, M.; Liu, X. Research on Multi-UAV Cooperative Dynamic Path Planning Algorithm Based on Conflict Search. Drones 2024, 8, 274. [Google Scholar] [CrossRef]
- Kuyffer, E.D.; Joseph, W.; Martens, L.; Pessemier, T.D. Travel route and formation optimization for flocks of drones in package delivery by using an ACO based V-Shape algorithm. Results Eng. 2024, 24, 103627. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Tian, J. UAV formation path planning for mountainous forest terrain utilizing an artificial rabbit optimizer incorporating reinforcement learning and thermal conduction search strategies. Adv. Eng. Inform. 2024, 62, 102947. [Google Scholar] [CrossRef]
- Fang, X.; Xie, L.; Li, X. Distributed localization in dynamic networks via complex laplacian. Automatica 2023, 151, 2574–2587. [Google Scholar] [CrossRef]
- Fang, X.; Li, X.; Xie, L. 3-D Distributed Localization with Mixed Local Relative Measurements. IEEE Trans. Signal Process. 2020, 68, 5869–5881. [Google Scholar] [CrossRef]
- Fang, X.; Xie, L. Distributed formation maneuver control using complex laplacian. IEEE Trans. Autom. Control 2023, 69, 1850–1857. [Google Scholar] [CrossRef]
- Fang, X.; Xie, L.; Li, X. Integrated relative-measurement-based network localization and formation maneuver control. IEEE Trans. Autom. Control 2023, 69, 1906–1913. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).