Hyperspectral Estimation of Tea Leaf Chlorophyll Content Based on Stacking Models
Abstract
1. Introduction
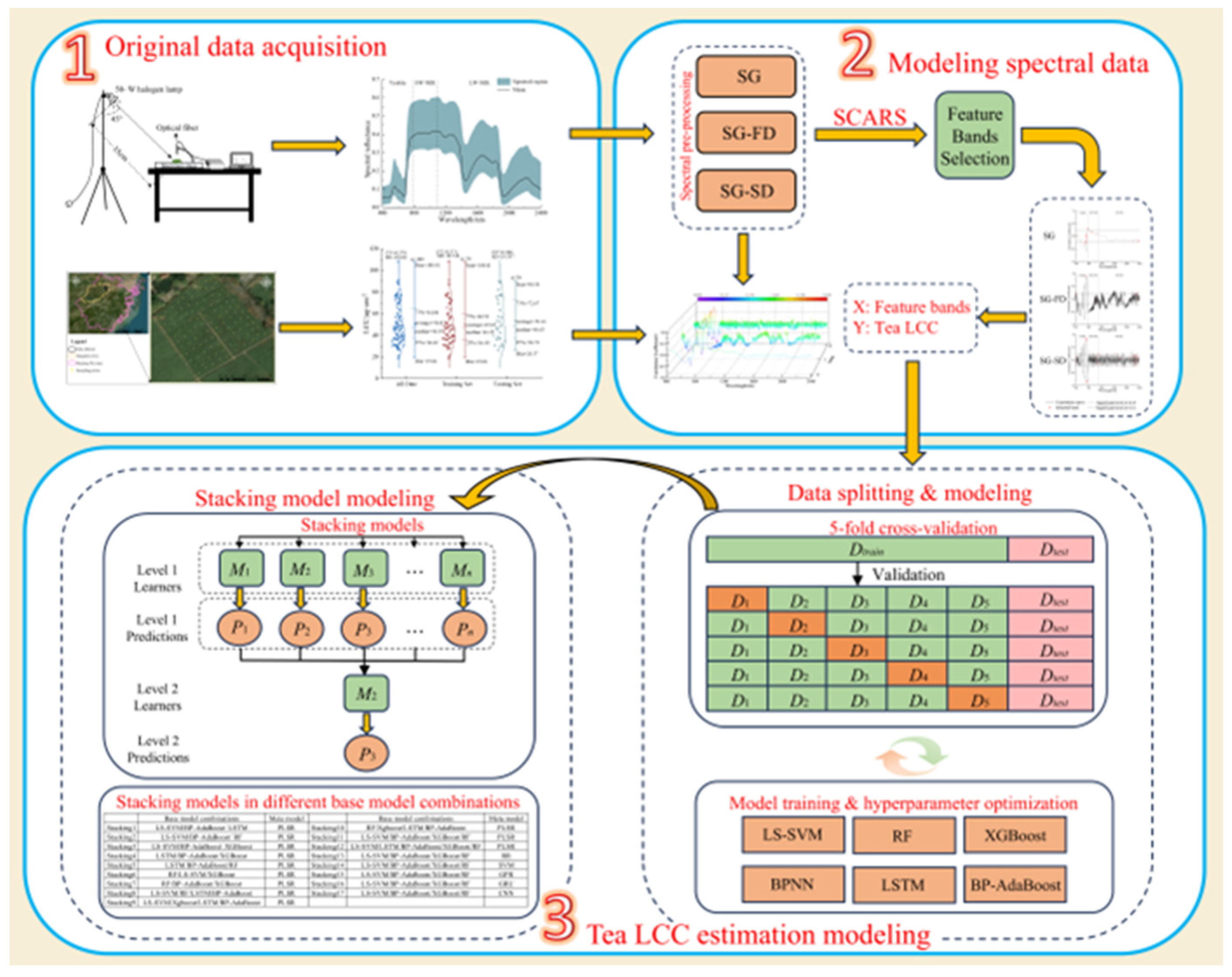
2. Materials and Methods
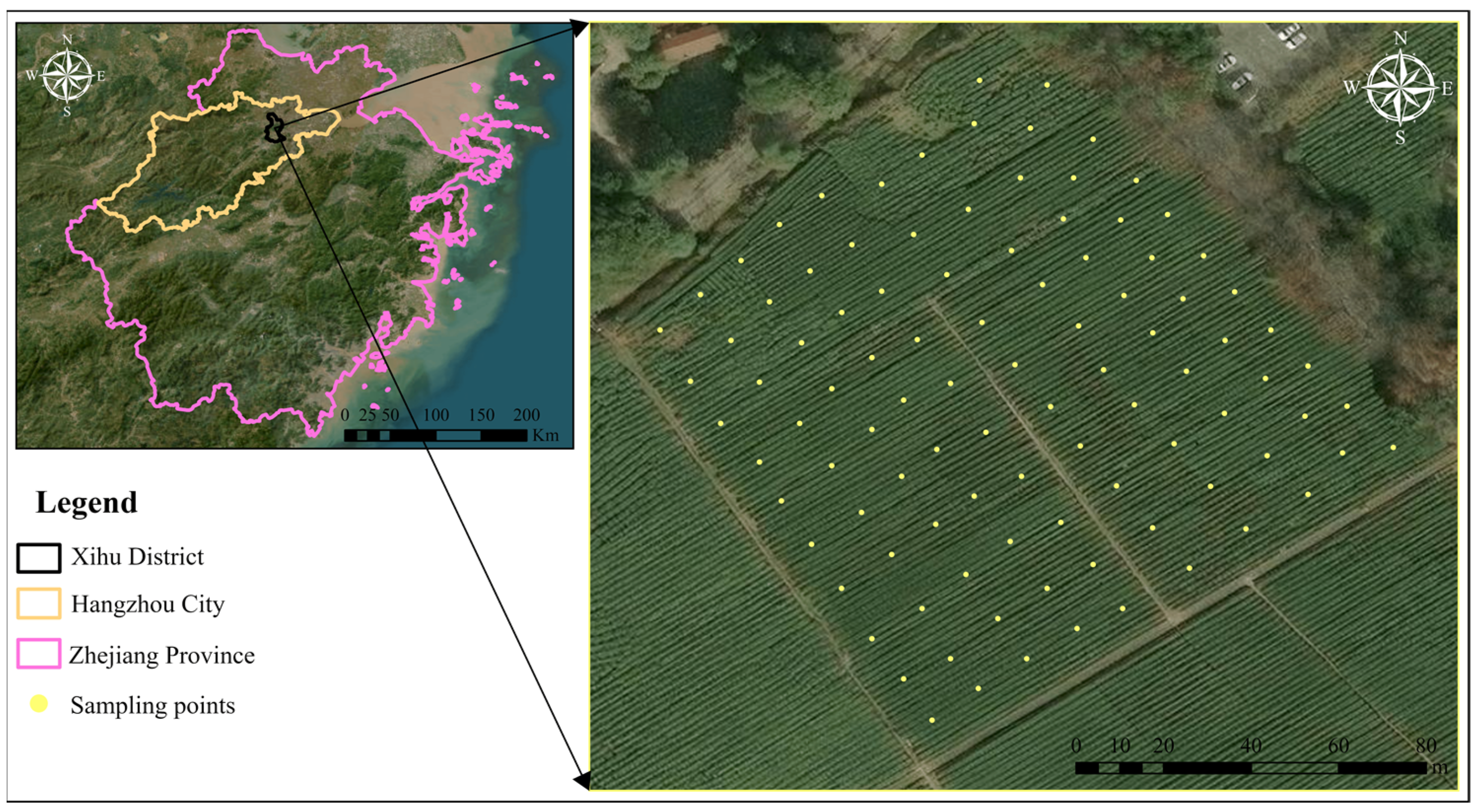
2.1. Experimental Design
2.2. HYPERSPECTRAL Data Measurement and Pre-Processing
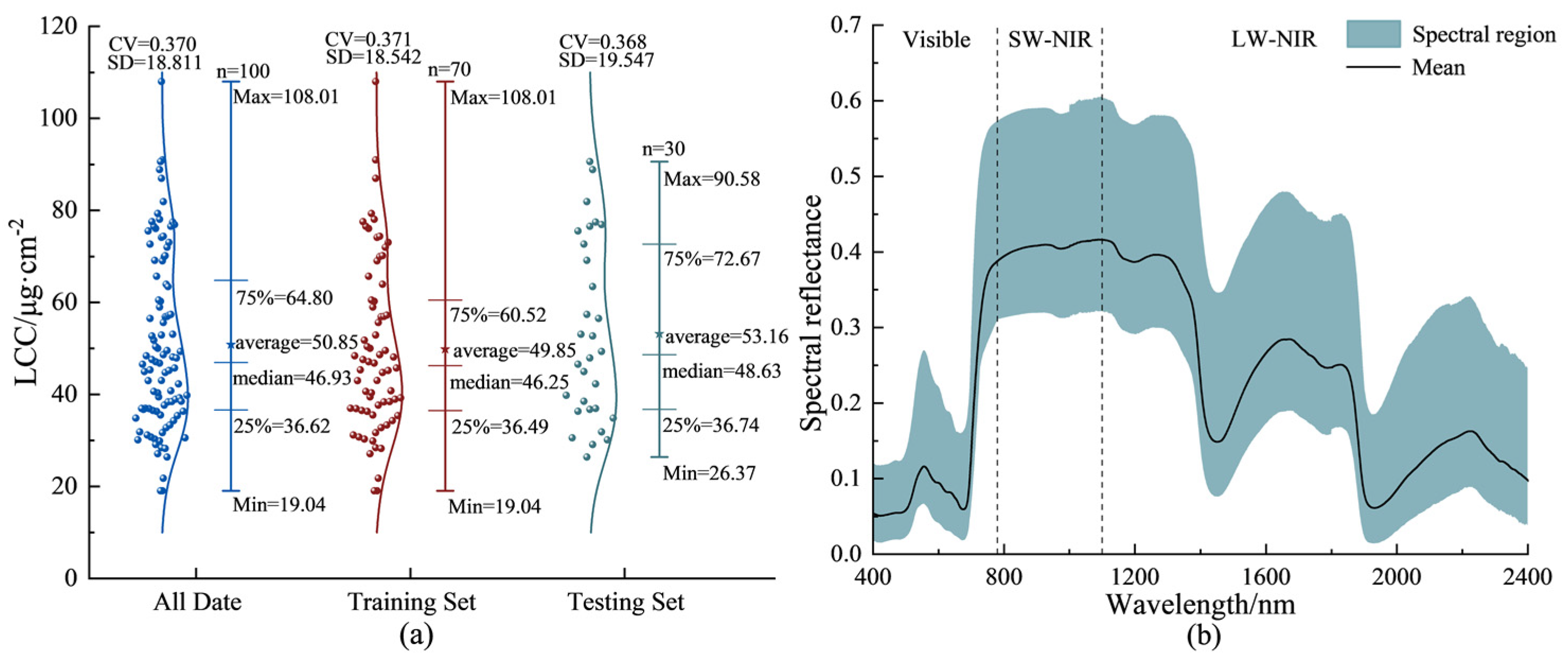
2.3. LCC Measurement
2.4. Variable Selection Algorithm
2.5. Constructing Models
2.5.1. LS-SVM
2.5.2. RF
2.5.3. XGBoost
2.5.4. LSTM
2.5.5. BPNN
2.5.6. BP-AdaBoost
2.5.7. PLSR
2.5.8. RR
2.5.9. SVM
2.5.10. GPR
2.5.11. GRU
2.5.12. CNN
2.5.13. Stacking Model
2.6. Evaluation Indicators
3. Results
3.1. Descriptive Statistics
3.2. Feature Variable Selection
3.3. Tea LCC Estimation Model
3.3.1. Tea LCC Single Model Construction
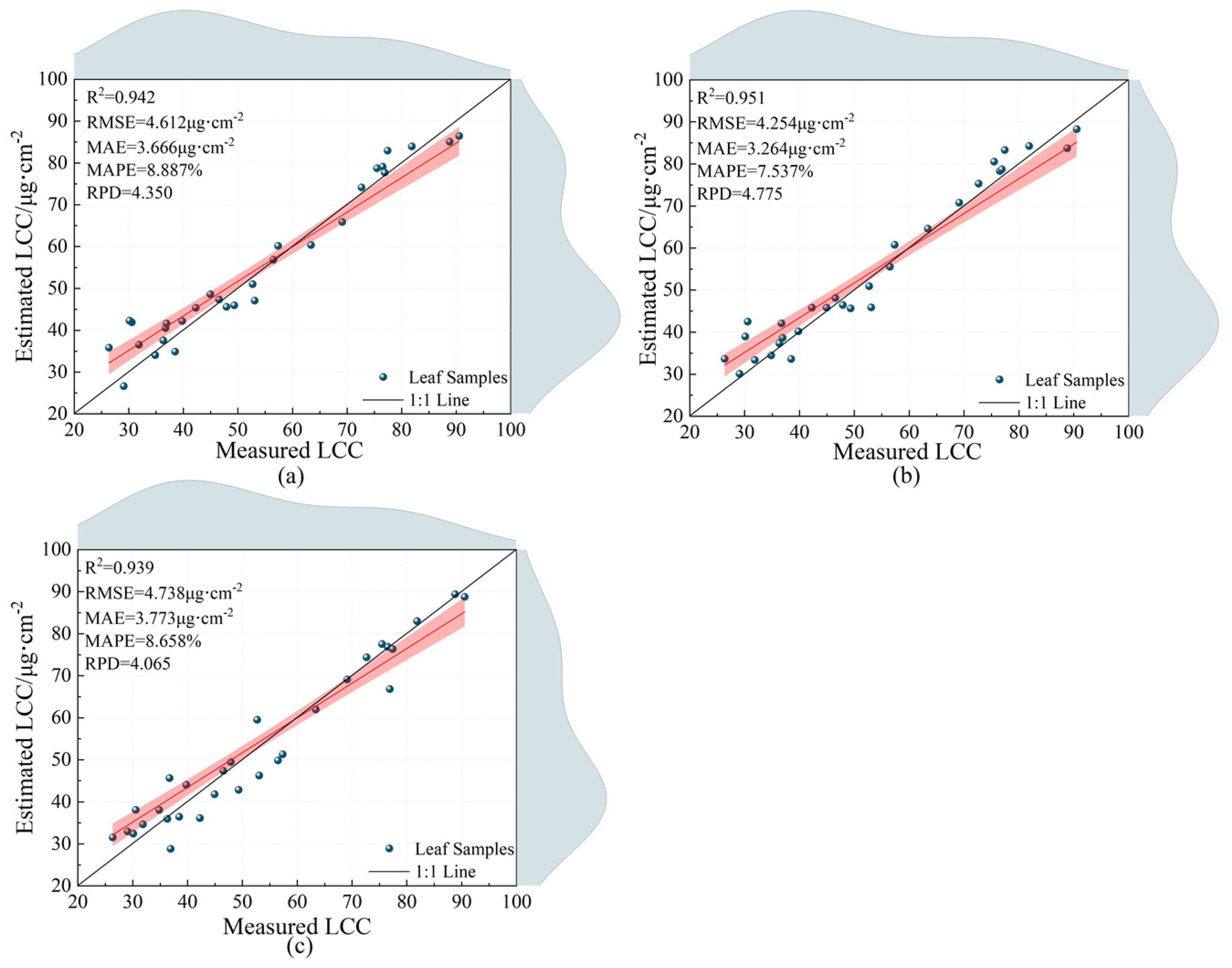
3.3.2. Stacking Integrated Learning Algorithm and Model Estimation Results
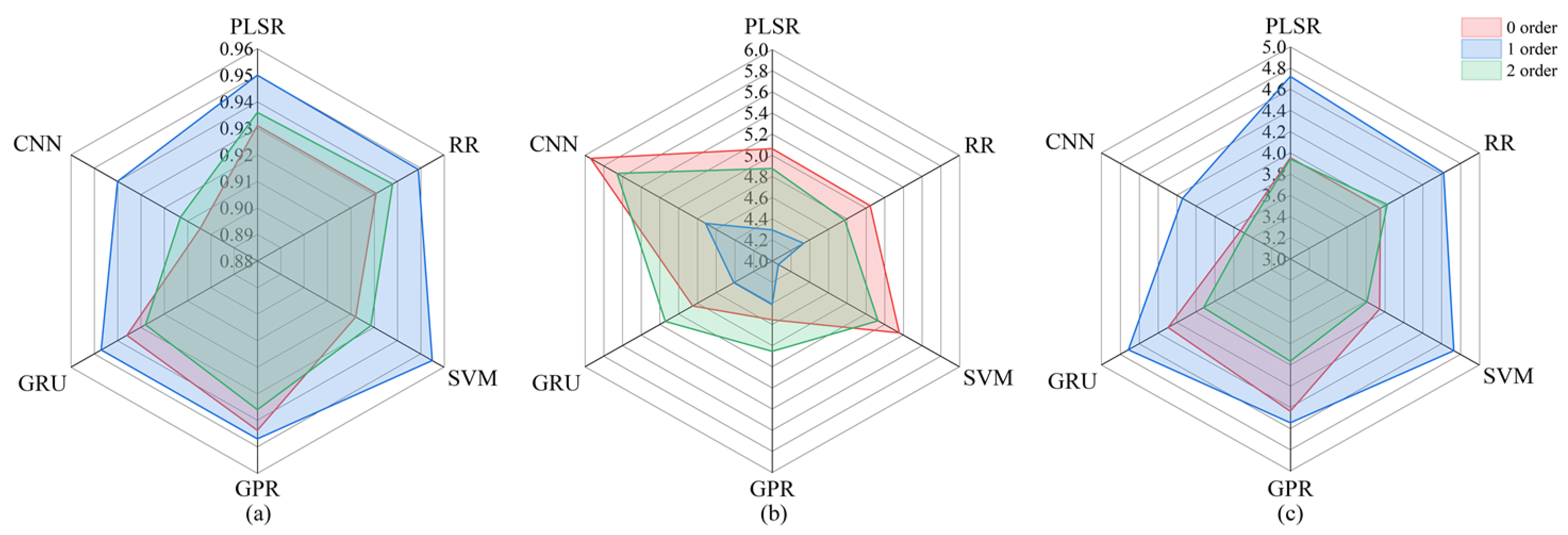
3.4. Analysis of the Impact of Metamodel Selection on Stacking Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nürnberg, D.J.; Morton, J.; Santabarbara, S.; Telfer, A.; Joliot, P.; Antonaru, L.A.; Ruban, A.V.; Cardona, T.; Krausz, E.; Boussac, A.; et al. Photochemistry beyond the Red Limit in Chlorophyll f–Containing Photosystems. Science 2018, 360, 1210–1213. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Wang, L.; Zhou, J.; He, W.; Zeng, J.; Jiang, Y.; Cheng, H. Catechin Contents in Tea (Camellia sinensis) as Affected by Cultivar and Environment and Their Relation to Chlorophyll Contents. Food Chem. 2011, 125, 44–48. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Wang, R.; Mo, G.; Luo, S.; Luo, X.; He, L.; Gonsamo, A.; Arabian, J.; Zhang, Y.; et al. The Global Distribution of Leaf Chlorophyll Content. Remote Sens. Environ. 2020, 236, 111479. [Google Scholar] [CrossRef]
- Sun, Q.; Jiao, Q.; Qian, X.; Liu, L.; Liu, X.; Dai, H. Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations. Remote Sens. 2021, 13, 470. [Google Scholar] [CrossRef]
- Elango, T.; Jeyaraj, A.; Dayalan, H.; Arul, S.; Govindasamy, R.; Prathap, K.; Li, X. Influence of Shading Intensity on Chlorophyll, Carotenoid and Metabolites Biosynthesis to Improve the Quality of Green Tea: A Review. Energy Nexus 2023, 12, 100241. [Google Scholar] [CrossRef]
- Sun, Z.; Bu, Z.; Lu, S.; Omasa, K. A General Algorithm of Leaf Chlorophyll Content Estimation for a Wide Range of Plant Species. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Zhang, Y.-H.; Han, Z.-M.; Liu, X.-Y.; Jian, Y.-F.; Hu, C.-G.; Dian, Y.-Y. Evaluating the Performance of Hyperspectral Leaf Reflectance to Detect Water Stress and Estimation of Photosynthetic Capacities. Remote Sens. 2021, 13, 2160. [Google Scholar] [CrossRef]
- Hasan, U.; Jia, K.; Wang, L.; Wang, C.; Shen, Z.; Yu, W.; Sun, Y.; Jiang, H.; Zhang, Z.; Guo, J.; et al. Retrieval of Leaf Chlorophyll Contents (LCCs) in Litchi Based on Fractional Order Derivatives and VCPA-GA-ML Algorithms. Plants 2023, 12, 501. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Liu, L.; Xie, Y.; Zhu, B.; Song, K. Rice Leaf Chlorophyll Content Estimation with Different Crop Coverages Based on Sentinel-2. Ecol. Inform. 2024, 81, 102622. [Google Scholar] [CrossRef]
- Xiao, B.; Li, S.; Dou, S.; He, H.; Fu, B.; Zhang, T.; Sun, W.; Yang, Y.; Xiong, Y.; Shi, J.; et al. Comparison of Leaf Chlorophyll Content Retrieval Performance of Citrus Using FOD and CWT Methods with Field-Based Full-Spectrum Hyperspectral Reflectance Data. Comput. Electron. Agric. 2024, 217, 108559. [Google Scholar] [CrossRef]
- Ravikanth, L.; Jayas, D.S.; White, N.D.G.; Fields, P.G.; Sun, D.-W. Extraction of Spectral Information from Hyperspectral Data and Application of Hyperspectral Imaging for Food and Agricultural Products. Food Bioprocess Technol. 2017, 10, 1–33. [Google Scholar] [CrossRef]
- He, J.; He, J.; Liu, G.; Li, W.; Li, C.; Li, Z. Inversion Analysis of Soil Nitrogen Content Using Hyperspectral Images with Different Preprocessing Methods. Ecol. Inform. 2023, 78, 102381. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Hyperspectral Indices Based on First Derivative Spectra Closely Trace Canopy Transpiration in a Desert Plant. Ecol. Inform. 2016, 35, 1–8. [Google Scholar] [CrossRef]
- Geng, J.; Lv, J.; Pei, J.; Liao, C.; Tan, Q.; Wang, T.; Fang, H.; Wang, L. Prediction of Soil Organic Carbon in Black Soil Based on a Synergistic Scheme from Hyperspectral Data: Combining Fractional-Order Derivatives and Three-Dimensional Spectral Indices. Comput. Electron. Agric. 2024, 220, 108905. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, Q.; Chen, Y.; Liu, Y.; Jiang, D.; Zhang, Z. Hyperspectral Estimation of Chlorophyll Content in Apple Tree Leaf Based on Feature Band Selection and the CatBoost Model. Agronomy 2023, 13, 2075. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, C.; Sun, J.; Yao, K.; Xu, M.; Cheng, J. Nondestructive Testing and Visualization of Compound Heavy Metals in Lettuce Leaves Using Fluorescence Hyperspectral Imaging. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 291, 122337. [Google Scholar] [CrossRef]
- Balabin, R.M.; Smirnov, S.V. Variable Selection in Near-Infrared Spectroscopy: Benchmarking of Feature Selection Methods on Biodiesel Data. Anal. Chim. Acta 2011, 692, 63–72. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef][Green Version]
- Yun, Y.-H.; Liang, Y.-Z.; Xie, G.-X.; Li, H.-D.; Cao, D.-S.; Xu, Q.-S. A Perspective Demonstration on the Importance of Variable Selection in Inverse Calibration for Complex Analytical Systems. Analyst 2013, 138, 6412–6421. [Google Scholar] [CrossRef]
- Duan, H.; Zhu, R.; Xu, W.; Qiu, Y.; Yao, X.; Xu, C. Hyperspectral Imaging Detection of Total Viable Count from Vacuum Packing Cooling Mutton Based on GA and CARS Algorithms. Spectrosc. Spectr. Anal. 2017, 37, 847–852. [Google Scholar]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key Wavelengths Screening Using Competitive Adaptive Reweighted Sampling Method for Multivariate Calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Determination of Soil Properties with Visible to Near- and Mid-Infrared Spectroscopy: Effects of Spectral Variable Selection. Geoderma 2014, 223, 88–96. [Google Scholar] [CrossRef]
- Tan, K.; Wang, H.; Zhang, Q.; Jia, X. An Improved Estimation Model for Soil Heavy Metal(Loid) Concentration Retrieval in Mining Areas Using Reflectance Spectroscopy. J. Soils Sediments 2018, 18, 2008–2022. [Google Scholar] [CrossRef]
- Chen, Y.; Li, S.; Zhang, X.; Gao, X.; Jiang, Y.; Wang, J.; Jia, X.; Ban, Z. Prediction of Apple Moisture Content Based on Hyperspectral Imaging Combined with Neural Network Modeling. Sci. Hortic. 2024, 338, 113739. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Estimating the Distribution of Chlorophyll Content in CYVCV Infected Lemon Leaf Using Hyperspectral Imaging. Comput. Electron. Agric. 2022, 198, 107036. [Google Scholar] [CrossRef]
- Tan, K.; Ma, W.; Chen, L.; Wang, H.; Du, Q.; Du, P.; Yan, B.; Liu, R.; Li, H. Estimating the Distribution Trend of Soil Heavy Metals in Mining Area from HyMap Airborne Hyperspectral Imagery Based on Ensemble Learning. J. Hazard. Mater. 2021, 401, 123288. [Google Scholar] [CrossRef]
- Zheng, K.; Li, Q.; Wang, J.; Geng, J.; Cao, P.; Sui, T.; Wang, X.; Du, Y. Stability Competitive Adaptive Reweighted Sampling (SCARS) and Its Applications to Multivariate Calibration of NIR Spectra. Chemom. Intell. Lab. Syst. 2012, 112, 48–54. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, H.; Chen, Q.; Mei, C.; Liu, G. Identification of Solid State Fermentation Degree with FT-NIR Spectroscopy: Comparison of Wavelength Variable Selection Methods of CARS and SCARS. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 149, 1–7. [Google Scholar] [CrossRef]
- Mao, B.; Cheng, Q.; Chen, L.; Duan, F.; Sun, X.; Li, Y.; Li, Z.; Zhai, W.; Ding, F.; Li, H.; et al. Multi-Random Ensemble on Partial Least Squares Regression to Predict Wheat Yield and Its Losses across Water and Nitrogen Stress with Hyperspectral Remote Sensing. Comput. Electron. Agric. 2024, 222, 109046. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, J.; Li, P.; Zeng, F.; Wang, H. Hyperspectral Detection of Salted Sea Cucumber Adulteration Using Different Spectral Preprocessing Techniques and SVM Method. LWT 2021, 152, 112295. [Google Scholar] [CrossRef]
- Subi, X.; Eziz, M.; Zhong, Q.; Li, X. Estimating the Chromium Concentration of Farmland Soils in an Arid Zone from Hyperspectral Reflectance by Using Partial Least Squares Regression Methods. Ecol. Indic. 2024, 161, 111987. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Z.; Fu, Y.; Rao, F. Time Series Prediction of COVID-19 Transmission in America Using LSTM and XGBoost Algorithms. Results Phys. 2021, 27, 104462. [Google Scholar] [CrossRef]
- Yue, J.; Wang, J.; Zhang, Z.; Li, C.; Yang, H.; Feng, H.; Guo, W. Estimating Crop Leaf Area Index and Chlorophyll Content Using a Deep Learning—Based Hyperspectral Analysis Method. Computers and Electronics in Agriculture 2024, 227, 109653. [Google Scholar] [CrossRef]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD Values of Summer Maize Using UAV Hyperspectral Data Based on Multiple Machine Learning Algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Chang, R.; Chen, Z.; Wang, D.; Guo, K. Hyperspectral Remote Sensing Inversion and Monitoring of Organic Matter in Black Soil Based on Dynamic Fitness Inertia Weight Particle Swarm Optimization Neural Network. Remote Sens. 2022, 14, 4316. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Sun, W.; Wang, J.; Ding, S.; Liu, S. Effects of Hyperspectral Data with Different Spectral Resolutions on the Estimation of Soil Heavy Metal Content: From Ground-Based and Airborne Data to Satellite-Simulated Data. Sci. Total Environ. 2022, 838, 156129. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Qu, Y.; Gao, L.; Sun, X.; Qi, H.; Zhang, B.; Shen, T. Ensemble-Based Information Retrieval With Mass Estimation for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5508123. [Google Scholar] [CrossRef]
- Vicente, L.E.; de Souza Filho, C.R. Identification of Mineral Components in Tropical Soils Using Reflectance Spectroscopy and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Data. Remote Sens. Environ. 2011, 115, 1824–1836. [Google Scholar] [CrossRef]
- Saha, A.; Pal, S.C. Application of Machine Learning and Emerging Remote Sensing Techniques in Hydrology: A State-of-the-Art Review and Current Research Trends. J. Hydrol. 2024, 632, 130907. [Google Scholar] [CrossRef]
- Huang, X.; Guan, H.; Bo, L.; Xu, Z.; Mao, X. Hyperspectral Proximal Sensing of Leaf Chlorophyll Content of Spring Maize Based on a Hybrid of Physically Based Modelling and Ensemble Stacking. Comput. Electron. Agric. 2023, 208, 107745. [Google Scholar] [CrossRef]
- Lin, N.; Jiang, R.; Li, G.; Yang, Q.; Li, D.; Yang, X. Estimating the Heavy Metal Contents in Farmland Soil from Hyperspectral Images Based on Stacked AdaBoost Ensemble Learning. Ecol. Indic. 2022, 143, 109330. [Google Scholar] [CrossRef]
- Cui, B.; Dong, W.; Yin, B.; Li, X.; Cui, J. Hyperspectral Image Classification Method Based on Semantic Filtering and Ensemble Learning. Infrared Phys. Technol. 2023, 135, 104949. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Z.; Fu, Y.; Zhao, L.; Ren, Y.; Nan, T.; Guo, H. Prediction of Arsenic and Fluoride in Groundwater of the North China Plain Using Enhanced Stacking Ensemble Learning. Water Res. 2024, 259, 121848. [Google Scholar] [CrossRef]
- Phong, T.N.; Duong, H.H.; Huu, D.N.; Tran, V.P.; Phan, T.T.; Al-Ansari, N.; Hiep, V.L.; Binh, T.P.; Lanh, S.H.; Prakash, I. Improvement of Credal Decision Trees Using Ensemble Frameworks for Groundwater Potential Modeling. Sustainability 2020, 12, 2622. [Google Scholar] [CrossRef]
- Osman, A.I.A.; Ahmed, A.N.; Huang, Y.F.; Kumar, P.; Birima, A.H.; Sherif, M.; Sefelnasr, A.; Ebraheemand, A.A.; El-Shafie, A. Past, Present and Perspective Methodology for Groundwater Modeling-Based Machine Learning Approaches. Arch. Comput. Method Eng. 2022, 29, 3843–3859. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Xiang, Y.; Geng, H.; Yang, X.; Yang, N.; Du, R.; Wang, Y.; Zhang, Z.; Shi, L.; et al. Improving UAV Hyperspectral Monitoring Accuracy of Summer Maize Soil Moisture Content with an Ensemble Learning Model Fusing Crop Physiological Spectral Responses. Eur. J. Agron. 2024, 160, 127299. [Google Scholar] [CrossRef]
- Yao, L.; Xu, M.; Liu, Y.; Niu, R.; Wu, X.; Song, Y. Estimating of Heavy Metal Concentration in Agricultural Soils from Hyperspectral Satellite Sensor Imagery: Considering the Sources and Migration Pathways of Pollutants. Ecol. Indic. 2024, 158, 111416. [Google Scholar] [CrossRef]
- Wu, M.; Dou, S.; Lin, N.; Jiang, R.; Zhu, B. Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images. Remote Sens. 2023, 15, 4713. [Google Scholar] [CrossRef]
- Zou, Z.; Zhen, J.; Wang, Q.; Wu, Q.; Li, M.; Yuan, D.; Cui, Q.; Zhou, M.; Xu, L. Research on Nondestructive Detection of Sweet-Waxy Corn Seed Varieties and Mildew Based on Stacked Ensemble Learning and Hyperspectral Feature Fusion Technology. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2024, 322, 124816. [Google Scholar] [CrossRef]
- Satish, N.; Anmala, J.; Varma, M.R.R.; Rajitha, K. Performance of Machine Learning, Artificial Neural Network (ANN), and Stacked Ensemble Models in Predicting Water Quality Index (WQI) from Surface Water Quality Parameters, Climatic and Land Use Data. Process Saf. Environ. Prot. 2024, 192, 177–195. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L. Chlorophyll Fluorescence Effects on Vegetation Apparent Reflectance: I. Leaf-Level Measurements and Model Simulation. Remote Sens. Environ. 2000, 74, 582–595. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. [34] Chlorophylls and Carotenoids: Pigments of Photosynthetic Biomembranes. In Methods in Enzymology; Plant Cell Membranes; Academic Press: Cambridge, MA, USA, 1987; Volume 148, pp. 350–382. [Google Scholar]
- Tang, H.-S.; Xue, S.-T.; Chen, R.; Sato, T. Online Weighted LS-SVM for Hysteretic Structural System Identification. Eng. Struct. 2006, 28, 1728–1735. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA; pp. 785–794. [Google Scholar]
- Dong, F.; Bi, Y.; Hao, J.; Liu, S.; Yi, W.; Yu, W.; Lv, Y.; Cui, J.; Li, H.; Xian, J.; et al. A New Comprehensive Quantitative Index for the Assessment of Essential Amino Acid Quality in Beef Using Vis-NIR Hyperspectral Imaging Combined with LSTM. Food Chem. 2024, 440, 138040. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, F.; Kung, H.; Shi, P.; Yushanjiang, A.; Zhu, S. Estimation of the Fe and Cu Contents of the Surface Water in the Ebinur Lake Basin Based on LIBS and a Machine Learning Algorithm. Int. J. Environ. Res. Public Health 2018, 15, 2390. [Google Scholar] [CrossRef]
- Lin, Q.; Yang, S.; Yang, R.; Wu, H. Transistor Modeling Based on LM-BPNN and CG-BPNN for the GaAs pHEMT. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3268. [Google Scholar] [CrossRef]
- Jiang, X.; Bu, Y.; Han, L.; Tian, J.; Hu, X.; Zhang, X.; Huang, D.; Luo, H. Rapid Nondestructive Detecting of Wheat Varieties and Mixing Ratio by Combining Hyperspectral Imaging and Ensemble Learning. Food Control 2023, 150, 109740. [Google Scholar] [CrossRef]
- Rumere, F.A.O.; Soemartojo, S.M.; Widyaningsih, Y. Restricted Ridge Regression Estimator as a Parameter Estimation in Multiple Linear Regression Model for Multicollinearity Case. J. Phys. Conf. Ser. 2021, 1725, 012021. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using Data Mining to Model and Interpret Soil Diffuse Reflectance Spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Arefi, A.; Sturm, B.; von Gersdorff, G.; Nasirahmadi, A.; Hensel, O. Vis-NIR Hyperspectral Imaging along with Gaussian Process Regression to Monitor Quality Attributes of Apple Slices during Drying. LWT 2021, 152, 112297. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Sun, M.; Liu, X.; Cao, L. A Study on Hyperspectral Soil Moisture Content Prediction by Incorporating a Hybrid Neural Network into Stacking Ensemble Learning. Agronomy 2024, 14, 2054. [Google Scholar] [CrossRef]
- Yu, S.; Fan, J.; Lu, X.; Wen, W.; Shao, S.; Liang, D.; Yang, X.; Guo, X.; Zhao, C. Deep Learning Models Based on Hyperspectral Data and Time-Series Phenotypes for Predicting Quality Attributes in Lettuces under Water Stress. Comput. Electron. Agric. 2023, 211, 108034. [Google Scholar] [CrossRef]
- Chatzimparmpas, A.; Martins, R.M.; Kucher, K.; Kerren, A. StackGenVis: Alignment of Data, Algorithms, and Models for Stacking Ensemble Learning Using Performance Metrics. IEEE Trans. Vis. Comput. Graph. 2021, 27, 1547–1557. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between Gross Primary Production, Green LAI, and Canopy Chlorophyll Content in Maize: Implications for Remote Sensing of Primary Production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, Y.; Geng, J.; Huang, Z. Pixel-Level Assessment Model of Contamination Conditions of Composite Insulators Based on Hyperspectral Imaging Technology and a Semi-Supervised Ladder Network. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 326–335. [Google Scholar] [CrossRef]
- Kusumo, B.H.; Hedley, M.J.; Hedley, C.B.; Hueni, A.; Arnold, G.C.; Tuohy, M.P. The Use of Vis-NIR Spectral Reflectance for Determining Root Density: Evaluation of Ryegrass Roots in a Glasshouse Trial. Eur. J. Soil Sci. 2009, 60, 22–32. [Google Scholar] [CrossRef]
- Leyden, K.; Goodwine, B. Fractional-Order System Identification for Health Monitoring. Nonlinear Dyn. 2018, 92, 1317–1334. [Google Scholar] [CrossRef]
- Huang, B.; Li, S.; Long, T.; Bai, S.; Zhao, J.; Xu, H.; Lan, Y.; Liu, H.; Long, Y. Research on Predicting Photosynthetic Pigments in Tomato Seedling Leaves Based on Near-Infrared Hyperspectral Imaging and Machine Learning. Microchem. J. 2024, 204, 111076. [Google Scholar] [CrossRef]
- Shi, T.; Cui, L.; Wang, J.; Fei, T.; Chen, Y.; Wu, G. Comparison of Multivariate Methods for Estimating Soil Total Nitrogen with Visible/near-Infrared Spectroscopy. Plant Soil 2013, 366, 363–375. [Google Scholar] [CrossRef]
- Kemper, T.; Sommer, S. Estimate of Heavy Metal Contamination in Soils after a Mining Accident Using Reflectance Spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Dong, Z.; Liu, J.; Wang, H.; Zhang, Y.; Chen, T.; Du, Y.; Shao, L.; Xie, J. Hyperspectral Characteristics and Quantitative Analysis of Leaf Chlorophyll by Reflectance Spectroscopy Based on a Genetic Algorithm in Combination with Partial Least Squares Regression. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 243, 118786. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.-M.; Ma, J.-H.; Zhao, Z.-M.; Yang, H.-Z.-Y.; Xuan, Y.-M.; Ouyang, J.-X.; Fan, D.-M.; Yu, J.-F.; Wang, X.-C. Pixel-Class Prediction for Nitrogen Content of Tea Plants Based on Unmanned Aerial Vehicle Images Using Machine Learning and Deep Learning. Expert Syst. Appl. 2023, 227, 120351. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Efficient RTM-Based Training of Machine Learning Regression Algorithms to Quantify Biophysical & Biochemical Traits of Agricultural Crops. ISPRS J. Photogramm. Remote Sens. 2021, 173, 278–296. [Google Scholar] [CrossRef]
- Du, R.; Lu, J.; Xiang, Y.; Zhang, F.; Chen, J.; Tang, Z.; Shi, H.; Wang, X.; Li, W. Estimation of Winter Canola Growth Parameter from UAV Multi-Angular Spectral-Texture Information Using Stacking-Based Ensemble Learning Model. Comput. Electron. Agric. 2024, 222, 109074. [Google Scholar] [CrossRef]
- Ji, Y.; Liu, R.; Xiao, Y.; Cui, Y.; Chen, Z.; Zong, X.; Yang, T. Faba Bean Above-Ground Biomass and Bean Yield Estimation Based on Consumer-Grade Unmanned Aerial Vehicle RGB Images and Ensemble Learning. Precis. Agric 2023, 24, 1439–1460. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1857, pp. 1–15. ISBN 978-3-540-67704-8. [Google Scholar]
- Wang, J.; Zhao, W.; Wang, G.; Pereira, P. Afforestation Changes the Trade-off between Soil Moisture and Plant Species Diversity in Different Vegetation Zones on the Loess Plateau. CATENA 2022, 219, 106583. [Google Scholar] [CrossRef]
- Wang, S.; Wu, Y.; Li, R.; Wang, X. Remote Sensing-Based Retrieval of Soil Moisture Content Using Stacking Ensemble Learning Models. Land Degrad. Dev. 2023, 34, 911–925. [Google Scholar] [CrossRef]
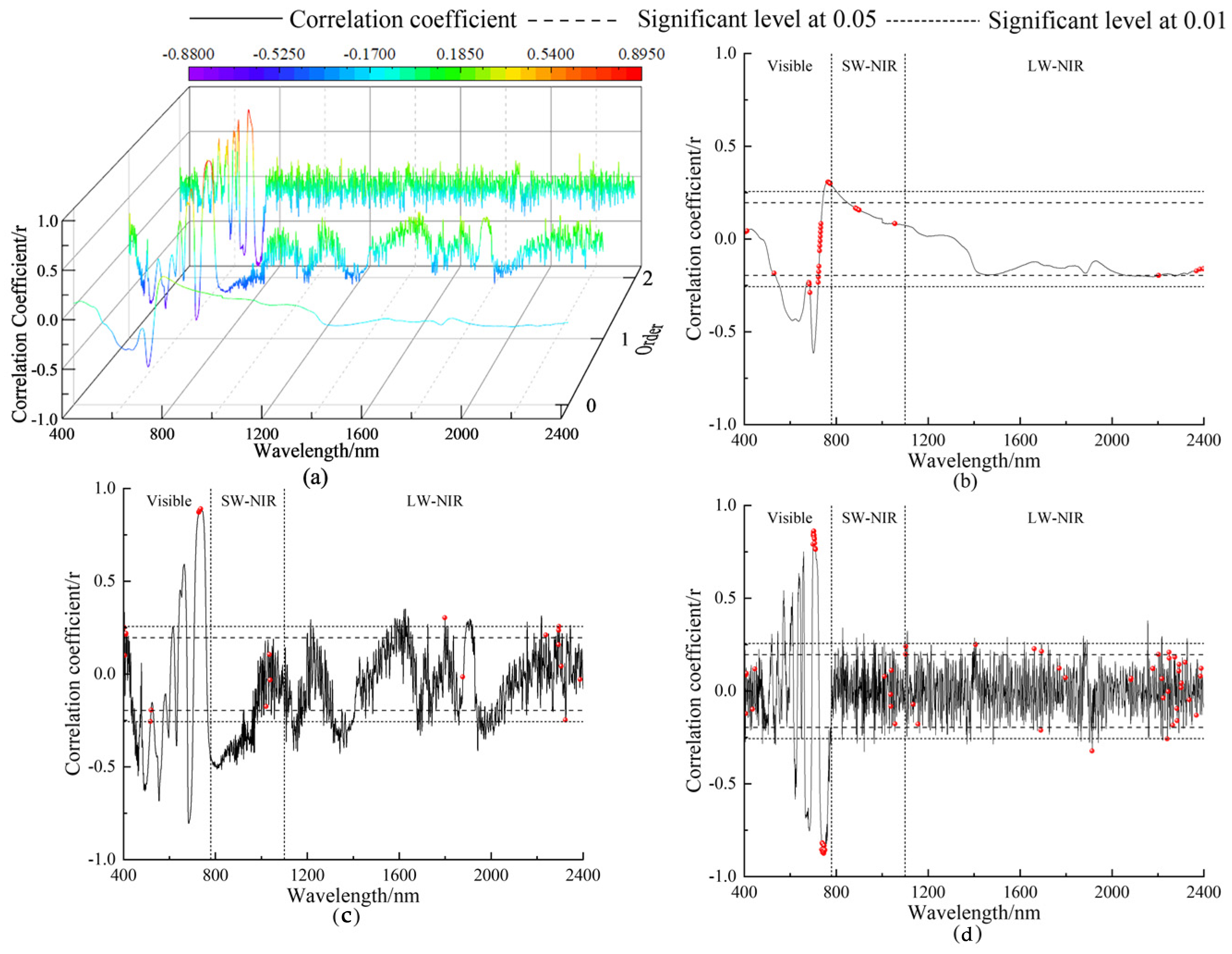
| Order | Pearson Correlation Analysis | ||||
|---|---|---|---|---|---|
| Pb | Nb | Tb | R_max | Corresponding Bands/nm | |
| 0 | 55 | 150 | 205 | 0.615 | 701 |
| 1 | 144 | 526 | 670 | 0.891 | 736 |
| 2 | 109 | 95 | 204 | 0.877 | 746 |
| Model | Order | Training Set | Testing Set | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | MAPE | R2 | RMSE | MAE | MAPE | RPD | ||
| LS-SVM | 0 | 0.984 | 2.348 | 1.641 | 3.880 | 0.654 | 11.309 | 6.525 | 15.798 | 1.759 |
| 1 | 1.000 | 0.014 | 0.010 | 0.024 | 0.801 | 8.582 | 6.453 | 16.152 | 2.356 | |
| 2 | 1.000 | 0.001 | 0.001 | 0.002 | 0.775 | 9.125 | 6.962 | 15.348 | 2.119 | |
| RF | 0 | 0.773 | 8.766 | 6.228 | 14.098 | 0.564 | 12.694 | 10.184 | 20.853 | 1.526 |
| 1 | 0.913 | 5.414 | 3.739 | 8.496 | 0.906 | 5.896 | 4.834 | 10.786 | 3.269 | |
| 2 | 0.927 | 4.966 | 3.424 | 8.152 | 0.887 | 6.457 | 5.442 | 11.593 | 2.981 | |
| XGBoost | 0 | 0.987 | 2.107 | 1.345 | 3.116 | 0.724 | 10.089 | 7.404 | 15.552 | 1.916 |
| 1 | 0.994 | 1.395 | 0.662 | 1.760 | 0.891 | 6.351 | 4.992 | 11.966 | 3.027 | |
| 2 | 0.994 | 1.378 | 0.469 | 1.251 | 0.867 | 6.999 | 5.280 | 12.299 | 2.746 | |
| LSTM | 0 | 0.859 | 6.920 | 5.017 | 11.824 | 0.903 | 5.971 | 4.670 | 10.659 | 3.224 |
| 1 | 0.955 | 3.918 | 3.095 | 7.461 | 0.926 | 5.235 | 4.370 | 9.749 | 4.535 | |
| 2 | 0.993 | 1.500 | 1.132 | 2.885 | 0.909 | 5.782 | 4.720 | 9.623 | 3.332 | |
| BPNN | 0 | 0.856 | 6.993 | 4.910 | 10.212 | 0.861 | 7.178 | 5.461 | 11.565 | 2.987 |
| 1 | 0.924 | 5.079 | 2.867 | 6.003 | 0.908 | 5.840 | 4.823 | 11.330 | 3.327 | |
| 2 | 0.866 | 6.738 | 2.960 | 6.693 | 0.815 | 8.260 | 6.750 | 15.029 | 2.404 | |
| BP-AdaBoost | 0 | 0.939 | 4.537 | 3.217 | 7.354 | 0.881 | 6.623 | 4.373 | 10.899 | 2.940 |
| 1 | 0.961 | 3.639 | 2.383 | 5.668 | 0.918 | 5.503 | 4.315 | 10.478 | 3.817 | |
| 2 | 0.958 | 3.755 | 2.937 | 6.460 | 0.832 | 7.884 | 6.401 | 14.131 | 2.475 | |
| Base Model Assembly | Base Model Assembly | ||
|---|---|---|---|
| Stacking1 | LS-SVM/BP-AdaBoost/LSTM | Stacking7 | RF/BP-AdaBoost/XGBoost |
| Stacking2 | LS-SVM/BP-AdaBoost/RF | Stacking8 | LS-SVM/RF/LSTM/BP-AdaBoost |
| Stacking3 | LS-SVM/BP-AdaBoost/XGBoost | Stacking9 | LS-SVM/XGBoost/LSTM/BP-AdaBoost |
| Stacking4 | LSTM/BP-AdaBoost/XGBoost | Stacking10 | RF/XGBoost/LSTM/BP-AdaBoost |
| Stacking5 | LSTM/BP-AdaBoost/RF | Stacking11 | LS-SVM/RF/XGBoost/BP-AdaBoost |
| Stacking6 | LS-SVM/RF/XGBoost | Stacking12 | LS-SVM/RF/XGBoost/LSTM/BP-AdaBoost |
| Model | Order | Training Set | Testing Set | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | MAPE | R2 | RMSE | MAE | MAPE | RPD | ||
| Stacking1 | 0 | 0.863 | 6.806 | 5.268 | 13.136 | 0.921 | 5.418 | 3.805 | 9.702 | 3.811 |
| 1 | 0.866 | 6.735 | 5.380 | 12.803 | 0.942 | 4.611 | 3.705 | 8.640 | 4.961 | |
| 2 | 0.919 | 5.232 | 4.083 | 9.333 | 0.938 | 4.791 | 3.826 | 8.817 | 4.017 | |
| Stacking2 | 0 | 0.863 | 6.803 | 5.214 | 12.930 | 0.932 | 5.017 | 3.819 | 9.738 | 4.102 |
| 1 | 0.853 | 7.070 | 5.611 | 13.461 | 0.951 | 4.254 | 3.264 | 7.537 | 4.775 | |
| 2 | 0.915 | 5.356 | 4.232 | 9.655 | 0.936 | 4.867 | 3.999 | 9.307 | 3.949 | |
| Stacking3 | 0 | 0.869 | 6.669 | 5.199 | 12.811 | 0.933 | 4.959 | 3.882 | 9.671 | 4.065 |
| 1 | 0.854 | 7.038 | 5.660 | 13.703 | 0.948 | 4.363 | 3.284 | 7.735 | 4.672 | |
| 2 | 0.915 | 5.363 | 4.286 | 9.791 | 0.934 | 4.940 | 4.012 | 9.383 | 3.890 | |
| Stacking4 | 0 | 0.847 | 7.210 | 5.834 | 14.101 | 0.942 | 4.612 | 3.666 | 8.887 | 4.350 |
| 1 | 0.849 | 7.157 | 5.656 | 13.749 | 0.947 | 4.426 | 3.324 | 7.917 | 4.610 | |
| 2 | 0.915 | 5.374 | 4.200 | 9.412 | 0.934 | 4.943 | 4.160 | 9.576 | 3.891 | |
| Stacking5 | 0 | 0.849 | 7.154 | 5.584 | 13.529 | 0.922 | 5.371 | 4.299 | 10.185 | 3.653 |
| 1 | 0.865 | 6.762 | 5.287 | 12.626 | 0.946 | 4.449 | 3.386 | 7.900 | 5.005 | |
| 2 | 0.917 | 5.299 | 4.194 | 9.450 | 0.933 | 4.970 | 4.058 | 9.175 | 3.877 | |
| Stacking6 | 0 | 0.749 | 9.215 | 6.772 | 16.751 | 0.817 | 8.228 | 5.944 | 13.621 | 2.338 |
| 1 | 0.785 | 8.541 | 6.568 | 14.957 | 0.912 | 5.686 | 4.808 | 10.476 | 3.384 | |
| 2 | 0.789 | 8.446 | 6.195 | 14.568 | 0.892 | 6.308 | 5.074 | 10.858 | 3.068 | |
| Stacking7 | 0 | 0.843 | 7.300 | 5.596 | 13.601 | 0.925 | 5.257 | 4.111 | 9.954 | 3.800 |
| 1 | 0.862 | 6.831 | 5.321 | 12.687 | 0.946 | 4.481 | 3.459 | 8.174 | 5.013 | |
| 2 | 0.918 | 5.278 | 4.122 | 9.308 | 0.937 | 4.814 | 3.925 | 8.896 | 4.004 | |
| Stacking8 | 0 | 0.864 | 6.785 | 5.307 | 13.131 | 0.916 | 5.559 | 4.083 | 10.075 | 3.697 |
| 1 | 0.868 | 6.682 | 5.233 | 12.363 | 0.948 | 4.379 | 3.445 | 7.899 | 5.157 | |
| 2 | 0.918 | 5.260 | 4.057 | 9.325 | 0.939 | 4.738 | 3.773 | 8.658 | 4.065 | |
| Stacking9 | 0 | 0.869 | 6.656 | 5.255 | 12.924 | 0.923 | 5.346 | 3.924 | 9.612 | 3.778 |
| 1 | 0.870 | 6.630 | 5.181 | 12.329 | 0.947 | 4.418 | 3.477 | 7.969 | 5.081 | |
| 2 | 0.919 | 5.225 | 4.097 | 9.390 | 0.936 | 4.844 | 3.879 | 8.942 | 3.972 | |
| Stacking10 | 0 | 0.849 | 7.145 | 5.477 | 13.365 | 0.869 | 6.963 | 5.926 | 13.362 | 2.777 |
| 1 | 0.866 | 6.736 | 5.325 | 12.773 | 0.943 | 4.577 | 3.526 | 8.263 | 4.918 | |
| 2 | 0.920 | 5.215 | 4.032 | 9.030 | 0.937 | 4.807 | 3.948 | 8.913 | 4.010 | |
| Stacking11 | 0 | 0.871 | 6.618 | 5.172 | 12.835 | 0.931 | 5.063 | 3.968 | 9.938 | 3.954 |
| 1 | 0.854 | 7.036 | 5.591 | 13.451 | 0.950 | 4.295 | 3.289 | 7.573 | 4.721 | |
| 2 | 0.916 | 5.330 | 4.179 | 9.508 | 0.936 | 4.875 | 4.018 | 9.367 | 3.943 | |
| Stacking12 | 0 | 0.869 | 6.665 | 5.140 | 12.812 | 0.918 | 5.514 | 4.614 | 11.229 | 3.557 |
| 1 | 0.870 | 6.644 | 5.159 | 12.216 | 0.948 | 4.393 | 3.461 | 7.840 | 5.100 | |
| 2 | 0.921 | 5.184 | 3.965 | 9.014 | 0.939 | 4.746 | 3.852 | 8.831 | 4.056 | |
| The Number of Base Models Is 3 | Add 1 Base Model | The Number of Base Models Is 4 | |
|---|---|---|---|
| Stacking1 | LS-SVM/BP-AdaBoost/LSTM | RF | Stacking8 |
| XGBoost | Stacking9 | ||
| Stacking2 | LS-SVM/BP-AdaBoost/RF | LSTM | Stacking8 |
| XGBoost | Stacking11 | ||
| Stacking3 | LS-SVM/BP-AdaBoost/XGBoost | LSTM | Stacking9 |
| RF | Stacking11 | ||
| Stacking4 | LSTM/BP-AdaBoost/XGBoost | LS-SVM | Stacking9 |
| RF | Stacking10 | ||
| Stacking5 | LSTM/BP-AdaBoost/RF | LS-SVM | Stacking8 |
| XGBoost | Stacking10 | ||
| Stacking6 | RF/LS-SVM/XGBoost | LSTM | Stacking9 |
| BP-AdaBoost | Stacking11 | ||
| Stacking7 | RF/BP-AdaBoost/XGBoost | LSTM | Stacking10 |
| LS-SVM | Stacking11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Cui, D.; Guo, J.; Hasan, U.; Lv, F.; Li, Z. Hyperspectral Estimation of Tea Leaf Chlorophyll Content Based on Stacking Models. Agriculture 2025, 15, 1039. https://doi.org/10.3390/agriculture15101039
Guo J, Cui D, Guo J, Hasan U, Lv F, Li Z. Hyperspectral Estimation of Tea Leaf Chlorophyll Content Based on Stacking Models. Agriculture. 2025; 15(10):1039. https://doi.org/10.3390/agriculture15101039
Chicago/Turabian StyleGuo, Jinfeng, Dong Cui, Jinxing Guo, Umut Hasan, Fengqi Lv, and Zixing Li. 2025. "Hyperspectral Estimation of Tea Leaf Chlorophyll Content Based on Stacking Models" Agriculture 15, no. 10: 1039. https://doi.org/10.3390/agriculture15101039
APA StyleGuo, J., Cui, D., Guo, J., Hasan, U., Lv, F., & Li, Z. (2025). Hyperspectral Estimation of Tea Leaf Chlorophyll Content Based on Stacking Models. Agriculture, 15(10), 1039. https://doi.org/10.3390/agriculture15101039







