Research on Grain Temperature Detection Based on Rational Sound-Source Signal
Abstract
1. Introduction
2. Materials and Methods
2.1. Modeling of Acoustic Temperature Measurement in Grain Storage
2.2. Calibration of Path-Correction Factor
2.3. Cross-Correlation Calculations
3. Experimental Setup and Signal Selection
3.1. Experimental Setup
3.2. Research on Attenuation Analysis of Acoustic Signals in Wheat
3.2.1. Calculation Method of Signal Propagation Attenuation Coefficient
3.2.2. Research on Attenuation Characteristics of Simulated Pulse Signals
3.2.3. Research on the Attenuation Characteristics of Linear Sweep Signals
3.2.4. Determination of Sound-Source Signal Types
3.3. Research on the Determination of Parameters for Optimal Sound-Source Signals
3.3.1. Research on the Determination of the Frequency Band of Linear Sweep Signals
3.3.2. Research on the Cycle Determination of Linear Frequency-Sweep Signal
4. Results and Discussion
4.1. Measurement of Acoustic Wave Propagation Time
4.2. Path-Correction Factor Calculation
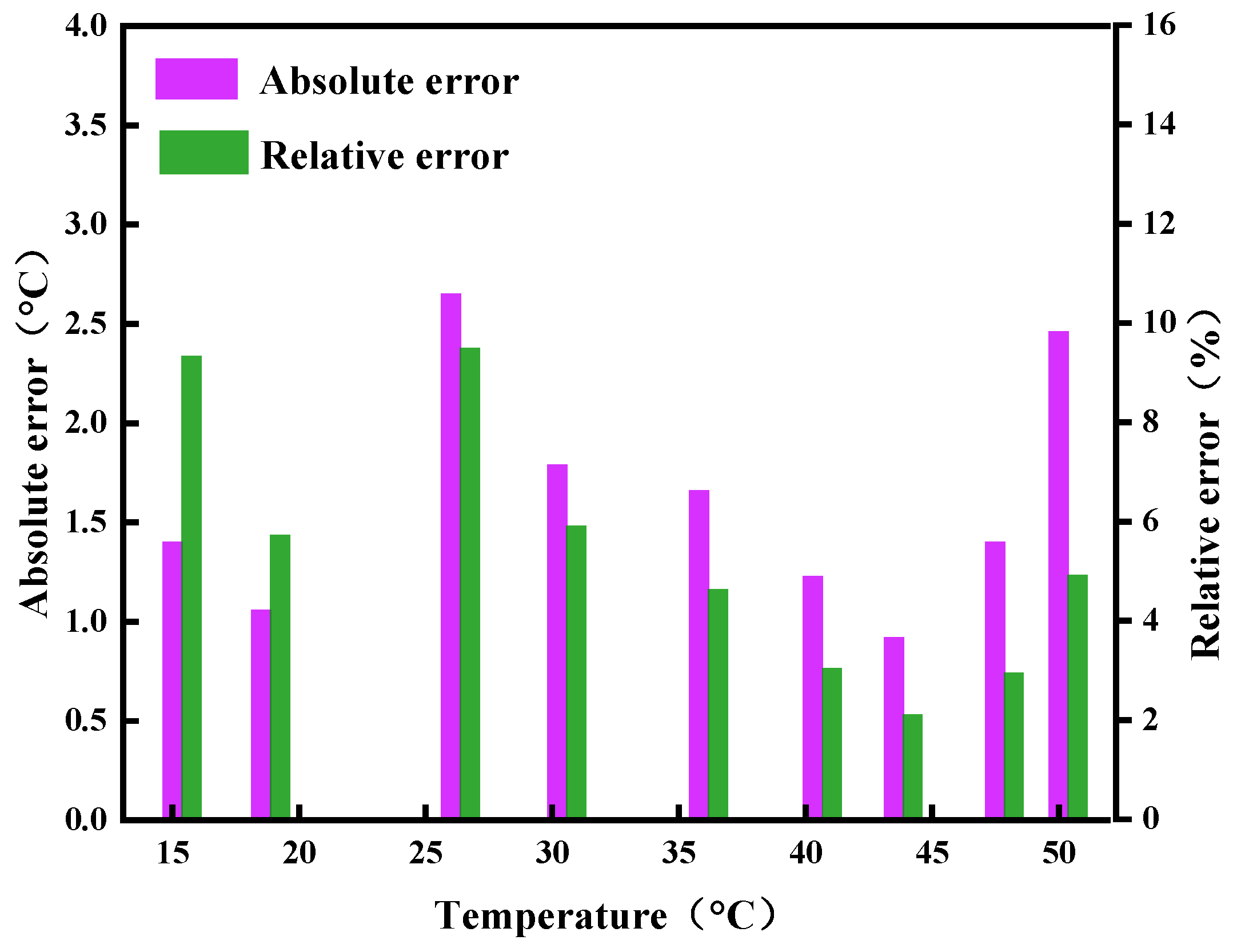
4.3. Temperature Measurement Results
4.4. Discussion
4.4.1. Influence of Grain Thermal Conductivity
4.4.2. Influence of Acoustic Propagation Time Measurement Errors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Duan, S.; Yang, W.; Wang, X.; Mao, S.; Zhang, Y. Temperature forecasting for stored grain: A deep spatiotemporal attention approach. IEEE Internet Things J. 2021, 8, 17147–17160. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, T.; Chen, Y.; Jin, X.; Feng, T.; Chen, X. Research on unmanned transfer vehicle path planning for raw grain warehousing. Intell. Fuzzy Syst. 2023, 45, 6513–6533. [Google Scholar] [CrossRef]
- Plumier, B.; Maier, D. Effect of temperature sensor numbers and placement on aeration cooling of a stored grain mass using a 3D finite element model. Agriculture 2021, 11, 231. [Google Scholar] [CrossRef]
- Neto, A.J.S.; Lopes, D.D.C. Thermistor based system for grain aeration monitoring and control. Comput. Electron. Agric. 2015, 116, 45–54. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Li, Z.; Hou, M.; Dong, G.; Liu, T.; Sun, T.; Grattan, K.T.V. Quasi-distributed fiber optic temperature and humidity sensor system for monitoring of grain storage in granaries. IEEE Sens. 2020, 20, 9226–9233. [Google Scholar] [CrossRef]
- Yang, G.; Yan, J.D.; Shen, G.; An, L.; Li, Z. Real-time monitoring of temperature field in piled pulverized coal based on acoustic method. Clean Coal Technol. 2022, 28, 59–65. [Google Scholar] [CrossRef]
- Dokhanchi, N.S.; Othmani, C.; Arnold, J.; Vogel, A.; Merchel, S.; Voelker, C.; Altinsoy, M.E. Indoor air temperature measurements using ultrasonic travel-time tomography. Appl. Acoust. 2024, 218, 109894. [Google Scholar] [CrossRef]
- Sukhanov, D.; Khalil, A. Two Dimensional Ultrasonic Air Temperature Tomography Based on Phase Shift Processing of Multi-Frequency Measurements. IEEE Trans. Instrum. Meas. 2024, 73, 4508706. [Google Scholar] [CrossRef]
- Lin, F.-S.; Huang, M.-C.; Tai, S.-K.; Chu, Y.-C.; Shen, S.-H.; Huang, C.-H. Investigation of an FPGA-based acoustic gas thermometer for monitoring indoor temperature distribution two-dimensionally. IEEE Sens. J. 2024, 24, 15197–15209. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, G.; Sun, J.; Liu, Y. Measurement the 3D temperature distribution in the combustion zone using acoustic tomography and nolinear wavefont tracing. J. Meas. 2024, 229, 114439. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, L.; Zhou, X.; Shi, Y.; Wu, N. Boiler Furnace Temperature Field Measurement and Reconstruction Error Elimination Based on Temperature Field Residual Correction Network. IEEE Trans. Instrum. Meas. 2024, 73, 2507215. [Google Scholar] [CrossRef]
- Kong, Q.; Jiang, G.; Liu, Y.; Sun, J. 3D high-quality temperature-field reconstruction method in furnace based on acoustic tomography. Appl. Therm. Eng. 2020, 179, 115693. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, X.; Yang, Q.; Chen, J.; Dong, C.; Zhao, L. A reconstruction method of boiler furnace temperature distribution based on acoustic measurement. IEEE Trans. Instrum. Meas. 2021, 70, 9600413. [Google Scholar] [CrossRef]
- Fan, W.; Chen, Y.; Pan, H.; Ye, Y.; Cai, Y.; Zhang, Z. Experimental study on underwater acoustic imaging of 2-D temperature distribution around hot springs on floor of Lake Qiezishan, China. Exp. Therm. Fluid Sci. 2010, 34, 1334–1345. [Google Scholar] [CrossRef]
- Yu, X.; Zhuang, X.; Li, Y.; Zhang, Y. Real-time observation of range-averaged temperature by high-frequency underwater acoustic thermometry. IEEE Access 2019, 7, 17975–17980. [Google Scholar] [CrossRef]
- Xu, S.; Li, G.; Feng, R.; Hu, Z.; Xu, P.; Huang, H. 3-D Water temperature distribution observation via coastal acoustic tomography sensing network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4206418. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, M.; Yan, Y.; Lu, G.; Cheng, X. Temperature measurement of stored biomass of different types and bulk densities using acoustic techniques. Fuel 2019, 257, 115986. [Google Scholar] [CrossRef]
- Zheng, L.J. Temperature Measurement of Biomass Piles Using Acoustic Sensors; North China Electric Power University: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Saito, I.; Mizutani, K.; Wakatsuki, N.; Kawabe, S. Measurement of vertical temperature distribution using a single pair of loudspeaker and microphone with acoustic reflection. Jpn. J. Appl. Phys. 2009, 48, 07GB05. [Google Scholar] [CrossRef]
- Guo, M. Research on Temperature Measurement of Stacked Biomass Based on Acoustic Method; North China Electric Power University: Beijing, China, 2019. [Google Scholar] [CrossRef]
- Hickling, R.; Wei, W.; Hagstrum, D. Studies of sound transmission in various types of stored grain for acoustic detection of insects. Appl. Acoust. 1997, 50, 263–278. [Google Scholar] [CrossRef]
- Hickling, R.; Wei, W. Sound transmission in stored grain. Appl. Acoust. 1995, 45, 1–8. [Google Scholar] [CrossRef]
- Ge, M.; Chen, G.; Liu, W.; Liu, C.; Zheng, D. Study on the pore structure characteristics of maize grain piles and their effects on air flow distribution. Comput. Electron. Agric. 2024, 224, 109136. [Google Scholar] [CrossRef]
- Guo, M.; Yan, Y.; Hu, Y.; Lu, G.; Zhang, J. Temperature measurement of stored biomass using low-frequency acoustic waves and correlation signal processing techniques. Fuel 2018, 227, 89–98. [Google Scholar] [CrossRef]
- Ribert, G.; Domingo, P.; Vervisch, L. Analysis of sub-grid scale modeling of the ideal-gas equation of state in hydrogen–oxygen premixed flames. Proc. Combust. Inst. 2019, 37, 2345–2351. [Google Scholar] [CrossRef]
- Yan, H.; Chen, G.; Zhou, Y.; Liu, L. Primary study of temperature distribution measurement in stored grain based on acoustic tomography. Exp. Therm. Fluid Sci. 2012, 42, 55–63. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, S.; Yang, Z.; Zhao, L.; Zhou, Y.; Zhou, D. Quality classification of stored wheat based on evidence reasoning rule and stacking ensemble learning. Comput. Electron. Agric. 2023, 214, 108339. [Google Scholar] [CrossRef]
- GB 1351-2023; People’s Republic of China National Standard Wheat. State Administration for Market Supervision and Administration of the People’s Republic of China: Beijing, China; National Standardization Administration of the People’s Republic of China: Beijing, China, 2023.
- Chen, J.H.; Li, J.X.; Zheng, D.Q.; Yin, J.; Huang, H.R.; Ge, M.M.; Zhang, J.Y. Prediction of Grain Porosity Based on GWO-BP Neural Network and Grain Compression Experiment. Sci. Technol. Cereals Oils Foods 2024, 32, 186–193. [Google Scholar] [CrossRef]
- Zhang, J.; Hao, R.; Gu, X. Amplitude attenuation laws of acoustic emission waves in plate structures. Dyna 2019, 94, 67–74. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Li, Z.S.; Wang, H.P.; Xin, J. A method based on power-law detector in deep-sea multi-path pulse signal joint detection. J. Acoust. Technol. 2025, 1–6. [Google Scholar] [CrossRef]
- Li, S.; Wang, F.; Zhang, Y.; Li, R.; Shi, S.; Li, Y.; Li, X.; da Costa, D.B. Orthogonal chirp division multiplexing assisted dual-function radar communication in IoT networks. IEEE Internet Things J. 2024, 13, 23752–23764. [Google Scholar] [CrossRef]
- Wu, R. Design of an Acoustic Temperature Measurement System Based on FPGA; North China Electric Power University: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, G.; Xu, L.; Zhang, X.; Liu, X.; Zhu, J. Characteristic analysis and data comparative of linear and nonlinear low-frequency sweep in vibroseis. J. Geophys. Eng. 2024, 21, 244–256. [Google Scholar] [CrossRef]
- GB/T 29890-2013; Technical Specification for Grain and Oil Storage. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China; Standardization Administration of the People’s Republic of China: Beijing, China, 2013.
- Tao, W.Q. Heat Transfer, 5th ed.; Higher Education Press: Beijing China, 2019; p. 536. [Google Scholar]


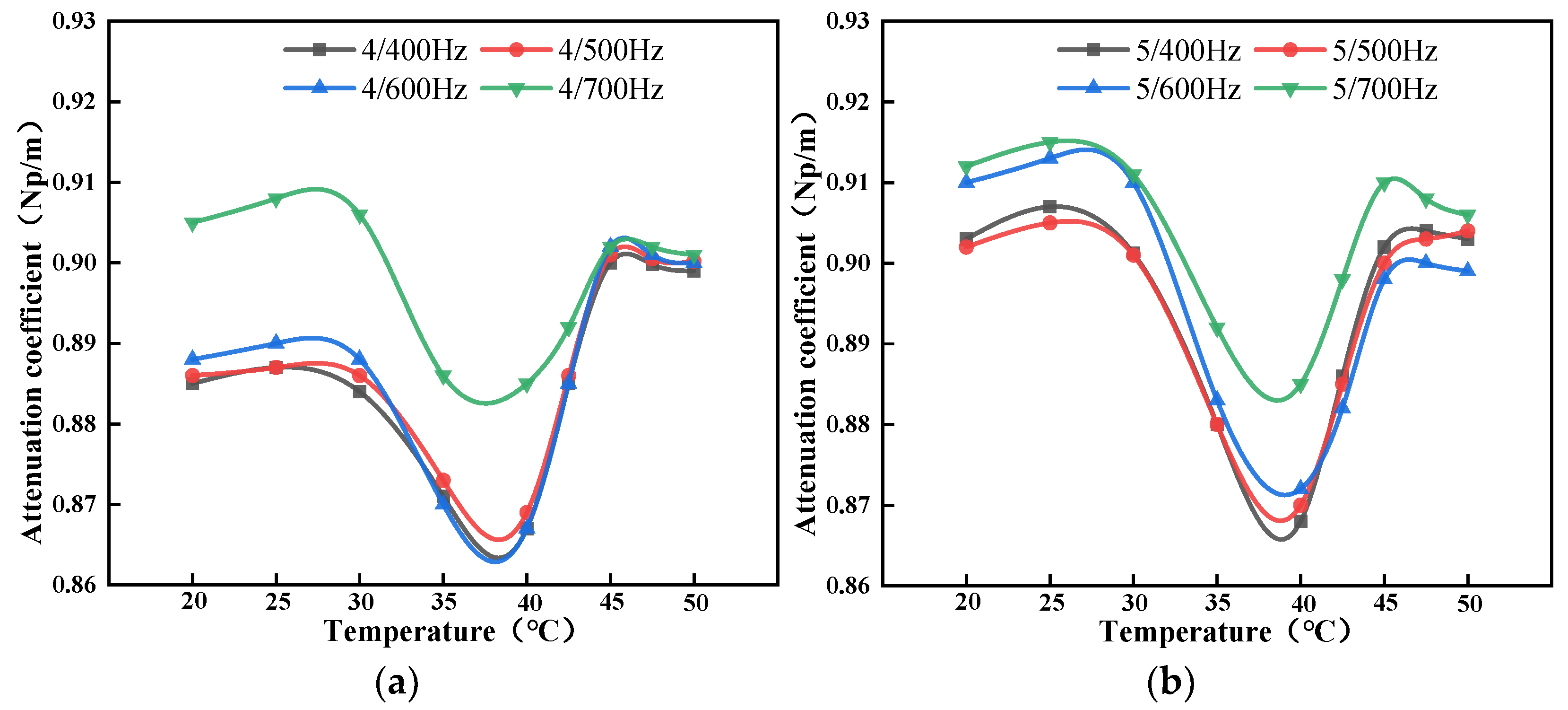
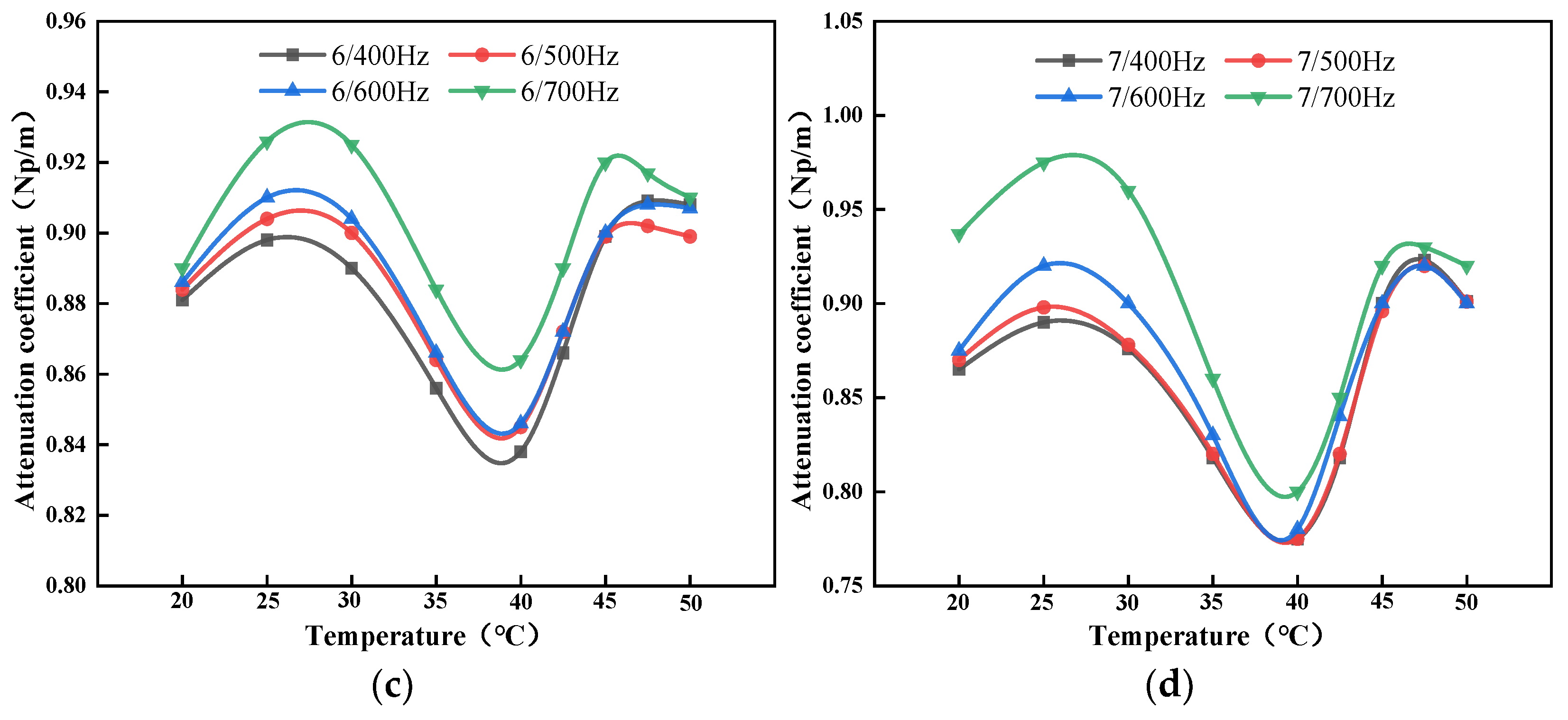
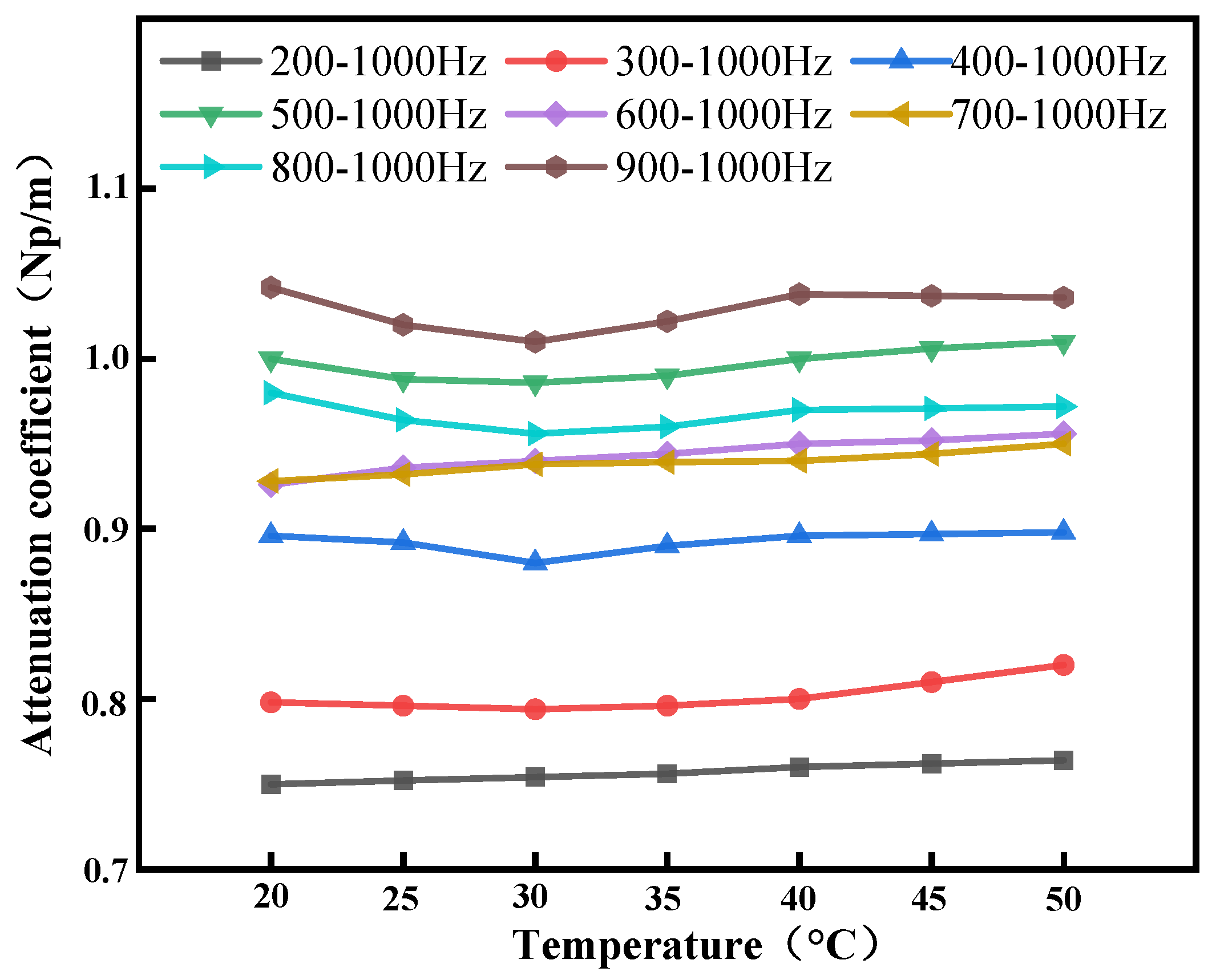

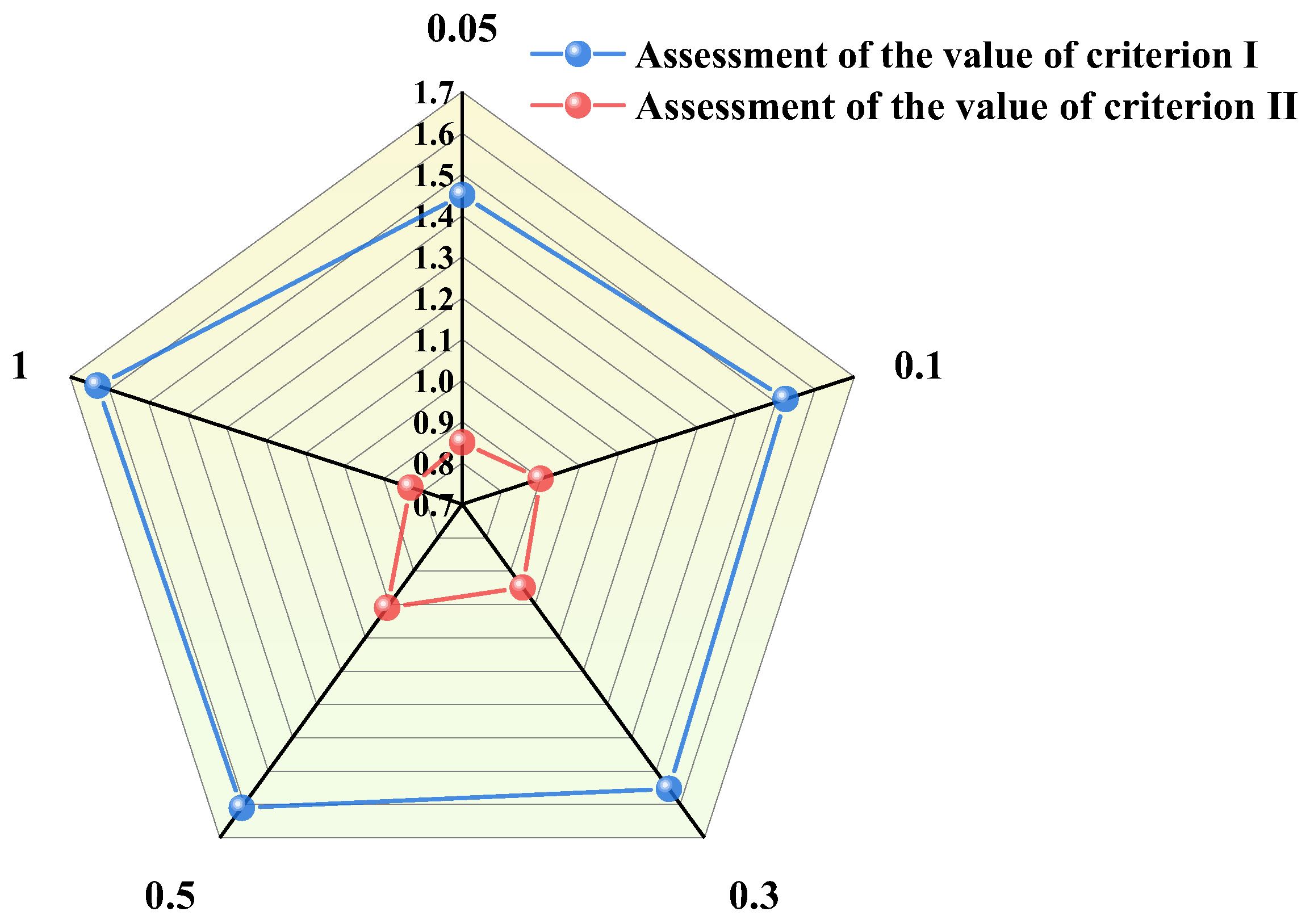

| Temperature Measurement Method | Advantages | Disadvantages |
|---|---|---|
| Thermocouple [3] | Wide temperature range; durability; fast response. | Lower accuracy; requires cold-junction compensation. |
| Thermistor [4] | High sensitivity; low cost; small size. | Non-linear; requires calibration. |
| Optical fiber [5] | High precision; high stability; safety. | Complex installation (fragile fibers); slower response. |
| Temperature (°C) | Microphone Depth: 0.1 m; Microphone Spacing: 1.3 m. | ||
|---|---|---|---|
| TOF (ms) | Standard Deviation (µs) | ||
| Normal | 15 | 4.823 | 0.43 |
| 18.5 | 4.791 | 0.32 | |
| Room temperature | 21 | 4.762 | 0.39 |
| Alert temperature | 26 | 4.743 | 0.32 |
| 30.2 | 4.703 | 0.41 | |
| 35.8 | 4.659 | 0.26 | |
| 40.3 | 4.622 | 0.35 | |
| 43.5 | 4.583 | 0.45 | |
| 47.5 | 4.551 | 0.50 | |
| 50 | 4.526 | 0.36 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, H.; Feng, B.; Jiang, Y.; Zhang, Y.; Cai, C.; Guo, C.; Wang, H.; Liu, Z.; Liu, X. Research on Grain Temperature Detection Based on Rational Sound-Source Signal. Agriculture 2025, 15, 1035. https://doi.org/10.3390/agriculture15101035
Ge H, Feng B, Jiang Y, Zhang Y, Cai C, Guo C, Wang H, Liu Z, Liu X. Research on Grain Temperature Detection Based on Rational Sound-Source Signal. Agriculture. 2025; 15(10):1035. https://doi.org/10.3390/agriculture15101035
Chicago/Turabian StyleGe, Hongyi, Bo Feng, Yuying Jiang, Yuan Zhang, Chengxin Cai, Chunyan Guo, Heng Wang, Ziyu Liu, and Xinxin Liu. 2025. "Research on Grain Temperature Detection Based on Rational Sound-Source Signal" Agriculture 15, no. 10: 1035. https://doi.org/10.3390/agriculture15101035
APA StyleGe, H., Feng, B., Jiang, Y., Zhang, Y., Cai, C., Guo, C., Wang, H., Liu, Z., & Liu, X. (2025). Research on Grain Temperature Detection Based on Rational Sound-Source Signal. Agriculture, 15(10), 1035. https://doi.org/10.3390/agriculture15101035





