CanKiwi: A Mechanistic Competition Model of Kiwifruit Bacterial Canker Disease Dynamics
Abstract
1. Introduction
2. Material and Methods
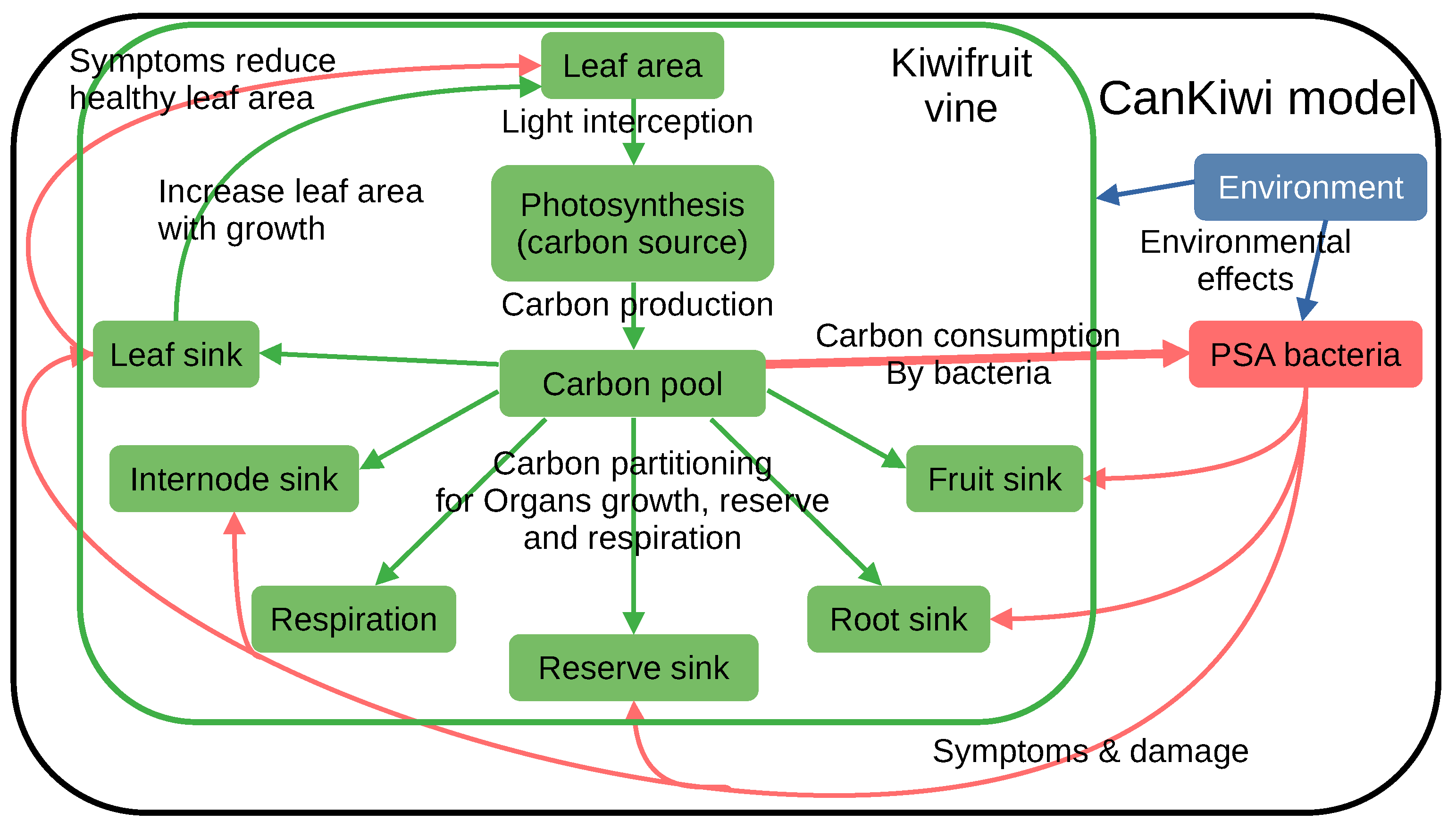
2.1. The Functional Kiwifruit Model
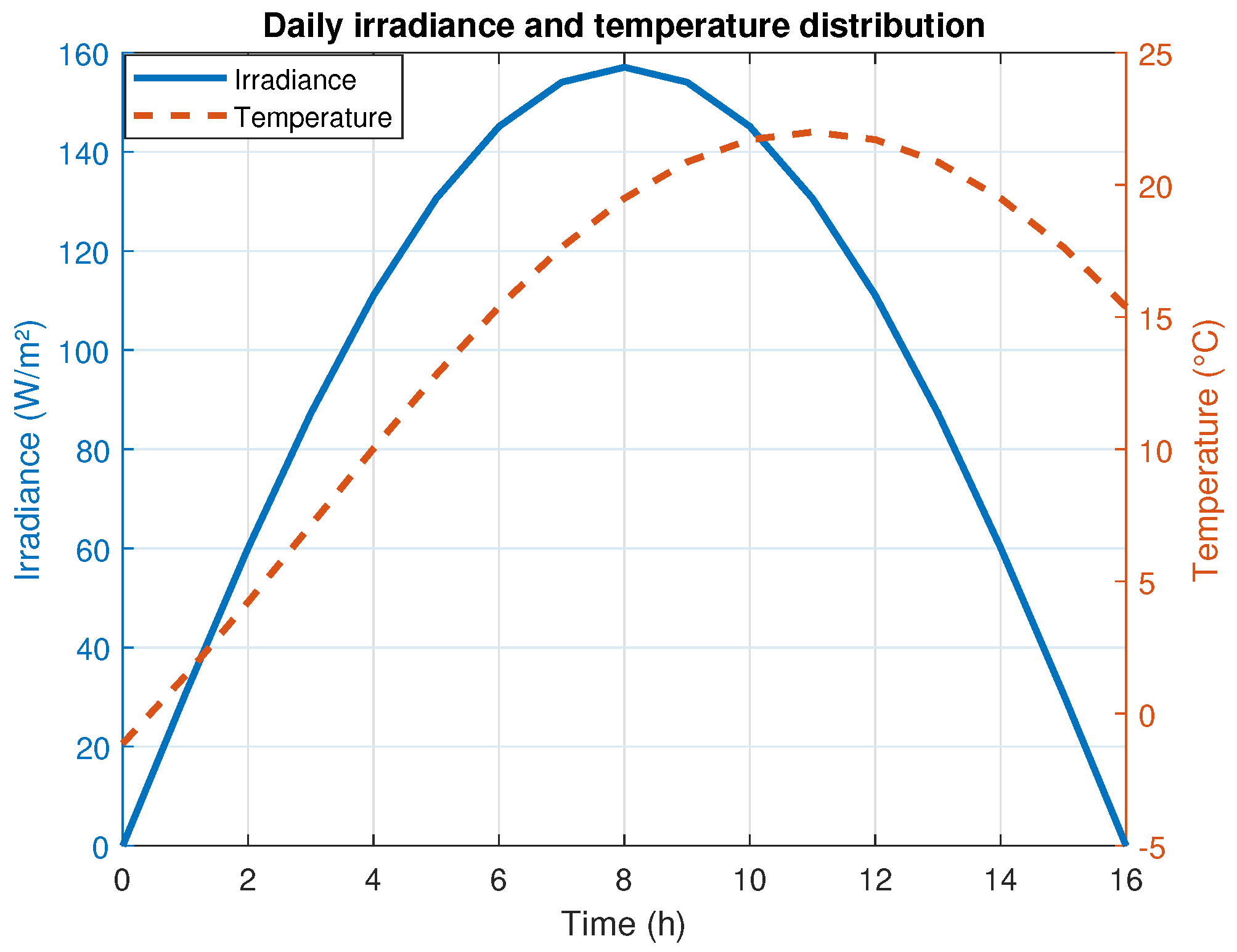
2.1.1. Carbon Acquisition (Photosynthesis)
2.1.2. Carbon Inflow into Sinks for Organ Growth
2.1.3. Vegetative Growth
2.1.4. Fruit Growth
2.1.5. Maintenance of Respiration
2.1.6. Carbon Acquisition Dynamics
2.1.7. Reserve Dynamics
2.2. Bacterial Population Dynamics
2.3. Competition for Resources (Carbon Balance)
2.3.1. Biotrophy Stage
2.3.2. Necrotrophy Stage
3. Results and Discussion
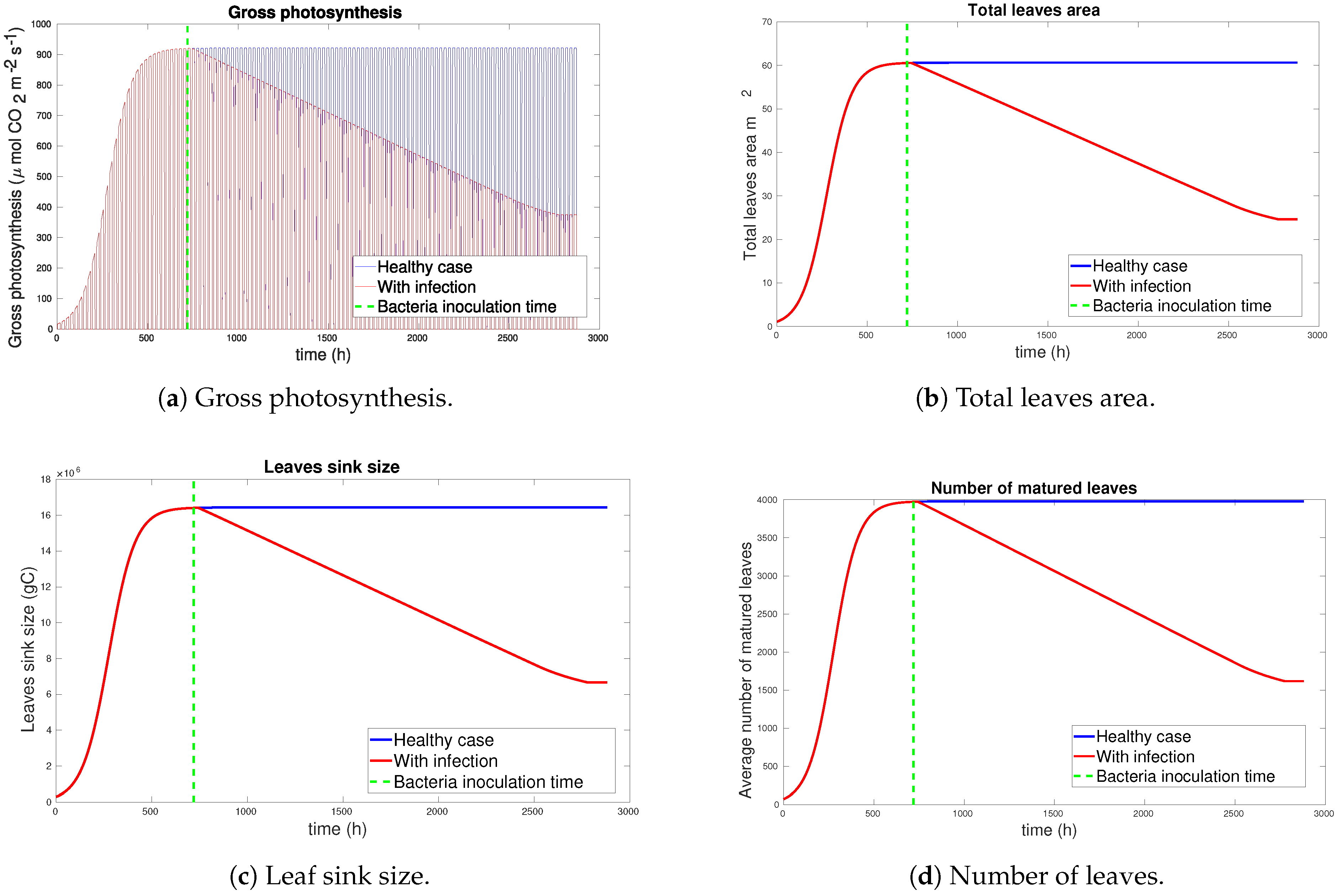
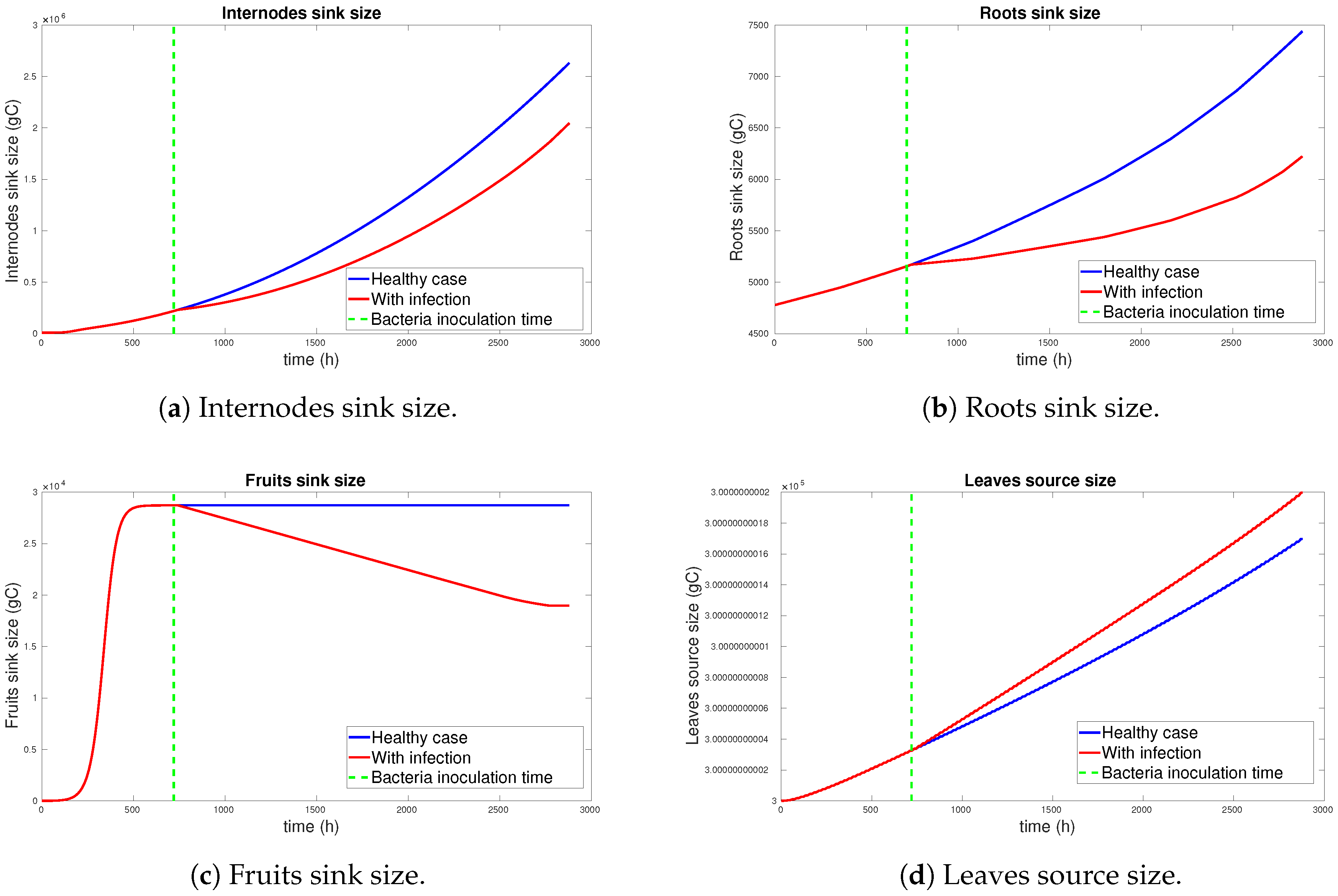
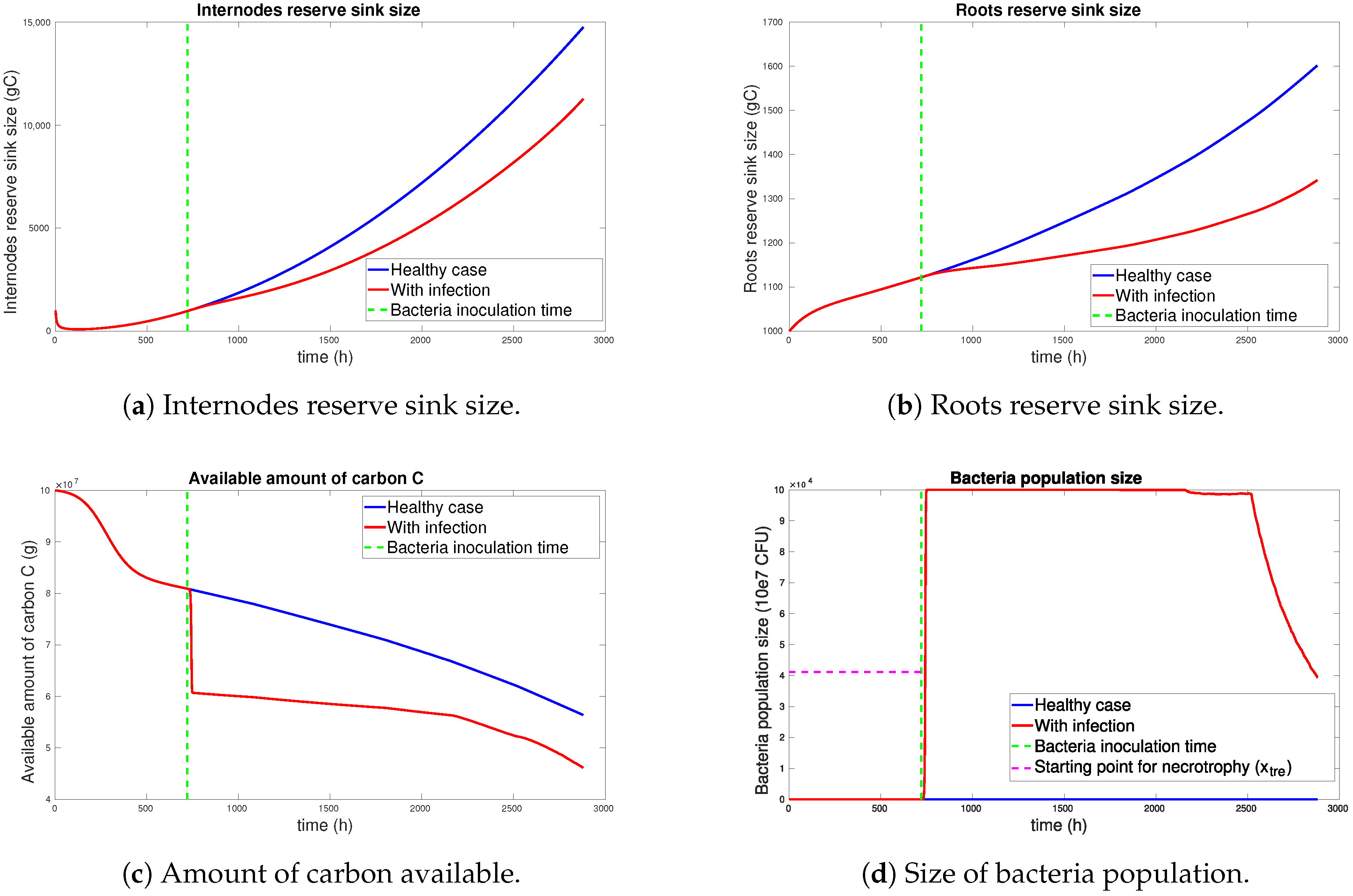
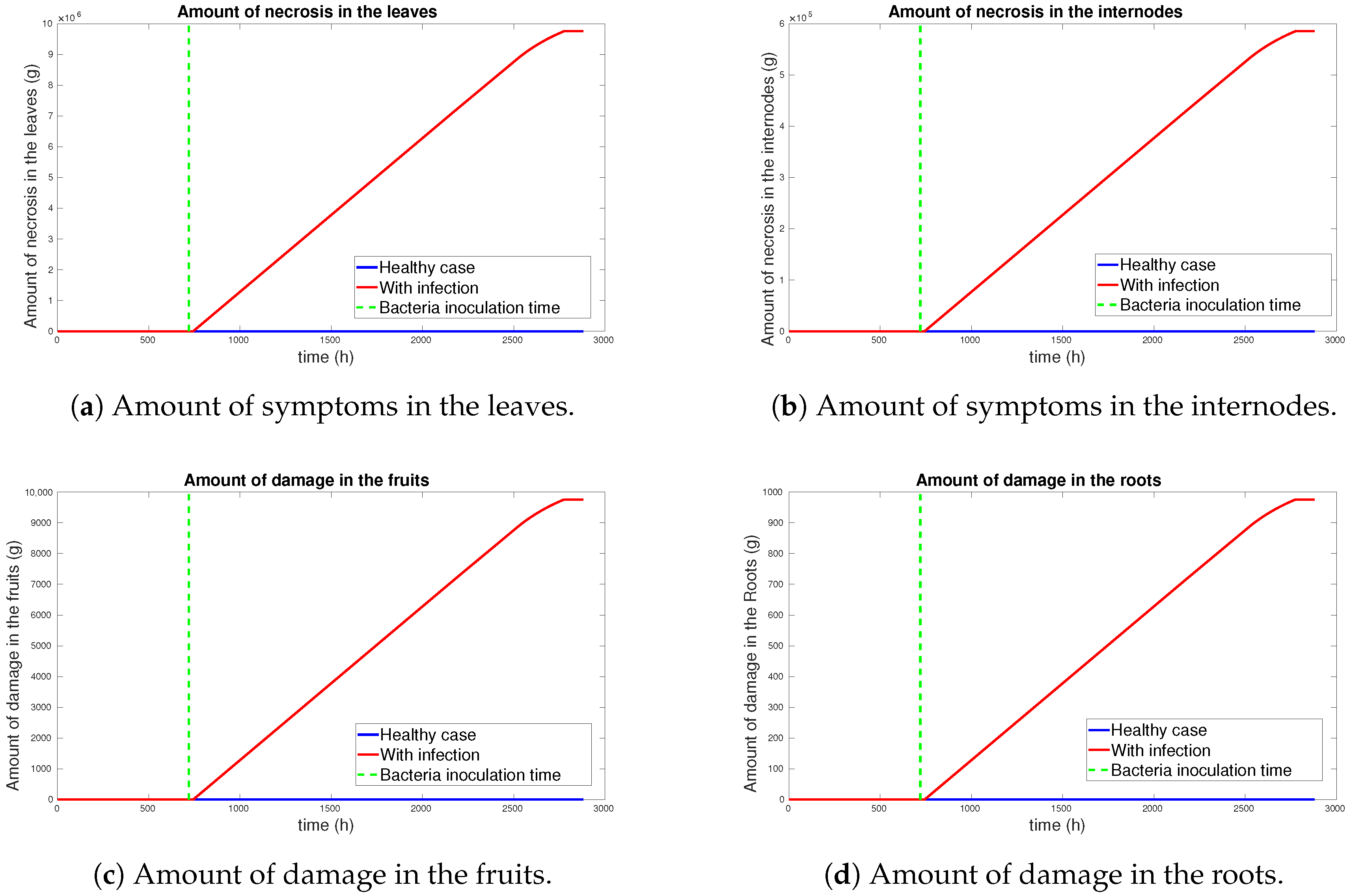
3.1. Simulation Results
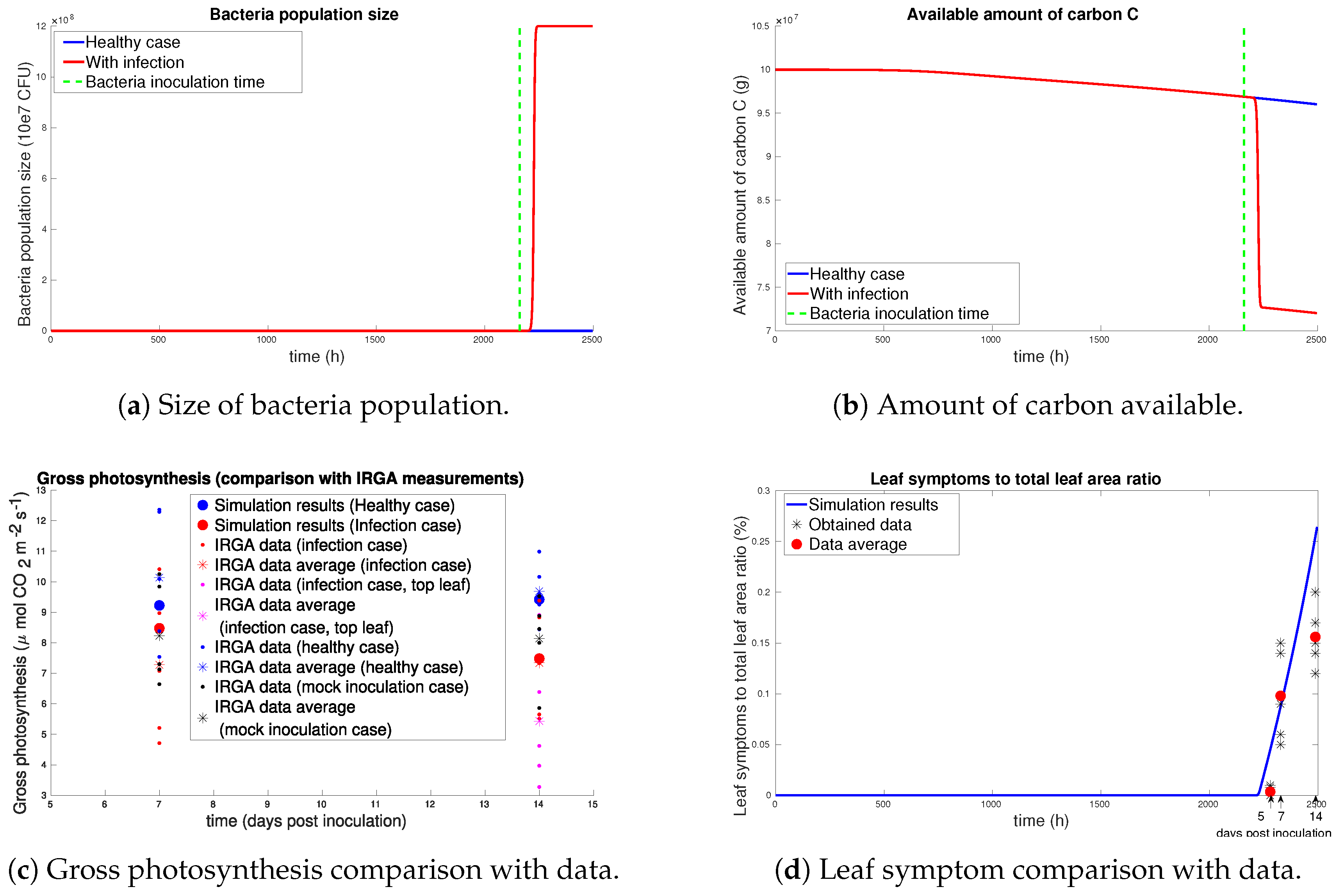
3.2. Experimental Validation
3.2.1. Preparation of the Plants and the Growth Environment
3.2.2. Preparation and Application of the Inoculum
3.2.3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CanKiwi | Model of Kiwifruit Bacterial Canker Disease Dynamics. |
| KBC | Kiwifruit Bacterial Canker. |
| PSA | Pseudomonas Syringae pv. Actinidiae. |
| FSPM | Functional-Structural Plant Model. |
| L-systems | Lindenmayer systems. |
| PPFD | Photosynthetic Photon Flux Density. |
| PAR | Photosynthetically Active Radiation. |
| CFU | Colony Forming Unit. |
| IRGA | Infrared Gas Analyzer. |
| MAE | Mean Absolute Error. |
References
- Kim, G.H.; Jung, J.S.; Koh, Y.J. Occurrence and epidemics of bacterial canker of kiwifruit in Korea. Plant Pathol. J. 2017, 33, 351. [Google Scholar] [CrossRef] [PubMed]
- Do, K.S.; Chung, B.N.; Joa, J.H. D-PSA-K: A model for estimating the accumulated potential damage on kiwifruit canes caused by bacterial canker during the growing and overwintering seasons. Plant Pathol. J. 2016, 32, 537. [Google Scholar] [CrossRef]
- Petriccione, M.; Di Cecco, I.; Salzano, A.; Arena, S.; Scaloni, A.; Scortichini, M. A proteomic approach to investigate the Actinidia spp./Pseudomonas syringae pv. actinidiae pathosystem. In Proceedings of the I International Symposium on Bacterial Canker of Kiwifruit, Mt. Maunganui, New Zealand, 19–22 November 2013; pp. 95–101. [Google Scholar]
- Doughari, J. An overview of plant immunity. J. Plant Pathol. Microbiol. 2015, 6, 322. [Google Scholar]
- Fernandes, A.P.G. Effect of Different Forms of Nitrogen Nutrition on Kiwifruit Development and Resistance to Pseudomonas Syringae pv. actinidiae. Master’s Thesis, Repositorio Aberto, Universidade do Porto, Porto, Portugal, 2019. [Google Scholar]
- Scortichini, M.; Marcelletti, S.; Ferrante, P.; Petriccione, M.; Firrao, G. Pseudomonas syringae pv. actinidiae: A re-emerging, multi-faceted, pandemic pathogen. Mol. Plant Pathol. 2012, 13, 631–640. [Google Scholar] [CrossRef]
- Donati, I.; Cellini, A.; Sangiorgio, D.; Vanneste, J.L.; Scortichini, M.; Balestra, G.M.; Spinelli, F. Pseudomonas syringae pv. actinidiae: Ecology, infection dynamics and disease epidemiology. Microb. Ecol. 2020, 80, 81–102. [Google Scholar]
- Cameron, A.; Sarojini, V. Pseudomonas syringae pv. actinidiae: Chemical control, resistance mechanisms and possible alternatives. Plant Pathol. 2014, 63, 1–11. [Google Scholar] [CrossRef]
- Santos, M.G.; Nunes da Silva, M.; Vasconcelos, M.W.; Carvalho, S.M. Scientific and technological advances in the development of sustainable disease management tools: A case study on kiwifruit bacterial canker. Front. Plant Sci. 2024, 14, 1306420. [Google Scholar] [CrossRef] [PubMed]
- Kraikivski, P. Mathematical Modeling in Systems Biology. Entropy 2023, 25, 1380. [Google Scholar] [CrossRef]
- Pinto, C.M.; Ionescu, C.M. Computational and Mathematical Models in Biology; Springer: Berlin/Heidelberg, Germany, 2023; Volum 38. [Google Scholar]
- Vittadello, S.T.; Stumpf, M.P. Open problems in mathematical biology. Math. Biosci. 2022, 354, 108926. [Google Scholar] [CrossRef] [PubMed]
- Ji, T.; Salotti, I.; Dong, C.; Li, M.; Rossi, V. Modeling the effects of the environment and the host plant on the ripe rot of grapes, caused by the Colletotrichum species. Plants 2021, 10, 2288. [Google Scholar] [CrossRef]
- Narouei-Khandan, H.A.; Worner, S.P.; Viljanen, S.L.; van Bruggen, A.H.; Balestra, G.M.; Jones, E. The Potential Global Climate Suitability of Kiwifruit Bacterial Canker Disease (Pseudomonas syringae pv. actinidiae (Psa)) Using Three Modelling Approaches: CLIMEX, Maxent and Multimodel Framework. Climate 2022, 10, 14. [Google Scholar] [CrossRef]
- Beresford, R.; Tyson, J.; Henshall, W. Development and validation of an infection risk model for bacterial canker of kiwifruit, using a multiplication and dispersal concept for forecasting bacterial diseases. Phytopathology 2017, 107, 184–191. [Google Scholar] [CrossRef] [PubMed]
- Froud, K.; Beresford, R.; Cogger, N. Impact of kiwifruit bacterial canker on productivity of cv. Hayward kiwifruit using observational data and multivariable analysis. Plant Pathol. 2018, 67, 671–681. [Google Scholar] [CrossRef]
- Thornley, J.; Johnson, I. Plant and Crop Modelling: A Mathematical Approach to Plant and Crop Physiology; Oxford University Press: Armidale, UK, 1990. [Google Scholar]
- Prusinkiewicz, P. Art and science of life: Designing and growing virtual plants with L-systems. In Proceedings of the XXVI International Horticultural Congress: Nursery Crops, Toronto, ON, Canada, 11–17 August 2002; Development, Evaluation, Production and Use 630. pp. 15–28. [Google Scholar]
- Louarn, G.; Song, Y. Two decades of functional–structural plant modelling: Now addressing fundamental questions in systems biology and predictive ecology. Ann. Bot. 2020, 126, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Thornley, J.H. Grassland Dynamics: An Ecosystem Simulation Model; CAB International: Wallingford, UK, 1998. [Google Scholar]
- Thornley, J.H.; Parsons, A.J. Allocation of new growth between shoot, root and mycorrhiza in relation to carbon, nitrogen and phosphate supply: Teleonomy with maximum growth rate. J. Theor. Biol. 2014, 342, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Orwin, K.H.; Kirschbaum, M.U.; St John, M.G.; Dickie, I.A. Organic nutrient uptake by mycorrhizal fungi enhances ecosystem carbon storage: A model-based assessment. Ecol. Lett. 2011, 14, 493–502. [Google Scholar] [CrossRef] [PubMed]
- Grisafi, F.; DeJong, T.M.; Tombesi, S. Fruit tree crop models: An update. Tree Physiol. 2022, 42, 441–457. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.; Prusinkiewicz, P.; Favreau, R.; DeJong, T. L-PEACH, an L-systems based model for simulating architecture, carbohydrate source-sink interactions and physiological responses of growing trees. In Functional-Structural Plant Modelling in Crop Production; Springer: Dordrecht, The Netherlands, 2007; pp. 139–150. [Google Scholar]
- DeJong, T.; Da Silva, D.; Negron, C.; Cieslak, M.; Prusinkiewicz, P. The L-ALMOND model: A functional-structural virtual tree model of almond tree architectural growth, carbohydrate dynamics over multiple years. In Proceedings of the X International Symposium on Modelling in Fruit Research and Orchard Management, Montpellier, France, 2 June 2015; pp. 43–50. [Google Scholar]
- Mirás-Avalos, J.M.; Uriarte, D.; Lakso, A.N.; Intrigliolo, D.S. Modeling grapevine performance with ‘VitiSim’, a weather-based carbon balance model: Water status and climate change scenarios. Sci. Hortic. 2018, 240, 561–571. [Google Scholar] [CrossRef]
- Zhu, J.; Dai, Z.; Vivin, P.; Gambetta, G.A.; Henke, M.; Peccoux, A.; Ollat, N.; Delrot, S. A 3-D functional–structural grapevine model that couples the dynamics of water transport with leaf gas exchange. Ann. Bot. 2018, 121, 833–848. [Google Scholar] [CrossRef] [PubMed]
- Boudon, F.; Persello, S.; Jestin, A.; Briand, A.S.; Grechi, I.; Fernique, P.; Guédon, Y.; Léchaudel, M.; Lauri, P.É.; Normand, F. V-Mango: A functional–structural model of mango tree growth, development and fruit production. Ann. Bot. 2020, 126, 745–763. [Google Scholar] [CrossRef] [PubMed]
- Lordan, J.; Reginato, G.H.; Lakso, A.N.; Francescatto, P.; Robinson, T.L. Natural fruitlet abscission as related to apple tree carbon balance estimated with the MaluSim model. Sci. Hortic. 2019, 247, 296–309. [Google Scholar] [CrossRef]
- Pallas, B.; Da Silva, D.; Valsesia, P.; Yang, W.; Guillaume, O.; Lauri, P.E.; Vercambre, G.; Génard, M.; Costes, E. Simulation of carbon allocation and organ growth variability in apple tree by connecting architectural and source–sink models. Ann. Bot. 2016, 118, 317–330. [Google Scholar] [CrossRef] [PubMed]
- Cieslak, M.; Seleznyova, A.N.; Hanan, J. A functional–structural kiwifruit vine model integrating architecture, carbon dynamics and effects of the environment. Ann. Bot. 2011, 107, 747–764. [Google Scholar] [CrossRef]
- DeJong, T. Simulating fruit tree growth, structure, and physiology using L-systems. Crop Sci. 2022, 62, 2091–2106. [Google Scholar] [CrossRef]
- Landis, F.C.; Fraser, L.H. A new model of carbon and phosphorus transfers in arbuscular mycorrhizas. New Phytol. 2008, 177, 466–479. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Cribb, B.; Clarke, A.R.; Hanan, J. A generic individual-based spatially explicit model as a novel tool for investigating insect-plant interactions: A case study of the behavioural ecology of frugivorous Tephritidae. PLoS ONE 2016, 11, e0151777. [Google Scholar] [CrossRef]
- Ney, B.; Bancal, M.O.; Bancal, P.; Bingham, I.; Foulkes, J.; Gouache, D.; Paveley, N.; Smith, J. Crop architecture and crop tolerance to fungal diseases and insect herbivory. Mechanisms to limit crop losses. Eur. J. Plant Pathol. 2013, 135, 561–580. [Google Scholar] [CrossRef]
- Combes, D.; Decau, M.L.; Rakocevic, M.; Jacquet, A.; Simon, J.C.; Sinoquet, H.; Sonohat, G.; Varlet-Grancher, C. Simulating the grazing of a white clover 3-D virtual sward canopy and the balance between bite mass and light capture by the residual sward. Ann. Bot. 2011, 108, 1203–1212. [Google Scholar] [CrossRef] [PubMed]
- Tivoli, B.; Andrivon, D.; Baranger, A.; Calonnec, A.; Jeger, M. Foreword: Plant and canopy architecture impact on disease epidemiology and pest development. Eur. J. Plant Pathol. 2013, 135, 453–454. [Google Scholar] [CrossRef]
- Robert, C.; Garin, G.; Abichou, M.; Houlès, V.; Pradal, C.; Fournier, C. Plant architecture and foliar senescence impact the race between wheat growth and Zymoseptoria tritici epidemics. Ann. Bot. 2018, 121, 975–989. [Google Scholar] [CrossRef] [PubMed]
- Calonnec, A.; Burie, J.B.; Langlais, M.; Guyader, S.; Saint-Jean, S.; Sache, I.; Tivoli, B. Impacts of plant growth and architecture on pathogen processes and their consequences for epidemic behaviour. Eur. J. Plant Pathol. 2013, 135, 479–497. [Google Scholar] [CrossRef]
- Madden, L.V.; Hughes, G.; van den Bosch, F. The Study of Plant Disease Epidemics; The American Phytopathological Society: Harpenden, UK, 2007. [Google Scholar] [CrossRef]
- Van Maanen, A.; Xu, X.M. Modelling plant disease epidemics. Eur. J. Plant Pathol. 2003, 109, 669–682. [Google Scholar] [CrossRef]
- Fedele, G.; Brischetto, C.; Rossi, V.; Gonzalez-Dominguez, E. A Systematic Map of the Research on Disease Modelling for Agricultural Crops Worldwide. Plants 2022, 11, 724. [Google Scholar] [CrossRef] [PubMed]
- Rossi, V.; Giosuè, S.; Caffi, T. Modelling plant diseases for decision making in crop protection. In Precision Crop Protection—The Challenge and Use of Heterogeneity; Springer: Dordrecht, The Nertherlands, 2010; pp. 241–258. [Google Scholar]
- Cucak, M.; Harteveld, D.O.; Wasko DeVetter, L.; Peever, T.L.; Moral, R.d.A.; Mattupalli, C. Development of a Decision Support System for the Management of Mummy Berry Disease in Northwestern Washington. Plants 2022, 11, 2043. [Google Scholar] [CrossRef]
- Salotti, I.; Rossi, V. A mechanistic weather-driven model for ascochyta rabiei infection and disease development in chickpea. Plants 2021, 10, 464. [Google Scholar] [CrossRef]
- Rossi, V.; Caffi, T.; Giosuè, S.; Bugiani, R. A mechanistic model simulating primary infections of downy mildew in grapevine. Ecol. Model. 2008, 212, 480–491. [Google Scholar] [CrossRef]
- González-Domínguez, E.; Fedele, G.; Salinari, F.; Rossi, V. A general model for the effect of crop management on plant disease epidemics at different scales of complexity. Agronomy 2020, 10, 462. [Google Scholar] [CrossRef]
- Wang, R.; Li, Q.; He, S.; Liu, Y.; Wang, M.; Jiang, G. Modeling and mapping the current and future distribution of Pseudomonas syringae pv. actinidiae under climate change in China. PLoS ONE 2018, 13, e0192153. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, J.; Jiang, Y.; Wang, R.; Wu, R. Predicting the potential distribution of Pseudomonas syringae pv. actinidiae in China using ensemble models. Plant Pathol. 2020, 69, 120–131. [Google Scholar] [CrossRef]
- Frisman, E.Y.; Zhdanova, O.; Kulakov, M.; Neverova, G.; Revutskaya, O. Mathematical modeling of population dynamics based on recurrent equations: Results and prospects. Part I. Biol. Bull. 2021, 48, 1–15. [Google Scholar] [CrossRef]
- Turchin, P. Complex population dynamics. In Complex Population Dynamics; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Salisbury, A. Mathematical Models in Population Dynamics. Bachelor’s Thesis, Natural Sciences New College of Florida, Sarasota, FL, USA, 2011. [Google Scholar]
- Bertoin, J. Mathematical Models for Population Dynamics: Randomness Versus Determinism, 2016. Preprint, hal-01262712v2, HAL Open Science. Available online: https://hal.science/hal-01262712/ (accessed on 21 December 2024).
- Baranyi, J.; Roberts, T.A. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 1994, 23, 277–294. [Google Scholar] [CrossRef]
- Xu, P. Dynamics of microbial competition, commensalism, and cooperation and its implications for coculture and microbiome engineering. Biotechnol. Bioeng. 2021, 118, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Cieslak, M.; Lemieux, C.; Hanan, J.; Prusinkiewicz, P. Quasi-Monte Carlo simulation of the light environment of plants. Funct. Plant Biol. 2008, 35, 837–849. [Google Scholar] [CrossRef] [PubMed]
- Alados, I.; Foyo-Moreno, I.; Alados-Arboledas, L. Photosynthetically active radiation: Measurements and modelling. Agric. For. Meteorol. 1996, 78, 121–131. [Google Scholar] [CrossRef]
- Franklin, J. Plant Growth Chamber Handbook.(Iowa Agriculture and Home Economics Experiment Station Special Report No. 99 (SR-99) and North Central Regional Research Publication No. 340.). Ed. by RW LANGHANS and TW TIBBITS. New Phytol. 1998, 138, 743–750. [Google Scholar] [CrossRef]
- Greer, D.H.; Seleznyova, A.N.; Green, S.R. From controlled environments to field simulations: Leaf area dynamics and photosynthesis of kiwifruit vines (Actinidia deliciosa). Funct. Plant Biol. 2004, 31, 169–179. [Google Scholar] [CrossRef]
- Seleznyova, A.N. Dissecting external effects on logistic-based growth: Equations, analytical solutions and applications. Funct. Plant Biol. 2008, 35, 811–822. [Google Scholar] [CrossRef]
- Pallardy, S.G. Physiology of Woody Plants; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Buwalda, J. A mathematical model of carbon acquisition and utilisation by kiwifruit vines. Ecol. Model. 1991, 57, 43–64. [Google Scholar] [CrossRef]
- Davison, R. The physiology of the kiwifruit vine. In Kiwifruit Science and Management; Warrington, I.J., Weston, G.C., Eds.; Ray Richards Publisher in association with the New Zealand Society for Horticultural Science: Auckland, New Zealand, 1990; pp. 127–154. [Google Scholar]
- Canell, M.; Dewar, R. Carbon allocation in trees: A review of concepts for modeling. Adv. Ecol. Res. 1994, 25, 59–104. [Google Scholar]
- Alonso, A.A.; Molina, I.; Theodoropoulos, C. Modeling bacterial population growth from stochastic single-cell dynamics. Appl. Environ. Microbiol. 2014, 80, 5241–5253. [Google Scholar] [CrossRef]
- Hoagland, D.R.; Arnon, D.I. The Water-Culture Method for Growing Plants Without Soil. 1950; Circular 347, 31p. Available online: https://www.nutricaodeplantas.agr.br/site/downloads/hoagland_arnon.pdf (accessed on 21 December 2024).
- Purohit, S.; Rawat, J.M.; Pathak, V.K.; Singh, D.K.; Rawat, B. A hydroponic-based efficient hardening protocol for in vitro raised commercial kiwifruit (Actinidia deliciosa). Vitr. Cell. Dev. Biol.-Plant 2021, 57, 541–550. [Google Scholar] [CrossRef]
- Nunes da Silva, M.; Vasconcelos, M.; Gaspar, M.; Balestra, G.; Mazzaglia, A.; Carvalho, S.M. Early pathogen recognition and antioxidant system activation contributes to Actinidia arguta tolerance against Pseudomonas syringae pathovars actinidiae and actinidifoliorum. Front. Plant Sci. 2020, 11, 1022. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Meaning | Value & Unit |
|---|---|---|
| t | Time | 1…2880 h |
| Daily average of irradiance | 100 | |
| Daily average photosynthetic photon flux density absorbed by leaves | 457 mol PAR | |
| p | Photoperiod | 16 h |
| Maximum rate of photosynthesis | 15.2 | |
| Apparent photon yield | 0.039 PAR | |
| Duration of rapid growth of leaves | 68.57 h | |
| Scaling parameter for developmental age | 4 dimensionless | |
| Sink priority for leaf growth | 0.01 gC | |
| n | Node number | 1 dimensionless |
| Initial growth rate depending on node number n | 0 gC | |
| L | Specific leaf area | C |
| Internode volumetric density | ||
| Duration of rapid growth of internodes | 34.285 h | |
| Sink priority for internode elongation | 0.01 | |
| Sink priority for internode thickening | 0.05 | |
| Rapid initial internode thickening rate | 0.28 dimensionless | |
| Long-term internode thickening rate | 0.003 dimensionless | |
| Sink priority for root growth | 30 gC | |
| Maximum potential growth rate for fibrous root | 0.003 | |
| Coefficient of root growth response to temperature | dimensionless | |
| Duration of rapid growth of fruits | 34.285 h | |
| Sink priority for fruit growth | 30 gC | |
| , , | Parameters controlling fruit growth rate | 0.8, 3, 9 |
| Sink priority for maintaining respiration of sink i | gC | |
| Coefficient of maintenance respiration for leaf | ||
| Coefficient of maintenance respiration for internode | ||
| Coefficient of maintenance respiration for root | ||
| Coefficient of maintenance respiration for fruit | 0.0596 | |
| Respiration temperature response coefficient for organ type i | dimensionless | |
| Constant units conversion coefficient | 0.0432 gC s | |
| Parameter regulating the leaf carbon supply rate | 1 gC | |
| Starch synthesis rate | 0.1 | |
| Starch hydrolysis rate | 1 | |
| Amount of starch made from 1 g of C | 2.5 g starch C | |
| Sink priority for starch synthesis | 0.1 gC | |
| Reserve carbon supply rate | 1 gC | |
| Maximum storage capacity level in internodes | 0.06 g starch C | |
| Maximum storage capacity level in roots | 0.22 g starch C | |
| Rate of adaptation of the bacteria to the new environment | 0.01 dimensionless | |
| Bacteria inoculation time | 720 h | |
| Maximum growth rate of bacteria | 1 | |
| Half saturation constant of bacteria growth | 0.5 gC | |
| Optimal temperature for bacteria | 21 °C | |
| Range of temperature tolerated by the bacteria | 10 °C | |
| Maximum temperature tolerated by the bacteria | 30 °C | |
| Maximum amount of bacteria the vine can accommodate | CFU | |
| Amount of carbon consumed by one unit of bacteria for reproduction | gC | |
| Threshold at which necrotrophy starts | CFU | |
| Rate of tissues death in the leaves and symptoms appearance | gC | |
| Rate of tissues death in the internodes and symptoms appearance | gC | |
| Rate of tissues death in the fruits and symptoms appearance | gC | |
| Rate of tissues death in the roots and symptoms appearance | gC | |
| Average area of one leaf | 0.015239 |
| Variable | Meaning | Value & Unit |
|---|---|---|
| Daily irradiance | 0 w/ | |
| I | Daily photosynthetic photon flux density absorbed by leaves | 0 mol PAR |
| T | Daily temperature | 16 °C |
| Gross rate of photosynthesis | 0 | |
| c | Carbon amount available for the sinks | gC |
| Size of leaf sink (in carbon amount) | gC | |
| Developmental age of leaf sink | 0 dimensionless | |
| Leaf area | ||
| Size of internode sink (in carbon amount) | gC | |
| Developmental age of internode sink | 0 dimensionless | |
| V | Volume of the internode | |
| Size of root sink (in carbon amount) | 4779 gC | |
| Size of fruit sink (in carbon amount) | 1 gC | |
| Developmental age of fruit sink | 0 dimensionless | |
| Carbon amount required for leaf respiration | 3 gC | |
| Carbon amount required for internode respiration | 0.1 gC | |
| Carbon amount required for root respiration | 4.7 gC | |
| Carbon amount required for fruit respiration | 0.0001 gC | |
| Size of carbon source in the leaves | gC | |
| Size of carbon reserve in the internode | gC | |
| Size of carbon reserve in the root | gC | |
| x | Size of bacteria population | CFU at h |
| q | Physiological state of the bacteria | 0.1 dimensionless |
| h | Relative humidity | 70% |
| Symptoms related to dead tissue in the leaves | 0 gC | |
| Symptoms related to dead tissue in the internodes | 0 gC | |
| Symptoms related to dead tissue in the roots | 0 gC | |
| Symptoms related to dead tissue in the fruits | 0 gC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadj Abdelkader, O.; Bouzebiba, H.; Santos, M.G.; Pena, D.; Aguiar, A.P.; Carvalho, S.M.P. CanKiwi: A Mechanistic Competition Model of Kiwifruit Bacterial Canker Disease Dynamics. Agriculture 2025, 15, 1. https://doi.org/10.3390/agriculture15010001
Hadj Abdelkader O, Bouzebiba H, Santos MG, Pena D, Aguiar AP, Carvalho SMP. CanKiwi: A Mechanistic Competition Model of Kiwifruit Bacterial Canker Disease Dynamics. Agriculture. 2025; 15(1):1. https://doi.org/10.3390/agriculture15010001
Chicago/Turabian StyleHadj Abdelkader, Oussama, Hadjer Bouzebiba, Miguel G. Santos, Danilo Pena, António Pedro Aguiar, and Susana M. P. Carvalho. 2025. "CanKiwi: A Mechanistic Competition Model of Kiwifruit Bacterial Canker Disease Dynamics" Agriculture 15, no. 1: 1. https://doi.org/10.3390/agriculture15010001
APA StyleHadj Abdelkader, O., Bouzebiba, H., Santos, M. G., Pena, D., Aguiar, A. P., & Carvalho, S. M. P. (2025). CanKiwi: A Mechanistic Competition Model of Kiwifruit Bacterial Canker Disease Dynamics. Agriculture, 15(1), 1. https://doi.org/10.3390/agriculture15010001








